Abstract
The second generation Mining Minima method yields binding affinities accurate to within 0.8 kcal/mol for the associations of α-, β-, and γ-cyclodextrin with benzene, resorcinol, flurbiprofen, naproxen, and nabumetone. These calculations require hours to a day on a commodity computer. The calculations also indicate that the changes in configurational entropy upon binding oppose association by as much as 24 kcal/mol and result primarily from a narrowing of energy wells in the bound versus the free state, rather than from a drop in the number of distinct low-energy conformations on binding. Also, the configurational entropy is found to vary substantially among the bound conformations of a given cyclodextrin-guest complex. This result suggests that the configurational entropy must be accounted for to reliably rank docked conformations in both host-guest and ligand-protein complexes. In close analogy with the common experimental observation of entropy-enthalpy compensation, the computed entropy changes show a near-linear relationship with the changes in mean potential plus solvation energy.
INTRODUCTION
Molecular recognition is of profound importance in biology and therapeutics, but the physical chemistry of this phenomenon is still not fully understood. For example, although it is accepted that binding is often associated with losses in configurational entropy, the magnitude and character of these entropy changes are not well understood. It is thus not surprising that accurate computer models of biomolecular binding remain elusive, despite the demand for such models for use in drug design and other applications. Part of the problem is that proteins and DNA are unwieldy objects for computational study, possessing so many degrees of freedom that one can rarely feel confident that a calculation has reached a converged result. This convergence problem can be addressed by crude simplifications, such as treating most or all of a protein as rigid, but only at the cost of introducing unpredictable errors. An alternative approach is to gain insight into molecular recognition by using host-guest systems as models of biomolecular binding. Chemical hosts bind their guests by the same physical mechanisms as biomolecules and often display similarly subtle structure-activity relationships, but are far simpler and thus far more tractable computationally.
The cyclodextrins (CDs) are of particular interest in this regard. These cyclic maltooligosaccharides bind a range of guest molecules in aqueous solution by both hydrophobic and polar interactions (Liu et al., 2004; Cao et al., 2003; Wang et al., 2003; Shehatta et al., 2002; Liu and Guo, 2002; Zheng et al., 2001). They are biomolecules, produced in nature by various bacterial species. Most studies have focused on CDs with glucose residues 6, 7, or 8, respectively termed α-CD, β-CD, and γ-CD. The shape of the CD macrocycle can be described as a truncated cone with a tapered cavity ∼8 Å deep. The narrow rim of the cavity of β-CD has a diameter of ∼6 Å and presents the primary hydroxyls of the glucose residues, whereas the wide rim has a diameter of ∼6.5 Å and presents the secondary hydroxyls of the glucose residues. The CDs have found increasing application as inert, nontoxic carriers of active compounds in drug formulations (Cao et al., 2003; Loftsson et al., 2004 and citations therein), cosmetics (Del Valle, 2004; Barse et al., 2003), and food (Del Valle, 2004), and their interactions with guest molecules have been extensively studied (see, e.g., Liu and Guo, 2002; Zheng et al., 2001). Although only limited structural data are available for the complexes of CDs with their guests, there is an extensive body of thermodynamic binding data (Rekharsky and Inoue, 1998) suitable for correlation with computational studies.
This study uses the second-generation version of the Mining Minima algorithm (Chang et al., 2003; Chang and Gilson, 2003), termed M2, to study the interactions of α-CD, β-CD (Fig. 1), and γ-CD with five guest molecules: benzene, resorcinol, and the nonsteroidal antiinflammatory drugs (NSAIDs) flurbiprofen, naproxen, and nabumetone (Fig. 2), of which one is neutral and two are anionic. The calculations yield excellent agreement with experimental affinities and also provide a detailed look at changes in configurational entropy and in various energy components upon binding. The results provide insight into the physical chemistry of molecular recognition and have implications for protein-ligand docking and scoring.
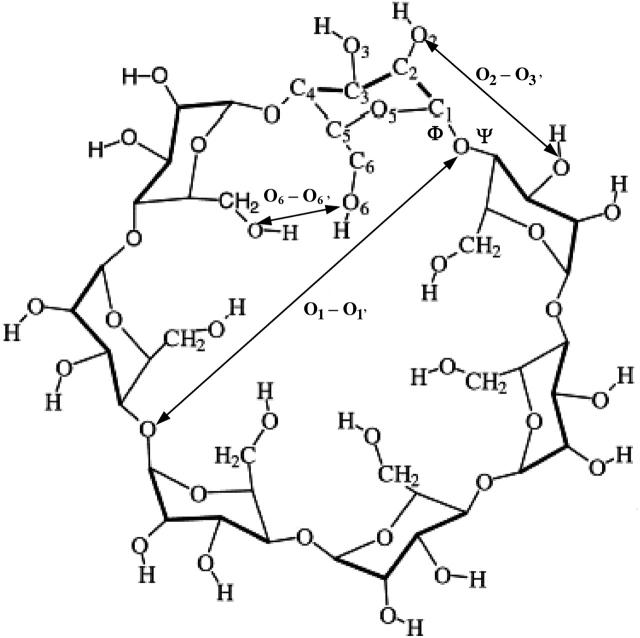
FIGURE 1.
Chemical structure of β-cyclodextrin, showing distances and angles used to describe overall conformation.
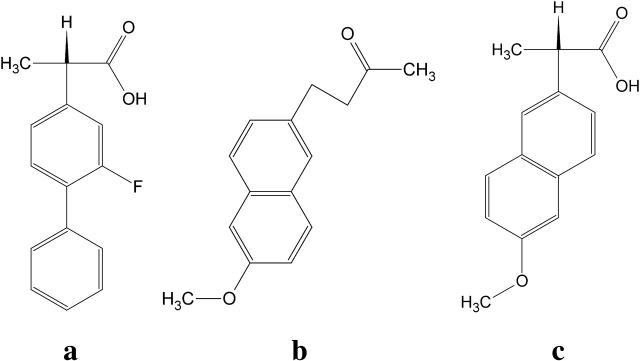
FIGURE 2.
Chemical structures of the nonsteroidal antiinflammatory drugs (a) flurbiprofen, (b) nabumetone, and (c) naproxen.
METHODS
Overview
The standard free energy of binding is the difference between the standard chemical potentials of the bound complex and of the free host and guest. These chemical potentials are computed here with the second-generation Mining Minima method, termed M2 (Chang et al., 2003; Chang and Gilson, 2003), which uses the predominant states approximation (Gilson et al., 1997) to compute the configuration integral of a molecule or complex as a sum of contributions from its low-energy conformations. The Tork algorithm (Chang and Gilson, 2003) is used to identify the low-energy conformations, and the configuration integral in each energy well is computed with the harmonic approximation/mode scanning (HA/MS) method (Chang et al., 2003). The energy model uses the CHARMM force field (MacKerell et al., 1995, 1998; Brooks et al., 1983) with an implicit solvation model. During conformational searching and integration, the effect of solvent is included with a generalized Born (GB) electrostatics model (Still et al., 1990; Gilson and Honig, 1991; Qiu et al., 1997); later, the solvation energy of each conformation is corrected by replacing the GB energy with the result of a more detailed, finite-difference solution (Warwicker and Watson, 1982; Klapper et al., 1986; Gilson et al., 1988) of the linearized Poisson-Boltzmann (PB) equation and by adding in a nonpolar solvation term proportional to the molecular surface area. The overall procedure may be summarized as follows.
Starting with six initial conformations of the molecule or complex, the following steps are iterated until the free energy (chemical potential) difference between successive iterations converges to <0.05 kcal/mol:
Starting from each of the six conformations, generate additional energy minima with Tork.
Delete conformations identical to ones that have already been discovered, including identities detectible only when symmetry is accounted for.
Repeat steps 1 and 2 twice for a total of three iterations.
Compute the configuration integrals (hence chemical potentials) of the resulting energy wells.
Correct the configurational integrals toward the more accurate finite-difference PB/surface area (PB/SA) model.
Add the corrected configuration integrals for the latest conformations to the running sum and evaluate the resulting change in free energy. Stop calculation if convergence criterion is reached.
Identify the six most stable new conformations as starting points for additional Tork searches in step 1, and return to step 1.
The method is now described in more detail.
Preparation of molecular structures
The starting structures of α-, β-, and γ-CD were taken from crystal structures (Manor and Saenger, 1974; Betzel et al., 1984; Harata, 1987) in the Protein Data Bank (Berman et al., 2000), and starting structures of flurbiprofen, naproxen, nabumetone, benzene, and resorcinol were prepared with the two-dimensional sketcher module of Quanta (Accelrys, San Diego, CA). Because the pKa values of flurbiprofen's and naproxen's carboxyl groups are in the 4–5 range, and the experiments were carried out at pH > 6, these compounds were treated as deprotonated. All hosts and guests were subjected to an initial energy minimization using CHARMM22 (MacKerell et al., 1995, 1998; Brooks et al., 1983), first by the conjugate gradient method with a root-mean-square (RMS) gradient tolerance of 0.01 kcal/mol, and then by the Newton-Raphson method with an RMS gradient tolerance of 0.0001 kcal/mol. For the complexes, initial conformations were generated by using Vdock (Kairys and Gilson, 2002; David et al., 2001) to dock the six lowest energy conformations of each free guest molecule into the lowest-energy conformation of each host. The six most stable resulting conformations were used as starting points for the procedure outlined in the “Overview” section.
Conformational search
The recently described Tork (Chang and Gilson, 2003) algorithm is used to discover new low-energy conformations. Briefly, Tork operates in bond-angle-torsion (BAT) coordinates (Chang and Gilson, 2003) in which the position of each atom i > 3 is specified by its bond length (bi), bond angle (θi), and dihedral angle (ϕi) with respect to three other atoms that are bonded in sequence and whose coordinates are already determined. (For atoms i ≤ 3, one or more coordinates are identified as external.) For a bimolecular complex, six additional coordinates are introduced to define the position (X, Y, Z) and the orientation (Θ, Φ, Ψ) of one molecule relative to the other. A single torsional angle is selected for each bond whose torsion is an important conformational determinant and the diagonalized matrix of the second derivatives of the energy with respect to these key torsions is computed and diagonalized. The resulting eigenvectors are used to construct displacement vectors in BAT space, termed drivers, which correspond to facile distortions of the molecule or complex, much as low force-constant eigenvectors are used to identify facile distortions in the low mode search algorithm (Kolossvary and Guida, 1996). The molecule is gradually distorted along a driver direction, or along a linear combination of drivers, until its energy reaches some predetermined threshold, at which point it is energy minimized to yield a low-energy conformation that usually is distinct from the initial conformation. For a bimolecular complex, distortion directions are modified by adding a separate random offset to each of the six additional coordinates defining the relative position of one molecule to the other.
Symmetry detection and removal of duplicate conformations
It is important to eliminate duplicate conformations so that no conformations are counted as contributing more than once to the chemical potential. Eliminating duplicates during the conformational search also avoids wastefully rerunning a Tork iteration from the same starting conformation. However, eliminating repeats is nontrivial when a molecule possesses chemical symmetries. For example, a β-cyclodextrin conformation in which glucose 1 is tilted inward while the other glucose residues are tilted outward should be considered identical to the other six conformations in which glucose residue 2, 3, 4, 5, 6, or 7 is tilted inward while the others are tilted outward. Here, a recently developed symmetry-detection algorithm (Chen et al., 2004), inspired by the work of Ivanov and Schuurman (1999), is used to eliminate all conformational repeats.
Briefly, a deterministic traversal of the atoms composing a molecule or complex is used to generate a molecular name consisting of a corresponding sequence of atom names. All traversals that generate the same name are identified, and the atom sequences associated with these traversals are identified as chemically equivalent and thus corresponding to global chemical symmetries. Subnames are also generated for molecular fragments initiated at branched atoms, and branches with identical subnames are identified as chemically equivalent and thus corresponding to local chemical symmetries. A symmetry operation then corresponds to an interchange of two or more groups of atoms with identical names. The list of symmetries is used to determine whether or not two conformations A and B of a molecule with Nsym symmetry operations are equivalent. This is done by applying all possible combinations of symmetrical atom interchanges to one of the conformations, say conformation A. The resulting symmetry-related conformations are screened to remove mirror images, leaving only conformations related by overall rotations or rotations at bonds linked to symmetrical chemical groups. The root-mean-square deviation (RMSD) of conformation B with respect to all the remaining symmetry-generated conformations of A is computed, and the lowest RMSD is taken as the true one. Conformations A and B are then considered equivalent if the lowest RMSD falls below a user-specified tolerance.
Symmetry numbers are used in computing chemical potentials (see “Calculation of free energies”), and determining these quantities requires identification of three-dimensional (3D) symmetries, not just the chemical equivalences discussed above. The 3D symmetries are identified by including dihedral angle information in the atom and molecular names so that two traversals match only if they are not only chemically equivalent but also conformationally equivalent. A reflectional symmetry is distinguished from a rotational symmetry by the fact that all dihedrals have their signs inverted, except for 180°, which is equivalent to 0°.
Calculation of free energies
The standard chemical potential of a molecule or complex is computed as
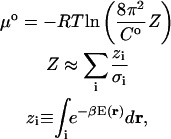 |
(1) |
where Z is the configuration integral over all conformations, C0 is the standard concentration, zi is the configuration integral within energy well i, σi is the symmetry number of conformation i, E(r) is the energy as a function of conformation r, β is (kT)−1 where k is Boltzmann's constant, and T is absolute temperature (Gilson et al., 1997a). Energy minima i are identified by the Tork search and conformational filtering methods described in “Conformational search” and “Symmetry detection and removal of duplicate conformations”. The local configuration integrals zi are evaluated with the recently developed HA/MS method, which uses the harmonic approximation with finite integration ranges, together with mode scanning, a fast correction for anharmonicity based upon internal bond-angle-torsion coordinates. The summation includes every energy well found to have a chemical potential within 20 kcal/mol of the global maximum of stability. A detailed description and results of numerical validation of the M2 algorithm can be found elsewhere (Chang et al., 2003).
Energy model
The energy E(r) in the configuration integrals (see “Calculation of free energies”) can be separated into a potential energy U(r) and a solvation energy W(r): E(r) = U(r) + W(r). The potential energy is computed here with the CHARMM22 parameter set (MacKerell et al., 1995, 1998; Brooks et al., 1983). The solvation energy has two parts, a nonpolar contribution Wnp, and an electrostatic contribution Welec. Wnp, the work of forming a nonpolar cavity in the solvent with the shape of the solute, is approximated by a surface area model Wnp = aA + b, where A is the solvent-accessible surface area of the solute (Å2), a is set to 0.006 kcal/(mol Å2), and b to zero (Friedman and Honig, 1995). The value of Welec is estimated with the generalized Born model (GB) during conformational search and harmonic approximation/mode scanning, then adjusted at each energy minimum toward a more accurate finite difference solution of the linearized Poisson-Boltzmann model (FDPB) obtained with the program UHBD (Davis et al., 1991). Thus, the corrected chemical potential of energy well i is
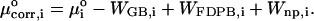 |
The solvent dielectric constant is set to that of water (80 at 298 K), atomic radii are set to the van der Waals (VDW) radii obtained from CHARMM22, the interior dielectric constant is set to 1, and the boundary between the low-dielectric interior and the high-dielectric exterior is defined by the Richards surface (Cortis and Friesner, 1997) with a 1.4-Å solvent probe.
Calculation of averaged energy terms and configurational entropy
The energy is the sum of various terms, such as van der Waals, Coulombic, and Welec, and it is of interest to determine how the averages of these quantities change upon binding. The Boltzmann average of an energy term, say the Coulombic energy UCoul is computed as
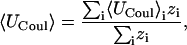 |
(2) |
where 〈Ucoul〉i is the mean of the Coulombic energy within energy well i, computed via the HA/MS method described above. This expression is also used to determine the changes in valence energy (〈Uval〉, the sum of bond stretch, angle bend, and intrinsic dihedral energies), the solute van der Waals (〈Uvdw〉), and Coulombic (〈UCoul〉) energies, and the nonpolar (〈Wnp〉) and electrostatic (〈Welec〉) solvation terms.
The binding free energy can be separated into the change in average energy 〈U + W〉 and the change in configurational entropy (Gilson et al., 1997a; Mardis et al., 2001), where the change in configurational entropy upon binding can be computed from
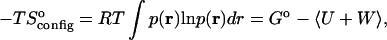 |
(3) |
where p(r) is the probability density of the configuration associated with coordinates r. Note that this quantity includes changes in the so-called rotational and translational entropy. However, it does not include the change in solvent entropy, because this is implicit in Δ〈W〉. As a consequence, the change in configurational entropy cannot be compared directly with the experimentally measured entropy change upon binding.
Structural analysis of cyclodextrins
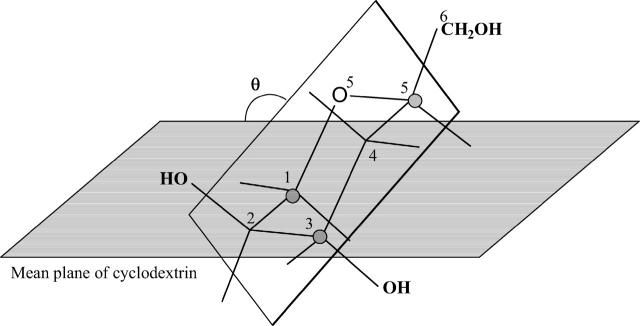
The conformations of the CDs are frequently characterized by descriptors that capture overall structural properties (Figs. 1 and 3). Each of the following descriptors is computed for a single conformation i and Boltzmann averages and variances are then computed across multiple conformations based upon their statistical weights zi. (See Eq. 2 and associated text.) As diagrammed in Fig. 3, the glucose tilt angle θ is the angle between the mean plane of the CD macrocycle, defined by all O1-atoms, and the mean plane of the glucose in question, defined by C1, C3, and C5. The average of the tilt angle over all the glucose monomers, here termed τ, indicates the taper of the molecule, where τ = 90 indicates a cylindrical shape and τ > 90 implies a taper from the secondary hydroxyl rim toward the primary hydroxyl rim. The intramolecularly averaged torsion angles Φ and Ψ are related quantities because these torsions control the glucose tilt angles. The circularity of a CD molecule can be described by the distortion parameter (Helden et al., 1992), the ratio of the smallest to the largest distance between any pair of glucose O1 atoms that lie across the ring from each other. (For β-CD, which has an odd number of glucoses, we take the average of the distance between the ith residue and the i + 3 and i + 4 residues.) The extent of hydrogen bonding along the rims of a CD is indicated by the mean distance between the oxygens of adjacent hydroxyls; i.e., by the mean O2–O3′ and O6–O6′ distances, respectively, for secondary and primary hydroxyls of adjacent residues.
FIGURE 3.
Diagram of glucose tilt angle θ in α-cyclodextrin.
RESULTS
The calculated free energies of binding agree with the available experimental data (Rekharsky and Inoue, 1998; Valero and Costa, 1999) to within 0.7 kcal/mol and accurately reflect the trends in each series of complexes, including the fact that the guests tend to bind most tightly to β-CD, rather than to α-CD or γ-CD. (See Table 1.) The following subsections analyze these results in detail. First, the conformational preferences of the free cyclodextrins are presented, both for comparison with published data and also as a baseline for comparison with the conformations of the complexes. Then each binding reaction is analyzed individually in terms of thermodynamics and structure, and the structural results are correlated with experimental nuclear Overhauser effect (NOE) data where available. (Site-specific chemical shift data are available in additional instances, but the structural information these provide is rather nonspecific.) Subsequent subsections provide more global analyses of configurational entropy, solvation entropy, densities of states, and the computational method.
TABLE 1.
Calculated ( (calc)) and experimental (
(calc)) and experimental ( (exp)) standard free energies of binding (kcal/mol) for cyclodextrin complexes (standard concentration 1 mol/liter), along with calculated results omitting mode scanning (
(exp)) standard free energies of binding (kcal/mol) for cyclodextrin complexes (standard concentration 1 mol/liter), along with calculated results omitting mode scanning (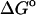 (HA)), omitting both the harmonic approximation and mode scanning (
(HA)), omitting both the harmonic approximation and mode scanning (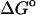 (U + W)), and omitting the correction towards finite difference solutions of the linearized Poisson-Boltzmann equation (
(U + W)), and omitting the correction towards finite difference solutions of the linearized Poisson-Boltzmann equation (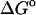 (GB))
(GB))
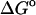 (calc) (calc) |
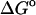 (exp) (exp) |
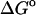 (HA) (HA) |
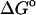 (U + W) (U + W) |
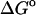 (GB) (GB) |
|
|---|---|---|---|---|---|
| Benzene | |||||
| α-CD | −1.96 | −2.05 | −2.77 | −5.45 | −0.87 |
| β-CD | −2.88 | −2.77, −3.04 | −3.47 | −6.09 | −2.36 |
| γ-CD | −1.47 | −1.31 | −1.22 | −4.94 | −0.78 |
| Resorcinol | |||||
| α-CD | −1.80 | −1.65 | −2.67 | −7.18 | 0.08 |
| β-CD | −3.11 | −2.77* | −3.21 | −10.45 | −1.80 |
| γ-CD | −1.92 | −1.84 | −2.47 | −5.78 | −0.23 |
| Flurbiprofen | |||||
| α-CD | −2.36 | −2.51† | −4.48 | −10.16 | −0.45 |
| β-CD | −5.41 | −4.97, −4.49† | −6.26 | −14.17 | −2.77 |
| γ-CD | −5.47 | −4.75† | −5.79 | −13.46 | −1.85 |
| Nabumetone | |||||
| α-CD | −2.09 | −2.13‡ | −2.27 | −6.31 | −1.09 |
| β-CD | −5.24 | −4.59‡ | −4.14 | −10.72 | −4.18 |
| γ-CD | −4.73 | n/a | −3.03 | −12.27 | −3.13 |
| Naproxen | |||||
| α-CD | −2.77 | n/a | −3.79 | −7.71 | −1.41 |
| β-CD | −4.52 | −4.32§ | −5.42 | −14.34 | −2.16 |
| γ-CD | −4.27 | n/a | −4.26 | −9.09 | −1.79 |
Except as otherwise noted, T = 298 K and solutions are not buffered. n/a, no experimental data available.
T = 303 K.
pH = 7.
T = 293 K.
T = 295 K.
Conformational preferences of free cyclodextrins
Structural descriptors (see “Structural analysis of cyclodextrins” and Figs. 1 and 3) of free α-, β-, and γ-CD are presented in Table 2, which shows the computed Boltzmann averages and RMSD from the averages, along with values obtained from crystal structures (Immel, 1995 and citations therein) for comparison. The tapers τ of the free CDs range between 100° and 110°; these results are consistent with the crystal structures to within the RMSD of the solution conformations. The roughly 20° difference between the mean torsion angles Φ and Ψ for each CD is directly related to the deviation of the glucose tilt angles from 90°. Interestingly, the CDs become more circular as the number of glucose residues increases from six in α-CD (circularity 0.852) to eight in γ-CD (circularity 0.996); note that a perfectly round conformation would have a circularity of 1. The larger CDs also are less flexible, as indicated by falling values of RMSD for every structural parameter in the table. This trend may result from the formation of stronger hydrogen bonds between the secondary hydroxyls of adjacent glucose residues for the larger rings, as reflected by the shortening of the oxygen-oxygen distances of adjacent secondary hydroxyls from 3.35 Å in α-cyclodextrin, to 2.89 Å in β-cyclodextrin, and then to 2.82 Å in γ-cyclodextrin. Crystal structures also indicate that these hydrogen bonds tighten up in the larger CDs (see Table 2), and this result is consistent with measurements of hydrogen/deuterium exchange in aqueous solution, which is rather slow in γ-cyclodextrin and thus suggestive of strong hydrogen bonding (Casu et al., 1968; Bergeron and Channing, 1976). For α-cyclodextrin, two out of the six O2–O3′ distances for adjacent secondary hydroxyls are much larger than 3.5 Å and hence inconsistent with hydrogen bonding. This result is consistent with the relatively elliptical shape of α-CD, indicated by its low circularity parameter, and implies that α-cyclodextrin is quite flexible in water, because the molecule possesses sixfold rotational symmetry and the defect in hydrogen bonding can therefore exist at any point around the rim. Finally, there is no significant hydrogen bonding between adjacent primary hydroxyls for any of the CDs, based upon the O6–O6′ distances of ∼4.5 Å. Overall, these results are consistent with those obtained from prior computational studies (Fermeglia et al., 2003; Bonnet et al., 2002).
TABLE 2.
Boltzmann-averaged (“mean”) conformational descriptors for free α-, β-, and γ-CD, together with literature data for crystals (Immel, 1995), with computed RMS deviations in parentheses
| Torsions
|
Distances
|
Circularity (distortion parameter) | |||||
|---|---|---|---|---|---|---|---|
| Φ | Ψ | Taper τ | Diagonal O1–O1′ | Adjacent 2° OH–OH | Adjacent 1° OH–OH | ||
| α-cyclodextrin | |||||||
| Crystal | 107.4 | 130.7 | 102.1 | 8.51 | 3.05 | 4.45 | 0.88 |
| Aqueous mean (RMSD) | 94.2 (6.7) | 127.3 (18.2) | 109.5 (12.2) | 8.46 (1.12) | 3.35 (0.62) | 4.44 (0.19) | 0.852 (0.017) |
| β-cyclodextrin | |||||||
| Crystal | 110.5 | 127.0 | 100.0 | 9.81 | 2.92 | 4.59 | 0.93 |
| Aqueous mean (RMSD) | 108.3 (1.3) | 116.4 (4.5) | 102.6 (2.4) | 9.77 (0.08) | 2.89 (0.03) | 4.47 (0.06) | 0.980 (0.003) |
| γ-cyclodextrin | |||||||
| Crystal | 110.1 | 129.4 | 104.4 | 11.76 | 2.84 | 4.39 | 0.98 |
| Aqueous mean (RMSD) | 111.6 (1.8) | 125.4 (1.5) | 101.5 (1.3) | 11.55 (0.01) | 2.82 (0.00) | 4.57 (0.04) | 0.996 (0.003) |
Analysis of the binding reactions
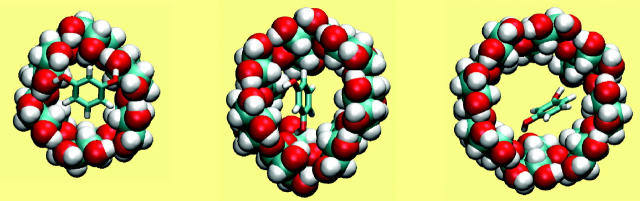
Benzene
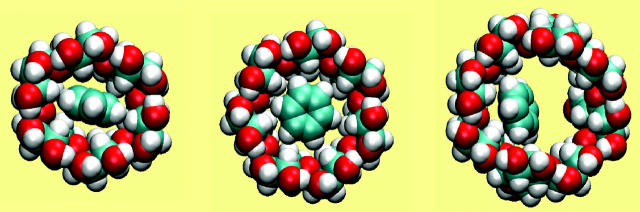
The association of benzene with all three CDs is driven primarily by attractive van der Waals interactions, which change by −10 to −13 kcal/mol upon binding. Binding is opposed most strongly by the loss of configurational entropy, which changes by 4–9 kcal/mol. (See Table 3.) Benzene binds within the cavities of all three CDs, fitting snugly into α-CD and increasingly loosely in β- and γ-CD, as illustrated in Fig. 4. The trends in the energy terms, from α-CD to γ-CD, are consistent with this assessment, because the change in van der Waals energy upon binding is most favorable for α-CD and least favorable for γ-CD, whereas the trend in configurational entropy is reversed, consistent with greatest conformational restriction on binding α-CD and least restriction on binding γ-CD. (Note that the change in configuration entropy reflects not only the mobility of benzene, but also the flexibility of the CDs themselves. Also, as stated in the “Calculation of averaged energy terms and configurational entropy” section, the changes in configurational entropy reported here do not include any contribution from solvent and therefore cannot be compared directly with experimental entropy changes upon binding.) The CDs are, in effect, preorganized to bind benzene, because binding causes little change in their conformations. Thus, the circularities change by at most 0.028 (from 0.852 to 0.824 for α-CD, from 0.980 to 0.994 for β-CD, and from 0.996 to 0.981 for γ-CD), the values of the taper (τ) decrease by only ∼2° in all cases, and the mean valence energies change by <1 kcal/mol upon binding (Table 3).
TABLE 3.
Calculated changes in Boltzmann-averaged energy components, configurational entropy, and standard free energy, for binding of benzene with cyclodextrins (kcal/mol)
| α-CD | β-CD | γ-CD | |
|---|---|---|---|
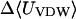 |
−12.6 | −11.8 | −10.06 |
 |
−0.46 | −0.17 | −0.078 |
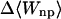 |
−1.68 | −1.73 | −1.58 |
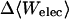 |
3.33 | 3.64 | 3.59 |
| −TΔSconfig | 8.75 | 7.2 | 6.23 |
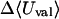 |
0.73 | 0.021 | 0.43 |
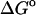 (calc) (calc) |
−1.96 | −2.88 | −1.47 |
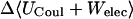 |
2.88 | 3.47 | 3.51 |
UVDW, van der Waals energy; Ucoul, Coulombic energy; Wnp, nonpolar solvation energy term; Welec, electrostatic solvation energy term; −TΔSconfig, free-energy contribution from change in configurational entropy; Uval, sum of bond, angle, and torsional energies; 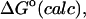 computed free energy of binding; Ucoul + Welec, electrostatic energy (sum of Coulombic and electrostatic solvation terms).
computed free energy of binding; Ucoul + Welec, electrostatic energy (sum of Coulombic and electrostatic solvation terms).
FIGURE 4.
Most stable conformation computed for complexes of benzene with α-CD, β-CD, and γ-CD (left to right). All views are from the wide (secondary hydroxyl) rim.
Resorcinol
As shown in Fig. 5, the calculations indicate that resorcinol tends to remain at the wide rim of α-CD, but to occupy the cavity of β-CD and γ-CD. All three CDs form hydrogen bonds to resorcinol's hydroxyl groups, but the structural patterns differ. In α-CD, only the secondary hydroxyls at the wide rim contribute; in the most stable complexes with β-CD, resorcinol forms a bridge between a primary hydroxyl and an ether oxygen or a secondary hydroxyl; and in γ-CD, resorcinol lies deep in the cavity and tends to bridge two primary hydroxyls. Binding is driven largely by van der Waals interactions of from −10 to −13 kcal/mol, as in the case of benzene, but resorcinol gains additional affinity from its hydrogen bonds, as reflected in favorable Coulombic energies of from −10 to −12 kcal/mol. These Coulombic attractions are only partly cancelled by electrostatic desolvation penalties of ∼7–8 kcal/mol (Table 4). Interestingly, the penalties in configurational entropy are much larger for resorcinol than for benzene, presumably due to additional conformational restrictions from hydrogen bonding as well as losses in the rotational freedom of hydroxyl groups. Relative to benzene, binding of resorcinol leads to larger distortions of α-CD and β-CD, but not γ-CD, as reflected in changes in valence energies of ∼2.3 kcal/mol for these two cases (Table 4). These changes in valence energy correlate with shifts in the taper (τ) of α- and β-CD to 80–90°, which tend to direct the secondary hydroxyls more toward the cavity and thus facilitate the formation of hydrogen bonds with the polar resorcinol molecule.
FIGURE 5.
Most stable conformation computed for complexes of resorcinol with α-CD, β-CD, and γ-CD (left to right). All views are from the wide (secondary hydroxyl) rim.
TABLE 4.
Calculated changes in Boltzmann-averaged energy components, configurational entropy, and standard free energy, for binding of resorcinol with cyclodextrins (kcal/mol)
| α-CD | β-CD | γ-CD | |
|---|---|---|---|
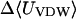 |
−12.85 | −11.58 | −10.09 |
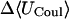 |
−9.71 | −12.23 | −9.53 |
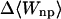 |
−1.80 | −2.04 | −1.94 |
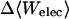 |
7.33 | 7.65 | 7.89 |
| −TΔSconfig | 12.84 | 12.79 | 11.32 |
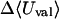 |
2.40 | 2.30 | 0.42 |
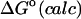 |
−1.80 | −3.11 | −1.92 |
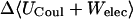 |
−2.38 | −4.58 | −1.64 |
See Table 3 for symbols.
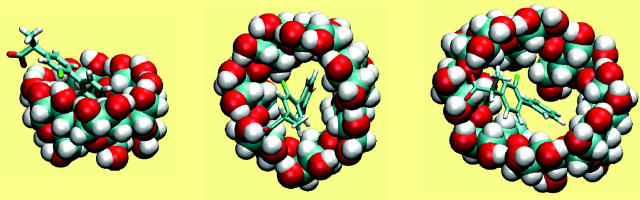
Flurbiprofen
Although flurbiprofen possess a carboxylate moiety, van der Waals interactions are arguably the main driving force for its association with the CDs, as for benzene and resorcinol. (See Table 5) It is true that the Coulombic part of the electrostatic energy is large and favorable, from −22 to −30 kcal/mol, due to interactions between the carboxylate group of the ligand and the hydroxyl groups of the host. However, these favorable interactions are strongly opposed by the cost of stripping high dielectric solvent from these groups during binding (Δ〈Welec〉 = 8–26 kcal/mol). Thus, although the net electrostatic contribution to binding is significant at from ∼−4 to −6 kcal/mol, it is much less than the van der Waals part. Binding strength is maximal for β-CD and less for α- and γ-CD, suggesting a more snug fit for β-CD. This suggestion is consistent with the fact that the loss in configurational entropy is greater on binding to β-CD than to α-CD or γ-CD. Overall, the losses in configurational entropy when flurbiprofen binds are remarkably large, contributing 20–24 kcal/mol to the overall binding free energy.
TABLE 5.
Calculated changes in Boltzmann-averaged energy components, configurational entropy, and standard free energy, for binding of flurbiprofen with cyclodextrins (kcal/mol)
| α-CD | β-CD | γ-CD | |
|---|---|---|---|
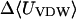 |
−17.62 | −23.89 | −21.06 |
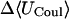 |
−22.3 | −30.43 | −29.66 |
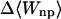 |
−2.40 | −3.15 | −3.15 |
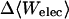 |
18.06 | 24.87 | 25.73 |
| −TΔSconfig | 19.99 | 24.10 | 19.52 |
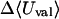 |
1.88 | 3.10 | 3.15 |
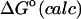 |
−2.36 | −5.41 | −5.47 |
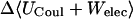 |
−4.21 | −5.57 | −3.93 |
See Table 3 for symbols.
Structurally, the calculations indicate that flurbiprofen tends to bind with its benzene moiety inserted and on the axis of the host, and with its carboxylate group forming hydrogen bonds with the secondary hydroxyls (Fig. 6). However, the detailed arrangement of the drug varies significantly across the three CDs. In α-CD (Fig. 6 left), flurbiprofen can be described as lying across the wide rim of the CD. The benzene ring does not insert deeply into the cavity of the CD and the fluorine atom forms polar interactions with a secondary hydroxyl group. In β-CD (Fig. 6 middle), the benzene moiety is deeply inserted, to the point where it interacts with the primary hydroxyls, the axis of the drug lies within ∼12° of the axis of the host, and the centers of mass of the two molecules lie within 0.8 Å of each other. However, the fluorine atom does not interact as closely with the hydroxyls as in the case of α-CD. The interactions of flurbiprofen with γ-CD (Fig. 6 right) are similar to those with β-CD, but the larger diameter of the cavity causes the drug to adopt more varied orientations that deviate by up to 25° from the axis of the host's ring. The bound conformations of the CDs differ significantly from their free conformations. Thus, the valence energy term rises by 2–3 kcal/mol upon binding and the macrocyclic rings become somewhat more distorted, with the circularities of α-, β-, and γ-CD dropping to 0.834, 0.885, and 0.944, respectively, and the taper parameter dropping by up to 10°.
FIGURE 6.
Most stable conformation computed for complexes of flurbiprofen with α-CD, β-CD, and γ-CD (left to right). All views are from the wide (secondary hydroxyl) rim.
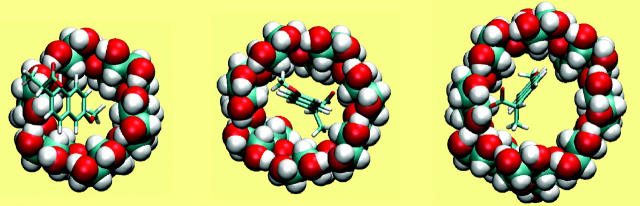
Naproxen
Like flurbiprofen, naproxen possesses a propanoate group linked to a system of two aromatic rings. However, the naphthyl moiety of naproxen form a more rigid unit than the biphenyl of flurbiprofen and the naphthyl of naproxen is decorated with a methoxy group that has no analog in flurbiprofen. Not surprisingly, then, the computed binding modes of naproxen differ from those of flurbiprofen. Naproxen's interactions with α-CD seem to be dominated by interactions involving its methoxy group and the ring to which it is bound, as shown in Fig. 7 (left). The propanoate group projects into solution in all 20 of the most stable conformations, whereas that of flurbiprofen interacts directly with the secondary hydroxyls. Accordingly, both the stabilizing Coulombic term and the destabilizing electrostatic desolvation term are several kcal/mol smaller in magnitude for naproxen than flurbiprofen, and the net electrostatic contribution to binding is ∼1 kcal/mol weaker (Table 6). Interestingly, this difference is approximately offset by a smaller configurational entropy penalty, so the computed binding constants of the two compounds differ by only ∼0.4 kcal/mol. The preferred binding mode of naproxen for β-CD is again distinct from that of flurbiprofen. As shown in Fig. 7 (middle), naproxen usually threads the cavity in a sense opposite to that of flurbiprofen, so the propanoate group forms hydrogen bonds with the primary, rather than the secondary, hydroxyls. However, in a few of the most stable 20 conformations, naproxen enters in the opposite sense, generally consistent with NOEs indicating close contacts between H5 of β-CD with aromatic proteins at both ends of naproxen (Sadlej-Sosnowska et al., 2000). For γ-CD, naproxen's computed binding modes are similar to those of flurbiprofen, with the aromatic groups in the cavity and the propanoate moiety forming hydrogen bonds to the secondary hydroxyls, as shown in Fig. 7 (right). As with flurbiprofen, binding of naproxen distorts the marocyclic rings somewhat: circularity decreases to 0.787, 0.894, and 0.885 for α-, β-, and γ-CD, respectively, and the mean valence energy rises ∼1–4 kcal/mol upon binding (Table 6). Binding of naproxen appears again to be driven primarily by van der Waals interactions; and again, the strongest van der Waals interactions and the greatest entropy penalty are seen for β-CD (Table 6), suggesting a particularly snug fit in this case.
FIGURE 7.
Most stable conformation computed for complexes of naproxen with α-CD, β-CD, and γ-CD (left to right). All views are from the wide (secondary hydroxyl) rim.
TABLE 6.
Calculated changes in Boltzmann-averaged energy components, configurational entropy, and standard free energy, for binding of naproxen with cyclodextrins (kcal/mol)
| α-CD | β-CD | γ-CD | |
|---|---|---|---|
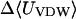 |
−17.32 | −25.34 | −21.12 |
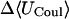 |
−17.09 | −17.69 | −30.91 |
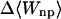 |
−2.28 | −3.11 | −3.03 |
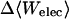 |
13.92 | 14.40 | 27.29 |
| −TΔSconfig | 18.75 | 23.56 | 20.32 |
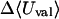 |
1.24 | 3.66 | 3.18 |
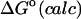 |
−2.77 | −4.52 | −4.27 |
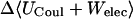 |
−3.17 | −3.29 | −3.62 |
See Table 3 for symbols.
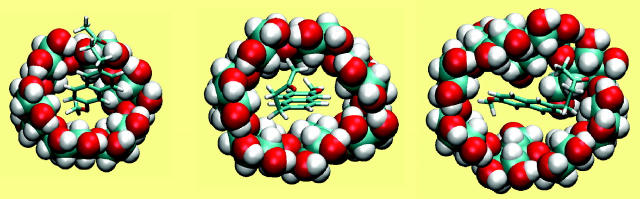
Nabumetone
Van der Waals interactions dominate in the binding of nabumetone (Table 7), as for the other drugs. Because nabumetone possesses an uncharged butanone group instead of the anionic propanoate group of naproxen and flurbiprofen, its electrostatic interactions are relatively weak. In α-CD, the calculations point to a preferred positioning of the rings and methoxy group like that of naproxen, but nabumetone's flexible butanone group curves down to accept hydrogen bonds from the secondary hydroxyls (Fig. 8 left) rather than projecting into solution like the propanoate group of naproxen. In β-CD, the methoxy group is threaded through to the primary hydroxyls, whereas the carbonyl tends to project into solution rather than interacting with the host (Fig. 8 middle). The fit appears to be snug, with the long axis of the drug, defined by the two substituted naphthyl carbons, lying along the rotational axis of the host to within ∼20°, and the host remaining rather circular (circularity 0.927). Van der Waals interactions with β-CD are strong, nearly −30 kcal/mol. In γ-CD, nabumetone may be described as lying nearly lengthwise within the cavity (Fig. 8 right), whereas the butanone group is accommodated by a local outward distortion of the secondary rim of the CD. The angle between the axis of the drug and that of the host is ∼70°, and the CD is distorted overall to a circularity of only 0.789. This arrangement is associated with particularly strong van der Waals interactions, ∼−28 kcal/mol. It is worth noting that, if flurbiprofen or naproxen were to bind in this conformation, desolvation of their anionic groups would impose a substantial energy penalty.
TABLE 7.
Calculated changes in Boltzmann-averaged energy components, configurational entropy, and standard free energy, for binding of nabumetone with cyclodextrins (kcal/mol)
| α-CD | β-CD | γ-CD | |
|---|---|---|---|
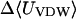 |
−18.88 | −29.60 | −27.90 |
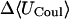 |
−2.83 | −7.31 | −7.10 |
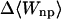 |
−2.23 | −3.19 | −3.61 |
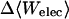 |
2.04 | 7.26 | 7.92 |
| −TΔSconfig | 19.06 | 24.35 | 23.32 |
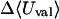 |
0.75 | 3.25 | 2.64 |
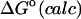 |
−2.09 | −5.24 | −4.73 |
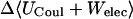 |
−0.79 | −0.05 | 0.82 |
See Table 3 for symbols.
FIGURE 8.
Most stable conformation computed for complexes of nabumetone with α-CD, β-CD, and γ-CD (left to right). All views are from the wide (secondary hydroxyl) rim.
Configurational and solvation entropy
Losses in configurational entropy strongly oppose binding in these systems, contributing 6–24 kcal/mol to the free energy of binding (Tables 3–7). These contributions are similar in magnitude to the large attractive van der Waals interactions that drive binding, and they vary strongly from one binding reaction to another. As a consequence, omitting these contributions would lead to large computational errors. This is illustrated in Fig. 9, which compares experimental binding energies with the computed free energy (top), and with the computed free energy less the change in configurational entropy (bottom).
FIGURE 9.
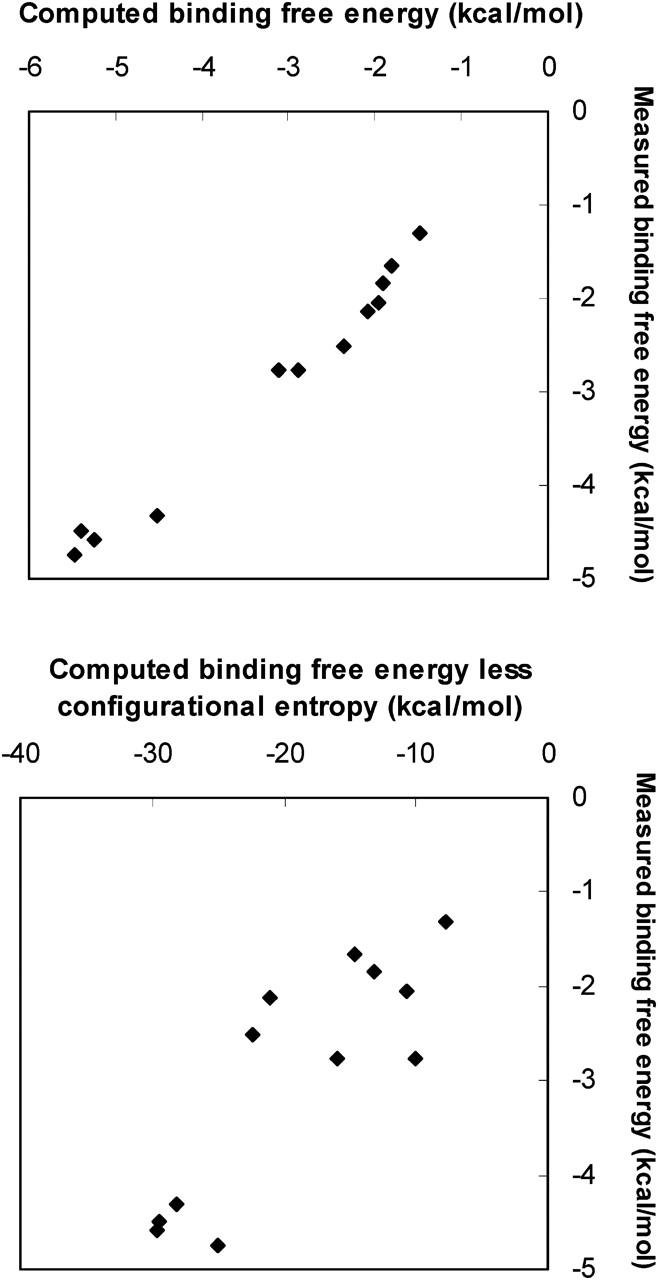
Scatter plot of measured binding free energy versus computed (top) binding free energy ΔGo and (bottom) Δ〈U + W〉.
The losses in configurational entropy observed here could result primarily from a reduction in the number of different low-energy conformations on binding or, alternatively, from a narrowing of energy wells in the bound complex relative to those of the free reactants. These possibilities can be roughly distinguished by examining the number of stable conformations before and after binding. To do this, we make the approximation that all energy wells whose free energies (chemical potentials) lie within thermal energy (RT = 0.6 kcal/mol) of the most stable energy well are equally and predominantly occupied. Then the change in entropy on binding due to the change in the number of these occupied energy wells contributes −T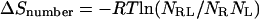 to the free energy of binding, where NX is the number of low-energy wells for the complex (X = RL), free receptor (X = R), and free ligand (X = L). The largest value of −TΔSnumber among all of the binding reactions studied here is only −1.2 to 1.8 kcal/mol at 300 K, which is far less than the entropic contributions that are actually computed. This result implies that the changes in configurational entropy upon binding result almost entirely from a tendency for the energy wells of the complexes to be much narrower than those of the free hosts and guests.
to the free energy of binding, where NX is the number of low-energy wells for the complex (X = RL), free receptor (X = R), and free ligand (X = L). The largest value of −TΔSnumber among all of the binding reactions studied here is only −1.2 to 1.8 kcal/mol at 300 K, which is far less than the entropic contributions that are actually computed. This result implies that the changes in configurational entropy upon binding result almost entirely from a tendency for the energy wells of the complexes to be much narrower than those of the free hosts and guests.
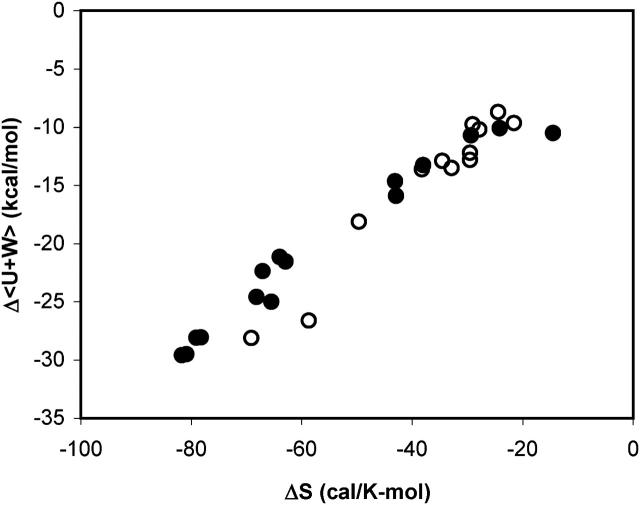
The changes in configurational entropy upon binding correlate strongly with the changes in the potential plus solvation energy, Δ〈U + W〉, as shown in Fig. 11. This result is consistent with the expectation that stronger binding forces (strongly negative Δ〈U + W〉) lead to greater immobilization of the bound species and hence greater losses in configurational entropy. This concept is often invoked to account for entropy-enthalpy compensation in experimental studies. Somewhat unexpectedly, the correlation found for these aqueous systems is remarkably similar to that found for a series of host-guest complexes in chloroform in a separate study with the M2 algorithm (Chang and Gilson, 2004), as also shown in the figure. Note that the change in configurational entropy, as defined here, accounts for the change in rotational, translational, and conformational freedom of the solutes, but not for the change in solvation entropy, which is discussed in the following subsection.
FIGURE 11.
Scatter plot of computed Δ〈U + W〉 versus ΔSconfig for all systems studied here (•) and for a series of host-guest systems in chloroform (○).
It is also of interest to examine the variation in configurational entropy among different bound conformations of a given ligand-cyclodextrin complex, especially because ligand-protein docking calculations almost universally assume that the configurational entropy of one docked conformation is similar to that of another. The present calculations allow the validity of this assumption to be assessed by comparing the stabilities of bound conformations (energy wells) with the energies at the bases of the same wells. That is, for conformations i of a given complex, we compare the free energy Gi (or the chemical potential μi) with the energy Ui + Wi. As shown in Fig. 10, the relationship between Gi and Ui + Wi varies from one complex to another. Thus, for benzene with β-CD, the chemical potential and energy correlate strongly, but for nabumetone with α-CD and resorcinol with β-CD, the conformation with the lowest energy Ui + Wi is not the most stable conformation. It is worth noting that most of the energy wells are close to harmonic, so the equipartition theorem applies and 〈U + W〉i − (Ui + Wi) is nearly constant at 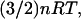 where n is the number of atoms. As a consequence, the differences between Gi and Ui + Wi shown here result almost entirely from variations in −TSconfig.
where n is the number of atoms. As a consequence, the differences between Gi and Ui + Wi shown here result almost entirely from variations in −TSconfig.
FIGURE 10.
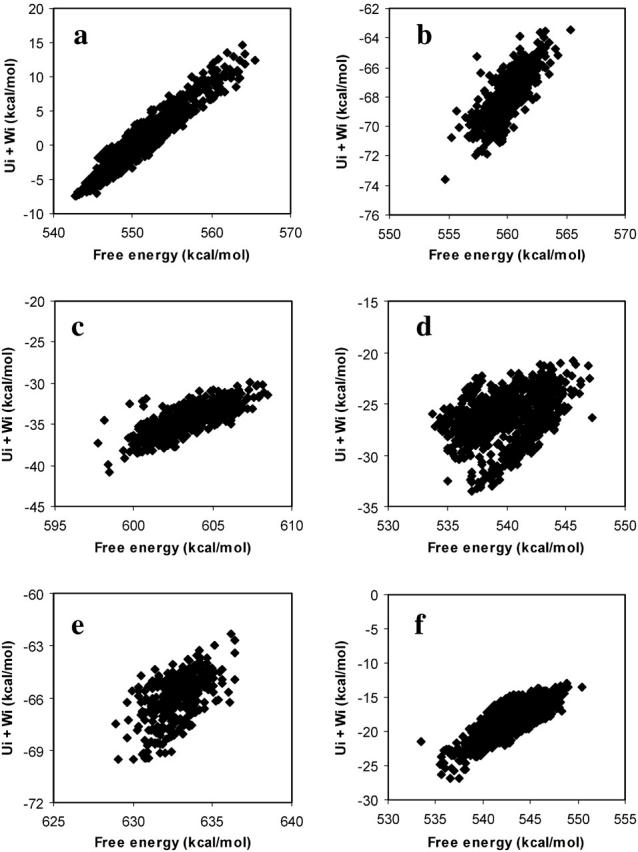
Scatter plots of the free energy μi of conformation i versus the potential plus solvation energy Ui + Wi for (a) benzene with β-CD, (b) naproxen with β-CD, (c) nabumetone with β-CD, (d) nabumetone with α-CD, (e) naproxen with γ-CD, and (f) resorcinol with β-CD.
Solvation entropy and enthalpy
It has previously been shown that the total entropy change upon binding can be decomposed rigorously into the sum of a change in configurational entropy and a change in solvation entropy (Gilson et al., 1997a). This implies that, if this solvation model could partition the solvation free energy into enthalpic and entropic contributions, it would be possible to compute the experimental entropy of binding. Unfortunately, no adequate solvation model for this purpose is currently available. (However, see Elcock and McCammon, 1997 for a thoughtful step in this direction). What is possible, however, is to subtract the computed change in configurational entropy from the experimental entropy (where available) to obtain the change in solvation entropy upon binding: 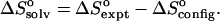 This exercise yields changes in solvation entropy ranging between 0.026 kcal/mol/K for benzene with α-CD and 0.077 kcal/mol/K for flurbiprofen with γ-CD; translating these entropy changes into free energy −TΔSsolv yields values of from −8 to −23 kcal/mol. These negative values are generally consistent with a strong hydrophobic contribution to the binding entropy. Interestingly, however, the overall change in solvation free energy ΔWPB + ΔWnp is consistently unfavorable (see Tables 3–7) due to the work of desolvating polar groups. Because the solvation entropy favors binding, the solvation enthalpy must strongly oppose binding. This observation is consistent with experimental observations that solvation of both polar and nonpolar chemical groups tends to be enthalpically favorable (see, e.g., data in Ben-Naim and Marcus, 1984; Marcus, 1994). Thus, desolvating such groups during binding is expected to be enthalpically unfavorable, as seen here.
This exercise yields changes in solvation entropy ranging between 0.026 kcal/mol/K for benzene with α-CD and 0.077 kcal/mol/K for flurbiprofen with γ-CD; translating these entropy changes into free energy −TΔSsolv yields values of from −8 to −23 kcal/mol. These negative values are generally consistent with a strong hydrophobic contribution to the binding entropy. Interestingly, however, the overall change in solvation free energy ΔWPB + ΔWnp is consistently unfavorable (see Tables 3–7) due to the work of desolvating polar groups. Because the solvation entropy favors binding, the solvation enthalpy must strongly oppose binding. This observation is consistent with experimental observations that solvation of both polar and nonpolar chemical groups tends to be enthalpically favorable (see, e.g., data in Ben-Naim and Marcus, 1984; Marcus, 1994). Thus, desolvating such groups during binding is expected to be enthalpically unfavorable, as seen here.
Distribution of stabilities of the cyclodextrins and their complexes (densities of states)
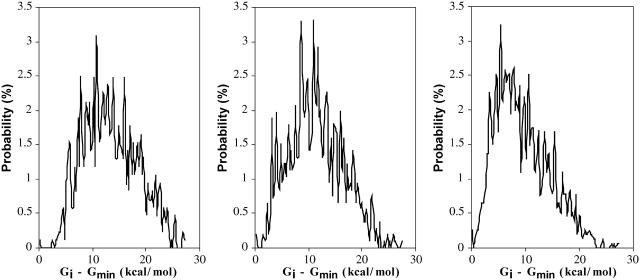
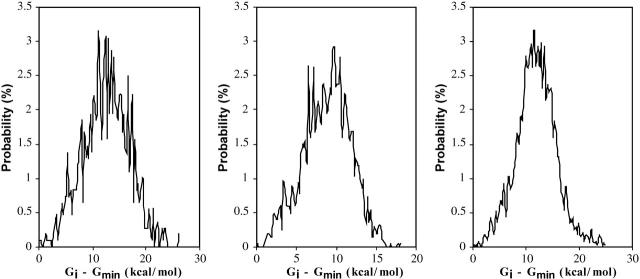
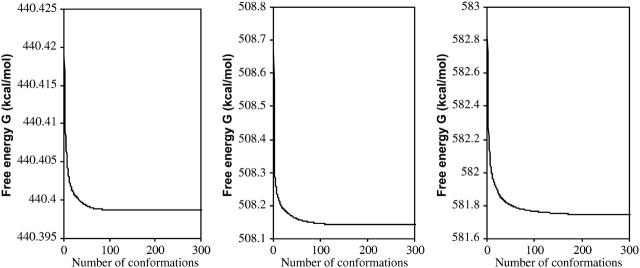
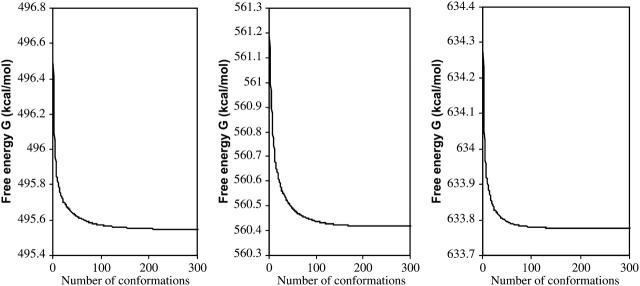
Figs. 12 and 13, respectively, show the conformational free-energy distributions for free α-, β-, and γ-CD and for α-, β-, and γ-CD complexed with flurbiprofen. (Similar results are obtained shown for the other NSAID complexes; data not shown.) The distributions all taper sharply at the low end, but most have a small cluster of very low-energy conformations, suggesting that the properties of these systems are dominated by the few most stable conformations. This is borne out by Figs. 14 and 15, which graph the cumulative chemical potentials as a function of the number N of conformations included in the summation of Eq. 1, where conformations are added from most to least stable. The figures show that just a few low-energy conformations are enough to yield a well-converged value of the chemical potential. Indeed, at most 39 conformations consistently suffice to account for the overall stability of these systems to within 0.1 kcal/mol. This observation is consistent with the predominant states concept (Gilson et al., 1997) which is the basis of this algorithm. It appears that the conformational searches used here go well beyond what is necessary to obtain converged thermodynamics properties for these systems. On the other hand, it is safest to extend the conformational search beyond what is strictly necessary to minimize the chance of missing an important low-energy conformation.
FIGURE 12.
Distribution of free energy μi for conformations i of free α-, β-, and γ-CD (left to right). The small peaks at the left of each distribution correspond to the most stable conformations.
FIGURE 13.
Distribution of free energy μi for conformations of complexes of flurbiprofen with α-, β-, and γ-CDs (left to right). The small peaks at the left of each distribution correspond to the most stable conformations.
FIGURE 14.
Cumulative free energies, 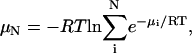 of free α-, β-, and γ-CD (left to right) as a function of the number of conformations included, N, where conformations are ranked from most to least stable.
of free α-, β-, and γ-CD (left to right) as a function of the number of conformations included, N, where conformations are ranked from most to least stable.
FIGURE 15.
Same as Fig. 14 for flurbiprofen with α-, β-, and γ-CD (left to right).
Importance of free-energy corrections in the calculations
As detailed in Methods, the present algorithm finds low-energy conformations (energy wells) and computes their stability based not only upon the depth of each well but also its width, via a corrected harmonic approximation, HA/MS. In addition, the generalized Born (Still et al., 1990; Gilson and Honig, 1991; Qiu et al., 1997) part of the solvation energy for each well is subtracted and replaced by the results of a presumably more accurate finite difference solution of the linearized Poisson-Boltzmann equation (Warwicker and Watson, 1982; Klapper et al., 1986; Gilson et al., 1988). Because these steps add complexity to the calculation, it is worth inquiring whether they improve the accuracy of the results.
First, the importance of the HA/MS calculation is evaluated by recomputing the standard free energies of binding without it. Instead, the quantity Ui + Wi is substituted for zi in Eq. 1, where Ui + Wi is the sum of potential and solvation energy at energy minimum i, and the solvation energy still includes the surface area and finite difference Poisson-Boltzmann corrections. The results, presented as 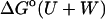 in Table 1, clearly do not agree with experiment as well as the full results,
in Table 1, clearly do not agree with experiment as well as the full results, 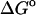 (calc), which do account for the widths of the energy wells via HA/MS integration.
(calc), which do account for the widths of the energy wells via HA/MS integration.
It is also of interest to examine the importance of correcting for anharmonicity with mode scanning (MS) by recomputing the binding free energies with the pure harmonic approximation. The resulting binding free energies, listed as 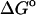 (HA) in Table 1, tend to be more negative than those obtained when the full HA/MS method is used. In fact, the changes in binding free energy are as large as 2 kcal/mol, for α-CD with flurbiprofen. Thus, omitting mode scanning degrades agreement with experiment in these systems.
(HA) in Table 1, tend to be more negative than those obtained when the full HA/MS method is used. In fact, the changes in binding free energy are as large as 2 kcal/mol, for α-CD with flurbiprofen. Thus, omitting mode scanning degrades agreement with experiment in these systems.
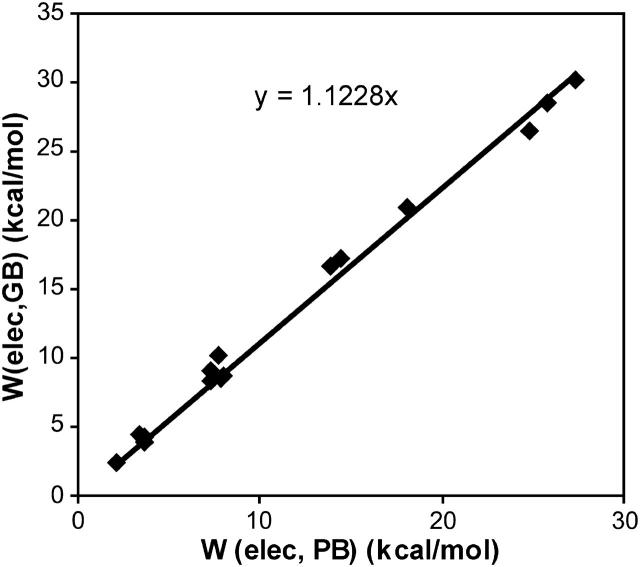
Finally, we examine the importance of the generalized Born to Poisson-Boltzmann correction by including the full HA/MS integrations but now omitting the correction from generalized Born toward Poisson-Boltzmann. This alteration in the method yields much less accurate results, listed as 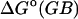 in Table 1. As shown in Fig. 16, the generalized Born and the finite difference Poisson-Boltzmann contributions to the overall binding free energy are strongly and linearly correlated for these systems, so it should be possible to obtain accurate results for these systems by adjusting the generalized Born calculations. However, it is not a given that such an adjustment would be applicable to other systems.
in Table 1. As shown in Fig. 16, the generalized Born and the finite difference Poisson-Boltzmann contributions to the overall binding free energy are strongly and linearly correlated for these systems, so it should be possible to obtain accurate results for these systems by adjusting the generalized Born calculations. However, it is not a given that such an adjustment would be applicable to other systems.
FIGURE 16.
Scatter plot of Boltzmann-averaged generalized Born versus Boltzmann-averaged finite difference Poisson-Boltzmann electrostatic solvation energies for all of the cyclodextrin complexes.
DISCUSSION
The M2 computational method
The M2 method yields accurate association constants for the cyclodextrin systems studied here: overall, the computed standard free energies of binding agree with experiment to within 1 kcal/mol for the association of various ligands with α-, β-, and γ-CD in aqueous solution. A full binding calculation can be completed for any of the systems studied here within a day of computer time. This study thus supports the validity of the predominant states concept that accurate free energies can be computed at modest computational cost by focusing on the lowest energy conformations of the free and bound molecules (Gilson et al., 1997b). The predominance of a small number of most stable conformations also is supported by the density of states and convergence data in Figs. 12–15. The M2 method should be useful not only for the interpretation of experimental data, but also for the design of chemically modified cyclodextrins to bind targeted ligands in applications such as encapsulation of pharmaceuticals and scavenging of environmental toxins. The method can also be applied more broadly in the design of other types of chemical hosts acting in aqueous and, as recently shown (Chang and Gilson, 2004), organic solvents.
It is worth noting that the binding free energies reported here are small differences between large opposing contributions. Thus, van der Waals and Coulombic interactions favor binding by from −10 to −50 kcal/mol in net, whereas configurational entropy losses and the electrostatic desolvation penalty oppose binding in roughly equal measure, leading to net binding free energies that are weaker than −6 kcal/mol in all instances. It is therefore striking that the computational method balances opposing contributions well enough to yield quite accurate results.
One might well have expected that an explicit representation of the molecular nature of water would have been necessary to adequately represent solvation of cyclodextrins and their complexes, given the large number of hydroxyl groups at various different spacings in these systems. However, good results are obtained here with an implicit solvation model that accounts for the granularity of water only in a rudimentary fashion, through the use of a solvent probe to define the molecular surface. The success of this model is presumably attributable to thermal averaging over many different conformations of the hydroxyls and solvent waters. In addition, the electrostatic part of the desolvation model appears to be well balanced with the Coulombic interaction term in the potential function because numerically similar, and similarly accurate, binding energies are obtained for the neutral ligand nabumetone and for the anionic ligands flurbiprofen and naproxen, despite large opposite changes in these two electrostatic terms.
This study has shown that the HA/MS calculations and the correction from generalized Born toward the linearized Poisson-Boltzmann model are necessary to obtain accurate results. Although the existence of a strong, linear relationship between the generalized Born and finite difference Poisson-Boltzmann energies suggests that the generalized Born model could be adjusted to give good results on its own for these systems, the same relationship between the two electrostatic models probably will not hold in other systems that are more or less strongly solvated (see, e.g., Marcus, 1994; David et al., 2000). As a consequence, it seems preferable to continue correcting toward the linearized PB model as done here, especially because most of the computer time is spent on conformational search, not on the PB calculations. We note, however, that ongoing work aimed at improving GB and other fast models of electrostatic solvation (see, e.g., Feig and Brooks, 2004 and citations therein) might ultimately make the correction used here unnecessary.
The M2 method bears some similarity to MM-PBSA (Srinivasan et al., 1998). However, it is expected to be more efficient because it includes an aggressive search for stable conformations rather than relying on a potentially lengthy molecular dynamics simulation to equilibrate the system. In addition, unlike the rigid-rotor harmonic oscillator method used in MM-PBSA, this method of calculating configuration integrals accounts for anharmonicity and has been numerically validated (Chang et al., 2003).
Changes in energy and entropy in binding
These calculations indicate that van der Waals interactions and the nonpolar solvation term provide the main driving force for binding in the systems studied here. Thus, although the Coulombic electrostatic term can be strongly stabilizing, especially for the anionic ligands, it is largely compensated by the electrostatic cost of desolvating the interacting charges. Interestingly, the losses in configurational entropy upon binding are found to be very substantial, and they approximately compensate the attractive van der Waals attractions. In fact, the magnitude of the entropic penalty in some cases exceeds that of the van der Waals attraction. The entropic penalty is greater for the drugs than for benzene and resorcinol, perhaps because the latter possess fewer degrees of freedom that can be restricted upon binding.
Interestingly, the change in configurational entropy upon binding does not result from a drop in the number of stable energy minima upon binding, but is better interpreted as an indicator of the tightness of the fit between the host and the guest. For example, the loss of configurational entropy of flurbiprofen is greatest for β-CD, consistent with the structural observations that flurbiprofen fits neatly into β-CD but is too bulky to penetrate deeply into the cavity of α-CD and too small to make a tight fit with γ-CD. More generally, the losses in configurational entropy observed here result almost entirely from the fact that the most stable energy wells for the complex are narrower than those for the free hosts and guests, rather than from a drop in the number of highly occupied wells upon binding. Similar results have been obtained for a series of host-guest interactions in chloroform (Chang and Gilson, 2004), so this may be a general result for host-guest systems. However, the situation might be different for binding reactions involving proteins, because they are far more flexible.
Entropic compensation
This study finds that stronger binding forces, as reflected by more negative values of Δ〈U + W〉, correlate with greater losses in configurational entropy, as shown in Fig. 11. This result is consistent with the intuitive concept that stronger attractive forces tend to reduce conformational flexibility, and is analogous to the entropy-enthalpy compensation frequently observed in experimental systems. However, it is not clear why the correlation seen here, like that seen in the experimentally observed correlation between total entropy and total enthalpy, has so linear a form, nor why it is so congruent with the results for a very different set of host-guest systems in chloroform (Chang and Gilson, 2004) (Fig. 11). It has been suggested that experimental enthalpy-entropy compensation may, in some cases at least, be a spurious result due to measurement error in the enthalpy (Lumry and Rajender, 1970; Krug et al., 1976; Sharp, 2001). However, in this study, the correlation between Δ〈U + W〉 and ΔSconfig appears to be physically meaningful because there is no reason why the 〈U + W〉 term, which is analogous to the enthalpy, should be particularly noisy. Moreover, the variations in configurational entropy observed here are consistent with structural interpretations related to the tightness of the host-guest fit. Thus, it appears that the correlation between Δ〈U + W〉 and ΔSconfig is real and physically meaningful.
Implications for molecular modeling and computer-aided drug design
This analysis has important implications for our understanding of biomolecular interactions, for theoretical modeling of molecular recognition, and for structure-based drug design. For one thing, it suggests that the energy and solvation models used here are reasonably accurate. In particular, the Coulombic and electrostatic solvation terms appear to be remarkably well balanced. On the other hand, proteins typically desolvate their ligands more than cyclodextrins do, so achieving a suitable balance between interaction and solvation may be more challenging for protein-ligand binding than for cyclodextrin-guest binding.
This study also bears on the nature and importance of changes in the configurational entropy on binding. We find that the change in configurational entropy contributes between 6 and 24 kcal/mol to the free energy of binding in the systems studied here. These numbers are far larger than those predicted by simple models that penalize rotatable bonds in the ligand by a few tenths of a kcal/mol per bond. Moreover, the rotatable bond count is completely unable to address the main reason for the loss of configurational entropy found here, the tightness of fit of the ligand in its binding site. Furthermore, we find that the configurational entropy varies significantly from one bound conformation to another of a given ligand-receptor complex (Fig. 10). This variation, which also is not captured by a count of rotatable bonds, is large enough in some cases to thoroughly shuffle the stability rankings of the conformations relative to those inferred from just potential plus solvation energy; i.e., from Ui + Wi. This result strongly suggests that it will be impossible to reliably rank docked conformations of ligands in proteins without accounting for the variation in configurational entropy from one bound conformation to another.
Perhaps this problem can be partially addressed based upon our empirical observation of a strong, near-linear relationship between the changes in configurational entropy and in mean energy 〈U + W〉. That is, even if nothing more sophisticated is done, it may be helpful to simply scale down the computed change in energy to account for a proportional loss in entropy. Although crude, this approach would probably be more accurate than the common approach of penalizing based upon the number of rotatable bonds in the ligand. Indeed, these results may help explain why straightforward physics-based energy models almost always grossly overestimate binding affinities and require scaling coefficients of less than unity (see, e.g., Morris et al., 1998): it is not that the energy model is wrong, but rather that it omits a large, compensatory entropic term. On the other hand, we do not know whether the energy-entropy relationship is sufficiently uniform across systems to permit a general parameterization of this approach. Also, some variations in configurational entropy certainly will not be captured by so simple a method, as highlighted in Figs. 9 and 10. Thus, it will be of interest to apply the M2 method to the calculation of protein-ligand binding affinities.
Acknowledgments
This publication was made possible by grant no. GM61300 from the National Institute of General Medical Sciences of the National Institutes of Health. Its contents are solely the responsibility of the authors and do not necessarily represent the official views of the National Institute of General Medical Sciences.
References
- Barse, B., P. Kaul, A. Banerjee, C. L. Kaul, and U. C. Banerjee. 2003. Cyclodextrins: emerging applications. Chim. Oggi. 21:48–57. [Google Scholar]
- Ben-Naim, A., and Y. Marcus. 1984. Solvation thermodynamics of nonionic solutes. J. Chem. Phys. 81:2016–2027. [Google Scholar]
- Bergeron, R., and M. A. Channing. 1976. Molecular disposition of para-nitrophenol and sodium para-nitrophenolate in cyclohexaamylose cavity: c-13 probe. Bioorg. Chem. 5:437–449. [Google Scholar]
- Berman, H. M., J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov, and P. E. Bourne. 2000. The Protein Data Bank. Nucleic Acids Res. 28:235–242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Betzel, C., C. Saenger, B. E. Hingerty, and G. M. Brown. 1984. Topography of cyclodextrin inclusion complexes, 20. Circular and flip-flop hydrogen-bonding in beta-cyclodextrin undecahydrate: a neutron-diffraction study. J. Am. Chem. Soc. 106:7545–7557. [Google Scholar]
- Bonnet, P., C. Jaime, and L. Morin-Allory. 2002. Structure and thermodynamics of alpha-, beta-, and gamma-cyclodextrin dimers. Molecular dynamics studies of the solvent effect and free binding energies. J. Org. Chem. 67:8602–8609. [DOI] [PubMed] [Google Scholar]
- Brooks, B. R., R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan, and M. Karplus. 1983. CHARMM: a program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 4:187–217. [Google Scholar]
- Cao, Y. J., X. H. Xiao, R. H. Lu, and Q. X. Guo. 2003. Theoretical study of the inclusion processes of ibuprofen enantiomers with native and modified beta-CDs. J. Incl. Phenom. Macro. 46:195–200. [Google Scholar]
- Casu, B., M. Reggiani, G. G. Gallo, and A. Vigevani. 1968. Conformation of O-methylated amylose and cyclodextrins. Tetrahedron. 24:803–821. [Google Scholar]
- Chang, C.-E., and M. K. Gilson. 2003. Tork: conformational analysis method for molecules and complexes. J. of Comput. Chem. 24:1987–1998. [DOI] [PubMed] [Google Scholar]
- Chang, C.-E., and M. K. Gilson. 2004. Free energy, entropy, and induced fit in host-guest recognition. J. Am. Chem. Soc. In press. [DOI] [PubMed]
- Chang, C.-E., M. J. Potter, and M. K. Gilson. 2003. Calculation of molecular configuration integrals. J. Phys. Chem. B. 107:1048–1055. [Google Scholar]
- Chen, W., J. Huang, and M. K. Gilson. 2004. Identification of symmetries in molecules and complexes. J. Chem. Inf. Comput. Sci. 44:1301–1313. [DOI] [PubMed] [Google Scholar]
- Cortis, C. M., and R. A. Friesner. 1997. An automatic three-dimensional finite element mesh generation system for the Poisson-Boltzmann equation. J. Comput. Chem. 18:1570–1590. [Google Scholar]
- David, L., R. Luo, and M. K. Gilson. 2000. Comparison of generalized Born and Poisson models: energetics and dynamics of HIV protease. J. Comput. Chem. 21:295–309. [Google Scholar]
- David, L., R. Luo, and M. K. Gilson. 2001. Ligand-receptor docking with the Mining Minima optimizer. J. Comput. Aided Mol. Des. 15:157–171. [DOI] [PubMed] [Google Scholar]
- Davis, M. E., J. D. Madura, B. A. Luty, and J. A. McCammon. 1991. Electrostatics and diffusion of molecules in solution: simulations with the University-of-Houston-Brownian dynamics program. Comput. Phys. Commun. 62:187–197. [Google Scholar]
- Del Valle, E. M. M. 2004. Cyclodextrins and their uses: a review. Process Biochem. 39:1033–1046. [Google Scholar]
- Elcock, A. H., and J. A. McCammon. 1997. Continuum solvation model for studying protein hydration thermodynamics at high temperatures. J. Phys. Chem. 101:9624–9634. [Google Scholar]
- Feig, M., and C. L. Brooks. 2004. Recent advances in the development and application of implicit solvent models in biomolecule simulations. Curr. Opin. Struct. Biol. 14:217–224. [DOI] [PubMed] [Google Scholar]
- Fermeglia, M., M. Ferrone, A. Lodi, and S. Pricl. 2003. Host-guest inclusion complexes between anticancer drugs and beta-cyclodextrin: computational studies. Carbohyd. Polym. 53:15–44. [Google Scholar]
- Friedman, R. A., and B. Honig. 1995. A free-energy analysis of nucleic-acid base stacking in aqueous-solution. Biophys. J. 69:1528–1535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilson, M. K., J. A. Given, B. L. Bush, and J. A. McCammon. 1997a. The statistical-thermodynamic basis for computation of binding affinities: a critical review. Biophys. J. 72:1047–1069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilson, M. K., J. A. Given, and M. S. Head. 1997b. A new class of models for computing receptor-ligand binding affinities. Chem. Biol. 4:87–92. [DOI] [PubMed] [Google Scholar]
- Gilson, M. K., and B. Honig. 1991. The inclusion of electrostatic hydration energies in molecular mechanics calculations. J. Comput. Aided Mol. Des. 5:5–20. [DOI] [PubMed] [Google Scholar]
- Gilson, M. K., K. A. Sharp, and B. H. Honig. 1988. Calculating the electrostatic potential of molecules in solution: method and error assessment. J. Comput. Chem. 9:327–335. [Google Scholar]
- Harata, K. 1987. The structure of the cyclodextrin complex, 20. Crystal-structure of uncomplexed hydrated gamma-cyclodextrin. Bull. Chem. Soc. Jpn. 60:2763–2767. [Google Scholar]
- Helden, S. P. V., B. P. V. Eijck, and L. H. M. Janssen. 1992. The conformational behavior of complexes of alpha-cyclodextrin with p-chlorophenol and p-hydroxybenzoic acid in water as studied by molecular-dynamics simulations. J. Biomol. Struct. Dyn. 9:1269–1283. [DOI] [PubMed] [Google Scholar]
- Immel, S. 1995. Computer simulation of chemical and biological properties of saccharides: sucrose, fructose, cyclodextrins, and starch. PhD thesis. Institute of Organic Chemistry, Darmstadt University of Technology, Darmstadt, Germany.
- Ivanov, J., and G. Schüürmann. 1999. Simple algorithms for determining the molecular symmetry. J. Chem. Inf. Comput. Sci. 39:728–737. [Google Scholar]
- Kairys, V., and M. K. Gilson. 2002. Enhanced docking with the mining minima optimizer: acceleration and side-chain flexibility. J. Comput. Chem. 23:1656–1670. [DOI] [PubMed] [Google Scholar]
- Klapper, I., R. Hagstrom, R. Fine, K. Sharp, and B. Honig. 1986. Focusing of electric fields in the active site of Cu-Zn superoxide dismutase. Proteins. 1:47–55. [DOI] [PubMed] [Google Scholar]
- Kolossvary, I., and W. C. Guida. 1996. Low mode search. An efficient, automated computational method for conformational analysis: application to cyclic and acyclic alkanes and cyclic peptides. J. Am. Chem. Soc. 118:5011–5019. [Google Scholar]
- Krug, R., W. Hunter, and R. Grieger. 1976. Statistical interpretation of enthalpy-entropy compensation. Nature. 261:566–567. [Google Scholar]
- Liu, L., and Q. X. Guo. 2002. The driving forces in the inclusion complexation of cyclodextrins. J. Incl. Phenom. Macro. 42:1–14. [Google Scholar]
- Liu, Y., E. C. Yang, Y. W. Yang, H. Y. Zhang, Z. Fan, F. Ding, and R. Cao. 2004. Thermodynamics of the molecular and chiral recognition of cycloalkanols and camphor by modified beta-cyclodextrins possessing simple aromatic tethers. J. Org. Chem. 69:173–180. [DOI] [PubMed] [Google Scholar]
- Loftsson, T., M. Masson, and M. E. Brewster. 2004. Self-association of cyclodextrins and cyclodextrin complexes. J. Pharm. Sci. 93:1091–1099. [DOI] [PubMed] [Google Scholar]
- Lumry, R., and S. Rajender. 1970. Enthalpy-entropy compensation phenomena in water solutions of proteins and small molecules: a ubiquitous property of water. Biopolymers. 9:1125–1227. [DOI] [PubMed] [Google Scholar]
- MacKerell, A., D. Bashford, M. Bellott, R. Dunbrack, J. Evanseck, M. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. Lau, C. Mattos, S. Michnick, T. Ngo, D. Nguyen, B. Prodhom, W. Reiher, B. Roux, M. Schlenkrich, J. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiorkiewicz-Kuczera, D. Yin, and M. Karplus. 1998. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B. 102:3586–3616. [DOI] [PubMed] [Google Scholar]
- MacKerell, A. D., Jr., J. Wiorkiewicz-Kuczera, and M. Karplus. 1995. An all-atom empirical energy function for the simulation of nucleic acids. J. Am. Chem. Soc. 117:11946–11975. [Google Scholar]
- Manor, P. C., and W. Saenger. 1974. Topography of cyclodextrin inclusion complexes. III. Crystal and molecular structure of cyclohexaamylose hexahydrate, the water dimer inclusion complex. J. Am. Chem. Soc. 96:3630–3639. [Google Scholar]
- Marcus, Y. 1994. A simple empirical-model describing the thermodynamics of hydration of ions of widely varying charges, sizes, and shapes. Biophys. Chem. 51:111–127. [Google Scholar]
- Mardis, K. L., R. Luo, and M. K. Gilson. 2001. Interpreting trends in the binding of cyclic ureas to HIV-1 protease. J. Mol. Biol. 309:507–517. [DOI] [PubMed] [Google Scholar]
- Morris, G. M., D. S. Goodsell, R. S. Halliday, R. Huey, W. E. Hart, R. K. Belew, and A. J. Olson. 1998. Automated docking using a Lamarckian genetic algorithm and empirical binding free energy function. J. Comput. Chem. 19:1639–1662. [Google Scholar]
- Qiu, D., P. S. Shenkin, F. P. Hollinger, and W. C. Still. 1997. The GB/SA continuum model for solvation. A fast analytical method for the calculation of approximate Born radii. J. Phys. Chem. 101:3005–3014. [Google Scholar]
- Rekharsky, M. V., and Y. Inoue. 1998. Complexation thermodynamics of cyclodextrins. Chem. Rev. 98:1875–1917. [DOI] [PubMed] [Google Scholar]
- Sadlej-Sosnowska, N., L. Kozerski, E. Bednarek, and J. Sitkowski. 2000. Fluorometric and NMR studies of the naproxen-cyclodextrin inclusion complexes in aqueous solutions. J. Incl. Phenom. Macro. 37:383–394. [Google Scholar]
- Sharp, K. 2001. Entropy-enthalpy compensation: fact or artifact? Protein Sci. 10:661–667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shehatta, I. S., M. S. Ibrahim, and M. R. Sultan. 2002. The antimicrobial nalidixic acid as a probe for molecular recognition of alpha- and beta-cyclodextrins. Can. J. Chem. 80:1313–1320. [Google Scholar]
- Srinivasan, J., T. E. Cheatham, P. Cieplak, P. A. Kollman, and D. A. Case. 1998. Continuum solvent studies of the stability of DNA, RNA, and phosphoramidate-DNA helices. J. Am. Chem. Soc. 120:9401–9409. [Google Scholar]
- Still, W. C., A. Tempczyk, R. C. Hawley, and T. Hendrickson. 1990. Semianalytical treatment of solvation for molecular mechanics and dynamics. J. Am. Chem. Soc. 112:6127–6129. [Google Scholar]
- Valero, M., and S. M. B. Costa. 1999. Complexation of the non-steroidal anti-inflammatory drug Nabumetone with modified and unmodified cyclodextrins. J. Incl. Phenom. Macro. 35:663–677. [Google Scholar]
- Wang, R. L., G. M. Zhang, Y. Yang, S. M. Shuang, and J. H. Pan. 2003. Inclusion behavior between methylene blue and neutral or charged beta-cyclo. Chinese J. Anal. Chem. 31:205–207. [Google Scholar]
- Warwicker, J., and H. C. Watson. 1982. Calculation of the electric-potential in the active-site cleft due to alpha-helix dipole. J. Mol. Biol. 157:671–679. [DOI] [PubMed] [Google Scholar]
- Zheng, X. M., W. M. Lu, and D. Z. Sun. 2001. Enthalpy and entropy criterion for the molecular recognize of some organic compounds with beta cyclodextrin. Acta. Phys-Chim. Sin. 17:343–347. [Google Scholar]