Permeation Properties of an Engineered Bacterial OmpF Porin Containing the EEEE-Locus of Ca²⁺ Channels

Abstract

The selectivity filter of the bacterial porin OmpF carries a small net charge close to −1 e and is therefore only slightly cation-selective. Calcium channels, on the other hand, contain four negatively charged glutamates, the EEEE-locus, and are among the most selective cation channels known. We aimed to turn the essentially nonselective OmpF into a Ca²⁺-selective channel. To that end, two additional glutamates (R42E and R132E) were introduced in the OmpF constriction zone that already contains D113 and E117. Mutant OmpF containing this DEEE-locus has a high Ca²⁺ over Cl⁻ selectivity and a Na⁺ current with a strongly increased sensitivity to 1 mM Ca²⁺. The charge/space competition model, initially applied to the L-type Ca²⁺ channel, identifies the fixed charge and filter volume as key determinants of ion selectivity, with the precise atomic arrangement having only second-order effects. By implication, the reproduction of fixed charge and filter volume should transform two channels into channels of similar selectivity, even if the two belong to entirely different ion channel families, as is the case for OmpF and the L-type Ca²⁺ channel. The results presented here fit quite well in the framework of charge/space competition theory.

INTRODUCTION

Membrane-embedded ion channels are electrolyte-filled proteinaceous nanotubes. Discrimination between ion species is crucial to ion channel function and electric charge is a critical parameter determining ion selectivity. At their narrowest part, cation-selective channels are lined with charged amino acids that determine (for the most part) the selectivity of the channel (although fixed charges elsewhere may participate, e.g., in the accumulation of ions at the end of the channel). The selectivity filters of both Na⁺ and Ca²⁺ channels contain several negatively charged aspartates and/or glutamates (Yang et al., 1993). A difference between the two channel types is that the signature sequence of Ca²⁺ channels (EEEE) contains two more of these negatively charged residues than the sequence of Na⁺ channels (DEKA), resulting in an overall charge of the selectivity filter of −4 e in Ca²⁺ channels compared to −1 e in Na⁺ channels. The seminal study of Heinemann and co-workers (1992) showed that the mere replacement of lysine by glutamate (DEKA→DEEA) turned the protein into a Ca²⁺-selective channel. Recently, Yamaoka et al. (2003) showed the inverse: they changed a Ca²⁺ channel into a Na⁺ channel. We still await the crystal structure of Na⁺ and Ca²⁺ channels, but even with the 64% sequence homology between the two proteins in mind (Lodish et al., 2000), it seems reasonable to assume that the positioning of the charged residues in the selectivity filter will be different. The ability to convert one channel type into the other inevitably leads to questions about the importance of the precise 3D structure of the selectivity filter. If atomic structural details of the filter were really that crucial, it is difficult to understand how a point mutation (DEKA→DEEA) can switch a Na⁺ channel into a functional Ca²⁺ channel. The notion that the charge and crowding of amino acid side chains—rather than their detailed structural arrangement—might be the main determinants of ion selectivity seems attractive in this context.

In an attempt to identify physical mechanisms underlying ionic selectivity, a model has been developed that describes the selectivity of the L-type Ca²⁺ channel exclusively in terms of the fixed charge, dielectric coefficient, and volume of the selectivity filter (Nonner et al., 2000; see also McCleskey, 2000). The simplest version of this charge/space competition (CSC) model uses the constraint of electroneutrality (see Eisenberg, 2003): fixed charge of the protein is exactly balanced by nearby mobile counter charge. The model then determines the thermodynamically optimal distribution of charged spheres in a limiting space as an output, not by assumption. The number of Na⁺ ions needed to electrically balance the −4 e charge of the four glutamates of the EEEE locus is twice the number of Ca²⁺ ions. The crowding of the extra Na⁺ ions is exactly why the channel prefers Ca²⁺ to Na⁺. According to the simplest version of CSC, all charges—fixed and mobile—float freely but are confined to the volume of the selectivity filter, emphasizing the irrelevancy of structural details to the model. The only difference between fixed and mobile charges is that the mobile charges are free to enter and leave the confined volume of the selectivity filter; fixed charges are not. The CSC model has also been used with some success to describe Na⁺-selective (Boda et al., 2002; Gillespie et al., 2002a) and anion channels (Gillespie et al., 2002c). The biological importance of crowded charge seems an inevitable consequence of the high density of fixed charge found at the active sites (i.e., selectivity filters) of many proteins and channels.

The work presented here is an extension of the pioneering mutation studies of Heinemann et al. (1992) and previous theoretical studies on ion permeation through L-type Ca²⁺ channels (Nonner and Eisenberg, 1998; Nonner et al., 1998). We address the question of the importance of exact structure for the mechanism of ion selectivity. By mimicking the fixed charge, and (we hope) the volume and dielectric coefficient of Ca²⁺ channels, we attempt to transmutate the nonselective OmpF into a channel selective for Ca²⁺.

OmpF is one of the nonselective porin molecules found in the outer membrane of Escherichia coli whose three-dimensional structure is known at high resolution (Cowan et al., 1992; Schirmer, 1998; Delcour, 2003). The OmpF molecule is a trimer of three identical polypeptides, each 340 amino acids long and folded and intertwined into a 16-stranded antiparallel β-barrel, ∼5 nm in length and 4 nm in diameter (Schulz, 2002). Half-way down the lumen of the pore, the channel narrows, resulting in a constriction zone ∼1 × 1 nm. Three positively charged arginines (R42, R82, and R132) located at one side of this constriction zone face a negatively charged aspartate (D113) and glutamate (E117) on the other side. Previous mutation studies emphasized already the role of these charged residues in OmpF selectivity (Saint et al., 1996; Saxena et al., 1999; Phale et al., 2001). We continued on this path and by replacing the three arginines with two glutamates (R42E and R132E) and one alanine (R82A), we created an EEEE-like locus (DEEE) in OmpF, whose properties are compared with those of the EEEE locus in Ca²⁺ channels.

Apart from the EEEE and DEEE locus, these two channels could not be more different. The monomeric L-type Ca²⁺ channel has four homologous domains, each containing six transmembrane α-helices; the trimeric bacterial channel, OmpF, is a folded β-barrel, a member of the family of channel-forming porins. Despite their evident differences, if the fixed charge and filter volumes are comparable, the CSC model predicts similarities in ion selectivity between these two types of channels. In this study, we analyze reversal potential and conductance measurements of wild-type (WT) and mutant OmpF protein that contains the DEEE locus.

MATERIALS AND METHODS

Chemicals

All chemicals were purchased from Sigma (Madison, WI), with the exception of n-octyl-oligo-polyoxyethylene OPOE (Alexis Biochemicals, San Diego, CA) and tetracyclin (Boehringer Mannheim, Brussels, Belgium).

Site-directed mutagenesis of OmpF

Plasmid pGompF—encoding the OmpF protein behind the PhoE leader sequence (Prilipov et al., 1998)—was kindly provided by Prof. T. Schirmer, University of Basel. To facilitate protein purification the leader sequence was removed and a ribosome-binding site and start codon were inserted directly before the sequence encoding mature OmpF, resulting in the plasmid pGompF-mature. This procedure resulted in the protein being expressed in large amounts in inclusion bodies, from which it was purified as described below. The plasmid pGompF-mature was used as a template in the QuikChange XL protocol from Stratagene (La Jolla, CA). First, the template was duplicated using reverse complement primers, containing the mutation of interest, resulting in mutated plasmid with staggered nicks. Then, the template was degraded and the mutated plasmid (with staggered nicks) was transformed to E. coli. Sequencing the DNA verified that the resulting mutated genes were only mutated in the intended codon and did not contain additional (silent) mutations. In some cases the ampicillin resistance marker was replaced with a marker for tetracycline.

OmpF isolation and purification

One-liter cell cultures of E. coli Bl21(DE3) or Omp8 (Prilipov et al., 1998) containing the desired plasmid were grown overnight in TY media supplemented with ampicillin (100 μg/ml) or tetracycline (5 μg/ml). Cell lysis was induced by the addition of lysozyme (0.35 mg/ml) and 1% Triton X-100. After sonication (3 × 30 s), inclusion bodies were pelleted and washed with 20 mM phosphate buffer, pH 6.5. After centrifugation, the pellet was dissolved in 8 M urea and diluted to a final protein concentration of 0.2 mg/ml in refolding buffer (20 mM sodium phosphate buffer, pH 6.5; 1 mM dodecylmaltoside and 1 mM Tris-(2-carboxyethyl)phosphine). After overnight refolding at room temperature, dimer-to-monomer conversion was accomplished by heating to 70°C for 1 h. Subsequent degradation of the monomers was induced by the addition of trypsin (trypsin/protein = 1:100 w/w). Final purification of trimer protein was achieved by ion exchange chromatography on MonoQ resin (Amersham Biosciences) using an elution buffer containing 200 mM NaPi, pH = 8.0, 1% OPOE and 1 mM Tris-(2-carboxyethyl)phosphine. Eluted fractions were analyzed by 12.5% SDS-PAGE (CBB stained) and protein concentration was determined with Lowry (BioRad, Hercules, CA). Typical total yield was 10–20 mg for WT and 5–6 mg for mutant protein. EAE and LEAE proteins were further purified by extracting out the SDS gel, using elution buffer, giving final protein yields of ≈50 μg.

Partially purified monomeric proteins were derived from inclusion bodies and checked by electron spray mass spectrometry. Theoretically predicted mass and experimentally obtained values were in excellent agreement and differed by <5 Da.

Solutions

The following buffers, supplemented with KCl or NaCl, were used for electrophysiological measurements: 20 mM Hepes (pK = 7.35), with N-methyl-d-glucamine (NMDG) adjusted to pH 7.4; 20 mM TAPS (pK = 8.4), with NMDG adjusted to pH 9.0 and 20 mM Na-Acetate, with 20 mM HCl adjusted to pH 3. Before use, all solutions were passed through a 0.2-μm nylon filter. Gradients are represented cis/trans; for instance, a 0.1 // 1 M KCl gradient indicates 0.1 M KCl in the cis compartment and 1 M KCl in the trans compartment.

Contamination of Na⁺- and K⁺-free solutions was avoided by using NMDG instead of NaOH or KOH to titrate the buffer solutions to the desired pH. We therefore compared WT conductance (in symmetrical 1 M KCl, pH 7.4) and selectivity (in 0.1 // 1 M KCl, pH 7.4) in Hepes-buffered solutions, pH-adjusted with either KOH or NMDG. The conductance values of single open trimers was found to be 4.15 ± 0.12 nS (n = 11) and 4.20 ± 0.12 nS (n = 17) in solutions titrated with KOH and NMDG, respectively. With KOH, the reversal potential was 26.4 ± 1.5 mV (n = 15), whereas with NMDG it was 28.2 ± 4.6 mV (n = 9). These data indicate that NMDG itself has no significant effect on either conductance or reversal potential.

Activity coefficients were calculated with Geochem-PC 2.0 software (Parker et al, 1995). At relatively low ionic strength (<0.5 M), Geochem calculates activity coefficients with the extended Debye-Hückel (or Davies) equation, whereas at higher ionic strength (>0.5 M) a modification of the Helgeson equation is used. Where appropriate, ion activities calculated by Geochem are given in figure legends.

Electrophysiology

Planar lipid bilayer (PLB) experiments were performed using a chamber and Delrin cuvet (models BCH-22A and CD22A, Warner Instruments, Hamden, CT). By means of 3 M KCl/2% agar salt bridges, the cis compartment was connected to the headstage and the trans compartment was connected to ground. The PLB was painted across a 250-μm diameter aperture and was composed of phosphatidylethanolamine and phosphatidylcholine in an 8:2 ratio, dissolved in n-decane (10 mg/ml). PLB formation was monitored electrically by observing the current output in response to a triangular wave (4 Hz, 1 V peak-to-peak). Data were sampled at 5 kHz and filtered at 1 kHz, using the Axopatch 200B amplifier (Axon Instruments, Union City, CA).

The pulse protocol used throughout this study (Fig. 1 A) started from a holding potential of 0 mV. After the potential (V) was jumped to −100 mV, V was held at −100 mV for 0.1 s, after which V was ramped to 100 mV in a little less than 2 s. Finally, after 0.1 s at 100 mV, V was jumped back to 0 mV. Fig. 1 B shows the current recorded from the PBL in the absence of protein, with 0.1 M NaCl, pH 7.4, on both sides of the membrane. The instantaneous current jumps (ΔI) at the beginning and end of the voltage ramp—indicated by a and b in Fig. 1 B, respectively—represent the rapid charging and decharging of the membrane capacitance C_m. That part of the trace between −50 and 50 mV was fitted by linear regression (dashed lines) and subtracted from “raw” traces measured with OmpF in the bilayer. Fig. 1 C shows raw data; Fig. 1 D shows corrected data. The control recording in Fig. 1 B serves several ends. First, it renders a correction for any seal and/or membrane leak conductance (R_m) as well as for the capacitive transients mentioned above. Second, it allows the assignment of the zero current level with the trimer completely shut, not a triviality because of the frequently observed residual conductance that remains after the apparent closure of all three monomers (compare b sections of the two IVs in Fig. 1 D). Finally, the followed procedure of current subtraction effectively corrects for current offsets.

FIGURE 1.

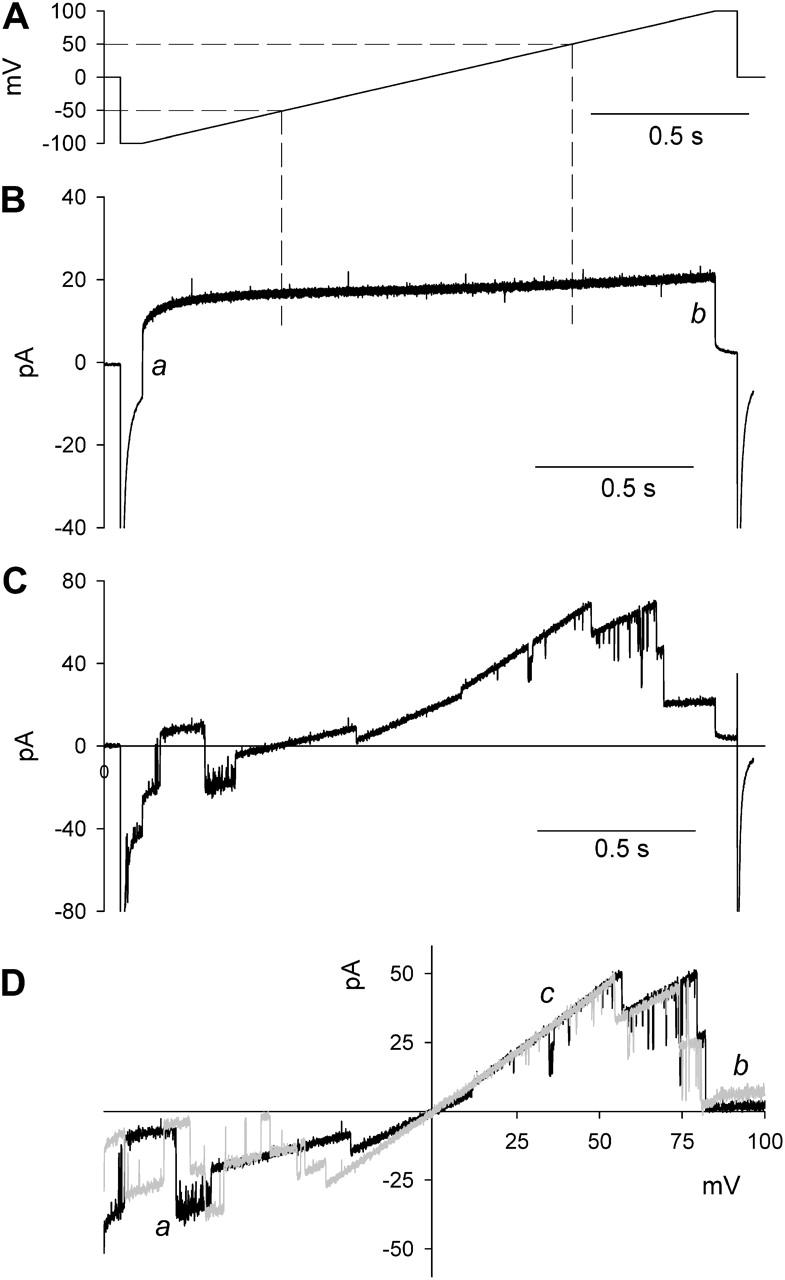
Recording protocol for OmpF conductance and selectivity measurements. (A) Voltage-ramp protocol used throughout the text. From a holding potential of 0 mV, the potential (V) was clamped at −100 mV for 0.1 s, after which V was ramped to 100 mV in a little less than 2 s (dV/dt = 111 mV/s). After 0.1 s at 100 mV, V was set back to 0 mV. (B) Control recording in the absence of protein with 0.1 M NaCl, pH 7.4, at both sides of the membrane. The instantaneous current jumps (ΔI) at the onset and offset of the voltage ramp, indicated by a and b, represent charging and decharging of the membrane capacitance, C_m (≈150 pF, according to ΔI = C_mdV/dt). That part of the control trace between −50 and 50 mV (dashed lines) was fit by linear regression and subtracted from traces as shown in C with OmpF in the bilayer. (C) Current trace with OmpF (EAE mutant) reconstituted in the bilayer and before correction. (D) Corrected current voltage or IV plot derived from the data in C. A second IV-plot (in gray) is shown to highlight the existence of subconductance states (indicated by a), the residual conductance after OmpF “closure” (b), and the current level with all three monomers fully open (c).

The value of the shunt resistance R_m depends on ionic conditions, notably Ca²⁺ concentration. It is essential therefore to obtain the control recording under exactly the same ionic conditions as the experimental recordings. The practical implication of this finding is that it is usually necessary to perform separate sets of experiments for each ionic condition instead of changing solutions during an experiment.

Potential differences (V) are defined as V = V_cis − V_trans. A positive (outward) current is defined as an efflux of cations from cis to trans. In experiments with predefined ionic gradient, measured reversal potentials (E_rev) were corrected for measured liquid junction potentials (LJP, mentioned in the figure legends where applicable). In addition, experiments were performed with PLBs painted under symmetrical ionic conditions and the gradient applied after membrane formation. Results rendered from both protocols were in excellent agreement.

Conductance (g) is defined as the slope conductance of the fully opened trimer protein, with equal concentrations of ions on both sides, and at 0 mV (measured over a 50-mV interval ranging from −25 to 25 mV), i.e., at E_rev. Conductance was derived from the trimeric current level (section c in Fig. 1 D) because it can be estimated precisely even in the presence of multiple subconductance states (see section a in Fig. 1 D).

Ion flux simulations

Here we consider six formal charged residues present in the constriction zone of WT OmpF: K16, R42, R82, R132, D113 and E117. It was assumed that the arginines (pK = ∼12) and lysines (pK = ∼10.4) all have charge +1 e and the glutamates and aspartates (pK = ∼4.4) all have a charge of −1 e, i.e., these residues are assumed to be either fully protonated or ionized (Varma and Jakobsson, 2003; cf. Karshikoff et al. 1994). Apart from these six charged residues in the constriction zone of OmpF (with a net charge of +2 e), negatively charged amino acids positioned in the entrance of the channel line the pore wall and contribute to the overall net negative electrostatic potential, thereby causing WT OmpF to be slightly cation-selective (Im and Roux, 2002a; Philippsen et al., 2002). It is for this reason that molecular dynamics calculations consistently included a surplus of monovalent cations (Suenaga et al., 1998; Tieleman and Berendsen, 1998; Im and Roux, 2002b). To make WT also behave as a (slightly) cation-selective channel during our calculations, we assumed the existence of three additional negative fixed charges, resulting in a net charge of −1 e. These three residues are supposedly always present, i.e., in WT and in mutant protein, are thought to be smeared out uniformly over the wall of the selectivity filter and therefore not modeled explicitly. The net charge of WT and the recombinant proteins used in this study are listed in Table 1. Experiments at pH 3 and 9 confirmed the ionization state of the residues involved (see also Nestorovich et al., 2003). Whereas recordings at pH 9 were essentially identical to those at pH 7.4, differences between WT and mutant protein vanished at pH 3, presumably because the newly introduced glutamates were protonated (“neutralized”) at such acidic pH (results not shown).

TABLE 1.

OmpF mutants used in this study that affect formal pore charge

Strain	Mutations	Charge*
Wild-Type		−1e
C	R82C	−2e
AAA	R42A, R82A, R132A	−4e
EAE	R42E, R82A, R132E	−6e
LEAE	K16L, R42E, R82A, R132E	−7e

^*Including a space charge of −3 e in WT and mutant protein.

Conductances, all in symmetrical solutions, were computed using a combination of density functional theory (DFT) and Poisson-Nernst-Planck (PNP) theory. Local excess chemical potentials of particles computed in the DFT are incorporated into the chemical potentials of the ions and water; these chemical potentials were included in the PNP description of ion flow. The approach followed has been described in detail in Gillespie et al. (2002b, 2003). The crowded charge term in the CSC model depends steeply on the volume of the pore, i.e., the amount of crowding, as one would expect intuitively. Therefore, apart from the fixed charge, another critical input parameter of CSC is the volume of the selectivity filter. Although we do not have the crystal structures of these mutant OmpF proteins at hand, we will nevertheless make an estimate of the filter volume involved. Fig. 2 shows a top view (A) and a side view (B) of a model of the EAE mutant with E42, A82, E132, D113, and E117 indicated. This model was created by simply substituting the side chains of the implicated residues without further refinement of any kind. Distances between the oxygens of E42 and D113 and between the oxygens of E117 and E132 are ∼1.6 nm. Based on these numbers, we hypothesized the pore to be formed by a cylinder with a radius of 0.8 nm and a length of 1 nm, enclosing a volume of ∼2 nm³. This central part is flanked by two symmetrical, conical atria (1 nm long, cone angle 45°) and embedded in a membrane 3 nm in thickness. The carboxylate groups of D113 and E117 and the guanidinium groups of K16, R42, R82, and R132 are represented as charged spheres 0.45 nm in diameter. These formal charged residues of Table 1 are modeled as ions that are confined to the cylindrical part of the pore but are otherwise free to move within the cylinder. The mobile, permeating ion species are represented as charged hard spheres (using the crystal diameters given in Table 1 of Nonner et al., 2000), and water as uncharged spheres (diameter 0.28 nm) in a uniform dielectric with a relative permittivity of 80. The diffusion coefficients are assigned bulk values, except in the cylindrical region of the pore; here, D_Na, D_Ca, and D_Cl (in 10⁻¹¹ m² s⁻¹) were 6, 0.6, and 6 (WT), or 1.5, 0.2, and 1.5 (EAE and LEAE), respectively. The ratio of D_Na and D_Ca in the pore was chosen to be ∼10 (D_Na/D_Ca = 2 g_Na/g_Ca; see Gillespie and Eisenberg, 2002) and inferred from a measured g_Na of ∼2.5 nS (in 1 M NaCl, see Table 2) and a g_Ca of ∼0.5 nS (in 0.1 M CaCl₂, see Fig. 8 A). Conductances were computed from the current at 10 mV applied potential and the DFT-PNP equations were solved as described in Gillespie et al. (2002b).

FIGURE 2.

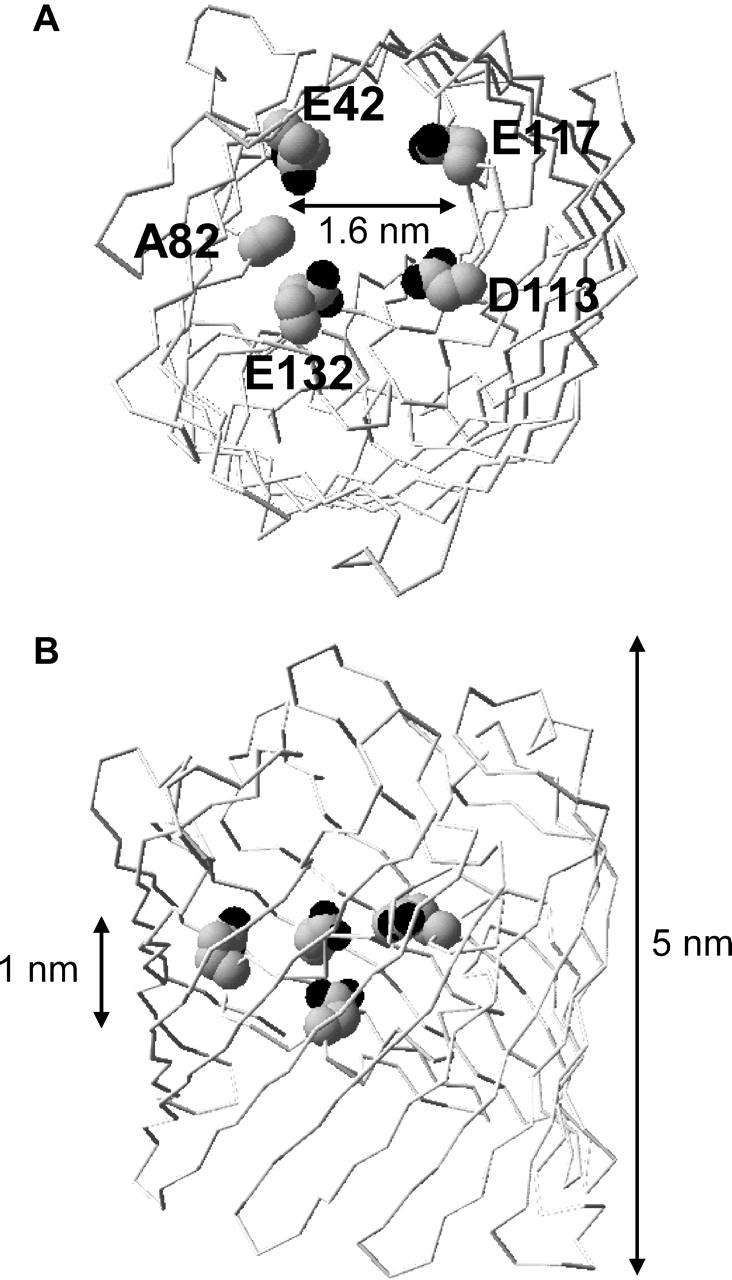
The constriction zone of the EAE mutant. Top (A) and side view (B) of a single monomer. The distance between the oxygens (all in black) of E42 and D113 and between the oxygens of E117 and E132 is ∼1.6 nm, indicating that all eight oxygens of E42, D113, E117, and E132 are positioned within a radius of 0.8 nm (top view in A) and within a plane of ∼1 nm (lateral view in B). Images were prepared in SwissPdbViewer 3.6b3.

TABLE 2.

Trimeric conductance (g) in nS in KCl and NaCl solutions

Symmetrical 0.1 or 1 M NaCl, pH 7.4
Strain	0.1 M	n	1 M	n
WT	0.50 ± 0.04	5	2.39 ± 0.09	8
AAA	ND*		ND*
EAE	0.80 ± 0.03	8	2.67 ± 0.03	6
LEAE	0.92 ± 0.05	5	2.84 ± 0.07	5
Symmetrical 0.1 or 1 M KCl, pH 7.4
Strain	0.1 M	n	1 M	n
WT	0.82 ± 0.07	11	4.20 ± 0.12	17
AAA	1.32 ± 0.04	9	4.58 ± 0.10	11
EAE	1.23 ± 0.04	9	4.61 ± 0.17	9
LEAE	ND*		ND*

^*Not determined.

FIGURE 8.

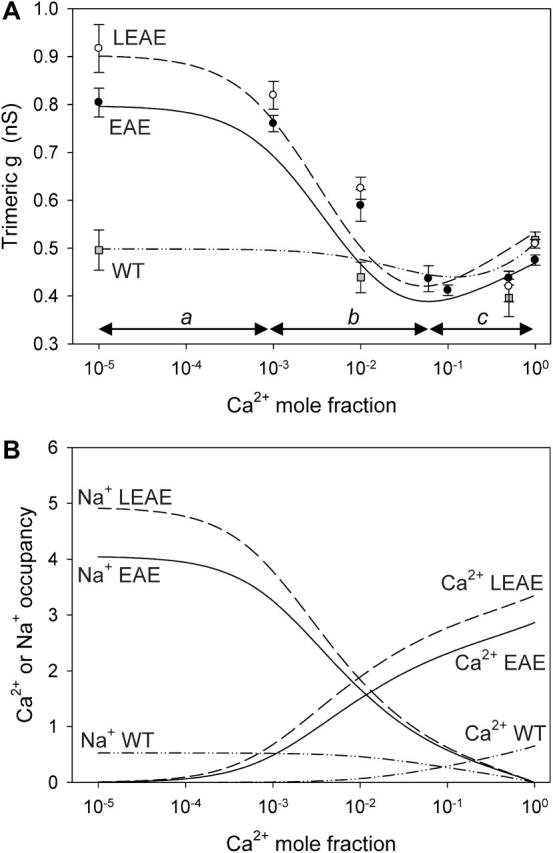
(A) Trimeric conductance (g) of WT and (L)EAE in mixtures of NaCl and CaCl₂, pH 7.4 (with Na⁺ + Ca²⁺ kept constant at 0.1 M), as a function of the mole fraction of Ca²⁺ (symbols). Each data point is based on at least five independent measurements. Curves represent simulated DFT-PNP data. The data points plotted over the left end of the abscissa were obtained with solutions that contained no added Ca²⁺. The Cl⁻ content of the solutions experimentally tested increased from left to right from (in mM) 74.1 (Ca²⁺ MF = 0) to 145.3 (Ca²⁺ MF = 1). (B) Number of Ca²⁺ and Na⁺ ions that on average occupy the pore of a single monomer in relation to the Ca²⁺ mole fraction.

Theoretical considerations were restricted to conductance calculations under symmetrical ionic conditions. Although the ratio of D_Na and D_Ca was estimated from experimentally obtained data, their absolute values remain unknown. The theory computes partitioning but not diffusion coefficients; the latter belong to the input parameters needed to calculate the flux. The shape of anomalous mole fraction effect (AMFE) curves as in Fig. 8 A is determined by the Ca²⁺ dependence of the Na⁺ current which, in turn, depends on the partioning of both ion species in the channel pore. Diffusion constants, on the other hand, only scale the conductance without affecting the overall shape. Therefore the flux calculations are far less prone to the (more or less) arbitrarily chosen numerical values of the diffusion constants inside the channel than E_rev calculations. In the latter, diffusion coefficients may have qualitative effects, i.e., they can swing the polarity of E_rev, and for that reason E_rev calculations were omitted.

RESULTS

Selectivity of cations versus anions

The monovalent cation versus anion selectivity of WT and mutant OmpF protein was estimated using a NaCl gradient (1 // 0.1 M, pH 7.4). Fig. 3 A plots E_rev versus the net charge of the lumen of the channel (see Materials and Methods and Table 1) with the theoretical equilibrium potential of Na⁺ indicated (E_Na = −49 mV). The introduction of more negative charge into the selectivity filter makes the protein more cation-selective. The mutations that replace positive charge by negative charge, or add negative charge, increase the conduction of Na⁺ over that of Cl⁻, an effect translated into a shift of E_rev toward E_Na and away from E_Cl of 49 mV. Fig. 3 B summarizes reversal potentials measured for a 1 // 0.1 M salt gradient using a different alkali metal ion, K⁺. The effects of the charge mutations are in the same direction as seen for Na⁺, but are smaller. The results with NaCl and KCl gradients are consistent with an electrostatic mechanism: cations are attracted to, and anions are repelled from, the pore as electronegative residues are introduced.

FIGURE 3.

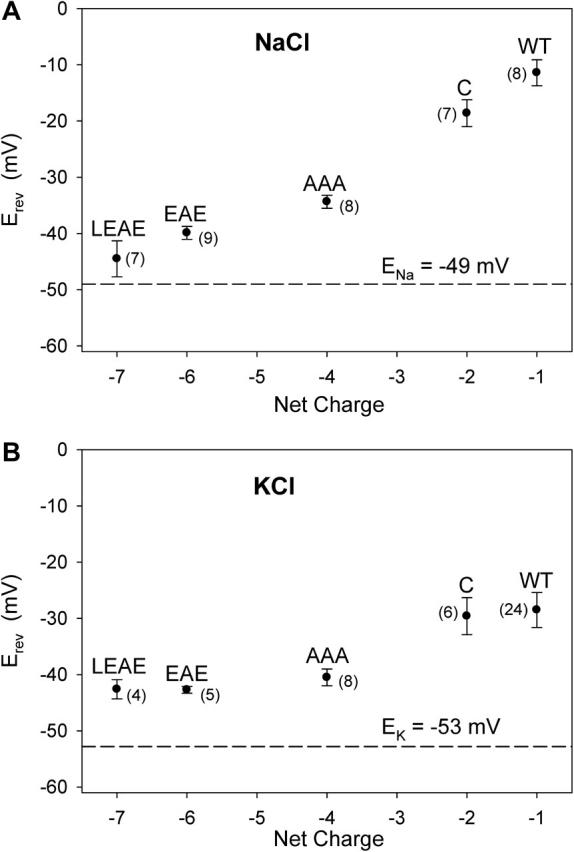
(A) Na⁺ over Cl⁻ selectivity. Measured reversal potentials (E_rev) recorded in 1 // 0.1 M NaCl (cis/trans), pH 7.4, are plotted against the net fixed charge in the lumen of OmpF porin. Nernst potential of Na⁺ (E_Na = −49 mV) and Cl⁻ (E_Cl = 49 mV) are based on ion activities of (in mM) Na⁺ = Cl⁻ = 74.1 (0.1 M NaCl) and Na⁺ = Cl⁻ = 514.2 (1 M NaCl). (B) K⁺ over Cl⁻ selectivity. Similar data as in A but with 1 // 0.1 M KCl, pH 7.4. Ion activities were (in mM) K⁺ = Cl⁻ = 77.2 (0.1 M KCl) and K⁺ = Cl⁻ = 620.1 (1 M KCl), resulting in an E_K of −53 mV and an E_Cl of 53 mV. Where appropriate, values of E_rev in A and B have been corrected for an LJP of 11 mV and 1 mV, respectively. Number in parentheses represents the number of independent measurements the data is based on.

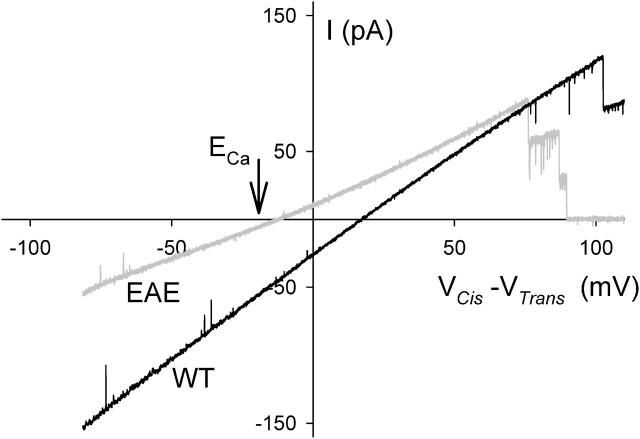
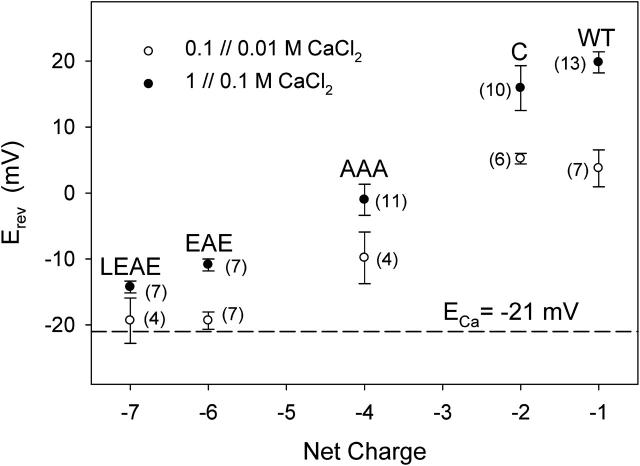
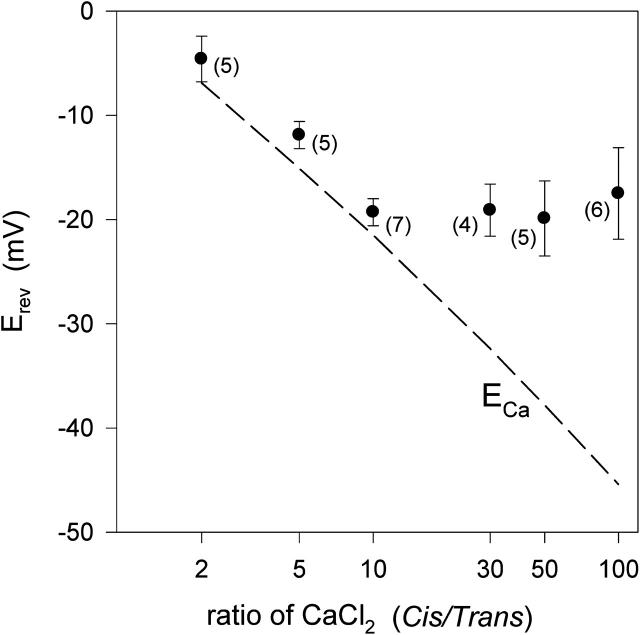
Currents recorded using a 1 // 0.1 M CaCl₂ gradient (see Fig. 4) show that E_rev of the more electronegative mutant EAE is more negative than that of WT porin. In experiments with this and the LEAE mutant, E_rev approached E_Ca as the electronegativity of the pore residues was increased (closed symbols in Fig. 5). This tendency was even stronger when a CaCl₂ gradient of lower ionic strength (0.1 // 0.01 M) was used in the test (open symbols in Fig. 5). Variation of the CaCl₂ gradient by maintaining the concentration of 0.1 M on the cis side while varying the concentration to lower values on the trans side reveal a limit in the reversal potential of ∼−20 mV (Fig. 6). It is possible that electronegative residues promote both stronger attraction but also less mobility for Ca²⁺. The effective screening of negative residues by Ca²⁺ could weaken the repulsion of the mutant pores for Cl⁻ and eventually even lead to charge inversion.

FIGURE 4.

Current traces obtained with WT (black) and EAE mutant (gray) and with 1 M CaCl₂, pH 7.4, in the cis compartment and 0.1 M CaCl₂, pH 7.4, in the trans compartment. Note the shift of E_rev into the direction of E_Ca (−20 mV) and away from E_Cl (54 mV), indicating the higher Ca²⁺ over Cl⁻ selectivity of EAE compared to WT. Data corrected for an LJP of 19 mV.

FIGURE 5.

Ca²⁺ over Cl⁻ selectivity. E_rev recorded at pH 7.4 in either 0.1 // 0.01 M (open symbols) or 1 // 0.1 M CaCl₂ (solid symbols), in relation to the net fixed charge accumulated in the pore. Indicated Nernst potential of Ca²⁺ (E_Ca) of −21 mV is the average of −22 mV (in 0.1 // 0.01 M) and −20 mV (in 1 // 0.1 M), based on the following ion activities (in mM) for the 0.01 M CaCl₂ solution, Ca²⁺ = 5.2 and Cl⁻ = 17; for the 0.1 M CaCl₂ solution, Ca²⁺ = 28.5 and Cl⁻ = 145.3 and for the 1 M CaCl₂ solution, Ca²⁺ = 137 and Cl⁻ = 1215. Where appropriate, values of E_rev in both 0.1 // 0.01 and 1 // 0.1 M have been corrected for an LJP of 19 mV. Number in parentheses represents the number of independent measurements the data is based on.

FIGURE 6.

Reversal potentials of EAE in relation to the ratio of CaCl₂, pH 7.4, in the cis and trans compartment. With 100 mM CaCl₂ in the cis compartment, CaCl₂ in trans was varied from 1 to 50 mM, resulting in gradients ranging from 2 to 100. The dashed line represents calculated equilibrium potentials of Ca²⁺. Ca²⁺ activities in the 1, 2, 3.33, 10, 20, 50, and 100 mM CaCl₂ solutions were (in mM) 0.8, 1.4, 2.2, 5.2, 8.6, 16.5, and 28.5, respectively. Measured LJPs for the 100/1, 100/2, 100/3.33, 100/10, 100/20, and 100/50 mM CaCl₂ gradient were 40, 34, 30, 20, 14, and 6 mV, respectively. Number in parentheses represents the number of independent measurements the data is based on.

Selectivity of Ca²⁺ versus Na⁺: reversal potential measurements

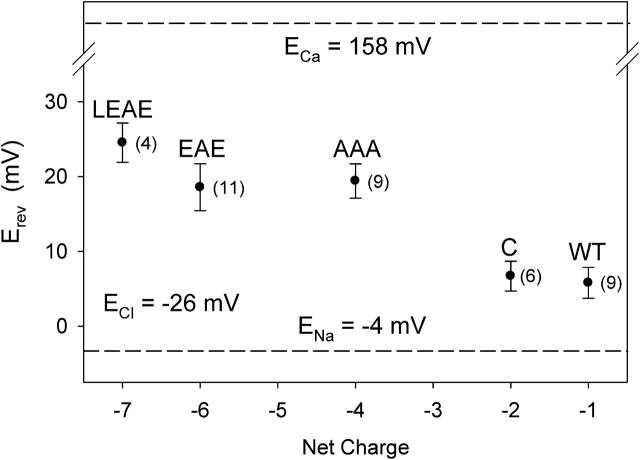
Reversal potentials measured with 0.1 M NaCl, pH 7.4, on the cis side and 0.1 M NaCl + 0.1 M CaCl2, pH 7.4, on the trans side are summarized in Fig. 7. The mutations that increase the negative charge in the pore shift E_rev away from E_Na and E_Cl and toward E_Ca, but none of the mutations produces an E_rev close to E_Ca. Similar, but smaller, shifts were observed under biionic conditions, with 0.1 M NaCl in cis and 0.1 M CaCl₂ in trans (results not shown). Given that gradients of the pure NaCl or CaCl₂ solutions indicate an increased cation over anion selectivity of the mutants (Figs. 3–5), the reversal potentials obtained under mixed or biionic conditions suggest a small but significant increase of the distinction made between Ca²⁺ and Na⁺. In L-type Ca²⁺ channels, already micromolar Ca²⁺ binds to the pore, thereby reducing (blocking) Na⁺-supported conductance (Kostyuk et al., 1983; Almers and McCleskey, 1984; Hess and Tsien, 1984). On the other hand, it needs millimolar Ca²⁺ to support substantial Ca²⁺ flow and shift E_rev significantly away from E_Na in the direction of E_Ca. In this case, the magnitude of the conductance thus is a stronger indicator of Ca²⁺/Na⁺ selectivity. To explore the possibility that our porin mutants behave the same way as the L-type Ca²⁺ channel, the next section focuses on conductance measurements.

FIGURE 7.

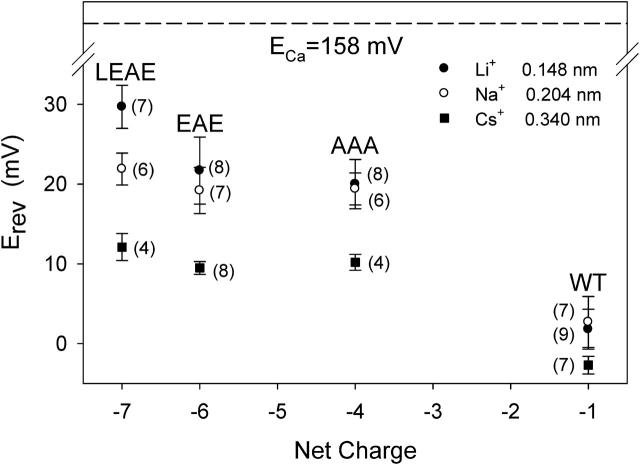
Ca²⁺ over Na⁺ selectivity. E_rev, recorded at pH 7.4 with 0.1 M NaCl in cis and 0.1 M NaCl + 0.1 M CaCl₂ in the trans compartment, in relation to the net fixed charge in the pore. Nernst potential of Na⁺ (E_Na = −4 mV) and Cl⁻ (E_Cl = −26 mV) are based on ion activities of (in mM): Na⁺ = Cl⁻ = 74.1 (0.1 M NaCl) and Ca²⁺ = 27.8, Na⁺ = 63.9, Cl⁻ = 207.6 (0.1 M NaCl + 0.1 M CaCl₂). The E_Ca value of 158 mV is an estimate assuming a contamination of the 0.1 M NaCl solution with 0.1 μM CaCl₂. Where appropriate, values of E_rev have been corrected for an LJP of −8 mV. Number in parentheses represents the number of independent measurements the data is based on.

Selectivity of Ca²⁺ versus Na⁺: AMFE experiments

Apart from a high selectivity for Ca²⁺ over Na⁺, Ca²⁺-selective channels are characterized by block of monovalent cation currents by low concentrations of divalent cations (Favre et al., 1996; Sun et al., 1997). We recorded OmpF conductance also in mixtures of NaCl and CaCl₂ and searched for block and AMFE. Because the total Na⁺ + Ca²⁺ concentrations of the solutions were constant at 100 mM, the Cl⁻ concentration varied and the AMFE experiments were necessarily not at constant ionic strength. In addition to conductance measurements (symbols in Fig. 8 A), we simulated OmpF conductance using the DFT-PNP calculations (curves in Fig. 8 A). AMFE behavior of conductance in the WT and (L)EAE proteins is clearly indicated by the nonlinear dependence of g on the mole fraction (MF) of Ca²⁺. Despite this similarity, g of WT and (L)EAE demonstrate quite a different sensitivity to the presence of low concentrations of CaCl₂. Whereas g(WT) is (almost) insensitive to the presence of 1 mM CaCl₂ (MF = 0.01), compared to g in Ca²⁺-free 0.1 M NaCl solution, at MF = 0.01 g of (L)EAE was inhibited by ∼30%. A second difference between WT and mutant proteins appears when comparing g in 0.1 M NaCl and in 0.1 M CaCl₂. Compared to its value in 0.1 M NaCl, (L)EAE conductance in 0.1 M CaCl₂ dropped by ∼42%. In contrast, WT conductance under both conditions was very similar (∼0.5 nS). Finally, in Na⁺-free 0.1 M CaCl₂ differences between g of WT and (L)EAE almost completely vanished, presumably because of the effective protein charge screening by Ca²⁺. It should be stressed that the curves in Fig. 8 A represent calculations rather than best fits to the experimental data points. We therefore conclude that the DFT-PNP approach is able to replicate experimental observations quite well.

Fig. 8 B shows the calculated number of Ca²⁺ and Na⁺ ions that, on average, occupy the pore of a single monomeric OmpF channel. Calculated numbers for Cl⁻ were on average >10 times lower than those for Ca²⁺ and Na⁺ and are therefore not shown. When bathed in pure NaCl or at low Ca²⁺ MF, the WT pore contains on average 0.5 Na⁺ ion and <0.05 Cl⁻ ion, whereas the pores of (L)EAE almost exclusively contain Na⁺. Values of g thus reflect Na⁺ passing the pore (region a in Fig. 8 A). The reduction of g that accompanies an increase in Ca²⁺-MF reflects an increase of occupancy by Ca²⁺, at the expense of Na⁺. Here we observe the hampering of Na⁺ current by bound Ca²⁺ (region b). As Ca²⁺ MF approaches unity, the WT pore carries on average only 0.5 Ca²⁺ vs. ∼3 Ca²⁺ in (L)EAE. Calcium effectively screens the fixed charge in the pore and with increasing Ca²⁺ MF, Cl⁻ repulsion becomes slightly less. Although in all three channels Cl⁻ starts to cooccupy the pore at high Ca²⁺ MF, Cl⁻ numbers in the pore of WT and (L)EAE remain low, ∼0.2. At high Ca²⁺ MF (region c), g is due to both Ca²⁺ (which has a high density but low mobility in the pore) and Cl⁻ (which has low density but high mobility in the pore). Despite the low number of Cl⁻ ions but because of its high mobility, the contribution of Cl⁻ to g translates into the measured and calculated increase of g at Ca²⁺ MF = 1.

Ca²⁺/alkali metal selectivity: reversal potential measurements

Fig. 9 compares the Ca²⁺ over alkali metal selectivity at pH 9 for three different ion species Li⁺, Na⁺, and Cs⁺. Li⁺ with an ionic radius of 0.148 nm is the smallest of the three, Cs⁺ with 0.340 nm the largest, while Na⁺ with 0.204 nm falls in between (see Nonner et al., 2000 and references therein). As is most clearly seen in the LEAE mutant, the smaller the alkali ion diameter, the higher the Ca²⁺ over alkali metal selectivity, i.e., the channel shows large-cation selectivity (see Gillespie et al., 2002c).

FIGURE 9.

Effect of monovalent cation species (Li⁺, Na⁺, and Cs⁺) on the Ca²⁺ over alkali metal selectivity at pH 9. Except for the alkali species and pH, ionic conditions were the same as in Fig. 7. E_rev values have been corrected for a LJP of −8 (with Na⁺) or −9 mV (with Li⁺ and Cs⁺). Number in parentheses represents the number of independent measurements the data is based on.

Conductance in KCl and NaCl

In a tiny system like an ion channel, the electrostatic potential is a sensitive function of all charges present (permanent and mobile) and conductance, in turn, depends on the potential profile (Eisenberg, 1996). Table 2 reports conductance measurements of WT and recombinant OmpF, obtained in symmetrical 0.1 or 1 M KCl or NaCl, pH 7.4. In both NaCl and KCl all mutants showed larger conductance than WT. Furthermore, the conductance in KCl, g(KCl), was consistently higher than the conductance in NaCl, g(NaCl). Differences between WT and mutant protein depended on the ionic strength (i.e., shielding) of the solution and were more pronounced in 0.1 than in 1 M salt solution. For instance, in 0.1 M KCl, g(EAE) is 1.5 times g(WT); but in 1 M KCl this ratio was reduced to ∼1.1. The normalized conductance (g/c, where c is concentration) shows the effects of charge and charge screening on conductance. Values of g/c in 0.1 M KCl of 8–13 nS/M were ∼2–3 times higher than those of ∼4.5 nS/M in 1 M KCl (see also Schirmer and Phale, 1999). Similar results were obtained in NaCl, though absolute values were lower.

DISCUSSION

With the substitution of up to four amino acids we introduced up to six additional negative charges in the constriction zone of OmpF and turned this essentially nonselective channel into a Ca²⁺-selective one. Most dramatic changes of selectivity to date have been found for genetically engineered anion-selective porins, e.g., the Paracoccus porin (Saxena et al., 1999) and Omp34 (Brunen and Engelhardt, 1995). However, these porins changed their selectivity from slightly anionic to slightly cationic. In the case of OmpF, an essentially nonselective porin has been turned into a highly cation-selective one.

As is apparent from the AMFE experiments in Fig. 8 A, against a background of 0.1 M NaCl the (L)EAE mutants have a millimolar affinity for Ca²⁺. Mutant OmpF and other “true” Ca²⁺ channels conduct cations perfectly well in either Ca²⁺- or Na⁺-free solutions and the disproportional inhibition of Na⁺ current by minute amounts of Ca²⁺ is one of the most remarkable features of Ca²⁺-selective channels. In mixtures of both ion species and with Ca²⁺ MF >0.01, Ca²⁺ predominantly occupies the pore (Fig. 8 B). The strong inhibition of Na⁺ current by low levels of Ca²⁺ seen in the (L)EAE mutants is due to a combination of the high affinity for Ca²⁺ (i.e., high partitioning), the lower Ca²⁺ diffusion rate inside the channel, and the low bulk Ca²⁺ concentration which limits the displacement of Ca²⁺ by another Ca²⁺.

In contrast to the clear picture arising from the AMFE data, the E_rev measurements of Fig. 7 show little Ca²⁺ over Na⁺ selectivity. The E_rev and AMFE experiments are not contradictory, however. In an analysis of a simple channel model, Gillespie and Eisenberg (2002) showed that E_rev includes at least two components. These partitioning and diffusive components measure ease of entrance into the channel and ease of movement through the channel, respectively, and can counterbalance each other. In other words, even though the additional negatively charged residues increase the partitioning of Ca²⁺ in the (L)EAE pore, these pores are more sticky to Ca²⁺, which in turn slows down the Ca²⁺ throughput rate, overall reflected in relatively small changes in E_rev.

Ca²⁺/alkali metal selectivity

Mutant OmpF shows the highest Ca²⁺ selectivity in the presence of the smallest alkali ion species, Li⁺, i.e., the channel is large-ion selective (Fig. 9). The L-type Ca²⁺ channel, on the other hand, shows a selectivity sequence that is exactly opposite and with Ca²⁺ selectivity highest in the presence of Cs⁺, i.e., small-ion selectivity (Nonner et al., 2000). With an estimated filter volume of 2 nm³ (see Materials and Methods), the filter volume of OmpF is more than five times that of the L-type Ca²⁺ channel (0.375 nm³, see Table 3). Only if space inside the selectivity filter is limited will small cations be favored (according to the theory) and only then do we expect to see small-ion selectivity as in the L-type Ca²⁺ channel. Also, numerous apolar residues line the channel wall of OmpF. Selectivity for large ions can then arise because of the (slightly) lower water density inside the channel causing larger ions to partition into the filter (Gillespie et al., 2002c).

TABLE 3.

Comparison of the L-type and RyR Ca²⁺ channels and mutant OmpF

Ca2+ channel type	Volume nm3	g in CaCl2 pS	DNa/DCa in filter	PCa/PNa	[Ca2+] to reduce g by 50%
L-type*	0.375	10 (saturated)	20	100	≈1 μM
RyR†	0.380	150 (in 50 mM)	≈10	5–7	≈5 mM
(L)EAE	2	158 (in 100 mM)‡	10	3–4¶	>1 mM

^*See Nonner and Eisenberg (1998) and references therein.

^†See Chen et al. (2003) and references therein.

^‡Monomeric conductance, see Fig. 8A.

^¶This study, under biionic conditions, 0.1 M NaCl // 0.1 M CaCl₂, pH 7.4 (unpublished results).

A discussion of alkali selectivity in this channel probably is complicated by the possibility that different species of ions can access different permeation paths in this large pore. Small alkali ions might be restricted to paths close to the negatively charged groups, whereas large alkali ions (and Cl⁻) might be able to access regions farther away from these groups due to the effects described by Gillespie et al. (2002c). Thus there might exist pathways for larger ions that are unavailable for smaller ions—so that larger ions, in effect, experience a wider pore. Screening of the negatively charged groups by Ca²⁺ then could reduce currents carried by small cations to a larger extent than currents carried by large cations, in contrast to the characteristics of Ca²⁺ block seen in L-type Ca²⁺ channels.

It is worth noting that the large-ion selectivity we find with mutant OmpF seems to disagree with the cation over anion selectivity of OmpF as reported recently (Danelon et al., 2003). This shows a selectivity sequence of LiCl > NaCl > CsCl, indicating OmpF acting as a small cation-selective channel, but it should be stressed, first, that this was a study on WT OmpF and, second, that Danelon et al. (2003) tested for Ca²⁺ over Cl⁻ selectivity rather than Ca²⁺ over alkali metal selectivity.

OmpF and CSC

Although it does not come as a surprise that the introduction of extra negative charge made OmpF more cation-selective, the observed rather high affinity for Ca²⁺ of (L)EAE containing the DEEE-locus should not be considered a trivial finding. The EEEE locus has been thought of as a diagnostic for Ca²⁺ selectivity but this view is challenged by recent findings on a bacterial Na⁺ channel, NaChBac (Ren et al., 2001; Yue et al., 2002). Despite the presence of the EEEE-locus, NaChBac is nevertheless Na⁺-selective. Apparently, the mere presence of the EEEE-locus does not guarantee Ca²⁺ selectivity per se (Catterall, 2001).

Even though the (L)EAE mutants may have more negative fixed charge accumulated in their filter volume than the L-type Ca²⁺ channel, the Na⁺ current through the latter is a thousand times more sensitive to added Ca²⁺. In the CSC model of Ca²⁺-selective channels, several parameters affect Ca²⁺ selectivity: volume, dielectric coefficient, and the number and size of the charged amino acid residues of the selectivity filter. The dramatic difference between the filter volume of the L-type Ca²⁺ channel and OmpF can explain the difference in the Ca²⁺ affinity between these two channel types. As found for the L-type Ca²⁺ channel, micromolar Ca²⁺ affinity is a steep function of filter volume and has already disappeared at 1.2 nm³. Thus, even without knowledge of dielectric properties of these channels, the experiments performed here confirm that high Ca²⁺ selectivity is not possible when the selectivity filter volume is large. In this context, it seems hardly coincidence that of all porins the one with the narrowest constriction zone, i.e., Omp34, is also the most selective (Zachariae et al., 2003).

According to CSC, Ca²⁺ selectivity in the L-type Ca²⁺ channel is produced by both electrostatics and excluded-volume effects due to the small size of the filter. Chloride, in particular, is rejected by both electrostatics and its relatively large size (compared to the cations). Considering the significantly larger filter volume of (mutant) OmpF protein, anion rejection seems predominantly based on electrostatics rather than excluded-volume effects. This conclusion is confirmed by the observation that the selectivity in CaCl₂ decreases with increasing ionic strength of the solution (Fig. 5).

But differences in filter volume might not tell the complete story. Table 3 compares the characteristics of three Ca²⁺-selective channels, the L-type Ca²⁺ channel, the ryanodine receptor Ca²⁺ channel (RyR) and (L)EAE. Remarkably, even though the estimated filter volume of (L)EAE is ∼5 times that of RyR, both channels show very similar characteristics (see Chen et al., 2003, and references therein): a high unitary Ca²⁺ conductance, a low Ca²⁺ over Na⁺ selectivity, and an amount of Ca²⁺ needed to reduce the monovalent cation current in the millimolar range. On the other hand, although the L-type Ca²⁺ channel and RyR have very similar estimated filter volumes (∼0.38 nm³), the Ca²⁺ affinity of RyR is more than three orders of magnitude lower. This observation may reflect the fact that both types of channels belong to an entirely different superfamily of ion channels with different global structures. Whereas the L-type Ca²⁺ channel comprises four homologous but not identical domains, the four domains of RyR are identical.

While the general properties of the OmpF mutants presented in this article can be explained in terms of the CSC model, each specific mutant is difficult to model exactly. Simplified equilibrium models that use bulk-liquid approximations (Nonner et al., 2000, 2001) or nonequilibrium models that use density functional theory (Gillespie et al., 2002b) rely on having the amino acid residues of the selectivity filters extend into the permeation pathway. The large selectivity filter of the OmpF mutants, however, invalidates this assumption. As a result of this, full three-dimensional models must be applied. Although molecular dynamics should be able to include the protein's dielectric properties, it cannot produce the current voltage curves needed to compute reversal potentials. Brownian dynamics can, in principle, fill this gap, but without the dielectric and elastic properties of the protein as inputs, Brownian dynamics is not a viable option.

CONCLUSION AND PERSPECTIVE

Considering the large pore diameter and the consequent lack of ion crowding in the (L)EAE pore, the high selectivity of these mutants is quite remarkable and emphasizes the role of electrostatics in ion selectivity. Anions are rejected from the pore (almost) exclusively by the electrostatic barrier originating from the four negatively charged residues in (L)EAE, whereas excluded volume effects and crowded charge terms that dominate the selectivity of the L-type Ca²⁺ channel are here of minor importance. The CSC model identifies the fixed charge and volume of the selectivity filter to be key determinants of ion selectivity whereas the precise orientation and positioning of the residues in the three-dimensional space of the filter are surprisingly irrelevant. The data presented here support this view. The (L)EAE mutants have more negative fixed charge accumulated in their filter volume than the L-type Ca²⁺ channel (−6 e or −7 e vs. −4 e) but the Na⁺ current through the latter is nevertheless a thousand times more sensitive to added Ca²⁺. Given the much larger filter volume of the porin mutants, this is exactly what CSC predicts: to impose Ca²⁺ selectivity on the OmpF porin, the introduction of an EEEE-locus alone does not suffice, the filter volume has to be taken into account as well. Although this study thus fits in the framework of CSC theory, it should not be considered as an attempt to prove or disprove CSC. Not only are the three-dimensional structures of mutant OmpF protein not known, but two other key parameters remain unknown, namely the permittivity and diffusion constants inside the pore. It seems to us, however, that the experimental findings fit well enough within CSC theory to provide useful guidelines for future mutations of OmpF and possibly other ion channel types as well.