Coupling Field Theory with Mesoscopic Dynamical Simulations of Multicomponent Lipid Bilayers

Abstract

A method for simulating a two-component lipid bilayer membrane in the mesoscopic regime is presented. The membrane is modeled as an elastic network of bonded points; the spring constants of these bonds are parameterized by the microscopic bulk modulus estimated from earlier atomistic nonequilibrium molecular dynamics simulations for several bilayer mixtures of DMPC and cholesterol. The modulus depends on the composition of a point in the elastic membrane model. The dynamics of the composition field is governed by the Cahn-Hilliard equation where a free energy functional models the coupling between the composition and curvature fields. The strength of the bonds in the elastic network are then modulated noting local changes in the composition and using a fit to the nonequilibrium molecular dynamics simulation data. Estimates for the magnitude and sign of the coupling parameter in the free energy model are made treating the bending modulus as a function of composition. A procedure for assigning the remaining parameters in the free energy model is also outlined. It is found that the square of the mean curvature averaged over the entire simulation box is enhanced if the strength of the bonds in the elastic network are modulated in response to local changes in the composition field. We suggest that this simulation method could also be used to determine if phase coexistence affects the stress response of the membrane to uniform dilations in area. This response, measured in the mesoscopic regime, is already known to be conditioned or renormalized by thermal undulations.

INTRODUCTION

The coupling between curvature and internal degrees of freedom is responsible for many shape transformations in biological membranes (Lipowsky, 1991; Sackmann, 1994). One example of such a coupling is echinocytosis, where a human red blood cell undergoes a transition from a biconcave shape to a crenated shape induced by an asymmetric adsorption of drugs into the two membrane monolayers (Sheetz et al., 1976). Another example, which is perhaps more relevant to our study, is giant unilamellar vesicle (GUV) budding induced by lateral phase separations within a closed lipid bilayer membrane composed of several molecular species (Jülicher and Lipowsky, 1993; Sackmann and Feder, 1995; Lipowsky and Sackmann, 1995; Baumgart et al., 2003). During budding, the interface between the two phases is located in a narrow neck interconnecting the mother and daughter cells. Provided the energy required to form a region of curvature at one phase is not large in comparison to the energy required to have an interface between two phase domains, the overall free energy of the membrane can be reduced by having a smaller, daughter vesicle of one phase sprout from the larger, mother vesicle of the other phase. Budding is sometimes the precursor to membrane fission; as a result, this phenomenon has received much attention. Experimentally, lipid domains in vesicles have been directly visualized using electron, two-photon excitation fluorescence, and confocal fluorescence microscopy techniques (Parasassi and Gratton, 1995; Bagatolli and Gratton, 1999, 2000a,b). Furthermore, the phases themselves have been characterized by fluorescence correlation spectroscopy, which monitors the translational diffusion of a fluorescent probe, typically 3,3′-dioadecylindocarboncynine (Korlach et al., 1999).

One motivation for studying GUVs is to understand the origins of the various shape changes in a biological vesicle subjected to variations in external conditions such as temperature, and internal conditions such as composition, at the different regions in a membrane (Baumgart et al., 2003). Composition is related to the concentrations of the different constituent molecules in the bilayer. A real, biological membrane has far more structure than an artificially synthesized GUV; for example, a biological membrane is supported by a cytoskeleton. Nonetheless, because of their simple structure, GUVs have been examined to simplify the identification of important physical mechanisms that might contribute to shape changes observed in real cells. Lateral phase separation is believed to be one of these mechanisms. Recent theoretical studies performed by Taniguchi (1995) and Jiang et al. (2000) have focused on determining the dominant, equilibrium states of a two-component membrane in the macroscopic regime by minimizing a Helfrich free energy model (Helfrich, 1973) extended to include composition as a degree of freedom. Here the membrane is treated as a continuum, that is, as a two-dimensional surface embedded in a three-dimensional space. Jiang et al. (2000) found these minima by solving analytically an equation where the gradient of the chemical potential associated with the free energy model is set to zero at all points on the membrane. Alternatively, Taniguchi (1995) found these minima by numerically integrating the Cahn-Hilliard (CH) equation (Cahn and Hilliard, 1958). Here the dynamics of the composition field (the composition at all points on the membrane) is driven by a diffusive flux, which is proportional to the gradient of the chemical potential (Langer, 1971; Castellano and Glotzer, 1995; Taniguchi, 1995; Kumar and Rao, 1998; Groves et al., 2000; Jiang et al., 2000). Some mixtures exhibit phase coexistence across a range of composition values, so the free energy model is made sufficiently general to allow for the possibility of phase separation. These studies have reproduced some of the vesicle structures seen in recent experiments on three-component GUVs (Baumgart et al., 2003).

Phase diagrams deduced from calorimetric, ESR, and SANS experiments on two-component membranes composed of DMPC and cholesterol suggest that these mixtures can phase-separate into coexisting liquid crystalline and fluid phases across a wide range of cholesterol mole fractions (Recktenwald and McConnell, 1981; Knoll et al., 1985; Vist and Davis, 1990; Almeida et al., 1992). However, although lateral phase separation has been observed directly using fluorescence microscopy for binary cholesterol lipid monolayers (Subramanian and McConnell, 1987; Keller and McConnell, 1999), phase domains have not been observed for binary cholesterol lipid bilayers. Ternary bilayer mixtures composed of cholesterol along with saturated and unsaturated lipids have exhibited binary phase separation (Dietrich et al., 2001; Baumgart et al., 2003) where it has been suggested that a cholesterol molecule becomes strongly correlated or binds with the unsaturated lipids to form a complex (Radhakrashnan et al., 2000). A simple theoretical model might suppose that each cholesterol molecule irreversibly dimerizes with a single unsaturated lipid so that the membrane behaves effectively as a two-component bilayer mixture where one of the components is now a complex (Komura et al., 2004). The material properties of these bilayer mixtures in GUVs have been measured using micropipette suction or pressurization (Kwok and Evans, 1981; Evans and Needham, 1987; Needham and Evans, 1988; Mui et al., 1993). These experiments show that even small amounts of cholesterol can dramatically change the stretching and bending elasticities of the membrane (Needham and Nunn, 1990). Equilibrium and nonequilibrium molecular dynamics (EMD and NEMD) simulations of atomistic model bilayers have also shown that the microscopic bulk modulus, λ, is affected by the addition of cholesterol to a membrane composed of primarily DMPC (Smondyrev and Berkowitz, 2001; Ayton et al., 2002b). In particular, λ increases with an increase in the concentration of cholesterol. The microscopic bulk modulus is a measure of the stress response of a small microscopic volume of bilayer with dimensions 3–10 nm to a local, isotropic in-plane strain: the stress, σ, is related to the strain, ε, via the constitutive relation, σ = 2λε (Evans and Needham, 1987). Across longer length scales, however, the stress versus strain curve of a GUV determined experimentally is nonlinear at low strains or surface area dilations (Rawicz et al., 2000). This nonlinear behavior is thought to be related to the existence of subvisible (not directly visible by microscopy) thermal ripples or bending modes (Evans and Rawicz, 1990, 1997). At low strains, the apparent, projected area is less than the actual, nonprojected area because of thermal undulations of the membrane's surface. The stress response of a mesoscopic volume of bilayer with dimensions 20–100 nm to a change in apparent area contains a contribution from the intrinsic, in-plane local area changes and a contribution from the force required to either smooth or buckle the membrane's surface. The stress response becomes linear once these soft bending modes are removed and the apparent area approaches the actual area. Therefore, the mesoscopic bulk modulus, λ_meso, characterizing this mesoscopic response, is not the same as the microscopic bulk modulus, λ: the stress response is conditioned by the existence of thermal undulations. The theoretical studies performed by Taniguchi (1995) and Jiang et al. (2000) do not treat thermal undulations; these studies do not examine how the material properties of a membrane are conditioned by thermal undulations and the coexistence of phase domains whose spatial dimensions are mesoscopic in size.

To theoretically verify whether these undulations do indeed affect the material properties of a membrane, various simulation strategies can be employed. Large-scale atomistic molecular dynamics (MD) simulations with length scales on the order of 20 nm have been performed (Lindahl and Edholm, 2000a,b). System sizes of this magnitude are required to remove finite size effects arising from periodic boundary conditions. With simulation box lengths on the order of the membrane thickness, 3–5 nm, these conditions inhibit the production of any long-wavelength, thermal bending undulations. Presently, to perform atomistic MD simulations with length scales on the order of 100 nm, electrostatic interactions are truncated (Marrink and Mark, 2001). However, it is known that transport properties such as the shear viscosity can be sensitive to these truncations (Wheeler et al., 1997). Alternatively, mesoscopic simulation methods such as dissipative particle dynamics (DPD) can examine longer length- and timescales (Espanol and Warren, 1995; Groot and Warren, 1997). However, the soft particle interactions employed in DPD allow particles to pass through one another; this might yield a large viscous response to uniform changes in area in comparison to the elastic response. Therefore, to bridge the gap between the microscopic regime, with length- and timescales on the order of 3–10 nm and several nanoseconds, and the mesoscopic regime, with length- and timescales on the order of 100 nm and 100 ns, we require a simulation method that accurately accounts for the effects of electrostatic particle interactions and accurately depicts the material behavior of the membrane subjected to various surface deformations.

One approach to overcoming these two simulation problems has been to abandon the molecular-level detail and instead adopt a coarse-grained description. The material properties of the membrane (for example, λ) are measured using microscopic atomistic EMD and NEMD simulations, and subsequently employed to parameterize effective forces between points in a mesoscopic, elastic membrane (EM) model (Ayton and Voth, 2002). Within the EM model, a membrane is decomposed into pseudoparticles that do not represent coarse-grained molecular models (Shelley et al., 2001; Marrink and Mark, 2003), but rather are more like continuum-level volumes that interact via a predetermined constitutive relation. The EM model is essentially a discretized constitutive model where interactions between neighboring points reproduces the microscopic stress response, σ, of a small, microscopic volume of bilayer to a local, in-plane isotropic strain, ε. In turn, the mesoscopic stress response of a patch of membrane with dimensions on the order of 20–100 nm can be determined by evaluating a virial expression for the pressure that incorporates the effective, constitutive forces.

In this article, we are interested in examining the dynamics of a composition field integrated in time over a thermally undulating surface. The EM model represents a computationally simple means for generating these undulations. For a membrane composed of many molecular species, an EM particle (point) can carry information about the composition at a particular region in space. Composition within the model is treated as an extended degree of freedom with its own governing equation of motion, the CH equation (Cahn and Hilliard, 1958). The strength of the bonds in the EM model can then be modulated given the dependence of the microscopic bulk modulus on composition (Ayton et al., 2002a,b). Again our main objective is to demonstrate how the dynamics of a composition field can be coupled to mesoscopic membrane surface dynamics that exhibits significant thermal undulations. The EM model serves as a tool for demonstrating our strategy; the EM model can be extended or replaced by another mesoscopic membrane model provided this new model and its accompanying dynamics generates accurate thermal undulations. For simplicity and the purpose of demonstration, we treat our two-component bilayer as if it could exhibit lateral phase separation; however, we stress that this phase separation has been exhibited for cholesterol lipid bilayers with at least three components. As a result, to obtain predictive results in the future our method should be generalized to accommodate more than just two components.

The remainder of this article is organized as follows. In Theory, we present the CH equation and its application to a membrane with a quasiplanar geometry. In Simulation Methodology, we describe the simulation methodology where the curvature and composition fields are coupled within the existing framework of the EM model; this model is reviewed in Appendix B. In Parameters, we give a procedure for systematically assigning approximate/reasonable values to all parameters in the free energy model. The present model omits the effects of the solvent on the motion of the thermal undulations; we describe the possible consequences of this omission and how the values of some model parameters can be adjusted to compensate. Finally, in Results, we present our simulation results, which should highlight some notable features of the dynamics. For a simulation of a critical quench producing a phase separation, we observe the effects of the dynamical feedback between the curvature and composition fields on the overall curvature of the membrane (the square of the mean curvature averaged over all EM points) and the local curvature at one of the two coexisting phases (the square of the mean curvature averaged over all EM points within a given phase). Finally a table of symbols, Table 1, has been included for the reader's convenience.

TABLE 1.

Essential symbols

Variable	Description
λ	Microscopic bulk modulus
Λ	Cubic coupling constant
Λ′	Bilinear coupling constant
h, h′	Membrane height and thickness
Fφ	Free energy of binary mixture
Ubin(φ)	Double-well potential in Fφ
FφH	Free energy of coupling
φI, φII	Locations of minima of Ubin
φc	Location of maximum of Ubin
φA	Mole fraction, A = DMPC
φB	Mole fraction, B = cholesterol
φ = φA−φB	Composition of membrane
CA, CB	Concentration, A and B
M, Dαβ	Mobility and diffusion coefficient
μ, μ*	Chemical potential and target
cl	Fourier coefficient of undulation mode
Fl	Sine/cosine function in Fourier series
rxy	Projected position on the x,y plane
kl	Two-dimensional wavevector
γL	Surface tension of membrane
Δx	Reference/input interfacial width
〈〈H2〉dmpc〉T	Curvature averaged over DMPC-rich phase
〈〈H2〉chol〉T	Curvature averaged over chol-rich phase
〈〈H2〉φ〉	Curvature averaged over “bin” of φ
Ngrid	Number of rectangular grid points

THEORY

The bilayer thickness, h′, and the microscopic bulk modulus, λ, depend on the composition, φ; later φ will be defined in terms of the concentrations of the constituent molecules in the bilayer. Composition in a microscopic, atomistic simulation is clearly a property of a collection of particles; by contrast, composition in a mesoscopic simulation is a property of a point because here a point conceptually represents a microscopic simulation cell of dimensions 3–5 nm. If we have a mesoscopic dynamics governing the composition of these points, then we can modulate the strengths of the bonds between the points in the EM model given the dependence of h′ and λ on φ estimated from atomistic EMD and NEMD simulations, respectively. We treat our membrane composed of DMPC and cholesterol as if it could undergo a lateral phase separation producing domains rich in DMPC (the liquid-disordered phase, ld) or rich in cholesterol (the liquid-ordered phase, lo) (Recktenwald and McConnell, 1981; Knoll et al., 1985; Almeida et al., 1992). In other words, our mesoscopic composition dynamics is designed to generate this phase separation and the subsequent movement of the phase domains in response to changes in the membrane's curvature, H.

The concentration of species α (either DMPC or cholesterol), C_α, satisfies the following balance equation in a local coordinate frame on the membrane's surface:

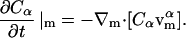(1)

Here ∇_m is the two-dimensional differential gradient operator tangent to the surface, 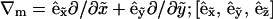is a local orthonormal basis set on the surface where 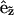is the normal unit vector. In addition, 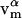is the flow or velocity of species α tangent to the membrane's surface. We emphasize that a fixed point on the membrane's surface where may not correspond to a fixed point in the lab frame if the membrane is undergoing thermal undulations. As a result, with the concentration of species α may appear to change with time in the lab frame even though ∂C_α/∂t|_m = 0 in a local frame on the membrane. Given Eq. 1 and provided the total concentration 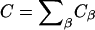is a constant, the balance equation for the mole fraction, 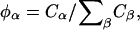of species α is

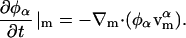(2)

The baricentric velocity, 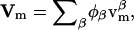is zero (deGroot and Mazur, 1962). The composition of the membrane at a point on its surface is then defined as

(3)

where A is DMPC and B is cholesterol. A membrane pure in DMPC or cholesterol has respectively φ = 1 or φ = − 1; furthermore, the DMPC-rich, ld phase occurs at φ > 0.8 (<10% cholesterol), whereas the cholesterol-rich, lo phase occurs at φ < 0.4 (>30% cholesterol) (Recktenwald and McConnell, 1981; Knoll et al., 1985; Almeida et al., 1992). If the composition averaged over all points in the membrane is between 0.4 and 0.8, then our simulation method is constructed to generate a phase separation starting with a uniform composition and ending with a mixture of ld and lo phase domains. Therefore, φ gives a measure of not only the composition of the membrane, but also some information on the structure of the resulting phase domains. Given Eq. 2, the balance equation for the composition is

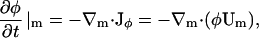(4)

where, within the diffusive flux, J_φ, we have a velocity 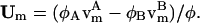If there is a net flow of material in the membrane where V_m ≠ 0, then a convective term must be added to Eq. 4 (this term is described later in Undulating Membrane; see below). Note that φ is the composition averaged over both monolayers or leaflets of our membrane. In some situations, for example a membrane composed of molecules with either conical or anticonical shapes (Lipowsky and Sackmann, 1995), φ cannot uniquely describe the state of the membrane at a point; as a result, here it is necessary to describe the composition of the membrane using two variables, φ⁽¹⁾ and φ⁽²⁾, which are the compositions of each individual monolayer.

Rather than including the species velocities in the dynamics, we write the flux in terms of a chemical potential, μ, via the constitutive relation (deGroot and Mazur, 1962)

(5)

Here μ = μ_A − μ_B is the chemical potential or free energy required to change the composition, specifically the energy required to remove a number of molecules of B = cholesterol and replace them with an equal number of molecules of A = DMPC. The constitutive coefficient, M > 0, is the mobility that can be expressed in terms of the self-diffusion constant of cholesterol at infinite dilution in a solvent of DMPC (see Parameters, below). The chemical potential in turn is written as the functional derivative with respect to φ of a free energy model, so that Eq. 4 becomes (Cahn and Hilliard, 1958; Langer, 1971; Metiu et al., 1976)

(6)

In principle, F[φ,H] is an effective, mesoscopic Hamiltonian obtained by coarse-graining the microscopic phase space integrated-over within the partition function, Z; the microscopic degrees of freedom spanning this space are weighted by a Boltzmann factor whose microscopic Hamiltonian represents the kinetic energies and potential interactions of the molecules in the system (Gunton et al., 1983). The partition function associated with F[φ,H] is

(7)

The curvature field, H, describes the texture of the membrane's surface, and 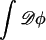is a field integral over all possible composition fields. The dominant contributions to this field integral come from those fields φ where δF/δφ = μ*. In practice, F[φ, H] is set to a physically reasonable phenomenological model. In turn, Eq. 6 is used to model the phase separation dynamics of a membrane suddenly quenched from a high temperature to a low temperature, T. Initially the membrane composition, φ, will be homogeneous but then, provided φ lies between the coexistence curves of the ld and lo phases, a phase separation occurs that is coupled to the membrane's curvature. We assume that after being suddenly quenched the membrane reaches thermal equilibrium much faster than phase equilibrium; in other words, we assume that the phase separation is driven by gradients in the chemical potential, μ, not the temperature. The CH dynamics drives μ toward a target chemical potential, μ*. If we are primarily interested in the movement of the phase domains in response to changes in the curvature field, H, and how this movement in turn affects H, then, at late times after the quench, Eq. 6 should give an accurate picture of this movement. The parameters in F[φ, H], which depend on T, are assigned values commensurate with what is known about the near-equilibrium phase domain structure obtained from atomistic MD simulations and experiment.

Equation 6 is the Cahn-Hilliard (CH) equation (Cahn and Hilliard, 1958) where F[φ, H] = F_φ + F_φH. The contribution to F from there being a binary mixture is

(8)

whereas the contribution from the coupling between the composition and curvature fields is (Lipowsky and Sackmann, 1995)

(9)

Here φ_r is a reference composition defined in Parameters, below (see the discussion/text surrounding Eq. 29). The first term on the right-hand side of Eq. 8 models the energy cost for having a nonuniform composition field. The second term is a double-well potential,

(10)

which should have minima at φ = 0.8 (ld phase) and at φ = 0.4 (lo phase), and should be zero for pure DMPC, U_bin(φ = 1) = 0. A differential element of area on the surface of the membrane is dA_m = g(x, y)dxdy where g is the metric (strictly speaking, the square-root of the metric). For an almost flat membrane parallel to the x,y plane with no overlaps, the shape of the membrane can be conveniently described in the Monge representation, [x, y, h(x, y)], where h(x, y) is the height of the membrane surface at (x, y) measured parallel to the z axis (Safran, 1994). In this representation, the metric is g(x, y) = [1 + (∂_xh)² + (∂_yh)²]^1/2, and the mean curvature, H, is approximately

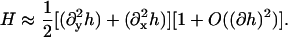(11)

To be concise in our notation, we have rewritten ∂h/∂x as ∂_xh and ∂²h/∂x² as The cubic coupling given by Eq. 9 is only suitable if the solvent environment above the membrane is identical to that below. However, if these environments are not the same so that there is a distinction between up and down (or for a closed membrane vesicle, a difference between in and out), then Eq. 9 should be replaced with a bilinear coupling (Jülicher and Lipowsky, 1993; Taniguchi, 1995; Kumar and Rao, 1998; Jiang et al., 2000),

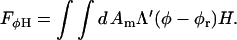(12)

Since the atomistic NEMD simulations of different DMPC/cholesterol mixtures were performed under symmetric, periodic boundary conditions, the appropriate coupling model is Eq. 9. Knowing the interfacial width and line tension between the two phase domains as well as the coexistence curve, we can then assign values to all the parameters in Eq. 8; however, we treat the coupling, Λ, as an adjustable parameter. Provided the deformations in the membrane from being flat are not appreciable, we have (see Appendix A)

(13)

where

(14)

B₁₁(x, y), B₂₂(x, y), and B₁₂(x, y) are given in Appendix A. To neglect the secondary coupling to curvature, we simply ignore the spatial derivatives of g arising from the operators 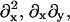and 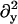in Eq. 13 acting on g(x, y)I.

The CH equation is not the only possibility available for generating the composition dynamics. We could alternatively use the time-dependent Landau-Ginzburg (LG) equation (Metiu et al., 1976),

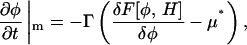(15)

where Γ > 0. Both equations result in the free energy, 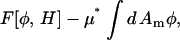approaching a local minimum; however, only the CH equation will conserve the mean composition, keeping 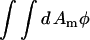a constant. As a result, the CH equation appears at first glance more suitable than the LG equation for studying a closed system such as a membrane vesicle, but the LG equation can be extended by adding a composition-stat (analogous to a thermostat), that is, a Nosé-Hoover feedback term that approximately conserves the mean composition (Evans and Holian, 1985; Evans and Morriss, 1990).

SIMULATION METHODOLOGY

To couple the composition and the curvature fields, the key quantity to be resolved instantaneously is the membrane's height function, h(x, y). Details in the construction of the EM model are highlighted in Appendix B and explained fully in Ayton and Voth (2002). The EM simulation dynamics generates a fluctuating curvature field whose Fourier modes have an average amplitude satisfying equipartition (Helfrich, 1973; Lindahl and Edholm, 2000a; Brown, 2003). These simulations use periodic boundary conditions where the membrane's surface is approximately parallel to the x,y plane; thus, h(x, y) can be written as a Fourier series expansion,

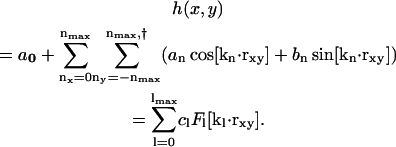(16)

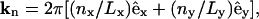
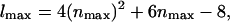
Here 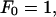and L_{x, y} are the dimensions of our central simulation box. The symbol † in the sum over n_y signifies that when n_x = 0, terms where n_y < 0 are excluded from the sum. Given the positions of the EM particles (points) projected onto the x,y plane, r_xy(j), and their heights above this plane, z_j, the coefficients, c_l, in this expansion can be found by minimizing a residual (Travis et al., 1995),

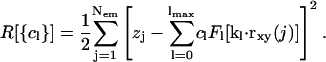(17)

This minimization (∂R/∂c_l = 0) yields a system of linear equations for the coefficients; solving this system during a simulation at every timestep is time-consuming and hence not feasible. Alternatively, if the number density (per unit area) or distribution of the EM points on the x,y plane is sufficiently dense, then the following approximation can be used:

(18)

Here the l = 0 coefficient is the mean height, 〈h〉.

The composition dynamics is coupled to the curvature by using Eq. 16 to evaluate H, then entering this H in F[φ, H]. To couple the curvature dynamics to the composition, the spring constants of the bonds in the EM model are set, given the compositions φ_i of the points within this network. Specifically, h′ and λ in ω (Eq. 45) are modulated based on fits to the thicknesses and microscopic bulk moduli of three DMPC/cholesterol mixtures estimated from atomistic EMD and NEMD simulations (Ayton et al., 2002b). This data was presented in an earlier article; here the data is presented again, except in units better reflecting the length- and timescales pertinent to our mesoscopic simulations (Table 2). The data for h and λ are well fit to f(φ) = a(φ − 1) exp [b(φ − 1)] + c with constants a, b, and c. Increasing the concentration of cholesterol increases the conformational ordering in the DMPC hydrocarbon tails (McMullen et al., 1994; Smondyrev and Berkowitz, 2001; Ayton et al., 2002b); as a result, the membrane's thickness, h, increases and the membrane becomes more resistant to local, in-plane changes in area (Table 2).

TABLE 2.

Various atomistic NEMD estimates for the membrane thickness, h′, and microscopic bulk modulus, λ

System	φ	h′ (nm)	λ (amu · nm−1 ps−2)
DMPC/pure	1	3.40	32.52
DMPC/cholesterol (2:1)	0.332	3.98	107.19
DMPC/cholesterol (1:1)	0	4.28	255.94

PARAMETERS

In this section, we give a rough guide for assigning reasonable values to the parameters in the free energy model, F[φ, H]. Whereas h′ and λ are estimated from atomistic EMD and NEMD simulations, ξ² and the parameters in U_bin(φ) are chosen to reproduce the coexistence points (compositions) in the phase diagram of a DMPC/cholesterol mixture at T = 308 Kelvin and what might be known about the interfacial properties of the boundary separating the phase domains of a perfectly flat membrane: the φ at the coexistence curves of the lo and ld phases; and the interfacial width, Δx, and line tension, γ_L, between these two phases. The binary mixture contribution to the free energy, U_bin(φ), should have a minimum at φ_I = 0.4 (lo phase) and at φ_II = 0.8 (ld phase); the maximum in U_bin(φ) lies at φ_c = 0.6, the critical composition (Recktenwald and McConnell, 1981; Knoll et al., 1985; Almeida et al., 1992). Assuming the minima in U_bin(φ) are degenerate, we let dU_bin(φ)/dφ = A(φ − φ_I)(φ − φ_II)(φ − φ_c) where

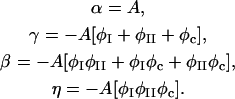(19)

To determine A and ξ², we minimize γ_L for a perfectly flat membrane.

The line tension, γ_L, is the difference in the free energy per unit interfacial length (measured along a line tangent to the interface between the two phases) and the free energy per unit interfacial length that the system would have if the properties of the bulk phases on both sides of the interface were constant up to a plane located so as to satisfy the following constraint (Rowlinson and Widom, 1982),

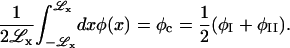(20)

Performing this minimization for U_bin(φ) symmetric at ∼φ = φ_c, we find given H = 0 that

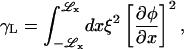(21)

where the composition profile is 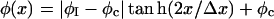and the interfacial width is

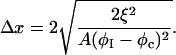(22)

In deriving Eq. 21, we considered an interface/phase boundary parallel to the y direction, where 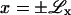are positions normal to the interface (x = 0) sufficiently far away from x = 0 that and 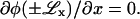Substituting φ(x) into Eq. 21, we find

(23)

Therefore, if we know γ_L and Δx, then we can determine A and ξ², and in turn α, γ, β, and η. The remaining parameter, ψ, can be set using the condition, U_bin(φ = 1) = 0 (Table 3), but since the composition dynamics is independent of ψ, ψ can be ignored. Crude experimental and theoretical estimates of the line tension yield (Lipowsky, 2002; Lipowsky and Dimova, 2003) γ_L ≈ 2 × 10⁻¹²N to 10⁻¹¹N; we chose γ_L = 6 × 10⁻¹²N or γ_L ≈ 3.595 amu · nm/ps². For the interfacial width, we chose Δx ∼ 5.6nm. The true interfacial width might be on the order of a few molecular diameters, so this choice is probably an overestimation. Choosing a smaller Δx will result in larger gradients in the composition field that will require more numerical effort to calculate accurately (that is, a smaller Δx requires a denser spatial grid to accurately calculate the spatial derivatives in the CH equation whose parameters are chosen using Δx as a reference). Since our main objective is simply to demonstrate that we have a mesoscopic simulation method that couples the dynamics of the curvature and composition fields, we chose for convenience a larger value of Δx than might be realistic.

TABLE 3.

Assignment of free energy and EM model parameters

Parameter	Value
α (amu/ps2)	1210.70
γ (amu/ps2)	−2179.26
β (amu/ps2)	−1259.13
η (amu/ps2)	−232.45
ξ2 (amu · nm2/ps2)	190
Λ (amu · nm2/ps2)	−900 to 900
M (nm2 · ps/amu)	0.0002
Box length, Lx = Ly (nm)	80
Number of EM points, Nem	6920
Fourier integer, nmax	4 to 6
ρm (amu/nm3)	723
Timestep, Δt (ps)	0.04

The mass density, ρ_m, agrees with the fit to the EMD data at φ = 0.6 = φ_c.

Once the parameters in F_φ are assigned, we can determine the mobility, M. For a perfectly flat membrane such that g(x, y) = 1 and H = 0, Eq. 6 becomes (Rogers et al., 1988)

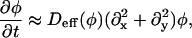(24)

provided ∂φ is small and 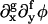such that f + g = 4 are negligible relative to 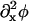and Here D_eff(φ) is an effective diffusion constant: D_eff(φ) = [3αφ² + 2γφ − β]M. Remembering φ = (C_A − C_B)/C then noting the diffusion equation (deGroot and Mazur, 1962), 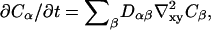valid only near equilibrium, we find from Eq. 24

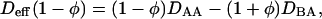(25)

(26)

If the total concentration C_A + C_B = C is constant, then further simplifications can be made; however, for the purpose of estimating M these simplifications are not necessary. In the infinite dilution limit where B (cholesterol) is the solute and A (DMPC) is the solvent, φ = 1, Eq. 25 shows that D_BA | _φ=1 = 0. Summing together Eqs. 25 and 26, then setting φ to 1, we obtain an expression for the mobility of

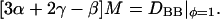(27)

Here D_BB | _φ=1 is the lateral self-diffusion constant of cholesterol in DMPC. From experiment and simulation (Lipowsky and Sackmann, 1995; Smondyrev and Berkowitz, 2001), D_BB | _φ=1 ∼10⁻⁵ nm²/ps; Eq. 27 then yields M ∼2 × 10⁻⁸ nm² · ps/amu. Short-range diffusion methods such as quasielastic neutron scattering give lateral diffusion constants that are two orders-of-magnitude larger than long-range methods such as fluorescence (Korlach et al., 1999). One possible reason for this discrepancy is that thermal undulations make the actual distances traveled by molecules much larger than the apparent, projected distances; as a result, the diffusion constant is conditioned by these undulations with increases in length scale, or equivalently decreases in the spatial resolution of the measurements. The quantity D_BB|_φ=1 entered into Eq. 27 is the short-range diffusion constant.

Another estimate of the mobility can be made by treating M more generally as a function of φ and then comparing the approximated CH equation, where 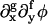such that f + g = 3 are ignored, to the diffusion equation, ∂C_B/∂t ∼ ∇_xy · [D_BB(φ)∇_xyC_B]. This comparison yields M(φ) ∂²U_bin/∂φ² = D_BB(φ). Replacing ∂²U_bin/∂φ² with its average from φ = 0.4 to 0.8 and D_BB(φ) with D_BB(φ = 1), we have the crude estimate, 〈M〉 ∼ 9 × 10⁻⁸ nm²ps/amu.

The EM model of a two-component membrane is composed of two parts: the Hamiltonian, F[φ, H], and the elastic energy model, 2E^l (Eq. 43), which is generalized to include cross-links between the two membrane leaflets (Ayton and Voth, 2002). Although ω (Eq. 45) is derived considering a perfectly flat membrane, Eq. 43 with this ω is applied to a nonflat membrane. Provided the peristaltic modes are ignored, the two-leaflet, EM model parameterized by λ can be equated to a single surface, continuum model parameterized by a bending modulus, κ_b, and a surface tension, γ_S (Safran, 1994). The Hamiltonian for this continuum model is the Helfrich free energy (Helfrich, 1973; Lipowsky and Sackmann, 1995),

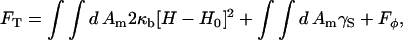(28)

where H₀ is the spontaneous curvature. To identify the cubic and bilinear coupling parameters in F[φ, H], we treat κ_b as a function of φ, expanding κ_b(φ) at some reference composition, φ_r,

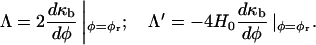(29)

If the spontaneous curvature, H₀, also depends on φ, then the expression for Λ′ should be modified. To relate κ_b to λ, we imagine a small, local bend in a bilayer membrane with two equal, finite principle radii of curvature where the local expansion in area of one monolayer is equal in magnitude to the local compression in area of the opposite monolayer (Safran, 1994; Sackmann, 1994; Lipowsky and Sackmann, 1995). Treating this asymmetric stretch as a bend is physically reasonable only across length scales comparable to the thickness of the bilayer, 3–5 nm. Therefore, the κ_b so derived is a microscopic bending modulus, not conditioned or renormalized by mesoscopic thermal undulations (Peliti and Leibler, 1985). Taking the membrane thickness, h′, to be fixed, then equating the elastic free energy per unit area given by Eq. 44 to the Helfrich free energy of bending per unit area, we find κ_b ∼ C(h′)³λ; depending on how the contribution to change in the elastic energy is distributed across the membrane, the prefactor C ranges from 1/12 to 1. Noting the fits to the NEMD and EMD data for λ and h′, we then have −Λ ∼2800–33,700, 1400–16,600, and 700–8100 amu · nm²/ps² for φ at ∼φ_r = φ_I = 0.4, φ_r = φ_c = 0.6, and φ_r = φ_II = 0.8, respectively. The derivation above is crude, so the most we can say with some confidence is that κ_b depends linearly on λ. Curiously, the sign of Λ appears unique. Nonetheless, Λ in our simulations is treated as an adjustable parameter so that we can examine the effects of the dynamics coupling φ and H. As such, Λ is assigned positive and negative values. The free energy model does not have to be restricted to a quadratic or cubic coupling between φ and H; the coupling model can made completely nonlinear by setting F_φH to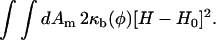

The values in our simulation assigned to the parameters in the free energy model, F[φ,H], are summarized in Table 2. Note that the values for Λ are 1–2 orders-of-magnitude lower than our estimates discussed above. Preliminary simulations showed that for very large |Λ| the composition of some EM points could be driven above φ = 1 (pure DMPC) for Λ < 0. A more modest assignment for Λ prevents this unphysical drift. Alternatively, we could have added to U_bin(φ) the following term representing the Flory-Huggins entropy of mixing for a two-component mixture consisting of a cholesterol-lipid dimer and a monomeric lipid (a simple model where each cholesterol irreversibly dimerizes with a single lipid) (Komura et al., 2004):

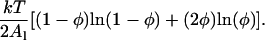(30)

Here A_l is the cross-sectional area of a lipid. The derivative of this term becomes infinite at φ = 0 and φ = 1, so this term acts as a caging potential. However, employing such a term necessitates abandoning our present, simple procedure for assigning α, γ, β, η, and ψ. In addition, M in our simulations is set four orders-of-magnitude larger than our estimate of 2 × 10⁻⁸ nm²ps/amu (Table 2). As we will discuss in Bare EM Dynamics, below, the EM model in the absence of a solvent moves 10–100 times faster than predicted by hydrodynamic theory and observed in experiments. To compensate for the absence of viscous dampening effects to the undulating motion of the membrane's surface, the mobility, M, should be set 10–100 times larger than its estimate. Once phase separation has occurred, the phase domains are expected to move in response to the curvature in the membrane. The normal front speed of a phase boundary should be roughly proportional to the local curvature, specifically 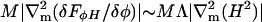(see the end of Undulating Membranes, below). Since |Λ| is set 10–100 times smaller than our estimate, M should also be multiplied by another factor of 10–100. Therefore, to balance both the effects of the absence of a solvent and a low setting for |Λ|, we set M in our simulations to 10,000 times its estimate, that is, to 2 × 10⁻⁴ nm² ps/amu.

In the microscopic regime, finite-size effects arising from periodic boundary conditions (Allen and Tildesley, 1987) may influence the phase separation observed in an atomistic simulation of a binary mixture (L_x ∼3−5 nm ∼ L_y), specifically the fluid structure at the interface. Similarly, these conditions might even affect the values of the mesoscopic bulk moduli, λ_meso, estimated using EM simulations if the dimensions of the central simulation box (L_x ∼80 nm ∼ L_y) are not chosen sufficiently large to contain several phase domains. Given the values listed in Table 2, it is therefore prudent to check before a simulation whether the Fourier modes characterizing the phase separation of the composition field fit within this box. According to a linear stability analysis of the CH equation for a perfectly flat membrane (Binder, 1986), immediately after a critical quench to T = 308 Kelvin at φ = φ_c = 0.6, the wavenumber of the fastest growing Fourier mode in the composition field is k_fast = [U″_bin(φ_c)/2ξ²]^1/2. Here U″ denotes the second derivative of U_bin with respect to φ. The corresponding wavelength is λ_fast ∼ 2π/k_fast ∼ 18 nm, which is approximately four times smaller than the length of our simulation box.

RESULTS

The results are presented in three parts. In Bare EM Dynamics, we examine the dynamics of the bare EM model where the composition field is static and uniform. Next we consider the composition dynamics integrated in time over a configurationally frozen EM snapshot. Finally in Undulating Membranes, we combine the two dynamical schemes propagating in time both the curvature field and the phase-separating composition field.

Bare EM dynamics

Including the dissipative and random forces in the EM equations of motion will generate a canonical distribution and thus correct thermodynamic averages (Espanol and Warren, 1995; Groot and Warren, 1997). However, whereas the effects of the membrane's hydration layer on the stress response are embedded in the microscopic bulk modulus, λ, an explicit, mesoscopic model for the solvent is still required to reproduce the dampening effects of the bulk solvent on the membrane's motion. We therefore suspect that the thermal undulations of the EM model, being in a vacuum, move faster than those of a membrane immersed in a bulk solvent. To check this motion, we performed an EM simulation with a homogeneous composition field, φ = φ_c = 0.6, where the area, A = L_xL_y, was fixed. The bond strengths were set according to the fits to the EMD and NEMD data for ρ_m, h′, and λ:ρ_m = 722.835 amu/nm³, h′ = 3.74 nm, and λ = 58.09 amu/(nm · ps²). The simulation was started from the final configuration with dimensions L_x ≈ 80.30 nm ≈ L_y taken from a zero surface tension (γ_S = 0) simulation of a pure DMPC EM model (φ = 1). The system was allowed to equilibrate for 500,000 timesteps of size Δt = 0.04 ps, followed by a production run of 1,000,000 Δt. The time autocorrelation functions of the undulation modes were averaged over 20 blocks of 100,000 Δt. The autocorrelation functions of those modes whose wavenumber, k_l, lay within the same interval, (p−1)Δk to pΔk, were then averaged:

(31)

Here p is an integer running from p = 2 to p = 10, Δk = k_max/10, and 〈·〉_T denotes a time average. The maximum value of k_l is 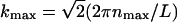where n_max = 4 is the maximum value chosen for n_x and n_y in the Fourier series expansion, h(x, y, t), Eq. 16.

Standard hydrodynamic coupling theory (Kramer, 1971; Crilly and Earnshaw, 1983; Hirn et al., 1999; Lindahl and Edholm, 2000a) predicts an oscillating regime at low wavenumbers, k, characterized by damped, oscillatory motion of the undulating modes, and an overdamped regime at high k characterized by overdamped, nonpropagated motion. This theory treats only the bending modes in the membrane, neglecting any possible coupling to the internal peristaltic modes that describe fluctuations in the membrane's thickness. The crossover between the two regimes occurs at a critical wavenumber, k_crit, which satisfies 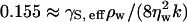where γ_{S, eff} = γ_S + κ_bk². Here ρ_w and η_w are, respectively, the mass density and shear viscosity of bulk water, κ_b is the bending modulus of the membrane, and γ_S is the surface tension of the membrane. Assuming κ_b ∼ 4 × 10⁻²⁰ J, η_w ∼ 0.891 × 10⁻³ kg · m⁻¹ s⁻¹, and γ_S ∼0.1 × 10⁻³ to 1.0 × 10⁻³ Nm⁻¹, we find k_crit ∼ 10³ to 10⁴ cm⁻¹. The wavenumbers, k_l, that we sample in our simulation range from 10⁵ to 10⁶ cm⁻¹. Since the initial EM configuration was selected from a zero-surface-tension, mesoscopic simulation (Ayton and Voth, 2002), the surface tension in our simulation is small, lying within 0.1 × 10⁻³ and 1.0 × 10⁻³ Nm⁻¹. Therefore, according to this estimate of k_crit, our simulation should be within the overdamped regime provided we include a mesoscopic model dynamics for bulk water. Fig. 1 shows the normalized autocorrelation function for several p. The function for p ≤ 10 undergoes oscillations. In the oscillating regime, the period of the oscillation in C_k(t) should be T₀ = 2π/ω₀ where ω₀ = [γ_{S, eff}k³/(2ρ_w)]^1/2. As shown in Fig. 1, the first peak in C_pΔk(t) for p = 8, 9, and 10 match the predicted times T₀ ∼ 700 ps, 500 ps, and 400 ps. For p > 10, C_pΔk(t) becomes a monotonically decreasing function of time. Therefore, our simulation actually lies on the crossover between the two undulating regimes. Despite this discrepancy, our simulation results are still consistent with the hydrodynamic theory. According to this theory, k_crit should increase as η_w, and thereby the dampening effects of the bulk water are decreased.

FIGURE 1.

Time autocorrelation functions of the coefficients in the Fourier series fit to the membrane's height, h(x,y,t). The composition of each point in the EM network is set to φ = φ_c = 0.6. Here k_max ≈ 4.44 × 10⁶ cm⁻¹ and Δk = k_max/10. The correlation function labeled k_* corresponds to a Fourier mode with a wavenumber ∼6.3 × 10⁶ cm⁻¹. As the wavenumbers increase above k_max, the undulating modes go from being damped to overdamped. Persistent oscillations (not shown) occur for p ≤ 5. These oscillations are particularly apparent if a single (no averaging over modes) Fourier mode is inspected.

In the overdamped regime, the hydrodynamic theory also predicts that C_k(t) will exponentially decay with a relaxation time, t_relax = 4η_w/(γ_{S, eff}k) (Brochard and Lennon, 1975; Messager et al., 1990; Levine and MacKintosh, 2002). Ignoring the character of the relaxation shown in Fig. 1, we find that the average relaxation rates shown in Fig. 1 are ∼10–100 times faster than the theoretical prediction. Nonetheless, our simulation results are still consistent with the theory because t_relax decreases with decreasing η_w. When we set the mobility to the estimate of M ∼ 2 × 10⁻⁸ nm⁻² · ps/amu, we found that the relaxation rate of the composition field (equivalently the rate at which the phase separation occurred) was much smaller than the undulation rate of the curvature field. Since our main purpose in this study was to demonstrate that a composition dynamics could be combined with the EM dynamics, we did not want a significant timescale separation to exist between the composition and the curvature fields: dynamical feedback between these two fields will not be observed with a significant timescale separation. As a result, we adjusted the mobility to M = 0.0002 nm⁻² · ps/amu to remove the timescale separation. The phase separation and subsequent movement of the phase domains are driven by the coupling to the local curvature. Consequently, the timescale separation will be breached if the coupling to the curvature is sufficiently strong. Furthermore, if the coupling parameter |Λ| is set too low, as we have done, then the mobility should be adjusted to a value much larger than M ∼2 × 10⁻⁸ nm⁻² · ps/amu to compensate. Finally, it is curious to note that in a recent theoretical analysis (Zilman and Granek, 1996), a stretched exponential decay, C_pΔk(t) = C_pΔk(t = 0) exp[−(Γ_pt)^2/3], was derived for the sponge and powder lamellar phases of a membrane bilayer, predicting relaxation rates 1000–10,000 times smaller than those evident in Fig. 1.

Static membrane

We simulate the phase separation of a critically quenched binary mixture by integrating the CH equation of motion for the composition field, φ. Since the membrane is static, so that the curvature field, H, does not vary in time, we can isolate the dynamics of φ. In addition, we can determine the timescales required for φ to reach a “steady state,” a phase-separated mesoscopic state where the free energy, has a local minimum. In this “steady state,” the extreme values of the composition field and the interfacial width between two phase domains are approximately constant. Along a given interface dividing two phase domains, the interfacial width will vary because of the coupling between the composition and the local curvature. Furthermore, because of this coupling, the actual width at some point on the interface will differ from the reference width, Δx = 5.6 nm, used to assign values to the free energy parameters (see Parameters, above). These parameters were estimated considering a perfectly flat membrane (H = 0). There can be many free energy local minima; however, in the absence of an external time-dependent field or internal source of noise, the dynamics will drive the φ field to only one of these minima; once there, φ is trapped. Specifically, starting from several different, approximately uniform composition fields with only slight deviations from complete uniformity, the phase separation for a critical quench on a perfectly flat membrane will yield after a given time several different labyrinthine patterns (Rogers et al., 1988). When a coupling to curvature is added to the dynamics, the number of such patterns for a frozen, nonflat surface becomes restricted: the pattern must conform to the underlying surface geometry or texture.

All simulations discussed in this section were started from a uniform composition field where φ = φ_c = 0.6. The curvature H was calculated using a Fourier series fit to the heights of the EM points of the final configuration generated by the bare EM simulation described earlier in Bare EM Dynamics (recall that in this simulation, the composition of each EM point was initially set to φ_c = 0.6, then the EM was free to undulate for 1,500,000 Δt with the φ at each EM point fixed at φ = φ_c = 0.6). Given the curvature field of this final configuration, the CH equation was then integrated in time using a fifth-order Gear predictor-corrector algorithm (Allen and Tildesley, 1987) with a timestep of Δt = 0.04 ps. The spatial derivatives of φ were calculated using simple finite difference approximations: parallel to the x,y plane, a rectangular grid was constructed consisting of N_grid = 6889 (83 × 83) grid points where the spacings between these points in the x and y directions were, respectively, L_x/83 and L_y/83. Periodic boundary conditions were also used to evaluate these derivatives. The accuracy of these approximations can be systematically improved given a fixed grid spacing by switching to distributed, approximating functional methods (Hoffman et al., 1991, 1992; Gunaratne et al., 1998). Monitoring the change in the free energy per unit area, Δ(F_φ + F_φH)/(L_xL_y) where ΔF_φ = F_φ(t) − F_φ(t = 0), we found that our integration of the CH equation on a less dense grid, 70 × 70 points, became numerically unstable: ΔF[φ, H]/(L_xL_y) diverged at large times, t. The integration on a more dense grid, 100 × 100, was identical to the integration on the 83 × 83 grid used in most of our calculations; however, the denser grid required a smaller timestep, Δt = 0.02 ps, for its integration to match the integration on the 83 × 83 grid. The mismatch between the results for these two grids at Δt = 0.04 ps might be a result of a subharmonic bifurcation (Rogers et al., 1988). Evidently, an integration of the CH equation on a denser spatial grid requires a smaller timestep to accurately resolve the fast motions of the shorter wavelength spatial modes in the composition field; these modes are made accessible by increasing the density of the spatial grid.

As shown in Fig. 2, increasing the magnitude of the parameter Λ in the cubic coupling model, Eq. 9, increases the relaxation rate of the composition field at times less than t ∼5000 ps; furthermore, although not shown in a figure, the evolution of ΔF[φ, H]/(L_xL_y) appears independent of the sign of Λ. This rate at early times can also be increased by increasing the resolution of the Fourier series fit to the heights of the points in the EM model. As shown in Fig. 3, increasing the number of terms in this series by increasing n_max from 4 to 6 increases the relaxation rate. It is also evident from Fig. 3 that the composition field for these different fits relaxes to different “steady states” since the final value of F[φ, H] is different for these fits. Secondary couplings to the curvature arising from the spatial derivatives of the metric, g(x, y), in Eq. 13 do not appear to significantly affect the evolution of ΔF[φ, H]/(L_xL_y) for n_max = 4; however, if the resolution of the fit is increased to n_max = 6, then the composition field does reach a different “steady state” if these secondary couplings are neglected (Fig. 4). At times >t ∼5000 ps, the relaxation rates for different Λ and n_max are more comparable than at times <t ∼5000 ps; however, at t > 5000 ps the rate does decrease as n_max increases. In short, the “steady state” reached by the composition field as well as the relaxation rate at early times depend on the degree to which this field sees the texture in the membrane's surface. We note that the fit to the heights of the two leaflets in the EM model map these two surfaces to a single, effective surface, and it is the curvature of this surface to which dynamics of the composition field is coupled.

FIGURE 2.

Relaxation of the model free energy, F[φ, H], with a static H for three different values in the cubic coupling parameter, Λ. As |Λ| increases, such that the coupling between the curvature and the composition becomes stronger, the relaxation rate at early times increases. At earlier times the relaxation appears to be exponential, whereas at later times it is linear and here the relaxation rates are comparable. All these simulations were started from a uniform composition field.

FIGURE 3.

Relaxation of the model free energy, F[φ, H], with a static H for three different Fourier series fits. As the number of terms in the fit increases, the relaxation rate at early times increases. At earlier times, the relaxations appears to be exponential, whereas at later times it is linear and here the relaxation rates are comparable. All these simulations were started from a uniform composition field.

FIGURE 4.

Relaxation of the model free energy, F[φ, H], with and without spatial derivatives of the metric, g(x,y), included in the CH equation. Here the membrane surface was static. For n_max = 4, there is no observable difference; however, here, for n_max = 6 the relaxation is different, resulting in a different steady-state approach.

CH dynamics implies that composition will be conserved; specifically, the mean composition, should be a constant. We found a very slight drift in 〈φ〉_i away from φ_c during an entire simulation run; small numerical errors could be corrected by shifting the compositions φ_i at each grid point, i, after every timestep. By contrast, an integration of the time-dependent LG equation with μ* set to zero did not conserve 〈φ〉_i: for Λ > 0, the entire composition field drifted toward ∼φ_I = 0.4, the cholesterol-rich phase; and for Λ < 0, this drift was toward ∼φ_II = 0.8, the DMPC-rich phase. However, if we knew before a simulation the value of μ* associated with φ_c, then although a 〈φ〉_i starting from an arbitrary initial condition will not be conserved, 〈φ〉_i(t) should approach φ_c as time increases.

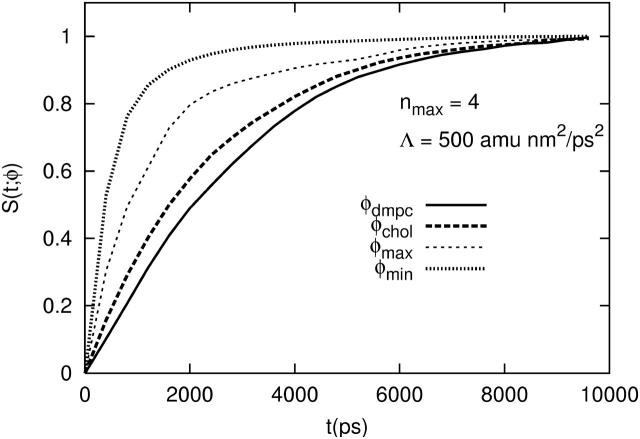
Our integration should also reproduce the characteristic behavior of the phase separation of a binary mixture (Langer, 1971). This separation occurs roughly in two stages. First, the minimum, φ_min(t), and maximum, φ_max(t), composition values should rapidly approach their respective limits of ∼φ_I and ∼φ_II. The mean composition over those grid points, i, whose φ_i is <φ_c, φ_chol ∼ φ_I, or whose φ_i is >φ_c, φ_dmpc ∼ φ_II, should evolve more slowly, lagging behind, respectively, φ_min(t) and φ_max(t). During this initial stage, the phase domains are poorly defined, having no sharp interface between them. Later, in the second stage of the separation, φ_chol(t) and φ_dmpc(t) catch up to φ_min(t) and φ_max(t), and the interfaces become more sharp. This behavior can be monitored by plotting relaxation functions, S(t;φ) = | [φ(t) − φ(t = 0)] | / | [φ(∞) − φ(t = 0)] |, with φ set to φ_min, φ_max, φ_chol, or φ_dmpc. Fig. 5 with S(t;φ) plotted for Λ = 500 amu · nm²/ps² and n_max = 4 shows that φ_min(t) and φ_max(t) evolve more rapidly than φ_chol(t) and φ_dmpc(t). In addition, when Λ > 0 the formation of the cholesterol-rich phase at ∼φ_I ∼ 0.4 appears faster than the formation of the DMPC-rich phase at ∼φ_II ∼ 0.8; the converse is seen when Λ < 0. In truth, there exists a third stage in the phase separation where the phase domain structure grows in size with increasing time in a self-similar manner so as to minimize the amount of perimeter between the two phases and thereby minimize the energetic cost for having interfaces between the phase domains (Gunton et al., 1983; Rogers et al., 1988). The beginnings of this growth are evident in Fig. 6. The transition from an exponential decay at early times to a linear decay at late times (Figs. 3 and 4) signals the onset of this asymptotic stage. We will further discuss this scaling regime in the following section.

FIGURE 5.

Relaxation functions of the extreme values in the composition field and the mean compositions of the cholesterol and DMPC-rich phases (n_max = 4). The membrane was static.

FIGURE 6.

Snapshots of the composition field morphology at t = 10,000 ps (top panel) and at t = 40,000 ps (bottom panel) on a static membrane (n_max = 4, Λ = 500 amu · nm² /ps²). Light- and dark-shaded regions mark the cholesterol-rich and DMPC-rich phases.

Given the cubic coupling model with Λ > 0 (Eq. 9), the free energy will be minimized if the cholesterol-rich phase domains are correlated with regions on the membrane's surface where the curvature, H², is large. In other words, when Λ > 0, there exists a thermodynamic force that attracts the cholesterol-rich domains to these regions. The opposite is true when Λ < 0: the DMPC-rich domains are attracted to these regions. Fig. 6 confirms these predictions; it shows the morphologies of the φ-field at t = 10,000 ps (250,000 timesteps) and at t = 40,000 ps (1,000,000 timesteps) superimposed on the single, effective surface generated by the Fourier series fit. The morphologies obtained from simulations using the bilinear coupling model, Eq. 12, appear quite different. When Λ′ > 0, the DMPC-rich phase domains lie on surface regions with negative mean curvature, H < 0, whereas the cholesterol-rich domains lie on surface regions with positive mean curvature H > 0; the converse is true when Λ′ < 0. Like the cubic coupling, the bilinear coupling also yields phase domains whose sizes grow in time, although this growth should slow as |Λ′| increases (Taniguchi, 1995).

For the cubic coupling model, increasing Λ when Λ > 0 decreases φ_min; φ_min shifts away from ∼φ_I = 0.4, where U_bin(φ) has a minimum (Table 4). Given this shift, the populations of the DMPC and cholesterol-rich phases, respectively P_dmpc and P_chol, cannot remain the same; P_dmpc must become larger than P_chol to conserve the mean composition, 〈φ〉 = φ_c = 0.6. The population of the DMPC-rich phase, P_dmpc, is defined as the fraction of the total number of grid points, i, whose composition φ_i is >φ_c; similarly, P_chol is defined as the fraction of i whose φ_i is <φ_c. When Λ < 0, the opposite is true: φ_max increases with increasing |Λ|, and P_chol becomes >P_dmpc. 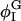These changes can be understood by grouping together the double-well and coupling contributions to F[φ,H]: When Λ > 0, decreases as Λ increases; 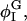where 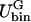has a local minimum, shifts away from 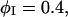where U_bin has a local minimum. The other minimum, also decreases; however, since the cholesterol-rich domains are correlated with surface regions where H² is large, the shift in from φ_I should be larger than the shift in 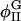from φ_II. Therefore, we do not expect when Λ > 0 to see as substantial a change in φ_max as in φ_min (Table 4). Furthermore, when Λ > 0, 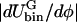is much larger on average for φ < φ_c than for φ > φ_c. As a result, the driving force on the cholesterol-rich phase to reach its final composition during the phase separation must be greater than the corresponding force acting on the DMPC-rich phase. The difference in the magnitudes of these two driving forces explains the faster relaxation of the cholesterol-rich phase observed in Fig. 5 when Λ > 0.

TABLE 4.

Extreme and mean values of the composition field, φ, and the population of the DMPC-rich phase at times t = 3000 ps and t = 10,000 ps for several values of the cubic coupling parameter, Λ (amu · nm² /ps²)

Λ	φmin	φchol	φdmpc	φmax	Pdmpc
t = 3000 ps
200	0.369	0.534	0.655	0.757	0.546
500	0.313	0.504	0.679	0.781	0.547
900	0.267	0.482	0.696	0.798	0.549
−200	0.443	0.545	0.666	0.831	0.454
−500	0.419	0.521	0.696	0.887	0.452
−900	0.402	0.504	0.718	0.933	0.450
t = 10,000 ps
200	0.343	0.478	0.716	0.802	0.510
500	0.303	0.467	0.722	0.807	0.521
900	0.261	0.455	0.730	0.815	0.527
−200	0.398	0.484	0.721	0.854	0.489
−500	0.392	0.478	0.734	0.897	0.479
−900	0.384	0.470	0.744	0.939	0.473

The populations of the DMPC and cholesterol-rich phases are P_dmpc and P_chol = 1–P_dmpc. Here the membrane's curvature, H, is nonuniform and independent of time.

Undulating membrane

Equation 4 gives the rate of change in the composition field at a fixed point on the membrane such that there are no net flows of material tangent to the membrane's surface but there can be thermal undulations. Because the membrane discussed in this section is now free to undulate, the projection of this point onto the x,y plane in the lab frame will not be fixed. In addition to the motions of the membrane in the direction normal to its surface, there are motions of the EM particles or points tangent to the surface. As a result, a convective term must be included to account for the net flow, V_m, of material parallel to the surface; the change in φ at a fixed point on the membrane is thus

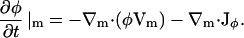(32)

Here, a fixed point on the membrane is not an EM point. If the divergence in V_m is zero, ∇_m · V_m = 0, then

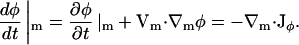(33)

Equation 33 is not the same as Eq. 4: the total time derivative, dφ/dt | _m, is the rate of change in φ from the perspective of a point moving with the flow, V_m, tangent to the surface. These points are exactly the EM points; therefore, when integrating Eq. 33, we should follow the motion and thereby the positions of the EM points. The difficulty is the calculation of the spatial derivatives within ∇_m · J_φ; in particular, the distribution of EM points projected onto the x,y plane does not have a uniform density. There are two ways to calculate these derivatives. The first is to use the moving least-squares method (Dilts, 1999; Kendrick, 2003), where the φ_i at the projections of the EM points onto the x,y plane are each fit to a polynomial expansion. The second is to map the compositions from the projections of the EM points on the x,y plane to a regular, rectangular grid of points on this plane; spatial derivatives are calculated on this grid, and then mapped back onto the irregular, EM grid.

The first method is computationally demanding whereas the second is inaccurate. Therefore, rather than working in the frame of the membrane, following the motion of the EM points and so using Eq. 33, we worked in the lab frame. The rate of change in the composition at a fixed point in the lab frame has a contribution from the change at a fixed point in a local frame on the membrane, ∂φ/∂t | _m, and a contribution from the motion of the membrane perpendicular to its surface. The latter contribution arises from the membrane undulations and accounts for the fact that a fixed point in the lab frame is not fixed in a local frame on the membrane. Therefore, the composition field at fixed point in the lab frame changes in time according to

(34)

For simplicity, we assumed that the first term on the right-hand side could be approximated by −∇_m · J_φ. We calculated this term in the same manner as described in the previous section: spatial derivatives of the composition were estimated by first constructing a rectangular grid with N_grid = 6889 (83 × 83) points on the x,y plane, then simple finite difference approximations were used. In Eq. 34, 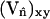is the projection of the membrane's normal velocity onto the x,y plane; this velocity was calculated using a Fourier series fit to the velocities of all the EM points.

All simulations were started from a uniform composition field with φ = φ_c = 0.6 and had n_max set to 4. The initial configuration of the EM grid of 6920 points was set to the final configuration generated by the bare EM simulation described earlier in Bare EM Dynamics. The membrane was allowed to relax during 500,000 timesteps of size Δt = 0.04 ps after which no further significant changes in the mean compositions of the cholesterol-rich and DMPC-rich phases were observed; “steady-state” averages were then accumulated during a subsequent 500,000 Δt. The total duration of a simulation run is 40 ns, on the same order as current coarse-grained molecular simulations of a similar size (Marrink et al., 2004). With our coarse-grained elastic model, ∼½ ns of simulation time per hour of wall time was achieved over one processor (although the actual timescale in this coarse-grained simulation is not rigorously defined: given the parameters chosen in our simulations, 40 ns may span a timescale of 1–2 orders-of-magnitude greater). Fully atomistic simulations with areas on the order of 300 nm² (Hofsab et al., 2003) were able to obtain ∼24 ps/h of wall time employing 32 processors. However, the ultimate goal of coupling CH or LG dynamics to an underlying mesoscopic membrane model like EM is not to replace atomistic-level or coarse-grained molecular models, but to offer an alternative conceptual framework, in order to examine composition dynamics. As such, a direct comparison between this method and coarse-grained molecular models is not exact.

In some simulations, the composition, φ, was dynamically decoupled (DEC) from the membrane's curvature; that is, φ was coupled to H, but H was not coupled to φ. Here the bonds in the EM network of cross-linked points were not modulated, but parameterized to the fit to the NEMD data at φ = φ_c = 0.6. For two DEC simulations whose cubic coupling constants only differed by a sign (positive or negative) and which started from the same initial membrane configuration with a uniform composition field (φ = φ_c = 0.6), the phase domain structure was identical at all times except that the placements of the two phases were exchanged. We did not explore the effects of the bilinear coupling model contribution to the free energy; our results strictly pertain to the cubic coupling model.

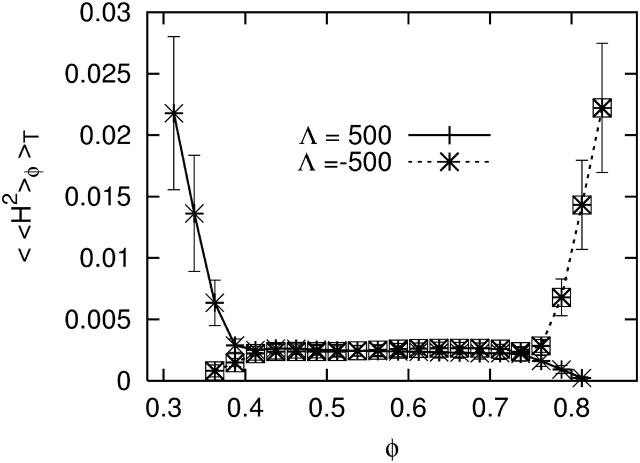
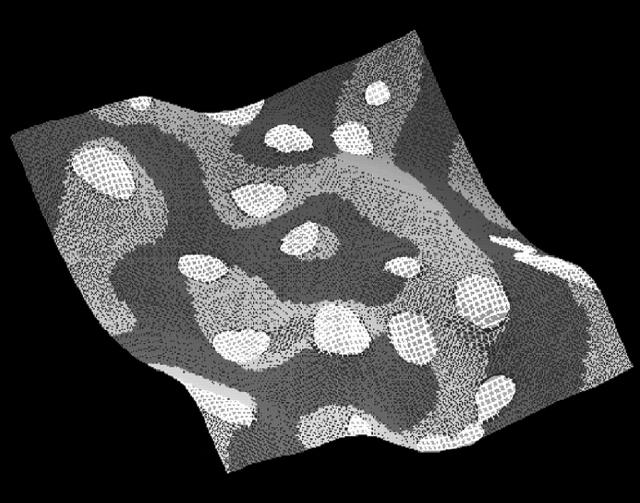
As discussed in the previous section, when Λ < 0 the free energy, F[φ,H], will be minimized if the DMPC-rich phase domains locate themselves at regions on the membrane's surface where H² is large. Conversely, when Λ > 0 the cholesterol-rich domains are driven to these regions. These predictions are confirmed by calculating the square of the curvatures averaged over EM points in the cholesterol-rich or DMPC-rich phases, respectively 〈〈H²〉_chol〉_T and 〈〈H²〉_dmpc〉_T. Here 〈·〉_T denotes a time average. Additional confirmation is obtained by calculating the curvature averaged over EM points with a given composition, 〈〈H²〉_φ〉_T (Fig. 7); notice here that the maximum value of the curvature is considerably larger than the average curvatures presented in Table 5. Fig. 8 is a snapshot of the membrane at t = 20,000 ps for Λ = 500 amu nm²/ps² where regions of relatively large curvature have been highlighted. Here the maximum curvature over all EM points is Max_iH² = 2.234 × 10⁻² nm⁻², and the average curvature over these points is 〈H²〉_i = 2.473 × 10⁻³ nm⁻². For this Λ, these regions are found predominately (but not exclusively) within the cholesterol-rich phase and near the boundaries of this phase. Of these highlighted regions, only two exist in the neighboring DMPC-rich phase; of the remaining, 13 overlap the boundaries, and four are exclusively within the cholesterol-rich phase.

FIGURE 7.

Curvature, H², averaged over EM points with a given composition, φ (bins of width 0.025), and then over time, 〈〈H²〉_φ〉_T (nm⁻²). Error bars give the standard deviation associated with the time average 〈·〉_T. Here the membrane was free to undulate (FC). For Λ = 500 amu · nm² /ps², cholesterol-rich phase domains are correlated with surface regions with large curvature. For Λ = −500 amu · nm² /ps², DMPC-rich domains are correlated with these regions.

TABLE 5.

The curvature averaged over the EM points, i, and then over time, 〈〈H²〉_i〉_T (nm⁻²); in addition, the curvature averaged over those points where φ_i < φ_c and over those points where φ_i > φ_c, respectively 〈〈H²〉_chol〉_T and 〈〈H²〉_dmpc〉_T

Λ	〈〈H2〉i〉T × 103	〈〈H2〉chol〉T × 103	〈〈H2〉dmpc〉T × 103
900 (FC)	2.688 ± 0.329	3.497 ± 0.263	1.805 ± 0.263
500 (FC)	2.616 ± 0.336	3.162 ± 0.474	2.015 ± 0.343
200 (FC)	2.509 ± 0.289	3.072 ± 0.436	1.905 ± 0.316
−200 (FC)	2.743 ± 0.370	2.355 ± 0.531	3.102 ± 0.449
−500 (FC)	2.702 ± 0.304	2.088 ± 0.321	3.268 ± 0.442
−900 (FC)	2.611 ± 0.337	1.886 ± 0.299	3.251 ± 0.493
500 (DEC)	2.439 ± 0.292	2.864 ± 0.460	1.987 ± 0.294
−500 (DEC)	2.439 ± 0.292	1.987 ± 0.294	2.864 ± 0.460

Standard deviations associated with 〈·〉_T are shown as errors; these errors give then a measure of the amplitude in the fluctuations. The cubic coupling parameter is Λ (amu · nm² /ps²). All these simulations were started from the same initial EM configuration with a uniform composition field. The terms FC and DEC, respectively, refer to fully coupled and dynamically decoupled simulations in which membrane was free to undulate.

FIGURE 8.

Snapshot of the two-component EM model at t = 20,000 ps generated by a fully coupled simulation (FC) with Λ = 500 amu · nm² /ps². Light- and dark-shaded regions mark the cholesterol-rich and DMPC-rich phases. If the curvature at a given EM point is approximately greater than the curvature averaged over all the EM points, specifically greater than 0.2[Max_i(H²) − 〈H²〉_i] + 〈H²〉_i, then the given point is white. The local curvature of the membrane is largest predominately within the cholesterol-rich phase.

When Λ < 0, we expect a positive feedback scenario to occur during a fully coupled simulation (FC): DMPC-rich domains are attracted to surface regions of large curvature, H², then the EM bonds in these regions become more slack, enhancing the local curvature, H². This increase in the local curvature should in turn attract more of the DMPC-rich phase. It might be more precise to say that the DMPC-rich phase is attracted regions of large curvature, then makes these regions more susceptible to extremes in curvature, H². Since the cholesterol-rich domains are driven to regions of relatively small curvature, H², when Λ < 0 we also expect that the curvature averaged over all the EM points and over time, 〈〈H²〉_i〉_T, for a FC simulation will be larger than the average curvature generated by the corresponding EM simulation where the composition of each EM point i is fixed at φ_i = φ_c = 0.6 (DEC). Table 5 shows this difference; in addition, it is evident in Table 5 that the 〈〈H²〉_dmpc〉_T for a FC simulation is larger than the 〈〈H²〉_dmpc〉_T for the corresponding DEC simulation at a given value of Λ < 0.

Curiously, when Λ > 0 the overall average curvature, 〈〈H²〉_i〉_T, for a FC simulation is also larger than the 〈〈H²〉_i〉_T for the corresponding DEC simulation where φ is uniform. When Λ > 0, F[φ,H] will be minimized if the cholesterol-rich domains locate themselves at regions of large local curvature, H². For a FC and a DEC simulation, if there are regions of maximum curvature, H², outside the cholesterol-rich phase, the phase boundary/interface will deform to include these regions within the cholesterol-rich phase; that is, the CH dynamics will move the phase domains so that the maxima of curvature are predominately located within the cholesterol-rich phase and near the boundaries of that phase (Fig. 8). Within the cholesterol-rich domain, the EM bonds are stiffer for a FC simulation than for a DEC simulation. As a result, within a cholesterol-rich domain, the susceptibility to extremes in curvature, H², should be less for an FC simulation than for the corresponding DEC simulation. Fig. 9 gives two instantaneous membrane configurations, one at t = 23,000 ps and one at t = 32,000 ps, taken from an FC simulation with Λ = 500 amu nm²/ps². Given these two snapshots and others like them, we observe that the especially extreme maxima in curvature, H² (shown in yellow), can usually be found near the boundaries of a cholesterol-rich domain for an FC simulation with Λ > 0, presumably because such extremes are not as favored within this phase. Originally, we expected that the cholesterol-rich domains would be attracted to surface regions of relatively large curvature, then for an FC simulation the EM bonds in these regions would become more stiff, reducing the local curvature, H². One might be inclined to designate this feedback scenario as being negative. Contrary to these expectations, however, the 〈〈H²〉_chol〉_T is larger for a FC simulation than the corresponding DEC simulation at a given value of Λ > 0 (Table 5). One possible explanation might be that, loosely speaking, although the curvature, H², is suppressed at surface regions within a cholesterol-rich domain for a FC simulation, it might simultaneously be enhanced in some surface regions (at some times) near the phase boundaries in the neighboring DMPC-rich domain: as the phase boundary deforms to meet a spot of maximum curvature outside a cholesterol-rich domain, the stiffening of bonds within surface regions now occupied by the cholesterol-rich domain might transmit a large elastic disturbance forward to the EM points in the spot of maximum curvature occupied by the neighboring DMPC-rich domain whose EM bonds are more slack. The EM bonds in the DMPC-rich phase of a FC simulation are also more slack relative to these bonds in the corresponding DEC simulation, implying that the DMPC-rich phase is more susceptible to large curvatures in a FC simulation compared to the DEC simulation. Finally, one should not have the preconception that regions most rich in cholesterol are located near the middle of a cholesterol-rich phase domain. When a spot of maximum curvature enters a cholesterol-rich domain the coupling contribution to the free energy of the composition field, Eq. 9 will be minimized for Λ > 0 if φ is made as small as possible; Fig. 7 confirms this prediction. This result also implies that at a spot of large curvature there will also be large gradients in the composition, φ. Note that the gradients in the curvature, H², can be inferred from the coloring scheme (white, green, then yellow) and the caption information of Fig. 9.

FIGURE 9.

Snapshots of the two-component EM model at t = 23,000 ps (left) and at t = 32,000 ps (right) generated by a FC simulation with Λ = 500 amu · nm² /ps². Blue and red regions mark the cholesterol-rich and DMPC-rich phases. If the curvature at a given EM point is >A[〈Max_i(H²)〉_T − 〈〈H²〉_i〉_T] + 〈〈H²〉_i〉_T, then it is colored yellow, green, or white (A = 0.75, yellow; A = 0.35, green; and A = 0.20, white). Yellow regions have the largest curvature, followed by green, then white. Above, 〈Max_i(H²)〉_T = 2.328 × 10⁻² nm⁻² and 〈〈H²〉_i〉_T = 2.616 × 10⁻³ nm⁻². Surface regions of especially large curvature, H², are usually found near the phase boundaries for Λ > 0 (FC).

To obtain a quantitative measure of the correlation between the positions of spots of large curvature (colored yellow in the snapshots, Fig. 9) and the positions of the points on the phase boundaries, we plot the fraction of the total number of yellow EM points that lie at a given distance, D_bnd, from the phase boundary. The distance of a given yellow EM point to the phase boundary is defined to be the distance between the yellow EM point and its nearest neighboring point on the phase boundary. In Fig. 10, N_y(D_bnd) is the total number of yellow EM points that lie within the interval [D_bnd – 0.5 nm, D_bnd + 0.5 nm], and N_y is the total number of yellow points. Totals are accumulated over the last 20,000 ps of the simulations. For the negative-feedback FC simulation, the maximum in this plot lies at D_bnd ≈ 1 nm; however, for the corresponding DEC and positive-feedback FC simulations, the maximum lies further out at D_bnd ≈ 4.5 nm and D_bnd ≈ 3.5 nm, respectively.

FIGURE 10.

Fraction of the total number of EM points of large curvature (colored yellow in the snapshots) that lie at a distance, D_bnd, from the phase boundary. Plots are given for two values of the coupling parameter, Λ (amu · nm²/ps²).

For the static membrane simulations where the composition field experienced no time-dependent external fields or internal sources of noise, when Λ < 0 the population of the DMPC-rich phase was less than the population of the cholesterol-rich phase: P_dmpc < P_chol. To understand the origin of this inequality, in the previous section we considered the shifts in the positions, 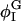and of the local minima in 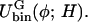However, for a simulation where the membrane was free to undulate and provide a time-dependent force acting on the φ_i, this inequality switched to P_dmpc > P_chol when Λ < 0. Again this inequality can be explained by examining When Λ < 0, the DMPC-rich phase domains are attracted to regions of large curvature, H², decreasing the value of at 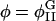relative to the value of 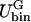at Here 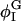and 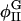are, respectively, the approximate compositions of the cholesterol-rich and DMPC-rich phases. Given that φ experiences a time-dependent field with a superimposed source of noise, it is now possible for the composition of an EM point, φ_i, to be thrown from the potential well 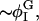then caught in the deeper potential well at 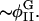The noise in our simulations originated from the random DPD force, 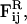and possibly from the changes in the cancellation error of the Fourier series fit, h(x, y, t), that occurred from one timestep to the next. To be strict, we could include in the CH equation a noise term that obeys a fluctuation-dissipation relation (Gardiner, 1985) so that a canonical distribution with a Hamiltonian, F[φ,H], is generated by the composition dynamics with a static H. However, we omitted this term. When Λ < 0 the inequality, P_dmpc > P_chol, was observed for both the fully coupled and dynamically decoupled simulations, but this inequality tended to be slightly more pronounced for the fully coupled simulations because here the DMPC-rich domains are allowed to enhance the local curvature, H², in the regions of already large curvature that initially attract these domains. As a result, the potential well at 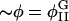becomes even deeper compared to the well at 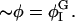The switch in the inequality can be seen in Fig. 11, which shows the instantaneous values of P_dmpc and P_chol = 1–P_dmpc during the “steady-state” approach at −900 amu · nm² / ps². At early times, just after the start of the fully coupled simulation, P_dmpc < P_chol but at late times this inequality switches to P_dmpc > P_chol. Similarly, when Λ > 0, we found the opposite inequality to be true after the “steady-state” approach—that is, P_dmpc < P_chol.

FIGURE 11.

Instantaneous values for the populations of the DMPC-rich and cholesterol-rich phases, P_dmpc and P_chol, during a fully coupled EM simulation at Λ = −900 amu · nm²/ps². Here the membrane was free to undulate (FC).

For a perfectly flat membrane, there exists a third stage in the phase separation of the composition field. In the first two stages, the interfaces between the two phases sharpen such that the phase domains become well defined. Later in the third stage, these domains grow in size so as to minimize the amount of perimeter between the two phases and in turn minimize the energetic cost for having interfaces. The structure of these domains coarsens in a self-similar manner eventually reaching a scaling regime in the long-time limit where the widths of domains, R(t), grow as R(t) ∼ t^1/3 (Rogers et al., 1988). Noise serves only to speed the completion of the first two stages, roughening the interfaces, and to impede the approach to the scaling regime. In other words, the continual growth of the domains occurs independently of noise being included, or not, in the composition dynamics. For a nonflat membrane, the contribution to free energy from the coupling between the composition and curvature fields, F_φH, competes with the contribution from the energetic cost for having interfaces between the two phases. If this coupling contribution is sufficiently large, then the domain growth occurring in the third stage can be impeded (Taniguchi, 1995). Furthermore, when R(t) becomes comparable to the dimensions of the simulation box, the domain growth will come to a halt because of the periodic boundary conditions imposed on the membrane. The linear stability analysis of the CH equation (end of Parameters, above) predicted that the phase domains should initially, before coarsening, have an average width of ∼9 nm, implying that our simulation box lengths would be too small to explore the later scaling regime. Nonetheless, the onset of this regime can be seen for t > 10,000 ps (the first two stages of the phase separation occur before t = 10,000 ps). Fig. 12 shows the number of EM points on the phase boundaries, N_b; this number decreases for the FC and DEC simulations, but given that our simulation box is too small, we cannot determine the scaling exponent z in N_b ∼ t^−z for t ≫ 40,000 ps. Curiously, the existence of the scaling regime implies that a true steady state can never be reached exactly. For this reason, we have put the phrase steady state within quotation marks in our discussion above.

FIGURE 12.

Number of EM points on the phase boundary between the cholesterol-rich and DMPC-rich phase domains. This boundary is defined as those points where 0.56 < φ < 0.64. These phase boundaries are only well defined once the phase domains have formed, that is, for t > 10,000 ps.

Knowing that the initial two stages of the phase separation occur on timescales comparable to the timescales of the membrane undulations does not necessarily imply that the characteristic timescale for the subsequent movement of the phase domains will also be comparable. In a steady state, we did observe a very slow growth in the phase domain structure; the phase domains ranged in projected width from 10 nm to 12 nm. However, these domains were not static. Looking at configuration snapshots taken during a simulation run, we saw considerable movement of the phase boundaries in response to changes in the local curvature, H². A front-velocity, c_m, at an interface can be estimated by letting Here φ_m(r_m, t) is the composition written as a function of coordinates, r_m, in some local axis system whose origin is fixed on the membrane. Provided c_m is weakly dependent on r_m and t, the magnitude of the projection of c_m onto the direction of ∇_mφ_m is Evaluating 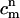for points only at the interface, we estimated, given 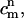that the time required for a domain to move across a distance of 10 nm ranged from 10³ ps to 10⁴ ps; this time decreased as Λ increased. Looking at Fig. 9, however, we saw that there was a slow change in the pattern of the phase domains. This change was faster for the negative feedback scenario, Λ > 0 (FC), than for the positive feedback scenario, Λ < 0 (FC): the EM model with Λ > 0 is more “frustrated” than the EM model with Λ < 0. By contrast, the change in the phase patterns for the dynamically decoupled simulations (DEC) was faster than the corresponding fully coupled simulations (FC): the membrane undulations in the DEC simulations are independent of the phase domains. Presumably, finite-size effects will also reduce the number of ways in which a phase pattern can change, slowing the transformation of these patterns.

DISCUSSION AND CONCLUSIONS

In this article, we presented and applied a method for simulating a two-component lipid bilayer membrane in the mesoscopic regime. The membrane was modeled as an elastic network of bonded particles or points where the strength of the bonds depended on the composition of these points. Composition in the mesoscopic regime can be treated as a property of a point rather than a property of a collection of points as it is in the microscopic regime. Therefore, rather than trying to simulate two types of molecular species, we let the composition be an extended degree of freedom. The dynamics of the composition field was generated by integrating in time the CH equation (Cahn and Hilliard, 1958), which incorporates a free energy functional to model a binary mixture. Knowing the coexistence curve of the mixture, and the interfacial width and line tension between two coexisting phase domains, the parameters in this functional can be set. A systematic procedure for assigning these parameters was outlined. Furthermore, knowing how the microscopic bulk modulus, thickness, and mass density vary with composition given fits to data determined in earlier atomistic NEMD simulations (Ayton et al., 2002b), the spring constants between the bonds in the EM network could be modulated. To couple the composition φ to the curvature H, the bending modulus was treated as a function of the composition. Expanding this modulus at some reference composition, we could then identify the coupling contribution to the free energy functional. This cubic coupling contribution was linear in the composition and quadratic in the curvature. A bilinear coupling contribution should also be included if the solvent environments on opposite sides of the membrane are not identical. We did not include this contribution in our study. We should stress that lateral phase separation for a cholesterol lipid bilayer has been observed by fluorescence for a ternary mixture, but not a binary mixture. Nonetheless, we treated the DMPC/cholesterol system in our study as if it could exhibit a phase separation. This treatment was warranted because the purpose of our study was to demonstrate a simulation strategy and examine its results for a simple model. In the future, our method should be extended to describe ternary mixtures, in order to make comparisons with experiments.

All our simulations began from a critically quenched, uniform composition field. Depending on the sign of the coupling parameter, either the cholesterol-rich phase or the DMPC-rich phase was attracted to regions of large local curvature, H². In the positive feedback scenario, the DMPC-rich phase is attracted to these regions; since the DMPC-rich phase is less rigid and less resistant to uniform changes in the local surface area than the cholesterol-rich phase, positive feedback yields an increase in the local curvature, H², at the DMPC-rich phase as well as an increase in the overall average curvature of the membrane. Our estimate of the cubic coupling constant, Λ, given our EMD data for the microscopic bulk modulus (Parameters, above), does yield a definite sign for Λ, predicting the positive feedback scenario (Λ < 0). Experimental results for ternary GUV mixtures composed of cholesterol, DOPC, and sphingomyelin (Baumgart et al., 2003) appear to agree with this prediction: the less rigid ld phase was found in the neck region of a budding domain, a region of extremely large curvature. It is obviously energetically more favorable to have the less rigid phase, whose bulk modulus is small relative to the lo phase, in the neck. By contrast, in the negative feedback scenario, the cholesterol-rich phase is attracted to regions of large local curvature, and here this curvature, H², should be suppressed. However, since cholesterol suppresses the same curvature that initially attracts it, the effect of this negative feedback on the overall average curvature is not as predictable as with positive feedback. Furthermore, we suspect that the stiffening of EM bonds, as the cholesterol-rich domain advances toward a spot of large curvature in the neighboring DMPC-rich domain, may transmit a disturbance to the motion of the EM points in this spot, enhancing the spot's already large curvature. Therefore, we should not designate this feedback as being negative. We stress that feedback in the mesoscopic regime will be observed only if there is not a significant timescale separation between the curvature and composition fields. This separation should become smaller as the coupling between these fields becomes stronger. As discussed in Parameters, the mobility was set four orders-of-magnitude larger than our estimates, primarily to compensate for the absence of a solvent and its dampening effects on the undulating motion of the membrane's surface. In the future, we need to include these effects, and have accurate values for our free energy parameters, to determine whether this timescale separation exists or not.

A purpose of this study was to demonstrate that the dynamics of the curvature and composition fields could be coupled within the existing framework of the EM model such that this coupling is parameterized by the microscopic material properties of the membrane. However, our ultimate goal is to use this method to investigate whether the mesoscopic bulk modulus (the effective modulus measured experimentally) depends on the existence of phase domains, which are mesoscopic in spatial width. This question cannot be addressed in the laboratory setting because it is impossible to prevent phase separation at temperatures below the critical temperature of mixtures lying between the coexistence curves. It is conceivable that the existence and movement of these domains may affect the stress response of the membrane to uniform changes in the membrane's projected area across mesoscopic length scales. For example, one can imagine a region of large local curvature, H², forming in the EM model whose bonds pull on the membrane's boundaries; with positive feedback, the DMPC-rich phase are attracted to these regions and weaken these bonds, thereby weakening their pull. Before answering this question, we require an explicit model for water in our mesoscopic dynamics to accurately reproduce the speed and character of the membrane undulations in a bulk solvent. In our earlier studies of a GUV under an osmotic pressure gradient, the modulus parameterizing the macroscopic material-point method (MPM) simulation (York et al., 1999; Ayton et al., 2001, 2002b) was set to the microscopic bulk modulus. However, it is known that subvisible thermal undulations can modify the stress response of a membrane (Evans and Rawicz, 1990, 1997; Rawicz et al., 2000): a zero-stress state simulated by molecular dynamics under periodic boundary conditions with simulation box lengths <∼10 nm actually corresponds to a highly stressed mesoscopic state (Ayton and Voth, 2002). Therefore, when parameterizing these MPM simulations of a macroscopic vesicle, the mesoscopic, not the microscopic, bulk modulus should be entered into the force calculation.

Integrating the CH equation, as it stands, is a computationally demanding method for simulating a multicomponent membrane in the macroscopic regime. Inasmuch as a point in a mesoscopic EM simulation represents a microscopic MD simulation box, a material point in a macroscopic MPM simulation represents a mesoscopic EM simulation box. Therefore, to obtain an equation of motion for the composition more pertinent to the macroscopic regime, we still need to spatially and temporally coarse-grain the CH equation (Goldenfeld et al., 1998). This averaging of the governing dynamics should yield a diffusion-like equation for a macroscopic composition field, defined by local averages of the composition field over the mesoscopic dimensions of the EM simulation box. This equation should govern the dynamics of the slow, long-wavelength modes in the composition field coupled to the slow, long-wavelength modes in the membrane's curvature, given that the affects of all the fast, short-wavelength modes in the membrane have been averaged. The short-wavelength modes in the composition field represent the phase-domain structure in the mesoscopic regime. However, this derivation will be difficult if a timescale separation exists where the short-wavelength modes in the curvature field move much faster than these modes in the composition field. Here, in the mesoscopic regime, the curvature will appear to the composition as a composition-dependent noise. In addition, an accurate assignment of the mobility will be important when the effects of an external field on the membrane dynamics are investigated. Here the mobility will govern the rate at which the composition field can respond either directly to these fields, such as to electric field (Groves et al., 2000), or indirectly through the changes in curvature resulting from these fields, such as a shear flow (de Haas et al., 1997; Kraus et al., 1996). To summarize, given a mesoscopic bulk modulus and a coarse-grained CH equation, we could attempt accurate and feasible simulations of a two-component GUV under various nonequilibrium conditions where the material properties of the membrane in the macroscopic regime are conditioned by the thermal undulations and possibly phase coexistence in the mesoscopic regime.

APPENDIX A: FUNCTIONAL DERIVATIVE

The composition can couple to the curvature directly through the free energy model and indirectly through the second-order spatial derivatives of the metric arising from 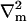in Eq. 6. To see this secondary coupling, we must evaluate the functional derivative with respect to φ in Eq. 6. First, the two-dimensional Laplacian operator 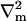in a local frame fixed on the membrane has to be rewritten in terms of differential operators in the lab frame. Given the rotation matrices relating these two frames, a coordinate transformation yields after some algebra

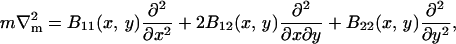(35)

and similarly

(36)

where

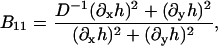(37)

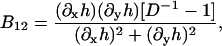(38)

(39)

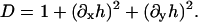(40)

If 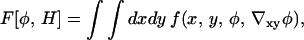then the functional derivative is

(41)

which when evaluated becomes

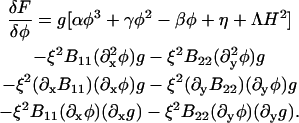(42)

The last four terms on the right-hand side of Eq. 42 are negligible compared to the remaining terms provided the spatial derivatives, ∂h, are sufficiently small. Specifically, if ∂h (representing 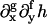where g and f are integers) is sufficiently small, then the last four terms in Eq. 42 are to order [(∂h)² + O((∂h)⁴)]∂φ, whereas the remaining terms are either to order 1 + O((∂h)²) or [1 + O((∂h)²)]∂φ.

APPENDIX B: EM MODEL AND DYNAMICS

The EM model is constructed by first considering two identical, perfectly flat leaflets above and below one another separated by 3 nm, each representing a monolayer. The initial area, A₀, of each leaflet is discretized into a number of small elements representing particles or points. After an in-plane dilation in area to A, the energy of one leaflet is

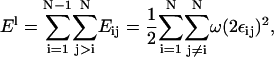(43)

where N is the number of points on one leaflet. Here ω is a constant to be determined, and 2ε _ij is related to the local strain between two points i and j arising from the area dilation. For a membrane parallel to the x,y plane, an in-plane stress, σ = −(1/2)(P_xx + P_yy), is related to an in-plane isotropic strain, 2ε = (A − A₀)/A₀ = ΔA/A₀, via the bulk constitutive relation σ = λ(ΔA/A₀) (Evans and Needham, 1987; Needham and Nunn, 1990; Hallet et al., 1993). Here λ is the microscopic bulk modulus describing the stress response of a perfectly flat membrane to an in-plane, isotropic change in area, ΔA; λ is estimated using cyclic compression NEMD (Hoover et al., 1980; Evans and Morriss, 1990) simulations starting from multiple configurations selected from an EMD trajectory under zero stress conditions, P = − σ = 0. Under adiabatic conditions, dE = − PdV = σh′dA, and the energy of the bilayer consistent with the constitutive relation is

(44)

The constant, ω, can be identified by noting that E(A) ∼2〈E^l〉 is a sum of the energies of the two identical, monolayer leaflets and by comparing Eq. 43 with Eq. 44. For small, in-plane deformations, the average local strain, 〈(2ε _ij)²〉, is ∼(ΔA/A₀)², and Eq. 43 becomes 〈E^l〉 ≈ 0.5N〈N_cut〉ω 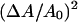; therefore, ω is

(45)

where initial area density is ρ₀ = N/A₀, and 〈N_cut〉 is the average number of points within a cutoff distance (defined below) from a given EM point.

When the membrane's area is A₀ such that σ = 0, the displacements between the EM points are given by 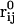; however, when this area is changed to A, the displacements become r_ij, and the local strain is to first order. The conservative force on i due to j is 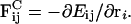In the derivation of the membrane is treated as being perfectly flat. When this constraint is removed and the membrane is allowed to undulate, bending away from the x,y plane, is retained as the conservative interaction between bonded points i and j. Furthermore, a bending resistance is created by bonding points on the same and opposite leaflets such that a given point is linked to those points lying within a sphere of radius r_cut = 3.4 nm ∼ h′ centered on that point. Heat is dissipated by using DPD dissipative and random forces (Espanol and Warren, 1995; Groot and Warren, 1997) or by using a Nosé-Hoover feedback (Evans and Holian, 1985).

The number of EM points on each leaflet is N = 3460 so that the reduced number density of the whole membrane is 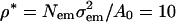where N_em = 2N and σ_em = 3.4 nm ∼ h′, which is the thickness of the DMPC bilayer membrane at P = 0 estimated from atomistic EMD simulations (Ayton et al., 2002a). The length of an EM particle is essentially σ_em. The mass of an EM particle is ρ_mAh′/N_em = m_i where ρ_m is the mass density also estimated from atomistic EMD simulations.