Mesoscopic Lateral Diffusion in Lipid Bilayers

Abstract

The lateral diffusion in bilayers is modeled with a multiscale mesoscopic simulation. The methodology consists of two simulations, where the first employs atomistic models to obtain exact results for the mesoscopic model. The second simulation takes the results obtained from the first to parameterize an effective force field that is employed in a new coarse-grained model. The multiscale aspect of this scheme occurs at the point where the microscopic time-averaged results of the first simulation are employed to parameterize the second simulation that operates in a higher spatial and temporal domain. The results of both simulation schemes give quantitative information on the details associated with lipid lateral diffusion.

INTRODUCTION

The computational limits of computer simulations of lipid bilayers are now at the point where atomistic-level models can be examined over timescales on the order of 100 ns (Lindahl and Edholm, 2001), or over lengthscales on the order of 20 nm (Lindahl and Edholm, 2000; Marrink and Mark, 2001; Hofsab et al., 2003). At these spatial and temporal regimes, long-wavelength phenomena such as slow bending modes begin to appear, as system sizes on the order of 20 nm can begin to exhibit significant thermal undulations (Lindahl and Edholm, 2000; Marrink and Mark, 2001). In the case of lipid bilayers, the thickness, h, of the bilayer is microscopic (nm), although the area, A, can persist up to nearly macroscopic lengthscales (μm) (Tieleman et al., 1997; Bagatolli and Gratton, 2000; Bagatolli et al., 2000; Forrest and Sansom, 2000; Lipowsky and Sackmann, 1995). Thus, the system effectively spans spatial and temporal regimes ranging from the microscopic to the macroscale. Furthermore, any process associated with a specific lengthscale (for example, the wavelength of a specific undulatory membrane mode) must be examined over a timescale relevant to that spatial domain. In other words, to fully examine systems such as bilayers that contain multiple spatial and temporal regimes, is it not enough to examine microscopic scale systems for long times, or conversely, macroscale systems over short times. Rather, the reality is that, to completely model the structure and dynamics of biological assemblies such as lipid bilayers, it is ultimately necessary to span not only the entire spatial regime from the atomistic to macroscopic scales, but also the corresponding temporal domain.

Presently, certain large-scale atomistic molecular dynamics (MD) simulations can reach mesoscopic spatial and temporal regimes with lengthscales on the order of 20 nm (Lindahl and Edholm, 2000; Marrink and Mark, 2001; Hofsab et al., 2003; Marrink et al., 2004) using the GROMACS force field (Spoel et al., 1996). The success of these simulations relies on some degree of coarse-graining of both the lipids and solvent. A number of coarse-grained lipid MD models have been developed (Marrink et al., 2004; Shelley et al., 2001; Goetz and Lipowsky, 1998; Goetz et al., 1999), and have been shown to reproduce various equilibrium structural properties; for example, the bilayer thickness. However, with these methods the truncation of electrostatics, combined with severe simplifications to the lipid molecular structure, can potentially alter the membrane's material properties; for example, the bulk modulus (Wheeler et al., 1997). Alternative schemes based on a more continuum-level membrane representation (Lin and Brown, 2004; Brown, 2003) incorporate, for example, the bending modulus as a primary parameterization. This approach to the problem could be particularly promising, especially in the context of a multiscale scheme, where the required parameters for the model are calculated at the atomistic level using, for example, nonequilibrium molecular dynamics (Ayton et al., 2002a,b). In recent articles from the present authors (Ayton and Voth, 2002, 2004), a mesoscale model for a membrane was proposed, called the elastic-membrane (EM) model, that was designed to operate within a multiscale simulation framework previously developed (Ayton et al., 2002a,b, 2001; Ayton and Voth, 2002). This model was used to examine the membrane's “bulk” elastic response to deformations. The general idea is to use the MD simulation cell as a “material property” template and then coarse-grain the membrane into domains with lengthscales approximately the size of the MD cell. These regions are then parameterized to respond to local plane-strain as predicted by atomistic-level (nonequilibrium molecular dynamics) bilayer simulations (Ayton et al., 2002a). The EM model employs the microscopically calculated bulk modulus, thickness, and density as key parameterizations to model to bulk elastic response of the membrane. The bending modulus is then found by explicitly creating a bending moment (Sackmann, 1994).

However, the full constitutive relation for bilayers includes the in-plane viscous shear viscosity, as bilayers are defined by a state of zero shear modulus (Hallet et al., 1993; Evans and Needham, 1987). This results from the fact that the lipids laterally diffuse within the plane of the bilayer. For example, lateral diffusion in lipid bilayers has been examined theoretically (Saffman, 1976; Saffman and Delbruck, 1975; Lipowsky and Sackmann, 1995), experimentally (Korlach et al., 1999; Rinn et al., 1999; Fahey et al., 1977; Almeida et al., 1992; Shin et al., 1991; Lipowsky and Sackmann, 1995), and with computer simulation (Hofsab et al., 2003; Essmann and Berkowitz, 1999; Lindahl and Edholm, 2001). Theoretically, Saffman modeled the hydrodynamic scenario of lateral diffusion by considering a cylinder of height h and radius r_c immersed in a thin membrane surrounded by viscous fluid (Saffman and Delbruck, 1975), where the viscosity of the surrounding fluid was less than that in the membrane. Including the viscosity of the surrounding fluid avoids a divergent diffusion coefficient in two dimensions (Saffman, 1976). The approximate result for the lateral diffusion constant, D_lat is given by

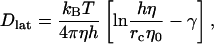(1)

where η₀ is the viscosity of the surrounding fluid and γ is Euler's constant (∼0.5772). Also, in (Saffman and Delbruck, 1975), a Langevin model of a similar particle in a sheet was also considered.

A wealth of experimental studies aimed at measuring the lateral diffusion coefficient in bilayers have been performed, and they can be loosely divided into short-range diffusion methods such as quasielastic neutron scattering (Lipowsky and Sackmann, 1995; Shin et al., 1991; Pfeiffer et al., 1988), and long-range diffusion methods such as fluorescence (Korlach et al., 1999), and magnetic resonance (Shin et al., 1991; Filippov et al., 2003; Oradd et al., 2002). Depending on whether short or long-range methods are used, different measurements of the lateral diffusion coefficient have been obtained (Vaz and Almeida, 1991). The origin of the discrepancy is believed to originate from short-time free volume displacements (Vaz and Almeida, 1991) versus long-time lipid motion. Experimentally, the short-time diffusion coefficient can be two orders-of-magnitude larger than the corresponding long-time diffusion coefficient.

Recent computer simulations of dipalmitoylphosphatidylcholine (DPPC) bilayers (Essmann and Berkowitz, 1999), employing 10-ns trajectories, calculated the lateral diffusion coefficient from the slope of the mean-square displacement; no discrepancy between the short-time and long-time diffusion coefficients was observed. The value of the lateral diffusion coefficient was found to be in reasonable agreement with neutron scattering experiments (Pfeiffer et al., 1988). Simulations over much longer times (100 ns) (Lindahl and Edholm, 2001), for the same system, indicate that the long-time diffusion coefficient is indeed smaller, and more in agreement with fluorescence techniques. However, large system size simulations (Hofsab et al., 2003) (1024 lipids compared to 64 in the previous work) examined over 10 ns exhibit a lateral diffusion similar to that found in Essmann and Berkowitz (1999). The main conclusion is that, perhaps, the time examined (length of simulation) and the accessible nonperiodic translational space (system size) are intrinsically coupled. That is, even though the system size was significantly larger in Hofsab et al. (2003), the lipid displacements occurred on the same timescale as in Essmann and Berkowitz (1999).

Importantly, most experimental scenarios do not measure the diffusion of actual lipids, but of test-probe molecules. For example, fluorescent probes in combination with confocal fluorescence microscopy (Korlach et al., 1999; Fahey et al., 1977) have been used to calculate the lateral diffusion coefficient in various bilayers. The idea is that the structure and amphipathic nature of the fluorescent probes are such that they should diffuse much like lipids. Thus, the probe particles combine with the lipids and couple with their dynamical behavior. In this case, the lateral diffusion coefficient is defined as in Lipowsky and Sackmann (1995),

(2)

where 〈r²〉 is the mean-square displacement of the randomly moving test probe which may, or may not, actually be a lipid.

Of course, with MD this approach is not generally used, as the coordinates of every atom are in hand. However, when the objective is to construct a mesoscopic model for lipid lateral diffusion, a carefully designed test probe, immersed in the bilayer, could itself become the new fundamental mesoscopic particle that would eventually be employed in a coarse-grained model of the entire membrane. Consider the following scenario: A test-probe with specially chosen dimensions (e.g., slightly larger than a lipid) is embedded into a detailed atomistic level MD simulation of a fully hydrated bilayer. The dynamical motion of the test probe is then used to define the new coarse-grained dynamics. The probe dynamics, resolved in terms of time correlation functions (TCFs) (Allen and Tildesley, 1987; Evans and Morriss, 1990), thus give an average description of the probe motion due to interactions with the surrounding environment. Then, the final step in creating the full mesoscale coarse-grained model involves “pulling out” the underlying MD, and replacing the detailed microscopic-level forces with an effective field designed to model dynamics of the probe. The effective field can be found, for example, by using linear response theory (Kubo, 1966; Evans and Morriss, 1990) combined with a Generalized Langevin equation (GLE) (Chandler, 1987; Evans and Morriss, 1990).

Employing this test-probe approach actually accomplishes two things. First, it defines the properties (i.e., the dimensions) of the new mesoscopic coarse-grained particle. Secondly, if it is designed carefully, it can give a wealth of information regarding the actual details of lipid diffusion. An interesting question in terms of lipid diffusion is the degree of correlated lateral lipid motion, and how locally correlated processes affect the lateral diffusion coefficient. In the free volume argument (Vaz and Almeida, 1991), the small vacancies or holes in the bilayer are a key mechanism involved in lateral lipid diffusion; however, superimposed on this process is the local collective motion of the bilayer itself (Fujitani, 2002). Not only does the membrane undulate in directions parallel to the local membrane normal; it also “sloshes” laterally. Of course, the magnitude of this collective motion depends on the size of the domain that is examined. A test probe will pick up all of this information: it will experience the fast-frequency Brownian motion due to interactions with lipids, as well as couple with the local collective motions (or lateral sloshing) that are present.

With the idea of a test-probe in mind, in this article we will extend the methodology developed for pure liquids in Ayton et al. (2004) to examine lateral diffusion from a mesoscopic and coarse-grained perspective. As such, this article will be divided into two parts. In the first part, a specially designed test-probe approach will be used to examine lateral diffusion in membranes. Both pure dimyristoylphosphatidylcholine (DMPC) and (1:1) DMPC/cholesterol mixtures will be examined. The implementation involves embedding a ghost probe, denoted a TUBE (two-dimensional undulating blob-like entity), into an atomistic-level simulation of a bilayer. The tube thus picks up any local lateral motions in the membrane. The dynamics of the TUBE are characterized by various TCFs (Allen and Tildesley, 1987; Evans and Morriss, 1990), and thus give a quantitative description of the specific mesoscopic diffusive processes in the membrane. Specifically, the resulting dynamical correlations can be employed to give information on the details associated with collective diffusion in the bilayer.

The second part of the article employs the results found in the first part to aid in the construction of a dynamical mesoscopic membrane model for lateral diffusive motion, which employs a methodology similar to that previously done for isotropic fluids (Ayton et al., 2004). The problem is cast within the framework of a GLE (in two dimensions), and is similar in spirit to the Langevin model discussed in Saffman and Delbruck (1975), where it was noted that a primary main challenge in describing membrane lateral diffusion with a GLE framework is the determination of the actual functional form of the memory function. If the memory function was known beforehand, then along the second fluctuation-dissipation theorem (Kubo, 1966; Chandler, 1987), it would be, in principle, possible to construct a GLE capable of describing membrane lateral diffusion.

THE TUBE SIMULATION METHOD

In the TUBE simulation method, a ghost probe (a tube) is embedded in an atomistic-level MD simulation of a bilayer surrounded by solvent (Ayton et al., 2002a), and the resulting dynamical motion of the tube is resolved employing the underlying MD. A snapshot of the embedded tube (denoted by the lighter region) is shown in Fig. 1. The term ghost refers to the fact that the probe particle does not alter either the structure or dynamics of the surrounding bilayer; however, it can respond to dynamical and structural changes originating at the molecular level. For this article, we will employ a DMPC bilayer with parameters as described in Ayton et al. (2002a), as well as a DMPC/cholesterol 1:1 mixture (Ayton et al., 2002b) as the underlying MD system.

FIGURE 1.

A snapshot of a TUBE ghost-probe in a DMPC bilayer simulation.

The means by which such a mesoscopic simulation is performed was previously discussed in detail in Ayton et al. (2004). Here, we will only highlight some key points. Very briefly, the TUBE simulation method involves embedding a cylindrical ghost-particle in an atomistic bilayer at some position R(t). For clarity, TUBE refers to the simulation method, whereas tube refers to the ghost particle itself. The volume of the TUBE is

(3)

where r_c is a predetermined cutoff radius, and h is the height of the cylinder. In this case, the tube is oriented along the z axis, and its height h spans the entire central MD simulation cell in the z direction. As such, the thin layer of solvent above and below the bilayer is also included (as shown in Fig. 1). The dynamics of the tube are only resolved in the x,y plane and thus it has two degrees of freedom. The mass of the tube, on average, is given by 〈m_B〉, where 〈m_B〉 = V_Bρ_N, and ρ_N is the average mass density.

Once embedded in the MD bilayer simulation, the tube will begin to move according to the forces acting on it, as well the collective flows present in its surroundings. The force acting on the tube from the surroundings is equal and opposite to the force the tube exerts on the rest of the system. Thus, by definition, the instantaneous force, is expressed as

(4)

where P_i is a time-dependent switching function such that P_i = 1 if atom i is within the tube at time t and is zero otherwise. The molecular force, f_i, is found from the gradient of the MD potential, f_i = −∇_riV(r), where r_i is the position of atom i. It should be noted that other choices for P_i are also possible (Flekkoy and Coveney, 1999). Unless otherwise explicitly stated, all vectors quantities (e.g., F(t)), will only contain the x and y components, as TUBE is designed to model the in-plane motion within the membrane only. The velocity of the tube is related to the local collective mass flows that are present, and is defined as

(5)

where the instantaneous mass of the tube is given by 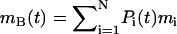and p_i(t) is the momentum of atom i at time t.

These forces and flows in a sense drag the tube around such that it samples the available space within the MD simulation. However, the atoms that are within the tube at any given moment are not bound within its volume, and are free to enter and exit. In fact, the atoms that enter and leave will carry their momentum, resulting in a convective component to the tube acceleration (Ayton et al., 2004). The translational motion can thus be resolved in terms of F(t) and U(t) by defining

(6)

where the integration timestep δt is that of the underlying molecular dynamics. At each time-step, the quantities F(t), U(t), and m_B(t) are recalculated, and the new position of the tube is updated. Note that since the atoms are free to enter and exit the tube, the equilibrium molecular correlations of the bilayer are not perturbed. In the case that the chosen tube corresponds to a well-defined molecule, for example a transmembrane protein (i.e., P_i = 1 for atoms that constitute the molecule, and is zero otherwise), then dR/dt = U, dU/dt = F/m_B, and Eq. 6 is the exact Taylor series expansion of R(t), the instantaneous center of mass, to second order.

Furthermore, under equilibrium dynamics at the MD level, the average kinetic energy of a tube will obey equipartition. In the molecular dynamics ensemble, where and m_B = 〈m_B(t)〉, the degrees of freedom must be correctly accounted for, and in the case where the fluctuations in m_B are small, we have

(7)

where d = 2(1 − m_B/M), k_B is Boltzmann's constant, T is the thermodynamic temperature, and M is the total mass of the MD system.

The dynamics of the tube are examined by various TUBE time-correlation functions (TCFs), in an analogous fashion to the more familiar molecular and atomic TCFs (Evans and Morriss, 1990; Allen and Tildesley, 1987). Time correlations of the instantaneous flow of the tube can be monitored by calculating the tube unnormalized velocity-velocity time correlation function, defined as

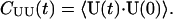(8)

Likewise, the corresponding mean-square displacement in terms of the x- and y-tube position components is given by

(9)

TUBE RESULTS

Underlying MD simulations of a fully solvated DMPC bilayer, as well as a 1:1 DMPC/cholesterol mixture, were performed using the DL_POLY (Smith and Forester, 1999) simulation package version 2.12. The bilayer consisted of 64 lipid molecules with 1312 water molecules resulting in ∼20.5 waters per lipid molecule. The DMPC lipids were modeled using a united-atom force field (Smondyrev and Berkowitz, 1999b) whereas the water model employed was TIP3P (Jorgensen et al., 1983). Details of the DMPC/cholesterol 1:1 simulation are described in Ayton et al. (2002b), and were composed of 32 DMPC molecules with approximately the same water/lipid ratio.

The MD timestep was set at 0.002 ps with a SHAKE tolerance of 10⁻⁴. Electrostatic interactions were calculated using particle-mesh Ewald (Sagui and Darden, 1999; Essmann et al., 1995) with a tolerance of 10⁻⁴. All interactions (real-space Ewald—de Leeuw et al., 1980—and van der Waals) were cut off at 1 nm. Constant temperature simulations in the canonical (NVT) ensemble were maintained using a Nosé-Hoover thermostat with a relaxation time of 0.2 ps. Constant energy (NVE) simulations were also employed as a cross-check. All simulations originated from equilibrated structures (with equilibration times well over 5 ns) and simulations were performed for over 2 ns to calculate the TUBE dynamics.

TUBE simulations were performed by randomly placing a tube in the central simulation cell. During the course of the MD simulation, the displacements of the tube were calculated via Eq. 6, where at each MD time-step, the switching function, P_i, that determines which atoms are in the tube and which ones are not, was updated. The results for the DMPC simulations will be discussed first, followed by the DMPC/cholesterol system.

DMPC TUBE simulations

Two DMPC TUBE simulations were performed: one with a tube with a radius of 1 nm, and one with a radius of 1.5 nm. With the DMPC area per lipid for this model calculated as ∼60 Ų (Smondyrev and Berkowitz, 1999a), the smaller tube will contain, on average, 10.4 lipid molecules within V_B (5.2 from each leaflet of the bilayer). Thus the tube is larger than one lipid molecule.

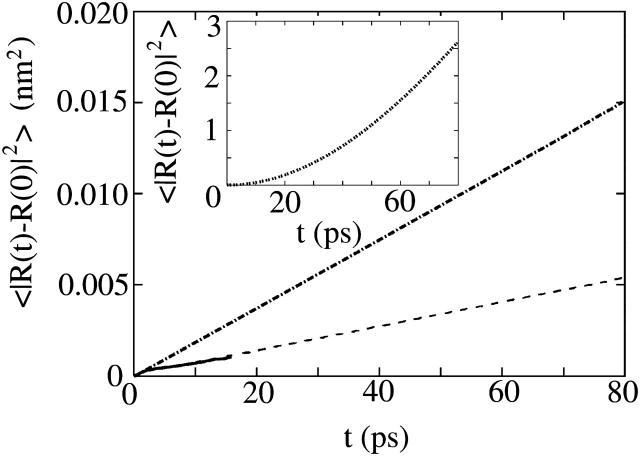
As the tube moves around in the x,y plane during the course of the simulation, both the tube velocity-velocity TCF, C_UU(t), as defined in Eq. 8, as well as the tube mean-square displacement are calculated. With that, in Fig. 2 is shown the short-time behavior of the velocity-velocity TUBE TCF C_UU(t), for a tube with r_c = 1 nm (solid line) and then with r_c = 1.5 nm (dotted). First, it is useful to note that the tube dynamics obeys equipartition via Eq. 7, and thus C_UU(0) for the r_c = 1 nm tube is proportionally greater than that for the r_c = 1.5 nm tube. As the radius of the tube becomes larger and larger, C_UU(0) becomes smaller until the tube basically does not really move. This effect is consistent with, for example, the motion of very large proteins embedded in membranes.

FIGURE 2.

The exact velocity-velocity TUBE TCF, C_UU(t), for a tube with r_c = 1 nm (solid line) and then with r_c = 1.5 nm (dashed line). The corresponding mean-square displacement over 16 ps is shown in the inset.

More interestingly, a closer inspection of C_UU(t) for r_c = 1 nm shows a distinct caged regime where C_UU(t) < 0. In fact, this regime persists to upwards of ∼4 ps. In this region, the tube undergoes a weak velocity caging effect where it is “going the other way.” The origin of this effect lies in the underlying molecular-level caging effects of all the molecules that constitute the tube, and it implies that the tube motion, at least for this tube size, contains a dynamical memory effect. When the radius of the tube is increased to r_c = 1.5, this memory effect is diminished, and the resulting dynamics are more reminiscent of Brownian motion.

The corresponding long-time mean-square displacement over 16 ps is shown in the inset of Fig. 2. We note that this time is still very short compared to that in Essmann and Berkowitz (1999) and Hofsab et al. (2003). With an underlying MD simulation of 2000 ps, 125 samples of the mean-square displacement at t = 16 ps are obtained. Since only one TUBE is placed in the simulation cell, a large number of samples are required to obtain fairly good statistics. Moreover, the idea behind the TUBE simulation is not to span long times (since it is resolved with a detailed atomistic-level model with full electrostatics), but to analyze the short-time dynamical correlations. As will be discussed in later sections, it is the subsequent coarse-grained model that is responsible for spanning both longer length as well as timescales. The mean-square displacements for these systems exhibit a linear regime after t ∼ 4 ps. The fast short-time mean-square displacement (which is up until t ∼ 4 ps) can be correlated to C_UU(t) as in the main panel of Fig. 2, and the linear regime begins at approximately the same time where the caging correlations in C_UU(t) have decayed. It still may be possible that a slower decay region at much longer times may be present, but in the case of the r_c = 1 nm tube, the resulting diffusion coefficient as calculated from Eq. 2, using a linear fit from t = 4 to t = 16 ps, is D_lat = 1.32 ± 0.005 × 10⁻⁷ cm²/s. Also, if D_lat is found from the integral of C_UU(t) (Allen and Tildesley, 1987) (using t = 0 to t = 10 ps), a corresponding value of D_lat = 1.2 ± 0.1 × 10⁻⁷ cm²/s is found, indicating that the tube equations of motion as given by Eqs. 5 and 6 are correctly linked. In the case of the r_c = 1.5 tube, a much smaller lateral diffusion was found from the mean-square displacement at D_lat = 0.65 ± 0.008 × 10⁻⁷ cm²/s. With TUBE, a definitive separation between short- and long-time estimates for the lateral diffusion do not seem to be apparent; however, the short timescales used in TUBE simulation do not really allow a clear separation of these quantities.

Experimentally, the lateral diffusion coefficient for DMPC has been measured with pulsed-field gradient NMR spectroscopy (Filippov et al., 2003; Oradd et al., 2002) where a value of D_lat = 1.1 × 10⁻⁷ cm²/s was found. It is interesting that the experimental lateral diffusion coefficient for the lipid is very similar to that of the r_c = 1.0 nm tube (where the cross-sectional area of the tube is approximately five times that of the calculated area per lipid).

This observation suggests that the diffusive process of the tube occurs through collective and correlated motions of lipids with a correlation lengthscale that is approximately the radius of the tube. It is important to keep in mind that the tube is not a well-defined molecule (e.g., a membrane protein), but is more like a two-dimensional fluid volume element. Furthermore, the structure of the surrounding membrane is not perturbed in any way. This scenario is in contrast to, say, a membrane-bound protein. In fact, since the tube is not anchored on a particular lipid, its location can change in response to any instantaneous flow or force. This effect will be discussed in more detail in the next subsection.

However, for larger tubes (i.e., r_c = 1.5 nm), the diffusion of the tube is significantly less (as shown in the inset of Fig. 2), and in fact, it is almost half that for the r_c = 1 nm tube.

TUBE: correlated lipid motions

The previous TUBE results can also give insight into the details associated with collective lipid motion. As such, at this point, some comments regarding the lateral diffusion in the TUBE simulations are in order. Recall that the tube is not a lipid, or even a well-defined probe molecule, but a cylindrical volume with height spanning the central MD simulation cell, and a radius r_c. For an r_c = 1 nm tube, the dynamics still contain strong residual molecular-level correlations, and the resulting mean-square displacement gives a lateral diffusion constant that is similar to the experimental estimate for lipids. However, with larger tubes (r_c = 1.5, for example) the lateral diffusion is much less, as noted before. That this new collective entity, the tube, has a lateral diffusion constant that depends on its size, suggests that the regime in which the tube D_lat is similar to the lipid D_lat corresponds to a critical lengthscale, wherein the collective motions of the atoms within the tube are correlated to the molecular mean-square displacement. In other words, a component of individual lipid diffusion could result from collective lipid motion that persists over a lengthscale of roughly 1 nm. Over this lengthscale, the motion of one lipid is highly correlated with that of the neighboring lipids, and for a period of time they move together as a loosely organized collection. At longer times, new lipids join the collection, whereas others leave. However, from the viewpoint of a single lipid molecule, it is always diffusing within a highly dynamically correlated local environment. This behavior might be reminiscent of that observed in cholesterol/phospholipid mixtures (Radhakrishnan and McConnell, 1999; Radhakrishnan et al., 2000) where condensed complexes of cholesterol and certain phospholipids (sphingomyelin) result in new collective diffusive entities. Of course, in the pure lipid case, there are no condensed complexes to speak of, but only highly correlated clusters of lipids over specific lengthscales. Still, these highly correlated motions could behave in a similar fashion to more organized complexes.

Also, since the tube spans the central simulation cell, it includes the lipids from both leaflets of the bilayer. Thus, in principle, the lipids that comprise the tube at a certain time could be separated into those in one monolayer, and then those in the opposing monolayer. If the lipids in one monolayer exhibit opposing, or highly uncorrelated motion with the lipids in the other leaflet, then the tube motion could, in principle, be cancelled out. This does not seem to be the case, and the situation is more along the lines with Korlach et al. (1999), where strong correlations in phase domains in opposing monolayers were observed. Furthermore, given that part of the atoms in the tube arise from the hydration layer above and below the bilayer, it is possible that the water motion adjacent to the lipid headgroups also experiences this highly correlated motion.

A stroboscopic snapshot of the tube location is given in Fig. 3, where the tube displacements in the x,y plane are clearly evident. The time separation between adjacent points is 16 ps, and the motion of the tube over this simulation shows significant movement. The tube displacement occurs from Eq. 6, where the resultant motion of the tube depends on the displacements of the molecules that reside inside the tube at time t. In this way, the tube probe will pick up the collective motions that occur in the region of space defined by Eq. 3.

FIGURE 3.

A stroboscopic snapshot of the exact MD tube position for the r_c = 1 nm system over 1000 ps. The time separation between adjacent points is 16 ps.

An interesting comparison can be made from the previous TUBE results with the theoretical model of Saffman (1976), given by Eq. 1. In Saffman (1976), the viscosity of the membrane is estimated to be ∼100 times that of the surrounding solvent, thus it would be interesting to see what is the measure of the apparent membrane viscosity as found from the TUBE simulation. We use the word apparent because in the theoretical model of Saffman, the exact height of the diffusing cylinder is required: here the height, h, is the height of the central simulation cell in the z direction, and thus it contains a thin layer of water. At this point, the TUBE simulation method does not allow for a direct calculation of the viscosity. This extension would require an external shear in the x,y plane (Evans and Morriss, 1990), and thus the TUBE simulation would be recast in a nonequilibrium regime. Alternatively, a predicted measure of the viscosity can be found from Eq. 1 by employing the previously calculated TUBE diffusion coefficient.

The predicted viscosity can be found from the solution of the equation g(η) = h(η), where

(10)

and h(η) = η. The solution where η ≫ η₀ can be found for the two different TUBE simulations. In the case where r_c = 1 and h = 5.5 nm (the thickness of the box in the z direction), η/η₀ ∼ 35. If instead a value of 3.4 nm is used (the thickness of the membrane), then η/η₀ ∼ 54. Since some of the solvent is employed in the TUBE simulation, its effect gets combined into the measured membrane viscosity. In practice, actually separating the membrane's contribution to the viscosity from that of the solvent (at least in terms of simulation methodologies) could be quite challenging. In the case where r_c = 1.5 nm, we find that, for h = 5.5 nm, η/η₀ ∼ 63, whereas for h = 3.4 nm, η/η₀ ∼ 108. From this comparison, it would appear that the TUBE results can be reasonably accounted for by hydrodynamic theory (Saffman, 1976). If a more precise separation of the membrane and solvent could be made (i.e., a precise measure of h), then a more direct comparison with the theory could also be made. However, even at this level, the results are quite encouraging.

DMPC/cholesterol TUBE simulation

In a previous study (Ayton et al., 2002b), it was found that the addition of cholesterol drastically alters the material properties of DMPC bilayers by a corresponding increase in the bulk modulus. Other properties—for example, the mass density and bilayer thickness—also increased. In the context of the previous pure lipid TUBE results, it is thus interesting to examine the collective mesoscopic TUBE dynamics for a lipid/cholesterol mixture. The idea here is to see how the addition of cholesterol affects the collective dynamical correlations that exist in the system.

Again, a tube is initially randomly placed in the simulation cell, where its displacement occurs through Eq. 6. All the relevant TUBE TCFs (Eqs. 8) along with the mean-square displacement (Eq. 9) were calculated. In Fig. 4, the TUBE C_UU(t), for a tube with r_c = 1 nm, is shown. For the same TUBE size as in the pure DMPC case (Fig. 2, solid line), the resulting correlations are quite different. First, the system again obeys equipartition as from Eq. 7, and at least qualitatively, the caged correlations are actually less than in a pure lipid, i.e., the system seems to exhibit more Brownian-like dynamics. Keeping in mind that at any particular time the tube may contain both lipids and cholesterol molecules (or even parts thereof), it is interesting that the collective dynamics seems to be more Brownian. Apparently the addition of cholesterol seems to disrupt the correlated lipid motions that occur in the pure membrane. When the corresponding mean-square displacement is examined (Fig. 4, inset), the resulting lateral diffusion is significantly less than the pure lipid case. It is very interesting that the TUBE dynamics can pick up such a change in mean-square displacement. In this case, the addition of cholesterol affects the collective dynamics by decreasing the lateral diffusion, but this effect is manifested not by strong caging effects, but in the equipartition (i.e., the time zero value of the TUBE velocity-velocity TCF), and the corresponding increase in mass density associated with the DMPC/cholesterol system.

FIGURE 4.

The exact MD velocity-velocity TUBE TCF, C_UU(t), for a tube with r_c = 1 nm for a 1:1 DMPC/cholesterol mixture. The corresponding mean-square displacement over 14 ps is shown in the inset. The X marks the mean-square displacement for the pure DMPC r_c = 1 nm system.

The fact that the addition of cholesterol apparently decreases the degree of correlated motion in the bilayer is very interesting. One possible explanation for this is an “impurity” model, where cholesterol acts like an impurity in an otherwise homogenous system (the pure DMPC bilayer). In the pure membrane case, the local collective dynamics contains a fairly strong residual caging or sloshing effect, where transient groups of lipids over lengthscales around a nanometer are dynamically correlated. The inclusion of cholesterol disrupts this soft sloshing via an interference effect. Consider the following scenario: a dynamically correlated motion is propagated across a lengthscale slightly larger than a lipid. This motion could be an oscillation to the right, for example. In the pure membrane case, this effect persists; however, in the case where cholesterol is included, this wave is disrupted. The origin of this disruption most likely lies in the rigid structure of cholesterol itself. Of course, at this point, this explanation is still very qualitative, and a more detailed analysis is required to make a more definitive statement.

A MESOSCOPIC MODEL FOR LATERAL LIPID DIFFUSION

The idea now is to construct a coarse-grained model for lateral lipid diffusion, employing the previous exact TUBE results as both a guide and for parameterization. The new coarse-grained model is denoted TUBEsys (i.e., TUBE system). The end result will be a space-filling system of interacting particles (denoted tubes), where the new forces between the tubes are such that the average dynamical behavior of the new mesoscopic particles reproduces that observed in the original TUBE simulation. The results from the previous TUBE simulation of the pure DMPC bilayer will be employed. Of course, by creating a new effective mean force between the particles, the original detailed atomistic interactions are removed, and, as a result, a significant jump in accessible lengthscales, as well as timescales, is achieved. As an aside, when developing a coarse-grained model, one typically has the choice as to the level of granularity, relative to the microscopic state. Most current coarse-grained bilayer models (Marrink et al., 2004; Shelley et al., 2001; Goetz and Lipowsky, 1998; Goetz et al., 1999) still retain lipid-like molecules. With TUBEsys, the fundamental particle has been significantly abstracted from the molecular level and is best thought of as a cylindrical volume with a mass density corresponding to the original underlying atomistic-level system. What must be done now is to develop a means of systematically building up a new set of coarse-grained forces between these new particles, such that the dynamics as well as the thermodynamics (at least a minimalist set of thermodynamic properties) of the new system matches that of the old one. As will be shown, there exists a hierarchy of forces that, when combined, result in a nearly complete dynamical and thermodynamic description of the system in a mesoscopic domain. This is because the set of new coarse-grained forces arise from the decomposition of the original forces observed in the TUBE simulation. The original TUBE force can be decomposed into four terms,

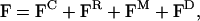(11)

where F^C is a conservative force that gives the required compressibility of the system, and will be discussed in more detail shortly. The next force component is F^R, which is a random force originating from the fast-frequency forces as observed in the original TUBE simulation (Ayton et al., 2004) and can be modeled with a Markovian approximation to a Generalized Langevin equation (GLE) (Chandler, 1987). The third component is a new force component, F^M, and it is denoted the harmonic memory force, because it incorporates the caging effects as observed in C_UU(t) (see the Appendix for more detail). Finally, the last component is F^D = −γUm_B, where γ is a drag term that satisfies both the first and second fluctuation-dissipation theorems (Chandler, 1987).

In a previous study of fluids (Ayton et al., 2004), a methodology was constructed that essentially projected out the random and drag components of F. The required remaining term in that study, the conservative force, was found to be much smaller than the other two components, suggesting that in mesoscopic liquid regimes the random/drag forces almost entirely dominate the dynamics. This result is very important: in mesoscopic models the random/drag effects should not be considered as a small perturbation; rather, they are the dominant forces in the system.

Here, in the case of lateral diffusion in a membrane, by decomposing the total TUBE force into the four components (Eq. 11), information will be obtained on the relative magnitudes of each of the components, and hence, on the interactions that will ultimately determine both the thermodynamic state and the dynamical correlations. Thus, the TUBEsys model not only allows for larger systems and longer times to be examined (via the coarse-graining of atomistic forces), but, by design it separates the complicated total mesoscopic force originally calculated in the TUBE simulation into a set of specific components.

The coarse-grained TUBEsys model will be systematically built up in three stages, rather than collating all four force terms from the onset. In this way, at each stage, the behavior of the model will be examined and will be compared to the previous stage. Thus, in a systematic way, the effect of each force component can be isolated.

The order of the buildup is as follows. First, the conservative interaction will be parameterized and the drag term will be included. At this stage, the drag term is nothing but a standard Nosé-Hoover thermostat. In the second stage, the required random force will be included, following the methodology as in Ayton et al. (2004), and details involved in that force component can be found there. The final stage will be to include the harmonic memory effect.

TUBEsys coarse-grained simulation

The new coarse-grained tube system is denoted TUBEsys, and consists of N_B-interacting particles that move in two dimensions. The acceleration of particle i is given by

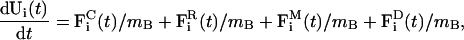(12)

where the different force components were introduced in Eq. 11, but now apply to each of the N_B tube particles. The only difference occurs in the last term, 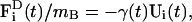where γ(t) is now a time-dependent drag term that enforces fluctuation-dissipation (Chandler, 1987). Again, in the case that only the conservative force is present, this term becomes a standard Nosé-Hoover thermostat (Evans and Holian, 1985; Evans and Morriss, 1990; Ayton et al., 2004).

We note that both 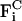and are evaluated via pairwise additive interactions between tube particles, i.e.,

(13)

where and 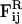are pair forces that have the property of F_ij = −F_ji, and thus conserve total momentum (which is advantageous in an MD-like simulation).

The requirements placed on the conservative interaction, can be found from continuum-mechanics, in particular smooth-particle applied mechanics (Kum et al., 1995; Hoover and Hoover, 2003; Hoover et al., 1996; Hoover and Posch, 1996), where it can be shown that systems that exhibit a quadratic dependence in pressure possess a repulsive interaction between different regions. In the case of membranes, it is the plane stress that is considered. In this manner, 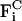can be found by considering the membrane's in-plane stress response to increases in density, i.e., ∂σ/∂ρ_B, where σ is the plane stress and ρ_B = N_B/(Ah), where A is the area. The constitutive relation for the bulk modulus in a bilayer is given by Ayton et al. (2002a) as

(14)

where λ is the bulk modulus of the membrane and 2ε = δA/A to first order. In the case that the initial state corresponds to a zero in-plane stress state, we can write

(15)

where P = − σ. Substituting the definition of the density in the previous equation gives

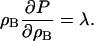(16)

One has considerable freedom in choosing the functional form of the repulsive interaction (Kum et al., 1995), as it essentially is modeling the mass distribution at some point in space. Following the methodology in Groot and Warren (1997), the conservative interaction can be modeled by a soft linear conservative force expressed as

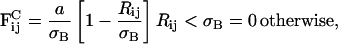(17)

where R_ij = |R_i−R_j| and σ_B will be defined soon. With the bulk modulus defined through Eq. 16, and with an approximation to the in-plane pressure given by

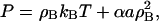(18)

where α is a scaling constant with units of nm³ and depends on σ_B, the value of a required to reproduce the bulk modulus upon small density changes can be found via

(19)

To find a, the required parameter for the conservative force, an initial TUBEsys simulation employing only the conservative interaction F^C and the drag F^D (which becomes just a Nosé-Hoover thermostat in the absence of a random force component) was performed. The simulation consisted of N_B = 1243 tube particles with a radius r_c = 1 nm at a reduced density of 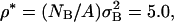and with σ_B = 3.98 nm. Other combinations are possible, but in general, once the mass of the tube is found from the original TUBE simulation (m_B = 10973 amu for the r_c = 1 nm tube), along with ρ*, and the actual mass density from the original MD simulation (defined as ρ′ = M/A where M is the total mass of the MD simulation cell and A is the area), then the TUBEsys cutoff is uniquely given by σ_B = (ρ*m_B/ρ′)^1/2. With this scheme, the mass of the tube remains consistent in going from TUBE to TUBEsys.

For values of a between 80 and 100 amu(nm/ps)² and we find α ∼ 1.81 nm³. With λ = 32.7 amu/(nm ps²) (Ayton et al., 2002a) we find a value of a ≈ 89 amu(nm/ps)² gives the correct pressure versus density at the initial state point of interest. In Fig. 5, ρ_B(∂P/∂ρ_B) versus ρ_B for the TUBE system with r_c = 1 nm is shown. From Eq. 16, this quantity should equal the bulk modulus at the initial density of ρ_B = 0.3515 nm⁻³, and from the results, it suggests that the current parameterization scheme works well.

FIGURE 5.

The quantity ρ_B(∂P/∂ρ_B) versus ρ_B for the TUBE system with the r_c = 1 nm system. The previously calculated bulk modulus of DMPC (Ayton et al., 2002a) is given by λ₀ as the dotted line. The initial density is ρ_B = 0.3515 nm⁻³.

At this stage, the resulting dynamics of the coarse-grained model can be calculated. Note that at this stage, where only the conservative and drag (thermostating) terms are included, the system corresponds to an MD-like simulation that samples a canonical distribution in the potential associated with the conservative force (Ayton et al., 2004; Ayton and Voth, 2004). The resulting tubes velocity-velocity TCF is shown in the inset of Fig. 6, where a very slow decay is observed. In fact, over 80 ps, the TCF still has not become fully decorrelated. The corresponding mean-square displacement is shown in the inset of Fig. 7, where a rough estimate of the diffusion coefficient is given by D_lat = 5.2 × 10⁻⁴ cm²/s, almost 5000 times greater than the experimental lateral diffusion coefficient for DMPC (Filippov et al., 2003; Oradd et al., 2002) as well as the estimated TUBE result as found in DMPC TUBE Simulations (see above). Clearly, at this level of parameterization, the TUBES simulation may have modeled the thermodynamic quantity of interest quite well, but the dynamics are completely inconsistent with the original exact TUBE results obtained from the underlying MD simulation.

FIGURE 6.

The TUBES velocity-velocity TCF employing F^C, F^R, and F^D (dash-dot line) from Eq. 11 and then with F^C, F^R, F^D, and the harmonic memory term F^M (dash line). The original exact MD TUBE C_UU(t) for the r_c = 1 nm is also shown for comparison as the solid line. The inset shows the raw TUBES velocity-velocity TCF where only F^C and F^D are present, and F^D/m_B becomes a standard Nosé-Hoover thermostat.

FIGURE 7.

The TUBEsys mean-square displacement employing F^C, F^R, and F^D (dash-dot line) from Eq. 11, where the resulting lateral diffusion coefficient is found to be D_lat = 4.8 × 10⁻⁷ cm²/s . The dash line corresponds to the TUBEsys mean-square displacement with F^C, F^R, F^D, and the harmonic memory term F^M, with a resulting lateral diffusion coefficient D_lat = 1.4 × 10⁻⁷ cm²/s. The solid line is the original exact MD TUBE results for the r_c = 1 nm system. The inset shows the TUBEsys mean-square displacement using only F^C and F^D.

Interestingly, this large diffusion effect has been observed in other coarse-grained simulations (Groot and Rabone, 2001). The solution there was to renormalize the diffusion coefficient by rescaling time, or effectively, by rescaling the masses of all the particles.

However, in the present case, when the required random force component, is included, a drastic change is observed in the dynamics of the system. Returning to Fig. 6, the dash-dot line in the main panel shows the new TUBEsys velocity-velocity TCF, which exhibits a sharp exponential decay over the course of two or three picoseconds. Thus the inclusion of the random force (and the accompanying drag force) completely alters the dynamics, and the diffusion drops drastically. As seen in the corresponding plot in Fig. 7, the mean-square displacement has dropped significantly, and the resulting lateral diffusion coefficient is found to be D_lat = 4.8 × 10⁻⁷ cm²/s (a similar value is found from integrating the velocity-velocity TCF). A close inspection of Fig. 6 reveals that including the random Brownian term results in a velocity-velocity TCF that is similar to the exact TUBE result (solid line), but, by design (Ayton et al., 2004), it still misses the caged correlation effects, and thus the resulting lateral diffusion is still approximately three-and-a-half times larger than the original TUBE result. Still, at this stage it is clear that the inclusion of the random and drag terms is crucial to recover, at least qualitatively, the correct dynamical behavior of the mesoscopic system. The conservative interaction alone cannot accomplish this.

In fact, a reverse buildup scheme can be employed, where the random and drag forces are parameterized first, and then the conservative interaction is added. This is the scheme that was employed in Ayton et al. (2004). Thus, to examine the relative strengths of the random/drag and conservative interactions, this reverse buildup scheme was also performed for the present system. A new set of TUBEsys simulations were done with exactly the same state parameters as previously discussed, but now the random/drag forces were initially parameterized and then the conservative interaction was included. The relevant TCFs, as well as mean-square displacement, were calculated during both stages. It was found that the dynamics were totally dominated by the random and drag forces, and that the inclusion of the conservative force made no difference. The resulting velocity-velocity TCFs, as well as the mean-square displacement were, for all purposes, identical to the results in the main panel of Figs. 6 and 7. Thus, even at this stage in the development it is clear that the dynamics of the system are almost entirely dominated by very strong random/drag forces. The effects of the weak conservative interaction, which ultimately give the thermodynamic state, are essentially buried in the “noise.”

The final stage of the force hierarchy still has to be performed—i.e., to complete the full coarse-grained model, the non-Markovian caged correlations in the tubes velocity-velocity TCF must be treated. The harmonic memory force, F^M, gives a relatively simple means of incorporating memory effects into the coarse-grained model, the details of which can be found in the Appendix. The resulting expression for F^M is given by

(20)

where in this expression is the average location of the tube from the present time, t, to a time t−τ_E in the past, i.e.,

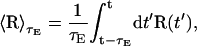(21)

and K_M is a spring constant with units of ps⁻². The effect of this final force contribution can be seen in the main panel of Fig. 6, where the dash line is the final TUBES velocity-velocity TCF including all four force components.

The inclusion of the harmonic memory force results in a small caged regime that matches the original TUBE result quite well. The two parameters in the harmonic force, K_M and τ_E, are easily found. The actual value of K_M corresponds to the magnitude of the harmonic force, which is by definition much smaller than the corresponding magnitude of the random force (see the Appendix). Values between 1 and 100 ps⁻² gave basically identical results. The other parameter, τ_E, is given by the wavelength of the caged effect. In this case, from the exact MD TUBE results Fig. 6 (solid line), the “cage” persists for ∼3–6 ps. A value of τ_E = 4 ps was therefore employed. It may be possible to extend the harmonic memory force to include more than one fundamental caged mode, so this topic will be explored in the future. For the present study, the inclusion of the memory effect can be seen in the mean-square displacement (dashed line, Fig. 7). The original exact MD mean-square displacement now agrees with the TUBEsys value up to 16 ps (the extent of the initial TUBE simulation). However, the TUBEsys simulation can now easily be examined over much longer times. The idea with TUBEsys, as alluded to in the DMPC TUBE simulations above, was to model the exact short-time dynamical correlations such that the mesoscale simulation can then access much longer times. At this point, the inclusion of the four different force components appears to give an accurate coarse-grained representation of the dynamical correlations, and thus the long-time mesoscopic dynamics take off where the initial exact TUBE result ended. For reference, the present TUBEsys simulation, employing all four force terms, and collecting TCFs out to 80 ps with averages accumulated over the course of a 8-ns simulation, took a mere 2 h in serial on a typical PC.

CONCLUSIONS

The article has been concerned with the construction of a mesoscopic model for a bilayer capable of modeling lateral diffusion in a membrane. The key feature is that the dynamics of the mesoscopic particle, the tube, are first calculated exactly using an MD simulation of a fully solvated bilayer. With these exact results at hand, a coarse-grained representation is then developed along the lines of a Generalized Langevin model that can reproduce the dynamics of the tube in the absence of the detailed underlying MD. The resulting space-filling coarse-grained model, TUBEsys, not only reproduces the time-correlations observed the in the original TUBE case, but the resulting lateral diffusion coefficient compares well with the original TUBE calculation.

In terms of new insights into the details behind correlated lipid motion, the TUBE simulation offers a wealth of information for both the pure and lipid/cholesterol systems. With TUBE, the resulting dynamical, rather than structural, correlations can be measured at the mesoscale, and the result is a very complex picture of mesoscopic correlated motion in bilayers. Recall that the tube is not a lipid, or even a well-defined molecule, but instead a ghost probe that does not alter the dynamics or structure of the bilayer. Instead, it inherits the collective dynamics of the underlying MD system. It is observed that the resulting lateral diffusion coefficient for tube sizes slightly larger than a lipid are in agreement with the estimated value of the pure lipid diffusion coefficient, suggesting that the diffusive mechanism in bilayers may contain a collective component where groups of lipids are transiently diffusing together in loosely organized clusters. It is also observed at this critical lengthscale, where the tube lateral diffusion matches the lipid lateral diffusion, that significant caging occurs in the tube velocity-velocity TCF, indicating that a fairly robust memory effect is present. On timescales of ∼4 ps, the tube shakes back and forth, due to the collective lipid motions inside of it. Upon coarse-graining, it was found that the force component responsible for the caging effect, the harmonic memory force, must be included above and beyond the conservative and random/drag forces to correctly model the dynamics. Without this term the calculated coarse-grained lateral diffusion was too large. Thus, the picture of collective lateral motion in bilayers is more complex that just Brownian motion, and it involves, at least on the lengthscales where the tube and lipid lateral diffusion coefficients overlap, significant organized collective motion. Interestingly, upon the addition of cholesterol (at a 1:1 ratio), the pronounced caging effect is decreased along with the lateral diffusion. Thus, not only is the collective lateral diffusion less in the DMPC/cholesterol mixture, but the actual dynamics are less organized and more Brownian. The origin of this effect is not immediately clear and is perhaps initially counterintuitive. However, a possible explanation for this effect is that cholesterol is acting much like an impurity in an otherwise homogenous system. In the pure case, since all the membrane molecules have the same molecular structure, a fairly large degree of locally correlated motion can persist. However, when cholesterol is introduced it acts to dampen or cancel out these motions by virtue of its drastically different molecular structure compared to a soft lipid molecule. Future work will focus on probing this effect.

In terms of the mesoscale model, TUBEsys, a key point with TUBEsys is that the model can be incrementally “built up,” where different force components originating from different sources are combined to, ultimately, reproduce the behavior observed in the original exact TUBE simulation. However, examining the behavior of the coarse-grained model at intermediate points in the full mesoscale model development gives quantitative information of exactly what the different force components are doing, i.e., which ones dominate and which ones do not. In this case, we find that the combination of the random and drag force components are by far the largest, and they completely dominate over the other components. In this case, the random and drag components essentially determine the dynamics, whereas the conservative interaction is nearly completely overwhelmed. In fact, if only the conservative interaction is employed (with the addition of a thermostat), then the resulting dynamics are wrong.

It is an interesting observation that a mesoscopic conservative force alone can give the correct thermodynamic state for a corresponding atomistic-level system, but completely wrong dynamics. Alternatively, if only the random/drag forces are employed, one can recover the dynamics of the system, but the equation of state of the system is that of an ideal gas. Thus, to fully complete the mesoscopic model, both the conservative and random/drag forces—along with their correct relative magnitudes—must be accounted for.

A significant time- and lengthscale jump is also achieved with TUBES. In terms of timescale, a jump from 0.002 ps at the MD level to 0.04 ps at the TUBEsys level is found. Spatially, ∼10 lipids, and the accompanying hydration layer, are mapped into one tube, which works out to an atom/tube ratio of ∼500:1. More importantly, since the electrostatics at the MD level have been mapped into drag forces via a GLE, the resulting tube-tube interactions are short-ranged. For comparison, in Hofsab et al. (2003) a DPPC membrane with an area ∼300 nm² (1024 lipids and 23,552 waters) required over 600 h of wall time over 32 processors to sample 16 ns of simulation time. In contrast, for a TUBEsys simulation with an area of 3900 nm², 4 h in serial on a typical Pentium PC is required to span approximately the same simulation time.

At this point in its development, TUBEsys is bound within a two-dimensional surface. The next step will be to include out-of-plane forces. One option is to couple TUBEsys with the undulating EM membrane (Ayton and Voth, 2002) to complete the mesoscopic bilayer description. In that regard, the EM membrane acts as a two-dimensional surface in which the tubes are bound. This development will be the topic of a subsequent article.

APPENDIX: EXTENDED LINEAR DECAY MODEL

In situations where nonexponential correlations in the TUBE velocity-velocity TCF, C_UU(t), are significant, a more detailed approximation of the GLE is required than was presented in Ayton et al. (2004). We note that this situation has been well studied (Evans and Morriss, 1990; Chandler, 1987) using the method of Laplace transforms. We begin with a GLE in two dimensions given by

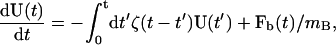(22)

where we approximate ζ(t) with a strong short-ranged contribution (Ayton et al., 2004), ζ_S(t), and an additional very weak longer-ranged component, ζ_M(t), as

(23)

The weak longer-ranged term is modeled as linear decay as ζ_M(t) = K_M(1 − t/τ_E) for 0 ≤ t ≤ τ_E and is zero otherwise. This component of the GLE can be integrated to give

(24)

where this additional perturbation contains the memory effects and is denoted the harmonic memory force. In this expression, is the average location of the tube from the present time, t, to a time t−τ_E in the past, i.e.,

(25)