Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Aug 31;87(5):3312–3322. doi: 10.1529/biophysj.104.046078

Simulation of the Early Stages of Nano-Domain Formation in Mixed Bilayers of Sphingomyelin, Cholesterol, and Dioleylphosphatidylcholine

Sagar A Pandit *, Eric Jakobsson †, H L Scott *
PMCID: PMC1304799  PMID: 15339797

Abstract

It is known from experimental studies that lipid bilayers composed of unsaturated phospholipids, sphingomyelin, and cholesterol contain microdomains rich in sphingomyelin and cholesterol. These domains are similar to “rafts” isolated from cell membranes, although the latter are much smaller in lateral size. Such domain formation can be a result of very specific and subtle lipid-lipid interactions. To identify and study these interactions, we have performed two molecular dynamics simulations, of 200-ns duration, of dioleylphosphatidylcholine (DOPC), sphingomyelin (SM), and cholesterol (Chol) systems, a 1:1:1 mixture of DOPC/SM/Chol, and a 1:1 mixture of DOPC/SM. The simulations show initial stages of the onset of spontaneous phase-separated domains in the systems. On the simulation timescale cholesterol favors a position at the interface between the ordered SM region and the disordered DOPC region in the ternary system and accelerates the process of domain formation. We find that the smooth α-face of Chol preferentially packs next to SM molecules. Based on a comparative analysis of interaction energies, we find that Chol molecules do not show a preference for SM or DOPC. We conclude that Chol molecules assist in the process of domain formation and the process is driven by entropic factors rather than differences in interaction energies.

INTRODUCTION

There is abundant evidence gathered in recent years suggesting that cellular plasma membranes contain phase-separated domains of different lipid composition. In particular, there is a major focus on nano-size membrane fragments that are not solubilized by the detergent Triton X-100. These domains are called detergent-resistant membrane domains (DRM) or “rafts” (Simons and Ikonen, 1997; Reitveld and Simons, 1998; Pralle et al., 2000; Jacobson and Dietrich, 1999). For reviews on the subject see Brown and London (1998) and Edidin (2003). In a biological context there is much recent evidence that nanometer-sized domains, presumably similar in structure to DRMs, are important membrane structural components in signal transduction (Manes et al., 1999; Aman and Ravichandran, 2001; Xavier et al., 1998; Kawabuchi et al., 2000), protein transport (Rozelle et al., 2000; Cheong et al., 1999; Viola et al., 1999), and sorting of membrane components (Manie et al., 2000; Harder et al., 1998; Sönnichsen et al., 2000; Zerial and McBride, 2001). There is also evidence for rafts functioning as sites for the binding and transport into the cell of several pathogens and toxins, including the human immunodeficiency virus 1 (HIV-1) and the prion protein PrPsc (Fantini et al., 2002).

At lower temperatures much of the sphingolipid and cholesterol components of mammalian cell membranes can be isolated in DRM fragments (Brown and Rose, 1992; Brown and London, 1998). Data from fluorescence polarization measurements of liposomes incorporating diphenylhexatriene show that the extracted DRM domains are in a liquid-ordered phase (Lo) (Schroeder et al., 1994) in which lipid chains are highly ordered but whole lipid molecules have rotational and lateral diffusion coefficients comparable to those in the liquid crystalline (Lα) phase. Subsequently a major focus of raft research has shifted to studies of bilayer systems in the Lo phase (Brown and London, 1998). These systems typically involve mixtures of saturated phospholipids, sphingolipids, and cholesterol. Reitveld and Simons suggested that the “rafts” are Lo-phase domains dispersed in a liquid crystalline (Lα) phase bilayer (Reitveld and Simons, 1998). Hence, the term “raft” is now used by many authors to denote not just a DRM but also a Lo-phase domain surrounded by Lα-phase lipids and other membrane components (Brown and London, 1998).

A variety of experimental techniques have been employed to study the properties of rafts or related Lo-phase domains in simple model membrane systems. The model membrane systems are generally multilamellar vesicles, monolayers, or giant unilamellar vesicle systems. Techniques employed typically include fluorescence microscopy (Dietrich et al., 2001; Samsonov et al., 2001; Veatch and Keller, 2002), single particle tracking (Dietrich et al., 2002), differential scanning calorimetry, and x-ray diffraction (Gandhavadi et al., 2002) and atomic force microscopy (AFM) (Rinia et al., 2001; Yuan et al., 2002; Lawrence et al., 2003). A recent comprehensive review of experimental studies of rafts and DRMs (Edidin, 2003) concludes that actual rafts in membranes may be very small (≲10 nm in diameter), and that the intermolecular interactions that drive the formation and stability of these nano-domains are still largely unknown.

Simulation studies offer the possibility of gaining atomic-level insights not easily obtained in experiments. In recent years numerous simulation studies have been performed on saturated phospholipid and cholesterol systems to investigate atomic level interactions and properties of bilayers in the Lo phase (see, e.g., Tu et al., 1998; Smondyrev and Berkowitz, 1999; Pasenkiewicz-Gierula et al., 2000; Róg and Pasenkiewicz-Gierula, 2001; Chiu et al., 2002; Hofsäß et al., 2003; Pandit et al., 2004a). Most of these simulations focus on the detailed interaction of cholesterol with the saturated phospholipid and the clustering behavior leading to the Lo phase. In our group, we recently used simulation to study the Lo phase of sphingomyelin (SM) in a 2:1 mixture of SM and cholesterol (Chol) (Khelashvili and Scott, 2004). We found that the Lo phase in SM/Chol mixtures persisted over a 30°C range in temperature. Despite these extensive simulations of systems in a Lo phase, there have been relatively few simulation and modeling attempts that directly focus on the issues related to the separation of Lo and Lα phases in bilayer systems (see, e.g., Huang et al., 1993; Anderson and McConnell, 2001; Pandit et al., 2004b). In previous work, we began to address this problem by carrying out a molecular dynamics (MD) simulation of a 2:1 sphingomyelin/cholesterol domain (in the Lo phase) in a large dioleylphosphatidylcholine (DOPC) bilayer that was in an Lα phase (Pandit et al., 2004b). Due to the extremely large size of this system (1424 DOPC, 264 SM, 122 Chol, and 62,561 SPC waters) the longtime behavior of this system was beyond current computational capacity. Hence, we have now carried out two MD simulations of smaller systems to examine the onset of spontaneous phase separation in DOPC, SM, and Chol mixtures. The results of these simulations are presented in this article.

METHODS

The MD simulations were performed on a ternary mixture of DOPC/SM/Chol with a 1:1:1 composition (system S1) and a binary mixture of DOPC/SM with a 1:1 composition (system S2). Both of these simulations were performed using the GROMACS package (Berendsen et al., 1995; Lindahl et al., 2001). Force-field parameters for the cholesterol molecules were those used by Höltje et al. (2001). The parameters for the phosphocholine polar groups were taken from our DPPC force field (Chiu et al., 1999a). The parameters for the sphingosine chain and polar groups were taken from the SM parameter set we developed for the simulation of a large pure 18:0 SM bilayer (Chiu et al., 2003). The hydrocarbon chain parameters were taken from our earlier determination of these quantities by fitting to density and heat of vaporization data (Chiu et al., 1999b). The LINCS algorithm was used to constrain all bonds in the system (Hess et al., 1997) allowing an integration time step of 4 fs. Periodic boundary conditions were applied in all three dimensions and long-range electrostatics were calculated using the SPME algorithm (Essmann et al., 1995) with a real space cutoff of 9.5 Å. A cutoff of 18 Å was employed for van der Waals interactions. The temperature in both S1 and S2 simulations was maintained at 300 K, using the Nose-Hoover scheme. The systems were equilibrated in an NPT ensemble using the Parrinello-Rahman pressure coupling scheme (Nose and Klein, 1983; Parrinello and Rahman, 1981) at a constant pressure of 1 atm.

The initial configurations for both the systems were generated by random placement of 100 DOPC and 100 SM molecules (taken randomly from our previous simulations of pure DOPC and pure SM bilayers) such that the phosphorus atoms of the headgroups were at the z = 25 Å and z = −25 Å planes and the hydrocarbon chain were pointing toward the z = 0 plane. System S1 also had 100 cholesterol molecules randomly placed equally in both the leaflets with hydroxyl oxygen in the planes z = 25 Å and z = −25 Å. Two slabs of 5000 and 3500 SPC waters were placed above and below the constructed bilayers for systems S1 and S2, respectively. The systems were energy minimized to remove bad contacts. A 200-ps MD simulation was performed on each system at 500 K. This was done to ensure proper disordering of the hydrocarbon chains. Then the temperature was brought down to 300 K in steps of 50 K. At each temperature step a small 100-ps MD simulation was performed on each system. Both the systems were simulated for 2 ns of MD with regeneration of velocities from a Maxwellian distribution at 300 K after every 100 ps. Then 3 ns of continuous MD simulations were performed on each system. At this point the velocities were regenerated as before and continuous 200-ns simulations were performed on both S1 and S2. Throughout the simulations we monitored the dimensions of the simulation cells. The simulation cells were stable over a short timescale, but decreased slightly in size during the full 200 ns of simulation time (see Fig. 2).

FIGURE 2.

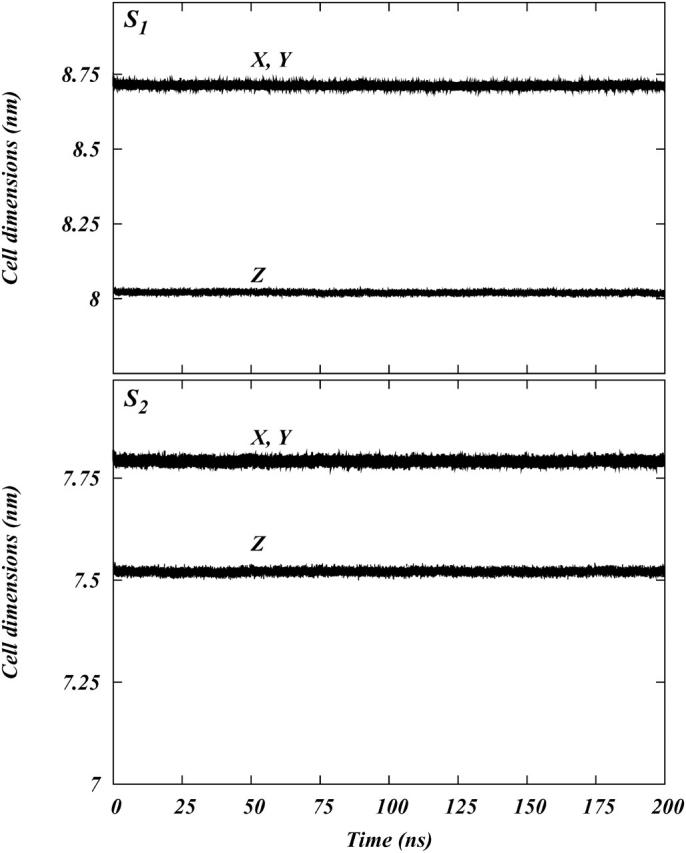
FIGURE 2

Open in a new tab

Plots of the X, Y, and Z dimensions of the simulation cells for the systems S1 and S2 as functions of time.

RESULTS AND DISCUSSION

Lateral diffusion coefficients for the lipids in the liquid crystalline phase, determined from experiment, are of the order of ∼5 × 10−12 m2/s (Filippov et al., 2003). This value along with Einstein's relation gives a root mean square (RMS) displacement of ∼20 Å for a single lipid in 200 ns. To address the basic question of whether such a small RMS displacement should allow for any domain formation in the simulation, we consider the following: The area of the simulation cell of system S2 was ∼6100 Å2. We have 50 points (SM lipids) uniformly randomly distributed over this area. Therefore, the average distance between nearest neighbors is ∼9 Å. If we assume that SM molecules in the neighborhood of each other tend to associate to begin to form a cluster then we should expect to see several pairs or triplets of SM molecules gather together to form small clusters on the simulation timescale. In system S1 we expect this effect to be more prominent as there are 100 points (SM/Chol) randomly distributed over the plane.

Before investigating the issues related to domain formation we first calculate standard structural and dynamic properties and compare them with experimental data. At the end of the simulation the MSD is ∼3.2 nm2, which corresponds to ∼18 Å of RMS displacement. The calculated RMS displacement of the molecules is similar to that estimated from the approximate diffusion coefficient (as discussed above). To obtain better sampling of the MSD we divided the 200-ns trajectory into four 50-ns trajectories and averaged the MSD over these four trajectories. Results of these averaged MSD are presented in Fig. 3. Because the molecules clearly exhibit diffusive behavior we use Einstein's relation,

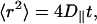graphic file with name M1.gif (1)

to calculate the lateral diffusion coefficient (D‖). Table 1 lists the resulting values of D‖ for both systems (calculated by fitting a straight line to the MSD traces in Fig. 3). We note that the diffusion coefficients of DOPC in systems S1 and S2 both are consistent with the experimental values (Filippov et al., 2003, 2004). Further, all the diffusion coefficients in system S1 are smaller than those in system S2. This is probably a result of the formation of localized clusters of cholesterol with the lipid molecules in system S1 (Pandit et al., 2004a), inhibiting lateral mobility of the lipids. Fillipov et al. have observed that the lateral diffusion of SM is significantly slower than that of DOPC in 1:1:1 mixtures of SM/DOPC/Chol (Filippov et al., 2004). We also observe a reduced diffusion of SM molecules. However, on the simulation timescale, the difference in diffusion coefficients of DOPC and SM is not large. One possible reason is that the SM in the simulations is still in a liquid crystalline phase rather than a gel or a liquid-ordered phase. If the simulation were continued further in time then we would expect a reduction in the diffusion of SM as it aggregates into dense, ordered clusters. Hence, the calculated reduced diffusion of SM is indicative of the onset of domain formation in the system, but the less-than-expected reduction in D‖ of SM implies that the process has not reached equilibrium in 200 ns.

FIGURE 3.

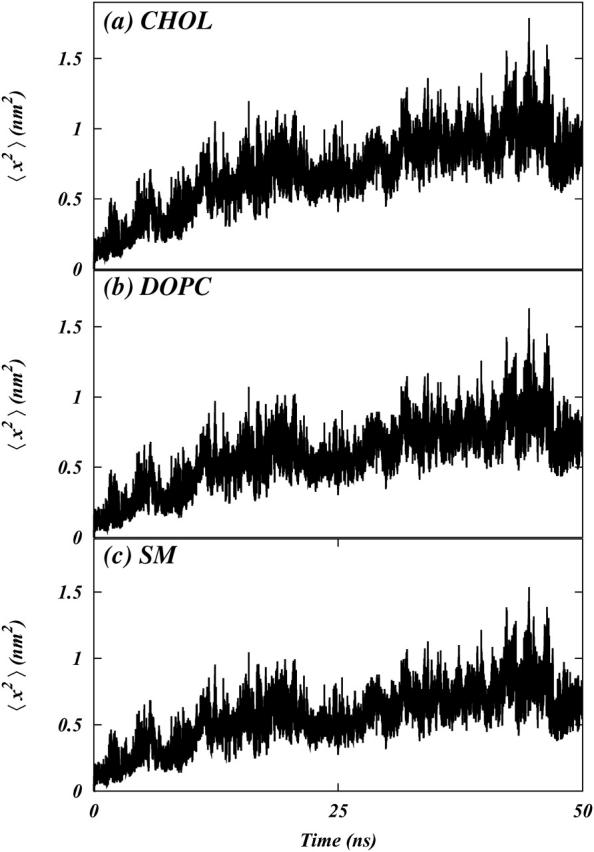
FIGURE 3

Open in a new tab

Lateral mean square displacement (MSD) of the centers of mass of (a) Chol, (b) DOPC, and (c) SM as a function of time averaged over four trajectories of 50-ns duration.

TABLE 1.

D‖ for various constituents of the systems

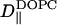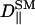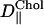System Inline graphic (× 10−12 m2/s) Inline graphic (× 10−12 m2/s) Inline graphic (× 10−12 m2/s)
S1 3.166 ± 0.011 2.853 ± 0.010 3.779 ± 0.011
S2 4.803 ± 0.013 4.471 ± 0.014 –
Open in a new tab

The values are calculated by averaging MSD over four 50-ns time slabs and fitting a straight line to the data over the last 30 ns of each slab. The error bars are the estimates of the error in straight-line fit.

A distinct feature of phase-separated domains is a difference in chain order and packing between ordered and fluid domains. The ordering of hydrocarbon tails is determined in NMR experiments by measuring the deuterium order parameters. The order parameter tensor, S, is defined as

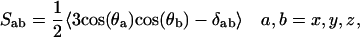graphic file with name M2.gif (2)

where θa is the angle made by ath molecular axis with the bilayer normal and δab is the Kronecker delta. In the simulations, with the united atom force field, the order parameter for saturated and unsaturated carbons SCD can be determined using the following relations

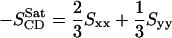graphic file with name M3.gif (3)
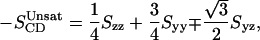graphic file with name M4.gif (4)

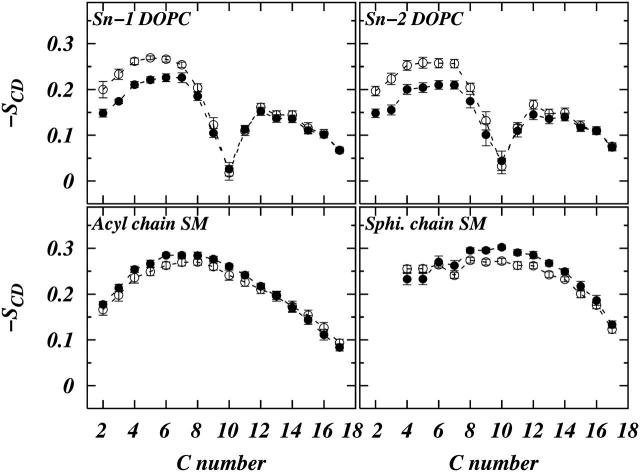
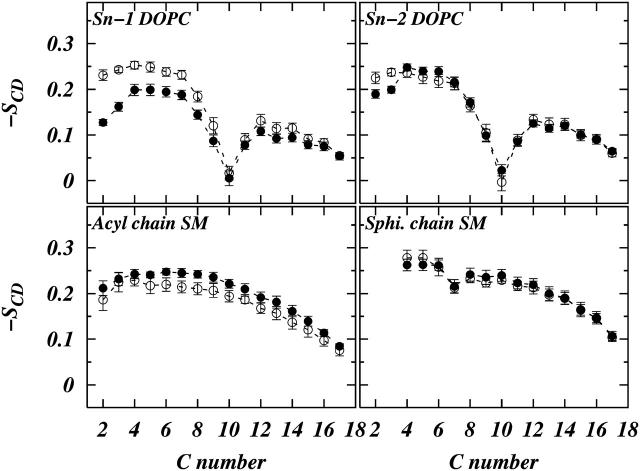
respectively, (Douliez et al., 1995). Figs. 4 and 5 show the calculated order parameter profiles for both the chains of DOPC and SM in systems S1 and S2, respectively. The calculated order parameter values after 200 ns for DOPC are lower in the plateau region compared to their initial values. On the other hand the SM order parameters after 200 ns are slightly larger than their initial values. This means that during the course of the 200-ns simulation time SM molecules became slightly more ordered on average and the DOPC molecules became less ordered, on average. This is indicative of a slow process of separation of the phases into domains. We also note that due to the presence of Chol the order parameters in system S1 are higher than those of system S2 for both DOPC and SM.

FIGURE 4.

FIGURE 4

Open in a new tab

Plots of chain-order parameter profiles for DOPC chains and SM chains in system S1. The symbols represent (○) values averaged over the first 10 ns of the simulation and (•) values averaged over the last 10 ns.

FIGURE 5.

FIGURE 5

Open in a new tab

Plots of chain-order parameter profiles for DOPC chains and SM chains in system S2. The symbols represent (○) values averaged over the first 10 ns of the simulation and (•) values averaged over the last 10 ns.

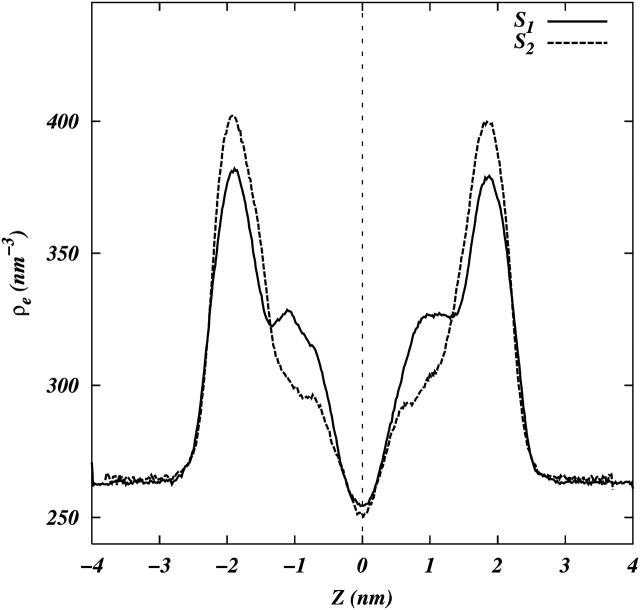
Fig. 6 shows the calculated electron densities for both simulated systems. The distance between the peaks in electron densities for both the systems, a measure of thickness of the bilayer, is ∼38 Å. The thickness reported by Gandhavadi et al. (2002) on 1:1:1 DOPC, bovine brain SM, and Chol is ∼43 Å. There are two possible reasons for this discrepancy: i), the bovine brain SM used in experiments include SM molecules with longer chains than the 18:0 SM used in this simulation; and ii), the simulated system is not yet in a completely phase-separated state where the SM chains are significantly ordered. Hence, we expect the thickness of the bilayer to increase over long simulation times. The electron density did not exhibit a bimodal structure due to regions of different thickness.

FIGURE 6.

FIGURE 6

Open in a new tab

Electron density profiles for systems S1 and S2.

Area per lipid and Voronoi tessellation

In simulations the area per lipid molecule is often used to assess the validity of the simulation. However, as described in our previous work (Pandit et al., 2004b), it is difficult to calculate the area per molecule in a ternary mixture. Hence, we used the voronoi tessellation technique introduced previously (Pandit et al., 2004b). We began by projecting each molecule onto a plane. We then approximated the projected molecule by a two-dimensional polygon of area

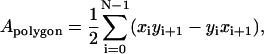graphic file with name M5.gif (5)

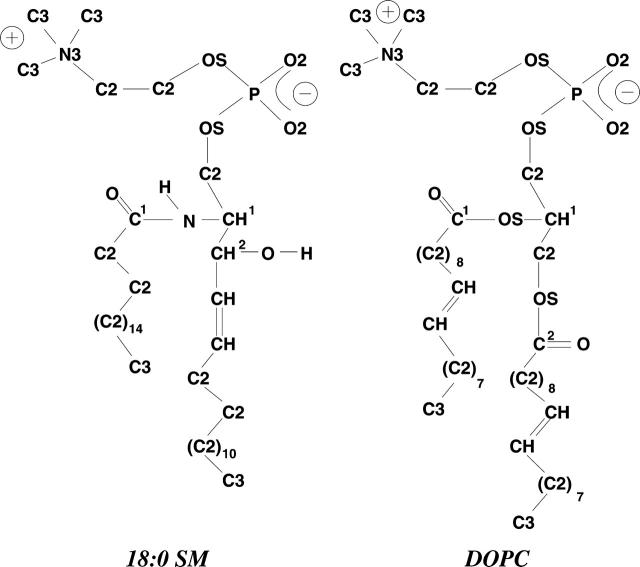
where N is the number vertices of the polygon and (xi, yi) with i mod(N) are the coordinates of the vertices of the polygon. A straightforward way of achieving this goal is by taking centers of masses of the molecules and generating a Voronoi tessellation (Jedlovszky et al., 2004; Falck et al., 2004; Gurtovenko et al., 2003; Patra et al., 2003; Shinoda and Okazaki, 1998). However, for any system with a mixture of molecules of different sizes, this method should overestimate the areas of smaller molecules and underestimate the areas of larger ones. We verified this by calculating areas per molecule in this and another simulation of ternary mixture of DOPC/SM/Chol (Pandit et al., 2004b). Hence, we decided to choose certain key atoms on molecules that lie approximately at the interface of hydrophobic and hydrophilic portions of each molecule type. To this end we chose C1, CH1, and C2 for DOPC (see Fig. 1) and C1, CH1, and CH2 for SM. The Chol was represented by the hydroxyl oxygen.

FIGURE 1.

FIGURE 1

Open in a new tab

Structure of the 18:0 SM and DOPC molecules, with the numbering scheme used in the simulations.

We projected each of these atoms on the z = 0 plane and constructed a Delaunay triangulation of these points. For each of these triangles we calculated the circumcenters. These circumcenters are the coordinates of the vertices of the Voronoi polygons corresponding to the projected coordinates of the key atoms. The vertices were then sorted to have a consistent orientation for all the polygons. The corresponding atomic polygons were combined to form a molecular polygon. Area analysis was performed on these molecular polygons. Because each polygon is associated with an individual molecule we can calculate the average area per molecule.

Fig. 7, a and b, show the traces of the average areas per molecule of DOPC, SM, and Chol as a function of time for systems S1 and S2, respectively. Both systems show an increase in the area per DOPC and a reduction in the area per SM over the initial values of these areas. The figure therefore provides evidence for a gradual separation of phases between DOPC and SM. However, it does not unequivocally prove the existence of equilibrated, phase-separated domains. We will revisit this issue in the next section. We note that in system S1, unlike system S2, the area per lipid changed rapidly (in ∼50 ns) to its steady-state (>200 ns) value. This suggests a possible role for Chol in accelerating the process of phase separation between DOPC and SM. The average area per lipid for SM, DOPC, and Chol at the end of 200 ns of the simulation are listed in Table 2. The value of area per DOPC for system S1 is closer to the pure DOPC area than that for system S2 (Nagle and Tristram-Nagle, 2000). A similar trend is also seen in the area per SM that again supports the possibility of cholesterol-assisted phase separation. Fig. 8 shows initial and final snapshots of one of the leaflets of systems S1 and S2. The figure shows, at a visual level, that small clusters have indeed formed for both SM and DOPC molecules, representing the initial stages in the aggregation of phase-separated regions in system S1. System S2 shows little or no such aggregation over 200 ns. Quantitative aspects of this process will be discussed below.

FIGURE 7.

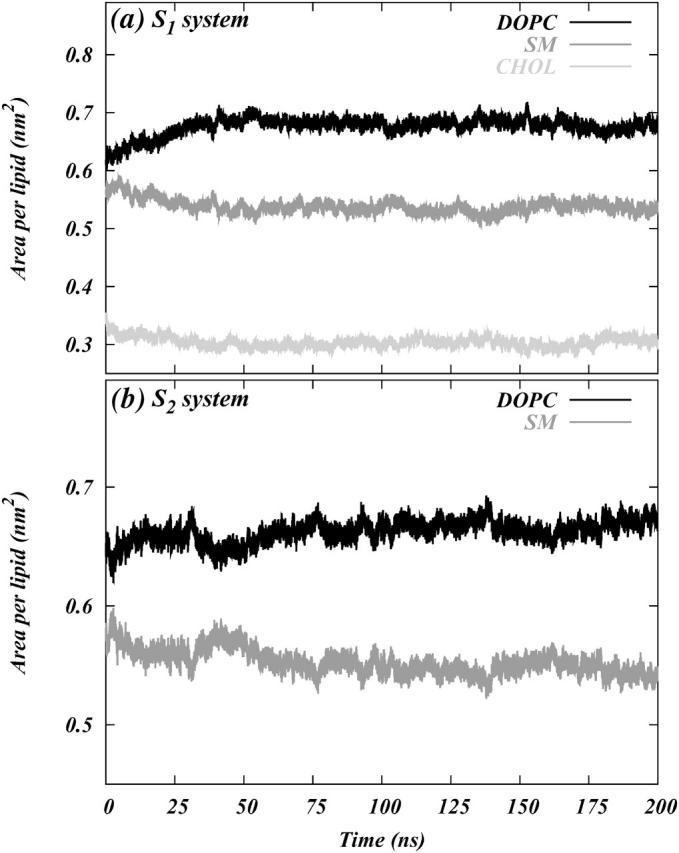
FIGURE 7

Open in a new tab

Area per molecule as a function of time for each of the constituents in (a) system S1 and (b) system S2.

TABLE 2.

Area per lipid for various constituents of the systems

System ADOPC (Å2) ASM (Å2) AChol (Å2)
S1 68.9 ± 0.7 52.7 ± 0.8 30.5 ± 0.7
S2 66.9 ± 0.7 54.4 ± 0.6 –
Open in a new tab

The values are calculated by averaging the area per lipids over the last 20 ns of the simulation.

FIGURE 8.

FIGURE 8

Open in a new tab

Snapshots of one of the leaflets in systems S1 and S2 at 0 ns (left) and 200 ns (right). The top snapshots are for system S1 and the bottom snapshots are for system S2. The DOPC molecules are represented by gray solid atoms, SM is represented by orange solid atoms, and Chol is represented by yellow solid atoms.

The definition of a domain

Lipid “rafts” are presumed to be Lo regions of membrane dispersed in regions having a different degree of order, e.g., an Lα phase (Brown and London, 1998; Reitveld and Simons, 1998). Fluorescence microscopy experiments are able to generate images of these domains (Dietrich et al., 2001; Samsonov et al., 2001; Veatch and Keller, 2002). In supported bilayers these domains are detected as regions of different membrane thickness. AFM experiments are able to detect these domains by measuring the height difference in supported bilayers (Rinia et al., 2001). Although we can calculate the chain order and height difference (Pandit et al., 2004b) in simulations, the large error bars on order parameters and height differences do not provide sufficiently well-resolved temporal description of the lateral organization of the system. Hence we decided to characterize the phase-separated domains in terms of a more robust criterion based on the projected polygonal areas of the molecules. As a rule of thumb, higher chain order gives rise to smaller areas per molecule. Hence, if we consider all molecules having their polygonal area below a certain cutoff value to be “ordered” and find connected aggregates based on polygon neighbors then we can identify domains based on this chosen cutoff value, as connected sets of molecules with areas less than the cutoff. We call such domains A-domains where A is the cutoff value used to identify the domains. Because the choice of a particular area cutoff does not uniquely characterize a nano-scopic domain, we examine A-domains for various cutoff values of A.

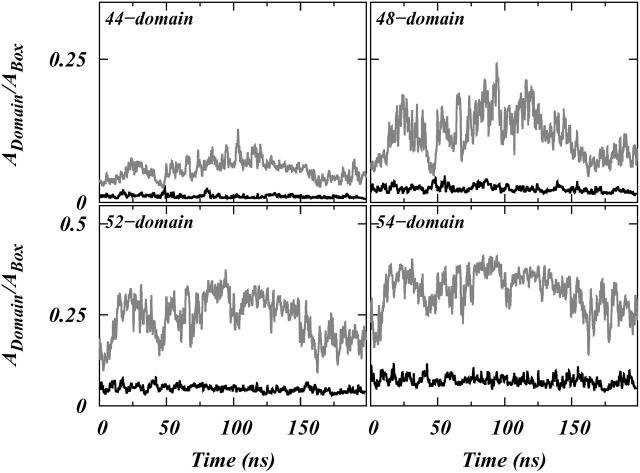
Fig. 9 shows the ratio of the area of a largest A-domain to the area of the box for systems S1 and S2 and for cutoff areas of 44, 48, 52, and 54 Å2. These cut offs are chosen to span the entire range of areas from the gel to the liquid crystalline phase of SM (Maulik et al., 1991; Koynova and Caffrey, 1995). Fig. 9 shows that the fraction of area occupied by the largest A-domain in system S2 is always much smaller than that in system S1. This suggests that, at least on a 200-ns simulation timescale, domain formation is favored and accelerated by the presence of Chol.

FIGURE 9.

FIGURE 9

Open in a new tab

Plots of ratios of largest connected A-domains to the total simulation box area, as functions of time, for systems S1 (shaded) and S2 (black) for 44-, 48-, 52-, and 54-Å2 area cutoffs. For the clarity of viewing, the plots are shown as moving averages calculated over 500-ps sliding windows.

By studying the rates of increase in domain size for various cutoff values we can extract additional information about the formation of A-domains. Domains in system S2 did not show significant growth from their initial size, which indicates that, on the 200-ns simulation timescale, the rate of association and dissociation of molecules into domains should be approximately equal for system S2. On the other hand in system S1 at higher area cutoff values, i.e., 48, 52, and 54 Å2, close to those associated with the Lα phase of SM, the domain increased in size in the first ∼20 nanoseconds and then remained approximately constant. Based on these findings, we suggest that either: i), the formation of domains in this system occurs in two steps; firstly, there is a localized “condensation,” or increase in order associated with nano-clusters of SM and SM/Chol (which we observe in the 200-ns simulations); secondly, there is a further aggregation of microclusters, and more cooperative chain ordering within aggregates over much larger length and timescales (which we do not observe in the 200-ns simulations); or ii), at the simulation temperature (300 K) lipid microdomains in a DOPC/SM/Chol system are in fact very small and localized (see, e.g., Dietrich et al., 2001; McMullen et al., 2004), and in the 200-ns simulation we see the full extent of lateral aggregation that will occur. Further simulations and accurate coarse-grained modeling may help to determine which alternative is correct.

The role of cholesterol

Having established that the Chol molecules play a significant role in domain formation, we have investigated further the nature of the interaction of cholesterol with lipids. To this end we calculated radial distribution functions (RDF) between the CH1 of DOPC (see Fig. 1) and the oxygen of Chol, and between the CH1 of SM and the oxygen of Chol. The RDF is defined as

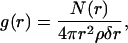graphic file with name M6.gif (6)

where N(r) is the number of CH1 atoms in the shell between r and r + δr around the oxygen atoms; ρ is the number density of CH1 atoms, taken as the ratio of the number of atoms to the volume of the simulation cell. Fig. 10 shows these RDFs. Fig. 10 shows that the first coordination shell of SM, with respect to Chol, as defined by the location of the sharp peak in the RDF, actually consist of two peaks, indicating two possible binding locations for SM. The plot for DOPC in Fig. 10 (top) shows only one peak. We calculated the coordination number, defined as the number of CH1 atoms in the first coordination shell around the Chol oxygens. The radius of the shell was set at 6 Å based on the location of the peaks in Fig. 9. The calculated coordination number of SM and DOPC around Chol is 0.55 ± 0.04 and 0.57 ± 0.04, respectively. This suggests that, even if there are two binding locations for SM, the coordination number of Chol with SM and DOPC is nearly the same, so that Chol does not show specific binding preference for SM or DOPC. Recent fluorescence spectroscopy and differential calorimetric studies performed on mixtures of PyrPC, PyrSM, and Chol also indicate a lack of specific interaction between SM and Chol (Holopainen et al., 2004). Hence, the RDFs by themselves do not provide direct insight into the role of Chol in domain formation.

FIGURE 10.

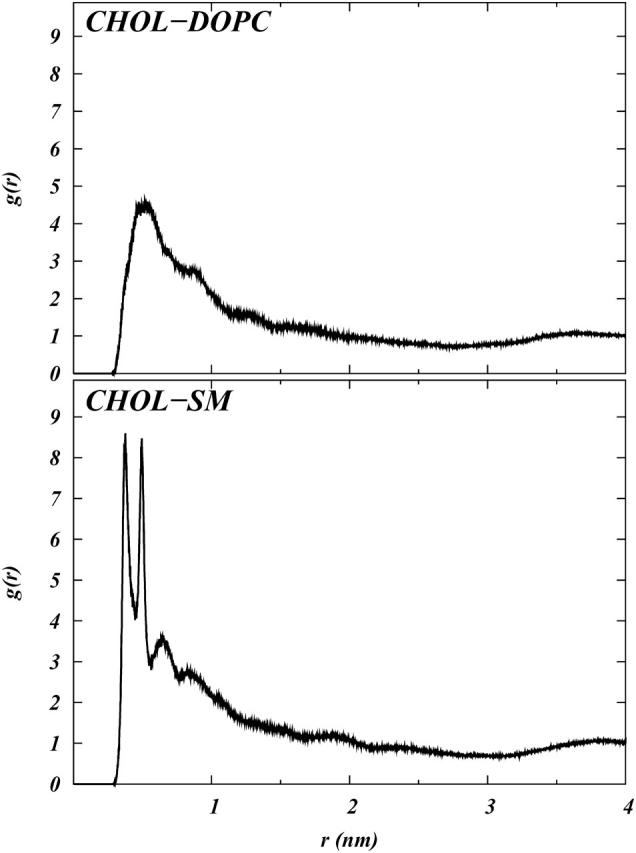
FIGURE 10

Open in a new tab

Radial distribution functions between the hydroxyl oxygen in Chol and CH1 (see Fig. 1) of DOPC and SM.

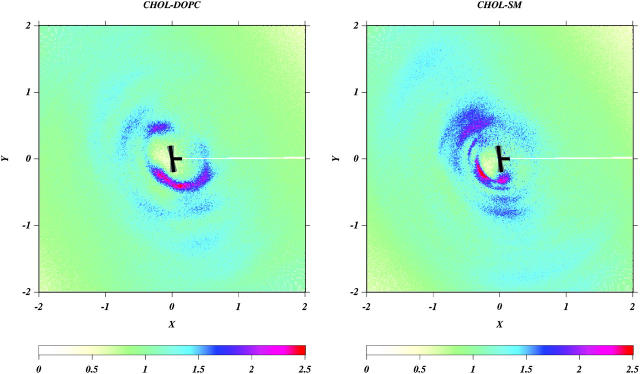
The Chol molecule has one flat face (denoted as the α-face) and one face that is rough due to protruding methyl groups (denoted as the β-face). Because Chol lies primarily in the hydrocarbon region of the bilayer, it is reasonable to question whether this specific design of the Chol molecule plays any role in promoting domain formation. Hence, we calculated a bivariate correlation function g(r, ϕ) between the CH1 atoms of DOPC and SM, respectively, and the oxygen atom of Chol, defined by

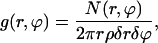graphic file with name M7.gif

where the distance r and ρ are defined as in RDFs, the angle ϕ is the angle made by the distance vector with respect to the positive x axis of the Chol body coordinate frame (see Fig. 11) and N(r, ϕ) is the number of CH1 atoms of lipids in an area element rδrδϕ at the point (r, ϕ) from the oxygen of Chol. Fig. 12 shows g(r, ϕ) for SM and DOPC averaged over the last 150 ns of the trajectory. The figure clearly shows that, on the simulation timescale, SM is associated with the α-face of Chol. On the other hand DOPC does not show a preference for either face of Chol. From the tail order parameters of SM and DOPC (Fig. 5), the nearly saturated chain of SM is more ordered than either chain of DOPC. The preferential arrangement of SM around Chol indicates that on the simulation timescales the Chol molecules tend to locate at the interface between the SM and the DOPC regions of the membrane, with the α-face of the Chol molecule interacting most strongly with SM chain. Such an arrangement again should be entropically favored because the saturated SM chains pack well around the α-face and more disordered unsaturated DOPC chains should pack well around the β-face.

FIGURE 11.

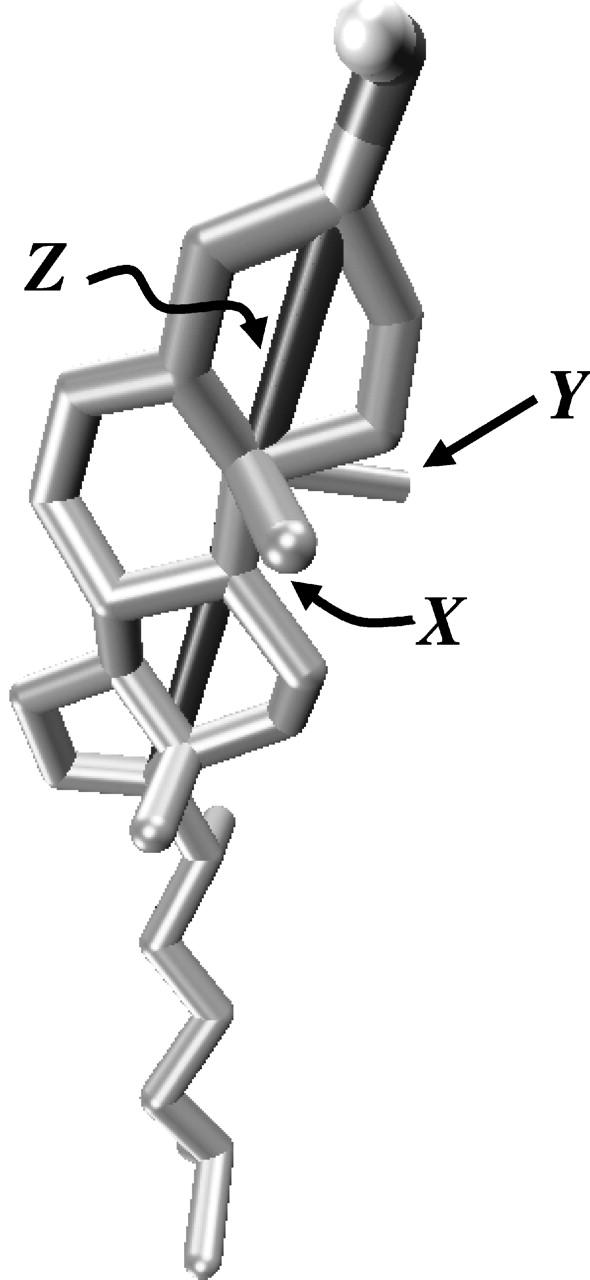
FIGURE 11

Open in a new tab

The body coordinate system used in calculation of g(r, ϕ) (see text).

FIGURE 12.

FIGURE 12

Open in a new tab

Density plot of g(r, ϕ) on the XY-plane of Chol body coordinate system. A Chol molecule is schematically shown as a black ⊢ where the small appendage denotes the β-face of the Chol molecule with possible fluctuation of its shape (with respect to the body coordinates) shown in gray.

To investigate the entropic role of Chol in promoting domains, we calculated the interaction energy between all pairs of Chol with SM and DOPC that are within 10 Å of each other and we binned these energies to obtain a distribution of Chol-lipid interaction energies. As a control case we also calculated the distribution of interaction energies between DOPC-DOPC and SM-SM pairs. (The distribution of interaction energy between DOPC-DOPC and SM-SM are calculated for S2 as well as S1 systems. The curves did not show significant quantitative difference. Hence, only plots corresponding to S1 systems are presented here.) Fig. 13, a and b, show the distributions of these energies. Unlike lipid-lipid interactions (Fig. 13 a) there are specific binding modes between Chol and lipid molecules. Hence, we observe peaks in the energy distribution favoring that particular interaction energy (Fig. 13 b). We find that the interaction energies of both DOPC and SM with Chol have peaks ∼−25 KJ/mol, indicating a binding possibility. However, the energy profiles are nearly identical for SM-Chol and DOPC-Chol, which leads us to speculate that the preferential organization of Chol at the interface of the domains may be due to entropic factors. Additional work is needed to verify this conjecture.

FIGURE 13.

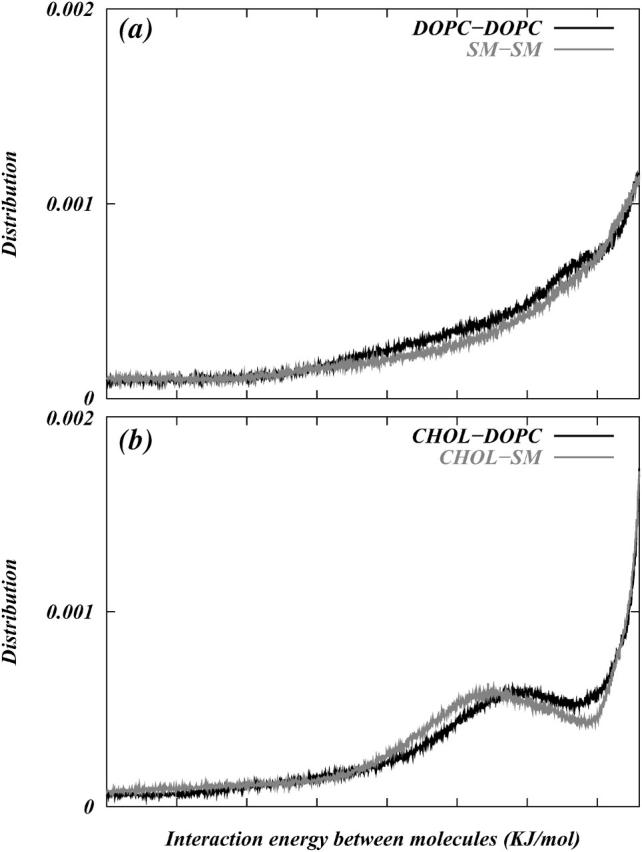
FIGURE 13

Open in a new tab

Distributions of pair interaction energies of (a) DOPC with DOPC and SM with SM, and (b) Chol with DOPC and SM. The distributions were calculated by summing over all atomic pair interactions between atoms of molecules whose centers of mass were <10 Å apart and sorting these energies into bins of width 0.1 KJ/mol.

SUMMARY

The aim of the simulations described in this article is to identify and quantify the molecular interactions in binary and ternary mixtures that may be responsible for the formation and stability of phase-separated domains. We have carried out long (200 ns) simulations of two mixed lipid bilayers. In both systems the initial placement of lipid molecules was random. Only in system S1, a 1:1:1 mixture of DOPC/SM/Chol did we observe initial stages of aggregation of SM and Chol into separate, elongated regions. We conclude that the initial stages of phase separation in our simulations are enhanced by the presence of Chol, which seems to form a natural interface between SM-rich and DOPC-rich regions.

It is conceivable that the preferential localization of Chol at the interface between SM-rich and DOPC-rich regions, observed in our simulations, contributes to the reduction of interfacial (line) tension between regions of different compositions. The reduced interfacial tension in this hypothesis is a consequence of Chol molecules orienting their α-face toward SM molecules leaving the rough β-face to interact with DOPC molecules. This allows and likely enhances the formation of Lo-phase SM domains and Lα-phase DOPC domains. In our earlier simulation of an SM-Chol nano-domain embedded in a DOPC matrix, the Chol molecules were largely situated, by design, in the interior of the SM-Chol region (Pandit et al., 2004b). We observed in this simulation that the Lo-phase central domain induced a marked increase in the order of the DOPC matrix. The insight gained from the simulations in this article suggests that, had we situated Chol at the edge of the SM-Chol central domain, in the previous simulation, the DOPC would have remained in its Lα-phase properties.

In light of these findings, we further conjecture that the shape of a spontaneously formed domain may be curvilinear in shape, as a consequence of the reduced interdomain line tension. If this results stands over a much larger timescale, then an implication is that the DRMs contain structures resembling stripe phases of alternating DOPC and SM domains, with Chol at the boundaries. We stress that the current simulation timescale, 200 ns, is too short by at least an order of magnitude to test these conjectures. However, to formulate models for lateral organization at longer timescales, it is necessary to carefully study the initial stages of domain formation at atomistic level. We are currently developing coarse-grained models based on these simulations that may help in this effort.

Acknowledgments

This work was supported by the National Institutes of Health (grant no. GM54651).

References

  1. Aman, M. J., and K. S. Ravichandran. 2001. A requirement for lipid rafts in B cell receptor induced Ca2+ flux. Curr. Biol. 10:393–396. [DOI] [PubMed] [Google Scholar]
  2. Anderson, T. G., and H. M. McConnell. 2001. Condensed complexes and the calorimetry of cholesterol-phospholipid bilayers. Biophys. J. 81:2774–2785. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Berendsen, H., D. van der Spoel, and R. van Drunen. 1995. Gromacs: a message-passing parallel molecular dynamics implementation. Comput. Phys. Commun. 91:43–56. [Google Scholar]
  4. Brown, D. A., and E. London. 1998. Functions of lipid rafts in biological membranes. Annu. Rev. Cell Dev. Biol. 14:111–136. [DOI] [PubMed] [Google Scholar]
  5. Brown, D. A., and J. K. Rose. 1992. Sorting of GPI-anchored proteins to glycolipid-enriched membrane subdomains during transport to the apical cell surface. Cell. 68:533–544. [DOI] [PubMed] [Google Scholar]
  6. Cheong, K. H., D. Zachetti, E. Schneeberger, and K. Simons. 1999. VIP17/MAL, a lipid raft-associated protein, is involved in apical transport in MDCK cells. Proc. Natl. Acad. Sci. USA. 96:6241–6248. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Chiu, S.-W., M. M. Clark, E. Jakobsson, S. Subramaniam, and H. L. Scott. 1999a. Application of a combined Monte Carlo and molecular dynamics method to the simulation of a dipalmitoylphosphatidylcholine lipid bilayer. J. Comput. Chem. 20:1153–1164. [Google Scholar]
  8. Chiu, S.-W., M. M. Clark, E. Jakobsson, S. Subramaniam, and H. L. Scott. 1999b. Optimization of hydrocarbon chain interaction parameters: application to the simulation of fluid phase lipid bilayers. J. Phys. Chem. B. 103:6323–6327. [Google Scholar]
  9. Chiu, S.-W., E. Jakobsson, R. J. Mashl, and H. L. Scott. 2002. Cholesterol-induced modifications in lipid bilayers: a simulation study. Biophys. J. 83:1842–1853. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Chiu, S.-W., S. Vasudevan, E. Jakobsson, R. J. Mashl, and H. L. Scott. 2003. Structure of sphingomyelin bilayers: a simulation study. Biophys. J. 85:3624–3635. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Dietrich, C., Z. N. Volovyk, M. Levi, N. L. Thompson, and K. Jacobson. 2001. Partitioning of Thy-1, GM1, and cross-linked phospholipids analogs into lipid rafts reconstituted in supported model membrane monolayers. Proc. Natl. Acad. Sci. USA. 98:10642–10647. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Dietrich, C., B. Yang, T. Fuiwara, A. Kusumi, and K. Jacobson. 2002. Relationship of lipid rafts to transient confinement zones detected by single particle tracking. Biophys. J. 82:244–284. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Douliez, J.-P., A. Léonard, and E. J. Dufourc. 1995. Restatement of order parameters in biomembranes: calculation of C-C bond order parameters for C-D quadrupolar splittings. Biophys. J. 68:1727–1739. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Edidin, M. 2003. The state of lipid rafts: from model membranes to cells. Annu. Rev. Biophys. Biomol. Struct. 32:257–283. [DOI] [PubMed] [Google Scholar]
  15. Essmann, U., L. Perera, M. L. Berkowitz, T. Darden, H. Lee, and L. G. Pedersen. 1995. A smooth particle mesh Ewald method. J. Chem. Phys. 103:8577–8593. [Google Scholar]
  16. Falck, E., M. Patra, M. Karttunen, M. T. Hyvönen, and I. Vattulainen. (2004). Lessons of slicing membranes: interplay of packing, free area, and lateral diffusion in phospholipid/cholesterol bilayers. http://www.arxiv.org/abs/cond-mat/0402290. [DOI] [PMC free article] [PubMed]
  17. Fantini, J., N. Garmy, R. Mahfoud, and N. Yahi. 2002. Lipid rafts: structure, function, and role in HIV, Alzheimers, and prion diseases. Exp. Rev. Mol. Med. 20:1–21. [DOI] [PubMed] [Google Scholar]
  18. Filippov, A., G. Orädd, and G. Lindblom. 2003. The effect of cholesterol on the lateral diffusion of phospholipids in oriented bilayers. Biophys. J. 84:3079–3086. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Filippov, A., G. Orädd, and G. Lindblom. 2004. Lipid lateral diffusion in ordered and disordered phases in raft mixtures. Biophys. J. 86:891–896. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Gandhavadi, M., D. Allende, A. Vidal, S. Simom, and T. Mcintosh. 2002. Structure, composition, and peptide binding properties of detergent soluble bilayers and detergent resistant rafts. Biophys. J. 82:1469–1482. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Gurtovenko, A. A., M. Patra, M. Karttunen, and I. Vattulainen. 2003. Cationic DMPC/DMTAP lipid bilayers: molecular dynamics study. http://www.arxiv.org/abs/cond-mat/0312400. [Online] [DOI] [PMC free article] [PubMed]
  22. Harder, T., P. Scheiffele, P. Verkade, and K. Simoms. 1998. Lipid domain structure of the plasma membrane revealed by patching of membrane components. J. Cell Biol. 141:929–942. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Hess, B., H. Bekker, H. J. C. Berendsen, and J. G. E. M. Fraaige. 1997. LINCS: a linear constraint solver for molecular simulations. J. Comput. Chem. 18:1463–1472. [Google Scholar]
  24. Hofsäß, C., E. Lindahl, and O. Edholm. 2003. Molecular dynamics simulations of phospholipid bilayers with cholesterol. Biophys. J. 84:2192–2206. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Holopainen, J. M., A. J. Metso, J.-P. Mattila, A. Jutila, and P. K. J. Kinnunen. 2004. Evidence for the lack of specific interaction between cholesterol and sphingomyelin. Biophys. J. 86:1510–1520. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Höltje, M., T. Förster, B. Brandt, T. Engels, W. von Rybinski, and H.-D. Höltje. 2001. Molecular dynamics simulations of stratum corneum lipid models: fatty acids and cholesterol. Biochim. Biophys. Acta. 1511:156–167. [DOI] [PubMed] [Google Scholar]
  27. Huang, J., J. E. Swanson, A. R. G. Dibble, A. K. Hinderliter, and G. W. Feigenson. 1993. Nonideal mixing of phosphatidylserine and phosphatidylcholine in fluid lamellar phase. Biophys. J. 64:413–425. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Jacobson, K., and C. Dietrich. 1999. Looking at lipid rafts? Trends Cell Biol. 9:87–91. [DOI] [PubMed] [Google Scholar]
  29. Jedlovszky, P., N. N. Medvedev, and M. Mezei. 2004. Effect of cholesterol on the properties of phospholipid membranes. 3. Local lateral structure. J. Phys. Chem. B. 108:465–472. [DOI] [PubMed] [Google Scholar]
  30. Kawabuchi, M., Y. Satomi, T. Takao, Y. Shimonishi, S. Nada, K. Nagai, A. Tarakhovsky, and M. Okada. 2000. Transmembrane phosphoprotein Cbp regulates the activities of Scr-family tyrosine kinases. Nature. 404:999–1002. [DOI] [PubMed] [Google Scholar]
  31. Khelashvili, G. A., and H. L. Scott. 2004. Combined Monte Carlo and molecular dynamics simulation of hydrated 18:0 sphingomyelin-cholestrol lipid bilayers. J. Chem. Phys. 120:9841–9847. [DOI] [PubMed] [Google Scholar]
  32. Koynova, R., and M. Caffrey. 1995. Phases and phase transitions of sphingolipids. Biochim. Biophys. Acta. 1255:213–236. [DOI] [PubMed] [Google Scholar]
  33. Lawrence, J. C., D. E. Saslowsky, J. M. Edwardson, and R. M. Henderson. 2003. Real-time analysis of the effects of cholesterol on lipid raft behavior using atomic force microscopy. Biophys. J. 84:1827–1832. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Lindahl, E., B. Hess, and D. van der Spoel. 2001. Gromacs 3.0: a package for molecular simulation and trajectory analysis. J. Mol. Model 7:306–317. [Google Scholar]
  35. Manes, S., E. Mira, C. Gomez-Moulton, R. A. Lacalle, P. Keller, J. P. Labrador, and A. C. Martinez. 1999. Membrane raft microdomains mediate front-rear polarity in migrating cells. EMBO J. 18:6211–6220. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Manie, S. N., S. Debreyne, S. Vincent, and D. Gerlier. 2000. Measles virus structural components are enriched into lipid raft microdomains: a potential cellular location for virus assembly. J. Virol. 74:305–311. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Maulik, P. R., P. K. Sripada, and G. G. Shipley. 1991. Structure and thermotropic properties of hydrated n-stearoyl sphingomyelin bilayer membranes. Biochim. Biophys. Acta. 1062:211–219. [DOI] [PubMed] [Google Scholar]
  38. McMullen, T. P. W., R. Lawis, and R. N. McElhaney. 2004. Cholesterol-phospholipid interactions: the liquid ordered phase and lipid rafts in model and biological membranes. Curr. Opin. Coll. Interf. Sci. 8:459–468. [Google Scholar]
  39. Nagle, J. F., and S. Tristram-Nagle. 2000. Structure of lipid bilayers. Biochim. Biophys. Acta. 1469:159–195. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Nose, S., and M. L. Klein. 1983. Constant pressure molecular dynamics for molecular systems. Mol. Phys. 50:1055–1076. [Google Scholar]
  41. Pandit, S. A., D. L. Bostick, and M. L. Berkowitz. 2004a. Complexation of phosphatidylcholine lipids with cholesterol. Biophys. J. 86:1345–1356. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Pandit, S. A., S. Vasudevan, S.-W. Chiu, R. J. Mashl, E. Jakobsson, and H. L. Scott. 2004b. Sphingomyelin-cholesterol domains in phospholipid membranes: atomistic simulation. Biophys. J. 87:1092–1100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Parrinello, M., and A. Rahman. 1981. Polymorphic transitions in single crystals: a new molecular dynamics method. J. Appl. Phys. 52:182–190. [Google Scholar]
  44. Pasenkiewicz-Gierula, M., T. Róg, K. Kitamura, and A. Kusumi. 2000. Cholesterol effects on the phosphatidylcholine bilayer polar region: a molecular simulation study. Biophys. J. 78:1376–1389. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Patra, M., M. Karttunen, M. Hyvönen, E. Falck, P. Lindqvist, and I. Vattulainen. 2003. Molecular dynamics simulations of lipid bilayers: major artifacts due to truncating electrostatic interactions. Biophys. J. 84:3636–3645. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Pralle, A., P. Keller, E. L. Florin, K. Simone, and J. H. K. Horber. 2000. Sphingolipid-cholesterol rafts diffuse as small entities in the plasma membrane of mammalian cells. J. Cell Biol. 148:997–1007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Reitveld, A., and K. Simons. 1998. The differential miscibility of lipids as the basis for the formation of functional membrane rafts. Biochim. Biophys. Acta. 1376:467–479. [DOI] [PubMed] [Google Scholar]
  48. Rinia, H. A., M. M. E. Snel, J. P. J. M. van der Eerden, and B. de Kruijff. 2001. Visualizing detergent resistant domains in model membranes with atomic force microscopy. FEBS Lett. 501:92–96. [DOI] [PubMed] [Google Scholar]
  49. Róg, T., and M. Pasenkiewicz-Gierula. 2001. Cholesterol effects on the phosphatidylcholine bilayer nonpolar region: a molecular simulation study. Biophys. J. 81:2190–2202. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Rozelle, A. L., L. M. Machesky, M. Yamamoto, M. H. Driessens, R. H. Insall, M. G. Roth, K. Luby-Phelps, G. Marriott, A. Hall, and H. L. Yin. 2000. Phosphatidylinositol 4,5-biphosphate induces actin-based movement of raft-enriched vesicles through WASP-Arp2/3. Curr. Biol. 6:311–320. [DOI] [PubMed] [Google Scholar]
  51. Samsonov, A. V., I. Mihalyov, and F. S. Cohen. 2001. Characterization of cholesterol-sphigomyelin domains and their dynamics in bilayer membranes. Biophys. J. 81:1486–1500. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Schroeder, R., E. London, and D. A. Brown. 1994. Interactions between saturated acyl chains confer detergent resistance on lipids and GPI-anchored proteins: GPI-anchored proteins in liposomes and cells show similar behavior. Proc. Natl. Acad. Sci. USA. 91:12130–12134. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Shinoda, W., and S. Okazaki. 1998. A Voronoi analysis of lipid area fluctuation in a bilayer. J. Chem. Phys. 109:1517–1521. [Google Scholar]
  54. Simons, K., and E. Ikonen. 1997. Functional rafts in cell membranes. Nature. 387:569–572. [DOI] [PubMed] [Google Scholar]
  55. Smondyrev, A. M., and M. L. Berkowitz. 1999. Structure of dipalmitoylphosphatidylcholine/cholesterol bilayer at low and high cholesterol concentrations: molecular dynamics simulation. Biophys. J. 77:2075–2089. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Sönnichsen, B., S. de Renzis, E. Nielsen, J. Reitdorf, and M. Zerial. 2000. Distinct membrane domains on endosomes in the recycling pathway visualized by multicolor imaging of Rab4, Rab5, and Rab1. J. Cell Biol. 149:901–914. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Tu, K., M. L. Klein, and D. J. Tobias. 1998. Constant-pressure molecular dynamics investigation of cholesterol effects in a dipalmitoylphosphatidylcholine bilayer. Biophys. J. 75:2147–2156. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Veatch, S. L., and Keller, S. L. (2002). Organization in lipid membranes containing cholesterol. Phys. Rev. Lett. 89:268101. [DOI] [PubMed] [Google Scholar]
  59. Viola, A., S. Schroeder, Y. Sakakibara, and A. Lanzavecchia. 1999. T lymphocyte costimulation mediated by reorganization of membrane microdomains. Science. 283:680–682. [DOI] [PubMed] [Google Scholar]
  60. Xavier, R., T. Brennan, Q. Li, C. McCormack, and B. Seed. 1998. Membrane compartmentation is required for efficient T cell activation. Immunity. 6:723–732. [DOI] [PubMed] [Google Scholar]
  61. Yuan, C., J. Furlong, P. Burgos, and L. J. Johnston. 2002. The size of lipid rafts: an atomic force microscopy study of ganglioside GM1 domains in sphingomyelin/DOPC/cholesterol. Biophys. J. 82:2526–2535. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Zerial, M., and H. McBride. 2001. Rab proteins as membrane organizers. Nat. Rev. Mol. Cell Biol. 2:107–117. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES