Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Aug 23;87(5):3413–3420. doi: 10.1529/biophysj.104.044719

Observation of the Energy-Level Structure of the Low-Light Adapted B800 LH4 Complex by Single-Molecule Spectroscopy

W P F de Ruijter *, S Oellerich *, J-M Segura *, A M Lawless †, M Papiz †, T J Aartsma *
PMCID: PMC1304807  PMID: 15326024

Abstract

Low-light adapted B800 light-harvesting complex 4 (LH4) from Rhodopseudomonas palustris is a complex in which the arrangement of the bacteriochloropyll a pigments is very different from the well-known B800-850 LH2 complex. For bulk samples, the main spectroscopic feature in the near-infrared is the occurrence of a single absorption band at 802 nm. Single-molecule spectroscopy can resolve the narrow bands that are associated with the exciton states of the individual complexes. The low temperature (1.2 K) fluorescence excitation spectra of individual LH4 complexes are very heterogeneous and display unique features. It is shown that an exciton model can adequately reproduce the polarization behavior of the complex, the experimental distributions of the number of observed peaks per complex, and the widths of the absorption bands. The results indicate that the excited states are mainly localized on one or a few subunits of the complex and provide further evidence supporting the recently proposed structure model.

INTRODUCTION

A wide variety of pigment-protein complexes are used as light-harvesting (LH) antennas to intercept light to meet the demand for energy of photosynthetic organisms. Each type of antenna complex has its own specific absorption spectrum, thereby optimizing the efficiency of light absorption depending on environmental conditions. In purple bacteria the most common antenna complexes are the light-harvesting complexes LH1 and LH2. In the near-infrared LH1 absorbs at 870 nm and LH2 at 800 nm and 850 nm. Light energy that is absorbed by an LH antenna is transferred to a reaction center (RC) through efficient energy transfer (Cogdell et al., 1996; Hu et al., 1997; van Grondelle et al., 1994). The number of antenna complexes per RC, and therefore the effective absorption cross section of the photosynthetic unit, depends on the light intensity in which the bacterium is grown. When grown under high-intensity conditions, less antenna complexes are required to let the RC operate at a maximal turnover rate. However, at low-intensity conditions the ratio of antenna to RC complexes increases significantly. Moreover, under these conditions some bacteria express new types of LH complexes such as the B800-820 LH3 complex in Rhodopseudomonas acidophila strain 7050 (Gardiner et al., 1993; McLuskey et al., 2001) or the B800 LH4 complex in Rhodopseudomonas palustris (Evans et al., 1990; Tharia et al., 1999).

In this article we consider the B800 LH4 complex in more detail. In contrast to the high resolution of the crystal structures of LH2 and LH3 (Koepke et al., 1996; McDermott et al., 1995; McLuskey et al., 2001; Papiz et al., 2003; Prince et al., 1997), the resolution of the electron density map of LH4 is currently only 7.5 Å (Hartigan et al., 2002). A pigment organization was proposed for LH4 that accounted for the near-infrared absorption and CD spectra and that was also consistent with the electron density map. An unusual feature of the model was the presence of four bacteriochlorophyll molecules per repeating unit rather than the usual three found in LH2 and LH3. This was also based on a quantification of the pigment to protein stoichiometry. Because of the relatively low resolution of the electron density map there is still some room for discussion about the validity of the proposed structural model of this complex. The general organization of the LH2 and LH4 complexes is the same: identical subunits are repeated cyclically in such a way that a ring-shaped structure is formed. However, the symmetries of these rings are different: LH2 and LH3 are usually nonameric but LH4 is octameric. In addition, the protein scaffold of the LH4 subunits, which keeps the functionally active components in place, is encoded by a specific pair of genes: pucBd and pucAd (Gall and Robert, 1999; Hartigan et al., 2002; Tharia et al., 1999).

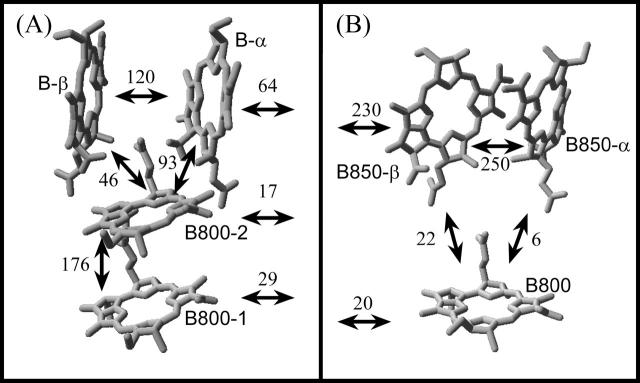
Although caution must be exercised with regard to details of the structural model, explicit predictions can be derived for the optical properties of the LH4 complex that can be easily tested, especially in comparison with LH2. The essential differences, which give rise to variations in the functional and spectral behavior of the complexes, can be seen in the bulk absorption spectra. For the case of LH2, there are two bands absorbing at ∼800 and 850 nm, whereas LH4 has only a single absorption band at 800 nm. Both bands in the LH2 spectrum are due to absorption of the Qy transition of the bacteriochlorophyll a (Bchl a) pigments. They are assigned to the two pigment rings in the complex, the B800 and B850 rings, respectively. The rings differ by their packing density and by the orientation of the pigments. For comparison, the Bchl a molecules of one subunit of the LH4 and LH2 rings are displayed in Fig. 1, A and B, respectively. The most striking difference is the occurrence of an additional Bchl a ring in the LH4 complex, the B800-2 ring, at a position approximately halfway between the densely packed B-α/B-β ring and the B800-1 ring that are both also present in LH2. This brings the number of Bchl a pigments in LH4 to 32, the same as in the larger LH1 complex (Qian et al., 2000; Roszak et al., 2003).

FIGURE 1.

FIGURE 1

Open in a new tab

Pigment arrangement and interaction strengths (in cm−1) of a subunit of (A) LH4 and (B) LH2. The interaction strengths have been derived by a structure-based calculation that uses a point monopole approximation (Hartigan et al., 2002). The different angles of the B-α/B-β pigments of LH4 with respect to the B850-α/B850-β pigments of LH2 (see text for details) are readily observed. Also, the position of the B800-2 pigment in LH4 can be seen. The phytyl chains of the BChl a molecules are omitted for clarity.

The second fundamental difference is the organization of the most densely packed pigment ring. In LH2, the B850 ring has nearly tangentially oriented Bchl a pigments, whereas in LH4 the equivalent B-α/B-β pigments are organized in a more radial fashion. Both these differences have implications for the way the complexes absorb and transfer energy. It is assumed that excitonic interactions are the major factor determining these properties. Excitonic interactions strongly depend on the alignment of and the distance between the dipole moments of the involved pigments. Therefore, the tangential orientation of the Qy transition dipole moments of the Bchl a pigments in the B850 ring is a key property for these interactions in LH2 (Didraga et al., 2002; Freer et al., 1996; Novoderezhkin and Razjivin, 1993). Because the alignment of the pigments is different in LH4, it is expected that excitonic interactions within the B-α/B-β ring and their effect on the spectral properties will differ from those in LH2. Due to the proximity of the additional B800-2 ring in the LH4 complex to the other rings, other excitonic interactions between the pigment rings become possible. Investigation of these interactions can serve as a test for the validity and the accuracy of the structural model.

Single-molecule spectroscopy (SMS) can provide information that is not accessible to bulk techniques. Spectra obtained by conventional techniques inherently display spectral broadening due to ensemble averaging of the spectra of the individual molecules. SMS resolves the optical spectrum of each individual complex and thus provides detailed information on the energy-level structure. Previous SMS studies on LH2 from Rps. acidophila have revealed the intriguing details of the band structure that arise due to the excitonic interactions as described above (Hofmann et al., 2003; Ketelaars et al., 2001; Matsushita et al., 2001; van Oijen et al., 1999a,b, 2000). Important questions on the electronic structure and excited-state dynamics in photosynthesis can therefore be resolved by SMS.

In this article, we present the results of a single-molecule spectroscopy study on the LH4 complex. Our spectra reveal important evidence supporting the structure model based on the 7.5-Å resolution electron density map and near-infrared modeling of absorption and CD spectra (Hartigan et al., 2002). We will elaborate on the two main differences with the existing LH2 structure model: the occurrence of an additional pigment ring and the more radial orientation of the pigments in the B-α/B-β ring. We observe spectral congestion due to the fact that all pigments absorb in the same region. In addition to that, there is a large variety in spectral behavior between complexes. Based on the structural model, simulations of single-molecule spectra were performed that reproduce the essential features of the observed spectra. It is shown that multiple pigment rings contribute significantly to the same absorption peak, indicating excitonic interactions within and between the pigment rings. Closer analysis reveals that interactions within the subunits are dominant.

MATERIALS AND METHODS

LH4 complexes of Rps. palustris (strain 2.1.6) were purified as described previously (Hartigan et al., 2002; Tharia et al., 1999). The purified protein was diluted with buffer (20 mM Tris, 0.05% dodecylmaltoside, 1.8% PVA, pH 8) to ∼10−11 M for single-molecule samples and to an optical density of 0.02 at 802 nm for bulk samples. Diluted protein solution (3 μl) was spin coated onto a LiF sample plate. The sample was then mounted in a cryostat and cooled down rapidly to a temperature of ∼1.2 K.

Fluorescence excitation spectra of single LH4 complexes and of bulk samples were obtained with a confocal microscope setup. Selection of individual complexes was performed as described previously (Ketelaars et al., 2001). Fluorescence was detected with an avalanche photodiode (SPCM-AQR-16; Perkin-Elmer, Wellesley, MA). For each complex, 200 polarization-dependent spectral scans were taken, accumulating to one hour illumination per studied complex at an intensity of 10–100 W/cm2. After each consecutive spectral scan, the polarization was rotated by an angle of 3.6°. To block the excitation light, a series of three or four band-pass filters was placed in the detection beam path. Several filter sets have been used, with transmission maxima varying from 826 to 870 nm and with a bandwidth between 20 and 40 nm. A total of 57 molecules was studied.

Simulations of the spectra were performed according to Frenkel exciton theory. It is assumed that only the Qy transitions of the Bchl a molecules contribute to the spectrum in the region of 780–840 nm. The Hamiltonian matrix for LH4 of Rps. palustris was calculated as described previously (Hartigan et al., 2002). A Gaussian distribution with a width of 175 cm−1 was applied to the site energies (the diagonal elements of the Hamiltonian) to introduce inhomogeneous energy broadening caused by stochastic variations in the protein environment. The width of the Gaussian distribution was optimized to resemble the bulk low-temperature absorption spectrum (data not shown). Diagonalization of the Hamiltonian results in a set of eigenvectors and eigenvalues. Each eigenvector represents a particular eigenstate of the complex and its elements correspond to the contribution of each pigment in the complex to the eigenstate. A measure for the contribution of a pigment to the eigenfunction of a particular exciton state is obtained when its eigenvector element is squared. Summation of the squared values that are associated with the pigments of one of the three rings in LH4 provides an indication for the contribution of that ring to an exciton state. The dipole strengths 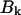Inline graphic of the excited states can be calculated according to the formula:

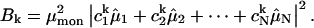graphic file with name M2.gif (1)

In this formula, 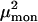Inline graphic is the dipole strength of a monomeric Bchl a pigment in the absence of coupling, 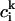Inline graphic is the element of eigenvector k at pigment i, and 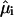Inline graphic is the unit dipole vector of pigment i.

A simulation produces a single-molecule stick spectrum in which the energies of the sticks are determined by the eigenvalues of the Hamiltonian and their amplitude by the associated dipole strengths. Each transition is then dressed by a Lorentzian lineshape of which the total area is normalized to the transition's dipole strength. The relative width is determined by modeling the excited-state lifetime of each individual state. The lifetime of an exciton state i is taken as the reciprocal of the population transfer rate Γi of that state, which is calculated according to the formula that has been derived by Leegwater et al. (1997):

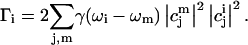graphic file with name M6.gif (2)

In this equation, γ(ω) represents the strength of the coupling of the complex to the surrounding phonon pool; ωi is the wavelength at which excited state i absorbs. Equation 2 only takes downhill energy transfer between exciton states into account, in accordance with the low-temperature conditions in the experiment. The function γ(ω) is taken to be similar to the empirical function in Vulto et al. (1999). This is a combination of a Lorentzian and an exponential function describing the high- and low-energy side of the phonon side band of an optical transition, respectively. The function contains three constants: the full width at half maximum of the Lorentzian function, Δω, the maximum of the phonon side band, ωc, and the scaling parameter γ0. Δω was taken to be 80 cm−1 and ωc was set at 24 cm−1, well within the range of values obtained by hole-burning measurements on LH2 (Freiberg et al., 2003; Reddy et al., 1991; van der Laan et al., 1990, 1993) The parameter γ0 scales the effective electron-phonon coupling strength. It has a strong effect on Γi and therefore on the distribution of the linewidths of the absorption bands. The simulated distribution of linewidths was fit to the experimental data by adjusting γ0 as the only fitting parameter (see Fig. 3).

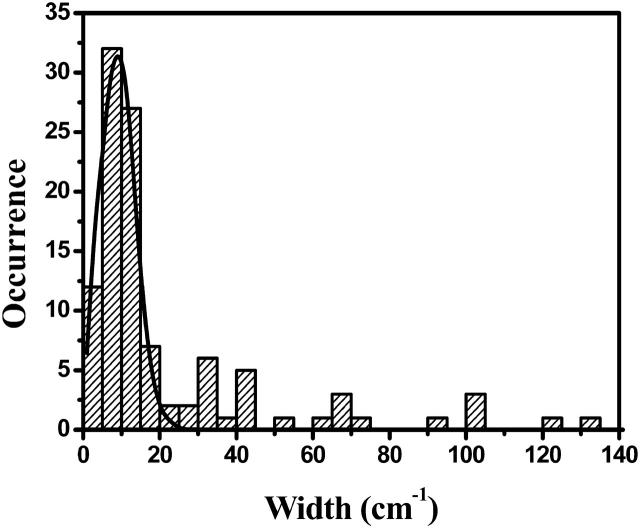
FIGURE 3.

FIGURE 3

Open in a new tab

Histogram of the widths of the peaks in the observed spectra (bars) and a simulation of the widths of the peaks in 1000 complexes. The simulated curve has been scaled to the height of the experimental distribution.

Polarization-dependent spectra of individual complexes with Gaussian inhomogeneous diagonal disorder were calculated by taking the inner product between the exciton transition moment and the polarization vector of the excitation light.

Monte Carlo simulations of an ensemble of LH4 were performed by summing the results of 10,000 randomly generated site-energy configurations. Only diagonal disorder was taken into account, assuming that the influence of off-diagonal disorder is negligible as it is in LH2 (Damjanovic et al., 2002; Dempster et al., 2001; Wu and Small, 1998).

RESULTS

In total 57 individual LH4 complexes have been studied. For 28 complexes the signal/noise level of the most intense band was at least 4, corresponding to a count rate of 100 cps. This is sufficiently high to allow an accurate determination of the width of the bands in the spectrum, taken to be the full width at half maximum. These complexes were studied in more detail. Summation of the single-molecule spectra did not lead to an exact reproduction of the bulk spectrum. This is not surprising, because the features in the spectra of individual complexes have such narrow bandwidths that only the summation of a significantly larger number of molecules would average out the structures of the single-molecule spectra. Simulations where up to 100 molecules were summed also displayed residual structure and therefore confirm this interpretation. Even though more data are required to fully reproduce the bulk spectrum, we consider our data to be representative for LH4. We will elaborate on this in the discussion section.

Unlike in the case of LH2, we do not, in general, observe two orthogonally polarized broad bands in the red-most part of the spectrum, which is the signature of a circular exciton state. For the LH4 complex, the single-molecule spectra are very heterogeneous and display heavy spectral congestion around 800 nm. Therefore, an assignment of individual bands or groups of transitions to specific exciton states or molecular transitions cannot be made.

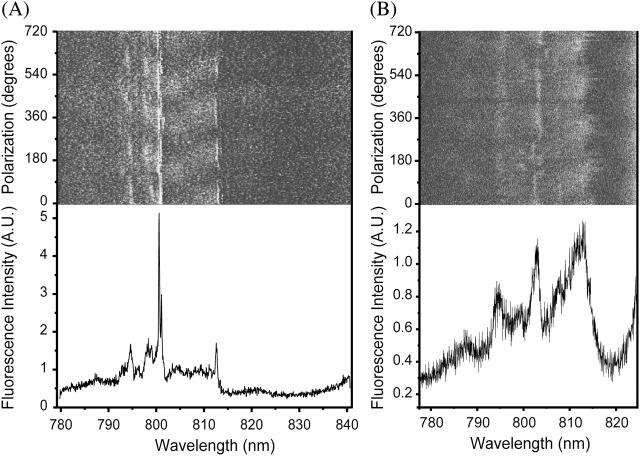
Fig. 2 shows the fluorescence excitation spectra of two individual LH4 complexes. The top parts of Fig. 2, A and B, show a two-dimensional representation of 200 spectra from consecutive wavelength scans. Each horizontal line in the image corresponds to an individual scan. Between scans, the polarization of the excitation beam is rotated by 3.6°. This representation makes it relatively easy to assess the behavior of the optical transitions at varying angles of polarization of the excitation light. The lower parts of Fig. 2, A and B, are the sum spectra of all scans in the two-dimensional representation. Single-molecule spectra did not depend on detection wavelength.

FIGURE 2.

FIGURE 2

Open in a new tab

Fluorescence excitation spectra of two individual LH4 complexes. (Top) Stack of 200 consecutive scans of the complex. After each scan, corresponding to a horizontal line in the images, the excitation polarization was rotated by 3.6°. The grayscale represents the intensity of fluorescence, ranging from 0 to 18 photon counts per measurement time unit of 10 ms in panel A and 0–9 counts in panel B. (Bottom) Sum of all 200 scans in the top image.

A histogram of the widths of the observed bands can be seen in Fig. 3. The bars in the figure represent the experimental data of the 28 complexes with a fluorescence signal level sufficient for the determination of the widths. The solid line is the result of a simulation of 1000 individual complexes, taking only those states into account that have an oscillator strength of at least one Bchl a. It has been numerically optimized to represent the experimental data by adjusting the value of γ0, as described in Materials and Methods. It was determined to have a value of 65 ps−1, comparable to the value that was previously found for the Fenna-Matthews-Olson complex (Vulto et al., 1999). There is only a single peak in the experimental distribution of linewidths, at 10 cm−1, and a long tail extending to larger widths.

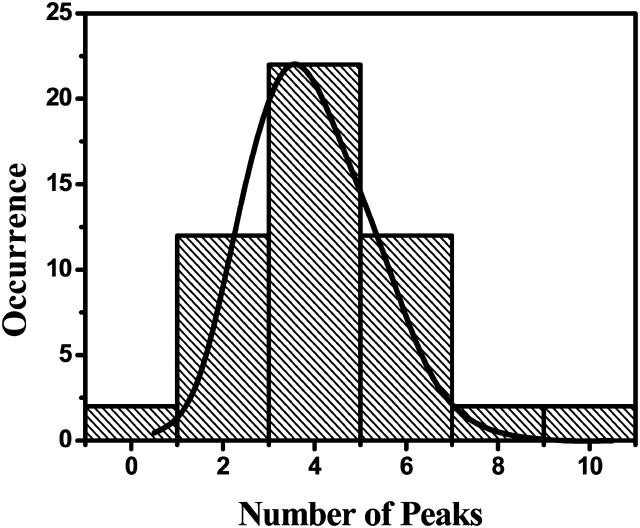
Each single-molecule spectrum typically displays four bands. A distribution of the experimentally observed number of bands per complex can be seen in Fig. 4. The distribution has a single peak and a short tail extending toward larger numbers. Only the most intense bands in the spectrum were counted, and this number can be compared with simulations in which we set an appropriate lower limit of the oscillator strength. There are more bands in the spectrum (depending on the extent of disorder), but they cannot all be distinguished experimentally because of signal/noise limitations. The maximum number of bands that was detected for a single complex was 10. The solid line in the figure is the result of a simulation of 1000 individual complexes. The simulated distribution was obtained by only taking into account those exciton states that have sufficient peak height to be detected above the experimental background level.

FIGURE 4.

FIGURE 4

Open in a new tab

Distribution of the number of detected bands in a single-molecule spectrum. The bars are the experimental data; the solid line represents a simulation of 1000 individual complexes. The maximum of the simulated distribution has been normalized to the maximum of the experimental distribution.

DISCUSSION

In general, there are four parameters that characterize an absorption band in a single-molecule spectrum: the polarization of the band, its energy, the linewidth, and the intensity. These spectral parameters are distinctly different for LH4 when comparing the results with the previously studied LH2. In particular, the single-molecule spectra of LH4 show a rather limited number of bands in the 800-nm region only. Furthermore, the distribution of the widths of the bands in the LH4 spectra has a single sharp peak around 10 cm−1 with a tail to larger widths as can be seen in Fig. 3. There is no clear distinction between broad and narrow peaks as in LH2, and the predominant linewidth lies between that of the two pigment pools of LH2, B800, and B850. Also, the characteristic orthogonal polarization of the k±1 bands is not observed although all spectra do show bands that are polarization dependent in the plane of excitation as well as an occasional band that is nearly polarization independent. The significant differences between the spectra of the two complexes, LH2 and LH4, indicate that they have rather different excited-state properties.

Numerical simulations based on the proposed structure model have been utilized to further investigate the nature of these differences. As in the case of LH2 (Dracheva et al., 1996; Sauer et al., 1996), an exciton model was applied to analyze the system in more detail. For LH2, such a model has provided significant insight. The values from structure-based calculations for the intermolecular interactions in LH4 and LH2 are indicated in Fig. 1. In the case of LH2, especially the strong interactions within the B850 ring have a profound effect on its spectral characteristics. The absorption of the ring is red-shifted by ∼50 nm and this is largely due to the head-to-head organization of the dipoles. The oscillator strength resides almost exclusively in the k±1 states of the red-most branch of exciton states (Dracheva et al., 1996; Sauer et al., 1996). The spectral linewidth is determined by the excited-state lifetime that, except for the k = 0 state, is very short because of fast energy relaxation between exciton states. These exciton transitions are observed as broad bands in the single-molecule spectra. In the B800 ring of LH2 the interactions are weaker by a factor of 10, but the excited states are still distributed over more than one Bchl a (Alden et al., 1997; Hofmann et al., 2003). The weaker interaction strength causes the energy to be localized, resulting in longer relaxation time constants (1–2 ps). Therefore, the B800 bands of LH2 are relatively narrow (1 cm−1) in the single-molecule spectra (van Oijen et al., 2000). The strength of the inter-ring interaction between the B800 and the B850 ring is similar to the interactions within the B800 ring and therefore energy transport between the rings occurs on the relatively slow timescale of 1 ps (Shreve et al., 1991).

When the LH4 results are compared to LH2, remarkable differences are observed. First of all, the strengths of the nearest-neighbor interactions within the B-α/B-β ring are about half of those interactions in the B850 ring of LH2. This difference is primarily due to the different orientation of the Bchl a molecules in the B-α/B-β ring. The second—and most prominent—difference between LH4 and LH2 lies in the inter-ring interactions involving the B800-2 ring. Based on the structure model, the largest interaction is the 176 cm−1 interaction between adjacent molecules in the B800-1 and B800-2 rings, whereas the intersubunit interactions are only 64 cm−1 or less as seen in Fig. 1. A consequence of this is that all Bchls a of the complex need to be taken into account in the simulations, whereas for LH2 the B800 and B850 rings could be studied separately due to their loose coupling. Nevertheless, we can draw two important conclusions from the model. It implies first of all, that the excited states are strongly delocalized over the Bchls a within a single subunit. Secondly, the intersubunit interaction is relatively small when compared to the variation in site energies, and therefore the excited states will be much more localized in LH4 than is the case in LH2. This has significant implications for the experimental observations, as we will discuss below.

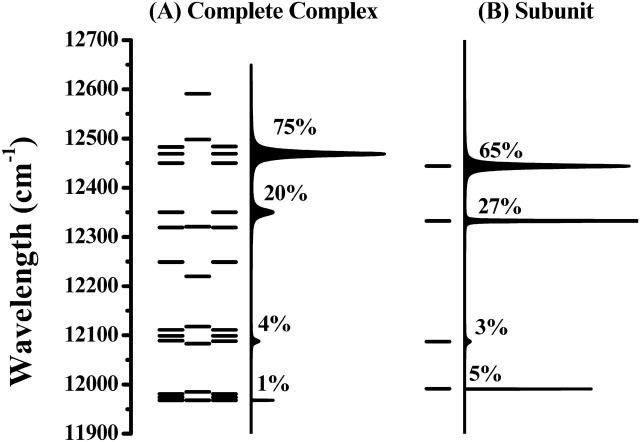
The eigenvalues of the LH4 Hamiltonian represent the energies of the 32 exciton states, according to the number of Bchl a molecules in the LH4 complex. We do not, however, observe 32 bands in our SMS spectra. This is due to a large variation in the peak amplitudes of the exciton states, which are determined by the oscillator strengths and lifetimes of those states. It is evident that the transitions with the highest oscillator strengths have a much higher probability to be detected than the transitions with the lowest strengths. Fig. 5 A shows a graph of the exciton manifold of LH4 without diagonal disorder, as well as the corresponding simulated single-molecule spectrum. For comparison, the manifold and the optical spectrum of a single subunit are included in Fig. 5 B. Both spectra appear roughly similar, but there are significant differences in oscillator strengths and widths of the bands indicating mixing of different subunit states. The exciton manifold of LH4 has states from ∼12,600 cm−1 to 11,900 cm−1 of which only two degenerate pairs have significant oscillator strength. The latter states must correlate with the most intense bands that are observed experimentally. This is consistent with the spectral position of the observed bands. The pronounced oscillator strength in the upper part of the manifold is in marked contrast with LH2, and is due to the parallel organization of the dipole moments of the Bchl a molecules in the case of LH4.

FIGURE 5.

FIGURE 5

Open in a new tab

Graph of the exciton manifold of LH4 without diagonal disorder. The percentual contribution to the total transition dipole strength is noted for the dominant transitions. (A) The energies of the exciton states of the complete complex. Due to the symmetry of the complex, a large part of the exciton states is degenerate. The right part shows the optical spectrum. (B) The energies of the exciton states of a single subunit. The right part shows the optical spectrum.

Diagonal disorder in the Hamiltonian shifts the energies of the dominant transitions, redistributes the total oscillator strength over the exciton manifold, and alters the energy transfer lifetimes. Even slight modifications of the site energies can have profound effects on the appearance of a single-molecule spectrum. Fitting a single-molecule spectrum is therefore by no means straightforward. Fig. 6 is an example of a simulation of a polarization-dependent single-molecule spectrum of LH4, without adjustment for instrument response or spectral diffusion. It has been selected from a series of spectra that were calculated after applying random diagonal disorder to the Hamiltonian because it has a strong resemblance with the spectrum that is displayed in Fig. 2 A, although it is not a numerically optimized fit. Nevertheless, the shape of the summed spectrum in the bottom panel of the figures as well as the polarization-dependent spectrum at the top are very similar, providing a first indication that a relatively simple model of the system is capable of adequately reproducing the experimental results. The narrow transitions in the simulated spectrum of Fig. 6 around 785 nm and 840 nm are difficult to observe experimentally, because they carry only ∼1–2% of the total oscillator strength. In general, out of a series of 40 random realizations of simulated single-molecule spectra, there is usually at least one that has a strong resemblance to a specific experimental spectrum. This shows that there are limited possibilities for the spectral behavior of the complex. From this we conclude that we have studied a sufficiently large number of complexes to observe the representative spectral variations. Because every individual complex has a different distribution of exciton states, we will elaborate on the statistics of the linewidths and the number of detected bands.

FIGURE 6.

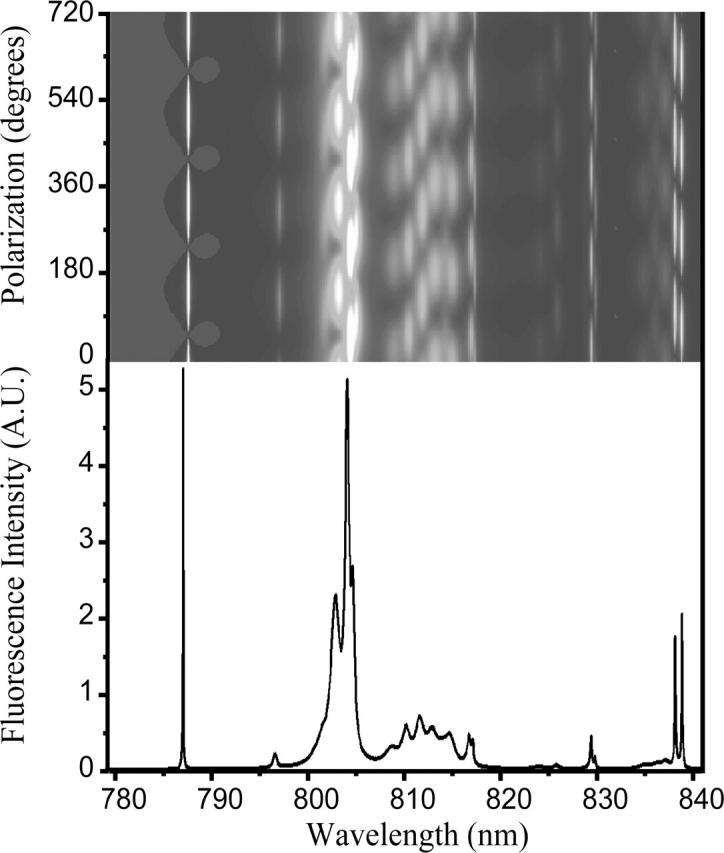
FIGURE 6

Open in a new tab

Simulated polarization-dependent single-molecule spectrum of LH4. This graph was selected from a series of 40 randomly generated spectra (see text for details) for having the most features in common with the experimental spectrum in Fig. 2 A. The narrow lines at the edges of the spectrum are difficult to observe experimentally because they contain only 1–2% of the total oscillator strength. Furthermore, the simulated spectrum has not been corrected for instrument response or spectral diffusion.

The width of a band is a direct measure for the dynamics of an exciton state. Most bands have a bandwidth of 10 cm−1, as can be seen in Fig. 3, which corresponds to internal energy transfer on a timescale of 0.5 ps. Our simulations reproduce the experimental results, except for the tail toward larger widths. We suspect this tail to consist of bands that are constituted by overlap of exciton transitions. An example of a band that appears in the tail of Fig. 3 can be seen in Fig. 2 A in the region between 805 and 810 nm. When comparing this experimentally observed band with the region around 810 nm in the simulation of Fig. 6, it can be seen that it is plausible that the band of Fig. 2 A is built up by multiple exciton states. The aforementioned internal energy transfer is slow compared to the dynamics of the B850 ring of LH2, where energy transfer takes place in 100 fs, but faster than the dynamics of the B800 ring (Kennis et al., 1997). The explanation for these slow dynamics lies in the structure of the exciton manifold. As indicated above, most of the oscillator strength is contained in the higher exciton states whereas the lower states hardly have any strength at all. The rate of internal energy transfer toward the lower states depends on the overlap of the probability densities of energetically adjacent exciton states, according to Eq. 2. This overlap is small unless the excited states are strongly delocalized. Therefore, the slower rate of interexciton relaxation as deduced from the linewidths in the single-molecule spectra of LH4 as compared to those of the B850 ring in LH2 lead to the conclusion that the excited states in LH4 are more localized.

We will now discuss the statistics of the number of detected bands in the experimental spectra. Redistribution of the oscillator strengths of the exciton states by diagonal disorder causes the number of states to vary between the complexes. Due to experimental limitations, we only observe the exciton transitions with significant oscillator strength. In the experiment we thus obtain a variation in the number of detected bands per complex, with a distribution as shown in Fig. 4. When comparing this with the exciton manifold in Fig. 5, it can be seen that without disorder there are only four distinct transitions that carry oscillator strength, one of which will dominate the absorption spectrum by accounting for 75% of the oscillator strength. After applying disorder, this oscillator strength is distributed over multiple exciton states. Therefore the complexes constituting the tail in the distribution presumably have a larger site energy disorder than the complexes for which fewer bands are detected. Our simulations with the model parameters of Fig. 1 confirm that there is only a limited number of exciton states—with respect to the number of Bchl a molecules in the complex—that carry significant oscillator strength. These results are a strong confirmation of the excitonic nature of the interactions within the complex.

For LH2, important conclusions on the overall structure of the complex could be drawn from polarized fluorescence excitation measurements (Hofmann et al., 2003; Ketelaars et al., 2001). Overlap of the exciton transition moments with the polarization direction of the excitation light causes all transitions to appear as polarized bands with a cos2 angular intensity profile in polarization-dependent single-molecule spectra as seen in Fig. 2. The symmetry-imposed orthogonality of the B850 bands in LH2 is a strong indication that the corresponding exciton states are largely delocalized over the whole B850 ring. Although the symmetry of the LH4 complex is similar to that of the LH2 complex we do not observe this distinct orthogonality of optical transitions, but rather a large, more or less random, variation of polarization angles (see Fig. 2). This can only occur if excitations are localized on relatively small parts of the ring, extending over a few pigments only. Simulations, like the one in Fig. 6, show a similar absence of orthogonality. No clear pattern could be distinguished in the relative polarization angles of the optical transitions. We conclude that the effect of disorder, and the concomitant localization of exciton states is much larger in the case of LH4, as expected on the basis of the structural model.

The picture that emerges from these observations is that intrasubunit interactions play an important role in the excited-state properties of LH4. According to the structure model, most of the oscillator strength is in the upper exciton state, even for a single subunit. This is corroborated by the large Stokes shift of the fluorescence in this system (Gall and Robert, 1999). The single-molecule spectra show that relaxation rates between exciton states are slower than in the B850 ring of LH2, and that characteristic features of a circular exciton are absent in the case of LH4. Because the intersubunit interaction strength is substantially less than the width of the site energy distribution, the exciton states are localized on one or a few subunits instead of delocalized over the complete ring as in the case of LH2. These observations are consistent with the Hamiltonian that has been derived from the structure model.

CONCLUSIONS

We have reported the first single-molecule experiments on LH4 and have performed model-based simulations to investigate the properties of the system. We have studied three properties of the complex in more detail. First of all we observe a number of bands that is less than the number of Bchl a molecules in the complex, reflecting the excitonic coupling of the Bchl a molecules in the complex. Second, the lifetimes of the excited states, which are observed as the widths of the experimental bands, are longer than those of the LH2 complex as a result of the smaller intersubunit interaction energies. Finally, the polarization characteristics of the complex confirm that the excited-state behavior of LH4 is unlike that of other bacterial LH complexes studied so far, and arises due to localization of the exciton states to at most a few subunits only.

We conclude that we have provided further independent evidence supporting the structure model for LH4 and the associated exciton dynamics. It is remarkable that this structure model has been used successfully to account for bulk near-infrared absorption and CD experiments, low resolution electron density maps (Hartigan et al., 2002), and now SMS experiments.

Acknowledgments

This work is supported by the Earth and Life Sciences (ALW) section of the Nederlandse Organisatie voor Wetenschapelijk Onderzoek (NWO) and by the Volkswagen Stiftung (Germany, Hannover). S.O. acknowledges a Marie Curie fellowship from the European Union.

S. Oellerich's present address is Experimentalphysik IV, Universität Bayreuth, Germany.

J.-M. Segura's present address is ISIC-LCPPM, Faculté des Sciences de Base, EPFL, Lausanne, Switzerland.

References

  1. Alden, R. G., E. Johnson, V. Nagarajan, and W. W. Parson. 1997. Calculations of spectroscopic properties of the LH2 bacteriochlorophyll-protein antenna complex from Rhodopseudomonas acidophila. J. Phys. Chem. B. 101:4667–4680. [Google Scholar]
  2. Cogdell, R. J., P. K. Fyfe, S. J. Barret, S. M. Prince, A. A. Freer, N. W. Isaacs, P. McGlynn, and C. N. Hunter. 1996. The purple bacterial photosynthetic unit. Photosynth. Res. 48:55–63. [DOI] [PubMed] [Google Scholar]
  3. Damjanovic, A., I. Kosztin, U. Kleinekathöfer, and K. Schulten. 2002. Excitons in a photosynthetic light-harvesting system: a combined molecular dynamics, quantum chemistry, and polaron model study. Phys. Rev. E. 65:031919. [DOI] [PubMed] [Google Scholar]
  4. Dempster, S. E., S. Jang, and R. J. Silbey. 2001. Single molecule spectroscopy of disordered circular aggregates: a perturbation analysis. J. Chem. Phys. 114:10015–10023. [Google Scholar]
  5. Didraga, C., J. A. Klugkist, and J. Knoester. 2002. Optical properties of helical cylindrical molecular aggregates: the homogeneous limit. J. Phys. Chem. B. 106:11474–11486. [Google Scholar]
  6. Dracheva, T. V., V. Novoderezhkin, and A. P. Razjivin. 1996. Exciton delocalization in the antenna of purple bacteria: exciton spectrum calculations using X-ray data and experimental site inhomogeneity. FEBS Lett. 387:81–84. [DOI] [PubMed] [Google Scholar]
  7. Evans, M. B., A. M. Hawthornthwaite, and R. J. Cogdell. 1990. Isolation and characterisation of the different B800–850 light-harvesting complexes from low- and high-light grown cells of Rhodopseudomonas palustris, strain 2.1.6. Biochim. Biophys. Acta. 1016:71–76. [Google Scholar]
  8. Freer, A. A., S. M. Prince, K. Sauer, M. Z. Papiz, A. M. Hawthornthwaite-Lawless, and G. McDermott. 1996. Pigment-pigment interactions and energy transfer in the antenna complex of the photosynthetic bacterium Rps. acidophila. Structure. 4:449–462. [DOI] [PubMed] [Google Scholar]
  9. Freiberg, A., M. Rätsep, K. Timpmann, and G. Trinkunas. 2003. Self-trapped excitons in circular cacteriochlorophyll antenna complexes. Luminescence. 102–103:363–368. [Google Scholar]
  10. Gall, A., and B. Robert. 1999. Characterization of the different peripheral light-harvesting complexes from high- and low-light grown cells from Rhodopseudomonas palustris. Biochemistry. 38:5185–5190. [DOI] [PubMed] [Google Scholar]
  11. Gardiner, A., R. J. Cogdell, and S. Takaichi. 1993. The effect of growth conditions on the light-harvesting apparatus in Rhodopseudomonas acidophila. Photosynth. Res. 38:159–167. [DOI] [PubMed] [Google Scholar]
  12. Hartigan, N., H. A. Tharia, F. Sweeney, A. M. Lawless, and M. Z. Papiz. 2002. The 7.5 Å electron density and spectroscopic properties of a novel low-light B800 LH2 from Rhodopseudomonas palustris. Biophys. J. 82:963–977. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Hofmann, C., M. Ketelaars, M. Matsushita, H. Michel, T. J. Aartsma, and J. Köhler. 2003. Single-molecule study of the electronic couplings in a circular array of molecules: light-harvesting-2 complex from Rhodospirillum molischianum. Phys. Rev. Lett. 90:013004. [DOI] [PubMed] [Google Scholar]
  14. Hu, X., T. Ritz, A. Damjanovic, and K. Schulten. 1997. Pigment organization and transfer of electronic excitation in the photosynthetic unit of purple bacteria. J. Phys. Chem. B. 101:3854–3871. [Google Scholar]
  15. Kennis, J. T. M., A. M. Streltsov, H. Permentier, T. J. Aartsma, and J. Amesz. 1997. Exciton coherence and energy transfer in the LH2 antenna complex of Rhodopseudomonas acidophila at low temperature. J. Phys. Chem. B. 101:8369–8374. [Google Scholar]
  16. Ketelaars, M., A. M. van Oijen, M. Matsushita, J. Köhler, J. Schmidt, and T. J. Aartsma. 2001. Spectroscopy on the B850 band of individual light-harvesting 2 complexes of Rhodopseudomonas acidophila I. Experiments and Monte Carlo simulations. Biophys. J. 80:1591–1603. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Koepke, J., X. Hu, C. Muenke, K. Schulten, and H. Michel. 1996. The crystal structure of the light-harvesting complex II (B800–850) from Rhodospirillum molischianum. Structure. 4:581–597. [DOI] [PubMed] [Google Scholar]
  18. Leegwater, J. A., J. R. Durrant, and D. R. Klug. 1997. Exciton equilibration induced by phonons: theory and application to PS II reaction centers. J. Phys. Chem. B. 101:7205–7210. [Google Scholar]
  19. Matsushita, M., M. Ketelaars, A. M. van Oijen, J. Köhler, T. J. Aartsma, and J. Schmidt. 2001. Spectroscopy on the B850 band of individual light-harvesting 2 complexes of Rhodopseudomonas acidophila. II. Exciton states of an elliptically deformed ring aggregate. Biophys. J. 80:1604–1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. McDermott, G., S. M. Prince, A. A. Freer, A. M. Hawthornthwaite-Lawless, M. Z. Papiz, R. J. Cogdell, and N. W. Isaacs. 1995. Crystal structure of an integral membrane light-harvesting complex from photosynthetic bacteria. Nature. 374:517–521. [Google Scholar]
  21. McLuskey, K., M. Prince, R. J. Cogdell, and N. W. Isaacs. 2001. The crystallographic structure of the B800–820 LH3 light-harvesting complex from the purple bacteria Rhodopseudomonas Acidophila strain 7050. Biochemistry. 40:8783–8789. [DOI] [PubMed] [Google Scholar]
  22. Novoderezhkin, V., and A. P. Razjivin. 1993. Excitonic interactions in the light-harvesting antenna of photosynthetic purple bacteria and their influence on picosecond absorbance difference spectra. FEBS Lett. 330:5–7. [DOI] [PubMed] [Google Scholar]
  23. Papiz, M. Z., S. M. Prince, T. D. Howard, R. J. Cogdell, and N. W. Isaacs. 2003. The structure and thermal motion of the B800–850 LH2 complex from Rps. acidophila at 2.0 Å resolution and 100 K: new structural features and functionally relevant motions. J. Mol. Biol. 326:1523–1538. [DOI] [PubMed] [Google Scholar]
  24. Prince, S. M., M. Z. Papiz, A. A. Freer, G. McDermott, A. M. Hawthornthwaite-Lawless, R. J. Cogdell, and N. W. Isaacs. 1997. Apoprotein structure in the LH2 complex from Rhodopseudomonas acidophila strain 10050: modular assembly and protein pigment interactions. J. Mol. Biol. 268:412–423. [DOI] [PubMed] [Google Scholar]
  25. Qian, P., T. Yagura, Y. Koyama, and R. J. Cogdell. 2000. Isolation and purification of the reaction center (RC) and the core (RC-LH1) complex from Rhodobium marinum: the LH1 ring of the detergent-solubilized core complex contains 32 bacteriochlorophylls. Plant Cell Physiol. 41:1347–1353. [DOI] [PubMed] [Google Scholar]
  26. Reddy, N. R. S., G. J. Small, M. Seibert, and R. Picorel. 1991. Energy transfer dynamics of the B800-B850 antenna complex of Rhodobacter sphaeroides: a hole burning study. Chem. Phys. Lett. 181:391–399. [Google Scholar]
  27. Roszak, A. W., T. D. Howard, J. Southall, A. Gardiner, C. J. Law, N. W. Isaacs, and R. J. Cogdell. 2003. Crystal Structure of the RC-LH1 Core Complex from Rhodopseudomonas palustris. Science. 302:1969–1972. [DOI] [PubMed] [Google Scholar]
  28. Sauer, K., R. J. Cogdell, S. M. Prince, A. Freer, N. W. Isaacs, and H. Scheer. 1996. Structure-based calculations of the optical spectra of the LH2 bacteriochlorophyll-protein complex from Rhodopseudomonas acidophila. Photochem. Photobiol. 64:564–576. [Google Scholar]
  29. Shreve, A. P., J. K. Trautman, H. A. Frank, T. G. Owens, and A. C. Albrecht. 1991. Femtosecond energy-transfer processes in the B800-850 light-harvesting complex of Rhodobacter sphaeroides 2.4.1. Biochim. Biophys. Acta. 1058:280–288. [DOI] [PubMed] [Google Scholar]
  30. Tharia, H. A., T. D. Nightingale, M. Z. Papiz, and A. M. Lawless. 1999. Characterisation of hydrophobic peptides by RP-HPLC from different spectral forms of LH2 isolated from Rps. palustris. Photosynth. Res. 61:157–167. [Google Scholar]
  31. van der Laan, H., C. De Caro, Th. Schmidt, R. W. Visschers, R. van Grondelle, G. J. S. Fowler, C. N. Hunter, and S. Völker. 1993. Excited-state dynamics of mutated antenna complexes of purple bacteria studied by hole-burning. Chem. Phys. Lett. 212:569–580. [Google Scholar]
  32. van der Laan, H., Th. Schmidt, R. W. Visschers, K. J. Visscher, R. van Grondelle, and S. Völker. 1990. Energy transfer in the B800-850 antenna complex of purple bacteria Rhodobacter sphaeroides: a study by spectral hole-burning. Chem. Phys. Lett. 170:231–238. [Google Scholar]
  33. van Grondelle, R., J. P. Dekker, T. Gillbro, and V. Sundstrom. 1994. Energy transfer and trapping in photosynthesis. Biochim. Biophys. Acta. 1187:1–65. [Google Scholar]
  34. van Oijen, A. M., M. Ketelaars, J. Köhler, T. J. Aartsma, and J. Schmidt. 1999a. Spectroscopy of individual LH2 complexes of Rhodopseudomonas acidophila: localized excitations in the B800 band. Chem. Phys. 247:53–60. [Google Scholar]
  35. van Oijen, A. M., M. Ketelaars, J. Köhler, T. J. Aartsma, and J. Schmidt. 1999b. Unraveling the electronic structure of individual photosynthetic pigment-protein complexes. Science. 285:400–402. [DOI] [PubMed] [Google Scholar]
  36. van Oijen, A. M., M. Ketelaars, J. Köhler, T. J. Aartsma, and J. Schmidt. 2000. Spectroscopy of individual light-harvesting 2 complexes of Rhodopseudomonas acidophila: diagonal disorder, intercomplex heterogeneity, spectral diffusion, and energy transfer in the B800 band. Biophys. J. 78:1570–1577. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Vulto, S. E., M. A. de Baat, S. Neerken, F. R. Nowak, H. van Amerongen, J. Amesz, and T. J. Aartsma. 1999. Excited state dynamics in FMO antenna complexes from photosynthetic green sulfur bacteria: a kinetic model. J. Phys. Chem. B. 103:8153–8161. [Google Scholar]
  38. Wu, H.-M., and G. J. Small. 1998. Symmetry-based analysis of the effects of random energy disorder on the excitonic level structure of cyclic arrays: application to photosynthetic antenna complexes. J. Phys. Chem. B. 102:888–898. [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES