The Protonation Status of Compound II in Myoglobin, Studied by a Combination of Experimental Data and Quantum Chemical Calculations: Quantum Refinement

Abstract

Treatment of met-myoglobin (Fe^III) with H₂O₂ gives rise to ferryl myoglobin, which is closely related to compound II in peroxidases. Experimental studies have given conflicting results for this species. In particular, crystallographic and extended x-ray absorption fine-structure data have shown either a short (∼170 pm) or a longer (∼190 pm) Fe–O bond, indicating either a double or a single bond. We here present a combined experimental and theoretical investigation of this species. In particular, we use quantum refinement to re-refine a crystal structure with a long bond, using 12 possible states of the active site. The states differ in the formal oxidation state of the iron ion and in the protonation of the oxygen ligand (O²⁻, OH⁻, or H₂O) and the distal histidine residue (with a proton on N^δ1, N^ε2, or on both atoms). Quantum refinement is essentially standard crystallographic refinement, where the molecular-mechanics potential, normally used to supplement the experimental data, is replaced by a quantum chemical calculation. Thereby, we obtain an accurate description of the active site in all the different protonation and oxidation states, and we can determine which of the 12 structures fit the experimental data best by comparing the crystallographic R-factors, electron-density maps, strain energies, and deviation from the ideal structure. The results indicate that Fe^III OH⁻ and Fe^IV OH⁻ fit the experimental data almost equally well. These two states are appreciably better than the standard model of compound II, Fe^IV O²⁻. Combined with the available spectroscopic data, this indicates that compound II in myoglobin is protonated and is best described as Fe^IV OH⁻. It accepts a hydrogen bond from the distal His, which may be protonated at low pH.

INTRODUCTION

Myoglobin is the major heme-containing protein of cardiac and skeletal muscle and serves as an oxygen buffer in respiring tissues. The oxygen affinity of myoglobin lies between that of hemoglobin, which releases oxygen in passing through respiring tissues, and cytochrome c oxidase, which uses molecular oxygen in oxidative respiration. It is the high myoglobin content that gives continually respiring tissues their red color.

Myoglobin has been studied intensively for decades (Philips, 2001) and it was the first protein for which the three-dimensional structure was solved (Kendrew et al., 1960). The structure showed a globular protein, built up mainly from α-helices. The active site of myoglobin is situated in a hydrophobic pocket near the center of the molecule and consists of a prosthetic heme group (iron protoporphyrin IX) with a Fe^II ion in the center of a porphyrin ring, coordinated by the four nitrogen atoms of the pyrrole rings. The ion is also bound to the N^ε2 atom of the conserved proximal histidine (His) residue. The sixth coordination site, completing the octahedral coordination around the iron ion, is empty or occupied by O₂. A nearby His residue (the distal His) forms a hydrogen bond to the bound O₂ molecule, thereby stabilizing the binding and favoring O₂ compared to other competing diatomic gases, e.g., CO and NO (Spiro and Kozlowski, 2001). Mutation of the proximal His ligand or surrounding hydrophobic side chains in general leads to dissociation of the heme group (Hargrove et al., 1996).

Heme groups are also present in many other proteins. They show an impressively varied chemistry, with functions ranging from electron transfer (cytochromes) to binding and transport of small molecules and catalysis of a great wealth of reactions (e.g., peroxidases, oxidases, and catalases; see da Silvia and Williams, 1994; Kaim and Schwederski, 1994; Smith and Veitch, 1998; Matsunaga and Shir, 2004). All these proteins bind heme, but the surrounding protein and the axial ligand vary extensively between different groups of proteins and are considered to tune the properties of the heme group (Poulos, 1996).

Much effort has been put into investigations of the reaction cycles of these heme proteins. The reaction cycle of peroxidases (Gajhede, 2001; and see Fig. 1, this article) starts with the resting Fe^III state, which is either six-coordinate with a water molecule (1) or five-coordinate with an empty coordination site (2). This state binds H₂O₂ (3), which is then deprotonated to a hydroperoxide intermediate (4). When this intermediate is re-protonated on the distal oxygen atom, the O–O bond breaks automatically in a heterolytic manner, resulting in water and compound I (5; formally Fe^V O²⁻, but one of the reducing equivalents is located in the porphyrin ring or on a nearby protein residue). Compound I is extremely reactive and can abstract an electron from almost any substrate (the reduction potential is close to 1 V; Gajhede, 2001). This results in a substrate radical and compound II (Fe^IV O²⁻; 6). Compound II is also reactive with a similar reduction potential and can abstract an electron from another substrate molecule, thereby returning to the resting state after the uptake of two protons.

FIGURE 1.

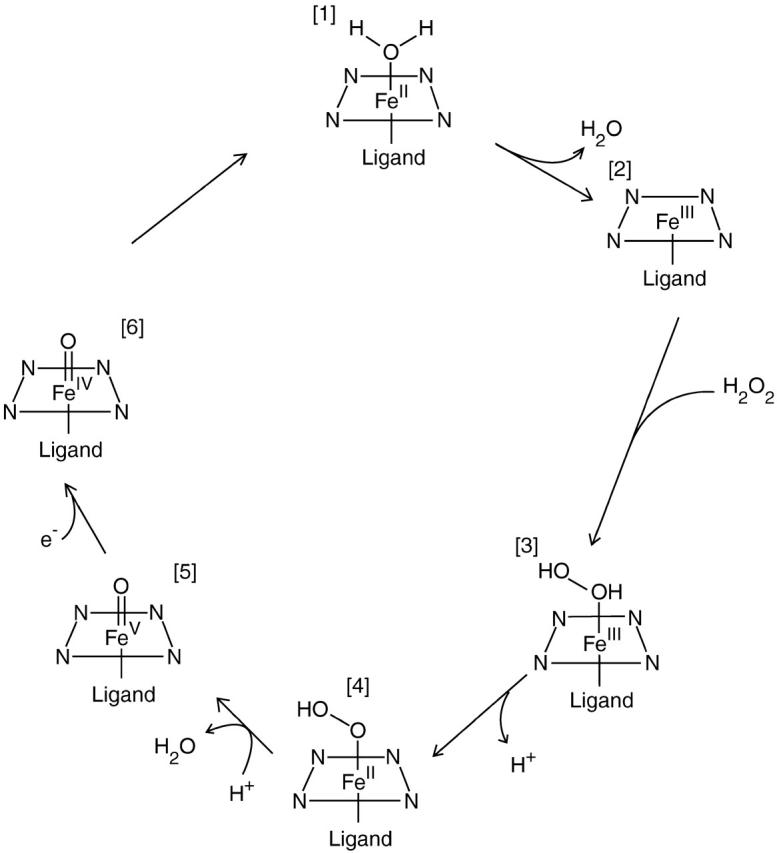
The proposed reaction cycle for peroxidases (Gajhede, 2001). Compounds I and II are complexes 5 and 6.

The normal function of myoglobin is to bind and store O₂. However, it has been shown that it may also support a peroxidase-like activity, i.e., a H₂O₂-dependent oxidation of many substrates (Giulivi and Cadenas, 1994). During the reversible O₂ binding, oxymyoglobin auto-oxidizes at a relatively slow rate (Tajima and Shikama, 1987) to yield met-myoglobin (i.e., Fe^III) and a superoxide radical (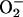). The latter disproportionates to H₂O₂ and O₂. H₂O₂ is a reactive species and can cause potential damage. The peroxidase activity of myoglobin may take care of this problem (Giulivi and Cadenas, 1994). The reaction product of H₂O₂ with met-myoglobin is considered to be compound I (Keilin and Hartree, 1950). This species is labile and rapidly takes up an electron by a poorly known mechanism to form compound II (ferryl myoglobin), which is quite stable (Giulivi and Cadenas, 1994). It has also been suggested that the O–O bond may break homolytically, giving rise to compound II and a hydroxyl radical (neutral OH^˙). Native myoglobins possess a lower peroxidase activity than peroxidases, which has been attributed to the absence of a distal arginine residue and the failure of the distal histidine to function as an acid-base catalyst (Matsui et al., 1999). By mutations that place the histidine in a similar distance to the heme as in the active site of peroxidases, compound I of myoglobin has been observed, probably owing to an increased rate of heterolysis (Ozaki et al., 1997; Matsui et al., 1999). However, compound I has also been observed for native myoglobin through stopped-flow rapid-scan spectrophotometry (Egawa et al., 2000).

Earlier crystallographic and extended x-ray absorption fine-structure (EXAFS) investigations have indicated that the Fe–O bond length in compound II in myoglobin, horseradish peroxidase (HRP), and catalase is 164–171 pm, i.e., close to what has been observed for compound I (Chance et al., 1986a; Penner-Hahn et al., 1986; Gouet et al., 1996), thereby indicating that it is a Fe^IV O²⁻ species. However, in three recent crystal structures of compound II in myoglobin, HRP, and catalase, appreciably longer Fe–O bonds were observed, 184–192 pm (Hersleth et al., 2002; Berglund et al., 2002; Murshudov et al., 2002). Such a long Fe–O bond was also observed in a recent crystal structure of compound I in cytochrome c peroxidase (187 pm), which is electronically equivalent to compound II of HRP, because the other oxidizing equivalent is on a tryptophane residue (Bonagura et al., 2003). A similar bond length (193 pm) has also been reported in an EXAFS study of compound II in HRP (Chance et al., 1984). This was interpreted as a protonation of O²⁻ to OH⁻ or even as Fe^III OH^˙. However, this interpretation was recently questioned in another EXAFS study of chloroperoxidase and HRP, which gave a long Fe–O bond only for the former enzyme (Green et al., 2004). Considering the importance of compound II in the catalytic cycle of many different types of enzymes, it is highly interesting to settle the actual character of compound II. In this article we therefore use our recently developed quantum-refinement method (Ryde et al., 2002) to re-refine the crystal structure of compound II in myoglobin using various oxidation and protonation states of the active site, to see which fit the experimental data best.

METHODS

Quantum refinement

Quantum refinement (Ryde et al., 2002; Ryde and Nilsson, 2003b) is essentially standard crystallographic refinement supplemented by quantum chemical calculations for a small part of the protein. Crystallographic refinement programs change the protein model (coordinates, occupancies, B-factors, etc.) to improve the fit of the observed and calculated structure-factor amplitudes (usually estimated as the residual disagreement, the R-factor). Owing to the limited resolution normally obtained for biomolecules, the experimental data are supplemented by some chemical information, usually in the form of a molecular-mechanics (MM) force field (Kleywegt and Jones, 1998). Then, the refinement takes the form of a minimization or simulated annealing calculation by molecular dynamics using an energy function of the form

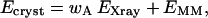(1)

where E_Xray is a penalty function that describes how well the model agrees with the experimental data (we have used a maximum-likelihood refinement target using amplitudes, MLF; see Pannu and Read, 1996; Adams et al., 1997). E_MM is an MM energy function with bond, angle, dihedral, and nonbonded terms, and w_A is a weight factor, which is necessary because E_MM is in energy units whereas E_Xray is in arbitrary units. It determines the relative importance of the crystallographic raw data and the MM force field for the final structure.

Quantum chemistry can be introduced in this function by replacing the MM potential for a small (but interesting) part of the protein (system 1) by a quantum mechanics (QM) calculation, yielding a QM energy for system 1, E_QM1. To avoid double counting we must then subtract the MM energy of system 1, E_MM1,

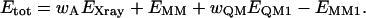(2)

Thereby, we introduce an accurate energy function for the system of interest. Such an energy function is implemented in the software ComQum-X (Ryde et al., 2002), which is a combination of the software TURBOMOLE (Ahlrichs et al., 2000) and the crystallography and NMR system (CNS) (Brünger et al., 2000). The factor w_QM in Eq. 2 is another weight, which is needed because the CNS MM force field is based on a statistical analysis of crystal structures (Engh and Huber, 1991). Therefore, the force constants are not energy-derived, as is the QM term, but they are in arbitrary statistical units. Experience has shown that the CNS force constants are typically three times larger than energy-based force constants (Engh and Huber, 1991), and w_QM = 3 has therefore been used throughout this work (Ryde et al., 2002).

Special attention is needed if there is a covalent bond between the QM system and the surrounding proteins. This is a well-known problem in the popular combined QM and MM methods (QM/MM; Monard and Merz, 1999; Mulholland, 2001; Ryde, 2003) (ComQum-X can also be seen as a QM/MM method with restraints to crystallographic raw data), and a simple and robust solution (Nicoll et al., 2001) is to truncate the QM system with hydrogen atoms, the positions of which are linearly related to the corresponding carbon atom in the protein (Ryde et al., 2002). Of course, E_MM1 is also calculated with these hydrogen atoms, so that artifacts introduced by the hydrogen truncation may cancel out. Following crystallographic custom, protons and electrostatic interactions are ignored in the refinement, except of course in the quantum chemical calculations.

ComQum-X has been tested by re-refining the structure of N-methylmesoporphyrin bound to ferrochelatase (Ryde et al., 2002). The results showed that we may improve the structure locally in terms of the R_free factor (the R_free factor is an R-factor calculated for a set of randomly chosen intensities, typically ∼5%, which are set aside from the beginning and not used during the refinement; Brünger, 1993). Moreover, we have shown (Ryde and Nilsson, 2003a) that refinement with ComQum-X of a medium-resolution (170 pm) crystal structure of cytochrome c₅₅₃ brings the geometry of the heme group and its ligands closer to that observed in an atomic-resolution structure (97 pm) of the same protein (Benini et al., 2000). For example, the errors in the Fe-ligand distances are reduced from 3–9, 12, and 32 pm to 1, 0, and 2 pm (for the porphyrin, histidine, and methionine ligands, respectively). We have also shown that ComQum-X can be used to deduce the protonation state of metal-bound solvent molecules in protein structures (Ryde and Nilsson, 2003b; Nilsson and Ryde, 2004). We used the catalytic zinc ion in alcohol dehydrogenase as a test case, because the pK_a of the zinc-bound water molecule is known from kinetic measurements, and we were able to reproduce the correct protonation state of both an alkoxide ion and a water molecule.

Computational details

The quantum-refinement calculations and vacuum geometry optimizations were performed with the density functional Becke-Perdew86 method (Becke, 1988; Perdew, 1986). They were sped up by expanding the Coulomb interactions in an auxiliary basis set, the resolution-of-identity approximation (Eichkorn et al., 1995, 1997). These calculations employed the DZpdf basis set for iron (Schäfer et al., 1992; Sigfridsson et al., 2001) and the 6-31G* basis set for all other atoms, except the O-ligand, for which a set of diffuse functions (6-31+G*) was also included (Hehre et al., 1986).

Most of the calculations were run on the model Fe(Por)(Im)(H₂O/OH⁻/O²⁻) (Im), where Por is porphine, i.e., the porphyrin ring without side chains (our previous calculations have shown that the porphyrin side chains have a minor effect on the geometry of the heme group; Sigfridsson and Ryde, 2003) and Im is imidazole, the standard model of His residues. Thus, the model includes both the proximal His ligand and the distal His residue. However, some vacuum calculations were run on a smaller complex without the model of the distal His residue.

All quantum-refinement calculations are based on the crystal structure of compound II in myoglobin at 135-pm resolution (collected at 100 K, pH 5.2; Hersleth et al., 2002). Coordinates, occupancies, B-factors, and structure factors of the structure were obtained from the Brookhaven Protein Data Bank files 1GJN. From these files we also obtained the space group, unit-cell parameters, resolution limits, R-factors, and the test set used for the evaluation of the R_free factor.

The full protein was used in all calculations, including all crystal water molecules in the Protein Data Bank file. The full geometry of the proteins was optimized until the change in E_tot was below 10⁻⁶ Hartree (2.6 J/mol) and the norm of the Cartesian gradients was below 10⁻³ a.u. In each cycle of the geometry optimization, the surrounding protein was allowed to relax by one cycle of crystallographic minimization and one cycle of individual B-factor refinement. However, the new coordinates and B-factors were accepted only if the R_free factor was reduced. For the protein, we used the standard CNS force field (protein_rep.param, water_rep.param, and ion.param) and for the heme group, the parameter file from the original refinement (these parameters are of little importance, because the heme group is treated by quantum chemistry in the refinement). For the other program parameters, we used data from the Protein Data Bank files or the default choices.

The w_A factor in Eq. 2, poses a special problem, because it is the only undetermined parameter in ComQum-X. In standard crystallographic refinements, it is determined so that the MM and crystallographic forces have a similar magnitude (Brünger and Rice, 1997). However, there is no warranty that this is the optimum choice, especially not if a part of the protein is supplemented by a QM energy function. Therefore, we have determined the optimum choice of w_A for each system by optimizing the R_free factor. This was done by refining each structure at (at least) five different values of w_A, 0.006, 0.06, 0.25 (the default choice of CNS), 1, and 6. The R_free factor was always lowest for w_A = 0.25 or 1 and increased monotonously for higher and lower values of w_A.

Relative energies of the various protein complexes were estimated by solving the Poisson-Boltzmann equation numerically using MEAD 2.2 software (Bashford, 1997; Tishmack et al., 1997). Charges for the quantum system were fitted to the electrostatic potential using the Merz-Kollman scheme (Besler et al., 1990), as implemented in Gaussian-98 software (Frisch et al., 1998). In the charge calculation, the wavefunction was perturbed by protein and solvent point charges, scaled by a factor of 4. For the rest of the protein (and side chains of the heme group), partial charges from the CHARMM param27 force field (MacKerell et al., 1998) were used. Optimized radii were used for all protein atoms in the MEAD calculations (Nina and Roux, 1997) and for the atoms that change protonation in the various calculations (the iron oxygen ligand and the distal imidazole group), a radii of 120, 155, and 150 PM were used for the H, N, and O atoms, respectively (Ullmann et al., 2002). A unity dielectric constant (ε = 1) was used for the quantum system, whereas ε = 4 in the remaining protein, and ε = 80 in the surroundings (water). These values have previously been shown to provide reasonable agreement with experimental results (Ullmann et al., 2002; Bashford et al., 1993; T. Rasmussen, K. Nilsson, and U. Ryde, unpublished).

The MEAD calculations were based on the quantum-refined geometries. All water molecules were removed. The MEAD calculations were performed with 151³ grid points, with a coarse grid with a spacing of 100 pm, centered on the geometric center of the protein, and a dense grid with a spacing of 20 pm, centered on the iron ion. The solvent energies are the average of seven calculations in which the grid origin was moved 10 pm in positive and negative directions along each Cartesian axis. The maximum difference among the four calculations is 2 kJ/mol.

The reported energies are the sum of the QM energies of the quantum system and the MEAD solvation energies of the QM system in the protein and the surrounding solvent. The intrinsic and solvation energy of the protein was assumed to be constant for the various states. The QM energies were calculated with the B3LYP function, as implemented in Gaussian-98 (Frisch et al., 1998; Hertwig and Koch, 1997), because this functional is known to give more accurate energies, especially for transition metal systems (Bauschlicher, 1995; Siegbahn and Blomberg, 2000; the same functional was used for the charge calculations). The wavefunction was perturbed by the protein and solvent point charges, scaled by a factor of 4, but the energy was calculated without these charges in a single SCF iteration.

RESULTS AND DISCUSSION

Vacuum calculations

As mentioned above, compound II is normally assumed to be Fe^IV O²⁻ (which is often written as Fe=O, but we prefer to explicitly show the formal oxidation and protonation states), but the Fe^IV OH⁻ and Fe^III OH^˙ forms have also been suggested (Hersleth et al., 2002). The aim of the present investigation is to determine the actual protonation and oxidation state of compound II in myoglobin, observed in the crystal structure of Hersleth et al. (2002). Therefore, we have studied three formal oxidation states for iron, Fe^III, Fe^IV, and Fe^V, and three protonation states for water, H₂O, OH⁻, and O²⁻. Based on the expected protonation states for the various ions, we decided to study the following six combinations: Fe^III H₂O, Fe^III OH⁻, Fe^III O²⁻, Fe^IV OH⁻, Fe^IV O²⁻, and Fe^V O²⁻.

To get a first feeling of the optimum structures of these complexes and also to get some insight in their most stable spin states (some have not been observed experimentally), we optimized the structures of the three reasonable spin states (high-, intermediate-, and low-spin), using the Fe(Por)(Im)(H₂O/OH⁻/O²⁻) model (Fig. 2). The results of these calculations are shown in Table 1.

FIGURE 2.

The small Fe(Por)(Im)(OH⁻) model of the heme active site used in some of the vacuum calculations.

TABLE 1.

Vacuum structures of the Fe(Por)(His)(O/OH/H₂O) model and relative energies of the various spin states (ΔE)

Ox. state		# Unpaired spin	Distance to Fe (pm)			ΔE kJ/mol
			Ligand		NPor		NHis	O
III	H2O	5	205–208	215	240
III	OH−	1	201–202	206	182	0.0
III		3	202–203	261	191	75.6
III		5	208–210	256	188	106.2
III	O2−*	1	203–204	219	166	0.0
III		3	203–204	218	165	5.8
IV	OH−	0†	196–205	204	179	24.2
IV		2	196–203	205	178	0.0
IV		4	196–213	218	183	101.2
IV	H2O	0†	200	194	205	3.1
IV		0	194–204	194	204	38.2
IV		2	198–199	194	205	0.0
IV		4	198	218	241	22.2
IV	O2−	0†	202	217	165	32.0
IV		2	202	217	165	0.0
IV		4	209	217	164	90.5
V	OH−	1	201–202	205	181	0.0
V		3	202–203	262	191	76.1
V		5	208–210	257	188	106.6
V	O2−	1	197–206	213	163	5.5
V		3	199	213	165	0.0
V		5	199	214	165	181.5
Crystal			197–205	214	192

^*The His ligand dissociates in the sextet state.

^†Open-shell singlet.

Fe^III H₂O (met-myoglobin) is experimentally known to be in the high-spin (sextet) state (Hersleth et al., 2002). The Fe^III OH⁻ model is most stable in the low-spin (doublet) state (Sitter et al., 1988), as can be seen in Table 1, whereas the Fe^III O²⁻ model has nearly degenerate double and quartet states (the former is 6 kJ/mol more stable). For the Fe^IV models, the triplet (intermediate-spin) state was found to be lowest in energy. Again, this is in accordance with experimental data for compound II in myoglobin, as well as in peroxidases (Foote et al., 1989). For the compound I model (Fe^V O²⁻), the doublet and quartet states are almost degenerate, but in our calculations, the quartet is slightly lower in energy. In the peroxidases, the doublet state is observed experimentally, with a J-coupling constant of only 0–10 cm⁻¹ (Green, 2001) to the radical on heme or on an amino acid. Since the axial ligation differs between myoglobin and peroxidases (the latter has a carboxylate group hydrogen-bonded to the His ligand, giving it some imidazolate character), and since the two states have very similar geometries, we decided to run all Fe^V O²⁻ calculations with the quartet state. In the following, we will only discuss these spin states.

The geometries of the various complexes are also shown in Table 1. For the most stable spin states, we get a Fe–O distance of 240 pm for Fe^III H₂O, 182 pm for Fe^III OH⁻, 166 pm for Fe^III O²⁻, 178 pm for Fe^IV OH⁻, 165 pm for Fe^IV O²⁻, and 163–165 pm for Fe^V O²⁻ Thus, based on these data, neither of the models give a Fe–O distance close to that observed in the crystal structure of compound II in myoglobin (192 pm), but that of Fe^III OH⁻ is closest to it.

Interestingly, the crystal structure shows a long Fe–N_His bond length of 214 pm. This is appreciably longer than in the OH⁻ models (204–206 pm), but similar to what is found for the H₂O and O²⁻ complexes (213–219 pm). Thus, these small models give little explanation to the observed crystal structure.

The results of these vacuum calculations are similar to those obtained in earlier studies of similar sites (Ghosh et al., 1994; Antony et al., 1997; Kuramochi et al., 1997; Wirstam et al., 1999; Harris, 2001; Harris and Loew, 2001; Rovira and Fita, 2003; Rydberg et al., 2004). In particular, a recent study of compound II in catalase and peroxidase gave Fe–O distances of 177 pm when protonated and 168–169 pm when unprotonated (Rovira and Fita, 2003).

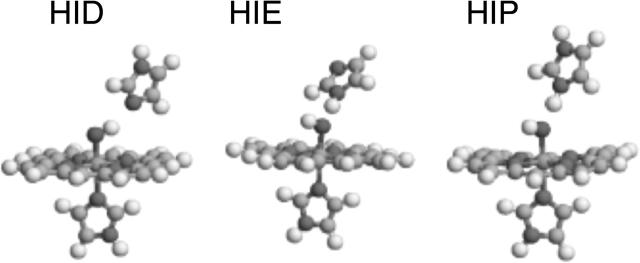
As mentioned above, the distal His forms a hydrogen bond to the oxygen ligand in myoglobin via the N^ε2 atom. It is conceivable that such a hydrogen bond may modify the Fe–O distance. Therefore, we added a model of the distal His to the quantum system, yielding the Fe(Por)(Im)(H₂O/OH⁻/O²⁻)(Im) model (Fig. 3). Unfortunately, the protonation state of a His residue is not clear from crystal structures; it can be protonated either on the N^δ1 atom, the N^ε2 atom, or on both atoms. We will call these three possibilities HID, HIE, and HIP. Clearly, if there is a water ligand, the distal His residue must be of the HID type, to accept a hydrogen bond (Fig. 3 a), whereas if the ligand is O²⁻, it must be either HIE or HIP, to donate a hydrogen bond. However, for the OH⁻ ligand, all three protonation states are possible. This gives us 12 different models of the active site, which were all optimized and are described in Table 2. For the Fe^IV H₂O–HIE state, the proton moved from H₂O to HIE, forming the Fe^IV OH⁻ HIP complex. Likewise, the Fe^III O²⁻ HIP complex reorganized to the Fe^III OH⁻ HIE complex.

FIGURE 3.

The Fe(Por)(Im)(OH⁻)(Im) model of the active heme site used in both the vacuum and quantum-refinement calculations. The three figures illustrate the three possible protonation states of the distal His model—HID, HIE, and HIP.

TABLE 2.

Vacuum structures of the Fe(Por)(Im)(O/OH/H₂O)(Im) model

			Distance to Fe (PM)
Ox. state	Ligand	His	NPor	NHis	O	O–N/H
III	H2O	HID	205–209	222	219	267/104
III	OH−	HID	201–202	207	180	292/100
III		HIE	201–202	206	184	282/178
III*		HIP	201–202	201	188	255/148
III	O2−	HIE	201–203	219	170	271/165
IV*	H2O	HID	196–202	197	194	253/105
IV	OH−	HID	201–202	209	171	253/111
IV		HIE	198–202	205	182	284/180
IV		HIP	195–203	201	186	268/161
IV		Arg	201–204	200	189	269/163
IV	O2−	HIE	202–203	217	166	286/182
IV		HIP	202–203	213	168	255/142
IV		Arg	202	212	167	277/172
V	O2−	HIE	200–201	211	166	282/179
V		HIP	200	209	167	270/164
Crystal			197–205	214	192	270/−

^*Fixed N–H distance.

From this table, it can be seen that the hydrogen bond has a quite strong influence on the Fe–O distance. Thus, if the O-ligand is a donator (the HID structures), the Fe–O distances decrease by 2–9 pm, whereas when it is an acceptor, the Fe–O distance increases by 1–8 pm, more for OH⁻ than O²⁻ and also more for HIP than HIE. Therefore, the Fe–O bonds in the Fe^IV OH⁻ HIP (186 pm) and Fe^III OH⁻ HIE structures (184 pm) are only 6–8 pm shorter than in the crystal structure.

However, the hydrogen bond to the distal His residue also affects the (quite flexible) distance to the proximal His residue. The HIP models give the shortest bonds and the HID models the longest with a variation of up to 8 pm. As with the small model, it is in general the models with the shortest Fe–O bond that give a Fe–N_His bond length most similar to the crystal structure. Yet, the Fe^IV OH⁻/HID model also gives a quite reasonable Fe–N_His bond length (209 pm).

This indicates that there actually may be a reasonable interpretation of the crystal structure, although the direct comparison with vacuum structures cannot unambiguously point out the best candidate because different models give the best results for the Fe–O and Fe–N_His bonds. If we simply take the sum of the absolute deviations of these two bonds, the Fe^IV OH⁻ HIP (16 pm) and Fe^III OH⁻ HIE (17 pm) models give the best results. However, such a treatment does not take into account the other bond lengths (and angles) in the structure, nor does it take into account the relative strength of the bonds (a Fe–O²⁻ bond is much stiffer than a Fe–H₂O bond). All this is considered in the quantum refinement procedure, which can be seen as a quantum chemical method with restraints to the crystallographic raw data. Thus, it also disregards possible errors in the crystallographic coordinates (which are not the raw data but the result of an involved process of interpretation) and it considers how well the positions of the various atoms are determined (giving a stronger restraint to a well-determined atom than to a more poorly determined one), thereby obtaining an optimum compromise between crystallography and quantum chemistry.

Finally, we also tested if the distal residues in heme peroxidases have a similar effect. Thus, we added CH₃NHC(NH₂)₂ as a model of the distal arginine (Arg) residue in these enzymes. To ensure that this model forms a hydrogen bond to the oxo group only with the inner nitrogen atom, we also added a water molecule, bridging the oxo group and the terminal nitrogen atom of the Arg model. The results of these optimizations (for Fe^IV OH⁻ and Fe^IV O²⁻) are also shown in Table 2 (Arg entries). It can be seen that the geometries are similar to those obtained with the His models, especially the charged HIP model; the Fe–O bond is 167 pm for the Fe^IV O²⁻ structure, but 189 pm in the Fe^IV OH⁻ structure. The latter estimate is close to the distance observed in the recent crystal structures of compound II in HRP and compound I in cytochrome c peroxidase (184–187 PM) (Berglund et al., 2002; Bonagura et al., 2003). This shows that myoglobin and peroxidase models behave in a similar manner.

Quantum refinement

We re-refined the crystal structure of compound II in myoglobin (Hersleth et al., 2002) using the same 12 models of the heme site as in the vacuum calculations. All 12 models converged to distinct structures, but two states, which we also tried, Fe^IV H₂O HID and Fe^III O²⁻ HIP, converged to Fe^IV OH⁻ HIP and Fe^III OH⁻ HID by an internal proton transfer. All structures were optimized for a range of values for the w_A factor, to find the optimum choice. For all models, either w_A = 1 or the default w_A = 0.25 gave the minimum in R_free factor and these results are presented in Table 3. It should be noted that most of the entries in this table are comparable only if the same value of w_A has been used.

TABLE 3.

ComQum-X results for the active site in myoglobin compound II (Hersleth et al., 2002)

					Distance to Fe (PM)
Ox. state	Ligand	His	wA	ΔEQM1 kJ/mol	NPor	NHis	O	O–N/H	Rfree	R
III	H2O	HID	0.25	41.9	202–209	212	206	259/107	0.20594	0.18058
III			1.0	56.2	199–206	210	200	262/107	0.20572	0.18020
III	OH−	HID	0.25	22.8	199–204	209	182	277/100	0.20560	0.18041
III			1.0	34.9	197–203	208	185	272/100	0.20561	0.18020
III		HIE	0.25	33.4	198–204	207	185	273/171	0.20565	0.18048
III			1.0	34.6	196–203	208	188	271/168	0.20568	0.18020
III		HIP	0.25	41.9	199–203	205	191	259/143	0.20594	0.18047
III			1.0	44.8	197–203	207	192	264/150	0.20577	0.18018
III	O2−	HIE	0.25	34.1	199–204	211	174	273/167	0.20587	0.18068
III			1.0	44.0	197–203	209	182	271/163	0.20579	0.18027
IV	OH−	HID	0.25	40.9	198–204	209	177	271/105	0.20573	0.18055
IV			1.0	47.9	197–203	209	183	271/104	0.20569	0.18024
IV		HIE	0.25	32.8	197–204	207	184	273/170	0.20567	0.18050
IV			1.0	34.4	196–203	208	187	270/168	0.20570	0.18027
IV		HIP	0.25	44.9	196–205	206	186	270/164	0.20564	0.18047
IV			1.0	45.9	195–204	207	189	270/163	0.20565	0.18020
IV	O2−	HIE	0.25	33.3	200–205	211	169	280/177	0.20587	0.18075
IV			1.0	46.2	197–204	210	176	276/173	0.20579	0.18037
IV		HIP	0.25	129.3	200–204	211	171	270/160	0.20572	0.18068
IV			1.0	152.2	197–204	210	179	271/161	0.20567	0.18032
V	O2−	HIE	0.25	41.4	200–204	210	169	277/174	0.20590	0.18075
V			1.0	51.5	197–204	209	176	274/170	0.20583	0.18037
V		HIP	0.25	125.1	200–204	210	170	275/167	0.20570	0.18062
V			1.0	146.5	197–203	209	178	274/167	0.20570	0.18033
Crystal					197–205	214	192	270/−	0.20593	0.18010

Fe–ligand distances, strain energies (ΔE_QM1), and R-factors are tabulated for the various oxidation and protonation states.

We will use six different criteria to evaluate which of the structures fit the crystal data best. These are the R and R_free factors, strain energies, the divergence of the Fe–O and Fe–N_His distances from those observed in vacuum, and electron-density maps. Strain energies (ΔE_QM1 in Table 3) are calculated as the difference in QM energy of the active site optimized in vacuum or in the protein, and therefore measures how much the structure has to be distorted to fit into the experimental electron density.

All calculations except one give improved structures in terms of the R_free factor. However, the reduction (and variation between the various structures) is very small, from 0.2056 to 0.2059. This is quite normal for the quantum refinement (Ryde and Nilsson, 2003b) and reflects that the R_free factor is a global property of the whole crystal structure, and we make only small changes for 57 atoms (out of 1412) in the active site. Our previous calculations (Ryde and Nilsson, 2003b) have shown that even if the variation in the R_free factor is small, it is reproducible and makes sense (e.g., R_free shows a nice minimum when the w_A factor is varied). Therefore, we have some confidence to compare R_free factors obtained for the various models.

From Table 3 it can be seen that the lowest R_free factors are obtained for Fe^III OH⁻ (especially with HID and HIE) and Fe^IV OH⁻ (especially with HIP), whereas Fe^III H₂O, Fe^III O²⁻, Fe^IV O²⁻, and Fe^V O²⁻ give high values.

The standard R-factor shows a similar variation, but it is always slightly higher than in the original crystal structure (0.1802–0.1807, compared to 0.1801). This actually also flags an improvement, because both the R_free factor and the difference between R_free and R should be minimized. The R-factor is smallest for Fe^III OH⁻ HID and Fe^III H₂O HID, whereas the O²⁻ models give the largest values. The R-factor is always lower for w_A = 1 than for w_A = 0.25, reflecting the stronger restraints toward the crystallographic data in the former calculations.

The strain energy (ΔE_QM1) is lowest (23–35 kJ/mol) for the Fe^III OH⁻ HID/HIE and Fe^IV OH⁻ HIE structures. Most of the other structures have a strain energy of 40–50 kJ/mol, but the two Fe^IV/Fe^V O²⁻ HIP structures have an appreciably higher strain energy (125–152 kJ/mol).

The Fe–O distances show a quite appreciable variation for the various models, 169–206 pm. This reflects that this bond is quite stiff in the quantum chemical calculations, especially for O²⁻ and OH⁻. It is notable that all structures, except those with Fe^III H₂O, give Fe–O bonds shorter than those in the original crystal structure, although the difference for Fe^III OH⁻ HIP is not large. The stiffness of this bond is also reflected in the small deviation between the ComQum-X and vacuum distances for the various models. It varies between 1 and 12 pm (19 pm for Fe^III H₂O) and is smallest for Fe^III OH⁻ HIE and Fe^IV OH⁻ HIP. As usual, the O²⁻ structures (but also the Fe^IV OH⁻ HID structure) give the worst results.

The Fe–N_His distance shows an even smaller variation, 205–212 pm, reflecting that it is quite flexible in the quantum chemical calculations. It is notable that it is always shorter than in the original crystal structure, indicating that this distance was somewhat too long. Interestingly, the smallest deviation from the vacuum structures is obtained for the Fe^V O²⁻ and the Fe^IV OH⁻ HID structures, i.e., those that gave the worst Fe–O bonds and strain energies. This reflects the inconsistency between the Fe–O and Fe–N_His bonds, observed already for the vacuum structures.

If we consider all of these results, it is clear that the normal interpretation of compound II, Fe^IV O²⁻ fits the crystal data worst. It is also clear that Fe^III O²⁻ and Fe^V O²⁻ are poor interpretations of the crystal structure. On the other hand, Fe^III OH⁻ HID and HIE seem to give the best results, both being always among the best structures with all criteria. The Fe^IV OH⁻ HIE and HIP structures also seem to give a reasonable fit to the crystallographic data.

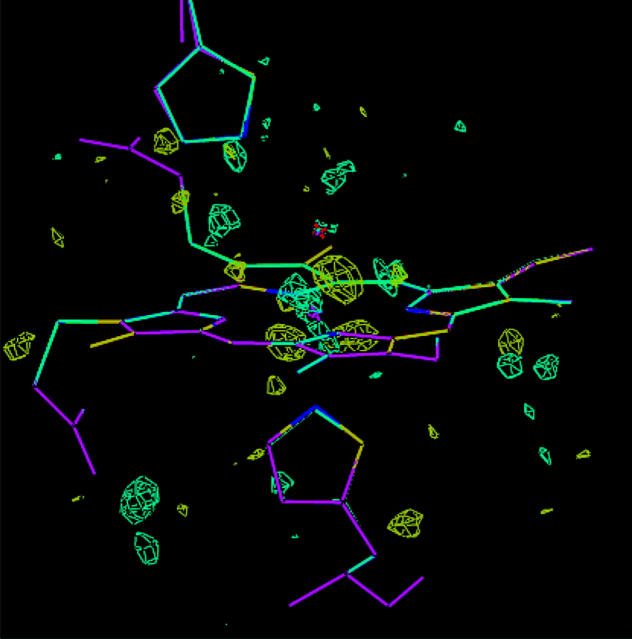
These conclusions are confirmed by an inspection of the electron-density maps. Fig. 4 shows a comparison of the original crystal structure and the re-refined structure with the Fe^IV OH⁻ HIE model. Only small differences between the two structures can be seen. This figure also shows the f_o–f_c difference map of the original crystal structure at the ±3σ level, which has quite a few features of both positive and negative residual density. However, if these are compared with the difference maps of two ComQum-X structures (the Fe^III OH⁻ HIE and Fe^IV OH⁻ HIE models), shown in Fig. 5, a strong improvement (less residual density) can be seen for both structures. On the other hand, it is very hard to distinguish between the two ComQum-X structures because they show similar features of almost equal volumes.

FIGURE 4.

A comparison of the original crystal structure (magenta) and the re-refined structure of Fe^IV OH⁻ HIE. Also included is the f_o−f_c difference map of the original crystal structure at the ±3.0σ level (cyan and yellow).

FIGURE 5.

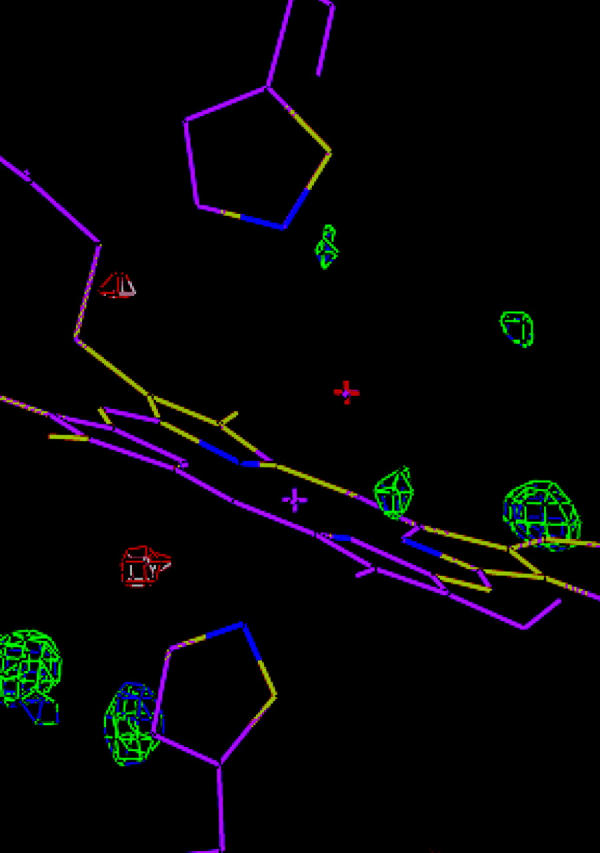
A comparison of the ComQum-X structures of the Fe^III OH⁻ HIE (magenta) and Fe^IV OH⁻ HIE models. Also included are the f_o−f_c difference maps of the two structures at the ±3.0σ level (blue and white for Fe^III and green and red for Fe^IV).

Concluding remarks

We have studied compound II in myoglobin by re-refining a 135-pm resolution crystal structure using 12 different protonation and oxidation states of the iron ion, the O-ligand, and the distal His residue. The results clearly show that the crystal structure does not contain a Fe^IV O²⁻ complex. Instead, it seems to contain a Fe^III OH⁻ or Fe^IV OH⁻ complex. However, none of the tested models fit perfectly into the electron density. Instead, there is an inconsistency between the observed Fe–O and Fe–N_His distances, which are not reproduced by any of the tested vacuum structures. This may indicate that the crystal structure is actually a mixture of at least two different oxidation or protonation states. Alternatively, the surrounding of the proximal His ligand in myoglobin may stabilize an elongated Fe–N_His bond length (Chance et al., 1986a).

The basis of our quantum refinement method is of course that our quantum chemical calculations give accurate results. Previous investigations and calibrations have shown that this is the case for metal complexes studied with the present density-functional method and basis set (Ryde and Nilsson, 2003b). In particular, the method reproduces Fe–N_Por, Fe–N_His, and Fe–S_Met bond lengths in cytochrome models within 3, 2, and 3 pm, respectively, and reproduce Fe–ligand bond lengths in a 95-pm crystal structure of cytochrome c₅₅₃ to within 3 pm (Ryde and Nilsson, 2003a).

In the present investigation, we see that our optimized Fe–O distance for compound I (Fe^V O²⁻), 165–167 pm, is in excellent accordance with experimental (crystallographic and EXAFS) data, 165–172 pm, for cytochrome P450, catalase, cytochrome c peroxidase, and HRP (Schlichting et al., 2000; Chance et al., 1986b; Gouet et al., 1996; Green et al., 2004). Moreover, our results reproduce the expectation that deprotonated compound II (Fe^IV O²⁻) should have a similar Fe–O distance (165–168 pm; it is 164–171 pm in a crystal structure of catalase and EXAFS structures of myoglobin and HRP; Chance et al., 1986a; Penner-Hahn et al., 1986; Gouet et al., 1996). Therefore, we have some confidence that our calculated structures can be trusted to within 3–5 pm.

Some of the systems studied have the same atoms and the same number of electrons. Therefore, their energies are comparable. It can be of some interest to compare these energies to get a feeling of the intrinsic stabilities and how they are changed in the protein. First, the HIE form of Fe^III (i.e., where OH⁻ is the acceptor of a hydrogen bond from the distal His) is 28 kJ/mol more stable than the HID form in vacuum. In the protein this has increased to 95 kJ/mol (for the structures obtained with w_A = 0.25). For Fe^IV, the HID form is most stable both in vacuum (by 46 kJ/mol) and in the protein (by 5 kJ/mol). Finally, we can also compare Fe^III H₂O HID with Fe^III OH⁻ HIP. It turns out that the latter form is most stable, both in vacuum and in the protein (by 83 and 23 kJ/mol, respectively).

In the original article of the crystal structure (Hersleth et al., 2002), it was suggested that the compound II structure represents a Fe^III OH^˙ state or possibly Fe^IV OH⁻. This conclusion was based on the long Fe–O distance and the short hydrogen bond to the distal His residue (N–O distance of 270 pm). In our vacuum calculations, the N–O hydrogen-bond length varies quite appreciably, e.g., from 252 to 293 pm in vacuum. All distances for HIE are ∼285 pm, whereas those of HID and HIP vary much more. The length of the H-acceptor interaction is 142–182 pm, indicating a quite strong interaction. In the ComQum-X structures, the variation is smaller, 259–280 pm—i.e., quite well centered around the value in the original structure. Thus, our results give no evidence that the oxidation and protonation state of the active site can be determined from the hydrogen-bond length.

The suggestion that the species observed is Fe^III OH^˙ also needs some comments. This state involves the same nuclei and the same number of electrons as the Fe^IV OH⁻ state. The only difference is the transfer of an electron from Fe^III to OH^˙. Thus, they are two electronic states of the same complex. In our calculations, one of them should therefore come out as the ground state, whereas the other is an excited state. To show the electronic structure of the various states, we have calculated the spin density of the different groups in the various complexes in Table 4. It can be seen that the Fe^IV OH⁻ complexes show a spin population of 1.39–1.55 on iron. This is intermediate between what is expected for Fe^III and Fe^IV. The spin population on OH⁻ varies with the distal His model. In the HIE and HIP complexes, there is 0.13–0.17 e on OH⁻, indicating almost a pure OH⁻ ion. The rest of the spin is located either in the porphyrin ring or on the distal His model. However, in the HID complex there are 0.46 unpaired electrons on the oxygen ligands, indicating that its electronic structure is almost between OH⁻ and OH^˙. These trends remain also in the ComQum-X structures, even if the length of the hydrogen bond is almost identical in these. We have made many attempts to find a pure wavefunction that corresponds to the Fe^III OH^˙ description, but without any success. Thus, it is hard to discern between the Fe^III OH^˙ and Fe^IV OH⁻ descriptions and it may actually be that the electron density is so delocalized that the truth is in between these two descriptions (as was seen for the HID complex). Moreover, it can be expected that the character varies significantly with small changes in the surroundings. A conclusive description of the actual electronic structure of the states can only be obtained with more advanced, multiconfigurational methods.

TABLE 4.

Spin densities of the Fe(Por)(Im)(H₂O/OH⁻/O²⁻)(Im) vacuum models

			Spin density on
Ox. state	Ligand	His	Fe	O-ligand	Por	Improx	Imdist
III	H2O		4.13	0.03	0.72	0.11
III		HID	4.16	0.07	0.66	0.10	0.01
III	OH−		0.87	0.21	−0.07	0.00
III		HID	0.84	0.24	−0.08	−0.01	0.00
III		HIE	0.92	0.14	−0.06	−0.01	0.00
III		HIP	0.97	0.08	−0.05	0.00	0.00
III	O2−		1.12	0.79	−0.90	−0.01
III		HIE	1.05	0.63	−0.67	−0.02	0.00
IV	H2O		1.07	0.01	0.92	0.01
IV		HID	1.21	0.03	0.75	0.00	0.00
IV	OH−		1.53	0.26	0.21	0.00
IV		HID	1.55	0.45	−0.02	−0.01	0.03
IV		HIE	1.43	0.17	0.12	−0.01	0.29
IV		HIP	1.39	0.13	0.48	0.00	0.00
IV	O2−		1.17	0.89	−0.05	−0.01
IV		HIE	1.25	0.81	−0.05	−0.01	0.00
IV		HIP	1.37	0.65	−0.06	0.02	0.02
V	OH−		0.87	0.21	−0.07	−0.01
V	O2−		1.43	0.94	0.63	0.00
V		HIE	1.38	0.84	0.44	0.00	0.33
V		HIP	1.16	0.82	0.99	0.05	−0.01

The fact that the crystal should contain compound II and not compound I or Fe^III is based on an investigation of the electron paramagnetic resonance spectrum, which shows that the Fe^III signal disappears when treating the crystals with H₂O₂ (Hersleth et al., 2002). It is replaced by a compound I signal, but it amounts to <2% of the original signal, indicating that the majority of the sites are in a different state with an even number of electrons. The conclusion that it is compound II is also supported by the change in color of the crystal (Hersleth et al., 2002). It has been checked by microspectrophotometry that the oxidation state of myoglobin compound II crystals does not change significantly during data collection at SNBL/BM1 at the European Synchrotron Radiation Facility in Grenoble, France.

The experimental evidence for compound II in heme proteins is somewhat messy. As mentioned before, a crystal structure of compound II in catalase (Gouet et al., 1996) gives a short Fe–O bond of 171 pm, indicating the Fe^IV O²⁻ state. However, the present crystal structure, two recent structures of compound II in HRP and catalase, as well as the crystal structure of compound I in cytochrome c peroxidase (with the extra oxidizing equivalent on a tryptophane radical), indicate a longer bond, 184–192 pm (Berglund et al., 2002; Hersleth et al., 2002; Murshudov et al., 2002; Bonagura et al., 2003). These long bonds were interpreted as a single Fe–O bond caused by the protonation of the oxygen atom. Likewise, there are three EXAFS studies that indicate a short Fe–O bond of compound II in myoglobin and HRP (164–170 pm; Chance et al., 1986a; Penner-Hahn et al., 1986; Green et al., 2004), but there is also another study on HRP that gave a long Fe–O bond (193 pm; Chance et al., 1984). The two spectra from HRP are clearly different, showing that the difference is not caused by errors in the fitting procedure (Penner-Hahn et al., 1986). Thus, at least two forms of compound II seem to exist. A long EXAFS Fe–O bond (182 pm) was also found for compound II in chloroperoxidase (with an axial cysteine Fe ligand), but the same authors obtained a short bond for HRP (170 pm) and they question the long bonds observed in the other enzymes (Green et al., 2004). Thus, the nature of compound II in heme proteins is still controversial.

The situation is even more complicated by the observation of two pH-dependent states of compound II in peroxidases by resonance Raman and variable-temperature magnetic circular dichroism (Paeng and Kincaid, 1988; Sitter et al., 1985; Andersson and Dawson, 1991; Foote et al., 1989). For HRP, the transition between the two states is around pH 8.5 and the alkaline form has a higher frequency of the Fe–O bond (788 compared to 776 cm⁻¹; Sitter et al., 1988). Both pH states are suggested to be Fe^IV O²⁻, but at high pH, there should be no hydrogen bond to the distal His residue (the Fe–O frequency is insensitive to deuterium exchange; Sitter et al., 1988). For myoglobin, a similar transition is observed around pH 3.5 and the form at normal pH is most similar to the alkaline form of HRP compound II (Sitter et al., 1985; Foote et al., 1989). The low-pH form is highly unstable and has been interpreted as having a protonated distal His residue that swings out into the solvent, making the heme site more exposed (Foote et al., 1989). Thus, these two pH forms cannot explain the differences in the Fe–O distance, observed by EXAFS and crystallography (concerning the protonation of the iron-bound water molecule).

This is in accordance with the resonance Raman spectrum of our myoglobin crystals and solution (T. Uchida, H.-P. Hersleth, T. Kitagawa, K. K. Andersson, unpublished data): It shows an appreciably lower Fe–O frequency (below 700 cm⁻¹), in agreement with the long Fe–O bond.

If we take all this experimental data together with our results and trust that the crystal is not reduced during data collection, the most probable interpretation of compound II in our crystals of myoglobin seems to be the Fe^IV OH⁻ state in the HIE or HIP forms, in which the distal His donates a hydrogen bond to the iron-bound OH⁻ group (these two states also fit the crystal structure best). It is possible that the distal His group protonates in the physiological pH range, which could explain the variation observed in the O–N distance between the O-ligand and the distal His group in crystal structures collected at pH 5.2 (270 pm), 6.8 (288 pm), and 8.7 (294 pm; H.-P. Hersleth, C. H. Görbitz, K. K. Andersson, unpublished data; Hersleth et al., 2001). These structures show no significant changes in the other structural parameters. This interpretation is in accordance with a 16-pm increase in the O–N distance for the Fe^IV OH⁻ HIE/HIP models in Table 2.