An Automatic Method for Predicting Transmembrane Protein Structures Using Cryo-EM and Evolutionary Data

Abstract

The transmembrane (TM) domains of many integral membrane proteins are composed of α-helix bundles. Structure determination at high resolution (<4 Å) of TM domains is still exceedingly difficult experimentally. Hence, some TM-protein structures have only been solved at intermediate (5–10 Å) or low (>10 Å) resolutions using, for example, cryo-electron microscopy (cryo-EM). These structures reveal the packing arrangement of the TM domain, but cannot be used to determine the positions of individual amino acids. The observation that typically, the lipid-exposed faces of TM proteins are evolutionarily more variable and less charged than their core provides a simple rule for orienting their constituent helices. Based on this rule, we developed score functions and automated methods for orienting TM helices, for which locations and tilt angles have been determined using, e.g., cryo-EM data. The method was parameterized with the aim of retrieving the native structure of bacteriorhodopsin among near- and far-from-native templates. It was then tested on proteins that differ from bacteriorhodopsin in their sequences, architectures, and functions, such as the acetylcholine receptor and rhodopsin. The predicted structures were within 1.5–3.5 Å from the native state in all cases. We conclude that the computational method can be used in conjunction with cryo-EM data to obtain approximate model structures of TM domains of proteins for which a sufficiently heterogeneous set of homologs is available. We also show that in those proteins in which relatively short loops connect neighboring helices, the scoring functions can discriminate between near- and far-from-native conformations even without the constraints imposed on helix locations and tilt angles that are derived from cryo-EM.

INTRODUCTION

TM proteins are crucial mediators of cell-to-cell signaling and transport processes, and constitute some 50% of contemporary drug targets (Fleming, 2000). In recent years the pace of structural determination of TM proteins has increased, but technical problems related to protein purification and crystallization still hamper TM-protein structure determination. Thus, despite their biomedical importance, <40 distinct folds of TM proteins have been solved to date by high-resolution methods such as x-ray crystallography. The lack of a large set of solved TM proteins also restricts the usefulness of computational methods based on the statistics of solved protein structures, and in particular, of comparative or homology modeling, which has been a very successful approach in soluble proteins.

In general, computational prediction of soluble-protein structures is difficult, largely because of the variety of possible folds, which implies a vast number of degrees of freedom. In contrast, all TM proteins that inhabit the plasma membrane of eukaryotic cells form α-helix bundles, thus reducing the desolvation penalty of exposing polar main-chain groups. The high propensity to form secondary structures reduces the number of degrees of freedom, which determine the protein's fold, and hence, lowers the complexity of predicting the structures of these proteins.

Structure prediction of TM proteins often relies conceptually on the two-stage model for protein assembly in the membrane (Popot and Engelman, 1990). According to this model, the first step of folding is the insertion of the TM domains into the membrane as α-helices. Only in the second stage do these helices associate to form bundles (reviewed by White and Wimley, 1999 and Popot and Engelman, 2000). One of the implications of the two-stage model is that, overall, the stability of individual TM domains is independent of that of other domains. Hence, prediction of TM-protein structures can begin with experimental determination (or prediction, reviewed by von Heijne, 1996 and Chen et al., 2002) of the locations of the TM helices in the amino-acid sequence of the protein.

Some early attempts were made to predict helix orientations relative to one another by using the concept of the hydrophobic moment (Eisenberg et al., 1984; Rees et al., 1989). However, in view of the low-dielectric character of the membrane, the hydrophobic driving force is probably less dominant in this medium than in soluble proteins, and the hydrophobic moment proved to be of limited use in TM-protein structure prediction (Pilpel et al., 1999; Stevens and Arkin, 1999).

Attempts were also made to predict the structures of specific TM proteins or protein families (Tuffery and Lavery, 1993; Stokes et al., 1994; Taylor et al., 1994; Adams et al., 1995; Baldwin et al., 1997; Heymann and Engel, 2000; Hirokawa et al., 2000; Zhdanov and Kasemo, 2001; Sorgen et al., 2002; Trabanino et al., 2004). For high-resolution structure prediction of pairs of TM α-helices, a method that was based on molecular dynamics was developed, in which data derived from large-scale mutational assays were utilized to derive constraints for the conformation search (Adams et al., 1995). Extensions to this method were suggested, which used phylogenetic instead of mutational data (Briggs et al., 2001) and lowered the computational load associated with the conformation search (Pappu et al., 1999). Recently, a method based on Monte-Carlo sampling of conformations, which selects tightly packed conformations, was shown to reproduce the structures of homooligomers (Kim et al., 2003). Another method that was founded on a knowledge-based potential constructed on the basis of TM proteins of known structures and energy terms that simulate the membrane environment was also shown to retrieve the conformations of small homooligomers (Pellegrini-Calace et al., 2003).

A major limitation of many of the methods in this class is the large computational load. In fact, computational complexity has restricted the applicability of these methods mostly to the cases of homooligomers of single-spanning TM proteins. A more fundamental handicap is the reliance of many of these methods on contemporary force fields. Recent results indicate that the forces specifying and stabilizing TM-helix interactions are still unclear (Bowie, 2000), casting doubt on the ability of methods based on existing force fields to yield accurate predictions.

We recently examined the possibility of reducing the computational burden by using low resolution from the outset (Fleishman and Ben-Tal, 2002), i.e., by considering only the helices' C^α traces. We developed a scoring function and a search methodology to seek stable conformations of pairs of closely packed TM helices. The use of a reduced representation of the helices allowed us to conduct an exhaustive search of conformation space, and to test the method systematically on many different examples. This approach proved useful in studying the involvement of the TM domain in the activation of the erbB2 receptor tyrosine kinase (Fleishman et al., 2002). However, it could only be applied reliably to helix pairs that are closely packed (<9 Å separation between the helix axes) (Fleishman and Ben-Tal, 2002). Because many of the helices in TM proteins have greater interhelical separations (Bowie, 1997), in general, this method cannot be used to predict entire protein domains.

Here, we explored whether such an approach can be extended to deal with large TM domains by incorporating the evolutionary-conservation profile of the protein and the hydrophobicity of its constituent amino-acid residues. The underlying idea is that amino-acid positions that mediate interhelical contacts would be more evolutionarily conserved than those that face the lipid (Donnelly et al., 1993; Stevens and Arkin, 2001; Beuming and Weinstein, 2004), because mutation of positions that form contact would most likely destabilize the protein, and render it dysfunctional (Fig. 1). Hydrophobicity can be used to discard potential conformations that expose charged positions (e.g., Arg and Glu) to the membrane environment (Cronet et al., 1993) due to the prohibitive cost in desolvation of their highly polar side chains (Honig and Hubbell, 1984).

FIGURE 1.

The conservation profile of the TM domain of rhodopsin (PDB code 1l9h). Conservation scores were computed using the ConSurf server with the Rate4Site algorithm (Pupko et al., 2002), and are mapped according to the color scale with turquoise through burgundy signifying variable through conserved positions. (A) Two side views looking from within the membrane plane. The space-filling models show that the lipid-facing parts of the protein are mostly variable. (B) Looking from the cytoplasmic side. Stick models of residues that belong to the two highest categories of the conservation scale (8 and 9) are indicated. The vast majority of these highly conserved residues face the protein interior. The arrows identify the highly conserved Trp-161, which is exceptional in that it is exposed to the membrane despite its high conservation. This and all other molecular representations were generated with MOLSCRIPT (Kraulis, 1991) and rendered with Raster3D (Merritt and Bacon, 1997).

To reduce the computational burden associated with conformational searches of large TM domains, the targets for our approach are those proteins for which intermediate-resolution (5–10 Å in-plane) structural data are available, e.g., from cryo-EM (Unger, 2001). At such resolution, cryo-EM maps reveal the organization of TM helices relative to one another including the helices' positions and tilt angles, but do not disclose the locations of the individual amino acids. Based on the cryo-EM data, it is possible to approximate the helices' principal axes either manually (Baldwin et al., 1997; Fleishman et al., 2004) or computationally (Jiang et al., 2001). Then, the conformational search need only explore the orientations of the helices around their principal axes.

Intermediate-resolution cryo-EM maps of TM proteins often provide accurate data on the lateral positions of the helices and their tilt angles within the lipid bilayer, but much poorer data on the positions of the helices along the vertical axis (Unger and Schertler, 1995; Unger et al., 1999). In this study, we limited the methods' validation to the hydrophobic portion of each of the TM helices. As these segments are most likely to align with one another within the hydrophobic core of the lipid bilayer, the inaccuracy due to the low vertical resolution of cryo-EM data does not present a significant problem. In a refinement stage of the conformational search described below, a limited exploration of all degrees of freedom, including the vertical axis, was conducted.

Baldwin et al. (1997) used a similar approach to predict the orientations of helices in rhodopsin based on the receptor's cryo-EM map at 9 Å in-plane resolution (Unger et al., 1997). This prediction was shown (Bourne and Meng, 2000) to compare very well with the high-resolution structure, which was solved a few years later (Palczewski et al., 2000). However, Baldwin et al.'s conservation analysis was highly labor intensive and required substantial subjective intervention at various stages (Baldwin et al., 1997), making it difficult to apply to a large set of proteins. As conservation analyses have grown in rigor and sophistication in recent years, we have employed automatic and more sensitive tools, to construct score functions for ranking conformations of TM proteins. This has allowed us to test various formulations of the prediction rule and search methodology on a variety of TM proteins. The tests were based on perturbations of the native-state structures as they are found in the PDB, except in the case of rhodopsin, in which they were conducted using data extracted (Baldwin et al., 1997) from its cryo-EM map at 9-Å resolution (Unger et al., 1997).

Our analysis leads us to conclude that an approach based on evolutionary conservation, hydrophobicity, and intermediate-resolution structures can retrieve near-native structures subject to two principal requirements. First, the cryo-EM map must show that all helices have a face that is buried in the protein bundle and another that is exposed to the membrane milieu or the pore lumen. This requirement is necessary because it is only the heterogeneity of environments that allows the correct orientation of the helices. Second, evolutionarily conserved and variable residues must be distributed in the TM domain in accordance with a helical pattern (Fig. 1). This distribution ensures that a clearly higher score is assigned to an orientation, in which conserved residues face the interior of the helix bundle, whereas the variable residues are directed toward the lipid. Hence, a typical case in which this approach is expected to yield a near-native structure is a protein or an oligomer, where all helices face the lipid environment or a relatively large internal pore, and a sufficiently heterogeneous set of sequences are available.

Score functions

In developing the conformation-search methodology and the score functions, we initially used the structure of bacteriorhodopsin for parameterization (Luecke et al., 1998). That is, various formulations of the scoring function were attempted with the aim of detecting the native structure among contending templates. For instance, formulations that gave a more dominant effect to hydrophobicity were found to do more poorly than the formulation that is given below, which stresses conservation, in agreement with the notion that the hydrophobic moment is a relatively poor indicator of helix orientations (Pilpel et al., 1999; Stevens and Arkin, 1999).

The so-called burial function, which we first introduced in Fleishman and Ben-Tal (2002), is a major component of the scoring schemes defined here. It is an estimate of the extent of an amino acid's contact with another helix. Because the model describes amino acids merely in terms of C^α positions, only an approximate measure of contact can be attained. To achieve this approximation, the function considers the distance between an amino acid's C^α position and the other helix's principal axis. It also considers the angle formed between two vectors: one that connects the two helix axes, and a second that connects the C^α position to its own axis (Fleishman and Ben-Tal, 2002). If both the angle and the distance are small, the burial function is assigned relatively high values (→1). Low values (→0) are assigned otherwise.

This burial function takes into account the details of the local interactions of the helices. The alternative use of a moment to account for hydrophobicity or conservation treats all helices as being perpendicular to the membrane plane (e.g., Eisenberg et al., 1982; Pilpel et al., 1999), thus giving a particular helix face the same weight in computing the optimal conformation throughout the TM span. In contrast, the use of the burial function tests the extent of contact for each amino-acid residue, and treats each position according to its actual contact with other helices, thus treating tilted and kinked helices more realistically (Fleishman and Ben-Tal, 2002).

We used three schemes for ranking template conformations. The simplest form is the “singlewise” score (Fleishman et al., 2004). This function assigns a high score to conformations that bury conserved faces in the α-helix bundle, and expose the helices' variable faces to the lipid. The function is singlewise in the sense that for any given amino acid, only the locations of the axes of its neighboring helices are taken into account. Because these locations can be derived from the cryo-EM data to a reasonable degree of confidence, the contributions of each amino-acid residue to the overall score is independent of the positions of other residues. The underlying notion in the singlewise score is that positions that are buried in the protein core are typically conserved evolutionarily (Fig. 1). Indeed, some conserved positions may be exposed to the membrane in contradiction to this “rule” (see the arrows in Fig. 1). However, summation across the entire helix span reduces the prediction's sensitivity to such cases.

Another term penalizes the exposure to the lipid (burial values <0.5) of the most polar amino-acid residues that are associated with high (>7 kcals/mol) desolvation energies upon transfer from water to membrane according to the Kessel & Ben-Tal scale (Kessel and Ben-Tal, 2002). The residues for which the penalty applies are Arg, Asn, Asp, Glu, and Lys. In essence, this term associates conformations that expose very polar residues with very unfavorable scores. Polar residues at the terminal turns (four amino-acid residues) of helices were disregarded in computing this penalty, because at these locations, residues may interact favorably with the relatively polar environment at the lipid-water interface (von Heijne, 1996). Proline residues are ignored in calculating the conservation scores because they are often conserved owing to kinks that they induce in the helix secondary structure rather than to the formation of interhelical contacts (Baldwin et al., 1997).

A second scheme, called the “pairwise” function, included, in addition to the singlewise score, a term that favors contact formation between highly conserved residues, and penalizes contacts among highly variable residues. Hence, this function takes into account the positions of pairs of residues in contrast to the singlewise score, which considers residues separately. The underlying concept here is that positions that form contact should be highly conserved, because introducing even mild changes in these positions would abrogate interhelical contact.

The singlewise and pairwise score functions do not include terms that penalize the formation of possible steric clashes between the helices. Generally, the positions and tilt angles can be derived from cryo-EM data. However, these data are potentially inaccurate due to limited resolution. A scoring function that contains an approximation of penalties due to steric clashes could be useful for a limited exploration of the conformation space with respect to helix positions and tilt angles. We thus defined a third score function, which included, in addition to the terms in the pairwise score, penalties for conformations, in which a helix is potentially in violation of another's approximate exclusion volume.

METHODS

Conservation analysis

The conservation of amino-acid residues in the TM domains of the proteins were calculated using the ConSurf server (Glaser et al., 2003) with the Rate4Site algorithm (Pupko et al., 2002). Homologs were collected using 5 PSI-BLAST iterations and a BLAST e-value cutoff of 1 (Altschul et al., 1997). We asserted by visual inspection of the alignments that there were no significant gaps in the TM domains of all the proteins under study.

Score functions

To each configuration of the helix bundle produced by the search method, we assign a score. The score is based on four terms, such that:

1. Hydrophobic residues face the lipid environment and hydrophilic residues are directed toward the protein core.

2. Conserved residues face the protein core and variable residues face the lipid environment (Fig. 1).

3. Highly conserved residues on different helices are in close proximity, whereas highly variable residues are distal.

4. A penalty for potential steric clashes.

For each conformation the score is generally defined as follows, where the summation is on every residue pair i,j in the TM domain:

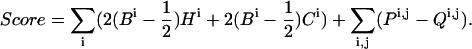(1)

In Eq. 1, Cⁱ are the normalized evolutionary-conservation scores assigned by Rate4Site (Pupko et al., 2002) (Fig. 1) and Hⁱ the desolvation free energies of transfer from water to membrane (Kessel and Ben-Tal, 2002); Bⁱ is the burial score associated with each residue, i.e., the extent of that residue's contact with other helices (Fleishman and Ben-Tal, 2002); P^i,j is a pairwise term that promotes contact between highly conserved residues and penalizes contact between highly variable residues; and Q^i,j is a penalty for formation of severe van der Waals clashes.

High Cⁱ and Hⁱ values indicate that a residue is conserved and hydrophilic, respectively. Hydrophobicity is taken into account only for residue types that are associated with free energies of transfer >7 kcal/mol (Kessel and Ben-Tal, 2002), and are counted only for residues i, for which the burial scores Bⁱ are <0.5. Thus the hydrophobicity scale serves as a significant penalty on the exposure of the most polar residues to the membrane environment. The terminal turns (four amino-acid residues) from each side of the TM segments are ignored in computing this penalty, because residues in these regions may be accommodated by the polar environment at the lipid-water interface (von Heijne, 1989). The contributions of proline residues to the score is also ignored because they are often conserved due to kinks they form in secondary structure rather than due to the promotion of interhelical contacts (Baldwin et al., 1997).

Cⁱ and Hⁱ are singlewise terms that depend on the amino-acid site itself, regardless of the protein conformation. In contrast, Bⁱ is the burial score associated with each residue i, and depends on the maximal contact formed by each residue with other helices in the bundle (elaborated below). It assumes values in the range 0−1, where zero indicates complete exposure to the membrane environment and 1 indicates complete burial in another helix.

Maximization of the score defined in Eq. 1 favors the burial of hydrophilic residues in the α-helix bundle and penalizes their exposure to the membrane (the first term in Eq. 1). Similarly, the second term in Eq. 1 favors the burial of conserved amino acids in the bundle interior and penalizes their exposure to the lipid. The third is a pairwise-contact term favoring contact between well-conserved residues and penalizing contact between highly variable residues.

(2)

where residues j and i are not >7 Å apart, and their respective burial scores (B) are >0.2.

The fourth term in Eq. 1, Q^i,j, produces a severe penalty on steric-clash formation, and is summed on all pairs of residues i, j in the TM domain:

(3)

where d^i,j is the distance between residues i and j, Θ is the threshold below which the penalty assumes infinite magnitude, and μ is the threshold above which the penalty cancels out. We chose this formulation for the penalty because it produces a function that is continuous for d^i,j > Θ, as is its first derivative. A value of 2 Å was chosen for Θ, to approximate the C^α van der Waals radius (1.88 Å) (Tsai et al., 1999), and 2.5 Å was chosen for μ. The penalty is very large for distances close to 2 Å, but drops off quickly toward zero at 2.5 Å. Thus, conformations are penalized only for severe steric clashes.

We tested different formulations of the score function presented in Eqs. 1–3 by assigning different weights to the various terms, and by using different hydrophobicity scales. This formulation was found to work well in identifying bacteriorhodopsin's native-state structure from decoys. Hydrophobicity appears to be a poor indicator on its own for TM-helix orientations, whereas contact between highly conserved residues is a good indicator.

The singlewise score function is defined as in Eq. 1 (Fleishman et al., 2004), except that the pairwise contact terms P and the penalties on steric clashes Q are neglected. Essentially this score function favors the burial of conserved and hydrophilic residues in the protein core, but does not favor contact between conserved residues. The pairwise score is similarly defined as in Eq. 1 with the penalties for steric clashes being neglected.

Assessing the extent of interresidue contact

The score function defined in Eq. 1 is based on a quantification of the burial of amino acids that mediate interhelical contact. In measuring the extent of burial Bⁱ of amino acid i we consider two criteria, as elaborated by Fleishman and Ben-Tal (2002). The first is the distance between the amino acid and the principal axis of the other helix; the smaller the distance, the more deeply buried the amino acid. The second is the orientation of the amino acid with respect to the principal axis of the other helix; the more the amino acid is directed toward the other helix, the better its burial.

Formally, we consider two parameters: the distance Dⁱ between amino acid i and the axis of the other helix, and the angular orientation Aⁱ of amino acid i with respect to the axis of the other helix. We define the burial of an amino acid as the intersection of these two criteria:

(4)

where S(Dⁱ) and S(Aⁱ) are transformations of the distance and angular criteria as defined in Eqs. 5 and 6 below.

The parameters used by Fleishman and Ben-Tal (2002) for the burial function B were tailored specifically to TM-helix pairs with short interaxial separations. In the more general case treated here, it was necessary to reparameterize the function. By manually modulating these parameters with regard to the structure of bacteriorhodopsin, we found the parameter values t = 60° and p = 4 to be suitable for transformation of the angle Aⁱ. For transformation of the distance, we first subtract 4.3 Å from the value of Dⁱ calculated for the distance between the amino acid and the axis of the other helix. This value approximates the smallest possible distance between an amino acid and another helix (the radius of an α-helix to its C^α atoms is 2.3 Å plus 2 Å for two exclusion radii), and approaches a value of 1 for S(Dⁱ) if the amino acid is as close as possible to the axis of the other helix. The parameter values chosen for transformation of the distance are t = 10 Å and p = 6. Thus the two transformations for amino acid i are:

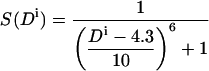(5)

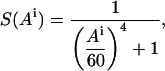(6)

where Aⁱ and Dⁱ are expressed in degrees and Ångstroms, respectively.

Conformation search in TM proteins with short loops

In those cases, where the TM helices are connected via short loops, e.g., rhodopsin, it is possible to sample the constrained conformation space available to the α-helix bundle by using a modification of the method of Monge et al. (1994), in which α-helices are treated as rigid bodies, and their exclusion volumes and the lengths of the interconnecting loops are taken into account. The software and low-resolution potential used were developed by Eyrich et al. (1999) (J. Gunn, private communication).

We began with the native-state structure, and systematically perturbed the helix positions as follows. One helix was selected and moved around its close-contact interfaces with other helices by shifting up and down, twisting, and rotating; all of these changes were made by adding appropriate quadratic bonus functions to the low-resolution potential and minimizing. The resulting structures were then used as starting points for another round of minimization of the low-resolution potential. In both cases, another bonus function was added to the potential to help reward the TM orientations of the helices. (Because in this software the conformational space is given in Φ-Ψ coordinates and no consistent embedding into Euclidean space is done by the program, it was not possible to impose the membrane constraints in the straightforward way.) This membrane function was based on the distances between the termini of all of the helices besides the one designated to move. It rewarded those intertermini distances (excluding those of the selected perturbed helix) that remained within 4.5 Å of their original values. Thus steric clashes resulting from the helix perturbations would tend to be resolved inside the membrane, and conformations that did not respect the TM orientations were penalized.

Several rounds of this procedure were completed using the best-scoring structures as the initial structures to perturb. The resulting structures were then screened for steric clashes and inappropriate TM orientations using the energy functions, and finally clustered at 0.8 Å to produce our test set.

RESULTS

Rhodopsin and the bacterial rhodopsins

We used rhodopsin as our main test case because it represents the typical case for which the method is intended. That is, it is a medium-size protein (7 TM segments), which has been solved at intermediate in-plane resolution (9 Å) (Unger et al., 1997), and shares sequence homology with a large set of other G-protein-coupled receptors. Moreover, its high-resolution structure (2.8 Å) (Palczewski et al., 2000) allows us to test the prediction's quality.

Baldwin et al. (1997) used the intermediate-resolution cryo-EM maps of rhodopsin (Unger et al., 1997), as well as conservation data, to manually infer a template structure, which included the coordinates of C^α atoms. We did not use their model structure of rhodopsin, but did employ the helix-tilt angles and positions that they extracted from the cryo-EM maps (Baldwin et al., 1997). The assignment of individual TM segments to the helices seen in the cryo-EM maps was also taken from Baldwin et al.'s analysis. In addition, we used their data on the positions, directions, and extents of kinks in the TM domain. In summary, the C^α positions of each helix were generated according to the helix parameters of canonical α-helices as observed in the intermediate-resolution data (Unger et al., 1997).

To test the singlewise function's performance, each helix was rotated in 5° increments around its principal axis (range: 0–360°), and its best-scoring orientation was selected. Because the contribution to the singlewise score of each of the helices is essentially independent of that of the others, we superimposed the best-scoring orientations of each of the seven helices to obtain an optimal template structure. The root-mean-square deviation (RMSd) of this template from the native-state structure of rhodopsin was 3.7 Å.

The search in orientation space is confined within a seven-dimensional hypercube, where each degree of freedom sets the orientation of one of the seven helices. To calculate the distribution of RMSd values of conformations within this hypercube to the native-state structure of rhodopsin, we generated 2000 template conformations. In each of these templates, every helix's orientation was randomly selected from a distribution with uniform probability in the range 0–360°. The RMSds of each of these templates from the native-state structure of rhodopsin (Palczewski et al., 2000) was then computed (Fig. 2). The optimal structure was found within the lowest 3.5 percentiles of RMSd values, demonstrating that even the relatively simple singlewise score function is capable of retrieving a near-native structure from a set of decoys (Table 1).

FIGURE 2.

A histogram of RMSd values to the native-state structure of 2000 randomly generated templates of rhodopsin. The templates were constructed according to the helical axes parameters obtained (Baldwin et al., 1997) from the cryo-EM data of rhodopsin at 9 Å in-plane resolution (Unger et al., 1997). The RMSd of the conformation with the best singlewise score (3.7 Å from native) is marked by a dashed line, a value that is at the lowest 3.5 percentiles of the random conformations.

TABLE 1.

Summary of the results of using the singlewise score function to calculate a near-native conformation of rhodopsin and the three bacterial rhodopsins, bacterio-, halo- and sensory rhodopsin II

Protein	RMSd of randomly generated conformations (± SD) Å	RMSd of the highest-score conformation from the native-state structure (Å)	Percentile of highest-scoring conformation
Bacteriorhodopsin	3.9 ± 0.4	3.2	5.6
Halorhodopsin	3.3 ± 0.4	2.5	4.2
Sensory rhodopsin II	3.5 ± 0.4	1.8	0.01
Rhodopsin	4.5 ± 0.4	3.7	3.5

The three bacterial proteins are related to one another in terms of sequences and structures, but show some local structural differences. Rhodopsin is different in terms of architecture and sequence. Templates for the three bacterial rhodopsins were constructed on the basis of their high-resolution PDB structures. Rhodopsin's templates were constructed on the basis of helix-axes parameters (Baldwin et al., 1997) taken from its 9-Å in-plane resolution structure (Unger et al., 1997). Percentiles were computed on the basis of a distribution of expected RMSd values for each protein (see Results). In all cases, the best-scoring conformation is significantly closer to the native state than predicted by chance.

We also tested the singlewise score on the three homologous bacterial rhodopsins, bacterio-, halo-, and sensory rhodopsin II (PDB codes are 1c3w, 1e12, and 1jgj, respectively). These three proteins share ∼30% sequence identity and their structures are quite similar (1–1.7 Å RMSd; Fischer et al., 1992), but show some local structural differences and no homology with rhodopsin. We extracted the helix-axes parameters (tilt angles and positions) (Fleishman and Ben-Tal, 2002) from the proteins' high-resolution structures, and constructed canonical α-helices accordingly, without modeling explicitly any deviations from helicity, such as kinks and bulges. We then employed the singlewise score and searched the conformation space (seven-dimensional hypercube) exhaustively in the same manner as explained above for rhodopsin. Table 1 summarizes the results of the conformation searches. In all cases, as in rhodopsin, the singlewise score detected templates that were much closer to native than expected by chance.

Using the result of the exhaustive singlewise search as a starting template structure of rhodopsin, we conducted a conformation search employing the pairwise score function that avoids steric clashes, and the Simplex optimization method, which is a line-search algorithm for finding a local optimum (Nelder and Mead, 1965). The RMSd of the predicted structure from the native state (PDB code 1l9h) was 3.1 Å, which is an improvement over the result obtained by using the singlewise score function alone (3.7 Å). This result is comparable with that obtained by Baldwin et al. (3.2 Å) (Baldwin et al., 1997). We tested whether subsequent use of the two scores constitutes a viable search strategy on the three homologous bacterial rhodopsin structures. However, in these cases the pairwise score improved the RMSd of the predicted conformations only marginally (data not shown).

The acetylcholine receptor

The nicotinic acetylcholine receptor (AchR) transfers the electrical signal at the nerve-muscle synapse by the gating of its TM pore (Hille, 2001). The channel is composed of five homologous subunits (β, γ, δ, or ɛ, and two α-subunits), where each monomer consists of four TM domains (M1–M4). The five M2 segments from each of the subunits line the pore. The recently solved structure of the closed AchR at 4-Å resolution revealed an unexpected architecture, in which the M2 helices appear to be embedded in water and surrounded by an outer ring of the other TM helices (Miyazawa et al., 2003), to which they form only a very loose attachment. These loose contacts are thought to facilitate the substantial changes in the orientations of the M2 helices (Unwin, 1995).

We constructed a model of the AchR TM domain by deriving the helix-tilt angles and positions (Fleishman and Ben-Tal, 2002) from its native-state structure (PDB code 1oed). Canonical α-helices that fit the parameters of these helix axes were then constructed. To predict the optimal structure based on the pairwise score, we sampled 20,000 different combinations of orientations of the four helices comprising a subunit. Fivefold symmetry across the AchR subunits was enforced, and the best-scoring conformation according to the pairwise score was selected. In contrast to the cases of the rhodopsins, the relatively small number of helices in each monomer of the AchR ensures that this number of orientations will adequately cover the conformation space. This search yielded a structure that was 2.5 Å RMSd from the native-state structure (Miyazawa et al., 2003) (Fig. 3 A).

FIGURE 3.

(A) A stereo view of the TM domain of AchR (blue) superimposed on the predicted template (red). Spheres mark the positions of the cytoplasmic ends of the helices for clarity. The RMSd between the native-state and the calculated structures is 2.5 Å. Helices M1 and M3 were predicted quite accurately, but helices M2 and M4 were skewed by 90 and 100°, respectively. (B) A view of the AchR structure from the cytoplasmic side. The residues are colored according to the evolutionary-conservation scale shown in Fig. 1. M2 is homogeneously conserved explaining the inaccurate prediction. M4 is highly exposed to the membrane. Hence, despite the clear conservation signal, there is a large degree of uncertainty in its orientation.

In this predicted conformation (Fig. 3 A) the orientations of helices M1 and M3 match the native state quite closely, except for deviations from helical ideality in M3. Helix M4 is largely exposed to the lipid (Fig. 3 B), a feature not typical of other solved TM protein structures, which usually show tighter interhelical interactions. Owing to this exposure, there is a larger degree of uncertainty concerning the prediction of this helix's orientation, and indeed the optimal orientation is skewed by ∼100° relative to the native state. The predicted orientation of M2 is offset to a slightly lesser extent. The reason for the deviation of M2 from the native state is that this helix is conserved quite homogeneously throughout the segment (Fig. 3 B). The lack of a clear conservation versus variability pattern precludes this helix's orientation with confidence.

Constraints imposed by short interconnecting loops instead of by cryo-EM data

Many of the extramembrane loops that connect TM helices are relatively short (<10 amino-acid residues) (Tusnady and Simon, 1998). In principle, such short loops can impose severe constraints on the conformation space that a pair of helices is free to sample. Here, we were interested in testing whether considering the constraints imposed by loop lengths improves the prediction's quality.

For conformation sampling, we adapted a technique that was developed by Monge et al. (1994) for sampling the conformations of secondary-structural elements in soluble proteins. The method starts from the native-state structure of the protein, and perturbs the secondary-structural elements' positions and tilt angles while treating them as rigid bodies. In contrast, the regions of the interconnecting loops that are devoid of defined secondary structure are allowed to sample conformations freely.

To construct a complete native-state structure, we added the positions of the loop residues that are missing from the PDB structure (1l9h). These missing loop residues were built into our native state via minimization of our low-resolution energy function of these loop residues, whereas the rest were constrained to their positions as observed in the PDB structure. The native state was then systematically perturbed, and the resultant conformations were assessed with a low-resolution energy function to penalize the formation of steric clashes and covalent-bond strains. Nonphysical conformations were thus penalized (Monge et al., 1994). Hence, the constraint on the helices' positions and tilt angles is that the lengths of the interconnecting loops are respected.

Another penalty was imposed on TM helices that assumed a nontransmembrane orientation, i.e., for helices whose termini were not located on opposite sides of the presumed membrane. Hence, the search method samples conformation space that is available to the helix bundle, but penalizes nonphysical orientations. Structures with high penalties were then discarded to eliminate those that were clearly nonphysical.

Based on the high-resolution structure of rhodopsin (PDB code 1l9h) as the template structure, we generated 108 modified templates, each differing from all the others by at least 0.8 Å RMSd (Table 2). The structures were quite evenly distributed in conformation space; sampled conformations were up to 6.2 Å RMSd from rhodopsin's native-state structure.

TABLE 2.

Summary of results using a modified version of the conformation-sampling method of Monge et al. (1994) in conjunction with the pairwise score function

Protein	Number of structures sampled	Maximal RMSd from native of sampled structures (Å)	RMSd of the highest-score conformation from the native-state structure (Å)	Score rank of the native structure	Correlation coefficient (r) of RMSd values versus pairwise scores
Rhodopsin	109	6.2	1.5	2	−0.78
Bacteriorhodopsin	96	4.0	1.9	30	−0.54
Aquaporin-1	26	3.7	0.9	6	−0.63

The three TM proteins that were tested are heterogeneous in terms of functions, structures, and sequences. The anticorrelations obtained in all three cases demonstrate that the pairwise score is capable of ranking conformations according to their similarity to the native-state structure in a variety of cases.

Because the conformation-sampling method usually does not generate conformations that form steric clashes (Monge et al., 1994), we used the pairwise score without the terms that penalize the formation of clashes. We note that in ranking the resultant conformations, the score did not incorporate any terms from the Monge et al. (1994) conformational sampling technique. Strikingly, the native-state structure of rhodopsin ranked second according to the pairwise function (Table 2), demonstrating that short interconnecting loops may indeed be used for identifying near-native conformations, even without the constraints on helix positions and tilts derived from cryo-EM data.

A more stringent criterion, testing the Pearson correlation coefficient between the conformations' scores and their RMSds from the native-state structure, resulted in r = −0.78 (Fig. 4). This high anticorrelation demonstrates that the pairwise score is capable not only of detecting the native-state conformation, but also of discriminating near-native and far-from-native conformations. We also analyzed the performance of this combination of pairwise score and search method on the structures of bacteriorhodopsin and aquaporin-1 (PDB codes 1c3w and 1j4n, respectively). The results are summarized in Table 2. Despite the sequence, structural, and functional heterogeneity of the three proteins, the results for all are encouraging.

FIGURE 4.

A scatter plot showing the RMSd values from the native state (PDB code 1l9h) versus the pairwise score for 109 different template structures of rhodopsin. The two measures are anticorrelated (r = −0.78). The solid line marks the linear regression of the data points. The arrow marks the point of the native state structure.

Deviations from α-helicity have only a local effect on the prediction's quality

Many TM helices exhibit deviations from α-helicity, including π-bulges and kinks. These deviations were shown to have functional importance in some cases (Ubarretxena-Belandia and Engelman, 2001). Kinks are sometimes discernible in cryo-EM maps, e.g., in rhodopsin's 9-Å map (Unger et al., 1997). When observed, the kinks can be incorporated into the conformational search methodology in a straightforward manner, as we have done for rhodopsin above. Recently, it was shown that the positions and directions (though not the magnitudes) of the majority of the kinks observed in high-resolution structures could also be inferred from sequence data alone (Yohannan et al., 2004). However, no computational method is yet available to identify π-bulges.

Fig. 5 shows the consequences of modeling as α-helices domains that contain π-bulges and bent regions in the case of sensory rhodopsin II. As mentioned above, to generate the calculated template (Fig. 5 B), the tilt angles and positions of the helix axes were inferred from the high-resolution structure (PDB code 1jgj), and canonical α-helices were constructed. The singlewise score was then used to rank all the possible orientations of each of the helices, and the best-scoring conformation was selected (Fig. 5 B). Obviously, the prediction's accuracy in the region surrounding the deviations from helicity is relatively low, but is quite high in other regions of the same helices, and in other helices (RMSd of the prediction from the native-state structure is 1.8 Å). Hence, we conclude that the adverse effects of helical deviations on the prediction quality are mostly local.

FIGURE 5.

(A) A view from the extracellular side of the TM domain of sensory rhodopsin II (PDB code 1jgj). The locations of a π-bulge and a kink are marked with arrows. (B) The template of sensory rhodopsin II that was assigned the highest singlewise score. Even though the calculated template shown in panel B is based on canonical α-helices, the deviations from α-helicity have a minor effect on the calculated conformation. Panels A and B are colored according to the evolutionary-conservation scale shown in Fig. 1.

Uncertainties in the TM helix boundaries have a negligible effect on the prediction's accuracy

Even when helix positions and tilts are derived reliably from cryo-EM measurements, different TM boundaries can be fitted into the intermediate-resolution images. Qualitatively, changes at the TM-domain termini are not expected to have very large effects on the prediction's quality according to the scoring schemes suggested here, because the calculations are based on the average properties of relatively long helical stretches (5–6 helical turns).

To examine the implications of erroneous choices of the boundaries, we changed the boundaries of the TM spans in the construction of templates of rhodopsin and reevaluated the prediction. Juxtamembrane regions are often spotted by charged residues. Because the score functions penalize conformations that expose very polar residues to the lipid environment, we tested only helix stretches that are shorter than the TM-domain definitions. Thus, in each iteration, every helix was shortened by variable amounts according to a uniform-probability distribution (0−4 positions). We drew 200 such domain definitions, and used the singlewise score to identify a near-native conformation for each of these definitions according to the method outlined above.

The RMSd values of the highest-scoring conformations to the native-state structure of rhodopsin for this sample were very dense around 3.7 Å, which is the value obtained for the original TM-boundary definition, with a standard deviation of 0.1 Å. This result demonstrates that the score function is indeed minimally sensitive to moderate changes in the hydrophobic boundaries.

DISCUSSION

Structure determination of TM proteins at high resolution remains an intricate task despite recent advances. On the other hand, several TM proteins have been solved at intermediate resolution (5–10 Å). These data have mostly been employed to gain a general understanding of the proteins' architectures, but the positions of individual amino-acid residues could not be inferred (e.g., Holm et al., 2002; Ubarretxena-Belandia et al., 2003)). Hence, it has been impossible to gain a clear view of the molecular determinants affecting protein stability and function from these data. Here, we have explored how TM helices' conservation profiles and hydrophobicity can be used in conjunction with data on helix tilts and positions for structure prediction.

We employed accurate measures of conservation (Pupko et al., 2002) and hydrophobicity (Kessel and Ben-Tal, 2002) in a fully automated method. Such measures have been used previously to predict structures from cryo-EM maps (e.g., Baldwin et al., 1997), but these methods were mostly manual, and often required an alignment of a large number of homologous sequences. Here, we showed that even a relatively small set of sequences (36 in the case of the bacterial rhodopsins) may be sufficient to engender accurate predictions thanks to the more sensitive measures of conservation that are currently available (Pupko et al., 2002).

Importantly, the fact that the methods are automatic provides a more objective and reproducible way of modeling TM domains. In particular, in many cryo-EM maps of TM proteins, the connectivity between helices is not discernible, leading to an ambiguity with regard to the assignment of hydrophobic sequences to the helices seen in the map (e.g., Ubarretxena-Belandia et al., 2003). In principle, there may be up to n! different assignments, where n is the number of helices in the bundle. In practice, many of the assignments may be eliminated at the outset if they imply the connection of distant helices by short loops (Enosh et al., 2004). In some cases, biochemical data may provide sufficient constraints for assignment, e.g., regarding the positions of pore-lining helices (Fleishman et al., 2004). Still, it may be that several contending assignments would need to be carefully considered in view of experimental data (Enosh et al., 2004). The methods we have suggested can be helpful in automatically generating and comparing models for different assignments, in which the combinatorial complexity would preclude manual model building.

Thus, after parameterization using bacteriorhodopsin, we tested and challenged this approach with a variety of different TM-protein structures, including rhodopsin, bacterial rhodopsins, aquaporin 1, and the AchR. We have used several different search methodologies for structure prediction, and all produced relatively promising results. This is encouraging, because it demonstrates that the score functions are robust, in the sense that their outcomes are sound independently of the search method used.

Our study has yielded a number of rules that must be met for the protein under study, if this approach is to succeed. First, the cryo-EM map must show that each helix is neither overly buried in the protein core nor overly exposed to the membrane (or the pore lumen in the case of large channels). Accordingly, it is due to the uncharacteristic exposure of the M4 helix in AchR that its calculated orientation is far from the native state (Fig. 5). Second, the conservation profile of each helix must be sufficiently variable. Helices that are highly conserved throughout (such as M2 of AchR) do not contain a clear enough signal to reveal their orientations. A threshold of sequence variability necessary for accurate predictions is difficult to set a-priori. However, a rule of thumb is that the TM domain should show a helical pattern of variability versus conservation, as seen in most of the cases studied here (e.g., Fig. 4).

Reassuringly, our results on AchR demonstrate, that even in those cases in which a number of helices in the structure cannot be oriented reliably (M2 and M4), the others can still be accurately retrieved (M1 and M3). In the setting of a structure-prediction exercise, it would be possible to determine which helices cannot be oriented reliably on the basis of their conservation profiles and their exposures to the membrane according to intermediate-resolution data.

Our results show that in other cases, the score functions can identify near-native conformations (Figs. 2 and 4; Tables 1 and 2). The fact that the parameterization, which was conducted to reproduce the native structure of bacteriorhodopsin, also retrieved quite closely the native structures of two homologous proteins (sensory rhodopsin II and halorhodopsin) and three very different TM proteins (rhodopsin, aquaporin-1, and AchR) is an indication of the method's predictive ability. The results show that this scoring scheme, though simple, is capable of reliably ranking decoy structures according to their RMSds from the native state (Table 2, Figs. 2–4).

The main focus of this study has been the development of score functions for structure prediction in conjunction with intermediate-resolution cryo-EM maps. However, the results using a conformational search method that takes into account interconnecting loop lengths (Monge et al., 1994) have been encouraging for proteins with small extra-membrane domains. Further research should be devoted to the possibility of predicting the structures of TM domains with short loops even without the constraints imposed by cryo-EM data on helix positions and tilt angles. Furthermore, the results based on rhodopsin's intermediate-resolution structure (Table 2) indicate that a limited exploration of the conformational space defined by the helix positions, tilt, and azimuthal angles may improve structure prediction in cases, in which these parameters cannot be approximated with high confidence from the cryo-EM data. The inclusion of atomistic detail may improve these results further by capturing the subtleties of helix-packing interactions.

It was demonstrated that short sequence motifs could drive the dimerization of TM domains (Lemmon et al., 1992; Javadpour et al., 1999; Russ and Engelman, 1999, 2000; Dawson et al., 2002). For instance, the GxxxG motif, in which two Gly residues are separated by three other residues was shown to induce the close association of two TM helices (MacKenzie et al., 1997). It was also shown that Ala and small polar residues (Ser and Thr) could replace the Gly residues in the motif and induce contact formation (Dawson et al., 2002). We previously used such sequence rules for predicting likely conformations of pairs of TM helices (Fleishman and Ben-Tal, 2002; Fleishman et al., 2002). Here, we did not explicitly utilize information regarding amino-acid packing propensities, because the importance of these residues for packing is reflected in their evolutionary conservation (Sternberg and Gullick, 1989).

We note that the results presented here show that the methods are quite robust in terms of sensitivity to structural or sequence differences. Changes in TM boundaries, for example, did not have a significant effect on the predicted templates of rhodopsin. Some recently solved TM protein structures show helices that are not straight (e.g., Jiang et al., 2002; Miyazawa et al., 2003). In the case of the AchR we used canonical α-helices, even though there are some marked deviations from α-helicity in M2 and M3, yet the predictions did not suffer to any great extent due to these deviations (Fig. 3). Nor have π-bulges and kinks affected the prediction's quality extensively (Fig. 5). Furthermore, although retinal was not modeled in the rhodopsins, the helices' orientations in all cases were reproduced quite accurately. Indeed, explicitly modeling these deviations from α-helicity and the addition of prosthetic groups should improve prediction accuracy. However, from the cases we have examined, we conclude that the strong conservation signal in many TM proteins (exemplified in Fig. 1) ensures that various structural deformations, that might not be accounted for in the cryo-EM data, have mostly a local effect on the accuracy of the prediction, and that this effect is much diminished in unaffected helices.