Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Aug 17;87(5):3536–3546. doi: 10.1529/biophysj.104.044404

Sound-Induced Motions of Individual Cochlear Hair Bundles

A J Aranyosi *,‡, Dennis M Freeman *,†,‡,§
PMCID: PMC1304819  PMID: 15315953

Abstract

We present motions of individual freestanding hair bundles in an isolated cochlea in response to tonal sound stimulation. Motions were measured from images taken by strobing a light source at the tone frequency. The tips and bases of hair bundles moved a comparable amount, but with a phase difference that increased by 180° with frequency, indicating that distributed fluid properties drove hair bundle motion. Hair bundle rotation increased with frequency to a constant value, and underwent >90° of phase change. The frequency at which the phase of rotation relative to deflection of the bundle base was 60° was comparable to the expected best frequency of each hair cell, and varied inversely with the square of bundle height. The sharpness of tuning of individual hair bundles was comparable to that of hair cell receptor potentials at high sound levels. These results indicate that frequency selectivity at high sound levels in this cochlea is purely mechanical, determined by the interaction of hair bundles with the surrounding fluid. The sharper tuning of receptor potentials at lower sound levels is consistent with the presence of a negative damping, but not a negative stiffness, as an active amplifier in hair bundles.

INTRODUCTION

The sharp frequency selectivity of auditory nerve fiber responses to sound is a hallmark of vertebrate cochlear function. This exquisite tuning is determined in large part by the mechanical properties of the cochlea (for review, see Robles and Ruggero, 2001). Although active mechanical amplification as driven by outer hair cell motility (Brownell et al., 1985) clearly plays a key role in cochlear function (Zheng et al., 2000; Liberman et al., 2002), the passive mechanical properties of most cochlear structures are just beginning to be understood.

These properties can be studied more easily in nonmammalian cochleae, where the same mechanical components are present in a simpler context. In this study we describe measurements of mechanical tuning at the level of individual hair bundles in the alligator lizard (Gerrhonotus multicarinatus) cochlea. Like the mammalian cochlea, the alligator lizard cochlea is driven by pressure differences across the basilar membrane (BM). However, the lack of a traveling wave on the alligator lizard BM (Peake and Ling, 1980) means that frequency selectivity in the alligator lizard cochlea is introduced at the individual hair cell (Weiss et al., 1978). This frequency selectivity is quite sharp: both neural responses and hair cell receptor potentials in the alligator lizard have best frequencies ranging from 0.2 to 4.5 kHz and Q10dB values ranging from 0.5 to 5 at the response threshold (Weiss et al., 1976; Holton and Weiss, 1983a,b), although the sharpness of tuning decreases at higher sound levels.

There is increasing consensus that the sharpness of this tuning in nonmammalian vertebrates is increased at low levels by an active mechanism within the hair bundle itself (Crawford and Fettiplace, 1985; Benser et al., 1996; Manley et al., 2001; Martin et al., 2001). However, significant evidence points to the passive mechanical response of the hair bundle as the basis for this tuning. In the freestanding region of the alligator lizard cochlea, which lacks a tectorial membrane, hair bundles are graded in height along the length of the cochlea. The most apical hair bundles in this region are ∼30 μm tall and have best frequencies near 1 kHz, and the most basal hair bundles are ∼12 μm tall and have best frequencies above 4 kHz (Mulroy, 1974; Weiss et al., 1978; Holton and Weiss, 1983b). This correlation of best frequency with hair bundle height has prompted models in which the frequency selectivity seen at the auditory nerve arises from a mechanical resonance between the compliance of the hair bundle and the mass of fluid entrained to move with the bundle (Weiss and Leong, 1985; Freeman and Weiss, 1990a; Shatz, 2000). Other models, however, have suggested that a mechanical resonance of hair bundles is not possible (Billone and Raynor, 1973).

Preliminary measurements have shown that taller hair bundles are deflected more than shorter ones at 1 kHz, and the opposite is true at 4 kHz (Holton and Hudspeth, 1983). In addition, the phase of motion of the tip relative to the base of the bundle increasingly lags with frequency, with taller hair bundles showing more lag at any given frequency (Frishkopf and DeRosier, 1983). Although these measurements are consistent with a mechanical resonance of hair bundles, there are many other possible interpretations.

To determine whether these hair bundles are mechanically resonant, we have made detailed measurements of the motion of freestanding hair bundles as a function of both frequency and bundle height. These measurements provide the most complete understanding of sound-induced motion of hair bundles in any species to date.

METHODS

Biological preparation

Cochleae of adult alligator lizards (G. multicarinatus, 20–49 g) were exposed using a dorsal approach, and lifted out by the eighth nerve using hydraulically-actuated forceps mounted on a micromanipulator. An artificial perilymph (AP) solution bathed the cochlea at all times as it was transferred to a chamber designed to allow simultaneous acoustic stimulation and microscopic imaging of the cochlea. The cochlea was clamped in place between two fluid spaces, similar to its attachment in vivo. An artificial endolymph (AE) solution was then perfused over the apical surface, and the vestibular membrane was removed, exposing the cochlea for imaging. Results are reported for hair bundles from four cochleae.

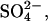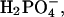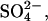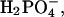Artificial perilymph contained (in mM): Na+, 168; K+, 3; Ca2+, 2; Mg2+, 1.2; Cl−, 174.9; Inline graphic 2; Inline graphic 0.5; D-glucose, 5; Hepes, 5. Artificial endolymph contained (in mM): Na+, 2; K+, 174; Ca2+, 0.02; Cl−, 171.5; Inline graphic 2; Inline graphic 0.5; D-glucose, 5; Hepes, 5. Solutions were adjusted to a pH of 7.30, and had an osmolality of 342 ± 8 mmol/kg. Both solutions contained MEM essential and nonessential amino acids and were oxygenated immediately before use. In some experiments Liebowitz' L-15 was used in place of artificial perilymph. All chemicals were purchased from Sigma Chemical Company (St. Louis, MO).

Experiment chamber

The experiment chamber (Fig. 1) was based on a design initially developed by Quentin Davis (Davis and Freeman, 1995; Davis, 1997). The Plexiglas experiment chamber allowed the cochlea to be clamped over a 0.74 mm hole separating two fluid spaces. The clamping ring was a thin slice of polyetheretherketone (PEEK) tubing (McMaster-Carr, NJ) with a 0.76 mm inner diameter. These dimensions match the size of the bony ring on which the cochlea sits in vivo (Mulroy, 1974; Freeman, 1990). The clamping ring encircled the triangular and neural limbi to avoid direct contact with the basilar membrane or sensory hair cells. Because otoconia from the lagena had a tendency to cover the cochlea and damage the hair bundles if the lagena was compressed, the outer edge of the clamping ring was trimmed by hand to reduce contact with the lagena.

FIGURE 1.

FIGURE 1

Open in a new tab

Schematic drawing of the experiment chamber. The cochlea was held by a clamping ring over a hole separating two fluid spaces. A piezoelectric disk generated pressures in the fluid below the cochlea, and the resulting pressures were sensed with a pressure transducer. To reduce electrical cross talk, the piezoelectric disk was shielded from the electrolytic fluid by a small volume of oil and a thin plastic membrane. The fluids above and below the cochlea could be perfused continuously. The chamber was designed so that both the objective and condenser could be brought into focus on the specimen to provide Köhler illumination (Inoué, 1986). In addition, the inverted v shape underneath the cochlea was designed to allow the widest angles of light coming from the condenser to reach the cochlea without being distorted by the Plexiglas chamber. The dashed circles indicate structures coming out of the plane of view. Some features of this drawing have been exaggerated for visibility.

The clamping ring was glued to a stainless steel tube which was attached on the distal end to a cantilevered piece of shim steel. The shim steel acted as a spring holding the clamp above the hole. A threaded rod with a glued-on nut pushed down on the shim steel when the rod was turned, allowing the clamp to be raised and lowered slowly. The rod contained a 90° bend near the top, creating a lever arm. This lever arm allowed the rod to be turned by hand, so the vertical motion of the clamping ring was ∼1/60th of the motion of the tip of the rod. This reduction in motion allowed the ear to be clamped gently, reducing potentially damaging vibrations.

Computer microvision

To perform the measurements reported in this study, we have developed a novel optical imaging system, which we call Computer Microvision (CMV), which combines the techniques of video microscopy, stroboscopic illumination, and computer vision. The cochlea was viewed through a 63×, 0.9 NA water immersion objective (Zeiss), with a transmitted light condenser with an NA of 0.8. Images were collected with a 12-bit, 1024 × 1024 pixel CCD camera (CAD7-1024A, Dalsa Inc., Waterloo, Ontario). Sound stimuli were generated in the basal fluid with a piezoelectric disk (Panasonic EFR Series) and were calibrated with a hydrophone (Model EPB-126W-100G, Entran Devices, Inc., Fairfield, NJ). Sound stimuli were adjusted to a pressure of 120 dB SPL in fluid, corresponding to 85–100 dB SPL at the tympanic membrane (Rosowski et al., 1985). The specimen was illuminated with an LED that was strobed with a 1/8 duty cycle synchronous with the voltage drive to the sound source. Strobing the LED modulated the high frequency cochlear motions to DC to allow the low noise camera to image the cochlea at any desired phase of motion. Images were taken at each of eight evenly spaced stimulus phases by exposing the camera for many stimulus cycles, with the strobe pulse centered on the desired phase. The resulting images captured the first 3½ harmonics of motion. (The Nyquist sampling theorem specifies that only the cosine phase component of the highest harmonic is captured.) This process was repeated at multiple planes of focus to capture the three-dimensional motion of the cochlea. The order of presentation of different stimulus frequencies was randomized to reduce any confounding effects of time on the measurements.

Motion measurements were made using computer vision algorithms (Davis and Freeman, 1998a,b; Timoner and Freeman, 2001) based on ones originally developed by Horn (Horn, 1986; Horn and Weldon Jr., 1988). Assuming the brightness E(x, y, z, t) of the object being imaged is shift invariant in time and space, then

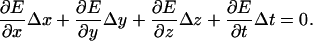graphic file with name M5.gif (1)

When the derivatives are evaluated at a single set of pixels then Eq. 1 is ill posed. If the derivatives are evaluated at each set of pixels within a region, however, the three displacements can be found by minimizing the squared error in the resulting set of equations. Such “optical flow” algorithms are limited primarily by fixed pattern noise in the imaging system and by quantization of gradient estimates, both of which bias the displacement estimate toward zero (Davis and Freeman, 1998b; Timoner and Freeman, 2001; Copeland, 2003). In practice, however, these limits were typically smaller than noise introduced by low-frequency vibrations of the optical table.

System calibration

The CMV system was calibrated by measuring the motion of a piece of scratched Plexiglas simultaneously using both CMV and a laser Doppler velocimeter (OFV 511, Polytec, Waldbronn, Germany). The results, shown in Fig. 2, demonstrate that computer microvision can measure sinusoidal motions accurately for peak displacements as small as 2 nanometers. These displacements correspond to <0.02 pixels in the images. Similar calibrations for three-dimensional measurements yielded a noise floor of 40 nm in the direction of the microscope axis. This noise floor represents a lower limit. The cochlea often exhibited a slow drift in position, and appeared to be more sensitive to external vibrations; these effects caused the effective noise floor to be somewhat higher than the lower limit.

FIGURE 2.

FIGURE 2

Open in a new tab

Calibration of the system against a laser Doppler velocimeter (LDV) in the plane of microscope focus. The target was a piece of scratched Plexiglas glued to the end of a piezoelectric crystal. The microscope was focused on the center of the Plexiglas at the same time that the LDV was aimed at a piece of retroreflective tape on the end of the Plexiglas. Circles show five independent measurements of motion at each of 20 stimulus intensities. The straight line has a slope of one. The maximum error in the CMV measurement is a consistent 5–10% underestimate at larger displacements introduced by the motion measurement algorithm.

For displacements in the range of 0.1–0.5 pixels (19–95 nm), CMV underestimates motion as determined by laser Doppler velocimetry by ∼5–10% due to biases in the brightness gradient estimates used by the motion detection algorithms (Davis and Freeman, 1998a). Since subpixel motions are always within ± 0.5 pixels, the maximum bias in the motion estimates is 5–10%.

Determining hair bundle motions

From the collected images we measured hair bundle motion in all three dimensions. However, images in some focal planes were corrupted by ambient vibrations. Corrupted image sequences could be detected by the presence of a jerkiness to the motion that was not present when viewing the motion directly. The most reliable results came from two-dimensional measurements made from images without any visible corruption. Consequently, the majority of results reported in this study were obtained from two-dimensional motion measurements of vertically oriented bundles. The plane containing the bundle base was identified as the lowest focal plane at which individual stereocilia could be recognized. The plane containing the bundle tip was identified as the highest focal plane at which the stereocilia images had both light and dark contrast edges. Multiple independent measurements of motion were obtained from images at nearby focal planes.

For each hair bundle at each frequency, the displacements dTip(t) of the bundle tip and dRL(t) of the reticular lamina (RL) at the bundle base were measured. Hair bundle deflection was given by dDefl(t) = dRL(t) − dTip(t), and rotation θ(t) was then computed by

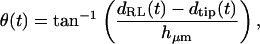graphic file with name M6.gif (2)

where hμm is the height of the hair bundle in micrometers. Tip and RL displacements were defined as positive for deflections toward the neural limbus, and hair bundle deflection was defined as positive away from the neural limbus, so that a positive displacement of the RL relative to the tip resulted in a positive deflection of the hair bundle. Although the orientation of hair bundles changes at the midline of the cochlea, this change was ignored in determining the direction of positive deflection.

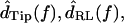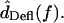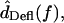Because motions were typically sinusoidal in response to sinusoidal sound stimuli, the fundamental component of the Fourier transform of motion was computed to yield Inline graphic and Inline graphic For Inline graphic the difference between the motion of the RL and tip was computed in the time domain before taking the Fourier transform.

RESULTS

Images of the freestanding region

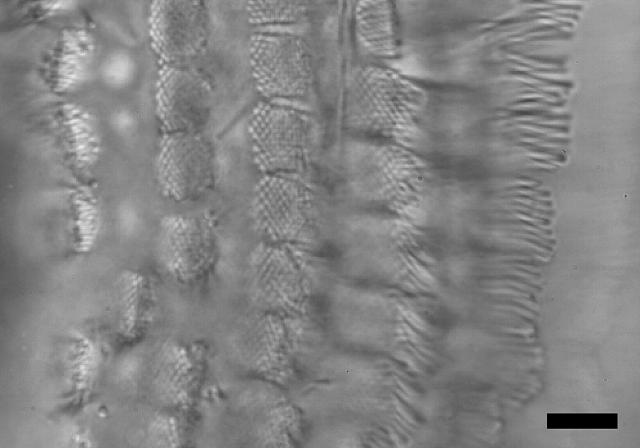
Three-dimensional images of the cochlea in motion were acquired in four preparations. The cochlea was oriented so that the basilar membrane lay in the x, y plane, the excitatory axis of hair bundles lay in the x direction, and the longitudinal axis of the cochlea lay in the y direction. Fig. 3 shows a typical image. The bases and tips of each hair bundle can be clearly seen. In addition, individual stereocilia can be resolved for most hair bundles. As is typical for this region of the alligator lizard cochlea, the hair bundles have no overlying tectorial structure. The tallest row of stereocilia in each bundle is significantly taller than the other rows, with a height varying systematically from >30 μm at the apical end to ∼12 μm at the basal end. Images were acquired at 1 μm spacing throughout the cochlea.

FIGURE 3.

FIGURE 3

Open in a new tab

Image of the freestanding region of the alligator lizard cochlea. This image shows a top-down view as seen through the microscope. The neural edge is to the left, the apical end is toward the top of the image. This image is focused at the level of the hair bundles, which are loosely arranged into five columns. Stereocilia within each bundle are packed in a hexagonal array. Stereocilia pointing upward are visible as light or dark circles. Stereocilia pointing to the side are visible as rods. Scale bar = 10 μm.

Visual examination of hair bundle motion

In all preparations, the motion of the hair bundles and cochlea was examined visually before being measured quantitatively. Visual examination was accomplished by driving the light source with a pulse wave having a 0.125 duty cycle and a frequency 1–3 Hz below that of the sound stimulus. The beating effect generated in this manner slowed the apparent motion of the cochlea. The motion of all structures was smooth and periodic, with a period corresponding to the beat frequency. In the absence of external noise, the motion qualitatively resembled that of structures known to move sinusoidally. No traveling wave was visible on the cochlea, although at frequencies above 4–5 kHz the basal end showed an increase in motion amplitude and a phase lag compared to the apical end.

The motions of the bases and tips of hair bundles were large enough to be visible through the microscope. Stereocilia remained rigid, and deflected about their bases, even at the highest frequencies. Hair bundles moved as a unit in response to sound stimulation; no detectable splaying of the hair bundles could be seen. In all respects, the observed motion agreed qualitatively with the measurements reported in the rest of this study. Animated images of the cochlea moving in response to sound stimulation are included as supplemental material.

Trajectories of motion

Fig. 4 shows typical trajectories of motion for the tip and base of a hair bundle. Both trajectories were nearly elliptical, with motion of the tip more nearly circular than that of the RL. Displacement in the x direction lagged that in the z direction, causing a clockwise trajectory; this lag was greater for dTip(t) than for dRL(t) . In addition, dTip(t) lagged dRL(t) in both directions. The major axes of both ellipses point nearly in the direction of maximum hair bundle excitation (perpendicular to the gray line).

FIGURE 4.

FIGURE 4

Open in a new tab

Trajectories of dTip(t) (+) and dRL(t) (○) of a 24.5 μm tall hair bundle in response to a 1 kHz tone. Symbols denote measured points; the lines connecting them represent a sum of the harmonic components determined from the measurements. The gray line is oriented in the direction of the stereocilia axis, connects the starting points of both trajectories, and has a scaled length of 1 μm. The wavy lines indicate that the trajectories come from locations spaced 24.5 μm apart.

Shear component of motion of a typical hair bundle

Fig. 5 shows the shear component of dTip(t) and dRL(t) of a 22 μm tall hair bundle in response to a tone at 1687 Hz, 120 dB SPL in fluid. The displacements were largely sinusoidal; higher harmonics were more than 20 dB smaller than the fundamental component, and near the noise floor of the measurement system. At this frequency, the tip moved slightly less than the RL and lagged the RL by 57.7°. Hair bundle deflection dDefl(t) was slightly smaller than and led dRL(t) by 56.9°. Hair bundle rotation θ(t) was 0.50° peak. Both dDefl(t) and θ(t) are represented by the same curve in Fig. 5, using two different scales.

FIGURE 5.

FIGURE 5

Open in a new tab

Motion of the tip and RL of a 22-μm tall hair bundle in response to a 1687 Hz, 120 dB SPL stimulus. Symbols denote measured points; the lines connecting these points are the sum of the harmonic components for each set of measurements. The RL moved by 0.21 μm peak. The tip moved 0.19 μm peak, and lagged the RL by 57.7°. The scale on the left applies to plots of dRL(t) and dTip(t) . The third plot shows both dDefl(t) according to the left scale and hair bundle rotation θ(t) according to the right scale, using the small angle approximation to the inverse tangent. θ(t) was 0.50° peak, and led deflection of the RL by 56.9°.

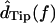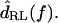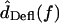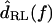The measurements of Fig. 5 were typical in that dTip(t) lagged dRL(t), and dDefl(t) led dRL(t) . The magnitude of the fundamental component of the Fourier transform Inline graphic was typically comparable to or slightly larger than that of Inline graphic The relation between Inline graphic and Inline graphic magnitudes was more dependent on frequency, as is shown below.

Motion of bundle tips

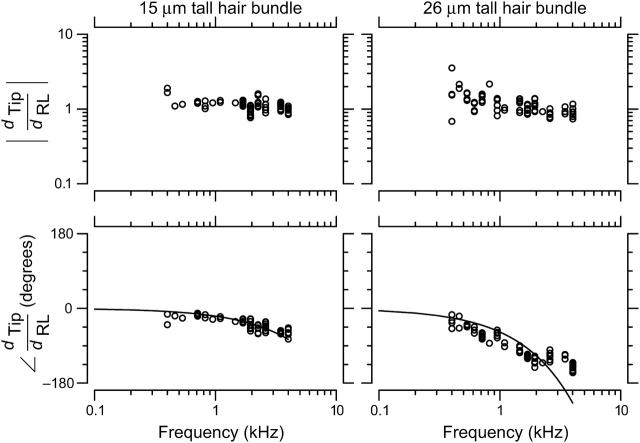
Fig. 6 shows the ratio 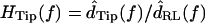Inline graphic as a function of frequency for two hair bundles with heights of 15 and 26 μm, respectively. The magnitude of HTip(f) was typically between 1 and 1.5, and dropped slightly with frequency. At low frequencies, dTip(t) and dRL(t) were nearly in phase. At high frequencies, the phase was near −90° for the shorter bundle, and near −180° for the taller bundle. At any given frequency, the phase lag was larger for the taller hair bundle. The solid lines in the bottom plots show the least squares fit of an ideal time delay to the phase measurements. For the taller bundle, this fit underestimated the phase lag at low frequencies and overestimated the phase lag at high frequencies.

FIGURE 6.

FIGURE 6

Open in a new tab

Magnitude and phase of the ratio HTip(f) of Tip to RL displacement for two hair bundles with heights of 15 μm (left) and 26 μm (right). Circles show individual measurements; at some frequencies, multiple independent measurements were made at each frequency by analyzing motion at different planes. The magnitude of HTip(f) was slightly >1, and nearly constant with frequency. The phase fell from near zero at low frequencies to near −90° for the shorter hair bundle, and near −180° for the taller hair bundle at high frequencies. Solid lines show the least squares fit of an ideal time delay to the phase; the delays were 16 μs and 52 μs for the shorter and taller bundles, respectively. For the taller bundle, the best-fit time delay overestimated the phase lag at low frequencies and underestimated the lag at high frequencies.

The features seen in Fig. 6 were similar for all hair bundles examined. Specifically, the magnitude of HTip(f) showed only a small drop with frequency, and the phase was near zero at low frequencies and decreased with frequency. The phase lag at any given frequency varied with hair bundle height; for the tallest bundles, the lag approached −180° at high frequencies. Fig. 7 plots the magnitude and phase of HTip(f) at 400 Hz and 4 kHz as a function of measured hair bundle height in micrometers hμm. At both low and high frequencies, the magnitude was nearly constant with bundle height. The magnitude was typically slightly >1 at low frequencies, and slightly <1 at high frequencies. The phase of HTip(f) varied significantly with both frequency and bundle height. At 400 Hz, φdeg = (− 1.5 ± 1)hμm + (3 ± 20) (r = −0.38, n = 47), where φdeg is the phase of HTip(f) in degrees and hμm is the hair bundle height in μm. The range of values for the slope and offset indicate the range for which the mean squared error was within 10% of the minimum value. Within this range of error the slope and offset of the fit had a strong inverse correlation; this correlation is true of all of the two parameter fits reported in this study. At 4 kHz, φdeg = (−7.3 ± 2.3)hμm + (46 ± 45) (r = −0.71, n = 72). The range of values are as per the previous fit. The difference in n at the two frequencies represents the difficulty of obtaining accurate measurements at low frequencies.

FIGURE 7.

FIGURE 7

Open in a new tab

Magnitude and phase of HTip(f) at 400 Hz (left) and 4 kHz (right), as a function of hair bundle height hμm. To a first approximation, the magnitude was independent of bundle height at any given frequency; least squares fits are 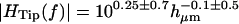Inline graphic at 400 Hz and 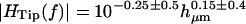Inline graphic at 4 kHz. The magnitude was larger on average at 400 Hz than at 4 kHz. The phase φdeg was linearly dependent on hμm, and was greater at high frequencies than at low frequencies for a given hμm. Least squares fits to the phase data are φdeg = (−1.5 ± 1)hμm + (3 ± 20) (r = −0.38, n = 47) (400 Hz) and φdeg = (−7.3 ± 2.3)hμm + (46 ± 45) (r = −0.71, n = 72) (4 kHz).

Deflection of hair bundles

In contrast to HTip(f), the ratio 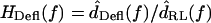Inline graphic had a magnitude that varied with frequency. Fig. 8 plots HDefl(f) versus frequency for the same hair bundles in Fig. 6. At the lowest frequencies, where dTip(t) is nearly in phase with dRL(t), dDefl(t) is dominated by noise. Above these frequencies, several trends are evident. The magnitude of HDefl(f) increased with frequency at low frequencies, and was roughly constant at high frequencies, consistent with the response of a high pass filter. The slope of HDefl(f) magnitude with frequency at low frequencies was steeper for the shorter hair bundle. In addition, the phase of HDefl(f) was positive at all frequencies. This phase lead exceeded 90° at low frequencies. For the taller hair bundle, the phase approached 0° at high frequencies. At all frequencies, the phase was more positive and the magnitude was smaller for the shorter hair bundle.

FIGURE 8.

FIGURE 8

Open in a new tab

Magnitude and phase of HDefl(f) for the two hair bundles of Fig. 6. The magnitude increased with frequency at low frequencies, and was nearly constant at high frequencies. The phase rolled off from >+90° at low frequencies to near 0° at high frequencies. For the shorter hair bundle, the magnitude was smaller and the phase lead was larger at all frequencies.

Dependence of frequency response on bundle height

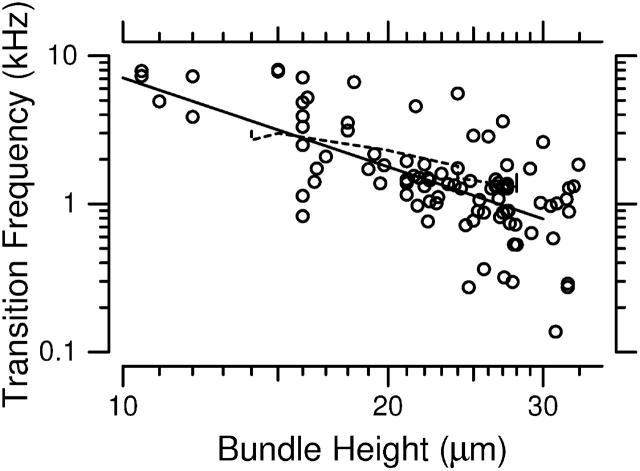
The changes in magnitude of HDefl(f) with frequency were gradual, making it difficult to estimate a single transition frequency from the magnitude measurements. To estimate the dependence of HDefl(f) on bundle height, we determined the frequency fd60 at which the phase of HDefl(f) fell below +60° for each bundle. Fig. 9 A plots fd60 as a function of hair bundle height. In general, fd60 fell with increasing hair bundle height; the exponent of the least squares fit power law was −2.0 ± 0.6, plotted as a solid line in the figure. The figure also plots the height dependence of best frequency of hair cell receptor potentials, by combining a frequency versus position map (Holton and Weiss, 1983b) with a height versus position map (Mulroy, 1974). This curve (dashed line) falls close to the current measurements, with a similar dependence on bundle height.

FIGURE 9.

FIGURE 9

Open in a new tab

(A) Frequency at which the phase of HDefl(f) was +60°, plotted versus bundle height. The solid line is 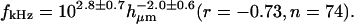Inline graphic The dashed line plots best frequencies of hair cell receptor potentials versus bundle height. (B) Frequency at which the phase of HTip(f) was −60°, plotted versus bundle height. The two lines are repeated from A. (C) Correlation between the two estimates of best frequency; the phase of HDefl(f) is plotted on the horizontal axis. The solid line has a slope of one.

Fig. 9 B plots the frequency at which HTip(f) dropped below −60° as a function of bundle height. The relation between transition frequency and bundle height is similar to that seen in Fig. 9 A. Fig. 9 C plots the two transition frequencies against each other for each hair bundle. The majority of points fall near the line of equality. However, the transition frequency estimated from HTip(f) is a stronger function of bundle height, so the slope of the least squares linear fit to the data in Fig. 9 C is ∼1.4.

Three-dimensional measurements

With the exception of Fig. 4, the results shown thus far are based on a two-dimensional analysis. Such measurements are technically simpler and provide more reliable measurements than three-dimensional analyses, allowing us to compare the motion of many hair bundles at many frequencies in a single preparation. However, such measurements are subject to the criticism that motion orthogonal to the plane of focus may confound the measurement of in-plane motion. To verify the accuracy of our measurements, we measured three-dimensional motions in a smaller number of hair bundles in four different preparations. In these measurements fewer reliable data points were available for each hair bundle, so the estimates of transition frequency are less reliable. Fig. 10 shows the transition frequency determined from these measurements. Although there is more scatter in the measurements, most of the data points fall close to the best fit line from Fig. 9, indicating that the results presented here are comparable for two- and three-dimensional analyses.

FIGURE 10.

FIGURE 10

Open in a new tab

The frequency at which the phase of HDefl(f) was +60°, plotted versus bundle height. These measurements are based on three-dimensional analyses of motion of hair bundles in four preparations. The solid line is repeated from Fig. 9 A. Note that the scale of this plot differs from that of Fig. 9.

DISCUSSION

Limitations of the measurements

The measurement of differential motion of the tip and base of the hair bundle is susceptible to noise, particularly at low frequencies for which both motions are nearly in phase. To obtain reliable measurements of hair bundle deflection it was necessary to use sound pressures at the high end of the physiological range. This limitation makes it extremely difficult to observe hair bundle mechanics at lower sound levels, and impossible to observe any spontaneous oscillations of hair bundles. In addition, the tuning measured at high sound levels in this study may not necessarily reflect the low-level tuning of the cochlea. For this reason we restrict our discussion to high-intensity sound, with the exception of one section that examines how putative active mechanisms might affect the tuning as a function of level.

Because of the time required to obtain these measurements, we were typically able to measure only a single frequency response from each preparation. As a result, it is impossible to determine whether tuning changed with time. However, since the order of frequency presentation was randomized, we can compare responses at two closely-spaced frequencies to estimate the magnitude of any such change. As can be seen in Figs. 6 and 8, the difference in motion at any two closely-spaced frequencies is comparable to or smaller than the variability of responses at any given frequency. For this reason we believe that time-dependent changes in tuning had little effect on the results of this study.

Micromechanical motions were sinusoidal

Visual observations of hair bundle motion showed sinusoidal or nearly sinusoidal motion. These observations were confirmed by the majority of quantitative measurements. Higher harmonics were typically at the noise floor of the measurement system, >20 dB and often >40 dB smaller than the fundamental component of motion. Most exceptions to this rule fell into one of two categories: either the motion was largely sinusoidal with a drift in one direction, or the motion was essentially random. Since our measurement technique involved modulating AC motions down to DC for imaging, slow drift in the setup and low frequency vibrations that were not isolated from the air table can account for both of these exceptions. Such corrupted measurements were clearly identifiable by the fact that they affected entire images, rather than individual hair bundles.

These results show that the mechanical properties of hair bundles at high sound levels do not generate significant harmonic distortion. However, Holton and Weiss (1983b) measured second harmonic components of hair cell receptor potential responses to tones that were as large as 14 dB below the fundamental. Similar distortions have been measured in hair cell responses of mammals (Dallos and Cheatham, 1989), although the distortions of basilar membrane mechanical responses near the best frequency are quite small (Ruggero et al., 1997; Cooper, 1998). The relation between hair bundle deflection and receptor potential is nonlinear in both frogs (Hudspeth and Corey, 1977) and mammals (Russell et al., 1986), which has led to the suggestion that the transduction apparatus is responsible for generating most of the distortion seen in hair cell responses (Dallos and Cheatham, 1989). These results provide additional support for this hypothesis by demonstrating that, at least at high sound levels, hair bundles do not contribute significant mechanical distortion.

Hair bundles are neither velocity nor displacement sensors

In the mammalian cochlea, it has been suggested based on the anatomy of the overlying tectorial membrane that outer hair cells sense RL displacement and inner hair cells are velocity sensors (Dallos et al., 1972). Intracellular recordings from hair cells have borne out this suggestion, at least at low frequencies (Sellick and Russell, 1980; Russell and Sellick, 1983; Dallos, 1985; Cheatham and Dallos, 1998; Cheatham and Dallos, 1999). In the freestanding region of the alligator lizard cochlea, which lacks a tectorial membrane, hair bundles act as neither velocity nor displacement sensors. At the highest frequencies, freestanding hair bundles are nearly displacement sensors, but these frequencies are far above the best frequencies of the bundles. At low frequencies hair bundle deflection leads RL velocity, so the bundles are not velocity sensors. The hair bundles can be considered to sense RL velocity only when the phase of HDefl(f) is near +90°. However, at frequencies corresponding to the peak response in vivo, the phase of HDefl(f) is +60°, suggesting that at their best frequency, freestanding hair bundles sense neither velocity nor displacement of the reticular lamina, but some linear combination of the two.

Hair bundle height determines transition frequency

As shown in Fig. 9, the frequency at which hair bundle deflection leads RL displacement by 60° can be predicted from the height of the hair bundle. The dependence of this frequency on bundle height is comparable to that of receptor potential best frequency. This result provides strong support for the idea that the mechanical properties of individual hair bundles determine the best frequency of the hair cell. With hair bundles ranging in height from ∼12 to 30 μm across the cochlea (Mulroy, 1974), the measurements in Fig. 9 predict best frequencies to range over a factor of 6.25. This result agrees roughly with measured best frequencies from neural recordings, which vary from 1 to 4.5 kHz (Weiss et al., 1976). Thus, variations in the mechanical properties of hair bundles can account for the range of best frequencies seen in this cochlea. These measurements do not imply that hair bundle height is the sole determinant of best frequency; other properties, such as the stiffness of the bundle, may also vary with height to contribute to the observed responses.

Frequency dependence of bundle tip motion demonstrates distributed fluid impedance

The measurements of HTip(f) show 180° of phase roll-off from low to high frequencies. Previous measurements of HTip(f) phase were analyzed on the assumption that this phase represented a second order system (Frishkopf and DeRosier, 1983). Although the magnitude of such a system should fall as the square of frequency when the phase lag becomes large, Fig. 6 shows only a very small change in magnitude at high frequencies, indicating that HTip(f) is not second order. An alternate possibility, that HTip(f) is an ideal time delay, fails to match measurements for tall hair bundles, for which the phase levels off near −180°. A more likely explanation comes from the distributed mechanical properties of the fluid bathing the hair bundles. At low frequencies, fluid viscosity causes the dominant motion of the fluid to be in phase with the motion of the RL (Freeman and Weiss, 1990c), causing HTip(f) to have a magnitude near one and a phase near zero, exerting little torque on the hair bundles. At high frequencies, viscous forces are less important and inertial fluid forces dominate (Freeman and Weiss, 1990b). As a result, the hair bundle pivots about a virtual point near the center of the bundle to minimize the flow of fluid over and around the bundle. This frequency-dependent fluid behavior gives HTip(f) a magnitude that remains nearly constant with frequency although the phase changes by up to 180°. The transition from one regime to the other depends on the mass of fluid moving with the bundle, and thus on bundle height.

Hair bundles are mechanical band pass filters

Unlike the constant magnitude with frequency seen in HTip(f), the transformation from dRL(t) to dDefl(t) in Fig. 8 is high pass, with a phase change >90° and <180°. Since the phase response of at least some hair bundles is not well-fit by a time delay, the hair bundle is most likely a second-order system, or nearly second-order as suggested by a model that accounts for distributed fluid impedance (Freeman and Weiss, 1990a). 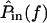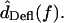To determine how hair bundle mechanical properties affect frequency selectivity in vivo, we must determine the transformation from the input sound pressure Inline graphic to Inline graphic Previous measurements (Peake and Ling, 1980; Rosowski et al., 1985) have shown that between 1 and 4 kHz, 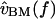Inline graphic is nearly proportional to 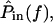Inline graphic with the deviations being introduced by the middle ear. 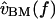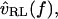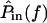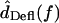In this cochlea Inline graphic is proportional to Inline graphic so the relation between Inline graphic and Inline graphic can be approximated by plotting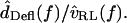 Inline graphic

The resulting transfer function magnitude clearly falls with frequency at high frequencies, but its behavior at low frequencies is less apparent. Since dTip(t) and dRL(t) are nearly in phase at low frequencies, small measurement errors can bias dDefl(t) magnitude to higher values. Thus from magnitude alone we cannot determine whether HDefl(f) is low pass or band pass. However, the phase changes by >90° with frequency, supporting the conclusion that freestanding hair bundles contribute a band pass tuning to measurements of hair cell electrical responses. Since the change in phase with frequency is relatively slow, this system is not highly resonant. The sharpness of tuning is most likely limited by fluid viscosity, in which case measurements made at higher temperatures or with low-viscosity fluids in place of water would reveal sharper tuning and make the band-pass responses more evident.

Mechanical properties account for frequency selectivity in this cochlea

A cascade of macro- and micromechanical systems is responsible for determining the frequency selectivity of hair cells in the freestanding region. The tuning curves of auditory nerve fibers innervating this region of the cochlea have low frequency slopes averaging ∼40 dB/decade, and high frequency slopes averaging from ∼−60 to −80 dB/decade (Weiss et al., 1976). These slopes are similar for hair cell receptor potentials, nearly independent of level (Holton and Weiss, 1983b), and indicate that in a linear approximation, the peripheral auditory pathway of this cochlea behaves as a fifth- or sixth-order system. The outer and middle ears act roughly as a second-order system, imparting a slope of 20 dB/decade below 1 kHz and −20 dB/decade above (Rosowski et al., 1985). The basilar membrane is a low-pass, first- or second-order system that imparts an additional −20 to −40 dB/decade above 2–3 kHz (Peake and Ling, 1980). The left plot of Fig. 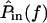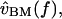11 shows the transformation from Inline graphic to Inline graphic which is broadly tuned and has a shallow high-frequency slope.

FIGURE 11.

FIGURE 11

Open in a new tab

Mechanical cascade of the alligator lizard cochlea at high sound levels. The left plot shows the transformation from sound pressure to basilar membrane velocity, which is broadly tuned in frequency. The right plot shows the transformation from sound pressure to hair bundle deflection for two hair bundles (solid lines), computed by cascading the left plot with the data of Fig. 8, and applying a −20 dB/decade slope to account for the transformation from 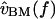Inline graphic to Inline graphic (assuming BM and RL motions are equal in magnitude). The dotted line shows measurements of hair cell receptor potential Vr in response to 85 dB SPL tones (from Holton and Weiss, 1983b).

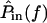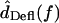The frequency dependence of hair bundle motion contributes a 20–40 dB/decade change in slope with frequency, and up to 180° of phase lag. This frequency dependence is a function of hair bundle height, as shown in Figs. 9 and 10. The right plot of Fig. 11 shows the transformation from Inline graphic to Inline graphic for two hair bundles, computed by combining the left plot with the data of Fig. 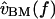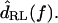8, and applying a slope of −20 dB/decade throughout to convert from Inline graphic to Inline graphic The difference in transition frequency between the two bundles causes the best frequency to differ slightly. The low-frequency slopes are between +20 and +40 dB/decade, comparable to measurements from auditory nerve fibers (Weiss et al., 1976). The high-frequency slopes are near −60 dB/decade, slightly shallower than those of auditory nerve fibers. This plot also shows the receptor potential of a hair cell with a best frequency near 2 kHz in response to 85 dB SPL tones in air (dotted line, from Holton and Weiss, 1983b). The sharpness of tuning of this receptor potential is comparable to that seen in this study, showing that at least at high sound levels, the measured mechanical properties of the cochlea are sufficient to account for hair cell tuning.

Implications for active bundle mechanics

The tuning of hair cell receptor potentials and auditory nerve fiber responses at low sound levels is significantly sharper than the high-level tuning of Fig. 11 (Weiss et al., 1976; Holton and Weiss, 1983a). Although the presence of tectorial structures, such as sallets, can increase the sharpness of tuning of hair cells (Authier and Manley, 1995; Manley, 2000), such a mechanism does not depend on sound level. Some nonlinear and most likely active mechanism must act to increase the sharpness of tuning at lower sound levels. Previous studies of this cochlea have shown that frequency selectivity occurs before mechano-electrical transduction (Weiss et al., 1978), or as a result of bidirectional transduction (Weiss, 1982), indicating that this active mechanism is at least partly mechanical. Measurements from other lizards have also shown that the active mechanism is in the hair bundle rather than the cell soma (Manley et al., 2001). This study has demonstrated directly that frequency selectivity is introduced at the individual hair bundle. Consequently, any active mechanism in this cochlea must interact with the mechanical properties of individual hair bundles.

Recent studies of hair bundles from both the turtle cochlea and the bullfrog sacculus have shown that the hair bundle can exert active movements (Crawford and Fettiplace, 1985; Benser et al., 1996), and that these movements can amplify mechanical stimuli (Martin et al., 2001). Two models for this amplification process have been proposed. In the first, the hair bundle has a position-dependent negative stiffness due to the gating of transduction channels (Martin et al., 2000, 2001). A competing model suggests that negative damping, possibly due to kinociliary motion, is the active process (Camalet et al., 2000). In this study, we have seen that hair bundles act as mechanical filters. Introducing a negative stiffness would reduce the cutoff frequency of these filters, causing the best frequencies of hair cells to be lower at low sound levels. However, the best frequencies measured from hair cell receptor potentials are nearly independent of level, and may even be slightly higher at low sound levels (Holton and Weiss, 1983b). Therefore, as in the mammalian cochlea (Shera, 2001), it is likely that a negative damping rather than a stiffness change constitutes the active mechanical process in this cochlea. Measurements of tuning at lower sound levels, although technically more difficult, might provide further insight into putative active mechanisms in this cochlea.

Implications for mammalian hearing

Since the structures and mechanisms responsible for mechanical tuning in this cochlea are also present in the more complex mammalian cochlea, the results presented here provide insights that are important for understanding the mammalian cochlea as well. For example, hair bundles as close together as 50 μm showed significantly different motions, supporting the idea that longitudinal coupling within the cochlea can be ignored. At high frequencies where the torque on the hair bundle is determined primarily by fluid mass, hair bundles are RL displacement detectors, indicating that the characterization of hair bundles as rotational compliances extends to high frequencies and to sound stimulation. All of the stereocilia within a bundle moved together, indicating that the effective mechanical coupling of hair bundles in response to dynamic stimuli is stronger than the coupling that has been measured from static deflections (Langer et al., 2001). Measurements of HTip(f) show that both viscous and inertial fluid properties play a key role in determining the frequency dependence of motion of cochlear structures. Finally, mechanical tuning at high levels is broad, providing direct support for the idea that an active mechanism at the level of individual hair cells is necessary to counteract fluid damping.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.

Supplementary Material

[supplemental file]
biophysj_87_5_3536__index.html (686B, html)

Acknowledgments

The authors thank Tom Weiss, Quentin Davis, David Mountain, and David Corey for valuable discussions. Chris Shera, Kinuko Masaki, Roozbeh Ghaffari, Aleem Siddiqui, Wendy Gu, Stanley Hong, and Chris Bergevin provided helpful comments on the manuscript.

This research was supported by grant R01-DC00238 from the National Institutes of Health. A.J.A. was supported in part by a training grant from the National Institutes of Health to the Speech and Hearing Biosciences and Technology program in the Harvard-MIT Division of Health Sciences and Technology.

References

  1. Authier, S., and G. A. Manley. 1995. A model of frequency tuning in the basilar papilla of the tokay gecko, gekko gecko. Hear. Res. 82:1–13. [DOI] [PubMed] [Google Scholar]
  2. Benser, M., R. Marquis, and A. Hudspeth. 1996. Rapid, active hair bundle movements in hair cells from the bullfrog's sacculus. J. Neurosci. 16:5629–5643. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Billone, M., and S. Raynor. 1973. Transmission of radial shear forces to cochlear hair cells. J. Acoust. Soc. Am. 54:1143–1156. [DOI] [PubMed] [Google Scholar]
  4. Brownell, W. E., C. R. Bader, D. Bertrand, and Y. de Ribaupierre. 1985. Evoked mechanical responses of isolated cochlear hair cells. Science. 227:194–196. [DOI] [PubMed] [Google Scholar]
  5. Camalet, S., T. Duke, F. Jülicher, and J. Prost. 2000. Auditory sensitivity provided by self-tuned critical oscillations of hair cells. Proc. Natl. Acad. Sci. USA. 97:3183–3188. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Cheatham, M., and P. Dallos. 1998. The level dependence of response phase: observations from cochlear hair cells. J. Acoust. Soc. Am. 104:356–369. [DOI] [PubMed] [Google Scholar]
  7. Cheatham, M., and P. Dallos. 1999. Response phase: a view from the inner hair cell. J. Acoust. Soc. Am. 105:799–810. [DOI] [PubMed] [Google Scholar]
  8. Cooper, N. P. 1998. Harmonic distortion on the basilar membrane in the basal turn of the guinea-pig cochlea. J. Physiol. 509:277–288. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Copeland, A. D. 2003. Robust motion estimation in the presence of fixed pattern noise. Master's thesis, Massachusetts Institute of Technology, Cambridge, MA.
  10. Crawford, A. C., and R. Fettiplace. 1985. The mechanical properties of ciliary bundles of turtle cochlear hair cells. J. Physiol. 364:359–379. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Dallos, P. 1985. Response characteristics of mammalian cochlear hair cells. J. Neurosci. 5:1591–1608. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Dallos, P., M. C. Billone, J. D. Durrant, C. Wang, and S. Raynor. 1972. Cochlear inner and outer hair cells: functional differences. Science. 177:356–358. [DOI] [PubMed] [Google Scholar]
  13. Dallos, P., and M. A. Cheatham. 1989. Nonlinearities in cochlear receptor potentials and their origins. J. Acoust. Soc. Am. 86:1790–1796. [DOI] [PubMed] [Google Scholar]
  14. Davis, C. Q. 1997. Measuring nanometer, three-dimensional motions with light microscopy. PhD thesis, Massachusetts Institute of Technology, Cambridge, MA.
  15. Davis, C. Q., and D. M. Freeman. 1995. Direct observations of sound-induced motions of the reticular lamina, tectorial membrane, hair bundles, and individual stereocilia. In Abstracts of the Eighteenth Midwinter Research Meeting, Association for Research in Otolaryngology, St. Petersburg, FL.
  16. Davis, C. Q., and D. M. Freeman. 1998a. Statistics of subpixel registration algorithms based on spatio-temporal gradients or block matching. Opt. Eng. 37:1290–1298. [Google Scholar]
  17. Davis, C. Q., and D. M. Freeman. 1998b. Using a light microscope to measure motions with nanometer accuracy. Opt. Eng. 37:1299–1304. [Google Scholar]
  18. Freeman, D. M. 1990. Anatomical model of the cochlea of the alligator lizard. Hear. Res. 49:29–38. [DOI] [PubMed] [Google Scholar]
  19. Freeman, D. M., and T. F. Weiss. 1990a. Hydrodynamic analysis of a two-dimensional model for micromechanical resonance of freestanding hair bundles. Hear. Res. 48:37–68. [DOI] [PubMed] [Google Scholar]
  20. Freeman, D. M., and T. F. Weiss. 1990b. Hydrodynamic forces on hair bundles at high frequencies. Hear. Res. 48:31–36. [DOI] [PubMed] [Google Scholar]
  21. Freeman, D. M., and T. F. Weiss. 1990c. Hydrodynamic forces on hair bundles at low frequencies. Hear. Res. 48:17–30. [DOI] [PubMed] [Google Scholar]
  22. Frishkopf, L. S., and D. J. DeRosier. 1983. Mechanical tuning of freestanding stereociliary bundles and frequency analysis in the alligator lizard cochlea. Hear. Res. 12:393–404. [DOI] [PubMed] [Google Scholar]
  23. Holton, T., and A. J. Hudspeth. 1983. A micromechanical contribution to cochlear tuning and tonotopic organization. Science. 222:508–510. [DOI] [PubMed] [Google Scholar]
  24. Holton, T., and T. F. Weiss. 1983a. Frequency selectivity of hair cells and nerve fibers in the alligator lizard cochlea. J. Physiol. 345:241–260. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Holton, T., and T. F. Weiss. 1983b. Receptor potentials of lizard cochlear hair cells with freestanding stereocilia in response to tones. J. Physiol. 345:205–240. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Horn, B. K. P. 1986. Robot Vision. MIT Press, Cambridge, MA.
  27. Horn, B. K. P., and E. J. Weldon, Jr. 1988. Direct methods for recovering motion. Int. J. of Comput. Vision. 2:51–76. [Google Scholar]
  28. Hudspeth, A. J., and D. P. Corey. 1977. Sensitivity, polarity, and conductance change in the response of vertebrate hair cells to controlled mechanical stimuli. Proc. Natl. Acad. Sci. USA. 74:2407–2411. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Inoué, S. 1986. Video Microscopy. Plenum Press, New York.
  30. Langer, M., S. Fink, A. Koitschev, U. Rexhausen, J. Hörber, and J. Ruppersberg. 2001. Lateral mechanical coupling of stereocilia in cochlear hair bundles. Biophys. J. 80:2608–2621. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Liberman, M., J. Gao, D. He, X. Wu, S. Jia, and J. Zuo. 2002. Prestin is required for electromotility of the outer hair cell and for the cochlear amplifier. Nature. 419:300–304. [DOI] [PubMed] [Google Scholar]
  32. Manley, G. A. 2000. Cochlear mechanisms from a phylogenetic viewpoint. Proc. Natl. Acad. Sci. USA. 97:11736–11743. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Manley, G. A., D. L. Kirk, C. Köppl, and G. K. Yates. 2001. In vivo evidence for a cochlear amplifier in the hair-cell bundle of lizards. Proc. Natl. Acad. Sci. USA. 98:2826–2831. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Martin, P., A. J. Hudspeth, and F. Jülicher. 2001. Comparison of a hair bundle's spontaneous oscillations with its response to mechanical stimulation reveals the underlying active process. Proc. Natl. Acad. Sci. USA. 98:14380–14385. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Martin, P., A. D. Mehta, and A. J. Hudspeth. 2000. Negative hair-bundle stiffness betrays a mechanism for mechanical amplification by the hair cell. Proc. Natl. Acad. Sci. USA. 97:12026–12031. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Mulroy, M. J. 1974. Cochlear anatomy of the alligator lizard. Brain Behav. Evol. 10:69–87. [DOI] [PubMed] [Google Scholar]
  37. Peake, W. T., and A. L. Ling, Jr. 1980. Basilar-membrane motion in the alligator lizard: its relation to tonotopic organization and frequency selectivity. J. Acoust. Soc. Am. 67:1736–1745. [DOI] [PubMed] [Google Scholar]
  38. Robles, L., and M. A. Ruggero. 2001. Mechanics of the mammalian cochlea. Physiol. Rev. 81:1305–1352. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Rosowski, J. J., W. T. Peake, T. J. Lynch, R. Leong, and T. F. Weiss. 1985. A model for signal transmission in an ear having hair cells with freestanding stereocilia: II. Macromechanical stage. Hear. Res. 20:139–155. [DOI] [PubMed] [Google Scholar]
  40. Ruggero, M. A., N. C. Rich, A. Recio, S. S. Narayan, and L. Robles. 1997. Basilar-membrane responses to tones at the base of the chinchilla cochlea. J. Acoust. Soc. Am. 101:2151–2163. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Russell, I. J., G. P. Richardson, and M. Kössl. 1986. Mechanosensitivity of mammalian auditory hair cells in vitro. Nature. 321:517–519. [DOI] [PubMed] [Google Scholar]
  42. Russell, I. J., and P. M. Sellick. 1983. Low-frequency characteristics of intracellularly recorded receptor potentials in guinea-pig cochlear hair cells. J. Physiol. 338:179–206. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Sellick, P. M., and I. J. Russell. 1980. The responses of inner hair cells to basilar membrane velocity during low frequency auditory stimulation in the guinea pig cochlea. Hear. Res. 2:439–445. [DOI] [PubMed] [Google Scholar]
  44. Shatz, L. F. 2000. The effect of hair bundle shape on hair bundle hydrodynamics of inner ear hair cells at low and high frequencies. Hear. Res. 141:39–50. [DOI] [PubMed] [Google Scholar]
  45. Shera, C. 2001. Intensity-invariance of fine time structure in basilar-membrane click responses: implications for cochlear mechanics. J. Acoust. Soc. Am. 110:332–348. [DOI] [PubMed] [Google Scholar]
  46. Timoner, S. J., and D. M. Freeman. 2001. Multi-image gradient-based algorithms for motion estimation. Opt. Eng. 40:2003–2016. [Google Scholar]
  47. Weiss, T. F. 1982. Bidirectional transduction in vertebrate hair cells: A mechanism for coupling mechanical and electrical processes. Hear. Res. 7:353–360. [DOI] [PubMed] [Google Scholar]
  48. Weiss, T. F., and R. Leong. 1985. A model for signal transmission in an ear having cells with freestanding stereocilia. III. Micromechanical stage. Hear. Res. 20:157–174. [DOI] [PubMed] [Google Scholar]
  49. Weiss, T. F., M. J. Mulroy, R. G. Turner, and C. L. Pike. 1976. Tuning of single fibers in the cochlear nerve of the alligator lizard: relation to receptor morphology. Brain Res. 115:71–90. [DOI] [PubMed] [Google Scholar]
  50. Weiss, T. F., W. T. Peake, A. Ling, and T. Holton. 1978. Which structures determine frequency selectivity and tonotopic organization of vertebrate cochlear nerve fibers? Evidence from the alligator lizard. In Evoked Electrical Activity in the Auditory Nervous System. R. Naunton and C. Fernandez, editors. Academic Press, New York. 91–112.
  51. Zheng, J., W. Shen, D. He, K. Long, L. Madison, and P. Dallos. 2000. Prestin is the motor protein of cochlear outer hair cells. Nature. 405:149–155. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[supplemental file]
biophysj_87_5_3536__index.html (686B, html)
biophysj_87_5_3536__4000Hz-motion.gif (5.4MB, gif)

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES