Oligomerization of Amyloid Aβ_16–22 Peptides Using Hydrogen Bonds and Hydrophobicity Forces

Abstract

The 16–22 amino-acid fragment of the β-amyloid peptide associated with the Alzheimer's disease, Aβ, is capable of forming amyloid fibrils. Here we study the aggregation mechanism of Aβ_16–22 peptides by unbiased thermodynamic simulations at the atomic level for systems of one, three, and six Aβ_16–22 peptides. We find that the isolated Aβ_16–22 peptide is mainly a random coil in the sense that both the α-helix and β-strand contents are low, whereas the three- and six-chain systems form aggregated structures with a high β-sheet content. Furthermore, in agreement with experiments on Aβ_16–22 fibrils, we find that large parallel β-sheets are unlikely to form. For the six-chain system, the aggregated structures can have many different shapes, but certain particularly stable shapes can be identified.

INTRODUCTION

The fibrillar aggregates that characterize amyloid diseases, such as the Alzheimer's disease, are formed by specific peptides or proteins. However, it is known that several non-disease-related proteins are capable of forming similar amyloid structures (Rochet and Lansbury, 2000; Dobson, 2003), and that the aggregation of such proteins can be cytotoxic (Bucciantini et al., 2002). This suggests, first, that polypeptide chains have a general tendency to form amyloid structures and, second, that natural proteins should have evolved mechanisms to avoid this tendency. Such mechanisms have indeed been proposed (Otzen et al., 2000; Broome and Hecht, 2000; Richardson and Richardson, 2002). The propensity of a given polypeptide chain to form amyloid fibrils depends, nevertheless, on its amino-acid sequence (West et al., 1999; Villegas et al., 2000; Hammarström et al., 2002; López de la Paz et al., 2002; Chiti et al., 2003), and short sequence stretches promoting amyloid formation have been identified (López de la Paz and Serrano, 2004; Ventura et al., 2004).

Although the structure of amyloid fibrils is not known in atomic detail, there is ample evidence from x-ray fiber diffraction studies that the core of the typical amyloid fibril is composed of β-sheets whose strands run perpendicular to the fibril axis (Sunde and Blake, 1997). More detailed information is available, for example, for fibrils made from different fragments of the Alzheimer's Aβ peptide. In particular, there is evidence from solid-state NMR studies for a parallel organization of the β-strands in Aβ_10–35 (Burkoth et al., 2000) and Aβ_1–40 (Petkova et al., 2002) fibrils, and for an antiparallel organization in Aβ_34–42 (Lansbury et al., 1995), Aβ_11–25 (Petkova et al., 2004), and Aβ_16–22 fibrils (Balbach et al., 2000; Gordon et al., 2004). Most of these fragments contain the hydrophobic Aβ_16–20 segment (KLVFF), which is known to be important in the Aβ–Aβ interaction (Tjernberg et al., 1996).

Small peptides like Aβ_16–22 are well suited as model systems for probing the mechanisms of aggregation and fibril formation, and are being studied not only in vitro but also in silico. Computer simulations of simplified (Bratko and Blanch, 2001; Harrison et al., 2001; Dima and Thirumalai, 2002; Jang et al., 2004; Friedel and Shea, 2004) and atomic (Ma and Nussinov, 2002a,b; Klimov and Thirumalai, 2003; Gsponer et al., 2003; Paci et al., 2004) models have provided useful insights into the aggregation behavior of some peptide systems. To properly explore the free-energy landscape of aggregation at the atomic level is, nevertheless, a computational challenge.

Here we investigate the formation and properties of Aβ_16–22 oligomers by unbiased Monte Carlo (MC) simulations of systems with up to six chains, using a sequence-based atomic model with an effective potential based on hydrogen bonds and hydrophobic attraction (no explicit water molecules). The same model has previously been used to study the folding of individual peptides (Irbäck et al., 2003; Irbäck and Sjunnesson, 2004; A. Irbäck and S. Mohanty, unpublished). It was shown that this model is able to fold several different peptides, both α-helical and β-sheet peptides, for one and the same choice of parameters. The calculated melting behaviors were, moreover, in good agreement with experimental data for all these peptides.

MODEL AND METHODS

The main object of study in this article is the peptide Aβ_16–22, given by acetyl-Lys-Leu-Val-Phe-Phe-Ala-Glu-NH₂. We consider systems of one, three, and six Aβ_16–22 peptides. The multichain systems are contained in periodic boxes. All the interactions are short range, which makes the implementation of the periodic boundary conditions straightforward. The box sizes are (35 Å)³ and (44 Å)³ for three and six chains, respectively, corresponding to a constant peptide concentration. For computational efficiency, the peptide concentration is taken to be high.

Our model (Irbäck et al., 2003; Irbäck and Sjunnesson, 2004; A. Irbäck and S. Mohanty, unpublished) contains all atoms of the peptide chains, including hydrogen atoms. The model assumes fixed bond lengths, bond angles, and peptide torsion angles (180°), so that each amino acid only has the Ramachandran torsion angles φ, ψ, and a number of side-chain torsion angles as its degrees of freedom. Numerical values of the geometrical parameters held constant can be found elsewhere (Irbäck et al., 2003).

The interaction potential

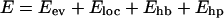(1)

is composed of four terms, which we describe next. Energy parameters are given on a scale (A. Irbäck and S. Mohanty, unpublished) such that a temperature of T = 300 K corresponds to kT ≈ 0.447 (k is Boltzmann's constant).

The first term in Eq. 1, E_ev, represents excluded-volume effects and has the form

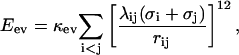(2)

where the summation is over pairs of atoms (i,j), κ_ev = 0.10, and σ_i = 1.77, 1.75, 1.55, 1.42, and 1.00 Å for S, C, N, O, and H atoms, respectively. The parameter λ_ij has the value 0.75 for all pairs except those connected by three covalent bonds, for which λ_ij = 1. When the two atoms belong to different chains, we always use λ_ij = 0.75. To speed up the calculations, Eq. 2 is evaluated using a cutoff of 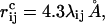and pairs with fixed separation are omitted.

The second energy term, E _loc, is a local intrachain potential. It has the form

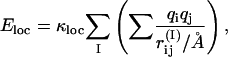(3)

where the inner sum represents the interactions between the partial charges of the backbone NH and C′O groups in one amino acid, I. This potential is not used for Gly and Pro amino acids which have very different φ, ψ distributions, but is the same for all other amino acids. The inner sum has four terms (NC′, NO, HC′, and HO) which depend only on the φ- and ψ-angles for amino acid I. The partial charges are taken as q_i = ±0.20 for H and N and q_i = ±0.42 for C′ and O (Brändén and Tooze, 1991), and we put κ_loc = 100, corresponding to a dielectric constant of ε_r ≈ 2.5.

The third term of the energy function is the hydrogen-bond energy E_hb, which has the form

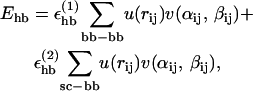(4)

where the two functions u(r) and v(α,β) are given by

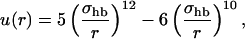(5)

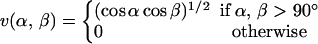(6)

We consider only hydrogen bonds between NH and CO groups, and r_ij denotes the HO distance, α_ij the NHO angle, and β_ij the HOC angle. The parameters 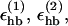and σ_hb are taken as 3.1, 2.0, and 2.0 Å, respectively. The function u(r) is calculated using a cutoff of r^c = 4.5 Å. The first sum in Eq. 4 contains backbone-backbone interactions, whereas the second sum contains interactions between charged side chains (Asp, Glu, Lys, and Arg) and the backbones. For intrachain hydrogen bonds we make two restrictions. First, we disallow backbone NH (C′O) groups to make hydrogen bonds with the two nearest backbone C′O (NH) groups on each side of them. Second, we forbid hydrogen bonds between the side chain of one amino acid with the nearest donor or acceptor on either side of its C_α. For interchain hydrogen bonds, we make no such restrictions. As a simple form of context dependence, we assign a reduced strength to hydrogen bonds involving chain ends, which tend to be exposed to water. Following the experimental studies of the Aβ_16–22 peptide (Balbach et al., 2000; Gordon et al., 2004), we have used acetyl and amide capping groups at the ends. A hydrogen bond involving one or two such groups is reduced in strength by factors of 2 and 4, respectively.

The fourth energy term, E_hp, represents an effective hydrophobic attraction between nonpolar side chains. It has the pairwise additive form

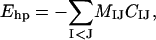(7)

where C_IJ is a measure of the degree of contact between side chains I and J, and M_IJ sets the energy that a pair in full contact gets. The matrix M_IJ is defined in Table 1. To calculate C_IJ we use a predetermined set of atoms, A_I, for each side chain I. We define C_IJ as

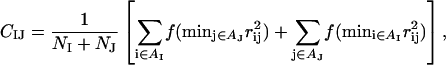(8)

where the function f(x) is given by f(x) = 1 if x < A, f(x) = 0 if x > B, and f(x) = (B–x)/(B–A) if A < x < B [A = (3.5 Å)² and B = (4.5 Å)²]. Roughly speaking, C_IJ is the fraction of atoms in A_I or A_J that are in contact with some atom from the other side chain. For Pro, the set A_I consists of the C_β, C_γ, and C_δ atoms. The definition of A_I for the other hydrophobic side chains has been given elsewhere (Irbäck et al., 2003). For pairs that are nearest or next-nearest neighbors along the same chain, we use a reduced strength for the hydrophobic attraction; M_IJ is reduced by a factor of 2 for next-nearest neighbors, and taken to be 0 for nearest neighbors.

TABLE 1.

The hydrophobicity matrix M_IJ

		I	II	III
I	Ala	0.0	0.1	0.1
II	Ile, Leu, Met, Pro, Val		0.9	2.8
III	Phe, Trp, Tyr			3.2

Hydrophobic amino acids are divided into three categories. The matrix M_IJ represents the size of hydrophobicity interaction when an amino acid of type I is in contact with an amino acid of type J.

To study the thermodynamic behavior of this model, we use simulated tempering (Lyubartsev et al., 1992; Marinari and Parisi, 1992; Irbäck and Potthast, 1995) in which the temperature is a dynamical variable. (For a review of simulated tempering and other generalized-ensemble techniques for protein folding, see Hansmann and Okamoto, 1999.) We study the one- and three-chain systems at eight different temperatures, ranging from 275 K to 369 K, and the six-chain system at seven temperatures, ranging from 287 K to 369 K.

Our simulations are carried out using two different elementary moves for the backbone degrees of freedom: first, the highly nonlocal pivot move in which a single backbone torsion angle is turned; and second, a semilocal method (Favrin et al., 2001) that works with up to eight adjacent backbone degrees of freedom, which are turned in a coordinated manner. Side-chain angles are updated one by one. In addition to these updates, we also use rigid-body translations and rotations of whole chains. Every update involves a Metropolis accept/reject step, thus ensuring detailed balance. All our simulations are started from random configurations. All statistical errors quoted are 1σ errors obtained from the variation between independent runs. We performed nine runs with 10⁸ elementary MC steps for N_c = 1, 11 runs with 10⁹ MC steps for N_c = 3, and 18 runs with 2 × 10⁹ MC steps for N_c = 6. Each of the N_c = 6 runs required ∼12 CPU days on a 1.6-GHz computer.

To characterize the behavior of these systems, we first determine the secondary structure. For a chain with N amino acids, we define the α-helix and β-strand contents as the fractions of the N–2 inner amino acids with their (φ,ψ) pair in the α-helix and β-strand regions of the Ramachandran space. We assume that α-helix corresponds to −90° < φ < −30°, −77° < ψ < −17° and that β-strand corresponds to −150° < φ < −90°, 90° < ψ < 150°. The average α-helix and β-strand contents, over all the chains of the system, are denoted by H and S, respectively.

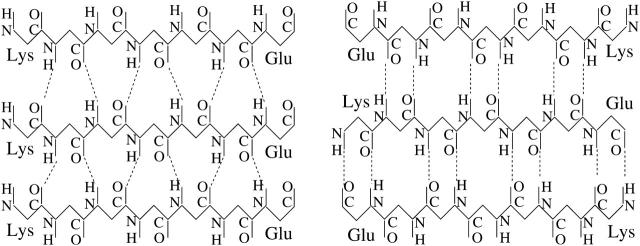
To distinguish between parallel and antiparallel β-sheet structure, we examine the orientation of end-to-end vectors. For a given multichain configuration, we first determine all pairs of chains such that 1), their interchain hydrogen bond energy is 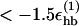(roughly corresponding to 2–3 hydrogen bonds), and 2), both chains have a β-strand content >0.5. For each such pair of chains, we then calculate the scalar product of their normalized end-to-end unit vectors. If this scalar product is >0.7 (<−0.7), we say that the two chains are parallel (antiparallel). We denote the numbers of parallel and antiparallel pairs of chains by n₊ and n₋, respectively. Fig. 1 illustrates the hydrogen-bond patterns in parallel and antiparallel β-sheets.

FIGURE 1.

Schematic illustrations of the hydrogen-bond patterns for in-register, parallel β-strands (left) and in-register, antiparallel β-strands (right).

RESULTS AND DISCUSSION

Using the model described in the previous section, we study the thermodynamics of systems of N_c Aβ_16–22 peptides for N_c = 1, 3, and 6. Fig. 2 illustrates the Monte Carlo evolution in one of 18 independent simulated-tempering runs for the six-chain system. In the course of the run, aggregated low-energy structures form and dissolve several times.

FIGURE 2.

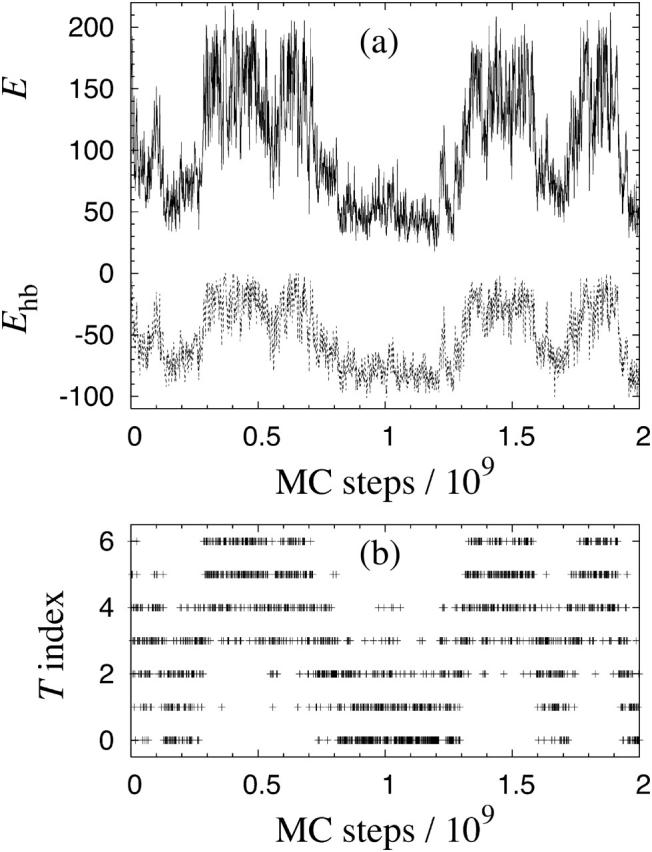
Monte Carlo evolution in a simulated-tempering run for N_c = 6 Aβ_16–22 peptides. (a) The total energy E (solid line) and the hydrogen-bond energy E_hb (dashed line), both in kcal/mol. (b) The temperature index k. There are seven allowed temperatures T_k, satisfying T₀ = 287 K < T₁ < … < T₆ = 369 K. Measurements are taken every 10⁶ MC steps.

Secondary structure

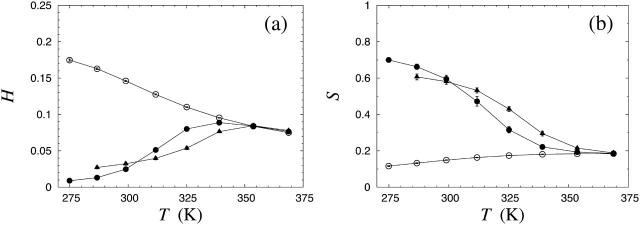
Fig. 3 shows the α-helix and β-strand contents H and S, as defined in the previous section, against temperature for different N_c. For N_c = 1, we see that both H and S are small at all temperatures studied, although H increases with decreasing temperature. So, in our model, the Aβ_16–22 monomer is mainly a random coil throughout this temperature range. The N_c = 3 and N_c = 6 systems show a qualitatively different behavior; S increases sharply with decreasing temperature, to values of S = 0.6 and higher, whereas H is very small. These results clearly demonstrate that unless the temperature is too high, the three- and six-chain systems self-assemble into ordered structures with a high β-strand content.

FIGURE 3.

(a) The α-helix content H against temperature T for Aβ_16–22 for N_c = 1 (○), N_c = 3 (•), and N_c = 6 (▴). Lines joining data points are only a guide for the eye. (b) Same for the β-strand content S; note, however, that the scales in a and b are different.

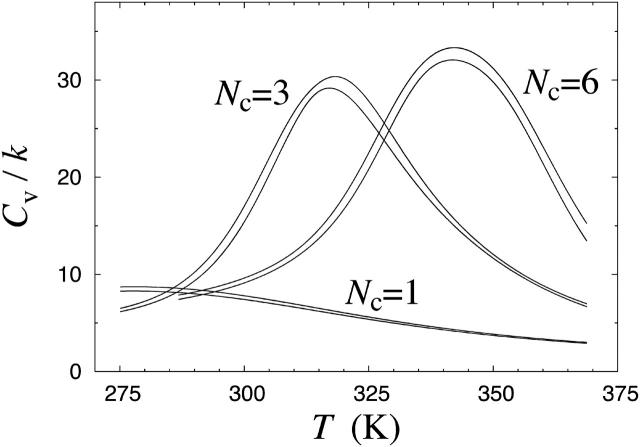
The temperature at which the aggregation sets in depends strongly on the peptide concentration, and exploring that dependence is beyond the scope of the present study. We note, however, that the β-sheet formation sets in at a higher temperature for N_c = 6 than for N_c = 3. This fact is also reflected in the behavior of the specific heat, as shown in Fig. 4. For N_c = 3 and N_c = 6, the specific heat C_v(T) exhibits a pronounced peak. As the system size increases from N_c = 3 to N_c = 6, the peak is shifted toward higher temperature. Near the peak, the energy distribution is broad (data not shown), showing that both aggregated low-energy and unstructured high-energy states occur with a significant frequency at these temperatures.

FIGURE 4.

Specific heat C_v against temperature T for N_c = 1, 3, and 6 Aβ_16–22 peptides, as obtained using histogram reweighting techniques (Ferrenberg and Swendsen, 1988). The bands are centered around the expected values and show statistical 1σ errors. C_v is defined as C_v = (N_cN)⁻¹d〈E〉/dT = (N_cNkT²)⁻¹(〈E²〉–〈E〉²), where N_c is the number of chains, N is the number of amino acids per chain, and 〈O〉 denotes a Boltzmann average of variable O.

Our results for N_c = 1 and N_c = 3 can be compared with results from molecular dynamics simulations with explicit water by Klimov and Thirumalai (2003). Using somewhat different definitions of H and S and a temperature of T = 300 K, these authors found that H = 0.11 and S = 0.33 for N_c = 1, and H = 0.26 and S = 0.30 for N_c = 3. Our N_c = 1 results (see Fig. 3) are in reasonable agreement with theirs, given that we use a stricter definition of β-strands. However, our N_c = 3 results disagree with theirs. They obtained a smaller β-strand content and a larger α-helix content compared to their own N_c = 1 results; whereas we observe a much larger β-strand content for N_c = 3 compared to N_c = 1.

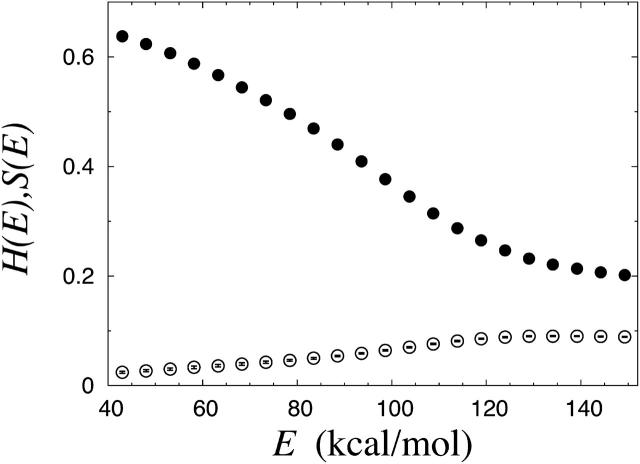
For the N_c = 3 system, Klimov and Thirumalai (2003) furthermore found evidence for an obligatory α-helical intermediate. To see whether or not such an intermediate exists in our model, we divided the energy axis into bins and calculated the average α-helix and β-strand contents for each bin, at a fixed temperature near the specific heat maximum. Fig. 5 shows the resulting α-helix and β-strand profiles H(E) and S(E). We see that the β-strand content S(E) increases steadily with decreasing energy. The α-helix content H(E), on the other hand, has its global maximum at E ∼ 130 kcal/mol. However, the maximum value of H(E) is very small. Hence, we find no sign of an obligatory α-helical intermediate in our model. Most of the amino acids in a typical configuration at intermediate energies are either random coils or β-strands.

FIGURE 5.

The α-helix (○) and β-strand (•) profiles H(E) and S(E) (see the text) for the six-chain Aβ_16–22 system at T = 325 K.

β-strand organization

As mentioned in the Introduction, there exist experimental results (Balbach et al., 2000; Gordon et al., 2004) suggesting that the β-strands in full Aβ_16–22 fibrils have an in-register, antiparallel organization. To find out whether our systems show a preference for either parallel or antiparallel β-sheets, we consider the joint probability distribution P(n₊,n₋), where n₊ and n₋ count the numbers of interacting chain pairs with high β-strand contents that are parallel and antiparallel, respectively (see Model and Methods).

Table 2 shows this distribution for the N_c = 3 system at T = 275 K. For this system, the most probable combination of (n₊,n₋) is (1,1), corresponding to a mixed β-sheet. At the same time, the distribution shows a clear asymmetry. The frequency of occurrence for antiparallel β-sheets with (n₊,n₋) = (0,2) is a factor of 7 higher than that for parallel β-sheets with (n₊,n₋) = (2,0).

TABLE 2.

The probability distribution P(n₊,n₋) for N_c = 3 Aβ_16–22 peptides at T = 275 K (see Model and Methods)

	n−
n+	0	1	2
0	0.17 (2)	0.22 (3)	0.14 (3)
1	0.13 (2)	0.32 (6)
2	0.020 (7)

P(n₊,n₋) values <10⁻³ are omitted. The numbers in parentheses are the statistical errors in the last digits.

The corresponding results for N_c = 6, at T = 287 K, are shown in Table 3. As in the N_c = 3 case, we find that a majority of the configurations contain mixed β-sheet structure, n₊ and n₋ both being nonzero. The asymmetry of the (n₊,n₋) distribution is even more pronounced for N_c = 6 than for N_c = 3. In particular, we see that large n₋ values are much more probable than large n₊ values; the combination (n₊,n₋) = (4,0) is, e.g., very unlikely to occur, whereas (n₊,n₋) = (0,4) does occur with a significant frequency.

TABLE 3.

Same as Table 2 for N_c = 6 Aβ_16–22 peptides at T = 287 K

	n−
n+	0	1	2	3	4
0	0.028 (5)	0.059 (11)	0.08 (2)	0.06 (2)	0.030 (15)
1	0.038 (6)	0.12 (2)	0.16 (3)	0.10 (3)	0.006 (3)

Tables 2 and 3 show the (n₊,n₋) distribution at the lowest temperatures studied. With increasing temperature, the average n₊ and n₋ steadily decrease. At the highest temperature studied, 369 K, ∼99% of the conformations have n₊ = n₋ = 0, for N_c = 3 as well as N_c = 6. The full (n₊,n₋) distribution for both N_c = 3 and N_c = 6 at all the different temperatures studied can be found as Supplementary Material.

Although the statistical uncertainties are somewhat large, the results in Tables 2 and 3 show some clear trends. The most striking one is that large n₊ values are strongly suppressed, which means that large parallel β-sheets are very unlikely to form. The probability of having large antiparallel β-sheets is much higher. Compared to purely antiparallel β-sheet structures, it is possible that mixed β-sheet structures are more difficult to extend to large stable structures. To be able to check whether or not this is the case, simulations of larger systems are required.

Why are antiparallel β-sheets favored over parallel ones? Klimov and Thirumalai (2003) concluded that Aβ_16–22 peptides make antiparallel β-sheets because of Coulomb interactions between charged side chains; the two end side chains of the Aβ_16–22 peptide carry opposite charges, which indeed should make the antiparallel orientation electrostatically favorable. However, our model completely ignores Coulomb interactions between side-chain charges and still strongly favors the antiparallel organization. Other mechanisms than Coulomb interactions between side-chain charges might therefore play a significant role, such as the geometry of backbone-backbone hydrogen bonds (see Fig. 1), steric effects, and the precise distribution of hydrophobicity along the chains. A recent experimental study (Gordon et al., 2004) highlights the importance of the hydrophobicity distribution. This study showed that the β-sheet structure of Aβ_16–22 fibrils can be changed from antiparallel to parallel by adding an octanyl end group to the peptide which increases its amphiphilicity.

To probe the registry of the β-sheets, we monitored backbone-backbone hydrogen bond patterns (see Fig. 1). Fig. 6 illustrates three possible antiparallel registries: 17 + k ↔ 20 − k (Fig. 6 a), 17 + k ↔ 21 − k (Fig. 6 b), and 17 + k ↔ 22 − k (Fig. 6 c). The 17 + k ↔ 21 − k registry is the one found in experiments on Aβ_16–22 fibrils (Balbach et al., 2000; Gordon et al., 2004), whereas experiments on fibrils made from the slightly larger segment Aβ_11–25 found evidence for the 17 + k ↔ 20 − k registry at pH 7.4 and for the 17 + k ↔ 22 − k registry at pH 2.4 (Petkova et al., 2004). In our calculations, the 17 + k ↔ 20 − k and 17 + k ↔ 21 − k registries occur with high and comparable frequencies. The 17 + k ↔ 22 − k registry is, by contrast, strongly suppressed, which probably is due to hydrophobic effects, although steric clashes between the large Phe side chains could play a role, too. As to the 17 + k ↔ 20 − k and 17 + k ↔ 21 − k registries, it would be very interesting to see whether their relative frequencies of occurrence depend on (n₊,n₋), but that will require higher statistics than those provided by the present calculations.

FIGURE 6.

(a–c) Schematic representations of three different registries for an antiparallel pair of Aβ_16–22 peptides.

Other peptides

To test our model, we performed simulations similar to those for the Aβ_16–22 peptide for some other peptides. Some of these peptides, including the polar one studied by Diaz-Avalos et al. (2003), had a low overall hydrophobicity. We found that the propensity to aggregate is much lower for such peptides than for the Aβ_16–22 peptide, and a higher peptide concentration was required to promote aggregation. These results clearly show that in our model, hydrophobic attraction is a major driving force for aggregation.

As an example of a peptide with a significant hydrophobicity but an uneven distribution of it, we studied the peptide acetyl-Lys-Phe-Phe-Ala-Ala-Ala-Glu-NH₂, in which the two strongly hydrophobic Phe amino acids are asymmetrically placed. For this peptide, we obtained aggregated β-sheet structures with a predominantly parallel β-strand organization, which in particular confirms that our model is capable of generating stable parallel β-sheets.

Examples of low-energy structures

It is known that relatively small assemblies formed early in the aggregation of full-length Aβ (Lambert et al., 1998; Walsh et al., 1999, 2002), as well as non-disease-related proteins (Bucciantini et al., 2002), can be toxic—which makes it very interesting to study possible oligomer shapes. In addition, such structures represent potential seeds for the fibril formation.

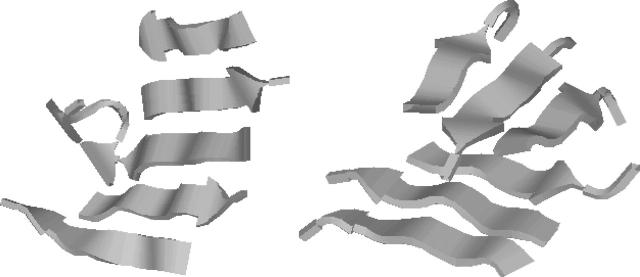
From our simulations, we find that the six-chain Aβ_16–22 system does not exhibit a single dominating free-energy minimum, but rather a number of more or less degenerate local minima. Fig. 7 shows two snapshots of such minima. The β-strand content is, as noted earlier, high, and the structures shown in Fig. 7 illustrate this property.

FIGURE 7.

Two typical low-energy structures from our simulations of six Aβ_16–22 peptides: a five-stranded β-sheet (left), and two three-stranded β-sheets “sandwiching” several of their hydrophobic side chains between them (right). Drawn with RasMol (Sayle and Milner-White, 1995).

In the simplest class of typical structures observed in our simulations, five of the chains form a relatively flat β-sheet, whereas the remaining chain is a random coil and held in contact with the β-sheet by hydrophobic attraction. Six-stranded β-sheets also occur in the simulations, but with a low frequency, as can be seen from the P(n₊,n₋) distribution in Table 3. Further, for the six-chain system, we observe the emergence of new nontrivial structures with no analogs in the three-chain simulations. The second structure in Fig. 7 illustrates this. Here stability is achieved by stacking two different, three-stranded, β-sheets together, which brings hydrophobic side chains from the two β-sheets in close contact. Such “sandwiches” occur with a non-negligible frequency in our simulations. To estimate the precise populations of these minima is difficult. However, five-stranded β-sheets did occur more frequently than sandwiches in the simulations. By visual inspection, we further estimate that of the order of 10% of the configurations are sandwich-like at the lowest temperature studied, at which the snapshots were taken. These low-energy structures also occur at higher temperatures, but become very rare above the specific heat maximum (see Fig. 4).

In none of our simulations did we find any indication of a free-energy minimum in which the β-strands are joined end-to-end to form the so-called β-helix (Wetzel, 2002). In our model, stability is enhanced by increasing the number of hydrogen bonds or by increasing hydrophobic contacts. For system sizes as small as those we examined, the β-helix is inferior to many competing structures in both of these respects, and hence its absence is expected.

CONCLUSION

Using a sequence-based atomic model which was originally developed for folding studies of single peptides (Irbäck et al., 2003; Irbäck and Sjunnesson, 2004; A. Irbäck and S. Mohanty, unpublished), we studied the aggregation properties of Aβ_16–22 peptides. In this model, we found that Aβ_16–22 peptides have a high propensity to self-assemble into aggregated structures with a high β-strand content, whereas the isolated Aβ_16–22 peptide is mainly a random coil. Both parallel and antiparallel arrangements of the β-strands occur in the model, with a definite preference for the antiparallel arrangement.

It is important to note that we find this preference for the antiparallel β-strand orientation despite ignoring the Coulomb interactions between the two charged side chains at the ends of the peptide. It has been suggested (Klimov and Thirumalai, 2003) that such Coulomb interactions are the main determinant for the antiparallel orientation. Although these Coulomb interactions might enhance the tendency for Aβ_16–22 peptides to form β-sheets with an antiparallel organization, our results strongly suggest that other factors play a significant role, too. It is worth noting that the orientation is not necessarily determined solely by sequence-specific side-chain interactions, as antiparallel β-sheets are widely held to be intrinsically more stable than parallel ones. For the Aβ_16–22 peptide, which in particular lacks a clear amphiphilicity, there is no obvious mechanism to overcome this tendency.

In our simulations, we did not observe an absolute free-energy minimum, but rather several nearly degenerate minima corresponding to different supramolecular structures, all consisting of arrangements of β-strands. Apart from single β-sheets, laminated multisheet structures were found near free-energy minima for the six-chain system. It should be pointed out that the six-chain system is still too small to permit the formation of, for example, a barrel-type structure. It will therefore be very interesting to try to extend these calculations to larger system sizes.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.