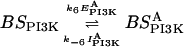Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Oct 1;87(6):3764–3774. doi: 10.1529/biophysj.104.045484

Two Complementary, Local Excitation, Global Inhibition Mechanisms Acting in Parallel Can Explain the Chemoattractant-Induced Regulation of PI(3,4,5)P3 Response in Dictyostelium Cells

Lan Ma *, Chris Janetopoulos †, Liu Yang *, Peter N Devreotes †, Pablo A Iglesias *
PMCID: PMC1304889  PMID: 15465874

Abstract

Chemotaxing cells, such as Dictyostelium and mammalian neutrophils, sense shallow chemoattractant gradients and respond with highly polarized changes in cell morphology and motility. Uniform chemoattractant stimulation induces the transient translocations of several downstream signaling components, including phosphoinositide 3-kinase (PI3K), tensin homology protein (PTEN), and phosphatidylinositol 3,4,5-trisphosphate (PI(3,4,5)P3). In contrast, static spatial chemoattractant gradients elicit the persistent, amplified localization of these molecules. We have proposed a model in which the response to chemoattractant is regulated by a balance of a local excitation and a global inhibition, both of which are controlled by receptor occupancy. This model can account for both the transient and spatial responses to chemoattractants, but alone does not amplify the external gradient. In this article, we develop a model in which parallel local excitation, global inhibition mechanisms control the membrane binding of PI3K and PTEN. Together, the action of these enzymes induces an amplified PI(3,4,5)P3 response that agrees quantitatively with experimentally obtained plekstrin homology-green fluorescent protein distributions in latrunculin-treated cells. We compare the model's performance with that of several mutants in which one or both of the enzymes are disrupted. The model accounts for the observed response to multiple, simultaneous chemoattractant cues and can recreate the cellular response to combinations of temporal and spatial stimuli. Finally, we use the model to predict the response of a cell where only a fraction is stimulated by a saturating dose of chemoattractant.

INTRODUCTION

Chemotaxis, the directed movement of cells toward chemoattractant or away from chemorepellent, is crucial for many biological processes such as inflammation (Lloyd, 2002), lymphocyte trafficking (Moser and Loetscher, 2001), axon guidance (Dickson, 2002) and yeast mating (Schrick et al., 1997). To move chemotactically, cells must perform and coordinate three basic physiological responses: directional sensing, polarization, and movement. Cells must first sense and interpret the extracellular chemoattractant field. Cells must then assume an asymmetric shape with well-defined anterior and posterior regions. They must then move in the direction of the spatial cue. To understand chemotaxis fully requires an understanding of the interactions among these three processes. However, each must first be understood individually. In this article, we focus on the first step, directional sensing, which can be observed in unpolarized immobilized cells by the translocation of proteins in the cell in response to chemoattractant stimulus. To this effect, we develop a computational model that can explain the temporal and spatial regulation of directional sensing in Dictyostelium discoideum cells.

During directional gradient sensing, eukaryotic cells such as Dictyostelium and neutrophils exhibit extraordinary sensitivity to external chemical gradients. By monitoring the translocation of green fluorescent protein (GFP)-tagged plekstrin homology (PH) domains, which bind to phosphatidylinositol 3,4,5-trisphosphate (PI(3,4,5)P3), as well as the enzymes that regulate PI(3,4,5)P3 production, it has been shown that signaling components are sharply localized at the leading edge when the chemoattractant concentration across the cell length can differ by as little as 5% (Parent and Devreotes, 1999; Servant et al., 2000; Chung et al., 2001; Dormann et al., 2002). This indicates that the intracellular signal transduction pathway can amplify a shallow signaling input into a much steeper internal response. Moreover, cells treated with inhibitors of actin polymerization, which removes polarization and immobilizes them, still show amplified responses, though the amplification is smaller than in polarized cells (Parent et al., 1998; Servant et al., 2000; Janetopoulos et al., 2004).

Because the upstream signaling components and biochemical reactions, such as receptor occupancy, G-protein subunits, and G-protein activation, are uniformly distributed along the perimeter of a cell during directional sensing, the response must become highly localized in events between the G-protein and PI(3,4,5)P3 (Xiao et al., 1997; Servant et al., 1999; Jin et al., 2000; Janetopoulos et al., 2001; Ueda et al., 2001). The complementary regulation of two classes of enzymes that govern the metabolism of PI(3,4,5)P3, the phosphoinositide 3-kinase (PI3K) and tensin homology protein (PTEN), likely play a role in this amplification (Funamoto et al., 2002; Iijima and Devreotes, 2002; Huang et al., 2003; Janetopoulos et al., 2004). Upon uniform cAMP stimulation, PI3K rapidly translocates from the cytosol to the plasma membrane and then dissociates with kinetics similar to those of PH-domain containing proteins. In contrast, PTEN, which is initially localized to the plasma membrane, dissociates transiently to the cytosol and returns to its original configuration within a few minutes. When a cell is exposed to a cAMP gradient, PI3K localizes to the front membrane whereas PTEN localizes to the rear sides and posterior membrane. Proper balance between the PI3Ks and PTEN is critical for local accumulation of PI(3,4,5)P3 as well as further signaling events that lead to pseudopodia production (Funamoto et al., 2002; Iijima and Devreotes, 2002). The receptor regulation of these enzyme movements occurs in both polarized and unpolarized cells, though they are not as dynamic in polarized cells (Janetopoulos et al., 2004).

Recent experimental quantification of the external chemoattractant gradient and the internal localized response provides a means for designing and validating mathematical models (Janetopoulos et al., 2004). Direct measurements of the gradient of the fluorescent Cy3-cAMP, and a readout of the binding of PH-GFP, PI3K-GFP, and PTEN-GFP to the cell membrane, have shed light on the amount of amplification between stimulus and response during gradient sensing. These experiments provide a means for quantitatively testing the predictive nature of a number of gradient sensing models. We propose a model that accounts for the observed transient localization of PI3K and PTEN during persistent homogeneous chemoattractant stimulation. The complementary regulation of PI3K and PTEN explains the observed amplification of membrane lipid PI(3,4,5)P3 in immobilized cells in a chemotactic gradient. Using this model, we duplicate the observed response of several mutants. Moreover, we predict the cellular response to several complex combinations of temporal and spatial stimuli.

MATERIALS AND METHODS

Model

The core of our model is a pair of local excitation, global inhibition (LEGI) response regulators (Fig. 1 A). In the LEGI model, the response to a stimulus is mediated through the balance between a fast, local excitation and a slower, global inhibition process, both of which are controlled by receptor occupancy (Parent and Devreotes, 1999; Levchenko and Iglesias, 2002; Krishnan and Iglesias, 2003; Kutscher et al., 2004). When stimulated by uniform concentration of chemoattractant, the faster local excitation rises with receptor occupancy, leading to an increase in the response. As the slower inhibition rises, the response subsides, ensuring perfect adaptation. When in a gradient, local excitation mirrors receptor occupancy, and hence, chemoattractant concentration gradients. The inhibition process integrates the global signal, leading to an inhibitory signal that is equivalent to the average level of receptor occupancy in the cell. Thus, a surplus of excitation over inhibition gives rise to a persistent response at the front of the cell; at the rear, inhibition exceeds excitation and there is a persistent depression from basal levels. As shown mathematically, the LEGI model can account for both perfect adaptation and, qualitatively, for the static spatial sensing observed in Dictyostelium cells (Levchenko and Iglesias, 2002). However, the basic regulator does not amplify external gradients.

FIGURE 1.

FIGURE 1

Open in a new tab

Model for regulation of PI(3,4,5)P3 through complementary local excitation, global inhibition (LEGI) response regulators. (A) Receptor occupancy regulates two LEGI mechanisms working in parallel. In LEGI-PI3K, the excitation process activates more binding sites for PI3K (BSPI3K→BS*PI3K), whereas in LEGI-PTEN, excitation destroys binding sites (BS*PTEN→BSPTEN). Binding and activation of the enzymes follows the spatial distribution of the binding sites. Together, the two enzymes enhance the spatial resolution of PI(3,4,5)P3 by increasing phosphorylation of PI(4,5)P2 (by activated PI3K) and decreasing dephosphorylation of PI(3,4,5)P3 (by activated PTEN) at the front. (B) Virtual Cell implementation of the model. Each species, together with its localization, is represented by the dark shaded circle. The solid lines indicate the inputs and outputs of the reactions, represented by the light shaded ovals. Catalytic activities are represented by dashed lines. Concentrations for all species are given in Table 1. Kinetic coefficients for the reactions are found in Table 2.

In the model described here, two LEGI mechanisms, acting independently in parallel, induce the complementary regulation of membrane binding/activation sites for PI3K and PTEN upon chemoattractant stimulation. Each regulator controls the number of membrane binding sites that allow for enzyme association and activation on the membrane of PI3K and PTEN, respectively. The two enzymes then catalyze the conversion between phosphatidylinositol 4,5-bisphosphate (PI(4,5)P2) and PI(3,4,5)P3.

The first LEGI mechanism generates PI3K binding sites on the membrane as described in Huang et al. (2003). The molecule responsible for fast excitation (EPI3K) is confined to the membrane, whereas the slower inhibitory molecule (IPI3K) is allowed to diffuse freely in the cytoplasm. This mechanism results in a transient increase of PI3K binding sites in response to uniform stimulus, and an accumulation of PI3K binding sites on the side of the cell facing the chemoattractant gradient. Images of fluorescently tagged PI3K distribution show that the PI3K gradient at the leading edge is slightly sharper than the external cAMP gradient (Funamoto et al., 2002; Janetopoulos et al., 2004). To account for this, we assume that the reaction dynamics governing the activation of the PI3K binding sites follows Michaelis-Menten kinetics with a Hill coefficient of 2. This limited positive cooperativity is used in our model to generate the initial amplification observed in PI3K binding (see supplementary material).

PTEN binding sites are controlled by a second LEGI mechanism using separate excitation (EPTEN) and inhibition (IPTEN) molecules (Fig. 1 A). In this case, however, the response regulator destroys active binding sites. This results in a transient depletion of membrane binding sites for PTEN under uniform stimulation and a localization of binding sites for PTEN at the posterior membrane under graded inputs. Our earlier findings (Janetopoulos et al., 2004) indicate that PTEN and cAMP concentrations are inversely correlated, and thus we have assigned a linear inhibition of PTEN binding sites.

Our model structure assumes no cross talk between the two channels of binding/activation of PI3K and PTEN. Biochemically, it has been shown that PI3K activation is independent of PTEN (Huang et al., 2003). The regulation of PTEN binding is also independent of PI3K and PI(3,4,5)P3 levels (Iijima et al., 2004).

Specifications and conditions of the model

  1. The model is implemented using the Virtual Cell modeling environment (Loew and Schaff, 2001), available at http://www.nrcam.uchc.edu/applications/applications.html, on a circular disc representing a cell of diameter 14 μm placed in a two-dimensional environment (22–30 μm squares) in which no-flux boundary conditions are imposed. A schematic of the reaction network from Virtual Cell is shown in Fig. 1 B. A listing of all elements in the model, specifying their initial concentrations and cellular localization, is found in Table 1. The model reactions and rate constants used are shown in Table 2.

  2. The two global inhibitors in the LEGI mechanisms (IPI3K, IPTEN), as well as the unbound PI3K and PTEN, are allowed to diffuse in the cytoplasm. Their diffusion coefficients are taken to be in the order of 50 μm2s−1, the observed value of free cytosolic proteins (Potma et al., 2001; Ruchira et al., 2004). All other elements are assumed to be immobile and located at the membrane. Lipid diffusion would have a small, blurring effect on the spatial profiles observed here (Krishnan and Iglesias, 2004); however, it is known that the dispersion of PI(3,4,5)P3 is small relative to other signaling components (Postma et al., 2004a).

  3. Since most of the reaction rates are unknown, the values used are determined by fitting data from experimentally observed PI3K, PTEN, and PH-GFP localization under homogeneous stimulation.

  4. Studies indicate that in unstimulated cells, the plasma-membrane concentration of PI(4,5)P2 is significantly higher than that of PI(3,4,5)P3 and remains at a high level during activation of G-protein-mediated signaling pathways and chemotaxis (Stephens et al., 1993). In our model, we assume an initial concentration of PI(4,5)P2 that is 500–1000 times higher than that of PI(3,4,5)P3.

TABLE 1.

Virtual Cell model variables

Parameter Description Location Initial conditions Units Diffusion coefficient
L_source Micropipette cAMP source Extracellular Variable μM
L Diffusible extracellular cAMP Extracellular Variable μM 300 μm2/s
R cAMP receptor density Membrane 70 No./μm2
S Receptor occupancy Membrane 0 No./μm2
E_pten Nonactivated PTEN excitation Membrane 100 No./μm2
EA_pten Activated PTEN excitation Membrane 0 No./μm2
E_pi3k Nonactivated PI3K excitation Membrane 100 No./μm2
EA_pi3k Activated PI3K excitation Membrane 0 No./μm2
I_pten Nonactivated PTEN inhibitor Intracellular 0.1 μM 50 μm2/s
IA_pten Activated PTEN exciter Intracellular 0 μM 50 μm2/s
I_pi3k Nonactivated PI3K inhibitor Intracellular 0.1 μM 50 μm2/s
IA_pi3k Activated PI3K inhibitor Intracellular 0 μM 50 μm2/s
BS_pten Nonactivated PTEN binding site Membrane 100 No./μm2
BSA_pten Activated PTEN binding site Membrane 0 No./μm2
BS_pi3k Nonactivated PI3K binding site Membrane 100 No./μm2
BSA_pi3k Activated PI3K binding site Membrane 0 No./μm2
PTENA Activated PTEN Membrane 0 No./μm2
PI3KA Activated PI3K Membrane 0 No./μm2
PTEN Free diffusible PTEN Intracellular 0.1 μM 10 μm2/s
PI3K Free diffusible PI3K Intracellular 0.1 μM 5 μm2/s
PIP2 PI(4,5)P2 Membrane 1000 No./μm2
PIP3 PI(3,4,5)P3 Membrane 1 No./μm2
Open in a new tab

TABLE 2.

Reactions and kinetic constants

Reactions Rate constants
graphic file with name M1.gif
 k0 = 15.6 μM−1 s−1
k−0 = 0.39 s−1
graphic file with name M2.gif
 k1 = 5e-5 (No./μm2)−1 s−1
k−1 = 0.05 s−1
graphic file with name M3.gif
 k2 = 2e-6 (No./μm2)−1 s−1
k−2 = 2 s−1
graphic file with name M4.gif
 k3 = 0.03 (No./μm2)−1 s−1
k−3 = 30 s−1
graphic file with name M5.gif
 k4 = 8e-4 (No./μm2)−1 s−1
k−4 = 80 s−1
graphic file with name M6.gif
 k5 = 1 nM−1 s−1
k−5 = 8 (No./μm2)−1 s−1
graphic file with name M7.gif
 k6 = 1 (No./μm2)−1 s−1
k−6 = 1 nM−1 s−1
graphic file with name M8.gif
 k7 = 1 μM−1 s−1
k−7 = 1 s−1
graphic file with name M9.gif
 k8 = 1 μM−1 s−1
k−8 = 1 s−1
graphic file with name M10.gif
 k9 = 0.01 (No./μm2)−1 s−1
k−9 = 10 (No./μm2)−1 s−1
Open in a new tab

RESULTS

Temporal regulation

Using our default parameter values, listed in Table 1, we simulated the response of a cell exposed to a homogeneous, constant external 1 μM cAMP dose. The simulation shows a rapid, fivefold increase in the concentration of membrane-bound PI3K. Within 25 s, 90% of the increase in membrane-bound PI3K returns to the cytosol, demonstrating the adaptation property of the LEGI mechanism. With slightly slower kinetics, membrane-bound PTEN moves to the cytosol. At its lowest concentration, ∼20% of basal membrane-bound PTEN remains. After 80 s, 90% of this PTEN returns to the membrane. For both enzymes, the membrane localization mirrors closely the existence of binding sites on the membrane, owing to the high KD and fast off-rate chosen for these binding events. The complementary behavior of membrane binding mirrors the transient localization of PI3K-GFP and PTEN-GFP observed experimentally in response to uniform cAMP (Funamoto et al., 2002; Iijima and Devreotes, 2002; Huang et al., 2003). In response to this complementary regulation, PI(3,4,5)P3 accumulation exhibits a sharper, 10-fold transient increase from basal level (Fig. 2 B). Within 50 s, PI(3,4,5)P3 had returned to within 10% of the basal level. These simulations were repeated using different parameter values. Though the results varied quantitatively (not shown), in all cases the complementary regulation of the enzymes elicits greater peak PI(3,4,5)P3 responses.

FIGURE 2.

FIGURE 2

Open in a new tab

Temporal responses of the model to uniform changes in chemoattractant. (A) Membrane localization of PI3K and PTEN elicited by a uniform increase in cAMP concentration from 1 nM to 1 μM. Both PI3K and PTEN concentrations have been normalized by their respective basal levels. (B) Corresponding membrane accumulation of PI(3,4,5)P3 for wild-type cells, as well as cells in which either only 10% of PI3K or PTEN is available, to a change in cAMP concentration from 1 nM to 1 μM. Data have been normalized to wild-type 1 nM steady-state response. (C) PI(3,4,5)P3 accumulation in wild-type cells is also compared with cells in which enzymes levels are simultaneously reduced as in B, or increased to 200% of wild-type levels. Data are normalized as in B.

To compare the transient regulation of PI(3,4,5)P3 between wild-type cells and known mutants, we simulated the response of cells in which one or both of the enzymes have been impaired. Dictyostelium cells in which two of the known PI3Ks have been disrupted show a decrease in PH domains recruited to the membrane and accumulating at the leading edge of cells in a gradient (Funamoto et al., 2001; Huang et al., 2003). To account for this partial impairment of PI3K, we remove 90% of the available PI3K in the model; the remaining 10% is regulated by the LEGI mechanism as in the simulations of wild-type cells. In Dictyostelium cells lacking PTEN, PI(3,4,5)P3 is removed by other lipid-degrading enzymes (Iijima and Devreotes, 2002). To account for this, we fixed a residual phosphatase activity at a fraction (10%) of basal level. In the simulated time course, PI(3,4,5)P3 accumulation in PTEN-deficient cells is higher, whereas that of PI3K-deficient cells is significantly lower, than for wild-type cells (Fig. 2 B). The time courses of these temporal simulations are consistent with observations from recent experiments (Iijima and Devreotes, 2002). Wild-type cells are also compared to cells in which the available PI3K and PTEN are simultaneously decreased or increased (Fig. 2 C). When both enzymes were reduced simultaneously, the peak and basal levels were lower than in the wild-type cells. In contrast, when both enzymes were overexpressed, the time course was similar to the wild-type cells.

Spatial regulation

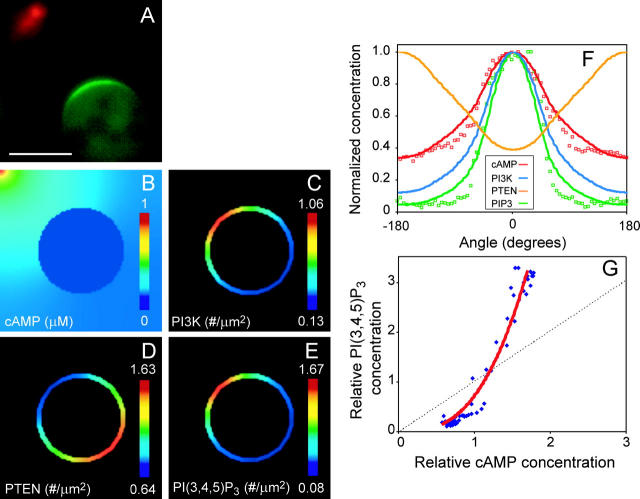
A cell's ability to detect static spatial gradients can be observed experimentally by exposing Dictyostelium cells treated with latrunculin, an inhibitor of actin polymerization, to a micropipette containing cAMP (Parent and Devreotes, 1999). Recent quantitative analysis of a series of these micropipette-assay experiments has made it possible to validate our model (Fig. 3 A and Janetopoulos et al., 2004). Spatial sensing is simulated by placing a circular cell of diameter 14 μm at the center of a 26 × 26 μm environment where a source with 1 μM cAMP is introduced in one corner. The cAMP diffuses away from the source and creates a concentration gradient around the cell perimeter (Fig. 3 B). A representative simulation result of membrane-associated PTEN, PI3K, and PI(3,4,5)P3 illustrates that, at steady state, PI3K and PI(3,4,5)P3 accumulate at the front, whereas PTEN localizes at the rear in response to the cAMP gradient (Fig. 3, C–E). To compare the gradient of different components along the cell periphery, intensities of PTEN, PI3K, and PI(3,4,5)P3, normalized to their maximum values, are plotted in polar coordinates and compared with experimentally obtained fluorescent levels (Fig. 3 F). In this simulation, the shallow external cAMP gradient gives rise to a slightly amplified membrane-bound PI3K gradient. Membrane-bound PTEN, on the other hand, is inversely distributed on the membrane, away from the micropipette. This complementary regulation elicits a sharp PI(3,4,5)P3 gradient. Qualitatively, the model demonstrates the membrane distribution of PTEN, PI3K, and PI(3,4,5)P3 observed in previous experiments (Funamoto et al., 2002; Iijima and Devreotes, 2002; Huang et al., 2003).

FIGURE 3.

FIGURE 3

Open in a new tab

Comparison of model with experiments for cells that are sensing spatial gradients. (A) A micropipette containing Cy3-cAMP (red) is placed near a latrunculin-treated Dictyostelium cell expressing PH-GFP. The PH-GFP translocates selectively toward the membrane closest to the pipette. White bar is 10 μm. (B–E) Virtual Cell simulation of this experiment, in which a two-dimensional spherical cell 14 μm in diameter is placed near a pipette at the top left corner of the 26 μm × 26 μm environment. Shown are the spatial distributions of cAMP outside the cell, as well as PI3K, PTEN, and PI(3,4,5)P3 on the cell membrane. The degree of spatial amplification of PTEN is the lowest, whereas that of PI(3,4,5)P3 is the highest. (F) Spatial amplification can be seen by plotting the intensity levels as a function of angle along the membrane. The “zero” angle is chosen to point toward the micropipette. Shown are both the experimental intensities for the cell in A (small red circles for cy3-cAMP, small green squares for PH-GFP), as well as simulation values (red, cAMP; green, PI(3,4,5)P3; blue, PI3K; orange, PTEN). All data sets have been normalized to their respective maxima. Experimental data was quantified as in Janetopoulos et al. (2004). (G) The degree of amplification can be observed by plotting the signal levels relative to their average values along the cell membrane. The dotted line shows the response one would expect if there were no amplification. The experimental data, from F, is shown in the blue dots. The red line shows the simulation data.

To verify our model quantitatively, we compare experimental and simulated data. We normalize both measured and calculated cAMP and PI(3,4,5)P3 concentrations by their respective average concentrations over the membrane, and plot the normalized response of PI(3,4,5)P3 against that of cAMP (Fig. 3 G). Experimentally, these data are highly reproducible between cells and in different chemoattractant gradients (Janetopoulos et al., 2004). The simulation results show strong agreement with the experimental data in latrunculin-treated cells. Taking this input-output response as an important quantitative characteristic of this signaling system, we find that our model can explain the amplification observed in latrunculin-treated cells. Similar comparisons with measured PI3K and PTEN intensities also agree with our earlier experimental results (data not shown).

To determine how the shape and size of the cAMP gradient affects the PI(3,4,5)P3 concentration profile, we simulated various situations in which either the position or the cAMP concentration of the micropipette is varied (Fig. 4 A), and monitor PI(3,4,5)P3 distribution along the membrane (Fig. 4 B). These simulations show that the shape of the PI(3,4,5)P3 response is affected both by the shape of the cAMP gradient as well as its midpoint concentration. Thus, two gradients having the same shape can elicit vastly different responses. For example, the cells in b and c have cAMP profiles with approximately the same shape and absolute gradient (the difference in concentrations between the maximum and minimum in Fig. 4 A). However, the cell in c has a higher response (Fig. 4 B) because the mean (global) level of chemoattractant is higher. Similarly, the cell in a has a large absolute cAMP gradient but the PI(3,4,5)P3 response is relatively muted because the mean level of cAMP is also very high. In the LEGI mechanism, the response depends on the ratio of excitation over inhibition (see supplementary material), which mirror local and global receptor occupancies, respectively. Thus, when the data from these simulations is plotted in terms of relative concentrations, all four cases yield essentially the same curve (Fig. 4 C). It is known that the overall chemotactic response depends on the relative gradient steepness (Zigmond, 1977; Fisher et al., 1989). The simulation results suggest that this feature is mediated by PI(3,4,5)P3, and agree with our recent experimental results (Janetopoulos et al., 2004).

FIGURE 4.

FIGURE 4

Open in a new tab

Dependence of the response on absolute and relative cAMP concentrations. Shown are the cAMP (A) and PI(3,4,5)P3 profiles (B) for four simulations in which either the location or the concentration of the cAMP source is changed. (C) The PI(3,4,5)P3 and cAMP concentrations, normalized to their respective means, are plotted against each other, showing nearly indistinguishable responses.

Dual stimulation

To investigate the response of our model of Dictyostelium cells to multiple sources, a cell is stimulated with two perfectly symmetric sources (Fig. 5 A). PI3K and PI(3,4,5)P3 responses exhibit symmetric double peaks facing each of the cAMP sources, whereas PTEN accumulates away from the micropipettes (Fig. 5, B–D). We vary the cAMP concentration of one source (Fig. 5 E), resulting in PI(3,4,5)P3 peaks with unequal distributions (Fig. 5 F). We also change the location of one source, so that the two are now 90° apart. Though the trough between them is much smaller, the two peaks can still be distinguished (Fig. 5 G). Finally, we investigate the response of the PTEN-deficient cells exposed to two sources, 180° apart. In this case, PI(3,4,5)P3 concentration levels are sufficiently elevated that a peak cannot be easily distinguished (Fig. 5 H). These results are consistent with the symmetric and asymmetric responses observed in similar experiments on latrunculin-treated cells (Janetopoulos et al., 2004).

FIGURE 5.

FIGURE 5

Open in a new tab

Spatial response of PI(3,4,5)P3 elicited by simultaneous steady stimulation of the cell. (A) Two 0.5 μM cAMP sources are applied close to the cell, but at opposite sides. (B–D) PI3K, PTEN, and PI(3,4,5)P3 localizations. The cAMP concentration of the pipette on the right is reduced to 0.4 μM, resulting in unequal stimulation at the sides (E), and the PI(3,4,5)P3 is monitored (F). (G) One pipette is relocated to obtain two symmetric 0.5 μM sources placed 90° apart. (H) PI(3,4,5)P3 response in cells in which PTEN has been reduced to 10% of basal level.

Response to simultaneous temporal and spatial stimulation

To examine the behavior of a cell to stimuli that combine temporal and spatial components, we simulate the response of a cell to one such complex stimulus (Fig. 6 and movie in supplementary material). A cell, initially in a gradient, is stimulated homogeneously by a saturating 10 μM dose of cAMP. After 100 s, this homogeneous chemoattractant source is removed, and the cAMP gradient is reestablished. Because of the uniform stimulus, PI(3,4,5)P3, which is initially found facing the cAMP source, increases everywhere along the membrane. Within 50 s, this response subsides and the PI(3,4,5)P3 concentration approaches basal levels everywhere on the membrane. After the removal of the uniform stimulus, PI(3,4,5)P3 disappears from the membrane, but later appears in the form of a crescent responding to the cAMP gradient.

FIGURE 6.

FIGURE 6

Open in a new tab

Spatial and temporal PI(3,4,5)P3 response to a complex stimulus. A cell, initially in a cAMP gradient as in Fig. 3 B, is stimulated with a 10 μM uniform dose at 0 s. The stimulus is removed at 100 s, allowing the cAMP gradient to reestablish. Shown is the spatial distribution of PI(3,4,5)P3 at five time instances (A–E) as well as the PI(3,4,5)P3 membrane concentrations at the front and rear as a function of time (F). The steady-state response to a uniform 1 nM stimulus is given as a reference, labeled as Basal. The five time instances corresponding to panels A–E are denoted by an arrow. (See accompanying movie.)

Fractional-cell stimulation

Finally, as a test of the model, we create an experimental condition, which, to our knowledge, has not been performed and for which the cellular response is not easy to predict. We simulate portions (50%, 75%, and 87.5%) of the cell membrane with a saturating concentration of cAMP, but leave the rest of the cell unstimulated. In all cases, the stimulated portion of the cell elicits a PI(3,4,5)P3 response, whereas the rest of the cell membrane has no PI(3,4,5)P3 present (Fig. 7). The simulations predict that as the fraction of the cell membrane exposed to chemoattractant increases, the level of the response decreases. Moreover, the concentration of PI(3,4,5)P3 is slightly higher near the boundary formed by the presence of cAMP.

FIGURE 7.

FIGURE 7

Open in a new tab

Spatial PI(3,4,5)P3 response in cells that are partially stimulated by saturating cAMP concentrations. Simulations are done in which 87.5% (A), 75% (B), or 50% (C) of the cell is exposed to a saturating dose of chemoattractant but the rest of the cell is not stimulated. (D) PI(3,4,5)P3 membrane concentrations are plotted as a function of the angle, labeled in A. (E) The predicted phenomenon can be explained by the model depicted here. Local receptor occupation (gray band in column 1) activates the excitation and inhibition processes (green and red bands in column 2). Although the local excitation remains where it is produced, the inhibitor diffuses evenly throughout the cell to a level that is proportional to the fraction of the cell that is stimulated (column 3). Throughout the cell, the response is dictated by the balance between the resulting excitation and inhibition processes (column 4). Thus, wherever the receptor is occupied, a cellular response is observed, because the local excitation concentration is higher than that of the inhibition. However, as the fraction of the cell stimulated increases, the concentration of the inhibitor also increases, leading to a smaller difference between excitation and inhibition, and consequently, a smaller response. Wherever the receptors are unoccupied, there is no excitation, but inhibitor is present, leading to an absence in the response.

DISCUSSION

Simulations of our mathematical model based on the reciprocal regulation of two important enzymes regulating PI(3,4,5)P3 reveal that the temporal and spatial localizations observed in fluorescently-tagged PI3K, PTEN, and PH domains are explained by two LEGI mechanisms acting in parallel. PI(3,4,5)P3 is synthesized by PI3K and degraded by PTEN on the membrane. As a consequence, the combination of complementary translocations of PI3K and PTEN increases the temporal response of PI(3,4,5)P3 to a uniform stimulus, as well as its spatial localization in response to a chemoattractant gradient. Our simulations of cells deficient in either one or both of the enzymes demonstrate the importance of maintaining a balance in their levels for proper gradient sensing. The need for this balance has been observed experimentally; cells lacking PTEN or PI3K show impaired chemotaxis (Funamoto et al., 2002; Iijima and Devreotes, 2002). However, PI3K inhibitors can partially restore the chemotactic response in pten− cells (Chen et al., 2003).

The model exhibits several important features of the chemotactic, spatial sensing response that we have demonstrated recently (Janetopoulos et al., 2004) and that are missing in other models proposed to explain gradient sensing (Meinhardt, 1999; Narang et al., 2001; Postma and Van Haastert, 2001; Rappel et al., 2002). Our model shows that the spatial distribution of the response is affected by the chemoattractant gradient, so that steeper gradients elicit more localized responses than shallower gradients. Similarly, the midpoint cAMP concentration affects the degree of localization since the response depends on the relative gradient (Janetopoulos et al., 2004). Both these features are direct consequences of the LEGI mechanisms. In contrast, several other models predict a steady-state response that is invariant with respect to the mean value and relative gradient of the chemoattractant concentration profile (Meinhardt, 1999; Narang et al., 2001), whereas others cannot account for the cell's ability to sense gradients of increasing midpoint concentration (Postma and Van Haastert, 2001). Our model also shows that the rear of a cell in a gradient remains responsive to further stimulation, be it spatial or temporal. These features agree with our recent experimental findings on latrunculin-treated cells (Janetopoulos et al., 2004). Other proposed models suggest that the rear of the cell becomes inhibited and so would not be able to sense further stimuli (Rappel et al., 2002). The simulation shown in Fig. 6 also explains the observed behavior in a recent experiment (Janetopoulos et al., 2004), and in doing so, provides support for the existence of a receptor-mediated, slower inhibitory process. The extinguishing of the PI(3,4,5)P3 response at the front of the cell after the removal of the uniform cAMP stimulus is a result of the slower decrease in the concentration of the inhibitor, relative to that of the excitation process, in response to a decrease in receptor occupancy.

The adaptation achieved through the LEGI mechanism is not affected by model parameter values and hence is a robust process. However, it is also known that the external gradient is not amplified with a single LEGI regulator (Iglesias and Levchenko, 2002; Levchenko and Iglesias, 2002). To introduce high amplification, a positive feedback mechanism can be added downstream of the standard LEGI mechanism. The resulting model inherits robust adaptation from the LEGI regulator, but the amplification performance is very sensitive to parameter values. Other methods of achieving amplification that are not sensitive to parameter variations have been considered (Meinhardt, 1999; Narang et al., 2001; Postma and Van Haastert, 2001). However, because of the hysteretic nature of their response, these models cannot account for the response seen in unpolarized Dictyostelium to rapidly changing sources (Iglesias and Levchenko, 2002; Devreotes and Janetopoulos, 2003). In contrast, the model presented in this article, through the dual spatial sensing mechanisms, exhibits robust adaptation as well as redundant amplification. From a biological standpoint, this mechanism offers considerable advantages as it allows a cell to sense gradients, and hence chemotax—though perhaps with reduced efficiency—even if the function of one of the two regulators is missing or impaired, as has been experimentally observed (Funamoto et al., 2002; Iijima and Devreotes, 2002).

In our model, we assume cooperative activation of PI3K with a Hill coefficient of 2 and linear inhibition for PTEN, both of which are activated by receptor occupancy. These model parameters were chosen so that the concentration of PI3K is proportional to the square, and the concentration of PTEN is inversely proportional to the first power of normalized cAMP concentration, respectively, to agree with our experimental data (Iijima et al., 2004; Janetopoulos et al., 2004). The need for cooperativity in PI3K binding suggests that additional regulatory elements exist. The resulting concentration of PI(3,4,5)P3 is proportional to the cubic power of normalized cAMP concentration, also in agreement with our experimental data observed in nonpolarized cells (see supplemental material).

The effect of varying cell geometry on the model was tested by importing various images of polarized cells into the Virtual Cell environment and simulating the cellular response. The simulations predicted that polarized cells exhibit slightly greater gradient amplification than the spherical cells (data not shown). Since no biochemical data were changed in the model, these results show that the streamlined cell morphology associated with moving cells can enhance the spatial heterogeneity of the PI(3,4,5)P3 distribution. However, when we compare the simulation to experimental data (Janetopoulos et al., 2004), we find that not all the experimentally observed amplification is achieved by the model. The experimental and virtual setups differ in several aspects. In vivo, neither the shape of the moving cell nor the observed chemotactic gradients is constant; this influences the observed response. In contrast, in our simulation, the polarized cell is assumed immobile in a static chemoattractant gradient. These differences between model and experiment do not arise in the spherical, static cells where a strong match between theory and experiment is observed. Nevertheless, our simulations suggest that there are additional amplification steps in the regulatory pathway of polarized cells. A positive feedback loop involving actin polymerization has been suggested (Weiner et al., 2002). This loop would have no effect on the immobilized cells, and might help to account for the missing amplification in the polarized cells. A positive feedback loop involving mild hysteretic effect may also explain some cell's ability to remain polarized even in the absence of external gradients (Devreotes and Janetopoulos, 2003).

Our simulations predict cellular responses to stimuli that are not easily implemented experimentally. For example, our model makes a very strong prediction as to the behavior expected when a fraction of the cell membrane is exposed to saturating concentrations of cAMP, but the rest of the cell is unstimulated. The cell experiences no chemoattractant gradient, only a steplike change in concentration. The predicted response suggests that a chemoattractant gradient is not necessary for a static spatial response. The inhibitory molecules acting in each LEGI mechanism diffuse away from the region of the cell membrane where they are activated, allowing a cellular response to develop (Fig. 7 E). Because the inhibitor is created by receptor occupancy, as the fraction of the cell stimulated is decreased, the total number of inhibitor molecules created is smaller. Moreover, since they diffuse around the whole cell membrane, the concentration at any one point along the membrane decreases. This explains the increase in the local response seen in Fig. 7. To our knowledge, this experiment has not been performed, but could be attempted using a clamp or microfluidic device (Dertinger et al., 2001) to stimulate only a fraction of the cell. Experimental determination of the cellular response would help greatly in our understanding of the chemotactic behavior of cells. Were the behavior predicted here to be observed, this experiment would provide further evidence for the existence of a receptor-mediated global inhibitor.

Although our simulations provide cellular responses that mirror most of the observed response of directional sensing Dictyostelium cells, there are several features that are not accounted for.

First, as stated at the outset, our model does not explain the other processes involved in gradient sensing, polarization, and movement. Polarization is known to have an effect on the accumulation of PI(3,4,5)P3, as it leads to greater amplification and the desensitization of the cell's rear (Jin et al., 2000; Janetopoulos et al., 2004). Although our model can accurately explain gradient sensing in latrunculin-treated cells, aspects of other models may be needed to account for the observed differences in the responses between treated and untreated cells.

Second, chemoattractant stimulation elicits a localized, second phase of PI(3,4,5)P3 accumulation on the membrane (Chen et al., 2003; Postma et al., 2003). The mechanics that underlie the two phases are unknown and are not taken into account in these models.

Thirdly, specific biochemical entities have not been assigned to the excitation (EPI3K, EPTEN) or inhibition (IPI3K, IPTEN) processes. All four of these processes must be mediated by receptor occupancy. The two excitation processes must mirror receptor occupancy so they could be expected to be bound near the G-protein. In contrast, the inhibitory processes should be diffusible to provide a global signal. These properties allow us to speculate on possible candidates. For PTEN, it is known that a putative N-terminal PI(4,5)P2 binding motif is necessary for binding to the membrane (Iijima et al., 2004). Thus, the excitation process for PTEN (EPTEN) may represent a receptor-mediated decrease in the binding affinity of the PI(4,5)P2 binding motif. A conformational change in PTEN, possibly phosphorylation (Vazquez et al., 2001; Das et al., 2003), could also affect this binding affinity. If this change takes place while PTEN is in the cytosol, this would represent a global signal and thus serve as the inhibitor in the PTEN LEGI mechanism. For the PI3K LEGI mechanism, several candidates exist for the excitation and inhibition processes. It is known that PI3K activation depends on Gβγ, and that the PI3Ks contain Ras binding motifs. Moreover, an N-terminal fragment of PI3K is sufficient for binding to the membrane. Molecules that may be involved as inhibitors in the LEGI mechanisms include the G-protein α-subunit, Gα9, which is believed to play a role in adaptation (Brzostowski et al., 2002) and RCK1 (Sun and Firtel, 2003) (see Manahan et al., 2004).

Finally, recent experiments suggest that Dictyostelium cells do not adapt perfectly when stimulated uniformly (Postma et al., 2003; Postma et al., 2004b). Although our simulation parameters have been chosen to adapt perfectly or nearly perfectly, our model of dual regulation through complementary LEGI mechanisms does not require this perfect adaptation. If we allow the parameter values to change (as described in the supplementary material), perfect adaptation can be lost. However, spatial sensing is still possible, though at a reduced efficiency.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.

Supplementary Material

[Supplemental File]
biophysj_104.045484_index.html (1KB, html)

Acknowledgments

This work has been supported in part by the National Science Foundation's Biocomplexity Program grant DMS-0083500 (P.A.I.), The Whitaker Foundation (P.A.I.), National Institutes of Health grants Nos. 34933 and 28007 (P.N.D.) and 71920 (P.A.I.), and American Cancer Society grant No. PF-00-334-01 (C.J.).

References

  1. Brzostowski, J. A., C. Johnson, and A. R. Kimmel. 2002. Gα-mediated inhibition of developmental signal response. Curr. Biol. 12:1199–1208. [DOI] [PubMed] [Google Scholar]
  2. Chen, L., C. Janetopoulos, Y. E. Huang, M. Iijima, J. Borleis, and P. N. Devreotes. 2003. Two phases of actin polymerization display different dependencies on PI(3,4,5)P3 accumulation and have unique roles during chemotaxis. Mol. Biol. Cell. 14:5028–5037. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Chung, C. Y., S. Funamoto, and R. A. Firtel. 2001. Signaling pathways controlling cell polarity and chemotaxis. Trends Biochem. Sci. 26:557–566. [DOI] [PubMed] [Google Scholar]
  4. Das, S., J. E. Dixon, and W. Cho. 2003. Membrane-binding and activation mechanism of PTEN. Proc. Natl. Acad. Sci. USA. 100:7491–7496. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Dertinger, S. K. W., D. T. Chiu, N. L. Jeon, and G. W. Whitesides. 2001. Generation of gradients having complex shapes using microfluidic networks. Anal. Chem. 73:1240–1246. [Google Scholar]
  6. Devreotes, P., and Janetopoulos C. 2003. Eukaryotic chemotaxis: distinctions between directional sensing and polarization. J. Biol. Chem. 278:20445–20448. [DOI] [PubMed] [Google Scholar]
  7. Dickson, B. 2002. Molecular mechanisms of axon guidance. Science. 298:1959–1964. [DOI] [PubMed] [Google Scholar]
  8. Dormann, D., G. Weijer, C. A. Parent, P. N. Devreotes, and C. J. Weijer. 2002. Visualizing PI3 kinase-mediated cell-cell signaling during Dictyostelium development. Curr. Biol. 12:1178–1188. [DOI] [PubMed] [Google Scholar]
  9. Fisher, P. R., R. Merkl, and G. Gerisch. 1989. Quantitative analysis of cell motility and chemotaxis in Dictyostelium discoideum by using an image processing system and a novel chemotaxis chamber providing stationary chemical gradients. J. Cell Biol. 108:973–984. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Funamoto, S., R. Meili, S. Lee, L. Parry, and R. A. Firtel. 2002. Spatial and temporal regulation of 3-phosphoinositides by PI 3-kinase and PTEN mediates chemotaxis. Cell. 109:611–623. [DOI] [PubMed] [Google Scholar]
  11. Funamoto, S., K. Milan, R. Meili, and R. A. Firtel. 2001. Role of phosphatidylinositol 3′ kinase and a downstream pleckstrin homology domain-containing protein in controlling chemotaxis in Dictyostelium. J. Cell Biol. 153:795–810. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Huang, Y. E., M. Iijima, C. A. Parent, S. Funamoto, R. A. Firtel, and P. Devreotes. 2003. Receptor mediated regulation of PI3Ks confines PI(3,4,5)P3 to the leading edge of chemotaxing cells. Mol. Biol. Cell. 14:1913–1922. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Iglesias, P. A., and A. Levchenko. 2002. Modeling the cell's guidance system. Sci. STKE. 2002:re12. [DOI] [PubMed] [Google Scholar]
  14. Iijima, M., and P. Devreotes. 2002. Tumor suppressor PTEN mediates sensing of chemoattractant gradients. Cell. 109:599–610. [DOI] [PubMed] [Google Scholar]
  15. Iijima, M., Y. E. Huang, H. R. Luo, F. Vazquez, and P. N. Devreotes. 2004. Novel mechanism of PTEN regulation by its phosphatidylinositol 4,5-bisphosphate binding motif is critical for chemotaxis. J. Biol. Chem. 279:16606–16613. [DOI] [PubMed] [Google Scholar]
  16. Janetopoulos, C., T. Jin, and P. Devreotes. 2001. Receptor-mediated activation of heterotrimeric G-proteins in living cells. Science. 291:2408–2411. [DOI] [PubMed] [Google Scholar]
  17. Janetopoulos, C., L. Ma, P. N. Devreotes, and P. A. Iglesias. 2004. Chemoattractant-induced phosphatidylinositol 3,4,5-trisphosphate accumulation is spatially amplified and adapts, independent of the actin cytoskeleton. Proc. Natl. Acad. Sci. USA. 101:8951–8956. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Jin, T., N. Zhang, Y. Long, C. A. Parent, and P. N. Devreotes. 2000. Localization of the G protein βγ complex in living cells during chemotaxis. Science. 287:1034–1036. [DOI] [PubMed] [Google Scholar]
  19. Krishnan, J., and P. A. Iglesias. 2003. Analysis of an adaptation module of gradient sensing. Bull. Math. Biol. 65:95–128. [DOI] [PubMed] [Google Scholar]
  20. Krishnan, J., and P. A. Iglesias. 2004. A modeling framework describing the enzyme regulation of membrane lipids underlying gradient perception in Dictyostelium cells. J. Theor. Biol. 229:85–99. [DOI] [PubMed] [Google Scholar]
  21. Kutscher, B., P. Devreotes, and P. A. Iglesias. 2004. Local excitation, global inhibition mechanism for gradient sensing: An interactive applet. Sci. STKE. 2004:pl3. [DOI] [PubMed] [Google Scholar]
  22. Levchenko, A., and P. A. Iglesias. 2002. Models of eukaryotic gradient sensing: application to chemotaxis of amoebae and neutrophils. Biophys. J. 82:50–63. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Lloyd, C. 2002. Chemokines in allergic lung inflammation. Immunology. 105:144–154. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Loew, L. M., and J. Schaff. 2001. The Virtual Cell: a software environment for computational cell biology. Trends Biotechnol. 19:401–406. [DOI] [PubMed] [Google Scholar]
  25. Manahan, C. L., P. A. Iglesias, Y. Long, and P. N. Devreotes. 2004. Chemoattractant signaling in Dictyostelium discoideum. Annu. Rev. Cell. Biol. 20:223–253. [DOI] [PubMed] [Google Scholar]
  26. Meinhardt, H. 1999. Orientation of chemotactic cells and growth cones: models and mechanisms. J. Cell Sci. 112:2867–2874. [DOI] [PubMed] [Google Scholar]
  27. Moser, B., and P. Loetscher. 2001. Lymphocyte traffic control by chemokines. Nat. Immunol. 2:123–128. [DOI] [PubMed] [Google Scholar]
  28. Narang, A., K. K. Subramanian, and D. A. Lauffenburger. 2001. A mathematical model for chemoattractant gradient sensing based on receptor-regulated membrane phospholipid signaling dynamics. Ann. Biomed. Eng. 29:677–691. [DOI] [PubMed] [Google Scholar]
  29. Parent, C. A., B. J. Blacklock, W. M. Froehlich, D. B. Murphy, and P. N. Devreotes. 1998. G protein signaling events are activated at the leading edge of chemotactic cells. Cell. 95:81–91. [DOI] [PubMed] [Google Scholar]
  30. Parent, C. A., and P. N. Devreotes. 1999. A cell's sense of direction. Science. 284:765–770. [DOI] [PubMed] [Google Scholar]
  31. Postma, M., L. Bosgraaf, H. M. Loovers, and P. J. Van Haastert. 2004a. Chemotaxis: signalling modules join hands at front and tail. EMBO Rep. 5:35–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Postma, M., J. Roelofs, J. Goedhart, T. W. Gadella, A. J. Visser, and P. J. Van Haastert. 2003. Uniform cAMP stimulation of Dictyostelium cells induces localized patches of signal transduction and pseudopodia. Mol. Biol. Cell. 14:5019–5027. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Postma, M., J. Roelofs, J. Goedhart, H. M. Loovers, A. J. Visser, and P. J. Van Haastert. 2004b. Sensitization of Dictyostelium chemotaxis by phosphoinositide-3-kinase-mediated self-organizing signalling patches. J. Cell Sci. 117:2925–2935. [DOI] [PubMed] [Google Scholar]
  34. Postma, M., and P. J. Van Haastert. 2001. A diffusion-translocation model for gradient sensing by chemotactic cells. Biophys. J. 81:1314–1323. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Potma, E. O., W. P. de Boeij, L. Bosgraaf, J. Roelofs, P. J. van Haastert, and D. A. Wiersma. 2001. Reduced protein diffusion rate by cytoskeleton in vegetative and polarized Dictyostelium cells. Biophys. J. 81:2010–2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Rappel, W. J., P. J. Thomas, H. Levine, and W. F. Loomis. 2002. Establishing direction during chemotaxis in eukaryotic cells. Biophys. J. 83:1361–1367. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Ruchira, M. A. Hink, L. Bosgraaf, P. J. van Haastert, and A. J. Visser. 2004. Pleckstrin homology domain diffusion in Dictyostelium cytoplasm studied using fluorescence correlation spectroscopy. J. Biol. Chem. 279:10013–10019. [DOI] [PubMed] [Google Scholar]
  38. Schrick, K., B. Garvik, and L. H. Hartwell. 1997. Mating in Saccharomyces cerevisiae: the role of the pheromone signal transduction pathway in the chemotropic response to pheromone. Genetics. 147:19–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Servant, G., O. D. Weiner, P. Herzmark, T. Balla, J. W. Sedat, and H. R. Bourne. 2000. Polarization of chemoattractant receptor signaling during neutrophil chemotaxis. Science. 287:1037–1040. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Servant, G., O. D. Weiner, E. R. Neptune, J. W. Sedat, and H. R. Bourne. 1999. Dynamics of a chemoattractant receptor in living neutrophils during chemotaxis. Mol. Biol. Cell. 10:1163–1178. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Stephens, L. R., T. R. Jackson, and P. T. Hawkins. 1993. Agonist-stimulated synthesis of phosphatidylinositol(3,4,5)-trisphosphate: a new intracellular signalling system? Biochim Biophys. Acta. 1179:27–75. [DOI] [PubMed] [Google Scholar]
  42. Sun, B., and R. A. Firtel. 2003. A regulator of G protein signaling-containing kinase is important for chemotaxis and multicellular development in dictyostelium. Mol. Biol. Cell. 14:1727–1743. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Ueda, M., Y. Sako, T. Tanaka, P. Devreotes, and T. Yanagida. 2001. Single-molecule analysis of chemotactic signaling in Dictyostelium cells. Science. 294:864–867. [DOI] [PubMed] [Google Scholar]
  44. Vazquez, F., S. R. Grossman, Y. Takahashi, M. V. Rokas, N. Nakamura, and W. R. Sellers. 2001. Phosphorylation of the PTEN tail acts as an inhibitory switch by preventing its recruitment into a protein complex. J. Biol. Chem. 276:48627–48630. [DOI] [PubMed] [Google Scholar]
  45. Weiner, O. D., P. O. Neilsen, G. D. Prestwich, M. W. Kirschner, L. C. Cantley, and H. R. Bourne. 2002. A PtdInsP(3)- and Rho GTPase-mediated positive feedback loop regulates neutrophil polarity. Nat. Cell Biol. 4:509–513. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Xiao, Z., N. Zhang, D. B. Murphy, and P. N. Devreotes. 1997. Dynamic distribution of chemoattractant receptors in living cells during chemotaxis and persistent stimulation. J. Cell Biol. 139:365–374. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Zigmond, S. H. 1977. Ability of polymorphonuclear leukocytes to orient in gradients of chemotactic factors. J. Cell Biol. 75:606–616. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[Supplemental File]
biophysj_104.045484_index.html (1KB, html)
biophysj_104.045484_1.pdf (42.7KB, pdf)
Download video file (19.5MB, mov)

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES