Filtering of Calcium Transients by the Endoplasmic Reticulum in Pancreatic β-Cells

Abstract

Calcium handling in pancreatic β-cells is important for intracellular signaling, the control of electrical activity, and insulin secretion. The endoplasmic reticulum (ER) is a key organelle involved in the storage and release of intracellular Ca²⁺. Using mathematical modeling, we analyze the filtering properties of the ER and clarify the dual role that it plays as both a Ca²⁺ source and a Ca²⁺ sink. We demonstrate that recent time-dependent data on the free Ca²⁺ concentration in pancreatic islets and β-cell clusters can be explained with a model that uses a passive ER that takes up Ca²⁺ when the cell is depolarized and the cytosolic Ca²⁺ concentration is elevated, and releases Ca²⁺ when the cell is repolarized and the cytosolic Ca²⁺ is at a lower concentration. We find that Ca²⁺-induced Ca²⁺ release is not necessary to explain the data, and indeed the model is inconsistent with the data if Ca²⁺-induced Ca²⁺ release is a dominating factor. Finally, we show that a three-compartment model that includes a subspace compartment between the ER and the plasma membrane provides the best agreement with the experimental Ca²⁺ data.

INTRODUCTION

A key element of glucose homeostasis is the secretion of insulin by pancreatic β-cells in response to changes in the blood glucose level. The signal transduction from external glucose to insulin secretion is a multistep process, involving cell depolarization and a subsequent elevation of the intracellular Ca²⁺ concentration. Specifically, glucose is transported across the cell membrane and metabolized, resulting in an increase in the intracellular ATP/ADP ratio. This increased ratio closes ATP-sensitive K⁺ channels, depolarizing the cell and activating voltage-dependent Ca²⁺ channels. The resulting Ca²⁺ influx increases the intracellular Ca²⁺ concentration and evokes exocytosis of insulin granules (Ashcroft and Rorsman, 1989).

While Ca²⁺ influx is clearly important in the β-cell's response to depolarization, there is a large body of evidence that the endoplasmic reticulum (ER) also plays a role (Arredouani et al., 2002b; Bertram et al., 1995; Gilon et al., 1999; Lemmens et al., 2001; Miura et al., 1997; Tengholm et al., 2001). The contribution that the ER makes to Ca²⁺ handling in pancreatic islets was the focus, in particular, of a recent study in which the free cytosolic Ca²⁺ concentration was measured during an oscillatory potassium pulse protocol. Each K⁺ pulse depolarizes the islet, and at the end of the pulse the cell repolarizes. The oscillatory pattern of K⁺ pulses was chosen to resemble electrical bursting patterns typically observed in islets (Arredouani et al., 2002b). By controlling the electrical subsystem, the authors were able to focus on the Ca²⁺ dynamics. Calcium rose during each depolarization and decayed to a level above baseline during each repolarization. Experiments were repeated in the presence of the SERCA pump inhibitor thapsigargin (Tg), which blocks uptake of Ca²⁺ into the ER and ultimately leads to Ca²⁺ depletion in the organelle. In the presence of Tg, the amplitude of the Ca²⁺ response to depolarization was increased significantly, and the Ca²⁺ nadir between depolarizations was close to the baseline level. In a related study using longer depolarizations, Gilon et al. (1999) also demonstrated that Tg increases the amplitude of the Ca²⁺ response, and additionally increases the rate of rise of Ca²⁺ during the depolarization. Another study demonstrated that the Ca²⁺ dynamics in SERCA3 knockout mice are similar to those in control mice in the presence of Tg during short burst-like K⁺ pulses, suggesting that SERCA3 is the SERCA isoform primarily responsible for filling the ER when the cytosolic Ca²⁺ concentration is elevated by depolarization (Arredouani et al., 2002a).

In this study we use mathematical modeling to address several questions related to the contribution of the ER to Ca²⁺ handling in β-cells. First, we ask whether a simple model with two Ca²⁺ compartments, the ER and cytosol, can account for the recent Ca²⁺ data of Arredouani et al. (2002b) and Gilon et al. (1999). Second, whereas these authors focused on the effects of SERCA blockers, we ask what effect other modulators such as carbachol, Li⁺, and calmidazolium would have on the cytosolic Ca²⁺ dynamics. Carbachol promotes efflux of Ca²⁺ from the ER via the production of inositol 1,4,5-trisphosphate (IP₃), whereas Li⁺ and calmidazolium inhibit Ca²⁺ exchangers and pumps in the plasma membrane, respectively (Nadal et al., 1994; Wolf et al., 1988). Third, we use the experimental data to constrain the speed at which the ER takes up and releases Ca²⁺, and find that ER Ca²⁺ must be much slower than cytosolic Ca²⁺, but not too slow.

Some have suggested that calcium-induced calcium release (CICR) from the ER is important in β-cells (Ämmälä et al., 1991; Gromada et al., 1996; Kang and Holz, 2003; Lemmens et al., 2001), and indeed there is little doubt that it is important when agonists such as acetylcholine or GLP-1 are present (Ämmälä et al., 1991; Gilon et al., 1995; Gromada et al., 1996; Kang and Holz, 2003; Lemmens et al., 2001). However, in the absence of these agonists the significance of CICR is unclear. A recent study (Beauvois et al., 2004) failed to find any CICR during brief depolarizations (<40 s) such as those that occur during a burst of action potentials. Also, mRNA for ryanodine receptors, the primary mechanism for CICR in the absence of cholinergic agonists, was only weakly expressed in β-cells. However, an atypical form of CICR was observed, which was not dependent on either IP₃R or RyR, in response to supraphysiological KCl pulses, much longer and stronger than the ones in Arredouani et al. (2002b) that we simulate. This atypical CICR appeared only infrequently in response to glucose-induced calcium oscillations and was not required for those oscillations.

In the analysis presented here, we find that a passive two-compartment model (cytosol and ER only) is able to account for all of the recent time-dependent Ca²⁺ data. Thus, the Ca²⁺ filtering properties of an ER with a Ca²⁺-dependent SERCA and slow passive leak that depends on the gradient between the ER and cytosolic Ca²⁺ levels accounts for the reported effects of Tg on the cytosolic Ca²⁺ during trains of depolarizations. Although CICR is not necessary, a modest CICR contribution is compatible with the data. However, if CICR is dominant, such that the ER drains during depolarization and refills during repolarization, then the model does not reproduce the Ca²⁺ data. Thus, if CICR is present in β-cells during normal glucose stimulation, then it must be present at modest levels.

The simple two-compartment model predicts that during long sustained depolarizations the cytosolic Ca²⁺ concentration will approach the same value with or without SERCA pump blockers. This is true whether or not CICR is present. Thus, whereas the SERCA pumping rate has a profound effect on the dynamics of the cytosolic Ca²⁺, it has no impact on the equilibrium level of cytosolic Ca²⁺. A slightly more complex model, called the subspace model, on the other hand, predicts that the measured equilibrium Ca²⁺ concentration will be lower when the ER is depleted of Ca²⁺. The subspace model postulates that Ca²⁺ from the ER is released primarily into a compartment that lies between the ER and the plasma membrane and was motivated by the observation that a slow K⁺ current (I_K(slow)) activated by burst-like trains of depolarizations (Goforth et al., 2002; Göpel et al., 1999; Kanno et al., 2002) is inhibited by SERCA pump blockade (Goforth et al., 2002). Our results suggest that the three-compartment subspace model is superior to a two-compartment model with or without CICR in reproducing the recent data on Ca²⁺ handling in β-cells.

METHODS

Basic two-compartment model

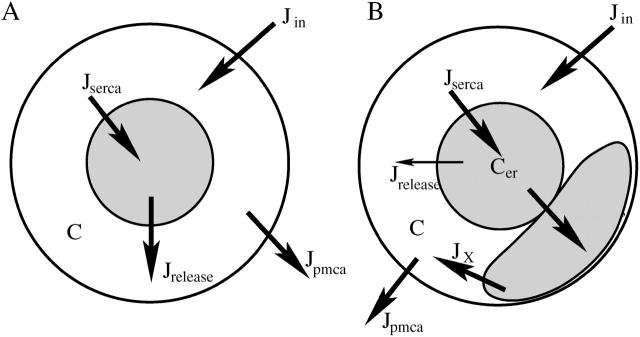
Whereas the experimental data that we simulate comes from intact islets, we use a single-cell model in our simulations. Although some phenomena, such as asynchronous Ca²⁺ releases, cannot be modeled with this approach, it suffices to explain most aspects of islet behavior because the cells are electrically coupled and their electrical activity and Ca²⁺ dynamics are synchronized. The basic two-compartment model is illustrated in Fig. 1 A. Calcium enters the cell through L-type Ca²⁺ channels in the plasma membrane, with flux (J_in) proportional to the Ca²⁺ current. Calcium is removed by Ca²⁺ pumps in the membrane, with flux (J_pmca) assumed to be proportional to the cytosolic free Ca²⁺ concentration (C). Thus,

(1)

where α converts current to concentration, and k_pmca is the plasma membrane pump rate. The Ca²⁺ current is voltage (V)-dependent, and is given by

(2)

where g_Ca is the whole cell conductance, V_Ca is the Ca²⁺ reversal potential, and m is the channel activation variable. Since channel activation is known to be rapid, we assume for simplicity that it is instantaneous, so

FIGURE 1.

Illustration of the Ca²⁺ fluxes incorporated in (A) the two-compartment model and (B) the three-compartment subspace model. The thin arrow in B represents a small flux from the ER to the bulk cytosol.

Calcium from the cytosol is transported into the ER by SERCA pumps in the ER membrane. Two SERCA genes are expressed in β-cells, SERCA2b and SERCA3. The SERCA2b ATPase has high Ca²⁺ affinity and is primarily responsible for setting the basal level of Ca²⁺ in the ER (Varadi and Rutter, 2002). The SERCA3 ATPase has lower Ca²⁺ affinity and is primarily responsible for transporting Ca²⁺ from the cytosol to the ER during Ca²⁺ elevations, such as those produced by bursts of action potentials (Arredouani et al., 2002a). We include terms for both SERCA2b and SERCA3 in our model. Flux through SERCA2b pumps is described by a small constant term (this pump is treated as saturated even at basal cytosolic Ca²⁺ levels), whereas flux through SERCA3 pumps is assumed to be proportional to C. Flux out of the ER (J_release) is assumed to be proportional to the gradient between the concentrations of free cytosolic Ca²⁺ and free ER Ca²⁺ (C_er). Thus,

(3)

where k_serca2b and k_serca3 are the SERCA2b and SERCA3 rate constants, and p_er is the rate of Ca²⁺ release from the ER. Release from the ER could be through inositol 1,4,5-trisphophate (IP₃) or ryanodine channels in the ER membrane, or some other route of passive leak. Thapsigargin (Tg) is modeled by setting both k_serca2b and k_serca3 to 0, whereas SERCA3 knockout is modeled by setting only k_serca3 to 0. The simple linear expressions used for ER fluxes demonstrate that no nonlinearities in the fluxes are needed to account for the data of Arredouani et al. (2002b). Similar linear ER fluxes were used by Gall and Susa (1999), but without the constant for SERCA2b.

The time-dependent concentrations of C and C_er are described using conservation equations. Thus,

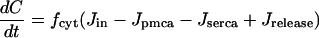(4)

(5)

where f_cyt, f_er are the fractions of free Ca²⁺ in the cytosolic and ER compartments, respectively, and ν_cyt and ν_er are the volumes of the cytosolic and ER compartments. All parameter values are listed in Table 1. The basic two-compartment model is used in Figs. 2–8.

TABLE 1.

Parameter values used in two-compartment model

gCa	1200 pS	VCa	30 mV	α	4.5 × 10−6μM fA−1 ms−1
vm	−15 mV	sm	8 mV	fcyt	0.01
fer	0.01	vcyt	10 μm3	ver	0.4 μm3
per	10−4 ms−1	pmin	10−5 ms−1	pmax	3 × 10−4 ms−1
Kcicr	0.5 μM	kpmca	0.08 ms−1	kserca3	0.08 ms−1
kserca2b	0.02 μM ms−1

FIGURE 2.

(A) Simulated voltage protocol mimicking the biphasic response to an increase in glucose concentration. (B) Cytosolic Ca²⁺ response with SERCA pumps enabled (solid line) and disabled (dashed line). During each imposed oscillation, the nadir is defined as the lowest value of C during the repolarized phase. The amplitude is the difference between the peak and the nadir. (C) The ER Ca²⁺ concentration. No driving force is established between the ER and the cytosol when SERCA pumps are disabled (dashed line).

FIGURE 3.

(A) Doubling the rate of Ca²⁺ release from the ER, p_er, has a transient effect on the cytosolic Ca²⁺ response (dashed line) to the voltage protocol, but no long-term effect. (B) C_er adapts to the doubling in p_er (dashed line) by declining to a value one-half that of the control.

FIGURE 4.

(A) Reducing the rate of pumping across the plasma membrane by half (dashed line) slightly increases the amplitude of the Ca²⁺ response to depolarization and greatly increases the Ca²⁺ nadir. (B) The increase in the Ca²⁺ nadir is due to an increase in C_er.

FIGURE 5.

(A) An increase in the glucose concentration is mimicked (at arrow) by increasing the depolarized phase duration from 8 s to 12 s, while keeping the oscillation period fixed at 24 s. (B) In the control simulation (solid line), increasing the duration of depolarization results in an increase in the Ca²⁺ nadir, but not in the amplitude, whereas there is no effect when SERCA pumps are disabled (dashed line). (C) In the control simulation, an increase in the ER Ca²⁺ concentration is responsible for the increased cytosolic Ca²⁺ nadir.

FIGURE 6.

(A) When the Ca²⁺ channel conductance, g_Ca, is doubled (at arrow), both the Ca²⁺ amplitude and nadir are increased. This is true with SERCA pumps enabled (solid line) or disabled (dashed line), although the nadir increase in the latter case is quite small. (B) As in Fig. 5, the nadir increase is due primarily to an increase in the ER Ca²⁺ concentration, although increased Ca²⁺ entry also plays a role.

FIGURE 7.

(A) Voltage protocol for compound bursting. (B) In the control system the Ca²⁺ nadir rises during a compound burst and slowly falls between (solid line). This does not occur when the SERCA pumps are disabled (dashed line). (C) The rise and fall of the nadir reflects the dynamics of ER Ca²⁺.

FIGURE 8.

Demonstration that the slow rise and fall of the cytosolic Ca²⁺ nadir depends critically on the speed at which the ER takes up and releases Ca²⁺. (A) The speed of the ER is increased by setting f_er = 0.1 (solid line), or decreased by setting f_er = 0.0002 (dashed line). (B) There are no slow C_er dynamics when f_er = 0.1, and there is only a small increase in C_er during a compound burst when f_er = 0.0002.

Two-compartment model with CICR

In simulations performed with the basic two-compartment model the ER Ca²⁺ release rate, p_er, is constant. In simulations involving calcium-induced Ca²⁺ release (CICR), p_er is an increasing function of C,

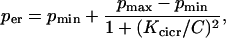(6)

which is constructed so that Ca²⁺ efflux from the ER is increased when cytosolic Ca²⁺ is elevated. The model with CICR is used in Figs. 9 and 10.

FIGURE 9.

Ca²⁺ response to a sequence of depolarizations when CICR dominates release from the ER. (A) Sequence of brief depolarizations. (B) Cytosolic Ca²⁺ rises during depolarization and falls during repolarization. (C) The ER releases Ca²⁺ during the depolarization due to CICR, and refills during the repolarization.

FIGURE 10.

(A) Biphasic voltage protocol applied to the model in which CICR dominates. (B) Even with active SERCA pumps the Ca²⁺ nadir is not elevated and the amplitude is large (solid line), so that blocking SERCA pumps has only a small effect (dashed line). (C) The cytosolic Ca²⁺ nadir is not elevated despite the fact that the ER is filled.

Three-compartment subspace model

The subspace model (Goforth et al., 2002) was motivated by experimental evidence for a Ca²⁺-activated K⁺ current (I_K(slow)) that develops during burst-like voltage-clamp depolarizations (Goforth et al., 2002; Göpel et al., 1999; Kanno et al., 2002). In this model, Ca²⁺ released from the ER primarily enters a subspace compartment adjacent to the plasma membrane, and from here can enter the bulk cytosol (Fig. 1 B). The Ca²⁺ concentration in the subspace (C_ss) is elevated compared with the bulk cytosolic Ca²⁺ (C) due to this preferential influx from the ER. Here, we assume that there is also some release from the ER directly into the bulk cytosol. In Goforth et al. (2002) it was proposed that the Ca²⁺-activated K⁺ channels that comprise a large component of I_K(slow) respond to this elevated C_ss rather than the lower bulk cytosolic Ca²⁺. We are interested here only in the Ca²⁺ handling, so ion channels other than the L-type channels are omitted from the model.

The Ca²⁺ flux terms in the subspace model are largely the same as in the two-compartment model, with the exception of the two release terms J_release,ss and J_release,cyt, and the new flux term between the subspace and the bulk cytosol (J_X). Thus,

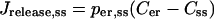(7)

(8)

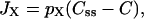(9)

where p_er,ss, p_er,cyt, and p_X are constants. The differential equations describing the Ca²⁺ concentrations in the three compartments are

(10)

(11)

(12)

where f_ss is the fraction of free Ca²⁺ in the subspace and ν_ss is the volume. The observable for this model is the average of the Ca²⁺ concentrations in the bulk cytosol and the subspace compartment weighted by the compartment volumes,

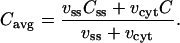(13)

All parameters for the subspace model are given in Table 2. This model is used in Fig. 11 only.

TABLE 2.

Parameter values used in the three-compartment subspace model

gCa	1450 pS	VCa	30 mV	A	4.5 × 10−6μM fA−1 ms−1
kpmca	0.12 ms−1	kserca3	0.3 ms−1	kserca2b	0.02 μM ms−1
fcyt	0.01	fer	0.01	fss	0.01
pX	0.045 ms−1	per,cyt	5 × 10−5 ms−1	per,ss	1.5 × 10−6 ms−1
νcyt	3.2 μm3	νer	0.4 μm3	νss	0.8 μm3
sm	8 mV	vm	−13 mV

FIGURE 11.

Ca²⁺ concentrations during a sustained depolarization from −70 mV to −30 mV with the three-compartment subspace model. (A) The weighted average of the bulk cytosolic Ca²⁺ and the subspace Ca²⁺ concentrations is lower when SERCA pumps are inhibited (dashed line) than in the control system (solid line). The ER Ca²⁺ concentration (B) and the subspace Ca²⁺ concentration (D) are lower when SERCA pumps are inhibited. (C) The bulk cytosolic concentration satisfies Eq. 16, so its steady state is independent of the C_er or ER parameters.

RESULTS

Ca²⁺ flux terms have differential effects on the Ca²⁺ profile

In the in vitro studies of pancreatic islets, when the bath glucose concentration is raised from a substimulatory to a suprastimulatory level the β-cell electrical response is typically biphasic. The cells first spike continuously for 1–2 min (phase 1), and then produce bursts of action potentials (phase 2) with periods ranging from 10 s to ∼1 min (Meissner and Atwater, 1976). This behavior was mimicked using K⁺ pulses in the experimental study by Arredouani et al. (2002b), and the average intracellular free Ca²⁺ concentration was measured. Each K⁺ pulse depolarizes the islet, and the islet repolarizes between pulses. Hence, the K⁺ pulse protocol is similar to a voltage-clamp protocol, with the advantage that it is applicable to intact islets. We simulated this voltage-clamp-like protocol with our mathematical models. As illustrated in Fig. 2 A, voltage is initially maintained at a resting potential of −70 mV. It is then elevated to −30 mV for 1 min, mimicking the first phase of electrical activity. After this, a voltage oscillation is imposed by periodically clamping V between −60 mV and −30 mV, mimicking the silent and active phases of bursting, respectively. The duration of the repolarized phase is 16 s, and that of the depolarized phase is 8 s.

The model cytosolic Ca²⁺ response to this protocol is shown in Fig. 2 B (solid curve), using the basic two-compartment model without CICR. (This model is used to generate Figs. 2–8.) Note that the Ca²⁺ nadir during the silent phases is elevated above the resting level. Also note the slow rise in Ca²⁺ during the initial depolarization, which reflects the time constant of ER filling. The model ER Ca²⁺ concentration is shown in Fig. 2 C. During the initial depolarization the ER fills, and during subsequent oscillatory activity C_er remains elevated. This maintained elevation of C_er provides the driving force for a net flux of Ca²⁺ from the ER into the cytosol during the repolarized phases of the oscillatory activity, elevating the cytosolic Ca²⁺ nadir.

Application of the SERCA pump blocker thapsigargin (Tg) is simulated by setting both k_serca2b and k_serca3 to 0 and allowing the system to equilibrate at the resting potential, so that the cytosolic and ER Ca²⁺ concentrations converge. When the voltage protocol is applied, the amplitude of the cytosolic Ca²⁺ response is much greater and the nadir is no longer elevated (Fig. 2 B, dashed curve). This twofold effect of blocking SERCA pumps reflects two important dynamical roles of the ER. First, the ER acts as a Ca²⁺ sink, slowing the rise of cytosolic Ca²⁺. When SERCA pumps are blocked, the filtering of cytosolic Ca²⁺ is reduced and C rises to a higher level. Second, the ER acts as a Ca²⁺ source when the cell is repolarized and there is little or no entry of Ca²⁺ into the cell. This latter role requires that a gradient be established between the ER and the cytosol, and this does not happen when SERCA pumps are blocked.

The simulation results in Fig. 2 reproduce the experimental data (Fig. 2, B and C, of Arredouani et al., 2002b, and Fig. 2 A of Gilon et al., 1999) very well, indicating that the simple two-compartment model with passive Ca²⁺ release from the ER is sufficient to describe the effects on cytosolic Ca²⁺ of disabling the SERCA pumps. Similar effects on cytosolic Ca²⁺ were observed in SERCA3 knockout mice (Arredouani et al., 2002b) and can be simulated with the model by setting k_serca3 = 0 (not shown). However, the model indicates that the ER does not empty in that case, demonstrating that it is the rise and fall of ER Ca²⁺, not the level of ER Ca²⁺, that governs the filtering effect of the ER.

Another way to reduce C_er is to increase the release rate from the ER. We investigated whether increasing the Ca²⁺ release rate would increase the cytosolic Ca²⁺ amplitude and decrease the nadir during the voltage protocol, as did blocking the SERCA pumps. This was tested by doubling p_er. Fig. 3 shows the control response (solid line) and the response with p_er doubled (dashed line). Increasing the Ca²⁺ release rate had no effect on the cytosolic Ca²⁺ amplitude, and although the nadir is initially elevated, this effect is only transient. The lack of effect on the Ca²⁺ amplitude is explained by noting that the Ca²⁺ influx into the ER during a depolarization is mainly determined by k_serca2b and k_serca3, not p_er. The lack of a long-term effect on the Ca²⁺ nadir can be understood by noting that J_release = p_er (C_er−C) ≈ p_erC_er. When p_er is doubled C_er adapts by falling to half its control value (Fig. 3 B), and J_release is ultimately the same as in the control simulation. Thus, the nadir is ultimately the same as in the control simulation. This model prediction can be readily tested experimentally by applying carbachol or some other muscarinic agonist to stimulate IP₃ production and increase Ca²⁺ release from the ER through IP₃ channels.

We next examined the effects of partially disabling the plasma membrane Ca²⁺ pumps by reducing k_pmca by half. Although this maneuver did cause a small increase in the cytosolic Ca²⁺ amplitude in response to the pulse protocol, it raised the Ca²⁺ nadir by a much larger amount (Fig. 4 A). The former effect is due to the reduced pumping, whereas the latter effect is due to the increased Ca²⁺ release from the ER during the repolarized phase of the oscillation. Indeed, the main consequence of reducing pumping out of the cell is to increase C so that more Ca²⁺ gets pumped into the ER, setting up a larger gradient between the ER and cytosol compartments (Fig. 4 B). As a result, when the cell is repolarized the ER is a greater source of Ca²⁺, increasing the cytosolic Ca²⁺ nadir above its control value. This model prediction can be tested experimentally by replacing Na⁺ with Li⁺ to inhibit Na⁺/Ca²⁺ exchange (Nadal et al., 1994) or applying calmidazolium to inhibit calmodulin and thus the plasma membrane Ca²⁺ pumps (Wolf et al., 1988).

In summary, reducing the uptake of Ca²⁺ into the ER by disabling the SERCA pumps yields an increased cytosolic Ca²⁺ amplitude and reduced nadir in response to the voltage protocol, consistent with the effects of the SERCA pump blocker Tg or SERCA3 knockout during a similar K⁺ pulse protocol (Arredouani et al., 2002a,b). Increasing Ca²⁺ efflux from the ER has only a transient effect on the Ca²⁺ nadir; ultimately the Ca²⁺ nadir returns to its control level. Decreasing the Ca²⁺ efflux from the cell by partially inhibiting plasma membrane Ca²⁺ pumps yields a slightly increased Ca²⁺ amplitude and a significantly increased Ca²⁺ nadir in response to the voltage protocol. Thus, alterations in the level of Ca²⁺ release from the ER or in the plasma membrane pump rate have effects on the cytosolic Ca²⁺ that are quite different from the effect of disabling SERCA pumps. All of these effects can be understood in terms of the dual role of the ER as a Ca²⁺ sink and a Ca²⁺ source.

The effects of increased Ca²⁺ entry depend on how entry is increased

When the bath glucose concentration is increased from one suprastimulatory level to a higher level pancreatic islets typically respond by increasing the plateau fraction of bursting, i.e., the ratio of active phase duration to the total burst period. This effect on the membrane potential was mimicked by Arredouani et al. (2002b) by increasing the K⁺ pulse duration while keeping the oscillation period fixed. (The effects of increasing the glucose concentration on pumps were found to be negligible compared to the effect on the plateau fraction.) We simulate this by increasing the depolarized duration from 8 to 12 s while decreasing the repolarized duration from 16 to 12 seconds, so that the oscillation period remains fixed at 24 s (Fig. 5 A). In the control simulation (SERCA intact), the increase in plateau fraction causes an increase in the Ca²⁺ nadir, with little change in the Ca²⁺ amplitude (Fig. 5 B). This is consistent with data shown in Fig. 3 A of Arredouani et al. (2002b). The cause of the nadir increase is a greater influx of Ca²⁺ into the cell, and consequently a higher concentration of Ca²⁺ in the ER (Fig. 5 C). Thus, release of Ca²⁺ from the ER is greater during the repolarized phase, yielding an increased Ca²⁺ nadir. The Ca²⁺ amplitude is not increased by the longer depolarization because C equilibrates rapidly to the depolarized voltage; it has already nearly equilibrated by the end of an 8-s depolarization, so increasing the duration of depolarization will not significantly increase the cytosolic Ca²⁺ amplitude.

When the simulation is repeated with SERCA pumps disabled (Fig. 5 B, dashed line) there is again little change in the Ca²⁺ amplitude when the plateau fraction is increased. However, unlike the control simulation, the Ca²⁺ nadir is almost unchanged by the increased plateau fraction. This simulation is consistent with Fig. 3 B of Arredouani et al. (2002b).

Increasing the plateau fraction is one way to increase the total Ca²⁺ entry into the β-cell. Another way to do this is to increase influx through the Ca²⁺ channels. Arredouani et al. (2002b) achieved this by raising the external Ca²⁺ concentration. The approach we take in the simulations shown in Fig. 6 is to increase the Ca²⁺ channel conductance. In the control simulation, doubling g_Ca increases both the Ca²⁺ nadir and amplitude (Fig. 6 A). As when the plateau fraction was increased, the nadir is increased primarily because C_er is elevated (Fig. 6 B). An increase in the Ca²⁺ influx during the repolarized phase adds an additional (small) component to the nadir, which is evident as a small nadir increase when the SERCA pumps are disabled (dashed line). The increased Ca²⁺ amplitude is evident whether the SERCA pumps are enabled or disabled, and is due to an increase in the Ca²⁺ entry per unit time. Thus, in contrast to the effects of doubling the plateau fraction (Fig. 5), where the total Ca²⁺ entry is increased by increasing the duration of cell depolarization (and not the Ca²⁺ entry per unit time), increasing the conductance increases the influx (J_in) relative to efflux (J_pmca) during the depolarized phase, resulting in an increased Ca²⁺ amplitude. Results from this simulation, both in control and with SERCA pumps inhibited, are consistent with data in Fig. 4 of Arredouani et al. (2002b).

In summary, the two methods of increasing total Ca²⁺ entry reported in Arredouani et al. (2002b) and simulated here have different effects on the cytosolic Ca²⁺. These differential effects can be understood with the two-compartment model, and do not require additional features such as CICR.

A compound bursting pattern provides a good test protocol for Ca²⁺ handling

Mixed Ca²⁺ oscillations are sometimes observed in single β-cells or β-cell clusters (Jonkers et al., 1999; Krippeit-Drews et al., 2000) and in islets (Bergsten et al., 1994; Valdeolmillos et al., 1989; Zhang et al., 2003). These oscillations are most likely due to episodes of bursts (Barbosa et al., 1998; Cook 1983; Henquin et al., 1982), which we call compound bursts (Bertram et al., 2004). Compound bursts were mimicked by Arredouani et al. (2002b), and we simulate this protocol in Fig. 7. Here a series of five voltage oscillations is applied, with each oscillation consisting of a 16-s depolarization followed by an 8-s repolarization (Fig. 7 A). Two episodes of compound bursts were applied, separated in time by 2 min. In the control conditions, the cytosolic Ca²⁺ nadir rose during the first episode and slowly fell during the time between (Fig. 7 B). The slow rise and fall of the nadir reflects the dynamics of the ER Ca²⁺ concentration (Fig. 7 C). When the SERCA pumps were disabled (k_serca2b = 0 and k_serca3 = 0) the ER Ca²⁺ concentration remained flat, and consequently there was no rise in the nadir during the oscillations, and C immediately returned to its baseline value at the end of an episode of bursts (Fig. 7 B, dashed line). These results are consistent with data shown in Fig. 6, B and C, of Arredouani et al. (2002b).

The impact of the ER on the rise and fall of the Ca²⁺ nadir is further demonstrated in Fig. 8, where the rate of change of C_er has been modified by adjusting the fraction of free Ca²⁺ in the ER (f_er). First, the speed of the ER was increased by a factor of 10 by changing f_er from 0.01 to 0.1 (solid curves). In this case, the slow increase in C_er exhibited previously during a compound burst (Fig. 7 C) is replaced by oscillations in C_er around an elevated, but constant, mean. As a result, the cytosolic Ca²⁺ nadir rises quickly during a bursting episode, exhibiting no slow upward ramp (Fig. 8 A). Also, with the faster ER the cytosolic Ca²⁺ falls quickly to its baseline value at the end of a compound burst, reflecting the rapid decline in C_er (Fig. 8 B). To examine the other extreme, we decreased the speed of the ER by a factor of 50, setting f_er = 0.0002 (dashed curves). In this case, the free ER Ca²⁺ concentration increases only slightly during a compound burst, and as a consequence the cytosolic Ca²⁺ nadir returns to baseline between each depolarization, so there is little elevation of the nadir. Thus, a very slow ER has effects on cytosolic Ca²⁺ that are in some ways similar to the effects of disabling the SERCA pumps. One key difference, however, is that the C amplitude is larger than that of the control when SERCA pumps are disabled (Fig. 7 B), whereas the amplitude is smaller than control when the ER dynamics are slowed by decreasing f_er (Fig. 8 A). This is because the filtering performed by the ER is reduced in the former case and increased in the latter case.

In summary, the compound bursting simulations in conjunction with the experimental data of Arredouani et al. (2002b) show clearly the influence that the ER has on the cytosolic Ca²⁺ dynamics, both during an episode of bursts and between episodes. They also put constraints on the speed of the ER. If the ER fills and empties too rapidly or too slowly, the slow rise and fall of the Ca²⁺ nadir, which was shown clearly in Arredouani et al. (2002b), is not produced. Although decreasing the speed of the ER by increasing its filtering capacity greatly reduces the rise in the cytosolic Ca²⁺ nadir during a compound burst, it also decreases the Ca²⁺ amplitude, in contrast to the increase produced when SERCA pumps are inhibited. Indeed, blocking SERCA pumps is the only manipulation we have found that suppresses the rise in the Ca²⁺ nadir while increasing the Ca²⁺ amplitude.

The Ca²⁺ response is inconsistent with experimental data when CICR is a dominant factor

We next investigate the potential role of Ca²⁺-induced Ca²⁺ release (CICR) in β-cells, by making the rate of efflux from the ER, p_er, an increasing function of the cytosolic Ca²⁺ concentration (Eq. 6). The extent of the contribution of CICR to the total release from the ER depends on the choice of parameters. The parameter p_min sets the passive release, whereas the magnitude of CICR is determined by p_max−p_min. For example, if p_min = p_max then CICR will contribute nothing to J_release. Figures shown thus far have used the basic two-compartment model, where release is passive. All results can be reproduced by a model in which some degree of CICR is included (not shown). However, since CICR tends to reduce the ER Ca²⁺ concentration relative to that in the cytosol, the effects of blocking SERCA pumps are blunted when CICR is included.

We consider now an extreme case, in which J_release is dominated by CICR. We saw previously that when release is passive the ER fills during depolarization and drains during repolarization. On the contrary, when release is dominated by CICR the Ca²⁺ entering the cell during depolarization induces release from the ER, so the ER initially fills, but then releases once the cytosolic concentration becomes sufficiently large. During repolarization the ER fills since the cytosolic Ca²⁺ is lower, inducing less release. The response to a train of three depolarizations is demonstrated in Fig. 9.

This CICR model was used to simulate the Ca²⁺ response during the biphasic voltage protocol (Fig. 10 A). Except for an initial transient period during which the ER was filling, blocking SERCA pumps had little effect on either the Ca²⁺ nadir or the Ca²⁺ amplitude (Fig. 10 B). That is, C returned to baseline after each depolarization, whether SERCA pumps were activated or disabled, and the Ca²⁺ amplitude was slightly decreased when SERCA pumps were blocked. The nadir was not elevated because with this model the ER takes up Ca²⁺ during the repolarized phase, and it is release of Ca²⁺ that produces the elevated nadir. The amplitude was abnormally large because the ER does not take up Ca²⁺ when the cell is depolarized; instead it amplifies the cytosolic Ca²⁺. Thus, a model in which CICR dominates release from the ER does not reproduce the experimental Tg data (Arredouani et al., 2002b; Gilon et al., 1999).

Continuous depolarization data support the subspace model

The simulations presented thus far highlight dynamic or time-dependent properties of Ca²⁺ handling. A much simpler simulation, continuous depolarization, highlights steady-state properties and yields some surprising results. During continuous depolarization with elevated K⁺, Table 1 of Arredouani et al. (2002b) shows that the cytosolic Ca²⁺ concentration was lower in the presence of Tg. Although they did not report this difference as statistically significant, we note that reductions were observed in each of eight conditions. A statistically significant reduction in steady-state Ca²⁺ in the presence of Tg was reported in single β-cells by Lemmens et al. (2001).

Contrary to these data, the basic two-compartment model indicates that the steady-state values should be identical whether or not pumps are blocked. This is easily seen from the equations. At steady state, Eq. 5 yields

(14)

and combined with Eq. 4 we obtain

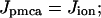(15)

so from Eq. 1,

(16)

where C_∞ is the equilibrium or steady-state cytosolic Ca²⁺ concentration. Thus, the steady state depends only on the Ca²⁺ influx and efflux across the plasma membrane, and is independent of the ER Ca²⁺ concentration or any parameters relating to the ER. This is true whether release from the ER is passive, as in our basic model, or active through CICR. Thus, the two-compartment models fail to reproduce the continuous depolarization data (Arredouani et al., 2002b; Lemmens et al., 2001).

A three-compartment model has been developed (Goforth et al., 2002) to explain recent data on the buildup and decay of a Ca²⁺-activated K⁺ current during a burst of short action-potential-like depolarizations (Goforth et al., 2002; Göpel et al., 1999; Kanno et al., 2002). As described in Methods, this model contains an ER compartment, a bulk cytosolic compartment, and a Ca²⁺ subspace postulated to exist between the ER and the plasma membrane. In this model, most of the release from the ER enters the subspace compartment, so that the Ca²⁺ concentration in this compartment is elevated above that of the bulk cytosol (Fig. 1 B). Like the basic two-compartment model, the three-compartment subspace model reproduces all the experimental data related to the dynamics of Ca²⁺ handling (not shown). However, whereas the two-compartment model (with or without CICR) fails to reproduce the steady-state Ca²⁺ data, the subspace model correctly predicts a decrease in cytosolic Ca²⁺when SERCA pumps are blocked.

Fig. 11 shows the Ca²⁺ concentrations in the three compartments during a continuous depolarization from −70 to −30 mV. Also shown is C_avg, the weighted average of the bulk cytosolic Ca²⁺ (C) and the subspace Ca²⁺ (C_ss) concentrations (Eq. 13). This weighted average is what would be observed in experiments measuring the Ca²⁺ concentration in the cell. As with the two-compartment model, the bulk cytosolic Ca²⁺ attains the same steady-state level whether or not the SERCA pumps are inhibited (Fig. 11 C), since the steady-state concentration in this compartment satisfies Eq. 16. However, the subspace Ca²⁺ concentration has a lower steady-state value when SERCA pumps are blocked (dashed line, Fig. 11 D) since the Ca²⁺ influx to this compartment is less when the ER is depleted (Fig. 11 B). In fact, the steady-state subspace concentration equals the bulk cytosolic concentration when SERCA pumps are blocked, whereas it is higher when the subspace is intact. Since the observable C_avg is the weighted average of C and C_ss, it is lower when SERCA pumps are inhibited than in the control case (Fig. 11 A), consistent with the experimental data.

DISCUSSION

We have demonstrated that a simple two-compartment model with passive Ca²⁺ release from the ER can reproduce recent time-dependent Ca²⁺ data (Arredouani et al., 2002a,b; Gilon et al., 1999). Although a modest contribution of CICR is compatible with the data, a model in which CICR is the dominant efflux pathway from the ER is not compatible.

Although the two-compartment model, with or without modest CICR, reproduces the time-dependent data, it is not compatible with steady-state Ca²⁺ data showing that the cytosolic Ca²⁺ concentration is lower when SERCA pumps are inhibited by Tg (Arredouani et al., 2002b; Lemmens et al., 2001). Prolonged stimulation with high KCl can produce an atypical form of CICR that does not involve the IP₃R or RyR in normal mouse β-cells (Beauvois et al., 2004). This could lead to a reduction in cytosolic Ca²⁺ when SERCA pumps are blocked. However, we note that the atypical CICR only gives a single, transient release in response to a maintained stimulus (Beauvois et al., 2004), which suggests that CICR is not the best explanation for the steady-state reduction. Here, we have shown a three-compartment model that includes a subspace compartment between the ER and the plasma membrane reproduces both the time-dependent and the steady-state data without recourse to CICR.

This subspace model was developed to account for data showing a transient rise and fall of a current tail that develops during a short train of action-potential-like depolarizations (Goforth et al., 2002), and that has been attributed largely to a voltage-independent, Ca²⁺-activated K⁺ current (Goforth et al., 2002; Göpel et al., 1999; Kanno et al., 2002). The subspace model accounts for this data, whereas the basic two-compartment model does not. If CICR is added to the two-compartment model and is the dominant factor in release, then the I_K(slow) data is reproduced. That is, if a substantial part of the rise in cytosolic Ca²⁺ that activates I_K(slow) is due to release from the ER, then Tg would reduce I_K(slow). However, we have shown here that a model with dominant CICR is not compatible with time-dependent Ca²⁺ data. Thus, in our view, the subspace model most accurately reflects the handling of Ca²⁺ in pancreatic β-cells.

The ER serves as both a Ca²⁺ sink and source. When the cell is depolarized Ca²⁺ enters the cell through ion channels, elevating the cytosolic Ca²⁺ concentration. This causes the ER to take up Ca²⁺, therefore acting as a sink, which slows and blunts the rise in cytosolic Ca²⁺. When the cell is repolarized the influx through ion channels stops and the cytosolic Ca²⁺ concentration drops due to removal through membrane Ca²⁺ pumps. As a result Ca²⁺ is released from the ER, which now acts as a source and slows and antagonizes the fall in cytosolic Ca²⁺. These dual roles provide the framework for understanding the effects of agents known to modify Ca²⁺ pathways in β-cells. For example, when Tg is used to block SERCA pumps, the ER will not have any active uptake mechanism and will no longer serve as a Ca²⁺ sink. Also, since the ER does not fill with Tg present, it will not serve as a Ca²⁺ source when the cell is repolarized. These two effects of SERCA pump blockage can explain all the time-dependent Tg data.

Knockout experiments (Arredouani et al., 2002b) show that ER sourcing and sinking is also eliminated by removal of SERCA3 alone. Thus, this low affinity isoform is solely responsible for ER Ca²⁺ oscillations and their attendant effects on cytosolic Ca²⁺. The high affinity isoform, SERCA2b, is likely nearly saturated at basal Ca²⁺ and accounts for the ability of the ER to fill, albeit slowly, in low Ca²⁺, provided sufficient ATP is present (Tengholm et al., 2001).

In addition to accounting for the known data, we have made some new predictions. The model predicts that agents such as carbachol, that increase the release from the ER, will have no long-term effects on the cytosolic Ca²⁺ dynamics. This prediction can readily be tested. Other agents such as Li⁺ or calmidazolium reduce efflux across the plasma membrane (Nadal et al., 1994; Wolf et al., 1988) and are predicted to increase the Ca²⁺ nadir, but have no effect on the Ca²⁺ amplitude during the biphasic burst-like voltage protocol.

Finally, we have demonstrated that the cytosolic Ca²⁺ dynamics are affected greatly by the speed at which the ER takes up and releases Ca²⁺. If the ER is too fast then it will not contribute a slow component to the cytosolic Ca²⁺ dynamics. This slow component is evident in the slow fall of Ca²⁺ often observed after bursts of action potentials in free-running (not voltage-clamped) islets (Gilon et al., 1999; Nadal et al., 1994; Valdeolmillos et al., 1989; Zhang et al., 2003). If the ER is too slow then it will take up only a small amount of Ca²⁺ during burst-like depolarizations. This will have an effect on cytosolic Ca²⁺ that is somewhat similar to the effect of having no ER compartment at all (i.e., SERCA pumps blocked), and subsequently the ER will not contribute any observable slow component to the Ca²⁺ signal. Thus, the uptake and release of Ca²⁺ from the ER must be slow compared to the timescale of cytosolic Ca²⁺, but not too slow.

There is experimental evidence that a store-operated current (SOC) is activated in β-cells when the ER is drained either through activation of IP₃ receptors or through inhibition of SERCA pumps (Mears and Zimliki, 2004; Miura et al., 1997; Worley et al., 1994b). This is a nonselective current, permeable to Ca²⁺ as well as other ions (Mears and Zimliki, 2004; Worley et al., 1994a). Although we have not included SOC in the simulations presented here, we have performed simulations to test its effects on the time-dependent Ca²⁺ dynamics (not shown). The extra Ca²⁺ that enters the model cell through SOC when the ER is depleted elevates both the Ca²⁺ peak and the Ca²⁺ nadir when the burst-like depolarization protocol is applied. However, if the Ca²⁺ component of SOC is relatively small, then the overall effect of draining the ER is to reduce the Ca²⁺ nadir. The Ca²⁺ amplitude is increased when the ER is drained regardless of the size of SOC. Also, the Ca²⁺ component of SOC increases the cytosolic Ca²⁺ concentration during long depolarizations when the ER is drained. Thus, the Tg-induced reduction in the Ca²⁺ concentration during long depolarizations reported by Arredouani et al. (2002b) and Lemmens et al. (2001) may be partially blunted by SOC; without SOC the reduction in Ca²⁺ concentration would be even greater. This provides additional support for the three-compartment subspace model, the only model that predicts a reduction in the steady-state cytosolic Ca²⁺ concentration when Tg is present. In this way, the effects of SOC make the case for a three-compartment subspace model more compelling.