Charged Lipid Vesicles: Effects of Salts on Bending Rigidity, Stability, and Size

Abstract

The swelling behavior of charged phospholipids in pure water is completely different from that of neutral or isoelectric phospholipids. It was therefore suggested in the past that, instead of multilamellar phases, vesicles represent the stable structures of charged lipids in excess water. In this article, we show that this might indeed be the case for dioleoylphosphatidylglycerol and even for dioleoylphosphatidylcholine in certain salts. The size of the vesicles formed by these lipids depends on the phospholipid concentration in a way that has been predicted in the literature for vesicles of which the curvature energy is compensated for by translational entropy and a renormalization of the bending moduli (entropic stabilization). Self-consistent field calculations on charged bilayers show that the mean bending modulus k_c and the Gaussian bending modulus 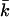have opposite sign and 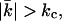especially at low ionic strength. This has the implication that the energy needed to curve the bilayer into a closed vesicle 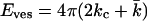is much less than one would expect based on the value of k_c alone. As a result, E_ves can relatively easily be entropically compensated. The radii of vesicles that are stabilized by entropy are expected to depend on the membrane persistence length and thus on k_c. Experiments in which the vesicle size is studied as a function of the salt and the salt concentration correlate well with self-consistent field predictions of k_c as a function of ionic strength.

INTRODUCTION

Phospholipid vesicles are often used as model systems to study the (physical) principles behind the behavior of biological membranes. Although most biological membranes are negatively charged, much of the research on vesicles has concentrated on vesicles of electrostatically neutral lipids. However, a large difference in swelling and phase behavior between electrostatically neutral and negatively charged phospholipids has been observed in the past (Hauser et al., 1982, 1984). In pure water, uncharged lipids show only limited swelling; this results in the formation of a multilamellar phase in excess water. Lipids that are net charged swell continuously in pure water. In excess water, the swelling of charged lipids results in fully hydrated unilamellar vesicles (Hauser, 1984). Vesicles have therefore been suggested to represent an equilibrium structure of the charged phospholipid bilayer (Hauser, 1984).

The stabilization mechanism of charged phospholipid bilayers is expected to be fundamentally different from that of catanionic vesicles. Catanionic vesicles of cetyltrimethylammonium bromide and perfluorooctanoate are, in a certain composition range, stabilized by a spontaneous curvature of the bilayer (Jung et al., 2001, 2002). This spontaneous curvature arises due to nonideal surfactant mixing, which causes the interior and exterior monolayers of the vesicle bilayer to have significantly different compositions (Safran et al., 1990, 1991). The size of these equilibrium vesicles stabilized by a spontaneous curvature is only determined by the ratio in which the different surfactants are mixed. Vesicles that consist of only one (charged) phospholipid species do not have a spontaneous curvature and can therefore only be stabilized against the formation of multilamellar sheets by their electrostatic charge and by entropic contributions linked to degrees of freedom of the membranes. When the undulational, translational, and possibly other entropic terms of the bilayers are sufficient to overcome the curvature free energy of the bilayer, a well-defined equilibrium radius is expected. This equilibrium size of the vesicles should in first order be determined by the mean bending modulus of the lipid bilayer. Another parameter that is expected to affect the size of these entropically stabilized vesicles is the total surfactant concentration (Safran, 1994; Simons and Cates, 1992; Herve et al., 1993; Morse and Milner, 1995).

The curvature free energy per unit of area can, in good approximation, be described as a second order expansion of the interfacial tension γ in the mean curvature 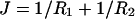and the Gaussian curvature 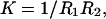in which R₁ and R₁ are the curvatures that locally describe the membrane bilayer

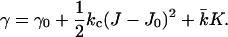(1)

The coefficients in Eq. 2 that are of particular interest are the bending modulus k_c, the spontaneous curvature J₀, and the saddle-splay modulus 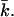These coefficients can be derived from the curvature dependence of the interfacial tension. The spontaneous curvature J₀ is thought to be the curvature that minimizes the surface free energy (of cylindrically shaped surfaces). The Gaussian bending modulus, 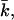determines the topology of the interface rather than its rigidity, which in turn, is determined by k_c. The mean bending modulus, k_c, must be positive for a bilayer, as any deformation from the equilibrium state has to increase the free energy. The sign of 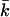is not determined a priori. For negative values of 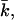the bilayer will prefer spherical deformations 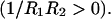For positive values of 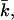the only way for the surface to lower its free energy is the formation of saddle surfaces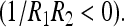

From the thermodynamics of small systems, it follows that, if the translational entropy of the membrane is neglected, a flat equilibrium bilayer membrane is tensionless, i.e., γ = 0. Therefore, Eq. 1 reduces to

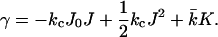(2)

If the membrane has no spontaneous curvature, as expected for bilayers composed of only one phospholipid species, the energy needed to curve a flat bilayer into a closed vesicle becomes equal to E_ves = γA, (A = 4πR²)

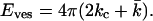(3)

One of the sources of entropy that can compensate for this curvature energy is the translational entropy. A population of many small vesicles has a larger translational entropy than a population of a few large vesicles (with equal surface area). The system can therefore increase its entropy by increasing the number and decreasing the size of the vesicles in solution. However, it is not possible to decrease the size of the vesicles indefinitely. The membrane has a certain stiffness given by persistence length ξ_p. On distances smaller than ξ_p, the membrane is stiff, whereas above this length the information on orientation is lost. This means that, in first order approximation, ξ_p sets the lower limit to the vesicle size. As the bilayer has no resistance to shape fluctuations at distances longer than ξ_p, the membrane freely undulates at these length scales. This means, however, that the bending moduli are no longer independent of the vesicle radii or the length scale L at which the system is studied. The bending moduli should therefore be replaced by effective bending moduli. The effective mean bending modulus 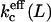can be written as

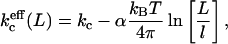(4)

where l is a length scale proportional to the size of the molecules. Besides the translational entropy and the bilayer undulations discussed above, other sources of entropy such as the polydispersity of the vesicle sizes can also contribute to compensate the curvature energy of the system.

Although knowledge of k_c and 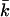is necessary to estimate the curvature free energy, and thus to understand the behavior of bilayer membranes, there are relatively few measurements of k_c and almost no measurements of 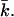Moreover, the micropipette pressurization technique (Evans and Needham, 1987; Rawicz et al., 2000) and the analysis of the shape fluctuations of giant vesicles (Meleard et al., 1998), which are often used to determine the mean bending modulus, probe k_c at length scales much larger than those relevant for submicrometer vesicles. The values for k_c that are found in this way differ between the different techniques that are used but are all in the range of 5–40 k_BT (Seifert and Lipowsky, 1995). Unfortunately, almost all measurements done so far refer to neutral or isoelectric phospholipids, and no information is available for both k_c and 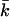of charged lipid bilayers. Realistic molecular model calculations are the only theoretical means to predict the curvature free energy and the mechanical parameters of a lipid bilayer. Recently, it was shown how these parameters can be determined unambiguously from self-consistent field (SCF) calculations (Oversteegen and Leermakers, 2000). We will apply this computation method to obtain systematic predictions for charged lipid systems in electrolyte solutions.

In this article, we investigate the entropic stabilization of charged lipid bilayers. For this purpose, the formation and the behavior of dioleoylphosphatidylglycerol (DOPG) vesicles in the presence of different salts and salt concentrations was studied. SCF calculations were used to get insight into the curvature free energy and the Helfrich mechanical parameters of charged lipid-like bilayers.

MATERIALS AND METHODS

Experiments

The anionic phospholipid DOPG was purchased as a sodium salt, and the zwitterionic phospholipid dioleoylphosphatidylcholine (DOPC) was purchased as a chloroform solution, from Avanti Polar Lipids (Birmingham, AL); both were used without further purification. Analytical grade NaCl and NaI were purchased from Merck (Darmstadt, Germany) and NaBr from J. T. Baker Chemicals (Deventer, Holland). Vesicles were made by drying the phospholipids from chloroform under a stream of nitrogen followed by at least 2 h under vacuum to remove the last traces of solvent. The dry lipid film was rehydrated with a salt solution of the desired ionic strength to a concentration of 2 mg lipid/ml unless stated otherwise. Three different methods were used for the final vesicle production. The lipid film was 1), rehydrated overnight to produce giant vesicles, 2), vortexed with the salt solution, or 3), sonicated in salt solution in a round bath sonicator to produce small unilamellar vesicles (SUVs).

Multilayered vesicles of phospholipids are known to fragment into small vesicles, whereas SUVs fuse to form larger vesicles when the electrolyte solution in which they are suspended is subjected to successive cycles of freezing and thawing. Dioleoyl derivatives are particularly susceptible to this freeze-thaw procedure (MacDonald et al., 1994; Traikia et al., 2000), and were therefore used in this study. The freeze-thaw procedure probably ruptures the vesicles into fragments the size of which is determined by the persistence length of the bilayer. When these bilayer fragments reseal, this may result in vesicles with a size that is determined by k_c. To test this hypothesis, both giant vesicles and SUVs were subjected to repetitive cycles of freezing and thawing; 1 ml of vesicle containing solution was immersed in liquid nitrogen until completely frozen. The samples were thawed in a water bath at ∼313 K. This procedure was repeated until the size of the vesicles no longer changed. As it took many freeze-thaw cycles before the final size was reached, the procedure was speeded up by vortexing the vesicle suspension during thawing. This vortexing had no influence on the final radius obtained.

To see if vesicles could spontaneously evolve to vesicle radii comparable to those found in the freeze-thaw procedure, the size evolution of vesicles was followed in time (without any freeze-thaw steps) in a different experiment. For this purpose, the dry DOPG film was brought into contact with solutions of 0, 25, or 200 mM NaCl. To remove the lipid layer from the wall of the glass tube, the solution was shaken. Once the lipid layer was removed from the wall, the vesicle suspension was not stirred anymore. While the suspension was standing, samples were taken and analyzed regularly. As explained above, the stabilization mechanism of more component membranes can be completely different from that of membranes consisting of only one component. To make sure that the interpretation of our measurements was not obscured by phospholipid degradation, the samples were tested for the presence of hydrolysis products. The lipids were separated by one-dimensional thin-layer chromatography (TLC plates No. 5721, Merck), with CHCl₃:MeOH:HAc, 60:25:8 as the developing solvents. Fractions were made visible by spraying with a 0.1% solution of 8-anilino-1-naphthalencesulfonic acid in MeOH and inspection under ultraviolet light. The spontaneous size evolution of the vesicles was terminated within 30 h after vesicle preparation, which was well within the time at which traces of breakdown products could be detected.

To check whether perturbations by salt gradients could lead to a reequilibration of the vesicles, DOPG samples were subjected to either hyper- or hypotonic salt gradients. The vesicles tested were prepared by the freeze-thaw method. Osmotic gradients were applied by stepwise changes in the NaBr concentration.

Both DOPG and DOPC samples were checked by eye for phase separation. If phase separation took place, the appearance of multilamellar phases was inspected with crossed polarizers. The results shown here all apply to solutions that only contain vesicles. The appearance of multilamellar phases is treated in a second study (M. M. A. E. Claessens, F. A. M. Leermakers, F. A. Hoekstra, and M. A. Cohen Stuart, unpublished).

The size of the vesicles was determined using dynamic light scattering. The instrumental setup consisted of an ALV-5000 correlator and a scattering device with an ALV-125 goniometer and a multiline Lexel AR-laser source. The presented data were collected at a scattering angle of 90° at a wavelength of 513 nm. During the measurements, the temperature was kept constant at 298 K. A cumulant analysis was used to determine the average vesicle size.

Self-consistent field calculations

The self-consistent field theory can be used to evaluate the distribution of surfactant molecules in association colloids, e.g., micelles, vesicles, or bilayers. As surfactant molecules can assume many different conformations, it is convenient to divide the surfactants into segments, and space into a set of discrete coordinates. The surfactant chains are then restricted to have their segments on these coordinates.

The set of restricted coordinates on which the surfactant segments can be placed is called the lattice. In this lattice, one can either have flat, cylindrical, or spherical lattice layers. These layers are used to reduce the complexity of the calculations. Within the lattice layers, no density gradients occur (mean-field approximation). Tangential to the layers, numbered z = 1, . . , m, gradients may develop. The lattice layers are composed of L(z) indistinguishable lattice sites. And, in principle, a three-dimensional problem can in this way be reduced to a one-dimensional problem. Surfactants are composed of a string of segments, each of the size of a water molecule. When the solvent molecules, ions, and the segments of the surfactant chains are placed on the lattice, they all occupy one lattice site. Thus, as all the lattice sites have the same volume, each segment has a fixed size. Differences between segments can by introduced by changing their interactions with surrounding segments; their chemical nature can be accounted for. It should be kept in mind that by placing the molecules in a certain geometry, the symmetry of the lattice imposes a certain aggregate structure; as a result aggregates are unable to seek their optimum geometry.

All chain segments and monomers in the system have interactions with surrounding segments. Therefore, a potential energy u_x(z) is assigned to each type of segment x relative to the bulk solution β. This potential energy belongs to the segment, irrespective of the chain to which the segment belongs. The potential energy u_x(z) depends on all possible interactions of segment x with its environment. Physically, this means that u_x(z) contains all the potential energy contributions needed to bring a segment x from the bulk (where u_x(∞) = 0) to position z. Taking into account excluded volume, nearest neighbor, and electrostatic interactions, u_x(z) becomes

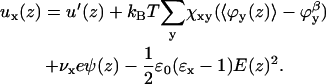(5)

Here, ϕ_y is the volume fraction of all other segment types, y; the superscript β refers to the bulk solution; and χ is the Flory-Huggins exchange energy parameter. The u′(z) term is the excluded-volume potential and originates from optimizing the partition function with an incompressibility constraint; in each coordinate z, the sum of the volume fractions should be unity, 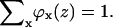This means that u′(x) is the (free) energy needed to generate a vacant site in layer z so that the segment can be inserted. The second term in Eq. 5 accounts for all short-range nearest-neighbor contact energies that a segment x has with all other segments in the system (again relative to the interactions it has in the bulk). The angular brackets indicate averaging of ϕ(z) over the neighboring cells of a site in layer z. This term contains information on the lattice symmetry, which can be flat, cylindrical, or spherical. The Flory-Huggins parameter χ_xy describes the interaction between segments of type x and type y. This dimensionless parameter has a positive value when the attractive interactions between xx and yy pairs are larger than those between two xy pairs. At negative χ-parameters, it is the other way around, i.e., the attractive interactions between the xy pairs are larger than the average of xx and yy pairs. In the term, the electrostatics are taken into account. The electrostatic potential in a certain layer, ψ(z), determines how much energy it costs to place a charge, 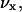on this lattice layer. The valence of segment x is given by ν_x; e is the elementary charge. The last term accounts for the fact that the segments can be polarized in the presence of an electric field. The polarization is a function of the electric field 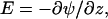and its polarizability given by dielectric permittivity (ɛ_x −). The energy gain due to this polarization is again proportional to E. It can be shown that the free energy gain is just half this value, i.e., there is a term 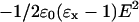in the segment potential. The electrostatic potential ψ(z), and thus E(z) follow from the total charge distribution as will be discussed below.

The distribution of a free segment over the layers , is given by its Boltzmann factor G_x(z),

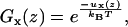(6)

which is generalized to

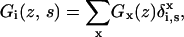(7)

where 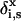is unity when segment s of molecule i is of type x and zero otherwise. To find the volume fraction profile ϕ_i(z, s) of a particular segment s in chains of type i, a more complicated procedure is needed. For this purpose, the segment distribution functions G_i(z, s | 1) are introduced. These functions are evaluated by step-weighted walks along the contour of chains i, starting at segment 1 at all allowed positions and finishing after s – 1 steps with segments s in layer z. The segment distribution function G_i(z, s | 1) can be obtained from the segment-weighting factor G_i(z, s) by the recurrence relation

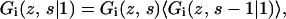(8)

which implies a first-order Markov approximation In Eq. 8, the angular brackets again denote averaging over neighboring cells. If segment s is of type x, the weight of segment s in layer z, G_i(z, s | s), of course equals G_i(z, s). A similar segments distribution function, G_i(z, s | N), can be obtained by starting at segment N at the end of the chain instead of segment 1. Now, ϕ(z, s) can be calculated, taking into account that the segment s in chain i is connected to both segment s − 1 and s + 1:

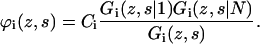(9)

Since segment s appears in the segment distribution functions of both chain ends, the division by G_i(z, s) is needed to correct for double counting. In the case one chooses to fix the bulk concentration, the normalization factor C_i is related to the equilibrium volume fraction 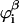in the bulk solution:

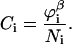(10)

When, on the other hand, the number of molecules of type i, n_i, is fixed, the sum of the volume fractions over all layers will yield the total number of monomers 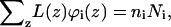and therefore C_i is given by

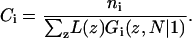(11)

The volume fractions of all moieties in the system can now be determined from the segment-weighting factors, which follow from the potential energies u_x(z). However, the energies u_x(z), in turn, determine the volume fractions as can be seen from Eq. 5. The total charge distribution q(z) follows from the densities of all charged components in the system:

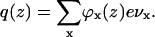In addition, the dielectric permittivity profile can be estimated by

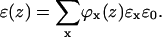These quantities are then used in the Poisson equation generalized for dielectric permittivity gradients:

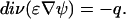Consequently, the set of equations has to be solved iteratively until the segment potentials and volume fractions are consistent.

Once the self-consistent solution is found from the potential energies and the segment distribution functions, the equilibrium density profiles and the potential profiles are known. Moreover, the self-consistent solutions give access to the thermodynamic quantities such as the free energy, chemical potential, and the grand potential in the system.

At the self-consistent field solution, the bulk solution is in equilibrium with the inhomogeneous system. In the bulk solution, the densities of all the components are known. From these bulk densities, the chemical potentials, with respect to the pure amorphous reference state, can be calculated:

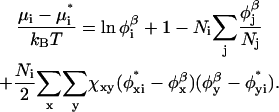(12)

The superscript asterisk denotes the reference state of the pure unmixed components and 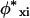is the fraction of segments of molecule i of type x. The grand potential is given by

(13)

in which

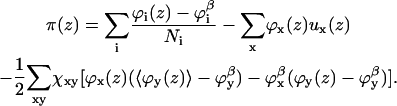(14)

The volume fractions and electrostatic potentials are known everywhere in the system and therefore the interfacial tension γ can be calculated from the grand potential according to Eq. 13. The values obtained for the grand potential from the SCF calculations are unequivocal (Oversteegen and Leermakers, 2000) and therefore the Helfrich constants can be determined unambiguously. For the calculation of the Helfrich constants, the curvature dependence of the interfacial tension γ is required. The curvature of a lipid bilayer can be varied in the calculations by changing the amount of lipids in the system of cylindrical or spherical geometry.

Parameters

Phospholipids were modeled as linear chains with segment sequence C₁₈X₂C₂X₂C₁₈. The two C₁₈ groups represent the hydrophobic tails; the X₂C₂X₂ group stands for the hydrophilic headgroup. The X segments carry some charge (specified below). Water was modeled by a simple solvent monomer W. The ionic strength of the solution was determined by two monomer types, cation and anion, with valency +1 e and −1 e, respectively. The contact energy between the hydrocarbon and water is reflected in the Flory-Huggins interaction parameter χ_{C – W}. χ_{C – W} is the most important parameter for membrane formation, as it is the driving force for self-assembly. The value was chosen to be χ_{C – W} = 1.6, similar to the value used in earlier studies (Meijer et al., 1994; Leermakers and Scheutjens, 1988b,a) and consistent with the dependency of the critical micelle concentration on the surfactant tail length (Leermakers et al., 1989). The χ_{C – X} and χ_{C – ion} are also set to 1.6 to mimic the unfavorable interactions of the X segments and ions with the hydrocarbons. The lipid headgroup was made soluble in water by choosing a χ-value of −2 for the interaction between the solvent W and the headgroup segment X. Of course, the ions will differ in their interactions with water from the lipid molecules. To make the interaction between the water and the ions more realistic, the χ-values were varied, as will be discussed in the Results. In all calculations, the following dielectric constants were used: ɛ_C = 2, ɛ_X = ɛ_cation = ɛ_anion = 5, and ɛ_W = 80.

RESULTS

Effect of the number of freeze-thaw cycles on vesicle size

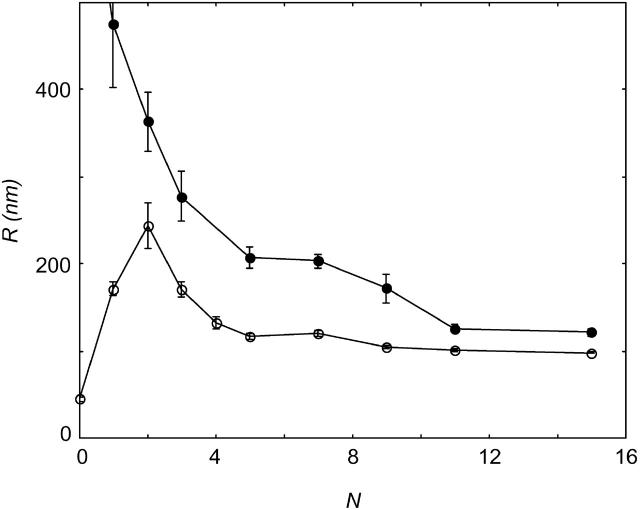
The effect of freezing and thawing on the size of phospholipid vesicles was investigated with dynamic light scattering. Fig. 1 shows the radius of DOPG vesicles in 200 mM (SUVs) and 300 mM (giants) NaBr solutions as a function of the number of freeze-thaw cycles.

FIGURE 1.

Radius of large multilamellar DOPG vesicles in 300 mM NaBr (•) and small sonicated DOPG vesicles in 200 mM NaBr (○) as a function of the number of repeated freeze-thaw cycles, N.

Giant DOPG vesicles fragmented into smaller ones during freeze-thawing. After 12–15 cycles, their size was judged to stabilize. When small unilamellar DOPG vesicles (SUVs) were subjected to the same procedure, they grew in size. Again, after 12–15 freeze-thaw cycles, their size did not change anymore. With increasing number of freeze-thaw cycles, the standard deviation of the vesicle radii distribution became smaller, indicating an increase in homodispersity. The final radius of the DOPG vesicles did not depend on the starting size, but was determined only by the ionic strength of the salt solution.

Evolution of vesicle size in time

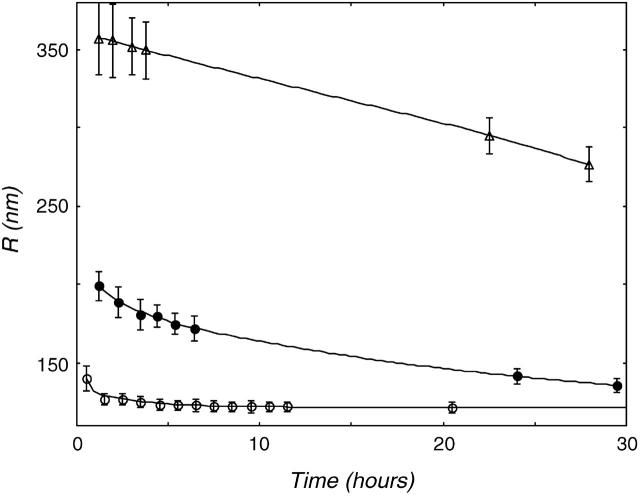
Though the starting size had no influence on the final vesicle size in the freeze-thaw experiment, it is not clear whether this size represents the stable size of the vesicle, or is just a result of the preparation method. Therefore, the size evolution of vesicles that were brought into suspension was followed in time. These vesicles were not subjected to the freeze-thaw method. Fig. 2 shows the results of the size evolution of DOPG vesicles in three different salt concentrations.

FIGURE 2.

Size evolution of multilamellar DOPG vesicles was followed in time. Data are shown for DOPG vesicles in (○) demineralized water, (•) 25mM NaCl, and (▵) 200mM NaCl. The higher the electrolyte concentration, the slower the vesicle size decreases. In demineralized water, the radius evolves to the radius found after 15 freeze-thaw cycles.

At all salt concentrations, the vesicle radius decreased with time, but the higher the ionic strength of the solution, the slower the observed size decrease. The initial vesicle radius, as it was found after suspending, was also significantly higher at higher salt strength. This is probably due to the increased screening of the charge on the phospholipid by the salt, which renders the phospholipid less soluble (Marsh and King, 1986; Cevc, 1993), giving rise to larger aggregates and a slower exchange of lipids between them. Vesicles normally change in size by the diffusion of lipid monomers between the vesicles (Madani and Kaler, 1990; Olsson and Wennerström, 2002). Only in the case of no added salt is the exchange of material between vesicles fast enough to reach a stable size. In demineralized water, the suspended DOPG vesicles evolved to the same radius as the ones obtained after the freeze-thaw experiment. This result implies that the vesicles we observe probably represent the entropically stabilized structure of charged phospholipids. If the exchange of material between the aggregates can take place fast enough, completely different methods of vesicle preparation give rise to vesicles of the same size. Apparently, the freeze-thaw procedure just accelerates the exchange of lipid and the reconstruction of vesicles.

Concentration dependence of vesicle radius

Below we will argue that the vesicles, produced by the freeze-thaw method, are entropically stabilized. In this case, one expects that there is an effect of dilution on size. Moreover, for membranes with a high bending modulus vesicles will only be stable in the very dilute regime. The values reported for the bending moduli of phosphatidylcholine (PC) membranes are in the order of 10–40 k_BT (Seifert and Lipowsky, 1995; Meleard et al., 1998; Rawicz et al., 2000), which is rather high. The dependence of the lipid concentration during production on the vesicle size therefore deserves attention.

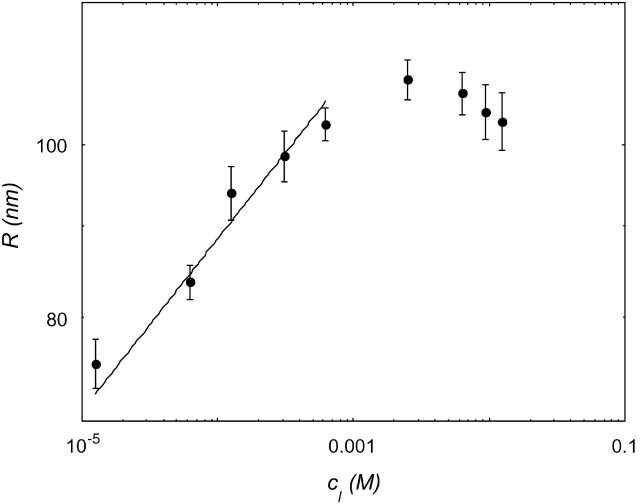
Suspensions of 10⁻³–10 mM DOPG were subjected to the freeze-thaw procedure. Fig. 3 shows the dependence of the vesicle radius, after 15 freeze-thaw cycles, on the phospholipid concentration (c_DOPG) in a 300 mM NaCl solution.

FIGURE 3.

Vesicle size as a function of the concentration of DOPG. Data are shown for DOPG in 300mM NaCl.

At a low lipid concentration, the size of the vesicles grew with increasing c_DOPG; the data can be fitted with a power ∼0.1.

In the case where the total curvature energy is lowered due to contributions of the translation entropy only, R is expected to scale 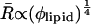(Safran et al., 1991). When the undulational entropy is also taken into account by renormalization of the bending modulus, R scales as 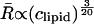(Simons and Cates, 1992; Herve et al., 1993). This value is very close to the experimentally found power law. It is therefore most likely that DOPG vesicles in salt solution prepared by the freeze-thaw method are stabilized by undulation entropy.

Around c_DOPG = 2 mM, the vesicle size stabilized, or decreased slightly with increasing c_DOPG. At these high lipid concentrations, the packing of vesicles becomes more dense (volume faction of vesicles, φ_vesicle ≈ 0.1), excluded volume interactions can no longer be neglected (Simons and Cates, 1992), and the radius levels off (or decreases slightly) with increasing c_DOPG.

DOPC behaved slightly different from DOPG. We were able to produce vesicles of DOPC in NaBr by freeze-thawing, but not in NaCl. In NaCl, multilamellar sheets were formed up to very high salt concentrations. At high concentrations of NaBr, a well-defined vesicle size was obtained after freezing and thawing, for different starting conditions. But at low concentrations of salt, the system phase-separated into a vesicle-rich and a lamellar phase. Therefore, it seemed interesting to have a look at the size of DOPG and DOPC vesicles in a range of salt concentrations.

Salt dependence of the entropically stabilized vesicle radius

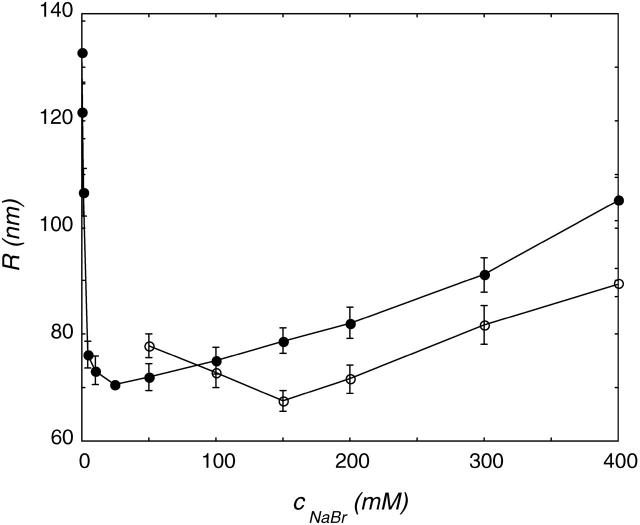
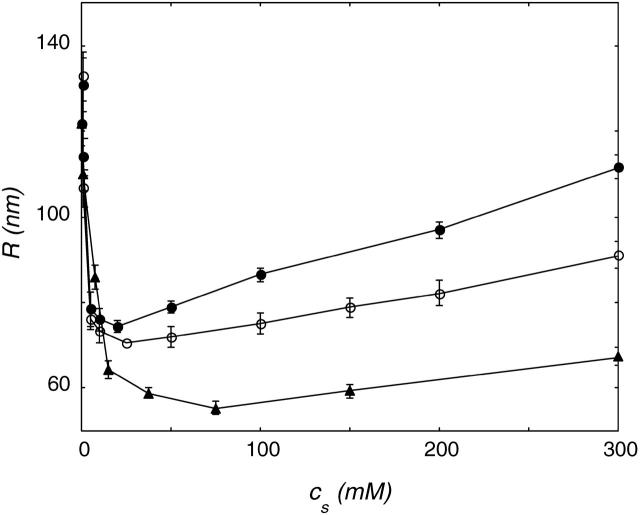
The freeze-thaw procedure was applied to DOPG and DOPC vesicle suspensions in a range of NaBr concentrations. The effect of the ionic strength on the final (after 15 cycles) vesicle radius is shown in Fig. 4.

FIGURE 4.

Size of DOPG (•) and DOPC (○) vesicles in NaBr after 15 freeze-thaw cycles as a function of ionic strength. The phospholipid concentration during freezing and thawing was 2 mg/ml. The R versus c_s curves can be divided into two regimes: at low ionic strength, the vesicle radius decreases, whereas it increases at higher salt concentrations.

In Fig. 4, two regimes are visible for DOPG vesicles. At a low NaBr concentration, the vesicle radius decreased with increasing ionic strength. At a low ionic strength, the radius of the DOPG vesicles decreased fast with NaBr concentration. At a high NaBr concentration, a modest size increase was visible with increasing salt strength. The freeze-thaw method only gave stable DOPC vesicles at high NaBr concentration. The radius of these DOPC vesicles decreased slightly up to 150 mM NaBr; in even higher NaBr concentrations, R increases with ionic strength. The slopes of the DOPG and DOPC curves at higher ionic strength were comparable, but here the less-charged DOPC vesicles are always smaller. At concentrations higher than 400 mM salt, the polydispersity of the samples increased, and with increasing salt concentration, aggregates became visible. At these high salt concentrations, the dynamic light scattering results were therefore assumed not to represent the radius of single vesicles.

It is known from literature that PC lipids in salt solutions behave in some ways as if they were slightly negatively charged (Tatulian, 1983). Despite their zwitterionic nature, PC lipid vesicles in salt solution show electrophoretic mobility. The charging can be ascribed to a binding of anions to the trimethylammonium group of the PC lipid. The net charge on the vesicle surface depends on the salt concentration and the kind of salt used. The order of effectiveness to increase the headgroup charge is in agreement with the lyotropic series; in this respect, I⁻ is more effective than Br⁻, and Br⁻ is more effective than Cl⁻. Comparing DOPG and DOPC vesicles in a certain salt solution is actually the same as comparing vesicles with a difference in surface charge density. Initially, a lower surface charge density gives rise to a slower size decrease. But at higher ionic strength, the curves for high and low surface charge density cross (Fig. 4). Vesicles with a low surface charge density reach a smaller vesicle radius at high ionic strength.

Ions do not only influence the vesicle radius by specific binding. Variations in ion hydration can have a large influence on vesicle size. To test the role of ion hydration on the radius of DOPG vesicles, three different salts in the lyotropic series were tested. In this series, the strength of hydration decreases in the order Cl⁻ > Br⁻ > I⁻. Fig. 5 presents the data obtained for DOPG in NaCl, NaBr and NaI solution.

FIGURE 5.

Radius R of DOPG vesicles as a function of ionic strength. Vesicles were prepared by freeze-thawing DOPG vesicles 15 times in NaCl (•), NaBr (○), and NaI (▴).

The initial size decrease with ionic strength was comparable for all salts used. However, at high ionic strength, the size of vesicles in NaI was always smaller than that of vesicles in NaBr, and these were in turn smaller than those in NaCl. The stronger the ion is hydrated, the more the bilayer membrane is dehydrated. Therefore, the ionic strength at which the vesicle radius starts to increase is much lower for strongly hydrated ions. As a consequence, vesicles reach smaller radii in solutions of weakly hydrated ions at high ionic strength.

Perturbations

Osmotic gradients over the lipid bilayer may force the vesicles to equilibrate to the new situation. When salts are used to apply this osmotic gradient, the vesicle radii can be compared to those obtained with the freeze-thaw method for different salt concentrations. The radius of vesicles, prepared in demineralized water, was observed to decrease when subjected to sudden increases of osmotic strength. A stepwise increase from 0 to 400 mM NaBr led to a decrease in the hydrodynamic radius of ∼40 nm. For vesicles in 400 mM NaBr, a decrease in the radius of ∼10 nm was observed when the salt concentration was lowered to 25 mM. The vesicles did not obtain the same size, but changed in the direction of those that were prepared by the freeze-thaw method.

Self-consistent field calculations

The mechanical parameters from the Helfrich equation can be determined unambiguously from SCF calculations. They follow from the curvature dependence of the interfacial tension (Oversteegen and Leermakers, 2000). The curvature of the bilayer can be varied by changing the number of lipid molecules in the system. For a given number of lipid molecules, the constrained (i.e., the geometry is an input constraint) equilibrium density profiles were calculated. From the resulting interfacial tensions of both a spherical and a cylindrical vesicle as a function of the vesicle radius, the Helfrich constants are calculated. For a cylindrical vesicle (K = 0, 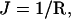and A = 2πRh, where h is the length of the cylinder), Eq. 2 can be written as

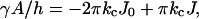(15)

in which h is the length of the cylinder. For a spherical vesicle (J² = 4K = 4/R² and A = 4πR²), γA can be written as

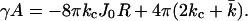(16)

Thus, k_c was determined from a cylindrical interface, by varying the total curvature J. This k_c was subsequently used to derive from the data on the spherical geometry. Fig. 6 shows the dependence of γA on the mean curvature J for a bilayer composed of C₁₈X₂C₂X₂C₁₈ in cylindrical lattice geometry.

FIGURE 6.

γA/h as a function of the mean curvature J for a lipid bilayer in a cylindrical lattice geometry at a volume fraction of salt, φ_s = 0.01.

As predicted in Eq. 15, γA depended linearly on J. By extrapolating the γA versus J data, J₀ can be calculated. For the one-component systems studied here, extrapolation of the γ versus J data to zero interfacial tension yielded a zero abscissa for all ionic strengths studied. This means that a bilayer composed of a single charged lipid species has no spontaneous curvature, J₀ = 0. The mean bending modulus k_c follows from the slope of the curve. Fig. 7 gives the corresponding result for a spherical vesicle.

FIGURE 7.

γA as a function of the vesicle radius R (lattice layers) at φ_s = 0.01. The calculations were performed in spherical lattice geometry.

The curve is in agreement with Eq. 16, provided that the vesicle does not have a spontaneous curvature. For small values of R, γA is no longer constant. One method to deal with small values of R (and large values of the curvatures J and K) is to extend the Helfrich equation to include higher-order terms in the curvature. When this route is chosen, one will obtain values for yet more mechanical parameters (related to terms of order 1/R⁴). One can also insist on the Helfrich equation (i.e., use only terms of order 1/R²). Then, the bending moduli k_c and 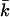become a function of R. Bilayer stability depends on the values of the bending moduli k_c and 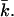Mechanically stable bilayers are only found if the total free energy of bending is positive. 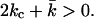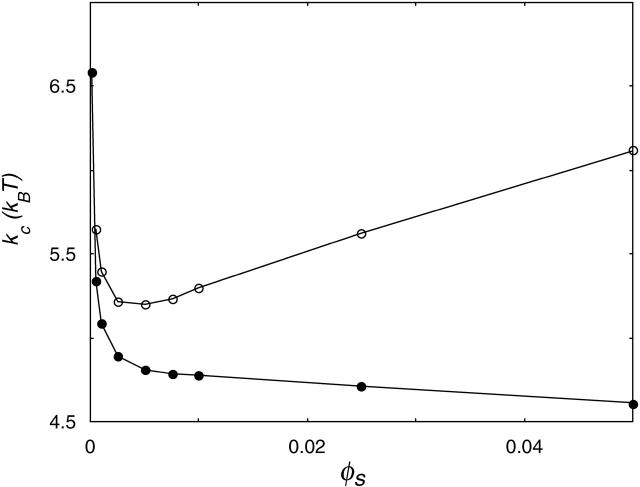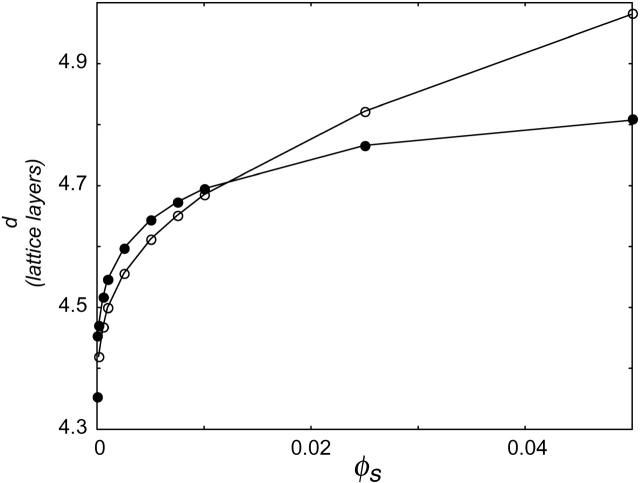In a spherical geometry, this means that At very low ionic strength, the total bending energy of the bilayers becomes negative and the vesicle will break up into small micelles. All the data shown below pertain to mechanically stable vesicles. It should be kept in mind that the k_c found in the calculations represents an intrinsic instead of an effective k_c, as shape fluctuations are not taken into account in the SCF calculations. To obtain k_c and 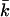for phospholipid-like bilayers, the calculations were first performed with the default choice of χ-parameters. This default choice can be made by assuming that, except for their charge, the electrolyte ions are identical to the solvent monomers in their interactions with water and the hydrophobic tails. The total charge on the headgroup was chosen to be −1; this corresponds to a valence of −1/4 per X. With these assumptions, k_c is found to decrease with ionic strength (Fig. 8). This decrease indicates that the bending is dominated by electrostatic effects. With increasing salt concentration, the diffuse double layer around the negatively charged vesicle surface will become thinner, and therefore k_c will decrease. However, the bilayer itself will become thicker, as closer lipid packing is possible when the charges get screened at high salt concentrations. The increase in bilayer thickness is apparently not as effective as the decrease in diffuse double layer thickness. The result is a decrease in total thickness of the bilayer plus the electric double layer, and therefore a decrease in k_c. The assumption that χ_{W − ion} = 0 is probably an oversimplification, as ions are hydrated. The introduction of a negative χ-parameter for the interaction between the solvent W and the ions therefore seems justified. When a value of −2 is chosen for χ_{W − ion}, two regimes become visible in the k_c versus ionic strength plot (Fig. 8). In the low ionic strength regime, k_c decreases, whereas at higher ionic strengths it increases significantly with salt concentration. Apparently, the increase in bilayer thickness overrules the decrease in double layer thickness at high ionic strength. As the ionic strength increases, the dehydration effect becomes more important. Membrane dehydration will cause the lipids to pack into a more dense bilayer at a high salt concentration (Fig. 9).

FIGURE 8.

Mean bending modulus, k_c, of a charged C₁₈X₂C₂X₂C₁₈ bilayer membrane as a function of the ionic strength. If ideal (athermal) interaction between water and ions is assumed (χ_{W − ion} = 0), k_c is decreasing (•); when ion hydration is taken into account (χ_{W − ion} = −2), two regimes become visible (○).

FIGURE 9.

Half the bilayer thickness d in lattice layers, as a function of ionic strength for χ_{W − ion} = −2 (○) and χ_{W − ion} = 0 (•).

The decrease in solvent quality causes the membrane to become thicker and thus k_c to increase; this effect is the dominating one at high ionic strength.

Our calculations can be further refined by making a difference in the affinity of cations and anions for the solvent W. Cations are known to be much smaller than anions; as a result their surface charge is more concentrated, and they are therefore more strongly hydrated. The difference in affinity of anions and cations for the solvent has been modeled by choosing a more negative value for χ_{W − cation} than for χ_{W − anion}.

Experimental results on the vesicle radius as a function of ionic strength were obtained for three different anions all with the same cation. The anions differ in their degree of hydration. The difference in hydration has been modeled in the calculations by choosing three different values for χ_{W − anion} while keeping χ_{W − cation} constant (Fig. 10).

FIGURE 10.

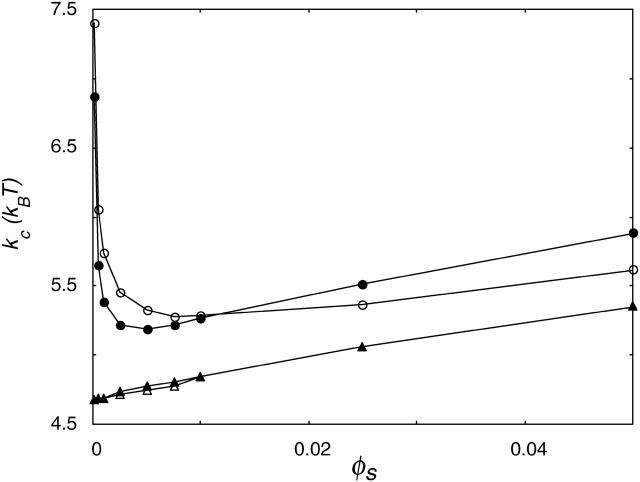
Mean bending modulus k_c versus ionic strength. Data are shown for χ_{W − anion} = 0 (•), χ_{W − anion} = −1 (○), and χ_{W − anion} = −2 (▴); in all cases, χ_{W − cation} = −2.

With decreasing χ_{W − anion}, the bilayer becomes slightly more dehydrated. The initial decrease in k_c with ionic strength is the same for all χ-parameters used; the differences can be found in the increase in k_c at higher ionic strength. The more negative the value for χ_{W − anion}, the lower the ionic strength at which the increase in k_c starts. As a result, lower k_c values are reached for lower values of χ_{W − anion}. The increase in k_c at high ionic strength is much faster for a high value of χ_{W − anion} than for lower values. Variations in the hydration of ions seem to be the main reason for the ion-specific behavior of k_c with ionic strength.

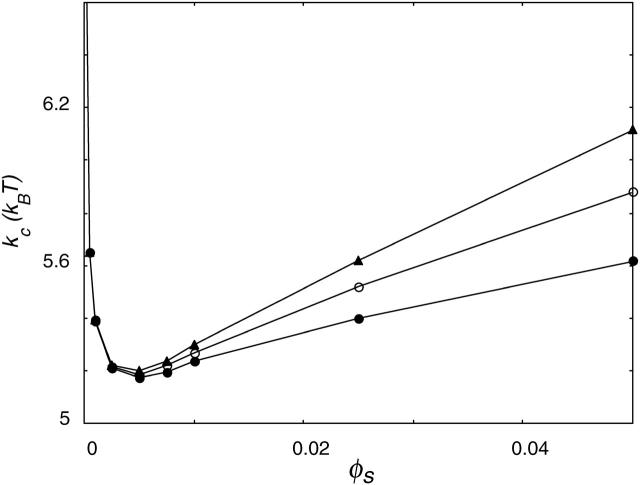
DOPG is a negatively charged phospholipid, whereas DOPC is zwitterionic. Until now, we only dealt with lipids carrying a net charge. These lipids are probably not representative for DOPC lipids. Therefore, the model lipid was slightly modified by replacing one of the X₂ segments by a segment Y₂ (C₁₈X₂C₂Y₂C₁₈), in which Y carries the same but opposite charge as X. Aggregates of these lipids behaved similar to vesicles of neutral lipids, as can be seen in Fig. 11.

FIGURE 11.

Mean bending modulus, k_c, of a bilayer membrane as a function of ionic strength. The charges on the lipids' headgroup were −1 (•), or −1/2 (○), or the headgroup was zwitterionic (▴) or not charged (▵).

On the other hand, it is well known from the literature (Tatulian, 1983) that vesicles of PC lipids in salt solution have an electrophoretic mobility. This effect has been ascribed to the specific binding of ions to the PC membrane. Anions increase the surface charge of PC vesicles, by specific binding to the trimethylammonium group, in the order of the lyotropic series, Cl⁻ < Br⁻ < I⁻ < SCN⁻ (Tatulian, 1983). But although PC membranes are supposed to have a net negative charge, this charge will not be as large as the charge on the anionic PG bilayers. To gain insight into the effect of the headgroup charge, calculations have been done for amphiphiles with a different headgroup charge. Fig. 11 shows k_c as a function of ionic strength for two headgroup charges. Again two regimes can be distinguished. The decrease in k_c is faster for lipids with a higher headgroup charge. In the decreasing regime, k_c of the higher-charged lipid is always smaller than that of the less-charged one. In the regime where k_c increases as a function of the ionic strength, it is the other way around: k_c of the higher charged lipid is always larger. The energy needed to curve a flat bilayer into a closed vesicle E_ves is determined by the sum of 2k_c and 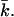If the bilayer has no spontaneous curvature, E_ves becomes

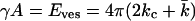(17)

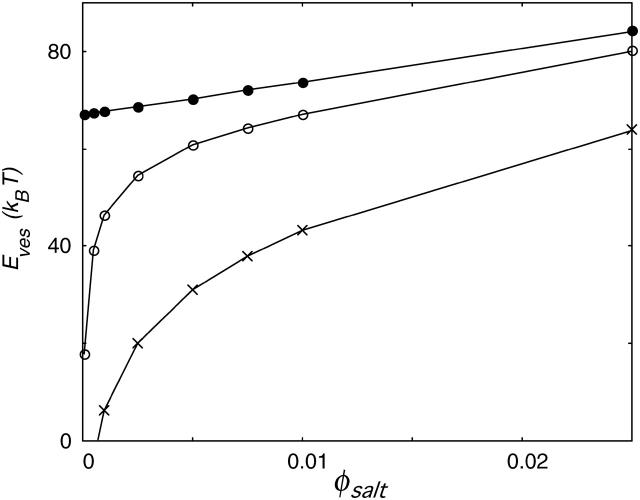
and can be determined from the calculations in a spherical geometry. The value of E_ves is of great interest for the understanding of vesicle stability. To get more insight into the behavior of the curvature energy of charged lipid bilayers with ionic strength, E_ves was calculated for bilayers composed of lipids that differ in headgroup charge (Fig. 12). In these calculations, we made use of the same parameter set as in Fig.11. For all headgroup charges, E_ves increases as a function of the ionic strength. But at all salt concentrations, the curvature energy is the highest for the uncharged bilayers and decreases with increasing headgroup charge. The differences in the bending energy of the bilayer between charged and uncharged lipids are particularly large at low ionic strength. For the charged lipid bilayers, E_ves becomes even negative at very low ionic strength. Then the mechanical stability of the bilayer is lost and the formation of micellar structures is preferred. With increasing ionic strength, the charge on the bilayer gets screened; the curvature energy therefore becomes comparable to that of the uncharged membrane. The mean bending modulus k_c is higher for the charged lipid bilayer compared to the uncharged membrane. The lower curvature energy of the uncharged bilayers must therefore be the result of more negative values of 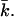The Gaussian bending modulus can be calculated from the known values of E_ves and k_c. Fig. 13 shows the behavior of 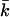as a function of salt concentration. For all headgroup charges, 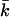becomes less negative with increasing ionic strength. The more negatively charged bilayers, however, have a much more negative value of 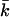at low salt concentrations.

FIGURE 12.

Curvature energy E_ves as a function of the ionic strength for bilayers that carry no charge (•), a charge of −2/5 e (○), and a charge of −1 e per lipid molecule (×).

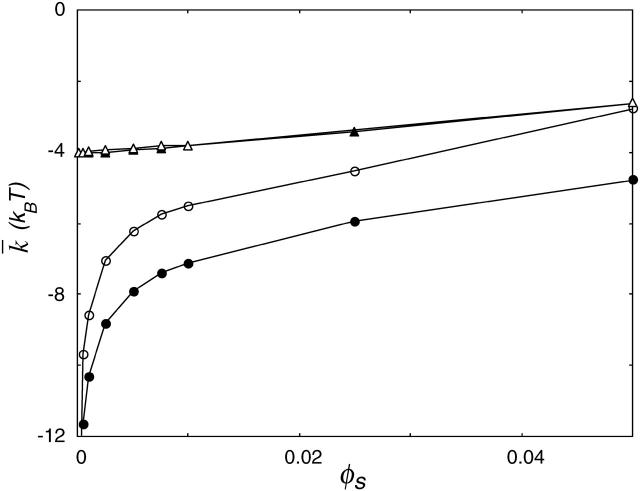
FIGURE 13.

Gaussian bending modulus, 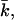of a bilayer membrane as a function of ionic strength. The value of 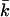strongly depends on the charge on the headgroup. The less charge on the headgroup, the closer the membrane is to 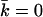. The charges on the lipids' headgroup were −1 (•), or 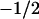(○), or the headgroup was zwitterionic (▴) or not charged (▵).

DISCUSSION AND CONCLUSIONS

Despite the high mean bending moduli that have been reported in the literature, our experiments indicate that (charged) phospholipid bilayers may form vesicles that are stabilized by entropy. The experiments show that vesicles in salt solution made by freeze-thaw experiments are very likely close to their entropically stabilized size. When vesicles are subjected to the freeze-thaw method, the initial size of the vesicles has no influence on the vesicle radius that is finally obtained (Fig. 1). The final vesicle radius only depends on the kind of salt, the salt concentration, the phospholipid concentration, and the phospholipid used. In addition, a complementary preparation method shows that, if the exchange of material between the vesicles is fast enough, vesicles tend to evolve spontaneously to the size obtained with the freeze-thaw method (Fig. 2). The fact that these vesicles do not form spontaneously upon addition of a salt solution is probably due to the very low solubility of the phospholipids. Although the critical micelle concentration (CMC) of charged phospholipids is much higher than the CMC of zwitterionic or uncharged phospholipid species, the CMC of the charged phospholipids decreases dramatically as the ionic strength increases (Marsh, 1986; Cevc, 1993). The bulk concentration of lipid becomes very low, and therefore the exchange of material between vesicles becomes slower with increasing ionic strength. Presumably, this is also the reason why phospholipid vesicles can be prepared in particular sizes and remain as such without fast reequilibration. In this respect, the freeze-thaw procedure is very helpful; it seems to be a method for fast vesicle equilibration. It is, however, not clear how the freeze-thaw procedure helps to redistribute lipid material between the vesicles. One possibility is that freeze-thaw cycling disrupts the vesicle membrane into small fragments, which recombine to form new vesicles. For vesicles of a single lipid species, the spontaneous curvature J₀ is expected to be zero; this was also found in the self-consistent field calculations. If the vesicles found in our experiments are in thermodynamic equilibrium, the curvature energy of the bilayer must be compensated for by entropy.

Our SCF calculations show that the curvature energy is a function of the charge on the lipid bilayer and the ionic strength of the solution (Fig. 12). At low ionic strength, the curvature energy of a charged lipid bilayer is considerably lower than that of a bilayer carrying less or no electric charge. At relatively low ionic strength, k_c and 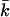of charged lipid bilayers are opposite in sign but of the same order of magnitude. The curvature energy of the charged lipid bilayer is therefore lower than what one would expect based on the value of k_c alone. At low ionic strength, the curvature energy of the charged lipid bilayer is probably low enough to be compensated for by entropy. For entropically stabilized vesicles, a dependence of the vesicle radius on the lipid concentration was predicted. In the limit where translational entropy plays a role, vesicles with 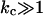are only stable at low volume fractions of lipid (Safran, 1994).

In our experiments, two regimes can be distinguished in the dependence of the vesicle radius, R, on the DOPG concentration. In the dilute regime, R increases with the lipid concentration. The power law dependence between phospholipid concentration and vesicle size agrees with the behavior predicted for vesicles that are stabilized by translational entropy and a renormalization of the bending moduli (Simons and Cates, 1992; Herve et al., 1993). At higher lipid concentrations, R stays constant, or decreases slightly with increasing lipid concentrations. There are several ways in which the additional membrane surface area that arises at higher lipid concentrations can be accommodated (Simons and Cates, 1992). The system can simply form a lamellar phase, or the vesicles can shrink in size and so accommodate the extra mass fraction while remaining at the overlap threshold, and finally the vesicles may become nested in onions.

It is not entirely clear which of the two last possibilities refers to our system. The system did not show any birefringence, and the polydispersity of the sample did not change much. The results we obtained with the SCF calculations on the behavior of k_c as a function of the ionic strength agree qualitatively with theoretical predictions. Using a Poisson-Boltzmann (Lekkerkerker, 1989) or a Debeye-Huckel (Winterhalter and Helfrich, 1988) approximation, it was shown that given a certain charge density, the electrostatic contribution to k_c, 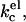decreases with increasing ionic strength. The decrease in 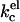can be attributed to a decrease in the thickness of the electric double layer. Increasing the ionic strength, however, also results in a screening of the charges on the lipid headgroups. In a real lipid bilayer, the predicted decrease in 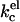is therefore partly compensated for by a closer packing of the lipids in the bilayer. As headgroup area adjustments are included in our SCF-calculations, the overall k_c we observe decreases not as fast as was predicted for 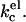When entropic contributions make the formation of vesicles possible by compensating for the curvature energy of the bilayer, the size of these vesicles is expected to be determined by the mean bending modulus of the bilayer. The trends seen in the k_c curves (calculations, Fig. 11) as a function of ionic strength strongly resemble those of the vesicle size (experiments, Fig. 4) as a function of ionic strength. When the vesicle size is indeed determined by k_c, the initial decrease in vesicle size can be attributed to the decreasing thickness of the diffuse double layer with increasing salt concentration. The size increase at high ionic strength is due to a thickening of the lipid bilayer. Calculations show that with increasing ionic strength, the membrane dehydrates, which leads to closer lipid packing, a thicker membrane, and therefore a higher k_c. The behavior of k_c observed at high ionic strength was not predicted by theory and can be understood in terms of ion and membrane hydration as will be discussed below.

To understand the effect of Cl⁻, Br⁻, and I⁻ on the bilayer membrane, ion hydration has to be taken into account. Cl⁻ ions are more strongly hydrated than Br⁻ and I⁻ ions; therefore, ions tend to dehydrate the membrane in the series Cl⁻ > Br ⁻ > I⁻. In the calculations, this was simulated by choosing different χ-parameters for the interactions between the anions and the solvent. The more negative χ-parameter corresponds to the more strongly hydrated anion. The cation Na⁺ is, due to its surface charge density, even more strongly hydrated than both anions and therefore its χ-parameter is the most negative. In the calculations, the most negative χ_{W − anion} gives rise to the highest k_c values. For entropically stabilized vesicles, higher vesicle radii are expected for higher k_c values. Ion hydration does not only affect the absolute value of k_c, the increase in k_c with ionic strength is also faster for the lowest χ_{W − anion}. Experiments on DOPG vesicles in NaCl, NaBr, and NaI show that the vesicles in NaCl are always larger than the ones in NaBr, and these are always larger than the ones in NaI. In the high ionic strength regime, the radii of the DOPG vesicles in NaCl also increase faster with ionic strength than similar vesicles in the other salt solutions. Also, for this situation, k_c from the calculations and the experimentally determined vesicle radius show the same trends in their behavior as a function of ionic strength (Figs. 10 and 5).