Basal Sliding and the Mechanics of Oscillation in a Mammalian Sperm Flagellum

Abstract

The mechanism of oscillation in cilia and flagella has been a long-standing mystery. This article raises the possibility of a mechanical explanation based on new findings relating to where in the flagellum microtubule sliding can occur—and where it cannot occur. All theoretical analyses of flagellar bending have until now made the assumption that sliding displacements at the base of the flagellum cannot occur. One consequence of this has been the need to accept that sliding must be transmitted through propagating bends, an idea that has been tolerated even though it becomes paradoxical if bends are the result of resistance to sliding. Our observations, of spermatozoa from the chinchilla, have led us to a contradictory view. We have shown directly, by light microscopy and by two methods of electron microscopy, that basal sliding does occur. Also, evidence from video microscopy indicates that a propagating bend cannot transmit sliding through it. We have analyzed a movement pattern in which the beat frequency increases fourfold in a phasic manner. Our analysis of this suggests that new bends terminate when no further sliding is possible. At this point the bend direction immediately reverses. That is, the flagellar beat frequency increases when there is a limitation to sliding. One can see directly the alternation in basal sliding direction under these circumstances. This suggests a mechanism for the initiation of a new bend in the opposite direction to the bend just completed: we propose that the initiating trigger is the reversal of elastic deformations at the base, which reverses the direction of interdoublet sliding.

INTRODUCTION

Eukaryotic flagella, and cilia, are characterized by rhythmic movement. Flagellar movement is often planar or near-planar and results in bends of alternating direction—this is the oscillation. The explanation for flagellar oscillation is unknown, despite a large body of relevant experimental work that extends back over many decades (reviewed by Brokaw, 1982, 1989).

An initial question is whether the oscillatory behavior is generated in some localized region of the flagellum. At first sight, it might seem obvious that “an oscillator” must exist at the flagellar base, because bending typically begins at the flagellar base and it is known that greatly shortened flagella continue to oscillate (Goldstein, 1981). But in a few well-documented flagella, the oscillation originates at the tip (Holwill and McGregor, 1976; Baccetti et al., 1989; Ishijima et al., 1994). Also, oscillations can sometimes originate in the flagellar shaft (Shingyoji and Takahashi, 1995; Woolley and Bozkurt, 1995; Woolley and Vernon, 2002) and oscillating forces have even been recorded from small groups of dynein arms on isolated doublets (Shingyoji et al., 1998). Nevertheless, the idea prevails that the beat frequency is controlled by some property of the basal region and that the basal region, as a pacemaker, dominates other possible oscillators (Douglas and Holwill, 1972).

The supposed basal pacemaker region, however, does not generate its rhythm independently of events in the flagellar shaft, for its frequency can be entrained mechanically (Murakami, 1963; Machemer, 1974; Okuno and Hiramoto, 1976; Eshel and Gibbons, 1989; Shingyoji et al., 1995), and, if the bending cycle is interrupted for a period, its phase when it restarts is unrelated to its phase before interruption (Murakami, 1963; Eshel et al., 1992), unless the wave is preserved in rigor (Tani and Kamimura, 1998). All this is evidence that the rhythm is not intrinsic but is in some way proprioceptive.

Now, it follows from the sliding doublet theory of flagellar bending (Satir, 1968; Brokaw, 1991; Vernon and Woolley, 2002) that the initiation of a new bend at the flagellar base involves a change in the sliding direction of the doublet microtubules (Gibbons, 1982). Thus the “proprioceptive problem” becomes: what change in the basal region causes a reversal of sliding direction? The change could be the development of a critical curvature (Brokaw, 1985). The apparently limiting effect of curvature has been followed visually when pairs of doublets show repetitive sliding (Kamiya and Okagaki, 1986). However, experimental reduction of basal curvature did not halt the oscillation (Kaneda, 1965; Okuno and Hiramoto, 1976). Also, oscillations that arise on the flagellar shaft can develop with very low (Woolley and Bozkurt, 1995; Woolley and Vernon, 2002) or even with zero curvature (Kamimura and Kamiya, 1989). Currently then, the mechanism that initiates sliding in new bends has not been identified.

Almost all the experimental work mentioned above has been performed on simple “9 + 2” flagella (e.g., from sea urchin sperm), where the axoneme has a diameter of ∼200 nm. In this work, however, we have used a mammalian sperm flagellum, the general structure of which is already well known (Fawcett, 1975). Here the 9 + 2 complex is augmented by extra, passive structures, the outer dense fibers (ODFs)—but as far as we know, the mechanism of motility is fundamentally the same, with the dynein architecture highly conserved (Bozkurt and Woolley, 1993). We have taken advantage of the fact that the base of the flagellum here is more than twice as thick as that of a simple flagellum and is relatively easy to observe. The structure that thickens the base is known as the connecting piece (Conn.P), a composite of nine segmented columns, each of which fuses distally to an ODF, which, in turn, attaches to the abaxial edge of its axonemal doublet microtubule (Fawcett and Phillips, 1969; Zamboni and Stefanini, 1971; Hamasaki et al., 1994).

The interpretation of sliding in this system has been that the force of sliding is transmitted to the sperm head through the Conn.P by the motion of the ODFs, driven by the doublets. The Conn.P forms an anchorage for the nine ODFs (Lindemann and Gibbons, 1975). In planar bending the “9 + 9 + 2” axoneme behaves as two functional “halves”, alternating with respect to sliding direction during each cycle of bending; the two ODF doublet subsets (9, 1, and 2) and (4, 5, 6, and 7) are thought to move relative to the ODF doublet 3–8 axis, which acts as a partition (reviewed in Vernon and Woolley, 2002). The pattern of active force generation among the nine doublets, deduced from the unidirectional polarity of dynein motors, is that activity in the 1–4 subset alternates with activity in the 6–9 subset, such that in a given location there will be active sliding within one of these subsets and passive sliding within the other (Wais-Steider and Satir, 1979). There is an unexplained asymmetry in the angles of the alternate bends (Woolley, 2003). The ODFs of mammalian spermatozoa provide increased stiffness. At the same time, they proportionately raise the bending torque, thus overcoming the additional flexural rigidity (Lindemann, 1996).

This study began with a chance new observation made on a motile chinchilla spermatozoon from which the head had become detached. The base was undergoing a repetitive shear distortion in phase with the highly asymmetric beat cycle. Part of our study uses light and electron microscopy to document this basal shear strain in intact spermatozoa. The remainder of the article explores the importance of basal strain in permitting bend growth, in regulating oscillation frequency, and more speculatively, in triggering sliding reversal and in imposing beat asymmetries.

METHODS AND MATERIALS

Spermatozoa were taken post mortem from the cauda epididymidis of adult chinchillas (Chinchilla lanigera). Small (unmeasured) quantities were allowed to suspend in 1 ml aliquots of Hanks' balanced salt solution supplemented with 3 mg/ml bovine serum albumin. Then, under a supported coverslip, at room temperature, ∼20 μl of the sperm suspension was interfaced against ∼20 μl of the same saline but now supplemented further with 2% w/v methyl cellulose (Sigma, St. Louis, MO) to give a nominal viscosity of 4.0 Pa s (4000 cP). The spermatozoa were vigorously motile after they had entered the viscous medium; they swam against the coverslip but nevertheless rolled (spun) about their progression axes. Eventually, however, some of the cells adopted planar waveforms against the coverslip, at first intermittently, then persistently (Woolley, 2003). These planar waves have been selected for study.

Video recordings were made of spermatozoa swimming with planar waveforms beneath the coverslip (Woolley, 2003). Dark-field illumination was used throughout, with either 40× or 100× oil immersion objectives. For further details of equipment, see Woolley (2003). The images in Fig. 2 were obtained by using a projector lens in front of the charge-coupled device camera. Video sequences were digitized and analyzed using a Scion LG-3 frame grabber and Scion Image, the PC version of NIH Image (Scion, Frederick, MD).

FIGURE 2.

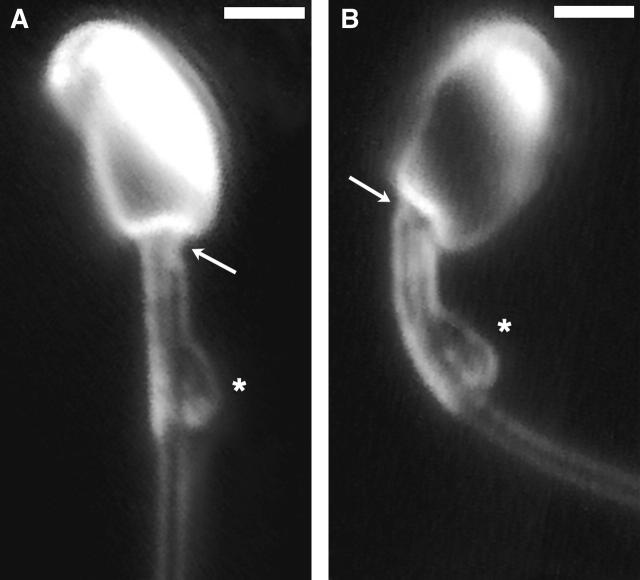
Images corresponding to Fig. 1 of an intact spermatozoon, showing how the basal angulation tilts the head. (A) At R_max, a niche is noticeable (arrow). (B) At P_max, the head engages in the niche but a gap opens up on the opposite side (arrow) as the connecting piece extrudes beyond the mitochondrial sheath. The cytoplasmic droplet (asterisk) has a constant, asymmetric position. Scale bar, 2 μm.

For publication, composite images were constructed by superimposing selected frames and offsetting them to avoid confusing overlap. Flagellar curvature was measured directly from the digitized sequences within Scion Image. Flagellar bend position was decided subjectively, then measured by fitting multiple straight lines to the image of the flagellum and summing their lengths. Flagellar bend angles (as in Fig. 7) were obtained as the included angle between perpendiculars to tangents drawn at the base and first interbend.

FIGURE 7.

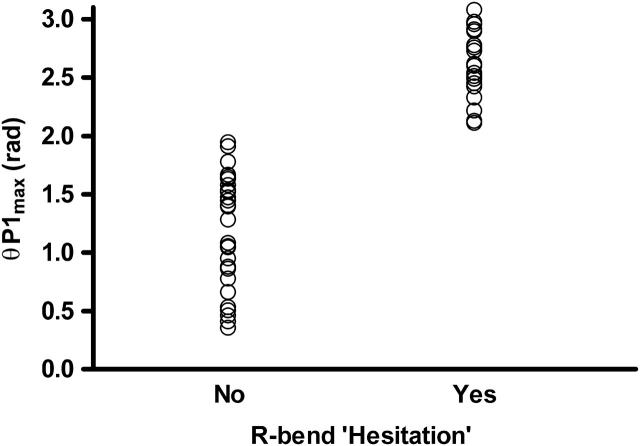
Measurements of the maximum angle reached by bend P1, taken from 21 beat cycles, from six spermatozoa. They are arranged in two columns according to whether or not bend P1 was followed by hesitations (i.e., rapid oscillations before the next full-size R-bend). The angle was measured just before the hesitations or normal propagations began.

Excised pieces of cauda epididymidis were processed for electron microscopy by a standard method (Vernon and Woolley, 2002). Serial transverse sections of the sperm neck were photographed from silver-gold sections; silver-gray sections were used for the longitudinal sections. The images from serial transverse sections were digitized using a negative scanner, and models constructed using WinSurf, a three-dimensional reconstruction software package for PCs (SURFdriver Software, Kailua, HI).

RESULTS

The evidence for basal sliding in chinchilla spermatozoa

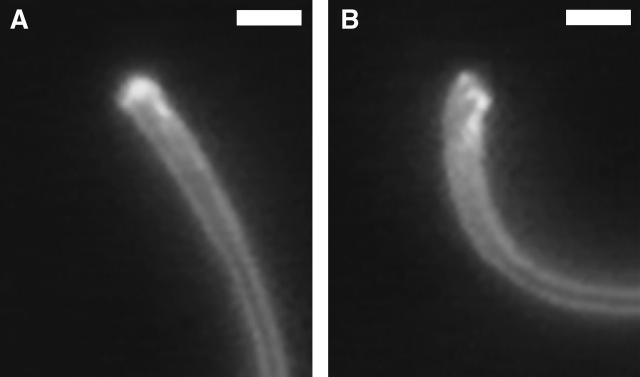
Basal sliding, in principle, may occur in two ways: 1), by inducing compressive and tensile strain in the columns of the connecting piece, and 2), by inducing shear strain between the opposing columns of the Conn.P. The first type of strain, which by itself produces no angulation in the basal profile of the neck and no tilting of the head, is the type previously detected in Chinese hamster spermatozoa (Vernon and Woolley, 2002); it is sliding that is accommodated without being manifested as bending. The second type does affect the profile of the flagellar base and does tilt the head; these effects are more easily visible by light microscopy. We first observed the rhythmic change in basal profile in a motile spermatozoon that had become decapitated (Fig. 1). The sperm swam just beneath the coverslip, with a planar waveform, for an indefinite period. Its cycle of bending was asymmetric and the P-bend (greater angle) produced a much greater change in basal profile than the R-bend (Fig. 1). This phenomenon could be recorded in intact spermatozoa (Fig. 2), in which it was easier to see that the neck structures on the left-hand side of the image had extended out of the mitochondrial sheath at the maximum development of the principal bend (Fig. 2 B).

FIGURE 1.

Video frames of the basal end of a headless chinchilla spermatozoon at the maximum growth of (A) the reverse bend (R_max) and (B) the principal bend (P_max). At P_max, there is a distinct angulation of the basal profile; at R_max there is a very slight angulation in the opposite direction. Scale bar, 2 μm.

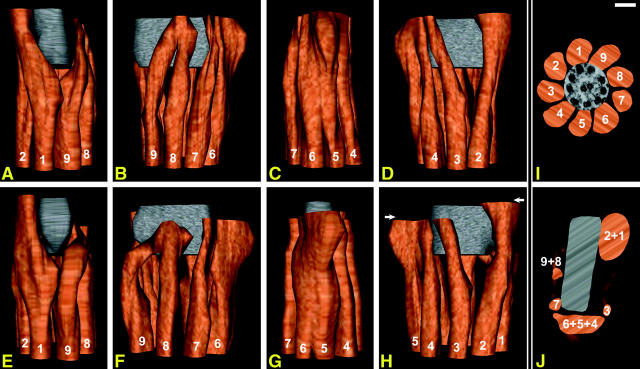
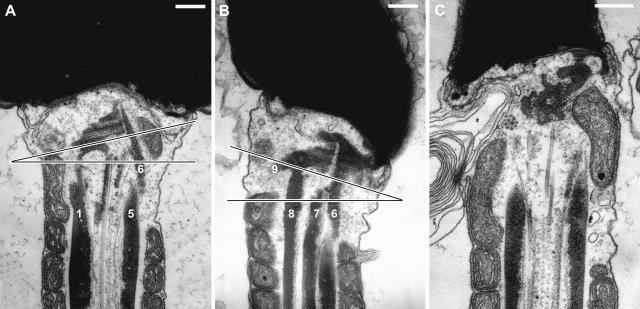
From electron microscopy, the basal shear strain could be related to the structures within the neck. Four reconstructions of the neck were made, and two of them are shown as Fig. 3: each is presented in a row of four images (Fig. 3, A–D and E–H), rotated successively by 90° to give views of the dorsal, right, ventral, and left sides in that order (arbitrary anatomical terms used by Woolley, 2003). The structures shown in these reconstructions are surface models of the ODF-Conn.P system. The columns are built of the transversely striated Conn.P proximally (upper part of reconstruction) and the ODFs distally (lower part). (The points of fusion between the Conn.P columns and ODFs cannot be decided from transverse sections, though we can say that the transition from ODF to Conn.P columns occurs about halfway up the reconstructions.) Views of the neck from the distal and proximal ends are also included (Fig. 3, I and J, respectively). The proximal centriole is given a gray color. To recall the difference between a mammalian sperm flagellum and a simple flagellum, the position of the 9 + 2 axoneme is shown on the distal surface of Fig. 3, I. No attempt is made to picture the well-known reduction and disappearance of the 9 + 2 axoneme in the more proximal part of the neck.

FIGURE 3.

(A–D) A reconstruction, based on serial transverse sections of the neck region, rotated to provide four orthogonal perspectives. The side view, corresponding to that in Fig. 2 A, is in B. The individual outer dense fibers are numbered and colored orange-brown. The level at which an ODF fuses to its connecting piece column could not be established from transverse sections. The proximal centriole has been colored gray. (E–H) Another example, but showing shear displacement, with the fused columns 1 + 2 extending more proximally than the fused columns 4 + 5 + 6 (displacement arrowed in H). The side view, corresponding to that in Fig. 2 B, is in F. (I) A view of the reconstruction (A–D), looking from the distal end toward the proximal end. A cross section of the 9 + 2 axoneme has been superimposed to show its relationship to the ODFs. (J) The reconstruction (A–D) again, looking from the proximal end. Arbitrary texture maps have been applied to the surface of the models. Scale bar, 100 nm. Supplementary videos show rotation sequences of these reconstructions.

If the reader examines the aspect of the sperm neck in Fig. 2 A, then the corresponding aspect in the reconstructions is Fig. 3 B. Detailed analysis of the reconstructions showed that Conn.P columns 3, 7, 8, and 9 terminate on the sides of the proximal centriole; the remaining two groups (1 and 2, and 4, 5, and 6) fuse into two masses, M₁₊₂ and M₄₊₅₊₆, between which lies the proximal centriole, approximately in the plane of the beat, and with its open end toward M₁₊₂ (Fig. 3, A–I). From this, it would seem that basal shear strain must involve the alternating protrusion and retraction of these two masses and tilting (and possible stretching) of the proximal centriole. Protrusion and retraction were confirmed in our second reconstruction, which showed that basal shear strain can be preserved by routine chemical fixation (Fig. 3, E–H). Thus the reconstruction of Fig. 3, E–H, has fortuitously preserved the displacements found at the maximal development of the principal bend. The aspect of the neck presented in Fig. 2 B is represented by the image in Fig. 3 F. In Fig. 3 H, the shear displacement is indicated by the separation of the two white arrows.

Evidence for dynamic tilting of the proximal centriole emerged from a series of 14 longitudinal sections cut approximately in the plane of the beat. The angle of the long axis of the proximal centriole, relative to the flagellar axis, showed extreme values different by 0.44 rad (Fig. 4, A and B). The latch-like shape of M₄₊₅₊₆ over the base of the proximal centriole may promote its tilting during P-bending (Fig. 4 B).

FIGURE 4.

Electron micrographs of longitudinal sections through the neck. (A and B) Images chosen to show the variable angulation of the long axis of the proximal centriole, believed to result from basal shear strain. The numbering of the ODFs is based on Fig. 3. The niche (absence of mitochondria) shown in Fig. 2 A is seen on the right-hand edge of each specimen. (C) Section in a plane cutting the proximal centriole transversely, to show that the neck implants at one edge of the head (the right-hand edge, as shown). Scale bar, 200 nm.

All these observations refer to basal shear strain. It has not been possible to measure tensile and compressive strains in the columns of the Conn.P (i.e., changes in periodicity).

We next needed to establish formally the relationship between the neck reconstructions of Fig. 3 and the asymmetry of the bending cycle seen in Fig. 2 (which has already been pointed out). In thin sections (e.g., Fig. 4, A and B), we saw a characteristic gap in the mitochondrial sheath, opposite ODF doublets 4 and 5. Since this feature could be seen in living spermatozoa, as a permanent niche accommodating the baso-lateral angle of the sperm head at the moment when the P-bend is maximally developed (Fig. 2), it is certain that the full development of the P-bend involves the basal protrusion of M₁₊₂ and an upward tilt and possible stretching of the proximal centriole. The mitochondrial morphology is thus adapted to this bending asymmetry. Development of the R-bend by contrast involves a relative basal protrusion of M₄₊₅₊₆, though to a lesser extent. Several other structural cues, such as the consistent positioning of the cytoplasmic droplet on the ODF doublet 5, 6 edge (from electron microscopy) and its position on the convex side of the R-bend (from light microscopy), confirm these conclusions. This establishes that the direction of sperm head asymmetry and the direction of bend asymmetry, in relation to the numbered ODF doublets, are the same as in the mouse (Woolley, 2003).

The serial transverse sections revealed a further feature, relevant to the kinematics of mammalian spermatozoa. The implantation fossa in the base of the sperm nucleus, to which the base of the flagellum is attached, is much nearer one surface of the head than the other (conveniently seen in Fig. 4 C): it is nearer the surface of the head that is against the coverslip in Fig. 2. (Applying the thrust asymmetrically in this way may add a hydrodynamic component to the observed tilting between head plane and beat plane that causes such spermatozoa to become trapped at liquid—solid and liquid—air interfaces (Woolley, 2003).)

The flagellar oscillation is influenced by antecedent bends

It was possible to recognize a characteristic bending pattern on the flagellum and relate it to the basal shear strain visible at the neck. Though first observed in a headless flagellum, where the change in basal profile is most obvious, the pattern was later confirmed on numerous intact spermatozoa. The key feature is that the flagellum seems to “hesitate” several times at a certain phase of the cycle before it proceeded to form a bend.

The “hesitating” pattern was characteristic of sperm at the surface of the coverslip that were executing two-dimensional waves—the hesitations occurred when these waves included P-bends of large angle (as will be shown). The change to this pattern was reversible: rolling sperm were seen to approach and stabilize at the surface, to adopt the hesitating pattern for a few cycles, then to swim away, rolling again, usually without the hesitations.

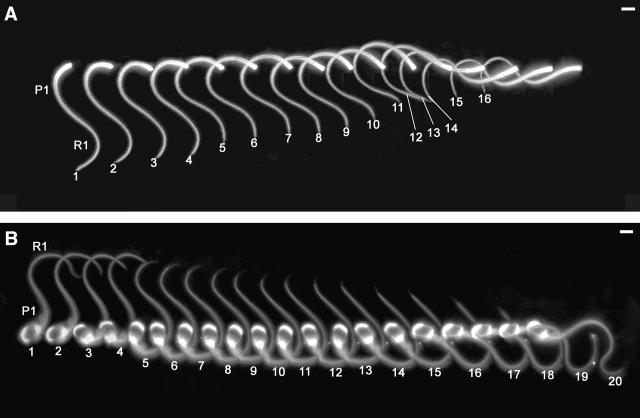
The hesitating pattern is illustrated in Fig. 5. Beginning with that stage of the cycle shown by image 1 in both panels of Fig. 5, the stage at which a bend R1 is already far down the flagellum and a P-bend, P1 is nearing full development. There is distinct rostral protrusion of M₁₊₂ from the flagellar base (best seen in panel A, images 1–3, but also seen enlarged in Figs. 1 B and 2 B). The following R-bend is so reduced in angle that it merely reduces the angle of P1 slightly. But it is clearly seen as a straightening of the proximal flagellum and there is a concomitant loss of basal angulation—the basal profile becomes perpendicular (image 4 in panel A; image 6 in panel B). Because of its small angle, at most ∼0.7 rad, this cryptic R-bend is denoted R2. Next, the basal curvature reverses again, signaling the next P-bend, but this is of similar small angle (hence P2) and simply restores the angle of P1, causing another maximal protrusion of M₁₊₂ from the base. Thus there is no persistence of R2 on the flagellum, nor of a recognizable P2. This sequence of alternating small angle bends repeats several times: ….R3….P3….R4….P4…. (see legends for the detail). It is this that gives the appearance of hesitation in the full development of an R-bend (see also supplementary videos). The next fully formed R-bend will be called R6 (arbitrarily, since the number of hesitation cycles is variable. It does not develop until the moment that bend R1, the last fully formed R-bend, has entirely propagated off the tip of the flagellum. When R6 develops fully, it achieves an angle of ∼1.2 rad. At its height, there is a slight rostral protrusion of M₄₊₅₊₆ from the flagellar base such that the angulation in the basal profile deviates slightly from the perpendicular in the opposite direction to when P1 was fully developed (enlarged in Figs. 1 A and 2 A). After R6 has begun to propagate, the next full-scale P-bend, P6, begins to grow—without any hesitations—and reaches its full angle. The early stages of the growth of P6 are seen in Fig. 5 A, images 15 and 16, and in Fig. 5 B, image 20. With P6 reaching maximum development, the whole cycle repeats indefinitely.

FIGURE 5.

(A) Sequential images, from left to right, of a headless sperm in motion, during a beat cycle that showed “hesitation” in developing the reverse (R) bend. Bends P1 and R1 are identified in image 1. P1 reaches its greatest curvature proximally in image 3. Then in image 4, a slight proximal straightening indicates that the cryptic bend R2 has developed. Image 5 shows the cryptic bend P2. The rapid oscillation continues with cryptic R-bends in images 6, 8, and 10, and cryptic P-bends in images 7, 9, and 11. Only when bend R1 finally leaves the tip, in image 12, does the next full-size R-bend develop (images 13 and 14), followed without hesitation by (the first stages of) the next full-size P-bend (images 15 and 16). Duration of sequence 3.84 s. Time intervals (left to right) were 0.23, 0.12, 0.07, 0.41, 0.12, 0.12, 0.07, 0.17, 0.36, 0.67, 0.36, 0.41, 0.43, 0.24, and 0.05 s. (B) Sequential images, as in A but showing an intact sperm. P1 reaches its maximal angle in image 5. Cryptic R-bends are maximally developed in images 6, 8, 10, 12, and 14. Cryptic P-bends are seen in images 7, 9, 11, and 13. Bend R1 leaves the tip in image 15. Only then does the next full-size R-bend develop (images 16–19), followed immediately by the next full-size P-bend (beginning in image 20). Duration of sequence 3.54 s. Time intervals (left to right) were 0.12, 0.24, 0.05, 0.72, 0.07, 0.17, 0.07, 0.14, 0.05, 0.12, 0.12, 0.19, 0.29, 0.12, 0.24, 0.19, 0.17, 0.24, and 0.24 s. In both A and B, the individual frames have been selected to show the peaks of the oscillation, which is more obvious in B because of the tilting of the head. At this scale, the basal protrusions in A are difficult to see but are represented in Fig. 1. The sequence of frames has been spread from left to right to minimize confusing superimposition. Frame-by-frame quantitative analyses of these specimens is given in Fig. 6, A and C. Scale bar, 4 μm. (Also see supplementary videos.)

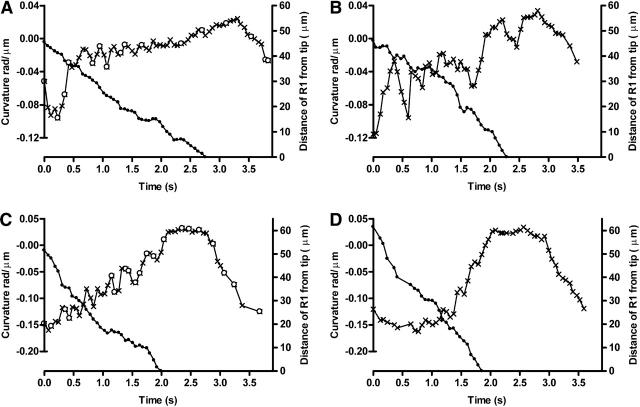
These events are shown graphically in Fig. 6, A and C (which correspond to the images in Fig. 5, A and B). Further examples are shown as Fig. 6, B and D. Here, the curvature of the proximal flagellum is plotted against time. It shows the hesitation sequences and the fact that they come to an end when the trailing edge of bend R1 has propagated off the flagellar tip.

FIGURE 6.

(A) Frame-by-frame analysis of the movements illustrated in Fig. 5 A. The curvature of the proximal 10 μm of the flagellum is plotted using a mixture of open circles and crosses; the open circles represent video frames illustrated in Fig. 5 A. The curvature is seen to oscillate rapidly until the trailing edge of the antecedent full-sized R-bend (solid circles) has propagated off the tip. Downward deflection of curvature represents cryptic P-bends. (B) Another example of a hesitation cycle from the same headless sperm. (C) Frame-by-frame analysis, as in Fig. 6 A, of the intact specimen illustrated in Fig. 5 B. (D) Another example from a different intact sperm. In all four graphs, the velocity of propagation of the full-size R-bend shows irregularities that may possibly be related to the oscillatory movements on the proximal flagellum.

It is likely also, from the graphs (Fig. 6), that the propagation velocity of R1 is modulated in a rhythmic way by the hesitation oscillations on the proximal flagellum. However, the positional judgments are too problematical to answer the question, “Do bends R2, R3, etc., accelerate or retard bend R1?”. A related question is whether the velocity of propagation of bend R1 is different in hesitating versus nonhesitating sperm. This was tested by finding sperm that showed phases of hesitating cycles interspersed among phases of nonhesitating cycles. Five of these very rare cells were located. In each situation, we compared the propagation speed of an R-bend over the distal 50 μm of the flagellum. The five pairs of velocities were (Hesitating:Nonhesitating) 70:79, 53:58, 40:76, 40:78, and 46:77 μm.s⁻¹. The mean rise in propagation velocity when the hesitation ceased was 54.9%. The difference between the means of the two sets of velocities was significant (P < 0.05).

The average frequency (± SD) of the hesitation phase cycles was 6.7 ± 1.9 Hz (n = 21, from six sperm). The average beat frequency of cycles without hesitation was 1.6 ± 0.4 Hz (n = 6 spermatozoa, 4–8 cycles from each). Thus the hesitation phase is a time when the oscillation or beat frequency increases fourfold. The importance of a large P-bend angle in predisposing the flagellum to the hesitation oscillations is documented in Fig. 7. The critical P-angle necessary for hesitation was ∼2 rad.

DISCUSSION

It is important to consider first whether hesitating chinchilla sperm are functioning normally. The amount of basal shear displayed is certainly greater than in other mammalian spermatozoa that we have examined. We could not detect it at all in the mouse, for example, even though an early three-dimensional reconstruction showed that the connecting piece fuses into two masses, similar to those described here (Iwashita and Ōura, 1980). Neither have we been able to see basal shear in rat spermatozoa. This is less surprising since the connecting piece in the rat seems to fuse into a cylinder (Woolley and Fawcett, 1973). However, the spermatozoa of all mammals (and many birds) have striated connecting piece columns, and we assume that basal sliding will occur by compressive and tensile strains in these columns, whether or not it produces a visible degree of basal shear strain. The large basal strain in chinchilla sperm relates to a large principal bend and a pronounced tilting of the sperm head. There is a cavity in the mitochondrial sheath that accommodates the angle of the sperm head, suggesting that the degree of tilt is not abnormal. Spermatozoa swimming with hesitations at the coverslip sometimes swam away, deeper, and resumed the typical rolling movement, which indicates that their movement at the surface was not pathological, at least not irreversibly so.

We think it plausible that in free-swimming spermatozoa, some of the basal strain is accommodated in torsion. It has been argued that torsion in the neck region at the point of full bend development is responsible for the three-dimensional flagellar waveform in mammalian spermatozoa (Woolley, 2003).

Interpretation of the ‘hesitating’ bending pattern

Following the notation of Brokaw (1997), the sliding that generates a P-bend at the flagellar base is P-sliding; sliding that generates an R-bend is R-sliding. From our ultrastructural results, doublets 1–4 are active in P-sliding and doublets 6–9 are active in R-sliding—based on the common assumption that dynein can operate only as a minus-end-directed motor. P-bend propagation is driven by R-sliding, and R-bend propagation is driven by P-sliding (Gibbons, 1982; Brokaw 1997).

In the conditions for hesitation, we argue the following:

1. P-sliding generates bend P1, contributes to the growth of bend R1, and continues in the propagation of R1 (Fig. 5, first images). The basal shear due to this P-sliding is clearly seen on the protrusion of M₁₊₂. Our calculations suggest that none of this sliding need be transmitted through the R-bend propagating on the distal flagellum.

2. The proximal flagellum should next switch to R-sliding. R2 should grow and P1 should move rapidly distally. But R2 is cryptic (denoted R2) and the curvature of P1 is reestablished proximally by P2.

3. This situation is relieved when R1 is lost from the tip. We conclude that the propagation of R1 limits sliding on the proximal flagellum (i.e., “synchronous sliding” does not occur). This mechanical interaction is further supported by the effect that bends R2, R3, etc., may possibly have in modulating the propagation speed of R1. The conclusion that propagating bends are regions that do not allow the transmission of sliding was anticipated in our earlier study of mouse spermatozoa (Woolley and Vernon, 2002). In general it accords well with the plentiful evidence that flagellar bends, once they have begun propagating, are structurally stable, as compared with developing bends (Eshel et al., 1990; Shingyoji et al., 1991) or with interbend regions (Woolley and Vernon, 2001).

4. A surprising deduction from the above is that R-sliding proximally (doublets 6–9 active) is being prevented by P-sliding distally (doublets 1–4 active), i.e., within the propagating R1 bend. This forces us to propose that doublets 6–9 must also be actively involved in propagating R1—with their polarity of force generation necessarily reversed!

5. The hesitation results only when P1 exceeds ∼2 rad. We conclude that bend R2 can grow normally if P1 still has capacity for growth (by R-sliding throughout the R-P bend pair). We think that P1 bends >2 rad may be at the limit of their curvature. This means that the cryptic R2 bend can grow only through basal sliding.

6. We now investigate whether the amount of basal sliding required for the growth of R2 is credible in terms of the ultrastructure. We assume that the ODF-doublet structure is itself neither compressible nor extensible. The cryptic R2 bend involves a loss of angle in P1 of at most ∼0.7 rad. To calculate the sliding necessary for this (ΔL), one has to use an estimate of functional diameter (d), i.e., the distance between the centers-of-mass of the ODF doublet complexes in the bending plane (Vernon and Woolley, 2002). Our estimate of the average d for the proximal 10 μm of the flagellum is 350 nm. The estimate of ΔL is given by dθ (Satir, 1968). Thus bend R2 is underlain by ∼245 nm of sliding. Now, the basal shear strain is measured by constructing a perpendicular to the tangent drawn to the flagellar axis, at the base, and measuring the deviation (α) of the basal surface from this perpendicular. The sliding (Δs) underlying a given change in basal angulation (Δα) is given by 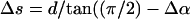). For the change from P1 to R2, our estimate of Δα was 0.37 ± 0.17 rad, (n = 7). Taking d, the basal diameter, to be 450 nm (Fig. 3 J), Δs is ∼75 nm. Therefore, we conclude that the change from bend P1 to bend R2 must involve the provision of 245 − 75 nm, i.e., 170 nm, of sliding accommodated as compressive/tensile strain, meaning a ±85 nm length change of the columns of the Conn.P on each edge as they change from being loaded in one direction to being loaded in the other. This limiting strain in the columns is credible, since their length in fixed cells is ∼600 nm.

7. Thus bend R2 seems to be terminated when no more sliding is possible. It is immediately followed by P-sliding, giving bend P2, also cryptic in that it merely restores the prior curvature of P1 and renews the basal protrusion. The development of P2 will involve the reversal of the sliding that formed R2, and it terminates when no more sliding is possible (either at the base, within P1, or through R1). Under these circumstances, bend termination and the reversal of sliding direction occur when basal sliding reaches its limit. This oscillation continues while R1 propagates. The hesitation can be regarded as a phase of high-frequency oscillation.

8. At the end of this high frequency (hesitation) phase, when R1 finally leaves the flagellum, an R-bend (say R6) now develops to an angle of ∼1.2 rad, at which point the R-sliding has produced a slight basal shear strain (protrusion of M₄₊₅₊₆).

9. The following full-size P-bend (P6) develops most of its angle while P1 is still propagating (data not presented). We assume that the propagating P1 blocks proximal P-sliding (the reciprocal scheme to that described), and that the P-sliding underlying the considerable growth of P6 is distributed between the basal strains and additional growth of R6 (i.e., until P1 is lost from the tip). This last point requires confirmation when suitable analytical methods have been developed.

10. Data for the propagation speed of the R-bends indicate clearly a retardation during the hesitation cycles as compared with nonhesitating cycles. Our preferred interpretation is that in a nonhesitating cycle, the presence of a following P-bend causes the R-bend ahead of it to travel more quickly. This echoes the phenomenon described in iii above, where the higher frequency bending proximally seems to modulate the speed of R1 distally. The cause of these interactions is unknown.

General implications for the mechanics of flagellar oscillation

In this article, basal shear strain has been demonstrated and compressive/tensile strain has been inferred. In a previous article, using a different species, we showed compressive/tensile strain both visually and as reflected in the tip displacements (Vernon and Woolley, 2002). Since these deformations recur indefinitely, without any disruption, they must be regarded as elastic. It is recognized that the oscillation involves a reversal of sliding direction, and this implies a termination of activity in one dynein subset (at the proximal flagellum) and an initiation of activity in the opposing subset (Brokaw, 1982). We have found that bend termination occurs when the scope for further sliding tends to zero. From this, we theorize that resistance to further sliding terminates activity in the dynein, representing a stalling force. At this point, the composite basal strain can unload and will reverse the direction of sliding. Sliding that was in the active direction becomes sliding in the passive direction. The converse will also be true because the active sliding just terminated will have loaded (i.e., deformed) the connecting piece as a whole, owing to the fusions within it, and the linkage through the proximal centriole, and also because basal sliding will have occurred in the passive set (since the distal sliding restriction will have applied to both sets of doublets). Finally, oscillation is explained if passively generated sliding in the active direction triggers dynein arms to become active. Hence a reciprocating motion will become established. Thus we are proposing that the connecting piece, through its elasticity, is the switching device at the flagellar base.

In this study, the rebound action of the connecting piece will have been controlled by the sliding resistance coincident with the propagating bend. But a sudden rebound, with overshoot, was seen in our study of hamster sperm flagella, where there were no propagating bends to slow the effect (Vernon and Woolley, 2002).

This explanation for the oscillation might be true for all cilia and flagella if the role of the connecting piece could be played by the basal body. Perhaps the intertriplet links, the basal plate, and the “cartwheel” linkages deform elastically. There is no mention of this in the literature, except for a comment on a micrograph of Elliptio cilia, in which a basal body showed shear strain (Warner and Satir, 1974). Kinosita and Kamada (1939) proposed that elastic deformation of ciliary rootlets triggered the ciliary stroke. Eshel and Gibbons (1989) speculated that linear compliance of the doublets might explain the high basal sliding velocities seen when beat frequency was imposed on sea urchin spermatozoa. Brokaw (1989) has discussed the bending elasticity of the doublets as a possible switch for the direction of active sliding.

If elastic materials are responsible for timing the oscillation, subordinate oscillations might become explicable. Very high frequency oscillations (Kamimura and Kamiya, 1989) might be based on the elasticity of radial spokes or nexin links. Minor, propagating oscillations (Woolley and Vernon, 2002) might be based on the elasticity of dynein cross-bridges. The apparent need for a basal anchorage to establish regular oscillations (Woolley and Bozkurt, 1995) is perhaps the need for an anchorage with appropriate elasticity. Beat asymmetry might be explained by anisotropy in the basal structures. The basal knobs attached to ciliary basal bodies might determine the plane of the effective stroke (Gibbons, 1961) by imposing anisotropy on the intertriplet linkages. These ideas are in accord with a long-recognized relationship, namely that motility pattern and basal body structure are both very diverse, whereas axonemal structure is relatively invariable.

The idea that dyneins inactivate when the active force is in balance with the elastic restoring force is supported by experiments in which the pattern of force generation was measured for a few dynein arms (Shingyoji et al., 1998). There was a fall in force when displacement was maximal, with recovery corresponding to the beat cycle period, thus generating an oscillation. We considered also what would happen if the force was lowered, without changing the sliding velocity, reasoning that the oscillation frequency should increase: this would presumably have been the case for the shortened sperm flagella, in which (with the ATP concentration unchanged) the beat frequency increased above that of controls (Gibbons, 1974; Goldstein, 1981; Brokaw, 1996).

The idea that dyneins activate when sliding is imposed on them in the “active” direction finds support in the literature. Pushing arrested cilia and macrocilia in the direction of the “next stroke” stimulates completion of another cycle of bending (Murakami, 1963; Thurm, 1968; Tamm, 1983; Stommel, 1986), leading Tamm (1983) to claim that passive sliding induces active sliding in the same direction. In other work, beat frequency has been modulated, either by a vibrating probe adjacent to the flagellar base (Okuno and Hiramoto, 1976) or by a vibrating micropipette attached to the sperm head (Eshel and Gibbons, 1989). The modulation may work because the natural trigger (the unloading of elastic distortion) is overridden, with active sliding being induced by imposing passive sliding in the same direction. These experiments seem to reveal how axonemes can entrain each other, as in flagellar synchronization and ciliary metachronism (Machemer, 1974).

Basal sliding has been discussed in relation to the oscillation. An additional aspect, drawing from the results in this study, is that where basal sliding does occur, “synchronous” sliding appears not to occur. The best experimental evidence for synchronous sliding is found in the measurements on Ciona sperm by Brokaw (1991). On the other hand, his report of proximal axonemal disruptions in relation to heightened asymmetry could, we think, indicate distal sliding restriction (Brokaw, 1997). In mouse spermatozoa, synchronous sliding was not possible in propagating P-bends but seemed to be possible in R-bends and in secondary waves (Woolley and Vernon, 2002). The difficulty with synchronous sliding is that sliding displacements are required to be transferred through bends that are already propagating (Gibbons, 1982). Might basal sliding be a factor in simple flagella? Without basal sliding, synchronous sliding has to be invoked to explain two modes of bend development:

1. “Non-oscillatory” synchronous sliding (i.e., where bending is asymmetric). Here, the amount of synchronous sliding accumulating at the tip with each cycle is proportional to θ_Pmax − θ_Rmax, or ∼0.8 rad using sea urchin data from Goldstein (1977). If this were accommodated basally, instead, it would create a shear strain between the edges of the basal body of 160 nm (using ΔL = dθ, where d = 200 nm), representing a maximal stretch of intertriplet linkages to ∼26 nm from a rest length of ∼20 nm (using ΔL = dθ, where d = 20 nm; stretched length = 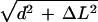). A shear strain of 160 nm would certainly be obvious by electron microscopy if it could be stabilized. The length of this basal body is ∼400 nm (Sale, 1986).

2. “Oscillatory” synchronous sliding (i.e., where new bends grow to >½ magnitude before being succeeded). For sea urchin sperm, the amount of sliding of this type was proportional to 0.2–0.6 rad (Gibbons, 1982); for tunicate sperm, a value of 0.4 rad was measured (Brokaw, 1991). A basal accommodation of such sliding would thus produce a smaller strain than that just estimated. However, whereas sliding within the basal body might in theory render synchronous sliding unnecessary, the direct measurements of displacement in Ciona sperm show synchronous sliding occurring (Brokaw, 1991).

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.