Abstract
We present a theoretical study of the self-complementary single-stranded 30-mer d(TC*TTC*C*TTTTCCTTCTC*CCGAGAAGGTTTT) (PDB ID: 1b4y) that was designed to form an intramolecular triplex by folding back twice on itself. At neutral pH the molecule exists in a duplex hairpin conformation, whereas at acidic pH the cytosines labeled by an asterisk (*) are protonated, forming Hoogsteen hydrogen bonds with guanine of a GC Watson-Crick basepair to generate a triplex. As a first step in an investigation of the energetics of the triplex-hairpin transition, we applied the Bashford-Karplus multiple site model of protonation to calculate the titration curves for the two conformations. Based on these data, a two-state model is used to study the equilibrium properties of transition. Although this model properly describes the thermodynamics of the protonation-deprotonation steps that drive the folding-unfolding of the oligomer, it cannot provide insight into the time-dependent mechanism of the process. A series of molecular dynamics simulations using the ff94 force field of the AMBER 6.0 package was therefore run to explore the dynamics of the folding/unfolding pathway. The molecular dynamics method was combined with Poisson-Boltzmann calculations to determine when a change in protonation state was warranted during a trajectory. This revealed a sequence of elementary protonation steps during the folding/unfolding transition and suggests a strong coupling between ionization and folding in cytosine-rich triple-helical triplexes.
INTRODUCTION
Since the first triple-helical nucleic acid complex containing two strands of poly(uridylic acid) and one strand of poly(adenylic acid) was discovered in 1957 (Felsenfeld et al., 1957) numerous other examples have been found and investigated (Frank-Kamenetskii and Mirkin, 1995). Among these structures much attention has been given to the H-DNA molecule, which contains both triple- and single-stranded regions (Mirkin et al., 1987; Lyamichev et al., 1985). H-DNA has been found in the genomes of vertebrates and invertebrates (Htun et al., 1984; Glikin et al., 1983) and is thought to play a regulatory role in replication (Rao et al., 1988; Brinton et al., 1991) and transcription (Shimizu et al., 1989; Kato and Shimizu, 1992). Thermodynamic and structural studies of triplex formation use intramolecular sequences of 20–30 nucleotides that fold back twice on themselves, forming a paperclip-like structure called a hairpin (Sklenar and Feigon, 1990; Chen, 1991). There are several reasons for this: first, the strands of these triplexes are always present in stoichiometric amounts; second, because the folded tertiary structure is defined by the primary sequence (Volker and Klump, 1994) there is only a small chance of the formation of competing structures; and third, these triplexes are more stable compared to intermolecular ones and may be formed in the absence of stabilizing agents over a wider range of temperature (Soyfer and Potaman, 1996).
Generally, a nucleic acid duplex composed of one homopyrimidine and one homopurine strand can form inter- as well as intramolecular triplexes by binding a homopyrimidine strand parallel to the homopurine strand (Riley et al., 1966). Antiparallel binding of a purine strand to the pyrimidine strand of such a duplex is also possible (Arnott and Selsing, 1974). The first mechanism involves the formation of the TA·T and CG·C+ triads stabilized by conventional Watson-Crick pairing in the original duplex and Hoogsteen pairing to the third strand. The formation of a GC+ Hoogsteen pair requires cytosine to be protonated at the N3 position, thus making the stability of these triads pH-dependent. It has been demonstrated that CG·C triads are more stable than TA·T triads at low pH (Roberts and Crothers, 1996) due to the formation of stronger hydrogen bonds in the Hoogsteen pair, electrostatic stabilization of the positively charged triad by the negative backbone (Sun et al., 1991), and favorable secondary interactions (Jorgensen and Pranata, 1990). An increase in pH induces cytosine deprotonation and destabilizes the CG·C triads, leading to dissociation of the third strand. Under this condition, intramolecular “paperclip” triplexes will unfold to hairpin duplexes. One of the factors determining the stability of triplexes is the pKa of cytosine N3 atoms of the third strand. These pKa values can be estimated by various methods including ultraviolet absorption spectroscopy, circular dichroism (CD) spectroscopy, fluorescence (Soyfer and Potaman, 1996), and nuclear magnetic resonance (NMR) (Leitner et al., 1998;Weisz et al., 2000). All of these methods indicate that the pKa depends upon the position of the particular cytosine within the molecule as well as the global molecular conformation.
Protonation constants of the titratable groups of a macromolecule in an electrolyte solution can be estimated computationally by solving the Poisson-Boltzmann (PB) equation (Pack et al., 1993; Nicholls and Honig, 1991; Madura et al., 1995). Bashford and Karplus (1990) have presented the standard approach for calculation of pKa values of titratable sites of amino acids in proteins based on the Debye-Hückel (DH) approximation to the PB equation. The method may be applied with reasonable accuracy to systems containing polyelectrolyte molecules that are not highly charged and, although neglecting polarization of the protonation sites (Sham et al., 1997), provides satisfactory results for many systems (Antosiewicz et al., 1996, 1994). A few methods that account for the local conformational flexibility of proteins have been proposed (You and Bashford, 1995; Ripoll et al., 1996; Zhou and Vijayakumar, 1997; Georgescu et al., 2002; Lim et al., 1991; Li et al., 2002). However, triple-helical DNA systems pose two difficulties when using the Bashford-Karplus approach to calculate pKa values. First, nucleic acids are highly charged macromolecules and the DH approximation severely overestimates the electrostatic potential at the surface (Pack et al., 1998; Lamm, 2003). Second, the Bashford-Karplus method, as typically applied to proteins, assumes that protonation and folding processes are not strongly coupled—an approximation which, although valid in those cases, fails for hairpin-triplex transitions. Details of the PB calculations are presented in Methods.
Because protonation is very sensitive to local and global conformation, structural changes are an important consideration in understanding triple-helix formation. In computer studies of folding, conformational changes can, in principle, be taken into account by molecular dynamics (MD) methods. In practice, major structural reorganization occurs on a timescale of micro- to milliseconds that is much longer than the typical nanosecond range of simulations. Early simulations were also confronted with problems in the parameter sets: the standard AMBER (Cornell et al., 1995) and CHARM (MacKerell et al., 1995) parameter sets were unable to describe the formation of a GC+ Hoogsteen pair due to absence of parameters for a protonated cytosine. MD simulations on triple helices were first performed on structures that contained only TA·T triads (Kiran and Bansal, 1995; Shields et al., 1997) or on triplexes stabilized by GC·G and CG·C triads containing unprotonated cytosines (Ojha and Tiwari, 2002). The development of additional parameters (Sponer et al., 1997) for the iminohydrogen of cytosine (H3) presented an opportunity to simulate nucleic acid molecules containing three (Spackova et al., 1998; Basye et al., 2001) or four (Csaszar et al., 2001) strands stabilized by GC+ Hoogsteen basepairs. These studies confirmed the stability of CG·C+ triads. In these calculations the cytosines were protonated a priori, regardless of their pKa values, and the number of protons was fixed.
Hairpin tetraloops are important structural fragments of RNA and DNA molecules and are often involved in the formation of tertiary structures from secondary units (Moore, 1999; Brion and Westhof, 1997). It has been proposed that tetraloops regulate the activity of macromolecules by shifting the equilibrium between alternate structures (Gluck et al., 1994; Wool et al., 1992) and that they may serve as recognition elements for proteins and nucleic acids (Michel and Westhof, 1990; Zwieb, 1992; Murphy and Cech, 1994). According to a classification proposed by Hilbers et al. (1991) tetraloops can be divided into three groups depending on the position of the second and third bases of the loop. Particularly, loops belonging to group II are of major interest because they can be found in both DNA and RNA (van Dongen et al., 1999; Jucker and Pardi, 1995). The conformation of loops in this group is characterized by the following feature: a base of the second residue at the 5′ end of a molecule is turned into or toward the minor groove, whereas a base of the third residue stacks over a (noncanonical) basepair formed by the two remaining residues of the tetraloop. It has been shown that the formation of group II loops is determined predominantly by the nature of the second residue in a loop rather than by the conformation of underlying helical stem. This folding pattern will be realized if a base of this residue is a pyrimidine (van Dongen et al., 1996).
Elucidation of the mechanism of formation of C-containing triplexes requires an understanding of how pH change alters the population of protonation substates and how this in turn affects the global conformation of the molecule. This article presents calculations on the self-complementary single-stranded DNA 30-mer d(TC*TTC*C*TTTTCCTTCTC*CCGAGAAGGTTTT), where C* indicates a protonation site. This sequence folds back twice on itself forming GCCC and TTTT tetraloops in an intramolecular triple helix (PDB ID: 1b4y). NMR studies have shown the triple-helical structure to be stable at pH 4.5 and that an increase to pH 7.0 induces unfolding into a double-helical hairpin structure (van Dongen et al., 1999). The first part of this article discusses an equilibrium two-state model that illuminates the conformational transition by taking into account the pKa values of protonation sites for the hairpin and triplex endstates. In the second part of the article we describe MD simulations which show the effect of protonation of titratable sites on the local and global conformation of DNA. Particularly, we tested the influence of the protonated incoming third strand on the conformation of the CCCG tetraloop. The calculations indicated that it is necessary to treat the conformational and electrostatic factors as highly coupled to obtain a quantitative description of the folding mechanism.
METHODS
Charge derivation procedure
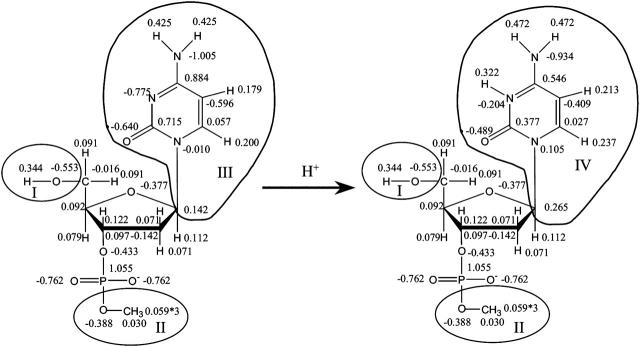
When atom N3 on cytosine (C) is protonated, the added charge is distributed over the entire ring so a recalculation of charges from the standard AMBER data set is necessary. A cytosine base was extracted from a canonical B-DNA structure and terminated by hydrogenating N1. A similar procedure was performed to obtain the geometry of a deoxycytosine nucleotide (dC) in which the O5′ atom bound to phosphate was methylated and another O5′ atom bound to carbon C5′ hydrogenated to terminate the nucleotide (Fig. 1). ESP charges were derived according to the Merz-Kollman scheme (Singh and Kollman, 1984) at the RHF/6-31G(d) level for the unprotonated and protonated forms of dC and C. These charges were used as input to calculate RESP charges using the RESP program implemented in the AMBER package (Pearlman et al., 1995). RESP charges for C and C+ were calculated without any constraints. To ensure an integral amount of charge on each nucleotide, a constraint was applied to the nucleotides in their unprotonated and protonated forms (i.e., QI − QII = 0 in Fig. 1). The calculation of pKa values according to the Bashford-Karplus scheme (discussed below) requires the same set of charges for the model compound (in our case cytosine) and the protonation site dC in DNA. Two extra constraints were therefore applied for dC and dC+ (QIII = 0 and QIV = 1 in Fig. 1) and the charges of these fragments were replaced by those obtained for C and C+, respectively. The derived sets of RESP charges for nucleotides dC and dC+ with constrained fragments are presented in Fig. 1. The AMBER ff94 parameter set was used for all other nucleotide charges (Cornell et al., 1995).
FIGURE 1.
Scheme used to derive the RESP charges for dC and dC+; charges derived at HF/6-31G(d) level and used in the MD simulations are shown (see Methods for details).
Electrostatic calculations
We used the finite difference method as implemented in the University of Houston Brownian Dynamics program to calculate the electrostatic potential at the titratable sites (Davis et al., 1991). Determination of the potential φ due to a highly-charged molecule requires solving the full nonlinear Poisson-Boltzmann equation
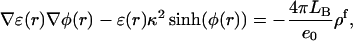 |
(1) |
where ɛ(r) is the local dielectric coefficient, κ2 = 8πLBC is the square of the Debye constant, C is the concentration of added salt (the experimental value 0.1 M was used; van Dongen et al., 1999), 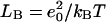 is the Bjerrum length, e0 is the proton charge, kBT is the temperature, and ρf is the distribution of fixed charges. For comparison we also tested the (linear) Debye-Hückel (DH) version:
is the Bjerrum length, e0 is the proton charge, kBT is the temperature, and ρf is the distribution of fixed charges. For comparison we also tested the (linear) Debye-Hückel (DH) version:
 |
(2) |
The potential at the boundary of a coarse grid (65 × 65 × 65) with grid spacing 3.0 Å was set to zero. A focusing procedure was performed at each titratable site using a finer grid (0.4 Å) with the same number of grid points. Calculations were performed using dielectric coefficients of 20 and 78.5 for the DNA and solvent, respectively. The set of atomic radii of the AMBER 94 force field was used in all electrostatic calculations.
pKa calculations
In the present work a titratable site consists of all cytosine base atoms including either C1′ (for the polynucleotide) or H1 (for the model compound); this assignment conforms to the reduced site approximation (Bashford and Karplus, 1991) in which protonation of phosphate ions are neglected (their pKintr is lower by 2–3 units than that of cytosine and outside the range of the simulations), but allows the charge in protonating cytosine atom N3 to be distributed throughout the base.
According to the Tanford-Kirkwood approach (Tanford and Kirkwood, 1957), the intrinsic pKa of a titratable site μ (pKintr, μ) of a macromolecule can be calculated from the pKa of the site in the absence of the molecule (for cytosine, pKmodel, μ = 4.3) by taking into account the effect of the dielectric property of the macromolecule of the electrostatic free energy of the complex. That is,
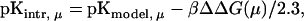 |
(3) |
where ΔΔG(μ) is the difference in the free energy changes between the process of dissolving cytosine μ in DNA in its protonated (H) and unprotonated (0) forms. In the (linear) Bashford-Karplus approach, the free energy difference can be expressed as the sum of two terms, ΔΔGBorn(μ) and ΔΔGback(μ), where each free energy term can be calculated provided that both the site μ of DNA and the model compound have the same internal geometry, the same set of charges, and the same arrangement of grid points (to eliminate the self energy term). Thus, following Bashford and Karplus, but with the understanding that protonation of a single site μ may alter the charges of multiple atoms i within that site (to give the charge set 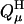 ), we have (Lamm, 2003)
), we have (Lamm, 2003)
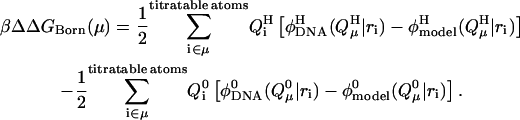 |
(4) |
The notation 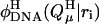 denotes the value of the electrostatic potential in the DNA (as opposed to that in the model compound) at position ri of atom i belonging to site μ due to the protonated charge set
denotes the value of the electrostatic potential in the DNA (as opposed to that in the model compound) at position ri of atom i belonging to site μ due to the protonated charge set 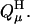 The Born term accounts for the difference in the energies of transferring the protonated and unprotonated forms of the cytosine site into a low dielectric DNA cavity. (Note that all atoms of a site are titratable in this site-distributed charge approach.)
The Born term accounts for the difference in the energies of transferring the protonated and unprotonated forms of the cytosine site into a low dielectric DNA cavity. (Note that all atoms of a site are titratable in this site-distributed charge approach.)
Because the DNA oligomer is highly charged, to calculate the influence of the background charges upon the pKa, we used an approach that differs slightly from one proposed by Bashford and Karplus (1990). In their approach the background free energy contribution is calculated as the product of the background charges and the potential due to a model compound embedded into the dielectric cavity of the macromolecule. This assumes that the energy is linear in the background charges, as obtained, for example, in a Guntelberg-type charging process in which the linear Poisson-Boltzmann equation is used. However, because DNA is highly charged, we choose instead to charge the much smaller protonatable sites in the presence of the nonlinear PB-determined background potential. We thus write the background free energy contribution as
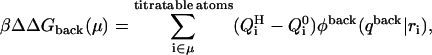 |
(5) |
where φback(qback|ri) is the potential due to background charges qback of the DNA molecule calculated at the positions ri of the charges Qi of the model compound.
We must also take into account the presence of other mutually titratable sites in the molecule. The protonation of site μ in the presence of a proton on site ν costs an energy Wμν due to the electrostatic interaction between these sites:
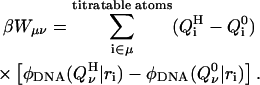 |
(6) |
Site-site interaction energies have been obtained explicitly for each of the 16 possible protonation states. In the spirit of Tanford and Roxby (1972) and Bashford and Karplus (1990), an “approximate” or “apparent” pKa (or pKapp) can be defined by
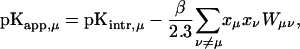 |
(7) |
where xμ is either 1 or 0 depending on whether site μ is protonated or not. These pH-independent pKapp values are useful as a more accurate indicator of site protonation (at a given pH) than the intrinsic values. By knowing the pKintr, μ for each site μ and the interaction energy Wμν between sites, we can calculate the fraction of molecules having site σ protonated as a function of pH. The titration curve for site σ is given by
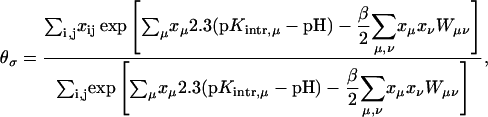 |
(8) |
where the sum over i and j accounts for all possible protonation states (with elements xij, see Appendix for details). The total titration curve is then the sum of the titration curves for all sites.
MD simulations
Molecular dynamics (MD) simulations were carried out using the AMBER 6.0 suite of programs (Pearlman et al., 1995) and the force field developed by Cornell et al. (1995) Additional force field parameters for protonated cytosine were taken from Sponer et al. (1997) The set of charges previously derived for the PB calculations was used for protonated cytosines.
Each system was prepared using the XLeaP module by surrounding the molecule in a water box that typically contained ∼6500 water molecules and 25–29 Na+ ions, depending on the number of protonated cytosines. MD simulations were performed in the NTP ensemble with a time step of 2 fs using the SHAKE algorithm (Ryckaert et al., 1977). Coupling to an external heat bath and volume scaling were applied every 0.2 ps to keep the system at 300 K and 1 atm; a 9.0 Å cutoff was applied for van der Waals interactions.
Water molecules and counterions were equilibrated by minimizing the system (1000 steps) under positional restraints on the DNA with a force constant of 500 kcal mol−1 Å−2. This was followed by a restrained MD run of 25 ps with heating from 100 K to 300 K during the first ps. The restrained MD run was continued for 25 ps more using the particle-mesh Ewald method (Darden et al., 1993). After this the restraints on the DNA molecule were reduced by the following scheme: 1000 minimization steps with 25 kcal mol−1 Å−2 position restraints; then 3 ps dynamics at 300 K with 25 kcal mol−1 Å−2 position restraints with five consecutive rounds of 600 steps minimization, removing positional restraints by 5 kcal mol−1 Å−2 for each run. The system with no positional restraints was heated from 100 K to 300 K during a 20-ps MD run followed by the 1-ns production run; snapshots of the trajectory were saved every 1 ps.
Trajectories were analyzed using the Carnal module of the AMBER suite and CURVES 5.3 (Lavery and Sklenar, 1988, 1989) was used to obtain global and local helix parameters, sugar pucker conformations, and backbone dihedral angles.
RESULTS
The two-state equilibrium model
Initial structures
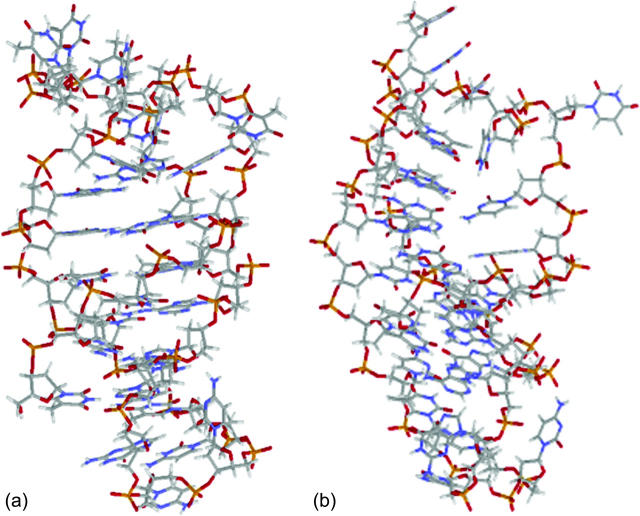
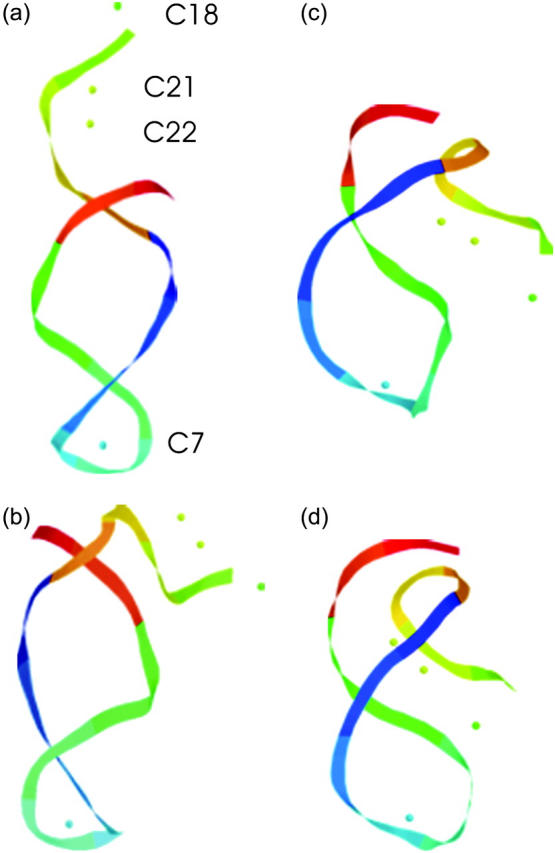
The DNA oligomer schematically shown in Fig. 2 a exists in a triple-helical conformation (the τ-state, Fig. 2 b) at low pH due to protonation of the N3 atoms of C18, C21, C22, and C7, which form Hoogsteen basepairs with guanines (PDB ID:1b4y, Structure 10). The first three cytosines are located in the triple-helical stem and form CG·C+ triads; C7 is located in a CCCG tetraloop and forms a Hoogsteen basepair with G10. At neutral pH all cytosines are unprotonated and the DNA molecule exists as a hairpin duplex (the δ-state; for example, see Fig. 2 c). Overall, the equilibrium can be expressed as
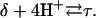 |
(9) |
Within the framework of a two-state model, we assume that the molecule adopts either the τ- or δ-conformation and that each of these states has four protonation sites with 24 = 16 protonation substates. Only the four aforementioned cytosine bases are considered protonatable in this reduced-site approximation (see Methods, above; see also Bashford and Karplus, 1991). The triplex structure predominates at low pH, where all four cytosines favor protonation, whereas the hairpin form predominates at neutral (and high) pH where a shift toward unprotonated bases occurs. The population of protonation substates within each conformation, in addition to the τ–δ structural free energy difference, determines the relative concentration of conformations in the equilibrium mixture. Most observables, such as ultraviolet absorbance, depend only on the ratio of the concentrations of the two conformations, not on the population of protonation substates. The calculation of pKa values and titration and absorbance curves are discussed in the following sections.
FIGURE 2.
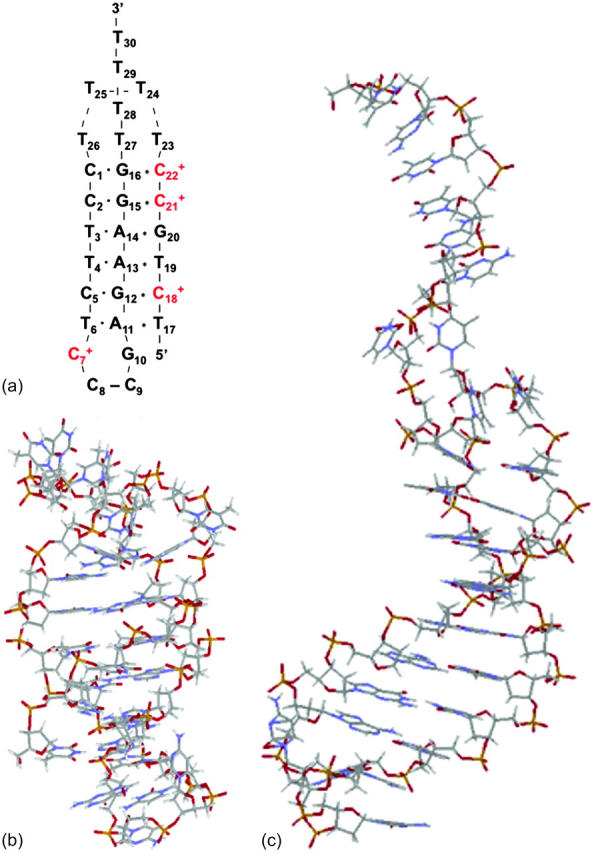
(a) Schematic representation of triple-helical DNA (PDB ID: 1b4y). Protonated cytosines are highlighted in red. The original (NMR) triplex (b) and relaxed duplex (c) conformations used in the two-state model.
The structure of the triplex conformation used for the equilibrium calculations was that of the PDB file. All atomic charges were obtained from the AMBER ff94 parameter set except those for cytosine for which an RESP recalculation was performed (see Methods, above). The hairpin duplex structure was generated from the triplex by changing the dihedral angles of T23, T24, and T25 originally located in the TTTT loop, and rearranging the Hoogsteen  pair into a Watson-Crick G10–C7 pair by flipping the guanine base. This significant structural difference in the CCCG tetraloop was noted previously (van Dongen et al., 1996). A 1-ns MD trajectory was generated to obtain the equilibrated hairpin conformation. Conformations of the NMR triplex (denoted
pair into a Watson-Crick G10–C7 pair by flipping the guanine base. This significant structural difference in the CCCG tetraloop was noted previously (van Dongen et al., 1996). A 1-ns MD trajectory was generated to obtain the equilibrated hairpin conformation. Conformations of the NMR triplex (denoted  in Eq. 14 below) and hairpin duplex after equilibration (denoted
in Eq. 14 below) and hairpin duplex after equilibration (denoted 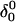 in Eq. 15 below) are shown in Fig. 2, b and c, respectively.
in Eq. 15 below) are shown in Fig. 2, b and c, respectively.
Calculation of intrinsic pKa values
Tanford and Kirkwood introduced the concept of an intrinsic pKa (or pKintr), defined as the pKa of a site on a molecule when all other sites are unprotonated (Tanford and Kirkwood, 1957). The pKintr values of the titratable sites for the triplex and hairpin conformations (Table 1) were calculated as described in Methods, above, according to the method of Bashford and Karplus (1991) by solving the PB equation using the University of Houston Brownian Dynamics program (Davis et al., 1991). The pKintr values of the third-strand cytosines of the triplex conformation lie between 8.4 and 9.5 and increase as the position of the titratable site moves from one end of the molecule toward the middle. This variation of pKa with position is readily understood by noting that the electrostatic potential is more negative in the center of the triplex than at an end. Asensio et al. (1998) have performed NMR measurements of the pKa values of triplexes containing a single CG·C+ triad with this triad positioned at different locations along the strand and have shown that the pKa of cytosine N3 of the triad “must be at least 9.5 for internal positions.” The pKa values in these experiments are identical to pKintr values because the molecules have only a single protonation site. These experimental data are in a good agreement with theoretical calculations of pKintr values performed by Pack et al. (1998).We mention that experimental studies of similar systems using indirect methods, in which the measured pKa values are in the 6–7 range (Volker and Klump, 1994; Asensio et al., 1998; Plum and Breslauer, 1995; Sugimoto et al., 2001), actually record the average pKa values of the triplex and hairpin conformations.
TABLE 1.
Intrinsic and apparent pKa values calculated for site N3 of the protonatable cytosine bases for the triplex (τ) and hairpin (δ) conformations used in the two-state model
| Site | pKintr(τ) | pKintr(δ) | pKapp(τ) | pKapp(δ) |
|---|---|---|---|---|
| C18 | 8.4 | 5.2 | 8.1 | 5.1 |
| C21 | 9.5 | 5.4 | 8.2 | 4.7 |
| C22 | 9.0 | 5.5 | 7.9 | 4.9 |
| C7 | 7.7 | 4.2 | 7.5 | 4.2 |
Our calculations show that the pKintr values calculated for cytosines located in the single-strand region of the hairpin conformation lie between 5.2 and 5.5 and reflect the same position dependence as in the triplex. Even in the absence of complementary guanines, the acidity of these cytosines is still less than that of free cytosine (pKa = 4.3) because of the negative electrostatic field of the molecule.
The calculation of the pKa using Eqs. 6 and 7 assumes that the potential due to a set of charges equals the sum of the potentials of the individual charges, a property inherent in the linear Debye-Hückel equation but not necessarily applicable to the full Poisson-Boltzmann equation (Eq. 1). To test the accuracy of Eqs. 6 and 7, we calculated the pKintr of C18 in the hairpin conformation using a more accurate two-step approach. First, the Born and background terms were calculated in the absence of electrolyte by solving the (linear) Poisson equation. After that, corrections due to added salt were obtained separately by solving the nonlinear Poisson-Boltzmann equation. (A detailed description of this method will appear in a forthcoming article, Petrov et al., 2005.) The pKintr of C18 calculated by this method is 5.0, which is only 0.2 units less than that calculated obtained by using Eqs. 6 and 7, suggesting that the interactions are still within (or near) the linear regime, and that the approximation is tolerable.
Influence of neighboring cytosines
The definition of an intrinsic pKa assumes that two titratable sites in a molecule do not interact, and thus pKintr may be considered as an approximation to the apparent pKa if the sites are shielded from one another by distance, solvent, and/or ions. In the present oligomer, C21 and C22 are neighbors, whereas C18 has two nucleotides separating it from C21; in the triplex form C7 is within one base triad of C18. NMR measurements have shown that the pKa of cytosine in a CG·C+ triad in a triplex drops from 9.5 to 8.0 when an adjacent CG·C triad becomes protonated (Asensio et al., 1998). Tanford and Roxby modified the original Tanford-Kirkwood method for calculating pKa values by taking into account site-site interactions (Tanford and Roxby, 1972). Accordingly, protonation of a particular site μ decreases the pKa of a nearby site ν by βWμν/2.3 units from its intrinsic value, with Wμν being the site-site interaction energy. These site-site interaction energies can be estimated from the solution of the PB equation using Eq. 6; values for these energies are presented in Table 2.
TABLE 2.
Pairwise site-site interactions Wμν, the total influence of the neighboring sites calculated as a sum of all pairwise site-site interactions and the resulting apparent pKa values calculated according to Eq. 7 used in the two-state model
| Site ν → | C18 | C21 | C22 | C7 | 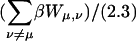 |
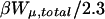 |
pKapp |
|---|---|---|---|---|---|---|---|
| Site μ↓ | Triplex | ||||||
| C18 | 0.10 | 0.03 | 0.18 | 0.33 | 0.32 | 8.05 | |
| C21 | 0.10 | 1.10 | 0.02 | 1.22 | 1.23 | 8.23 | |
| C22 | 0.03 | 1.08 | 0.01 | 1.13 | 1.13 | 7.88 | |
| C7 | 0.18 | 0.02 | 0.01 | 0.21 | 0.23 | 7.49 | |
| Hairpin | |||||||
| C18 | 0.07 | 0.03 | 3.87 × 10−5 | 0.10 | 0.10 | 5.13 | |
| C21 | 0.07 | 0.57 | 1.00 × 10−4 | 0.64 | 0.63 | 4.72 | |
| C22 | 0.03 | 0.58 | 1.00 × 10−4 | 0.61 | 0.61 | 4.87 | |
| C7 | 3.60 × 10−5 | 1.01 × 10−4 | 1.40 × 10−4 | 2.7 × 10−4 | 3 × 10−3 | 4.15 |
All values are given in pH units.
The strongest interaction is found between adjacent cytosines C21 and C22 (WC21,C22 are 1.10 and 0.57 for the triplex and hairpin states, respectively) and this interaction decays rapidly as the distance between two titratable sites increases. It is seen that all site-site interactions energies are higher in the triplex than in the hairpin, although the distances between the titratable sites (except those involving C7) are almost identical. The titratable sites in the triplex are contained a low dielectric cavity, whereas in the hairpin they are shielded by the solvent. The site-site interaction energy is almost symmetric with respect to site indexes because the main factor in determining its magnitude is the distance between the sites; minor corrections due to nonlinearity of the free energy on the potential, as noted above, account for the slight asymmetry.
The site-site interactions of the fully protonated molecules were calculated by two different methods. According to the first method these energy terms are assumed to be additive, therefore, the total interaction 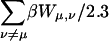 was calculated as the sum of the pairwise terms βWμν/2.3. However, these terms are strictly additive only within the linear DH theory. To test this approximation, we also calculated the corrections to the pKa of each site βWμ,total/2.3 explicitly, assuming that the other three sites were simultaneously protonated. These values are also presented in Table 2, columns 6 and 7. The site-site interactions calculated by these two methods are in extremely good agreement, indicating that the linear DH approximation is valid for these interactions.
was calculated as the sum of the pairwise terms βWμν/2.3. However, these terms are strictly additive only within the linear DH theory. To test this approximation, we also calculated the corrections to the pKa of each site βWμ,total/2.3 explicitly, assuming that the other three sites were simultaneously protonated. These values are also presented in Table 2, columns 6 and 7. The site-site interactions calculated by these two methods are in extremely good agreement, indicating that the linear DH approximation is valid for these interactions.
Titration and absorbance curves
The titration curves were calculated according to Eq. 8 using the intrinsic pKa values of Table 1 and the pairwise site-site interaction energies of Table 2 by averaging the Boltzmann-weighted site occupancies over all possible protonation states. This use of fixed conformations assumes that the free energy change upon protonation is much larger than that due to any subsequent structural changes within a particular (triplex or hairpin) conformation and that structural free energy changes may be described solely by the free energy difference between the unprotonated triplex and hairpin conformations.
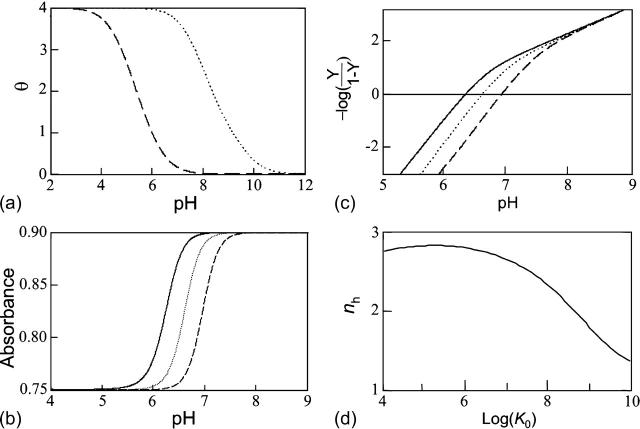
The shift between the hairpin and triplex titration curves (Fig. 3 a) reflects the differences in the pKintr values of their titratable sites (Table 1). The fact that the two curves are not exactly parallel results from different shifts between pKa values for the titratable sites in the two conformations and in the conformational dependence of Wμν. The midpoints of the titration curves are 5.7 and 8.0 for the hairpin and triplex conformations, respectively.
FIGURE 3.
(a) The theoretical titration curves (fraction of protonated cytosines, θ versus pH) calculated for the triplex (dotted) and duplex (dashed) conformations, respectively. (b) The titration curves (absorbance versus pH) for which the observable accounts for the triplex-duplex transition calculated using Eq. A10 with different K0: 108 (solid), 107 (dotted), and 106 (dashed). (c) Hill plots (−logY/(1–Y)) calculated using Eq. A14 with different K0: 108 (solid), 107 (dotted), and 106 (dashed). (d) Dependence of the Hill coefficient, nh, on folding constant K0.
The equilibrium constant Kτ–δ for the triplex-hairpin duplex (τ–δ) conformational transition in our pH-dependent two-state model is given by Eqs. A5–A7 in the Appendix. This leads to an expression for the absorbance A as a function of DNA concentration (CDNA), triplex (ɛτ), and duplex (ɛδ) extinction coefficients, and pH (Eq. A13) as
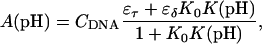 |
(10) |
where
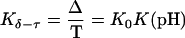 |
(11) |
is the relative amount of DNA in the duplex (δ) and triplex (τ) conformations in the two-state model. In Eq. 10 K0 is the equilibrium constant for the unprotonated triplex-hairpin conformational transition and, although difficult to estimate, can be obtained by fitting an experimental absorption curve. In Fig. 3 b we show the absorbance as a function of pH for three values of K0 (106, 107, and 108) using the calculated pKa values and the extinction coefficients ɛδ = 0.76 and ɛτ = 0.90 (Asensio et al., 1998). The predicted absorbance is seen to depend strongly on K0. Given that the duplex-triplex transition occurs between 4.5 and 7.0 pH (van Dongen et al., 1999), the absorbance curves suggest that K0 lies in the range 106–108. It then follows that the fully unprotonated oligomer is more stable in the hairpin than in the triplex conformation by ln(K0)/β ∼10 kcal/mol. By contrast, the difference in free energy change gained by protonating all cytosines in the triplex versus those in the hairpin is 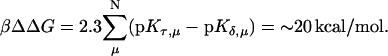
To investigate the cooperativity of the triplex-hairpin transition, we performed a Hill analysis (see Eqs. A14 and A15 in the Appendix). Fig. 3 c shows a plot of 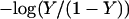 versus pH, where Y is the fraction of molecules with any cytosine protonated (Voet and Voet, 1995), for several values of K0. The slope of this curve at Y = 0.5 (zero on the ordinate) gives the Hill coefficient (nh), which is shown in Fig. 3 d as a function of log(K0). Values for nh are seen to fall in the range 2.3–2.8 for K0 between 106 and 108, indicating that protonation of the molecule is highly cooperative (and similar to that in hemoglobin-oxygen binding) and that protonation and conformation processes are strongly coupled. Fig. 3 d also shows that cooperativity vanishes at extreme values of K0 due to the uncoupling of the protonation and folding processes.
versus pH, where Y is the fraction of molecules with any cytosine protonated (Voet and Voet, 1995), for several values of K0. The slope of this curve at Y = 0.5 (zero on the ordinate) gives the Hill coefficient (nh), which is shown in Fig. 3 d as a function of log(K0). Values for nh are seen to fall in the range 2.3–2.8 for K0 between 106 and 108, indicating that protonation of the molecule is highly cooperative (and similar to that in hemoglobin-oxygen binding) and that protonation and conformation processes are strongly coupled. Fig. 3 d also shows that cooperativity vanishes at extreme values of K0 due to the uncoupling of the protonation and folding processes.
Simulations of unfolding
Overview
The simple two-state model presented above is useful in verifying experimental conclusions about the influence of protonation site position as well as site-site interactions on pKa values. The calculations also demonstrate a strong dependence of the pKa values on macromolecular conformation. Furthermore, this approach explains the general behavior of experimental titration curves obtained for triple-helical DNA. The two-state model, however, neglects any conformational difference between different protonation substates and so is unable to shed light on the folding or unfolding pathway, a simple example of which is the opening of a GC+ Hoogsteen pair preceding, and allowing, cytosine deprotonation (Gueron et al., 1987). Therefore, we have used molecular dynamics simulations to investigate the relationship between protonation and subsequent conformational changes.
Basepair opening
The importance of going beyond a two-state model and considering the effect of protonation or deprotonation on an initial conformation is illustrated by the following example. It has been suggested that deprotonation of cytosine at N3, which forms a Hoogsteen bond with guanine N7 in the triplex, is caused by, rather than causes, disruption of the bond (Leitner et al., 2000). This process can be described by the scheme
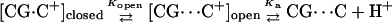 |
(12) |
and
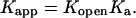 |
(13) |
If basepair opening is a prerequisite for the triplex-duplex transition, it should be taken into account in a description of triplex unfolding. Basepair opening has been studied experimentally by measuring the exchange rate between iminoprotons using NMR (Gueron et al., 1987; Leroy et al., 1988) and has been applied to a 31-mer paperclip DNA molecule (Macaya et al., 1992a), revealing the following features (Powell et al., 2001). First, the opening constants Kopen obtained for AT Hoogsteen pairs are higher than that for GC+ pairs, indicating the greater stability of the latter due to background (phosphate) charges stabilizing the positively charged basepair. Second, Kopen for GC+ basepairs located in the center of the molecule are lower than those for GC+ at the ends, showing increased stability at the center of the triplex. This observation is consistent with our calculation of triplex pKintr values discussed above. The increased stability of the central GC+ basepairs also results from positional constraints imposed by stacking interactions involving the two neighboring basepairs. This basepair opening has also been observed in MD simulations (Cieplak et al., 1997; van Aalten et al., 1999).
Coupling pKa calculations to dynamic structural changes
The two-state model of the triplex-hairpin transition discussed in a previous section cannot provide insight into the dynamic mechanism of the process. To couple protonation with time-dependent structural changes, such as basepair opening, we combined electrostatic pKa calculations, as described above, with MD simulations of DNA in an electrolyte plus water bath. To investigate the triplex-hairpin unfolding process we started with the molecule in the fully protonated triplex NMR conformation (denoted 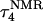 in Eq. 14 below) and, after adding and relaxing solvent (water) and counterions, performed a 20-ps equilibration run to obtain the starting geometry for the system
in Eq. 14 below) and, after adding and relaxing solvent (water) and counterions, performed a 20-ps equilibration run to obtain the starting geometry for the system  A complete 1-ns trajectory showed the NMR triplex conformation to be stable with structural changes within ∼2.8 Å of the initial NMR structure. However, some local conformational changes, e.g., reversible basepair opening, especially for the
A complete 1-ns trajectory showed the NMR triplex conformation to be stable with structural changes within ∼2.8 Å of the initial NMR structure. However, some local conformational changes, e.g., reversible basepair opening, especially for the 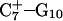 Hoogsteen pair located in the CCCG tetraloop, was observed. Apparent pKa calculations for the complex (Eq. 7 and Table 2) indicate that at pH 4.5 all Hoogsteen cytosines should be protonated, consistent with the observed NMR structure.
Hoogsteen pair located in the CCCG tetraloop, was observed. Apparent pKa calculations for the complex (Eq. 7 and Table 2) indicate that at pH 4.5 all Hoogsteen cytosines should be protonated, consistent with the observed NMR structure.
To find a specific conformation for which one might reasonably deprotonate C7 (or another cytosine), we ran a 1-ns simulation starting from 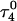 and analyzed the resulting trajectory by plotting the N3(C)–N7(G) hydrogen bond distances as function of time. A large fluctuation in this distance would indicate when a basepair opened and one of the bases becomes more exposed to solvent. This would suggest when the simulation could be interrupted and the pKapp values recalculated to determine if a change in the protonation state of a base was warranted. A proton was therefore removed (concomitant with charge rearrangement; see Methods, above) and a new trajectory generated.
and analyzed the resulting trajectory by plotting the N3(C)–N7(G) hydrogen bond distances as function of time. A large fluctuation in this distance would indicate when a basepair opened and one of the bases becomes more exposed to solvent. This would suggest when the simulation could be interrupted and the pKapp values recalculated to determine if a change in the protonation state of a base was warranted. A proton was therefore removed (concomitant with charge rearrangement; see Methods, above) and a new trajectory generated.
The entire process can be summarized by the scheme
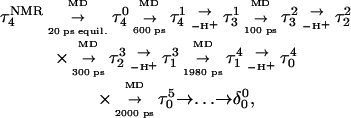 |
(14) |
where superscripts denote a particular conformation, subscripts indicate the number of protonated cytosine bases, and τ and δ refer to the triplex and hairpin structures. This alternating MD/PB(pKa) procedure was continued until the molecule was fully deprotonated. This general approach, for which specifics are related below, was also used to investigate the initial steps in the hairpin-to-triplex folding pathway. Our approach explores the behavior of single MD trajectory and is thus different from the MM/PBSA (Massova and Kollman, 2000) and MCCE (Georgescu et al., 2002) approaches that perform electrostatic calculations on macromolecules in various conformations. A detailed account of the triplex-hairpin unfolding investigation now follows.
Instability and deprotonation of the C+CCG tetraloop
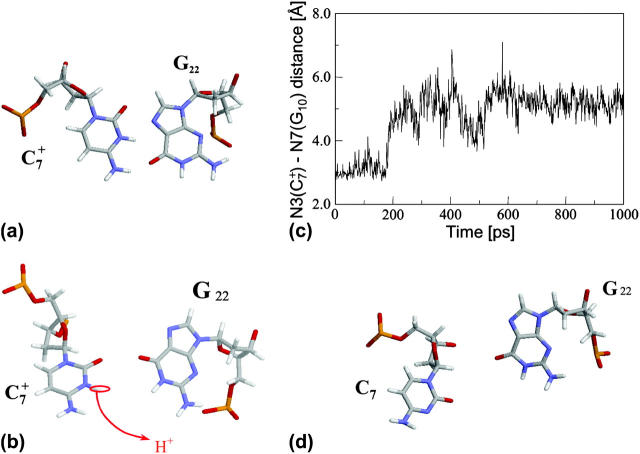
Analysis of the triplex structure 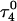 indicated that all four basepairs containing protonated cytosines, including those in the C+CCG loop (Fig. 4 a), were in the closed state (van Dongen et al., 1999). As mentioned above, analysis of a 1-ns trajectory displayed major structural changes in the C+CCG tetraloop (Fig. 4 b) with the
indicated that all four basepairs containing protonated cytosines, including those in the C+CCG loop (Fig. 4 a), were in the closed state (van Dongen et al., 1999). As mentioned above, analysis of a 1-ns trajectory displayed major structural changes in the C+CCG tetraloop (Fig. 4 b) with the 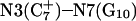 and
and 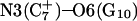 distances (Fig. 4 c) undergoing a significant increase of ∼7 Å first at 400 ps and again at 600 ps. A comparison of snapshots of the initial conformation (
distances (Fig. 4 c) undergoing a significant increase of ∼7 Å first at 400 ps and again at 600 ps. A comparison of snapshots of the initial conformation (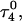 almost identical to
almost identical to 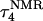 displayed in Fig. 4 a) and that after 600 ps
displayed in Fig. 4 a) and that after 600 ps 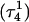 showed a distinct opening of the
showed a distinct opening of the 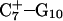 Hoogsteen basepair (Fig. 4 b). Analysis of the N3–N7 distances in the CG·C+ triads in the triple-helical region also illustrated the instability of this region. Poisson-Boltzmann calculations performed on the
Hoogsteen basepair (Fig. 4 b). Analysis of the N3–N7 distances in the CG·C+ triads in the triple-helical region also illustrated the instability of this region. Poisson-Boltzmann calculations performed on the 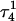 structure gave a pKapp of 6.7 for site
structure gave a pKapp of 6.7 for site 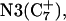 the lowest value among all protonated cytosines (Table 3). The
the lowest value among all protonated cytosines (Table 3). The 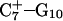 basepair opening indicated by the large fluctuation in the N3–N7 distance would expose the cytosine N3 atom to solvent, deprotonating it based on its calculated pKapp value.
basepair opening indicated by the large fluctuation in the N3–N7 distance would expose the cytosine N3 atom to solvent, deprotonating it based on its calculated pKapp value.
FIGURE 4.
(a) The NMR conformation of 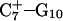 in the C+CCG tetraloop
in the C+CCG tetraloop 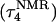 of the triplex. (b) Snapshot of the protonated C+CCG tetraloop at 600 ps
of the triplex. (b) Snapshot of the protonated C+CCG tetraloop at 600 ps  (c) The
(c) The 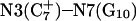 distance during a 1-ns MD simulation after a 20-ps equilibrium run on
distance during a 1-ns MD simulation after a 20-ps equilibrium run on 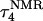 (that is, starting from conformation
(that is, starting from conformation 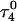 ). (d) Snapshot of the deprotonated CCCG tetraloop after an additional 1-ns simulation (that is,
). (d) Snapshot of the deprotonated CCCG tetraloop after an additional 1-ns simulation (that is, 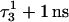 ) to illustrate the separation between bases. Conformational notation follows that of Eq. 14 for this figure and for Figs. 5–8.
) to illustrate the separation between bases. Conformational notation follows that of Eq. 14 for this figure and for Figs. 5–8.
TABLE 3.
Apparent pKa values for site N3 of the protonatable cytosine bases for the triplex conformation during unfolding (at pH 7.0)
| Site | 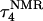 |
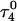 |
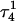 |
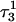 |
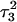 |
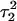 |
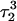 |
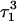 |
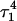 |
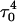 |
|---|---|---|---|---|---|---|---|---|---|---|
| C18 | 8.1 | 8.0 | 8.0 | 8.1 | 7.7 | 7.7 | 7.6 | 7.6 | 6.5 | 6.6 |
| C21 | 8.2 | 7.9 | 8.2 | 8.2 | 7.7 | 7.8 | 8.8 | 8.9 | 7.4 | 7.4 |
| C22 | 7.9 | 8.2 | 8.3 | 8.3 | 7.2 | 7.2 | 6.8 | 6.8 | 6.1 | 7.2 |
| C7 | 7.5 | 7.4 | 6.7 | 6.7 | 5.5 | 5.5 | 5.4 | 5.6 | 5.9 | 5.9 |
The pKapp values for the unprotonated sites are shown in bold (the notation corresponds to that in Eq. 14).
Deprotonation of N3(C7) (to yield conformation 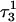 ), along with the addition of an equilibrated sodium counterion to maintain system electroneutrality, followed by a 1-ns simulation, revealed that the CCCG tetraloop expanded during the first hundred picoseconds due to electrostatic repulsion between N3(C7) and the N7 and O6 atoms of G10. This repulsion led to tilting of G10 as well as severe changes in the backbone dihedral angles during the first 100 ps of the trajectory; a snapshot of basepair C7–G10 of the CCCG loop conformation obtained after 1 ns is shown in Fig. 4 d. An extremely interesting feature of C7–G10 is the switch between Hoogsteen pairing in the fully protonated triplex and Watson-Crick pairing in the fully deprotonated hairpin duplex (van Dongen et al., 1999). Although we were unable to observe the flipping of the G10 base necessary for this switch to occur, either during this or later trajectories, undoubtedly due to the limited nanosecond time regime investigated by the dynamics, we feel that the noted base tilting and backbone angle changes strongly hint at the instability of the loop.
), along with the addition of an equilibrated sodium counterion to maintain system electroneutrality, followed by a 1-ns simulation, revealed that the CCCG tetraloop expanded during the first hundred picoseconds due to electrostatic repulsion between N3(C7) and the N7 and O6 atoms of G10. This repulsion led to tilting of G10 as well as severe changes in the backbone dihedral angles during the first 100 ps of the trajectory; a snapshot of basepair C7–G10 of the CCCG loop conformation obtained after 1 ns is shown in Fig. 4 d. An extremely interesting feature of C7–G10 is the switch between Hoogsteen pairing in the fully protonated triplex and Watson-Crick pairing in the fully deprotonated hairpin duplex (van Dongen et al., 1999). Although we were unable to observe the flipping of the G10 base necessary for this switch to occur, either during this or later trajectories, undoubtedly due to the limited nanosecond time regime investigated by the dynamics, we feel that the noted base tilting and backbone angle changes strongly hint at the instability of the loop.
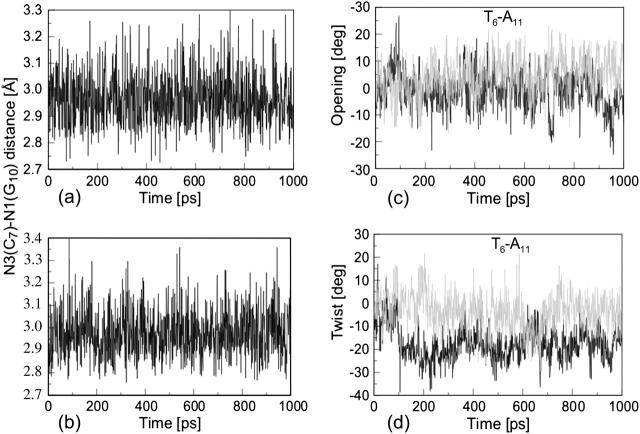
Deprotonation of C22+
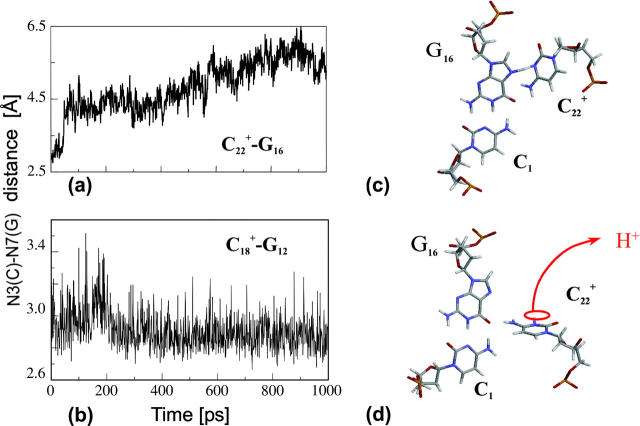
The conformational changes induced by deprotonation of 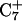 are not confined to the CCCG loop but are transmitted to the rest of the molecule. The result of these structural changes, as well as the influence of solvent interactions, is to affect the N3–N7 distances of the remaining protonated G–C+ Hoogsteen pairs. Fig. 5 displays these distances for the
are not confined to the CCCG loop but are transmitted to the rest of the molecule. The result of these structural changes, as well as the influence of solvent interactions, is to affect the N3–N7 distances of the remaining protonated G–C+ Hoogsteen pairs. Fig. 5 displays these distances for the 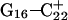 (Fig. 5 a) and
(Fig. 5 a) and 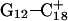 (Fig. 5 b) pairs. After 100 ps the N3–N7 distance in the
(Fig. 5 b) pairs. After 100 ps the N3–N7 distance in the 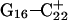 pair, adjacent to the TTTT tetraloop at the top of the molecule (Fig. 2 a), increased significantly from 2.9 Å to ∼5.0 Å (Fig. 5 a). Snapshots of the
pair, adjacent to the TTTT tetraloop at the top of the molecule (Fig. 2 a), increased significantly from 2.9 Å to ∼5.0 Å (Fig. 5 a). Snapshots of the 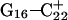 pair at the beginning of the trajectory
pair at the beginning of the trajectory 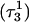 and after 100 ps
and after 100 ps 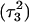 are shown in Fig. 5, c and d, respectively, and show that base
are shown in Fig. 5, c and d, respectively, and show that base 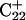 has opened out into the solvent. In contrast, the corresponding distance in the
has opened out into the solvent. In contrast, the corresponding distance in the 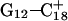 basepair temporarily increased much less, from 2.8 Å to 3.2 Å, returning to its initial value at 250 ps (Fig. 5 b). The same parameter for the
basepair temporarily increased much less, from 2.8 Å to 3.2 Å, returning to its initial value at 250 ps (Fig. 5 b). The same parameter for the 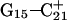 basepair remained unchanged, fluctuating around its initial value of 2.9 Å. As a control, we monitored these distances in the initial system with C7 protonated and found that they fluctuated around their initial values with no significant changes. These observations strongly suggest that deprotonation of C7 not only induces changes in the tetraloop conformation but is also responsible for structural changes throughout the entire molecule and is a key event in initiating the subsequent transformation toward full deprotonation and the unfolded hairpin duplex state (van Dongen et al., 1999). In a study of the reactivity of intermolecular triplexes, Shimizu et al. (1994) showed that a triad (either TA·T or CG·C+) adjacent to a loop displayed increased reactivity to OsO4 and so concluded that this is an unstable region. This would explain an enhanced sensitivity of
basepair remained unchanged, fluctuating around its initial value of 2.9 Å. As a control, we monitored these distances in the initial system with C7 protonated and found that they fluctuated around their initial values with no significant changes. These observations strongly suggest that deprotonation of C7 not only induces changes in the tetraloop conformation but is also responsible for structural changes throughout the entire molecule and is a key event in initiating the subsequent transformation toward full deprotonation and the unfolded hairpin duplex state (van Dongen et al., 1999). In a study of the reactivity of intermolecular triplexes, Shimizu et al. (1994) showed that a triad (either TA·T or CG·C+) adjacent to a loop displayed increased reactivity to OsO4 and so concluded that this is an unstable region. This would explain an enhanced sensitivity of 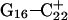 to local structural perturbations.
to local structural perturbations.
FIGURE 5.
The N3–N7 distance for the (a) 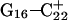 and (b)
and (b) 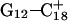 basepairs of the triplex during a 1-ns MD simulation after deprotonation of
basepairs of the triplex during a 1-ns MD simulation after deprotonation of 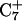 (starting from conformation
(starting from conformation 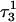 ). Snapshots of the
). Snapshots of the 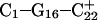 triad at (c) 0 ps
triad at (c) 0 ps 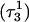 and (d) 100 ps
and (d) 100 ps 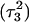 .
.
The energy of deprotonation of 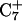 induces conformational changes in the tetraloop. Relaxation of the loop in turn leads to energy transfer either along the dihedral angles of the sugar-phosphate backbones or through the base triads by altering the helical parameters, or both. Full rotation about the most flexible dihedral angles α, β, and ξ is capable of transferring ∼2.5–2.8 kcal/mol, as found from the AMBER ff94 force field (Cornell et al., 1995). These values correspond to the maximal energy transfer through the sugar-phosphate backbone. The force constants for slide and shift, the two principal helical degrees of freedom for stacked Watson-Crick bases (Gardiner et al., 2003), are in the range 1–2 kcal/(mol per Å2) (Olson et al., 1998). Analysis of the same trajectory showed the largest change occurred for the slide parameter, which is a translation of one basepair with respect to its neighbor toward the backbone (shift is a translation perpendicular to slide and moves a basepair into the major or minor groove in B-DNA). Fig. 6 displays the slide parameter for the Watson-Crick and Hoogsteen basepairs as a function of time for trajectory
induces conformational changes in the tetraloop. Relaxation of the loop in turn leads to energy transfer either along the dihedral angles of the sugar-phosphate backbones or through the base triads by altering the helical parameters, or both. Full rotation about the most flexible dihedral angles α, β, and ξ is capable of transferring ∼2.5–2.8 kcal/mol, as found from the AMBER ff94 force field (Cornell et al., 1995). These values correspond to the maximal energy transfer through the sugar-phosphate backbone. The force constants for slide and shift, the two principal helical degrees of freedom for stacked Watson-Crick bases (Gardiner et al., 2003), are in the range 1–2 kcal/(mol per Å2) (Olson et al., 1998). Analysis of the same trajectory showed the largest change occurred for the slide parameter, which is a translation of one basepair with respect to its neighbor toward the backbone (shift is a translation perpendicular to slide and moves a basepair into the major or minor groove in B-DNA). Fig. 6 displays the slide parameter for the Watson-Crick and Hoogsteen basepairs as a function of time for trajectory 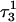 (0–100 ps) before deprotonation of
(0–100 ps) before deprotonation of 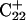 and for the first 100 ps after deprotonation (trajectory
and for the first 100 ps after deprotonation (trajectory 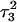 ). (As helical slide has not yet been parameterized for Hoogsteen stacking, Watson-Crick values—see Olson et al., 1998—were used.) During the trajectory the slide changed by 1.5–2.0 Å, corresponding to a basepair-basepair interaction energy of 6–8 kcal/mol. There is a slight indication (Fig. 6) that this structural perturbation propagates primarily along the duplex stem, reaching the TTTT loop at ∼70 ps and just before the observed base flipping of
). (As helical slide has not yet been parameterized for Hoogsteen stacking, Watson-Crick values—see Olson et al., 1998—were used.) During the trajectory the slide changed by 1.5–2.0 Å, corresponding to a basepair-basepair interaction energy of 6–8 kcal/mol. There is a slight indication (Fig. 6) that this structural perturbation propagates primarily along the duplex stem, reaching the TTTT loop at ∼70 ps and just before the observed base flipping of 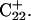 As the amount of slide energy is much larger than that which could be transmitted along the sugar-phosphate backbone, energy transfer through basepair stacking appears to be responsible for disruption of the weak
As the amount of slide energy is much larger than that which could be transmitted along the sugar-phosphate backbone, energy transfer through basepair stacking appears to be responsible for disruption of the weak 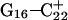 basepair, and leads to conditions for the deprotonation of
basepair, and leads to conditions for the deprotonation of 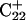 .
.
FIGURE 6.
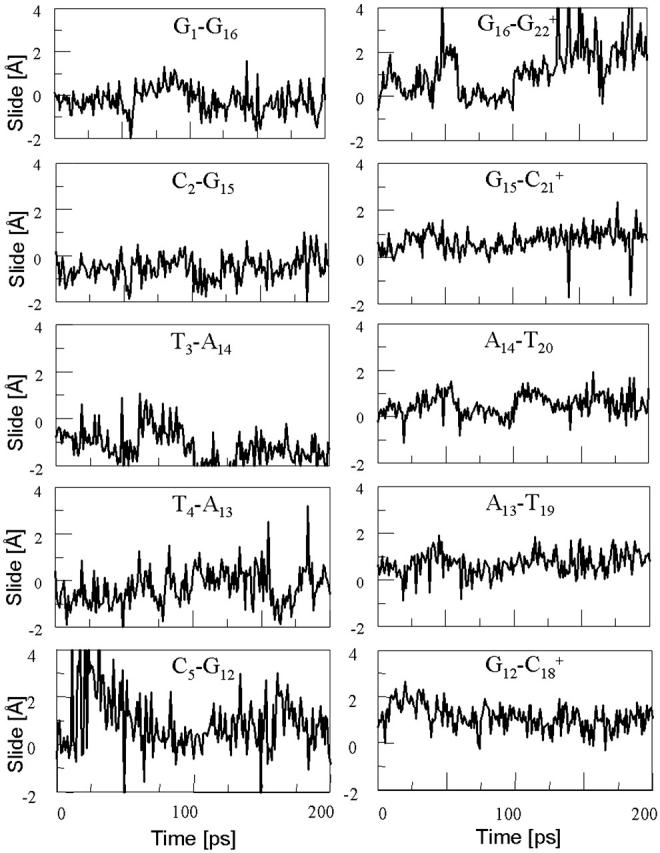
The helical parameter slide (in Å) for the indicated basepairs during trajectory 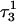 before deprotonation of
before deprotonation of 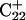 (0–100 ps) and the first 100 ps of trajectory
(0–100 ps) and the first 100 ps of trajectory 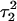 after deprotonation (100–200 ps).
after deprotonation (100–200 ps).
Returning to the observation concerning the increased 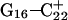 distance after 100 ps of trajectory
distance after 100 ps of trajectory 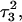 we then extracted the DNA coordinates and recalculated the pKapp values (Table 3). The pKapp of C7 in the CCCG tetraloop was found to have been further lowered from 6.7 to 5.5, indicating that reprotonation of C7 and reformation of the Hoogsteen-paired loop structure is unlikely at this point. The pKapp values of the third-strand cytosines also decreased with the largest decrease observed for
we then extracted the DNA coordinates and recalculated the pKapp values (Table 3). The pKapp of C7 in the CCCG tetraloop was found to have been further lowered from 6.7 to 5.5, indicating that reprotonation of C7 and reformation of the Hoogsteen-paired loop structure is unlikely at this point. The pKapp values of the third-strand cytosines also decreased with the largest decrease observed for 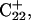 from 8.3 to 7.2 and in agreement with the N3–N7 distance analysis discussed earlier. The preference among the three third-strand cytosines for
from 8.3 to 7.2 and in agreement with the N3–N7 distance analysis discussed earlier. The preference among the three third-strand cytosines for 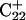 to deprotonate first is not, as might first be thought, due to its position near one end of the molecule where the negative electrostatic potential is weaker. If this were so then the pKapp for this base would be the lowest of the three for structure
to deprotonate first is not, as might first be thought, due to its position near one end of the molecule where the negative electrostatic potential is weaker. If this were so then the pKapp for this base would be the lowest of the three for structure 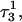 when in fact it is the highest (or at least equal, within error). Rather this preference is due to basepairing instability near the TTTT loop, as mentioned above. Also, structural changes resulting from deprotonation of the C+CCG loop were transmitted to the other end of the molecule, further destabilizing the
when in fact it is the highest (or at least equal, within error). Rather this preference is due to basepairing instability near the TTTT loop, as mentioned above. Also, structural changes resulting from deprotonation of the C+CCG loop were transmitted to the other end of the molecule, further destabilizing the 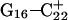 basepair. The result after 100 ps of dynamics is a rolling and tilting of
basepair. The result after 100 ps of dynamics is a rolling and tilting of 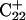 from its original position, exposing the protonation site to the solvent (Fig. 5, c and d). The instability of CG·C+ triads adjacent to the TTTT loop has also been inferred from measurements of cytosine pKapp values (Leitner et al., 2000). These values were found to be lower by a few units than those measured for cytosines near the interior of DNA structures, suggesting that the H3 atom of a cytosine adjacent to a loop may no longer be involved in Hoogsteen pairing but exposed to solvent.
from its original position, exposing the protonation site to the solvent (Fig. 5, c and d). The instability of CG·C+ triads adjacent to the TTTT loop has also been inferred from measurements of cytosine pKapp values (Leitner et al., 2000). These values were found to be lower by a few units than those measured for cytosines near the interior of DNA structures, suggesting that the H3 atom of a cytosine adjacent to a loop may no longer be involved in Hoogsteen pairing but exposed to solvent.
Deprotonation of C18+
On the basis of the sudden and stable increase in the 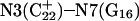 distance after 100 ps of the
distance after 100 ps of the 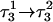 trajectory, we interrupted the simulation at this point and deprotonated
trajectory, we interrupted the simulation at this point and deprotonated 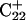 (to give
(to give 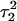 ). Recalculated pKapp values are given in Table 3. After updating the charges (including an added counterion), the simulation was restarted from these coordinates and a 1-ns trajectory generated. The N3–N7 distances for the two remaining Hoogsteen pairs (
). Recalculated pKapp values are given in Table 3. After updating the charges (including an added counterion), the simulation was restarted from these coordinates and a 1-ns trajectory generated. The N3–N7 distances for the two remaining Hoogsteen pairs (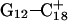 and
and 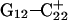 ) were then analyzed as before; Fig. 7 a displays these data for the
) were then analyzed as before; Fig. 7 a displays these data for the 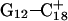 pair. The transient instability of
pair. The transient instability of 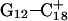 observed during the first 200 ps of the previous trajectory (Fig. 5 b) is perhaps evident in the more severe fluctuations seen in Fig. 7 a. However, an obvious point at which to interrupt the simulation was much more difficult to discern in this case; we chose, somewhat arbitrarily, 300 ps
observed during the first 200 ps of the previous trajectory (Fig. 5 b) is perhaps evident in the more severe fluctuations seen in Fig. 7 a. However, an obvious point at which to interrupt the simulation was much more difficult to discern in this case; we chose, somewhat arbitrarily, 300 ps 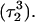 Recalculation of the pKapp values showed that for this conformation
Recalculation of the pKapp values showed that for this conformation 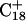 was indeed more likely to be deprotonated than
was indeed more likely to be deprotonated than 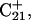 although most (80%) would remain protonated. The slight conformational changes in the triad coordinates may be gleaned by comparing Fig. 7, b
although most (80%) would remain protonated. The slight conformational changes in the triad coordinates may be gleaned by comparing Fig. 7, b 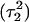 and c
and c 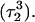 To model those molecules for which
To model those molecules for which 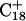 was deprotonated at this point, we updated the charges based on the neutral base
was deprotonated at this point, we updated the charges based on the neutral base 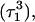 added a counterion, and generated a 2-ns trajectory, starting at the interrupted coordinates.
added a counterion, and generated a 2-ns trajectory, starting at the interrupted coordinates.
FIGURE 7.
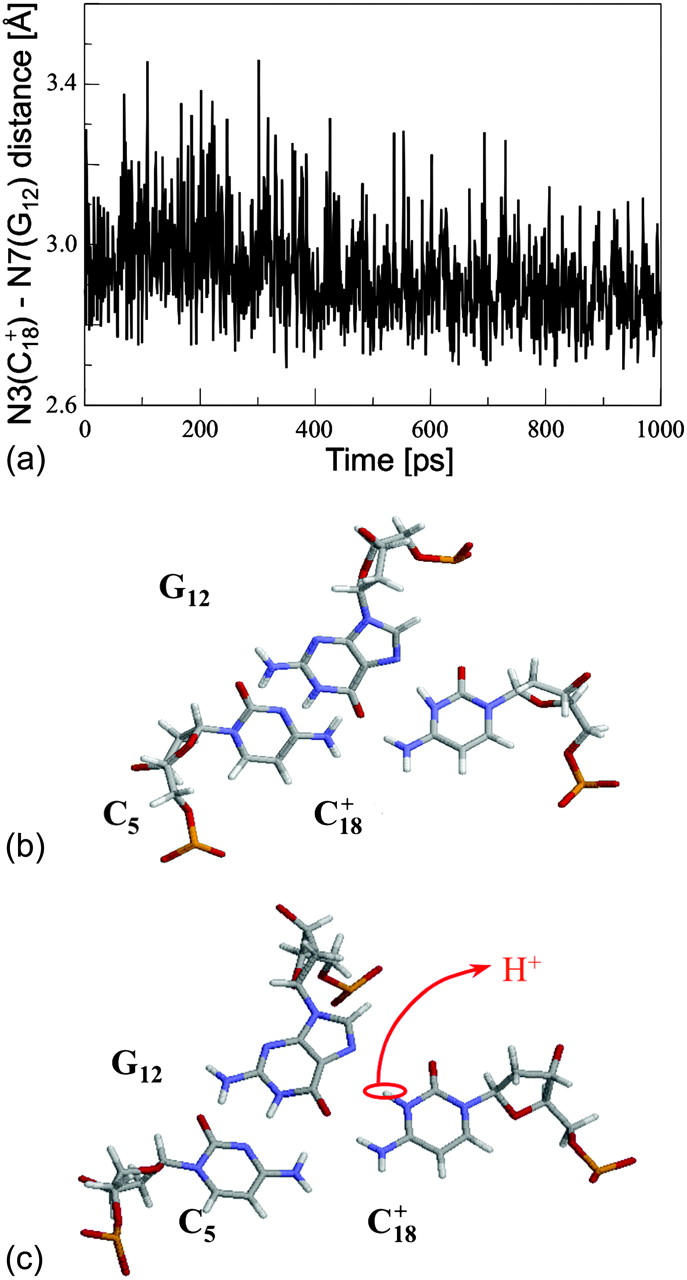
(a) The 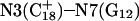 distance during a 1-ns MD simulation after deprotonation of
distance during a 1-ns MD simulation after deprotonation of 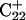 (starting from conformation
(starting from conformation 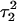 ). Snapshots of the
). Snapshots of the 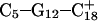 triad at (b) 0 ps
triad at (b) 0 ps 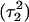 and (c) 300 ps
and (c) 300 ps 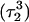 .
.
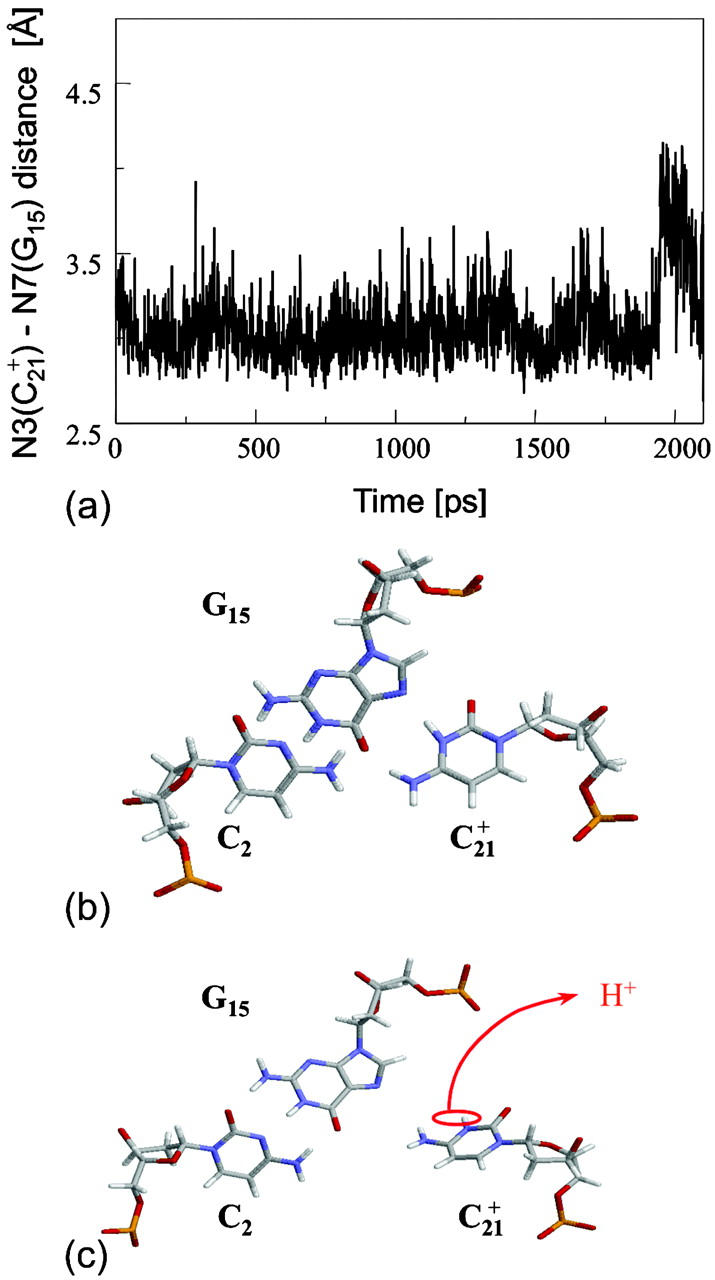
Deprotonation of C21+
The remaining protonated Hoogsteen pair is 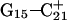 and the N3–N7 distances during the penultimate simulation are shown in Fig. 8 a, where a significant increase can be seen at 1980 ps. This conformational change was reversible as long as the protonation state of
and the N3–N7 distances during the penultimate simulation are shown in Fig. 8 a, where a significant increase can be seen at 1980 ps. This conformational change was reversible as long as the protonation state of 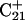 remained unchanged. Snapshots of the
remained unchanged. Snapshots of the 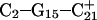 triad geometry at the start
triad geometry at the start 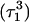 and end
and end 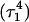 of the run are shown in Fig., 8 b and c, respectively. To check if the implied base opening was fortuitous, we generated a second trajectory starting from conformation
of the run are shown in Fig., 8 b and c, respectively. To check if the implied base opening was fortuitous, we generated a second trajectory starting from conformation 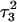 but with bases
but with bases 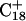 and
and 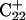 simultaneously deprotonated. A similar increase in the
simultaneously deprotonated. A similar increase in the 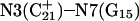 displacement was observed at 1450 ps (data not shown). Apparent pKa values for
displacement was observed at 1450 ps (data not shown). Apparent pKa values for 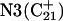 calculated at the start
calculated at the start 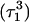 and end
and end 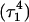 of the trajectory are listed in Table 3, with the substantial decrease from 8.9 to 7.4 evident. Also listed are the pKapp values after deprotonation of
of the trajectory are listed in Table 3, with the substantial decrease from 8.9 to 7.4 evident. Also listed are the pKapp values after deprotonation of 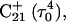 which shows a unit increase in the pKapp for N3(C22) resulting from a strong site-site interaction with neighboring C21. A final 2-ns trajectory was generated after the last deprotonation to verify stability of the fully deprotonated structure. Fig. 9 compares the NMR structure (
which shows a unit increase in the pKapp for N3(C22) resulting from a strong site-site interaction with neighboring C21. A final 2-ns trajectory was generated after the last deprotonation to verify stability of the fully deprotonated structure. Fig. 9 compares the NMR structure (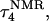 Fig. 9 a) with that obtained at the end of the final simulation (
Fig. 9 a) with that obtained at the end of the final simulation ( Fig. 9 b), illustrating the separation of the third strand as well as expansion of the CCCG tetraloop.
Fig. 9 b), illustrating the separation of the third strand as well as expansion of the CCCG tetraloop.
FIGURE 8.
(a) The 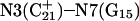 distance during a 1-ns MD simulation after deprotonation of
distance during a 1-ns MD simulation after deprotonation of 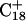 (starting from conformation
(starting from conformation 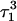 ). Snapshots of the
). Snapshots of the 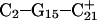 triad at (b) 0 ps
triad at (b) 0 ps 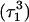 and (c) 1980 ps
and (c) 1980 ps 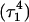 .
.
FIGURE 9.
(a) The NMR triplex conformation 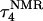 compared with (b) the final conformation
compared with (b) the final conformation 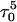 obtained after a 2-ns simulation on the fully deprotonated structure
obtained after a 2-ns simulation on the fully deprotonated structure 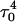 .
.
Summary of unfolding
A picture of the initial part of the unfolding dynamics may be obtained by splicing together the separate 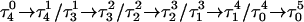 segments. The presence of the third strand influences the double-helical region by pushing the Watson-Crick basepairs toward the minor groove. This distortion is characterized by an x displacement of −2.5 ± 0.9 Å (versus the averages −5.4 Å and −0.7 Å for the canonical A and B forms, respectively; Cieplak et al., 1997). Also, the analysis of this super-trajectory indicated that the sugar puckers remain in the range of 126 ± 23° (versus ∼190° and ∼12°), which corresponds to C1′-exo and C2′-endo conformations, and the values of the dihedral angle δ are found to be in a range of 117 ± 25° (versus ∼80° and ∼130°). These observations suggest that triple-helical DNA assumes a conformation intermediate between the canonical A and B forms. Our data are in a good agreement with experimental results (Radhakrishnan and Patel, 1994; Macaya et al., 1992b).
segments. The presence of the third strand influences the double-helical region by pushing the Watson-Crick basepairs toward the minor groove. This distortion is characterized by an x displacement of −2.5 ± 0.9 Å (versus the averages −5.4 Å and −0.7 Å for the canonical A and B forms, respectively; Cieplak et al., 1997). Also, the analysis of this super-trajectory indicated that the sugar puckers remain in the range of 126 ± 23° (versus ∼190° and ∼12°), which corresponds to C1′-exo and C2′-endo conformations, and the values of the dihedral angle δ are found to be in a range of 117 ± 25° (versus ∼80° and ∼130°). These observations suggest that triple-helical DNA assumes a conformation intermediate between the canonical A and B forms. Our data are in a good agreement with experimental results (Radhakrishnan and Patel, 1994; Macaya et al., 1992b).
This combined MD/PB approach suggests that the C+CCG tetraloop in the particular triplex plays the role of a conformational switch, supporting the contention of van Dongen et al. (1996) Deprotonation of C7 not only induces local changes in the loop structure but, we believe, also leads to conformational changes in the helical stem. The data show that the 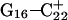 Hoogsteen pair is much less stable than either the
Hoogsteen pair is much less stable than either the 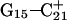 and
and 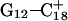 pairs and that prior deprotonation of
pairs and that prior deprotonation of 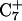 could also help influence
could also help influence 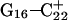 to open first. Subsequent deprotonation of
to open first. Subsequent deprotonation of 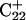 then aids the opening first of
then aids the opening first of 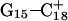 and then of
and then of 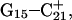 with their loss of protons. Deprotonation of these four cytosines is seen as cooperative in the sense that structural changes induced by Hoogsteen pair repulsion after loss of the binding proton as well as site-site interactions play lead roles. In fact, the presence of the latter accounts for the nonzipper order of basepair opening.
with their loss of protons. Deprotonation of these four cytosines is seen as cooperative in the sense that structural changes induced by Hoogsteen pair repulsion after loss of the binding proton as well as site-site interactions play lead roles. In fact, the presence of the latter accounts for the nonzipper order of basepair opening.
The simulation of unfolding was not continued after the fourth and final cytosine deprotonation as it appeared, as indicated by a few sample trajectories that full or even partial extension of the third strand was now governed by electrostatic and solvent-mediated effects in the diffusive time regime and, as such, were too long for the nanosecond dynamics investigated here. To obtain a more nearly complete view of the entire pathway, we therefore repeated the above MD/PB procedure but from the point of view of folding by beginning with the unprotonated hairpin duplex structure of Fig. 2 c.
Dynamics simulations of folding
Summary of folding
The main question we wanted to address in simulating the folding pathway is whether the sequence of cytosine protonation would be the reverse of that found for deprotonation during unfolding. We were also interested in the stability of the CCCG tetraloop. The folding simulation began with the hairpin duplex coordinates used for the equilibrium studies (labeled 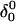 in Eq. 15 below and shown as a cartoon in Fig. 10 a and in detail in Fig. 2 c). In analogy with the unfolding scheme shown in Eq. 14, we give that for folding
in Eq. 15 below and shown as a cartoon in Fig. 10 a and in detail in Fig. 2 c). In analogy with the unfolding scheme shown in Eq. 14, we give that for folding
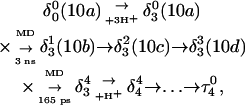 |
(15) |
where the notation in parentheses refers to the cartoons of Fig. 10. Calculated pKapp values for particular conformations of the hairpin are listed in Table 4. These show that, for the extended hairpin structure 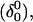 all cytosines remain unprotonated at neutral pH, hence implying the stability of the hairpin duplex under this condition. Lowering the pH to 4.5 to initiate folding, results in the protonation of all cytosines in the extended third strand. However, C7 in the CCCG tetraloop would remain unprotonated (67%) and retain its Watson-Crick pairing with G10. Because protonation of most of the titratable sites occurs immediately upon lowering of the pH (the three sites are already exposed to solvent), we may already conclude that the sequence of events involved in folding do not mirror those of unfolding.
all cytosines remain unprotonated at neutral pH, hence implying the stability of the hairpin duplex under this condition. Lowering the pH to 4.5 to initiate folding, results in the protonation of all cytosines in the extended third strand. However, C7 in the CCCG tetraloop would remain unprotonated (67%) and retain its Watson-Crick pairing with G10. Because protonation of most of the titratable sites occurs immediately upon lowering of the pH (the three sites are already exposed to solvent), we may already conclude that the sequence of events involved in folding do not mirror those of unfolding.
FIGURE 10.
The artificially generated (a) hairpin and (b–d) partially folded hairpin conformations used to investigate the folding pathway. The hairpin conformation (a, 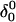 ) was constructed as described in the text in connection with Fig. 2 c; conformation (b,
) was constructed as described in the text in connection with Fig. 2 c; conformation (b, 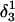 ) was obtained by protonating the three cytosines on the extended arm of the hairpin and running a 3-ns MD simulation; conformations (c,
) was obtained by protonating the three cytosines on the extended arm of the hairpin and running a 3-ns MD simulation; conformations (c, 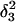 ) and (d,
) and (d, 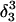 ) were artificially constructed from the hairpin conformation by changing dihedral angles in the TTTT tetraloop and equilibrating the structures (see the text for additional details).
) were artificially constructed from the hairpin conformation by changing dihedral angles in the TTTT tetraloop and equilibrating the structures (see the text for additional details).
TABLE 4.
Apparent pKa values for site N3 of the protonatable cytosine bases for the hairpin during folding (at pH 4.5)
| Site |
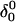 (10a) (10a) |
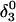 (10a) (10a) |
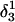 (10b) (10b) |
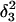 (10c) (10c) |
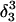 (10d) (10d) |
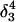 |
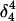 |
|---|---|---|---|---|---|---|---|
| C18 | 5.2 | 5.1 | 5.2 | 5.3 | 6.3 | 6.5 | 6.4 |
| C21 | 5.4 | 4.7 | 5.1 | 5.4 | 5.8 | 5.9 | 5.9 |
| C22 | 5.5 | 4.9 | 5.6 | 6.0 | 6.3 | 6.4 | 6.4 |
| C7 | 4.2 | 4.2 | 4.2 | 4.3 | 4.3 | 4.4 | 4.4 |
The pKapp values for the protonated sites are shown in bold (the notation corresponds to that in Eq. 15).
To investigate the effect of third-strand protonation on the folding dynamics, we ran a 3-ns MD simulation starting from conformation 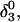 at the end of which the extended third strand of the molecule was bent by ∼90° with respect to the double-helical region (
at the end of which the extended third strand of the molecule was bent by ∼90° with respect to the double-helical region (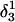 and shown in Fig. 10 b). To verify that this bend was due to reduced electrostatic repulsion between the extended strand and the duplex, we also generated a 2-ns trajectory based on the fully unprotonated structure
and shown in Fig. 10 b). To verify that this bend was due to reduced electrostatic repulsion between the extended strand and the duplex, we also generated a 2-ns trajectory based on the fully unprotonated structure 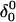 and observed no significant global conformational change during the run. Analysis of the helix parameters for the
and observed no significant global conformational change during the run. Analysis of the helix parameters for the 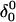 duplex region showed the x displacement to lie in the range −1.6 ± 0.8 Å. This value is more positive than that calculated for the folded triple-helical structure and indicates that the hairpin conformation at neutral pH is closer to the canonical B-form of DNA than the triplex structure. However, this value, along with data of the time-averaged sugar puckers (118 ± 34°) and dihedral angles (123 ± 21°), still suggests that the hairpin structure lies between the A and B forms.
duplex region showed the x displacement to lie in the range −1.6 ± 0.8 Å. This value is more positive than that calculated for the folded triple-helical structure and indicates that the hairpin conformation at neutral pH is closer to the canonical B-form of DNA than the triplex structure. However, this value, along with data of the time-averaged sugar puckers (118 ± 34°) and dihedral angles (123 ± 21°), still suggests that the hairpin structure lies between the A and B forms.
As complete protonation of the extended strand followed by three nanoseconds of simulation had moved the pathway into the diffusive regime, we suspended the MD/PB procedure at this point. However, the results of the method have allowed us to elicit the essential features of the folding mechanism. To summarize, the unprotonated hairpin is stable at neutral pH. Lowering of the pH to 4.5 immediately leads to protonation of all extended-strand cytosines and a reduction in the electrostatic repulsion between this strand and the duplex. This decrease appears to be enough for the extended arm to bend approximately at right angle to the duplex, at which point diffusive fluctuations cause it to approach closer to the duplex, ultimately providing a conformation suitable for Hoogsteen pairing between bases of the third strand and the duplex to occur. Before or after this pairing, G10 in the CCCG loop flips over and Hoogsteen-pairs with a protonated 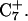 To gain insight into the sequence of events involved in the reorganization of the CCCG loop, we performed several additional MD simulations which we now describe.
To gain insight into the sequence of events involved in the reorganization of the CCCG loop, we performed several additional MD simulations which we now describe.
Conformational changes in the CCCG tetraloop
To investigate the stability of the unprotonated CCCG loop in the Watson-Crick conformation, we artificially created two hairpin structures intermediate between the triply-protonated 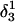 conformation and the NMR triplex
conformation and the NMR triplex 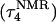 in the same manner as the extended hairpin
in the same manner as the extended hairpin 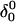 was made (including 20 ps of MD equilibration). These conformations,
was made (including 20 ps of MD equilibration). These conformations, 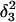 and
and 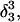 in which the angles between the third strand and the duplex are ∼20° and 5°, are shown in Fig. 10, c and d, respectively, and were intended to model the later stages of folding. In the sequence
in which the angles between the third strand and the duplex are ∼20° and 5°, are shown in Fig. 10, c and d, respectively, and were intended to model the later stages of folding. In the sequence 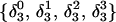 of comparative structures, C7–G10 forms a Watson-Crick pair and the third-strand bases
of comparative structures, C7–G10 forms a Watson-Crick pair and the third-strand bases 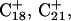 and
and 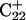 are protonated. Calculated pKapp values for these conformations are listed in Table 4 and show that bending the protonated third strand with respect to the duplex from 180°
are protonated. Calculated pKapp values for these conformations are listed in Table 4 and show that bending the protonated third strand with respect to the duplex from 180° 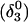 to 90°
to 90° 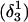 to 20°
to 20° 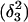 has little effect on the proclivity for N3(C7) to protonate. A 1-ns MD simulation on conformation
has little effect on the proclivity for N3(C7) to protonate. A 1-ns MD simulation on conformation 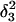 also showed the C7–G10 pair to remain intact in the Watson-Crick bonding pattern with a final, essentially unchanged pKapp for N3(C7) of 4.23. From these data we infer that it is only when the extended strand approaches to <5° of the duplex that N3(C7) is protonated at pH values near 4.5.
also showed the C7–G10 pair to remain intact in the Watson-Crick bonding pattern with a final, essentially unchanged pKapp for N3(C7) of 4.23. From these data we infer that it is only when the extended strand approaches to <5° of the duplex that N3(C7) is protonated at pH values near 4.5.
We therefore focused more closely on a comparison between the CCCG loop structure in the unprotonated hairpin conformation 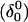 and that with the 5° third-strand-duplex bend
and that with the 5° third-strand-duplex bend 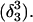 Two 1-ns MD trajectories were generated, one starting from the unprotonated extended conformation
Two 1-ns MD trajectories were generated, one starting from the unprotonated extended conformation 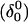 and a second starting from the triply-protonated, partially-bent conformation
and a second starting from the triply-protonated, partially-bent conformation 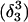 and the N3(C7)–N1(G10) distances compared (Fig. 11, a and b). For the latter trajectory the analysis of the data disclosed large fluctuations, indicating that H-bonds in the C7–G10 pair had become weaker. This results from the approach of T17 to basepair T6–A11 adjacent to pair C7–G10, inducing the former to open by a few degrees (Fig. 11 c). This then leads to an unwinding of the double-helical fragment as shown by a change in the twist measured for C7–G10 relative to T6–A11 (Fig. 11 d), consequently weakening the H-bonds in the CCCG loop. In the first significant fluctuation during the
and the N3(C7)–N1(G10) distances compared (Fig. 11, a and b). For the latter trajectory the analysis of the data disclosed large fluctuations, indicating that H-bonds in the C7–G10 pair had become weaker. This results from the approach of T17 to basepair T6–A11 adjacent to pair C7–G10, inducing the former to open by a few degrees (Fig. 11 c). This then leads to an unwinding of the double-helical fragment as shown by a change in the twist measured for C7–G10 relative to T6–A11 (Fig. 11 d), consequently weakening the H-bonds in the CCCG loop. In the first significant fluctuation during the 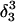 trajectory, this distance has increased from 2.95 Å to 3.17 Å by 165 ps (Fig. 11 b), compared to the average value of 2.96 Å for the
trajectory, this distance has increased from 2.95 Å to 3.17 Å by 165 ps (Fig. 11 b), compared to the average value of 2.96 Å for the 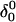 (Fig. 10 a). At this point the distance decreases back down, only to repeat this cycle ∼160 ps later. As seen in Fig. 10 d, there is some correlation with the change in twist angle. Extracting the coordinates of the conformation at 165 ps
(Fig. 10 a). At this point the distance decreases back down, only to repeat this cycle ∼160 ps later. As seen in Fig. 10 d, there is some correlation with the change in twist angle. Extracting the coordinates of the conformation at 165 ps 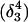 provided a slight increase in the pKapp for N3(C7) to 4.4. Protonating this structure
provided a slight increase in the pKapp for N3(C7) to 4.4. Protonating this structure 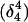 and running a 2-ns MD simulation revealed a partial rearrangement of the C+CCG loop (G10 flips out of the stack, but does not turn over); however, the complete Watson-Crick-to-Hoogsteen transition for
and running a 2-ns MD simulation revealed a partial rearrangement of the C+CCG loop (G10 flips out of the stack, but does not turn over); however, the complete Watson-Crick-to-Hoogsteen transition for 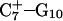 was not observed.
was not observed.
FIGURE 11.
The N3(C7)–N7(G10) distance during a 1-ns MD simulation of (a) the unprotonated extended hairpin (starting from conformation 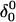 ) and (b) the triply-protonated, partially bent hairpin (starting from conformation
) and (b) the triply-protonated, partially bent hairpin (starting from conformation 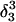 ). Also shown are comparisons of the two helix parameters (c) opening (symbol σ in Lavery and Sklenar, 1989) and (d) twist (symbol Ω in Lavery and Sklenar, 1989) of the T6–A11 pair during these two simulations (
). Also shown are comparisons of the two helix parameters (c) opening (symbol σ in Lavery and Sklenar, 1989) and (d) twist (symbol Ω in Lavery and Sklenar, 1989) of the T6–A11 pair during these two simulations (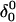 in black and
in black and 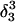 in shading).
in shading).
From these observations, and in agreement with the sequence of events observed in the folding study discussed earlier, the data suggest that transformation from an unprotonated Watson-Crick C7–G10 pair to a protonated Hoogsteen 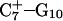 pair is probably coupled to structural changes induced by binding of the third strand to the duplex. This would suggest that although deprotonation of the C+CCG tetraloop might act as a conformational switch during unfolding of the triplex by inducing the third strand to dissociate from the duplex, binding of the third strand to the duplex during folding is the switch that induces opening of C7–G10, leading to protonation of C7 and rebinding with G10 as a Hoogsteen pair. This is, of course, speculative but consistent with the data.
pair is probably coupled to structural changes induced by binding of the third strand to the duplex. This would suggest that although deprotonation of the C+CCG tetraloop might act as a conformational switch during unfolding of the triplex by inducing the third strand to dissociate from the duplex, binding of the third strand to the duplex during folding is the switch that induces opening of C7–G10, leading to protonation of C7 and rebinding with G10 as a Hoogsteen pair. This is, of course, speculative but consistent with the data.
Van Dongen et al. (1996) have hypothesized two possible mechanisms for the formation of the 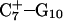 basepair. According to their first mechanism the Watson-Crick-to-Hoogsteen transition results directly from the lowering of the pH and is subsequently followed by protonation of C7. In this case the conformational changes in the CCCG loop would be independent of third-strand folding. Our dynamics data tend to discount this. Alternatively, they suggested that the transition might be mediated by conformational changes in the duplex that are induced by folding of the third strand, in agreement with the view posited above. However, longer timescale studies appear necessary to clarify this picture.
basepair. According to their first mechanism the Watson-Crick-to-Hoogsteen transition results directly from the lowering of the pH and is subsequently followed by protonation of C7. In this case the conformational changes in the CCCG loop would be independent of third-strand folding. Our dynamics data tend to discount this. Alternatively, they suggested that the transition might be mediated by conformational changes in the duplex that are induced by folding of the third strand, in agreement with the view posited above. However, longer timescale studies appear necessary to clarify this picture.
DISCUSSION
The hairpin/triplex transition of DNA is a complex process that is driven by the exchange between the electrostatic energy of protonation/deprotonation and the internal (bond) energy of the macromolecule, aided by interactions with the solvent. A simple two-state equilibrium model is useful in explaining the general behavior of the experimental titration curves and can in fact be used to provide an estimate of the free energy difference between the unprotonated (or protonated) endstates. This model also shows that protonation and folding of this H-DNA oligomer are coupled and highly cooperative. The observation that evolutionary processes commonly take advantage of cooperativity lends support for a biological role for H-DNA.
A more detailed approach is required to investigate intermediate states along the folding pathway and the combined MD/PB method used here seems noteworthy. Of particular interest is the asymmetry in the protonation/deprotonation sequence for the pH-induced folding/unfolding of this molecule. Also, it appears that the C+CCG tetraloop plays a central role in the unfolding transition. Containing the first cytosine to deprotonate, the loop may act as a conformational switch, initiating structural changes throughout the molecule, thus inducing deprotonation and dissociation of the third strand in preparation for unfolding. Perhaps a better description of the CCCG loop would be as a conformational lock. Only when the third strand is protonated and in close proximity to the duplex, and perhaps Hoogsteen-paired with it, does it appear that the CCCG loop protonates, with the guanine base flipping from its Watson-Crick position to form a Hoogsteen pair, essentially locking the entire structure in place. Unfolding the molecule then requires that the structure first be unlocked through deprotonation of the C+CCG loop.
Finally, we make one comment regarding the lack of a C+CCG tetraloop in H-DNA for which the system studied here was used as a model (van Dongen et al., 1996). The effect of a conformational change in the tetraloop leading to deprotonation of the first cytosine in the third strand 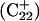 may be viewed as a structural perturbation due to the binding by, or at least influence of, another molecule (protein, drug, or cation) six-basepairs distant, and may thus not be entirely irrelevant to the regulatory role of H-DNA in transcription and replication.
may be viewed as a structural perturbation due to the binding by, or at least influence of, another molecule (protein, drug, or cation) six-basepairs distant, and may thus not be entirely irrelevant to the regulatory role of H-DNA in transcription and replication.
In summary, the complementary use of a two-state equilibrium model and a combined MD/PB dynamic approach has provided a fairly detailed picture of this simple yet rich system. Extension of these techniques to similar problems such as the magnesium-induced folding of RNA should be equally rewarding.
Acknowledgments
We thank Professors S.S. Wijmenga, C.W. Hilbers, and A.N. Lane for helpful insights and discussions.
This work was supported in part by National Institutes of Health grant GM29079.
APPENDIX
Consider a molecule (DNA) that can assume two conformations, which we designate as τ (triplex) and δ (duplex). Consider also that this molecule and hence each conformation possesses N (necessarily nonidentical) protonatable sites. We identify the protonation state of a conformation by the total number of sites which are protonated, thus giving N + 1 possible states for each conformation and ranging from fully unprotonated to fully protonated. Within each of these protonation states are 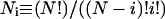 protonation substates determined by the specific sites that are protonated. The τ–δ conformational transition can be described by the two-state equilibrium constant
protonation substates determined by the specific sites that are protonated. The τ–δ conformational transition can be described by the two-state equilibrium constant
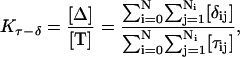 |
(A1) |
where Δ and T are total concentrations of duplex and triplex, and i and j indicate the protonation state and substate of the particular conformation, respectively. To express Kτ–δ in terms of pH, we require the free energy change as a function of pH between the fully unprotonated state (δ0 ≡ δ01; no second subscript is necessary since this state is unique) and a particular protonation substate. (We could also start from the fully protonated state δ4.) That is, we want the equilibrium constant 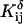 for the protonation scheme
for the protonation scheme
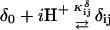 |
(A2) |
or
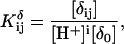 |
(A3) |
as well as the corresponding expression for the τ-conformation. Assuming that no structural changes contribute to the free energy upon protonation, the Bashford-Karplus method can be used to obtain the equilibrium constant for reaction A2 (Bashford and Karplus, 1990):
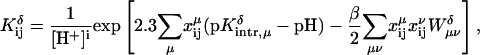 |
(A4) |
where xμ denotes a protonation state “vector” for a site μ which takes the value 1 or 0 depending on whether substate ij of site μ is protonated or not. Equation A4 also contains a correction term Wμν (Wμμ ≡ 0) that accounts for the interaction between mutually protonated sites in a substate. Combining Eqs. A1, A3, and A4, along with the corresponding expression for the τ-conformation, gives the desired result for the τ–δ equilibrium constant of
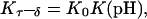 |
(A5) |
where
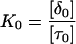 |
(A6) |
is the high-pH limit of Kτ–δ corresponding to the free energy change (βΔG0 = −2.3 pK0) for the transition between unprotonated conformations, and the pH-dependent part of the equilibrium constant is contained in the quantity
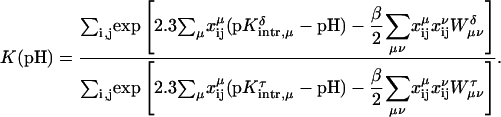 |
(A7) |
The equilibrium constant has the obvious limits corresponding to the fully protonated and unprotonated states of
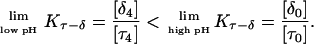 |
(A8) |
Proton exchange NMR measurements can be used to obtain Kτ–δ at different pH. The apparent equivalence point is the pH at which the triplex and duplex concentrations are equal, and corresponds to the condition Kτ–δ = 1. By using Eqs. A1 and A5, and along with the conservation requirement
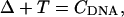 |
(A9) |
where CDNA is the total concentration of DNA, the total concentration of each conformation is given by
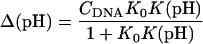 |
(A10) |
and
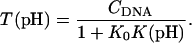 |
(A11) |
For a measured property of the system that depends linearly on the concentrations of the conformations and is independent of protonation substates, such as the absorbance A, we can write
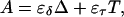 |
(A12) |
where ɛδ and ɛτ are the extinction coefficients of the duplex and triplex conformations, respectively, and are assumed to be independent of pH. Equations A10–A12 allow us to express the absorbance in terms of pH:
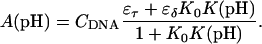 |
(A13) |
The low- and high-pH limits of Eq. A8 show that the absorbance curve displays the expected sigmoidal shape. Using Eq. A13 to fit an absorbance curve allows one to determine the sole fitting parameter K0 and hence the free energy for the unprotonated conformational transition.
A similar analysis can be used to calculate the Hill coefficient (nh) describing the cooperativity of the transition. The Hill coefficient is given by the slope of 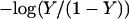 versus pH at Y = 0.5, where Y is the protonated fraction of DNA (Voet and Voet, 1995). Following the notation above, the protonated fraction is given by
versus pH at Y = 0.5, where Y is the protonated fraction of DNA (Voet and Voet, 1995). Following the notation above, the protonated fraction is given by
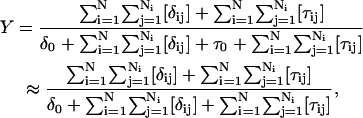 |
(A14) |
with the second line of Eq. A14 following from K0 = δ0/τ0 ≫ 1. Use of Eqs. A3, A4, and A6 then give
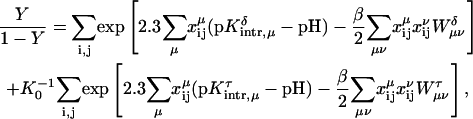 |
(A15) |
which, when plotted as 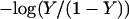 versus pH, yields the Hill coefficient.
versus pH, yields the Hill coefficient.
References
- Antosiewicz, J., J. A. McCammon, and M. K. Gilson. 1994. Prediction of pH-dependent properties of proteins. J. Mol. Biol. 238:415–436. [DOI] [PubMed] [Google Scholar]
- Antosiewicz, J., J. A. McCammon, and M. K. Gilson. 1996. The determinants of pKas in proteins. Biochemistry. 35:7819–7833. [DOI] [PubMed] [Google Scholar]
- Arnott, S., and E. Selsing. 1974. Structures for polynucleotide complexes poly(dA)·poly(dT) and poly(dT)·poly(dA)·poly(dT). J. Mol. Biol. 88:509–521. [DOI] [PubMed] [Google Scholar]
- Asensio, J. L., A. N. Lane, J. Dhesi, S. Bergqvist, and T. Brown. 1998. The contribution of cytosine protonation to the stability of parallel DNA triple helices. J. Mol. Biol. 275:811–822. [DOI] [PubMed] [Google Scholar]
- Bashford, D., and M. Karplus. 1990. pKas of ionizable groups in proteins: atomic detail from a continuum electrostatic model. Biochemistry. 29:10219–10225. [DOI] [PubMed] [Google Scholar]
- Bashford, D., and M. Karplus. 1991. Multiple-site titration curves of proteins: an analysis of exact and approximate methods for their calculation. J. Phys. Chem. 95:9556–9561. [Google Scholar]
- Basye, J., J. O. Trent, D. Q. Gao, and S. W. Ebbinghaus. 2001. Triplex formation by morpholino oligodeoxyribonucleotides in the HER-2/neu promoter requires the pyrimidine motif. Nucleic Acids Res. 29:4873–4880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brinton, B. T., M. S. Caddle, and N. H. Heintz. 1991. Position and orientation-dependent effects of a eukaryotic Z-triplex DNA motif on episomal DNA-replication in COS-7 cells. J. Biol. Chem. 266:5153–5161. [PubMed] [Google Scholar]
- Brion, P., and E. Westhof. 1997. Hierarchy and dynamics of RNA folding. Annu. Rev. Bioph. Biom. 26:113–137. [DOI] [PubMed] [Google Scholar]
- Chen, F. M. 1991. Intramolecular triplex formation of the purine·purine·pyrimidine type. Biochemistry. 30:4472–4479. [DOI] [PubMed] [Google Scholar]
- Cieplak, P., T. E. Cheatham, and P. A. Kollman. 1997. Molecular dynamics simulations find that 3′ phosphoramidate-modified DNA duplexes undergo a B to A transition and normal DNA duplexes an A to B transition. J. Am. Chem. Soc. 119:6722–6730. [Google Scholar]
- Cornell, W. D., P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell, and P. A. Kollman. 1995. A second generation force-field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc. 117:5179–5197. [Google Scholar]
- Csaszar, K., N. Spackova, R. Stefl, J. Sponer, and N. B. Leontis. 2001. Molecular dynamics of the frame-shifting pseudoknot from Beet Western Yellow virus: the role of non-Watson-Crick basepairing, ordered hydration, cation binding and base mutations on stability and unfolding. J. Mol. Biol. 313:1073–1091. [DOI] [PubMed] [Google Scholar]
- Darden, T., D. York, and L. Pedersen. 1993. Particle mesh Ewald: an N·Log(N) method for Ewald sums in large systems. J. Chem. Phys. 98:10089–10092. [Google Scholar]
- Davis, M. E., J. D. Madura, B. A. Luty, and J. A. McCammon. 1991. Electrostatics and diffusion of molecules in solution: simulations with the University of Houston Brownian Dynamics program. Comput. Phys. Commun. 62:187–197. [Google Scholar]
- Felsenfeld, G., D. R. Davis, and A. Rich. 1957. Formation of a three-stranded polynucleotide molecule. J. Am. Chem. Soc. 79:2023–2024. [Google Scholar]
- Frank-Kamenetskii, M. D., and S. M. Mirkin. 1995. Triplex DNA structures. Annu. Rev. Biochem. 64:65–95. [DOI] [PubMed] [Google Scholar]
- Gardiner, E. J., C. A. Hunter, M. J. Packer, D. S. Palmer, and P. Willett. 2003. Sequence-dependent DNA structure: a database of octamer structural parameters. J. Mol. Biol. 332:1025–1035. [DOI] [PubMed] [Google Scholar]
- Georgescu, R. E., E. G. Alexov, and M. R. Gunner. 2002. Combining conformational flexibility and continuum electrostatics for calculating pKas in proteins. Biophys. J. 83:1731–1748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glikin, G. C., G. Gargiulo, L. Renadescalzi, and A. Worcel. 1983. Escherichia coli single-strand binding: protein stabilizes specific denatured sites in superhelical DNA. Nature. 303:770–774. [DOI] [PubMed] [Google Scholar]
- Gluck, A., Y. Endo, and I. G. Wool. 1994. The ribosomal-RNA identity elements for ricin and for α-sarcin: mutations in the putative CG pair that closes a GAGA tetraloop. Nucleic Acids Res. 22:321–324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gueron, M., M. Kochoyan, and J. L. Leroy. 1987. A single-mode of DNA basepair opening drives imino proton-exchange. Nature. 328:89–92. [DOI] [PubMed] [Google Scholar]
- Hilbers, C. W., M. J. J. Blommers, F. J. M. Vandeven, J. H. van Boom, and G. A. van der Marel. 1991. High-resolution NMR: studies of DNA hairpins with four nucleotides in the loop region. Nucleos. Nucleot. 10:61–80. [Google Scholar]
- Htun, H., E. Lund, and J. E. Dahlberg. 1984. Human U1 RNA genes contain an unusually sensitive nuclease S1 cleavage site within the conserved 3′ flanking region. Proc. Natl. Acad. Sci. USA. 81:7288–7292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jorgensen, W. L., and J. Pranata. 1990. Importance of secondary interactions in triply hydrogen-bonded complexes: guanine-cytosine vs. uracil-2,6-diaminopyridine. J. Am. Chem. Soc. 112:2008–2010. [Google Scholar]
- Jucker, F. M., and A. Pardi. 1995. Solution structure of the CUUG hairpin loop: a novel RNA tetraloop motif. Biochemistry. 34:14416–14427. [DOI] [PubMed] [Google Scholar]
- Kato, M., and N. Shimizu. 1992. Effect of the potential triplex DNA region on the in vivo expression of bacterial β-lactamase gene in superhelical recombinant plasmids. J. Biochem. 112:492–494. [DOI] [PubMed] [Google Scholar]
- Kiran, M. R., and M. Bansal. 1995. Structural polymorphism in d(T)(12)·D(A)(12)*d(T)(12) triple helices. J. Biomol. Struct. Dyn. 13:493–505. [DOI] [PubMed] [Google Scholar]
- Lamm, G. 2003. The Poisson-Boltzmann equation. In Reviews in Computational Chemistry. K.B. Lipkowitz, R. Larter, and T. R. Cundari, editors. Wiley & Sons, Hoboken, NJ. 147–365. We point out two typographic errors in Lamm, 2003, in Eq. 407; the superscript of the free energy in the first line should read B and that of the second line should read C. Also, the sign in front of the summation over background charges in Eq. 412 should be positive. Additional errata will appear on the Reviews in Computational Chemistry web site.
- Lavery, R., and H. Sklenar. 1988. The definition of generalized helicoidal parameters and of axis curvature for irregular nucleic acids. J. Biomol. Struct. Dyn. 6:63–91. [DOI] [PubMed] [Google Scholar]
- Lavery, R., and H. Sklenar. 1989. Defining the structure of irregular nucleic acids: conventions and principles. J. Biomol. Struct. Dyn. 6:655–667. [DOI] [PubMed] [Google Scholar]
- Leitner, D., W. Schroder, and K. Weisz. 1998. Direct monitoring of cytosine protonation in an intramolecular DNA triple helix. J. Am. Chem. Soc. 120:7123–7124. [Google Scholar]
- Leitner, D., W. Schroder, and K. Weisz. 2000. Influence of sequence-dependent cytosine protonation and methylation on DNA triplex stability. Biochemistry. 39:5886–5892. [DOI] [PubMed] [Google Scholar]
- Leroy, J. L., M. Kochoyan, T. Huynhdinh, and M. Gueron. 1988. Characterization of basepair opening in deoxynucleotide duplexes using catalyzed exchange of the imino proton. J. Mol. Biol. 200:223–238. [DOI] [PubMed] [Google Scholar]
- Li, H., A. W. Hains, J. E. Everts, A. D. Robertson, and J. H. Jensen. 2002. The prediction of protein pKas using QM/MM: the pKa of lysine 55 in Turkey ovomucoid third domain. J. Phys. Chem. B. 106:3486–3494. [Google Scholar]
- Lim, C., D. Bashford, and M. Karplus. 1991. Absolute pKa calculations with continuum dielectric methods. J. Phys. Chem. 95:5610–5620. [Google Scholar]
- Lyamichev, V. I., S. M. Mirkin, and M. D. Frank Kamenetskii. 1985. A pH-dependent structural transition in the homopurine-homopyrimidine tract in superhelical DNA. J. Biomol. Struct. Dyn. 3:327–338. [DOI] [PubMed] [Google Scholar]
- Macaya, R., E. Wang, P. Schultze, V. Sklenar, and J. Feigon. 1992a. Proton nuclear-magnetic resonance assignments and structural characterization of an intramolecular DNA triplex. J. Mol. Biol. 225:755–773. [DOI] [PubMed] [Google Scholar]
- Macaya, R. F., P. Schultze, and J. Feigon. 1992b. Sugar conformations in intramolecular DNA triplexes determined by coupling constants obtained by automated simulation of P·COSY cross peaks. J. Am. Chem. Soc. 114:781–783. [Google Scholar]
- MacKerell, A. D., J. Wiorkiewicz-Kuczera, and M. Karplus. 1995. An all-atom empirical energy function for the simulation of nucleic acids. J. Am. Chem. Soc. 117:11946–11975. [Google Scholar]
- Madura, J. D., J. M. Briggs, R. C. Wade, M. E. Davis, B. A. Luty, A. Ilin, J. Antosiewicz, M. K. Gilson, B. Bagheri, L. R. Scott, and J. A. McCammon. 1995. Electrostatics and diffusion of molecules in solution: simulations with the University of Houston Brownian Dynamics program. Comput. Phys. Commun. 91:57–95. [Google Scholar]
- Massova, I., and P. A. Kollman. 2000. Combined molecular mechanical and continuum solvent approach (MM-PBSA/GBSA) to predict ligand binding. Perspect. Drug Discov. 18:113–135. [Google Scholar]
- Michel, F., and E. Westhof. 1990. Modeling of the three-dimensional architecture of group-I catalytic introns based on comparative sequence analysis. J. Mol. Biol. 216:585–610. [DOI] [PubMed] [Google Scholar]
- Mirkin, S. M., V. I. Lyamichev, K. N. Drushlyak, V. N. Dobrynin, S. A. Filippov, and M. D. Frank Kamenetskii. 1987. DNA H-form requires a homopurine homopyrimidine mirror repeat. Nature. 330:495–497. [DOI] [PubMed] [Google Scholar]
- Moore, P. B. 1999. Structural motifs in RNA. Annu. Rev. Biochem. 68:287–300. [DOI] [PubMed] [Google Scholar]
- Murphy, F. L., and T. R. Cech. 1994. GAAA tetraloop and conserved bulge stabilize tertiary structure of a group-I intron domain. J. Mol. Biol. 236:49–63. [DOI] [PubMed] [Google Scholar]
- Nicholls, A., and B. Honig. 1991. A rapid finite-difference algorithm, utilizing successive over-relaxation to solve the Poisson-Boltzmann equation. J. Comp. Chem. 12:435–445. [Google Scholar]
- Ojha, R. P., and R. K. Tiwari. 2002. Molecular dynamics simulation study of DNA triplex formed by mixed sequences in solution. J. Biomol. Struct. Dyn. 20:107–126. [DOI] [PubMed] [Google Scholar]
- Olson, W. K., A. A. Gorin, X. J. Lu, L. M. Hock, and V. B. Zhurkin. 1998. DNA sequence-dependent deformability deduced from protein-DNA crystal complexes. Proc. Natl. Acad. Sci. USA. 95:11163–11168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pack, G. R., G. A. Garrett, L. Wong, and G. Lamm. 1993. The effect of a variable dielectric coefficient and finite ion size on Poisson-Boltzmann calculations of DNA-electrolyte systems. Biophys. J. 65:1363–1370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pack, G. R., L. Wong, and G. Lamm. 1998. pKa of cytosine on the third strand of triplex DNA: preliminary Poisson-Boltzmann calculations. Inter. J. Quantum. Chem. 70:1177–1184. [Google Scholar]
- Pearlman, D. A., D. A. Case, J. W. Caldwell, W. S. Ross, T. E. Cheatham, S. Debolt, D. Ferguson, G. Seibel, and P. Kollman. 1995. AMBER, a package of computer programs for applying molecular mechanics, normal mode analysis, molecular dynamics and free energy calculations to simulate the structural and energetic properties of molecules. Comput. Phys. Commun. 91:1–41. [Google Scholar]
- Petrov, A. S., G. Lamm, and G. R. Pack. 2005. Calculation of binding free energy for magnesium-RNA interactions. Biopolymers. In press. [DOI] [PubMed]
- Plum, G. E., and K. J. Breslauer. 1995. Thermodynamics of an intramolecular DNA triple helix: a calorimetric and spectroscopic study of the pH and salt dependence of thermally induced structural transitions. J. Mol. Biol. 248:679–695. [DOI] [PubMed] [Google Scholar]
- Powell, S. W., L. H. Jiang, and I. M. Russu. 2001. Proton exchange and basepair opening in a DNA triple helix. Biochemistry. 40:11065–11072. [DOI] [PubMed] [Google Scholar]
- Radhakrishnan, I., and D. J. Patel. 1994. DNA Triplexes: solution structures, hydration sites, energetics, interactions, and function. Biochemistry. 33:11405–11416. [DOI] [PubMed] [Google Scholar]
- Rao, B. S., H. Manor, and R. G. Martin. 1988. Pausing in Simian virus-40 DNA: replication by a sequence containing (dG-dA)27·(dT-dC)27. Nucleic Acids Res. 16:8077–8094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riley, M., B. Maling, and M. J. Chamberlin. 1966. Physical and chemical characterization of two- and three-stranded adenine·thymine and adenine·uracil homopolymer complexes. J. Mol. Biol. 20:359–389. [DOI] [PubMed] [Google Scholar]
- Ripoll, D. R., Y. N. Vorobjev, A. Liwo, J. A. Vila, and H. A. Scheraga. 1996. Coupling between folding and ionization equilibria: effects of pH on the conformational preferences of polypeptides. J. Mol. Biol. 264:770–783. [DOI] [PubMed] [Google Scholar]
- Roberts, R. W., and D. M. Crothers. 1996. Prediction of the stability of DNA triplexes. Proc. Natl. Acad. Sci. USA. 93:4320–4325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ryckaert, J. P., G. Ciccotti, and H. J. C. Berendsen. 1977. Numerical integration of Cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comp. Phys. 23:327–341. [Google Scholar]
- Sham, Y. Y., Z. T. Chu, and A. Warshel. 1997. Consistent calculations of pKas of ionizable residues in proteins: semi-microscopic and microscopic approaches. J. Phys. Chem. B. 101:4458–4472. [Google Scholar]
- Shields, G. C., C. A. Laughton, and M. Orozco. 1997. Molecular dynamics simulations of the d(T·A·T) triple helix. J. Am. Chem. Soc. 119:7463–7469. [Google Scholar]
- Shimizu, M., J. C. Hanvey, and R. D. Wells. 1989. Intramolecular DNA triplexes in supercoiled plasmids. I. Effect of loop size on formation and stability. J. Biol. Chem. 264:5944–5949. [PubMed] [Google Scholar]
- Shimizu, M., K. Kubo, U. Matsumoto, and H. Shindo. 1994. The loop sequence plays crucial roles for isomerization of intramolecular DNA triplexes in supercoiled plasmids. J. Mol. Biol. 235:185–197. [DOI] [PubMed] [Google Scholar]
- Singh, U. C., and P. A. Kollman. 1984. An approach to computing electrostatic charges for molecules. J. Comp. Chem. 5:129–145. [Google Scholar]
- Sklenar, V., and J. Feigon. 1990. Formation of a stable triplex from a single DNA strand. Nature. 345:836–838. [DOI] [PubMed] [Google Scholar]
- Soyfer, V., and V. N. Potaman. 1996. Triple-Helical Nucleic Acids. Springer, New York.
- Spackova, N., I. Berger, M. Egli, and J. Sponer. 1998. Molecular dynamics of hemiprotonated intercalated four-stranded I-DNA: stable trajectories on a nanosecond scale. J. Am. Chem. Soc. 120:6147–6151. [Google Scholar]
- Sponer, J., J. V. Burda, P. Mejzlik, J. Leszczynski, and P. Hobza. 1997. Hydrogen-bonded trimers of DNA bases and their interaction with metal cations: ab initio quantum-chemical and empirical potential study. J. Biomol. Struct. Dyn. 14:613–628. [DOI] [PubMed] [Google Scholar]
- Sugimoto, N., P. Wu, H. Hara, and Y. Kawamoto. 2001. pH and cation effects on the properties of parallel pyrimidine motif DNA triplexes. Biochemistry. 40:9396–9405. [DOI] [PubMed] [Google Scholar]
- Sun, J. S., J. L. Mergny, R. Lavery, T. Montenaygarestier, and C. Helene. 1991. Triple helix structures: sequence dependence, flexibility and mismatch effects. J. Biomol. Struct. Dyn. 9:411–424. [DOI] [PubMed] [Google Scholar]
- Tanford, C., and J. G. Kirkwood. 1957. Theory of protein titration curves. I. General equations for impenetratable spheres. J. Am. Chem. Soc. 79:5333–5339. [Google Scholar]
- Tanford, C., and R. Roxby. 1972. Interpretation of protein titration curves: application to lysozyme. Biochemistry. 11:2192–2198. [DOI] [PubMed] [Google Scholar]
- van Aalten, D. M. F., D. A. Erlanson, G. L. Verdine, and L. Joshua-Tor. 1999. A structural snapshot of basepair opening in DNA. Proc. Natl. Acad. Sci. USA. 96:11809–11814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Dongen, M. J. P., J. F. Doreleijers, G. A. van der Marel, J. H. van Boom, C. W. Hilbers, and S. S. Wijmenga. 1999. Structure and mechanism of formation of the H-y5 isomer of an intramolecular DNA triple helix. Nat. Struct. Biol. 6:854–859. [DOI] [PubMed] [Google Scholar]
- van Dongen, M. J. P., S. S. Wijmenga, G. A. van der Marel, J. H. van Boom, and C. W. Hilbers. 1996. The transition from a neutral-pH double helix to a low-pH triple helix induces a conformational switch in the CCCG tetraloop closing a Watson-Crick stem. J. Mol. Biol. 263:715–729. [DOI] [PubMed] [Google Scholar]
- Voet, D., and J. G. Voet. 1995. Biochemistry. J. Wiley & Sons, New York.
- Volker, J., and H. H. Klump. 1994. Electrostatic effects in DNA triple helices. Biochemistry. 33:13502–13508. [DOI] [PubMed] [Google Scholar]
- Weisz, K., D. Leitner, C. Krafft, and T. Welfle. 2000. Structural heterogeneity in intramolecular DNA triple helices. Biol. Chem. 381:275–283. [DOI] [PubMed] [Google Scholar]
- Wool, I. G., A. Gluck, and Y. Endo. 1992. Ribotoxin recognition of ribosomal RNA and a proposal for the mechanism of translocation. Trends Biochem. Sci. 17:266–269. [DOI] [PubMed] [Google Scholar]
- You, T. J., and D. Bashford. 1995. Conformation and hydrogen ion titration of proteins: a continuum electrostatic model with conformational flexibility. Biophys. J. 69:1721–1733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou, H. X., and M. Vijayakumar. 1997. Modeling of protein conformational fluctuations in pKa predictions. J. Mol. Biol. 267:1002–1011. [DOI] [PubMed] [Google Scholar]
- Zwieb, C. 1992. Recognition of a tetranucleotide loop of signal recognition particle RNA by protein-SRP 19. J. Biol. Chem. 267:15650–15656. [PubMed] [Google Scholar]