Doming modes and dynamics of model heme compounds

Abstract

Synchrotron far-IR spectroscopy and density-functional calculations are used to characterize the low-frequency dynamics of model heme FeCO compounds. The “doming” vibrational mode in which the iron atom moves out of the porphyrin plane while the periphery of this ring moves in the opposite direction determines the reactivity of oxygen with this type of molecule in biological systems. Calculations of frequencies and absorption intensities and the measured pressure dependence of vibrational modes in the model compounds are used to identify the doming and related normal modes.

The biological functions of heme proteins such as myoglobin in reversible transport of O₂ as well as CO and NO for regulation of physiological functions are well known (1–7). The myoglobin active center is a five-coordinated iron porphyrin (heme) complex in which the axial ligand is an imidazole ring from a histidine residue of the protein. This system is capable of binding the sixth ligand in an axial position, which, due to the size of the pocket left open by the encompassing globin, can be a small molecule like oxygen, carbon monoxide, or nitroxide. Binding of this small molecule changes the spin state of the Fe-porphyrin group and pulls the iron atom into the porphyrin ring plane, triggering conformational change of the protein. It also ensures a cooperative binding of oxygen to the four heme units in hemoglobin. Although significant progress has been made in understanding the dynamics of the heme after ligand binding and release (e.g., after dissociation) (8, 9), the dynamics of the Fe atom bound to the heme-bearing protein as well as the heme molecule itself have not been fully characterized. It is clear that iron atom motion is of utmost importance in triggering a conformational change in myoglobin on binding a small polar molecule to the axial position (10–19).

It is indeed the dynamics of the heme prosthetic group and that of the surrounding protein that determine the physiological properties of hemoglobin. It has been shown that access of small molecules such as oxygen, CO, or NO to the heme is controlled by the protein (21). There have thus been numerous experimental studies of the molecular vibrations in heme and heme-related chromophores. These studies have included resonance Raman (12, 13), femtosecond coherence spectroscopy (14), and inelastic x-ray scattering with synchrotron radiation (10, 11). The theoretical studies include molecular dynamics (2) as well as density functional theory (DFT) geometry and force field studies (15–19), calculated resonance Raman (18), and IR intensities (19). Each of these techniques has provided useful information for describing the dynamics of this important class of biomolecules. Molecular dynamics studies (2) in particular demonstrate the importance of precise knowledge of the dynamics of the heme. The motion of bound groups such as CO, NO, or O₂ can be accurately characterized only with a complete knowledge of the binding forces and dynamics of the heme molecule. Undoubtedly, the most discussed dynamical feature in these molecules is the “doming” mode that involves the motion of Fe out of the plane of the molecule and a distortion of the heme from its planar configuration. Many of the techniques mentioned above have been used with the goal of characterizing the doming mode but the investigations carried out to date have not yet unequivocally identified and characterized this mode.

In this study, we used synchrotron far-IR spectroscopy and diamond-anvil cell methods in combination with DFT calculations of vibrational frequencies and intensities to characterize the low-frequency dynamics in iron-porphyrin compounds. These compounds are models for the oxygen-transporting heme compounds such as myoglobin. Recently, it has been shown that DFT can yield efficiently accurate potential energy surfaces, including the effects of electron correlation for complex molecules. It is therefore possible to predict with high reliability the frequencies, vibrational amplitudes, and IR absorption or Raman scattering intensities that can be combined to give a detailed characterization of molecular motions that define their biological reactivity. The remarkably accurate results obtained for metalloporphyrins (18, 19, 21) indicate that this would be an ideal class of materials for the study of low-frequency motions including the biologically important doming mode.

Experimental and Theoretical Methods

Samples of COFe(OEP)Py (carboxy-octaethyl-ironporphyrin-pyridine) with both natural abundance of isotopes and with ¹³C on the CO group were prepared as follows.

Octaethylporphine (OEP) was purchased from Porphyrin Products, Logan, UT. All solvents were obtained from Aldrich and used without further purification. Pyridine-d₅ (D, 99.5%) and ¹³CO gas (¹³C, 99%; ¹⁸O, 10%) were purchased from Cambridge Isotope Laboratories, Andover, MA. Iron(II) acetate and its ⁵⁴Fe isotopomer in hot acetic acid were used to incorporate iron into the free-base porphyrin (22). The mixture was stirred for 1 h at 50–60°C. The dried solids were chromatographed on basic alumina (grade III, Aldrich) with toluene after elution with methylene chloride. The nonfluorescent fraction eluted with methylene chloride was washed with 1 M solution of HCl and evaporated to dryness. COFe(OEP)Py was synthesized according to a modification of a previously published procedure (23). Fe(OEP)Cl was dissolved in neat tetrahydrofuran and reduced with freshly prepared zinc amalgam, and 1.1 molar equivalent of pyridine and excess of CO were added to the filtrated solution after centrifugation of the mixture for 3–5 min. The solution of COFe(OEP)Py was filtrated again and addition of degassed water-precipitated COFe(OEP)Py, which was collected by centrifugation and dried over nitrogen. Mid- and low-frequency IR spectra in KBr pellets were recorded at room temperature with a conventional IR source to confirm the identity of prepared complexes. Isotopomers with ⁵⁷Fe and a sample of carboxy-ethio-ironporphyrin-pyridine were also prepared and used for assignment of IR modes. Conventional mid-IR spectra of all samples were obtained to verify the purity of the samples.

Subsequently, detailed IR absorption experiments, including far-IR measurements, were performed at beamline U2A at the National Synchrotron Light Source, Brookhaven National Laboratory, Upton, NY. The spectra were obtained with a Bruker 66v/S vacuum Fourier transform interferometer by using a boron doped Si bolometer (Infrared Laboratories, Tucson, AZ) for the far-IR. A HgCdTe type A detector was used for mid-IR spectra to verify sample purity and assignment of mid-IR bands. Spectra were obtained by using either mylar beamsplitters with thicknesses of 3.5, 6, and 23 μm to cover the frequency ranges from 30 to 600 cm⁻¹ or a Si beamsplitter on a KBr substrate for the mid-IR frequency range from 600 to 4,000 cm⁻¹ both with a resolution of 4 cm⁻¹. Samples were mounted either on the working face of a diamond anvil without a gasket or mounted in a gasket in a diamond-anvil high-pressure cell. Stainless steel gaskets with thicknesses of 25–500 μm and apertures of 200–500 μm were used to hold the samples. Ruby chips with diameters of ≈10 μm were loaded with the samples and used for pressure measurement. Pressures were measured by the wavelength shift of the ruby fluorescence (24). The pressure range used in this study was 0.1 MPa to 1.5 GPa. All spectra were obtained at room temperature.

Calculations were performed by using gradient-corrected DFT methods with a hybrid Becke-Lee-Young-Parr exchange correlation functional (B3-LYP) implemented in GAUSSIAN 98 quantum chemistry software (25). Optimization of geometry and force field calculation were performed with 6–31G* basis set on N, C, O, and H atoms and the Ahlrichs VTZ basis set on Fe atom.

Results and Discussion

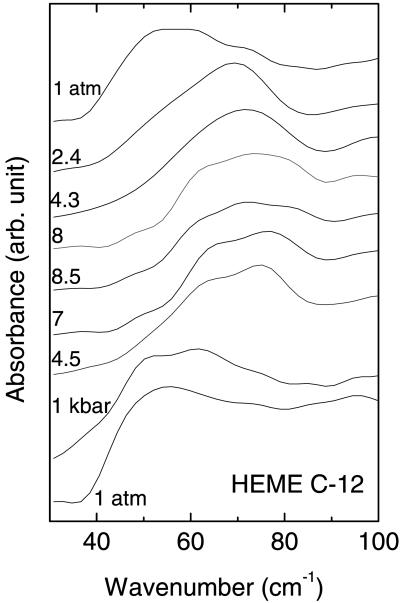
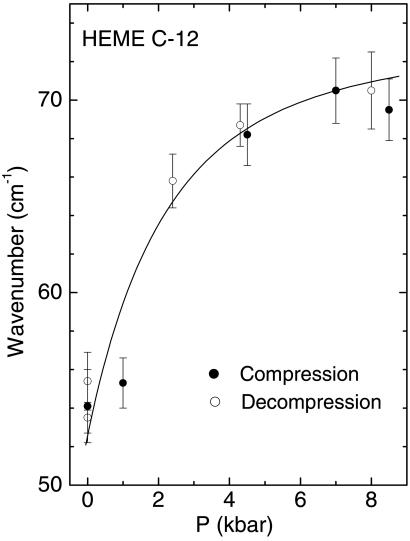
The IR spectra of COFe(OEP)Py as a function of pressure are shown in Figs. 1 and 2. The measured pressure dependence of absorption peaks in the pressure range 0.1 MPa to 1.5 GPa was greatest for the broad peak observed at ≈53 cm⁻¹. This absorption peak shifted rapidly with a small increase in pressure. It shifted by ≈20 cm⁻¹ within 0.24 GPa and then more slowly up to 0.85 GPa. Due to the very broad and somewhat weak absorption, a sample thickness of 500 μm was required to observe this peak. This requirement restricted the pressure range used to prevent extrusion of the gasket and to enable the recording of spectra on decompression. The pressure dependence of the lowest frequency absorption is shown in Fig. 2. The pressure dependences of the peak positions were completely reversible on increasing and decreasing pressure. Several of the other absorption peaks in the spectra at higher frequencies also had complex structure, indicating multiple peaks within a single broad absorption feature.

Figure 1.

Far-IR absorption spectra of CoFe(OEP)Py determined with a 23-μm thick mylar beamsplitter. The gasket and sample were ≈500 μm thick with a 500 μm diameter.

Figure 2.

Pressure dependence of the low-frequency (53 cm⁻¹) peak.

The results of the calculations for COFe(OEP)Py and the description of each vibrational mode with non-negligible IR intensity are given in Table 1. The calculated integrated intensities and frequencies can be compared with the experimental result to identify the key modes for this molecule. In particular, the calculated harmonic frequency of the doming mode for the molecule is predicted to be at ≈39 cm⁻¹. This mode is expected to have a marked negative anharmonicity due to the quartic terms in the potential. The sign of anharmonicity results from rigidity of the poprhyrin ring combined with the strength of the Fe-N(P) bonds. Thus the observed fundamental of this mode should be at a somewhat larger energy than calculated at this level. Moreover, the calculations are performed for the isolated molecule due to the practical system size limitations of the DFT technique. Thus there may be additional lattice vibrations at lower frequencies that overlap with the intramolecular vibrations. In addition, crystal field effects are not accounted for in these calculations. On the other hand, intermolecular interactions in such molecular systems are in general weaker than the intramolecular interactions, allowing assignments of major features to be made with reasonable certainty. Notably, a very large pressure dependence is expected for those vibrational modes associated with large amplitude molecular distortions or molecular translations (i.e., lattice vibrations).

Table 1.

Calculated frequencies, integrated intensities, and vibrational mode description for COFe(OEP)Py

Calculated frequency, cm−1	Calculated integrated intensity, cm/mmol	Frequency, cm−1 (Experiment)	Mode description
33	0.46	53*	Pyridine ring wagging
39	0.66	53*	Doming mode
129	0.55	140	Inverse doming
155	0.47	158*	Py bending + ethane twist
160	0.77	158*	Ethane twist
166	0.32	158*	Ethane twist + Py bend
224	0.26	233	P op deformation
240	0.56	233	CH3 ethane torsion
241	0.33	233	CH3 ethane torsion
253	0.46	250	P op deformation
255	0.43	250	P op deform + CH3 ethane deformation
262	0.88	260	Cm P op deformation + Fe-Py stretch
277	0.47	275	Cm op P deformation
292	0.20	293	N op P deformation
308	0.44	310	Fe in-plane motion, ethane rocking
321	0.41	334	Cm, N(P) op P deformation
340	0.30	352	Fe in-plane motion, ethane rocking
369	7.15	361	op P deformation (Cm and N)
455	0.89	444*	C(CO)-Fe-N(Py) deformation, Py op deformation
458	2.04	444*	op P deformation, Cα, Cβ Pyrrole twist
465	0.34	470	op P deformation (Cα, Cβ) Pyrrole twist
471	1.98	478*	Fe-CO stretch, Fe-N(Py) stretch
480	0.43	478*	op P deformation (N, Cβ)
491	5.02	497*	op P deformation (N, Cβ)
514	4.02	497*	N-Fe-N deformation
532	0.51	520	op P deformation
535	3.23	542	N-Fe-N deformation, pyrrole rocking
575	1.32	572*	Fe-C-O deformation, Fe in-plane motion
576	1.53	572*	Fe-C-O deformation, Fe in-plane motion
588	1.25	588	Pyrrole op deformation

Only modes with calculated integrated intensities greater than 0.2 cm/mmol and frequencies less than 600⁻¹ are listed. Frequencies with asterisks denote peaks that are close in frequency or part of a broad peak and that cannot be clearly separated at 1 bar. These peaks are identified by the same frequency in the table. The following notation is used: P, porphine ring; op, out of P-plane; ip, in the P-plane; C_m, C_α,β-methine bridge and pyrrole rings carbon atoms; Py, axially bound pyridine. 

The largest pressure dependence is for the peak observed at 53 cm⁻¹ at 1 bar. The pressure dependence for this mode is highly nonlinear (Figs. 2 and 3) and decreases rapidly with increasing pressure. This finding reflects the extremely weak binding force constant calculated for the Fe atom in the molecule and the large magnitude of the fourth-order anharmonicity for this mode. This anharmonicity apparently decreases with increasing pressure. We therefore identify the peak observed at 53 cm⁻¹ as a fundamental excitation of the doming mode. Inspection of the character of motions for this vibration shows that the Fe atom amplitude is quite small and it is the periphery of the porphyrin ring that undergoes the largest displacement during vibration.

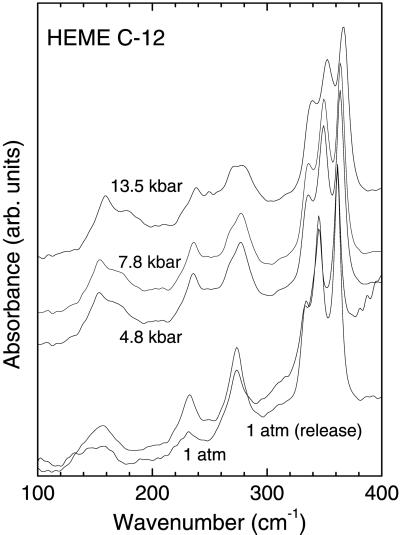
Figure 3.

Far-IR absorption spectra of CoFe(OEP)Py with 6-μm thick mylar beamsplitter. The sample thickness was ≈300 μm.

Comparing the calculated results for COFePy, we find that heavy ethyl substituents on the periphery of the porphyrin ring are responsible for damping of the amplitude of the Fe atom. Such heavy substituents are a rule in all naturally occurring heme complexes including myoglobin, which plausibly explains the failure to identify this mode by means of Mössbauer spectroscopy (11). The experimental pressure dependence of the inverted doming mode, calculated at 129 cm⁻¹, is apparently less than that for the doming mode. Its pressure dependence cannot be estimated with high accuracy since it is calculated to be located in the wide absorption feature with a maximum intensity at 158 cm⁻¹ that includes three other bands with similar absorption strengths. It is expected, however, that the inverted doming mode would have a lower pressure dependence than the doming mode since the atomic motions in this mode involve Fe and Cβ atoms moving in one direction and N(P), C_m, and Cα atoms moving in the opposite directions. The atoms denoted Cβ are on the periphery of the porphine ring attached to the Fe, the C_m, and atoms are in the methine bridges joining the four pyrrole rings of poprhine, and the Cα atoms are adjacent to the N atoms of the pyrrole rings. It should be noted that the calculations reported here are for a molecule with a low spin state. Calculations on this class of molecules in other low-lying spin states close in energy in five-coordinated complexes like deoxy heme can lead to a shift of the mode frequency by 20 cm⁻¹ or more for the doming or inverted doming modes (26). The agreement between the calculated and observed frequencies can nevertheless be considered to be very good.

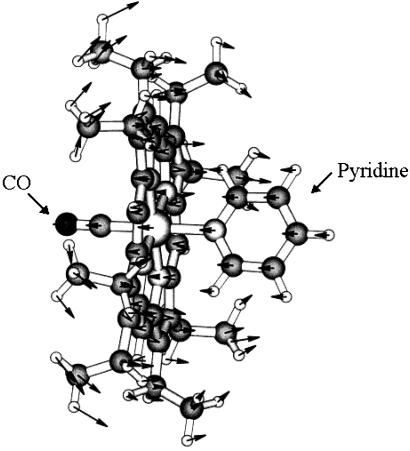
The approximate integrated intensities of peaks relative to the strongest peaks in the absorption spectrum are in reasonable agreement with the calculated ratios with one possible exception. This is the group of peaks in the 310- to 370-cm⁻¹ region. The calculated absorption intensity of a particular out-of-plane porphine deformation is substantially greater than other peaks in this region (see Table 1). The apparent difference between the experimental and the calculated intensity distribution may be due to the effects of intermolecular interactions that result in sharing of IR absorption intensities and are not accounted for in the calculations. This mixing could occur since all modes in this region with calculated intensities >0.2 km/mmol have the same symmetry. The total calculated intensity ratio of the peaks in the 310- to 370-cm⁻¹ region to that the doming mode is ≈12 if one excludes the contribution of the pyridine ring wagging mode that is close to that of the mode identified as the doming vibration. This agrees well with experiment. The calculated rms vibrational amplitude of the Fe atom perpendicular to the plane of the molecule for the doming mode is 0.04 Å (Fig. 4). This finding compares with calculated vibrational amplitudes of 0.03 Å for the N atoms and maximum vibrational amplitudes of 0.06 Å for C atoms perpendicular to the plane of the molecule and the maximum amplitude of 0.09 Å for the peripheral hydrogen atoms on the methyl ends of the ethane groups. The conformational change in hemoglobin is triggered by the binding of the sixth ligand to the iron atom. This switches the spin state of the complex from a (tense) quintet into a (relaxed) singlet and causes a large (about 0.3–0.4 Å) displacement of the iron atom along the doming mode coordinate (26). The softness of the potential energy surface along the doming coordinate facilitates such a large conformational change.

Figure 4.

COFe(OEP)Py molecule showing atom displacements for doming mode. The Fe atom is located between the CO and pyridine molecules. Nitrogen atoms are bonded to the Fe atom.

Summary

A number of experimental studies have reported low-frequency modes in closely related compounds (5, 10–12). These studies identified low-frequency vibrations but, in contrast to the present study, the authors were unable to make a definitive assignment due to either lack of theoretical calculations or incomplete experimental information such as intensity data or the use of pressure dependence. The assignments in the present work were made through the combined use of pressure studies and DFT calculations. DFT methods had earlier proven to be accurate for the modes in the mid-IR frequency range for these materials (19). As a further test of these conclusions, we also measured the mid-IR spectrum due to ¹³CO in an isotopically doped sample. It is interesting that the high sensitivity of the current apparatus yielded the peaks for ¹³C¹⁶O, ¹²C ¹⁶O, as well as for ¹³C ¹⁸O, and the observed frequencies are in excellent agreement with the earlier predictions from DFT calculations (13).

In summary, we have used synchrotron IR spectroscopy, in particular far-IR and high-pressure measurements together with DFT calculations, to identify the low-frequency modes including the long-sought doming mode. It is believed that the present techniques can be successfully applied to this wide class of biologically important materials to lead to a detailed understanding of the reaction dynamics of heme proteins.

Abbreviations

DFT

density functional theory

COFe(OEP)Py

carboxy-octaethyl-ironporphyrin-pyridine

OEP

octaethylporphine