Abstract
The quinol:fumarate reductase of Wolinella succinogenes binds a low- and a high-potential heme b group in its transmembrane subunit C. Both hemes are part of the electron transport chain between the two catalytic sites of this redox enzyme. The oxidation-reduction midpoint potentials of the hemes are well established but their assignment in the structure has not yet been determined. By simulating redox titrations, using continuum electrostatics calculations, it was possible to achieve an unequivocal assignment of the low- and high-potential hemes to the distal and proximal positions in the structure, respectively. Prominent features governing the differences in midpoint potential between the two hemes are the higher loss of reaction field energy for the proximal heme and the stronger destabilization of the oxidized form of the proximal heme due to several buried Arg and Lys residues. According to the so-called “E-pathway hypothesis”, quinol:fumarate reductase has previously been postulated to exhibit a novel coupling of transmembrane electron and proton transfer. Simulation of heme b reduction indicates that the protonation state of the conserved residue Glu C180, predicted to play a key role in this process, indeed depends on the redox state of the hemes. This result clearly supports the E-pathway hypothesis.
INTRODUCTION
The quinol:fumarate reductase (QFR) of the anaerobic ɛ-proteobacterium Wolinella succinogenes is a diheme-containing membrane protein complex, which couples the two-electron reduction of fumarate to succinate (reaction Eq. 1a) to the two-electron oxidation of quinol to quinone (reaction Eq. 1b):
 |
(1a) |
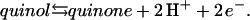 |
(1b) |
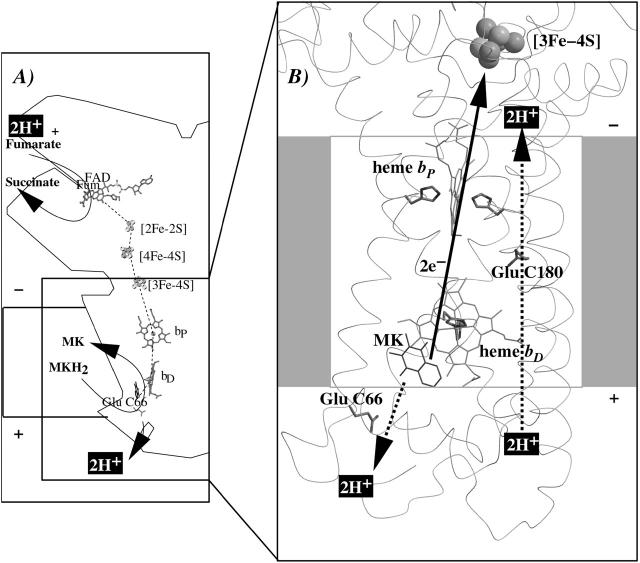
Together with the succinate:quinone reductases, which catalyze the reverse reaction in aerobic respiration, QFRs form the enzyme superfamily of succinate:quinone oxidoreductases (EC 1.3.5.1; Hägerhäll, 1997; Ohnishi et al., 2000; Lancaster, 2003a). According to the composition of their hydrophobic domains, i.e., the membrane anchors of the enzymes, and the respective heme content (Hägerhäll and Hederstedt, 1996; Hederstedt, 1999), succinate:quinone oxidoreductases are classified in five types, i.e., A–E (see Lancaster, 2001, 2002a, for a detailed description and recent overview). Following this scheme, the QFR from W. succinogenes, as well as the succinate:quinone reductase from the Gram-positive bacterium Bacillus subtilis, are type B enzymes with one large hydrophobic subunit and two heme groups. These heme groups are termed proximal and distal based on their relative proximity to the hydrophilic subunits. The QFR from W. succinogenes is involved in anaerobic respiration with various electron donor substrates, such as formate or molecular hydrogen, and with fumarate as the terminal electron acceptor (Kröger, 1978; Lancaster, 2004). The crystal structure of W. succinogenes QFR in the oxidized state has been determined at 2.2 Å resolution (Lancaster et al., 1999). The site of menaquinol oxidation is located close to the periplasmic side of the membrane in the vicinity of amino acid residue Glu C66 (C is the designator of the respective subunit), which has been shown to be selectively essential for menaquinol oxidation (Lancaster et al., 2000). The functional role and location of Glu C66 indicate that the two protons, which are liberated during menaquinol oxidation, are released on the periplasmic side of the membrane (Lancaster et al., 2000). On the other hand, two protons are invariably bound on the cytoplasmic side of the membrane upon fumarate reduction (Lancaster et al., 2001). Thus, the catalytic reaction of W. succinogenes QFR should contribute to the generation of a transmembrane electrochemical proton potential. However, experimental measurements on inverted vesicles and proteoliposomes containing QFR indicated repeatedly that the enzymatic reaction of QFR is an electroneutral process (Geisler et al., 1994; Kröger et al., 2002; Biel et al., 2002). To reconcile this apparent contradiction, the so-called “E-pathway hypothesis” of coupled transmembrane electron and proton transfer, which is summarized in Fig. 1, A and B, was proposed (Lancaster, 2002b). It states that transmembrane electron transfer via the two QFR heme b groups upon menaquinol oxidation is coupled to a compensatory cotransfer of one proton per electron from the periplasmic to the cytoplasmic side of the membrane. This proton transfer occurs via a pathway, which is transiently open during the reduction of the hemes and inactive in the oxidized state of the enzyme. The two most prominent constituents of the E-pathway were suggested to be the ring C-propionate of the distal heme bD and amino acid residue Glu C180.
FIGURE 1.
(A and B) E-pathway hypothesis of coupled transmembrane proton and electron transfer in the QFR from W. succinogenes. The negative side of the indicated membrane is the bacterial cytoplasm; the positive side corresponds to the periplasm. (A) Hypothetical establishment of a transmembrane electrochemical potential (without an E-pathway) as suggested by the essential role of Glu C66 for menaquinol oxidation by W. succinogenes QFR (Lancaster et al., 2000). Panel A features the prosthetic groups of the W. succinogenes QFR dimer (coordinates as in 1QLA; Lancaster et al., 1999). Also indicated are the side chain of Glu C66 and a tentative model of menaquinol (MKH2) binding. The position of bound fumarate (Fum) is taken from PDB entry 1QLB (Lancaster et al., 1999). (B) Hypothetical cotransfer of one proton per one electron across the membrane (E-pathway hypothesis; Lancaster, 2002b). The two protons that are liberated upon menaquinol oxidation are released toward the periplasmic side of the membrane via residue Glu C66. In compensation, coupled to electron transfer via the two heme groups, protons are transferred from the periplasm via the ring C-propionate of the distal heme bD and residue Glu C180 to the cytoplasm, where they counterbalance the two protons which are bound during fumarate reduction. In the oxidized state of the enzyme the E-pathway is required to be inactive to prevent discharging of the proton potential (Lancaster, 2003a).
In the context of rationalizing the E-pathway hypothesis, this study investigated computationally the effect of transmembrane electron transfer (via the distal and proximal hemes of QFR) on the protonation states of residues in the vicinity of the heme groups. If the E-pathway hypothesis is valid, then transmembrane electron transfer via the heme groups is predicted to be associated with transmembrane proton transfer. This in particular should be reflected in changed ionization states of titratable residues that are actively involved in the suggested proton transfer. Other electron transfer-associated proton transfer events in the enzyme, such as those at the active sites of menaquinol oxidation and fumarate reduction, have not been investigated here.
The second aspect of this contribution was to investigate the electrochemistry of the heme groups of QFR (via simulated Eh and pH titrations) and the assignment of the low- and high-potential hemes to the distal and proximal positions in the structure of QFR. This is also of relevance to the catalytic mechanism and the general understanding of the enzyme since all other prosthetic groups of QFR are already characterized by their oxidation-reduction (midpoint) potentials and their unique position in the structure (Lancaster et al., 1999; Lancaster, 2004).
Finally, the presented results based on electrostatic calculations are compared and discussed with respect to available experimental results.
METHODS
Multiconformation continuum electrostatics method
The employed method of multiconformation continuum electrostatics (MCCE) has been developed and previously been described by M. R. Gunner and co-workers (see Alexov and Gunner, 1997, and Gunner and Alexov, 2000a, for a more detailed description of the MCCE method). In the following the main features are summarized. For our calculations, we used version w-m015 of MCCE. The method allows us to determine the equilibrium conformational and ionization states of all protein side chains, nonsolvent-exposed water molecules, ions, ligands, cofactors, and prosthetic groups at a given pH and ambient redox potential Eh. It makes use of several preselected atomic positions and ionization states for amino acid side chains or heme propionates, cofactors, prosthetic groups, buried waters, and ligands. Thus, the use of MCCE permits the consideration of multiple positions for hydroxyl and water protons; alternative side-chain rotamers for residues with strong electrostatic interactions are based on a heavy atom rotamer library (Dunbrack and Karplus, 1994; Dunbrack and Cohen, 1997). Every individual side-chain conformation and, for practical reasons, also the ionization state of a residue as well as the reduced or oxidized state of a cofactor (or prosthetic group) is characterized as a conformer. In this way, the entirety of conformers represents all allowed states of the protein, which are incorporated into the calculations.
The MCCE program generates the various conformers for all amino acid residues, cofactors or prosthetic groups. The preselection of conformers attempts to create as many good choices as possible without including positions, which will never be selected during the Monte Carlo sampling, since badly chosen conformers will not be part of a low energy microstate (Georgescu et al., 2002).
As described in Gunner and Alexov (2000), crystallographic waters and ions on the protein surface are removed and replaced with the high dielectric surroundings; buried waters are retained and are provided with conformers with different positions for their protons. Furthermore, waters and ions are provided with a conformer, which does not have any interactions with the protein enabling them to move into the solvent.
Arg and Lys side chains are provided with one neutral and one charged conformer. His residues obtain four neutral and two ionized conformers. Two basic His conformers are created by rotation of the side chain around the CB–CG bond. Each of the two cases is further divided into two neutral forms (either atom ND1 or NE2 is deprotonated) and one ionized form. Asn and Gln have two conformers with the terminal N and O atoms in exchanged positions. Asp, Glu, and Tyr are supplied with one charged and two neutral (with the proton placed in the torsion minimum) conformers. In addition, residues with hydroxyl groups (Ser, Thr, and the neutral forms of Asp, Glu, and Tyr) are each provided with an extra conformer, which is capable of donating a hydrogen bond to all surrounding acceptors. All other amino acid residues (Ala, Cys, Gly, Ile, Leu, Met, Phe, Pro, Trp, and Val) are not provided with conformers. The ring C- and D-propionates of the heme groups are provided with conformers analogously to Asp and Glu residues. Water molecules obtain conformers, which donate and accept hydrogen bonds, as well as an additional conformer which does not interact with the protein, hence corresponding to bulk water.
The program DelPhi (Nicholls and Honig, 1991) is used to calculate the electrostatic potential of the protein by solving the Poisson-Boltzmann equation. In this calculation, the protein interior was assigned a dielectric constant of ɛ = 4 and ɛ = 80 was chosen for water (Gilson and Honig, 1986).
The assigned atomic partial charges and radii in the MCCE calculations for the amino acid side chains were taken from the PARSE charge set (Sitkoff et al., 1994). As was stated in Gunner and Alexov (2000), the PARSE parameter set optimized atomic charge and radius to fit transfer energies, and these provide calculated pKa values that compare favorably with other parameter sets (Antosiewicz et al., 1996). Furthermore, these parameters have previously been used in other electrostatic studies—e.g., Alexov and Gunner (1999), Georgescu et al. (2002), Mao et al. (2003), Song et al. (2003), and Hauser et al. (2004).
The partial charges of the heme groups and their His ligands, and also the reference midpoint potential of −220 mV for the bis-His ligated hemes (in aqueous solution) were taken from Gunner and Honig (1991). This value has also been used successfully in other electrostatic studies, e.g., Mao et al. (2003) and Ullmann and Knapp (1999), and the original experimental values are from Wilson (1974).
The partial charges that were assigned to the three iron-sulfur centers were extracted from Stephens et al. (1996) for the [3Fe-4S] center, from Li et al. (1998) for the [2Fe-2S] center, and from Jensen et al. (1994) for the [4Fe-4S] center. For comparison, uniform charge distributions for the iron-sulfur clusters were tested. These did not have a significant influence on the obtained results. The corresponding deviations for the calculated heme b midpoint potentials (not shown) were not more than ±5 mV, and below ±0.04 ΔpK units for the pKa value of Glu C180, which is much less than the accuracy of the employed method compared to experimental data (Georgescu et al., 2002; Mao et al., 2003).
The solution pKsol values used for the ionizable residues were 12.5 (Arg), 4.75 (Asp), 4.75 (Glu), 6.5 (His), 10.8 (Lys), 8.0 (Ntr), and 4.75 (Paa, Pdd). Those reference values were previously utilized and described in other reports of electrostatic calculations (e.g., see Georgescu et al., 2002). The reference pKsol values for Asp and Glu of 4.75 are values corresponding to a simple carboxylic acid, and this value does not strongly depend on the length of the acid alkyl chain (Gunner et al., 2000). Since the influence of the backbone lowers the pKa of Glu and Asp even in peptides (Oliveberg et al., 1995; and Gunner et al., 2000) and since the backbone is explicitly considered in the MCCE calculations, the simple carboxylic acid value for pKsol was employed in this study to avoid double-counting the contributions of the protein backbone (Georgescu et al., 2002). In numerous other electrostatic studies on proteins (e.g., Antosiewicz et al., 1994; Demchuk and Wade, 1996), the values used for pKsol of Asp and Glu were 4.0 and 4.4, respectively. Those values were obtained from experimental studies of peptides (see Richarz and Wüthrich, 1978; Matthew et al., 1985) and their use here would involve double-counting the impact of the peptide backbone by both explicit consideration in the electrostatic calculations and implicit consideration in the reference pKsol values.
The employed solution solvation energies (desolvation penalties) in ΔpK units were −9.9 (Arg+), −12.6 (Asp−), −13.1 (Glu−), −8.9 (His+), −13.6 (Lys+), −10.4 (Ntr+), −12.4 (Paa−, Pdd−), −7.0 (Hem+), −26.6 [4Fe-4S], −30.6 [3Fe-4S], and −29.7 [2Fe-2S]. The values for the oxidized iron-sulfur centers were calculated with the help of MCCE, all others were unchanged from previous MCCE studies as quoted in the literature (e.g., Alexov and Gunner, 1999; Georgescu et al., 2002; Mao et al., 2003; Song et al., 2003; and Hauser et al., 2004).
A single protein microstate n is characterized by selecting one particular conformer for every residue, cofactor, and water molecule of the protein, which is present in the investigated structural model. Thus, the total number of possible microstates is very high if several hundreds or more conformers are being considered in the calculations. Facing a vast number of microstates, MCCE uses Monte Carlo sampling to efficiently determine the probability for every conformer in the Boltzmann distribution for a given set of the parameters Eh and pH. The energy ΔG(n) of any microstate n is calculated as
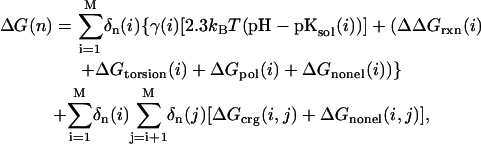 |
(2) |
with kBT = 0.43 ΔpK units = 0.59 kcal/mol (at room temperature); M the total number of conformers; δn(i) = 1 for conformers which are present in microstate n, and δn(i) = 0 for conformers which are absent; γ(i) = −1 for acids, γ(i) = 1 for bases, and γ(i) = 0 for neutral groups. The pKsol(i) is the pKa of an ionizable group i in solution, and ΔΔGrxn(i) is the difference of the reaction field energy for residue i in solution and embedded in the protein, and ΔΔGtorsion(i) is the torsion energy of residue i. The terms ΔGpol(i) and ΔGnonel(i) are the electrostatic and nonelectrostatic (Lennard-Jones) interaction energies between conformer i and the backbone, respectively the residues with no conformers. The terms ΔGcrg(i,j) and ΔGnonel(i,j) are the pairwise electrostatic and nonelectrostatic interaction energies between conformer i and conformer j. The individual terms of Eq. 2 were calculated with the help of MCCE as described in Alexov and Gunner (1997), Gunner and Alexov (2000), and Georgescu et al. (2002).
The so-called intrinsic pK (pKint; Tanford and Kirkwood, 1957) is defined as the pKa of a titrating group in the protein which it would adopt if all other ionizable groups were in their neutral state:
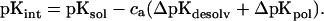 |
(3) |
The parameter ca is −1 if the site is an acid and +1 for a base. The second and third terms of Eq. 3 correspond to ΔΔGrxn and ΔGpol, respectively.
Simulated redox potential (Eh) titrations are performed by setting a fixed pH value before an individual Monte Carlo sampling run; analogously, for pH titrations a fixed ambient redox potential Eh is set. In a similar way, possible intermediate states of electron transfer via the heme groups can be simulated by keeping the oxidation state of the hemes and the other cofactors fixed throughout the Monte Carlo sampling. Subsequently, the found protein microstates can be analyzed with respect to the effect that the fixed charge distribution has on the occupancy of the individual conformers (i.e., the protonation state of an acidic residue in terms of occupancy of the ionized and neutral conformer as well as the side-chain conformation).
Structural model of QFR and coordinates
The structural model that was used in the presented study was based on the crystal structure of the oxidized QFR dimer of a molecular mass of 260 kDa (PDB access code: 1QLA) determined at pH 6.0 as it has been described earlier (Lancaster et al., 1999). Due to the large size of the protein complex, it was necessary to restrict the calculations to the coordinates of subunits B and C and the respective prosthetic groups of one QFR monomer. No membrane model was included in the calculations, since it is not likely that the inclusion of a membrane model would significantly affect the results, as has been discussed earlier for other membrane protein complexes (see Lancaster et al., 1996, and references therein; and Rabenstein et al., 1998). The omission of the majority of crystallographic water molecules was advisable since their number is too great to be entirely incorporated in the multiconformation calculations without increasing the necessary computing time disproportionately. As a sensible compromise and to take advantage of the capability of the MCCE method to explicitly take into account water molecules (and especially different water conformers), a set of 21 water molecules, which were found in the crystal structure within a radius of 9 Å around the heme propionates of the two heme b groups and amino acid residue Glu C180, was included in the QFR model. A similar approach of omitting all crystallographic water molecules, except for a small set of water molecules, which are ligated to the metal binding sites, has been applied in a recent electrostatic study on bovine heart cytochrome c oxidase (Popović and Stuchebrukhov, 2004). The QFR model including the 21 water molecules will be referred to as model W in the following, and the model without water molecules will be addressed as model X. To test the influence of the water molecules on the results, the calculations were performed both on model W and on model X for comparison.
Due to the absence of a crystallographically defined model for menaquinone (MK) or menaquinol (MKH2) in the available coordinate files of W. succinogenes QFR, no quinone species was included in the calculations. As experimentally determined, the in vitro activity of wild-type QFR enzyme is essentially restricted to the region between pH 5 and pH 9 (C. R.D. Lancaster, unpublished). Furthermore, the coordinates, which were taken from the original crystal structure (1QLA), represent the enzyme in its oxidized state at pH 6, and it is by no means clear how the protein structure is affected by more extreme pH values. Thus, although data were computed from pH 0 to pH 14, only results for the intermediate pH range are presented and discussed in this study.
Simulated redox potential titrations
For simulating ambient redox potential (Eh) titrations of the heme b groups of QFR (at a fixed pH), first a range of ambient redox potentials was chosen, which was divided into equidistant potential steps. Subsequently, Monte Carlo simulations were performed at each chosen ambient redox potential value Eh to determine the occupancy of the reduced and oxidized heme conformers, respectively. The occupancy data of the reduced heme species were then fitted with a standard Nernst equation (derived by W.H. Nernst in 1889),
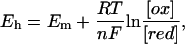 |
(4) |
(with Eh, ambient redox potential; Em, midpoint potential; R, universal gas constant; T, absolute temperature; n, number of transferred electrons; F, Faraday constant; [ox], concentration of oxidized species; and [red], concentration of reduced species), to deduce the midpoint potentials of the distal and proximal heme b groups. For the simulations, the two heme b groups were allowed to electrostatically interact with each other, and their redox states were not fixed during the calculations. The experimental data (which are based on the redox-dependent absorbance differences related to the Soret- and α-bands of the hemes) that will be included for comparison in Results, below, were normalized to match the simulated curves. The simulated data as well as the fitted Nernst curves will be shown as two-step curves, which represent the sum of two single heme titration curves.
Simulation of heme reduction
The exact order of individual electron transfer steps of electrons along the chain of cofactors and prosthetic groups of QFR is not known. For simulating heme reduction, a possible scenario for intermediate states of electron transfer via the heme b groups of QFR was chosen. The order which seems to be most probable is described as follows: The reference redox state was chosen to be the oxidized state (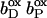 ), i.e., both, the distal (bD) and the proximal (bP) heme b groups were oxidized (the three iron-sulfur clusters in enzyme subunit B remained oxidized for all presented simulations). The second intermediate state and first step of simulated heme reduction was to consider the distal heme b group, which is closest to the menaquinol binding site (Lancaster et al., 2000), to be reduced and the proximal heme to remain oxidized (
), i.e., both, the distal (bD) and the proximal (bP) heme b groups were oxidized (the three iron-sulfur clusters in enzyme subunit B remained oxidized for all presented simulations). The second intermediate state and first step of simulated heme reduction was to consider the distal heme b group, which is closest to the menaquinol binding site (Lancaster et al., 2000), to be reduced and the proximal heme to remain oxidized (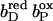 ). Thus, the first of two electrons has been transferred from the menaquinol to the nearest prosthetic group in the structure of QFR (Lancaster et al., 1999). In the second step, the electron is transferred from the distal heme to the proximal heme. This leaves the distal heme oxidized and the proximal heme reduced (
). Thus, the first of two electrons has been transferred from the menaquinol to the nearest prosthetic group in the structure of QFR (Lancaster et al., 1999). In the second step, the electron is transferred from the distal heme to the proximal heme. This leaves the distal heme oxidized and the proximal heme reduced ( ). The third step introduces a second electron, which is transferred to the distal heme leaving both hemes reduced (
). The third step introduces a second electron, which is transferred to the distal heme leaving both hemes reduced ( ). The considered steps of electron transfer are in line with the arrangement of the prosthetic groups of QFR as it was found in the crystal structure of QFR (Lancaster et al., 1999, 2000).
). The considered steps of electron transfer are in line with the arrangement of the prosthetic groups of QFR as it was found in the crystal structure of QFR (Lancaster et al., 1999, 2000).
These initial steps of electron transfer in the catalytic reaction of QFR (i.e., menaquinol oxidation by fumarate reduction) have been simulated by preselecting the respective redox states of the two involved heme groups of the cytochrome b (QFR subunit C) and subsequent calculation of the corresponding ionization states and side-chain orientations of the individual groups of the QFR model as a function of pH. The presented calculations were carried out at fixed ambient redox potentials of +25 mV (standard midpoint potential of the fumarate/succinate redox couple at pH 7; see Ohnishi et al., 2000).
RESULTS
Our calculations on the W. succinogenes QFR model W comprised 1638 (1267) conformers (the numbers in parentheses refer to model X). Among those were a total of 140 protonatable residues: 24 Arg, 30 Lys, 8 nonligated His, 29 Asp, 27 Glu, 16 Tyr, 4 heme propionates, and 2 N-termini of subunits B and C. For these 140 residues, 711 (677) neutral and 348 (343) ionized conformers are created for model W. For the 21 selected water molecules in model W, 310 conformers are generated. The remaining 269 (247) conformers are built for nonprotonatable amino acid residues such as Ser and Thr, which are not provided with heavy atom rotamers but only different hydrogen atom positions. Ionizable amino acid residues (in three-letter code) will be distinguished with a superscript +, −, or 0, depending on the side-chain charge (e.g., Glu0 for a neutral and Glu− for an ionized glutamate conformer). Individual conformers are specified explicitly (with arbitrarily chosen lower-case letters) only if the relevant conformer differs from the side-chain conformation in the crystal structure (PDB entry 1QLA) or if it is necessary to distinguish the specific conformers.
Electrostatic interactions of hemes and their propionates with the protein
Using the MCCE program, we calculated the interaction energies of every conformer of the QFR model with all others, which yields a symmetric interaction matrix with n × n entries (n being the total number of conformers). Table 1 contains a list of 37 conformers interacting with the proximal and distal heme b groups and their propionates which were chosen according to the following criteria: All conformers which are listed have both an interaction energy with one of the hemes or their propionates of ±2 ΔpK units or greater as well as a minimum occupancy of 5% at pH 7 in the oxidized state of the QFR model. The entries are ordered according to the z coordinate of the residues since this coordinate approximately coincides with the membrane normal, with the hydrophobic region ranging from z = −25 Å to z = −55 Å (C. R. D. Lancaster, unpublished). The initial state was defined to be the state in which all heme groups are oxidized. For practical reasons, Table 1 also contains the three conformers, b, d, and f of water molecule W33, and a second ionized conformer k of Glu− C180. As will be explained later in the text, conformer k of Glu− C180 is necessary for the discussion, and the three conformers of W33 are strongly interacting with conformer k of Glu− C180.
Figure .
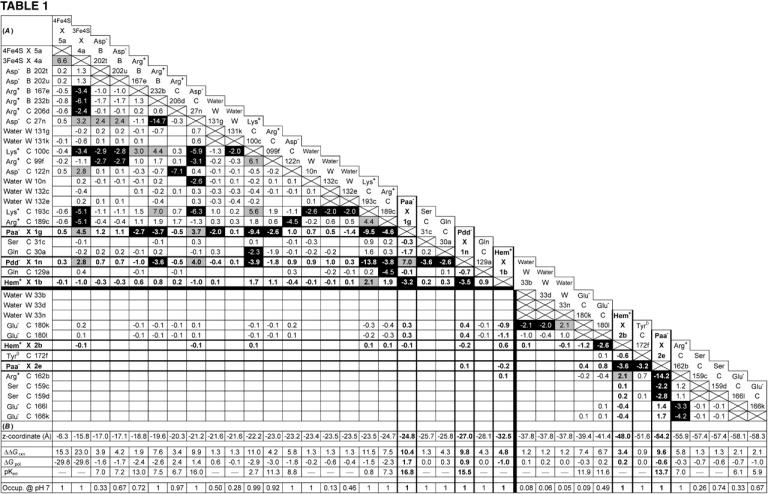
(A and B) Mutual electrostatic interaction energies in the oxidized state  of model W. (A) All interaction energies are given in ΔpK units. Entries above ±2 ΔpK units are highlighted: positive values in shading and negative values in black. Residues are specified by the residue name, the protein chain, the residue number in the chain, and the individual conformer. Entries of value 0.0 have been omitted for clarity. The five rows and columns containing entries for hemes (Hem) and propionates (Paa− X 1, Pdd− X 1, Hem+ X 1, Hem+ X 2, and Paa− X 2) are highlighted with bold frames and bold numbers. All entries are sorted with respect to the z coordinate of the conformer. The horizontal and vertical black lines indicate the separation of strong interactions within the upper-left part and within the lower-right part of the table, respectively. (B) The z coordinate of the listed conformers in Å, starting with the [4Fe-4S] center on the cytoplasmic side and ending with Glu C166 close to the periplasmic side of the membrane (the z axis is normal to the membrane plane). The z coordinates of the following residue atoms (nomenclature as in the PDB file) are quoted: CZ (Arg), CG (Asp), CD (Glu), NZ (Lys), CD (Gln), OG (Ser), OH (Tyr), FE (Hem), CGA (Paa), CGD (Pdd), FE1 [4Fe-4S], FE1 [3Fe-4S], and OH (HOH). Additional entries are the contributions of loss of reaction field energy (ΔΔGrxn) and pH-independent polar interactions (ΔGpol) to the intrinsic pKint value of the specific conformer. The last row of this table features the conformer occupancy at pH 7.
of model W. (A) All interaction energies are given in ΔpK units. Entries above ±2 ΔpK units are highlighted: positive values in shading and negative values in black. Residues are specified by the residue name, the protein chain, the residue number in the chain, and the individual conformer. Entries of value 0.0 have been omitted for clarity. The five rows and columns containing entries for hemes (Hem) and propionates (Paa− X 1, Pdd− X 1, Hem+ X 1, Hem+ X 2, and Paa− X 2) are highlighted with bold frames and bold numbers. All entries are sorted with respect to the z coordinate of the conformer. The horizontal and vertical black lines indicate the separation of strong interactions within the upper-left part and within the lower-right part of the table, respectively. (B) The z coordinate of the listed conformers in Å, starting with the [4Fe-4S] center on the cytoplasmic side and ending with Glu C166 close to the periplasmic side of the membrane (the z axis is normal to the membrane plane). The z coordinates of the following residue atoms (nomenclature as in the PDB file) are quoted: CZ (Arg), CG (Asp), CD (Glu), NZ (Lys), CD (Gln), OG (Ser), OH (Tyr), FE (Hem), CGA (Paa), CGD (Pdd), FE1 [4Fe-4S], FE1 [3Fe-4S], and OH (HOH). Additional entries are the contributions of loss of reaction field energy (ΔΔGrxn) and pH-independent polar interactions (ΔGpol) to the intrinsic pKint value of the specific conformer. The last row of this table features the conformer occupancy at pH 7.
Both oxidized hemes feature strong (negative) stabilizing, thus stabilizing interactions of comparable magnitude (∼−3.4 ΔpK units) with respect to their accompanying ionized propionates. In addition, the proximal heme shares several (positive) destabilizing interactions with ionized Lys and Arg residues (as shown in Table 1 and illustrated in Fig. 3). The strongest individual destabilizing interaction of +2.1 ΔpK units is due to Lys+ C193, and the additional destabilizing interactions below the threshold of 2.0 ΔpK units are due to Arg+ C189, Lys+ C100, and Arg+ C99. No further strong stabilizing interactions of larger magnitude than the threshold of −2.0 ΔpK units (except the two propionates mentioned) exist for the proximal heme bP.
FIGURE 3.
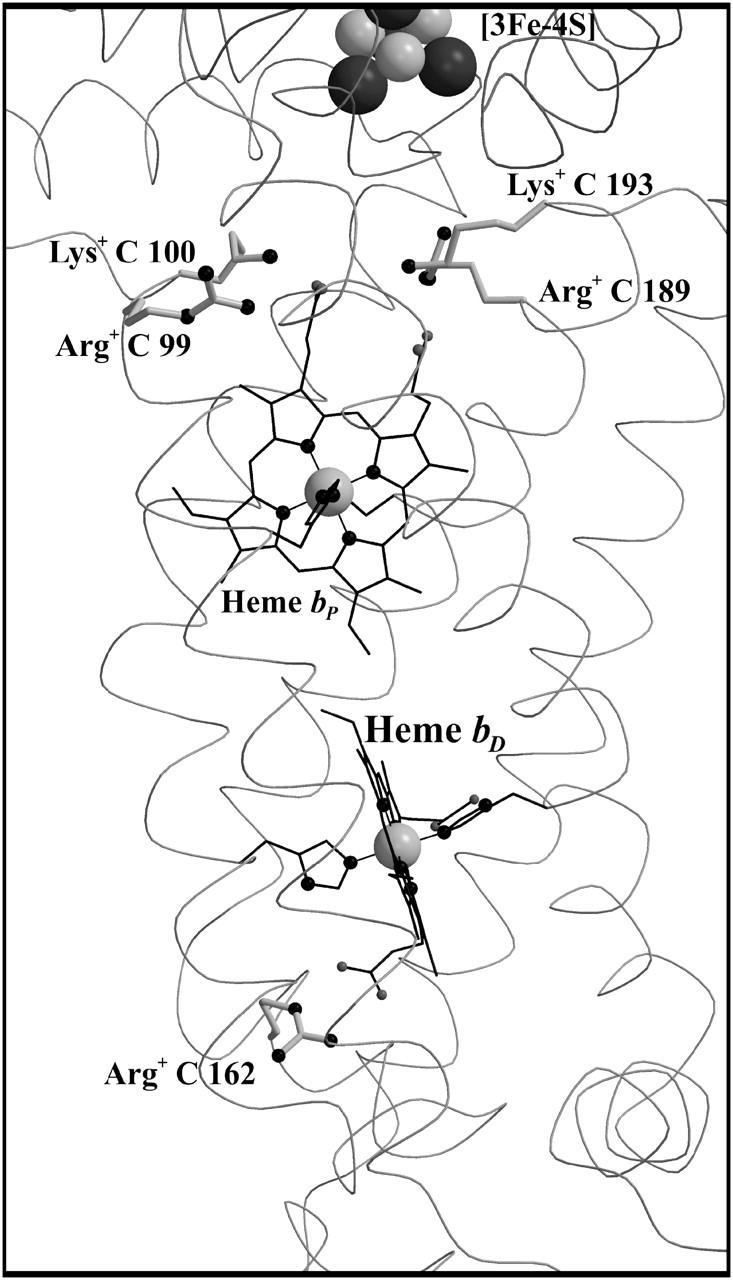
Ionized bases interacting with the heme b groups of QFR. The figure shows a detail of QFR structure, including the positions of the proximal heme bP and the distal heme bD and the buried bases (Arg C99, Lys C100, Arg C189, and Lys C193 for bP, and Arg C162 for bD, respectively), which are fully ionized in the oxidized state, and thus destabilize the oxidized heme species. The coordinates were taken from PDB entry 1QLA (Lancaster et al., 1999).
The distal heme bD has fewer destabilizing interactions and only Arg+ C162 (see Fig. 3) exceeds the threshold with +2.1 ΔpK units. Instead, heme bD has an additional, strongly stabilizing interaction of −2.6 ΔpK units with conformer l of Glu− C180. This conformer also stabilizes the oxidized species of the proximal heme, but only by −1.1 ΔpK units. Also conformer k of Glu− C180 stabilizes the two oxidized hemes, but to a lesser extent compared to conformer l. It is conformer k that corresponds to the conformation of Glu C180 in the crystal structure 1QLA (see Fig. 7 below for a detailed picture).
FIGURE 7.

Side-chain orientation of the Glu C180 conformers. Conformation “intermediate” (in solid representation, corresponding to the orientation of the ionized k-conformer) and conformation “distal” (shaded representation, corresponding to l) of Glu C180 with respect to the heme groups and the two crystallographic water molecules W11 and W33. The figure also explains the terminology intermediate and distal, since the intermediate conformation displays no preference in orientation with respect to the two hemes, whereas the distal conformation is oriented toward the distal heme group. In the case of the alternate conformers, solid representation indicates an increase of occupancy upon reduction of heme bD; shaded representation indicates a decrease. For each of the waters, the two conformers (which undergo the strongest increase and decrease, respectively, in occupancy) are depicted exemplarily.
The arrangement of the conformers in Table 1 with respect to their z coordinates also reflects the higher number of possible interaction partners for the proximal heme bP and its propionates in the structure of QFR. Furthermore, Table 1 can be subdivided in two parts, which do not have any strong interactions in common that would exceed the threshold of ±2.0 ΔpK units. This is indicated by the black lines, which divide the respective sections of the interaction table. The strongest link between the two groups is amino acid residue Glu C180, as the two ionized conformers k and l stabilize the proximal oxidized heme by −0.9 and −1.1 ΔpK units, respectively.
Similarly to Glu and Asp side chains, MCCE generates several different conformers for the four heme propionates. As a result of the calculations, all four propionates adopt a single conformation (i.e., 100% occupancy in the oxidized state at pH 7). By comparison it was identified that the orientations of the respective four heme propionate conformers do not differ from the original x-ray crystal structure. In the oxidized state, the two propionates of the proximal heme are fully ionized, and they both meet the criteria to appear in Table 1. In the case of the distal heme, the ring D-propionate is also fully ionized, whereas the ring C-propionate is in its neutral, fully protonated state. The neutral species is not engaged in strong electrostatic interactions exceeding ±2 ΔpK units, and is consequently not listed in Table 1. Inspection of the electrostatic interaction energies of the ionized conformer of the distal ring C-propionate shows that it would strongly interact with the oxidized distal heme, the ionized ring D-propionate of the distal heme, and with the ionized Glu C180.
The described protonation pattern of the four heme propionates does not change in the neutral pH range throughout the course of the modeled electron transfer steps. The three ionized heme propionates are all strongly stabilized by several favorable interactions with positively charged residues (see Table 1). The two propionates of the proximal heme are also subjected to some large destabilizing interactions, particularly with each other (+7.0 ΔpK units), but also with the oxidized [3Fe-4S] cluster and with the ionized Asp− C27.
Protonation states of residues interacting with hemes (in the oxidized state of the enzyme)
In the oxidized state at pH 7, all conformers of ionizable residues that display strong interactions with the hemes and their propionates (listed in Table 1) have an occupancy of very close or identical to 100% with the exception of Arg+ B167 and Glu− C180. Residue Arg B167 is also fully ionized, but the conformer of Arg+ B167 that is strongly interacting with the ring D-propionate of the proximal heme only accounts for 72% of the total occupancy. Another ionized conformer, whose side chain is tilted by roughly 90° and is pointing away from the ring D-propionate of the proximal heme, covers the remaining 28%. Glu C180 is only partially ionized in the oxidized state at pH 7, and the contribution of the relevant l conformer to the total occupancy is 49%. The role and protonation state of residue Glu C180 will be discussed in detail later in the text. The conformers with high occupancy for the proximal heme and its propionates are Arg+ B167, Arg+ B232, Asp− C27, Lys+ C100, Arg+ C99, Lys+ C193, and Arg+ C189; and the conformers with high occupancy for the distal heme and its propionates are Glu− C180, Tyr0 C172, and Arg+ C162.
All of the residues mentioned above, except for Glu− C180 and Tyr0 C172, are found to be in their original conformation as deduced by x-ray crystallography (Lancaster et al., 1999). The different conformations of Glu− C180 have already been introduced above (see Fig. 7); and in the case of Tyr0 C172 the phenol ring is slightly tilted compared to the original orientation in the crystal structure.
Comparison of simulated and experimental Eh titrations and heme assignment
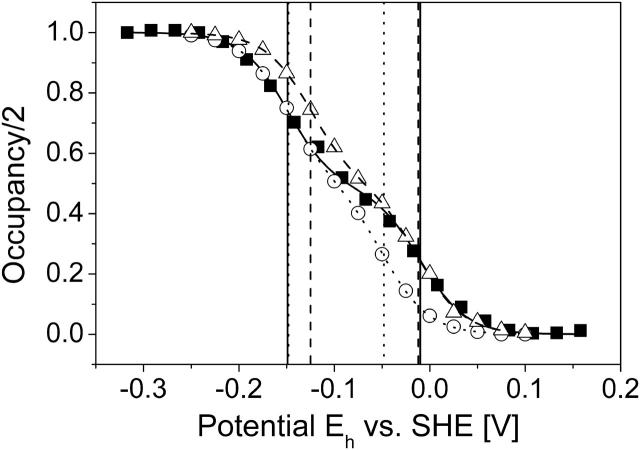
Fig. 2 shows the results of the simulated Eh titrations at pH 7 for model W and model X, as well as a comparison with experimental QFR wild-type data measured at pH 7 (Lancaster et al., 2000). The experimentally derived midpoint potentials, which are included in Fig. 2, are −149 mV for the low-potential and −9 mV for the high-potential heme. Furthermore, Fig. 2 shows the simulated data for model X, and the obtained midpoint potentials are −149 mV for the low- and −48 mV for the high-potential heme. For model W the midpoint potentials, which were found, are −125 mV for the low- and −12 mV for the high-potential heme. Thus, the net effect of inclusion of the water molecules in model W was an increase of the midpoint potentials of +24 mV for the low- and +36 mV for the high-potential heme.
FIGURE 2.
Simulated heme redox titrations. The simulated data as well as the fitted Nernst curves are shown as two-step curves, which represent the sum of two single heme titration curves. The figure shows the simulated and experimental (Lancaster et al., 2000) redox titrations of hemes bP and bD of QFR at pH 7. ▪, Experimental data; ○, simulated data using model X; and ▵, simulated data for model W. The three fitted Nernst curves are also included: ——, experimental; · · · · , simulation, model X; and - - - -, simulation, model W. The vertical lines (same labeling as for the Nernst curves) indicate the positions of the individual oxidation-reduction (midpoint) potentials as they were obtained by the Nernst fit: low-potential heme, −149 mV (experiment), −149 mV (simulation, model X), and −125 mV (simulation, model W); and high-potential heme, −9 mV (experiment), −48 mV (simulation, model X), and −12 mV (simulation, model W). The low-potential heme corresponds to heme bD and the high-potential to bP.
Since the obtained midpoint potentials are directly related to the heme coordinates, the lower midpoint potential could be assigned to the distal heme position, and the higher midpoint potential to the proximal position in the structure as a result of this study. Previous tentative assignments of the low- and high-potential heme to the distal and proximal position in a related enzyme have been made (Hägerhäll et al., 1995) but were partly based on assumptions, thus leaving some uncertainty (see Discussion).
The way in which the protein environment modulates the two different midpoint potentials such that the two values differ by 113 mV for model W (and 101 mV for model X) is reflected in Table 1 B, and ultimately in the sum of all mutual electrostatic interactions. The relevant properties are the loss of reaction field energy ΔΔGrxn and the direct electrostatic interactions with the surrounding ionized bases, which were mentioned above and which are listed in Table 1. These residues are responsible for the most part of the difference in destabilization of the oxidized state of the two hemes. The oxidized form of the high-potential proximal heme is more destabilized than the low-potential distal heme because of four basic residues, namely Arg+ C99, Lys+ C100, Arg+ C189, and Lys+ C193 in the vicinity of the heme propionates of the proximal heme. In contrast to the proximal heme, the distal heme is only significantly destabilized by Arg+ C162. The orientation of the heme groups of QFR with respect to the relevant ionized basic residues in the structure is shown in Fig. 3.
An explanation of the total difference in midpoint potential between the high- and low-potential heme requires the addition of all energetic contributions listed in Table 1, A and B. For the oxidized proximal heme, the respective results in Table 1 B are ΔΔGrxn = 4.8 ΔpK units and ΔGpol = −1.0 ΔpK units, and for the oxidized distal heme, ΔΔGrxn = 3.4 ΔpK units and ΔGpol = 0.2 ΔpK units. As mentioned above, the most dominating direct electrostatic interactions ΔGcrg with the hemes are listed in Table 1 A. Yet the sum of many smaller energetic contributions (<2 ΔpK units) from other interacting conformers not present in Table 1 A might be of considerable influence. Thus, the sum of all interaction energy terms of the two oxidized hemes has to be calculated individually. In addition, every interaction energy value must be weighted with the product of the occupancies of the respective pair of conformers in the oxidized state at pH 7. The numbers, which were obtained for all mutual interactions ΔGcrg, were −0.6 ΔpK units for the proximal and −2.6 ΔpK units for the distal heme. (If only the conformers included in Table 1 were taken into account, the respective numbers were −0.1 ΔpK units for the proximal and −3.3 ΔpK units for the distal heme.) Thus, the total sum for the oxidized proximal heme is ΔΔGrxn + ΔGpol + ΔGcrg = (4.8 − 1.0 − 0.6 =) 3.2 ΔpK units, and ΔΔGrxn + ΔGpol + ΔGcrg = (3.4 + 0.2 − 2.6 =) 1.0 ΔpK units for the oxidized distal heme. Hence, the oxidized form of the proximal heme is destabilized by 2.2 ΔpK units more than the oxidized form of the distal heme. This difference in energy corresponds to a difference in midpoint potential of 132 mV, which essentially accounts for the midpoint potential difference value of 113 mV found in the simulated redox titration of the hemes (see Fig. 2). Thus, the consideration of the oxidized states alone is sufficient to explain the midpoint potential difference of the proximal and distal heme. The remaining deviation of ∼19 mV is due to additional differential contributions of the reduced heme species, which have been left aside in the estimation above.
Comparison of the different energy terms for the proximal and distal hemes shows that the oxidized species of the proximal heme bP is more stabilized than the distal heme group bD due to permanent polar interactions ΔGpol with the backbone and polar residues. This contribution of ΔGpol partly counterbalances the effect of the desolvation energy ΔΔGrxn and the charge-charge interactions ΔGcrg, as both latter terms are more favorable with respect to the oxidized distal heme bD. Otherwise, the midpoint potential difference of the two heme groups would be even larger than the observed 113 mV.
Nonstandard protonation states of residues in the QFR model at pH 7
Most ionizable residues in the QFR model adopt standard protonation states at pH 7. Only a limited number of protonatable residues were found to adopt nonstandard protonation states in the oxidized state as well as in the other simulated redox states at pH 7. Nonstandard protonation states at pH 7 were considered to be Lys0, Arg0, His+, Asp0, Glu0, Paa0, Pdd0, and Tyr−. Since most residues are provided with several conformers, it should be noted that the quoted residue occupancies in this paragraph are given for the sum of the occupancies of the conformer fraction, which belongs to a nonstandard protonation state. As a threshold, a value of 5% was chosen to qualify for significant nonstandard protonation. The following residues of interest in the context of this study (with their occupancies in parentheses) were identified among the entirety of residues in model W in the oxidized state at pH 7: the ring C-propionate of the distal heme, called Pdd0 X2 (100%); Glu0 C180 (42%); and Glu0 C66 (100%). Other residues with nonstandard protonation states were His+ B128 (60%), His+ B187 (79%), His+ B123 (99%), His+ B22 (64%), Lys0 C213 (53%), and Lys0 C251 (11%). The only residue quoted here, which will significantly change (>5%) its protonation state at pH 7 with respect to the other simulated heme redox states, is Glu C180 and will be discussed below in detail.
Simulated heme reduction and its effect on conformer occupancy
Upon simulated heme reduction, the ionization state of the ionizable groups of the enzyme as well as the general contribution of conformers was analyzed. Table 2 shows a list of conformers that change their occupancy at pH 7 by >5% in the course of the simulated heme reduction. As for Table 1, the conformers are sorted according to their z coordinate (i.e., the membrane normal). A different way of presenting the results, which are summarized in Table 2, is to plot the occupancy of every conformer in a subsequent state against the occupancy of the same conformer in the preceding state (see Fig. 4). The further an entry is off the diagonal, the greater the change of the respective conformer occupancy was for the considered step. This representation also allows displaying all conformers in one plot.
TABLE 2.
Significant occupancy changes between the different modeled heme redox states
| Occupancies in states:
|
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
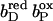 minus minus 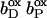
|
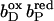 minus minus 
|
 minus minus 
|
z-coordinate (Å) | |||||||||
| Arg+ | B | 167g | −0.13 | −14.5 | ||||||||
| Arg+ | B | 167e | 0.13 | −18.8 | ||||||||
| Water | W | 110c | −0.06 | −17.0 | ||||||||
| Water | W | 110o | −0.06 | −17.0 | ||||||||
| Arg+ | C | 99i | −0.08 | −20.7 | ||||||||
| Arg+ | C | 99f | 0.08 | −23.0 | ||||||||
| Water | W | 131g | 0.09 | −21.6 | ||||||||
| Water | W | 132c | −0.07 | −23.5 | ||||||||
| Water | W | 132e | 0.11 | −23.5 | ||||||||
| Lys | C | 213a | 0.08 | Lys | C | 213a | −0.14 | −31.1 | ||||
| Lys+ | C | 213b | −0.08 | Lys+ | C | 213b | 0.14 | −31.1 | ||||
| Thr | C | 33b | 0.06 | −31.5 | ||||||||
| Thr | C | 33c | −0.07 | −31.5 | ||||||||
| Thr | C | 214a | 0.05 | −32.2 | ||||||||
| Thr | C | 214b | −0.07 | −32.2 | ||||||||
| Water | W | 11b | 0.07 | Water | W | 11b | 0.07 | −37.8 | ||||
| Water | W | 11f | 0.07 | Water | W | 11f | −0.08 | −37.8 | ||||
| Water | W | 33b | −0.06 | −37.8 | ||||||||
| Water | W | 33e | −0.06 | −37.8 | ||||||||
| Water | W | 33f | −0.07 | −37.8 | ||||||||
| Glu | C | 180a | 0.10 | −39.4 | ||||||||
| Glu | C | 180b | 0.08 | −39.4 | ||||||||
| Glu | C | 180c | 0.11 | Glu | C | 180c | 0.06 | −39.4 | ||||
| Glu | C | 180e | 0.06 | −39.4 | ||||||||
| Glu− | C | 180k | −0.09 | −39.4 | ||||||||
| Glu | C | 180f | 0.20 | Glu | C | 180f | −0.12 | Glu | C | 180f | 0.09 | −41.4 |
| Glu | C | 180g | 0.06 | −41.4 | ||||||||
| Glu− | C | 180l | −0.49 | Glu− | C | 180l | 0.07 | Glu− | C | 180l | −0.07 | −41.4 |
| Ser | C | 49c | −0.06 | Ser | C | 49c | 0.06 | −51.0 | ||||
| Thr | C | 227a | −0.06 | Thr | C | 227a | 0.08 | −51.8 | ||||
| Thr | C | 227b | 0.06 | Thr | C | 227b | −0.08 | −51.8 | ||||
| Ser | C | 160a | −0.07 | Ser | C | 160a | 0.08 | Ser | C | 160a | −0.06 | −60.3 |
| Ser | C | 160b | 0.07 | Ser | C | 160b | −0.07 | Ser | C | 160b | 0.06 | −60.3 |
Significant changes of conformer occupancy (>5%) at pH 7 were calculated as differences of occupancies: occupancy in final state minus occupancy in initial state. Conformers are sorted according to descending z coordinates in Å.
FIGURE 4.
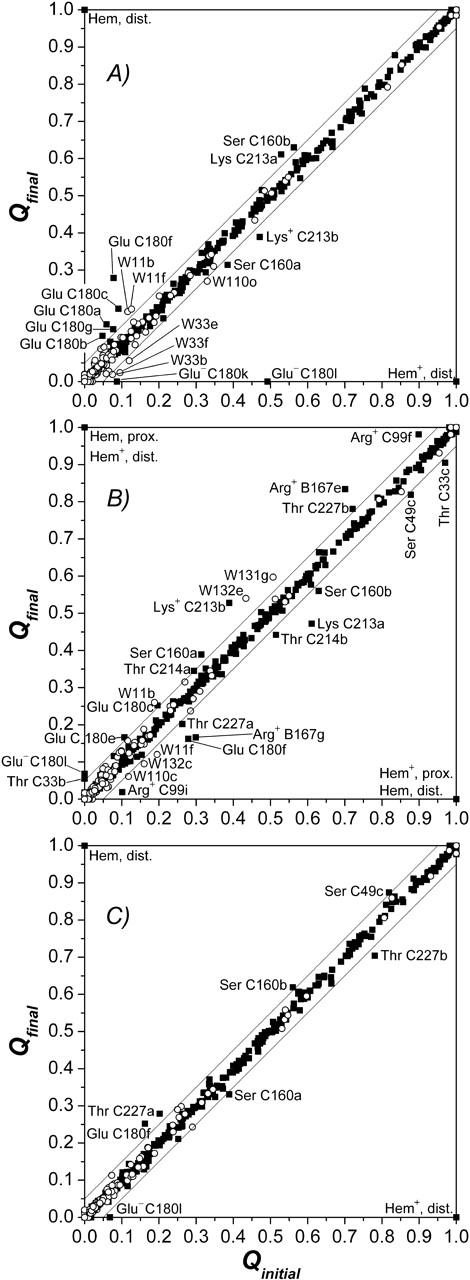
(A–C) Graphical representation of significant occupancy changes. The figure shows a plot of the occupancy in final state (Qfin) against occupancy in initial state (Qini) for all conformers of model W at pH 7. Occupancy deviations by >5% off the diagonal are considered significant, the corresponding conformers are labeled. Conformers represented by points close to the diagonal do not experience significant conformational changes, whereas conformers below the diagonal decrease their occupancy, and conformers above the diagonal raise their occupancy upon the respective subsequent intermediate state of electron transfer. ▪, Protein conformers; ○, water conformers. Abscissa in A, 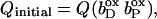 ordinate in A,
ordinate in A, 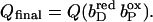 Abscissa in B,
Abscissa in B, 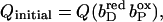 ordinate in B,
ordinate in B, 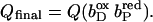 Abscissa in C,
Abscissa in C,  ordinate in C,
ordinate in C, 
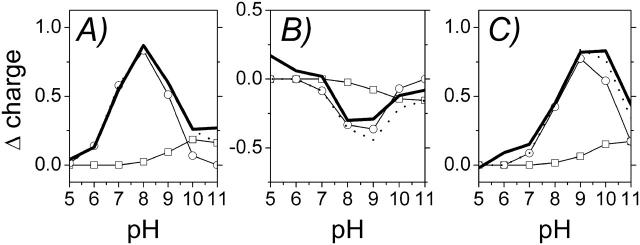
The adjustment of ionization states as a consequence of the changed redox states is also reflected in a change of the total charge of the QFR model. The sum of all changes gives the total change of charge, but separate contributions can be assigned to individual groups or side chains in the protein. To visualize the obtained results, the difference of the total charge of model W between the four individual redox states of the heme b groups (after the corresponding step of electron transfer) as a function of pH is shown in Fig. 5, A–C. The results show that the largest changes of the total charge between the four considered heme redox states occur at intermediate pH values around the maximum at pH 8 (steps 1 and 2 in Fig. 5, A and B) and pH 9 (step 3 in Fig. 5 C). To analyze the origin of the curves, which reflect the change of the total charge of QFR, the contributions of individual residues were checked and the two dominant ones were included in Fig. 5. The two residues that exhibit the largest changes in ionization state between pH 5 and 11 were identified to be the amino acid residues Glu C180 and Glu C66. The obtained results show that the major contribution to the change of the total charge at physiologically relevant pH values (i.e., ∼pH 7) is due to amino acid residue Glu C180.
FIGURE 5.
(A–C) Change of the total charge in the course of simulated heme reduction. Comparison of the change of the total charge of model W (——) as a function of pH for the three considered electron transfer steps with the summed contribution of two individual residues (· · · · ), which are in detail: □, Glu− C66, and ○, Glu− C180. The data show the sum of the occupancies of the respective deprotonated, charged species. The change of charge in A is calculated as the difference of the total charge in state  minus
minus  ; in B,
; in B, 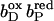 minus
minus 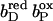 ; and in C,
; and in C, 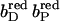 minus
minus 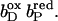
Fig. 5 A shows that upon reduction of the distal heme, which represents the first step of electron transfer following the oxidized state, Glu C180 contributes strongest between pH 6 and 10. The total charge at pH 7 is increased by +0.55 in units of proton charge, and a comparison with the corresponding result for Glu C180 clearly states that this particular residue is by far the dominating reason for the observed increase. This can be interpreted in terms of a partial proton uptake of Glu C180 upon reduction of the distal heme. A similar behavior is observed for Glu C66, although the relevant contribution only occurs at higher pH values (i.e., above pH values that are of physiological relevance) with a much lower magnitude.
In the second step, depicted in Fig. 5 B, the proximal heme is reduced and the distal heme is reoxidized. Yet the protonation state of Glu C180 at pH 7 does not change significantly upon electron transfer to the proximal heme.
Upon re-reduction of the distal heme by the second electron (with the proximal heme still being reduced), shown in Fig. 5 C, the protonation state of Glu C180 again does not feature a significant change, i.e., Glu C180 remains protonated at pH 7.
To underline the above findings, the sum of the occupancy changes of the two identified residues, Glu C180 and Glu C66, was compared with the change of total charge, showing that the course of the change of the total charge is well reproduced by the sum of the two residues alone. The protonation state of Glu C180 is substantially increased upon heme reduction, and the residue is predominantly protonated at pH 7 as long as at least one heme group is reduced. The same analysis based on the data obtained with model X exhibits very comparable results, which are shifted to lower pH values by ∼1 pH unit (data not shown).
Simulated pH titrations of residue Glu C180 as a function of the heme redox states
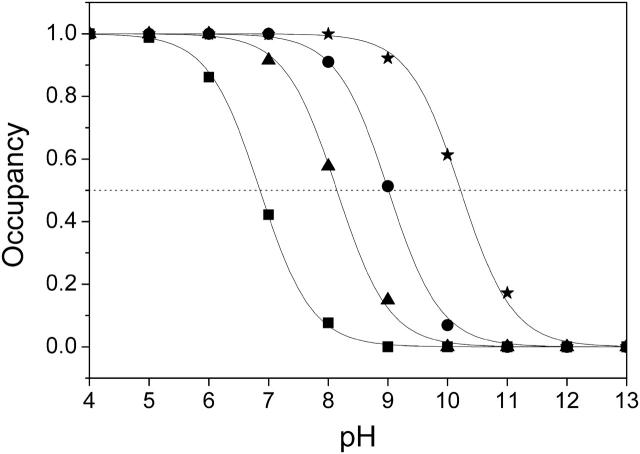
Fig. 6 shows simulated pH titrations of amino acid residue Glu C180 (i.e., the cumulative occupancy of all neutral Glu0 C180 conformers) for the different redox states of model W that were considered in this study. In the oxidized state, the pKa of Glu C180 is lowest with a value of pKa = 6.9. When the distal heme is reduced, the pKa increases by 2.1 ΔpK units to pKa = 9.0. In a second step, the electron is shifted to the proximal heme, which has a comparatively minor effect on the pKa, shifting it to pKa = 8.2. Upon re-reduction of the distal heme with the proximal still reduced, the pKa increases by 2.0 ΔpK units to a value of 10.2. All four quoted pKa values were obtained by fitting the data points with a simple Henderson-Hasselbalch equation (see de Levie, 2003, for a recent evaluation of the origin and history of the Henderson-Hasselbalch equation). Analysis of the electrostatic interaction energies and respective conformer occupancies in the different modeled redox states directly shows that the main influence on the pKa of Glu C180 is due to the charge on the heme groups. There are two ionized conformers of Glu C180, namely conformers k and l of Glu− C180, which exhibit relevant occupancies and electrostatic interactions with the oxidized heme groups (see Table 1). Fig. 7 shows the position and orientation of the two ionized conformers k and l of Glu− C180 together with the two heme groups and the two water molecules (waters W11 and W33) in detail. The electrostatic interaction energy of conformer k of Glu− C180 and the proximal heme bP is −1.1 ΔpK units, and −2.6 ΔpK units for the distal heme bD (see Table 1). The respective interactions for conformer l of Glu− C180 are −0.9 ΔpK units for the proximal heme bP, and −1.2 ΔpK units for the distal heme bD (see Table 1). The quoted interaction energies also explain the observation that the reduction of the distal heme bD has a slightly stronger influence on the pKa of Glu C180 than the reduction of the proximal heme bP (see Fig. 6).
FIGURE 6.
The pKa of Glu C180 depends on the heme b redox states. The pH titration curves of Glu0 C180 (sum of all neutral conformers) are shown as a function of the four considered heme redox states. ▪, Both hemes oxidized; •, distal heme reduced; ▴, proximal heme reduced; and ★, both hemes reduced. Solid lines represent fitting curves according to a simple Henderson-Hasselbalch equation. The corresponding pKa values are 6.9 in the oxidized state 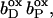 9.0 for
9.0 for 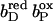 (distal heme reduced), 8.2 for
(distal heme reduced), 8.2 for 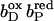 (proximal heme reduced), and 10.2 for
(proximal heme reduced), and 10.2 for  (both hemes reduced).
(both hemes reduced).
The difference between, for example, the lowest and highest pKa values (corresponding to the fully oxidized state and the state with both hemes reduced, respectively) is 3.3 pH units. The above stated heme interactions with the two ionized conformers k and l of Glu− C180 and their respective occupancies yield an energetic difference between the respective redox states of 3.7 ΔpK units, which accounts for almost all of the observed total difference of 3.3 pH units. Again, in the case of model X, a similar behavior is observed but at lower pH values (by ∼1 pH unit, data not shown).
Conformational change of Glu C180 mediated by water molecules W11 and W33
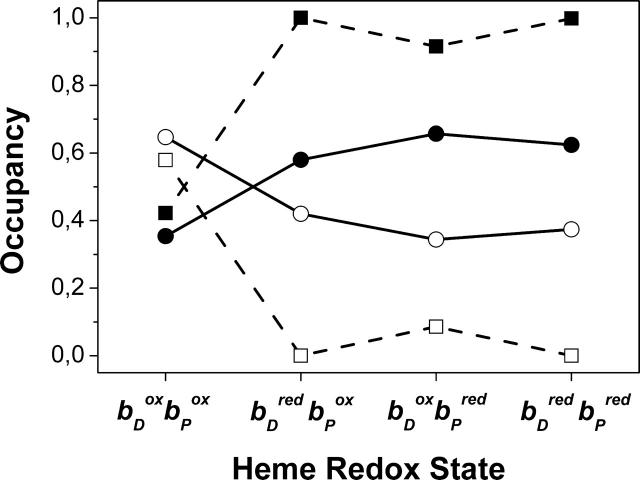
In addition to the original side-chain orientation of amino acid residue Glu C180, called intermediate conformation (corresponding to the orientation of conformer k), as it is found in the crystal structure 1QLA of QFR, one other conformation, termed distal (corresponding to l; see Fig. 7), was identified to be relevant. The occupancy distribution of all Glu C180 conformers at pH 7 with respect to the two major conformations shows that the reduction of the distal and/or proximal heme favors the intermediate over the distal conformation. Fig. 8 shows the sum of occupancies of all Glu C180 conformers, which are either in the intermediate or distal conformation, irrespective of the protonation state of the conformers, as a function of the modeled heme redox states. To complement this, Fig. 8 also shows the progression of the protonation state of Glu C180, i.e., the sum of all protonated and deprotonated conformers, respectively. Upon reduction of the distal heme, the occupancy of the intermediate conformation increases at the expense of the distal from 0.35 to 0.58. The conformational change upon reduction of the distal heme is accompanied by proton uptake of Glu C180, and the residue remains strongly protonated during the subsequent electron transfer steps as long as the heme groups are reduced.
FIGURE 8.
Conformational change of the Glu C180 side chain. The figure depicts the summed occupancies of all conformers in intermediate (•) and distal (○) conformations, and summed occupancies of all protonated (▪) and deprotonated (□) conformers at pH 7 as a function of the heme b redox state.
In the case of model X, there is no such effect to be detected as described above, suggesting that the observed conformation change of Glu C180 is mediated by the water molecules W11 and W33 in the vicinity of the side chain (see Fig. 7). The two water molecules are provided with several conformers (8 for W11 and 15 for W33), but only three conformers of W33 meet the criteria to be listed in Table 1 (all interactions of W11 with Glu C180 conformers are below ±1 ΔpK unit, data not shown). Just like Glu C180, water molecules W11 and W33 undergo an alternation of their orientation with respect to the reduction of heme bD. This is exemplified in Fig. 7 for the first step of electron transfer.
DISCUSSION
The electrostatic method employed here, MCCE, previously yielded reliable results with respect to available experimental data in studies on lysozyme (Alexov and Gunner, 1997), coupled electron and proton transfer in bacterial photosynthetic reaction centers (Alexov and Gunner, 1999), the simulation of pKa values in small soluble proteins (Georgescu et al., 2002), the calculation of proton transfer in bacteriorhodopsin intermediates (Song et al., 2003), and the simulation of heme midpoint potentials in various cytochromes (Mao et al., 2003; Hauser et al., 2004). Thus, the results generated in this study can be discussed with an adequate level of confidence.
Simulated heme Eh titrations
The results of the simulated Eh titrations of QFR presented in Fig. 2 clearly reproduce the redox behavior of the heme groups of the detergent-solubilized enzyme as determined experimentally (Lancaster et al., 2000). The values calculated for the midpoints of the high- and low-potential heme b groups agree very well with available experimental data, and the obtained agreement of heme midpoint potentials between simulation and experiment is in line with results from other studies using comparable (Gunner and Honig, 1991) or identical approaches (Mao et al., 2003). The agreement for the high-potential heme based on model W is excellent. The agreement for the low-potential heme is better in the case of model X. However, the proximal heme site in the crystal structure is better defined than the distal site, as is reflected in higher temperature factors in the environment of the distal heme site (Lancaster et al., 1999). Thus, the slight discrepancy of the simulation, based on the favored model W and the experiment, could be due to the higher temperature factors of the crystal structure around the distal heme. Also the inevitable backbone rigidity in the MCCE simulations might be inappropriate with respect to the different redox states of the hemes. It has been shown (e.g., Mao et al., 2003) that the calculated Em values can largely depend on the starting structure of the investigated cytochrome. For instance, MCCE calculations with oxidized and reduced structures of the same cytochrome might yield very different midpoint potentials. The most dominating origin for this discrepancy is that the heme-containing protein might undergo a conformational change upon reduction, which involves the polypeptide backbone. Thus, the structure of the reduced cytochrome is not optimized to stabilize the oxidized heme. Such a backbone conformational change cannot be accounted for by the MCCE method since the conformational flexibility within the scope of MCCE is restricted to different side-chain orientations of polar and ionizable residues and polar hydrogen positions. In this respect, it should be kept in mind that the employed QFR model was based on an oxidized crystal structure, and it is presently not clear which structural changes QFR enzyme might undergo upon reduction. Yet the comparison of the obtained results with available experimental data shows that many effects, which are observed in the simulations, are directly reflected in the experiment. This finding enhances the level of confidence in the employed MCCE method, which is necessary for the evaluation of the generated results.
The obtained midpoint potentials of the high- and low-potential hemes are slightly decreased (by −24 mV for the low-potential, and by −36 mV for the high-potential heme) in the case of model X. In principle, the oxidized, charged heme species is always destabilized due to the loss of reaction field energy if it is removed from aqueous solution and instead introduced into the protein (Kassner, 1972, 1973). This destabilization of the oxidized state is then reflected in an elevated midpoint potential. Thus, the observed effect with waters is somewhat contradictory. But comparison of the electrostatic interaction energies in both cases (with and without water) shows that the positive Arg and Lys bases, which are highlighted in Fig. 3, have slightly higher positive interaction energies with the oxidized heme groups in the case with the waters. This indicates a stronger destabilization of the oxidized heme species in the presence of the water molecules, which are included in model W.
The obtained relative difference between high and low midpoint potentials of the two hemes in the QFR model agrees very well with the previously measured experimental data (Lancaster et al., 2000). This relative difference is of greater relevance than the consistence of the absolute midpoint potential values as this absolute value depends on the initial reference (midpoint) potentials that have been chosen for the bis-histidine-ligated heme b groups of QFR (Gunner and Honig, 1991). The presented results of simulated redox titrations show how well the employed method is able to reproduce the influence of the protein environment on the reference (midpoint) potentials of the heme groups and how the presented interactions of individual groups with the hemes modify the absolute value of the midpoint potentials which were obtained as a result of the simulations.
All effects related to the hemes (and also individual amino acid residues like Glu C180) in the QFR model, which were observed and discussed in this study, are related to the various mutual electrostatic interaction energies, as they are shown in Table 1. The 37 entries are only a small excerpt of the n × n interaction matrix, and in principle every conformer in the model interacts with all others. But as shown in Results, above, for the different heme midpoint potentials (and the redox-dependent pKa values of Glu C180), it is feasible in most cases to restrict the analysis to the direct strong electrostatic interactions around the residue or group of interest. Only taking into account the strong electrostatic interactions listed in Table 1 was sufficient to explain the result that the protein environment destabilizes the oxidized heme species for the proximal site more strongly than for the distal site. Yet, for a more exact reproduction of the difference in the two midpoint potentials, as it was found in the simulated titration at pH 7 (see Fig. 2), it was necessary to sum over all occupancy-weighted interactions of the individual heme groups.
Assignment of the low- and high-potential heme to bD and bP
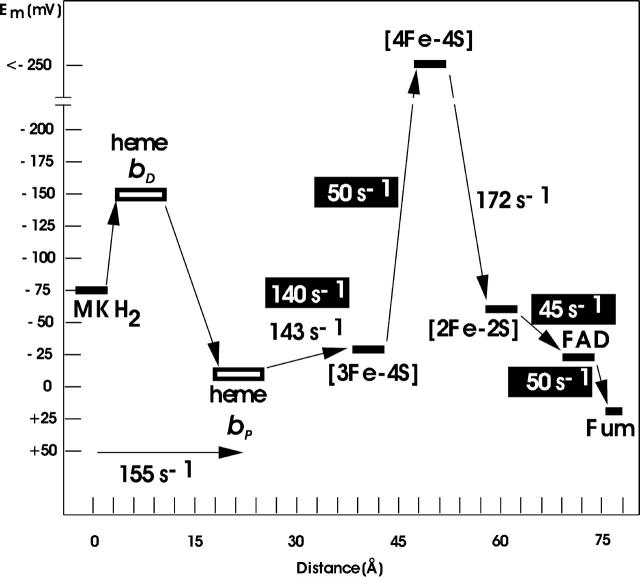
As a second main aspect of the simulated heme redox titrations, it was possible to assign the low-potential heme to the distal position and the high-potential heme to the proximal position in the QFR structure. For the two heme groups of the cytochrome b of QFR, this assignment was still a matter of debate. With the help of spectroscopically monitored heme redox titrations of a cytochrome, it is feasible to determine the presence of multiple heme groups and their respective midpoint potentials. Yet an unequivocal assignment of an individual heme to its position in a known structure is not a straightforward task. A tentative assignment, based on mutagenesis experiments, has been made for a close relative of W. succinogenes QFR, the succinate:quinone reductase of B. subtilis (Hägerhäll et al., 1995); but in this cited study, with respect to their assignment, the authors explicitly state: “However, the properties of the mutant cytochromes could be misleading since the loss of one heme may change the properties of the remaining heme.” For the performed electrostatic calculations the situation is different, as the results can directly be correlated with the individual coordinates on which the simulation is based. Thus, it becomes immediately apparent which site accommodates the low- and which the high-potential heme in the structure. The reliability of this assignment is increased by the fact that the employed approach has been well established for many years, and also by how well the simulated and experimental data match. Fig. 9 shows the experimentally deduced midpoint potentials of the substrates, prosthetic groups and cofactors (as well as the corresponding electron transfer rates) of QFR, which are involved in the catalytic mechanism of the enzyme. The scheme shows that some of the involved electron transfer steps are endergonic and some are exergonic. Efficient tunneling of electrons is ensured due to the spatial proximity of the prosthetic groups and cofactors (Page et al., 1999). This scheme has so far been incomplete due to the missing proper assignment of the two hemes with respect to their position in the structure. The now-accomplished assignment of the low-potential heme to the distal position and of the high-potential heme to the proximal position in the structure of QFR gives a precise picture of the electron transport chain of the W. succinogenes quinol:fumarate reductase.
FIGURE 9.
Oxidation-reduction (midpoint) potentials (in mV and at pH 7) of the constituents of the electron transport chain of the W. succinogenes QFR. The distances are given in Å and refer to inter-cofactor distances. Electron transfer rates in white are reoxidation rates of the fully reduced enzyme by fumarate; those in black are reduction rates of the fully oxidized enzyme, as compiled in Lancaster (2004). The assignment of the hemes (bDistal = bLow and bProximal = bHigh) is indicated as obtained by simulated heme redox titrations in the study presented here. The experimental heme midpoint potentials are taken from Lancaster et al. (2002); all others have been compiled in Lancaster (2004).
Simulated heme reduction and affected ionizations states as a function of pH
There are some drawbacks to the employed MCCE method. For example, if one wants to describe the in vivo activity of an enzyme such as QFR, the catalytic mechanism is inevitably described unsatisfactorily by a method which considers static equilibrium states of the protein only, as the simulated redox states are at the utmost transiently populated in vivo. Yet this approach has proven to yield valuable results in other studies on other membrane-bound enzymes before (see Lancaster, 2003b, for a recent review) and to be very useful to identify the potential importance and function of individual groups or residues and their possible interplay with respect to the enzymatic activity of the protein.
On the other hand, the evaluation of the employed static method can be completely different if it is compared to results from other static experimental methods such as electrochemical redox titrations in combination with methods like Fourier-transform infrared (FTIR) and ultraviolet/visible spectroscopy (Moss et al., 1990). Those types of experiments are more comparable to the results of electrostatic calculations, since they also deal with equilibrium states. Thus, the titrations simulated here are an ideal complement to the experimental redox titrations of the heme b groups of QFR (Lancaster et al., 2000).
The results presented in Fig. 5 show which residues of QFR undergo a change of their ionization state (as a function of pH) in response to the changed redox state of the two heme b groups of QFR. The observed changes reflect the putative importance of the involved groups or residues for the catalytic mechanism of QFR, especially in the framework of coupled electron and proton transfer. When discussing redox-related changes of the protonation state of Glu C180 with respect to the physiological activity of QFR enzyme, it is sensible to restrict the analysis to intermediate pH values, although data have been obtained from pH 0 to pH 14. In the intermediate pH range the highly dominant contribution incorporates a single amino acid residue, which was identified to be Glu C180.
The change of protonation state of Glu C180 is directly related to the pKa value of the particular residue in the four different modeled heme b redox states (see Fig. 6), and the differences in pKa directly come into play as the system is taken from one redox state to the next. Again, direct and indirect (via other residues that are influenced by the heme charges) interactions of residue Glu C180 with the reduced and especially oxidized heme species lead to different occupancies of neutral and ionized Glu C180 conformers in the different redox states. This adjustment of conformer distribution between neutral and ionized states is then reflected in a changed pKa value or, in other words, in protonation or deprotonation of the residue if a fixed pH value is considered as a point of reference.
Reorientation of the Glu C180 side chain upon heme reduction
Results in Figs. 5 and 6 show net effects concerning the protonation state of Glu C180. But one major advantage of the multiconformation method is the possibility to study conformational changes of individual residues, as it has been described for Glu C180 (see Fig. 7) in Results, above. This observed reorientation upon reduction of the distal heme bD is apparently mediated by the neighboring water molecules, as the effect could not be observed for model X. As mentioned before and indicated in Table 1, conformers k and l of Glu− C180 have several stabilizing and destabilizing interactions with the conformers of water molecules W33 and, to a lesser extent, also with W11 in common. The presence of the two crystallographically determined water molecules in the vicinity of Glu C180 in model W increases the number of possible microstates that have to be considered in the Monte Carlo simulation. Thus, in contrast to model X, a scenario is created in which the energies of the different Glu C180 conformers are subjected to a more subtle selection and the resulting distinction is reflected in a pronounced dependency of the intermediate and distal conformations of Glu C180 with respect to the different heme b redox states. Another indication for the correctness and relevance of the two different side-chain conformations of Glu C180 was given by recent structural data on QFR wild-type enzyme at 1.78 Å resolution (C. R. D. Lancaster, unpublished), where significant electron density is observed for another side-chain conformation of Glu C180 that resembles the conformer which was created by MCCE and which could not be resolved in the previous original structure (1QLA) at 2.2 Å resolution.
The observed combination of (de)protonation and conformational changes of Glu C180 as a consequence of the modified heme b redox states was also found from the comparison of electrochemically induced FTIR difference spectra on the wild-type enzyme and of a corresponding variant, in which the relevant amino acid residue Glu C180 has been replaced by a glutamine (A. H. Haas, U. S. Sauer, R. Gross, J. Simon, W. Mäntele, and C. R. D. Lancaster, unpublished).
Protonation state of the ring C-propionate of heme bD
In addition to Glu C180, the ring C-propionate of the distal heme b group of QFR was also suggested to be involved in the proposed E-pathway of QFR. Unfortunately, this could not readily be deduced from the presented simulations, since the obtained protonation states of all four heme propionates were very stable around neutral pH and did not change as a function of the heme redox state. Interestingly, the ring C-propionate of the distal heme was the only one, which was calculated to be protonated in all investigated cases. The crystal structure (1QLA) of QFR does not feature any water molecules in the vicinity of the ring C-propionate of the distal heme. If water molecules would serve as proton donors and acceptors for this propionate in the tentative E-pathway, the lack of water sites in the model could be a possible reason why MCCE falls short of properly simulating protonation changes of the ring C-propionate of QFR. In a recent electrostatics study on the bovine heart cytochrome c oxidase (Popović and Stuchebrukhov, 2004), the authors discuss a possible drawback of the continuum solvent model, which neglects the directed dipoles of explicit water molecules, to create artifacts in the form of strong salt bridges between the involved heme propionates and surrounding arginines. As a result, the propionates could not serve as pumping elements. In their simulations, the authors obtained coupling strengths of ∼10–15 ΔpK units between the ionized propionates and arginines. Similar values were found in this study for the ionized heme propionates of QFR and the respective Arg+ and Lys+ residues (see Table 1). Furthermore, an estimation is made in Popović and Stuchebrukhov (2004), which leads to the conclusion that the influence of water dipoles could indeed weaken a strong salt bridge, but unlikely to an extent that would result in deprotonation of the respective arginine/propionate pair and enable the propionate to accept a proton.
In the case of QFR, such strong salt bridges can be identified for the two propionates of the proximal heme and the ring D-propionate of the distal heme (see Fig. 3). For the ring C-propionate of the distal heme, no evident acceptor for a salt bridge can be identified. Thus, the observed full protonation of this site could indicate that the ring C-propionate might serve as a transient proton donor/acceptor of the proposed E-pathway. For this function, the residue does not necessarily need to exhibit different protonation in the various modeled redox states. The internal pKint value of this propionate was calculated to be 15.5. Thus, it could easily donate a proton at neutral pH and be immediately reprotonated. Furthermore, as stated above, there are no relevant electrostatic interactions available for the ring C-propionate of the distal heme to possibly stabilize an ionized equilibrium state.
In this line of argumentation, two other examples can be given: Glu L212 in the bacterial photosynthetic reaction center (RC) is a key residue for proton transfer in this enzyme. In electrostatic calculations on the RC of Rhodopseudomonas viridis (Lancaster et al., 1996), this residue is predominantly protonated in all modeled redox states, and the simulated proton uptake between the two states  is negligible at neutral pH, which is in line with FTIR measurements on this enzyme (Breton et al., 1997 and 1999). The second example is Glu 278 of the cytochrome c oxidase from Paracoccus denitrificans, which was found to be neutral at pH 7 for all simulated redox states in comparable electrostatic calculations (Kannt et al., 1998) and in redox-induced FTIR difference spectra (Hellwig et al., 1998, 2002).
is negligible at neutral pH, which is in line with FTIR measurements on this enzyme (Breton et al., 1997 and 1999). The second example is Glu 278 of the cytochrome c oxidase from Paracoccus denitrificans, which was found to be neutral at pH 7 for all simulated redox states in comparable electrostatic calculations (Kannt et al., 1998) and in redox-induced FTIR difference spectra (Hellwig et al., 1998, 2002).
Implications for the E-pathway hypothesis
The obtained results and interpretation of the data with respect to transmembrane proton transfer via Glu C180, which is coupled to the redox states of the heme groups, strengthen the proposed model of catalytic action of QFR enzyme. The main aspect of the proposed E-pathway hypothesis (Lancaster, 2002b) is the existence of a transient proton transfer pathway in the QFR structure leading from the periplasm to the cytoplasm. A requirement of this hypothesis is that the E-pathway is active only upon reduction of the hemes but closed in the oxidized state. Two protons were suggested to be transferred via this pathway, which should compensate for the two protons that are released toward the periplasm via Glu C66 (Lancaster et al., 2000) and the two protons, which are bound on the cytoplasmic side of QFR upon fumarate reduction (Lancaster et al., 1999). The ionization state changes of Glu C180 can be interpreted as proton uptake and release that is directly coupled to the redox state of the distal and proximal heme. This observation under the applied conditions is consistent with in vivo proton translocation via Glu C180. Thus, the localization of Glu C180 and its strong interactions with the two heme groups give it the necessary characteristics to be the key element for the coupling of transmembrane electron transfer (via the hemes) to transmembrane proton transfer via the proposed E-pathway.
CONCLUSIONS
Simulations of the electrochemical redox titration behavior of the high- and low-potential heme b groups of the quinol:fumarate reductase from W. succinogenes by multiconformation continuum electrostatics calculations exhibit a very high degree of agreement with respect to the experimentally determined midpoint potentials of the hemes. Several ionized basic (Lys and Arg) residues have been identified to have a relevant electrostatic interaction with the oxidized heme species, hence tuning the two midpoint potentials to the observed values. The incorporation of water molecules in the calculations has a noticeable effect on the absolute values of the obtained midpoint potentials although the relative difference of the two obtained midpoints does not change significantly. The MCCE calculations clearly show that the low-potential heme corresponds to the distal position in the structure, and the high-potential is identical to the proximal heme. This assignment could not be achieved unequivocally with experimental methods. In addition, the currently discussed mechanism or E-pathway hypothesis of coupled electron and proton transfer in the QFR of W. succinogenes is further supported by the results of this study. The simulations show that the protonation state of the key amino acid residue Glu C180 depends on the redox states of the heme groups as suggested by the E-pathway hypothesis. This result yields a possible mechanism for the coupling of transmembrane proton transfer via Glu C180 to the electron transfer via the heme b groups, since Glu C180 could be part of a proton wire and its redox-dependent protonation state could serve as the regulatory element for the E-pathway. Furthermore, the results of simulated heme reduction indicate that the side chain of Glu C180 also changes its conformation with respect to the redox state of the hemes. Both major results concerning the role of Glu C180, the change of protonation as well as the reorientation of the side chain upon reduction of the heme groups, are consistent with results from electrochemically induced FTIR difference spectroscopy on the QFR from W. succinogenes (A. H. Haas, U. S. Sauer, R. Gross, J. Simon, W. Mäntele, and C. R. D. Lancaster, unpublished). The ring C-propionate of the distal heme is found to be fully protonated in all simulated redox states, indicating a possible role as a transient proton donor/acceptor in the E-pathway.
Acknowledgments
We thank Marilyn Gunner for providing the MCCE program code, Elena Herzog for providing scripts for data processing, and Hartmut Michel for his support of this project.
This work was supported by the Deutsche Forschungsgemeinschaft (SFB 472, P19) and the Max-Planck-Gesellschaft.
APPENDIX: GLOSSARY
Abbreviations
Arg+, ionized arginine.
Arg0, neutral arginine.
FAD, flavin adenine dinucleotide.
Glu−, ionized glutamate.
Glu0, neutral glutamate.
MK, menaquinone.
MKH2, menaquinol.
Paa, heme ring D-propionate.
Pdd, heme ring C-propionate.
SHE′, standard hydrogen electrode at pH 7.
Symbols
Eh, ambient redox potential.
Em, oxidation-reduction (midpoint) potential.
ΔG(n), free energy of protein microstate n.
pKsol(i), pKa of ionizable group i in aqueous solution.
ΔΔGrxn(i), reaction field energy (desolvation penalty) of residue i.
ΔGpol(i), interaction energy of residue i with polypeptide backbone and polar side chains.
ΔGnonel(i), nonelectrostatic (Lennard-Jones) interaction of residue i with the backbone and side chains with no conformational degrees of freedom.
ΔGcrg(i,j), pairwise electrostatic interaction energy of residues i and j.
ΔGnonel(i,j), pairwise nonelectrostatic (Lennard-Jones) interaction of residues i and j.
pKint, pKint = pKsol − ca(ΔpKdesolv + ΔpKpol), the pKa of an ionizable group in the protein with all other groups in their neutral state, with cα = 1 for bases and cα = −1 for acids.
Interconversion of energy units
1 kcal/mol = 4.184 kJ/mol.
1 ΔpK unit = 1.38 kcal/mol.
1 kT = 0.59 kcal/mol = 0.43 ΔpK units.
1 eV = 23.06 kcal/mol = 16.71 ΔpK units.
References
- Alexov, E. G., and M. R. Gunner. 1997. Incorporating protein conformational flexibility into the calculation of pH-dependent protein properties. Biophys. J. 74:2075–2093. [DOI] [PMC free article] [PubMed] [Google Scholar]
-
Alexov, E. G., and M. R. Gunner. 1999. Calculated protein and proton motions coupled to electron transfer: electron transfer from
 to QB in bacterial photosynthetic reaction centers. Biochemistry. 38:8253–8270. [DOI] [PubMed] [Google Scholar]
to QB in bacterial photosynthetic reaction centers. Biochemistry. 38:8253–8270. [DOI] [PubMed] [Google Scholar] - Antosiewicz, J., J. A. McCammon, and M. K. Gilson. 1994. Prediction of pH-dependent properties in proteins. J. Mol. Biol. 238:415–436. [DOI] [PubMed] [Google Scholar]
- Antosiewicz, J., J. M. Briggs, A. H. Elcock, M. K. Gilson, and J. A. McCammon. 1996. Computing ionization states of proteins with a detailed charge model. J. Comput. Chem. 17:1633–1644. [Google Scholar]
- Biel, S., J. Simon, R. Gross, T. Ruiz, M. Ruitenberg, and A. Kröger. 2002. Reconstitution of coupled fumarate respiration in liposomes by incorporating the electron transport enzymes isolated from Wolinella succinogenes. Eur. J. Biochem. 269:1974–1983. [DOI] [PubMed] [Google Scholar]
- Breton, J., E. Nabedryk, J. P. Allen, and J. C. Williams. 1997. Electrostatic influence of QA reduction on the IR vibrational mode of the 10a-Ester C=O of HA demonstrated by mutations at residues Glu L104 and Trp L100 in reaction centers from Rhodobacter sphaeroides. Biochemistry. 36:4515–4525. [DOI] [PubMed] [Google Scholar]
- Breton, J., M. Bibikova, D. Oesterhelt, and E. Nabedryk. 1999. Conformational heterogeneity of the bacteriopheophytin electron acceptor HA in reaction centers from Rhodopseudomonas viridis revealed by Fourier transform infrared spectroscopy and site-directed mutagenesis. Biochemistry. 38:11541–11552. [DOI] [PubMed] [Google Scholar]
- de Levie, R. 2003. The Henderson-Hasselbalch equation: its history and limitations. J. Chem. Educ. 80:146.
- Demchuk, E., and R. Wade. 1996. Improving the continuum dielectric approach to calculating pKas of ionizable groups in proteins. J. Phys. Chem. 100:17373–17387. [Google Scholar]
- Dunbrack, R. L., and F. E. Cohen. 1997. Bayesian statistical analysis of protein side-chain rotamer preferences. Protein Sci. 6:1661–1681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dunbrack, R. L., and M. Karplus. 1994. Conformational analysis of the backbone-dependent rotamer preferences of protein side-chains. Nat. Struct. Biol. 1:334–340. [DOI] [PubMed] [Google Scholar]
- Geisler, V., R. Ullmann, and A. Kröger. 1994. The direction of the proton exchange associated with the redox reactions of menaquinone during the electron transport in Wolinella succinogenes. Biochim. Biophys. Acta. 1184:219–226. [Google Scholar]
- Georgescu, R. E., E. G. Alexov, and M. R. Gunner. 2002. Combining conformational flexibility and continuum electrostatics for calculating pKas in proteins. Biophys. J. 83:1731–1748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilson, M. K., and B. Honig. 1986. The dielectric constant of a folded protein. Biopolymers. 25:2097–2119. [DOI] [PubMed] [Google Scholar]
- Gunner, M. R., and B. Honig. 1991. Electrostatic control of midpoint potentials in the cytochrome subunit of the Rhodopseudomonas viridis reaction center. Proc. Natl. Acad. Sci. USA. 88:9151–9155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gunner, M. R., and E. G. Alexov. 2000. A pragmatic approach to structure based calculations of coupled proton and electron transfer in proteins. Biochim. Biophys. Acta. 1458:63–87. [DOI] [PubMed] [Google Scholar]
- Gunner, M. R., M. A. Saleh, E. Cross, A. ud-Doula, and M. Wise. 2000. Backbone dipoles generate positive potentials in all proteins: origins and implications of the effect. Biophys. J. 78:1126–1144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hägerhäll, C., H. Fridén, R. Aasa, and L. Hederstedt. 1995. Transmembrane topology and axial ligands to hemes in the cytochrome b subunit of Bacillus subtilis succinate:menaquinone reductase. Biochemistry. 34:11080–11089. [DOI] [PubMed] [Google Scholar]
- Hägerhäll, C., and L. Hederstedt. 1996. A structural model for the membrane-integral domain of succinate:quinone oxidoreductases. FEBS Lett. 389:25–31. [DOI] [PubMed] [Google Scholar]
- Hägerhäll, C. 1997. Succinate:quinone oxidoreductases: variations on a conserved theme. Biochim. Biophys. Acta. 1320:107–141. [DOI] [PubMed] [Google Scholar]
- Hauser, K., J. Mao, and M. R. Gunner. 2004. pH dependence of heme electrochemistry in cytochromes investigated by multiconformation continuum electrostatic calculations. Biopolymers. 74:51–54. [DOI] [PubMed] [Google Scholar]
- Hederstedt, L. 1999. Respiration without O2. Science. 284:1941–1942. [DOI] [PubMed] [Google Scholar]
- Hellwig, P., J. Behr, C. Ostermeier, O. M. H. Richter, U. Pfitzner, A. Odenwald, B. Ludwig, H. Michel, and W. Mäntele. 1998. Involvement of glutamic acid 278 in the redox reaction of the cytochrome c oxidase from Paracoccus denitrificans investigated by FTIR spectroscopy. Biochemistry. 37:7390–7399. [DOI] [PubMed] [Google Scholar]
- Hellwig, P., U. Pfitzner, J. Behr, B. Rost, R. P. Pesavento, W. v. Donk, R. B. Gennis, H. Michel, B. Ludwig, and W. Mäntele. 2002. Vibrational modes of tyrosines in cytochrome c oxidase from Paracoccus denitrificans: FTIR and electrochemical studies on Tyr-D4-labeled and on Tyr280His and Tyr35Phe mutant enzymes. Biochemistry. 41:9116–9125. [DOI] [PubMed] [Google Scholar]
- Jensen, G. M., A. Warshel, and P. J. Stephens. 1994. Calculation of the redox potentials of iron-sulfur proteins: the 2-/3-couple of [Fe4S4*Cys4] clusters in Peptococcus aerogenes ferredoxin, Azotobacter vinelandii ferredoxin I, and Chromatium vinosum high-potential iron protein. Biochemistry. 33:10911–10924. [DOI] [PubMed] [Google Scholar]
- Kannt, A., C. R. D. Lancaster, and H. Michel. 1998. The coupling of electron transfer and proton translocation: electrostatic calculations on Paracoccus denitrificans cytochrome c oxidase. Biophys. J. 74:708–721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kassner, R. J. 1972. Effects of nonpolar environments on redox potentials of heme complexes. Proc. Natl. Acad. Sci. USA. 69:2263–2267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kassner, R. J. 1973. Theoretical model for effects of local nonpolar heme environments on redox potentials in cytochromes. J. Am. Chem. Soc. 95:2674–2677. [DOI] [PubMed] [Google Scholar]
- Kröger, A. 1978. Fumarate as terminal acceptor of phosphorylative electron transport. Biochim. Biophys. Acta. 505:129–145. [DOI] [PubMed] [Google Scholar]
- Kröger, A., S. Biel, J. Simon, R. Gross, G. Unden, and C. R. D. Lancaster. 2002. Fumarate respiration of Wolinella succinogenes: enzymology, energetics and coupling mechanism. Biochim. Biophys. Acta. 1553:23–38. [DOI] [PubMed] [Google Scholar]
- Lancaster, C. R. D., H. Michel, B. Honig, and M. R. Gunner. 1996. Calculated coupling of electron and proton transfer in the photosynthetic reaction center of Rhodopseudomonas viridis. Biophys. J. 70:2469–2492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lancaster, C. R. D., A. Kröger, M. Auer, and H. Michel. 1999. Structure of fumarate reductase from Wolinella succinogenes at 2.2 Å resolution. Nature. 402:377–385. [DOI] [PubMed] [Google Scholar]
- Lancaster, C. R. D., R. Gross, A. Haas, M. Ritter, W. Mäntele, J. Simon, and A. Kröger. 2000. Essential role of Glu C66 for menaquinol oxidation indicates transmembrane electrochemical potential generation by Wolinella succinogenes fumarate reductase. Proc. Natl. Acad. Sci. USA. 97:13051–13056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lancaster, C. R. D., R. Gross, and J. Simon. 2001. A third crystal form of Wolinella succinogenes quinol:fumarate reductase reveals domain closure at the site of fumarate reduction. Eur. J. Biochem. 268:1820–1827. [PubMed] [Google Scholar]
- Lancaster, C. R. D. 2001. Succinate:quinone oxidoreductases. In Handbook of Metalloproteins, Vol. 1. A. Messerschmidt, R. Huber, T. Poulos, and K. Wieghardt, editors. John Wiley & Sons, Chichester, UK. 379–401.
- Lancaster, C. R. D. 2002a. Succinate:quinone oxidoreductases: an overview. Biochim. Biophys. Acta. 1553:1–6. [DOI] [PubMed] [Google Scholar]
- Lancaster, C. R. D. 2002b. Wolinella succinogenes quinol: fumarate reductase—2.2-Å resolution crystal structure and the E-pathway hypothesis of coupled transmembrane proton and electron transfer. Biochim. Biophys. Acta. 1565:215–231. [DOI] [PubMed] [Google Scholar]
- Lancaster, C. R. D. 2003a. The structure of Wolinella succinogenes quinol:fumarate reductase and its relevance to the superfamily of succinate:quinone oxidoreductases. Adv. Prot. Chem. 63:131–149. [DOI] [PubMed] [Google Scholar]
- Lancaster, C. R. D. 2003b. The role of electrostatics in proton-conducting membrane protein complexes. FEBS Lett. 545:52–60. [DOI] [PubMed] [Google Scholar]
- Lancaster, C. R. D. 2004. Structure and function of succinate:quinone oxidoreductases and the role of quinol:fumarate reductases in fumarate respiration. In Respiration in Archaea and Bacteria, Vol. 1: Diversity of Prokaryotic Electron Transport Carriers. D. Zannoni, editor. Kluwer, Dordrecht, NL. 57–85.
- Li, J., M. R. Nelson, C. Y. Peng, D. Bashford, and L. Noodleman. 1998. Incorporating protein environments in density functional theory: a self-consistent reaction field calculation of redox potentials of [2Fe2S] clusters in ferredoxin and phthalate dioxygenase reductase. J. Phys. Chem. A. 102:6311–6324. [Google Scholar]
- Mao, J., K. Hauser, and M. R. Gunner. 2003. How cytochromes with different folds control heme redox potentials. Biochemistry. 42:9829–9840. [DOI] [PubMed] [Google Scholar]
- Matthew, J. B., F. R. N. Gurd, B. Garcia-Moreno, M. A. Flanagan, K. L. March, and S. J. Shire. 1985. pH-dependent processes in proteins. CRC Crit. Rev. Biochem. 18:191–197. [DOI] [PubMed] [Google Scholar]
- Moss, D. A., E. Nabedryk, J. Breton, and W. Mäntele. 1990. Redox-linked conformational changes in proteins detected by a combination of infrared spectroscopy and protein electrochemistry: evaluation of the technique with cytochrome c. Eur. J. Biochem. 187:565–572. [DOI] [PubMed] [Google Scholar]
- Nicholls, A., and B. Honig. 1991. A rapid finite difference algorithm utilizing successive over-relaxation to solve the Poisson-Boltzmann equation. J. Comp. Chem. 12:435–445. [Google Scholar]
- Ohnishi, T., C. C. Moser, C. C. Page, P. L. Dutton, and T. Yano. 2000. Simple redox-linked proton-transfer design: new insights from structures of quinol-fumarate reductase. Structure. 8:R23–R32. [DOI] [PubMed] [Google Scholar]
- Oliveberg, M., V. L. Arcus, and A. R. Fersht. 1995. pKa values of carboxyl groups in the native and denatured states of barnase. The pKa values of the denatured state are on average 0.4 units lower than those of model compounds. Biochemistry. 34:9424–9433. [DOI] [PubMed] [Google Scholar]
- Page, C. C., C. C. Moser, X. Chen, and P. L. Dutton. 1999. Natural engineering principles of electron tunnelling in biological oxidation–reduction. Nature. 402:47–52. [DOI] [PubMed] [Google Scholar]
- Popović, D. M., and A. A. Stuchebrukhov. 2004. Electrostatic study of the proton pumping mechanism in bovine heart cytochrome c oxidase. J. Am. Chem. Soc. 126:1858–1871. [DOI] [PubMed] [Google Scholar]
- Rabenstein, B., G. M. Ullmann, and E.-W. Knapp. 1998. Energetics of electron-transfer and protonation reactions of the quinones in the photosynthetic reaction center of Rhodopseudomonas viridis. Biochemistry. 37:2488–2495. [DOI] [PubMed] [Google Scholar]
- Richarz, R., and K. Wüthrich. 1978. Carbon-13 NMR chemical shifts of the common amino acid residues measured in aqueous solutions of the linear tetrapeptides H-Gly-Gly-X-L-Ala-OH. Biopolymers. 17:2133–2141. [Google Scholar]
- Song, Y., J. Mao, and M. R. Gunner. 2003. Calculation of proton transfer in bacteriorhodopsin bR and M intermediates. Biochemistry. 42:9875–9888. [DOI] [PubMed] [Google Scholar]
- Stephens, P. J., D. R. Jollie, and A. Warshel. 1996. Protein control of redox potentials of iron-sulfur proteins. Chem. Rev. 96:2491–2513. [DOI] [PubMed] [Google Scholar]
- Sitkoff, D., K. A. Sharp, and B. Honig. 1994. Accurate calculation of hydration free energies using macroscopic solvent models. J. Phys. Chem. 98:1978–1988. [Google Scholar]
- Tanford, C., and J. G. Kirkwood. 1957. Theory of protein titration curves. I. General equations for impenetrable spheres. J. Am. Chem. Soc. 79:5333–5339. [Google Scholar]
- Ullmann, G. M., and E.-W. Knapp. 1999. Electrostatic models for computing protonation and redox equilibria in proteins. Eur. Biophys. J. 28:533–551. [DOI] [PubMed] [Google Scholar]
- Wilson, G. S. 1974. Electrochemical studies of porphyrin redox reactions as cytochrome models. Bioelectrochem. Bioenerg. 1:172–179. [Google Scholar]