Donor-bridge-acceptor energetics determine the distance dependence of electron tunneling in DNA

Abstract

Electron transfer (ET) processes in DNA are of current interest because of their involvement in oxidative strand cleavage reactions and their relevance to the development of molecular electronics. Two mechanisms have been identified for ET in DNA, a single-step tunneling process and a multistep charge-hopping process. The dynamics of tunneling reactions depend on both the distance between the electron donor and acceptor and the nature of the molecular bridge separating the donor and acceptor. In the case of protein and alkane bridges, the distance dependence is not strongly dependent on the properties of the donor and acceptor. In contrast, we show here that the distance decay of DNA ET rates varies markedly with the energetics of the donor and acceptor relative to the bridge. Specifically, we find that an increase in the energy of the bridge states by 0.25 eV (1 eV = 1.602 × 10⁻¹⁹ J) relative to the donor and acceptor energies for photochemical oxidation of nucleotides, without changing the reaction free energy, results in an increase in the characteristic exponential distance decay constant for the ET rates from 0.71 to 1.1 Å⁻¹. These results show that, in the small tunneling energy gap regime of DNA ET, the distance dependence is not universal; it varies strongly with the tunneling energy gap. These DNA ET reactions fill a “missing link” or transition regime between the large barrier (rapidly decaying) tunneling regime and the (slowly decaying) hopping regime in the general theory of bridge-mediated ET processes.

Electron transfer (ET) processes in which an electron donor and acceptor are separated by a molecular spacer or bridge (D-B-A systems) are encountered widely in biological systems (proteins and DNA; refs. 1–4) and molecular wires (5–7). The dynamics of such processes are known to depend, inter alia, on the length and nature of the bridge (8, 9). The dynamics of single-step photoinduced ET in D-B-A systems, a process referred to as tunneling, is generally found to display an exponential dependence on the D-A distance as described by Eq. 1,

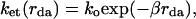1

where k_o is a temperature-dependent prefactor, r_da is the D-A separation, and β characterizes the steepness of the experimental distance dependence. The values of β for D-B-A systems vary with the nature of the bridge. For example, values of β ≈ 1.3 and 1.0 Å⁻¹ are observed for protein bridges possessing α-helix or β-sheet geometries, respectively, and values of β ≈ 0.9 Å⁻¹ are observed for rigid alkane bridges (2, 5). This range of β values is well accounted for in theories that include the specific nature of the through-bond and through-space electronic interactions in these bridges. Values as large as 1.7 Å⁻¹ are observed for tunneling through water (10, 11). These larger values in water are likely associated with the noncovalent interactions and the large ionization potential (IP) of water. Much smaller values of β ≈ 0.1 Å⁻¹ are observed for bridges consisting of conjugated polyenes (5, 12), which probably arise from delocalization of the donor and acceptor states onto the bridge. DNA systems apparently are unique in that a wide range of values of β (0.1–1.5 Å⁻¹) have been observed for similar duplex DNA bridge structures (13, 14). The very smallest β values for DNA ET may arise from an alternative ET mechanism, multistep hole hopping (15–18). The distance dependence of the reorganization energy may enhance some of the observed β values (19). A question in DNA ET is how much the donor and acceptor energetics can influence the β value by tuning the electronic coupling strength. By making donor-acceptor modifications that do not change the ET-activation free energies, we find that β values can be changed by more than 50%. We interpret these results in terms of tunneling energy gap effects on bridge-mediated coupling, a long-sought but elusive effect in bridge-mediated ET chemistry. We also describe why the tunneling energy dependence of β is pronounced in DNA ET, while it is seemingly weak in protein and alkane ET systems.

The Tunneling Energy Gap

The distance dependence of k_et originates from both the electronic coupling and the Franck–Condon factor (Eq. 2), and it is difficult (experimentally) to separate these two influences. The squared electronic coupling is expected to decrease approximately exponentially with distance and is characterized by the decay exponent β^c (Eq. 3).

2

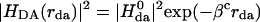3

The Franck–Condon factors may also introduce distance dependence to the ET rate (for example, through the distance dependence of the reaction free energy and reorganization energy), so β^c and β (Eq. 1) need not be identical. The decay exponent in Eq. 3 depends on the strength of the interactions among bridge sites and the magnitude of the tunneling energy gap, ΔE_tun, between the donor (or acceptor) and bridge units. In the semiclassical view of ET processes, nuclear motion causes fluctuations in the donor and acceptor energetics, and when these levels are equal (i.e., the system is in the transition state), ET may occur. We define the tunneling energy, E_tun, as the negative IP of the system in the transition-state complex (the energy of the transferred electron) and the tunneling energy gap as the difference between E_tun and the negative IP of the nearest bridging state, IP_br (Eq. 4; ref. 20).

The role of the tunneling energy gap is illustrated in the McConnell model (21). The McConnell model assumes that the bridge consists of a periodic chain of orbitals with nearest-neighbor interaction elements, t_mn, and energy gap, ΔE, between the donor (or acceptor) and bridge localized orbitals. As such, the exponential decay constant β^c can be described by Eq. 5.

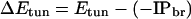4

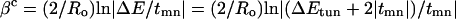5

In the McConnell model, ΔE_tun is smaller than ΔE by an amount equal to half of the energy “band-width” of the “mixed” bridge eigenstates. More elaborate methods of analyzing bridge-mediated coupling predict dependencies of β^c on ΔE_tun qualitatively similar to the prediction of Eq. 5 (9).

Tunneling energies are derived from the properties of the (nonequilibrium) activated complex and thus are difficult to determine experimentally. Experimental verification of the influence of tunneling energy on the bridge-mediated coupling has proved elusive for D-B-A model compounds with fixed-bridge structures, although there is some evidence of ΔE_tun effects in studies of mutated and model photosynthetic reaction centers (22). ΔE_tun is closely related to the “injection free energy,” ΔG_inj, which is defined as the minimum free energy difference between the state with the hole localized on the bridge (A⁻B⁺D) and the initial or the final state (A*BD or A⁻BD⁺) (23, 24). ΔG_inj is an ensemble property and can be estimated from electrochemical data and excitation energies. Both ΔE_tun and ΔG_inj increase as the bridge states are moved further in energy from the donor-acceptor states. However, ΔE_tun depends on the reorganization energy of the ET process, whereas ΔG_inj does not. It has been shown that ΔE_tun is equal to the injection free energy plus one half of the reorganization energy when simplifying assumptions are made (13, 20).

Experimental Determination of β

Synthetic DNA hairpins containing a stilbene-4,4′-dicarboxamide (SA) chromophore (Fig. 1) have provided a versatile platform for investigations of the dynamics of photoinduced ET in DNA (14, 25). The SA chromophore serves both as a rigid linker for the construction of remarkably stable synthetic hairpins and as an electron acceptor, which selectively photooxidizes guanine but not the other three common DNA nucleobases. Selective oxidation of G is consistent with the energetics of the photochemical ET process, estimated from the Rehm–Weller relationship (Eq. 6; ref. 26),

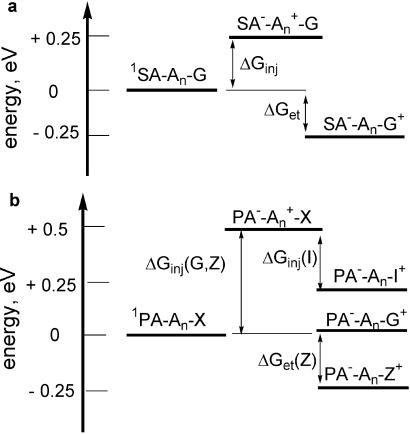
6

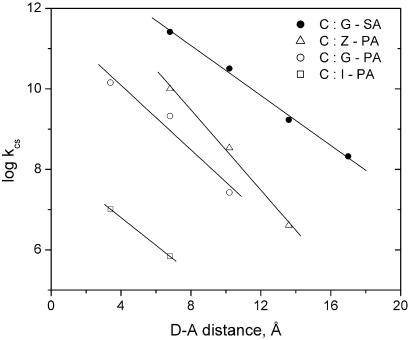
using the SA singlet excitation energy, E_s, ground-state reduction potential, E_rdn, (Fig. 1a), and G oxidation potential, E_ox (Fig. 1b; refs. 27 and 28). As shown schematically in Fig. 2a, oxidation of the G donor (ΔG_et) is exergonic, whereas injection of a hole into the polyA:T bridge (ΔG_inj) is endergonic. Calculated values of ΔG_et and ΔG_inj are summarized in Table 1. The other bases, T and C, are more difficult to oxidize than A (27). Determination of the dynamics of photoinduced ET from G to singlet SA for the G-SA family of hairpins in which SA and G are separated by a variable number of T:A base pairs (Fig. 1c) provides a value of β = 0.71 ± 0.07 Å⁻¹ (Fig. 3), assuming a normal DNA π-stacking distance (3.4 Å per step; refs. 29 and 30).

Figure 1.

(a) Structure, singlet energy, and reduction potentials of SA and PA linkers. (b) Structure and oxidation potential of nucleobase donors. (c) Schematic structures of SA- and PA-linked hairpins.

Figure 2.

Energetics of charge separation singlet SA acceptor with G donor (a) and singlet PA acceptor with I, G, and Z donors (b).

Table 1.

Free energies for electron transfer and hole injection and values of β for distance-dependent electron transfer in DNA

Hairpin*	ΔGet†‡, eV	ΔGinj‡§, eV	β¶, Å−1
G-SA‖	−0.20	0.25	0.71  ± 0.07
Z-PA**	−0.24	0.50	1.1  ± 0.15
G-PA**	0.05	0.45	0.92  ± 0.09
I-PA**	0.21	0.29	0.8  ± 0.2

^*See Fig. 1 for structures. 

^† Calculated using Eq. 5 and the electrochemical data in Fig. 1. The difference in equilibrium oxidation potentials for G⁺Z vs. GZ⁺ is 0.19 ± 0.03 eV, smaller than the value 0.29 eV obtained from the electrochemical oxidation potentials for single nucleotides (Fig. 1; ref. 27). 

^‡ Estimated error ± 0.05 eV. 

^§ See Fig. 1. 

^¶ Calculated from the slopes in Fig. 3. Errors are estimated from the kinetic data. 

^‖ The value of β = 0.71 Å⁻¹ was obtained for G located in the polyA strand. A slightly smaller value of β = 0.64 ± 0.1 was obtained for G located in the polyT strand (29, 30). 

^**Data from this study. 

Figure 3.

Distance dependence of the rate constant for photoinduced ET between the singlet PA and SA acceptors and nucleobase donors.

It is possible to alter the values of both ΔG_et (Eq. 6) and ΔG_inj by changing the redox potentials of the donor and acceptor (31). The use of a phenanthrene-2,7-dicarboxamide (PA) linker (Fig. 1a) as the acceptor and G as the donor results in a small positive value of ΔG_et and a larger value of ΔG_inj (Table 1; Fig. 2b). The preparation of PA-linked hairpins has been described previously (31). Use of the nucleobase analog deazaguanine (Z) with a PA linker results in a value of ΔG_et similar to that for oxidation of G by SA, whereas use of inosine (I) results in endergonic ET. The values of ΔG_inj are approximately the same for the Z and G hole donor nucleobases. Photooxidation of I by PA is thermodynamically “uphill” (Fig. 2b), and thus ΔG_inj is smaller for the oxidation of I. Molecular modeling using the AMBER force field indicates that SA- and PA-linked hairpins adopt similar B-form DNA structures with SA or PA π-stacked with the adjacent base pair. The melting temperatures and circular dichroism (CD) spectra of the SA- and PA-linked hairpins are similar also.

The fluorescence quantum yields and decay times for the PA-linked hairpins with Z, G, and I donors determined in the present study are reported in Table 2. The nanosecond decay times were obtained using stroboscopic detection (31) and are best fit by a single exponential in all cases. The decay times for very weak fluorescence of hairpins 1G-PA and 2Z-PA were obtained with a Ti:sapphire-pumped system with single-photon counting having an instrument response function of 50 ps (32). These decays are best fit by a dual exponential (the shorter-lived picosecond component is reported in Table 2). The longer-lived components (≈2–4 ns), by analogy to the behavior of duplexes containing the fluorescent nucleobase analog 2-aminopurine (33), are attributed to poorly stacked minor hairpin conformers. The values of Φ_f and τ_s are seen to decrease as ΔG_et becomes more negative and as the D-A separation decreases, in accord with an ET mechanism for fluorescence quenching. Values of k_et calculated from the singlet decay times also are reported in Table 2. For a given D-A separation, values of k_et decrease with increasing (more positive) ΔG_et, as previously observed for the SA linker. The values of k_et for 1I-PA and 1G-PA and the extrapolated value for 1Z-PA fall on the plot of k_et vs. ΔG_et previously obtained for nearest-neighbor quenching of SA and other acceptor linkers by nucleobases (31). This indicates that the D-A electronic coupling and reorganization energies for PA- and SA-linked hairpins, as well as their structures, are similar.

Table 2.

Fluorescence quantum yields, lifetimes, and dynamics of electron transfer

Hairpin*	Φf†	τs‡, ns	ket§, s−1
A-PA	0.41	24.8	<106
1I-PA	0.27	19.8	1.0  × 107
2I-PA	0.33	24.4	≈1  × 106
1G-PA	≈0.001	0.07	1.4  × 1010
2G-PA	0.01	0.47	2.1  × 109
3G-PA	0.22	14.9	2.7  × 107¶
4G-PA	0.37	25.9	<106
2Z-PA	≈0.002	0.10	1.0  × 1010
3Z-PA	0.02	2.6	3.4  × 108
4Z-PA	0.28	22.5	4  × 106

Data from this study, except as noted, are for deoxygenated solutions of 5 × 10⁻⁶ M hairpin in aqueous buffer containing 0.1 M NaCl. 

^*See Fig. 1 for structures. 

^† Fluorescence quantum yields determined by comparison to quinine sulfate. Limits of error for multiple determination ±10%. 

^‡ Fluorescence decay times. Nanosecond decays determined as described in ref. 33 are all single exponential. Subnanosecond decays determined as described in ref. 34 can be fit to either single or double exponential functions with long-lived decay components of 2.9 ns for 1G-PA and 3.9 ns for 2Z-PA. 

^§ k_et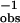 = τ − τ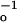, where τ_o is the decay time of the hairpin A-PA. 

^¶ Data from ref. 33. 

Plots of log k_et vs. D-A separation for PA-linked hairpins with Z, G, and I as donors are shown in Fig. 3. The slopes of these plots decrease in the order Z > G > I, providing values of β = 1.1 ± 0.1, 0.92 ± 0.15, and 0.8 ± 0.2 Å⁻¹, respectively, according to Eq. 1. In the case of the G-PA and I-PA hairpins, the data points for nearest-neighbor ET have been included in the calculation of β, as is the standard practice (30, 34, 35). Nearest-neighbor quenching is not strictly DNA-mediated, and thus we have the greatest confidence in the values of β for G-SA and Z-PA. The difference in their β values is well outside the experimental limits of error (Table 1). Values of β, in principle, could also be determined from the fluorescence quantum yield data. However, the possible existence of minor hairpin conformers in which fluorescence quenching is relatively inefficient renders quantum yield data less reliable than kinetic data.

Interpretation of the Experimental Results

The reorganization energy for DNA hole transfer is expected to increase with distance, and this dependence has been probed theoretically by several groups (19, 36–38). The reorganization energies at a given distance for the four families of data in Fig. 3 are expected to be approximately equal, because the structures of the corresponding donor and acceptor groups and the DNA bridge are nearly the same in these hairpin families. This suggests that the differences in β values arise from the electronic coupling element rather than from the Franck–Condon factor (Eq. 2). Chemical differences among the donors and acceptors can influence the intercepts of the distance decay curves in Fig. 3 because of different H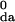 values (Eq. 3), but should not influence their slopes strongly. As such, the differences in these slopes are attributed to tunneling energy effects (Eq. 5), which are shown schematically in Fig. 4. This analysis assumes that the geometry of the A:T stack is similar for the four hairpin families. Changes in geometry of the A:T stack resulting from changes in the donor and acceptor would be expected to alter the value of the t_mn elements (Eq. 5) and thus the value of β. Recent theoretical studies indicate that changes in base-pair stacking can alter the t_mn elements (18, 23, 24, 38–41). However, the similar CD spectra and thermal dissociation profiles for the SA- and PA-linked hairpins suggest that differences in structure are minimal. It is important to note that local structural changes associated with the donor and acceptor may influence the overall value of the coupling without changing its distance dependence, β.

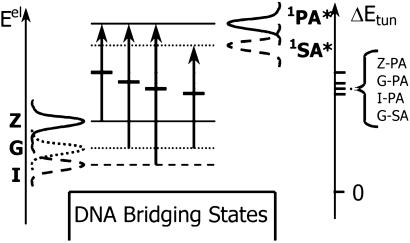
Figure 4.

Spectral functions for electron removal (from Z, G, and I) and insertion (on ¹SA* and ¹PA*). It is assumed that |ΔG⁰| < λ. Τhe arrows represent the ET from the bases to the excited acceptor species. The peak in the product between insertion and removal functions defines the most probable tunneling energy for the ET process, indicated by the short, dark, horizontal bars for each process. The tunneling energy gaps are indicated (Right). The larger the tunneling energy gap, the larger the predicted value of β is.

The tunneling energy dependence of the D-A coupling is described readily in terms of electron insertion and removal functions (20, 42). This formulation of nonadiabatic ET theory employs Gaussian spectral functions, which are temperature-, redox potential-, and reorganization energy-dependent (20). It is equivalent to conventional high-temperature nonadiabatic ET theory but clearly shows the distribution of electron-tunneling energies. The probability of electron removal from the reduced donors (and insertion onto the oxidized acceptors) is expected to appear as shown qualitatively in Fig. 4, in which the three curves on the far left are the removal probability functions, and the two curves on the right are the insertion probability functions. Peaks in the electron-donor removal functions will lie at energies below the peaks in the acceptor-insertion functions, consistent with the “normal” Marcus regime (|ΔG⁰| < λ; ref. 8). The positive energy offset between the removal (left-hand side of diagram) and insertion functions (right-hand side of diagram) is equal to λ + ΔG⁰, the familiar energy offset between the two Marcus parabolas for the equilibrium geometry of the reactants in the normal free energy regime. Since ET occurs when the donor-removal and acceptor-insertion energies are equal, the most probable tunneling energy associated with the ET transition occurs at the peak of the product of the insertion and removal functions. Assuming that the insertion and removal functions have equal widths, their product will be optimized midway between the maxima of the individual functions, as indicated by the short, dark, horizontal lines in Fig. 4. This treatment is based on the assumption that the fluctuations of the donor and acceptor energy levels are not correlated. When the donor and acceptor are at shorter distances, this assumption is not strictly valid. However, it will not influence our qualitative conclusions.

The predicted trend in the tunneling energy gaps (ΔE_tun) is Z-PA > G-PA > I-PA > G-SA, which parallels the calculated values of ΔG_inj and the experimental β values (Table 1). We emphasize that β is controlled by the tunneling energy gap, the energy difference between the quasidegenerate donor-acceptor states, and closest bridge state in the transition state rather than the injection free energy, which is an equilibrium property. This conclusion is supported by the observed difference in β values for the Z-PA and G-PA hairpin families, which have the same injection free energy but different tunneling energy gaps (Fig. 4). The observed difference in Z-PA and G-PA β values (1.1 and 0.92 Å⁻¹, respectively) is smaller than the sum of the uncertainties in their β values (0.15 and 0.09 Å⁻¹, respectively). Thus the confidence in the observed difference in their β values is relatively low. It follows from Fig. 4 that the tunneling energy should increase with reorganization energy, although we do not have experimental data yet to support this prediction (20).

The measured difference in β values for the G-SA and Z-PA hairpin families can be compared with a theoretically predicted dependence of β upon the tunneling energy reported in figure 4 of ref. 20. This figure indicates that a tunneling energy offset of ≈0.25 eV (1 eV = 1.602 × 10⁻¹⁹ J) from the point where β = 0.7 Å⁻¹ should generate a β of ≈1.1 Å⁻¹. The excellent correspondence between theory and experiment (Table 1) requires that the source of all distance dependence in the ET rate is the electronic coupling (i.e., β = β^c). This qualification is in conflict with the theoretical prediction of a strong distance dependence of the outer-sphere reorganization energy (20, 43). Some physical aspects of the stilbene/guanine ET systems apparently are misrepresented by the continuum-electrostatics analysis of the outer-sphere reorganization energy. Large delocalization or polarizability of the initially excited or product states could lead to smaller outer-sphere reorganization energies than are estimated theoretically (20, 43).

Comparison of Tunneling in DNA and Alkanes

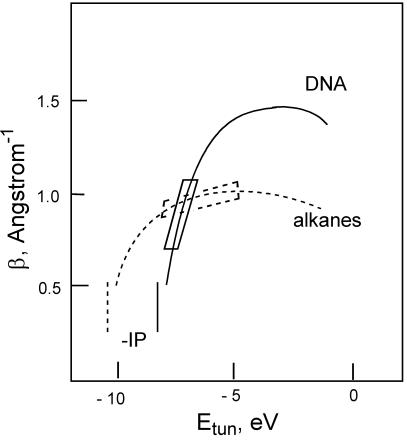
The dependence of β on tunneling energy (E_tun) in DNA and all-trans alkanes is shown schematically in Fig. 5. The difference between the tunneling energy and IP of the A:T bridge (IP_br) determines the tunneling energy gap (Eq. 4). In accord with the McConnell and more advanced models (43), the value of β is expected to decrease as the tunneling energy gap decreases, as indicated in Fig. 5. Because the IP values for alkanes are larger than for DNA bases, the dropoff in β occurs at more negative tunneling energies in alkanes than in DNA. As the tunneling energy approaches the (negative) electron affinity of the bridge, we expect to enter the electron mediation regime, in which β will decrease. The maximum value of β is expected to be larger for DNA than for the alkane bridge because of the stronger through-bond interactions in the alkane chain (20) compared with the through-space interactions between the π-stacked bases that mediate electron tunneling in DNA.

Figure 5.

The qualitative tunneling energy dependence of β according to Eqs. 4 and 5 in DNA hairpins (solid line) and all-trans alkanes (dashed line). Maximum values of β are estimates based on experimental data. Vertical lines represent the negative IPs for alkanes and T:A base pairs. The boxes represent the range of tunneling energies for the DNA hairpins in the present study, in which the tunneling energies are nearly as large in magnitude as the base-pair IPs, and for studies of ET in systems with alkane bridges, in which the tunneling energies are much smaller in magnitude than the alkane IPs.

The combination of low bridge IP (44) and relatively large negative E_tun values for photoinduced ET in DNA can result in values of β that strongly depend on ΔE_tun, as observed in the present investigation. Values of β ≈ 0.6–0.8 Å⁻¹ have been reported recently for systems in which a singlet aminopurine, acridine dye, or thionine dye acceptor is separated from a guanine donor by a variable number of A:T base pairs (34, 35, 45). These systems have values of ΔG_inj (and ΔE_tun) similar to that of our G-SA system (Table 1), and thus it is not surprising that they have similar β values (14). The use of D-A pairs intercalated (46, 47) or end-tethered (48) in duplexes containing both A:T and G:C base pairs results in values of β as large as 1.5 Å⁻¹, in accord with the larger values of ΔE_tun expected for acceptors that cannot oxidize G. This value of β is used as an upper bound in Fig. 5; however, Franck–Condon effects may contribute to the magnitude of β in these systems. Whereas the upper bound of β for DNA is yet to be determined by experiment, calculations suggest that β could be as large as ≈2 Å⁻¹ for noncovalent π-stack-mediated tunneling (20). Values of β < 0.4 Å⁻¹ for tunneling in DNA would seem to require very small values of ΔE_tun, in which case oxidation of the T:A bridge is likely to compete with bridge-mediated oxidation of G. In the case of tunneling via alkane or protein bridges, E_tun − (−IP_bridge) is substantially larger than that for A:T base-pair bridges, because the IP is larger for alkane or protein bridges than for DNA bases, and the range of E_tun is limited to a window of a few electron volts for stable donor-acceptor species (49). As a consequence, little variation is observed in values of β for alkane- or protein-mediated ET as donor and acceptor energetics are varied (1, 50).

In conclusion, we have shown experimentally that the distance dependence of the tunneling rate in DNA is strongly dependent on the energetic proximity of the base-pair bridge states to the donor and acceptor initial and final states. From a theoretical point of view, we have demonstrated that the different β values for ET process in DNA can be understood in the context of tunneling energy gap-modulated electron donor-acceptor interactions. These results provide the “missing link” in our understanding of electron transport in DNA. Namely, as the tunneling energy gap decreases from ≈0.5 to ≈0.25 eV, β changes from a typical “large” value of 1.1 to a “small” value of 0.6 Å⁻¹. A further decrease in the tunneling energy gap may cause a transition, especially at longer distances, to a hopping mechanism with a qualitatively weaker distance dependence. The dynamics and theory of hole transport in DNA have also been studied in our laboratories (38, 51, 52).

Abbreviations

ET

electron transfer

SA

stilbene-4,4′-dicarboxamide

PA

phenanthrene-2,7-dicarboxamide

Z

deazaguanine

IP

ionization potential