Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Nov 8;88(1):147–155. doi: 10.1529/biophysj.104.046375

Folding Trp-Cage to NMR Resolution Native Structure Using a Coarse-Grained Protein Model

Feng Ding *, Sergey V Buldyrev †, Nikolay V Dokholyan *
PMCID: PMC1304993  PMID: 15533926

Abstract

We develop a coarse-grained protein model with a simplified amino acid interaction potential. Using this model, we perform discrete molecular dynamics folding simulations of a small 20-residue protein—Trp-cage—from a fully extended conformation. We demonstrate the ability of the Trp-cage model to consistently reach conformations within 2-Å backbone root-mean-square distance from the corresponding NMR structures. The minimum root-mean-square distance of Trp-cage conformations in simulations can be <1 Å. Our findings suggest that, at least in the case of Trp-cage, a detailed all-atom protein model with a molecular mechanics force field is not necessary to reach the native state of a protein. Our results also suggest that the success of folding Trp-cage in our simulations and in the reported all-atom molecular mechanics simulation studies may be mainly due to the special stabilizing features specific to this miniprotein.

INTRODUCTION

In 2001 Neidigh et al. discovered that the 18-residue-long segment Leu-21–Pro-38 of exendin-4—a naturally occurring 39-amino-acid protein—is the shortest-known independently folding fragment (Neidigh et al., 2001), designated as Trp-cage by Barua and Andersen (2001). Neidigh et al. (2002) have truncated and redesigned the exendin-4 to a 20-residue miniprotein that exhibits cooperative folding transition and is significantly more stable than any other known miniprotein (Dahiyat and Mayo, 1997; de la Paz et al., 2001; Kortemme et al., 1998; Ottesen and Imperiali, 2001; Qiu et al., 2002) (ΔGU ≈ 8.6 kJ mol−1 at 3°C). Due to its fast folding kinetics, high thermodynamic stability, and small size, the Trp-cage received considerable attention in the computational community (Chowdhury et al., 2003; Pitera and Swope, 2003; Simmerling et al., 2002; Snow et al., 2002; Zagrovic and Pande, 2003; Zhou, 2003). These studies have demonstrated the abilities of all-atom molecular mechanics simulations to reach the native state of the Trp-cage within ∼1-Å backbone root-mean-square deviation (RMSD) from a completely unfolded conformation.

A central paradigm of molecular biology is that a protein's structure is determined by its amino acid sequence. However, the relationship between a protein's amino acid sequence and its structure (protein folding problem; Anfinsen, 1973; Fersht and Shakhnovich, 1998; Levitt et al., 1997; Onuchic et al., 1997; Pande et al., 2000; Plaxco et al., 1998; Shakhnovich, 1997) remains largely unknown despite a large number of studies (e.g., Abkevich et al., 1994; Bryngelson and Wolynes, 1987, 1989; Dill, 1985, 1990; Go and Abe, 1981; Irback and Potthast, 1995; Klimov and Thirumalai, 1998; Micheletti et al., 1998; Nymeyer et al., 1998; Pande et al., 1997; Shakhnovich, 1994, 1996; Taketomi et al., 1975). Although a success of folding Trp-cage in computer simulations (Chowdhury et al., 2003; Pitera and Swope, 2003; Snow et al., 2002; Zagrovic and Pande, 2003; Zhou, 2003) may be perceived as a triumph in solving the protein-folding problem, we ask here whether the folding dynamics of the Trp-cage is governed by a few key factors that may not be applicable to the majority of proteins. The physical force fields employed in molecular mechanics simulations capture these factors, which solely determine the folding dynamics of the Trp-cage.

To answer this question we employ discrete molecular dynamics (DMD) simulations (Ding et al., 2002a, 2003; Dokholyan et al., 1998; Zhou and Karplus, 1997). Unlike molecular mechanics simulations driven by physical forces, DMD simulations are driven by collision events due to ballistic motion of the particles and constraints between these particles (Dokholyan et al., 2003). Due to its high efficiency, the DMD algorithm has been recently applied to study protein folding and aggregations (Ding et al., 2002a,b; Dokholyan et al., 2000; Smith and Hall, 2001b,c). Thus, DMD simulations provide us with an opportunity to test whether just a set of key interactions can be imposed to capture the key factors governing the Trp-cage folding dynamics.

The evidence for the key factors determining the Trp-cage folding dynamics has been suggested by Neidigh et al. (2001), who designed a stable fast-folding Trp-cage sequence—NLYIQWLKDGGPSSGRPPPS—by mutagenesis studies of a common amino acid sequence pattern for Trp-cage fold, XFXXWXXXXGPXXXXPPPX, where X is any amino acid. These three key factors (i–iii) are listed below. i), Interactions of proline with aromatic residues, such as Pro-Trp, stabilize the Trp-cage. Gellman and Woolfson (2002) and Neidigh et al. (2001) argue that several small proteins, such as WW domains (Zarrinpar and Lim, 2000), villin headpiece (McKnight et al., 1997), Trp zipper (Cochran et al., 2001), and avian pancreatic polypeptide (Blundell et al., 1981), employ Pro-Trp stacking as a means of stabilization. ii), The high proportion of proline residues (20%) results in a more rigid Trp-cage structure than the majority of protein structures, drastically reducing the entropy of the Trp-cage unfolded state. Gellman and Woolfson (2002) pointed out that Trp-cage is also rich in Gly residues that contrary to Pro residues increase backbone flexibility and, thus, favor unfolded conformations. We hypothesize that Gly enrichment is essential for the Pro-Trp stacking to occur, and despite their destabilizing effect, Gly residues allow this favorable Pro-Trp interaction. iii), Pitera and Swope (2003) pointed out that a salt bridge between Asp-9 and Arg-16 in the TC5b variant provides an additional stabilization to the Trp-cage.

We develop a coarse-grained protein model that mimics protein backbone flexibility and side-chain packing, and a model of amino acid interactions that are likely to be the key factors determining Trp-cage folding dynamics (i–iii). We demonstrate that our model consistently undergoes a folding transition from fully extended conformation to a near-native set of conformations that are within 2-Å RMSD from the NMR structure (Neidigh et al., 2002). We show that some states reach the average NMR structure within <1-Å backbone RMSD.

METHODS

Discrete molecular dynamics

The DMD algorithm is based on pairwise spherically symmetrical-potentials that are discontinuous functions of an interatomic distance (Alder and Wainwright, 1959; Dokholyan et al., 1998; Rapaport, 1997; Zhou and Karplus, 1997). The earliest molecular dynamics simulations (Alder and Wainwright, 1959) were performed with the discrete algorithm, before the advent of continuous potentials and thus the modern molecular mechanics. In DMD all atoms move with constant velocity unless they reach the interatomic distance where the stepwise potential function changes. At this moment of time their velocities change instantaneously. This change satisfies the laws of energy, momentum, and angular momentum conservations. When the kinetic energy of the particles is not sufficient to overcome the potential barrier, the atoms undergo a hard core reflection with no potential energy change.

Protein model

We model the protein by beads-on-a-string with beads corresponding to the backbone and side-chain heavy atoms. It has been shown that a four-bead DMD model with three backbone beads—N, Cα, C′—and one minimalist side-chain bead Cβ can capture dynamics of the polypeptide backbone (Ding et al., 2003; Smith and Hall, 2000, 2001a). Due to the coarse-grained nature, the four-bead DMD model cannot estimate the side-chain entropy, packing in the protein core, etc., all of which makes critical contributions to protein folding (Creamer and Rose, 1992). To observe protein folding, the model needs to correctly capture not only the backbone entropy but also the side-chain entropy and the size effect for the packing of side chains. Therefore, to keep the model simple while effectively capturing all the important features, we add one or two additional effective side-chain atoms into the four-bead model (Ding et al., 2003; Smith and Hall, 2000, 2001c). For the β-branched amino acids—Thr, Ile, and Val—we introduce two γ-beads representing the two branches after Cβ. For bulky amino acids—Arg, Lys, and Trp—we include an additional δ-bead (see Fig. 1 A).

FIGURE 1.

FIGURE 1

Open in a new tab

(A) The schematic diagram of the model peptide. Only two consecutive residues are presented. The shaded γ2- and δ-beads—Cγ2 and Cδ—indicate that not all amino acids have them. Covalent bonds are represented as thick lines and the constraints that need to fix the bond angles and the planar property of peptide bonds are denoted as thin dashed lines. (B) The schematic diagram of the hydrogen bond among backbone. Only the backbone beads of the model are shown. The thick dash lines represent the hydrogen bonds and the thin dashed lines indicate the auxiliary constraints for the formation of the hydrogen bond. (C) The histogram of distances between the hydrogen-bonded oxygen and nitrogen as well as the distance of the auxiliary constraints, which is calculated for the hydrogen bonds in crystal structures.

To model the bond lengths and bond angles, we introduce constraints between the neighboring beads (Dokholyan et al., 1998). We use the same parameters as in Ding et al. (2003) to model the protein backbone. We list the parameters related to the side-chain beads in Table S1 of the Supplementary Material. We model the nonbonded interactions by assigning stepwise potentials between pairs of beads. Each bead is modeled as an interacting soft ball with a hardcore radius HC and its interaction range IR, which are also listed in Table S1 (see Supplementary Material). Due to introduction of the γ-and δ-beads in the model, we are able to model the side-chain dihedral angles. For proline, we also model the unusual properties of the backbone and side-chain dihedral angels by mimicking the covalent bond between the side chain and the backbone. For details of the parameters (Table S2) and modeling of the backbone and side-chain dihedral angles, please refer to the Supplementary Material.

Nonbonded interactions

We model amino acid interactions by assigning square-well potentials between pairs of the nonbonded beads (the pairs that have no covalent linkages or no constraints). We include in our model the hydrophobic interaction HHP, salt-bridge interaction HSB, aromatic interaction between aromatic amino acids HAR, aromatic-proline interaction between proline and aromatic residues HAR-PRO, hydrogen bond interaction among backbones 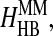Inline graphic hydrogen bond interactions between side chains and backbones 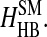Inline graphic Thus the total Hamiltonian of the model, H, consists of six contributions:

graphic file with name M3.gif (1)

Here, hydrophobic, salt-bridge, and aromatic interaction are solely between β-, γ-, and δ-beads of different side chains. To assign various types of interactions for all pairs of beads, we categorize all the side-chain beads into following six types: hydrophobic (H), amphipathic (A), aromatic (AR), neutral polar (P), positively charged (PC), and negatively charged (NC). One bead can belong to more than one category, for example, the γ-bead of phenylalanine is both hydrophobic and aromatic (listed in Table S3 of Supplementary Material).

Only pairwise interactions between side-chain beads are considered in this model and the potential functions are stepwise:

graphic file with name M4.gif (2)

where, i and j indicate different side-chain beads, the HC is the hardcore radius of each bead and the IR is the radius of interaction range for each bead (Table S1). The parameter IRext is introduced to allow a small attraction before the two beads comes to their interaction ranges. In our study, we set IRext as 0.75 Å.

Side-chain–side-chain interactions

Hydrophobic interactions are assigned between two hydrophobic beads or between one hydrophobic and another amphipathic bead if both beads are not aromatic and/or proline. The interaction strengths are assigned ɛHH and ɛHA, respectively. The aromatic interactions are assigned between two aromatic beads—namely Cγ of Phe and Tyr and Cδ of Trp—with the strength ɛAR. The aromatic-proline interaction is assigned between the γ-bead of proline and the aromatic bead. The interaction strength is ɛAR-PRO. The salt-bridge interactions are assigned between the positively charged and the negatively charged beads and the salt-bridge strength is ɛSB. Two beads of the same charge experience the hardcore repulsion.

Hydrogen bond interactions

Hydrogen bond interactions are introduced among the backbones and between the backbone and polar side-chain beads using an algorithm similar to Ding et al. (2003). The hydrogen bond interaction is between the backbone hydrogen bond donor (HBD), nitrogen Ni, and hydrogen bond acceptor (HBA), carbonyl oxygen Oj. To mimic the angular dependence of the backbone hydrogen bond, we introduce three auxiliary constraints: Ni–Cj, Cαi–Oj, and Ci-1–Oj, which are presented in Fig. 1 B as the thin dashed lines. To assess the interaction ranges for a hydrogen bond, we calculate the above four distances for actual hydrogen bonds by sampling over all native structures from the Protein Data Bank (PDB; Berman et al., 2000). We define a hydrogen bond in the native structures from PDB by the following criteria: a), the distance of oxygen and hydrogen is <2.5 Å; and b), the angles NiHiOj and CiOiHj are >90°. The histograms of the four distances are presented in Fig. 1 C. The distributions of all the distances are Gaussian. 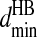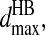We define the minimum and maximum interaction distances, Inline graphic and Inline graphic for each of the related pairs according to their average values and variances (listed in Table S4 of Supplementary Material). 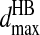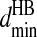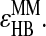When any one of the four pairs, Ni–Oj, Ni–Cj, Cαi–Oj, or Ci-1–Oj, comes to their corresponding Inline graphic distance, we verify that the distances of the other three pairs are within their ranges, Inline graphic and Inline graphic If so, a hydrogen bond is formed and the potential energy is decreased of Inline graphic The corresponding oxygen and nitrogen change their types into their hydrogen bonded types, 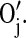Inline graphic and Inline graphic Once changed in their types, they cannot form any other hydrogen bond unless the existing hydrogen bond breaks. The mechanism for the dissociation of the hydrogen bond is similar. Once any one of the four pairs comes to the distance of 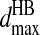Inline graphic and the kinetic energy is enough to overcome the loss of the potential energy 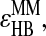Inline graphic the hydrogen bond breaks and the nitrogen and oxygen return to their original types, Ni and Oj.

It has also been pointed out (Aurora and Rose, 1998; Presta and Rose, 1988; Stickle et al., 1992) that the hydrogen bonds between the polar side chain and backbones are important for the starting and ending of α-helices and also for the formation of turns in proteins. We introduce this type of hydrogen bond interaction into our model for those polar residues, namely Thr, Ser, Asn, Asp, Gln, and Glu, which are observed to frequently form this type of hydrogen bond in the PDB structures. There are two types of possible hydrogen bonding interactions between side chain and backbones:

  1. Side-chain beads as hydrogen bond donor. We allow the polar side-chain γ-beads of Asn, Asp, Gln, Glu, Ser, and Thr to form hydrogen bonds with the backbone nitrogen. To mimic the angular dependence of hydrogen bond, we introduce additional constraints between the γ-bead and the two neighboring beads of the corresponding nitrogen beads—C′ and Cα—along the backbone. Because the γ-beads are coarse grained, we do not introduce any constraints between the backbone nitrogen beads and the neighboring beads of the effective γ-beads.

  2. Side-chain beads as hydrogen bond acceptor. We also allow the polar side-chain γ-beads of Ser, Thr, Asn, and Gln to form hydrogen bonds with the backbone carbonyl oxygen. The auxiliary constraints are between the neighboring prime carbon and the side-chain γ-beads. Side-chain γ-beads of Asn, Gln, Ser, and Thr can be either HBD or HBA. For simplicity, we only allow one type of hydrogen bond to be formed at one time. The parameters for the side-chain and backbone interactions are assigned by analyzing the corresponding hydrogen bonds in the PDB structures and are listed in Table S4 (see Supplementary Material).

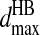Once a side-chain γ-bead encounters a free backbone nitrogen or oxygen at the hydrogen bonding range Inline graphic we check the distances of the corresponding auxiliary constraints between the γ-beads and the neighboring beads of nitrogen or oxygen: Cα and C′ beads near the N or C′ bead near oxygen. If all the constraints are satisfied, the potential energy is decreased by Inline graphic and a temporary bond is assigned for the auxiliary pairs so that the orientation is maintained during the lifetime of the hydrogen bond. Both the backbone nitrogen/oxygen and the γ-bead change their types upon the formation of the hydrogen bond. Once the hydrogen-bonded γ-bead and its corresponding backbone hydrogen partner, N or O, come to the distance Inline graphic again, the dissociation might happen. If the kinetic energy is enough to overcome the gain of potential energy, the hydrogen bond breaks. Upon the dissociation of the hydrogen bonds, the involved beads change their types back to their original types.

Importantly, we treat these two types of hydrogen bonds, among backbones and between side chains and backbones, differently. A hydrogen bond between two backbone beads may form or dissociate if the oxygen-nitrogen distance or any other distance of the three auxiliary pairs (Ni–Cj, Cαi–Oj, or Ci-1–Oj) becomes equal to its maximal value Inline graphic In contrast, a hydrogen bond between a side-chain bead and a backbone bead may form or dissociate only if the donor-acceptor distance becomes equal to Inline graphic In this type of hydrogen bond, the auxiliary bonds act as temporary bonds with infinitely high potential wells and can form or break only simultaneously with the donor-acceptor bond.

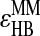In summary, our model has seven interaction parameters: ɛHH, ɛHA, ɛAR, ɛAR-PRO, ɛSB, Inline graphic and ɛχ, where ɛχ is the interaction strength used to model the dihedral angles (see Supplementary Material). To fold Trp-cage, we have assigned the initial values to the parameters according to Srinivasan and Rose (1999) and adjust these values using feedback from our folding simulations. In this study, we set the parameters of the bonded and nonbonded interaction strengths ɛχ = 1.5ɛ, ɛHH = 1.05ɛ, ɛHA = 0.60ɛ, ɛAR = 1.80ɛ, ɛAR-PRO = 1.50ɛ, ɛSB = 2.70ɛ, Inline graphic = 5ɛ, and Inline graphic = 2.50ɛ, where the energy unit, ɛ, is of the order of 1 kcal mol−1. Starting from fully extended polymers, we perform molecular dynamics simulations at various temperatures. The temperature unit is related to the energy unit, ɛ/kB. The temperature is controlled by a Berendsen thermostat (Berendsen et al., 1984) with the heat exchange rate equal to 0.1 per time unit. The time unit is the derivative of the units of length, mass, and energy, which are defined as Å, mass of carbon atom mC, and ɛ, respectively.

RESULTS AND DISCUSSION

To study the folding process of Trp-cage, we perform equilibrium molecular dynamics simulations of a coarse-grained model of the miniprotein at various temperatures (see Methods) starting from an extended conformation. Throughout this study, the temperature is measured in units of energy ɛ, divided by Boltzmann constant, ɛ/kB (see Methods). The calculation of RMSD is based on the positions of the backbone Cα atoms and the native state is chosen as the first NMR model of Trp-cage (PDB code: 1L2Y). At very high temperatures, i.e., T = 1.00, the protein is completely unfolded and remains in the random coil state with the average radius of gyration (Rg) of ∼12 Å. As we decrease the temperature below T = 0.80, the protein collapses to a compact conformation similar to the coil-globular transition (Grosberg and Khokhlov, 1994), which is a noncooperative process and is manifested as the shoulder in the specific heat plot in Fig. 2 A.

FIGURE 2.

FIGURE 2

Open in a new tab

The folding thermodynamics of Trp-cage. (A) The specific heat Cv as the function of temperature. The potential energy (P.E.), radius of gyration (Rg), and the Cα RMSD are plotted as the functions of simulation time for different temperatures: (B) T = 0.72, (C) T = 0.63, and (E) T = 0.57. To show the initial collapsing and folding, we present in panel F the folding trajectories of the initial 104 time units at T = 0.63. (F) The distributions of the RMSD at different temperatures. (G) The histogram of RMSD for the randomly generated globule structures of a 20-residue homopolymer. A Gaussian fit suggests that the average RMSD is ∼6 Å and the mean ± SD is 0.8 Å. (F) The distribution of RMSD with the key interactions weakened or excluded.

Within the temperature range 0.70 < T < 0.80 the protein remains mostly in the globular state and remains unfolded during most of the simulation time. In Fig. 2 B, we present a typical simulation trajectory at temperature T = 0.72. The average radii of gyration (Rg) of the native, random coil, and fully extended states of Trp-cage are ∼7 Å, 12 Å, and 19 Å, respectively. The average Rg of the unfolded state at T = 0.72 is ∼9.5 Å. Thus, the unfolded state in the simulation is significantly collapsed and the extent of reduction of Rg upon folding from these collapsed states is only ≈30%. We also observe that the RMSD of this unfolded state from the native state is on average 4.3 Å. Rapid fluctuations in the RMSD suggest that the model protein is mostly present in the unfolded state without populating any specific stable state. According to the studies of Reva et al. (1998), the RMSD distribution for a 20-residue protein with randomly selected/constructed globular protein-like structures is Gaussian with an average of 9 Å and a mean ± SD of 2 Å. Because the empirical RMSD distributions of proteins with different lengths (Reva et al., 1998) is derived from studies of proteins >60 residues, it is possible that this distribution for short proteins such as Trp-Cage may not hold. To test the significance of our and other's folding simulations of Trp-cage, we study the RMSD distribution of globular states of a 20-residue homopolymer, having nonspecific attractions between all side chains, computed with respect to the native state of Trp-cage. We perform 1200 independent DMD simulations to quench the homopolymer into the condensed globule state and present the histogram of RMSD in Fig. 2 G. The distribution is Gaussian with an average value of 6 Å and a mean ± SD of 0.8 Å, which is different from Reva et al. (1998). Therefore, the probability to find a globular structure with RMSD < 4 Å is 10−4, according to either Reva et al. (1998) or the above quenching studies. Thus, the model protein remains in a highly collapsed state with a nontrivial similarity to the native state, a so-called “molten-globular” state (Ptitsyn and Uversky, 1995) within the temperature range of 0.70 < T < 0.80.

Another important observation during our high-temperature simulations is that fluctuations can approach the folded state with RMSD as low as 2 Å (Fig. 2 B), indicating the availability of the native state even at these relatively high temperatures. However, the native state is not stable at these temperatures and the protein rapidly unfolds to a denatured molten-globular state, because the potential energy gain upon folding due to thermal fluctuation is not sufficient to overcome the loss in the entropic contribution to the free energy that is proportional to the temperature. By decreasing the temperature, we expect to observe more folded species, defined as the structures with RMSD < 2 Å.

At the temperature T = 0.63, we observe the model protein in the folded state with a significantly high probability (Fig. 2 C). Once the protein reaches the folded state, it remains in the folded state for a long simulation time—longer than 104 time units—and then unfolds. Approximately equal probability of the folded and the unfolded (molten-globular) states (Fig. 2 F) and multiple folding/unfolding transitions along the simulation trajectory (Fig. 2 C) indicates the proximity of this simulation temperature to the folding transition temperature of Trp-cage. To demonstrate the initial folding from the initial stretched-chain conformation, we present in Fig. 2 D the trajectory of the initial 104 time units. The initial collapse from the stretched chain is very rapid and occurs within 1000 time units as the value of Rg approaches 10 Å while the RMSD is still 4 Å. After ∼104 time units, this molten-globular state rearranges itself and reaches the folded state with RMSD < 2 Å. In Fig. 2 E, we present a trajectory for the simulation at low temperature T = 0.57. At this temperature, the probability of observing the folded state is much larger than that of observing an unfolded state. At low temperatures (T < TF), the folding dynamics become slow and the protein model free-energy landscape develops kinetic traps upon folding (the first 105 time units trajectories in Fig. 2 E). Once the protein folds, it is stable in the folded state with some infrequent and short-lived unfolding fluctuations. In approximately one out of 10 simulations at low temperatures, we observe the kinetic trapping that may extend to nearly 5 × 105 time units (data not shown). However, the potential energy of the traps is always larger than that for the folded state as in Fig. 2 E.

In Fig. 2 D, we present the distribution of RMSD for various temperatures. As temperature decreases, the population of folded states increases, so the folding transition temperature can be identified to be approximately TF = 0.63. At this temperature, the distribution is bimodal with two peaks of equal area with maxima at 1.7 Å and 3.5 Å corresponding to folded and unfolded states, respectively.

To test the importance of the key interactions—aromatic-proline and hydrogen bond interactions—we study the effect of excluding or weakening these key interactions on folding. Starting for the near-native state, we perform DMD simulations at a low temperature T = 0.60 < TF with these key interactions weakened or excluded. As presented in Fig. 2 H, we observe that the exclusion and weakening of these key interactions leads to nonnative conformations with RMSD > 3.5 Å, whereas the simulations with these interactions intact lead to folded conformations with RMSD < 2 Å. It is also interesting to notice that the interaction strength of the hydrogen bonds is the strongest among all interaction strengths, which is due to the short-range and angular-dependent nature of our hydrogen bond model. The formation of a hydrogen bond accompanies a large loss of entropy that requires large potential energy change to balance it.

As shown in Fig. 2, our simplified model can reproducibly reach the folded state with an average RMSD of <2 Å and can reach structures with RMSD as small as 1.0 Å in a wide range of temperatures. To characterize the structure of the folded state obtained in DMD simulations, we show in Fig. 3, A and B, a typical DMD configuration with RMSD of 0.96 Å from two opposite view points. In these figures, we show coarse-grained representation of the side chains for different residues (see Methods and Supplementary Material). In agreement with NMR structures, the hallmark residue of Trp-cage, Trp-6, is closely packed with residues Tyr-3, Pro-12, Pro-18, Pro-19, forming the core. We also observe the formation of the salt bridge between the Asp-9 and Arg-16. The two helices, α-helix of residues 1–8 and the 310 helix around Ser-13, coincide with those in the NMR structures. Keeping in mind that our model includes only a set of key interactions and has coarse-grained side-chain representations with simplified stepwise interaction potential functions (see Methods and Supplementary Material), the proximity of the DMD folded state to the experimental native state is not guaranteed a priori.

FIGURE 3.

FIGURE 3

Open in a new tab

The snapshot of one of folded ensemble from DMD simulation is shown in two opposite views (A and B). The simulation structure is aligned with respect to the NMR structure, which is shown in cartoon representation. The native structure is colored purple and the MD structure is in cyan. In the structure from MD simulations, residues Trp-6, Tyr-3, and Pro-12, 17, 18, and 19 are shown in solid representation and are colored as golden. We also show the salt bridge formed between Asp-9 and Arg-16, which are drawn as meshed spheres. Because our model is coarse grained, only the reduced side-chain beads are shown. The scatter plot of RMSD versus the potential energy for various temperatures: (C) T = 0.72; (D) T = 0.63; and (E) T = 0.57.

One important question in assessing a protein model with a set of amino acid interaction parameters is whether the potential energy of the native state corresponds to the ground state, i.e., the lowest energy state of all available structures. To address this question for our model with the given simple interaction parameters, we present in Fig. 3, C–E, the contour plots of the number of states observed in a simulation trajectory with a given potential energy and RMSD at different temperatures. In general, we observe a significant correlation between the potential energy and RMSD for different temperatures. However, even below the folding transition temperature, we observe some outliers: structures with small RMSD but large potential energies, and structures with large RMSD (≈4.0 Å) whose potential energy is close to that of the folded states. Nevertheless, the probability to observe these outliers is very low, of the order of 10−5 (Fig. 3, C–E). Therefore, the entropy of those states is small and thus the corresponding free energy is higher than that of the folded states with low RMSD and low potential energy. A similar problem of the existence of the outliers has also been observed in the all-atom molecular mechanics studies (Simmerling et al., 2002; Yang et al., 2004; Zhou, 2003).

The simplified model combined with a fast dynamics algorithm gives us the opportunity to study the folding process for many successful folding events starting from the extended chain. We find that the time needed for folding and also the detailed pathways of folding are extremely heterogeneous for different trajectories at different temperatures. However, an initial collapse is common to all of these folding processes. For the Trp-cage, the initial collapse is mainly due to the aromatic and aromatic-proline interactions. These collapsed structures are nonspecific, i.e., have no persistent secondary structures. We present in Fig. 4, A and B, two different collapsed structures where the aromatic and/or aromatic-proline contacts are present. Although the salt-bridge interaction is assigned to be the strongest term in the side-chain interactions (see Methods and Supplementary Material), the salt bridge between Asp-9 and Arg-16 is not necessarily present in the collapsed states. To better understand the ensemble properties of the collapsed states, we calculate the frequency map (Fig. 4 E) from the trajectories at T = 0.72. At this temperature the protein is mainly present in the molten-globular states that are flexible and can unfold into completely extended states (see Fig. 2, B and E). A contact between two residues is defined to exist when any of the interacting side-chain beads are within their interaction ranges (see Methods and Supplementary Material). In the frequency map of the collapsed state of Fig. 4 E, the formation of the short-range hydrophobic contacts near the N-terminus have high probability. The probability to observe the salt bridge between Asp-9 and Arg-16 is only ≈0.2. The long-range contacts between the poly-proline 17–19 and the Trp-6 and Tyr-3 also have low probability due to the nonspecific nature of the collapse state (the contacts within the elliptical circles in Fig. 4 E).

FIGURE 4.

FIGURE 4

Open in a new tab

(A and B) Two different collapsed “molten-globular” states. (C) A snapshot along the folding pathway is similar to the intermediate observed in Zhou (2003). (D) The structure of the model protein that is committed to fold with all the helical secondary structures formed. (E) The contact frequency map of the molten-globular state measured at T = 0.72. We only plot the contacts with frequency >0.05. The long-range aromatic-proline contacts are encircled by ellipses. (F) The probability of formation various secondary structure elements during simulation at T = 0.72.

To fold from the collapsed molten globular states into its native state, the protein has to develop the native secondary structure. It is interesting to quantify the propensity of different secondary structures in these collapsed states. Following the method proposed by Rose et al. (Srinivasan and Rose, 2002), we calculate the propensity of different secondary structures at T = 0.72 where the protein remains mostly in the molten-globular state (Fig. 4 F). Because the calculation of secondary structure propensity in Srinivasan and Rose (2002) is based only on the backbone dihedral angles, the propensity of strand formation actually measures the propensity to be in extended conformations. The dominant secondary structure is random coil-like except that the poly-proline 17–19 is extended. Interestingly, the probability to observe helices for residues 2–9 is significant, ≈10%, indicating a strong helical propensity for first-half residues of the Trp-cage even in the molten-globular state.

It is of great interest to study the folding mechanism from many successful folding transitions observed in our simulations. However, our simulations are done in vacuum, in absence of water. The lack of diffusive friction due to the absence of surrounding water might lead to artifacts in folding dynamics in the event sequences and timescales of formation of different secondary and tertiary structures. We believe that although the population of different folding pathways might be different with and without the explicit solvent, the analysis of multiple folding transitions in the absence of solvent might provide us the information about the possible pathways.

According to our simulations, the protein in the collapsed molten-globular state must form all the secondary structures including the α-helix, 310-helix, as well as the salt bridge, which are present in the native fold. This rearrangement process is highly heterogeneous. Typically the formation of the first α-helix is faster than the formation of 310-helix. The preformed salt bridge behaves as a trap for the formation of the 310-helix and needs to break in order for the short helix to form. We also observe in some folding processes a folding pathway similar to what is described in Zhou (2003): the preformed salt bridge between Asp-9 and Arg-16 separates two prepacked subcores of Try-3, Trp-6, Pro-12, and the poly-proline 17–19 (Fig. 4 C); the preformed salt bridge must break in order for the global folding to occur (Fig. 4 D).

CONCLUSION

We reproduce folding of the 20-residue-long Trp-cage using a simplified protein model. Introducing only key interactions to stabilize the Trp-cage, namely the aromatic-proline, salt bridge, and the hydrogen bond interaction, our coarse-grained model of the miniprotein is able to fold into the native state with an average RMSD of <2 Å, whereas some conformations reach the NMR structure with RMSD < 1.00 Å. The exclusion and weakening of these interactions in simulations lead to nonnative conformations. Several all-atom molecular dynamics studies for the Trp-cage were reported to fold into structures with similar backbone RMSD (Chowdhury et al., 2003; Pitera and Swope, 2003; Snow et al., 2002; Zagrovic and Pande, 2003; Zhou, 2003). In our DMD model, the protein is simplified into a string of interconnected beads that interact with each other via square-well interaction potentials. Therefore, our success to fold Trp-cage into its NMR native state suggests that an all-atom protein model and a sophisticated force field is not necessary to fold a protein into its native state, at least in the case of Trp-cage.

In addition, we find that once the key stabilizing interactions—the aromatic-proline, salt-bridge, and the hydrogen bond interaction—are emphasized, the resulting folding is not very sensitive to assigned interaction strengths (data not shown). This persistent ability of our Trp-cage model to fold under the emphasis of the important interactions is due to the special sequence and structural properties specific to Trp-cage. For instance, the inclusion of a large number of prolines reduces the available conformation space, as well as increases the number of aromatic-proline contacts. The aromatic-proline interaction is commonly observed to stabilize the protein-protein and protein-ligand interactions (Gellman and Woolfson, 2002). This might also be one of the reasons for the success of different all-atom molecular mechanics studies of Trp-cage using different force fields (Chowdhury et al., 2003; Pitera and Swope, 2003; Snow et al., 2002; Zagrovic and Pande, 2003; Zhou, 2003). Therefore, we conclude that it might be too early to draw any conclusions about the “correctness” of the current molecular mechanics force fields from the recent success in the all-atom molecular dynamics folding studies of Trp-cage and that additional tests on a large set of proteins are necessary.

An important advantage of the coarse-grained model with simplified interaction potential is the ability to reach an effective timescale of the simulation trajectories several orders of magnitude longer than the traditional all-atom molecular dynamics. We show in this study that our model of the miniprotein is able to undergo multiple folding and unfolding transitions in a single simulation trajectory that is yet to be observed in all-atom molecular mechanics simulations.

In our simulations, we observe a significant correlation between the potential energy and RMSD, i.e., small RMSD states usually correspond to low potential energy states. However, we still observe some outliers or decoy states that have low potential energy but high RMSD. It is possible to train the parameters of the model, which, in our simplified case, include only seven interaction variables, to better satisfy the ground-state criteria by trying various potential training methods such as minimizing the Z-score (Abkevich et al., 1996) or perceptron learning (Vendruscolo et al., 2000; Vendruscolo and Domany, 1998). More detailed potential energy functions of side-chain interactions may also improve the proximity of the folded state of the model to the experimental native state. However, these methods applied to a single protein do not guarantee the transferability to other proteins (Khatun et al., 2004). To improve the predictive power of this model, one must design transferable potential energy functions using multiple proteins.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.

[Supplemental File]
biophysj_104.046375_index.html (736B, html)

Acknowledgments

We thank Charles W. Carter, Jr., Sagar Khare, Brian Kulhman, and Kyle Wilcox for helpful discussions.

This work is supported in part by the University of North Carolina Junior Faculty Development IBM Fund Award, Muscular Dystrophy Association (grant MDA3720), and the March of Dimes Birth Defect Foundation (research grant No. 5-FY03-155 to N.V.D.). S.V.B. acknowledges support from the National Science Foundation.

References

  1. Abkevich, V. I., A. M. Gutin, and E. I. Shakhnovich. 1994. Specific nucleus as the transition-state for protein-folding: evidence from the lattice model. Biochemistry. 33:10026–10036. [DOI] [PubMed] [Google Scholar]
  2. Abkevich, V. I., A. M. Gutin, and E. I. Shakhnovich. 1996. Improved design of stable and fast-folding model proteins. Fold. Des. 1:221–230. [DOI] [PubMed] [Google Scholar]
  3. Alder, B. J., and T. E. Wainwright. 1959. Studies in molecular dynamics. I. General method. J. Chem. Phys. 31:459–466. [Google Scholar]
  4. Anfinsen, C. B. 1973. Principles that govern the folding of protein chains. Science. 181:223–230. [DOI] [PubMed] [Google Scholar]
  5. Aurora, R., and G. D. Rose. 1998. Helix capping. Protein Sci. 7:21–38. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Barua, B., and N. H. Andersen. 2001. Determinants of miniprotein stability: can anything replace a buried H-bonded Trp sidechain? Letters in Peptide Science. 8:221–226. [Google Scholar]
  7. Berendsen, H. J. C., J. P. M. Postma, W. F. Vangunsteren, A. DiNola, and J. R. Haak. 1984. Molecular-dynamics with coupling to an external bath. J. Chem. Phys. 81:3684–3690. [Google Scholar]
  8. Berman, H. M., J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov, and P. E. Bourne. 2000. The protein data bank. Nucleic Acids Res. 28:235–242. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Blundell, T. L., J. E. Pitts, I. J. Tickle, S. P. Wood, and C. W. Wu. 1981. X-ray analysis (1.4-A resolution) of avian pancreatic-polypeptide: small globular protein hormone. Proc. Natl. Acad. Sci. USA. 78:4175–4179. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Bryngelson, J. D., and P. G. Wolynes. 1987. Spin-glasses and the statistical-mechanics of protein folding. Proc. Natl. Acad. Sci. USA. 84:7524–7528. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Bryngelson, J. D., and P. G. Wolynes. 1989. Intermediates and barrier crossing in a random energy-model (with applications to protein folding). J. Phys. Chem. 93:6902–6915. [Google Scholar]
  12. Chowdhury, S., M. C. Lee, G. M. Xiong, and Y. Duan. 2003. Ab initio folding simulation of the Trp-cage mini-protein approaches NMR resolution. J. Mol. Biol. 327:711–717. [DOI] [PubMed] [Google Scholar]
  13. Cochran, A. G., N. J. Skelton, and M. A. Starovasnik. 2001. Tryptophan zippers: stable, monomeric beta-hairpins. Proc. Natl. Acad. Sci. USA. 98:5578–5583. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Creamer, T. P., and G. D. Rose. 1992. Side-chain entropy opposes alpha-helix formation but rationalizes experimentally determined helix-forming propensities. Proc. Natl. Acad. Sci. USA. 89:5937–5941. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Dahiyat, B. I., and S. L. Mayo. 1997. De novo protein design: fully automated sequence selection. Science. 278:82–87. [DOI] [PubMed] [Google Scholar]
  16. de la Paz, M. L., E. Lacroix, M. Ramirez-Alvarado, and L. Serrano. 2001. Computer-aided design of beta-sheet peptides. J. Mol. Biol. 312:229–246. [DOI] [PubMed] [Google Scholar]
  17. Dill, K. A. 1985. Theory for the folding and stability of globular-proteins. Biochemistry. 24:1501–1509. [DOI] [PubMed] [Google Scholar]
  18. Dill, K. A. 1990. Dominant forces in protein folding. Biochemistry. 29:7133–7155. [DOI] [PubMed] [Google Scholar]
  19. Ding, F., J. M. Borreguero, S. V. Buldyrev, H. E. Stanley, and N. V. Dokholyan. 2003. A mechanism for the alpha-helix to beta-hairpin transition. Proteins. In press. [DOI] [PubMed]
  20. Ding, F., N. V. Dokholyan, S. V. Buldyrev, H. E. Stanley, and E. I. Shakhnovich. 2002a. Direct molecular dynamics observation of protein folding transition state ensemble. Biophys. J. 83:3525–3532. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Ding, F., N. V. Dokholyan, S. V. Buldyrev, H. E. Stanley, and E. I. Shakhnovich. 2002b. Molecular dynamic simulation of the SH3 domain aggregation suggests a generic amyloidogenesis mechanism. J. Mol. Biol. 324:851–857. [DOI] [PubMed] [Google Scholar]
  22. Dokholyan, N. V., J. M. Borreguero, S. V. Buldyrev, F. Ding, H. E. Stanley, and E. I. Shakhnovich. 2003. Identifying the importance of amino acids for protein folding from crystal structures. In Macromolecular Crystallography. C. W. Carter, Jr. and R. M. Sweet, editors. 618–640. [DOI] [PubMed]
  23. Dokholyan, N. V., S. V. Buldyrev, H. E. Stanley, and E. I. Shakhnovich. 1998. Discrete molecular dynamics studies of the folding of a protein-like model. Fold. Des. 3:577–587. [DOI] [PubMed] [Google Scholar]
  24. Dokholyan, N. V., S. V. Buldyrev, H. E. Stanley, and E. I. Shakhnovich. 2000. Identifying the protein folding nucleus using molecular dynamics. J. Mol. Biol. 296:1183–1188. [DOI] [PubMed] [Google Scholar]
  25. Fersht, A. R., and E. I. Shakhnovich. 1998. Protein folding: think globally, (inter)act locally. Curr. Biol. 8:R478–R479. [DOI] [PubMed] [Google Scholar]
  26. Gellman, S. H., and D. N. Woolfson. 2002. Mini-proteins Trp the light fantastic. Nat. Struct. Biol. 9:408–410. [DOI] [PubMed] [Google Scholar]
  27. Go, N., and H. Abe. 1981. Noninteracting local-structure model of folding and unfolding transition in globular proteins. I. Formulation. Biopolymers. 20:991–1011. [DOI] [PubMed] [Google Scholar]
  28. Grosberg, A. Y., and A. R. Khokhlov. 1994. Statistical Physics of Macromolecules. American Institute of Physics, New York.
  29. Irback, A., and F. Potthast. 1995. Studies of an off-lattice model for protein-folding: sequence dependence and improved sampling at finite-temperature. J. Chem. Phys. 103:10298–10305. [Google Scholar]
  30. Khatun, J., S. D. Khare, and N. V. Dokholyan. 2004. Can contact potentials reliably predict stability of proteins? J. Mol. Biol. 336:1223–1238. [DOI] [PubMed] [Google Scholar]
  31. Klimov, D. K., and D. Thirumalai. 1998. Cooperativity in protein folding: from lattice models with sidechains to real proteins. Fold. Des. 3:127–139. [DOI] [PubMed] [Google Scholar]
  32. Kortemme, T., M. Ramirez-Alvarado, and L. Serrano. 1998. Design of a 20-amino acid, three-stranded beta-sheet protein. Science. 281:253–256. [DOI] [PubMed] [Google Scholar]
  33. Levitt, M., M. Gerstein, E. Huang, S. Subbiah, and J. Tsai. 1997. Protein folding: the endgame. Annu. Rev. Biochem. 66:549–579. [DOI] [PubMed] [Google Scholar]
  34. McKnight, C. J., P. T. Matsudaira, and P. S. Kim. 1997. NMR structure of the 35-residue villin headpiece subdomain. Nat. Struct. Biol. 4:180–184. [DOI] [PubMed] [Google Scholar]
  35. Micheletti, C., F. Seno, A. Maritan, and J. R. Banavar. 1998. Protein design in a lattice model of hydrophobic and polar amino acids. Phys. Rev. Lett. 80:2237–2240. [PubMed] [Google Scholar]
  36. Neidigh, J. W., R. M. Fesinmeyer, and N. H. Andersen. 2002. Designing a 20-residue protein. Nat. Struct. Biol. 9:425–430. [DOI] [PubMed] [Google Scholar]
  37. Neidigh, J. W., R. M. Fesinmeyer, K. S. Prickett, and N. H. Andersen. 2001. Exendin-4 and glucagon-like-peptide-1: NMR structural comparisons in the solution and micelle-associated states. Biochemistry. 40:13188–13200. [DOI] [PubMed] [Google Scholar]
  38. Nymeyer, H., A. E. Garcia, and J. N. Onuchic. 1998. Folding funnels and frustration in off-lattice minimalist protein landscapes. Proc. Natl. Acad. Sci. USA. 95:5921–5928. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Onuchic, J. N., Z. Luthey-Schulten, and P. G. Wolynes. 1997. Theory of protein folding: the energy landscape perspective. Annu. Rev. Phys. Chem. 48:545–600. [DOI] [PubMed] [Google Scholar]
  40. Ottesen, J. J., and B. Imperiali. 2001. Design of a discretely folded mini-protein motif with predominantly beta-structure. Nat. Struct. Biol. 8:535–539. [DOI] [PubMed] [Google Scholar]
  41. Pande, V. S., A. Y. Grosberg, and T. Tanaka. 1997. Statistical mechanics of simple models of protein folding and design. Biophys. J. 73:3192–3210. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Pande, V. S., A. Y. Grosberg, and T. Tanaka. 2000. Heteropolymer freezing and design: towards physical models of protein folding. Reviews of Modern Physics. 72:259–314. [Google Scholar]
  43. Pitera, J. W., and W. Swope. 2003. Understanding folding and design: replica-exchange simulations of “Trp-cage” fly miniproteins. Proc. Natl. Acad. Sci. USA. 100:7587–7592. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Plaxco, K. W., D. S. Riddle, V. Grantcharova, and D. Baker. 1998. Simplified proteins: minimalist solutions to the ‘protein folding problem’. Curr. Opin. Struct. Biol. 8:80–85. [DOI] [PubMed] [Google Scholar]
  45. Presta, L. G., and G. D. Rose. 1988. Helix signals in proteins. Science. 240:1632–1641. [DOI] [PubMed] [Google Scholar]
  46. Ptitsyn, O. B., and V. N. Uversky. 1995. Pre-molten globule: a new equilibrium state of protein molecules. FASEB J. 9:A1469. (Abstr.) [Google Scholar]
  47. Qiu, L. L., S. A. Pabit, A. E. Roitberg, and S. J. Hagen. 2002. Smaller and faster: the 20-residue Trp-cage protein folds in 4 micros. J. Am. Chem. Soc. 124:12952–12953. [DOI] [PubMed] [Google Scholar]
  48. Rapaport, D. C. 1997. The Art of Molecular Dynamics Simulations. Cambridge University Press, Cambridge, UK.
  49. Reva, B. A., A. V. Finkelstein, and J. Skolnick. 1998. What is the probability of a chance prediction of a protein structure with an RMSD of 6 angstrom? Fold. Des. 3:141–147. [DOI] [PubMed] [Google Scholar]
  50. Shakhnovich, E. I. 1994. Proteins with selected sequences fold into unique native conformation. Phys. Rev. Lett. 72:3907–3910. [DOI] [PubMed] [Google Scholar]
  51. Shakhnovich, E. I. 1996. Modeling protein folding: the beauty and power of simplicity. Fold. Des. 1:R50–R54. [DOI] [PubMed] [Google Scholar]
  52. Shakhnovich, E. I. 1997. Theoretical studies of protein-folding thermodynamics and kinetics. Curr. Opin. Struct. Biol. 7:29–40. [DOI] [PubMed] [Google Scholar]
  53. Simmerling, C., B. Strockbine, and A. E. Roitberg. 2002. All-atom structure prediction and folding simulations of a stable protein. J. Am. Chem. Soc. 124:11258–11259. [DOI] [PubMed] [Google Scholar]
  54. Smith, A. V., and C. K. Hall. 2000. Bridging the gap between homopolymer and protein models: a discontinuous molecular dynamics study. J. Chem. Phys. 113:9331–9342. [Google Scholar]
  55. Smith, A. V., and C. K. Hall. 2001a. Alpha-helix formation: discontinuous molecular dynamics on an intermediate-resolution protein model. Proteins. 44:344–360. [DOI] [PubMed] [Google Scholar]
  56. Smith, A. V., and C. K. Hall. 2001b. Assembly of a tetrameric alpha-helical bundle: computer simulations on an intermediate-resolution protein model. Proteins. 44:376–391. [DOI] [PubMed] [Google Scholar]
  57. Smith, A. V., and C. K. Hall. 2001c. Protein refolding versus aggregation: computer simulations on an intermediate-resolution protein model. J. Mol. Biol. 312:187–202. [DOI] [PubMed] [Google Scholar]
  58. Snow, C. D., B. Zagrovic, and V. S. Pande. 2002. The Trp cage: folding kinetics and unfolded state topology via molecular dynamics simulations. J. Am. Chem. Soc. 124:14548–14549. [DOI] [PubMed] [Google Scholar]
  59. Srinivasan, R., and G. D. Rose. 1999. A physical basis for protein secondary structure. Proc. Natl. Acad. Sci. USA. 96:14258–14263. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Srinivasan, R., and G. D. Rose. 2002. Ab initio prediction of protein structure using LINUS. Proteins. 47:489–495. [DOI] [PubMed] [Google Scholar]
  61. Stickle, D. F., L. G. Presta, K. A. Dill, and G. D. Rose. 1992. Hydrogen-bonding in globular-proteins. J. Mol. Biol. 226:1143–1159. [DOI] [PubMed] [Google Scholar]
  62. Taketomi, H., Y. Ueda, and N. Go. 1975. Studies on protein folding, unfolding and fluctuations by computer simulations. Int. J. Pept. Protein Res. 7:445–459. [PubMed] [Google Scholar]
  63. Vendruscolo, M., and E. Domany. 1998. Pairwise contact potentials are unsuitable for protein folding. J. Chem. Phys. 109:11101–11108. [Google Scholar]
  64. Vendruscolo, M., L. A. Mirny, E. I. Shakhnovich, and E. Domany. 2000. Comparison of two optimization methods to derive energy parameters for protein folding: perceptron and Z score. Proteins. 41:192–201. [PubMed] [Google Scholar]
  65. Yang, W. Y., J. W. Pitera, W. C. Swope, and M. Gruebele. 2004. Heterogeneous folding of the trpzip hairpin: full atom simulation and experiment. J. Mol. Biol. 336:241–251. [DOI] [PubMed] [Google Scholar]
  66. Zagrovic, B., and V. Pande. 2003. Solvent viscosity dependence of the folding rate of a small protein: distributed computing study. J. Comput. Chem. 24:1432–1436. [DOI] [PubMed] [Google Scholar]
  67. Zarrinpar, A., and W. A. Lim. 2000. Converging on proline: the mechanism of WW domain peptide recognition. Nat. Struct. Biol. 7:611–613. [DOI] [PubMed] [Google Scholar]
  68. Zhou, R. H. 2003. Trp-cage: folding free energy landscape in explicit water. Proc. Natl. Acad. Sci. USA. 100:13280–13285. [DOI] [PMC free article] [PubMed] [Google Scholar]
  69. Zhou, Y. Q., and M. Karplus. 1997. Folding thermodynamics of a model three-helix-bundle protein. Proc. Natl. Acad. Sci. USA. 94:14429–14432. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[Supplemental File]
biophysj_104.046375_index.html (736B, html)
biophysj_104.046375_1.pdf (659.7KB, pdf)

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES