Entropy Calculation of HIV-1 Env gp120, its Receptor CD4, and their Complex: An Analysis of Configurational Entropy Changes upon Complexation

Abstract

The HIV-1 gp120/CD4 interaction shows a large, unprecedented entropy/enthalpy compensation, with the capacity to fine-tune recognition over a broad range of affinity. The intermolecular interaction involves stable hydrophobic contacts with a unique protruding CD4-Phe⁴³ structure surrounded by an intermolecular hydrogen-bond network that covers the hemisphere of the CD4 D1 domain. We have applied a heuristic formula based on the covariance matrix of atom-positional fluctuations to assess the configurational entropy of the gp120/CD4 complex at different levels. The system was dissected into various subsets of atoms to evaluate the entropic contributions of different functional elements. By combining the trajectories of the free and complex forms, further insight into the conformational sampling was extracted. Despite the limited sampling time of 10 ns, the theoretically derived changes in configurational entropy are in fair agreement with the experimentally determined data. The simultaneous evaluation of different interaction modes through a decomposition approach is only feasible with the knowledge of the atomic trajectory of the system. The configurational entropy analysis in terms of combined trajectories presented here shall potentially provide accurate estimations of thermodynamic properties of biomolecules given sufficient sampling of conformational space.

INTRODUCTION

Conformational changes are central to the viral entry of human immunodeficiency virus type-1 (HIV-1), which is initiated by the mutual recognition of the HIV-1 envelope protein (Env) gp120 and the cellular receptor CD4 (Olshevsky et al., 1990; Sattentau and Moore, 1991). This is followed by the binding of the chemokine co-receptor to gp120 (Berger et al., 1999; Rizzuto et al., 1998; Trkola et al., 1996; Wu et al., 1996) and the extension or stretching of the coiled-coil gp41, leading to the insertion of the membrane fusion peptide into the host membrane, which induces fusion of the viral and host membranes (Chan and Kim, 1998). Specific recognition of CD4 by gp120 is evidently the linchpin of the CD4-mediated viral infection pathway. Recent extensive biochemical and biophysical studies have provided ample evidence of a substantial structural rearrangement during the gp120-CD4 recognition process (Wyatt and Sodroski, 1998). Large enthalpic (−259 ± 13 kJ mol⁻¹) and entropic changes (220 ± 13 kJ mol⁻¹ at 310 K) upon binding were observed experimentally (Kwong et al., 2002; Myszka et al., 2000). The free energy of binding, however, is small due to a remarkable entropy/enthalpy compensation. This means that the affinity of gp120 for CD4 and CD4-induced monoclonal antibodies (CD4MAb) is relatively small, and can be fine-tuned by small variations in those two rather large contributions. The gp120/CD4 interaction is predominantly determined by the core of gp120: removal of the hypervariable loops corresponding to nearly 40% of the total sequence shows little effect on the thermodynamic properties of binding (Myszka et al., 2000).

Comprehensive structural insight is, however, limited by the intrinsic flexibility of the system. The structure of the ternary complex of the core of gp120, CD4, and a CD4-induced antibody is the only available atomic information to date (Kwong et al., 2000, 1998). This truncated form of gp120 (core gp120) does not compromise much the biophysical and biological properties compared to the full-length wild-type (Kwong et al., 2002; Myszka et al., 2000; Pollard et al., 1992; Wyatt et al., 1993). It provides a suitable structural template for molecular dynamics (MD) studies allowing a significant reduction in the size for the simulation system as compared to full-length gp120. Using MD simulations we have identified concerted loop motion around the CD4 binding site in gp120 upon binding (Hsu and Bonvin, 2004). The enthalpic change upon gp120/CD4 complex formation, calculated as the difference in protein-protein plus protein-solvent potential energy between the simulations of the complex and of the separate proteins (−127 kJ mol⁻¹ at 300 K with a standard error, SE, of 11 kJ mol⁻¹), is of the same order of magnitude as the experimentally determined value (−259 ± 13 kJ mol⁻¹ at 310 K; Myszka et al., 2000). (Note that SE is defined as the standard deviation SD divided by the square-root of the number of sampling point N. The energies were calculated every 5 ps as reported earlier by Hsu and Bonvin, 2004, and therefore N is 16,001 when analyzing the 2–10 ns simulation segments.) Encouraged by the rough agreement between the theoretical and experimental binding enthalpies, we aimed at extracting the binding entropy from our simulations and at gaining insight into CD4 binding-induced conformational changes in gp120 that are related to entropy changes.

The estimation of configurational entropy from molecular dynamics trajectories was first proposed by Karplus and Kushick (1981) using a quasiharmonic method. The difference in configurational entropy between two molecular conformations a and b can be estimated as ΔS = k_B/2 ln(detσ_a/detσ_b), where σ_a and σ_b are the covariance matrices of atomic positional fluctuations of the two conformers and k_B is Boltzmann's constant. The method was formulated in terms of internal (non-Cartesian) coordinates, which made it less easily applicable. This approach was extended and applied to various biomolecular systems (Di Nola et al., 1984; Edholm and Berendsen, 1984; Levy et al., 1984). A decade later, Schlitter (1993) introduced a heuristic formula, based on Cartesian coordinates, to compute an upper bound to the absolute entropy of a molecule from a simulation trajectory. Calculation of the absolute molecular entropy would require a complete translational and rotational sampling. This is not yet reachable for proteins with the current computation timescale of nanoseconds. Instead, an assessment of the configurational entropy can be obtained from a MD trajectory based on the covariance matrix σ of the Cartesian atom-positional fluctuations after elimination of translational and overall rotational motion by atom-positional least-squares fitting of molecular trajectory structures onto each other. This method was successfully tested for biomolecular simulations of peptide folding (Schäfer et al., 2001, 2000) and applied to simulations of protein molten globule states (Schäfer et al., 2002). Recently Andricioaei and Karplus (2001) revised the quasiharmonic approach to allow for the use of Cartesian coordinates.

One advantage of approaches based on the covariance matrix of atomic fluctuation is the possibility to compute this quantity for different subsets of atoms or degrees of freedom. One can, for example, resolve the entropic contributions of hydrophilic and hydrophobic residues to protein-protein binding, which is experimentally impossible. It should be noted, though, that entropies originating from different degrees of freedom need not be additive and that a decomposition will neglect correlation of motions along different degrees of freedom. Yet, the neglect of correlation between a particular subset of atoms and the rest of the molecule is a reasonable first-order approximation. Such analysis nonetheless enables us in the current study to estimate the entropic contribution of subsets of atoms, or degrees of freedom of interest, down to residue and atomic levels. Comparison of the configurational entropies of gp120 and the CD4 D1 domain (denoted CD4 for simplicity in the following) in the free and bound states suggests that the formation of intermolecular hydrogen bonds and hydrophobic contacts contributes most to the entropy changes. In line with previous postulates based on thermodynamic data (Kwong et al., 2002; Myszka et al., 2000; Xiang et al., 2002), the conformational rearrangement in the bridging sheet of gp120 upon CD4 binding is accompanied by a significant loss of entropy. The large-amplitude relocalization of the V3 loop of gp120 upon binding is, however, free from any substantial entropic cost.

METHODS

Three simulations of 10 ns at 300 K, 1 atm, were carried out for three different systems in explicit solvent: free HIV-1 gp120 with the truncated LAI strain sequence (SWISS-PROT accession number P03377; 346 residues and 29,047 water molecules), free CD4 (99 residues of the D1 domain and 7768 water molecules), and their complex (445 residues and 30,242 water molecules). Core gp120 is defined as the construct present in the crystal structure with the truncated V1–V3 loops and N- and C-termini. The V4 loop (residues 398–409), for which electron density is missing in all crystal structures, and the V3 loop, which has been proposed to undergo significant rearrangements upon CD4 binding, were modeled onto the gp120 core, together with the six core mutations of the LAI strain (98.1% sequence identity with HxBc2, PDB entry number 1G9M; for details, see Hsu and Bonvin, 2004).

The GROMACS program package (Lindahl et al., 2001) was used for the MD simulations with the GROMOS96 43A1 force field (Daura et al., 1998; van Gunsteren et al., 1996), and the simple point-charge water model (Berendsen et al., 1981) with rectangular periodic boxes with a 1.4-nm solute-wall minimum distance. Nonbonded interactions were calculated using twin-range cutoffs of 0.8 and 1.4 nm. Long-range electrostatic interactions beyond the cutoff were treated with a generalized reaction field model (Tironi et al., 1995), using a dielectric constant of 54. For further simulation details, we refer to Hsu and Bonvin (2004). Owing to the large system sizes, ∼2 ns was required to reach equilibrium. The entropy analysis was therefore performed on the last 8 ns of each simulation, using molecular configurations that are two picoseconds apart.

Schlitter's formula was used for the configurational entropy calculation, which yields an upper bound to the true entropy S_true,

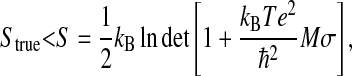(1)

where k_B is Boltzmann's constant, T the absolute temperature, e Euler's number, 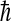Plank's constant divided by 2π, M the mass matrix that holds on the diagonal the masses belonging to the atomic Cartesian degrees of freedom, and σ the covariance matrix of atom-positional fluctuations. The elements of σ are given by

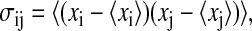(2)

where x_i are the Cartesian coordinates after least-squares superposition of the trajectory configurations with respect to a particular subset of atoms. Although the choice of this set of atoms will determine which motions are excluded as translational and rotational ones, and so will influence the calculated internal configurational entropy, it has little effect for relative comparisons.

Two sets of atoms were used in the superposition of molecular configurations:

1. The backbone atoms (N, Cα, and C′) of the most stable structural elements of both proteins, the first α-helix of gp120 (residues 17–31), and part of the β-sheet of CD4 consisting of residues 26–30 and 82–86 (see Fig. 1). The set of atoms is indicated by the code 2nd.

2. The backbone (N, Cα, and C′) atoms of individual residues were used for superposition of trajectory configurations when calculating the entropy per residue (code: fir).

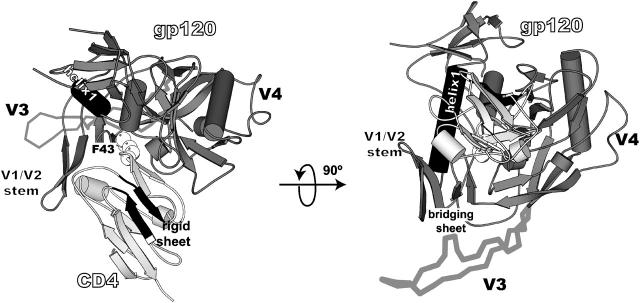
FIGURE 1.

Structure of the gp120/CD4 complex. Gp120 (core) and CD4 (D1 domain) are dark- and light-shaded, respectively. CD4-F43 is shown in open spheres to indicate the position of the binding cavity. The four β-strands of the bridging sheet that link the inner and outer domains are indicated. The secondary structure elements that are used for superposition before the configurational entropy calculation are solid-colored (for CD4 β-strands, β3, residues 26–30; β8, residues 82–86; and for gp120, α-helix 1, residues 17–31). The structure corresponds to a simulated configuration taken at 6 ns, representative of the most populated V3 conformation (shaded backbone, Cα trace). The figure was generated using MOLSCRIPT (Kraulis, 1991).

The covariance matrix and thus the configurational entropy were calculated for three different sets of atoms (see Table 1):

1. The gp120 molecule without the V3 loop and the CD4 molecule, both using all atoms (code: all) or using only backbone (N, Cα, and C′) atoms (code: bb); see Fig. 4.

2. Segments or regions that are directly involved in intermolecular interactions or that are indirectly affected upon binding: residue F43 of CD4 (code: F43) and the residues of gp120 forming a cavity to hold F43 (code: F43cav), residues of gp120 that form intermolecular hydrogen bonds (code: interHb) and their counterparts in CD4 (code: interHb); see Fig. 5; and the bridging sheet (code: bridge) and the V3 loop (code: V3) of gp120; see Fig. 6. Detailed lists of residues are given in Table 1.

3. The atoms of each residue (code: res); see Fig. 7.

TABLE 1.

Code definitions of atom sets used for configurational entropy calculations

Set code	Molecule	Residue number	Number of atoms
all	gp120	83–296, 331–492	3101
	CD4	1–99	1021
bb	gp120	83–296, 331–492	936
	CD4	1–99	297
F43	CD4	F43	17
F43cav	gp120	E370, N425, W427, G473	47
interHb	gp120	K97, C126, V127, A129, S131, N280, A281, S365, G366, G367, D368, Q428, E429, V430, G473, D474	130
	CD4	K22, Q25, K29, K35, S42, F43, L44, K46, D53, R59, Q64, N66, E87, D88	166
bridge	gp120	120–124, 198–202, 422–426, 431–435	198
V3	gp120	297–330	359

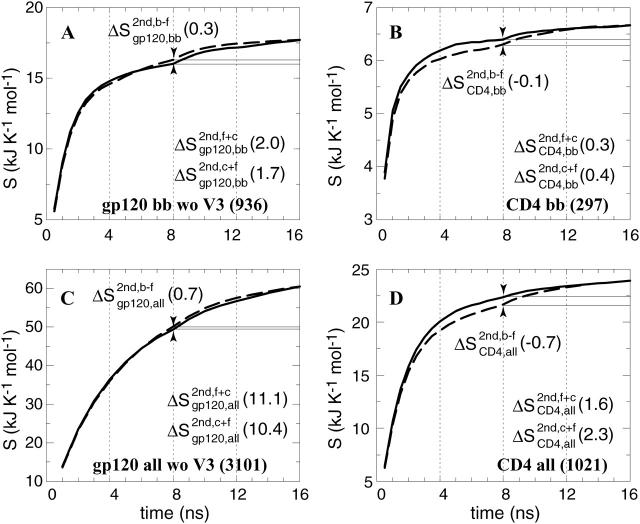
FIGURE 4.

Configurational entropy of gp120 and CD4-D1 domain. (A and C) Backbone and all atoms of gp120 excluding the V3 loop. (B and D) Backbone and all atoms of CD4. The buildup curves of the free+complex combined trajectory is shown in solid lines and the ones of the complex+free combined trajectory in dashed lines. The numbers of atoms used for the calculations are indicated between parentheses at the lower right of each panel. All covariance matrices were generated after positional least-squares fitting of backbone atoms of the β-sheet of CD4 and of α-helix 1 of gp120, respectively (see Fig. 1). The configurational entropy buildup was calculated every 0.5 ns except for the all-atom analysis of gp120 (1 ns/step). The configurational entropy difference between the free and complex forms 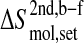(Eq. 4) is indicated at the midpoint of the curves (8 ns). The configurational entropy gains after combining trajectories, 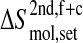and 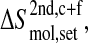Eqs. 8 and 7, are calculated by subtracting the midpoint values indicated by the horizontal lines from the end point values (see Methods).

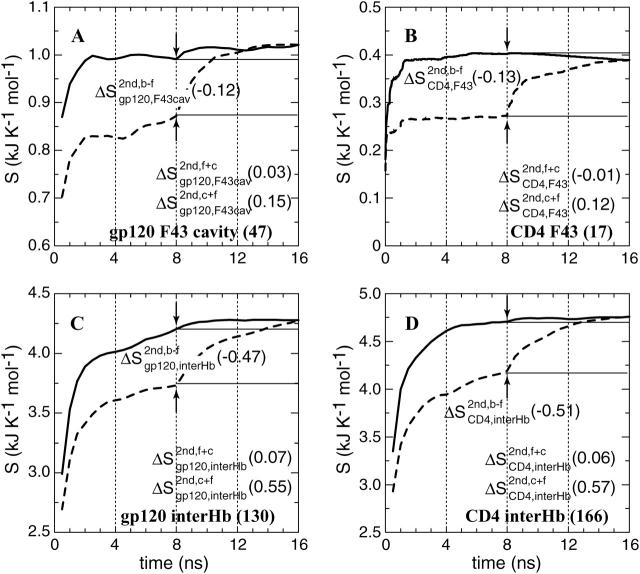
FIGURE 5.

Configurational entropy of the structural elements involved in gp120/CD4 intermolecular interactions. (A) Receptive cavity of gp120 formed by residues that have hydrophobic contacts with CD4-F43. (B) CD4-F43. (C, D) Residues of gp120 and CD4 that are involved in a stable intermolecular hydrogen-bond network. The configurational entropy buildup was calculated every 0.1 ns because of the fast equilibration within 1 ns. For further explanation, see Fig. 4's legend.

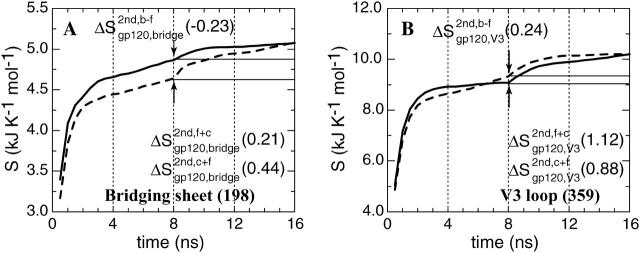
FIGURE 6.

Configurational entropy of the structural elements in gp120 that experience conformational changes upon CD4 binding. (A) The bridging sheet. (B) The V3 loop (see Fig. 1). The configurational entropy buildup was calculated every 0.5 ns. For further explanation, see Fig. 4's legend.

FIGURE 7.

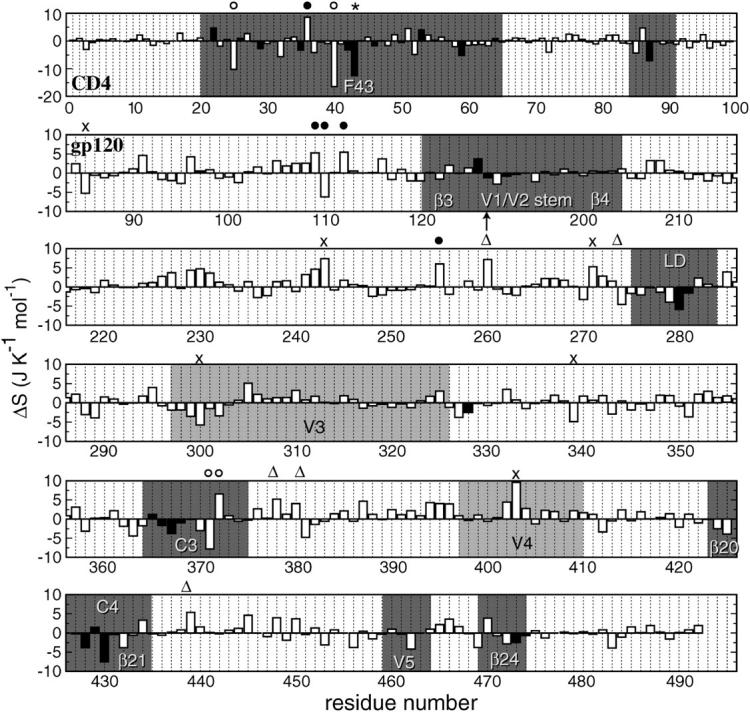
Differences in intraresidue configurational entropy in J K⁻¹ mol⁻¹ between complex and free MD simulations as a function of residue number. The intraresidue configurational entropies were calculated after positional least-squares fitting of backbone atoms of the respective residues. (Top row) CD4-D1 domain. The sequence numbering of gp120 follows the HxBc2 construct with an arrow indicating the missing V1/V2 loop (residues 128–194). Residues involved in the stable intermolecular hydrogen-bond network are shown in solid bars. CD4-F43 is highlighted with an asterisk. Residues not involved in stable intermolecular hydrogen bonds that exhibit entropy changes larger than two times the standard deviation from the average value are highlighted with the following symbols indicative of their minimum intermolecular distance d: (○) d < 0.5 nm; (•) 0.5 nm < d < 1 nm; (▵) 1 nm < d < 2 nm; and (×) d > 2 nm. The intermolecular distance is defined as the minimum interatomic distance from any atom of the residue of interest to any atom of the other molecule in the structure taken at 6 ns, which is well-equilibrated and is representative of the most populated V3 conformation (see Fig. 1). Regions in gp120 and CD4 that are involved in intermolecular contacts are in dark shading. The modeled V3 and V4 loops in gp120 are in light shading.

We use the following notation for the entropy of a set (set; all, bb) of atoms of a molecule (mol; gp120, CD4, complex) calculated from a trajectory (traj; free-gp120, free-CD4, complex) after superposition of the trajectory structures onto the first structure based on fitting a particular set of atoms (fit; 2nd, fir),

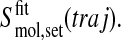(3)

The entropy difference between the bound (b) and free (f) states of CD4 is then

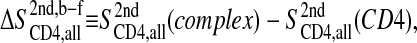(4)

and likewise for gp120 instead of CD4.

To assess the degree of overlap between the configurational spaces sampled in two simulations, one may append one trajectory to the other trajectory and compute the development of the configurational entropy S with time; see Fig. 2. Denoting the trajectories by I and II we then obtain

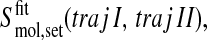(5)

or alternatively

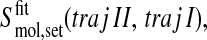(6)

depending on the sequence of appending.

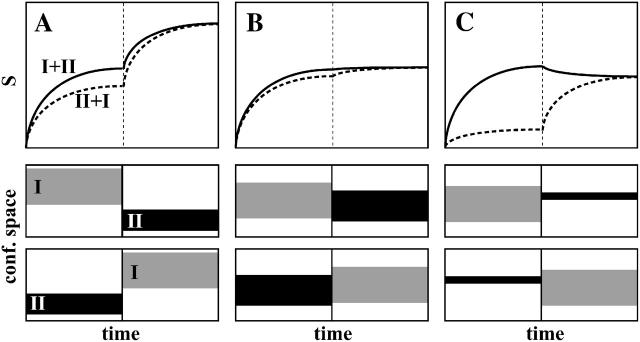
FIGURE 2.

Schematic of three possible results of the configurational entropy analysis of the combined trajectory of two simulations, i.e., I and II. (A) The two trajectories I and II sample different regions of conformational space; (B) the two trajectories I and II sample largely overlapping regions of conformational space; and (C) the two trajectories overlap, but one (II) only samples a small subspace of the conformational space of the other (I). For an explanation, see Methods. (Top) Configurational entropy buildup curves as a function of the length of the combined MD trajectory. The solid line corresponds to the configurational entropy of the combined trajectory, I+II, and the dashed line corresponds to the entropy obtained from the reversely combined trajectory, II+I, where I and II indicate the single trajectories. The conformational space sampling of the trajectories in the two combinations (I+II and II+I) is indicated in the lower panels.

Configurational entropy analysis of appended or combined trajectories can provide insight into the relative size and overlap of the conformational space sampled by a pair of single trajectories. For a molecule existing in two different states but with similar atom-positional fluctuations, similar configurational entropies are expected for the two states. Little information can be extracted by comparing the entropy of the two states. By combining the trajectories of these states, however, more information can be obtained. One can distinguish three cases (Fig. 2):

1. A stepwise increase in configurational entropy after appending a second trajectory that has no overlap, or only a small overlap, in conformational space with the first trajectory (Fig. 2 A).

2. A rather smooth continuation of the configurational entropy buildup profile without observable change or perturbation, after appending a second trajectory that has a large conformational overlap with the first one (Fig. 2 B).

3. A decrease in conformational entropy after appending a second trajectory that samples a much smaller conformational space than the first one, and is contained in the conformational space of the first trajectory (Fig. 2 C).

These three situations, denoted cases A, B, and C, will be used in Results, below. Analysis of combined trajectories can yield information on the difference in the conformational spaces visited by the two trajectories, e.g., of bound and unbound states, whereas analysis of the single trajectories only provides information about the extent of the respective conformational spaces, and not about their degree of overlap.

The coverage of the conformational space of the second trajectory segment with respect to the first segment of a combined trajectory can be quantitatively measured by the difference between S at the end of the second segment of the combined trajectory buildup curve and S at the end of the first segment. For example, the coverage of the free trajectory with respect to the complex trajectory is

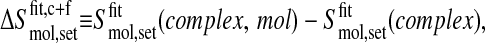(7)

and the coverage of the complex trajectory with respect to the free trajectory is

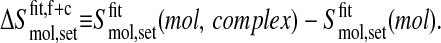(8)

RESULTS

Configurational entropy of gp120 and CD4

The configurational entropy of various sets of atoms of the free gp120 and CD4 molecules and their complex are shown in Figs. 4–6. Unlike other structural parameters such as the atom-positional root mean-square deviations (RMSD) of the trajectory structures from the starting structure, which seem to reach equilibrium after 2 ns for CD4 and 4 ns for gp120 (Fig. 3; for details see Hsu and Bonvin, 2004), only the backbone configurational entropy starts to level off after ∼4 ns (Fig. 4, A and B), and the all-atom values are still in the buildup phase throughout the 8-ns trajectories (Fig. 4, C and D). Unexpectedly, the configurational entropies of both backbone and all atoms of gp120 (Fig. 4, A and C) in the complex formed (dashed lines until 8 ns) toward the 8-ns time point are slightly higher (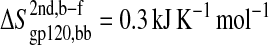 and 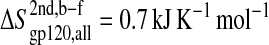) than those in the free form (solid lines until 8 ns). This increase, however, only amounts to <2% of the absolute value.

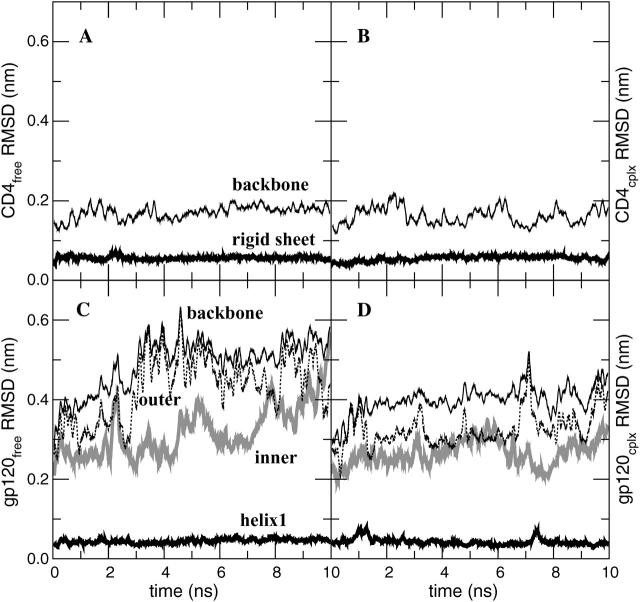
FIGURE 3.

Atom-positional (backbone atoms, N, Cα, and C′) root mean-square deviation (RMSD) of trajectory structures from the respective starting structure of CD4-D1 domain and gp120 (without the V3 loop) in the free and complex forms. (A, B) CD4 in the free and complex forms, respectively. (C, D) Gp120 in the free and complex forms, respectively. The RMSD values of the structural elements subjected to the least-squares superposition of backbone atoms are shown in thick solid lines (see Fig. 1) and those of the backbone atoms (N, Cα, and C′) of all residues are shown in thin solid lines. The RMSD values of the inner and outer domains of gp120 are shown in shaded and dashed lines, respectively; these values were smoothed for clarity using a 0.1-ns averaging window.

Due to the large number of atoms of gp120, the conformational sampling is not yet complete within the 8-ns simulation. The crossing-over of the complex and free buildup curves at ∼6 ns (Fig. 4, A and C) is due to a leveling off of the curve for the free form, which suggests that convergence is near for the free molecule. Appending the free and complex trajectories of CD4 gives rise to a small stepwise increase of the entropy buildup of the backbone atoms (Fig. 4 B at 8 ns), regardless of the order of appending. This suggests that two slightly different conformational spaces are sampled in the free and complex forms of the molecule, representing a situation of case A (Fig. 2 A). For the all-atom analysis of CD4 (Fig. 4 D), on the other hand, a smooth continuation at 8 ns of the configurational entropy buildup is observed when the complex trajectory is appended to the free one (solid line), whereas a slight stepwise increase is visible when the trajectories are appended in the reverse order (dashed line). This illustrates case B (Fig. 2 B), where a subspace of the conformational space of the free molecule is sampled in the complex state.

Configurational entropy of interacting elements and CD4 binding-induced conformational changes in gp120

The gp120/CD4 interface involves two major interaction modes:

1. The unique knob-and-socket hydrophobic interaction between CD4-F43 (17 atoms) and the gp120 receptive cavity, including E370, N425, W427, and G473 (47 atoms).

2. The stable intermolecular hydrogen-bond network (166 and 130 atoms for CD4 and gp120, respectively; for details see Table 1).

These intermolecular contacts restrict the mobility of the involved residues and, in turn, their configurational entropy. In the combined trajectory analysis (Fig. 5), the entropy buildup curves show a substantial jump at the appending point when the trajectory of the free form is appended to that of the complex form (dashed line), indicating that the free molecule samples conformational space not visited in the complex simulation (case A; Fig. 2 A). Note that whereas the configurational entropy of the whole system is still in the early stage of equilibration (Fig. 4), the entropy of most of the structural elements involved in the gp120/CD4 interface starts to level off after 4 ns as a result of their smaller number of atoms.

The loss of entropy stemming from the rigidification of the residues in gp120 forming stable hydrophobic contacts to CD4-F43 (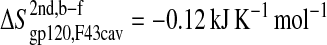; see Fig. 5 A) is of the same size as the corresponding loss of entropy in CD4-F43 ( 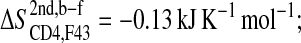see Fig. 5 B). Appending the complex trajectory of gp120 to the free one gives rise to a small increase (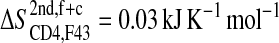), indicating that the complex form samples slightly different parts of conformational space (Fig. 5 A). Interestingly, for CD4-F43, the corresponding value is negative, −0.01 kJ K⁻¹ mol⁻¹ (solid line in Fig. 5 B). This would only occur when the averaged atom-positional fluctuations, i.e., the determinant of the covariance matrix, are reduced due to the addition of the second trajectory segment (case C, Fig. 2 C). In other words, the second MD trajectory segment covers a small subspace of the conformational space sampled by the first segment and hence reduces the overall size of the elements of the covariance matrix σ through averaging over the combined trajectories. As an illustration of this, the root mean-square fluctuations of the phenyl ring of CD4 Phe⁴³ after least-squares fitting on all heavy atoms of CD4 decreases from 0.30 ± 0.07 nm in the free form to 0.08 ± 0.01 nm in the complex form. Moreover, all Phe⁴³ side-chain conformations in the complex are contained within the ensemble of conformations of the free form.

In addition to the changes directly related to the intermolecular contact, CD4 binding also induces conformational changes away from the binding interface that are crucial for the subsequent events of viral entry into the host cell. It is generally accepted from thermodynamic and biochemical data that the β-sheet of gp120 that bridges the inner and outer domain of the gp120 core, the bridging sheet, is only fully formed and stabilized upon complexation with CD4 (Fig. 1), and that this stabilization contributes a sizeable entropic loss and/or enthalpic gain (Jardetzky, 2002; Kwong et al., 2002; Xiang et al., 2002). Concomitantly, the third hypervariable loop (V3) undergoes a rearrangement to a somewhat different conformation leading to accessibility of the epitope for co-receptor binding. Our previous MD study revealed that lid-closure motions upon CD4 binding are accompanied by concerted structural changes leading to a substantial increase of rigidity of the bridging sheet and a large-amplitude translocation of the V3 loop (Hsu and Bonvin, 2004). The corresponding changes in entropy are shown in Fig. 6. The bridging sheet shows a clear entropy difference between the free and complex forms of gp120 with a loss of entropy of 0.23 kJ K⁻¹ mol⁻¹. Not only is its flexibility reduced, but its configuration is also altered. This can be concluded from the subsequent change after appending the trajectories of the complex and of the free form to each other, which is consistent with the previously defined case A (Fig. 2 A). The entropy of the V3 loop in the CD4-bound form initially builds up more slowly than the entropy in the free form, but crosses the latter curve in the last 1.5 ns, resulting in a final increase of 0.24 kJ K⁻¹ mol⁻¹ (Fig. 6 B). In addition, the V3 loop shows an increase in entropy when the two trajectories are combined, irrespective of the order of appending. These observations suggest that the V3 loop undergoes major changes in conformation and/or localization upon CD4 binding, although its intrinsic flexibility persists, or even possibly increases.

Configurational entropy changes per residue

Changes in conformational entropy upon binding can also be calculated per residue. For this, the atom-positional least-squares fitting of trajectory structures was performed using backbone atoms (N, Cα, and C') of the individual residues to exclude from the entropy contributions of collective motions of larger structural segments. The intraresidue conformational entropy obtained in this way provides, therefore, only information about side-chain motions. The intraresidue configurational entropy per residue was calculated using Eq. 1 and then normalized by dividing it by the number of atoms of each residue. Intraresidue entropy differences between the free and complex forms 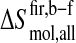(Eq. 4) are plotted as a function of residue number in Fig. 7.

On average, CD4 shows an intraresidue entropy decrease of −0.5 kJ K⁻¹ mol⁻¹ per atom, although gp120 shows an unexpected increase of 0.3 kJ K⁻¹ mol⁻¹. Most of the residues of CD4 and gp120 that are involved in the intermolecular hydrogen-bond network (solid bars in Fig. 7) show reductions in intraresidue configurational entropy upon complexation, except for K22 and D53 in CD4, and C126, S365, and E429 in gp120. The relative large entropy of these five residues illustrates their intrinsic flexibility that is reflected in their large B-factors in the crystal structure (Kwong et al., 1998). In addition, our previous MD analysis of the intermolecular hydrogen bonding shows that all these residues, except CD4-K22, form only marginally stable intermolecular hydrogen bonds. Despite its high occurrence (78%), the salt bridge between CD4-K22(Nζ) and gp120-E429(Cδ) located at the edge of the interface of the molecular complex might be subject to fewer structural limitations than those in the center of the interface. Furthermore, the relatively long side chains of both residues might also tolerate a higher degree of flexibility despite the presence of a salt bridge.

In line with the previous analysis of the functional elements, CD4-F43 shows a large intraresidue entropy reduction upon complexation (Fig. 7) due to the steric restriction imposed by the receptive cavity of gp120. The neighboring residue Q40, which lies at the center of the complex interface, shows the largest reduction among all residues (top row in Fig. 7). Although less confined than CD4-F43, it is in close contact (<0.5 nm interatomic distance) with T283, G473, and D474 of gp120, of which the latter two were found to form intermolecular hydrogen bonds with F43 and Q25 of CD4, respectively (Hsu and Bonvin, 2004). In gp120, regions that show concerted lid-closure motions upon CD4 binding, namely LD, C3, C4, and V5, display substantial intraresidue entropy reductions upon complexation especially for those residues that are involved in intermolecular hydrogen bonding (Fig. 7). Note that the outer half of the bridging sheet (β3 and β4) and the tip of the hairpin structure of the V3 loop (residues 297–330) do not exhibit significant entropy changes, most likely due to the lack of direct contact with CD4. This illustrates that changes in conformation do not necessarily involve a change in entropy or extent of motion.

In addition to the residues that are directly involved in intermolecular contacts or are in close proximity to the intermolecular interface, there are a few residues in gp120 that show large intraresidue entropy changes upon complexation (see Fig. 7). Some residues show positive intraresidue entropy change upon complexation. Several are located in the putative trimerization interface, S243, C378, and I439, and two of them, V255 and L260, are located in the β-turn that connects the inner and outer domains of gp120. This indicates that the intermolecular interactions between gp120 and CD4, although decreasing the intraresidue entropy of residues in direct contact, can induce intraresidue entropy changes at the interdomain interface within the gp120 monomer and at the putative trimeric gp120 interface.

Error analysis of configurational entropies

The configurational entropy differences between complex and free forms reported above were obtained from the entropy differences at 8 ns (the full trajectory length used for analysis). To estimate errors, several independent simulations could be performed and compared. This is, however, rather prohibitive, considering the system size in this particular case. An alternative is to divide a trajectory into N blocks of equal size over which sub-averages and standard errors can be calculated; the standard error is given by the standard deviation divided by squared root of the number of sampling points. An upper limit to the standard error at equilibrium can then be estimated by fitting the block average standard errors as a function of increasing trajectory block sizes to a single-exponential function. This so-called block average procedure has been applied, for example, to obtain standard errors of the average area per lipid molecule in membrane simulations (Anezo et al., 2003).

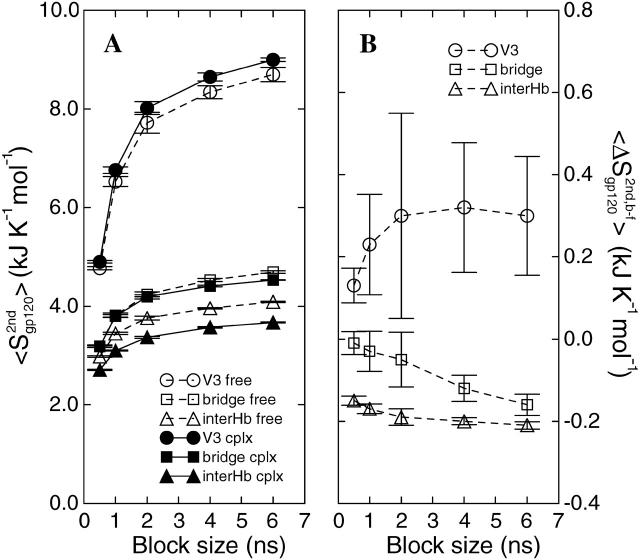
We followed here a similar procedure to estimate errors on the conformational entropy changes upon complex formation for the sets of atoms that are involved in intermolecular interactions and/or show conformational changes (Table 1). Each 8-ns trajectory was divided into 16, 8, and 4 blocks of non-overlapping trajectory segments of 0.5-, 1-, and 2-ns length, respectively, and five and three partially overlapping blocks of 4- and 6-ns length, respectively, by shifting the time origin by 1-ns increments. As an illustration, conformational entropy buildup curves as a function of block size with error bars derived from the block averaging procedure are presented for gp120 atom sets in Fig. 8. Since overlap between blocks can reduce the standard deviation and hence the standard error (Fig. 8 B), only the first three data points derived from non-overlapping blocks (0.5-, 1-, and 2-ns block sizes) were used for fitting the standard errors to an exponential function using the xcrvfit software (http://www.pence.ca/software/xcrvfit/) and extrapolating the standard error to infinite block size. The V3 loop of gp120 shows a monotonous increase of the average configurational entropy difference (circles in Fig. 8 B) with markedly larger standard errors than the other structural elements. This may reflect the large structural change and the crossing of the free and bound buildup curves (Fig. 6 B). The intermolecular hydrogen-bonded residues in gp120 and CD4 both show fast equilibration and small standard errors with increasing block size (triangles in Fig. 8). The same is observed for the bridging sheet of gp120 (squares in Fig. 8), for F43 of CD4 (F43), and the F43-cavity of gp120 (F43cav) (not shown). This suggests that, for these sets, sufficient sampling of conformational space has been achieved and that relatively precise conformational entropy differences between the two states can be obtained, although the values for the V3 loop should be taken with caution. The corresponding conformational entropy differences with their respective standard error estimates from the block averaging analysis are summarized in Table 2.

FIGURE 8.

Block average error analysis of configurational entropy. (A) Representative buildup curves of the average configurational entropies 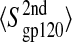with standard errors, SE, for various sets of atoms in the free (open symbols and dashed lines) and complex (solid symbols and solid lines) states as a function of the trajectory block size. (Circles) gp120 V3 loop; (squares) gp120 bridging sheet; and (triangles) gp120 intermolecular hydrogen-bounded residues (for definition, see Table 1). (B) Average configurational entropy differences 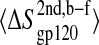between bound and free forms and standard errors SE_diff as a function of the trajectory block size. The standard error SE_diff of the entropy difference is calculated as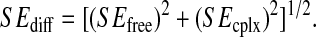

TABLE 2.

Configurational entropy differences ΔS with standard errors SE_diff for various functional sets of gp120 and CD4^‖

Set code*	Molecule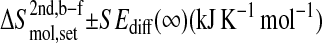
F43cav	gp120	−0.12 ± 0.03
F43	CD4	−0.13 ± 0.004
interHb	gp120	−0.47 ± 0.03
	CD4	−0.51 ± 0.08
bridge	gp120	−0.23 ± 0.08
V3	gp120	0.24 ± 0.25†

The configurational entropy differences 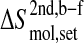are those reported in Figs. 5 and 6. The standard errors SE_diff are upper limits estimated from a block averaging procedure by fitting standard errors as a function of non-overlapping trajectory block size L (L = 0.5, 1.0, and 2.0 ns; see Fig. 8) to a single-exponential function 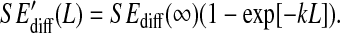The standard errors SE_diff(∞) are reported.

^*See Table 1.

^†Fitting of the data points did not converge and therefore the maximum value of the data set is reported.

DISCUSSION

Sufficient conformational sampling is a prerequisite for a reliable estimation of the conformational entropy. The required simulation time is correlated to the size of the system, i.e., the number of atoms taken into account in the calculation. For a moderate system size such as the entire CD4-D1 domain with 1021 atoms, convergence of conformational entropy of both the free and bound states is only observed in the later stage of the 8-ns trajectory segments. Nevertheless, the stabilizing effect of complexation on backbone and side chains can be unambiguously identified when comparing the buildup curves of the two states (Fig. 4, B and D). It is, however, not obvious to explain the slight, unexpected gain in entropy upon complexation for gp120 (Fig. 4 A). The conformational sampling requires more time than for CD4. When considering all protein atoms, the number of atoms in gp120 becomes too large to obtain sufficient sampling in the timescale of our simulation (10 ns); the buildup curves have not yet converged (Fig. 4 C). In contrast to the compact CD4, gp120 undergoes a number of significant loop contractions and translocations upon CD4 binding, which occur on a more extended timescale than the high-frequency local fluctuations. Complete sampling of these movements would require much longer simulations.

The conformational entropy change of gp120/CD4 complexation roughly agrees with the experimental value despite the fact that the contribution from bulk solvent was neglected in our analysis. Assessment of the complete system was not yet feasible due to insufficient sampling, especially for gp120. Nevertheless, by considering functionally important sets of atoms, a localized, rather than global, analysis provided insights into the entropic contribution of various degrees of freedom. The intermolecular hydrogen bond network and the insertion of CD4-F43 into its receptive cavity seem to predominantly determine the large entropy loss upon complexation. The bridging sheet of gp120 also plays a key role in the entropy change, as has been proposed experimentally (Myszka et al., 2000; Xiang et al., 2002). Although in some cases, conventional structural parameters such as atom-positional fluctuations may fail to identify thermodynamic differences between two states, the conformational entropy analysis of combined trajectories can provide a complementary way of evaluating spatial distributions and their statistical weight. This is essentially equivalent to the clustering approach, which was previously proposed to assess equilibration and convergence of biomolecules simulations (Smith et al., 2002). With the rapid advance in computing power and methodology, we are hopeful that a thorough description of the thermodynamics of such complex systems can be ultimately achieved via computer simulations and will meet experimental data in the near future.