Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Oct 8;88(1):412–421. doi: 10.1529/biophysj.104.050898

Flash-Induced Oxygen Evolution in Photosynthesis: Simple Solution for the Extended S-State Model that includes Misses, Double-Hits, Inactivation, and Backward-Transitions

Vladimir P Shinkarev 1
PMCID: PMC1305018  PMID: 15475587

Abstract

Flash-induced oxygen evolution in higher plants, algae, and cyanobacteria exhibits damped period-four oscillations. To explain such oscillations, Kok suggested a simple phenomenological S-state model, in which damping is due to empirical misses and double-hits. Here we developed an analytical solution for the extended Kok model that includes misses, double-hits, inactivation, and backward-transitions. The solution of the classic Kok model (with misses and double-hits only) can be obtained as a particular case of this solution. Simple equations describing the flash-number dependence of individual S-states and oxygen evolution in both cases are almost identical and, therefore, the classic Kok model does not have a significant advantage in its simplicity over the extended version considered in this article. Developed equations significantly simplify the fitting of experimental data via standard nonlinear regression analysis and make unnecessary the use of many previously developed methods for finding parameters of the model. The extended Kok model considered here can provide additional insight into the effect of dark relaxation between flashes and inactivation.

INTRODUCTION

Photosystem II (PSII) is the membrane-protein complex of higher plants, algae, and cyanobacteria, which uses the energy of light to oxidize water (with release of oxygen and protons) and reduce plastoquinone (with uptake of protons). PSII is the main source of the oxygen on the Earth, and is also implicated in the primary production of biomass in the biosphere. The complex multisubunit structure of PSII is needed to couple together the capture of light energy, oxidation of water, reduction of plastoquinone, and formation of a transmembrane proton gradient (reviewed in Cramer and Knaff, 1990; Debus, 1992; Diner and Babcock, 1996; Ke, 2001; Blankenship, 2002; Renger, 2003, 2004; Ferreira et al., 2004).

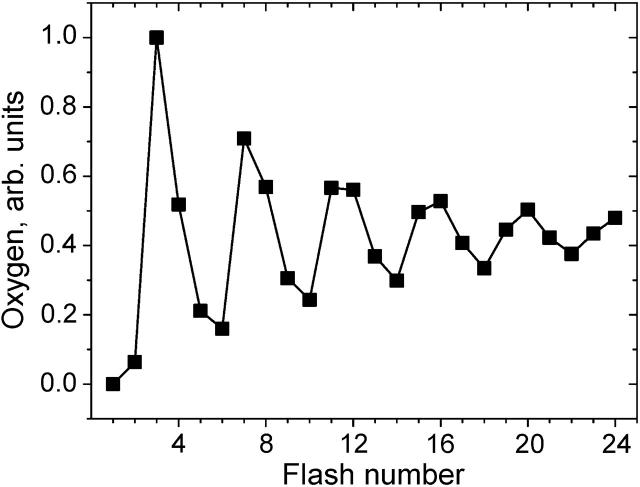
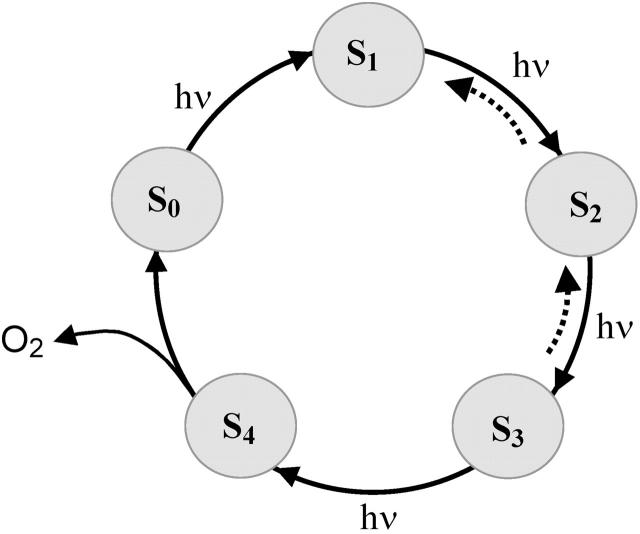
Photoactivation of dark-adapted PSII by a series of single-turnover flashes leads to period-four oscillations (Fig. 1) in the oxygen evolution (Joliot et al., 1969, 1971; Kok et al., 1970; Forbush et al., 1971). Several phenomenological models were proposed to explain such oscillations (see e.g., Joliot et al., 1969; Mar and Govindjee, 1972), but the only model suggested by Kok and coauthors (Kok et al., 1970; Forbush et al., 1971) withstood the test of time. According to oxygen evolution occurs in independent units called oxygen-evolving complexes (OEC). In the model (Fig. 2), four light-activation steps are needed for complete cycle of reactions leading to O2 evolution. Five formal states of PSII (S0, S1, S2, S3, and S4) were introduced to describe observed oscillations of oxygen evolution. According to the model, the oxygen evolution occurs during the S4→S0 transition. It was suggested that damping of oscillations in O2 yields is due to the presence of misses (i.e., zero-step advances, α) and double-hits (i.e., double-step advances, β).

FIGURE 1.

FIGURE 1

Open in a new tab

Flash-induced O2 evolution in spinach chloroplasts published by Forbush et al. (1971). Original data were independently digitized twice, averaged, and normalized.

FIGURE 2.

FIGURE 2

Open in a new tab

The Kok model of O2 evolution, consisting of four stable states (S0, …, S3) and one transient state (S4). The dashed arrows indicate dark relaxation of S-states.

Double-hits are mostly due to actual double PSII turnovers during a long flash and can be reduced significantly by the use of laser activation (Weiss and Sauer, 1970; Joliot et al., 1971; Joliot and Kok, 1975). Because electron transfer from QA to non-heme iron is significantly faster than electron transfer from primary (QA) to secondary (QB) acceptor quinones (Diner and Petrouleas, 1987), and re-reduction of P680 by YZ is very fast (reviewed in Ke, 2001), the double-hit could be observed when non-heme iron is oxidized before the flash. Indeed, Jursinic (1981) found that the incubation of chloroplasts with ferricyanide leads to threefold increase of double-hits induced by 3-μs xenon flashes. In addition, the double-hits in the laser or short xenon flash-induced O2 evolution can arise not because there is double turnover of reaction centers (RC), but because of the application of the oversimplified model of oxygen evolution. Indeed, if one introduces extra parameters in the model such as initial conditions (Delrieu and Rosengard, 1991), or unequal misses (Delrieu, 1983; Naber, 1989), the double-hit usually decreases. The artificial appearance of double-hits during application of the simple Kok model can be illustrated by fitting theoretical curves generated with zero double-hits (Shinkarev, 2005).

Misses can originate from different sources. Some RCs are inactive at the time of the saturating flash, due to the presence of either oxidized primary donor, P680+, or reduced primary quinone, 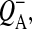Inline graphic as determined by the electron transfer (quasi)equilibria on the donor and acceptor sides of the RC (see e.g., Shinkarev and Wraight, 1993a). Misses may also arise from the rapid 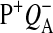Inline graphic charge recombination, which can partially compete with the forward electron transfer reactions (Joliot and Kok, 1975; Shinkarev and Wraight, 1993b; de Wijn and van Gorkom, 2002). Some misses can also originate from the reduction of S-states by YD in the dark interval between flashes (Babcock and Sauer, 1973). Delrieu (1974) and Etienne (1974) suggested that misses could reflect equilibrium between active and inactive forms of PSII. Lemasson and Etienne (1975) pointed out that the dark relaxation between flashes can also attribute to the observed misses. Lavorel and Lemasson (1976) indicated that some misses could have a nonphotochemical character. Frequently the source of misses is more trivial and is due to the absence of light saturation.

Current understanding of miss origination indicates that they should be S-state-dependent (see e.g., Delrieu, 1974, 1983; Lavorel, 1976; Bouges-Bocquet, 1980; Renger and Hanssum, 1988; Shinkarev and Wraight, 1993a,b; de Wijn and van Gorkom, 2002; Shinkarev, 2005). Calculation of misses using known or estimated values of the rate and equilibrium constants at the donor and acceptor sides of PSII demonstrated unambiguously that misses are different for each flash-induced transition (Shinkarev and Wraight, 1993a,b). Investigators de Wijn and van Gorkom (2002) reached a similar conclusion by analyzing the kinetics of chlorophyll a fluorescence yield transients induced by a flash series.

The majority of researchers agree that misses should be S-state-dependent. Despite that, equal miss and double-hit probabilities are predominantly used during analysis of oxygen evolution (reviewed in Shinkarev, 2005). There are at least two reasons for this. First, it was found that equal misses and double-hits provide a satisfactory fitting of experimental points (Kok et al., 1970; Thibault, 1978; Messinger and Renger, 1994). Similarly, model curves with unequal misses can be approximated nicely by the model with equal misses (Shinkarev, 2005). The second reason is more fundamental, and results from the fact that finding the transition probabilities and initial states from the oxygen evolution is an underdetermined problem (Lavorel, 1976; Meunier et al., 1996). As a result, the measured oxygen evolution could not be used for finding all unknown transition probabilities. The situation can be resolved only in the case where transition probabilities satisfy some restrictions. The simplest of such restrictions is the suggestion of equal misses and double-hits. In this case these transition probabilities can be restored from the measured oxygen evolution sequences.

To fit the observed O2 evolution pattern, Kok et al. (1970) assumed that, after prolonged dark adaptation, only S0 (≈20–30%) and S1 (≈80–70%) states are accumulated. There are at least two explanations for the apparent ratio of S0 and S1 found in experiments. The first explanation (which is currently obsolete) was originally suggested by Kok et al. (1970), and assumes equilibrium between S0 and S1. The second explanation (Velthuys and Visser, 1975; Vermaas et al., 1984) assumes that, in the dark, only the S1 state is stable, and that the S0 state is apparent only due to the presence of an electron donor, which reduces the S-states between flashes.

Only state S1 is stable in the dark. All other states deactivated back to S1 (Joliot and Kok, 1975). S2 and S3 states can be reduced by 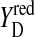Inline graphic (Babcock and Sauer, 1973; Velthuys and Visser, 1975; Vermaas et al., 1984; Styring and Rutherford, 1987), acceptor quinones (Radmer and Kok, 1973; Diner, 1977; Rutherford et al., 1982; Robinson and Crofts, 1983), or cyt b559 (Buser et al., 1992). It was also shown that 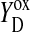Inline graphic could oxidize S0 to S1 in a pH-dependent manner (Plijter et al., 1986; Vass and Styring, 1991; Messinger and Renger, 1994).

Small exogenous reductants like hydrazine and hydroxylamine can generate additional super-reduced S-states (S−1, S−2, and S−3) of the OEC (Bouges, 1971; Messinger et al., 1991, 1997). It has been also noticed that formal introduction of the S−1 state, even in the absence of exogenous reductants, frequently improves the fitting of observed O2 evolution sequences (Bader et al., 1983; Messinger et al., 1993; Meunier et al., 1996; Isgandarova et al., 2003). However, in the latter case it is not clear if other extensions of the classic Kok model, such as S-state or flash-number dependence of misses, could provide similar improvement of the fitting (Isgandarova et al., 2003).

Over the years, many different extensions of the original Kok model have been proposed to explain different aspects of oxygen evolution. These include the introduction of additional states (see e.g., Bouges, 1971; Messinger et al., 1997; Isgandarova et al., 2003); additional transition probabilities (Delrieu and Rosengard, 1987; Meunier, 1993); or even an additional S-state cycle (Shinkarev and Wraight, 1993a). The dependence of transition probabilities on the S-state (Delrieu, 1974; Shinkarev and Wraight, 1993a,b), on flash-number (Meunier and Popovic, 1989), or upon relaxation between flashes (Joliot and Kok, 1975; Meunier et al., 1996), were also frequently considered.

Delrieu and Rosengard (1987) suggested that the classic Kok model should be extended to include flash-induced inactivation of the PSII, which is frequently observed experimentally (see e.g., Delrieu et al., 1985; Delrieu and Rosengard, 1987; Messinger et al., 1997). It is believed that many different factors are contributing to the observed effect, including the reduction of acceptor quinones influenced by the negative potential of the bare Pt-electrode and by electron balancing between photosystems.

In addition to misses and double-hits, Packham et al. (1988) introduced backward-transitions (double-misses), which could reflect dark relaxation of S-states between flashes (see e.g., Packham et al., 1988; Meunier, 1993; Meunier et al., 1996; Quigg et al., 2003).

Many advanced and frequently complicated procedures were developed and used previously to estimate values of parameters of different Kok models (see e.g., Delrieu, 1974; Lavorel, 1976; Beckwith and Jursinic, 1982; Lavergne, 1987, 1991; Messinger et al., 1991; Meunier, 1993; Meunier et al., 1996; Isgandarova et al., 2003). These numerical procedures are especially useful for the analysis of the extended S-state models (see e.g., Meunier et al., 1996; Isgandarova et al., 2003), which include additional S-states, additional transition probabilities, or relaxation between flashes, for which a simple analytical solution is not yet known. However, in the case of the classic Kok model, it is significantly easier to use a recently found, simple solution (Shinkarev, 2003).

In this article we obtain an analytical solution for the extended Kok model (four S-states, one inactive state, a miss, a double-hit, a backward-transition, and an inactivation). Developed equations significantly simplify the fitting of experimental data via standard nonlinear regression analysis.

RESULTS

Analytical solution for the extended Kok model with inactivation and backward-transitions incorporated

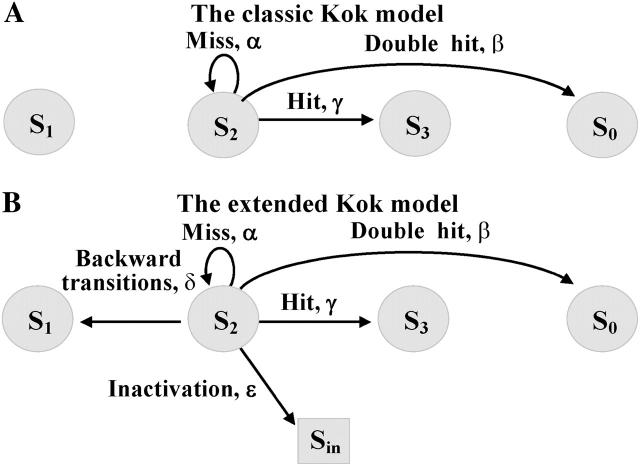
In the classic Kok model, four formal stable states with a differing number of oxidizing equivalents, S0, S1, S2, and S3, are used to describe observed oscillations of oxygen evolution (Kok et al., 1970). In addition to that we will assume the presence of an inactive stable state of OEC, i.e., Sin (Delrieu and Rosengard, 1987). Kok originally suggested that, for each S-state, the flash could induce only three transitions: miss (zero-step advance, α); hit (one-step advance, γ); and double-hit (two-step advance, β)—only two of which are independent. In the extended Kok model considered here we will assume also that each flash can induce inactivation of the PSII with probability ɛ, and can induce the backward-transition (Packham et al., 1988) with probability δ. Fig. 3 shows the transition probabilities in the classic (A) and in the extended (B) Kok models.

FIGURE 3.

FIGURE 3

Open in a new tab

Flash-induced transitions for S-states in the classic (A) and extended (B) Kok models of O2 evolution. For simplicity, only transitions for S2 are shown. The classic Kok model (A) has four stable states, whereas the extended Kok model (B) has five stable states, one of which (Sin) is an inactive state of OEC.

Lavorel (1976) noticed that the Kok model is a classic Markov chain (see e.g., Feller, 1968). In this model, flash-induced transitions between discrete states of an oxygen-evolving complex are described by taking into account all possible transitions of the given state after one flash. The matrix of one-step transition probabilities describes these possible transitions. As a result, the time evolution of the Markov chain could be described via the initial state of the chain and the one-step transition probabilities. The matrix of one-step transition probabilities for the extended Kok model can be presented in the form

graphic file with name M5.gif (1)

Here each element mij of the matrix M is the probability of transition between states Si−1 and Sj−1 (i,j ≤ 4). The inactive state, Sin, is the fifth state. For each row the sum of transition probabilities should be equal to 1, so we assume that α + β + γ + δ + ɛ = 1. We use here traditional notations for transition probabilities—namely, α for miss, γ for hit, β for double-hit, δ for backward-transition, and ɛ for inactivation. Note that these notations are different from those of Shinkarev (2003), who used alphabetical ordering of transition probabilities (a for miss, b for hit, and c for double-hit). We also use here a new notation for the matrix of one-step transition probabilities. The previously used notation (Q) is replaced here by M to avoid confusion with notation for acceptor quinones. Other than that, the procedure of obtaining the solution of the extended Kok model is quite similar to that used previously for the classic Kok model and is repeated here briefly.

Let s(n) = (s0(n), s1(n), s2(n), s3(n), sin(n)) be the row-vector of probabilities of S-states, where si(n) is the probability to find the OEC of PSII in the Si state (i = 0,1,2,3), or in the inactive state Sin, sin(n), after the nth flash (n = 0,1,2,…). For n = 0 row vector, s(0) = (s0(0), s1(0), s2(0), s3(0), sin(0)) ≡ (s0, s1, s2, s3, sin) describes initial (before-the-first-flash) conditions. The probabilities of individual S-states after the nth flash can be found by application of a matrix M of one-step transition probabilities to a row-vector of probabilities of S-states after n−1 flash,

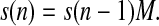graphic file with name M6.gif (2)

Frequently Eq. 2 is written via column-vectors, s(n)T = MTs(n−1)T (see e.g., Delrieu, 1974; Lavorel, 1976; Messinger et al., 1991; Isgandarova et al., 2003). We still prefer the form of Eq. 2 because in this case matrix M has direct probabilistic interpretation, namely each element mij of the matrix M is the probability of transition between states i and j.

The probability for OEC to be in a certain state after the nth flash is given by the respective component of the vector s(n) = (s0(n), s1(n), s2(n), s3(n), sin(n)), which can be evaluated by iterating Eq. 2, as

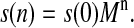graphic file with name M7.gif (3)

The matrix M can be diagonalized with matrix U, such that

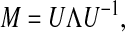graphic file with name M8.gif (4)

where Λ is the diagonal matrix with eigenvalues of matrix M as

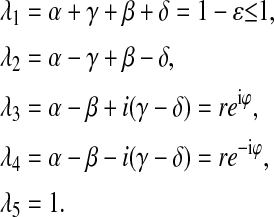graphic file with name M9.gif (5)

Here α, γ, β, and δ are miss, hit, double-hit, and backward-transition, respectively; ɛ is the probability of inactivation; r = [(α−β)2 + (γ−δ)2]1/2; and ϕ = arcsin((γ−δ)/r), i2 = −1.

Thus, Eq. 3 can be written as

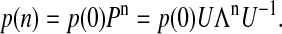graphic file with name M10.gif (6)

This gives us the possibility to calculate the probabilities (fractions) of individual S-states as a function of the flash-number for the extended Kok model with inactivation and backward-transitions,

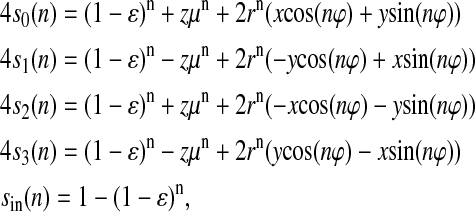graphic file with name M11.gif (7)

where μ ≡ α−γ + β−δ; r ≡ [(α−β)2 + (γ−δ)2]1/2; ϕ ≡ arcsin((γ−δ)/r); n is the number of flashes; si = si(0) are initial conditions for Si; x ≡ s0−s2; y ≡ s3−s1; and z ≡ s0−s1 + s2−s3.

Equation 7 for the flash-number dependence of individual S-states for arbitrary initial conditions takes the following form in the case of the classic Kok model with zero backward-transitions (δ = 0) and zero inactivation (ɛ = 0),

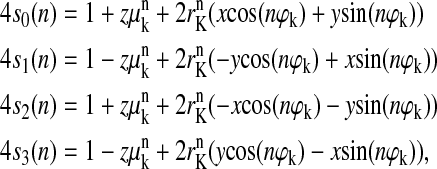graphic file with name M12.gif (8)

where μK = α−γ + β = 1−2γ; rK = [(α−β)2 + γ2]1/2; and ϕK = arcsin(γ/rK). All other parameters are as in Eq. 7.

Thus, we see that there is no significant difference in general expression for flash-number dependence of individual S-states in the original (classic) Kok model (Eq. 8) and in the extended Kok model (Eq. 7)—although the latter can take into account two additional parameters, which reflects the inactivation and relaxation between flashes. Equation 8 is identical to that obtained by Shinkarev (2003), but was written here using traditional notations for transition probabilities and simplified notations for probabilities (fractions) of S-states and other terms.

Oxygen evolution by PSII after the nth flash is determined by probabilities of S-states after the n−1 flash,

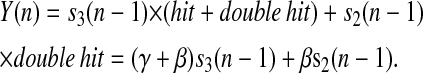graphic file with name M13.gif (9)

Binary oscillations of semiquinone in PSII and release of electrons from PSII

In the case of the classic Kok model, the equation for behavior of the acceptor side of PSII can be obtained by summing the solutions for the respective S-states (Shinkarev, 1996, 2003). A similar result is valid for the extended Kok model considered here. For example, by adding p0 and p2 from Eq. 7, one can obtain the equation for binary oscillations of 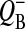Inline graphic as a function of flash-number, n,

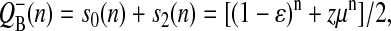graphic file with name M15.gif (10)

where ɛ is inactivation factor; α is miss; β is double-hit; γ is the hit; δ is the backward-transition μ ≡ α−γ + β−δ; and z ≡ s0−s1 + s2−s3.

Usually hit, γ, is close to 1, whereas miss, α, and double-hit, β, are closer to 0. As a result, the term μ = α−γ + β−δ is negative. In this case μn is positive for each even n, and is negative for each odd n. This alternating adding and subtracting of μn in Eq. 10 is the source of binary oscillations. The amplitude of these binary oscillations is modulated by initial conditions for S-states, z ≡ s0−s1 + s2−s3.

The determined flash-number dependence of semiquinone allows one to estimate the release of reducing equivalents from the acceptor side of PSII and periodic activation of the b6f complex by plastoquinol. The amount of plastoquinol formed in PSII immediately after the nth flash is proportional to the semiquinone formed by the previous flash.

Analysis of model data with the classic and extended Kok models

To check the applicability of Eqs. 7 and 9 for parameter estimation we synthesized the extended Kok model curve for oxygen yields with the following parameters: n = 20; α = 0.1; β = 0.03; δ = 0.02; ɛ = 0.01; s0 = 0.23; s1 = 0.7; s2 = 0.02; and s3 = 0.05, and added 1% or 5% random noise to it. Parameters were estimated by using the nonlinear least-squares curve fitter provided in Origin 6.1 software (OriginLabs, Northampton, MA). The advantage of this fitter and other analogous fitters is the possibility of estimation of standard errors for individual parameters. The other advantage is the ability to use any data points of the curve to find parameters during the fitting procedure. The application of nonlinear regression analysis to the model curve with 1% noise gave parameter values that were almost identical to those of the original curve, namely: α = 0.1 ± 0.002; β = 0.03 ± 0.002; δ = 0.018 ± 0.002; ɛ = 0.01 ± 0.001; s0 = 0.23 ± 0.004; s1 = 0.7 ± 0.01; and s2 = 0.017 ± 0.003. Similarly, the model curve with 5% random noise gave the following parameters: α = 0.11 ± 0.01; β = 0.030 ± 0.005; δ = 0.016 ± 0.005; ɛ = 0.009 ± 0.001; s0 = 0.21 ± 0.02; s1 = 0.69 ± 0.02; and s2 = 0.05 ± 0.02. We conclude that the nonlinear regression analysis provides reasonable values for all unknown parameters of the extended Kok model, even with a 5% noise level.

When the same curve with a 5% noise level was analyzed using the classic Kok model, we obtained the following parameters: α = 0.14 ± 0.01; β = 0.04 ± 0.01; s0 = 0.13 ± 0.04; s1 = 0.79 ± 0.05; and s2 = 0.014 ± 0.031. The data illustrate that if a model does not have some parameters (here we disregarded inactivation and backward-transitions), the artificial values could be assigned during the fitting procedure to included parameters to compensate for the effects of those absent. In this particular case, larger values of miss (0.14 instead of 0.1) and double-hit (0.04 instead of 0.03), as well as redistribution of initial conditions for S-states, are needed to compensate for the absence of ɛ and δ.

Analysis of experimental data with the classic and extended Kok models

Simultaneous analysis of all data points

Table 1 shows the parameters of the classic and extended Kok models determined from the data of Forbush et al. (1971) shown in Fig. 1. The extended Kok model gave smaller values for misses and double-hits in the studied data set. The inactivation parameter was significantly less than double-hit, whereas the value of backward-transition was similar to that of double-hit. The classic and extended Kok models gave similar values of initial conditions for S-states. During the fitting procedure it was assumed that all initial conditions are non-negative.

TABLE 1.

Parameters of the classic and extended Kok model determined for the data of Forbush et al. (1971) shown in Fig. 1

Model Classic (Eqs. 8 and 9) Extended (Eqs. 7 and 9)
Flashes used 1–24 1–24
Miss, α 0.084 ± 0.003 0.072 ± 0.004
Double-hit, β 0.028 ± 0.002 0.018 ± 0.004
Inactivation, ɛ — −0.001 ± 0.001
Backward-transition, δ — 0.013 ± 0.004
Initial condition for S0 0.25 ± 0.02 0.26 ± 0.01
Initial condition for S1 0.73 ± 0.02 0.72 ± 0.02
Initial condition for S2 0 0.01 ± 0.01
Initial condition for S3 ∼0.02* ∼0.01*
Error (reduced χ-square) 0.00026 0.00015
Open in a new tab
*

Calculated as (1 − ɛ)n −s0 − s1−s2.

From comparison of data presented in Table 1 we conclude that the application of the extended model gives results close, but not identical, to those of the classic Kok model.

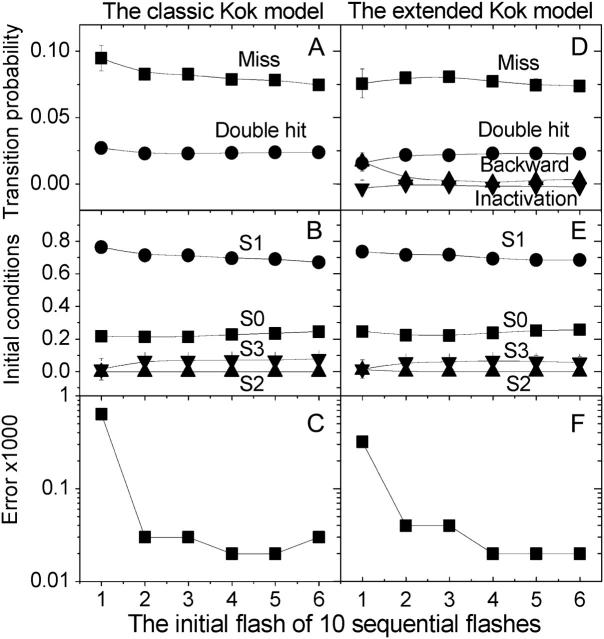
Analysis of flash-number dependence using moving window of 10 flashes

Fig. 4 shows the results of fitting of data of Forbush et al. (1971) using either the classic Kok model (Fig. 4, A–C) or the extended Kok model (Fig. 4, D–F) determined from 10 consecutive flashes. The classic and the extended Kok models gave almost identical parameters when determined from flashes 2–11, 3–12, etc. The main difference is observed for parameters determined for flashes 1–10.

FIGURE 4.

FIGURE 4

Open in a new tab

Analysis of the data of Forbush et al. (1971) using the classic Kok model (A–C) and the extended Kok model (D–F). Ten sequential oxygen evolution yields were used for the estimation of parameters of the model. Parameters determined from oxygen yields induced by flashes 1–10 are shown for the initial flash-number 1; parameters determined from flashes 2–11 are shown for the initial flash-number 2; etc. (A) Misses and double-hits; (B) initial conditions for S-states; (C) errors; (D) misses and double-hits; (E) initial conditions for S-states; and (F) errors. Calculations in A–C were made using Eqs. 8 and 9, whereas calculations in D–F were made using Eqs. 7 and 9. All calculations were made using the nonlinear least-squares curve fitter provided in Origin 6.1 software (OriginLabs, Northampton, MA). No boundary was assumed for the inactivation parameter during the fitting. All other parameters and initial conditions were assumed to be non-negative. Errors in C and F are calculated using the expression [Σi(yi −f(ni))2]/(N–p), where yi and f(xi) are the measured and the calculated oxygen yields induced by the flash ni, respectively; N is the number of data points used in the fit (here N = 10); and p is the number of free parameters in the fit (p = 5 in the case of the classic Kok model and p = 7 in the case of the extended Kok model).

The initial value for S1 is decreasing steadily whereas the initial value for S0 slightly increases. The initial condition for S2 is close to 0 for all flashes. The initial state for S3 increases after the initial flash and stays at ∼6% thereafter. Non-zero values of initial conditions for S3 were reported previously (see e.g., Bader et al., 1983; Burda and Schmid, 2001).

When first-flash is included into calculations, the fitting error is almost one order-of-magnitude larger than when it is excluded from the analysis.

DISCUSSION

The extended Kok model

Many different extensions of the original Kok model were suggested over the years to explain particular experiments. These include introduction of additional states (Bouges, 1971; Messinger et al., 1993; 1997; Meunier et al., 1996; Isgandarova et al., 2003); flash-induced inactivation of reaction centers (Delrieu and Rosengard, 1987, 1988; Messinger et al., 1997); backward-transitions (Packham et al., 1988; Meunier, 1993; Meunier et al., 1996; Quigg et al., 2003); and others. Here we considered only extension of the Kok model, which includes inactivation and backward-transitions. This satisfied the need to keep a reasonable balance between the simplicity of the solution and the number of parameters and states to be analyzed.

The significant advantage of the model developed here is its close identity with the classic Kok model (Kok et al., 1970), wherein both extra parameters, δ (backward-transition) and ɛ (inactivation), are set to 0. Simple equations describing the flash-number dependence of individual S-states and oxygen evolution in both cases are almost identical, meaning that the classic Kok model does not offer a significant advantage in simplicity over the extended Kok model that is used here. At the same time, the extended model also allows us to determine inactivation and backward-transitions if they play some role in a particular case.

In some sense, one can consider the solution developed here as an analog of application of the Michaelis-Menten equation to the enzyme catalysis. Both of these equations are wrong in most actual cases but, nevertheless, they are the simplest models available and should be the standard models used for the analysis of experimental data, unless experiments indicate otherwise.

The inactivation parameter in the extended Kok model

The extended Kok model considered here allows extracting information about the parameter, ɛ, which can be interpreted as the fraction of centers inactivated after each flash of the series. This parameter is directly connected to the parameter z, introduced by Delrieu and Rosengard (1987, 1988), which characterizes the fraction of centers remaining active in oxygen evolution after each flash of the series (ɛ = 1−z). According to Delrieu and Rosengard (1987), the value of ɛ = 1−z depends on the flash intensity and sample type, and in many cases is larger than double-hit.

Unexpectedly, our analysis presented in Fig. 4 revealed that, in the case of the data of Forbush et al. (1971), the inactivation is insignificant and is less than double-hit. The small inactivation in this particular case is possibly due to a modulated detecting beam of long wavelength (λ ≥ 700 nm) used by the authors “to insure oxidation of Q and A and optimal performance of system II” (Forbush et al., 1971).

It should be stressed, however, that in many cases good fitting of the original sequence of oxygen evolution is impossible without taking into account either inactivation (see e.g., Delrieu and Rosengard, 1987, 1988), or backward-transitions (see e.g., Meunier et al., 1996), or both. Data presented in a recent article by Clausen et al. (2004, Fig. 1) are typical in this respect. The classic Kok model gives poor fitting with miss, 0.143 ± 0.023; double-hit, 0.043 ± 0.021; and error, 0.004. The extended Kok model gives significantly better fitting with miss, 0.097 ± 0.007; double-hit, 0.028 ± 0.006; backward-transition, 0.020 ± 0.008; inactivation, 0.020 ± 0.001; and error, 0.0001.

Expressions for s0(n), …, s3(n) in Eq. 7 have meaning for both positive and negative ɛ, although, originally, it was expected to be only non-negative. Indeed, according to Eq. 7 the sum s0(n) + s1(n) + s2(n) + s3(n) is equal to (1−ɛ)n. So for negative ɛ this sum increases with n, which can be interpreted as activation. This is the main reason why no boundary was assumed for the inactivation parameter during the fitting of experimental data.

To describe the change of the number of active PSII centers during the flash series, Messinger et al. (1997) suggested using the parameter d in Eq. 2, s(n) = s(n−1)Md. The introduction of this parameter is equivalent to simultaneous normalization of parameters of the Kok model in Eq. 7, using the following replacements: 1−ɛ → (1−ɛ)/d, μ→ μ/d and r→ r/d. Thus, the parameter d could be significantly different from the inactivation parameter ɛ considered in this article.

The backward-transition parameter in the extended Kok model

The parameter, δ, corresponds to the flash-induced backward-transition and is sometimes called double-miss (Packham et al., 1988). The meaning of this parameter is blurred. Due to the symmetry of the S-state transitions, one step back is the same as three steps forward. Thus, this parameter can also be considered as a triple-hit. However, the probability of triple-hit is negligible, so, as a first approximation, one can interpret δ only as a parameter responsible for the relaxation of S-states between flashes (Meunier, 1993; Meunier et al., 1996). It was suggested that backward-transition could be a result of a single hit combined with two deactivations from S3 to S1 (Packham et al., 1988; Meunier 1993).

In the simple extension of the Kok model considered here we assume, for simplicity, that this backward-transition probability is the same for each S-state. In reality, they should be S-state-dependent, because only S3 and S2 deactivate quickly enough to influence the S-state distribution between flashes. Thus, independence of δ on S-states is only a first approximation to the real situation. When all flashes were considered for the data set of Forbush et al. (1971), the value of backward-transition was found to be comparable to double-hit (Table 1). However, when only 10 flashes were used for analysis, the backward-transitions were significant only for the first few initial flashes (Fig. 4).

Meaning of the parameters of the Kok model

It is clear now that some of the original postulates of the Kok model should be modified (for example, misses are different for each S-state, the initial conditions should be different, etc.), or extended. Thus, the classic Kok model is just convenient first-order approximation to the real case. Despite the original intention, the classic Kok model approximates the observed oxygen evolution with some apparent parameters. The current consensus in the field is that the classic Kok model can be used for semiquantitative analysis of the oxygen evolution and S-states transitions, if only one interprets the determined misses and double-hits as average values. Similarly, one can expect that additional transitional probabilities in the extended Kok model also can be interpreted as representing average values, namely, ɛ = ɛav = (ɛ0 + ɛ1 + ɛ2 + ɛ3)/4, δ = δav = (δ0 + δ1 + δ2 + δ3)/4.

The values of determined parameters could significantly depend on the model used. When the classic and extended Kok models were applied to Forbush et al. (1971) data, the values of misses and double-hits were significantly different when determined from the first 10 sequential flashes. Thus, if the model does not have some of its parameters (as in the classical Kok model, which disregards inactivation and backward-transitions), the artificial values could be assigned during the fitting procedure to included parameters to compensate for the effects of the absent parameters. Therefore, we conclude that in rationalizing the observed values of parameters of the extended Kok model, one can suggest either their mechanistic interpretation, or assume that the observed parameters are the result of application of an oversimplified model. Frequently both of them are needed to explain a particular case.

The meaning of different parameters in the Kok model can be clarified by using dynamic models, which include kinetics and thermodynamic information about PSII and allow easy incorporation of relaxation of S-states between flashes (see e.g., Shinkarev and Wraight, 1993a,b). The main conclusion from application of this approach is that all parameters of the Kok model are S-state-dependent and frequently flash-number-dependent.

Flash-number dependence of parameters

The flash-number dependence of the parameters of the Kok model could provide useful insight into mechanism of oxygen evolution. Previously such analysis was done using so-called sigma analysis, which frequently disregards information about initial conditions (Lavorel, 1976; Meunier and Popovic, 1989). As far as we know, this is the first report of direct calculation of flash-number dependence of all parameters of the Kok model to include initial conditions.

One can notice several trends in the flash-number dependencies of some parameters in Fig. 4, which are common for both the classic and the extended Kok models. These include the decrease of the miss factor and the initial condition for S1 with the flash-number. The decrease of miss with the flash-number was also observed by Meunier and Popovic (1989), who connected it to the changes of the redox state of the plastoquinone pool.

The significant difference between parameters observed for windows including or excluding the first flash (Fig. 4) is possibly due to the presence of YD, which donates electrons to the S-states after the first flash (Velthuys and Visser, 1975; Vermaas et al., 1984; Styring and Rutherford, 1987; Naber, 1989; Isgandarova et al., 2003). An extension of the Kok model of oxygen evolution, which takes into account the effect of electron donation from YD, has been suggested by Vass et al. (1990) and by Isgandarova et al. (2003), and is not considered here.

CONCLUSIONS

The Kok model has been successfully used for more than 30 years for interpretation of experimental data. Many advanced methods were developed over the years to estimate the values of parameters of the Kok model because a simple analytical solution for the oxygen evolution was unknown. Here we developed a simple analytical solution for the extended Kok model, which, in addition to misses and double-hits, also includes flash-induced inactivation and backward-transitions. The classic Kok model can be used as a particular case of this extended model. Simple equations developed for the extended Kok model significantly simplify the fitting of experimental data via the nonlinear regression analysis tools commonly present in standard data analysis packages. As a result, it made the use of previously developed (and frequently complicated) methods for the analysis of this version of the Kok model, unnecessary. With this simple solution, the main problem is shifting from finding the value of parameters to their interpretation.

The comparison of parameters, determined for the same data set using both the classic and the extended Kok models, shows that the artificial values could be assigned to misses and double-hits in the classic Kok model to compensate for effects of absent parameters responsible for the dark relaxation of PSII between flashes and inactivation.

Binary oscillations of the secondary acceptor, semiquinone, at the acceptor side of the reaction center of PSII, and the release of reducing equivalents to the b6f complex, can also be determined in the framework of the extended Kok model. Hence, the extended Kok model considered in this article allows the simultaneous description of individual S-states, oxygen evolution, and acceptor quinone states, and provides a basis for the quantitative description of the charge accumulation processes at the donor and acceptor sides of Photosystem II.

Acknowledgments

This work was partially supported by United States Department of Agriculture grant 9401725 and by National Institutes of Health grant GM 53508.

APPENDIX: ABBREVIATIONS

MK, M, matrices of one-step transition probabilities for the classic Kok model, and for the extended Kok model with both inactivation and backward-transitions, respectively.

  • n, the number of flashes.

  • OEC, oxygen evolving complex.

  • P680, primary electron donor of the reaction center of PSII.

  • PSII, Photosystem II.

  • QA, primary acceptor plastoquinone.

  • r ≡ [(α−β)2 + (γ−δ)2]1/2.

  • rK ≡ [(α−β)2 + γ2]1/2.

  • s(0), the row vector of initial conditions, s(0) = (s0(0), s1(0), s2(0), s3(0), sin(0)) ≡ (s0, s1, s2, s3, sin).

  • s(n), the row vector of probabilities of S-states after the nth flash, s(n) = (s0(n), s1(n), s2(n), s3(n), sin(n)) in the extended Kok model.

  • si, initial conditions for ith S-state, s0 = s0(0), s1 = s1(0), s2 = s2(0), s3 = s3(0).

  • si(n), the probability (fraction) of the Si state after the nth flash.

  • Sin, inactive state of the OEC.

  • sin(n), the probability (fraction) of the inactive state of OEC after the nth flash.

  • Sn, redox states of the OEC, where n = 0,1,2,3 represents the number of oxidizing equivalents.

  • U, matrix, transforming matrix M to diagonal form.

  • x ≡ s0−s2.

  • y ≡ s3−s1.

  • Y(n), oxygen yield after the nth flash.

  • YD, redox active tyrosine slowly interacting with S-states.

  • YZ, redox active tyrosine, fast electron donor to P680.

  • z ≡ s0−s1 + s2−s3.

  • α, traditionally used notation for the miss (zero-step advancement) in the Kok model.

  • β, traditionally used notation for the double-hit (two-step advancement) in the Kok model.

  • γ, traditionally used notation for the hit (one-step advancement) in the Kok model.

  • δ, the probability of backward-transition.

  • ɛ, the probability of inactivation.

  • μ ≡ α−γ + β−δ.

  • μK, value of μ in the classic Kok model, μK ≡ α−γ + β = 1−2γ.

  • λ1,…, λ5, eigenvalues of matrix M.

  • Λ, the diagonal matrix with eigenvalues λ1, …, λ5 of matrix M.

  • ϕ ≡ arcsin((γ−δ)/r).

  • ϕK, value of ϕ in the classic Kok model (ϕK = arcsin(γ/rK)).

References

  1. Babcock, G. T., and K. Sauer. 1973. Electron paramagnetic resonance signal in spinach chloroplasts. I. Kinetic analysis for untreated chloroplasts. Biochim. Biophys. Acta. 325:483–503. [DOI] [PubMed] [Google Scholar]
  2. Bader, K. P., P. Thibault, and G. H. Schmid. 1983. A study on oxygen evolution and on the S-state distribution in thylakoid preparations of the filamentous blue-green alga Oscillatoria chatybea. Z. Naturforsch. 38c:778–792. [Google Scholar]
  3. Beckwith, A. C., and P. A. Jursinic. 1982. An alternative approach to the analysis of photosynthetic oxygen evolution. J. Theor. Biol. 97:251–265. [Google Scholar]
  4. Blankenship, R. E. 2002. Molecular Mechanisms of Photosynthesis. Blackwell Science, Oxford, UK.
  5. Bouges, B. 1971. Effect of small hydroxylamine concentrations on the oxygen evolution by Chlorella and spinach chloroplasts. Biochim. Biophys. Acta. 234:103–112. [DOI] [PubMed] [Google Scholar]
  6. Bouges-Bocquet, B. 1980. Kinetic models for the electron donors of Photosystem II of photosynthesis. Biochim. Biophys. Acta. 594:85–103. [DOI] [PubMed] [Google Scholar]
  7. Burda, K., and G. H. Schmid. 2001. Heterogeneity of the mechanism of water splitting in photosystem II. Biochim. Biophys. Acta 1506:47–54. [DOI] [PubMed] [Google Scholar]
  8. Buser, C. A., B. A. Diner, and G. W. Brudvig. 1992. Photooxidation of cytochrome B559 in oxygen-evolving Photosystem. Biochemistry. 31:11449–11459. [DOI] [PubMed] [Google Scholar]
  9. Clausen, J., R. J. Debus, and W. Junge. 2004. Time-resolved oxygen production by PSII: chasing chemical intermediates. Biochim. Biophys. Acta. 1655:184–194. [DOI] [PubMed] [Google Scholar]
  10. Cramer, W. A., and D. B. Knaff. 1990. Energy Transduction in Biological Membranes. Springer-Verlag, New York.
  11. de Wijn, R., and H. J. van Gorkom. 2002. S-state dependence of the miss probability in Photosystem II. Photosynth. Res. 72:217–222. [DOI] [PubMed] [Google Scholar]
  12. Debus, R. J. 1992. The manganese and calcium ions of photosynthetic oxygen evolution. Biochim. Biophys. Acta. 1102:269–352. [DOI] [PubMed] [Google Scholar]
  13. Delrieu, M. J. 1974. Simple explanation of the misses in the cooperation of charges in photosynthetic oxygen evolution. Photochem. Photobiol. 20:441–454. [Google Scholar]
  14. Delrieu, M. J. 1983. Evidence for unequal misses in oxygen flash yield sequence in photosynthesis. Z. Naturforsch. 38c:247–258. [Google Scholar]
  15. Delrieu, M. J., and F. Rosengard. 1987. Fundamental difference between period-4 oscillations of the oxygen and fluorescence yield induced by flash excitation in inside-out thylakoids. Biochim. Biophys. Acta. 892:163–171. [Google Scholar]
  16. Delrieu, M. J., and F. Rosengard. 1988. Characterization of two types of oxygen-evolving Photosystem II reaction centers by the flash-induced oxygen and fluorescence yield. Biochim. Biophys. Acta. 936:39–49. [Google Scholar]
  17. Delrieu, M. J., and F. Rosengard. 1991. Changes in the S0 and S1 properties during dark adaptation in oxygen-evolving Photosystem-II-enriched thylakoid membranes. Biochim. Biophys. Acta. 1057:78–88. [Google Scholar]
  18. Delrieu, M. J., S. H. Hung, and F. de Kouchkovsky. 1985. pH dependence of the S2 → S3 transition associated evolution in inside-out thylakoids. FEBS Lett. 187:321–326. [Google Scholar]
  19. Diner, B. A. 1977. Dependence of the deactivation reactions of Photosystem II on the redox state of plastoquinone pool varied under anaerobic conditions equilibria on the acceptor side of Photosystem II. Biochim. Biophys. Acta. 460:247–258. [DOI] [PubMed] [Google Scholar]
  20. Diner, B. A., and G. T. Babcock. 1996. Structure, dynamics, and energy conversion efficiency in Photosystem II. In Oxygenic Photosynthesis: The Light Reactions. D.R. Ort and C.F. Yocum, editors. 213–247. Kluwer Academic Publishers, Dordrecht, The Netherlands.
  21. Diner, B. A., and V. Petrouleas. 1987. Q400, the non-heme iron of the Photosystem II iron-quinone complex. A spectroscopic probe of quinone and inhibitor binding to the reaction center. Biochim. Biophys. Acta. 895:107–125. [Google Scholar]
  22. Etienne, A. L. 1974. New results on the properties of Photosystem II centers blocked by 3-(3,4-dichlorophenyl)-1,1-dimethylurea in their different photoactive states. Biochim. Biophys. Acta. 333:320–330. [DOI] [PubMed] [Google Scholar]
  23. Feller, W. 1968. An Introduction to the Probability Theory and its Applications, Vol. 1. John Wiley and Sons, New York.
  24. Ferreira, K. N., T. M. Iverson, K. Maghlaoui, J. Barber, and S. Iwata. 2004. Architecture of the photosynthetic oxygen evolving center. Science. 303:1831–1838. [DOI] [PubMed] [Google Scholar]
  25. Forbush, B., B. Kok, and M. McGloin. 1971. Cooperation of charges in photosynthetic O2 evolution-II. Damping of flash yield oscillation, deactivation. Photochem. Photobiol. 14:307–321. [DOI] [PubMed] [Google Scholar]
  26. Isgandarova, S., G. Renger, and J. Messinger. 2003. Functional differences of Photosystem II from Synechococcus elongates and spinach characterized by flash-induced oxygen evolution patterns. Biochemistry. 42:8929–8938. [DOI] [PubMed] [Google Scholar]
  27. Joliot, P., A. Joliot, B. Bouges, and G. Barbieri. 1971. Studies of system II photocenters by comparative measurements of luminescence, fluorescence and oxygen emission. Photochem. Photobiol. 14:287–305. [Google Scholar]
  28. Joliot, P., and B. Kok. 1975. Oxygen evolution in photosynthesis. In Bioenergetics of Photosynthesis. Govindjee, editor. Academic Press, New York. 388–413.
  29. Joliot, P., G. Barbieri, and R. Chabaud. 1969. A new model for the photochemical centers of the system II. Photochem. Photobiol. 10:309–329. [Google Scholar]
  30. Jursinic, P. 1981. Investigation of double turnovers in Photosystem II charge separation and oxygen evolution with excitation flashes of different duration. Biochim. Biophys. Acta. 635:38–52. [DOI] [PubMed] [Google Scholar]
  31. Ke, B. 2001. Photosynthesis: Photobiochemistry and Photobiophysics. Kluwer, Dordrecht, The Netherlands.
  32. Kok, B., B. Forbush, and M. McGloin. 1970. Cooperation of charges in photosynthetic O2 evolution. I. A linear four-step mechanism. Photochem. Photobiol. 11:467–475. [DOI] [PubMed] [Google Scholar]
  33. Lavergne, J. 1987. Optical-difference spectra of the S-state transitions in the photosynthetic oxygen-evolving complex. Biochim. Biophys. Acta. 894:91–107. [Google Scholar]
  34. Lavergne, J. 1991. Improved UV-visible spectra of the S-transitions in the photosynthetic oxygen-evolving system. Biochim. Biophys. Acta. 1060:175–188. [Google Scholar]
  35. Lavorel, J. 1976. Matrix analysis of the oxygen evolving system of photosynthesis. J. Theor. Biol. 57:171–185. [DOI] [PubMed] [Google Scholar]
  36. Lavorel, J., and C. Lemasson. 1976. Anomalies in the kinetics of photosynthetic oxygen emission in sequences of flashes revealed by matrix analysis effects of carbonyl cyanide m-chlorophenylhydrazone and variation in time parameters. Biochim. Biophys. Acta. 430:501–516. [DOI] [PubMed] [Google Scholar]
  37. Lemasson, C., and A. L. Etienne. 1975. Photo-inactivation of system II centers by carbonyl cyanide m-chlorophenylhydrazone in Chlorella pyrenoidosa. Biochim. Biophys. Acta. 408:135–142. [DOI] [PubMed] [Google Scholar]
  38. Mar, T., and Govindjee. 1972. Kinetic models of oxygen evolution in photosynthesis. J. Theor. Biol. 36:427–446. [DOI] [PubMed] [Google Scholar]
  39. Messinger, J., and G. Renger. 1994. Analyses of pH-induced modifications of the period four oscillation of flash-induced oxygen evolution reveal distinct structural changes of the Photosystem II donor side at characteristic pH values. Biochemistry. 33:10896–10905. [DOI] [PubMed] [Google Scholar]
  40. Messinger, J., G. Seaton, T. Wydrzynski, U. Wacker, and G. Renger. 1997. S-3 state of the water oxidase in Photosystem II. Biochemistry. 36:6862–6873. [DOI] [PubMed] [Google Scholar]
  41. Messinger, J., U. Wacker, and G. Renger. 1991. Unusual low reactivity of the water oxidase in redox state S3 toward exogenous reductants. Analysis of the NH20H- and NH2NH2-induced modifications of flash-induced oxygen evolution in isolated spinach thylakoids. Biochemistry. 30:7852–7862. [DOI] [PubMed] [Google Scholar]
  42. Messinger, J., W. P. Schröder, and G. Renger. 1993. Structure-function relations in PSII. Effects of temperature and chaotropic agents on the period four oscillation of flash induced oxygen evolution. Biochemistry. 32:7658–7668. [DOI] [PubMed] [Google Scholar]
  43. Meunier, P. C. 1993. Oxygen evolution by Photosystem II: the contribution of backward-transitions to the anomalous behavior of double-hits revealed by a new analysis method. Photosynth. Res. 36:111–118. [DOI] [PubMed] [Google Scholar]
  44. Meunier, P. C., and R. Popovic. 1989. Evidence for a linear variation of the miss and single-hit S-state probabilities with the flash-number, measured by oxygen evolution in Dunaliella tertiolecta. Photosynth. Res. 22:131–136. [DOI] [PubMed] [Google Scholar]
  45. Meunier, P. C., R. L. Burnap, and L. A. Sherman. 1996. Improved five-step modeling of the Photosystem II S-state mechanism in cyanobacteria. Photosynth. Res. 47:61–76. [DOI] [PubMed] [Google Scholar]
  46. Naber, J. D. 1989. Molecular aspects of herbicide binding in chloroplasts. Thesis. Wageningen University, Wageningen, The Netherlands.
  47. Packham, N. K., M. Hodges, A. L. Etienne, and J. M. Briantais. 1988. Changes in flash-induced oxygen yield pattern by thylakoid membrane phosphorylation. Photosynth. Res. 15:221–232. [DOI] [PubMed] [Google Scholar]
  48. Plijter, J. J., A. de Groot, M. A. van Dijk, and H. J. van Gorkom. 1986. Destabilization by high pH of the S-state of the oxygen-evolving complex in Photosystem II particles. FEBS Lett. 195:313–318. [Google Scholar]
  49. Quigg, A., J. Beardall, and T. Wydrzynski. 2003. Photoacclimation involves modulation of the photosynthetic oxygen-evolving reactions in Dunaliella tertiolecta and Phaeodactylum tricornutum. Funct. Plant Biol. 30:301–308. [DOI] [PubMed] [Google Scholar]
  50. Radmer, R., and B. Kok. 1973. A kinetic analysis of the oxidizing and reducing sides of the oxygen evolving system of photosynthesis. Biochim. Biophys. Acta. 314:28–41. [DOI] [PubMed] [Google Scholar]
  51. Renger, G. 2003. Apparatus and mechanism of photosynthetic oxygen evolution: a personal perspective. Photosynth. Res. 76:269–288. [DOI] [PubMed] [Google Scholar]
  52. Renger, G. 2004. Coupling of electron and proton transfer in oxidative water cleavage in photosynthesis. Biochim. Biophys. Acta. 1655:195–204. [DOI] [PubMed] [Google Scholar]
  53. Renger, G., and B. Hanssum. 1988. Studies on the deconvolution of flash induced absorption changes into the difference spectra of individual redox steps within the water oxidizing enzyme system. Photosynth. Res. 16:243–259. [DOI] [PubMed] [Google Scholar]
  54. Robinson, H. H., and A. R. Crofts. 1983. Kinetics of the oxidation-reduction reactions of the Photosystem II quinone acceptor complex, and the pathway for deactivation. FEBS Lett. 153:221–226. [Google Scholar]
  55. Rutherford, A. W., A. R. Crofts, and Y. Inoue. 1982. Thermoluminescence as a probe of Photosystem II photochemistry the origin of the flash-induced glow peaks. Biochim. Biophys. Acta. 682:457–465. [Google Scholar]
  56. Shinkarev, V. P., and C. A. Wraight. 1993a. Oxygen evolution in photosynthesis: from unicycle to bicycle. Proc. Natl. Acad. Sci. USA. 90:1834–1838. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Shinkarev, V. P., and C. A. Wraight. 1993b. Kinetic factors in the bicycle model of oxygen evolution by Photosystem II. Photosynth. Res. 38:315–321. [DOI] [PubMed] [Google Scholar]
  58. Shinkarev, V. P. 1996. Binary oscillations in the Kok model of oxygen evolution in oxygenic photosynthesis. Photosynth. Res. 48:411–417. [DOI] [PubMed] [Google Scholar]
  59. Shinkarev, V. P. 2003. Oxygen evolution in photosynthesis: simple analytical solution for the Kok model. Biophys. J. 85:435–441. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Shinkarev, V. P. 2005. Flash-induced oxygen evolution and other oscillation processes in Photosystem II. In Photosystem II: The Water/Plastoquinone Oxido-Reductase In Photosynthesis. T. Wydrzynski and K. Satoh, editors. Kluwer Academic Publishers, Dordrecht, The Netherlands.
  61. Styring, S., and A. W. Rutherford. 1987. In the oxygen-evolving complex of Photosystem II the S0 state is oxidized to the S1 state by D+ (signal IIslow). Biochemistry. 26:2401–2405. [Google Scholar]
  62. Thibault, P. 1978. A new attempt to study the oxygen evolving system of photosynthesis: determination of transition probabilities of a state i. J. Theor. Biol. 73:271–284. [DOI] [PubMed] [Google Scholar]
  63. Vass, I., and S. Styring. 1991. pH-dependent charge equilibria between tyrosine-D and the S-states in Photosystem II. Estimation of relative midpoint redox potentials. Biochemistry. 30:830–839. [DOI] [PubMed] [Google Scholar]
  64. Vass, I., Z. Deak, and E. Hideg. 1990. Charge equilibrium between the water-oxidizing complex and the electron donor tyrosine-D in Photosystem II. Biochim. Biophys. Acta. 1017:63–69. [Google Scholar]
  65. Velthuys, B. R., and J. W. M. Visser. 1975. The reactivation of EPR signal II in chloroplasts treated with reduced dichlorophenol-indophenol: evidence against a dark equilibrium between two oxidation states of the oxygen evolving system. FEBS Lett. 55:109–112. [DOI] [PubMed] [Google Scholar]
  66. Vermaas, W. F. J., G. Renger, and G. Dohnt. 1984. The reduction of the oxygen evolving system in chloroplasts by thylakoid components. Biochim. Biophys. Acta. 764:194–202. [Google Scholar]
  67. Weiss, C., and K. Sauer. 1970. Activation kinetics of photosynthetic oxygen evolution under 20–40 nanosecond laser flashes. Photochem. Photobiol. 11:495–501. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES