Abstract
Despite the enormous interest that has been devoted to the study of farnesyltransferase, many questions concerning its catalytic mechanism remain unanswered. In particular, several doubts exist on the structure of the active-site zinc coordination sphere, more precisely on the nature of the fourth ligand, which is displaced during the catalytic reaction by a peptide thiolate. From available crystallographic structures, and mainly from x-ray absorption fine structure data, two possible alternatives emerge: a tightly zinc-bound water molecule or an almost symmetrical bidentate aspartate residue (Asp-297β). In this study, high-level theoretical calculations, with different-sized active site models, were used to elucidate this aspect. Our results demonstrate that both coordination alternatives lie in a notably close energetic proximity, even though the bidentate hypothesis has a somewhat lower energy. The Gibbs reaction and activation energies for the mono-bidentate conversion, as well as the structure for the corresponding transition state, were also determined. Globally, these results indicate that at room temperature the mono-bidentate conversion is reversible and very fast, and that probably both states exist in equilibrium, which suggests that a carboxylate-shift mechanism may have a key role in the farnesylation process by assisting the coordination/displacement of ligands to the zinc ion, thereby controlling the enzyme activity. Based on this equilibrium hypothesis, an explanation for the existing contradictions between the crystallographic and x-ray absorption fine structure results is proposed.
INTRODUCTION
Protein farnesyltransferase (FTase) is a zinc metalloenzyme, comprised of two nonidentical subunits (α and β), that catalyzes the addition of isoprenoid farnesyl, from farnesyl diphosphate (FPP), to a cysteine residue of a protein substrate containing a C-terminal, CAAX motif, in which C is the cysteine that is farnesylated, A is usually an aliphatic amino acid, and X is the terminal amino acid, normally methionine, serine, alanine, or glutamine (Goodman et al., 1990; Reiss et al., 1990, 1991, 1992; Moores et al., 1991). Known substrates for FTase include H-, N-, K-Ras proteins, nuclear lamins A and B, the γ-subunit of heterotrimeric G-proteins, centromeric proteins, and several proteins involved in visual signal transduction (Zhang et al., 1996).
The discovery that Ras proteins are modified by the farnesyl group, and most of all, the finding that such an alteration is critical for the oncogenic forms of these proteins to transform cells (Hancock et al., 1989; Jackson et al., 1990; Kato et al., 1992), has promoted widespread interest in protein farnesylation, because mutant Ras proteins have been implicated in ∼30% of all human cancers (Dolence and Poulter, 1995; James et al., 1996; Takai et al., 2001). Several farnesyltransferase inhibitors (FTIs) have been undergoing clinical trials for the treatment of cancer (Johnston, 2001; Ayral-Kaloustian and Salaski, 2002; Ohkanda et al., 2002), and some are already in an advanced stage of clinical testing (Ayral-Kaloustian and Salaski, 2002; Ohkanda et al., 2002; Huang and Rokosz, 2004; Wiesner et al., 2004). More than 100 patents describing FTIs have been published since 2000 (Huang and Rokosz, 2004). A few recent studies have also suggested FTIs as alternative drugs in the treatment of some diseases caused by pathogens, such as malaria (Chakrabarti et al., 2002; Wiesner et al., 2004) and the African sleeping sickness (Ohkanda et al., 2004), and as antiviral agents against a broad diversity of viruses that use prenylation, by the host FTase, in key aspects of their own life cycles, which includes a large set of medically important viruses but also several potential agents of bioterrorism (Bordier et al., 2003).
Despite the enormous curiosity surrounding FTase research, a significant amount of uncertainties regarding the catalytic mechanism remains. Even the active-site zinc coordination sphere is not exactly defined. It is known that the zinc ion is located in the β-subunit, near the subunit interface (Park et al., 1997) and that it is coordinated by residues Asp-297β, Cys-299β, and His-362β (Dolence et al., 1997; Kral et al., 1997; Park et al., 1997; Fu et al., 1998; Tobin et al., 2003). However, despite the high number of crystallographic structures currently available, doubts exist on the exact nature of the fourth ligand, although it is known that it coordinates through a low Z-atom (nitrogen or oxygen), and that the bond length is approximately within a 2.0–2.2-Å interval (Tobin et al., 2003). This feature is of particular importance for an atomic level understanding of the farnesylation mechanism, because it is this specific ligand that is displaced, during the catalytic reaction, by the CAAX motif cysteine residue from the protein substrate. Furthermore, it is this ligand that subsequently regenerates the zinc environment by replacing the product (or intermediate) (Huang et al., 1997; Tschantz et al., 1997; Long et al., 2002; Tobin et al., 2003) in the zinc coordination sphere, although closing the catalytic cycle still requires the entrance of an additional FPP substrate molecule (Tschantz et al., 1997).
From the reported crystallographic structures (Park et al., 1997; Long et al., 1998; Dunten et al., 1998), and particularly from recent x-ray absorption fine structure (EXAFS) studies (Tobin et al., 2003), two likely possibilities emerge. The first alternative suggests that a water molecule, seen in the 1FT1 crystallographic structure (Park et al., 1997) (the structure without a peptide substrate with a highest resolution) at 2.74 Å from the Zn2+ ion, is actually at a much smaller distance, and coordinates zinc. Within a classical view of the problem, this water molecule would be replaced by the peptide substrate during the reaction, subsequently returning to its place, after the chemical step has taken place, a mechanism extremely common in zinc enzymes (Vallee and Auld, 1990; McCall et al., 2000).
The other hypothesis suggests that residue Asp-297β (with reported Zn-O bond lengths in the 1FT1 structure of 2.00 and 2.56 Å) is in reality an almost symmetrical bidentate ligand. In light of this theory, Asp-297β would change from bidentate to monodentate (carboxylate shift), with the entrance of a CAAX substrate, changing back to bidentate with product (or intermediate) release from the zinc coordination sphere. This could imply an effective mechanism by which the enzyme would facilitate the nucleophilic addition during the prenylation reaction (Tobin et al., 2003).
Even though over the last few years some very interesting results with inhibitors have been obtained (Ayral-Kaloustian and Salaski, 2002; Ohkanda et al., 2002; Huang and Rokosz, 2004; Wiesner et al., 2004), a detailed knowledge on the farnesylation mechanism of the natural substrates of this enzyme is absolutely vital for the rational design and development of more specific enzyme inhibitors, with increased activity and potential value in the treatment of cancer, malaria, sleeping sickness, or even of infections caused by some viruses. However, some key points in the mechanism remain unexplained. The exact nature of the fourth ligand in the zinc coordination sphere is currently one of the most fundamental doubts, because the two possibilities for its identity imply completely different enzymatic mechanisms. Therefore, solving this fundamental dilemma represents a major step in the path toward mastering the FTase activity.
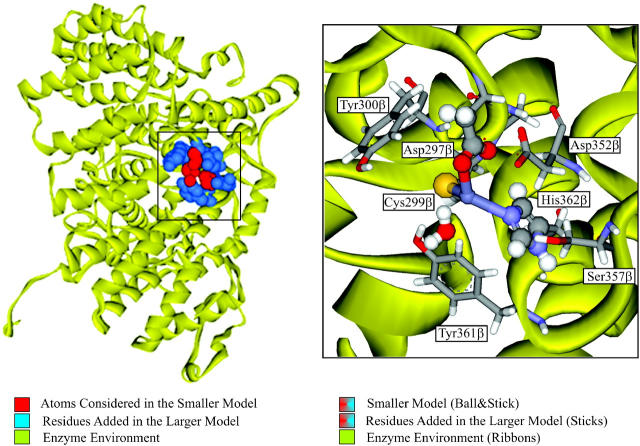
In this study, we have tried to unveil some key features of the farnesylation mechanism, using high-level theoretical calculations, focusing mainly on the zinc's coordination sphere paradigm. The two hypotheses presented above were analyzed using two models of different sizes (see Fig. 1): a smaller active-site model, including the zinc ion and all the residues directly coordinated, and a larger model, which also includes, in a second layer, all the residues within the active site that directly interact with the first coordination sphere of the metal atom, namely through hydrogen bonds. It is well known that enzymes are capable of generating a highly anisotropic environment, and that specific interactions originated by such an environment are usually important for their catalytic effect. The inclusion of a second layer was done with the purpose of accounting for those specific anisotropic interactions and for the mechanical restrictions of the enzyme environment on the first coordination sphere of the zinc ion.
FIGURE 1.
Farnesyltransferase enzyme. Representation of the 1FT1 crystallographic structure (Park et al., 1997), with major emphasis being given to the two models considered in this study.
Globally, the results seem to indicate that the bidentate hypothesis is the most stable. Additionally, the small energetic difference observed between the two coordination alternatives, together with the vanishing energetic barrier determined for the conversion from mono to bidentate, points to a reversible and fast coordination interchange at room temperature, and possibly to the existence of the two states in equilibrium. These aspects are of the uttermost importance to the prenylation reaction indicating that the Asp-297β carboxylate group performs a vital function, via a carboxylate shift mechanism. This carboxylate shift allows the coordination of new ligands to the zinc (changing from bidentate to monodentate) and/or the displacement of ligands (changing from monodentate to bidentate). As a result, the enzyme overall activity is modulated by the carboxylate shift mechanism.
METHODOLOGY
Smaller model
Minima determination and characterization
Calculations were performed on an active site model (smaller model) including the zinc ion and all its ligands (Asp-297β, Cys-299β, His-362β, and water). Conventional modeling of the amino acid side chains was used, that is, the zinc ligands aspartate, cysteinate, and histidine were modeled by acetate, methylthiolate, and imidazole, respectively. The validity of this type of approach has been demonstrated before with great success in the mechanistic study of several different enzymes (Siegbahn, 1998; Melo et al., 1999; Ryde, 1999; Fernandes and Ramos, 2003a,b; Lucas et al., 2003; Pereira et al., 2004). Models were prepared starting from the 1FT1 structure (Park et al., 1997), the crystallographic structure of FTase without a peptidic substrate, or an inhibitor with the highest resolution (2.25 Å).
The geometry of the model was first freely optimized rendering a structure with a monodentate Asp-297β ligand and a water-bound zinc ion (Minimum 1). The water molecule was subsequently removed and the geometry was reoptimized, leading to a structure with an almost symmetrical bidentate Asp-297β ligand. Afterwards, a water molecule was inserted at a 2.74-Å distance from the zinc atom, as reported in the 1FT1 crystallographic structure, and the geometry was again reoptimized, resulting in a structure with an Asp-297β bidentate ligand and a water molecule nonzinc coordinated. This third optimization was by far the most delicate, frequently rendering the same monodentate structure with a zinc-bound water as obtained for Minimum 1. To avoid the risk of being trapped in local minima several starting structures were tested, leading to two different minima (Minima 2 and 3). These starting structures were prepared by changing the orientation of the water molecule in relation to the zinc atom, while keeping the same Zn-water initial distance (2.74 Å). No geometric constraints were imposed on any of the calculations. All calculations were performed using the Gaussian 03 software package (Frisch et al., 2003).
This study makes use of the density functional theory with the B3LYP functional (Lee et al., 1988; Becke, 1993). Density functional theory calculations have been shown to give very accurate results for systems involving transition metals (Ziegler, 1991), particularly when using the B3LYP functional (Bauschlicher, 1995; Holthausen et al., 1995; Ricca and Bauschlicher, 1995). For zinc complexes, the superior accuracy of the B3LYP functional in comparison with Hartree-Fock and second-order Moller-Plesset perturbation theory has also been previously demonstrated (Ryde, 1999). Optimizations were carried out using the SDD basis set, as implemented in Gaussian 03 (Frisch et al., 2003). This basis set uses the small core quasi-relativistic Stoll-Preuss (SP) electron core potentials (also known as Stuttgart-Dresden) (Dolg et al., 1987; Andrae et al., 1990) for transition elements. For zinc, the outer electrons are described by a (311111/22111/411) valence basis specifically optimized for this metal and for use with the SP pseudopotentials. C, N, and O atoms are accounted by a (6111/41) quality basis set, whereas S and H atoms are treated respectively by a (531111/4211) and a (31) quality basis sets. The high-performance of SP pseudopotentials in calculations involving transition metals compounds, particularly within closed-shell systems, has been previously demonstrated (Frenking et al., 1996). The final electronic energies were calculated using the all-electron 6–311+G(2d,2p) basis set. Zero-point corrections, thermal, and entropic effects (T = 310.15 K, P = 1 bar) were added to all calculated energies.
The effect of the environment was evaluated by using a polarized continuum model, the IEF-PCM model, as implemented in Gaussian 03 (Cances et al., 1997; Mennucci and Tomasi, 1997; Cossi et al., 1998, 2002). This model has been shown to give better results for solvents with low dielectric constants than the alternative model C-PCM (Cossi et al., 2003). This feature is of particular importance to the study of enzymatic catalysis because the use of a continuum model is normally taken as an approximation to the effect of the global enzyme environment in a reaction, having been shown in previous studies on active sites in proteins (Blomberg et al., 1998; Siegbahn, 1998; Siegbahn et al., 1998) that an empirical dielectric constant (ɛ) of 4 gives generally good agreement with experimental results, and accounts for the average effect of both the protein and buried water molecules. In this study, IEF-PCM calculations were done primarily using ether as solvent (ɛ = 4.335) in an attempt to reproduce the enzyme global environment. IEF-PCM calculations were later extended to water (ɛ = 78.39), because in FTase the active site is known to be located in a crevice, with significant access to solvent in the absence of the peptide substrate. Previous studies have demonstrated that the effect of the continuum in geometries is, in general, rather small, even in charged systems (Fernandes et al., 2002; Fernandes and Ramos, 2004). Therefore, in all PCM calculations, it was assumed that gas-phase geometries could be transferred without the introduction of significant errors. Energies, within the continuum model, were also calculated using the 6–311 + G(2d,2p) basis set, and zero point corrections, thermal, and entropic effects (T = 310.15 K, P = 1 bar) were added to all calculated energies as well.
Transition states
A scan along the Zn-water oxygen distance was performed, starting from the monodentate-optimized structure (Minimum 1), using B3LYP/SDD. From the electronic energy chart, three minima connected by two transition states were identifiable. The regions on the potential energy surface closer to the maxima were further rescanned at narrower distance intervals, and the maximums subsequently obtained were used as starting guesses to find the correspondent transition states. The two transition state structures were subsequently optimized freely. Frequency analyses were performed at each stationary point on the potential energy surface. Therefore, all minima and transition states were verified taking in account the number of imaginary frequencies. The minima were confirmed as being the coordination alternatives previously obtained (Minima 1, 2, and 3). The final electronic values were calculated using the all electron 6–311 + G(2d,2p) basis set, and zero-point corrections, thermal, and entropic effects (310.15 K, 1 bar) were added to all calculated energies. IEF-PCM calculations for ɛ = 4.335 and ɛ = 78.39 were further applied to both transition states.
Conformer X
A previous analysis of the active site geometries on a significant number of zinc enzymes highlighted that most of the structures with a water molecule and a carboxylate group in the first-coordination sphere adopt a very particular geometry, where the water molecule establishes a very strong hydrogen bond with the free carboxylate oxygen (Chakrabarti, 1990; Ryde, 1999). However, in FTase, contrary to what has been reported for the other enzymes, available crystallographic structures and preliminary calculations indicated that an eventual free carboxylate oxygen would point not to the water molecule, but precisely in the opposite direction, rendering a very different geometry. Nonetheless, in this study, such a coordination hypothesis for FTase was evaluated. A model was built starting from the smaller model optimized geometry with a zinc-bound water molecule (Minimum 1). The initial structure was prepared by rotating the carboxylate group around the zinc-carboxylate bond. The obtained minimum was named Conformer X. Optimization and energy calculations, in gas phase and in continuum (ɛ = 4.335 and ɛ = 78.39), were performed as previously described for the alternative conformers.
Larger model
Minima determination and characterization
Enzymes have highly anisotropic charge distributions, which confers them the ability to attain very specific stabilizing effects. These features are not always perfectly described by a continuum model, taking into consideration that such a model is, by nature, isotropic. In an attempt to address this problem, a significant enlargement of the model size was made, within a two-layers ONIOM approach (Dapprich et al., 1999; Vreven and Morokuma, 2000), as implemented in Gaussian 03.
Calculations were performed on a 127-atoms active site model (designated “Larger model”), based on an 8-Å cut around the zinc atom in the 1FT1 structure. The overall procedure described for the minima determination in the smaller model was again used. The inner layer (layer H) included 22 atoms, in conformity with the smaller model presented in the previous section. The outer layer (layer L) included 105 atoms, comprising a total of five complete residues (Gly-298β, Tyr-300β, Asp-352β, Ser-357β, and Tyr-361β). The inner layer was treated with B3LYP/SDD, in analogy with the calculations already described for the smaller model. In the treatment of the outer layer, the semiempirical method PM3 (Stewart, 1989a,b, 1991) was used. There are not many semiempirical or molecular mechanics methods parameterized for metals. An evaluation of the applicability of PM3, AM1, and MNDO/d to the study of zinc complexes, and organometallic compounds containing Zn2+, clearly confirms PM3 as the most accurate of these three methods (Brauer et al., 2000). Moreover, it is known that the final energy is not very sensitive to the refinement of a correct geometry (Fernandes and Ramos, 2003a,b). Final energy values were determined using B3LYP/6–311+G(2d,dp) in the inner layer, and B3LYP/6–31+G(d) in the outer layer. Zero-point corrections, thermal, and entropic effects (T = 310.15 K, P = 1 bar) were added to all calculated energies.
In Gaussian 03, the use of the ONIOM with IEF-PCM model is not yet possible. However, an ONIOM calculation is based on several distinct calculations that can be done separately. Given the overall structure of our model, it would be expected that the inclusion of a dielectric constant would mainly alter the value for the first partial energy, that is, the one determined with the lower-theoretical-level method for the entire system. The inner layer interacts mainly with the outer layer, not with the solvent. Therefore, by keeping the second and third partial energies (as obtained in the gas phase) and recalculating in continuum the energy for the entire system with the lower-theoretical-level method it is possible to obtain an energy value for a two-layers ONIOM model placed in a medium with a specific dielectric constant. Accordingly, this procedure was followed for ɛ = 4.335 and ɛ = 78.39.
RESULTS
Smaller model
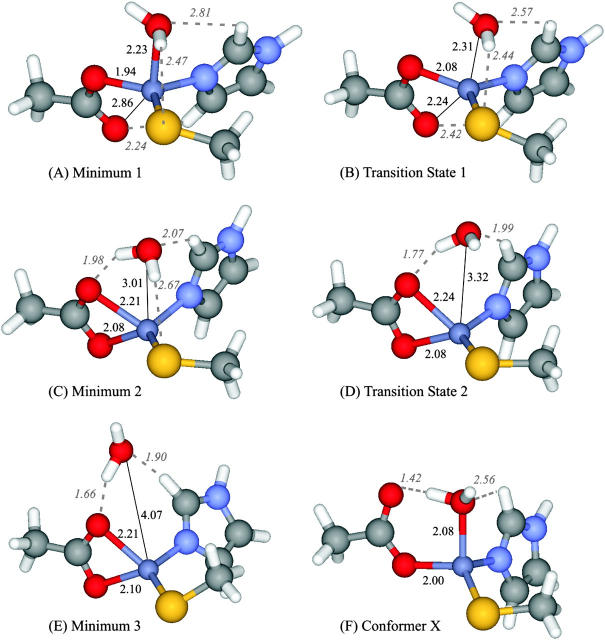
Three energy minima were obtained: one for the monodentate alternative (Minimum 1) and two for the bidentate hypothesis (Minima 2 and 3). These minima retain the overall topography of the active site reported in the crystallographic structure 1FT1, with the major differences observed deriving from the expected refinement in zinc bond lengths. The corresponding structures are depicted in Fig. 2. Table 1 lists the most important structural characteristics.
FIGURE 2.
Structures obtained for the stationary points studied, considering the 25-atoms model (Smaller model). Optimizations performed using B3LYP/SDD. Bond lengths and relevant hydrogen bonds reported in Å.
TABLE 1.
Structural characterization of all stationary points determined
| Distances to Zn2+ atom (Å) |
|||||||
|---|---|---|---|---|---|---|---|
| Model | Stationary point | S (Cys-299) | N (His-362) | Oa (Asp-297) | Ob (Asp-297) | H2O | Relevant hydrogen bonds |
| Smaller | Minimum 1 (monodentate) | 2.31 | 2.02 | 1.94 | 2.86 | 2.23 | Ob (Asp-297) with H (His-362) 2.24 Å |
| H2O with H (His-362) 2.81 Å | |||||||
| H20 with S (Cys-299) 2.47 Å | |||||||
| Transition state 1 | 2.30 | 2.02 | 1.99 | 2.51 | 2.31 | Ob (Asp-297) with H (His-362) 2.42 Å | |
| H2O with H (His-362) 2.57 Å | |||||||
| H20 with S (Cys-299) 2.44 Å | |||||||
| Minimum 2 (bidentate) | 2.26 | 2.02 | 2.08 | 2.21 | 3.01 | H2O with Ob (Asp-297) 1.98 Å | |
| H2O with H (His-362) 2.07 Å | |||||||
| H20 with S (Cys-299) 2.67 Å | |||||||
| Transition state 2 | 2.24 | 2.02 | 2.08 | 2.24 | 3.32 | H2O with Ob (Asp-297) 1.77 Å | |
| H2O with H (His-362) 1.99 Å | |||||||
| Minimum 3 (bidentate) | 2.25 | 2.02 | 2.10 | 2.21 | 4.07 | H2O with Ob (Asp-297) 1.66 Å | |
| H2O with H (His-362) 1.90 Å | |||||||
| Conformer X (monodentate) | 2.26 | 2.06 | 2.00 | 3.26 | 2.08 | H2O with Ob (Asp-297) 1.42 Å | |
| H2O with H (His-362) 2.56 Å | |||||||
| Larger | Monodentate (Minimum 1) | 2.30 | 2.02 | 2.02 | 2.88 | 2.13 | H2O with Oa (Asp-297) 1.95 Å |
| Ob (Asp-297) with NαH (Cys-299) 1.86 Å | |||||||
| Ob (Asp-297) with H (Cys-299) 2.61 Å | |||||||
| Ob (Asp-297) with NαH (Gly-298) 2.83 Å | |||||||
| Bidentate (Minimum 3) | 2.30 | 1.99 | 2.07 | 2.27 | 3.73 | H2O with Oa (Asp-297) 1.71 Å | |
| H2O with H (His-362) 1.97 Å | |||||||
Minimum 1 is a clearly monodentate structure, with Zn-O (Asp-297β) distances of 1.94 and 2.86 Å. In this minimum, the water molecule is located at a 2.23-Å distance from the zinc atom. This structure is stabilized by a 2.24-Å hydrogen bond between the free oxygen atom from Asp-297β (Ob) and His-362β. The water molecule is stabilized by two weak hydrogen bonds with the Cys-299β sulfur atom and with the His-362β imidazole.
Minimum 2 is bidentate, exhibiting Zn-O (Asp-297β) bond lengths of 2.08 and 2.21 Å. This minimum does not display a hydrogen bond between Asp-297β and His-362β, as seen in Minimum 1. The water molecule is located 3.01 Å away from zinc and is stabilized by three hydrogen bonds. Two of these bonds have also been reported in the previous structure. However, the interaction with His-362β in Minimum 2 is ∼0.7 Å shorter. A third hydrogen bond, between water and one of the Asp-297β oxygen atoms, is of particular relevance having the shortest length of all (1.98 Å).
Minimum 3 is also bidentate, presenting Zn-O (Asp-297β) bond lengths of 2.10 and 2.21 Å, very similar to the previous minimum. However, in this structure, the water molecule is positioned at a 4.07-Å distance from the metal atom. Although this minimum exhibits a lower number of hydrogen bonds than the structures reported before, it is worth nothing that these interactions are appreciably shorter, and naturally stronger.
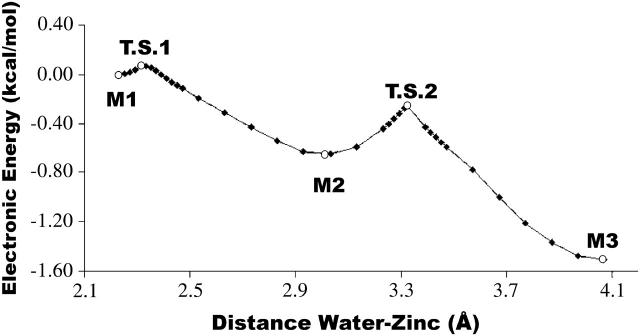
Fig. 3 illustrates the electronic energy variation with the water-zinc distance, showing the three energy minima already described and the transition states in between them. This curve only represents electronic energy values and therefore does not take into account thermal and entropic effects. The transition state structures are also represented in Fig. 2 and further characterized in Table 1.
FIGURE 3.
Electronic energy variation with water displacement, starting from the monodentate structure (Minimum 1). All stationary points included. Values obtained with B3LYP/SDD//B3LYP/SDD. Minimum 1 taken as reference. (M1) Minimum 1 (monodentate), (M2) Minimum 2 (bidentate), (M3) Minimum 3 (bidentate), (TS1) Transition State 1, (TS2) Transition State 2.
Transition State 1 connects Minima 1 and 2 and corresponds to a Zn-Ob stretching normal mode. The structure is stabilized by a 2.42-Å hydrogen bond between the free oxygen atom from Asp-297β (Ob) and the His-362β imidazole ring. The water molecule is positioned 2.31 Å away from zinc, and establishes hydrogen bonds with His-362β and with the sulfur atom from Cys-299β.
Transition State 2 connects the two bidentate coordination alternatives (Minima 2 and 3). A frequency mode analysis indicates that this transition state corresponds to a normal mode in which a stretching of the water-sulfur hydrogen bond (reported for Minima 1 and 2, and for TS1), is dominant. The water molecule is located at 3.32 Å from the zinc ion and establishes relevant hydrogen bonds with His-362β and Asp-297β, as described for the other stationary states.
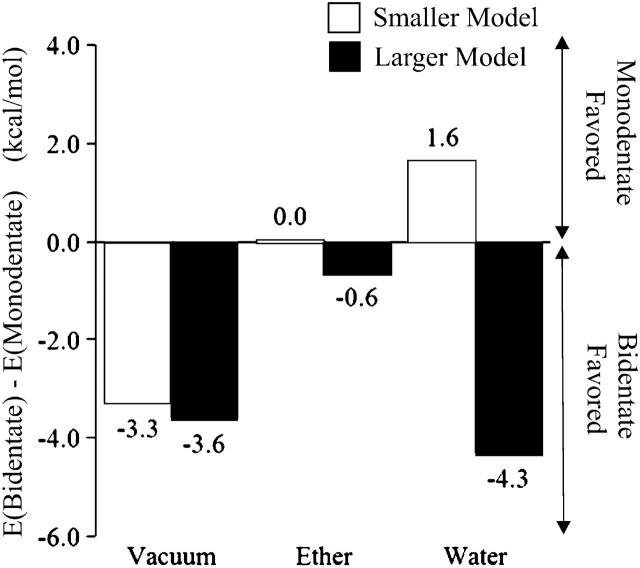
The Gibbs free energy values for the five stationary states discussed for the smaller model, in vacuum, ether (ɛ = 4.335), and water (ɛ = 78.39), are presented in Table 2, considering in each medium the energy value of Minimum 1 as reference. These values account for the electronic energy, the zero point, thermal, and entropic corrections (T = 310.15 K, P = 1 bar). This explains the reason why in certain cases the energy of a transition state is in fact lower than the reported value for one of the two minima it connects. Fig. 4 illustrates the Gibbs energy variation observed with water displacement. A comparison of the energy values obtained for the three minima clearly shows that Minimum 3 corresponds to the bidentate structure with the lowest energy, whereas Minimum 2 denotes only a local minimum. Therefore, the minima that illustrate mono- and bidentate coordination, to be discussed throughout the text, are Minima 1 and 3, respectively. Table 2 presents the differences in energy for both coordination alternatives in different media. Although in vacuum bidentate coordination is preferred, the results show that in ether mono- and bidentate coordination have more or less the same energy. In water, the monodentate alternative is favored.
TABLE 2.
Gibbs energy values for all stationary points in vacuum, ether, and water
| ΔG (kcal/mol)* |
||||
|---|---|---|---|---|
| Model | Stationary point | Vacuum | Ether | Water |
| Smaller | Minimum 1 | 0.0 | 0.0 | 0.0 |
| TS1 | −0.3 | 0.4 | 1.0 | |
| Minimum 2 | −2.1 | 2.0 | 3.6 | |
| TS2 | −1.0 | 2.4 | 3.3 | |
| Minimum 3 | −3.3 | 0.0 | 1.6 | |
| Conformer X | −6.7 | −6.5 | −6.7 | |
| Larger | Minimum 1 | 0.0 | 0.0 | 0.0 |
| Minimum 3 | −3.6 | −0.6 | −4.3 | |
The energy values for Minimum 1 were taken as reference in each medium.
FIGURE 4.
Gibbs energy values (kcal/mol) for all stationary points in vacuum, ether (ɛ = 4.335) and water (ɛ = 78.39). Values include zero-point, thermal, and entropic corrections (T = 310.15 K, P = 1 bar), and electronic energy results at the B3LYP/6–311 + G(2d,2p)//B3LYP/SDD level of theory. The energy values for the monodentate structure (Minimum 1) were taken as reference in each medium.
Fig. 2 F represents the optimized structure obtained for Conformer X, which corresponds to the most common monodentate structure observed for zinc enzymes with a carboxylate group and a water molecule in the first coordination sphere. The results presented in Table 2 show that this structure is by far the most stable in all media studied.
Larger model
The use of the 127-atoms model (Larger model) rendered only two energy minima: one for the monodentate hypothesis (Minimum 1), and another for the bidentate alternative (Minimum 3). In both minima, the overall topography of the active site reported in the 1FT1 crystallographic structure is retained. The structures are depicted in Fig. 5, and described in detail in Table 1.
FIGURE 5.
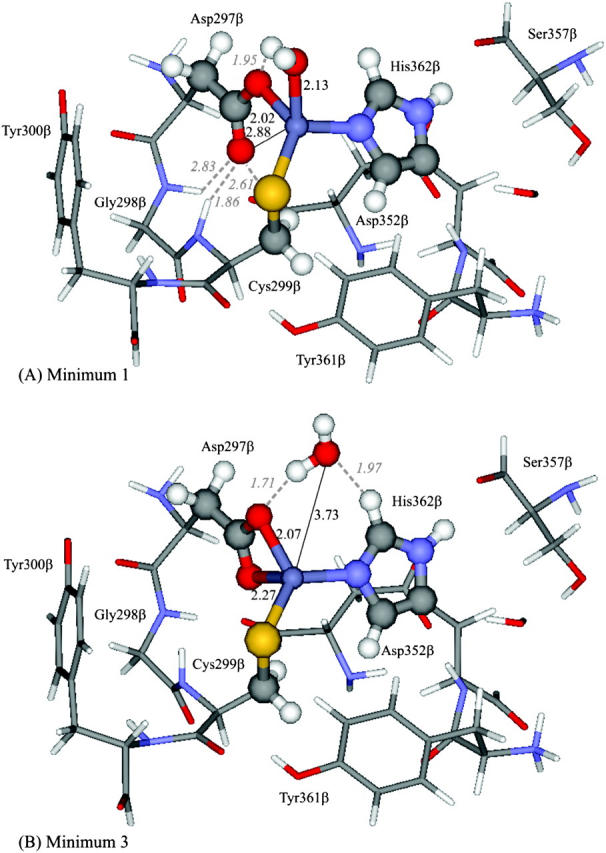
Structures obtained for the two minima studied, considering a 127-atoms model (Larger model). Geometries optimized at the ONIOM(B3LYP/SDD:PM3) level of theory. High-level atoms depicted in ball and stick. Low-level atoms represented in sticks. Designations given in analogy with the smaller model minima: (A) Minimum 1, (B) Minimum 3. Bond lengths and relevant hydrogen bonds reported in Å.
In Minimum 1 the water molecule is tightly bound, being located at a 2.13-Å distance from the zinc atom. The Zn-O (Asp-297β) distances are longer than the ones obtained for the smaller model (2.02 Å and 2.88 Å in this model, against 1.94 Å and 2.86 Å in the smaller model). The structure is stabilized by a 1.86-Å hydrogen bond, between the carboxylate free oxygen (Ob) and the peptidic hydrogen from Cys-299β. This carboxylate oxygen atom is further stabilized by two weak hydrogen bonds, with a hydrogen from the Cβ atom in Cys-299β, and with a peptidic hydrogen from Gly-298β. The water molecule is stabilized by a 1.95-Å hydrogen bond with the other carboxylate oxygen (Oa). The other interactions of the water molecule, seen in the smaller model, do not exist in this structure, mainly due to a slight rotation of the imidazole ring from His-362β, which displaces the ring from the plane described by the zinc-water-nitrogen bonds.
Minimum 3 has a water molecule located at 3.73 Å from the zinc atom, significantly shorter than the 4.07-Å distance reported for the Minimum 3 in the smaller model. This minimum was referred to as Minimum 3 in analogy with the designations attributed to the smaller model's minima, taking particularly into account the absence of a hydrogen bond between the water molecule and Cys-299β sulfur atom, but also due to the similarities observed, in terms of length and orientation, of the other two hydrogen bonds reported. In fact, in this minimum the water molecule establishes a hydrogen bond (1.71 Å) with one of the carboxylate oxygen atoms (Oa) and another with His-362β (1.97 Å), similar to the situation described for Minimum 1 in the smaller model.
A comparison between the structures obtained using the smaller and larger models presents two main differences: 1), considering the smaller model, for most of the minima studied (Minima 2 and 3 and Transition State 2), the longer zinc-Asp-297β bond length (Zn-Ob) is established with the carboxylate oxygen atom that lies closer to the water molecule, whereas the use of the larger model rendered structures in which the carboxylate oxygen atom located closer to water is in fact at a closer distance from the zinc atom (therefore labeled Oa); and 2), structures optimized for the larger model exhibit a slight rotation of the imidazole ring from His-362β, in relation to the smaller model, which displaces the ring from the plane defined by the zinc-water-nitrogen bonds and makes the existence of a minimum equivalent to Minimum 2 (from the smaller model) unfeasible.
The relative energies for the two coordination alternatives in vacuum, ether (ɛ = 4.335), and water (ɛ = 78.39), considering the larger model, are reported in Table 2, taking the value for the monodentate structure (Minimum 1) as reference. Fig. 4 illustrates the energetic differences between both structural hypotheses in the three media considered. The results show that the bidentate hypothesis is preferred.
DISCUSSION
Zinc exhibits certain specific characteristics that are very different from other first-row transition metals. Due to the filled d10 orbital, the zinc ion (Zn2+) does not participate in electron transfer reactions. Additionally, the d10 configuration results in a ligand field-stabilization energy of zero, for all possible geometries, leading to spatially not directed (isotropic) polarization effects. Therefore, no geometry is intrinsically more stable than another, which confers on zinc metalloenzymes an ability to accommodate, during an enzymatic catalysis process, several different coordination environments without significant energetic cost (McCall et al., 2000). Nevertheless, the geometry most often encountered in zinc metalloenzymes is a distorted tetrahedral, although a pentacoordinated geometry has also been suggested for intermediate species, and for some specific systems (Alberts et al., 1998; Coleman, 1998; McCall et al., 2000).
In FTase, zinc is known to play a catalytic role (Huang et al., 1997; Fu et al., 1998). In the first crystallographic structure of a farnesyltransferase enzyme, obtained in 1997 (structure 1FT1) (Park et al., 1997), the zinc coordination sphere was interpreted as being distorted pentacoordinated, with three residues from the β-subunit (Asp-297 bidentate, Cys-299, and His-362), plus a water molecule, as ligands. The nature of the amino acid residues present in the zinc coordination sphere is not the subject of any doubt, and is in agreement with several mutagenesis studies (Dolence et al., 1997; Kral et al., 1997; Fu et al., 1998). However, some aspects are still far from clear. In particular, the 2.74-Å distance observed between the zinc ion and the water molecule does not allow an unequivocal assignment of this molecule to the first coordination sphere. Furthermore, in subsequently determined crystallographic structures from FTase complexed with FPP, the water molecule is located at an even higher distance—3.22 Å in structure 1FPP (Dunten et al., 1998) or not identifiable at all in structure 1FT2 (Long et al., 1998). Another important and unclarified aspect of the zinc coordination sphere lies on the bidentate character of the aspartate ligand. In the 1FT1 structure, the reported Zn-O (Asp-297β) distances are 2.00 and 2.56 Å. In most of the structures subsequently determined, the differences between these two distances are even higher (Long et al., 1998, 2000, 2001; Strickland et al., 1998). Therefore, the assignment of this ligand as bidentate is at the very least questionable.
Despite the high number of crystallographic structures available for FTase, the above-mentioned aspects remain unclear. Most of all the available structures have a resolution of 2.0 Å or worse, which is insufficient for an atomic level structural analysis, given that for such a level of resolution the expected uncertainty in bond length is at least 0.3 Å (Tobin et al., 2003). Studies using extended EXAFS have provided evidence that the zinc atom is coordinated to only three low-Z ligands (oxygen or nitrogen), plus a cysteine sulfur, arranged within a distorted tetrahedral geometry (Tobin et al., 2003). Although EXAFS data do not allow a distinction between nitrogen or oxygen coordination, the average Zn-(N/O) and Zn-S distances determined are consistent with typical values found in small zinc molecules (Harding, 2001; Tobin et al., 2003), and significantly shorter than the reported values for FTase crystallographic structures (Park et al., 1997; Dunten et al., 1998; Long et al., 1998).
Two of the three Zn-(O/N) bonds are known to be established with a His-362β nitrogen atom and with an Asp-297β oxygen atom. Furthermore, the Zn-S bond is known to be between the zinc ion and the Cys-299β sulfur atom. However, the nature of the third low-Z ligand is still the subject of many doubts, not answered by the EXAFS studies. The two obvious candidates are the water molecule (located 2.74 Å away from zinc in the 1FT1 structure) and the second Asp-297β oxygen (placed at 2.56 Å in the same structure). However, despite its limitations EXAFS data clearly indicate the lack of significant dispersion in the three Zn-(N/O) values (not larger than 0.10 Å). Therefore, the three bond lengths should be ∼2.0–2.2 Å, which points toward a geometry with a tightly bound water or an almost symmetrical bidentate carboxylate ligand, not seen in any crystallographic structure of the farnesyltransferase enzyme so far. What is known, for sure, is that such a ligand disconnects when the protein or peptide substrate binds giving its place to the sulfur atom of the cysteine residue, within the substrate CAAX motif, rendering a distorted tetrahedral geometry with two low-Z ligands (N/O), and two sulfur atoms, directly connected to zinc.
The presence of a water molecule is a characteristic hallmark of catalytic zinc sites (Park et al., 1997; Hightower et al., 1998). In fact, in most of the catalytically active zinc sites, H2O is the fourth ligand, being activated by ionization or polarization in the course of a reaction for subsequent attack on a substrate, or simply being displaced by a substrate molecule in the zinc coordination sphere (Vallee and Auld, 1990). In FTase, as a prime argument against such an hypothesis, it has been argued that the presence of a zinc-coordinated water would be deleterious to the farnesylation reaction due to possible hydrolysis of the FPP substrate (Tobin et al., 2003). However, from the reported crystallographic structures of FTase complexed with the FPP substrate (Dunten et al., 1998; Long et al., 1998) it is seen that the zinc atom is located ∼7 Å away from FPP, which places an hypothetical zinc-coordinated water molecule very far away from the FPP carbon 1 target. Furthermore, the conformational change that leads to an approach between the zinc atom and FPP, and allows the farnesylation reaction to occur, only takes place after the coordination of the peptide substrate to the enzyme (Long et al., 2002; Pickett et al., 2003a,b), that is, after the displacement of the hypothetical zinc-coordinated water by the cysteine's sulfur from the CAAX motif. Therefore, the water molecule would never be a true menace to the farnesylation reaction, and the zinc-bound water molecule hypothesis cannot be ruled out simply by such an argument.
The other possible hypothesis would involve an almost symmetrical bidentate carboxylate group. Carboxylate ligands are common in many zinc enzymes (Lipscomb and Strater, 1996), and it is known that these carboxylate groups, in some cases, shift between mono- and bidentate coordination, which may function as an effective mechanism to balance the catalytic activity of such enzymes (Ryde, 1999). Bidentate coordination has been suggested for ∼30% of the zinc-carboxylate enzymes (Alberts et al., 1998; Ryde, 1999). However, these enzymes normally exhibit a very evident elongation of one of the Z-O carboxylate bonds by as much as 0.3–0.4 Å (Alberts et al., 1998), which would be in apparent contradiction with the evidence obtained by EXAFS studies for FTase, that clearly point to three Zn-(N/O) bonds with very similar lengths (Tobin et al., 2003).
Knowledge of the zinc coordination sphere is vital for an understanding of the global mechanism that rules the FTase activity. A better comprehension of the farnesylation mechanism could lead to significant progresses in the development of FTase inhibitors—rationally designed, more specific, with increased activity for cancer treatment, with potential value in the treatment of malaria and sleeping sickness, or even with application as antiviral agents.
The use of the smaller and larger models has allowed us to analyze the two coordination alternatives. The preparation of the larger model was carefully planned to capture both the intrinsic characteristics of the zinc complex and the influence of the anisotropic enzyme environment on the zinc coordination sphere. Several studies using this type of model have rendered very interesting results in the mechanistic study of other enzymes (Morokuma et al., 2001; Pelmenschikov and Siegbahn, 2002; Torrent et al., 2002; Kuno et al., 2003). All residues interacting directly with the zinc complex were included to preserve the specific interactions of the enzyme environment with the metal coordination sphere. Special care was taken to include all the hydrogen bonds between the zinc ligands and the surrounding residues. The remaining portion of FTase not included in the larger model was replaced by a dielectric continuum (ɛ = 4.335), which is a standard procedure in the treatment of the long-range nonspecific effects of the enzyme environment (Blomberg et al., 1998; Siegbahn, 1998; Siegbahn et al., 1998; Fernandes and Ramos, 2003a). Therefore, the conclusions drawn from this model can be extrapolated to the enzymatic system. The main purpose of considering also the first smaller model was to discriminate between the intrinsic characteristics of the zinc complex and the influence of the enzyme. This can be achieved by comparing the results of the two models, whose differences can be fully attributed to the enzyme.
Geometrically, both the mono- and bidentate structures considered in this study are in agreement with the distances envisioned by the EXAFS studies for FTase (Tobin et al., 2003), with three Zn-O/N bonds around a 2.0–2.2-Å interval. Our results have shown that the energy differences between both alternatives are generally small. Furthermore, our results indicate that the potential energy barriers between different minima are almost meaningless, and that the conversion mono-bidentate is reversible and fast, even at room temperature. Nevertheless, smaller model calculations in vacuum rendered an appreciably lower energy for the bidentate coordination hypothesis (Minimum 3), with the minor energy conformation being chiefly determined by the number of hydrogen bonds and by their strength. For calculations in continuum (ether or water), intermolecular hydrogen bonds become less important because the solvent stabilizes (in a minor or major extension) the groups more prone to interact by hydrogen bonds, namely the water molecule and the noncoordinated carboxylate oxygen. The degree to which these groups are exposed to the solvent is an aspect to be taken into account. In the monodentate structure (Fig. 2 A, Minimum 1), the water molecule and the second carboxylate oxygen adopt an orientation that promotes stabilization by the solvent, in comparison with the situation that arises from the bidentate geometry (Fig. 2 E, Minimum 3), where there is no carboxylate free oxygen. Therefore, solvation will stabilize the monodentate alternative to a greater major extent than the bidentate hypothesis. In ether (ɛ = 4.335), the referred stabilization, together with the decrease in importance of the intermolecular hydrogen bonds, results in energies virtually identical for both alternatives. In water, due to the higher dielectric constant (ɛ = 78.39), such stabilizations are even more intense, resulting in an energy considerably lower for the monodentate alternative.
For the larger model, calculations in vacuum are in agreement with the results obtained for the smaller model because the bidentate structure is, once again, more stabilized by hydrogen bonds than the monodentate alternative. The enzyme environment, represented by the additional five residues closer to the first coordination sphere (Gly-298β, Tyr-300β, Asp-352β, Ser-357β, and Tyr-361β), stabilizes both alternatives in practically the same amount with a small prevalence for the bidentate structure (by 0.3 kcal/mol). For continuum calculations, the main advantage that the monodentate structure exhibited in relation to the bidentate alternative in the smaller model—a free carboxylate oxygen atom exposed to the solvent—does not occur in the larger model due to the enzyme environment that avoids solvation of this atom. Therefore, contrary to the situation reported for the smaller model, in the larger model the continuum will tend to favor the bidentate structure. Naturally, this stabilization is significantly higher in water than in ether as discussed for the smaller model.
Taking into consideration the small variation observed in the change from the smaller to the larger model, and because the latter includes all the relevant residues that could interact directly with the first coordination sphere and that are responsible for the specific interactions of the enzyme environment with the zinc sphere, it is not expected that subsequent enlargements of the atomistic region of the model system could lead to meaningful alterations in the energetic difference between the two coordination hypotheses. Furthermore, given the subtle geometric differences existent between the two conformations, any long-range influence of the enzymatic environment beyond our second layer is highly unlikely to markedly favor one of the conformers over another. Hence, as the heterogeneous nature of the enzyme environment is accounted for by the second layer in our model, and the nonspecific distant effects are modeled by a continuum, the conclusions obtained with the larger model should be valid for the enzyme.
We recall that a typical B3LYP calculation with a standard basis set has an uncertainty of ∼2.5–3.0 kcal/mol in the determination of absolute values (Ricca and Bauschlicher, 1995; Holthausen et al., 1995; Bauschlicher, 1995). In this work we only present relative values between highly related structures, where the positions of just three or four atoms change considerably. The bulk of the system is not significantly altered. Therefore, most of the factors that might contribute to the error cancel, and the final error is expected to be much smaller. Nevertheless, the energy differences in some of the cases are most probably within the experimental error. This explains our reserves in pointing the bidentate conformer as the most stable alternative for the zinc coordination sphere in the FTase resting state. The results obtained point in that direction, the observed trend in the change from the smaller to the larger model is coherent with that conclusion, but the small differences observed do not allow a strong and definitive conclusion in this matter. However, it is precisely this very small energetic difference that is fascinating. In fact, one of the most important aspects derived from this study, which arises from the results with both the smaller and larger models, is the surprisingly small energetic differences envisioned between the two coordination hypotheses, particularly in terms of electronic energy. This feature led us to postulate the existence of an equilibrium involving the two coordination alternatives, with the correspondent populations being determined by the difference in the energy between the two hypotheses, following a Boltzmann distribution. For example, a difference of only 0.5 kcal/mol in the energy favoring the bidentate hypothesis would correspond to a mono/bidentate distribution of 30:70%, and a weighted average for the distance between the zinc ion and the second carboxylate oxygen atom (Zn-Ob) of ∼2.46 Å.
We have conducted a statistical analysis of this type of Zn-Ob bond lengths in all FTase crystal structures with a better resolution than 2.5 Å, a total of 17 structures. Details can be found in the supporting information. The result shows that 85% of these structures have reported bond lengths that fall in a 2.40–2.60-Å range, the average value being 2.49 Å. These values are absolutely atypical for a Zn-Ob distance, being significantly longer than a normal covalent bond but also considerably shorter than a characteristic ionic interaction. We have also arranged these 17 crystallographic structures into five groups, designated as resting state, binary complex, ternary complex with two Zn-thiolate bonds, ternary complex with one Zn-thiolate bond, and product complex. The structural analysis performed for each group shows that, even though the Zn-Ob bond lengths within each set of structures greatly vary (sometimes by as much as 0.4 Å), the average values for the five different groups are remarkably similar. The results seem to indicate the absence of a direct relationship between the existence, or not, of a second zinc-thiolate bond and the Zn-Ob distance. Furthermore, from our studies it is clear that a value in a 2.40–2.60-Å range would never correspond to one of the minima, but rather to a structure similar to the one presented for the transition state for a mono-bidentate conversion (Zn-Ob distance of 2.51 Å), which is, of course, highly unlikely to occur in a crystallographic structure. Therefore, we conclude that the atypical values reported for the Zn-Ob distance in FTase crystallographic structures arise from the existence of two different states populated, and consequently that both coordination alternatives—bidentate and monodentate with an extra ligand—exist in equilibrium, the ratio of which depends on the type of ligand. Taking all these aspects into consideration we conclude that in reasonable crystallographic structures of zinc enzymes with a carboxylate ligand a simple inspection of the Zn-Ob bond length is enough to verify the existence or not of two states in equilibrium. This conclusion is of major biological significance, being also extensible to a huge amount of metallo-enzymes, not only zinc-carboxylate enzymes but also other enzymes in general, which exhibit metal-carboxylate atypical bond lengths characteristic neither from a covalent bond nor from an ionic interaction.
Previous studies have demonstrated that most zinc enzymes with a water molecule, and a monodentate carboxylate group in the first coordination sphere, adopt a specific conformation where the free carboxylate oxygen interacts with the water molecule by a very strong hydrogen bond, almost defining a ring (Ryde, 1999). Our results showed that such a structure—referred to as Conformer X (Fig. 2 F)—has an energy at least 3–7 kcal/mol lower than all the other mono- and bidentate coordination alternatives considered (see Table 2), which is in agreement with the high prevalence of this structure within zinc enzymes. However, in the particular case of FTase such hypothesis is not realistic, because just a visual inspection of the crystallographic structures shows that such a conformer would require a major rotation of the Asp-297β carboxylate group, to which would undoubtedly correspond a very high distortion energy.
CONCLUSIONS
The results obtained in this study have shown that a bidentate coordination to zinc by the Asp-297β residue in the active site of FTase is not only possible but it is also the most stable realistic alternative. Interestingly, however, our results demonstrate that the two coordination alternatives for the zinc sphere in the FTase resting state—bidentate Asp-297β without water or monodentate Asp-297β with a water molecule—lie in a notably close energetic proximity. The Gibbs energy for a conversion between both alternatives and the correspondent transition state were also determined. The small Gibbs energy value obtained indicates that at room temperature a mono-bidentate conversion (carboxylate shift) with water elimination is reversible and very fast, which together with the small energetic difference observed between the two conformers suggests the existence of the two states in equilibrium. This equilibrium hypothesis could explain the atypical values observed in FTase crystallographic structures, namely the reported bond lengths between the zinc and the second carboxylate oxygen atom of Asp-297β, too long for a normal covalent bond but at the same time excessively short for a simple ionic interaction.
A reversible and fast mono-bidentate conversion, such as the one suggested, will perform a central catalytic function by assisting ligand entrance and/or release. These features are of the uttermost importance for the FTase activity, providing an effective mechanism for balancing Ras entrance, Ras attack on the FPP substrate, or even product release. Just as with FTase and the related enzyme geranylgeranyltransferase I, mechanisms of this type may also be important in other zinc enzymes with a carboxylate group coordinating the zinc ion.
SUPPLEMENTARY MATERIAL
An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.
Acknowledgments
We thank the FCT (Fundação para a Ciência e a Tecnologia) for a doctoral scholarship for Sérgio Filipe Sousa (SFRH/BD/12848/2003) and the National Foundation for Cancer Research Centre for Computational Drug Discovery, University of Oxford, Oxford, UK for financial support.
References
- Alberts, I. L., K. Nadassy, and S. J. Wodak. 1998. Analysis of zinc binding sites in protein crystal structures. Protein Sci. 7:1700–1716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andrae, D., U. Haussermann, M. Dolg, H. Stoll, and H. Preuss. 1990. Energy-adjusted ab initio pseudopotentials for the second and third row transition elements. Theor. Chim. Acta. 77:123–141. [Google Scholar]
- Ayral-Kaloustian, S., and E. J. Salaski. 2002. Protein farnesyltransferase inhibitors. Curr. Med. Chem. 9:1003–1032. [DOI] [PubMed] [Google Scholar]
- Bauschlicher, C. W. 1995. A comparison of the accuracy of different functionals. Chem. Phys. Lett. 246:40–44. [Google Scholar]
- Becke, A. D. 1993. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 98:5648–5652. [Google Scholar]
- Blomberg, M. R. A., P. E. M. Siegbahn, and G. T. Babcock. 1998. Modeling electron transfer in biochemistry: a quantum chemical study of charge separation in Rhodobacter sphaeroides and photosystem II. J. Am. Chem. Soc. 120:8812–8824. [Google Scholar]
- Bordier, B. B., J. Ohkanda, P. Liu, S. Y. Lee, F. H. Salazar, P. L. Marion, K. Ohashi, L. Meuse, M. A. Kay, J. L. Casey, S. M. Sebti, A. D. Hamilton, and J. S. Glenn. 2003. In vivo antiviral efficacy of prenylation inhibitors against hepatitis delta virus. J. Clin. Invest. 112:407–414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brauer, M., M. Kunert, E. Dinjus, M. Klussmann, M. Doring, H. Gorls, and E. Anders. 2000. Evaluation of the accuracy of PM3, AM1 and MNDO/d as applied to zinc compounds. J. Mol. Struct. 505:289–301. [Google Scholar]
- Cances, E., B. Mennucci, and J. Tomasi. 1997. A new integral equation formalism for the polarizable continuum model: theoretical background and applications to isotropic and anisotropic dielectrics. J. Chem. Phys. 107:3032–3041. [Google Scholar]
- Chakrabarti, P. 1990. Interaction of metal ions with carboxylic and carboxamide groups in protein structures. Protein Eng. 4:49–56. [DOI] [PubMed] [Google Scholar]
- Chakrabarti, D., T. Da Silva, J. Barger, S. Paquette, H. Patel, S. Patterson, and C. M. Allen. 2002. Protein farnesyltransferase and protein prenylation in plasmodium falciparum. J. Biol. Chem. 277:42066–42073. [DOI] [PubMed] [Google Scholar]
- Coleman, J. E. 1998. Zinc enzymes. Curr. Opin. Chem. Biol. 2:222–234. [DOI] [PubMed] [Google Scholar]
- Cossi, M., V. Barone, B. Mennucci, and J. Tomasi. 1998. Ab initio study of ionic solutions by a polarizable continuum dielectric model. Chem. Phys. Lett. 286:253–260. [Google Scholar]
- Cossi, M., N. Rega, G. Scalmani, and V. Barone. 2003. Energies, structures, and electronic properties of molecules in solution with the C-PCM solvation model. J. Comput. Chem. 24:669–681. [DOI] [PubMed] [Google Scholar]
- Cossi, M., G. Scalmani, N. Rega, and V. Barone. 2002. New developments in the polarizable continuum model for quantum mechanical and classical calculations on molecules in solution. J. Chem. Phys. 117:43–54. [Google Scholar]
- Dapprich, S., I. Komaromi, K. S. Byun, K. Morokuma, and M. J. Frisch. 1999. A new ONIOM implementation in Gaussian98. Part I. The calculation of energies, gradients, vibrational frequencies and electric field derivatives. J. Mol. Struct. 461:1–21. [Google Scholar]
- Dolence, J. M., and C. D. Poulter. 1995. A mechanism for posttranslational modifications of proteins by yeast protein farnesyltransferase. Proc. Natl. Acad. Sci. USA. 92:5008–5011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dolence, J. M., D. B. Rozema, and C. D. Poulter. 1997. Yeast protein farnesyltransferase. Site-directed mutagenesis of conserved residues in the beta-subunit. Biochemistry. 36:9246–9252. [DOI] [PubMed] [Google Scholar]
- Dolg, M., U. Wedig, H. Stoll, and H. Preuss. 1987. Energy-adjusted ab initio pseudopotentials for the first row transition elements. J. Chem. Phys. 86:866–872. [Google Scholar]
- Dunten, P., U. Kammlott, R. Crowther, D. Weber, R. Palermo, and J. Birktoft. 1998. Protein farnesyltransferase: structure and implications for substrate binding. Biochemistry. 37:7907–7912. [DOI] [PubMed] [Google Scholar]
- Fernandes, P. A., L. A. Eriksson, and M. J. Ramos. 2002. The reduction of ribonucleotides catalyzed by the enzyme ribonucleotide reductase. Theor. Chem. Acc. 108:352–364. [Google Scholar]
- Fernandes, P. A., and M. J. Ramos. 2003a. Theoretical studies on the mechanism of inhibition of ribonucleotide reductase by (E)-2′-fluoromethylene-2′-deoxycitidine-5′-diphosphate. J. Am. Chem. Soc. 125:6311–6322. [DOI] [PubMed] [Google Scholar]
- Fernandes, P. A., and M. J. Ramos. 2003b. Theoretical studies on the mode of inhibition of ribonucleotide reductase by 2′-substituted substrate analogues. Chemistry. 9:5916–5925. [DOI] [PubMed] [Google Scholar]
- Fernandes, P. A., and M. J. Ramos. 2004. Theoretical insights into the mechanism for thiol/disulfide exchange. Chemistry. 10:257–266. [DOI] [PubMed] [Google Scholar]
- Frenking, G., I. Antes, M. Bohme, S. Dapprich, A. W. Ehlers, V. Jonas, A. Neubaus, M. Otto, R. Stegmann, A. Veldkamp, and S. F. Vyboishchikov. 1996. Pseudopotential calculations of transition metal compounds: scope and limitations. Rev. Comp. Chem. 8:63–144. [Google Scholar]
- Frisch, M. J., G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchin, J. B. Cross, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malik, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, A. Al-Lahan, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez, and J. A. Pople. 2003. Gaussian 03: Revision A.1. Gaussian, Pittsburg, PA.
- Fu, H. W., L. S. Beese, and P. J. Casey. 1998. Kinetic analysis of zinc ligand mutants of mammalian protein farnesyltransferase. Biochemistry. 37:4465–4472. [DOI] [PubMed] [Google Scholar]
- Goodman, L. E., S. R. Judd, C. C. Farnsworth, S. Powers, M. H. Gelb, J. A. Glomset, and F. Tamanoi. 1990. Mutants of Saccharomyces cerevisiae defective in the farnesylation of Ras proteins. Proc. Natl. Acad. Sci. USA. 87:9665–9669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hancock, J. F., A. I. Magee, J. E. Childs, and C. J. Marshall. 1989. All Ras proteins are polyisoprenylated but only some are palmitoylated. Cell. 57:1167–1177. [DOI] [PubMed] [Google Scholar]
- Harding, M. M. 2001. Geometry of metal-ligand interactions in proteins. Acta. Crystallogr. D. Biol. Crystallogr. 57:401–411. [DOI] [PubMed] [Google Scholar]
- Hightower, K. E., C. C. Huang, P. J. Casey, and C. A. Fierke. 1998. H-Ras peptide and protein substrates bind protein farnesyltransferase as an ionized thiolate. Biochemistry. 37:15555–15562. [DOI] [PubMed] [Google Scholar]
- Holthausen, M. C., M. Mohr, and W. Koch. 1995. The performance of density functional/Hartree-Fock hybrid methods: the bonding in cationic first-row transition metal methylene complexes. Chem. Phys. Lett. 240:245–252. [Google Scholar]
- Huang, C. C., P. J. Casey, and C. A. Fierke. 1997. Evidence for a catalytic role of zinc in protein farnesyltransferase. J. Biol. Chem. 272:20–23. [DOI] [PubMed] [Google Scholar]
- Huang, C. Y., and L. Rokosz. 2004. Farnesyltransferase inhibitors: recent advances. Expert Opin. Ther. Pat. 14:175–186. [Google Scholar]
- Jackson, J. H., C. G. Cochrane, J. R. Bourne, P. A. Solski, J. E. Buss, and C. J. Der. 1990. Farnesol modification of Kirsten-Ras exon 4B protein is essential for transformation. Proc. Natl. Acad. Sci. USA. 87:3042–3046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- James, G., J. L. Goldstein, and M. S. Brown. 1996. Resistance of K-RasBV12 proteins to farnesyltransferase inhibitors in Rat1 cells. Proc. Natl. Acad. Sci. USA. 93:4454–4458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnston, S. R. 2001. Farnesyl transferase inhibitors: a novel targeted therapy for cancer. Lancet Oncol. 2:18–26. [DOI] [PubMed] [Google Scholar]
- Kato, K., A. D. Cox, M. M. Hisaka, S. M. Graham, J. E. Buss, and C. J. Der. 1992. Isoprenoid addition to Ras protein is the critical modification for its membrane association and transforming activity. Proc. Natl. Acad. Sci. USA. 89:6403–6407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kral, A. M., R. E. Diehl, S. J. deSolms, T. M. Williams, N. E. Kohl, and C. A. Omer. 1997. Mutational analysis of conserved residues of the beta-subunit of human farnesyl:protein transferase. J. Biol. Chem. 272:27319–27323. [DOI] [PubMed] [Google Scholar]
- Kuno, M., S. Hannongbua, and K. Morokuma. 2003. Theoretical investigation on nevirapine and HIV-1 reverse transcriptase binding site interaction, based on ONIOM method. Chem. Phys. Lett. 380:456–463. [Google Scholar]
- Lee, C., W. T. Yang, and R. G. Parr. 1988. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B. 37:785–789. [DOI] [PubMed] [Google Scholar]
- Lipscomb, W. N., and N. Strater. 1996. Recent advances in zinc enzymology. Chem. Rev. 96:2375–2434. [DOI] [PubMed] [Google Scholar]
- Long, S. B., P. J. Casey, and L. S. Beese. 1998. Cocrystal structure of protein farnesyltransferase complexed with a farnesyl diphosphate substrate. Biochemistry. 37:9612–9618. [DOI] [PubMed] [Google Scholar]
- Long, S. B., P. J. Casey, and L. S. Beese. 2000. The basis for K-Ras4B binding specificity to protein farnesyltransferase revealed by 2 A resolution ternary complex structures. Struct. Fold. Des. 8:209–222. [DOI] [PubMed] [Google Scholar]
- Long, S. B., P. J. Casey, and L. S. Beese. 2002. Reaction path of protein farnesyltransferase at atomic resolution. Nature. 419:645–650. [DOI] [PubMed] [Google Scholar]
- Long, S. B., P. J. Hancock, A. M. Kral, H. W. Hellinga, and L. S. Beese. 2001. The crystal structure of human protein farnesyltransferase reveals the basis for inhibition by CaaX tetrapeptides and their mimetics. Proc. Natl. Acad. Sci. USA. 98:12948–12953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lucas, M. F., P. A. Fernandes, L. A. Eriksson, and M. J. Ramos. 2003. Pyruvate formate lyase: a new perspective. J. Phys. Chem. B. 107:5751–5757. [Google Scholar]
- McCall, K. A., C. C. Huang, and C. A. Fierke. 2000. Function and mechanism of zinc metalloenzymes. J. Nutr. 130:1437–1446. [DOI] [PubMed] [Google Scholar]
- Melo, A., M. J. Ramos, W. B. Floriano, J. A. N. F. Gomes, J. F. R. Leão, A. L. Magalhães, B. Maigret, M. C. Nascimento, and N. Reuter. 1999. Theoretical study of arginine–carboxylate interactions. J. Mol. Struct. 463:81–90. [Google Scholar]
- Mennucci, B., and J. Tomasi. 1997. Continuum solvation models: a new approach to the problem of solutes's charge distribution and cavity boundaries. J. Chem. Phys. 106:5151–5158. [Google Scholar]
- Moores, S. L., M. D. Schaber, S. D. Mosser, E. Rands, M. B. O'Hara, V. M. Garsky, M. S. Marshall, D. L. Pompliano, and J. B. Gibbs. 1991. Sequence dependence of protein isoprenylation. J. Biol. Chem. 266:14603–14610. [PubMed] [Google Scholar]
- Morokuma, K., D. G. Musaev, T. Vreven, H. Basch, M. Torrent, and D. V. Khoroshun. 2001. Model studies of the structures, reactivities, and reaction mechanisms of metalloenzymes. IBM. J. Res. and Dev. 45:367–395. [Google Scholar]
- Ohkanda, J., F. S. Buckner, J. W. Lockman, K. Yokoyama, D. Carrico, R. Eastman, K. Luca-Fradley, W. Davies, S. L. Croft, W. C. Van Voorhis, M. H. Gelb, S. M. Sebti, and A. D. Hamilton. 2004. Design and synthesis of peptidomimetic protein farnesyltransferase inhibitors as anti-Trypanosoma brucei agents. J. Med. Chem. 47:432–445. [DOI] [PubMed] [Google Scholar]
- Ohkanda, J., D. B. Knowles, M. A. Blaskovich, S. M. Sebti, and A. D. Hamilton. 2002. Inhibitors of protein farnesyltransferase as novel anticancer agents. Curr. Top. Med. Chem. 2:303–323. [DOI] [PubMed] [Google Scholar]
- Park, H. W., S. R. Boduluri, J. F. Moomaw, P. J. Casey, and L. S. Beese. 1997. Crystal structure of protein farnesyltransferase at 2.25 angstrom resolution. Science. 275:1800–1804. [DOI] [PubMed] [Google Scholar]
- Pelmenschikov, V., and P. E. Siegbahn. 2002. Catalytic mechanism of matrix metalloproteinases: two-layered ONIOM study. Inorg. Chem. 41:5659–5666. [DOI] [PubMed] [Google Scholar]
- Pereira, S., P. A. Fernandes, and M. J. Ramos. 2004. Theoretical study of ribonucleotide reductase mechanism-based inhibition by 2′-azido-2′-deoxyribonucleoside 5′-diphosphates. J. Comput. Chem. 25:227–237. [DOI] [PubMed] [Google Scholar]
- Pickett, J. S., K. E. Bowers, and C. A. Fierke. 2003a. Mutagenesis studies of protein farnesyltransferase implicate aspartate β352 as a magnesium ligand. J. Biol. Chem. 278:51243–51250. [DOI] [PubMed] [Google Scholar]
- Pickett, J. S., K. E. Bowers, H. L. Hartman, H. W. Fu, A. C. Embry, P. J. Casey, and C. A. Fierke. 2003b. Kinetic studies of protein farnesyltransferase mutants establish active substrate conformation. Biochemistry. 42:9741–9748. [DOI] [PubMed] [Google Scholar]
- Reiss, Y., M. S. Brown, and J. L. Goldstein. 1992. Divalent cation and prenyl pyrophosphate specificities of the protein farnesyltransferase from rat brain, a zinc metalloenzyme. J. Biol. Chem. 267:6403–6408. [PubMed] [Google Scholar]
- Reiss, Y., J. L. Goldstein, M. C. Seabra, P. J. Casey, and M. S. Brown. 1990. Inhibition of purified p21ras farnesyl:protein transferase by Cys-AAX tetrapeptides. Cell. 62:81–88. [DOI] [PubMed] [Google Scholar]
- Reiss, Y., S. J. Stradley, L. M. Gierasch, M. S. Brown, and J. L. Goldstein. 1991. Sequence requirement for peptide recognition by rat brain p21ras protein farnesyltransferase. Proc. Natl. Acad. Sci. USA. 88:732–736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ricca, A., and C. W. Bauschlicher. 1995. A comparison of density functional theory with ab initio approaches for systems involving first transition row metals. Theor. Chim. Acta. 92:123–131. [Google Scholar]
- Ryde, U. 1999. Carboxylate binding modes in zinc proteins: a theoretical study. Biophys. J. 77:2777–2787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siegbahn, P. E. M. 1998. Theoretical study of the substrate mechanism of ribonucleotide reductase. J. Am. Chem. Soc. 120:8417–8429. [Google Scholar]
- Siegbahn, P. E. M., L. A. Eriksson, F. Himo, and M. Pavlov. 1998. Hidroge atom transfer in ribonucleotide reductase (RNR). J. Phys. Chem. B. 102:10622–10629. [Google Scholar]
- Stewart, J. J. P. 1989a. Optimization of parameters for semiempirical methods. 1. Method. J. Comput. Chem. 10:209–220. [Google Scholar]
- Stewart, J. J. P. 1989b. Optimization of parameters for semiempirical methods. 2. Applications. J. Comput. Chem. 10:221–264. [Google Scholar]
- Stewart, J. J. P. 1991. Optimization of parameters for semiempirical methods. 3. Extension of PM3 to Be, Mg, Zn, Ga, Ge, As, Se, Cd, In, Sn, Sb, Te, Hg, Tl, Pb, and Bi. J. Comput. Chem. 12:320–341. [Google Scholar]
- Strickland, C. L., W. T. Windsor, R. Syto, L. Wang, R. Bond, Z. Wu, J. Schwartz, H. V. Le, L. S. Beese, and P. C. Weber. 1998. Crystal structure of farnesyl protein transferase complexed with a CaaX peptide and farnesyl diphosphate analogue. Biochemistry. 37:16601–16611. [DOI] [PubMed] [Google Scholar]
- Takai, Y., T. Sasaki, and T. Matozaki. 2001. Small GTP-binding proteins. Physiol. Rev. 81:153–208. [DOI] [PubMed] [Google Scholar]
- Tobin, D. A., J. S. Pickett, H. L. Hartman, C. A. Fierke, and J. E. Penner-Hahn. 2003. Structural characterization of the zinc site in protein farnesyltransferase. J. Am. Chem. Soc. 125:9962–9969. [DOI] [PubMed] [Google Scholar]
- Torrent, M., T. Vreven, D. G. Musaev, K. Morokuma, O. Farkas, and H. B. Schlegel. 2002. Effects of the protein environment on the structure and energetics of active sites of metalloenzymes. ONIOM study of methane monooxygenase and ribonucleotide reductase. J. Am. Chem. Soc. 124:192–193. [DOI] [PubMed] [Google Scholar]
- Tschantz, W. R., E. S. Furfine, and P. J. Casey. 1997. Substrate binding is required for release of product from mammalian protein farnesyltransferase. J. Biol. Chem. 272:9989–9993. [DOI] [PubMed] [Google Scholar]
- Vallee, B. L., and D. S. Auld. 1990. Active-site zinc ligands and activated H2O of zinc enzymes. Proc. Natl. Acad. Sci. USA. 87:220–224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vreven, T., and K. Morokuma. 2000. On the application of the IMOMO (integrated molecular orbital plus molecular orbital) method. J. Comput. Chem. 21:1419–1432. [Google Scholar]
- Wiesner, J., K. Kettler, J. Sakowski, R. Ortmann, A. Katzin, E. Kimura, K. Silber, G. Klebe, H. Jomaa, and M. Schlitzer. 2004. Farnesyltransferase inhibitors inhibit the growth of malaria parasites in vitro and in vivo. Angew. Chem. Int. Ed. 43:251–254. [DOI] [PubMed] [Google Scholar]
- Zhang, F. L., H. W. Fu, P. J. Casey, and W. R. Bishop. 1996. Substitution of cadmium for zinc in farnesyl:protein transferase alters its substrate specificity. Biochemistry. 35:8166–8171. [DOI] [PubMed] [Google Scholar]
- Ziegler, T. 1991. Approximate density functional theory as a practical tool in molecular energetics and dynamics. Chem. Rev. 91:651–667. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.