Kinetic Pathways of β-Hairpin (Un)folding in Explicit Solvent

Abstract

We examine the dynamical (un)folding pathways of the C-terminal β-hairpin of protein G-B1 at room temperature in explicit solvent, by employing transition path sampling algorithms. The path ensembles contain information on the folding kinetics, including solvent motion. We determine the transition state ensembles for the two main transitions: 1), the hydrophobic collapse; and 2), the backbone hydrogen bond formation. In both cases the transition state ensembles are characterized by a layer (1) or a strip (2) of water molecules in between the two hairpin strands, supporting the hypothesis of the solvent as lubricant in the folding process. The transition state ensembles do not correspond with saddle points in the equilibrium free-energy landscapes. The kinetic pathways are thus not completely determined by the free-energy landscape. This phenomenon can occur if the order parameters obey different timescales. Using the transition interface sampling technique, we calculate the rate constants for (un)folding and find them in reasonable agreement with experiments, thus supporting the validation of using all-atom force fields to study protein folding.

INTRODUCTION

In the last decade, the 16-residue C-terminal fragment (41–56) of protein G-B1 (sequence GEWTYDDATKTFTVTE) which forms a stable β-hairpin in solution, has become a model system to investigate β-sheet formation (Blanco et al., 1994; Blanco and Serrano, 1995; Muñoz et al., 1997, 1998; Honda et al., 2000; Kolinski et al., 1999; Klimov and Thirumalai, 2000; Dinner et al., 1999; Zagrovic et al., 2001; Pande and Rokhsar, 1999; Roccatano et al., 1999; Ma and Nussinov, 2000; Eastman et al., 2001; García and Sanbonmatsu, 2001; Zhou et al., 2001; Tsai and Levitt, 2002). Seminal fluorescence experiments by Muñoz et al. (1997, 1998) revealed a two-state kinetics between the folded and unfolded hairpin, with a relaxation time of 6 μs. This work inspired many simulation studies on the β-hairpin using either simplified models (Kolinski et al., 1999; Klimov and Thirumalai, 2000), full atom models in implicit solvent (Dinner et al., 1999; Zagrovic et al., 2001), or in an explicit solvent (Pande and Rokhsar, 1999; Roccatano et al., 1999; Ma and Nussinov, 2000; Eastman et al., 2001; García and Sanbonmatsu, 2001; Zhou et al., 2001; Tsai and Levitt, 2002). The first investigations, high temperature molecular dynamics (MD) in explicit solvent by Pande and Rokhsar (1999) and multicanonical Monte Carlo sampling in implicit solvent by Dinner et al. (1999), demonstrated that the folding takes place via a number of discrete steps. After the initial β-turn formation the hydrophobic residues in the peptide collapse into a hydrophobic core, followed by formation of the backbone hydrogen bonds. Other simulations, notably by García and Sanbonmatsu (2001) and Zhou et al. (2001), determined the β-hairpin free-energy landscape in explicit solvent.

The kinetics of the folding of the β-hairpin in explicit solvent at room temperature, including the folding rate constant, has received less attention—and still poses a computational challenge. Several authors (Klimov and Thirumalai, 2000; Zagrovic et al., 2001) studied the thermodynamics and kinetics of an off-lattice model in implicit solvent, but from the differences in results between implicit and explicit solvent simulations it has become clear that the inclusion of the solvent is mandatory to describe the kinetics of the folding properly (Zhou and Berne, 2002; Shen and Freed, 2002; Nymeyer and García, 2003). Straightforward MD is a widely used tool for kinetic simulation studies, but can only access simulation times up to a microsecond. Although the β-hairpin has a relaxation time of only 6 μs, it is considered a very fast folder, and most proteins fold on a much longer timescale. Moreover, even if a folding event takes place within a microsecond of MD simulation time, it is only one possible pathway out of the many available to the system. The long folding times are partly caused by the existence of free-energy barriers between folded and unfolded states (and possible intermediates). The kinetics could be investigated by standard methods for the calculation of rate constants such as the transition-state-theory-based Bennett-Chandler approach (Chandler, 1978; Bennett, 1977). However, these methods are ineffective for high dimensional complex systems as it is difficult to find the correct reaction coordinates for an (un)folding. In the last decade, several methods have been developed to tackle the timescale and reaction coordinate problems simultaneously. In a previous article we showed that the transition path sampling (TPS) method (Dellago et al., 1998a,b, 1999, 2002; Bolhuis et al., 1998, 2000, 2002; Bolhuis and Chandler, 2000) can be used to investigate the β-hairpin formation process, including the unfolding rate constant (Bolhuis, 2003a). This article investigates the nature of the kinetic folding pathways of the β-hairpin in explicit solvent at room temperature in more detail, determines the transition state ensembles (TSE), and includes a new calculation of the folding rate constant. The main conclusion of this work is that the transition state ensembles for folding are characterized by a layer or strip of water molecules bridging the important groups in the molecule. This indicates the role of the solvent as a lubricant in the folding process, a hypothesis already put forward in Shea and Brooks (2001), Sheinerman and Brooks (1998a,b), Cheung et al. (2003), and García and Onuchic (2003). A second major conclusion is that the kinetic pathways do not always follow the free-energy landscape. This phenomenon has been recognized in several previous studies (ten Wolde and Chandler, 2003; Hagan et al., 2003). A third conclusion is that the computed free-energy barriers can be a bad indicator for the rate constants of folding processes, because of the wrong choice of the order parameters. This clearly demonstrates the need for methods such as TPS.

METHODS

System preparation

The β-hairpin system was prepared by extracting the C-terminus (residues 41–56) from the PDB structure of protein G-B1 (PDB code: 2gb1). Hydrogen atoms were added and the resulting 247-atom peptide was solvated in a cubic box of 1741 TIP3P water molecules. The system was equilibrated at 300 K at constant pressure until a density of 0.99 g/ml was reached (corresponding to a box size of 38.4 ų). This density was chosen to approach ambient conditions, yet not force the protein to denature by high pressure.

All MD simulations are carried out with NAMD (Kale et al., 1999) using the CHARMM22 force field (MacKerell et al., 1998). Newton's equations were integrated using the velocity Verlet algorithm. In all simulations the time step was 2 fs, periodic boundary conditions were applied, and long- range electrostatic interactions were calculated by Ewald summation. Bonds involving hydrogen atoms were constrained by the RATTLE algorithm (Andersen, 1983). In the straightforward MD simulations we kept the temperature constant by velocity rescaling; all transition path sampling trajectories were done at constant energy (see next section).

Transition path sampling

Straightforward MD shows that at 300 K there is a barrier to unfolding, preventing the system from unfolding or folding spontaneously in an accessible simulation timescale (Pande and Rokhsar, 1999; Roccatano et al., 1999; García and Sanbonmatsu, 2001; Zhou et al., 2001). TPS has proven to be a viable method for studying transitions between stable states separated by high free-energy barriers in complex environments (Dellago et al., 1998a,b, 1999, 2002; Bolhuis et al., 1998, 2000; Bolhuis and Chandler, 2000). Starting from an existing initial transition pathway, TPS gathers a collection of paths connecting a reactant with a product stable region by employing the Monte Carlo shooting algorithm. This MC algorithm changes the momenta of a randomly chosen time slice on an existing path, and determines a new trajectory from this time slice by integrating the equations of motion backward and forward in time using a standard NVE-MD integrator. When the new trajectory connects the initial with the final region, the new path is accepted, otherwise the old path is retained. Repeating this procedure with different time slices results in a random walk through path space and a collection of transition paths, i.e., the path ensemble. Because detailed balance is obeyed, the paths are properly sampled according to their statistical weight (for more information on the methods, see Dellago et al., 2002). Subsequent analysis of the path ensemble gives an unbiased insight into the mechanism of the reaction. The major advantage of TPS is that one does not have to impose reaction coordinates on the system, but rather extracts these from the simulation results. TPS has been successfully applied to such diverse systems as cluster isomerization, auto-dissociation of water, ion pair dissociation, and on isomerization of a dipeptide, as well as reactions in aqueous solution (for an overview, see Bolhuis et al., 2002).

Transition path sampling algorithms employing the deterministic shooting move run into problems for long deterministic trajectories over rough energy landscapes that cause the process to behave more diffusively (Bolhuis, 2003b). These types of diffusive transitions are found in, for example, crystal nucleation or, as in this article, protein folding. The original shooting method fails for such barriers, because when the path is becoming too long, the old and the new trajectories will have diverged completely before the other basin of attraction is reached. In that case, a small change in momenta will cause the forward as well as the backward trajectory to return to the same stable region. These nonreactive trajectories will make up the majority of the trial moves. We can improve the efficiency dramatically by making use of a stochastic TPS scheme (Bolhuis, 2003b). In the stochastic TPS scheme one can accept a forward or backward shot independent of the other (Dellago et al., 2002). Stochastic trajectories are obtained by coupling the system to a heat bath using a thermostat similar to the Andersen thermostat (Andersen, 1980). During the integration of the equations of motion we choose a random atom at a certain frequency and assign new random velocities according to the Maxwell-Boltzmann distribution. The frequency of the coupling is chosen low enough to keep the dynamics virtually deterministic to ensure realistic mechanisms and rate constants, while still having a quick but controlled divergence from the old path. Energy is kept constant by rescaling the kinetic energy of the system back to the old value after having obeyed constraints (RATTLE algorithm).

Further efficiency is obtained by making the path length variable (van Erp et al., 2003). As only shots from the barrier itself are useful in stochastic path sampling, it is natural to stop with the integration of the equation of motion once one reaches a stable state, provided that the trajectory is then really committed to a stable state. Alternatively, one can shoot a trial path of a fixed length l starting from a random time slice, as long as this length l is longer than the molecular commitment time (Dellago et al., 2002).

The stochastic path sampling algorithm now becomes as follows: Start with an initial path connecting A and B (for more details on how to create an initial path, see Dellago et al., 2002). Let 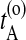be the time just before leaving A and 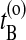the first time the system enters B on the old path. The barrier is thus between 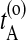and 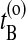. Now choose a slice x_t′ between 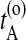and 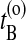with a uniform probability. (This uniform probability can be also replaced with a biasing function. Of course, one has to take into account the change in generating probability in the acceptance rule, in order to obey detailed balance.) In the original stochastic algorithm (Dellago et al., 2002) one either integrates the equations of motion forward or backward in time with equal probability. As we are actually almost performing deterministic MD, we sometimes expect a shooting move (simultaneous forward and backward integration) to succeed. We therefore start from x_t′ two simultaneous trajectories, forward and backward in time, for a duration of l time slices using the Andersen thermostat as a stochastic noise generator.

If the new trial path still connects A with B, the shot is accepted with a probability of

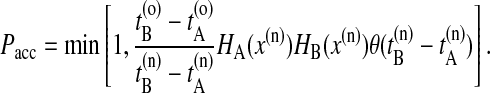(1)

Here, H_A(x) = 1 if the path visits A and equals zero otherwise, and x denotes the phase space coordinates of the entire path of length τ. The superscripts o and n refer to the old and the new path, respectively. The step-function θ(x) = 1 for x > 0 and zero otherwise, and ensures that B is reached after A. The last slice of the backward trajectory is renamed time slice 0, the last one of the forward trajectory is renamed time slice 2l, and the shooting point x_t′, becomes time slice l. If the backward path reaches A but the forward shot fails to visit B, the forward trajectory is rejected and the old forward part is retained. The old backward path from t = t′ to t = t′ – lΔt is then replaced by the new backward trajectory, and accepted with the above rule (Eq. 1). Similarly, if the forward path reaches B but the backward shot fails to visit A, the forward trajectory is substituted from t = t′ to t = t′ + lΔt and accepted with the above acceptance ratio. The new path is shifted such that the first slice is at t = 0. Detailed balance is conserved in this scheme. If 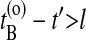or 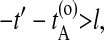trial moves are not long enough and l should be increased.

During the sampling the path length fluctuates, but remains bounded, because of the fraction inside the acceptance probability Eq. 1. In previous TPS studies, shifting moves were used to enhance statistics in the correlation functions for the calculation of rate constants. Here, we do not have to perform such shifting moves, since these have no effect on the path ensemble. The enhancement of statistics the shifting moves provide, is taken care of in the transition interface sampling (TIS) rate expression (van Erp et al., 2003).

Order parameters

Path sampling relies on a proper definition of the stable states by order parameters. Several requirements have to be fulfilled for these order parameters (Dellago et al., 2002). First, they should distinguish the different stable states sufficiently, excluding any overlap between the phase spaces of the different stable states. Otherwise, a path that seemingly has reached the final state could, in fact, still be in the basin of attraction of the initial state. All subsequent paths will then relax to this state, and hence sampling fails. This situation can be avoided by choosing the stable state boundaries entirely inside its basin of attraction. On the other hand, the order parameters should be characteristic for the stable states. When the system is committed to one of the stable states, a trajectory should visit the region defined by the order parameters frequently during a path of length l. Otherwise, not all relevant paths will be sampled, yielding just a subset of the proper path ensemble, or even the wrong ensemble. These requirements can only be fulfilled by trial and error.

We found that the following order parameters were most useful for the frayed-hydrophobic (F-H) transition (see Fig. 1):

1. The number of native hydrogen bonds N_hb between the carbonyl (C=O) and amide groups (N-H) in the peptide backbone. We take only the first five into consideration (Zhou et al., 2001).

2. The number of broken native backbone hydrogen bonds N_nb, defined by a distance between donor and acceptor >7 Å. This parameter indicates that the backbone hydrogen bond involved has been replaced by two solvent hydrogen bonds. The large distance ensures the hydrogen bond is truly broken and not merely undergoing a fluctuation. (Also, if the order parameter would have been chosen adjacent to the order parameter of the H-bond—i.e., 3.5 Å—the stable states will not be distinguished sufficiently. The sampling algorithm will then select those paths that are just crossing the edge at 3.5 Å, and, as this edge will be in one of the basins of attraction, sampling will fail.)

3. The number of hydrogen bonds N_solv between the backbone and the solvent, which gives the amount of solvation. In fact, we found it is more convenient to use the difference order parameter Δ = 2 × N_hb–N_solv. This parameter is ∼+10 for completely folded structures, and −10 for completely solvated configurations. The value Δ turns out to be more sensitive than N_hb, and can distinguish between true solvation of backbone and configurations in which the backbone hydrogen bonds are merely fluctuating.

4. The sum of the O-H distances of the backbone hydrogen bonds R_OH provides a clear distinction between the F- and H-states, and allows for a continuous measure for the number of hydrogen bonds, whereas all the above variables are discrete.

FIGURE 1.

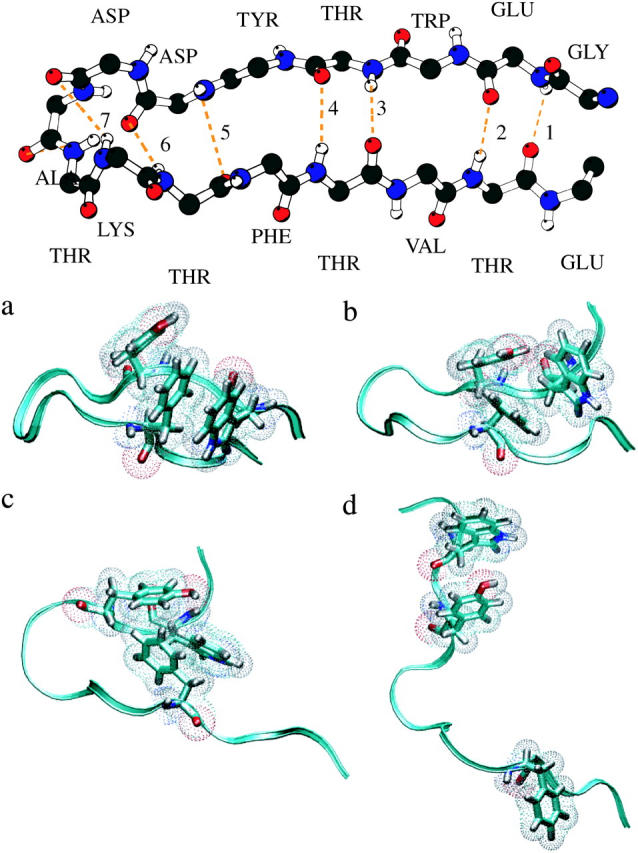
(Top) Native PDB structure of the β-hairpin. The side chains are left out. The seven backbone hydrogen bonds are indicated by dotted lines, and counted from the tail (following García and Sanbonmatsu, 2001). (Bottom) Spatial three-dimensional structures of the several stable states. (a) Native (N)-state, (b) Frayed (F)-state, (c) Hydrophobic (H)-state, and (d) Unfolded (U)-state. The backbone is represented as a ribbon, the hydrophobic core in a stick-model with dots to indicate the size of the atoms. All other residues and solvent molecules are left out. Figures were made with VMD (Humphrey et al., 1996).

For the hydrophobic-unfolded (H-U) transition (see Fig. 1), we need order parameters that describe the solvation of the hydrophobic core:

1. The radius of gyration of the group defined by the atoms in the hydrophobic residues phenylalanine (F52), tyrosine (Y45), and tryptophan (W43).

2. The minimum distance d_min between F52 and Y45 or W43 residues. This variable changes dramatically when the hydrophobic core is dissolving, and is more sensitive than R_g.

3. The number of solvent molecules N_wat between F52 and either Y45 or W43. This parameter that ensures a mere fluctuation in the R_g or minimum distance d_min is not counted as a barrier crossing. The number of solvent molecules is measured inside a cylinder of radius 2 Å along the axis between the centers of mass of the two hydrophobic residues involved.

In both transitions we also used the number of native contacts N_nc. A contact is a pair of C_α-atoms within 6 Å of each other. A contact is native if it also exists in the native state. However, this variable is of less importance, as it cannot distinguish the stable states properly, leading to bad sampling.

Transition state ensemble

The transition state ensembles were computed using the methods described in Dellago et al. (2002). For several randomly chosen paths from the path ensemble we calculated, at regular intervals of 10 slices (= 10 ps), the probability p_B to reach the final state. This commitment probability was computed by starting many (10–100) trajectories from a particular configuration with randomized velocities and counting the relative fraction that reaches the final instead of the initial state. The stable state definitions are given in Table 1. For some 10-ps intervals on the path we refined the search for the transition states by calculating p_B every ps.

TABLE 1.

Order parameters (OP) defining the upper (u) and lower (l) boundaries of the stable states

F-H transition					N-F transition					H-U transition
OP	Fl	Fu	Hl	Hu	OP	Nl	Nu	Fl	Fu	OP	Hl	Hu	Ul	Uu
ROH	1	20	50	99	ROH	1	14	23	99	RG	0	5	7.5	20
Nhb	3	20	0	0	Nhb	4	20	0	2	dmin	0	3	9	20
Nnb	0	1	4	20	Nnb	0	0	2	20	Nwat	0	0	5	20
Nnc	8	20	0	4	Nnc	12	20	0	8	Nnc	3	20	0	0
Δ	2	20	−20	−9

For each transition the initial and final states are defined; all distances are in Ångstroms.

Replica exchange method

To compare the TSE results with predictions by free-energy calculations we repeated the replica exchange (parallel tempering) method (REM) employed in Zhou et al. (2001), using NAMD (Kale et al., 1999) with the β-hairpin topology and CHARM22 force field (MacKerell et al., 1998). The number of replicas was 48, with temperatures ranging from 280 K to 570 K. The temperatures were set so that each subsequent replica pair had a swapping acceptance of 30–40%. Replica exchanges were done every 1 ps. The total amount of simulation time was 10 ns (amounting to a total simulation time of 480 ns), during which the order parameters were monitored. The FE-landscapes were obtained by taking the negative logarithm of the order parameter histograms. The equilibrium thermodynamics of the β-hairpin is discussed by other authors (Zhou et al., 2001). Here, we just use the REM results to compare the TPS and TSE results directly with the FE landscape using the same force field. (The question of whether or not the REM really samples the equilibrium FE landscape, remains unanswered. To answer this question one has to initiate the sampling with unfolded structures and check for convergence. This has not been done in Zhou et al., 2001, and we have not done it here, because of computational expenses.)

Transition interface sampling

Conventional methods such as the Bennett-Chandler technique (Chandler, 1978; Bennett, 1977) are not efficient to calculate the rate constant for complex transitions. If the order parameters used to estimate the barrier do not correspond to the reaction coordinates, the constraining techniques to calculate the free-energy barrier (such as umbrella sampling) can lead to unrealistic free-energy profiles and extreme hysteresis. Even if the free-energy barrier is properly sampled, the barrier will likely be lower than the real barrier, and the calculation of a statistically accurate transmission coefficient will be exceedingly difficult (Dellago et al., 2002; van Erp et al., 2003). Within the TPS framework, however, it is possible to calculate the rate constant for the β-hairpin accurately and efficiently using the transition interface sampling (TIS) method (van Erp et al., 2003). In short, the TIS method calculates the flux to leave a stable state and, subsequently, the conditional probability to reach the final state, provided that the boundary describing the initial state has been crossed. The basis of the method is the equation

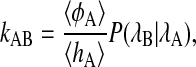(2)

where the forward rate constant k_AB is separated into two factors. The first factor is the flux 〈φ_A〉/〈h_A〉 to leave region A and the second factor in Eq. 2 is the conditional probability P(λ_B|λ_A) to reach region B (defined by order parameter λ_B) once the surface λ_A defining region A is passed. The flux factor can be measured by starting an MD simulation in stable state A. The interface λ_A will be crossed often, resulting in a statistically accurate value for the first factor. In contrast, the value of P(λ_B|λ_A) is very low for a high barrier, and cannot be measured directly. The statistics can be considerably improved by employing a biased sampling scheme. By sampling paths with the constraint that it comes from region A, crosses an interface λ_i, and then either goes to B or returns to A, we can measure the probability P(λ|λ_A) to reach values of λ > λ_i. These probabilities are binned in a histogram, and after having performed several simulations for different interfaces λ_i, these histograms are joined into a master curve, from which the value of P(λ_B|λ_A) can be extracted. A more detailed description of TIS can be found in van Erp et al. (2003).

RESULTS AND DISCUSSION

Molecular dynamics

After preparing and equilibrating (see Methods) the β-hairpin system, we performed a 2-ns MD run at 300 K. The β-hairpin is stable in solution, with, on average, four-to-five native backbone hydrogen bonds of the possible seven formed (a hydrogen bond is occupied if the distance between donor and acceptor is <3.5 Å and the O–H–N angle is >150°), and the hydrophobic core intact (see Fig. 1): the native or N-state (Pande and Rokhsar, 1999).

Next we conducted a 2-ns run at an elevated temperature of 400 K to force the unfolding process (Pande and Rokhsar, 1999). Several events took place spontaneously. First, the hydrophobic core rearranged and compacted, several hydrogen bonds broke, and the ends frayed. This so-called frayed (F)-state has, on average, two backbone hydrogen bonds. Then the remainder of the backbone hydrogen bonds broke, and the hairpin shortly remained in the so-called hydrophobic (H)-state in which the hydrophobic contacts still exists (see Fig. 1). Subsequently, in a short time of tens of picoseconds, the hydrophobic core dissolved and the peptide relaxes into the unfolded (U)-state.

Starting from three configurations along the 400-K trajectory, corresponding to the F-, H-, and U-states, we performed MD simulations at 300 K for 2 ns. Each state is (meta)stable, in qualitative agreement with free-energy calculations (Zhou et al., 2001). The number of stable native hydrogen bonds in the N- and F-states is, on average, ∼0.5 hydrogen bonds lower than found in Zhou et al. (2001). This disagreement is probably due to small differences in the force field, and/or the fact that we did not cap ends. After dissolution to the U-state the coordination of water molecules around the tryptophan increased by ∼20% with respect to the N- and F-states, thus qualitatively explaining the experimental quench in fluorescence (Muñoz et al., 1997). In the U-state the β-turn itself is still intact. We did not observe any helical content in any of the states.

In the following section we will investigate the F-H and the H-U transition independently at room temperature, as TPS simulations can tackle only one free-energy barrier at the time. The N-F was also studied (Bolhuis, 2003a), but is of less interest for the current article.

TPS of the F-H transition

We initiated the path sampling (see Methods) using a 100-ps pathway from the 400-K trajectory. TPS was performed at a constant energy corresponding to a temperature T = 295 K. The shot-length l = 300 ps and the time-slice interval was 2 ps. The paths were saved every 10th shooting attempt. The stable state definitions are given in Table 1. The ensemble could be sampled, albeit rather slowly. A collection of a few hundred pathways took approximately three months on an 8-node, 1-GHz Athlon PC cluster. In total we collected ∼2000 paths. An example of a path ensemble is given in Fig. 2. As the stochastic Andersen TPS algorithm accepts backward shots independently from the forward shot (see Methods), one may ask if the path ensemble is sampled properly. If this is not the case, the ensemble would show a part of the path ensemble that never changes. Fig. 2 clearly shows that none of the time slices have just a singular value, suggesting a proper sampling. To illustrate the sampling efficiency we plotted the complete F-H path sampling tree in Fig. 3. This tree shows that indeed the path ensemble is well sampled, as the forward and backward shots overlap many times. The modified sampling algorithm (see Methods) is actually very effective as the acceptance of a simultaneous backward and forward shot was extremely low. In Fig. 3, we also show the acceptance ratios for the forward and backward shots. If we had applied the original shooting algorithm the percentage of accepted paths would have been <0.01.

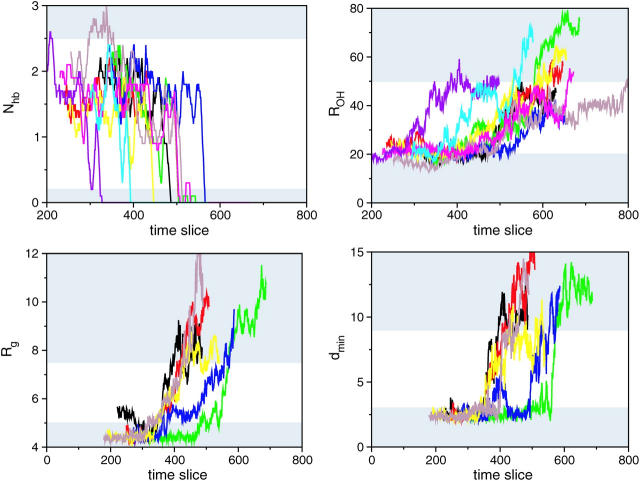
FIGURE 2.

Order parameters for typical pathways in the F-H and H-U path ensemble plotted as a function of time-slice index. Shaded areas indicate stable states. (Top left) Number of backbone hydrogen bonds N_hb in F-H ensemble. (For clarity, the data is smoothed by taking a 10 time-slice running average along the path. Due to this averaging some of the paths seem unable to reach the stable states.) (Top right) Sum of distances R_OH in F-H ensemble. (Bottom left) Core radius of gyration R_g in the H-U ensemble. (Bottom right) Minimum distance d_min in the H-U ensemble.

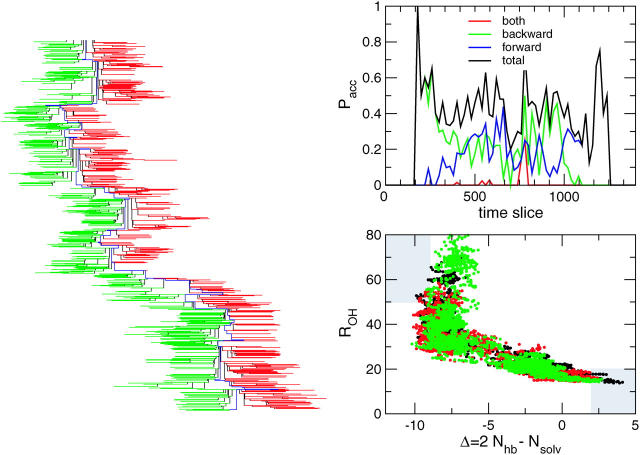
FIGURE 3.

Several indicators of proper sampling. (Left) The sampling of the F-H path ensemble represented as a tree. The x axis represent the time slices along each path, the y axis Monte Carlo simulation time. Starting with the initial path at the top, one shoots backward (left) and forward (right) in time. The solid vertical lines indicate the shooting points. Accepted (partial) paths are indicated in green (backward) and red (forward). While moving through the Monte Carlo time (downward), the entire path changes many times during the sampling. The thick blue line indicates the parts of the path ensemble that change the least. (Top right) Acceptance ratio for the F-H-path ensemble as a function of shooting-point time-slice index. The forward shooting is more accepted at the high end of the path, because it is already there in the basin of attraction of the H-state. The backward shooting is more accepted in the beginning of paths. Note that the simultaneous acceptance of both a forward and backward shot is extremely low, indicating the need for a stochastic algorithm. (Bottom right) Every 100th shooting attempt at a path, smoothed by running the averaging over 10 slices, is plotted in the (R_OH–Δ) plane. Every circle denotes a time slice. Groups of five subsequent paths are rendered in different colors to show that the sampling is reasonable. There is no apparent change in the ensemble over Monte Carlo simulation time (at least in this order parameter plane).

In Fig. 3 we plotted every 100th path in the path ensemble in the (R_OH–Δ) plane. Color-coding shows that the ensemble hardly changes over Monte Carlo time, again indicating a good sampling.

From analysis of the path ensemble we conclude that the mechanism for F-H unfolding is as follows. In the initial part of the paths the system is in the F-state, with the residues around the β-turn forming a fluctuating loop, the ends frayed, and with strong backbone hydrogen bonds 3 and 4 (see Fig. 1). Then, in several picoseconds these hydrogen bonds break almost in unison, to undergo the transition to the H-state. The unfulfilled backbone amide and carbonyl groups form a hydrogen bond to the solvent within a few time-slices (ps), whereas it takes a few tens of picoseconds before the criterion for the broken hydrogen bonds (N-O > 7 Å) is fulfilled (Bolhuis, 2003a). The solvent hydrogen bond formation is also clearly visible in Fig. 3, where almost all paths show a quick transition between Δ ≈ −3 and Δ ≈ −8. From this figure it also follows that R_OH slowly increases during and after the fast backbone hydrogen bond breaking and formation of the solvent bonds. For R_OH > 30 it seems that the number of hydrogen bonds to the solvent actually decreases again in the H-state.

TPS of the H-U transition

The F-H transition is followed by the H-U transition: dissolution of the hydrophobic core. As this transition has a relatively low free-energy barrier it probably has an unfolding rate constant in the order of nanoseconds. However, straightforward simulations showed a reasonable stability of the H- and U-states. We concluded that the unfolding is therefore too slow to study straightforwardly, and decided to study this transition with TPS. The time-slice separation was 1 ps with a shot-length of l = 100 ps. The stable state criteria are given in Table 1. The path sampling is very efficient, and an example of a path ensemble is given in Fig. 2. Inspection of the pathways reveal that during the H-U transition the R_g has to increase first to ∼6 Å, before the number of solvent molecules can rise. This is probably due to the fact that the hydrophobic residues must be a minimum distance apart to make enough space for the solvent. This behavior is visualized in Fig. 4, where several snapshots along a H-U unfolding path are depicted, together with the solvent structure. These snapshots show that when the hydrophobic core is intact, there is a ring-shaped hydrogen bond network around the core. When the hydrophobic residues are moving apart, this hydrogen bond network is rearranged and the water moves in.

FIGURE 4.

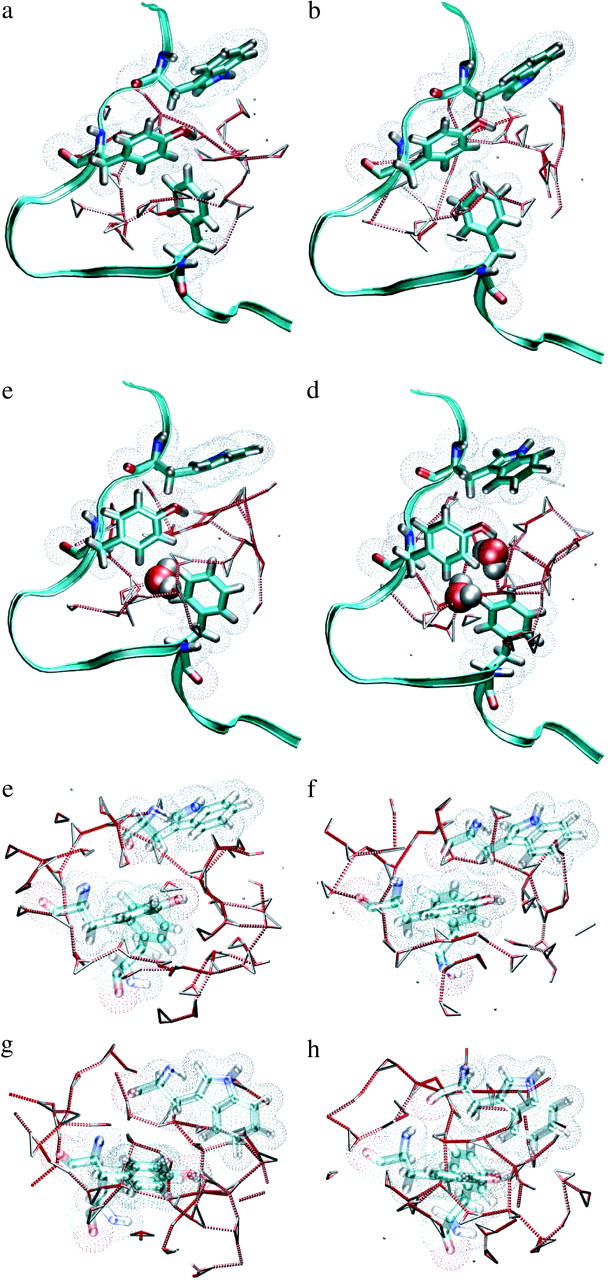
(a–d) Solvent structures around the transition states of the H-U paths. The hydrogen bond network is broken and solvent molecules occupy the space between the hydrophobic groups. The last structure is a transition state. The solvent is depicted as triangles connected with dotted lines for hydrogen bonds. The space-filling molecules are the waters used for the N_wat parameter. (e–h) The same solvent structures around the transition states, now viewed from the top. A ring of hydrogen bonds is broken and solvent molecules occupy the space between the hydrophobic groups. The hydrophobic residues are rendered as open (i.e., transparent) for clarity.

In hindsight, we could have used straightforward MD simulation to study this transition as the rate constant for unfolding turns out to be rather high.

The TSE of the F-H transition

We determined the TSE by computing the commitment probabilities (see Methods) p_B for several paths from the F-H ensemble. In Fig. 5, p_B is plotted as a function of time for several paths. Clearly there are many recrossings of the dividing surface. The configurations for which 0.4 < p_B < 0.6 were taken to be part of the transition state ensemble (TSE). This broad interval was chosen to obtain enough data points, but narrowing down the interval will not change the qualitative features. In Fig. 6, we show several snapshots of the transition state ensemble on top of each other, aligned by translation to match centers of mass and by rotation to minimize root mean-square deviation. The backbone is already in the β-hairpin shape, whereas the side chains are flexible. The relatively narrow distribution in the configurations might be caused by the fact that we only sample a local minimum in the path ensemble, and do not allow enough time to sample completely different part of the trajectories space. On the other hand, however, one should not be surprised to find the hairpin almost completely formed, as the H-F transition we are looking at is the final stabilizing transition to the native state.

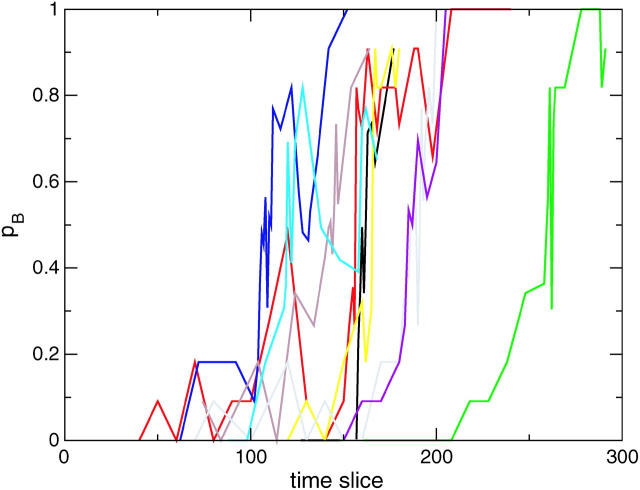
FIGURE 5.

The commitment probability p_B as a function of time slice for several paths from the F-H ensemble. There are several recrossings of the p_B = 0.5 surface, as expected for a diffusive transition.

FIGURE 6.

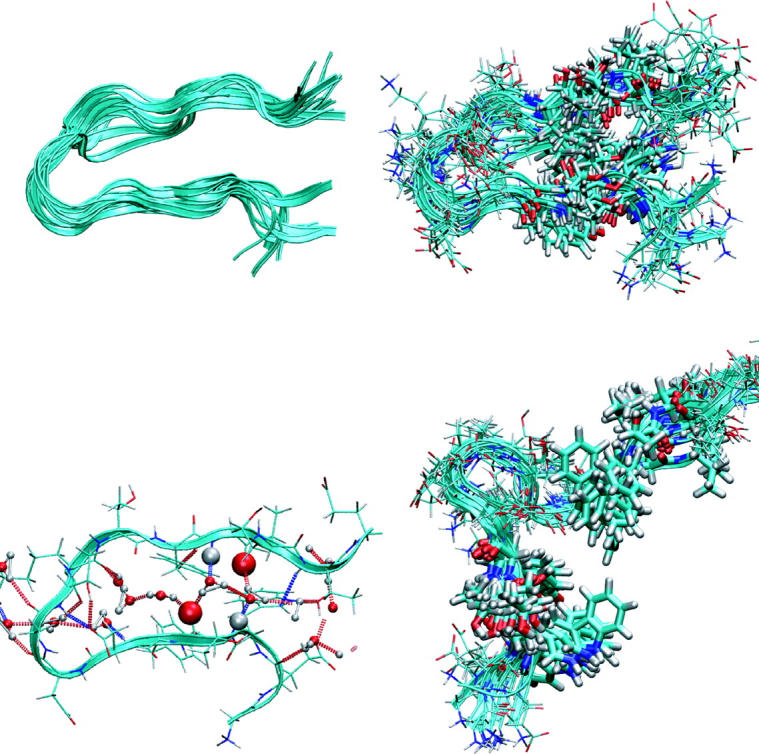
(Top left) TSE for the F-H transition in ribbon representation. (Top right) TSE in line representation. The solvent is left out. The configurations are quite similar, indicating that only a local sampling is possible. (Bottom left) Typical transition state configuration. The two strands are separated by a strip of water molecules. In particular, the important backbone hydrogen bonds 3–4 (indicated by large spheres) are bridged by water molecules. (Bottom right) Aligned TSE configurations for the H-U transition. The hydrophobic core is rendered in thick solid lines. The solvent is left out. The configurations are quite similar, suggesting that the path sampling is local.

Interestingly, the configurations in the TSE are characterized by the fact that the important hydrogen bonds 3 and 4 are not formed, and a strip of water molecules is in between the two strands, forming hydrogen bonds to the backbone donors and acceptors. This seems to be the overall generic picture for all configurations in the transition state ensemble. It supports the hypothesis brought forward by several authors that the solvent plays the role of lubricant in the final stages of folding (Shea and Brooks, 2001; Sheinerman and Brooks, 1998a,b; Cheung et al., 2003; García and Onuchic, 2003), bringing together the native backbone hydrogen bonds.

Comparison with the FE landscape

In Fig. 7 a we plot the free-energy from the REM simulations (see Methods) for T = 295 K in the N_hb–R_g plane, which are thought to be the most important order parameters for describing the folding (Zhou et al., 2001). The transition state saddle-point region seems to be located at R_g ≈ 4.7 and a N_hb ≈ 0.5, where the free-energy difference between the saddle point and the F-state minimum is ΔF = F_TS–F_F ≈ 1.5 k_BT (as we will see later, this very low value is caused by the choice of order parameters for the FE projection), where k_B is Boltzmann's constant. However, if we plot the TSE in the same plane, it is located around R_g ≈ 4.7 and N_hb = 0. This suggests that the TSE is not at the saddle point of the free-energy landscape, and that the order parameters N_hb and R_g do not entirely describe the kinetic pathways of folding. We also plotted in the same plane part of the p_B < 0.2 ensemble, and a part of the p_B > 0.9 ensemble in the figure to give an indication of the basin of attraction and commitment to the stable states.

FIGURE 7.

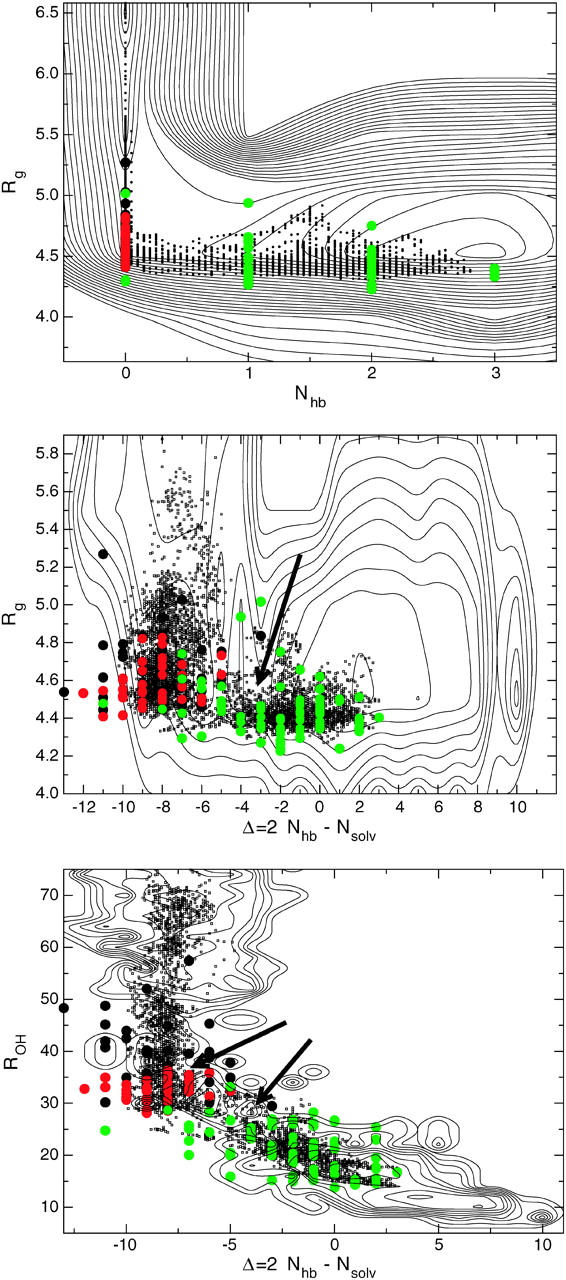
Representations of the F-H transition in three different order parameter planes. The free-energy landscape from replica exchange is given by solid thin contour lines separated by 0.2 k_BT. A few smoothed paths in the F-H ensemble are denoted by a scatter plot (small dots). Each dot represents a time slice along a path. Also given are the different committor ensembles: p_B < 0.2 green, 0.4 < p_B < 0.6 in red, and p_B > 0.9 in black. The transition state saddle points in the F-E landscape are indicated by arrows.

The discrepancy between the saddle point and the TSE is more clear in the Δ–R_g FE landscape, where the transition state region seems to be characterized by low R_g ≈ 4.6 and a Δ ≈ −3.5. In contrast, the TSE is located in a region around R_g ≈ 4.6 and Δ ≈ −9, suggesting that not only must all backbone hydrogen bonds be broken, but also that the hydrogen bonds to the solvent must be formed before the transition can occur. This can also be concluded from the transition state ensemble configurations in Fig. 6. In Fig. 7 c, we plotted the TSE in the R_OH–Δ plane, and here it is clear that besides the hydrogen bond parameter Δ, the total O-H distance between the two backbone strands R_OH also first has to reach a certain threshold (R_OH ≈ 30) before the transition can take place. Again, there is a difference between the saddle point at R_OH = 28 and Δ = −4, although one might argue that the TS saddle region in the FE landscape is actually located at R_OH ≈ 30 and Δ ≈ −9. In that case, the R_OH seems to be the proper reaction coordinate for the F-H transition. In the section on rate constants we will indeed use the R_OH as an order parameter to calculate the F-H rate.

Clearly the TSE does not correspond with the saddle points in all FE landscapes. One might think that this discrepancy could be caused by insufficient sampling of the free energy or transition paths. However, the free-energy minima of the F- and H-state are well characterized (e.g., in the (N_hb–R_g)-plane), and better sampling will not change the qualitative location of the saddle points. The transition-paths ensemble might also not be complete, but the transition states on each path indicate that it is not close to the FE-saddle point (at least in the (N_hb–R_g)-plane). Instead, the discrepancy is due to fact that the FE is a projection of all degrees of freedom on the chosen order parameters. This projection can obscure the location of true transition state (Dellago et al., 2002).

The Δ–R_g plot shows the largest differences between TSE and FE saddle points, probably because the solvent hydrogen bonds can adjust very quickly to the environment and are thus a fast variable, whereas R_g is a relatively slow variable that only changes dramatically when solution of the core takes place. Starting from the H-state, the folding transition is described by a slowly decreasing R_g. When the water molecules acting as a bridge between the two strands are in the right place, they quickly move out, and the backbone hydrogen bonds are formed. This mechanism is similar in spirit to the mechanism discussed by ten Wolde and Chandler (2003) on the collapse of a hydrophobic polymer. They also identified a slow R_g and a fast solvent variable, in which the solvent variable very quickly adapted to the environment, thus avoiding the free-energy saddle point.

The general picture is then that the kinetic pathways to unfolding go from a state in which hydrogen bonds 3 and 4 are tightly bound, via a transition state in which a strip of water bridges the backbone strands and form hydrogen bonds to the backbone. Only then are the paths really committed to the H-state. The folding takes place in the reverse fashion. In the H-state, the hairpin has to find the transition state conformation in which the backbone hydrogen bonds 3–4 are bridged by water, before they are actually formed. Hydrogen bonds 3–4 are formed first, as they are driven together by the nearby hydrophobic core. The expulsion of bridging waters might also be caused by the vicinity of the core.

The TSE of the H-U transition

We determined the H-U TSE in the same way as above. Configurations from the TSE are rendered in Fig. 6. The similarity between the transition states is large, indicating that possibly only a part of path space is sampled. However, the total number of paths sampled was only a few hundred, possibly too few to sample the entire trajectory space. In Fig. 8, we plot the REM free energy in the (N_wat,R_g), (d_min,N_wat), and (d_min,R_g) planes together with the path ensemble and the TSE, and part of the p_B < 0.2, 0.2 < p_B < 0.4, 0.6 < p_B < 0.8, and 0.8 < p_B < 1 ensembles. Here the discrepancy between the TSE and the FE saddle points is less clear. However, the 0.8 < p_B < 1 ensemble seems to overlap with the 0.4 < p_B < 0.6 ensemble in the d_min variable, suggesting that d_min has to be large enough to allow the waters to go inside the core before commitment to the U-state occurs. Likewise, the water rushes out of the core in the collapse, but the d_min is probably not the correct reaction coordinate, since as there are many configurations with a lower value of d_min in the p_B > 0.9 ensemble than the average d_min-value in the 0.4 < p_B < 0.6 ensemble. Fig. 4 suggests that the hydrogen bond network is responsible for the transition. However, there is no strong candidate for a reaction coordinate describing this network. Also, the H-U transition does not show a very high barrier, which makes it harder to describe the reaction.

FIGURE 8.

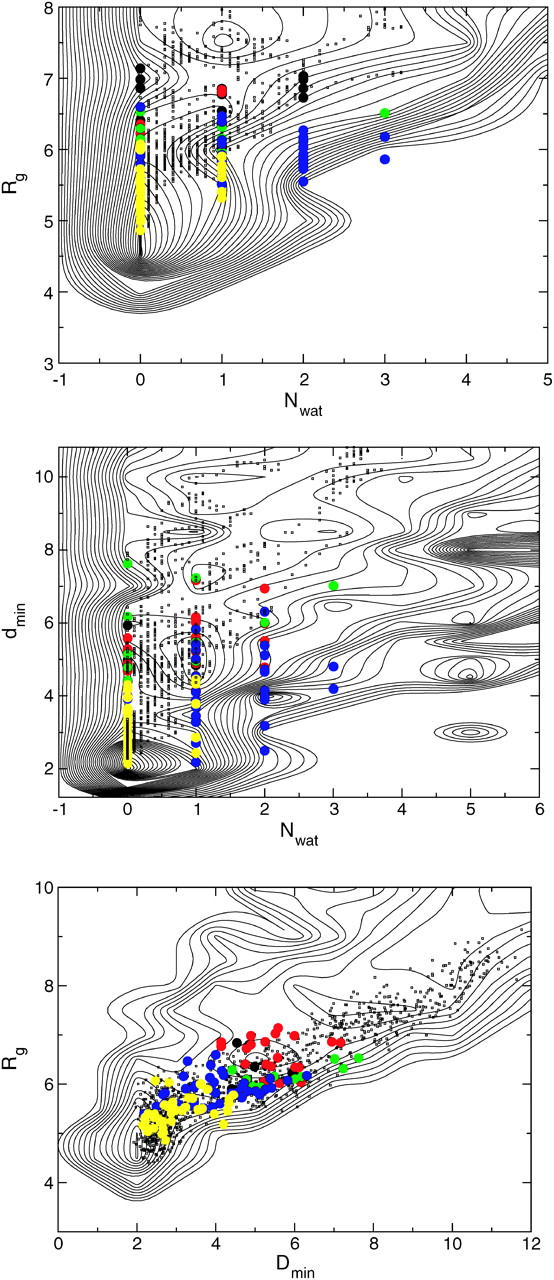
Representations of the H-U transition in three different order parameter planes. The free-energy landscape from replica exchange is given by solid thin contour lines separated by 0.5 k_BT. The H-U path ensemble is denoted by a scatter plot (small dots). Each dot represents a time slice along a path. Also given are the different committor ensembles: p_B < 0.2 yellow circles, 0.2 < p_B < 0.4 blue, 0.4 < p_B < 0.6 green, 0.6 < p_B < 0.8 red, and p_B > 0.8 in solid circles.

Rate constants

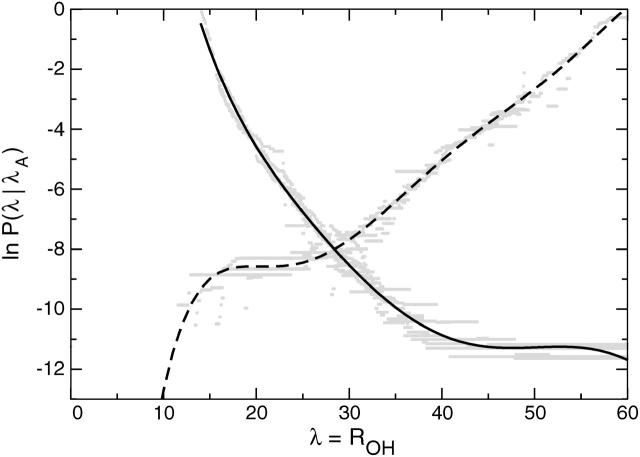
We presented the rate constant calculation for the rate-limiting F-H transition in Bolhuis (2003a). Here we will briefly repeat the results but also include results for the reverse folding reaction. We measured the crossing probability P(λ_B|λ_A) by conducting transition interface sampling (TIS) simulations for several interfaces λ_i (see Methods). The order parameter for the interfaces was the distance R_OH, which is a continuous variable and distinguishes the stable states quite well. Stable state definitions are the same as in Table 1. For the unfolding, the values for the interfaces were λ_i = R_OH = 14, 16, 20, 23, 28, 32, 36, 40, and 44. For each interface a TIS simulation was performed and the crossing probability was measured as a function of λ. From the resulting master curve shown in Fig. 9, it follows that the probability P(λ_B|λ_A) = 1.1 × 10⁻⁵. The flux term in Eq. 2 was measured directly from a MD simulation of the N-state and is ∼20 per ns. The total rate constant at 295 K for unfolding is then 0.20 μs⁻¹, in reasonably good agreement with the experimental result k = 0.17 μs⁻¹ (Muñoz et al., 1997, 1998). The folding rate can be deduced from the equilibrium constant K = k_AB/k_BA. Experiments show that at 300 K, the equilibrium constant is almost unity, hence the folding rate constant will almost equal the unfolding rate (Muñoz et al., 1997).

FIGURE 9.

Crossing probabilities P(λ_A|λ) for the unfolding F-H transition (solid) and the folding H-F transition (dashed) as a function of λ = R_OH. This function clearly shows a plateau in both cases, indicating that the final state has been reached.

To calculate the rate for the folding transition, starting from the H-state and going to the F-state, we also used λ ≡ R_OH as an order parameter. The H-state was defined as in Table 1, with R_OH ≥ 60 instead of 50, because the straightforward MD calculations indicated that the flux through λ = 50 was very low. The values for the interfaces were λ_i = 24, 26, 28, 30, 32, 34, 36, 38, 42, 46, 50, 55, and 60. The crossing probabilities were measured and joined together in the master curve in Fig. 9, yielding P(λ_B|λ_A) ≈ 2 × 10⁻⁴. The flux was once more obtained from a straightforward MD calculation and was estimated at 2 per ns. The resulting estimate for the H-F folding rate constant is ∼0.4 μs⁻¹. This is also surprisingly close to the experimental folding rate (Muñoz et al., 1997, 1998).

The agreement between the experimental and simulated rate constants is probably fortuitous, since the error in our calculation can be quite large. Nevertheless, inspection of Fig. 9 suggests that this error is approximately a factor 2. The values of the rate constants also agree with previous theoretical estimates in implicit solvent by Zagrovic et al. (2001). One might conclude that the solvent apparently does not play an important role in the folding rate, but it clearly is important for the mechanism and transition state ensemble.

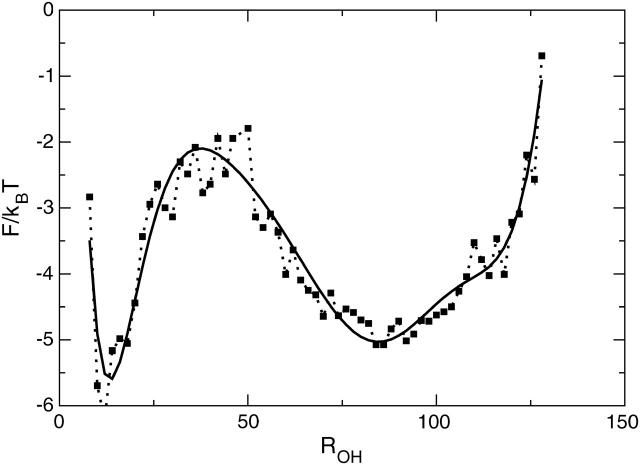
The above TIS results indicate that there is a free-energy barrier of >10 k_BT between the F- and H-states. However, if we plot the free energy F from the REM simulations as a function of R_OH in Fig. 10 we only obtain a barrier of ∼3–4 k_BT. This value is similar to the barrier found in the free-energy landscapes of Zhou et al. (2001). The large discrepancy between the rate constant and FE results is caused by an overlap between the F- and H-states, thus apparently lowering the barriers in the projection on not only the R_OH, but also the N_hb,R_g plane and other representations. It follows that free-energy landscapes cannot always be trusted to give correct barrier heights. The low barrier also shows that TST-based methods (Chandler, 1978; Bennett, 1977) cannot be used to calculate rates, as they will result in extremely low transmission coefficients. To ensure that the F-H barrier really should be higher than the FE estimate, we computed the F-H transition rate using a one-dimensional high friction Langevin description in the fitted R_OH free-energy landscape (see Fig. 10). The effective diffusion constant was obtained from a 4-ns straightforward MD simulation in the H-state and was D_eff ≈ 2.1 Ų/ps. The resulting Langevin rate constant was 80 ± 5 μs⁻¹, approximately a factor 500 too high with respect to the experimental and TIS rates. This indicates that the barrier should in fact be ln500 ≈ 6 k_BT higher, as correctly predicted by the TIS crossing probabilities.

FIGURE 10.

Free energy as a function of R_OH from REM simulations at T = 300 K. The solid smooth line is a ninth-order polynomial fit to the data.

In Bolhuis (2003a), we also calculated the rate constant for the H-U process with TIS. We chose λ = d_min as an order parameter, as that seemed to be the most sensitive parameter for the transition. Values for interfaces were λ_i = d_min = 3, 4, and 5. From the master curve and the flux, it followed that the total rate constant is 0.6 ns⁻¹, ∼3 orders-of-magnitude faster than the F-H transition. This confirmed that the folding obeys two-state behavior, as well as the notion that the F-H transition is the rate-limiting step in the unfolding process, and also the observation by several authors that the H-state is not extremely stable. García and Sanbonmatsu (2001) and Zhou et al. (2001) claim that the H-state is not well populated, hence has a higher free energy than the F- and U-state. Straightforward MD simulation showed reasonable stability of the H-state, but when continued for several nanoseconds more, the unfolding takes place spontaneously, in line with the calculated rate constant.

On the other hand, the fact that the F-H and the reverse H-F transition have similar rates indicates that the H-state is actually similar in free energy with respect to the U- and F-states (on the order of 1 k_BT difference), and that the two-state behavior is entirely caused by the barrier between H and F. This is in agreement with an elongated MD simulation in the U-state, which returned to the collapsed H-state, indicating that both solvation and hydrophobic collapse take place within nanoseconds. It is also supported by both our REM free-energy landscapes and those of Zhou et al. (2001), which all show a difference in free energy between the H-state and the U-state of <1 k_BT.

CONCLUSIONS

We presented the mechanistic details of an ensemble of kinetic pathways for β-hairpin folding in explicit solvent at room temperature. The overall folding mechanism as described in terms of intermediate states is in agreement with predictions from free-energy calculations. First, the hydrophobic core collapses, followed by the rate-limiting search for the backbone hydrogen bonds. The kinetic pathways, however, do not follow the free-energy landscapes. In particular the TSE is different from the prediction of the free-energy saddle points. The TSE for the F-H transition is characterized by an almost completely formed hairpin with a strip of water molecules separating the two strands. The TSE for the H-U transition is reached when the first water layer has entered the hydrophobic core. Both transitions indicate a role for the solvent as a lubricating agent in the folding process (Shea and Brooks, 2001; Sheinerman and Brooks, 1998a,b; Cheung et al., 2003; García and Onuchic, 2003). The finding of water bridges in the folding transition state ensemble begs the question if this is a general mechanism for folding. It would be interesting if these transition states are also found in other fast folders. Research in that direction is currently underway.

The computed rate constants for the folding and unfolding are in agreement with experiments. These results support the validation of the use of all-atom force fields to study protein folding. The computed free-energy barrier is much lower than one would expect, because adjacent stable states can overlap in their order parameter space. The use of TST-based methods to address the kinetics is therefore limited.

In summary, we have shown that the TPS methodology is a viable way of studying rare events in complex biomolecular systems. The important main advantage is that one does not have to impose the reaction coordinate, but can extract the transition states from the true dynamical paths. We stress that our methodology works irrespective of the quality of the force field. The main drawback is the computational effort, which can be huge for biomolecules in explicit solvent. Recently, we introduced the partial path sampling method for diffusive barriers, thus reducing the necessary simulation time (Moroni et al., 2004). Also, Singhal et al. (2004) have proposed a way to combine deterministic TPS as used here, with a stochastic Markovian description of protein folding, thus potentially reducing computational effort dramatically. Such stochastic approaches should be the future direction of atomistic simulations of protein folding kinetics.