Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Oct 22;88(1):579–589. doi: 10.1529/biophysj.104.048827

Quantitative Imaging of Lymphocyte Membrane Protein Reorganization and Signaling

Peter M Kasson *,†, Johannes B Huppa ‡,§, Michelle Krogsgaard ‡,§, Mark M Davis ‡,§, Axel T Brunger ‡,¶,∥
PMCID: PMC1305035  PMID: 15501943

Abstract

Changes in membrane protein localization are critical to establishing cell polarity and regulating cell signaling. Fluorescence microscopy of labeled proteins allows visualization of these changes, but quantitative analysis is needed to study this aspect of cell signaling in full mechanistic detail. We have developed a novel approach for quantitative assessment of membrane protein redistribution based on four-dimensional video microscopy of fluorescently labeled proteins. Our analytic system provides robust automated methods for cell surface reconstruction, cell shape tracking, cell-surface distance measurement, and cluster formation analysis. These methods permit statistical analyses and testing of mechanistic hypotheses regarding cell signaling. We have used this approach to measure antigen-dependent clustering of signaling molecules in CD4+ T lymphocytes, obtaining clustering velocities consistent with single-particle tracking data. Our system captures quantitative differences in clustering between signaling proteins with distinct biological functions. Our methods can be generalized to a range of cell-signaling phenomena and enable novel applications not feasible with single-particle studies, such as analysis of subcellular protein localization in live organ culture.

INTRODUCTION

Relocalization and clustering of signaling proteins in the plasma membrane accompany and drive a diverse array of biological processes, including lymphocyte activation, neuronal synapse formation, apoptosis, and cell motility (Boldin et al., 1995; Gautam et al., 1996; Ghosh et al., 2002; Grakoui et al., 1999; Monks et al., 1998; Sanes and Lichtman, 2001; Wang et al., 2003). In all of these cases, redistribution of membrane-associated signaling proteins has been linked with the initiation of cellular signaling cascades and the establishment of cellular polarity. Protein localization is commonly monitored using fluorescent probes, which can be covalently or genetically attached, as in the case of green fluorescent protein (GFP) fusion constructs, or associated via antibodies or other affinity tags. Recent advances in imaging technology allow the visualization of these probes with increasing specificity and spatiotemporal resolution (Agard et al., 1989; Gustafsson et al., 1999; Kam et al., 2001; McNally et al., 1999; Thomas et al., 1996).

Methods for quantitative analysis of these data, however, have lagged behind the progress in experimental detection techniques. Measurement of plasma membrane protein movements is challenging because these movements occur across four dimensions (x, y, z, time) and on a surface that is moving, rotating, and often deforming. Furthermore, experimental data from fluorescence microscopy frequently have low signal/noise levels. Previous work in this area has begun to address some of these issues (Gerlich et al., 2001; Moss et al., 2002; Tvarusko et al., 1999), but an integrated system for analysis has thus far been lacking. Such a system is necessary to measure receptor movement and patterning in a statistically valid manner and to study the underlying signaling processes in mechanistic detail.

Applied to one instance of cell signaling, fluorescence-labeling techniques have been used extensively to monitor membrane receptor clustering during T-lymphocyte activation (Davis et al., 2003; Grakoui et al., 1999; Krummel et al., 2000; Monks et al., 1998; Montoya et al., 2002; Purbhoo et al., 2004). Although the precise function of these phenomena remains to be determined, numerous signaling proteins cluster at the interface between the T cell and the antigen-presenting cell in an organized fashion. Proteins that cluster at this interface include the T-cell receptor (TCR) and its associated CD3 signaling proteins, the major histocompatibility complex protein (the TCR ligand), and the signaling protein linker for activation of T cells (LAT) (Davis et al., 2003; Grakoui et al., 1999; Huppa and Davis, 2003; Krummel et al., 2000; Monks et al., 1998; Montoya et al., 2002). Major challenges in the study of T-cell activation include determining the physical basis for these clustering phenomena and developing a mechanistic model for the signaling network they control. Both of these tasks require the ability to obtain quantitative measures of protein distribution and movement on the cell surface.

In this report, we describe the development of a means for quantitative assessment of protein redistribution and apply it to the analysis of the aforementioned phenomena. Our overall strategy for quantitative analysis is as follows (Fig. 1). We first identify the cell membrane in microscopy images and determine a consistent reference framework for measurement of cell-surface distances. We then use these distances to measure protein localization patterns over time and to assess protein redistribution behavior. We utilize the Moss segmentation filter previously reported by Yang et al. (2001) to detect membrane structures, followed by a level-set surface reconstruction technique to build a fully connected approximation of the cell surface. For analysis of membrane protein clustering, an automated cluster analysis technique identifies the cluster most likely to be of biological relevance at a single time point shortly after the onset of clustering. This information yields a reference point to track cluster formation throughout the course of the experiment. To track membrane changes over time, we then employ rigid-body cell shape alignment. We measure distances on the cell surface relative to the reference point via a graph-labeling algorithm that determines the shortest distance to each surface point. Applying this approach to T-lymphocyte activation, we measure velocities of signaling proteins undergoing stimulation-induced clustering. We have validated our approach on simulated receptor clustering data and experimentally by comparing our measurements of CD3ζ clustering to single-particle tracking measurements of T-cell receptor movement (Moss et al., 2002). We have subsequently extended our analysis to another signaling protein, LAT, measuring clustering behavior similar to that which has been qualitatively described in the literature. Neither of these proteins can be labeled for whole-cell single-particle studies because they lack extracellular domains suitable for external labeling. In contrast, our analytic system can readily be used to obtain measurements from microscopy of cytoplasmically labeled GFP fusion proteins.

FIGURE 1.

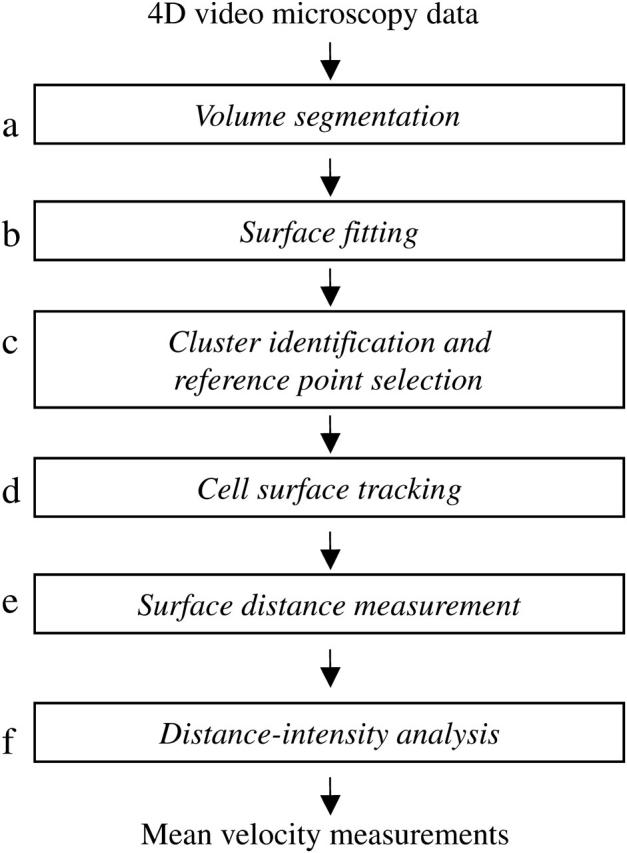
FIGURE 1

Open in a new tab

Analytic process for measuring membrane protein velocities. This schema depicts the stages of cell surface reconstruction, clustering analysis, and alignment performed by our system. (a) The volume segmentation filter serves to detect membrane structures in the image volume. Surface reconstruction performed at stage b uses a level-set method to fit a smooth surface to the membrane data points. (c) Clustering analysis is performed at a single time point to identify the center of the brightest cluster, which will serve as the reference point for further analysis. Cell surface tracking information obtained in stage d is then used to propagate this spatial reference point to all time points. (e) Cell surface distances are measured at each time point by a surface walking technique, using the reference point identified in stage d as the origin. (f) The distance information obtained in stage e is combined with membrane voxel intensity information to yield a distance-intensity distribution for each time point, from which the mean velocity can be calculated.

METHODS

Volume segmentation

Our analytic approach is outlined schematically in Fig. 1, and accompanying images from the analysis of a CD3ζ-GFP microscopy data set are shown in Fig. 2. The goal of the segmentation filter (Fig. 1 a) is to detect cell membranes in noisy images, as depicted in Fig. 2 a. For this task, we employ the Moss filter (Moss et al., 2002; Yang et al., 2001), which was developed for the identification of membrane structures and offers increased specificity compared to conventional edge-finding filters. As detailed below, the filter selects voxels that have high intensity and a high ratio of the second derivative to the first derivative of intensity with respect to position in each lateral image dimension. The filter selects membrane voxels with fairly high specificity but moderate sensitivity (Fig. 2 b), generating a membrane that may have some μm-scale “holes”. Subsequent cell-surface fitting via a level-set-based method largely compensates for errors of this nature (see below). Briefly, the volume segmentation filter functions as follows (Yang et al., 2001). A discriminant matrix ψ is calculated for each x-y plane of the image along the z axis, or z-slice, of a volume image:

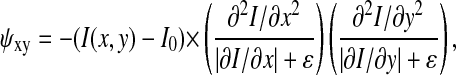graphic file with name M1.gif (1)

where I(x,y) is the intensity at pixel coordinate (x,y), I0 is the background intensity, and ɛ is a small arbitrary constant (set to 1 × 10−10). Thresholding as used in the Moss filter program is applied to this discriminant matrix to create a binary mask, from which isolated pixels are removed. Finally, z-connectivity is established by inclusion in the mask only of pixels that have a nonzero neighbor in an adjacent z-slice.

FIGURE 2.

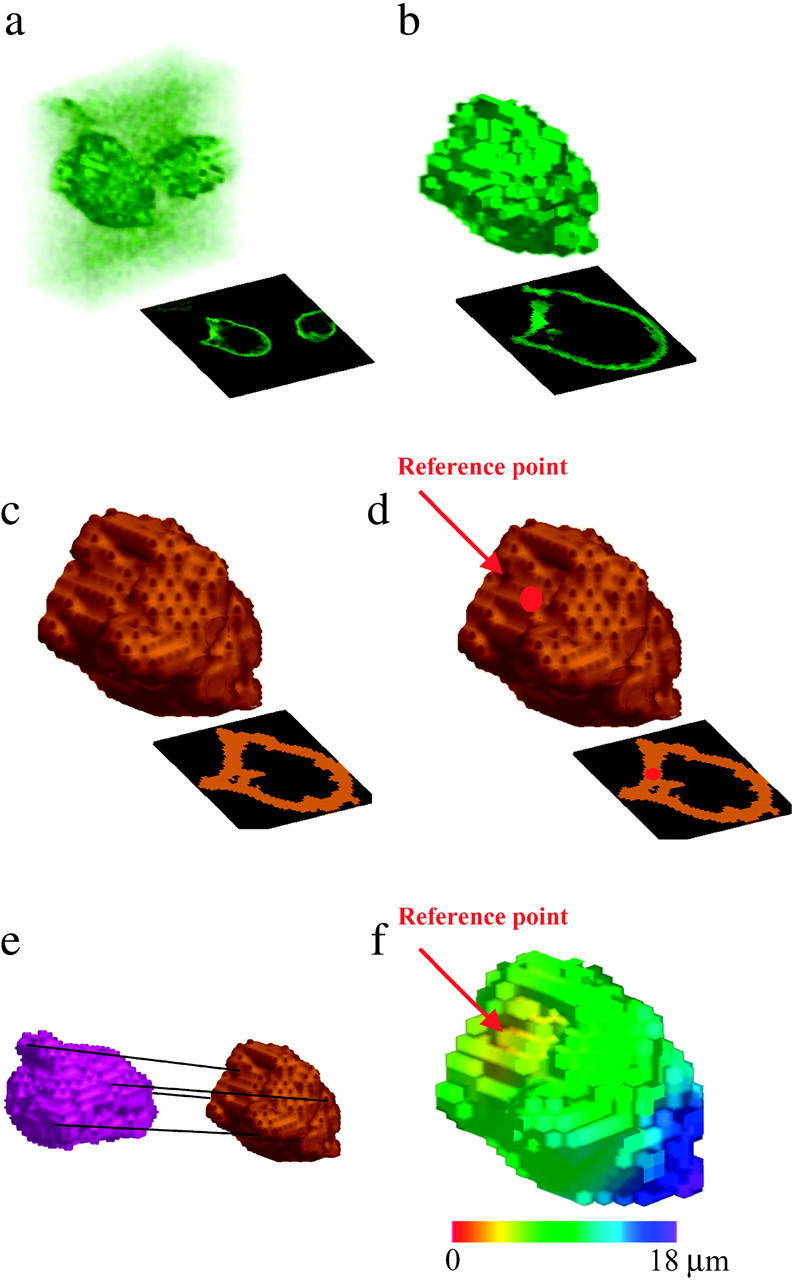
FIGURE 2

Open in a new tab

Images from the analysis of a single T-cell volume and renderings shown are from progressive analytic stages of a single time point from a CD3ζ-GFP data set. Each rendering shows the input data to the correspondingly lettered process in Fig. 1. Shown in panel a is the deconvolved microscopy data set. The set of membrane voxels identified by the segmentation filter is shown in panel b, and the reconstructed cell surface is shown in panel c. Shown in panel d is the cell surface with the reference point identified at 90 s after calcium flux, and shown in panel e are two aligned surfaces from the same cell at different time points. Shown in panel f is a distance map of the cell surface. Figure insets show x-y midsections through the cell.

Surface fitting

Surface fitting (Fig. 1 b) is performed on the largest connected region in the segmentation filter output. Starting with a set of cell membrane data voxels that is not necessarily complete, the goal is to obtain a smooth continuous surface approximating the cell surface (Fig. 2 c), which is necessary for accurate surface distance measurement. Such a surface also greatly aids subsequent cell surface tracking by providing a more consistent representation of cellular features for alignment. An ɛ-outer contour around the segmentation filter output data is taken as the initial surface. We implement a level-set-based formulation previously described by Zhao et al. (2000) and defined as follows:

Consider a scalar field ϕ(x,t) such that:

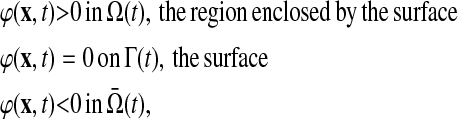graphic file with name M2.gif (2)

where x is a surface voxel and t is the evolution parameter of the field. As per Zhao et al. (2000), we define a surface energy:

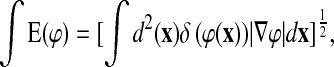graphic file with name M3.gif (3)

and a gradient flow for ϕ:

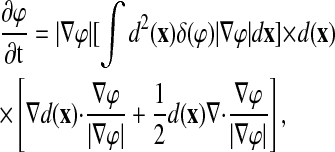graphic file with name M4.gif (4)

where d(x) is the distance from x to the nearest input data voxel and δ is the Dirac δ-function. Solution of these equations produces a surface that is attracted to the input data voxels yet minimizes surface curvature.

We solve the above gradient flow equation (Eq. 4) on a discrete grid to find a local minimum for ϕ using a partial-differential equation evolution method by Peng et al. (1999). Taking as the initial surface an ɛ-shell around the segmentation filter output data voxels for a small arbitrary ɛ, let ϕ0(x) = d(x) − ɛ, where d(x) is a distance function from the data voxels. Values for ɛ were tested in the range 0.3–3.3 μm; results shown in this study use ɛ = 1.5 μm. ϕ is then evolved in the local region of its level set according to a third-order Runge-Kutta method for numerical solution of differential equations. After ϕ converges, surface voxels x are selected by thresholding on ϕ such that ϕ(x) is less than the voxel grid spacing. This cutoff value is used because ϕ(x) approximates a signed distance function, as discussed below.

As discussed by Peng et al. (1999), over the course of level-set evolution the function ϕ will deviate from its desired behavior as a signed distance function. To maintain a well-behaved function ϕ, we periodically reinitialize ϕ such that its level set (and thus the evolving surface) is preserved but the new function ϕ more closely resembles a distance function, as per Sussman et al. (1994). Redistancing is obtained by solving a discretized version of the following equation to steady state:

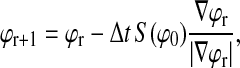graphic file with name M5.gif (5)

where S is the sign function.

To test how well our surface reconstruction method fits the data, we compared it to the method used in previous work (Moss et al., 2002), where a sphere is used to approximate the cell surface. Using root-mean-squared deviation (RMSD) from the segmentation filter output as a goodness-of-fit metric, our level-set-based reconstruction yields an average RMSD of 0.80 μm over the time points examined, substantially less than the 2.8 μm average RMSD obtained using the sphere-fitting method (data not shown). Additional validation tests of our volume segmentation and surface reconstruction methods are shown in Fig. 1 of the Supplementary Material.

Cluster identification and reference point selection

We next use the reconstructed cell surfaces to identify a consistent and relevant reference point and to track cell motion (Fig. 1, c and d). Reference point selection is performed at a single time point (not necessarily the first image), and the movement of this reference point is tracked through time using cell shape alignment as described below. In the absence of external information specifying an initial reference point of physiological interest, we infer a reference point based on general hypotheses regarding the expected behavior of the protein being measured (Figs. 1 c and 2 d). For example, during T-lymphocyte activation the biologically relevant reference point for T-cell receptor clustering is the center of the T-cell-antigen-presenting cell interface, identified by clustering analysis on the intensity data at a single time point shortly after calcium flux. A k-nearest-neighbors clustering analysis is used for this purpose. The following clustering metric is maximized over all surface points p:

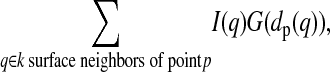graphic file with name M6.gif (6)

where I(q) is the observed intensity, dp(q) is the surface distance from p to q (determined as described below), and G is a Gaussian with ± SD σ = 2.5 μm. Tests in which the value of σ was varied from 1 to 5 μm do not show a substantial difference in performance (data not shown). The number of neighbors k was similarly varied between 15 and 200 without a substantial effect on reference point selection (data not shown); the results shown in this study use k = 50.

Cell surface tracking

Cell surface tracking is performed using a pairwise volume registration scheme (Figs. 1 d and 2 e). Aligning cell volumes using intensity information from the protein whose movements are being tracked would risk introducing artificial clustering behavior. Intensity information is therefore discarded for the purposes of cell surface alignment, and alignment is performed solely using cell surface geometry. The inputs to the alignment algorithm are thus binary volume data sets, the thresholded output of surface reconstruction (Fig. 1 c).

The problem of three-dimensional image alignment has been studied extensively in the context of medical image registration (Davatzikos et al., 1996; Maes et al., 1997; Viola and Wells, 1997; West et al., 1997). The standard method currently used in the field is maximization of mutual information, which is implemented via a random image subsampling approach (Viola and Wells, 1997). In the often noisy and rapidly deforming images acquired through microscopy, however, the alignment problem becomes somewhat different. Given two images with sufficiently low overlap, a randomized sampling algorithm for maximization of mutual information (Viola and Wells, 1997) often does not converge with a point sample size within fivefold of previously reported limits (data not shown).

To address this problem, we align the reconstructed cell surface at each time point against each adjacent time point using a pairwise registration scheme. We approximate cellular motion via a series of rigid-body movements. For most cells we have examined, cellular deformations are small on the timescale of observation. The minority of cells that undergo a rapid deformation require special treatment for the time points bridging the deformation. In the course of T-cell activation, local deformation at the cell-cell contact region creates a characteristic and consistent interface that further assists the tracking algorithm. Considering the set of all rigid-body transformations, we perform a global optimization search across quaternion rotation and translation space using iterative line searches with descending step size. Our search metric is a maximum likelihood criterion: p (D|M,T), where D is the data image (the reconstructed surface at time t), M is the model image (the reconstructed surface at time t ± 1), and T is the transform.

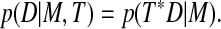graphic file with name M7.gif (7)

By conditional probability,

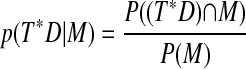graphic file with name M8.gif (8)
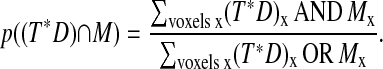graphic file with name M9.gif (9)

We maximize this probability p(D| M, T) across quaternion rotation and translation space as described above to obtain a set of rigid-body transformations describing the motion of the cell membrane over the period of observation. These transformations are used to track the movement of the reference point, providing a consistent framework for cell surface distance measurement as described below.

Surface distance measurement

Given a reconstructed surface and a reference point on that surface at each time point, we wish to create a map of the cell membrane giving the shortest surface distance from each point to the reference point (Fig. 2 f). This distance measurement is performed using an upwinding or surface walking strategy (Fig. 1 e). This algorithm provides a means of distance labeling a graph in an ordered manner, from closest to farthest. Three lists are maintained: visited nodes, nearby nodes, and unvisited nodes. Initially, all nodes are unvisited and have an infinite distance, and the reference point is visited and assigned a distance of 0 to begin the labeling process. The procedure for visiting a node n is as follows:

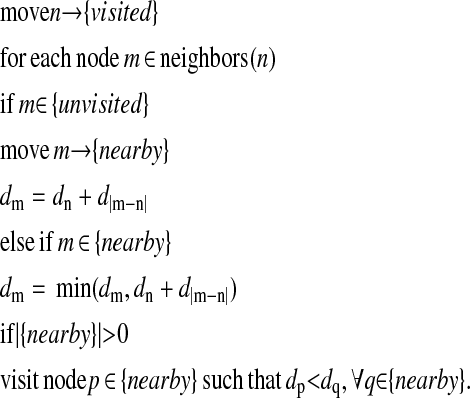graphic file with name M10.gif

This algorithm will visit all connected nodes on the reconstructed surface and will label them with a good approximation of the surface distance to the reference point. We allow neighbors to be found using either 6-connectivity (cube faces) or 26-connectivity (including diagonals); results reported here used 6-connectivity. Once a distance-labeled surface is obtained, the original data points are distance labeled by mapping each one to the closest surface point.

Distance-intensity analysis

By combining our cell-surface distance labeling with the cell membrane voxel intensities identified by the segmentation filter we obtain distance and intensity values for each data voxel on the cell membrane. We then compute radial profiles of distance versus fractional intensity (Fig. 1 f, examples in Fig. 3). Shifts in these profiles over time reflect bulk movement of the membrane protein being measured. Mean receptor velocities relative to the reference point are calculated using the change in intensity-weighted mean distance over time, where the intensity-weighted mean distance is computed as follows:

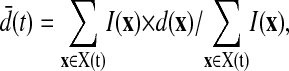graphic file with name M11.gif (10)

where X(t) is the cell membrane voxel data set (as determined by the segmentation filter) at time t, I(x) is the intensity of each membrane voxel x, and d(x) is the surface distance to x. Although these velocities fail to capture some of the subtleties of membrane protein redistribution, they provide a concise first-order encapsulation of the time evolution of distribution profiles. Our method of velocity estimation also assumes that any internalization of membrane proteins or delivery of protein to the surface occurs in a spatially unbiased manner. Local cluster size calculation is performed analogously to our k-nearest-neighbors calculation. The cluster size is defined as

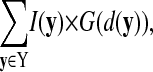graphic file with name M12.gif (11)

where Y are all voxels with a surface distance of <5 μm from the reference point and G is a Gaussian weighting function with ± SD σ = 1 μm. Cluster size values are normalized at 1 min before calcium flux to yield relative values.

FIGURE 3.

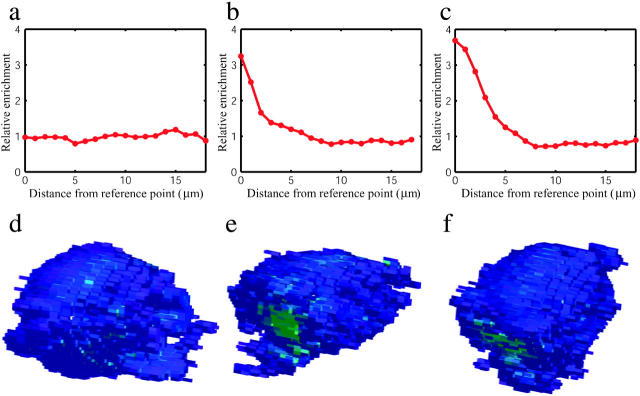
FIGURE 3

Open in a new tab

Radial distribution of intensity. Plotted are distributions showing the relative enrichment of CD3ζ-GFP at each surface distance increment from the reference point. The distribution plotted in panel a is at 1 min before Ca2+ flux, the distribution in panel b is at 0.5 min after Ca2+ flux, and the distribution in panel c is 1.5 min after Ca2+ flux. Mean intensity-distance values are 9.8, 8.4, and 8.1 μm, respectively. Distributions are corrected for the total surface area present at each distance from the reference point (calculated as the fraction of total CD3ζ-GFP present at each distance divided by the fraction of surface area at that distance). The intensity profile shifts from a close approximation of a uniform distribution to one that is substantially skewed toward the reference point, consistent with clustering behavior. Renderings of the cell membrane points selected by our segmentation filter are shown in panels d, e, and f for time points corresponding to the distributions plotted, colored by voxel intensity.

T-cell imaging

5C.C7 T lymphoblasts derived from T-cell-receptor transgenic mouse lymph nodes were grown, retrovirally transfected with CD3ζ-GFP or LAT-GFP constructs, and stimulated in vitro with the moth cytochrome c peptide 88–103 presented on antigen-presenting cells (CH27 / I-Ek) as previously reported (Ehrlich et al., 2002; Fink et al., 1986; Huppa et al., 2003). For calcium imaging, T cells were incubated with 5 μg/mL fura-2-am (Molecular Probes, Eugene, OR) for 30 min at room temperature and then washed once in imaging buffer before antigen exposure. The ratio of fura-2 emission at 510 ± 40 nm when excited at 340 and 380 nm, respectively, was used to assess intracellular calcium concentrations (Tsien, 1989).

Images were acquired on a Zeiss Axiovert S100TV microscope with a 1.3 numerical aperture 40× Fluar objective (Carl Zeiss, Jena, Germany). Samples were illuminated by a 300-W xenon light source with a Sutter DG-4 filter changer (Sutter Instruments, Novato, CA). Detection was performed using a cooled charge-coupled device camera (Roper Scientific, Tucson, AZ). Z-scanning was accomplished using a piezo-driven motor (Physik Instrumente, Waldbronn, Germany). Cells were imaged at 37°C in phenol red-free RPMI. Metamorph 5.0 (Universal Imaging, Downingtown, PA) was used for microscope control; images were further processed using 40 iterations of blind deconvolution (Deblur 9.2, AutoQuant Imaging, Watervliet, NY). Calcium flux was used as a temporal marker for the initiation of T-cell stimulation as has been done previously (Ehrlich et al., 2002; Huppa et al., 2003). Data sets were collected at a resolution of 0.3 × 0.3 × 1 μm; the time for acquisition of a single volume data set or “z-stack” was ∼3 s. Our analytic system used 26 min of CPU time to process one cell (63 × 70 × 27 voxels, 14 time points) on a 2.4-Ghz Intel Xeon processor (Intel, Santa Clara, CA). Renderings for visualization were produced using T3D (Research Systems, Boulder, CO), and Matlab (The MathWorks, Natick, MA).

RESULTS

Tests on simulated data

We validated our approach first by testing its ability to measure membrane protein clustering in a simulated system. We modeled receptor clustering by simulating individual protein molecules undergoing Brownian motion on a surface subject to an attractive force. We approximated the cell surface as a spheroid with radii of 7 μm and 4.7 μm and calculated receptor motion using a discrete-time, continuous-position simulation, adapting the time-evolution equations derived by Brillinger (1997):

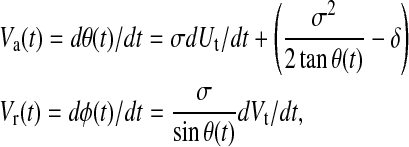graphic file with name M13.gif (12)

where θ ε [0,π] is the spherical coordinate corresponding to axial angle, φ ε [0,2π] is the spherical coordinate corresponding to radial angle, δ is the attractive drift term, and Ut and Vt are normally distributed random processes with mean 0 and variance σ2. The simulation was initialized with particles distributed randomly on the spheroid. A value of 1.4 μm was used for σ, corresponding to a two-dimensional diffusion constant D = 1 × 10−12 m2/s. Simulations were performed with attractive terms δ = 0.032 and 0.095 μm/s, chosen to produce velocities roughly similar to those observed experimentally for CD3ζ (units are converted to radians/s for use in Eq. 13). To simulate image formation, voxel occupancies were calculated from particle positions at each time, and the resulting images were processed using our analytic system as outlined in Fig. 1 (excluding the segmentation step) as if they were observed data. Particle positions were also analyzed directly for use as a reference standard as follows, letting the mean distance at time t be:

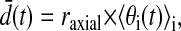graphic file with name M14.gif (13)

where raxial is the axial radius of 7 μm and 〈θi(t)〉i is the mean of the axial angle coordinates for all particles i at time t. Sixteen simulations were performed for each attractive velocity. The interquartile range was used as a means of nonparametric error estimation (Tukey, 1977). The results of these simulations (Fig. 4) show a good agreement between our image analysis measurements and the particle position data. Mean percentage errors were 10% and 9% for simulations with δ = 0.032 and 0.095 μm/s, respectively. As clustering becomes particularly punctate, small errors in reference point tracking can result in larger velocity measurement errors. This can be seen at long times in Fig. 4 a; the corresponding distance-intensity distribution is given in Fig. 4 e. Fig. 4 a also demonstrates that these errors shrink substantially when the reference point is artificially fixed. These results show the ability of our system to measure particle clustering velocities accurately in an ideal system when the reference point is determined from the observed images; we next demonstrate our system's performance on data from microscopy of labeled T-cell signaling proteins.

FIGURE 4.

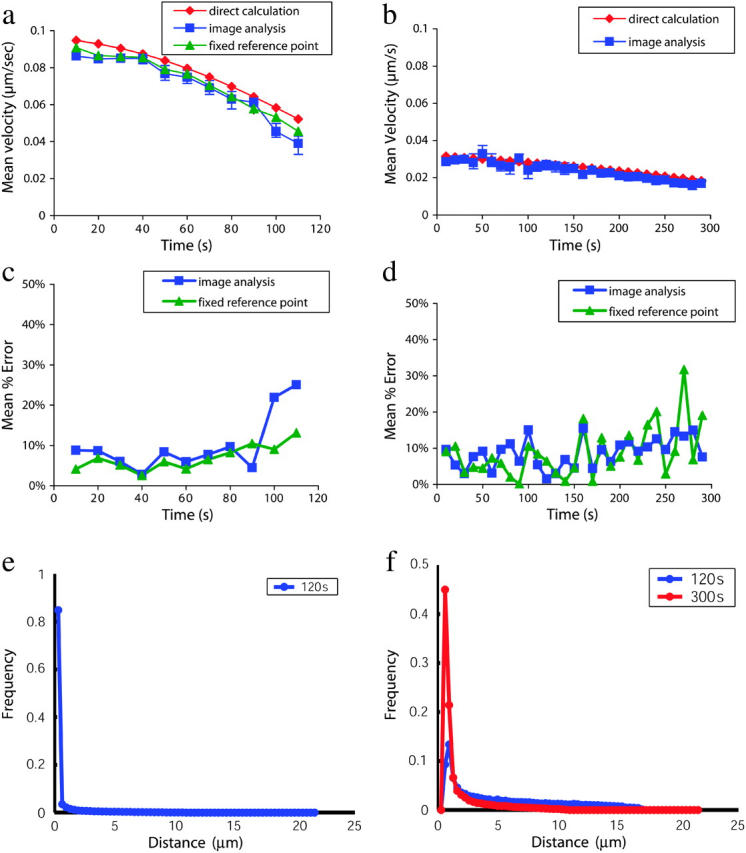
FIGURE 4

Open in a new tab

Tests on simulated data. Receptor motion on the cell surface was simulated by modeling a large number of particles undergoing Brownian motion with an attractive drift term. Particle motion was calculated using discrete time steps on the surface of a spheroid with radii 7 and 4.7 μm using the time-evolution equations derived by Brillinger (1997). Voxel occupancies were calculated from particle positions at each time, and the resulting images were processed using our analytic system as if they were observed four-dimensional data. Particle positions were also analyzed directly for use as a reference standard (see text). Clustering with attractive velocity component δ = 0.032 μm/s is plotted in panel a. Clustering with attractive velocity component δ = 0.095 μm/s is plotted in panel b. The mean percentage error introduced by our image analysis system is plotted in panels c and d. In the case of a very punctate distribution, small spatial errors in reference point alignment can result in large percentage errors. The effects of reference point error were also analyzed by fixing the reference point and comparing the percentage error. Histograms in panels e and f show the distribution of particle distances from the reference point in the simulations analyzed in panels a and b. The greater directed motion in panel a results in very punctate clustering of most particles after 2 min (e), whereas the smaller directed motion in panel b results in a smaller punctate clustering component and a more disperse distribution at 2 min, with a more completely clustered (but still less punctate, as can be seen by the difference in peak widths) distribution at 5 min (f). Sixteen simulations were performed for each attractive velocity; all error bars shown represent the first and third quartiles of the data.

Experimental measurements in T lymphocytes

Having developed a novel analytic system for measuring membrane protein localization and movement using bulk fluorescence microscopy data, we applied it to the measurement of signaling protein rearrangements in T lymphocytes undergoing antigenic stimulation. We first analyzed the clustering behavior of CD3ζ, a molecule closely associated with the T-cell receptor that has been observed to cluster at the cell-cell interface during T-cell stimulation. Profiles of CD3ζ distribution during the activation of a single T cell are shown in Fig. 3, accompanied by corresponding fluorescence intensity images for the cell surface. Measurements of CD3ζ velocity obtained using our system (Fig. 5 a) were similar in magnitude and time profile to previously reported single-particle tracking data for the T-cell receptor (Fig. 5 b) (Moss et al., 2002), an approximately comigratory molecule. We found a rapid increase in mean velocity relative to the reference point upon activation, peaking at ∼0.1 μm/s, followed by a return to baseline within 90 s. The single-particle trace shows a somewhat more extended decay phase. This subtle difference likely results from the fact that the single-particle trace depicts the motion of only a few molecules (it is the only published trace available for the T-cell receptor) and is thus a small sample from what is likely an inhomogeneous receptor population. Because detectable CD3ζ persists over the entire cell surface during antigenic stimulation, some molecules exhibit no net motion toward the interface. Trajectories may vary among moving molecules, potentially displaying dependence on starting position. Differences in the cell type used (D.10 lines versus 5C.C7 lymphoblasts) or subtle differences between T-cell receptor and CD3ζ motions may also account for some of the observed variation.

FIGURE 5.

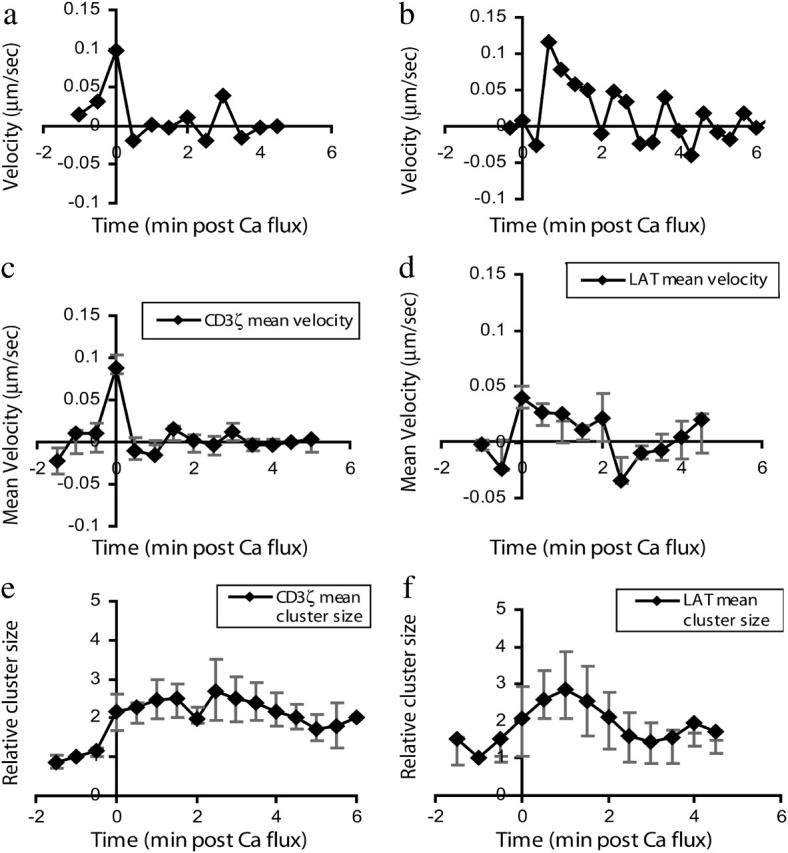
FIGURE 5

Open in a new tab

Receptor velocity in response to T-lymphocyte stimulation. (a) CD3ζ velocity measurements derived from bulk fluorescence measurements via our analytic system are plotted for a single cell. (b) A T-cell receptor velocity trace from the average of eight single-particle measurements is plotted using published data (Moss et al., 2002). (c) Shown are CD3ζ mean velocity measurements calculated based on analysis of six cells. (d) Plotted are mean velocity measurements for LAT movement toward the cell-cell interface. Values represent the mean of six cells. (e) Plotted are measurements of local CD3ζ cluster size near the interface. Values represent the mean of six cells. (f) Plotted are measurements of LAT local cluster size near the interface. Values plotted represent the mean of six cells. Both mean velocity and cluster size measurements show rapid LAT cluster formation followed by dissipation over the next 2 min, in contrast to the more stable cluster formation by CD3ζ. As our data are not normally distributed, nonparametric error analysis is used and error bars depict the first and third quartiles of the data in each plot.

We have also measured the activation-induced redistribution of LAT, a transmembrane protein that serves as a critical adaptor molecule in T-cell activation and has qualitatively been observed to cluster at the T-cell-antigen-presenting cell interface (Montoya et al., 2002; Purbhoo et al., 2004; Zhang et al., 1998). As has been qualitatively and heuristically observed, we found a rapid increase in mean velocity upon T-cell activation that then switches to a mild net dissipation of LAT after ∼2 min (Fig. 5 d). Because LAT enrichment at the interface is somewhat punctate, we also measured the local cluster size at the interface over time. As our data are not normally distributed, the interquartile range (Tukey, 1977) was used as a means of nonparametric error estimation for both clustering velocity and local cluster size measurements. Results (Fig. 5 f) are consistent with the mean velocity behavior: the cluster size increases two- to fourfold upon activation and returns to baseline within 3 min. This transient local clustering of LAT contrasts with the sustained greater than twofold increase in CD3ζ local cluster size (Fig. 5 e; velocity in Fig. 3 c) over the first 5 min.

Robustness testing

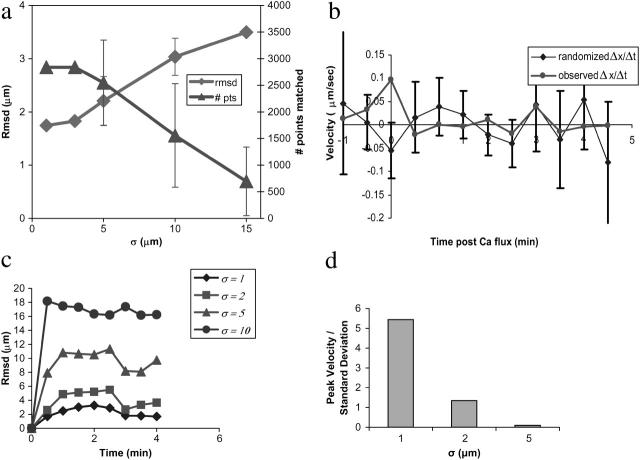
We have performed several analyses, using CD3ζ-GFP microscopy data, of our system's robustness to error. Surface reconstruction robustness to missing values (Fig. 6 a) was tested by performing surface reconstruction on microscopy data sets with points deleted from the segmentation filter output, mimicking lower filter sensitivity. For each test set, a data voxel was selected at random and all data voxels within a given radius were deleted. Surface reconstruction was performed as described above and the results compared to reconstruction on the unmodified data via a closest-point matching algorithm. Our method is robust to deletions up to ∼5 μm in radius (Fig. 6 a).

FIGURE 6.

FIGURE 6

Open in a new tab

Robustness testing. Robustness of surface reconstruction to missing data is shown in panel a. Missing data were generated by randomly selecting a membrane surface voxel and deleting all voxels within a given radius. Surface reconstruction was performed on the data sets thus generated, and the resulting surface voxels were compared to the unperturbed surface via a closest point matching strategy. The number of matched points (# pts) and the root-mean-squared deviation (rmsd) of matched points are plotted as a function of increasing deletion radius. Surface reconstruction is robust to deletions of as large as 5 μm; larger deletions are unrealistic, as the mean radius of a T lymphocyte is 7 μm. To test the potential biasing effect of cluster analysis for reference point determination, we compare in panel b experimentally observed clustering velocities to those calculated on data sets with randomly permuted intensities. Initial peak receptor velocities for the observed experimental data significantly exceed those in the randomized data (p < 0.01). Error bars represent one standard deviation of the mean. Robustness of cell surface alignment to stepwise perturbation error is plotted in panel c. Root-mean-squared deviation (rmsd) from the unperturbed alignment is plotted as a function of time based on 20 perturbation experiments. Our method is robust to stepwise error of σ ≤ 2 μm. Robustness of cell surface alignment and subsequent velocity measurements to choice of reference point is shown in panel d. The ratio of clustering velocity to standard deviation for each error level is plotted for different error levels σ based on 24 perturbation experiments each.

Our reference point identification approach is designed to minimize the introduction of spurious clustering behavior, yet it does utilize some clustering information in selecting a reference point. To test more rigorously for a potential biasing effect, we randomized membrane fluorescence intensity information for a single cell, generating 150 random intensity data sets for each time point by resampling the cell surface and randomly permuting intensity values. Clustering velocities were calculated from these randomized data sets and compared to those obtained from the experimentally observed data. The resulting data (Fig. 6 b) show initial peak receptor velocities for the experimental data significantly exceeding randomized velocities (p < 0.01 using the Mann-Whitney U test), thereby demonstrating that we detect biologically significant clustering distinct from any bias-induced artifacts.

We have also analyzed the robustness of cell shape tracking to errors in alignment and in initial reference point identification. For each error level σ, we performed 20 perturbation experiments where at each pairwise registration step the calculated alignment (i.e., the optimal rigid-body transformation) was perturbed by a normally distributed error term ɛR ∼ N(0,σ). Our algorithm is robust to random translational perturbations in cell shape alignment of σ = 2 μm at each time point (Fig. 6 c). Similarly, robustness of cell surface alignment and subsequent velocity measurements to choice of reference point was tested by randomly perturbing the initial reference point coordinates by a normally distributed error term ɛR ∼ N(0,σ). Cell shape alignment was performed using this perturbed reference point, and the mean clustering velocity was calculated. Perturbations in reference point identification of σ < 2 μm did not mask the observed response (Fig. 6 d). This robustness to perturbations in alignment and therefore in reference point tracking confirms empirical observations that our method allows measurement of protein redistribution even in the presence of small-to-moderate cellular deformations.

DISCUSSION

Our analyses of fluorescence microscopy data acquired using routine experimental methods have produced estimates of T-cell-receptor velocity that agree well with data from single-particle tracking experiments. We have also employed our method to measure the movement of another key signaling molecule in T-cell activation, LAT. The translocation of LAT to the cell-cell interface immediately after calcium flux followed by its dissipation after two minutes corresponds to the temporal pattern of its phosphorylation in T cells, which is required for T-cell activation (Zhang et al., 1998; Zhu et al., 2003). Our analysis of bulk fluorescence data thus provides important information regarding large-scale membrane protein redistribution.

Single-particle tracking experiments provide a critical means of analyzing individual membrane protein motions, particularly in a heterogeneous population. However, these experiments are difficult to perform and require numerous repetitions to build population statistics. Current labeling techniques for single-particle imaging in which the whole cell is visualized require an externally accessible domain on the protein being tracked and may introduce the possibility of labeling-associated artifacts (Michalet et al., 2003). Proteins such as LAT that lack a substantial extracellular domain are not amenable to current whole-cell single-molecule approaches but can easily be visualized using bulk methods. Quantitative analysis of bulk fluorescence is particularly well suited for measurements on the spatial and temporal scales of whole-cell protein redistribution. Our analytic system provides population statistics more readily, is applicable to a broader range of imaging conditions, and may be adapted to high-throughput measurements. Because it yields quantitative information on protein movement in situations where single-particle measurements would be difficult or impracticable, it represents an important complement to single-particle tracking.

Measuring movement using cell surface distances instead of Euclidean distances is another way in which our system provides additional information not available from current single-particle tracking methods. This advantage is dependent on accurate surface reconstruction, and we have shown that our system performs well on noisy images. However, extremely noisy images can result in poor capture of membrane voxels by the segmentation algorithm. In the presence of extensive intracellular protein aggregates or labeled cells clumped together, additional delineation of the membrane may be required for accurate analysis. Also, proteins very specifically concentrated in one portion of the cell may not label the membrane uniformly enough to allow surface reconstruction. To analyze such proteins, our system is extensible to two-color fluorescence microscopy using a membrane marker. Other possible extensions include the use of external information for reference point identification and the analysis of more complex polarization patterns, including multipolar signaling and the ring and exclusion patterns observed with some signaling proteins (Delon et al., 2001; Ehrlich et al., 2002; Krummel et al., 2000; Sperling et al., 1998; Wulfing et al., 1998). In addition, our analytic system is scalable to high-throughput experiments. Localization profiles could be screened across a large number of experimental conditions or, alternatively, localization profiles could be rapidly measured for a large number of signaling proteins, creating a sort of “localization proteomics.” This could form the basis for more complete quantitative models of signaling networks.

Our system measures changes in relative protein distribution to derive rates of protein motion. Our approach can also take advantage of further experimental information to estimate absolute protein distributions, calculating the absolute numbers of molecules present in local clusters and the net molecular rates of arrival in those clusters. The total number of fluorophores present on the cell surface throughout the experiment can be estimated in terms of four major factors: the number of fluorophores on the surface at the start of the experiment, the rate of fluorophore bleaching, and the rates of fluorophore internalization and delivery of new fluorophores to the cell surface. Fluorescence-activated cell sorting with quantitative standards immediately before the start of the experiment allows the determination of absolute fluorophore numbers, and one can set arbitrarily tight gating criteria to isolate a population of cells expressing a given number of fluorophores (with error given by the gating width). Fluorophore bleaching under imaging conditions can be estimated by imaging fixed cells over time and measuring the rate of signal decay. Finally, assuming constant illumination intensity, one can estimate the net change in fluorophores present on the surface as the change in total fluorescence signal from the cell surface after accounting for bleaching. Measurement of this quantity has the advantage of allowing more accurate measurements of protein clustering under conditions where substantial amounts of protein are being internalized or delivered to the surface in a targeted fashion.

Our analytic methods are also applicable to a major area of recent development in the cellular imaging field: optical microscopy of cellular interactions and signaling events in vivo (Bajenoff et al., 2003; Miller et al., 2002; Reichert et al., 2001; Stoll et al., 2002; Svoboda et al., 1997). The observation of subcellular signal protein rearrangements within a living animal will permit quantitative analysis of signaling in this more complex cellular milieu where single-particle observations are infeasible. For instance, cellular behavior during lymphocyte activation can be notably different in native organs than in model systems (Bousso et al., 2002; Mempel et al., 2004; Miller et al., 2004; Stoll et al., 2002). Therefore the ability to measure cell-signaling events in these more physiologically relevant systems is of particular interest to understanding the physiologic function of protein redistribution. Image acquisition and probe detection are challenging in vivo and in organ culture, so the use of bulk fluorescence imaging in our system becomes a distinct advantage. Thus our analytic system enables quantitative measurement of protein movements and signaling networks in this more physiological context.

We have presented a novel analytic system for quantitative measurement of membrane protein movements on the cell surface. Our methods are fully three-dimensional and use a surface-based, model-free approach. We measure activation-induced clustering of the CD3ζ receptor in a robust and automated fashion, obtaining results consistent with previously reported single-particle tracking measurements of the T-cell receptor. Measurements of the velocity and clustering behavior of the signaling protein LAT in CD4+ lymphocytes illustrate the ability of our system to capture quantitative differences between signaling processes. Because our analytic framework is generally applicable to membrane protein movements, it will benefit other investigations of cell signaling such as neuronal synapse formation and cellular direction sensing.

Software availability

A general-release version of our software is under development and will be made available at http://atb.slac.stanford.edu.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.

[Supplemental File]
biophysj_104.048827_index.html (724B, html)

Acknowledgments

We thank O. Troyanskaya, M. Vrljic, and T. Fenn for many helpful discussions. W. Moss allowed use of code for the Moss filter.

This work was supported in part by the National Institutes of Health and the Medical Scientist Training Program.

References

  1. Agard, D. A., Y. Hiraoka, P. Shaw, and J. W. Sedat. 1989. Fluorescence microscopy in three dimensions. Methods Cell Biol. 30:353–377. [DOI] [PubMed] [Google Scholar]
  2. Bajenoff, M., S. Granjeaud, and S. Guerder. 2003. The strategy of T cell antigen-presenting cell encounter in antigen-draining lymph nodes revealed by imaging of initial T cell activation. J. Exp. Med. 198:715–724. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Boldin, M. P., I. L. Mett, E. E. Varfolomeev, I. Chumakov, Y. Shemer-Avni, J. H. Camonis, and D. Wallach. 1995. Self-association of the “death domains” of the p55 tumor necrosis factor (TNF) receptor and Fas/APO1 prompts signaling for TNF and Fas/APO1 effects. J. Biol. Chem. 270:387–391. [DOI] [PubMed] [Google Scholar]
  4. Bousso, P., N. R. Bhakta, R. S. Lewis, and E. Robey. 2002. Dynamics of thymocyte-stromal cell interactions visualized by two-photon microscopy. Science. 296:1876–1880. [DOI] [PubMed] [Google Scholar]
  5. Brillinger, D. R. 1997. A particle migrating randomly on a sphere. J. Theor. Probab. 10:429–443. [Google Scholar]
  6. Davatzikos, C., J. L. Prince, and R. N. Bryan. 1996. Image registration based on boundary mapping. IEEE Trans. Med. Imaging. 15:112–115. [DOI] [PubMed] [Google Scholar]
  7. Davis, M. M., M. Krogsgaard, J. B. Huppa, C. Sumen, M. A. Purbhoo, D. J. Irvine, L. C. Wu, and L. Ehrlich. 2003. Dynamics of cell surface molecules during T cell recognition. Annu. Rev. Biochem. 72. [DOI] [PubMed]
  8. Delon, J., K. Kaibuchi, and R. N. Germain. 2001. Exclusion of CD43 from the immunological synapse is mediated by phosphorylation-regulated relocation of the cytoskeletal adaptor moesin. Immunity. 15:691–701. [DOI] [PubMed] [Google Scholar]
  9. Ehrlich, L. I., P. J. Ebert, M. F. Krummel, A. Weiss, and M. M. Davis. 2002. Dynamics of p56lck translocation to the T cell immunological synapse following agonist and antagonist stimulation. Immunity. 17:809–822. [DOI] [PubMed] [Google Scholar]
  10. Fink, P. J., L. A. Matis, D. L. McElligott, M. Bookman, and S. M. Hedrick. 1986. Correlations between T-cell specificity and the structure of the antigen receptor. Nature. 321:219–226. [DOI] [PubMed] [Google Scholar]
  11. Gautam, M., P. G. Noakes, L. Moscoso, F. Rupp, R. H. Scheller, J. P. Merlie, and J. R. Sanes. 1996. Defective neuromuscular synaptogenesis in agrin-deficient mutant mice. Cell. 85:525–535. [DOI] [PubMed] [Google Scholar]
  12. Gerlich, D., J. Beaudouin, M. Gebhard, J. Ellenberg, and R. Eils. 2001. Four-dimensional imaging and quantitative reconstruction to analyse complex spatiotemporal processes in live cells. Nat. Cell Biol. 3:852–855. [DOI] [PubMed] [Google Scholar]
  13. Ghosh, P. K., A. Vasanji, G. Murugesan, S. J. Eppell, L. M. Graham, and P. L. Fox. 2002. Membrane microviscosity regulates endothelial cell motility. Nat. Cell Biol. 4:894–900. [DOI] [PubMed] [Google Scholar]
  14. Grakoui, A., S. K. Bromley, C. Sumen, M. M. Davis, A. S. Shaw, P. M. Allen, and M. L. Dustin. 1999. The immunological synapse: a molecular machine controlling T cell activation. Science. 285:221–227. [DOI] [PubMed] [Google Scholar]
  15. Gustafsson, M. G., D. A. Agard, and J. W. Sedat. 1999. I5M: 3D widefield light microscopy with better than 100 nm axial resolution. J. Microsc. 195:10–16. [DOI] [PubMed] [Google Scholar]
  16. Huppa, J. B., and M. M. Davis. 2003. T-cell-antigen recognition and the immunological synapse. Nat. Immunol. 3:973–983. [DOI] [PubMed] [Google Scholar]
  17. Huppa, J. B., M. Gleimer, C. Sumen, and M. M. Davis. 2003. Continuous T cell receptor signaling required for synapse maintenance and full effector potential. Nat. Immunol. 4:749–755. [DOI] [PubMed] [Google Scholar]
  18. Kam, Z., B. Hanser, M. G. Gustafsson, D. A. Agard, and J. W. Sedat. 2001. Computational adaptive optics for live three-dimensional biological imaging. Proc. Natl. Acad. Sci. USA. 98:3790–3795. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Krummel, M. F., M. D. Sjaastad, C. Wulfing, and M. M. Davis. 2000. Differential clustering of CD4 and CD3zeta during T cell recognition. Science. 289:1349–1352. [DOI] [PubMed] [Google Scholar]
  20. Maes, F., A. Collignon, D. Vandermeulen, G. Marchal, and P. Suetens. 1997. Multimodality image registration by maximization of mutual information. IEEE Trans. Med. Imaging. 16:187–198. [DOI] [PubMed] [Google Scholar]
  21. McNally, J. G., T. Karpova, J. Cooper, and J. A. Conchello. 1999. Three-dimensional imaging by deconvolution microscopy. Methods. 19:373–385. [DOI] [PubMed] [Google Scholar]
  22. Mempel, T. R., S. E. Henrickson, and U. H. Von Andrian. 2004. T-cell priming by dendritic cells in lymph nodes occurs in three distinct phases. Nature. 427:154–159. [DOI] [PubMed] [Google Scholar]
  23. Michalet, X., A. N. Kapanidis, T. Laurence, F. Pinaud, S. Doose, M. Pflughoefft, and S. Weiss. 2003. The power and prospects of fluorescence microscopies and spectroscopies. Annu. Rev. Biophys. Biomol. Struct. 32:161–182. [DOI] [PubMed] [Google Scholar]
  24. Miller, M. J., A. S. Hejazi, S. H. Wei, M. D. Cahalan, and I. Parker. 2004. T cell repertoire scanning is promoted by dynamic dendritic cell behavior and random T cell motility in the lymph node. Proc. Natl. Acad. Sci. USA. 101:998–1003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Miller, M. J., S. H. Wei, I. Parker, and M. D. Cahalan. 2002. Two-photon imaging of lymphocyte motility and antigen response in intact lymph node. Science. 296:1869–1873. [DOI] [PubMed] [Google Scholar]
  26. Monks, C. R., B. A. Freiberg, H. Kupfer, N. Sciaky, and A. Kupfer. 1998. Three-dimensional segregation of supramolecular activation clusters in T cells. Nature. 395:82–86. [DOI] [PubMed] [Google Scholar]
  27. Montoya, M. C., D. Sancho, G. Bonello, Y. Collette, C. Langlet, H. T. He, P. Aparicio, A. Alcover, D. Olive, and F. Sanchez-Madrid. 2002. Role of ICAM-3 in the initial interaction of T lymphocytes and APCs. Nat. Immunol. 3:159–168. [DOI] [PubMed] [Google Scholar]
  28. Moss, W. C., D. J. Irvine, M. M. Davis, and M. F. Krummel. 2002. Quantifying signaling-induced reorientation of T cell receptors during immunological synapse formation. Proc. Natl. Acad. Sci. USA. 99:15024–15029. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Peng, D. P., B. Merriman, S. Osher, H. K. Zhao, and M. J. Kang. 1999. A PDE-based fast local level set method. J. Comput. Phys. 155:410–438. [Google Scholar]
  30. Purbhoo, M. A., D. J. Irvine, J. B. Huppa, and M. M. Davis. 2004. T cell killing does not require the formation of a stable mature immunological synapse. Nat. Immunol. 5:524–530. [DOI] [PubMed] [Google Scholar]
  31. Reichert, P., R. L. Reinhardt, E. Ingulli, and M. K. Jenkins. 2001. Cutting edge: in vivo identification of TCR redistribution and polarized IL-2 production by naive CD4 T cells. J. Immunol. 166:4278–4281. [DOI] [PubMed] [Google Scholar]
  32. Sanes, J. R., and J. W. Lichtman. 2001. Induction, assembly, maturation and maintenance of a postsynaptic apparatus. Nat. Rev. Neurosci. 2:791–805. [DOI] [PubMed] [Google Scholar]
  33. Sperling, A. I., J. R. Sedy, N. Manjunath, A. Kupfer, B. Ardman, and J. K. Burkhardt. 1998. TCR signaling induces selective exclusion of CD43 from the T cell-antigen-presenting cell contact site. J. Immunol. 161:6459–6462. [PubMed] [Google Scholar]
  34. Stoll, S., J. Delon, T. M. Brotz, and R. N. Germain. 2002. Dynamic imaging of T cell-dendritic cell interactions in lymph nodes. Science. 296:1873–1876. [DOI] [PubMed] [Google Scholar]
  35. Sussman, M., P. Smereka, and S. Osher. 1994. A level set approach for computing solutions to incompressible 2-phase flow. J. Comput. Phys. 114:146–159. [Google Scholar]
  36. Svoboda, K., W. Denk, D. Kleinfeld, and D. W. Tank. 1997. In vivo dendritic calcium dynamics in neocortical pyramidal neurons. Nature. 385:161–165. [DOI] [PubMed] [Google Scholar]
  37. Thomas, C., P. DeVries, J. Hardin, and J. White. 1996. Four-dimensional imaging: computer visualization of 3D movements in living specimens. Science. 273:603–607. [DOI] [PubMed] [Google Scholar]
  38. Tsien, R. Y. 1989. Fluorescent probes of cell signaling. Annu. Rev. Neurosci. 12:227–253. [DOI] [PubMed] [Google Scholar]
  39. Tukey, J. W. 1977. Exploratory Data Analysis. Addison-Wesley, Reading, MA.
  40. Tvarusko, W., M. Bentele, T. Misteli, R. Rudolf, C. Kaether, D. L. Spector, H. H. Gerdes, and R. Eils. 1999. Time-resolved analysis and visualization of dynamic processes in living cells. Proc. Natl. Acad. Sci. USA. 96:7950–7955. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Viola, P., and W. M. Wells. 1997. Alignment by maximization of mutual information. Int. J. Comput. Vision. 24:137–154. [Google Scholar]
  42. Wang, J., Z. Jing, L. Zhang, G. Zhou, J. Braun, Y. Yao, and Z. Z. Wang. 2003. Regulation of acetylcholine receptor clustering by the tumor suppressor APC. Nat. Neurosci. 6:1017–1018. [DOI] [PubMed] [Google Scholar]
  43. West, J., J. M. Fitzpatrick, M. Y. Wang, B. M. Dawant, C. R. Maurer, R. M. Kessler, R. J. Maciunas, C. Barillot, D. Lemoine, A. Collignon, F. Maes, P. Suetens, et al. 1997. Comparison and evaluation of retrospective intermodality brain image registration techniques. J. Comput. Assist. Tomogr. 21:554–566. [DOI] [PubMed] [Google Scholar]
  44. Wulfing, C., M. D. Sjaastad, and M. M. Davis. 1998. Visualizing the dynamics of T cell activation: intracellular adhesion molecule 1 migrates rapidly to the T cell/B cell interface and acts to sustain calcium levels. Proc. Natl. Acad. Sci. USA. 95:6302–6307. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Yang, J., U. Nagavarapu, K. Relloma, M. D. Sjaastad, W. C. Moss, A. Passaniti, and G. S. Herron. 2001. Telomerized human microvasculature is functional in vivo. Nat. Biotechnol. 19:219–224. [DOI] [PubMed] [Google Scholar]
  46. Zhang, W., J. Sloan-Lancaster, J. Kitchen, R. P. Trible, and L. E. Samelson. 1998. LAT: the ZAP-70 tyrosine kinase substrate that links T cell receptor to cellular activation. Cell. 92:83–92. [DOI] [PubMed] [Google Scholar]
  47. Zhao, H. K., S. Osher, B. Merriman, and M. Kang. 2000. Implicit and nonparametric shape reconstruction from unorganized data using a variational level set method. Comput. Vis. Image Und. 80:295–314. [Google Scholar]
  48. Zhu, M., E. Janssen, and W. Zhang. 2003. Minimal requirement of tyrosine residues of linker for activation of T cells in TCR signaling and thymocyte development. J. Immunol. 170:325–333. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[Supplemental File]
biophysj_104.048827_index.html (724B, html)
biophysj_104.048827_1.pdf (194.6KB, pdf)

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES