Static and Dynamic Errors in Particle Tracking Microrheology

Abstract

Particle tracking techniques are often used to assess the local mechanical properties of cells and biological fluids. The extracted trajectories are exploited to compute the mean-squared displacement that characterizes the dynamics of the probe particles. Limited spatial resolution and statistical uncertainty are the limiting factors that alter the accuracy of the mean-squared displacement estimation. We precisely quantified the effect of localization errors in the determination of the mean-squared displacement by separating the sources of these errors into two separate contributions. A “static error” arises in the position measurements of immobilized particles. A “dynamic error” comes from the particle motion during the finite exposure time that is required for visualization. We calculated the propagation of these errors on the mean-squared displacement. We examined the impact of our error analysis on theoretical model fluids used in biorheology. These theoretical predictions were verified for purely viscous fluids using simulations and a multiple-particle tracking technique performed with video microscopy. We showed that the static contribution can be confidently corrected in dynamics studies by using static experiments performed at a similar noise-to-signal ratio. This groundwork allowed us to achieve higher resolution in the mean-squared displacement, and thus to increase the accuracy of microrheology studies.

INTRODUCTION

The use of video microscopy to track single micron-sized colloids and individual molecules has attracted great interest in recent years. Because of its numerous advantages and great flexibility, video microscopy has become the primary choice in many diverse tracking experiments encompassing numerous applications. In biophysical studies, it has been used to observe molecular level motion of kinesin on microtubules and of myosin on actin (Gelles et al., 1988; Yildiz et al., 2003), to investigate the infection pathway of viruses (Seisenberger et al., 2001), and to study the mobility of proteins in cell membranes (see Saxton and Jacobson, 1997 for a review). Rheologists have tracked the thermal motion of Brownian particles to derive local rheological properties (Mason and Weitz, 1995; Chen et al., 2003) and to resolve microheterogeneities (Apgar et al., 2000; Valentine et al., 2001) of complex fluids. Colloidal scientists have pioneered the use of video microscopy in particle tracking experiments to study phase transitions (Murray et al., 1990) and to elucidate pair interaction potentials (Crocker and Grier, 1994).

The standard setup for particle tracking video microscopy includes a charge-coupled device (CCD) camera attached to a microscope that acquires images of fluorescent molecules or spherical particles. This setup gives access to a wide range of timescales, from high-speed video rate to unbounded long time-lapse acquisitions, that are particularly suitable for studying biological phenomena. Subpixel spatial resolution is obtained by locating the particle at the extrapolated center of its diffraction image when it covers several pixels (Cheezum et al., 2001). At usual magnifications of hundreds of nanometers per pixels, spatial resolutions of tens of nanometers is commonly achieved (Crocker and Grier, 1996; Cheezum et al., 2001). These values are well below the optical resolution of ∼250 nm (Inoué and Spring, 1997).

Tracking particles with even higher precision has also been shown to be feasible with the use of more complex setups. Among the video-based techniques, low-light-level CCD detectors operated in photon-counting mode are used to increase signal (Kubitscheck et al., 2000; Goulian and Simon, 2000) in single-molecule tracking. For such studies, background noise and signal levels (number of detected photons) are the limiting factors (Thompson et al., 2002). Improved observation techniques (such as internal reflection, near-field illumination, multiphoton or confocal microscopy) have been used to reduce the background fluorescence signal. Furthermore, elaborate extrapolation algorithms have been employed to refine particle positioning (Cheezum et al., 2001). Under optimized conditions, spatial resolution as low as a few nanometers has been achieved (Gelles et al., 1988). However, in addition to their inherent complexity, these techniques are not well suited for studying large length-scale dynamics, as they probe a reduced volume of sample (Kubitscheck et al., 2000). Furthermore, subnanometer resolution can be achieved using laser interferometry (Denk and Webb, 1990) or laser deflection particle tracking (Mason et al., 1997; Yamada et al., 2000). Although interferometric detection has been recently extended to track simultaneously two particles (C. F. Schmidt, Vrije Universiteit Amsterdam, personal communication, 2004), these methods cannot easily be extended to track several particles at the same time, unlike video microscopy.

Among the applications of particle tracking, investigation of local mechanical properties of a medium, using the particle as a local probe, is frequently performed. In these studies, averaged quantities such as the mean-squared displacement or the power spectral density of the position (Schnurr et al., 1997) are calculated to quantify the particle's dynamics. Thus, a large amount of data must be acquired to ensure high statistical accuracy, and the enhanced techniques described above are then not suitable for most studies. To this regard, video microscopy is both widely available and allows the acquisition of a large amount of data in minutes leading to a great statistical accuracy. However, a study by Martin et al. (2002) recently showed that the limited spatial resolution of standard video microscopy particle tracking leads to errors that can significantly alter the physical interpretations. Thus, a compromise arises in the choice of the tracking technique between: on one hand, video microscopy with great flexibility and high statistical accuracy but a low spatial resolution that limits the validity of microrheological measurements, and on the other hand, enhanced tracking techniques with a high spatial resolution but a limited extensibility to multiple-particle tracking. The spatial resolution of particle tracking video microscopy has been thoroughly, both qualitatively and quantitatively, studied by observing immobilized particles (Cheezum et al., 2001; Thompson et al., 2002). In this study we refer to this contribution of the spatial resolution as the “static error” in particle localization. Due to the finite video frame acquisition time (also called exposure or shutter time), another sort of localization error arises when moving particles are observed. This contribution to the spatial resolution depends on the dynamics of the imaged particles and thus will be referred to as “dynamic errors” in the text. To our knowledge, no quantitative studies have been performed on the effect of these dynamic errors on the mean-squared displacement or the power spectral density of the position. However, both types of error should be considered when calculating these two averaged quantities. We present methods to efficiently quantify the influence of these two types of errors on the estimation of the mean-squared displacement. We provide precise ways to correct for the static errors and derive expressions for the dynamic errors of several model fluids. Therefore, we show that accurate values of the mean-squared displacement can be obtained using standard video microscopy.

The balance of this article is organized as follows. We first present a generalized theoretical model to quantify the sources of error in particle tracking experiments, without restriction to video-based detection. We focus on the propagation of these errors on the mean-squared displacement and on the power spectral density. We then verify the model on purely viscous fluids using both simulation and experimental methods, and extend our theoretical prediction to other model fluids. Finally, we discuss the results, particularly in terms of rheological properties, to illustrate how these errors can mislead physical interpretations. Descriptions of correction methods are also presented.

THEORY

In this section, we develop a model to calculate how the errors in the estimated particle position propagate on the power spectral density and the mean-squared displacement. To consider all sources of localization error, we separate the static contribution from the dynamic contribution. The so-called “static error” arises from noise inherent to any particle-tracking experiment (Bobroff, 1986). The “dynamic error” comes from the acquisition time (or shutter time) required for position measurements. In the calculations that follow, we perform averages on infinitely populated statistical ensembles and thus do not consider the inherent inaccuracy associated with the sample statistics of finite-sized ensembles. This is a good approximation in most particle tracking techniques adapted to studying local rheology as these setups are designed to acquire a large amount of data (at least 10⁴ data points in most cases). In the text, 〈…〉 designates time averages for single-particle tracking, whereas for multiple-particle tracking, it designates a population and/or time average. Furthermore, the following models are general and do not require any assumptions about the dynamics of the tracked particles. For instance, results are equally valid for thermally fluctuating or actively manipulated (e.g., using optical tweezers) particles.

Static error

We consider a setup that exhibits an intrinsic error in the determination of a particle's position as a result of the underlying noise in the measurements (Bobroff, 1986). Systematic errors such as calibration inaccuracy or position- and time-independent offset are not considered here. The origin of the noise depends on the tracking setup, but without loss of generality, we assume that the true position x(t) of the particle at time t is estimated by 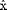(t) with the following relation:

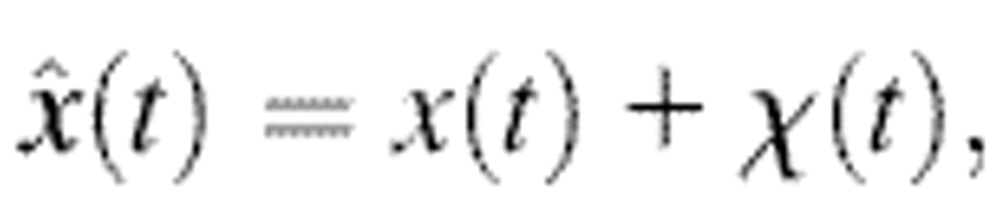(1)

where χ is a stationary random offset with zero mean 〈χ(t)〉 = 0 and constant variance 〈χ²(t)〉 = ɛ² that defines the spatial resolution ɛ of the setup. The error χ is also assumed to be independent of the position such that 〈x(t)χ(t′)〉 = 0 for any (t, t′). The autocorrelation function of the position C_x(τ) = 〈x(t + τ)x(t)〉 − 〈x(t)〉² (where τ is the lag time), is modified to

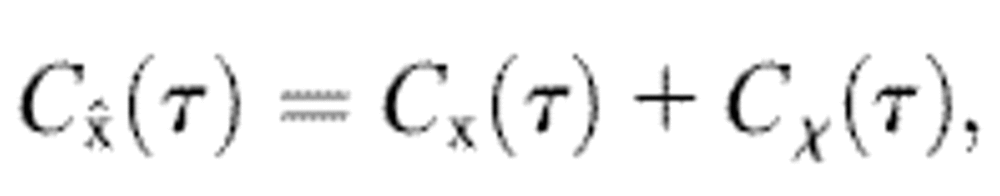(2)

when the static errors in the measurement are taken into account. In Eq. 2, C_χ(τ) is the autocorrelation function of the error. In the frequency domain, the power spectral density of the position becomes

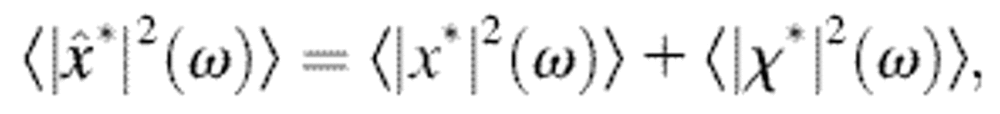(3)

as obtained by taking the Fourier transform on both sides of Eq. 2 and using the Wiener-Khinchin Theorem (Papoulis, 1991). When the mean-squared displacement 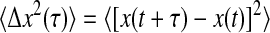is to be calculated, we use the relation

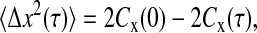(4)

to find

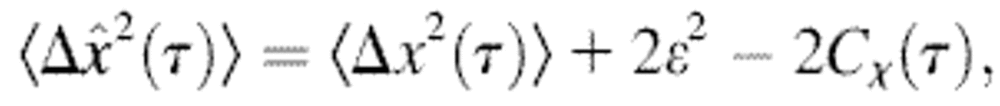(5)

where we have used the definition of the spatial resolution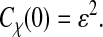

Dynamic error

For all experimental setups, a single measurement requires a given acquisition time σ during which the particle is continually moving. Thus, the position that is acquired at time t contains the history of the successive positions occupied by the particle during the time interval [t − σ, t]. We model this dynamic error by calculating the measured position as the average 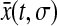of all the positions the particle takes while the shutter is open:

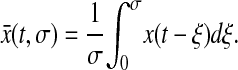(6)

Note that by performing an average over the time σ, any dynamics involving variation of x(t) over a characteristic time τ_R < σ cannot be resolved. This has important ramifications as shown in several examples given later (see the Further Theoretical Results section). In the frequency domain, Eq. 6 becomes 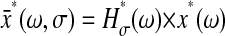with 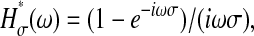so that the power spectral density of the position is (Papoulis, 1991):

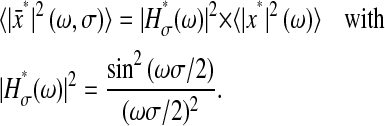(7)

In the time domain, Eq. 7 is written 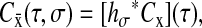where h_σ(τ) is the inverse Fourier transform of 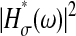(that is h_σ(τ) = (σ − |τ|)/σ² for |τ| ≤ σ and h_σ(τ) = 0 elsewhere) and 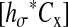designates the convolution of h_σ and C_x. We can then calculate the mean-squared displacement using Eq. 4:

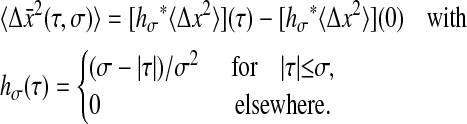(8)

This relation is linear, but as opposed to the propagation formula for the power spectrum density (Eq. 7), it is rather difficult to invert. After simplifying, Eq. 8 can be written for τ ≥ σ:

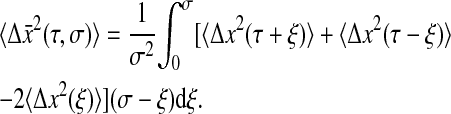(9)

We present in the Further Theoretical Results section three relevant examples for model fluids that give specific insight on how the mean-squared displacement depends on this dynamic error. After combining the contributions from the two errors, we obtain

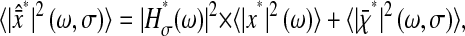(10)

for the measured power spectrum density, and

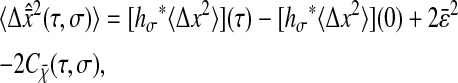(11)

for the measured mean-squared displacement, where we have written the measured static error:

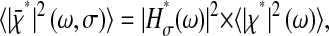(12)

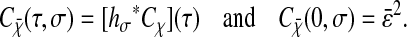(13)

Note that the ideal static localization errors 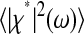and 2ɛ² − 2C_χ(τ) considered at first in Eqs. 3 and 5 are also transformed by the dynamic error during the course of the demonstration. It is the resulting quantities 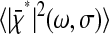and 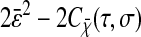that are actually measured for immobilized particles, because any experimental measurement has a finite σ. This effect is usually implicitly considered in all models that relate the spatial resolution to the number of detected photons or the signal level (such as the one presented in the Appendix). The former quantities are indeed themselves connected to the exposure time σ through the emission rate of the light source, which is detector independent. Additionally, we could have considered the dynamic errors first and then start from 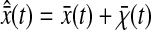to obtain the same results as Eqs. 10 and 11. In the rest of the article, 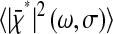and 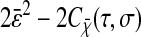will be referred to as “static” errors.

Applications

The static localization errors are easily corrected in Eqs. 10 and 11. However, to successfully replace the value of 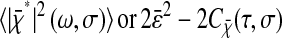in a dynamic experiment by the one measured in a static study, one must ensure that the experimental conditions in both cases are identical. In particular, noise and signal quality must be reproduced, as χ(t) commonly depends on these parameters in the experimental data. To illustrate the importance of the dynamic errors, one can calculate the value of 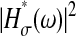at the Nyquist frequency ω = π/σ (because the acquisition rate is ≤1/σ). We find 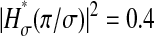, meaning that the apparent (measured) power spectral density is only 40% of its true value. In general, both the static and dynamic localization errors will have greater effect at high frequencies. As pointed out earlier, high-frequency corrections can be applied on 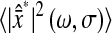because the inversion of Eq. 7 to calculate 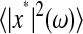is straightforward. Moreover, low-frequency statistical inaccuracy of the microrheology techniques, not taken into account in the derivation, will limit the applicability of the propagation formulas (Eqs. 10 and 11).

In this article, we used video microscopy to perform multiple-particle tracking. In this setup, the noise primarily comes from background signal (that includes for example out-of-focus particles or autofluorescence of the rest of the sample), the photon shot noise, the CCD noise (readout noise and pattern noise, the dark current noise being usually negligible at video rate) and digitization noise in the frame grabber. Measurements of the noise in the electronic chain (CCD and frame grabber) is given in the Appendix. The tracking measurements are based on a centroid localization algorithm performed on images of particles. In this procedure, the spatial resolution can be related to the tracking parameters used for data processing and to the noise-to-signal ratio of the raw measurement. In particular, the spatial error will follow the same temporal distribution as the pixel intensity noise in the movie. From the noise characterization shown in the Appendix, the spatial error can thus be considered temporally white up to at least the frame-rate frequency as well as independent of the shutter time at constant brightness. Then we can write 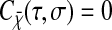for τ ≥ σ. Plugging this expression and 〈Δx²(τ)〉 = 2D|τ| into Eq. 11, we find the apparent mean-squared displacement of a particle in a Newtonian fluid (see Eq. 24) for τ ≥ σ:

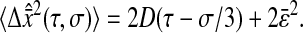(14)

The self-diffusion coefficient for a spherical particle is calculated from D = k_BT/(6πaη), where k_B is the Boltzmann's constant, T the absolute temperature, η the viscosity of the fluid, and a the particle radius. This model is verified in subsequent sections of the article through simulations and experiments.

Finally, a tracking setup may suffer from another sort of error called bias. It is defined as an inaccuracy in locating the particle that depends on the position (Cheezum et al., 2001). In that case, χ depends on x and the correlation term 〈x(t)χ(t′)〉 can be nonzero, so that our theoretical predictions do not apply. For example, localization errors from pixelization are position dependent, as shown later in the article. However, we also demonstrate that these bias errors are small at typical noise-to-signal ratios encountered in our tracking technique, in accordance with the results of Cheezum et al. (2001).

METHODS

Experiments

We used a multiple-particle tracking technique that has been described in detail elsewhere (Crocker and Grier, 1996). Briefly, 2a = 0.925 μm fluorescent beads (Polysciences, Warrington, PA) were dispersed in the sample at low volume fraction, φ < 0.1%. The samples were first deoxygenated to avoid photobleaching and then sealed in a chamber made of two microscope slides separated by 100-μm thick spacers. The slides were preconditioned in successive baths of NaOH (1 M) and boiling water for cleaning. The samples were then imaged using a fluorescent video microscopy setup consisting of an industrial grade CCD camera (Hitachi KP-M1A, Woodbury, NY) with variable shutter speed ranging from 1/60 s to 1/10,000 s, set to frame integration mode, and attached to the side port of an inverted microscope (Zeiss Axiovert 200, Jena, Germany). We used a 63× water-immersion objective (N.A. = 1.2) leading to an on-screen magnification of 210 nm/pxl. The focal plane was chosen near the center of the chamber (at least 40 μm away from the microscope slides) to minimize the effect of bead-surface hydrodynamic interactions on the observed dynamics. Movies were digitized with a frame grabber (Scion LG-3, Frederick, MD) providing 8-bit dynamic range (that is a range from 0 to 255 analog-to-digital units (ADU)), and recorded using the software NIH Image. The movies were analyzed offline using programs (Crocker and Grier, 1996) written in IDL language (Research Systems, Boulder, CO). Because a single video frame consists of two interlaced fields (each of them containing either the odd or the even rows of the CCD matrix) that are exposed 1/60 s apart, 60 Hz temporal resolution is achieved by analyzing each field independently. However, resolution is lost in the direction perpendicular to the interlacing (Crocker and Grier, 1996). Thus, in our study we analyzed particle motion in the horizontal direction (hereafter defined to be the x direction). Estimation of the spatial resolution in this direction is discussed throughout this article.

To verify the models we present in this article, we needed to evaluate average quantities on sufficiently populated ensembles to minimize the inaccuracy inherent to finite sample statistics. To calculate the mean-squared displacement at a given lag time τ, an ensemble of displacements is built by subdividing each trajectory into fragments of length τ. Thus a particle labeled i tracked over a length T_i leads to a sample containing ∼T_i/τ trajectory steps in the statistical ensemble. Consequently, higher statistical accuracy is achieved at short lag times. In all the following, we chose the maximum lag times such that at least 5 × 10⁴ data points were used to compute the mean-squared displacement. This leads to a relative error estimated by (5 × 10⁴)^−1/2 ∼ 0.5% that we verified to be well below any other sources of error.

Simulations

Static measurements

We first created an ensemble of 1000 images containing static Gaussian spots following the brightness distribution given by Eq. 44. The particles were randomly placed in the initial image and their positions did not change throughout the length of the movie. Signal-independent Gaussian noise was generated and added to each frame. Such an additive model is justified for the video microscopy method used here, as shown in the Appendix. The apparent radius was varied around the typical values observed for the particles imaged in the experiments: from 4 pxl to 5 pxl. We have investigated different noise-to-signal ratios by changing both the level of the signal and the level of the noise. The multiple-particle tracking algorithms have been applied to these movies after deinterlacing the fields (see the previous section), and the spatial resolution was measured from the mean-squared displacement 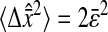computed in the x direction of the interlacing. Fig. 1, A–C, show typical particle images created for these movies at different noise-to-signal ratios, compared to an experimental image (Fig. 1 D) of a particle obtained using the static measurement described later.

FIGURE 1.

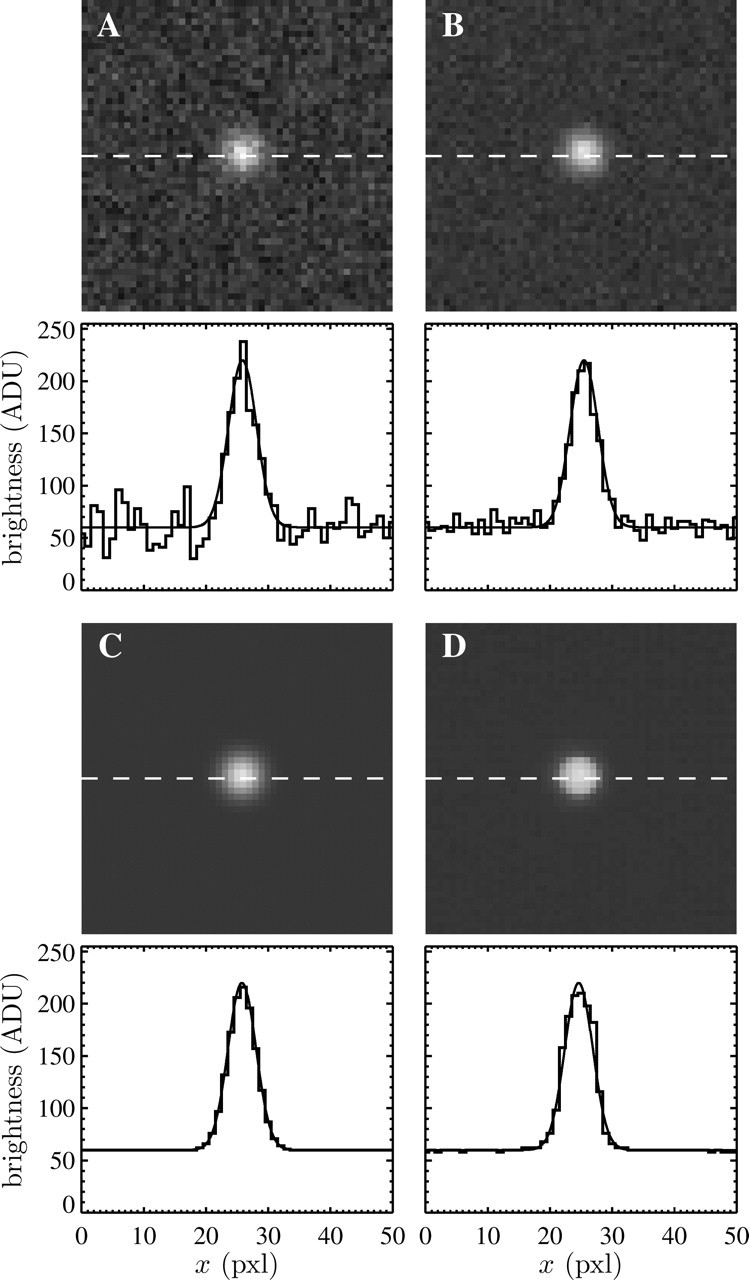
Sample particle images created during the simulations and extracted from a typical static experiment. Corresponding brightness profiles along the white dashed line are displayed under each image, as well as the corresponding Gaussian function (solid line). The apparent radius in all images is 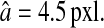(A–C) Simulated Gaussian spots with the same signal levels but different noise levels. The resulting noise-to-signal ratios are, respectively, N/S = 0.1, N/S = 0.05, and N/S = 0. (D) Typical experimental profile of an in-focus particle image. The noise-to-signal ratio is N/S = 0.01 as extracted from our procedure. The profile differs slightly from a Gaussian function (solid line) and the image of the particle presents sharper edges than the theoretical Gaussian profile displayed in panel C.

Dynamic measurements

A Brownian dynamics simulation was developed to create bead trajectories. An explicit first-order algorithm (Öttinger, 1996) was used to advance the position of a particle at time t, r(t):

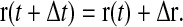(15)

The displacement Δr was chosen from a Gaussian distribution satisfying

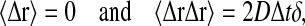(16)

where Δt is the time step and δ is the unit second-order tensor. Each trajectory was 10⁶ time steps long and was then transformed in the following manner:

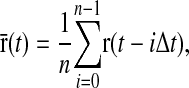(17)

where σ = nΔt defines the shutter time. We chose D = 0.5 μm²/s, varied n between 10 and 100, and set the time step to Δt = 1/6000 s, which is 1/100 the value of the frame rate (1/60 s). Thus, the shutter time varied between 1/60 and 1/600 s and we spanned a range of Dσ that is comparable to that found in the experiments. Also, we verified that our results did not appreciably change for smaller values of the time step Δt. On the resulting walks, a Gaussian distributed random offset with different standard deviations 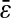ranging from 0.01 to 0.05 μm was added to each position. Fig. 2 illustrates the different stages of the simulation. Results were generated from an ensemble of 100 trajectories.

FIGURE 2.

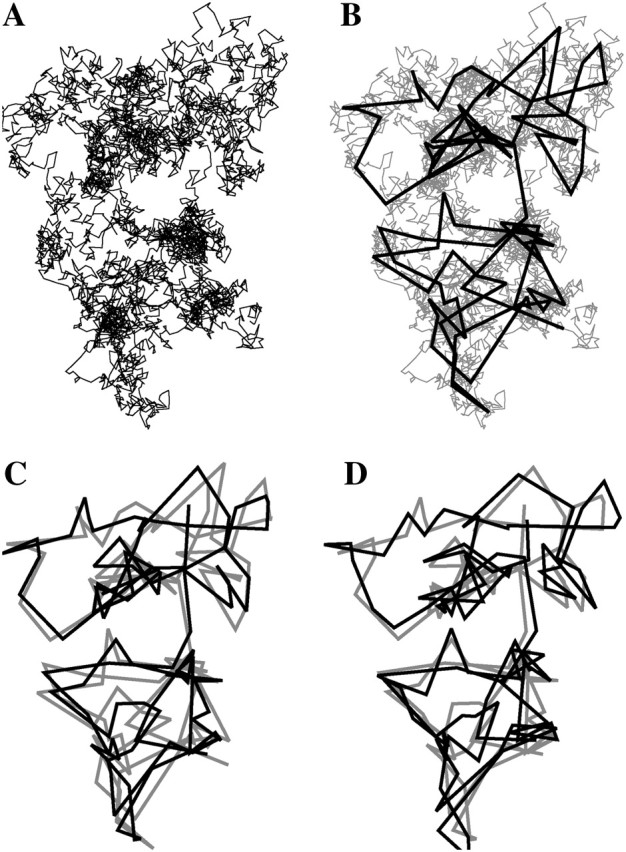
Illustration of the dynamic simulation process to create trajectories of a Brownian particle that are sampled with a finite shutter time. First, a trajectory with a large number of time steps is created (A). In the second image, positions every 50 time steps are retained (B). In the third image, a position is recalculated by averaging the position of the particle at the previous 20 time steps (C). Finally, Gaussian random noise is added in each position (D). Gray trajectories are displayed to compare successive steps of calculation.

Noise-to-signal ratio extraction

Extracting the statistics of noise present in typical images produced by video microscopy particle tracking experiments is a challenging task. As explained in the Appendix, noise in the images is the result of several independent contributions, and its smallest correlation length is l_n = 1 pxl. However, the signal's spatial frequency domain also includes the frequency 1 pxl⁻¹, as the edges of the particle images are sharp. Thus, performing high-pass linear filtering using spatial operators (convolution) or frequency operators (Fourier transformation) that select only the noise frequency in the image will not provide a true estimate of the noise. Nonlinear filters (like the median operator) and morphological grayscale operators (for example, the opening operator) are often used to reduce the noise in an image (Pratt, 1991). However, they possess the property of retaining the extreme brightness values of the raw image in the filtered result. Furthermore, an image obtained by subtracting the pixel values of the filtered image from the raw image contains black spots (zero brightness) where the particles are located. Thus, the brightness distribution of the noise isolated in this image includes an over-populated peak at 0 ADU, and the noise level is underestimated.

This suggests that the noise cannot be evaluated at the particle positions, but only in the region of the raw image that is around the particles. We explain later some limitations of our method following from this observation. To isolate this region of interest, we used similar methods encountered in the tracking algorithms. We calculated two filtered images out of the raw data array: a noise-reduced image G, obtained after convolution with a Gaussian kernel of half width l_n = 1 pxl, and a background image B, obtained by convolving the raw image with a constant kernel of size 2w + 1 (w is the typical radius of the mask used for centroid computation; see Crocker and Grier, 1996 and the Appendix for more details). We used the criterion G − B ≥ 1 ADU (or equivalently G − B ≥ 0.5 if the images G and B are higher precision data arrays) to define the signal region that is complementary to the region of interest in the whole image (see Fig. 3 B). As this criterion is very efficient in discriminating signal from sharp-edged spots (compare Fig. 3, A and B), it does not select the whole signal arising from a larger object with smooth edges. This effect is illustrated in Fig. 4. To solve this issue, we then applied a binary dilation morphological operation on the resulting image with a 2w diameter disk as the structuring element. This has the effect to extend the area of influence of each of the spot revealed by the previous criterion (compare Fig. 3, B and C). This last operation potentially eliminates several valid data points, but it significantly prevents the noise distribution from being biased by unwanted high brightness values that might be found near the particle images. Fig. 3 illustrates the different steps of our method, applied on a typical dynamic image. The noise is then the standard deviation of the brightness values of the raw image mapped to the region of interest.

FIGURE 3.

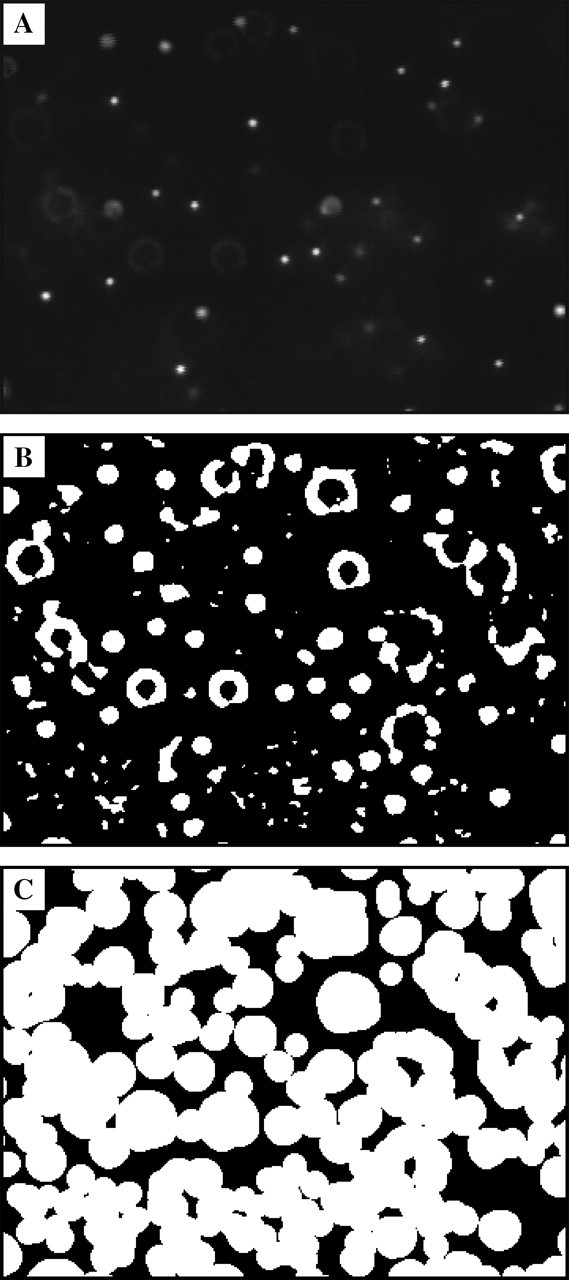
Principle for the extraction of the noise-to-signal ratio from a single movie frame. (A) A raw image taken out of a typical experimental movie for dynamic measurements. For clarity, intensity has been scaled to lie in the whole range from 0 to 255 ADU. (B) Regions of signal (white regions) selected based on the criterion that in these regions the noise-reduced image exceeds the background image by 1 ADU or more (see text). (C) Result of the binary dilation operation applied on the previous image. This operation is required as the previous signal extraction does not include large images of out-of-focus particles (see Fig. 4). The black area is the region of interest that will be used to calculate the noise.

FIGURE 4.

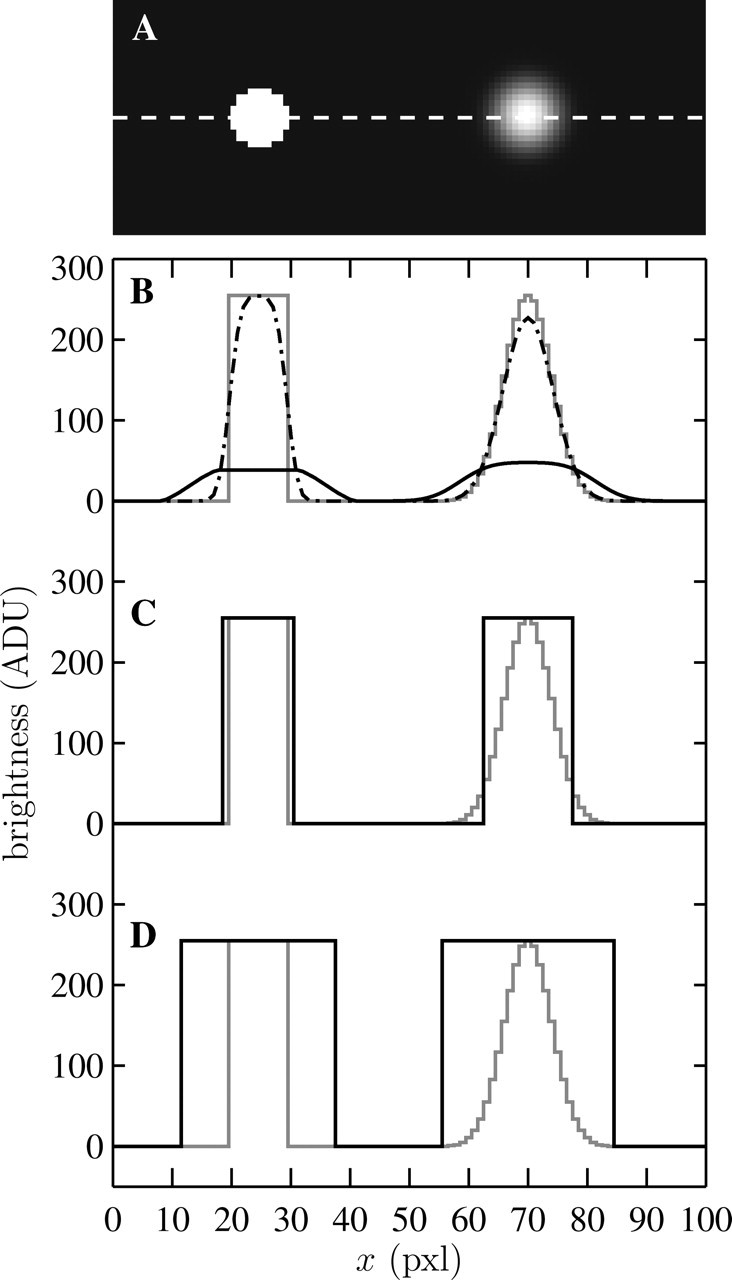
The use of the binary dilation operation for signal area selection. (A) Model particle images: a hat-like spot on the left and a Gaussian spot on the right, both with comparable apparent radius. In panels B–D, gray lines are brightness profiles along the white dashed line seen in panel A. (B) Brightness profile of the results of the background filter (solid line) and the noise-reduction filter (dashed-dotted line). (C) The solid line represents the signal selection using the criterion that the noise-reduced image exceeds the background image by 1 ADU or more; this criterion is efficient for the hat-like profile whereas the Gaussian profile is not fully selected. (D) Selected signal after applying the binary dilation operation on the previous selection; both profiles are now fully included in this selection.

Extraction of the signal is more straightforward. Only images of particles that participate in the statistical study are considered. The signal is then well defined by the difference between the local maximum brightness value of the spot and the average brightness value around the spot.

This method has been successfully verified on the simulated images and on the static experiments presented in the next section to an accuracy of 96%. However, this method has several limitations. For example, the concentration of particles cannot be too high because the region of interest for the noise extraction will not be found. Another important limitation is the assumption that the noise is spatially uniform. This is required to have a noise level in the region around the particles (where the noise is extracted by our procedure) that is identical to the one found where the particles are located (which influences the particle position estimation). By construction, this is the case for the simulations. In real images, nonuniformity of noise can be caused by its signal dependency (as it is the case for the shot noise contribution, for example). However, we show in the Appendix that this has a negligible effect. Other sources of nonuniformity include uneven illumination in the field of view or autofluorescence of the rest of the sample. Thus, the background noise can have a wide range of spatial frequencies. We explain in the Appendix that even background noise with a large correlation length has negligible influence in our setup. In addition, for dynamic experiments the computation of noise on a single frame can be biased by background fluorescence coming from particles that are out of focus and do not influence the estimation of positions for detected particles. An average over all frames takes advantage of the background fluorescence time fluctuations to accurately determine the noise involved in the particle localization. However, if the medium is too stiff or viscous, large motions of the particles are suppressed over the timescale of a movie. Thus, this eventual bias in the noise is constant throughout the entire length of the movie and the noise is not accurately estimated.

RESULTS

Estimation of ɛ̄ using fixed beads

To experimentally estimate 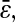we fixed the fluorescent probes on a glass microscope slide, recorded movies containing 1000 frames of the immobilized beads with different shutter times, and performed the multiple-particle tracking algorithm on the deinterlaced movies. We retained only the x position for each particle, and discriminated isolated particles from aggregates of several particles. We were able to vary the noise-to-signal ratio by changing the intensity of the excitation light source using neutral density filters. By varying the plane of observation, the particle images were captured in and out of focus to provide images that are similar to those actually observed in dynamic studies. Apparent radius and signal level were also varied in this manner. The noise-to-signal ratio was extracted from each frame using the procedure described in the Methods section, and the overall ratio was estimated by averaging over the entire movie. The resulting estimate of noise-to-signal ratio compared well with measurements performed on manually extracted background regions in several frames.

We successfully compared the standard deviation 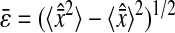that defines the spatial resolution 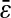calculated from the individual trajectories with the value calculated from the mean-squared displacement 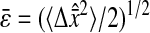at short lag times, for which statistical accuracy is best (see the Methods section). Fig. 5 A shows the experimental variation of 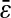with noise-to-signal ratio N/S, as compared to the theoretical predictions given by Eqs. 50 and 55 obtained using, respectively, Gaussian and hat-like spots for the particle images (cf. Fig. 4 A). We found good agreement between the theory applied on Gaussian spots (Eq. 50) and the experimental data. The scatter of the points around the linear fit (solid line in Fig. 5) comes from different apparent radii encountered in the experiment. Fig. 5 B compares the results of the simulation with the theoretical slopes. Because the Gaussian form was chosen for the spot in the simulations, the slight difference of the results with theory comes only from the pixelization of the images that is taken into account in the simulations. However, in the experiments, the pixelization is also inherent and the linear fit mainly exhibits values of 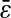smaller than found in the simulations: for the experimental data (solid line in Fig. 5) as compared to on average for the simulation (not shown in Fig. 5). This difference arises from the true experimental shape of the spot seen in Fig. 1 D, which has sharper edges than the Gaussian form. Thus we found that the experimental behavior slightly deviates from the Gaussian behavior toward the hat-spot behavior.

FIGURE 5.

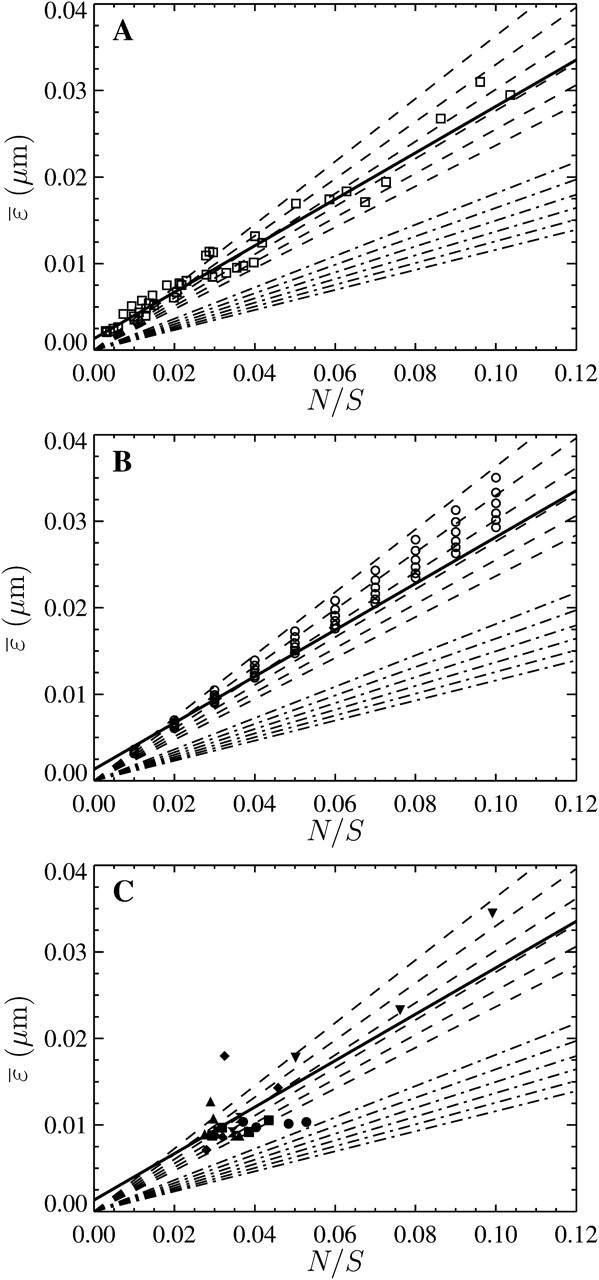
Evolution of the spatial resolution with the noise-to-signal ratio N/S. For all three plots, the dashed lines and the dashed-dotted lines are theoretical slopes calculated from Eqs. 50 and 55, respectively, with w = 7 pxl and 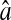evenly incremented from 4 to 5 pxl (the slopes increase as 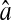decreases). The solid line is the linear fit to the experimental static measurements: 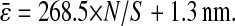(A) Experimental evaluation of 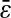at different N/S using fixed beads (□). Apparent radius 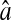extracted from particle images ranged from 4.09 to 4.96 pxl. The nonzero y-intercept in the linear fit comes from the constant offset between positions calculated from odd and even field images (see text and Fig. 6). (B) Result of the simulations (○) for w = 7 pxl and 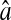ranging from 4 to 5 pxl. We verify the linear behavior of 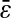versus N/S, with increasing slopes as decreases. However, because the pixelization is inherent in the simulations, there are systematic deviations from the corresponding theoretical slopes computed using Eq. 50 with same 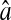(dashed lines). (C) Data extracted from the same set of dynamic experiments shown in Fig. 7, using values of 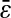as calculated by Eq. 20 (symbols are the same as in Fig. 7).

Another effect of pixelization is to create a constant offset 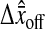between the position estimated in the odd and even field for a single immobile particle. We show in Fig. 6 A an experimental observation of this constant shift. As a result, the trajectory 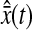of a single particle exhibits a 30-Hz periodic signal with amplitude 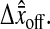The resulting mean-squared displacement averaged over an ensemble of fixed beads also oscillates between 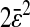and 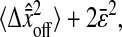so that our estimation of 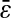is biased. Furthermore, one cannot expect to see 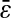vanishing as N/S approaches 0. From our experiments at low noise-to-signal ratio, we measured 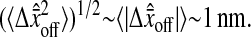The causes of such an offset can be multiple: different noise and/or signal in the even and odd field coming from the acquisition, spatial distortion, etc. We investigated one cause that is closely related to image pixelization. As illustrated in Fig. 6 B, this offset depends on the position (δx, δy) of the real profile center inside a single pixel (see Fig. 6 B for precise definition of δx and δy). We calculated the distribution of the values taken by 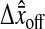as both δx and δy uniformly spans the range [−0.5, 0.5[ pxl, by using our simulation technique with Gaussian spots and N/S = 0. We found that 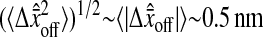and is fairly independent of the apparent radius of the particle in the range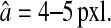

FIGURE 6.

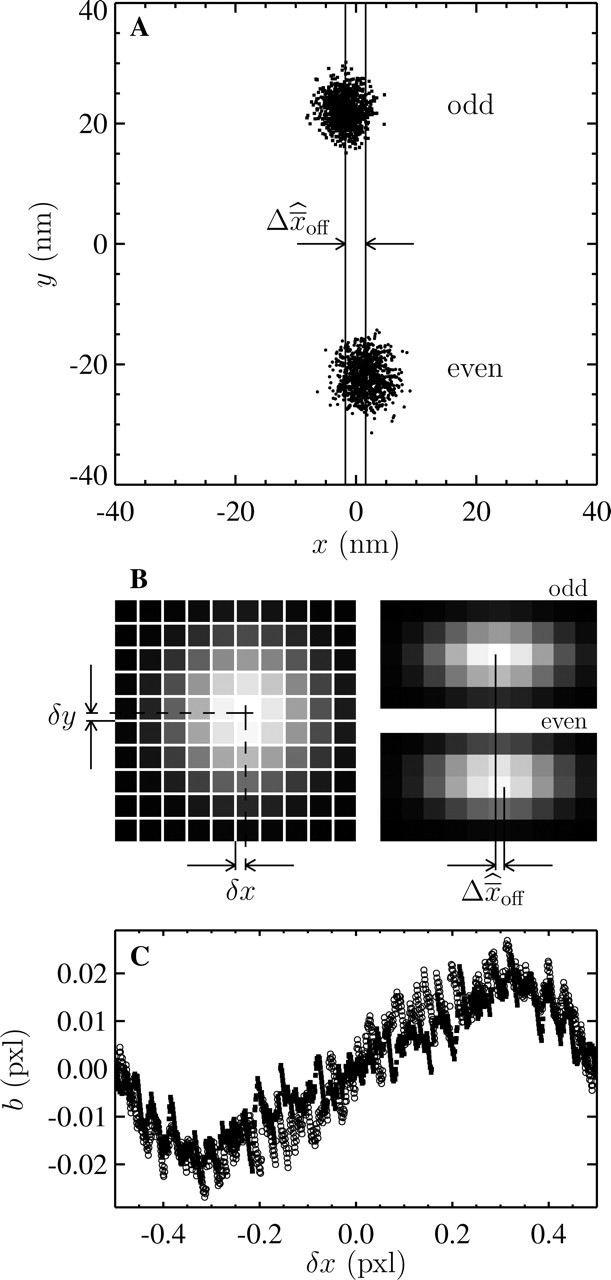
Illustration of the position offset and bias measured from the two different camera fields. (A) Experimental position measurements of a single particle fixed to a slide at low noise-to-signal ratio (N/S = 0.005). The dots are results of 1000 measurements, and present two distinctly different positions extracted from the two fields. The offset in the y direction perpendicular to the interlacing is significant. The offset 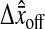is calculated by differencing the averaged position estimated in each field (the two solid lines). (B) Schematic of a model to explain the observed offset. On the left, the center of a Gaussian spot is positioned at (δx, δy) of a pixel corner. On the right, the resulting positions estimated from the odd and the even field of the same image are shifted (the magnitude of 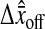has been increased for clarity). (C) Measurement of the bias as a function of the position of the particle from a pixel corner at low N/S. The different symbols correspond to the two different fields, such that the difference of the two plots corresponds to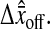

Finally, we used the static simulations to evaluate the bias error described in the Theory section. In each frame we compared the true position of each particle (an input in our simulation) with the corresponding value found by the tracking algorithm. After time averaging over all frames, we found the bias 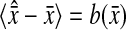to be a 1-pxl periodic function of the x position of the bead, fairly independent of the noise-to-signal ratio for N/S < 0.1 and of the apparent radius for 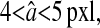comparable to results obtained by Cheezum et al. (2001). In Fig. 6 C, we show the measured bias b(δx) on both fields, odd and even, and for δx in the range [−0.5, 0.5[ pxl and δy = 0 (the shape is not appreciably modified for other values of δy). Also, when averaged over all particles, 〈b²〉^1/2 ∼ 〈|b|〉 ∼ 10⁻² pxl ∼ 2 nm. As opposed to the field offset described in the previous paragraph, the bias is not a component of the mean-squared displacement for the static experiments, as it adds a time-independent offset to each immobile particle position. In dynamic experiments, it will have negligible influence because 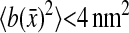is much smaller than a typical value of 100 nm² for 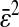(see next section). Additionally, the cross-correlation of 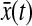and 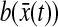needs to be evaluated (see the Theory section) and is negligible in many circumstances as shown in the next section.

Dynamic error

To verify Eq. 14, we applied multiple-particle tracking on water and on solutions of glycerol at concentrations 20%, 40%, 55%, and 82% volume fraction. The expected viscosities for these five Newtonian solutions at room temperature (T = 23°C) are ∼1, 2, 5, 10, and 100 mPa × s, respectively, weakly modified by the addition of particles at low volume fraction. We recorded movies of the fluorescent beads for a length of 5000 frames at 30 Hz (2 min, 45 s), that is 10,000 fields at 60 Hz. Four shutter times were used for acquisition: σ = 1/60, 1/125, 1/250, and 1/500 s. These long movies provided enough statistics to accurately estimate the mean-squared displacement at small lag times, and the intercept 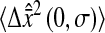and the slope 2D were evaluated by linear fit of the mean-squared displacement for lag times ranging from 1/60 s to 0.1 s (i.e., using the first six experimental points). We verified that at these lag times, at least 5 × 10⁴ trajectory steps were used to compute the mean-squared displacement (see the Methods section).

Fig. 7, A and B, shows the variation of the intercept with the scaled shutter time Dσ for both these experiments and the simulations described earlier. According to relation Eq. 14, the theoretical model predicts

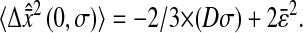(18)

FIGURE 7.

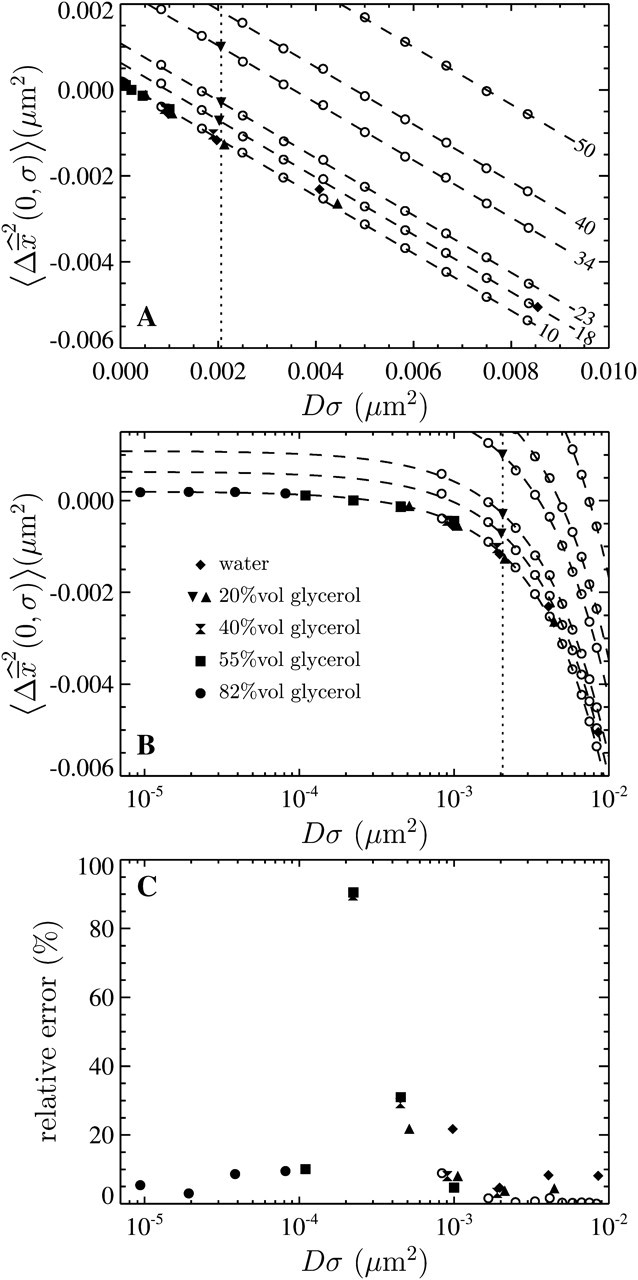
Dependence of the mean-squared displacement intercept 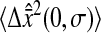on the scaled shutter time Dσ. Both 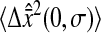and D are evaluated from a linear fit at small lag times. The solid symbols are from experimental results and the open circles are from simulations. For all experiments, the noise-to-signal ratio was kept constant, except for the inverted triangles that are extracted from a set of experiments in 20% glycerol with σ = 1/125 s that have been performed with different noise-to-signal ratio (the dotted lines in panels A and B indicate the averaged Dσ for this set of experiments). (A) Linear-linear plot. The dashed lines represent slopes of −2/3 with intercept 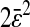(the value of 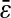is indicated in nanometers on the right-hand side of each line). The simulation results lie on the lines with corresponding input values of 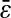(see text), and the experimental points obtained at identical noise-to-signal ratio (see Fig. 5) are in accordance with an intercept of 2 × 10⁻⁴ μm² (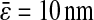). The set of experiments performed at fixed Dσ but with different N/S lie on lines with different intercepts corresponding to different values of 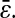(B) Linear-log plot to expand the region at small scaled shutter time Dσ. (C) Relative error to the theoretical trend 2 × 10⁻⁴ − 2Dσ/3 μm², as calculated using Eq. 19. The peak in the error corresponds to the regime where 2Dσ/3 ∼ 2 × 10⁻⁴ μm² (see text).

This formula was verified by our experiments and simulations. For the simulations, we found the slope of −2/3 and the intercepts of the lines compared well with 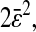where 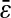is the spatial resolution we input into the simulation. For the experimental data, we also found a slope of −2/3 and extracted a constant intercept of 2 × 10⁻⁴ μm² leading to an average spatial resolution 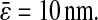We show in Fig. 7 C the error in the measured mean-squared displacement intercept as compared to the theoretical behavior expected for 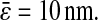For both simulations and experiments, we computed this error in the following way:

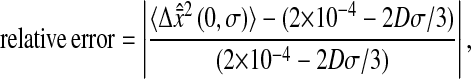(19)

where both 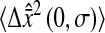and Dσ are expressed in μm². When 2Dσ/3 ∼ 2 × 10⁻⁴ μm², the values of 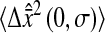are small and the corresponding relative error can reach large values. This explains the peak observed in Fig. 7 C at Dσ ∼ 3 × 10⁻⁴ μm². For other values of Dσ, the relative error is ∼2% or less and ∼10% or less for simulations and experiments, respectively.

Our results were aligned on a unique master line of slope −2/3 and intercept 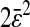only if 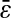was kept identical from one tracking experiment to the other. As suggested by our static study, we had to verify that the noise-to-signal ratio was kept identical from one movie to another. This is an experimental challenge because the noise-to-signal ratio cannot be evaluated a priori. Because the illumination collected by the CCD decreases as the shutter time is reduced, identical signal was recovered by raising the intensity of the excitation light source. However, we had no control over the resulting noise. Thus, to validate our measurements, we computed the exact spatial resolution 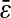using the inverted formula

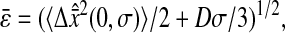(20)

and we extracted the noise-to-signal ratio using the procedure explained earlier. The resulting points compare well with the static study, as shown on Fig. 5 C. However several data points present significant deviation from the averaged static measurements. The noise-to-signal ratio of two points extracted from experiments made with 82% glycerol (solid circles) are overestimated. In the movies corresponding to these two data points, the background fluorescence is not uniform, and the noise level calculated by our algorithm deviates from the actual noise influencing the particle centroid positioning. This bias constantly affects the noise estimation because the highly viscous medium eliminates relevant variations of the background fluorescence over the duration of the movie. Thus, the noise-to-signal ratio resulting from a time average over the whole movie is inaccurate. This limitation of our N/S extraction procedure was pointed out earlier. Also, two points exhibits larger values of 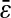than expected. They correspond to the larger values of Dσ encountered in our set of experiments: in water (diamonds) and in 20% glycerol (triangles) with σ = 1/60 s. However, as seen in Fig. 7 C, the corresponding relative error, more relevant because given in terms of mean-squared displacement, does not exceed 10%.

To complete the experimental verification of Eq. 18, we performed an additional set of experiments in which Dσ was kept constant, but the noise-to-signal ratio was varied. Beads were tracked in 20% glycerol solution and movies were acquired at σ = 1/125 s, giving Dσ ∼ 2 × 10⁻³ μm². The results are shown in Figs. 5 and 7 by the inverted triangles. For N/S evenly incremented from 0.03 to 0.1, identical Dσ were extracted (see the dotted line in Fig. 7 A), and the exact spatial resolution calculated using Eq. 20 is in good agreement with the static experiments (cf. Fig. 5 C).

Finally, we investigated the influence of bias on the mean-squared displacement. We used the Brownian dynamics simulations to create one-dimensional trajectories 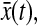and added a position dependent localization error 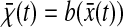at each time step. The bias is well modeled by b(x) = 0.02 × sin(2πx) where both b and x are expressed in pixels (see Fig. 6 C). The bias is negligible when particle motions amplitude (Dt_tot)^1/2 (where t_tot is the duration of tracking) is large as compared to the bias period of 1 pxl. We observe that for 1-μm-diameter beads tracked for 3 min, the bias remains negligible for solutions up to 1000 times more viscous than pure water when only time average on a single particle is performed, but to much higher values when a population average is performed on several particle trajectories.

FURTHER THEORETICAL RESULTS

In this section we use Eq. 9 to calculate the dynamic error for three standard model fluids. The Voigt and Maxwell fluids are the simplest viscoelastic model fluids that are commonly used to model the mechanical response of biological materials (Fung, 1993; Bausch et al., 1998). A third model in which the mean-squared displacement exhibits a power-law dependency with the lag time is also investigated. This model is relevant to microrheological studies, where data are often locally fit to a power law to easily extract viscoelastic properties (Mason, 2000). This last model is also known as the structural damping model, recently used to fit the mechanical response of living cells (Fabry et al., 2001).

Voigt fluid

We first examine the Voigt model (Fung, 1993) for which the complex shear modulus frequency spectrum is of the form 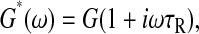where τ_R is the fluid's relaxation time. In such a medium, the mean-squared displacement of an inertialess bead is that of a particle attached to a damped oscillator:

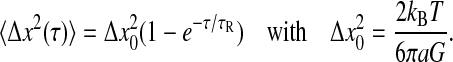(21)

Using Eq. 9, we then calculate

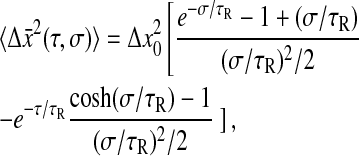(22)

for which we verify

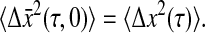(23)

The viscous limit is obtained for 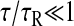(because σ ≤ τ, we have also ):

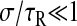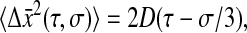(24)

where D = k_BT/(6πaη) is the bead self-diffusion coefficient and η is the viscosity of the fluid (η = Gτ_R in the Voigt model). Equation 24 was found by Goulian and Simon (2000) and is experimentally verified in our study. The elastic limit is obtained when 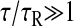for which

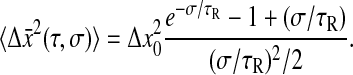(25)

Furthermore, if 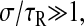as is the case for a purely elastic solid (τ_R = 0), we find that 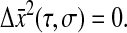As previously mentioned, dynamics occurring at timescales smaller than σ cannot be resolved. This is a fundamental problem encountered when studying Maxwell fluids, as outlined in the next section.

Maxwell fluid

For the Maxwell fluid model (Fung, 1993), 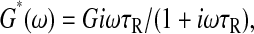and the mean-squared displacement of an inertialess embedded bead is (van Zanten and Rufener, 2000)

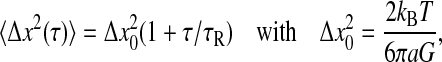(26)

for which we calculate:

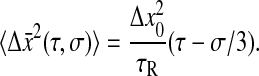(27)

This result is identical to that found for a purely viscous fluid (Eq. 24). The plateau region observed in Eq. 26 for τ < τ_R corresponds to a frictionless bead in a harmonic potential. Because we also neglect inertia in this model, it is a peculiar limit where the particle can sample all possible positions infinitely fast. Thus, after position averaging over any finite timescale, the particle is apparently immobile and the resulting mean-squared displacement is zero. Consequently, the elastic contribution in Eq. 26 is unobservable.

Power-law mean-squared displacement

The propagation of the dynamic error can be applied to a regime in which the mean-squared displacement follows a power law:

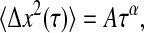(28)

or in a dimensionless form with 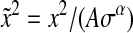and :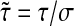

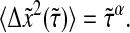(29)

We find

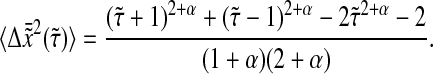(30)

In Fig. 8 A we compare the true mean-squared displacement 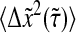with the one that includes our model dynamic error 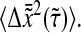We see that the amplitude of the Brownian fluctuation is decreased by this error (lower apparent mean-squared displacement). At the smallest lag time 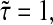we calculate the apparent diffusive coefficient as a function of the true α:

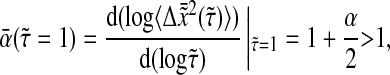(31)

which means that apparent superdiffusion will always be induced by the dynamic error. This can lead to significant misinterpretation of experimental data (see the Discussion section).

FIGURE 8.

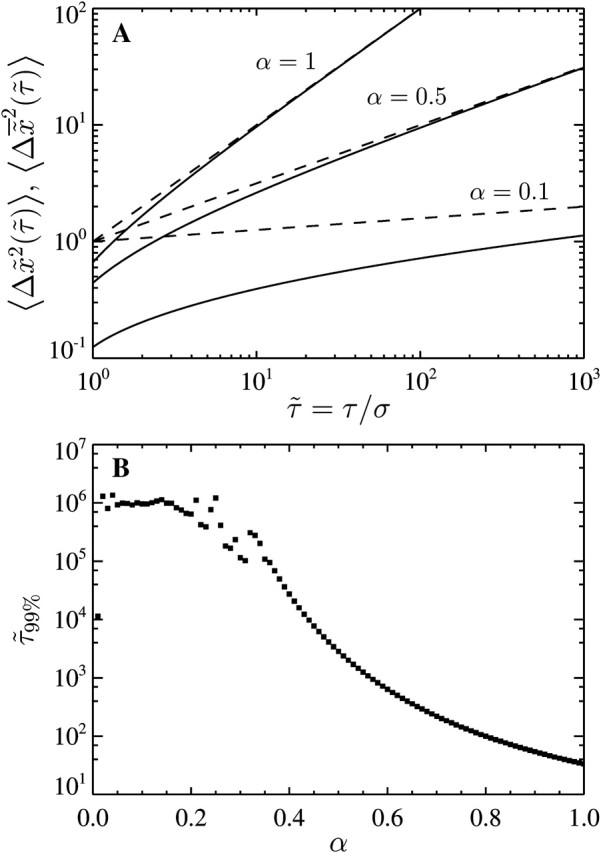
Effect of the dynamic error on particles that exhibit a power-law mean-squared displacement. (A) Comparison of (solid lines) with the true (dashed lines) for different values of α. Short lag time behavior is always superdiffusive. (B) Minimum lag times required to consider that the dynamic error has negligible effect. To solve 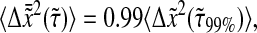we use a globally convergent Newton's method that becomes inefficient for α < 0.35.

To establish a criterion to neglect dynamic error, we evaluate the minimum dimensionless lag time 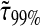such that, for 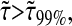we have 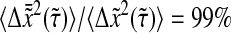at least. In Fig. 8 B, we computed 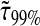for α ranging in ]0, 1]. We see that as the material gets stiffer (that is, as α decreases), the criterion 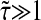is not sufficient to avoid large dynamic error.

DISCUSSION

We have classified the sources of spatial errors of particle tracking into two separate classes: static and dynamic. We have been able to precisely quantify each contribution for the particular case of Brownian particles moving in purely viscous fluids. Theoretical models for the errors were developed and validated using both simulations and experiments. The magnitudes of the static and dynamic errors were varied by, respectively, changing the noise-to-signal ratio and the shutter time of the measurements. In the Newtonian fluids we studied with video microscopy, both dependencies are linear. We found that the contributions from the two errors have antagonistic effects, and in some cases comparable values.

One parameter frequently used to characterize thermal motion is the diffusive exponent α(τ) introduced in the previous section, and defined as:

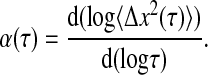(32)

When directly computed from the estimate of mean-squared displacement of probes in a purely viscous fluid, one finds the apparent diffusive exponent:

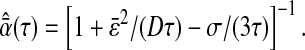(33)

Thus 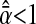if 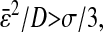and an apparent subdiffusion is observed. On the other hand, 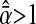if 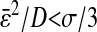and the particles exhibit an apparent superdiffusion in a purely viscous fluid. Fig. 9 A illustrates these two artifacts by showing experimentally measured mean-squared displacements in the two different regimes. Note that the results for 82% glycerol (solid circles) exhibit oscillations at short lag times. In this viscous fluid, particle displacements from one frame to the next are much smaller than 1 pxl. Thus, the offset between the position estimated in the odd and even field, as described in the previous section, becomes relevant. Furthermore, computation of the diffusive exponent from the mean-squared displacement is altered by these oscillations.

FIGURE 9.

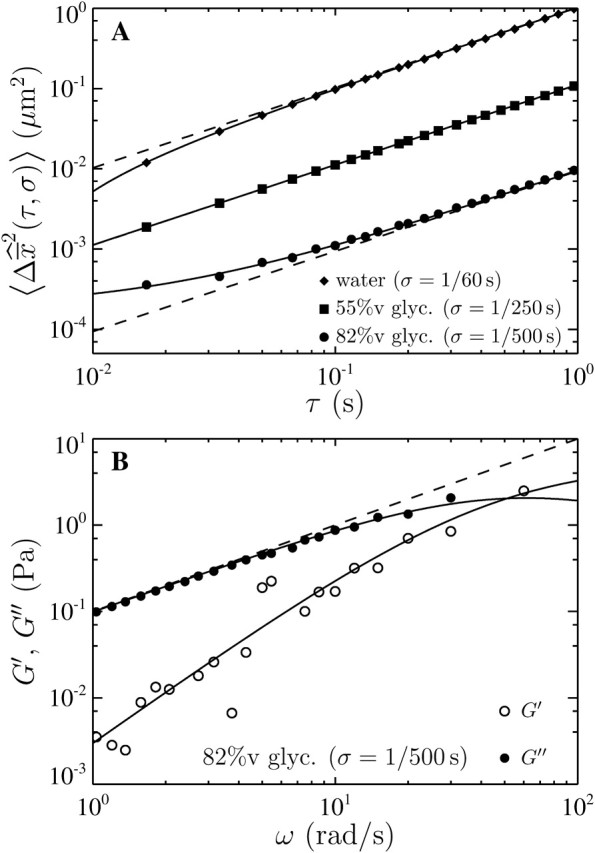
Demonstration of how the errors in the mean-squared displacement can lead to spurious rheological properties. On both plots, solid lines are data computed from linear fit extracted from the mean-squared displacement at small lag times, and dashed lines are data obtained after applying corrections explained in the Discussion section. (A) Mean-squared displacements from three experiments. For an experiment in water with σ = 1/60 s and 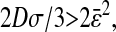an apparent superdiffusion can be observed. In 82% glycerol with σ = 1/500 s and 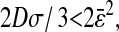the mean-squared displacement exhibits apparent subdiffusion. The errors compensate one another, 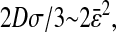in 55% glycerol with σ = 1/250 s. (B) Elastic and viscous moduli computed from the mean-squared displacement using the generalized Stokes-Einstein relation (Eq. 34). The apparent subdiffusion observed in 82% glycerol with σ = 1/500 s leads to an apparent elastic behavior at high frequencies. The scatter in the experimental data comes from the inaccurate estimation of the diffusive exponent from the measured mean-squared displacement with a numerical differentiation using three-point Lagrangian interpolation.

More striking are the errors arising in the rheological properties of the medium computed from the mean-squared displacement of the embedded particles. Using the generalized Stokes-Einstein equation, the complex shear modulus frequency spectrum 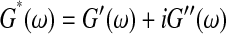can be evaluated by (Mason, 2000):

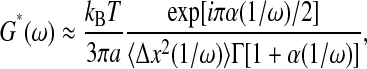(34)

where Γ designates the Γ-function. If α < 1, the material exhibits a storage modulus G′(ω) ≠ 0. Thus, when calculated from 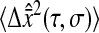in the regime where 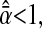the shear modulus of glycerol has an apparent elastic component. We illustrate this effect in Fig. 9 B. Furthermore, Fig. 9 A shows a third regime where the two sources of error compensate: 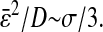These results suggest that more subtle mistakes can be made when interpreting the microrheology of complex fluids. Because dynamic error attenuates high-frequency elasticity, they can mask true subdiffusive behavior at short lag times and lead to an apparent diffusive mean-squared displacement. Several physical interpretations can arise from the observation of the mean-squared displacement, and it is thus essential to quantify the sources of errors to avoid any mistakes in one's line of reasoning.

Once the errors are quantified, corrections can be confidently made. The static error can be evaluated by fixing the particles on a substrate, and by performing measurements in similar noise and signal conditions as the rest of the experiments. The trivial subtraction of the measured static mean-squared displacement is validated, but not sufficient to recover the true mean-squared displacement. Further theoretical studies must be done to find ways to correct for the dynamic error. As stated earlier, corrections for this type of error can be applied on the power spectral density of the position by using Eq. 7, and additionally on the mean-squared displacement if an analytic model describing its variation is available. However, this dynamic contribution can be reduced by ensuring 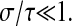Nevertheless, this criterion must be carefully verified for stiffer materials, as explained in earlier sections. As the exposure time is reduced, the collected illumination decreases, and thus the noise-to-signal ratio increases. Thus, a compromise between reducing the dynamic error or the static error follows if nonaveraged quantities are extracted. On the other hand, if the interest is focused on averaged properties, the shutter time should be decreased and correction for the static error should be performed. In this study, noise-to-signal ratios as high as 0.1 were examined. As N/S = 1 represents a fundamental limit, further studies should be performed in the range of N/S between 0.1 and 1 encountered in single-molecule tracking. On the other hand, noise-to-signal ratios N/S <0.03 is difficult to achieve with standard video microscopy setup used for dynamic experiments at small shutter time. Thus, the spatial resolution in the tracks cannot be lower than 10 nm (∼5 × 10⁻² pxl), in accordance with results obtained in similar conditions by other groups (Crocker and Grier, 1996; Cheezum et al., 2001). Also, we predict that the resolution of the mean-squared displacement can be reduced to values between 1 nm² and 10 nm² after corrections, limited only by statistics, accuracy in the estimation of 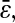and/or the position offset inherent to pixelization that were described earlier. However, further analysis should be performed to accurately evaluate this effective resolution, because this study is limited to purely viscous fluids, for which the corrections are straightforward to apply.

We have used a video microscopy multiple-particle tracking technique to perform the experiments. The methods employed here for noise measurements, as well as the relation between noise and spatial resolution are specific to this technique. However, static and dynamic errors from noise and finite exposure time are actually intrinsic to any particle tracking setup without restriction to the video-microscopy-based method. Also, the propagation formulas are valid for any dynamics, and should be considered even in active microrheology methods. For example, the spring constant of the trap created by optical tweezers is sometimes computed from the equilibrium mean-squared displacement of the trapped bead (Lang and Block, 2003), and can be biased by these errors. Moreover, Yasuda et al. (1996) already suggested that the amplitude of Brownian fluctuations can be underestimated when video detection is used in optical tweezers experiments.

To conclude, we demonstrated that dynamic and static errors can cause great deviations in the experimental results obtained using particle tracking techniques. We provided procedures to both quantify and correct these errors. We show that standard video microscopy (using simply industrial grade cameras) can then be used to perform high-resolution microrheology, and thus could become a primary choice for such experiments. Overall, our study brings to light the fact that great care must be taken in interpreting data obtained from particle tracking experiments.

APPENDIX

Noise characterization

To characterize the noise in our system we used the CCD transfer method described by Janesick et al. (1987). This technique provides a robust estimation of the different sources of noise. We observed a sample of fluorescein to evaluate the camera response at similar wavelengths as the beads. Regions of interest that exhibit uniform illumination were chosen on the camera field. For a given illumination, we found that the sources of noise characterized here are independent of the shutter time (see Fig. 10).

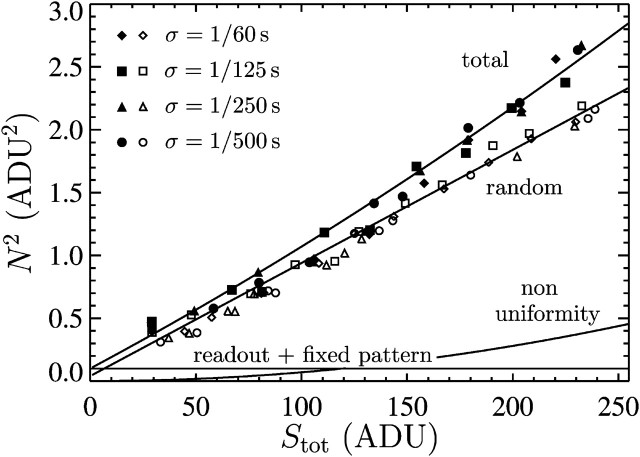
FIGURE 10.

Photon transfer curve for our setup. The open symbols designate pattern-independent noise estimation, the solid symbols are the total noise measurements. The readout and fixed-pattern noise contributions are signal independent, 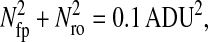the photon shot noise is 0.009 × S_tot, and the photo response nonuniformity noise follows 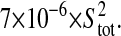The total noise curve is the sum of the four noise contributions and compares well with its experimental estimation, thus proving negligible effects of nonlinearity. Note that the photon transfer curve is independent of the shutter time.

The random pattern-independent noise, which includes the photon shot noise and the signal-independent readout noise, is estimated by half the variance of the brightness distribution obtained on the image resulting from the difference between two successive frames taken at the same illumination (Reibel et al., 2003). When estimated over the whole dynamic range of the camera, we found that this noise contribution is Gaussian distributed (as expected at high-light-level detection), with a variance linearly dependent on the illumination S_tot that we estimated by the average brightness value in the sample. Note that S_tot is expressed in ADU. We designate this noise contribution by N_rn and we write:

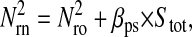(35)

where we found experimentally 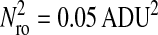for our camera readout noise and β_ps = 0.009 ADU for the photon shot noise coefficient of our setup (Fig. 10).

The fixed-pattern noise, and the photo-response nonuniformity noise estimation are evaluated in the following manner: the photo response of individual pixel is evaluated independently for 10 different illuminations with 100 frame-long movies being acquired for each illumination. A linear fit of response versus signal is produced for each pixel. The fixed-pattern noise is obtained as the variance of the intercept distribution over all the pixels. The photo-response nonuniformity noise coefficient is given by the variance of the slope distribution (Reibel et al., 2003). The pattern-dependent noise N_pd is then written:

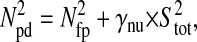(36)

where we found experimentally 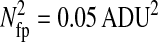for the fixed-pattern noise and γ_nu = 7 × 10⁻⁶ for the photo response nonuniformity noise coefficient of our camera (see Fig. 10).

The total noise is the variance of the raw image brightness distribution. Estimated at different illuminations, we found that the total noise compares well with the sum of the random noise with the pattern-dependent noise in the whole dynamic range of the camera, indicating that nonlinear contributions are negligible (see Fig. 10).

Another contribution to the total noise in an image can arise from uneven autofluorescence in the sample (in cells, for example) or signal from out-of-focus particles. We call this contribution “background noise” N_bg. It is negligible in the static experiments we performed in this study, but becomes important in dynamic studies. Finally the total noise is written:

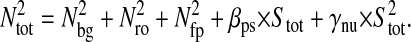(37)

The noise contributions considered here are by nature spatially white, except for the pattern-dependent noise and the background noise that might exhibit correlation lengths >1 pxl. The two-dimensional autocorrelation function calculated for regions of an image that are selected by our noise extraction procedure gives information on the distribution of noise correlation lengths. In movie frames obtained from both static and dynamic experiments, we found that the autocorrelation function is sharply peaked at 0 pxl with negligible occurrence at larger lag distances (data not shown). This suggests that a spatially white noise model, as used in the next section of this Appendix, is a reasonable assumption. It is expected that this assumption will hold for many microrheology experiments where a low concentration of probes is usually used in signal-free (e.g., nonfluorescent) medium. However, a different conclusion can be reached in other experimental scenarios, where for example out-of-focus autofluorescence of the sample might exhibit large patterns covering several pixels.

In the time domain, we characterized the CCD noise by calculating the power spectral density of the temporal variation of the noise intensity in a movie. We found in both static and dynamic experiments that the noise is temporally white from the frame-rate frequency for the upper limit of our spectrum, and at least down to a frequency of 0.1 Hz.

Relation between noise and spatial resolution

The multiple-particle tracking algorithms we use in this study have been explained in detail elsewhere (Crocker and Grier, 1996). In this Appendix we develop a model to relate the spatial resolution of the technique to the noise-to-signal ratio of the data. In the method, movies of particles are acquired using a CCD camera. Usual CCD chips contain 640 × 480 pxl, and typical trackable particles have an apparent radius 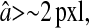which is usually different from the actual radius a of the bead. The particle position is determined by a brightness weighted average over a circular mask of radius 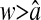applied on the filtered image of the particle. As noticed by Crocker and Grier (1996), if 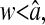clipping of the particle image by the mask deteriorates the resolution. For 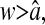this clipping effect is negligible as compared to the noise contribution, which will be the only consideration retained in the following model. Our aim is to evaluate the position of the particle that is determined from its filtered image. We define S_tot(ρ, r) = S_tot(ρ − r) the ideal brightness value at a location ρ on the particle image centered at the true position r = (x, y) (r = 0, 0 in the following). A convenient way to account for noise is to add a spatially white offset δS_ρ to the ideal brightness profile:

(38)

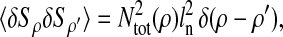(39)

where l_n is the correlation length of the noise, and N_tot(ρ) is the noise level. We know from the noise characterization, Eq. 37, that the noise level depends on the brightness distribution through:

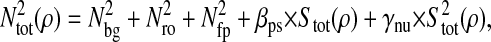(40)

with 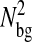the background noise, 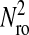the readout noise, 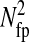the fixed-pattern noise, 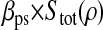the photon shot noise, and 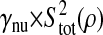the photo-response nonuniformity noise. Also, usual mask sizes satisfy 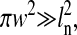which justifies the use of continuous integrals rather than finite summations. However, we find slight differences between our measurements on pixelized images and the following model, as discussed in the Results section. Under the continuous assumption, we can infer

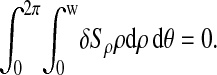(41)

Depending on the spatial repartition of the noise on the particle image, the brightness-weighted centroid of the filtered image will suffer a shift that we can estimate by the following:

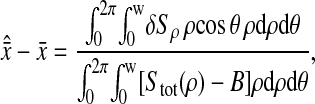(42)

where B designates the background brightness value assumed uniform at the scale of one particle. We then write

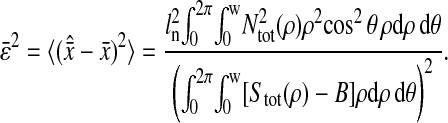(43)

By assuming a Gaussian brightness distribution for the particle image,

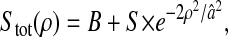(44)

where S is the signal level and 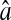is the apparent radius of the particle image, we find

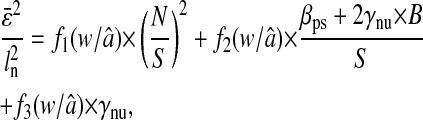(45)

where

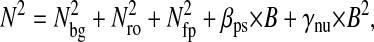(46)

is the noise amplitude evaluated at the background level and we have introduced the following functional forms:

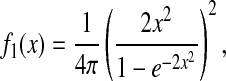(47)

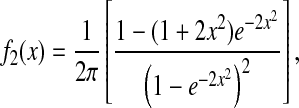(48)

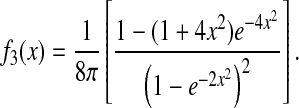(49)

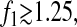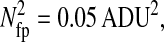
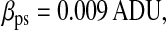
Note that Eq. 45 is formally equivalent, in terms of scaling, to theoretical results obtained by Thompson et al. (2002). We can evaluate the order of magnitude of each term for a typical mask size w = 7 pxl, with typical apparent radius from 4 to 5 pxl; then f₂ ∼ 0.15 and f₃ ∼ 0.04. Also, in most cases the background level is around B ∼ 50 ADU. Typical values obtained for our camera are: 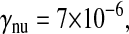and ranging from ∼0 ADU² for static experiments to ∼2 ADU² for dynamic experiments. We find that the first term in Eq. 45 always dominates in the range S between 10 and 200 ADU. This justifies both our method for estimating noise in regions without particles as well as our simulations that include only signal-independent noise. Furthermore, we will use the following formula obtained by keeping only the first term (in which noise is S independent) of Eq. 45:

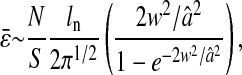(50)

as obtained by Crocker and Grier (1996). A Gaussian profile is usually a good approximation for a typical particle image. However, in some cases when the particle is close to the focal plane of the setup, its image presents a flatter peak and sharper edges (see Fig. 1 D). It is thus interesting to consider a flat brightness distribution,

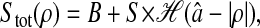(51)

where H is the Heaviside step function. In that case we find the same form to Eq. 45 with:

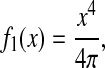(52)

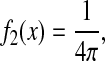(53)

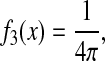(54)

for which we verify that the first term in Eq. 45 also dominates. Thus, we will write for the hat-like spot:

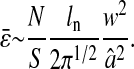(55)

Overall, we proved that even though the noise level increases at the particles location due to its signal dependency, this has negligible effect on the spatial resolution. In both cases (Eqs. 50 and 55), we find that the spatial resolution is proportional to the noise-to-signal ratio, and the slope depends only on the ratio of the mask area over the particle image area. It is essential at this point to notice that this slope is sensitive to the value of 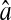: for a typical mask size 2w + 1 = 15 pxl, the slope increases by >30% as the apparent radius of the particle increases from 4 to 5 pxl. Often video particle tracking is performed on half-frames, as single frames are usually composed of two interlaced fields. In that case, both the image and the mask are shrunk by a factor of 2 in the direction perpendicular to the interlacing. It is easy to verify that the same result is found for such elliptical masks and particles. However, we explain in the Results section how this deinterlacing of pixelized images affects the measured trajectory.