Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Oct 22;88(1):680–689. doi: 10.1529/biophysj.104.048025

Mechanical Properties of Xenopus Egg Cytoplasmic Extracts

M T Valentine *, Z E Perlman †,‡, T J Mitchison †, D A Weitz *
PMCID: PMC1305045  PMID: 15501931

Abstract

Cytoplasmic extracts prepared from Xenopus laevis eggs are used for the reconstitution of a wide range of processes in cell biology, and offer a unique environment in which to investigate the role of cytoplasmic mechanics without the complication of preorganized cellular structures. As a step toward understanding the mechanical properties of this system, we have characterized the rheology of crude interphase extracts. At macroscopic length scales, the extract forms a soft viscoelastic solid. Using a conventional mechanical rheometer, we measure the elastic modulus to be in the range of 2–10 Pa, and loss modulus in the range of 0.5–5 Pa. Using pharmacological and immunological disruption methods, we establish that actin filaments and microtubules cooperate to give mechanical strength, whereas the intermediate filament cytokeratin does not contribute to viscoelasticity. At microscopic length scales smaller than the average network mesh size, the response is predominantly viscous. We use multiple particle tracking methods to measure the thermal fluctuations of 1 μm embedded tracer particles, and measure the viscosity to be ∼20 mPa-s. We explore the impact of rheology on actin-dependent cytoplasmic contraction, and find that although microtubules modulate contractile forces in vitro, their interactions are not purely mechanical.

INTRODUCTION

Cellular cytoplasm includes: the cytosol, a background fluid of globular proteins; the cytoskeleton, a complex filamentous network consisting of filamentous actin (F-actin), microtubules and intermediate filaments; and organelles. Cytoskeletal filaments form a continuous three-dimensional network that provides the scaffolding upon which motor proteins move as well as a large surface area for localization and immobilization of specific cytoplasmic molecules; moreover, this network can remodel and deform in response to external stress (Janmey, 1998). These interactions are essential for such biological processes as cell polarization, locomotion, adhesion, and division (Howard, 2001; Alberts et al., 2002; Boal, 2002). Yet, despite great interest in cellular mechanics and detailed structural information about the molecular components, our understanding of integrated cytoplasmic mechanics remains incomplete.

Here, we present crude interphase cytoplasmic extracts obtained from Xenopus laevis eggs as a model system for the study of cytoplasmic mechanics. Xenopus extracts support the formation of actin, microtubule, and cytokeratin networks, contain numerous binding proteins that mediate mechanical interactions between different filament systems, as well as a concentrated suspension of globular proteins that permeates the network to serve as a model cytosol (Clark and Merriam, 1978; Mandato et al., 2000). Initial studies have explored the biophysics of microtubule-dependent transport phenomena in this system (Salman et al., 2002); however, Xenopus extracts remain generally underused as an environment in which to examine the mechanical properties of complex cytoplasmic protein mixtures in the absence of preorganized cellular structures.

Xenopus egg extracts have unique technical advantages that make them especially useful for our studies. The cytosol is diluted very little, only 10–20%, during homogenization (Murray, 1991). Extracts remain metabolically active, with energy in the form of ATP supplied by the metabolism of endogenous glycogen and added phosphocreatine; this prevents myosin motors from forming rigor bonds onto actin filaments which would result in artifactual stiffening of the gel. Actin, microtubules, and cytokeratin, the only intermediate filament present in the extract, may be removed or stabilized by addition of pharmacological or immunological agents, allowing us to probe their different mechanical roles and isolate the molecular basis of gel elasticity (Franz et al., 1983; Franz and Franke, 1986). Moreover, it is possible to harvest relatively large amounts of cytoplasm to perform conventional mechanical tests.

Xenopus egg extracts are commonly used as model systems for the study of a wide range of biological processes, many of which involve structural rearrangements. In particular, these extracts have been essential to our understanding of a number of intrinsically mechanical cytoskeletal processes, including microtubule-based spindle assembly (Desai et al., 1999); actin-based propulsion of organelles (Theriot et al., 1994; Cameron et al., 1999; Taunton et al., 2000); the control of microtubule dynamics (Shirasu et al., 1999); and interactions of the different polymer networks in cytoplasm (Sider et al., 1999; Waterman-Storer et al., 2000; Weber and Bement, 2002). Xenopus extracts have also been used as a model system to study bulk physiological sol-gel transitions and actin-dependent contraction, which may underlie cell spreading and crawling (Clark and Merriam, 1978) and may be a useful model for meiotic spindle-cortex interactions (Z. E. Perlman, T. J. Mitchison, unpublished observations). Despite great interest in the biological characteristics of egg extracts, few experiments have focused on quantitative measurements of the viscoelastic properties of this material, limiting our understanding of the ways in which these mechanical properties underlie or constrain biological behaviors in this system.

In this article, we characterize the mechanical properties of Xenopus-derived bulk cytoplasm. We demonstrate that F-actin, microtubules, and cytokeratin form a composite network with a large mesh size of several microns, giving rise to viscoelastic responses that vary greatly depending on the length scales at which we probe the material. To measure the macroscopic properties of the extract, we use a mechanical rheometer to investigate the onset of gelation, and the frequency- and strain-dependent network response. We demonstrate that the composite network forms a soft viscoelastic solid with elastic modulus G′ in the range 2–10 Pa and viscous modulus G″ in range of 0.5–5 Pa and further that the F-actin and microtubule networks cooperate to give mechanical strength. To measure the microscopic properties of the extract, we use a multiple particle tracking technique to observe the thermal motions of embedded colloidal particles. At length scales of a micron, we find that the elastic filaments do not contribute and the sample is predominantly viscous with viscosity η ∼ 20 mPa-s. We explore the impact of this rheological response on actin-dependent cytoplasmic contractility, and demonstrate that microtubules oppose contractile forces in vitro.

MATERIALS AND METHODS

Xenopus egg cytoplasmic extracts

Crude interphase cytoplasmic extracts are prepared from Xenopus laevis as previously described, with minor modifications (Leno and Laskey, 1991). Briefly, 20–25 adult Xenopus females are preinjected with 500U pregnant mare serum gonadotropin (Sigma, St. Louis, MO) 4 days before injection with 500U human chorionic gonadotropin (Sigma, St. Louis, MO). Laid eggs are harvested the next day and washed with MMR (5 mM HEPES, pH 7.8; 0.1 mM EDTA, 100 mM NaCl, 2 mM KCl, 1 mM MgCl2, 2 mM CaCl2), taking care to discard activated, puffy, or irregular eggs. To maximize yield, frogs are returned to MMR at 16°C for a second preparation in which both laid and squeezed eggs are collected. Eggs are dejellied in 2% cysteine in water, with KOH added to pH 7.8, then washed twice with XB (10 mM HEPES, pH 7.7; 1 mM MgCL2, 0.1 mM CaCl2, 100 mM KCl, 50 mM sucrose) containing cycloheximide at a concentration of 1 μg/mL. Cycloheximide is included in all subsequent buffer exchanges to prevent production of cyclin and thereby block cell cycle progression. Eggs are driven into interphase by incubating for 7.5 min in 0.2 μg/mL A23187, a calcium ionophore (Sigma, St. Louis, MO). The eggs are exchanged into fresh XB and incubated for 10 min, then exchanged into XB plus protease inhibitors (10 μg/mL leupeptin, pepstatin, and chymostatin; Sigma, St. Louis, MO) at 4°C. All subsequent steps are performed at 4°C. After 10 min further incubation the eggs are gently transferred into 50 mL centrifuge tubes using a 25-mL plastic pipette that has been cut off to enlarge the opening and fire-polished to remove sharp edges. The first packing spin is performed in a clinical centrifuge at 1000 rpm for 30 s, after which excess buffer is removed and light oil (Nyosil M-25; Nye Lubricants, Fairhaven, MA) is gently added. After a second packing spin at 1000 rpm for 1 min then 2000 rpm for 30 s, excess buffer and oil are removed. The crushing spin is performed in an SS-630 rotor at 12,500 rpm for 15 min at 4°C to separate cytoplasmic proteins from pigment, organelles, lipids, and fats. Crude extract is recovered, supplemented with protease inhibitors (10 μg/mL final concentration each of leupeptin, pepstatin, and chymostatin), cycloheximide (1 μg /mL), 50 mM sucrose, and energy mix (7.5 mM creatine phosphate, 1 mM ATP, 1 mM MgCl2, final concentrations), to prevent depletion of endogenous ATP. Aliquots of 500 μL for use in rheology experiments and 100 μL for use in particle tracking are flash frozen in liquid nitrogen and stored at −70°C until use.

Sample preparation

In all cases, extracts are thawed immediately before use and kept on ice until loaded into experimental chambers. To probe the molecular basis for viscoelasticity, we use a variety of pharmacological and immunological techniques to selectively disrupt or stabilize a single component of the cytoskeleton. Actin is disassembled by addition of 30 μM latrunculin B (Calbiochem, San Diego, CA) and microtubules are disrupted by addition of 10 μM nocodazole (Sigma-Aldrich, St. Louis, MO). Phalloidin and taxol (Cytoskeleton, Denver, CO) are each added at a concentration of 10 μM to stabilize actin and microtubule networks, respectively. All drugs are dissolved in dimethyl sulfoxide (DMSO) such that the final experimental concentration is 1%. Cytokeratin assembly is blocked by the addition of 1 mg/mL of the cytokeratin monoclonal antibody C11 (Sigma-Aldrich, St. Louis, MO). Control experiments with the addition of 1 mg/mL of the nonspecific antibody IgG or an equivalent amount of pure phosphate-buffered saline (PBS; pH = 7.4) are also performed. Due to difficulties in obtaining highly concentrated IgG samples, the addition of antibodies to the extract introduces a 1:8 dilution. No DMSO is added to native gels or those treated with C11, IgG, or PBS.

Macroscopic rheology

To measure the bulk viscoelastic response, we use a mechanical strain-controlled rheometer (ARES: TA Instruments, New Castle, DE) with a cone and plate geometry, with a cone radius of 25 mm, cone angle of 0.02 rad, and minimal gap of ∼800 μm; the required sample volume is 500 μL. The lower plate fixture is chilled to 5°C, and the upper cone fixture is chilled on ice before mounting. To reduce the likelihood of the sample drying during the course of the measurement, we use a room humidifier and surround the cone and plate with a humid chamber. Once the sample is loaded, we raise the temperature of the lower tool to 22°C, and wait for the temperature to equilibrate. To probe the rheological response of the isolated cytoplasm, we apply a small amplitude, oscillatory shear strain, γ(t) = γo sin(ωt), where ω is the frequency of oscillation and γo is the strain amplitude and measure the resultant shear stress 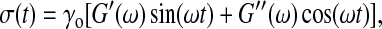Inline graphic where G′ is the storage or elastic modulus and G″ is the loss or viscous modulus. The smallest torque we are able to detect is ∼1 × 10−7 N-m, corresponding to a minimum stress of ∼0.1 Pa. To study the onset of gelation, we perform measurements with ω = 1 rad/s and γo = 0.05 every several minutes for ∼1 h after warming and monitor the change in G′ and G″ as a function of time. For times significantly beyond 1 h, our measurement often becomes unreliable. Drying and denaturing of the sample sometimes occur, forming a crust at the edge of the cone and plate and causing a large and sudden increase in the modulus; we also sometimes observe monotonic decreases in modulus at long times. We suspect that this decrease is a hallmark of macroscopic gel contraction, which allows slip at the interface of the sample and tool. For those samples that exhibit steady-state behavior, we perform frequency-dependent measurements, with γo = 0.01 or 0.05, and ω ranging from 1 to 100 rad/s. We also probe the nonlinear viscoelastic regime by measuring σ, G′, and G″ as a function of γo for ω = 1 rad/s and γo ranging from 0.005 to 25.

Multiple particle tracking

Measurements of microscopic viscoelasticity are made as previously described (Valentine et al., 2004). Briefly, protein-resistant polyethylene glycol (PEG)-coated particles are added to the extracts, and the sample is loaded into a chamber consisting of a microscope coverslip, slide, and 170-μm thick spacer. The slides are then gently transferred to an inverted research microscope (Leica DM-IRB) for observation with a 40× oil-immersion lens. Particles are imaged with brightfield microscopy, and each particle's thermally induced Brownian movements are recorded with a CCD camera (Cohu, San Diego, CA) onto S-VHS video tape or are digitized in real time using custom-written image analysis software (Keller et al., 2001); the magnification is 250 nm per pixel. Video frames are acquired to obtain tracer positions with 30 Hz temporal resolution. In each frame, the positions of the particles are identified by finding the brightness-averaged centroid position with a subpixel accuracy of ∼25 nm (Crocker and Grier, 1996). Positions are then linked in time to create two-dimensional particle trajectories. To quantify particle motions, we calculate the ensemble averaged mean-squared displacement (MSD), 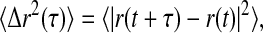Inline graphic as a function of lag time, τ, where the angled brackets indicate an average over many starting times t and the ensemble of particles in the field of view. For spherical tracers that are embedded in a homogeneous and incompressible medium, the MSD is directly related to the viscoelastic response of the surrounding material (Mason and Weitz, 1995; Gittes et al., 1997; Mason et al., 1997a,b; Levine and Lubensky, 2000). For a heterogeneous material, tracers that resist protein adsorption and are approximately equal to or smaller than the structural length scales move within mechanically distinct microenvironments and their dynamics are no longer directly related to the bulk viscoelastic response. Rather, their Brownian movements are sensitive to the viscosity of the solvent, effects of macromolecular crowding, and steric and hydrodynamic interactions with the network (Jones and Luby-Phelps, 1996; Luby-Phelps, 2000; Chen et al., 2003). PEG-coated tracers are required for these measurements to prevent aggregation and uncontrolled adsorption of proteins (Valentine, et al., 2004). In particular, active molecular motors bind to and transport unmodified beads through the cytoplasm, thereby confounding simple measurements of diffusion of the embedded probes.

Contraction assay

To investigate the role of the microtubule network in the actin-dependent contraction of interphase Xenopus egg extracts, we observe the contractile behavior of samples exposed to various pharmacological treatments as a function of time. Extracts are placed into six-well flat-bottomed Petri dishes and imaged by a CCD camera that is mounted to the table and suspended over the plate. Images are analyzed using custom-written IDL software to quantify the contraction.

RESULTS AND DISCUSSION

Bulk Xenopus extracts form soft viscoelastic solids

To investigate the macroscopic mechanical properties of the crude interphase cytoplasmic extracts, we use a strain-controlled rheometer to measure the time-evolution of viscoelasticity and probe both the linear and nonlinear rheological response. We measure the linear viscoelasticity using a dynamic measurement with ω = 1 rad/s and a strain of γ0 = 0.05. Untreated extracts form weak viscoelastic solids, with elastic moduli G′ in the range of 2–10 Pa, and viscous moduli G″ in the range of 0.5–5 Pa, as shown by their time evolutions in Fig. 1. Each curve represents an independent measurement, and demonstrates the variation in response from run to run. For extracts that are harvested on the same day and pooled before freezing, we measure slightly smaller differences in the moduli among repeated runs, suggesting that some of the variation in G′ and G″ may reflect differences in extract composition among harvests. The onset of gelation, defined as the time at which the sample produces a measurable stress with γo = 0.05 and ω = 1 rad/s occurs between 15 and 50 min after warming. Although the details of the time evolution vary from run to run, there are common features: in each case the extract gels to form a soft solid, and the elastic modulus dominates the loss modulus for all times, with the loss ratio G″/G′ ≈ 0.3–0.5. The value of the elastic modulus is 10–100 times larger than is typically measured for entangled reconstituted F-actin networks, and is similar to that measured for cross-linked actin gels (Janmey et al., 1990; Ruddies et al., 1993; Wachsstock et al., 1994; MacKintosh et al., 1995; Tempel et al., 1996; Xu et al., 1998; Palmer et al., 1999; Gardel et al., 2003).

FIGURE 1.

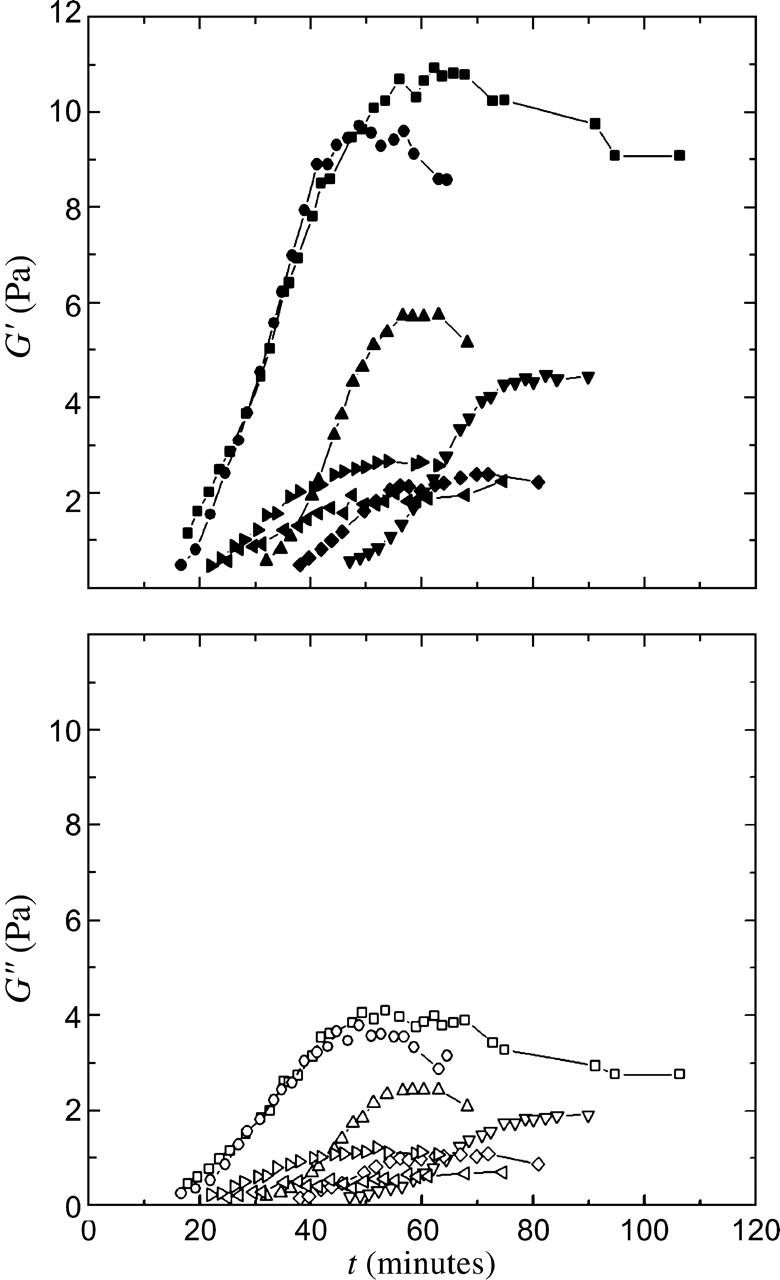
FIGURE 1

Open in a new tab

Time-evolution of the viscoelastic response of untreated cytoplasmic extracts, with measurements taken every 2–3 min with ω = 1 rad/s and γo = 0.05. Each curve represents an independent measurement, showing the variation in the response. In all cases, the extracts form weak viscoelastic solids, with elastic moduli G′ (top, solid symbols) in the range of 2–10 Pa, and viscous moduli G″ (bottom, open symbols) in the range of 0.5–5 Pa.

For long waiting times, the moduli reach an approximate steady-state value, allowing frequency-dependent measurements. In all cases, the elastic modulus dominates, and both G′ and G″ display a similar weak dependence on frequency, as shown in Fig. 2. Each curve represents an independent measurement, and demonstrates the variation in response. In contrast to strongly cross-linked gels, we find a significant loss modulus at all frequencies and we measure no characteristic crossover frequency, suggesting a broad spectrum of relaxation processes. In addition to thermally activated rearrangements that dissipate energy and relax network stress, it is possible that in the cytoplasm, athermal fluctuations, such as those caused by the ATP-driven movements of motor proteins, could give rise to unconventional relaxation mechanisms and increase G″ (LeGoff et al., 2002; Lau et al., 2003).

FIGURE 2.

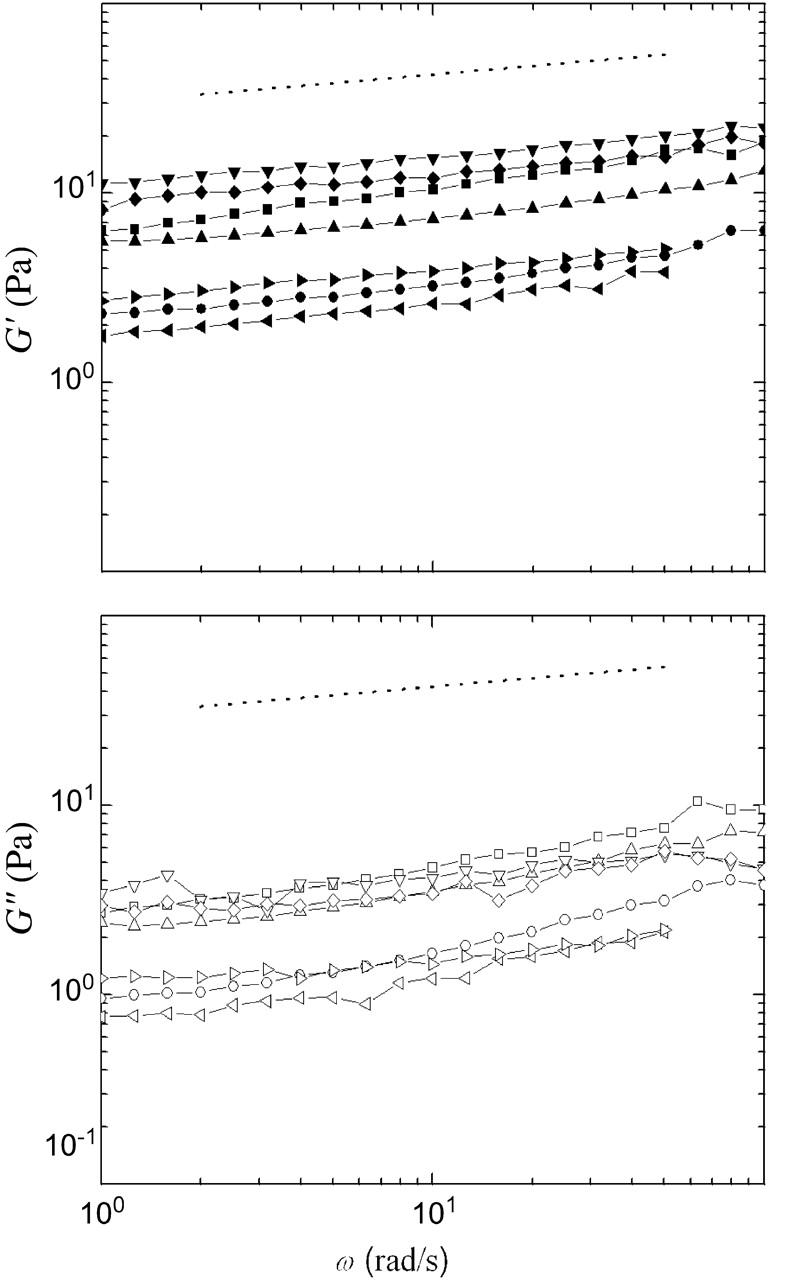
FIGURE 2

Open in a new tab

Frequency-dependence of the viscoelastic response of untreated cytoplasmic extracts, with γo = 0.05. Each curve represents an independent measurement, showing the variation in the response. In all cases, the elastic modulus dominates the loss modulus, and both G′ (top, solid symbols) and G″ (bottom, open symbols) show a weak dependence on frequency. The dotted line has a slope of 0.15, indicating that at these frequencies the extract responds as a viscoelastic solid.

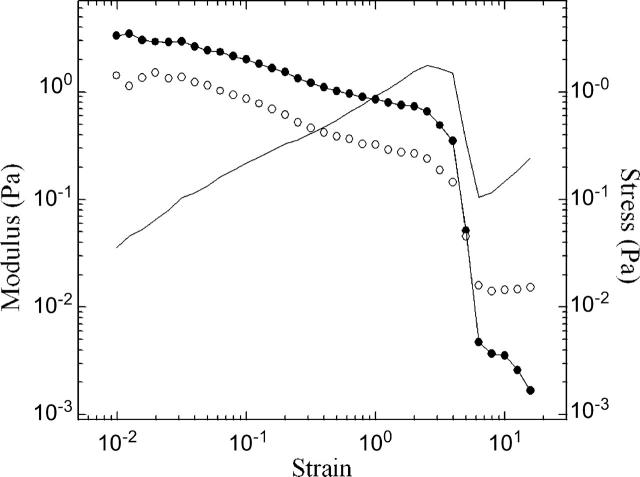
To explore cytoplasmic response to large deformations, we investigate the nonlinear rheological response by measuring stress, G′ and G″ as a function of strain at a fixed frequency ω = 1 rad/s. The regime in which stress is linearly dependent on strain is small, with strain softening occurring for γo > 0.01, as shown with a representative data set in Fig. 3. At high strains, the time-dependent stress may become nonsinusoidal, causing uncertainties in the calculation of the moduli. We cautiously note that G′ appears to dominate until very large strains; at the highest strains, G″ prevails, and we estimate the apparent viscosity η = ω−1G″ ∼ 20 mPa-s.

FIGURE 3.

FIGURE 3

Open in a new tab

Representative data showing the strain-dependence of the stress (line), G′ (solid symbols), and G″ (open symbols), obtained with a constant frequency ω = 1 rad/s. The linear regime is small, with strain softening occurring for γo > 0.01. G′ dominates until very large strains. At the highest strains, G″ prevails; we cautiously estimate the viscosity η = ω−1 G″ ∼ 20 mPa-s.

To reveal the origins of this mechanical response, we use a variety of pharmacological and immunological disruption techniques to alter the cytoplasmic structure, and measure the resultant change in viscoelasticity. We selectively remove F-actin by the addition of latrunculin B, which binds to globular actin (G-actin) in a 1:1 ratio, causing the rapid depolymerization of the F-actin network. Latrunculin-treated samples are extremely weak and never develop a measurable elastic modulus. We selectively remove the microtubule network by the addition of nocodazole, a drug that effectively lowers the concentration of GTP-bound tubulin. Nocodazole-treated extracts exhibit weak viscoelastic behavior, with moduli at the limits of our ability to measure with this experimental apparatus, with G′ in the range of 0.1–0.5 Pa or smaller. Though still solid-like, these gels are ten times weaker than untreated extracts. We selectively remove the cytokeratin network by the addition of the anti-cytokeratin antibody C11 and compare the rheological response to that of extracts containing the nonspecific antibody IgG or an equivalent amount of pure PBS. The addition of antibodies introduces a dilution that is responsible for an overall reduction in elastic response, but we measure no specific reduction due to the removal of the cytokeratin network within the repeatability of the experiment (data not shown).

We also selectively promote the growth of actin filaments or microtubules using the actin-stabilizer phalloidin or the microtubule-stabilizer taxol. Experimentally, we observe similar responses for extracts treated with either drug at 10 μM, as shown in Fig. 4, A and B; several independent measurements are shown for each condition to indicate the variability in the response. In both cases, samples gel within 20–35 min of warming, forming a soft viscoelastic solid with moduli similar to that measured for the untreated native extracts. In both cases the moduli fail to reach a steady-state value within the experimental observation time, and we observe a decrease in the modulus at long waiting times.

FIGURE 4.

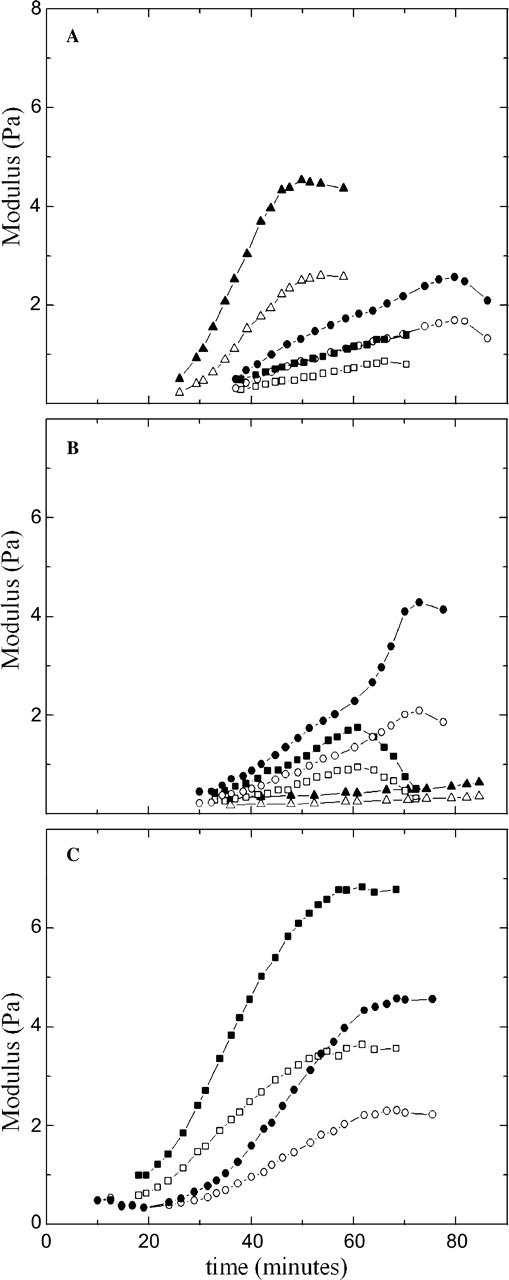
FIGURE 4

Open in a new tab

Storage (solid symbols) and loss (open symbols) moduli as a function of time after warming for extracts treated with (A) 10 μM phalloidin, (B) 10 μM taxol, and (C) 500 nM taxol. In each case, the extracts form weak viscoelastic solids, similar to the untreated native cytoplasmic gels. The time dependence of G′ and G″ is similar, and G″/G′ is ∼0.5.

The effects of taxol on microtubule morphology can vary with dose in a counterintuitive manner, since higher concentrations promote nucleation giving rise to many short polymers relative to the fewer but longer polymers that arise with a lower dose. To explore this effect, we repeat our measurements with 500 nM taxol, a 20-fold reduction in concentration. At this lower dose, the onset of gelation is more rapid, occurring within 10–20 min, and the moduli do reach steady state, indicating that filament length and number are important to the time-evolution of viscoelasticity, as shown in Fig. 4 C. However, in all cases, the overall value of the modulus, as well as the frequency- and strain-dependence of the viscoelastic response is similar to that of the untreated gels, suggesting that the native structure is sufficiently stable to maintain mechanical integrity.

Our mechanical measurements demonstrate that F-actin and microtubules play a crucial role in the mechanical response of the cytoplasm. Actin network disassembly eliminates network elasticity whereas the disruption of the microtubule network results in substantially weaker cytoplasm as compared to the untreated extract. Previous measurements of F-actin-microtubule interactions in Xenopus egg extracts have shown that microtubules, in conjunction with the motor protein cytoplasmic dynein, form physical contact with and exert force on F-actin, promoting the assembly of actin filaments into larger bundles (Sider et al., 1999; Waterman-Storer et al., 2000). As a result, the microtubule lattice may affect mechanical response directly by forming an independent stress-bearing network, with large bending modulus due to the extremely long persistence length of microtubules, of order 1 mm, or indirectly by remodeling the actin filaments into bundles that are better able to resist deformation (Waterman-Storer et al., 2000). In support of the latter, we observe colocalization of F-actin and microtubules using confocal fluorescence microscopy (data not shown).

Although both the actin and microtubule networks make important contributions to the elastic response of the cytoplasm, addition of the anti-cytokeratin antibody C11 results in no measurable change in viscoelastic response relative to IgG control, suggesting a minor role for the cytokeratin filament system in the mechanical properties of isolated cytoplasm. Our data indicate that despite their considerable tensile strength, cytokeratin filaments in this system deform more easily than F-actin or microtubules in response to shear stress. Intermediate filaments have been reported to contribute mechanical strength in vivo and are present in significant quantities in cells that undergo large tensile stresses, including nerve cell axons, muscle cells, and epithelial cells (Andra et al., 1997; Alberts et al., 2002). In cells, intermediate filaments are often anchored to the plasma membrane at cell-cell junctions and are found in the other membrane-associated structures such as the nuclear lamina (Herrmann and Aebi, 2000). Our measurements of isolated cytoplasm suggest that in cells, the organization of intermediate filaments by such membranous structures may be essential to their mechanical strength.

Previous measurements of the elastic properties of intact and adherent living cells have reported larger elastic moduli than what we measure in bulk cytoplasm; these differences likely arise from variations in polymer concentration, degree of cross-linking, and mesh size among cell types. For example, magnetic twisting cytometry measurements of human airway smooth muscle cells give elastic moduli in the range of 100–1000 Pa, with G″/G′ ∼ 0.4 (Fabry et al., 2001). For these measurements, beads are coated with a synthetic RGD (Arg-Gly-Asp)-containing peptide to specifically bind tracers to surface-bound integrin receptors and target the actin cytoskeleton and stiff actin-rich stress fibers. Experiments using atomic force microscopy (AFM) also measure cell response externally, and give elastic moduli of ∼1000 Pa (Mahaffy et al., 2000). Other AFM measurements of fibroblasts indicate that the elastic response arises predominantly from the actin cytoskeleton, and that the removal of F-actin reduces elasticity, whereas disassembly of the microtubules has no effect (Rotsch and Radmacher, 2000). Internal microrheological experiments using phagocytosed particles to probe the cytoplasm of macrophages measure a slightly weaker elastic response, with an average modulus of ∼ 350 Pa with values ranging from ∼20–750 Pa (Bausch et al., 1999). Our measurements of isolated cytoplasm give moduli in the range of 1–10 Pa, significantly smaller than that measured by techniques that selectively probe the actin cortex of adherent cells, but similar to the lower range of values reported for direct measurements of the macrophage cytoplasm. As with the cytokeratin network, it is likely that actin and microtubule networks are stiffened by the organization imposed by the organelles and internal membranes of the intact cell.

Extracts are viscous on micron length scales

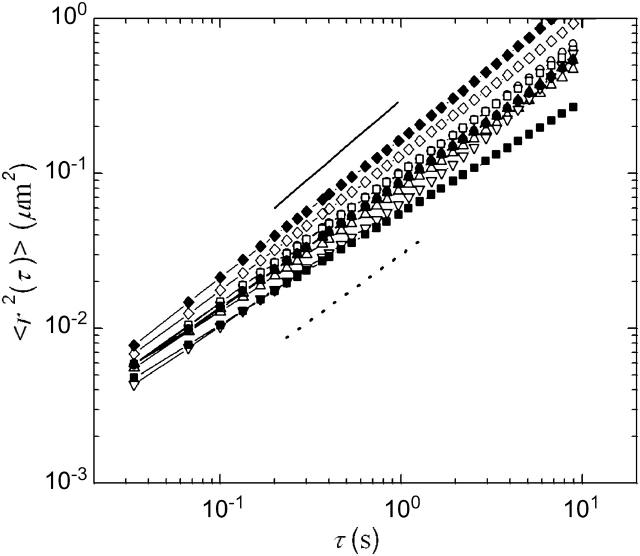
To characterize the mechanical microenvironments of the egg cytoplasm, we embed into the extracts 1-μm-diameter colloidal particles that have been rendered protein-resistant by the attachment of a PEG brush layer (Valentine et al., 2004), and record their thermal motions with video microscopy. Ten minutes after warming, particle dynamics are slightly subdiffusive, with 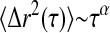Inline graphic with α ≈ 0.7–0.95, as shown in Fig. 5; this indicates that the material is not a pure fluid on micron length scales. Nevertheless, the material response is dominated by viscous dissipation. We determine an approximate value for the viscosity, η from 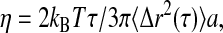Inline graphic where kBT is the thermal energy and a is the particle radius; we estimate η = 10–30 mPa-s. We measure no significant change in particle dynamics upon disassembly of either the actin or microtubule networks, or the addition of taxol to stabilize the microtubules, indicating that the elastic filaments are not playing a large role in the microscopic mechanical response. Microscopic contraction of the actin network prevents measurements of particle dynamics upon addition of phalloidin, and causes a slight upturn in the data for the extracts treated with nocodazole at the longest lag times. After 30 min, the extracts are still dominated by viscous relaxation, with viscosity in the range of 10–30 mPa-s; microscopic gel shrinkage prevents measurements of nocodazole- or phalloidin-treated gels at the 30-min time point. We compare this viscosity to that obtained with macroscopic measurements of G″ at high strains, a regime in which the elastic structures have likely yielded, and with steady shear measurements of extracts kept cold at 4°C (data not shown). In both cases the rheological response is dominated by the viscosity of the background fluid, and we find good agreement with that measured from the microscopic particle dynamics. Measurements with 0.2-, 0.5-μm PEG-coated tracers, and endogenous pigment granules of ∼0.8 μm also suggest viscosities in the range of 10–30 mPa-s (data not shown).

FIGURE 5.

FIGURE 5

Open in a new tab

Ensemble-averaged MSDs of particles moving in untreated extract (□) as well as extracts that have been treated with 30 μM latrunculin B (○), 10 μM nocodazole (▿), 10 μM taxol (⋄), and 500 nM taxol (▵), after a 10 min (open symbols) or 30 min incubation (solid symbols) at room temperature. Our data evolve slightly subdiffusively with lag time, indicating that the cytosol is not a pure fluid on these length scales. The solid line represents a slope of 1, as expected for a pure viscous fluid, and the dotted line a slope of 0.85. Although not a simple fluid, the material is predominantly viscous with viscosity in the range of 10–30 mPa-s. We measure no significant change in particle dynamics upon disassembly of either the actin or microtubule networks, or the stabilization of the microtubule network, and observe no significant changes in viscosity for waiting times of up to 30 min. At 30 min, the extracts are still dominated by viscous relaxation, with viscosity in the range of 10–30 mPa-s.

The viscosity we measure is significantly larger than that of pure water ηwater = 1 mPa-s. This increase is likely due to the high concentration of globular proteins found in egg extracts, typically 10–20% weight/volume (data not shown). Consistent with this, we have independently measured the viscosity of a solution of bovine serum albumin (BSA), a 67-kDa globular protein, at concentrations of 25% weight/volume, to be ∼25 mPa-s (data not shown). A previous study of the motion of 3-μm protein-absorbing particles in clarified Xenopus egg extract reported a slightly lower viscosity of 3 mPa-s when both microtubules and actin were depolymerized (Salman et al., 2002). In clarified extracts, additional high-speed centrifugation spins are used to eliminate vesicle fractions and reduce the overall protein concentration; these differences in extract preparation as well as particle size and surface chemistry make direct comparisons to our work difficult (Valentine et al., 2004). The viscosity we measure is similar to, although slightly larger than, previous measurements of the cytosol, the background fluid of globular proteins that surrounds the cytoskeleton in intact cells (Luby-Phelps, 2000).

In addition to the multiple particle tracking measurements of individual particles, we also attempted to use two-particle microrheology techniques, in which the correlated motion of pairs of particles is analyzed to measure the long wavelength deformation of a material (Crocker et al., 2000). We were unable to measure any correlated signal using our PEG-coated tracers, which we attribute to the very weak coupling of these probes to the protein network, which may reduce the long-range transmission of strain responsible for correlated particle movements in gels (Valentine et al., 2004).

We measure no significant change between the particle dynamics recorded after a 10-min and a 30-min incubation, no significant difference in particle movements when either the actin or microtubule networks are removed, and no correlated particle movements using two-particle microrheology analysis. This suggests that in all cases and all times, the filaments that are responsible for the macroscopic elastic response are well separated, with a mesh size larger than our particle diameter of 1 μm. We observe slightly subdiffusive particle dynamics, suggesting that local microstructure may provide some resistance to tracer movement; however, neither the actin nor microtubule networks are solely responsible for this resistance. Previous measurements of intact cells have reported similar heterogeneous local clusters of densely packed or strongly cross-linked filaments separated by soft regions (Luby-Phelps et al., 1986; Bausch et al., 1999).

Macroscopic gel contraction is actin-dependent and is opposed by microtubules

Upon warming to room temperature, native interphase Xenopus extracts contract and separate into an optically dense pellet surrounded by clear fluid, as shown in Fig. 6 A. Temperature-dependent gelation and contraction has been observed in many cytoplasmic extracts, and for Xenopus extracts is at least initially reversible (data not shown; Kane, 1976; Boxer and Stossel, 1976; Clark and Merriam, 1978; Kane, 1980). We investigate the role of cytoskeletal elasticity in this contraction using pharmacological treatments to selectively stabilize or remove F-actin and microtubules. The extracts are loaded into the observation chambers, initiating temperature-dependent polymerization and cross-linking of the filaments, and the resultant contraction is measured as a function of time. Untreated extracts contract little within the first 60 min, and ∼55% within 120 min, as determined by the change in the measured area of the extract, A, shown in the representative data set in Fig. 6 B. The selective removal of actin by the addition of latrunculin B prevents all contraction, consistent with an actomyosin driving mechanism (Clark and Merriam, 1978). By contrast, stabilizing the actin filaments with 10 μM phalloidin dramatically accelerates contraction, causing a 50% reduction in area within 60 min and a 65% reduction in 120 min. When we selectively remove the microtubules with nocodazole, we observe a significant reduction in the rate of contraction as compared to the untreated gels but similar time evolution overall, as shown in Fig. 6 C. When microtubules are stabilized with 10 μM taxol, the onset of contraction is significantly delayed to ∼100 min. Evidence of differences in the onset of contraction is also observed at the microscopic level using multiple particle tracking. Macroscopic contraction is accompanied by, and in some cases preceded by, the onset of nonuniform cytoplasmic flows. These streaming flows take up to an hour to develop in untreated extracts, but are observed in nocodazole-treated extract within 30 min and in phalloidin-treated extract within 10 min of warming. These differences in the onset of contraction are also consistent with our ability to measure a steady-state macroscopic viscoelastic response within our experimental observation time.

FIGURE 6.

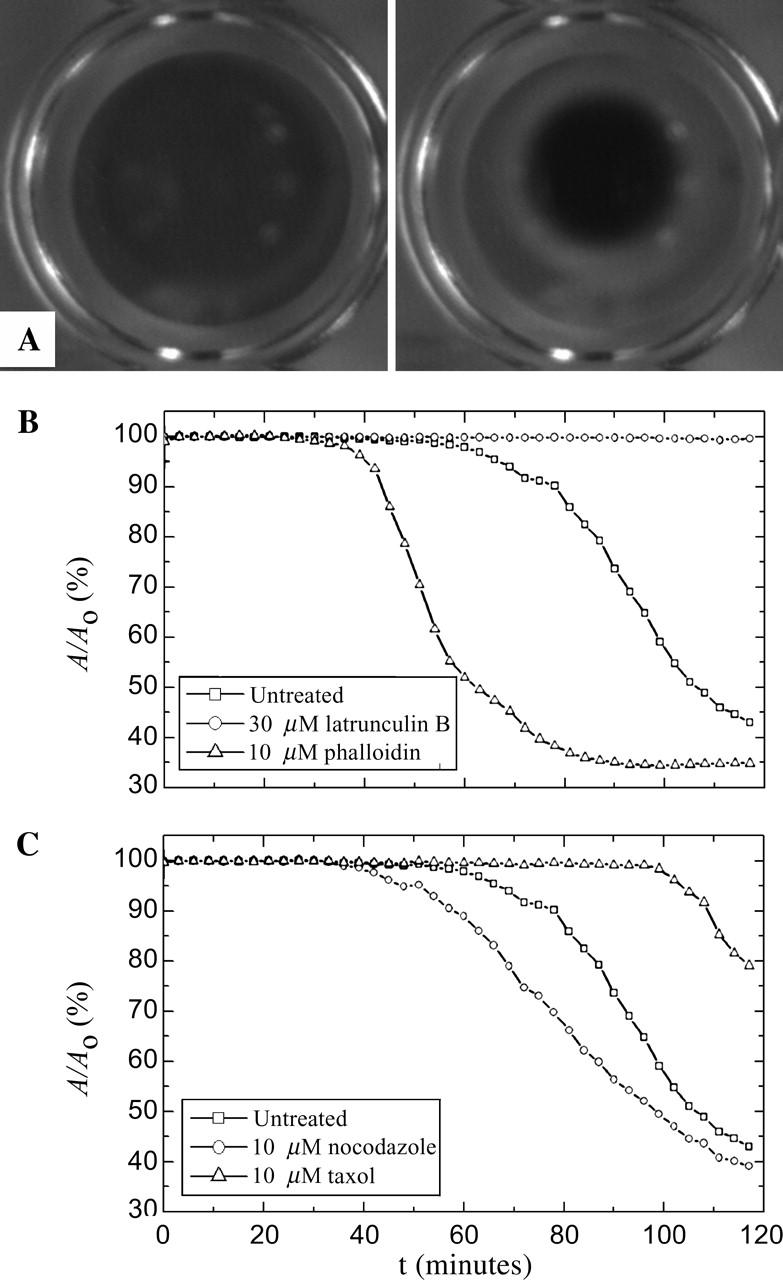
FIGURE 6

Open in a new tab

(A) Time-lapsed pictures demonstrating gelation/contraction for untreated extracts at t = 0 and t = 120 min. (B) Effect of actin depolymerizing and stabilizing drugs on contraction, here represented by the contracted gel area A normalized by initial gel area Ao. The disassembly of the actin network by latrunculin B prevents contraction, whereas addition of the stabilizing agent phalloidin accelerates the onset of contraction. (C) Effect of microtubule depolymerizing and stabilizing drugs on contraction. The disruption of the microtubule network by nocodazole accelerates whereas taxol stabilization inhibits contraction.

Taken together, our data reveal an intriguing relationship between gel structure, rheology, and contraction. Disassembly of the actin network eliminates both elastic response and actomyosin contractility. By contrast, the addition of phalloidin causes negligible changes in viscoelastic response, but accelerates contractility. This suggests that the degree of polymerization or steady-state actin filament length may limit the rate of contraction in egg extracts, even for gels of similar strength. The disruption of the microtubules both decreases bulk elasticity and accelerates contraction, suggesting that the microtubule network resists contractile forces in vitro. Although the addition of taxol has little effect on bulk elasticity, this treatment significantly slows the onset of contraction, suggesting that microtubule morphology or dynamics may directly modulate actin-based contractility.

Independent measurements have also reported that microtubules suppress the actomyosin-based contraction that drives cortical flow in cultured cells and Xenopus oocytes, as well as contraction near cell-substrate adhesions (Lyass et al., 1988; Danowski, 1989; Canman and Bement, 1997; Benink et al., 2000; Small et al., 2002). One hypothesis to explain this effect is that the microtubule network mechanically resists the compression and deformation that accompanies contraction (Benink et al., 2000; Waterman-Storer et al., 2000). In support of this mechanical model, previous measurements in fibroblasts and reconstituted composite networks, which consist of actin, the actin-cross-linking protein filamin, and smooth muscle myosin II, have demonstrated that contraction can be induced by a decrease in gel structure through partial solation of actin (Janson et al., 1991; Kolega et al., 1991). Our data suggest that in composite cytoplasmic networks, disassembly of the microtubule network also induces contraction. However, our data do not support the suggestion that changes in the elastic resistance of the microtubule network are solely responsible for modulating the actomyosin interactions. In the case of taxol-stabilized extracts, we measure little difference in network rheology as compared to the untreated gels, yet observe striking differences in their contractile behavior. In this case, the microtubules may biochemically interact with the actomyosin cytoskeleton; although such interactions remain poorly understood, microtubule regulation of actin based-contraction is suggested by observations in both Xenopus oocytes (Benink et al., 2000) and mammalian tissue culture (Palazzo and Gundersen, 2002). Alternatively, very local changes in gel structure and elasticity may dominate the contractile response without causing gross changes to the macroscopic rheology.

SUMMARY

This study provides an initial characterization of isolated bulk cytoplasm derived from Xenopus eggs. The crude egg extracts are spatially heterogeneous, as illustrated in a sketch in Fig. 7. At macroscopic length scales, interphase cytoplasm is a soft viscoelastic solid with an elastic modulus in the range of 2–10 Pa, and a considerable viscous modulus of 0.5–5 Pa. We have demonstrated that actin and microtubules cooperate to withstand shear deformation. Disruption of the microtubule network significantly weakens the elastic response, and the disassembly of actin filaments completely prevents gelation. We measure no contribution from the cytokeratin network to viscoelasticity. With multiple particle tracking methods, we probe the heterogeneous microenvironments within elastic meshwork. Using 1-μm-diameter probe particles, we measure a predominantly viscous response with a viscosity of 10–30 mPa-s, consistent with measurements of bulk cytoplasm under large strains, and similar to measurements of the cytosol of intact cells (Luby-Phelps, 2000). We have also measured the rate of actomyosin contraction in egg extracts; we find that microtubules suppress contraction, and that this suppression cannot be explained purely in terms of increased network elasticity.

FIGURE 7.

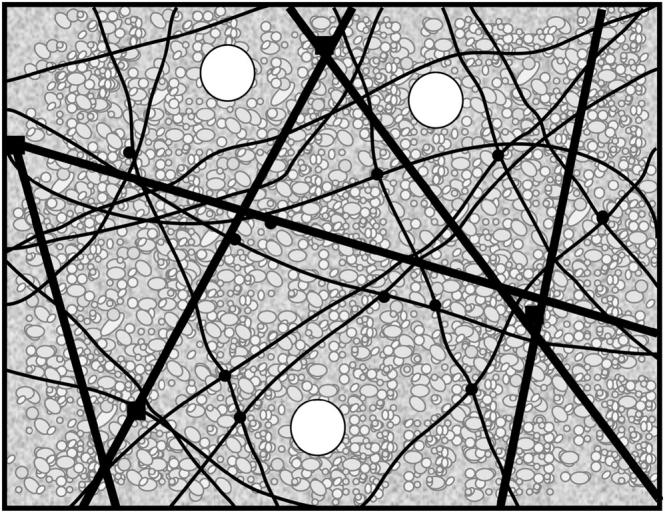
FIGURE 7

Open in a new tab

Sketch of the mechanically important structures in egg extract. F-actin, microtubules, and cytokeratin form a composite network stiffened by numerous cross-linking proteins (solid circles and squares). Protein-resistant micron-sized colloidal particles (white circles) do not interact with the elastic mesh; rather, they move within mechanically distinct microenvironments. The cytoskeleton is bathed in a concentrated protein solution, the cytosol, represented by the small macromolecules (grayscale, in background). This concentrated suspension increases the microscopic viscosity to ∼20 times that of water.

Our studies establish that Xenopus-based cell extract is a useful model system for the study not only of cytoskeletal structure (Sider et al., 1999; Waterman-Storer et al., 2000; Weber and Bement, 2002), but also cytoskeletal mechanics. The Xenopus egg is a specialized cell type, adapted for rapid division, and it remains to be determined how the mechanics of the egg cytoplasm we describe here compare to that of cells specialized for migration or secretion. Although the egg itself is not motile, quite large blastomeres, cells formed by division of the egg, can become motile when the cell cycle is arrested (Kimelman et al., 1987). Thus, we expect our conclusions can be cautiously generalized to the cytoplasm of smaller cells, where obtaining undiluted cytoplasm is difficult. It is known that the mechanical properties of the Xenopus egg change in a cell cycle-dependent manner (Rankin and Kirschner, 1997). Cell cycle state can be recapitulated in extracts, and one interesting direction for our approach will be to determine to what extent changes in the mechanical properties of whole eggs are governed by changes in the mechanics of bulk cytosol and cytoplasm, as opposed to changes in the mechanics of the egg cortex. In addition to investigations of the bulk properties of isolated cytoplasm, it may also be possible to use egg extracts to investigate the physical mechanisms that guide such localized cellular processes as active transport of organelles on microtubules or the microstructural properties of more geometrically complex structures such as the interphase nucleus and the mitotic spindle.

Acknowledgments

The authors thank Margaret Gardel, Cliff Brangwynne, Mimi Shirasu-Hiza, and Guillaume Charras for stimulating discussions, technical advice, and review of the manuscript.

This work was supported in part by grants from the National Science Foundation (DMR-0243715), the Materials Research Science and Engineering Center through the auspices of the National Science Foundation (DMR-0213805), the National Aeronautics and Space Administration (NAG3-2284), and the National Institutes of Health (GM39565). Z.E.P. is a Howard Hughes Medical Institute Predoctoral Fellow.

References

  1. Alberts, B., A. Johnson, J. Lewis, M. Raff, K. Roberts, and P. Walter. 2002. Molecular Biology of the Cell. Garland, New York.
  2. Andra, K., H. Lassman, R. Bittner, S. Shomy, R. Fassler, R. Propst, and G. Wiche. 1997. Targeted inactivation of plectin reveals essential function in maintaining the integrity of skin, muscle, and heart cytoarchitecture. Genes Dev. 11:3143–3156. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bausch, A. R., W. Möller, and E. Sackmann. 1999. Measurement of local viscoelasticity and forces in living cells by magnetic tweezers. Biophys. J. 76:573–579. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Benink, H. A., C. A. Mandato, and W. M. Bement. 2000. Analysis of cortical flow models in vivo. Mol. Biol. Cell. 11:2553–2563. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Boal, D. 2002. Mechanics of the Cell. Cambridge University Press, Cambridge.
  6. Boxer, L. A., and T. P. Stossel. 1976. Interactions of actin, myosin, and an actin-binding protein of chronic myelogenous leukemia leukocytes. J. Clin. Invest. 57:964–976. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Cameron, L. A., J. M. Footer, A. vanOudenaarden, and J. A. Theriot. 1999. Motility of Act A protein-coated microspheres driven by actin polymerization. Proc. Natl. Acad. Sci. USA. 96:4908–4913. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Canman, J. C., and W. M. Bement. 1997. Microtubules suppress actomyosin-based cortical flow in Xenopus oocytes. J. Cell Sci. 110:1907–1917. [DOI] [PubMed] [Google Scholar]
  9. Chen, D. T., E. R. Weeks, J. C. Crocker, M. F. Islam, R. Verma, J. Gruber, A. J. Levine, T. C. Lubensky, and A. G. Yodh. 2003. Rheological microscopy: local mechanical properties from microrheology. Phys. Rev. Lett. 90:108301. [DOI] [PubMed] [Google Scholar]
  10. Clark, T. G., and R. W. Merriam. 1978. Actin in Xenopus oocytes. J. Cell Biol. 77:427–438. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Crocker, J. C., and D. G. Grier. 1996. Methods of digital video microscopy for colloidal studies. J. Coll. Int. Sci. 179:298–310. [Google Scholar]
  12. Crocker, J. C., M. T. Valentine, E. R. Weeks, T. Gisler, P. D. Kaplan, A. G. Yodh, and D. A. Weitz. 2000. Two-point microrheology of inhomogeneous soft materials. Phys. Rev. Lett. 85:888–891. [DOI] [PubMed] [Google Scholar]
  13. Danowski, B. A. 1989. Fibroblast contractility and actin organization are stimulated by microtubule inhibitors. J. Cell Sci. 93:255–266. [DOI] [PubMed] [Google Scholar]
  14. Desai, A., A. Murray, T. J. Mitchison, and C. E. Walczak. 1999. The use of Xenopus egg extracts to study mitotic spindle assembly and function in vitro. Methods Cell. Biol. 61:385–412. [DOI] [PubMed] [Google Scholar]
  15. Fabry, B., G. N. Maksym, J. P. Butler, M. Glogauer, D. Navajas, and J. J. Fredberg. 2001. Scaling the microrheology of living cells. Phys. Rev. Lett. 87:148102. [DOI] [PubMed] [Google Scholar]
  16. Franz, J. K., L. Gall, M. A. Williams, B. Picheral, and W. W. Franke. 1983. Intermediate-size filaments in a germ cell: Expression of cytokeratin in oocytes and eggs of the frog Xenopus. Proc. Natl. Acad. Sci. USA. 80:6475–6479. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Franz, J. K., and W. W. Franke. 1986. Cloning of cDNA and amino acid sequence of a cytokeratin expressed in oocytes of Xenopus laevis. Proc. Natl. Acad. Sci. USA. 83:6475–6479. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Gardel, M. L., M. T. Valentine, J. C. Crocker, A. R. Bausch, and D. A. Weitz. 2003. Microrheology of entangled F-actin solutions. Phys. Rev. Lett. 91:158302. [DOI] [PubMed] [Google Scholar]
  19. Gittes, F., and F. C. MacKintosh. 1997. Dynamic shear modulus of a semi-flexible polymer network. Phys. Rev. E. 58:R1241–R1244. [Google Scholar]
  20. Herrmann, H., and U. Aebi. 2000. Intermediate filaments and their associates: multi-talented structural elements specifying cytoarchitecture and cytodynamics. Curr. Opin. Cell Biol. 12:79–90. [DOI] [PubMed] [Google Scholar]
  21. Howard, J. 2001. Mechanics of motor proteins and the cytoskeleton. Sinauer, Sunderland, MA.
  22. Janmey, P. A., S. Hvidt, J. Lamb, and T. P. Stossel. 1990. Effect of ATP on actin filament stiffness. Nature. 345:89–92. [DOI] [PubMed] [Google Scholar]
  23. Janmey, P. A. 1998. The cytoskeleton and cell signaling: component localization and coupling. Physiol. Rev. 78:763–781. [DOI] [PubMed] [Google Scholar]
  24. Janson, L. W., J. Kolega, and D. L. Taylor. 1991. Modulation of contractions by gelation/solation in a reconstituted motile model. J. Cell Biol. 114:1005–1015. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Jones, J. D., and K. Luby-Phelps. 1996. Tracer diffusion through F-actin: effect of filament length and cross-linking. Biophys. J. 71:2742–2750. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Kane, R. E. 1976. Actin polymerization and interaction with other proteins in temperature-induced gelation of sea urchin egg extracts. J. Cell Biol. 71:704–714. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Kane, R. E. 1980. Induction of either contractile or structural actin-based gels in sea urchin egg cytoplasmic extract. J. Cell Biol. 86:803–809. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Keller, M., J. Schilling, and E. Sackmann. 2001. Oscillatory magnetic bead rheometer for complex fluid microrheometry. Rev. Sci. Instrum. 72:3626–3634. [Google Scholar]
  29. Kimelman, D., M. Kirschner, and T. Scherson. 1987. The events of the midblastula transition in Xenopus are regulated by changes in the cell cycle. Cell. 48:399–407. [DOI] [PubMed] [Google Scholar]
  30. Kolega, J., L. W. Janson, and D. L. Taylor. 1991. The role of solation-contraction coupling in regulating stress fiber dynamics in nonmuscle cells. J. Cell Biol. 114:993–1003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Lau, A. W., B. D. Hoffman, A. Davies, J. C. Crocker, and T. C. Lubensky. 2003. Microrheology, stress fluctuations, and active behavior of living cells. Phys. Rev. Lett. 91:198101. [DOI] [PubMed] [Google Scholar]
  32. LeGoff, L., F. Amblard, and E. Furst. 2002. Motor-driven dynamics in actin-myosin networks. Phys. Rev. Lett. 88:018101. [DOI] [PubMed] [Google Scholar]
  33. Leno, G. H., and R. A. Laskey. 1991. DNA replication in cell-free extracts from Xenopus laevis. Methods Cell. Biol. 36:561–579. [DOI] [PubMed] [Google Scholar]
  34. Levine, A. J., and T. C. Lubensky. 2000. One- and two-particle microrheology. Phys. Rev. Lett. 85:1774–1777. [DOI] [PubMed] [Google Scholar]
  35. Luby-Phelps, K. 2000. Cytoarchitecture and physical properties of cytoplasm: volume, viscosity, diffusion, intracellular surface area. Int. Rev. Cytol. 192:189–221. [DOI] [PubMed] [Google Scholar]
  36. Luby-Phelps, K., D. L. Taylor, and F. Lanni. 1986. Probing the structure of cytoplasm. J. Cell Biol. 102:2015–2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Lyass, L. A., A. D. Bershadsky, J. M. Vasiliev, and I. M. Gelfand. 1988. Microtubule-dependent effect of phorbol ester on the contractility of the cytoskeleton of cultured fibroblasts. Proc. Natl. Acad. Sci. USA. 85:9538–9541. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Mahaffy, R. E., C. K. Shih, F. C. MacKintosh, and J. Kas. 2000. Scanning probe-based frequency-dependent microrheology of polymers and biological cells. Phys. Rev. Lett. 85:880–883. [DOI] [PubMed] [Google Scholar]
  39. Mandato, C. A., K. L. Weber, A. J. Zandy, T. J. Keating, and W. M. Bement. 2000. Xenopus egg extracts as a model system for analysis of microtubule, actin filament, and intermediate filament interactions. Methods Mol. Biol. 161:229–239. [DOI] [PubMed] [Google Scholar]
  40. Mason, T. G., K. Ganesan, J. H. van Zanten, D. Wirtz, and S. C. Kuo. 1997a. Particle tracking microrheology of complex fluids. Phys. Rev. Lett. 79:3282–3285. [Google Scholar]
  41. Mason, T. G., H. Gang, and D. A. Weitz. 1997b. Diffusing-wave-spectroscopy measurements of viscoelasticity of complex fluids. J. Opt. Soc. Am. A. 14:139–149. [Google Scholar]
  42. Mason, T. G., and D. A. Weitz. 1995. Optical measurements of frequency-dependent linear viscoelastic moduli of complex fluids. Phys. Rev. Lett. 74:1250–1253. [DOI] [PubMed] [Google Scholar]
  43. MacKintosh, F. C., J. A. Kas, and P. A. Janmey. 1995. Elasticity of semiflexible biopolymer networks. Phys. Rev. Lett. 75:4425–4428. [DOI] [PubMed] [Google Scholar]
  44. Murray, A. 1991. Cell cycle extracts. Methods Cell. Biol. 36:518–605. [PubMed] [Google Scholar]
  45. Palazzo, A. F., and G. G. Gundersen. 2002. Microtubule-actin cross-talk at focal adhesions. Sci. STKE. 139:PE31. [DOI] [PubMed] [Google Scholar]
  46. Palmer, A., T. G. Mason, J. Xu, S. C. Kuo, and D. Wirtz. 1999. Diffusing wave spectroscopy microrheology of actin filament networks. Biophys. J. 76:1063–1071. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Rankin, S., and M. Kirschner. 1997. The surface contraction waves of Xenopus eggs reflect the metachronous cell-cycle state of the cytoplasm. Curr. Biol. 6:451–454. [DOI] [PubMed] [Google Scholar]
  48. Rotsch, C., and M. Radmacher. 2000. Drug-induced changes of cytoskeletal structure and mechanics in fibroblasts: an atomic force microscopy study. Biophys. J. 78:520–535. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Ruddies, R., W. H. Goldman, G. Isenberg, and E. Sackmann. 1993. The viscoelasticity of entangled actin networks: the influence of defects and modulation by talin and vinculin. Eur. Biophys. J. 22:309–321. [DOI] [PubMed] [Google Scholar]
  50. Salman, H., Y. Gil, R. Granek, and M. Elbaum. 2002. Microtubules, motor proteins, and anomalous mean squared displacements. Chem. Phys. 284:389–397. [Google Scholar]
  51. Shirasu, M., A. Yonetani, and C. Walczak. 1999. Microtubule dynamics in Xenopus egg extract. Microsc. Res. Tech. 44:435–445. [DOI] [PubMed] [Google Scholar]
  52. Sider, J. R., C. A. Mandato, K. L. Weber, A. J. Zandy, D. Beach, R. J. Finst, J. Skoble, and W. M. Bement. 1999. Direct observation of microtubule-actin interactions in cell free lysates. J. Cell Sci. 112:1947–1956. [DOI] [PubMed] [Google Scholar]
  53. Small, J. V., B. Geiger, I. Kaverina, and A. Bershadsky. 2002. How do microtubules guide migrating cells? Nat. Rev. Mol. Cell. Biol. 3:957–964. [DOI] [PubMed] [Google Scholar]
  54. Taunton, J., B. A. Rowning, M. L. Coughlin, M. Wu, R. T. Moon, T. J. Mitchison, and C. A. Larabell. 2000. Actin-dependent propulsion of endosomes and lysosomes by recruitment of N-WASP. J. Cell Biol. 148:519–530. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Tempel, M., G. Isenberg, and E. Sackmann. 1996. Temperature-induced sol-gel transition and microgel formation in alpha-actinin cross-linked actin networks: a rheological study. Phys Rev. E. 54:1802–1810. [DOI] [PubMed] [Google Scholar]
  56. Theriot, J. A., J. Rosenblatt, D. A. Portnoy, P. J. Goldschmidt-Clermont, and T. J. Mitchison. 1994. Involvement of profilin in the actin-based motility of L. monocytogenes in cells and cell-free lysates. Cell. 76:505–517. [DOI] [PubMed] [Google Scholar]
  57. Valentine, M. T., Z. E. Perlman, M. L. Gardel, J. H. Shin, P. Matsudaira, T. J. Mitchison, and D. A. Weitz. 2004. Colloid surface chemistry critically affects multiple particle tracking measurements of biomaterials. Biophys. J. 86:4004–4014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Wachsstock, D. H., W. H. Schwartz, and T. D. Pollard. 1994. Cross-linker dynamics determine the mechanical properties of actin gels. Biophys. J. 66:801–809. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Waterman-Storer, C., D. Y. Duey, K. L. Weber, J. Keech, R. E. Cheney, E. D. Salmon, and W. M. Bement. 2000. Microtubules remodel actomyosin networks in Xenopus egg extracts via two mechanisms of F-actin networks. J. Cell Biol. 150:361–376. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Weber, K. L., and W. M. Bement. 2002. F-actin serves as a template for cytokeratin organization in cell free extracts. J. Cell Sci. 115:1373–1382. [DOI] [PubMed] [Google Scholar]
  61. Xu, J. Y., D. Wirtz, and T. D. Pollard. 1998. Dynamic cross-linking by alpha-actinin determines the mechanical properties of actin filament networks. J. Biol. Chem. 273:9570–9576. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES