Rapid Intracellular TEA Block of the KcsA Potassium Channel

Abstract

Intracellular tetraethylammonium (TEA) inhibition was studied at the single-channel level in the KcsA potassium channel reconstituted in planar lipid bilayers. TEA acts as a fast blocker (resulting in decreased current amplitude) with an affinity in the 75 mM range even at high bandwidth. Studies over a wide voltage range reveal that TEA block has a complex voltage-dependence that also depends on the ionic conditions. These observations are examined in the context of permeation models to extend our understanding of the coupling between permeant ions and TEA blockade.

INTRODUCTION

Quaternary ammonium ions (QAs) have been indispensable tools in dissecting the molecular details of gating and conduction in K⁺ channels (Armstrong, 1975; French and Shoukimas, 1981; Liu et al., 1997). Their utility stems largely from two important features: their structural diversity (including both symmetric molecules such as tetraethylammonium (TEA) and tetrabutylammonium as well as their asymmetric cousins) and the location at which they bind.

Data consistently support a model in which these agents act by blocking the permeation pathway, occluding the movement of K⁺ ions through the pore. Nearly all K⁺ channels are blocked by QAs on the intracellular side (Hille, 2001). The specificity of internal blockade is largely determined by the hydrophobicity of the blocker (Armstrong, 1971; French and Shoukimas, 1981). According to the simplest scenario, the blocking process can be viewed as being completely independent from permeation. In reality, however, it is clear that permeant ions also play important roles in blocker binding, either by direct competition with the blocker for the binding site, or indirectly through electrostatic repulsion (Hille and Schwarz, 1978; Spassova and Lu, 1998a, 1999; Thompson and Begenisich, 2000, 2001, 2003b). Due to these complexities of blocker binding, discerning the precise contribution of each factor ultimately requires knowledge of both the channel structure and permeation cycle. Because QAs are applied so widely in experimental studies, it is important to understand how these molecules interact and associate with K⁺ channels at the microscopic level.

In this context, the KcsA channel affords a singular framework for understanding the mechanism of pore block in molecular detail, as KcsA permits integration of data from crystallographic, functional, and computational experiments. The channel can be reconstituted into planar lipid bilayers, and its functional properties as well as its interaction with blockers can be probed over a wide range of ionic and voltage conditions (Heginbotham et al., 1999). The permeation cycle of K⁺ through the KcsA channel is uniquely better understood than for any other K⁺ channel, having been studied using both structural and computational approaches (Berneche and Roux, 2003; Morais-Cabral et al., 2001). The structure of KcsA with the tetrabutylammonium analog tetrabutylantimony bound within the cavity provides evidence for the physical location of QA binding site (Zhou et al., 2001a), a position that is supported by a long history of mutagenesis studies in homologous eukaryotic channels (Choi et al., 1993; Hartmann et al., 1991; Holmgren et al., 1997; Yellen et al., 1991).

In this article, we investigate the mechanism of fast intracellular TEA inhibition of the KcsA K⁺ channel. We examine both the voltage- and permeant ion-dependence of TEA block using high bandwidth recordings, and use a computational approach to establish that TEA is unlikely to bind within the selectivity filter. Our data are used to develop the first comprehensive kinetic model for TEA block, including the process of ion permeation, that describes the interaction of inhibitor, channel, and permeant ions. Our aim is to extend our understanding of the microscopic mechanism by which TEA blocks K⁺ channels, and through this, gain deeper insight into the mechanism of ion permeation through K⁺ channels.

METHODS

Materials

All the salts used were reagent grade or higher. Unless otherwise listed, chemicals were high purity and purchased from Sigma-Aldrich (St. Louis, MO). KCl and KOH (88.3%) were obtained from J. T. Baker (Phillipsburg, NJ), MOPS from American Bioanalytical (Natick, MA), K-Hepes from Fluka (Milwaukee, WI), and K₂ succinate from Great Western Inorganics (Arvada, CO). For protein extraction and purification, we used either n-dodecyl-β-d-maltoside (sol-grade) or n-decyl-β-d-maltoside (sol-grade); lipid for reconstitution was solubilized with CHAPS (anagrade) from Anatrace (Maumee, OH). Lipids for the reconstitution into vesicles and for planar lipid bilayer experiments were 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphoethanolamine (POPE) and 1-palmitoyl-2-oleoyl-sn-glycero-3-[phospho-rac-(1-glycerol)] (sodium salt) (POPG) from Avanti Polar Lipids (Alabaster, AL).

We used JM83 or XL-1 Blue Escherichia coli strains purchased, respectively, from ATCC (Manassas, VA) and Stratagene (La Jolla, CA) for protein expression. Cells were grown in Terrific Broth (24 g of yeast extract, 12 g of tryptone, 4 ml glycerol, 17 mM KH₂PO₄, and 72 mM K₂HPO₄).

Solutions for bilayer experiments were prepared fresh daily in the following two ways:

1. 16 mM KCl (for 20 mM K⁺), 96 mM KCl (for 100 mM K⁺), 196 mM KCl (for 200 mM K⁺), 396 mM KCl (for 400mM K⁺), and 10 mM succinic acid (trans solution) or 10 mM MOPS (cis solution), pH was adjusted to 4.0 (trans solution) and 7.0 (cis solution) with KOH.

2. For trans solutions, using 10 mM K₂ succinate and 0, 80, 180, or 380 mM KCl for 20 mM K⁺, 100 mM K⁺, 200 mM K⁺, and 400 mM K⁺ solutions, respectively, pH was adjusted to 4.0 using HCl; for cis solutions, using 10 mM K-Hepes and 10, 190, and 990 mM KCl for 20 mM K⁺, 200 mM K⁺ and 1000 mM K⁺ solutions, respectively, and adjusting pH to 7.0 using HCl.

Protein expression, purification, and reconstitution

KcsA protein was expressed and purified as previously described (Heginbotham et al., 1999; LeMasurier et al., 2001). Briefly, we used a plasmid construct (pASK90) containing the KcsA gene with an N-terminal His₆ tag with induction under the control of a tetracycline promoter. E. coli containing the plasmid were grown in Terrific Broth at 37°C until an OD₅₅₀ of 1.0, whence the expression of the protein was induced by the addition of anhydrotetracycline (Acros Chemicals, Pittsburgh, PA). After 90 min of induction, cells were collected and resuspended in buffer A (95 mM NaCl, 5 mM KCl, 50 mM MOPS pH 7.0). Cells were broken in the presence of protease inhibitors (1 μM leupeptin, 1 μM pepstatin A, 0.5 mM PMSF). Membranes were collected by high-speed centrifugation, after first removing unbroken cells with a low speed spin, and were resuspended in buffer B (95 mM NaOH and 5 mM KCl, pH 7.0 with H₃PO₄). Proteins were extracted by incubation with either 15 mM n-dodecyl-β-d-maltoside or 40 mM n-decyl-β-d-maltoside for 30 min. Protein was purified using nickel-affinity column in the presence of 40 mM imidazole and then eluted using 400 mM imidazole.

For reconstitution, 1–4 μg of protein was mixed immediately after purification with 400 μl of lipid (7.5 mg/ml POPE and 2.5 mg/ml POPG) solubilized in 34 mM CHAPS (Heginbotham et al., 1999). Detergent was removed using a Sephadex G-50 column, and vesicle aliquots were stored at −80°C for up to a month.

Lipid bilayer experiments

Single-channel recordings were performed using a horizontal planar bilayer system. The setup was prepared as described previously (LeMasurier et al., 2001). Briefly, two aqueous chambers are separated by a partition made from overhead transparency film. The partitions contained a hole in the middle over which bilayers of 20–100 pF were formed with a 3:1 mixture of POPE/POPG solubilized in decane.

Vesicles were fused under asymmetric conditions: 20 mM KCl, pH 4.0 trans solution and 200 mM KCl, pH 7.0 cis solutions. After the insertion of the channels, solutions in both chambers were perfused with the solutions to be used for each particular experiment (10 ml of solution was used for each perfusion). KcsA is activated by protons on its intracellular face; by maintaining cis solutions at pH 7.0, any channel inserting with its intracellular side facing the cis chamber is functionally silent. Hereafter, we will refer to solutions in the cis and trans chambers as “extracellular” and “intracellular”, respectively.

Data were acquired using Axopatch 200 and Clampex 8.0 software (Axon Instruments, Burlingame, CA). Data used in the raw trace of Fig. 1 were sampled at 50 kHz and filtered at 10 kHz; some were later digitally filtered at 5 kHz (effectively a filter cutoff of 4.5 KHz (Colquhoun and Sigworth, 1995)). Data for Figs. 1 b, 2, and 3 were acquired using 20 kHz sampling and 2 kHz filtering (at high TEA concentrations (≥100 mM) current was filtered at 1 kHz).

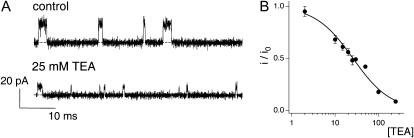
FIGURE 1.

Fast TEA block of KcsA. (A) Single-channel recordings at +200 mV with intra- and extracellular solutions of 200K4 and 200K7. Single-channel traces are shown for the indicated concentrations of TEA: 0 and 25 mM. Dotted lines indicate the closed state in this and subsequent figures. Data were sampled at 50 kHz and filtered at 10 kHz. (B) Current remaining (i/i_o) was plotted against the concentration of TEA. The solid line is a fit to the data using Eq. 1 with a K_1/2 of 25.8 mM. Data show mean ± SE of 3–4 independent determinations.

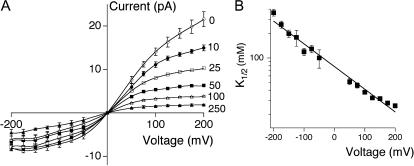
FIGURE 2.

Voltage-dependence of TEA block. (A) Current-voltage plots in the absence and presence of the indicated concentration of TEA, shown in millimolars. (B) At each voltage, a K_1/2 value was determined as in Fig. 1 B. The line shows a fit to Eq. 2, with K_1/2(0 mV) = 78 mM and δ = 0.16. Throughout figure, data show mean ± SE of 3–8 independent determinations.

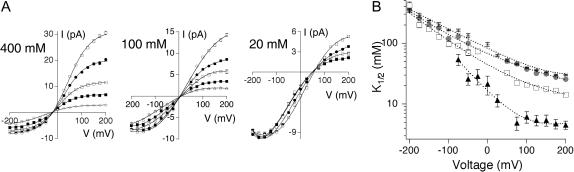
FIGURE 3.

Effect of internal [K⁺] on TEA affinity. (A) Single-channel current-voltage curves were generated at three different internal K⁺ concentrations (400, 100, and 20 mM, left to right) while maintaining constant 200K7 in the extracellular solution. Internal TEA concentrations were as follows: 20 mM K⁺: 0, 1, 5, and 10 mM TEA; 100 mM K⁺: 0, 10, 20, 50, and 100 mM TEA; and 400 mM K⁺: 0, 15, 50, 100, and 300 mM TEA. (B) K_1/2-voltage relation plotted for the four different intracellular [K⁺] (400 mM, stars; 200 mM, circles; 100 mM, squares; 20 mM, triangles). Dotted lines have no theoretical meaning. Throughout figure, data show mean ± SE of 3–12 independent determinations.

In experiments varying TEA concentration, K_1/2 values and errors were obtained from fits of the data to a 1:1 binding isotherm using the nonlinear least-squares fitting program in Igor Pro 4 (Wavemetrics, Lake Oswego, OR).

Single-channel amplitude was measured either from the peak of current histograms (QuB) or by direct inspection of current amplitude (Clampfit). Even under control conditions, KcsA enters a long-lived closed state (Irizarry et al., 2002); these events were manually removed before construction of the amplitude histograms. To confirm that the two methods yield comparable results, we used both to evaluate data obtained at 400 mM KCl (where openings are most brief and therefore susceptible to the largest error when measured by hand). Fifty openings taken in the absence of blocker and 50 taken in the presence of blocker were analyzed by hand before and after digitally refiltering the data at 1 kHz. The mean values of these data were within 1–2% of the values obtained analyzing the same events using all-points histograms.

Computational studies

The region of space accessible to TEA inside the cavity was explored using energy minimization calculations. The channel was kept rigidly fixed in the conformation determined by x-ray crystallography (Zhou et al., 2001b). The central nitrogen atom of TEA was fixed to lie at a prescribed position along the Z axis and the position of the molecule was optimized using 1000 cycles of adopted basis Newton Raphson energy minimization (Brooks et al., 1983). All the calculations were performed using the CHARMM program (Brooks et al., 1983) and the all-atom potential function PARAM22 (MacKerell et al., 1998). TEA can adopt two main conformations: fully symmetric or quasi-planar, and asymmetric pyramidal (Crouzy et al., 2001; Luzhkov and Aqvist, 2001). In all the calculations, it was assumed that TEA was in the symmetric conformation, which is the most stable (Crouzy et al., 2001).

Kinetic modeling

The kinetic models shown in Figs. 8, A and B, and 10, A and B, were evaluated using MATLAB 6.5.1. Rate constants for Model A in Fig. 8 A were as follows: AD¹, BE: 7.9 × 10⁷ s⁻¹ ; DA¹, EB: 7.9 × 10⁹ M⁻¹s⁻¹; AB¹, BA¹, DE, ED, GH¹, HG¹: 1 × 10¹⁰ s⁻¹; CD, FG: 6.3 × 10⁷ s⁻¹; DC, GF: 7.9 × 10⁸ M⁻¹s⁻¹; BC: 1 × 10⁹ s⁻¹; CB: 7.9 × 10⁹ s⁻¹; FC¹, GD¹, HE: 4.0 × 10⁵ s⁻¹; CF¹, DG¹, EH: 2.0 × 10⁸ M⁻¹s⁻¹. ¹A repulsive destabilization of 1.8 kcal/mol was added in addition to the rate constant shown above. TEA and K⁺ entry into the cavity each have voltage dependence of 0.07. Transitions between sites entirely within the selectivity filter (1 through 4) have equal voltage-dependence with δ of 0.233. Transitions into and out of the filter (site 0 ↔ site 1, site 4 ↔ cavity) have a voltage-dependence of 0.116. In voltage-dependent transitions, voltage-dependence is partitioned evenly between forward and backward rates.

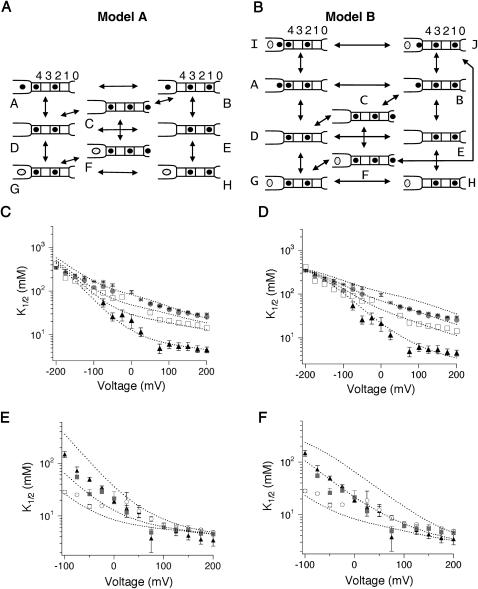
FIGURE 8.

Model for fast block by TEA. (A and B) Schematic diagrams of models used to evaluate TEA blockade of KcsA. K⁺ and TEA are depicted as solid circles and open ovals, respectively. Sites within the selectivity filter are shown as solid boxes, and are designated as 1–4; the cavity is located on the left, and site 0 is designated as 0. The four sites 1–4 are continuously occupied by two ions, located in either sites 1 and 3, or 2 and 4 (Aqvist and Luzhkov, 2000; Berneche and Roux, 2001; Morais-Cabral et al., 2001) Conducting ions enter either from the cavity site on the inside, or from 0 from the extracellular side. In the absence of blocker, ion conduction through the selectivity filter proceeds according to the concerted transitions: [3,1] ↔ [cavity,3,1] ↔ [4,2,0] ↔ [4,2] ↔ [3,1] (Berneche and Roux, 2003). (C–F). Predictions of how intracellular (C and D) or extracellular (E and F) [K⁺] affect TEA blockade in Models A (C and E) or B (D and F) are shown overlaid on the data from Figs. 3 and 4.

Rate constants for Model B in Fig. 8 B were as follows: AD¹, BE: 7.9 × 10⁶ s⁻¹ ; DA¹, EB: 1.6 × 10⁹ M⁻¹s⁻¹; AB¹, DE, GH¹, IJ¹ : 1 × 10⁸ s⁻¹; BA¹, ED, HG¹, JI¹: 1.3 × 10⁸ ; CD, FG: 1 × 10⁸ s⁻¹; DC, GF: 5 × 10⁸ M⁻¹s⁻¹ ; BC, JF^1,2: 1 × 10⁷ s⁻¹; CB, FJ^1,2: 3.2 × 10⁸ s⁻¹; FC¹, GD¹, HE, IA^1,2 JB² : 4.0 × 10⁵ s⁻¹; CF¹, DG¹, EH, AI^1,2, BJ²: 3.2 × 10⁸ M⁻¹s⁻¹. A repulsive destabilization of 1.8 kcal/mol for ¹ and of 0.8 kcal/mol for ² was added in addition to the rate constant shown above. TEA and K⁺ entry into the cavity each have a voltage dependence of 0.10. Transitions between sites entirely within the selectivity filter (1 through 4) have equal voltage-dependence with δ of 0.225. Transitions into and out of the filter (site 0 ↔ site 1, site 4 ↔ cavity) have a voltage-dependence of 0.112. In voltage-dependent transitions, voltage-dependence is partitioned evenly between forward and backward rates.

Rate constants for Fig. 10 A were as follows: AD¹, BE: 7.9 × 10⁷ s⁻¹ ; DA¹, EB: 7.9 × 10⁹ M⁻¹s⁻¹; AB¹, BA¹, DE, ED, GH¹, HG¹: 1 × 10¹⁰ s⁻¹; CD, FG: 6.3 × 10⁷ s⁻¹; DC, GF: 7.9 × 10⁸ M⁻¹s⁻¹; BC: 1 × 10⁹ s⁻¹; CB: 7.9 × 10⁹ s⁻¹; FC¹, GD¹, HE: 2.2 × 10⁶ s⁻¹; CF¹, DG¹, EH: 2.0 × 10⁹ M⁻¹s⁻¹. ¹A stabilization factor of 0.7 kcal/mol was added in addition to the rate constant shown above. Voltage dependence of all the transitions are the same as described for Model A.

FIGURE 10.

Modeling TEA block data from the Shaker channel using Model A. (A) Effect of internal K⁺ on TEA block with the introduction of stabilization between ions in the cavity site and the selectivity filter, evaluated at 20 (solid curve) and 100 mM (dashed curve) internal K⁺. (B) As in A, with rate constants modified to more closely mimic data obtained from the Shaker channel (see Methods).

Rate constants for Fig. 10 B were as follows: AD¹, BE: 1.6 × 10⁸ s⁻¹ ; DA¹, EB: 2.0 × 10⁹ M⁻¹s⁻¹; AB¹, DE, GH: 1 × 10¹¹ s⁻¹ ; BA¹, ED, HG¹: 1 × 10¹⁰ s⁻¹; CD, FG: 6.3 × 10⁷ s⁻¹; DC, GF: 6.3 × 10⁹ M⁻¹s⁻¹; BC: 1 × 10¹⁰ s⁻¹; CB: 1.3 × 10¹⁰ s⁻¹; FC¹, GD¹, HE: 1.6 × 10⁶ s⁻¹; CF¹, DG¹, EH: 2.0 × 10⁹ M⁻¹s⁻¹. ¹A stabilization factor of 0.7 kcal/mol was added in addition to the rate constant shown above. Voltage dependence of all the transitions are the same as described for Model A.

RESULTS

Fig. 1 A shows the basic phenotype of TEA block that this article examines in detail. Here, activity from a single channel is recorded in 200 mM symmetric K⁺ and at +200 mV. When TEA is added to the internal solution, the current amplitude decreases. This phenotype is expected for a class of inhibitors, fast or rapid blockers, for which the kinetics of block are much faster than the speed of data acquisition (Hille, 2001). In a basic survey of the KcsA channel, TEA was found to act as a rapid blocker in data filtered at 1 kHz (Heginbotham et al., 1999). The channel shown in Fig. 1 was recorded from a smaller bilayer and was filtered at 10 kHz, but despite the increased temporal resolution, we are still unable to resolve discrete blocking events. This indicates that the lifetime of the TEA-bound channel is <13 μs (Colquhoun and Sigworth, 1995), from which we calculate that the TEA off-rate is faster than ∼7.6 × 10⁴ s⁻¹. Fig. 1 B shows how i/i_o, the fraction of single-channel current remaining, varies with TEA concentration ranging from 2 to 250 mM. The data are well fit assuming a bimolecular interaction between the channel and TEA with K_1/2 of 25.8 ± 1.6 mM, as described by

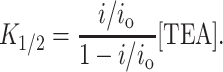(1)

This value is in good agreement with that previously published (Heginbotham et al., 1999). In combination with the lower limit for k_off measured above, this value indicates that the TEA association rate is at least 2.9 × 10⁶ M⁻¹s⁻¹.

Voltage-dependence of rapid block

We examined the voltage-dependence of TEA block in KcsA by collecting data similar to those shown in Fig. 1 B over a broad range of potentials (Fig. 2 A). TEA affinity is clearly voltage-dependent in KcsA (Fig. 2 B), and increases with depolarization. Interpolation of the data to 0 mV yields a voltage-independent apparent dissociation constant, K_1/2(0 mV), of 78.4 ± 2.6 mM. This value is considerably higher than the submillimolar values reported for most eukaryotic channels (∼0.7 mM for the Shaker channel, for instance (Yellen et al., 1991)), but is reminiscent of that observed in the Ca²⁺-activated K⁺ channel (values ranging from 27 to 60 mM (Blatz and Magleby, 1984; Villarroel et al., 1989; Yellen, 1984)).

At the simplest level, voltage-dependence of blocker affinity can be explained as arising from the interaction of a charged blocker with the electric potential across the pore (Woodhull, 1973). In this model, the dissociation constant of a blocker at an applied potential V, K_D (V), depends on its intrinsic magnitude in the absence of voltage, K_D (0 mV), as well as a voltage-dependent component derived from the valence z of the blocking molecule, and the fraction δ of the membrane potential the blocker traverses in reaching its binding site, according to

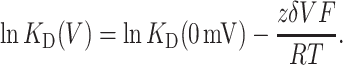(2)

A fit of the data shown in Fig. 2 B to Eq. 2 yields δ of 0.16. This value falls squarely within the range obtained from analogous measurements of rapid TEA block in the Ca²⁺-activated K⁺ channel (δ from 0.10 to 0.27 (Blatz and Magleby, 1984; Villarroel et al., 1989; Yellen, 1984)).

Effect of K⁺ concentration

The Woodhull model describes a simple and direct effect of membrane potential on blocker affinity, but there are also indirect sources of voltage-dependence. Permeant ions, for instance, can also influence the affinity of blockers that bind within the ion conduction pathway (Spassova and Lu, 1998a; Thompson and Begenisich, 2003a). Since changing the membrane potential can alter both the kinetics of ion conduction as well as the relative distribution of ions along the pore, voltage-dependence can also arise from interactions between blockers and permeant ions. The physical stability of our bilayer recording system allows experiments to be performed over a broad voltage range. This, together with the ability to exchange solutions in both cis and trans chambers, provides a unique opportunity to examine how blocker-permeant ion interactions are coupled to membrane potential.

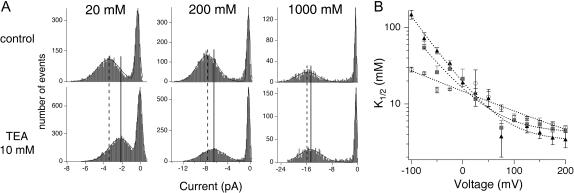
We first varied internal K⁺ from 20 to 400 mM, maintaining constant 200 mM external K⁺. Single-channel I/V curves (Fig. 3 A) were used to construct concentration-response curves, from which we determined K_1/2 values (as in Fig. 1 B); in all cases the data were well fit with Eq. 1, assuming a one-to-one interaction between channel and blocker. Fig. 3 B shows that changing internal [K⁺] affects both the affinity and the voltage-dependence of internal TEA block. Increasing the concentration of internal K⁺ decreases TEA affinity, shifting the curves upward. Changing internal [K⁺] also alters both the slope and the shape of the voltage-dependence plot; at 20 mM internal K⁺, a plateau becomes apparent at extreme positive potentials. The decrease in affinity with increasing [K⁺] is as expected from a competition model; in the Discussion we show that such models also predict both the slope and shape changes observed here.

We next examined the effect of external K⁺ at concentrations from 20 to 1000 mM. In these experiments, internal K⁺ was maintained at a low concentration, 20 mM, to minimize competition by internal permeant ions seen above. As with internal K⁺, external K⁺ influences both the affinity and voltage-dependence of TEA inhibition. Fig. 4 A shows amplitude histograms from single channels recorded at −75 mV with external solutions containing either 20, 200, or 1000 mM K⁺. Increasing external K⁺ decreases TEA block, a result that is qualitatively similar to the effects of external K⁺ observed in other channels (Armstrong and Binstock, 1965; Spassova and Lu, 1998a). Fig. 4 B illustrates that the extent of the external effect also depends on membrane potential: the effect of external K⁺ is larger at negative potentials than at positive voltages. This is easily grasped at an intuitive level: at positive potentials, both current and the occupancy of the binding sites along the conduction pathway are determined principally by the internal K⁺, which is maintained at a constant concentration in the experiments shown here, and by the membrane potential itself.

FIGURE 4.

Effect of external [K⁺] on TEA affinity. (A) Amplitude histograms generated at −75 mV with intracellular 20K4 and 20, 200, or 1000 mM extracellular K⁺ at pH 7.0, under control conditions (top) or in the presence of 10 mM TEA (bottom). Histograms were fitted with the sum of two Gaussians (one each to represent the closed and open states, solid lines). The decreased amplitude caused by TEA is reflected by the shift in the maximum amplitude of the open state—the control maximum is designated by the dashed line; the position of the maximum in TEA is shown with the solid line. (B) K_1/2-voltage relation plotted for the three different extracellular [K⁺] (1000 mM, triangles; 200 mM, squares; 20 mM, circles). Data show mean ±SE of 3–4 independent determinations.

Localizing the TEA binding site

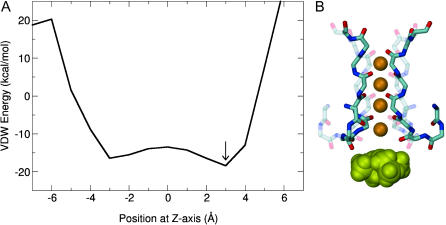
The observation that rapid block by internal TEA competes with both internal and external K⁺ indicates that TEA must physically bind in proximity to a K⁺ ion; a site within the inner cavity might fulfill this requirement, but a site within the selectivity filter proper could as well. The high-resolution crystal structure of KcsA shows seven distinct K⁺ binding sites along the ion conduction pathway: one within the inner cavity, four along the selectivity filter, and two located in the external vestibule (Zhou et al., 2001b). To specifically address the question of whether TEA might enter the selectivity filter, we calculated the van der Waals energy of TEA binding along the axis of the pore. These calculations were based on the structure of KcsA. Although this structure certainly corresponds to a closed conformation (Zhou et al., 2001a), the calculation is still informative because we are interested primarily in the selectivity filter and adjacent cavity region, which are not expected to undergo conformation changes with gating. Two K⁺ were positioned in the outer ion configuration (1 and 3, according to the nomenclature of Morais-Cabral et al., 2001), there were no explicit water molecules, and we used the simplifying assumption that TEA would bind along the central axis of the pore. TEA was translated through the cavity along the central axis in 1 Å steps. At each step, the nitrogen of TEA was fixed at this position and the energy was minimized. TEA carbon chains and the side chains of the protein were allowed to move; however, the protein backbone was kept rigid throughout the calculation. In Fig. 5, we show both the profile of the van der Waals interaction energy along the central axis of the pore (Fig. 5 A), and the position of TEA with lowest energy. Although TEA easily fits in the cavity, as evidenced by the negative van der Waals energy throughout this region, TEA binding into the selectivity filter is energetically prohibitive. Since TEA is unlikely to enter the selectivity filter, these data indicate that the competition previously observed between TEA and K⁺ must occur when TEA binds at a site below the selectivity filter.

FIGURE 5.

Energy variation of TEA-KcsA interaction with respect to the position of TEA in the cavity. (A) Van der Waals energy of interaction between TEA and KcsA was calculated using CHARMM where TEA was positioned along the central axis (Z) of the channel and moved 1 A at a time. Z = 0 corresponds to the center of the cavity. (B) Graphic illustration of the lowest energy position of TEA with respect to the selectivity filter. For illustrative purposes, four K⁺ ions were placed at positions 1–4 in the selectivity filter.

Because we have used the closed KcsA structure for this calculation, and examined only the van der Waals energy, our calculation does not address the question of where along the cavity TEA binds when inducing rapid block. It is interesting to note, however, that the minimum van der Waals energy occurs at a position 3 Å above the center of the cavity, slightly above the locations of both K⁺ and tetrabutylantimony found in cavity in crystal structures, and in a location similar to the binding site proposed previously by Luzhkov and Aqvist (2001) using molecular dynamics simulations with the symmetric conformer of TEA.

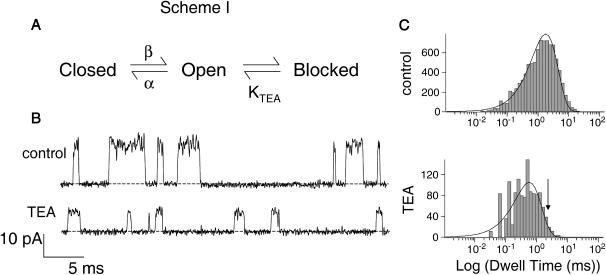
Test of an open channel block mechanism

We examined whether TEA acts as a strict classical open channel blocker in inducing rapid block. The properties of this class of inhibitors are shown in Scheme I (Fig. 6 A). Classical open channel blockers only bind to the open state of a channel; when bound, the blockers prevent the channel from closing (Hille, 2001). For the case of a rapid blocker, in which transitions between the open and blocked states are much faster than channel closing, the channel undergoes bursting behavior: fast transitions between open and blocked states are punctuated by longer entries into the closed state. Since individual blocking events cannot be resolved, the amplitude of the burst (the apparent single-channel current) reflects the relative amount of time spent in the open versus the blocked state, and the duration of each apparent opening actually reflects the length of time spent in a burst (Coronado and Miller, 1982). Scheme I predicts a quantitative relationship between TEA concentration and burst duration (τ) (Coronado and Miller, 1982) given by

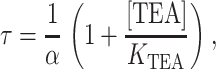(3)

where α is the closing rate of the channel. According to Eq. 3, adding TEA at a concentration equal to its K_TEA value should double the mean burst duration (the apparent open time) from its value in the absence of TEA. Fig. 6 B shows the current recorded from a single KcsA channel under control conditions and in the presence of 25 mM TEA. At the applied voltage of +200 mV, this is roughly the K_1/2 for rapid block (as evidenced by the appropriate decrease in current amplitude). However, inspection of both the raw data (Fig. 6 B) and open dwell-time histograms (Fig. 6 C) reveals that the open lifetimes actually decrease as TEA is added. This observation is inconsistent with TEA acting through a strict open channel block mechanism shown in Scheme I and Eq. 3, since in that case the burst duration should increase with blocker addition, as described above.

FIGURE 6.

Effect of TEA on burst duration. (A) Kinetic scheme for open channel block. Blocker binds only to the open state of the channel. (B) Single-channel records of KcsA in 200 mM symmetric K⁺ at +200 mV under control conditions and in the presence of 25 mM TEA. Data were sampled at 50 kHz and filtered at 5 kHz. (C) Open dwell-time histograms of single-channel activity recorded under control conditions and in the presence of 25 mM TEA. Single exponential fits to the data yield mean open times of 1.2 and 0.8 ms for control and TEA-blocked channels, respectively. Current is reduced by half at this voltage, indicating that the K_D value for rapid block is 25 mM. The open channel block scheme shown in A thus predicts a burst duration of 2.4 ms in the presence of TEA (position shown by arrow).

DISCUSSION

In this investigation of intracellular TEA with the KcsA channel, we have focused on rapid block. By using single-channel recordings, our data consider the process of rapid block in isolation from any potential effects of TEA on gating. We have found that TEA acts as a rapid blocker even at high bandwidth, that the affinity of fast TEA block is reduced by increasing K⁺ on either intracellular or extracellular surfaces, that TEA block displays a complex voltage-dependence, and that TEA is unlikely to bind within the selectivity filter. Coupled with the detailed knowledge of the permeation cycle in KcsA, these data permit a comprehensive quantitative modeling of rapid TEA block. As described below, our model in turn reveals two important features of TEA block in KcsA. First, although TEA appears to have a rather low intrinsic potency, the free energy of TEA binding to the “bare” channel is actually reasonably large. Second, that the interaction between TEA and KcsA is quite different than that seen in the Shaker K⁺ channel. The latter finding has important implications for the interpretation of structural studies of KcsA, as functional data acquired in the Shaker channel are frequently used as references.

Voltage-dependence of TEA block

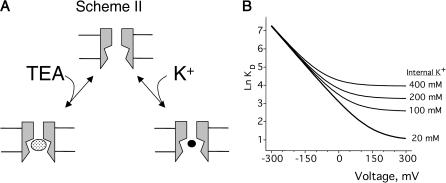
The basis of voltage-dependence of block can be quite complicated in multi-ion channels (Hille and Schwarz, 1978). Our use of single-channel recordings, coupled with the physical stability of artificial lipid bilayer, permitted our probing TEA block over a span of 400 mV. This extensive voltage range revealed clear deviations from the logarithmic relationship described by the classical Woodhull model (Woodhull, 1973). The model shown in Fig. 7 A, which is a slight modification of the original Woodhull model, is intended to provide an intuitive understanding of how deviations from the exponential relationship in the context of a Woodhull model may arise, and in particular, to highlight two important facts: that the measured voltage-dependence need not be constant over a broad range of potentials even if voltage-dependence comes from a single step, and that inhibition may appear voltage-independent even if the blocker binds deep within the electric field. In this scheme, conduction is still prohibited, and K⁺ bound within the cavity is in true equilibrium with the internal solution. K⁺ and TEA⁺ bind in a mutually exclusive manner to the same site, and both traverse the same fraction, δ, of the membrane potential, V, in reaching the binding site. The K_1/2 for TEA, 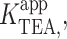depends on both the intrinsic voltage-independent dissociation constants for TEA and K⁺, K_TEA (0 mV), and K_K (0 mV), according to

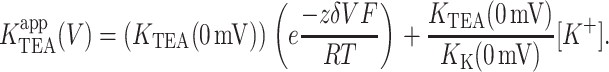(4)

FIGURE 7.

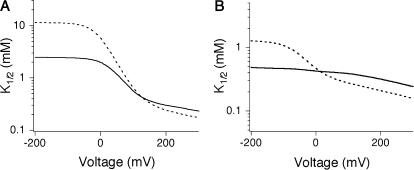
Competition model used in deriving Eq. 4. (A) Channels can bind either TEA or K⁺ within the cavity, but binding is mutually exclusive. (B) Simulation showing effect of changing internal [K⁺] on the K_1/2. The K_TEA and K_K were 20 and 150 mM, respectively, with δ = 0.36.

The introduction of competition has a profound effect on the observed voltage-dependence that is evident both arithmetically (Eq. 4) and graphically (Fig. 7 B). At negative voltages, the left term of the sum dominates, voltage-dependence arises as described by the basic Woodhull model, and the apparent K_TEA becomes independent of internal K⁺. A very different pattern emerges at positive voltages, where the second term dominates. The inner cavity site is saturated, and since the relative K⁺/TEA occupancy determined by the mole fraction in the medium, raising [K⁺] results in increased 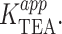Although the model in Fig. 7 qualitatively accounts for many features of our data, in a functioning channel, K⁺ has two egress routes: either the external or internal sides. Consequently, any model that includes K⁺ as a competing ion must explicitly consider permeation as well. This basic constraint is used in the models we consider below.

Coupling between rapid block and ion permeation

A growing body of literature indicates that internal TEA block is highly sensitive to permeant ions. Detailed investigations by Spassova and Lu (1998b, 1999) and Thompson and Begenisich (2000, 2001, 2003b) have shown that relatively simple competition models can account for the effects of external and internal [K⁺], respectively. Whereas these studies of TEA block use macroscopic current recordings, this study includes only data recorded at the single-channel level.

Our models of the interaction of TEA with KcsA are built from data provided by our experimental results and those of previous studies. On the basis of crystallographic and computational work, the structural, energetic, and dynamic features of the K⁺ permeation cycle are better known for KcsA than for any other K⁺ channel. We use this information as a foundation for modeling the conduction process (Berneche and Roux, 2003; Morais-Cabral et al., 2001; Zhou et al., 2001b). Although the precise position of the TEA binding site is unknown, our data place two restrictions on such a location: it must allow TEA to interact with K⁺, and it is not located within the selectivity filter proper. Because of the uncertainty associated with the physical location of the TEA binding site, we explored two slightly different kinetic models (A and B; Fig. 8, A and B) that both met the above criteria. The two models have identical K⁺ permeation cycles that were chosen to reflect as closely as possible the results of crystallographic studies (Morais-Cabral et al., 2001; Zhou et al., 2001b) and of detailed ion-flux simulations based on a multi-ion free energy surface calculated from molecular dynamics (Berneche and Roux, 2001, 2003). K⁺ binding sites along the conduction pathway correspond to those identified both in crystallographic and computational studies (Berneche and Roux, 2001; Zhou et al., 2001b); four (sites 1–4) are located within the selectivity filter, whereas the “0” and cavity sites are located at the extracellular entry and the cavity, respectively. A repulsive destabilization is assumed between ions bound within the cavity and at site 4.

The two models differ in where TEA binds, and as a consequence, in how TEA interacts with K⁺. In Model A (Fig. 8 A), TEA binds within the cavity at the same site normally occupied by a K⁺ ion. K⁺ and TEA bind in a mutually exclusive manner, and both ions cross the same fraction of the membrane potential in reaching the binding site. In Model B (Fig. 8 B), the TEA binding site is distinct from the cavity K⁺ binding site. The TEA binding site is located very close to the pore entrance, whereas the K⁺ binding site is higher in the cavity, close to the selectivity filter. TEA can bind even when K⁺ occupies the cavity site; once TEA is bound, K⁺ cannot leave the cavity into the internal solution, although it can still exit to the selectivity filter (the transition J ↔ F). TEA binding itself is voltage-independent, whereas K⁺ binding to the cavity does have voltage-dependence. This model includes repulsion between two ions in the cavity, as well as between cavity ions and K⁺ bound at site 4.

In both models, changes in internal potassium result in alterations of both slope and apparent affinity (dotted curves, Fig. 8, C and D). Both models can produce an apparent saturation of K_1/2 with increasing [K⁺]_int. This was initially unexpected in Model A in which K⁺ and TEA compete; in fact, the apparent saturation in this case reflects a local convergence over the K⁺ concentrations used in the study and disappears as K⁺ is increased even further (data not shown). The models also account for the effect of external potassium on internal TEA affinity (curves, Fig. 8, E and F). At extreme positive potentials, the K_1/2 becomes independent of external [K⁺] because the relative distribution among multi-ion occupancy states is determined largely by the concentration of internal K⁺ (kept constant during this experiment) and the membrane potential. The models predict a similar effect at extreme negative potentials when intracellular [K⁺] is varied; our data hint at such a convergence over the voltage range we examined.

Although Models A and B are distinct in their treatment of TEA binding, the dominant determinants of TEA binding converge in the two models under the conditions at which they were evaluated. In Model B, there is mutual destabilization between K⁺ and TEA when both are bound simultaneously in the cavity (state J). As repulsion increases, the occupancy of this state decreases. In the limit of infinite repulsion, state J disappears entirely, and Models A and B become identical except for their treatment of the voltage-dependence of TEA binding, and whether TEA and K⁺ occupy precisely the same position when they bind within the cavity. In fact, fitting our data to Model B required a high degree of repulsion (1.8 and 0.8 kcal/mol for the transitions such as those shown by B ↔ A and B ↔ J, respectively). As discussed below, the models reveal several important features of TEA binding (values from Model A are presented in the text body with those from Model B shown in parentheses).

The apparent binding affinity of TEA is dramatically affected by permeant ions. The true K_D of TEA binding is 2 mM (1.3 mM, Model B), reflecting a free energy of binding of 3.6 kcal/mol. Yet, under typical ionic conditions, the effective K_1/2 of block is 75 mM, or nearly 40-fold higher. The difference between these two values results from a combination of effects. Repulsive destabilization between ions bound in the adjacent cavity and site 4 disfavors states in which both sites are simultaneously occupied (on the order of 2 kcal/mol for both forward and backward rates). In addition, in Model A, both internal and external K⁺ compete with TEA for binding at its site.

In our models, the cavity displays a slight selectivity for TEA over K⁺. Interestingly, recent structural and functional evidence indicates that the cavity site displays only modest selectivity among small monovalent cations, with larger ions preferred over Na⁺ (Nimigean and Miller, 2002; Zhou and MacKinnon, 2004). By providing an estimate for the TEA K_D, our models extend the size comparison yet further. Our data indicate that TEA is favored over K⁺ by a ratio of ∼5:1 (∼4:1 for Model B), thus reinforcing the idea that the cavity site is not specifically tuned to bind K⁺, but actually prefers larger cations.

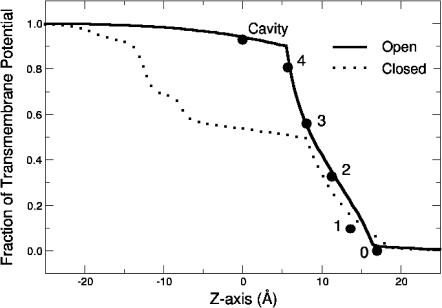
Our data are best fit by ascribing only a very modest voltage-dependence (δ = 0.07) to the actual binding of TEA or internal K⁺ within cavity (in Model B, δ_K = 0.10; δ_TEA = 0.0) with the majority of voltage-dependence (δ = 0.23 over modest potentials) resulting from the coupled movement of K⁺ ions within the pore. The relatively weak voltage-dependence of TEA binding fits well with calculations of the transmembrane potential using a modified Poisson-Boltzmann theory (Roux, 1999). Fig. 9 shows the potential profile of the ion binding sites of Model A superimposed upon the calculated transmembrane potential profiles of open and closed channels (Roux et al., 2000; Berneche and Roux, 2003); the overall voltage profile of our model closely follows that calculated for the KcsA channel in an “open” state based on the structure of the MthK channel (Jiang et al., 2002). The weak voltage-dependence of rapid block agrees well with that expected for TEA binding within the cavity of an open channel, (δ = 0.06), in contrast to that calculated from a closed state, where TEA binding in the cavity should sense >40% of the electric potential (Roux et al., 2000).

FIGURE 9.

Transmembrane potentials of the binding sites used in evaluating Model A (circles) superimposed on the profiles calculated for the open channel model (solid line) and closed channel structure (dashed line) of KcsA.

Comparison of rapid block in KcsA with TEA inhibition of eukaryotic channels

In many respects, the model shown in Fig. 8 A is quite similar to that previously proposed to explain the effects of external permeant ions on the Kir1.1 inward rectifier channel (Spassova and Lu, 1998a, 1999). Our results are qualitatively similar to those seen in the Kir1.1 channel (Spassova and Lu, 1998a), although in Kir1.1, both affinity and voltage-dependence are more sensitive to external K⁺ than we observe in KcsA. A larger disparity is seen between KcsA and the Shaker channels (Thompson and Begenisich, 2001). As described below, one obvious contrast can be explained by relatively slight differences between the two channels, but a second suggests the two channels differ fundamentally in the way ions interact along the conduction pathway.

Internal K⁺ has apparently diverse effects on TEA block in KcsA and Shaker channels, but this may in fact reflect only a subtle difference between them. Internal K⁺ clearly impacts internal TEA block in KcsA at 0 mV, but to see an analogous effect at the same voltage in Shaker, conduction must first be blocked by external TEA (Thompson and Begenisich, 2001). Thompson and Begenisich (2001) propose that the internal cavity of Shaker has a relatively low affinity for permeant ions; the site has a very low occupancy during conduction, and consequently internal K⁺ does not effectively compete with internal TEA. Correspondingly, when the channel is blocked with TEA from the outside, K⁺ within the cavity cannot escape to the outside, the cavity has a higher K⁺ occupancy, and K⁺ now competes with TEA. The competition observed in KcsA in the absence of external TEA is easily accommodated by this scenario if the cavity has a higher K⁺ occupancy than that of Shaker. The differences in channels and recording conditions are consistent with this possibility: the cavity site of KcsA appears to have slightly higher affinity for K⁺ than the equivalent site in Shaker (dissociation constants of 10 and ∼70 mM, respectively) (Thompson and Begenisich, 2001), and our recordings were made at higher K⁺ concentrations.

Close examination of the literature suggests a second, more dramatic, way in which data from Shaker and KcsA channels differ. In addition to their work at 0 mV mentioned above, Thompson and Begenisich (2001) have also examined the effect of internal [K⁺] in Shaker at positive voltages. Some of these data were collected in the absence of external TEA and, thus, more closely mirror the conditions used in our study. In these Shaker data, Thompson and Begenisich show that increasing internal [K⁺] results in increased voltage-dependence and a decreased K_1/2. This is precisely the opposite of the apparent competition between K⁺ and TEA that we observed in KcsA (Fig. 8 C). The difference between the two channels can be qualitatively reproduced at high positive potentials in Model A by altering the nature of the interaction between ions bound simultaneously in the cavity and site 4. Fig. 10 A shows the effect of changing the destabilization energy (used to model the KcsA data) between ions bound in these two sites to a stabilization energy of −0.7 kcal/mol. Internal potassium now decreases the K_1/2 at high potentials, mirroring the effect seen in Shaker. The voltages over which this occurs can be shifted into the range observed in Shaker (Fig. 10 B); this requires adjustment of most of the rate constants in the permeation cycle. The presence of effective stabilization between ions in the cavity and selectivity is unconventional, and may simply indicate that our KcsA permeation model is not appropriate for considering conduction and block in the Shaker channel. For instance, if the TEA binding site is closer to the selectivity filter in Shaker than in KcsA, it is possible that in Shaker, TEA could be trapped by internal K⁺ binding at a more peripheral site along the vestibule (thereby increasing its affinity). In fact, recent work on state-dependent accessibility changes suggests that the cytoplasmic entrance of the Shaker channel is narrow (Webster et al., 2004) and could differ from the open structure of the MthK channel (Jiang et al., 2002); a relatively narrow stretch at the bottom of the pore would facilitate TEA trapping. It is also possible that stabilization may result from subtle conformational changes of the TEA binding site induced by occupancy of ion located at site 4. In this scenario, the distinct effects of internal [K⁺] in Shaker and KcsA channels could reflect structural differences in the TEA binding sites or in the coupling of TEA binding and K⁺ occupancy of site 4 within the selectivity filter.

Finally, our data do not address whether the channel can close when TEA is bound, or whether TEA can bind to the closed states. The fast kinetics of block studied here suggest that little or no rearrangement occurs in response to binding, and are compatible with a model in which TEA binds to the open state. The possibility that block occurs through strict open channel block is consistent with much of our data, but a crucial test of this mechanism, namely an increase in the length of the channel open duration for rapid block, was inconclusive. The open times did not increase, but decreased instead, as though the channel can close around the blocker (Li and Aldrich, 2004; Zhou et al., 2001a), or the channel enters a second, long-lived, blocked state. Ongoing experiments examine these latter possibilities in detail.