The Dynamic Stress Responses to Area Change in Planar Lipid Bilayer Membranes

Abstract

The viscoelastic properties of planar phospholipid (dimyristoylphosphatidylcholine) bilayer membranes at 308 K are studied, many of them for the first time, using the nonequilibrium molecular dynamics simulation (NEMD) method for membrane area change. First, we present a unified formulation of the intrinsic three-dimensional (3D) and apparent in-plane viscoelastic moduli associated with area change based on the constitutive relations for a uniaxial system. The NEMD simulations of oscillatory area change process are then used to obtain the frequency-domain moduli. In the 4–250 GHz range, the intrinsic 3D elastic moduli of 20–27 kbar and viscous moduli of 0.2–9 kbar are found with anisotropy and monotonic frequency dispersion. In contrast, the apparent in-plane elastic moduli (1–9 kbar) are much smaller than, and the viscous moduli (2–6 kbar) comparable to, their 3D counterparts, due to the interplay between the lateral and normal relaxations. The time-domain relaxation functions, separately obtained by applying stepwise strains, can be fit by 4–6 exponential decay modes spanning subpicosecond to nanosecond timescale and are consistent with the frequency-domain results. From NEMD with varying strain amplitude, the linear constitutive model is shown to be valid up to 6 and 20% area change for the intrinsic 3D elastic and viscous responses, respectively, and up to 20% area change for the apparent in-plane viscoelasticity. Inclusion of a gramicidin A dimer (∼1 mol %) yields similar response properties with possibly smaller (<10%) viscous moduli. Our results agree well with available data from ultrasonic experiments, and demonstrate that the third dimension (thickness) of the planar lipid bilayer is integral to the in-plane viscoelasticity.

INTRODUCTION

Phospholipid bilayers are an important structural motif of cell membranes and serve as a model system in the study of many cellular functions (Sackmann, 1995). They exist in a liquid-crystalline state near physiological temperature. Thus, they can provide a mechanical barrier in an aqueous environment and, at the same time, act as a two-dimensional (2D) solvent accommodating biomolecules and proteins (Singer and Nicolson, 1972). This fluid nature produces, e.g., a lateral diffusion constant on the order of 10⁻¹² m²/s (Almeida and Vaz, 1995).

The elastic properties of membranes determine their stability against, and response to, mechanical deformation, e.g., under osmotic stress or inclusion of proteins (Evans and Hochmuth, 1978; Bloom et al., 1991). Experimental information exists on the area compressibility, the thickness compressibility, and the layer bending modulus (LePesant et al., 1978; Evans and Needham, 1987; Nallet et al., 1989; Yamamoto et al., 1992; Koenig et al., 1997; Rawicz et al., 2000). Recently, computer simulations employing coarse-grained or atomistic potential models have also begun to provide information on these properties (Goetz and Lipowsky, 1998; Lindahl and Edholm, 2000; Ayton et al., 2002). In contrast, the membrane viscous properties have received very limited attention. Regarding the in-plane shear viscosity, which is closely related to the lateral diffusion, there exist several reports estimating its magnitude for various lipid systems (Evans and Yeung, 1989; Weisz et al., 1992; Dimova et al., 2000). However, the dissipative effects of the membranes are sometimes referred to as “effective viscosity” or “microviscosity” without a clear specification of their nature or origin. Furthermore, partly due to experimental difficulties (Bloom et al., 1991), the viscosities associated with the area change have rarely been quantified (El-Sayed et al., 1986; Yamamoto et al., 1992). This state of affairs is not optimal because the viscosity, together with heat transport, provides a major dissipative mechanism. Various dynamic and relaxation phenomena, such as the propagation and attenuation of a sound wave, decay of thermal shape fluctuations, and translational and rotational diffusion of membrane constituents, will be closely related to the viscous or frictional properties.

In this article, we study the viscoelastic properties of bilayer membranes composed of dimyristoylphosphatidylcholine (DMPC) with the nonequilibrium molecular dynamics simulation (NEMD) method (Ayton et al., 2002), focusing on properties related to isotropic area change in planar membranes. We treat the elastic and viscous components on an equal footing within the relaxation function formalism appropriate for a system of uniaxial symmetry. Although the underlying theoretical ingredients have been in place for quite some time (Nye, 1985; Doi and Edwards, 1986; Tschoegl, 1989; Fung, 1993; Chaikin and Lubensky, 2000), it appears that the dynamic formulation of the linear viscoelasticity of a uniaxial system has not been presented in detail previously. The resulting three-dimensional (3D) linear constitutive relation contains three intrinsic complex viscoelastic moduli associated with the lateral and normal deformations and the coupling between them. The apparent 2D moduli relevant to many experimental situations naturally emerge from them by imposing the condition of zero normal stress. We determine these moduli from the NEMD simulations of the area change process. We find a simple yet highly nontrivial cooperation of the lateral and normal responses in producing the apparent 2D response. For example, it is found that the 2D apparent elastic moduli are about an order of magnitude smaller than the 3D elastic moduli, whereas the 2D viscous moduli are similar in magnitude to their 3D counterparts. Overall, the viscous effect relative to the elastic one is much more pronounced when the membrane system is allowed to adjust its thickness under applied tension. Also, the linear viscoelastic model appears to be valid at least up to 6% change in area for the DMPC membrane as far as the average response to area compression and expansion is concerned. We identify possible molecular mechanisms responsible for the observed viscoelastic behavior and make contact with various experimental results.

LINEAR VISCOELASTICITY OF A UNIAXIAL SYSTEM

In this section, we present a dynamic formulation of the linear viscoelasticity of membranes. We consider a hydrated lipid bilayer membrane with a planar geometry. This system is anisotropic with a uniaxial symmetry—the symmetry axis is the bilayer normal. Thus, the conventional dynamic stress-strain relation of an isotropic material (Doi and Edwards, 1986; Tschoegl, 1989; Goodwin and Hughes, 2000) needs to be generalized as a tensorial relation (Eq. 1) reflecting the system anisotropy and symmetry. Removing the shear deformation components from this equation, we are left with the 3D constitutive relation for the area and thickness change (Eq. 5) with three relevant relaxation functions (G_⊥(t), G_‖(t), G₁₃(t)). The corresponding frequency-domain expressions (Eq. 7) define three complex viscoelastic moduli (G_⊥*(ω), G_‖*(ω), G₁₃*(ω)) as Fourier transforms of the corresponding relaxation functions. These are the fundamental quantities characterizing the system viscoelasticity under the area change. Since most experiments are carried out under the ambient pressure in the normal direction, we can further simplify our formula by imposing the zero-normal-stress condition. This leads to the effective 2D constitutive relation (Eq. 9) with a single apparent 2D modulus G_2D*(ω). The 2D and 3D moduli are related by Eq. 10. This study is mainly concerned with determining these 2D and 3D moduli via NEMD simulations of the area change process. This is made possible by applying the stepwise and oscillatory area changes to an equilibrium system and then analyzing the stress responses in the lateral and normal directions. The details of this procedure and the required formula for the analysis are presented in two subsections, “Stepwise strain” and “Oscillatory strain”.

Linear viscoelastic properties of a planar lipid bilayer system, which has a uniaxial symmetry, are characterized by the following constitutive relations (Fung, 1993; Chaikin and Lubensky, 2000):

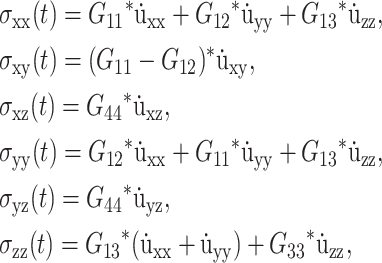(1)

where the symmetry axis is chosen to be in the z direction, σ(t) is the stress tensor, u(t) is the strain tensor with time derivative 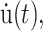and the G_ij(t)'s are five unique relaxation functions and f*g is defined as

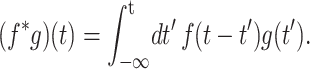(2)

The labeling of G_ij(t) in Eq. 1 follows the convention of Nye (1985). In Eq. 1, the stress tensor σ(t) is the response to the applied strain u(t). Depending on the experimental situation, this choice can be reversed such that u(t) is the response to applied σ(t). The response functions characterizing these two situations (relaxation and creep) are interconvertible if one is known in the entire time domain (Chapter 8 of Tschoegl, 1989). In an isotropic system, G_ij(t′)s are reduced to combinations of the bulk (G_B) and shear (G_S) relaxation functions as follows:

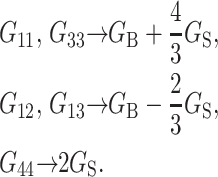(3)

In this article, we are concerned with the isotropic membrane area change and its coupling with the motion normal to the membrane. Thus, we do not consider the shear strain components, and the relevant strain tensor is given by

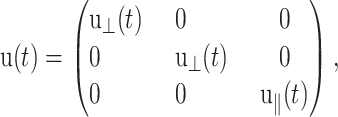(4)

where the z axis is perpendicular to the bilayer membrane. Then, Eq. 1 is simplified to

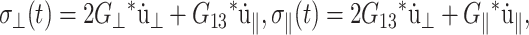(5)

with the following definitions:

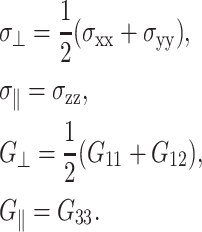(6)

Here, G_⊥ and G_‖ represent the response perpendicular and parallel to the symmetry axis (bilayer normal), respectively, and G₁₃ is the coupling between them. Hereafter, we will refer to G_⊥ as “lateral” or “in-plane”, and G_‖ as “normal” responses (with respect to the bilayer plane). As is usual in the theory of viscoelasticity (Tschoegl, 1989), we take the system at t = 0 as the reference state such that σ(t) = u(t) = 0 for t < 0. This makes it possible to limit our consideration to t ≥ 0. Then, the generalized half Fourier transform (GHFT, see below) of Eq. 5 yields the frequency-domain expressions as

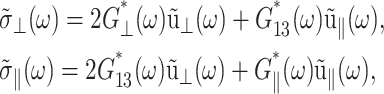(7)

where 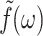is the GHFT of f(t) and G_α*(ω) (α = ⊥, 13, ‖) are complex moduli defined as

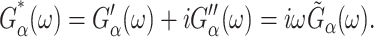(8)

(To ensure the existence of integral transforms, we define 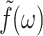as the GHFT, 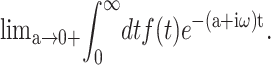For the stepwise strain u_⊥(t) of Eq. 13, 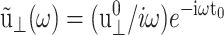and for the sine strain of Eq. 20 with frequency ω₀, · 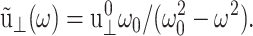A cosine strain with frequency ω₀ would yield 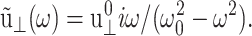See Tschoegl (1989) for details.) Here, 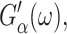the real part of G_α*(ω), is the storage modulus representing the elastic response of the system and 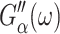is the loss modulus associated with dissipation. 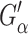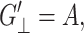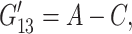corresponds to de Gennes' elastic constants A, B, C for smectic A (de Gennes, 1969; de Gennes and Prost, 1993) as follows: 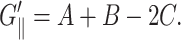Also, the anisotropic viscosity components η_α(ω), given by 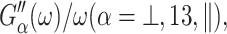are related to the viscosities of a uniaxial system, η₁, ⋯, η₅, defined by Martin et al. (1972): η_⊥ = η₄, η₁₃ = η₅, η_‖ = η₁.

If the area change takes place while the normal pressure is maintained at its equilibrium value 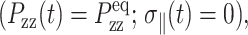Eq. 7 is further simplified to

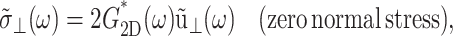(9)

in terms of the apparent 2D complex modulus G_2D*,

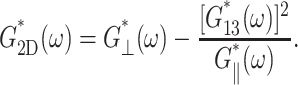(10)

Thus, the apparent 2D viscous (elastic) response depends not only on the 3D viscous (elastic) moduli but also on the 3D elastic (viscous) moduli. The area compressibility modulus K_A is often used to quantify the in-plane elastic properties of membranes (Evans and Needham, 1987). Similarly, the surface viscosity for area change κ_A, defined as the ratio of the lateral tension 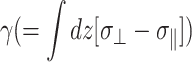to the rate of the relative area change, can be defined (Evans and Hochmuth, 1978; Bloom et al., 1991). In the linear regime and under the condition of zero normal stress, their frequency-dependent generalization is related to G_2D*(ω) as follows:

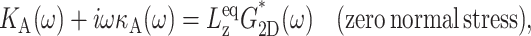(11)

where 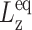is the equilibrium system size normal to the area under consideration.

The apparent thickness compressibility modulus 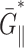under the zero lateral stress condition can also be obtained by setting 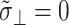in Eq. 7 as follows

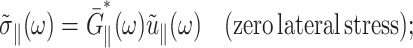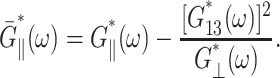(12)

To determine the three moduli (G_⊥, G₁₃, and G_‖) in Eq. 5 (or their frequency-domain equivalents, Eq. 7), we employ two different boundary conditions: i), a constant system size L_z along the normal direction (CLZ), and ii), a zero normal stress (ZNS). Below, we describe both boundary conditions when the stepwise and oscillatory lateral strains are applied.

Stepwise strain

If the system is expanded or contracted instantaneously at t = t₀ and isotropically along the xy plane, u_⊥(t) becomes

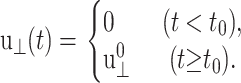(13)

When the system size L_z in the z direction is kept constant during this process (CLZ), 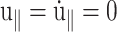and Eq. 5 yields

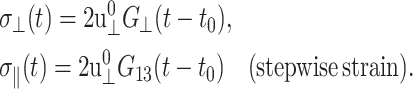(14)

Thus, G_⊥(t) and G₁₃(t) can be directly determined by monitoring the two stress components. On the other hand, if the normal pressure P_zz is maintained at the equilibrium value 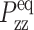(ZNS), the system will adjust L_z from its equilibrium value 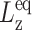in response to the lateral strain u_⊥(t), yielding the normal strain u_‖(t) as

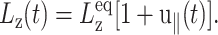(15)

We introduce the ratio ν(t) of u_‖(t) to 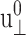in analogy with the Poisson's ratio associated with uniaxial tension (Tschoegl, 1989; Goodwin and Hughes, 2000),

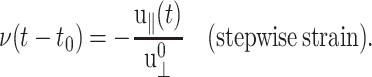(16)

In what follows, ν(t) will be referred to as the biaxial Poisson's ratio. For a general form of u_⊥(t), ν(t) can be defined as a convolution integral, similar to G_α(t),

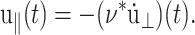(17)

ν(t) is a material function just as the relaxation functions G_α(t). ν(t) increases gradually from an initial value ν_g at t = 0 to its asymptotic value 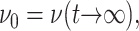which is 2 for an incompressible system. (ν_g can be expressed in terms of the instantaneous relaxation functions at time t = 0 (Tschoegl, 1989). The NEMD simulation results in the “Results” section indicate that ν_g = 0 for the systems studied here.) As will be shown in the section “Responses to oscillatory strain”, the transient behavior of ν(t) is closely related to the coupling of the elastic and viscous components in producing the apparent 2D response under the ZNS condition. In the frequency domain, we obtain

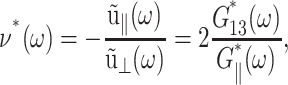(18)

where 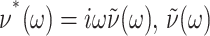is the GHFT of ν(t), and the relations hold for an arbitrary lateral strain 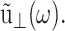However, the second identity above comes from Eq. 7 with 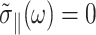and thus is valid only under the ZNS condition. In the static limit, 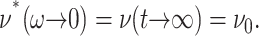In general, the imaginary part of ν*(ω) is negative unlike the loss modulus 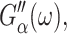which is always positive. This reflects the fact that the stress leads, whereas the normal strain lags, the applied lateral strain (Tschoegl, 1989). Despite the simple relations of Eq. 18, the integral equation relating ν(t) with G_α(t) does not yield a simple solution in the time domain. We also introduce the apparent 2D relaxation function G_2D(t) as the time-domain counterpart of G_2D*(ω). G_2D(t) can be determined from the lateral stress response via the relation

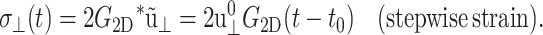(19)

Oscillatory strain

If an oscillatory lateral strain is applied such that

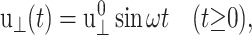(20)

Eq. 5 yields under the CLZ condition

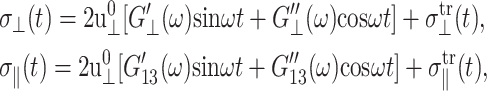(21)

where the first term in each equation is the steady-state oscillatory response 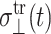and and 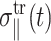denote transient terms present before the steady state is established. (Note that we apply the strain u_⊥(t) at t = 0.) Since we observe that the transient effects are smaller than the uncertainties of the computed moduli already in the first cycle of the applied strain at the highest frequency studied (ω = 251 GHz), we will ignore them hereafter. (If this condition is not met, it is necessary to model the transients explicitly or apply multiple cycles of strain and take the steady-state limit.) Then, G_⊥*(ω) and G_‖*(ω) can be determined from the in-phase and out-of-phase components of the stress responses in Eq. 21. When the same strain is applied under the ZNS condition, the strain in the normal direction, u_‖(t), comes into play. Under the steady-state assumption, we first invoke the following ansatz for u_‖(t),

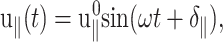(22)

in terms of the undetermined amplitude 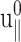and phase shift δ_‖. Equation 22 simply states that, in the steady-state limit, an oscillatory lateral strain will induce an oscillatory normal strain of the same frequency but with a possible phase shift. The constants 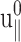and δ_‖ can be determined from the time dependence of L_z using Eqs. 15 and 22. This immediately yields ν*(ω) according to the first identity of Eq. 18,

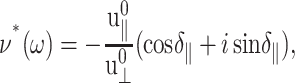(23)

and, in turn, G_‖*(ω) according to the second identity of Eq. 18,

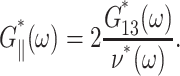(24)

Separately, the frequency-domain effective 2D modulus can be determined from the σ_⊥(t) data under the ZNS condition following the first identity of Eq. 19:

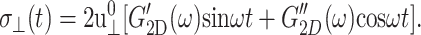(25)

We note that σ_⊥(t) under the ZNS condition is not utilized in determining G_⊥*, G₁₃*, and G_‖* as sketched above. Therefore, the relation between the 3D moduli and G_2D* in Eq. 10 can be used to check the internal consistency of the model employed.

SIMULATION DETAILS

We have performed NEMD simulation of lipid bilayer membranes under the stepwise and oscillatory strains. A similar approach has been taken previously in our group (Ayton et al., 2002), and we present a brief review of the method in the Appendix. Here, we only mention that the NEMD method provides the time-dependent stress profiles under the deformation (strain) of the system. In the following, we present the simulation parameters and details of the systems studied.

We have studied three different systems: i), hydrated phospholipid bilayer membranes composed of DMPC lipids, ii), a dimer of gramicidin A (gA) peptides embedded in the DMPC membrane in its open configuration, and iii), pure liquid water. Equilibrium configurations were generated as necessary from combinations of NVT, NP_nAT, i-NPT and a-NPT simulations. The reference DMPC system (D1) was composed of 64 DMPC lipids and 1312 water molecules in a box with 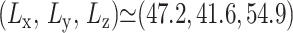Å. This yields the average density of 1.03 g/cm³ and the area per lipid of 61.4 Ų. The reference gA system (g1) contained 1 gA dimer, 88 DMPC, and 2514 water molecules in a box with size ∼(49.3, 59.3, 59.8) Å, giving the same density as the DMPC system. The pure water system contained 1795 water molecules at an average density of 0.995 g/cm³. To study the effects of system size and composition, DMPC systems with four times larger area (D2) and longer L_z (D3 and D4) were also studied. Similarly, a gA system with about a twice larger area containing 1 gA dimer, 184 DMPC, and 4998 water (g2) was also studied. For system D3 and D4, the increased volume was filled with water, resulting in a water concentration of 41.1 and 55.7 wt %, respectively, compared to 35.3 wt % for system D1. By comparison, the water concentration of system g1 and g2 were 41.7 and 41.2 wt %, respectively. Interaction potentials from Jorgensen et al. (1983) (TIP3P for water), Smondyrev and Berkowitz (1999) (for DMPC), and AMBER 94 (for gA, Cornell et al., 1995) were employed.

All simulations were performed at a temperature of 308 K using the Nose-Hoover thermostat with relaxation time τ_T of 0.2 ps. For constant pressure simulations, the barostat relaxation time τ_P of 0.25 ps was employed. We also used τ_P of 1.0 ps in part of simulations to see if the barostat relaxation interferes with the stress responses. Periodic boundary condition was imposed, and the long-range electrostatic interactions were taken into account by the smooth particle-mesh Ewald method as implemented in DL_POLY. Other parameters of the simulation are as follows: a time step size of 2 fs, cutoff distances for screened Coulomb and Lennard-Jones interactions of 7.0 Å, and a precision of bond constraints (SHAKE) of 1.0 × 10⁻⁶. Because we only consider homogeneous applied strains, all viscoelastic moduli below should be regarded as the zero-wavenumber limit apart from the constraints associated with the periodic boundary condition.

RESULTS

Since our approach relies heavily on the analyses of the stress tensor, it is important to first understand its behavior at equilibrium. The equilibrium simulations to generate the NEMD initial configurations show that the diagonal components of the stress tensor are close to zero, as was intended by the choice of barostat parameters. However, for the membrane systems, the lateral stress tensor depends sensitively on the area and it was found that the average lateral stress from the NP_nAT simulation is sometimes as large as 0.05 kbar even if the area is chosen from the a-NPT runs. Therefore, all the NEMD initial configurations should be regarded as having zero lateral stress with the maximum uncertainty of ∼± 0.05 kbar. The root mean-square fluctuations in stress are found to be anistropic: ∼0.3 kbar for σ_xx and σ_yy and 0.4–0.5 kbar for σ_‖ for systems D1 and g1. In contrast, the pure water system had isotropic stress fluctuations of ∼0.4 kbar. Results from larger systems (D2–D4 and g2) confirmed that this fluctuation decreases as the inverse square root of system size. We now turn to the NEMD results.

Responses to stepwise strain

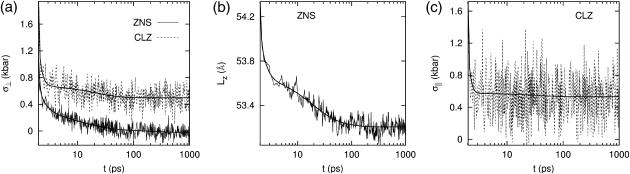
The response of the DMPC system D1 to the stepwise strain is shown in Fig. 1, a–c. In the simulation, the abrupt jump in strain was approximated by a linear increase from t = 1.95 to 2.00 ps and 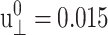was used (cf. Eq. 13). This corresponds to the expansion of the membrane area by ∼3%. The raw data used in the plots were averages over 16 independent NEMD runs. First, Fig. 1 a compares the lateral stresses under the ZNS and CLZ conditions. For the ZNS system, the large initial stress of ∼2.6 kbar decays to <1 kbar within 0.1 ps, and then slower decay mechanisms take over. There was no noticeable decay after 500 ps according to block averages, and the asymptotic stress measured by the average over the 500–1000 ps period was −0.02 kbar, indicating that the lateral stress completely relaxes to equilibrium after ∼500 ps. The initial stress response under the CLZ condition is similar. However, its asymptotic behavior is quite different, with a residual stress of 0.50 kbar. The latter value will be close to the new equilibrium lateral pressure corresponding to the increased volume under the CLZ condition. Similar decay is observed for L_z under the ZNS condition in Fig. 1 b. We note that the decrease in L_z almost completely compensates for the stepwise increase in lateral area, resulting in the final volume after 1 ns within 0.1% of the initial value. Therefore, the DMPC membrane behaves as an incompressible system at nanosecond timescales. Fig. 1 c shows the normal stress response under the CLZ condition with a relaxation behavior similar to the lateral stress under the same condition. The average normal stress for the 500–1000 ps period was 0.53 kbar.

FIGURE 1.

Responses of the reference DMPC system to the stepwise lateral strain (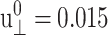). (a) The lateral stresses under the ZNS (thin solid line) and CLZ (short-dashed line) conditions. (b) The system size in the normal direction under the ZNS condition. (c) The normal stress under the CLZ condition. The thick smooth solid lines in each plot are numerical fit to the multi-exponential function (Eq. 26).

We have modeled the decay of all three stresses in Fig. 1 with a multi-exponential function of the form

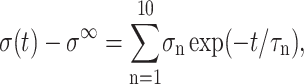(26)

where σ^∞ is the asymptotic stress, and similarly for L_z(t). A stable and reproducible fit could be obtained by excluding σ^∞ and 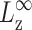from the fitting parameter space. These asymptotic values were separately determined as the average over the 500–1000 ps period and supplied to the fitting program. The lmder routine from the minpack package was used in the numerical fit (Garbow et al., 1980). The fit results, shown in Fig. 1 as thick solid lines, were then converted to relaxation functions and biaxial Poisson's ratio using Eqs. 14–16. They are summarized in Table 1 for the water, DMPC (D1), and gA (g1) systems. Also shown there is the apparent 2D response to the stepwise compression, 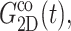with 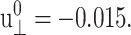We first note that the ultrafast components (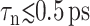) there carry uncertainties due to the finite lateral strain ramp-up time of 0.05 ps and the barostat relaxation time τ_P of 0.25 ps for the normal pressure under the ZNS condition. In addition, the asymptotic values G⁰ and ν₀ carry uncertainties related to the equilibrium stresses and L_z, respectively. For example, as mentioned above, the equilibrium stress components are uncertain by ≲0.05 kbar about its intended average of zero and it is transferred to Gⁿ as 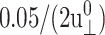or 1.67 kbar. The actual asymptotes of G_2D (−0.704 and −0.203 kbar for the DMPC and gA systems, respectively) are well within this uncertainty. Similarly, ν₀ is affected by the uncertainty in 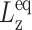and thus slightly larger than 2 for all three systems in Table 1. Transient terms with 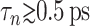are not affected by these uncertainties. With this caution, we note the following points: i), the stress relaxation of water is biexponential with the fast mode corresponding to one-half cycle of water librational motion and the slow mode twice faster than the single-molecule dipole relaxation (Jeon et al., 2003); ii), the distribution of relaxation times are wider for the DMPC and gA systems and the slowest modes extend to 100–200 ps; iii), 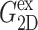has more decay components than 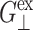or 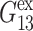but is comparable to ν^ex—whereas 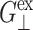and 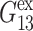are determined from the lateral stress alone, 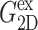and ν^ex have contributions from both lateral and normal responses; iv), ν₀ is close to 2 for all three systems, i.e., they are incompressible in the static limit, although it takes ∼1 ps and 100–200 ps for the water and membrane systems, respectively, to achieve that limit; and v), the response to a lateral expansion, 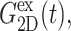is smaller than the response to a lateral compression, 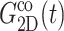—this difference is likely due to the excluded volume effect important only under compression. Also, 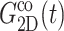has an additional slow decay component with τ ∼ 2 ns. The difference between the expansional and compressional responses is further demonstrated in Fig. 6 in the frequency domain via a GHFT of 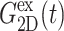and 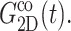There, the much larger elastic response to compression than to expansion is clearly seen. On the other hand, the difference in the loss modulus is smaller and more complicated than in the elastic modulus.

TABLE 1.

Relaxation times and their amplitudes in the multi-exponential approximations to the time-domain 2D and 3D relaxation functions and the biaxial Poisson's ratio

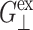
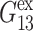
					νex
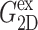
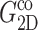
n	Gn	τn	Gn	τn	νn	τn	Gn	τn	Gn	τn
Water
0	-	-	-	-	2.18	-	0.117	-	-	-
1	-	-	-	-	−1.63	0.0395	98.3	0.0238	-	-
2	-	-	-	-	−0.0237	0.401	3.51	1.82	-	-
3	-	-	-	-	−0.422	1.22	-	-	-	-
DMPC
0	16.6	-	17.7	-	2.06	-	−0.704	-	−0.704	-
1	76.6	0.0145	70.3	0.0157	−0.0723	0.00347	69.1	0.00933	71.6	0.00811
2	19.6	0.219	20.2	0.222	−0.530	0.0805	10.6	0.151	24.4	0.177
3	5.16	0.561	1.43	34.3	−0.433	0.607	8.77	0.854	5.17	1.22
4	5.84	22.1	-	-	−0.421	16.9	3.27	4.05	4.31	9.72
5	-	-	-	-	−0.121	57.6	6.05	16.9	4.05	10.4
6	-	-	-	-	-	-	1.58	201	4.98	2080
gA
0	15.3	-	15.9	-	2.03	-	−0.203	-	-	-
1	79.2	0.0106	80.4	0.0188	−0.542	0.105	88.6	0.00959	-	-
2	19.7	0.225	9.85	0.110	−0.287	1.14	11.0	0.397	-	-
3	4.44	4.84	3.30	20.1	−0.382	3.11	3.46	3.98	-	-
4	1.96	121	-	-	−0.0723	52.3	3.76	4.47	-	-
5	-	-	-	-	−0.125	276	2.94	95.7	-	-

The superscripts “ex” and “co” denote responses to expansion and compression, respectively. 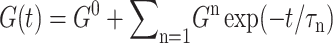and 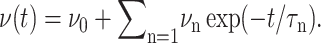Units: Gⁿ in kbar and τ_n in picoseconds.

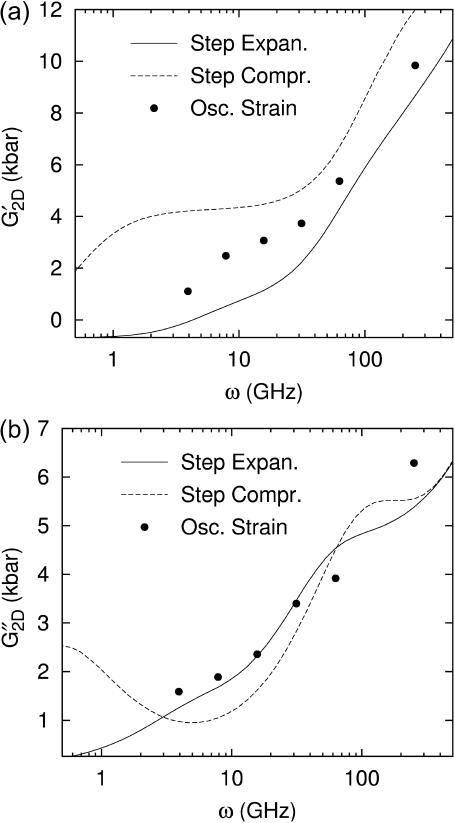
FIGURE 6.

Comparison of the time- and frequency-domain NEMD results for the apparent 2D viscoelastic moduli of the DMPC system (D1). The GHFT of the expansional relaxation function 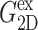(solid line) and the GHFT of the compressional relaxation function 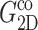(dashed line) are shown (cf. Table 1). The solid circles are from the oscillatory strain NEMD (cf. Table 3).

The observed relaxation modes for the membrane systems mainly reflect internal motions of lipid molecules. For example, the subpicosecond modes likely arise from molecular vibrations of lipid (Mendelsohn and Snyder, 1996) and intermolecular vibrations of water and lipid. At longer timescales, possible molecular motions contributing to the observed stress relaxations include the headgroup rotation (correlation time τ ∼ 400–700 ps from ³¹P NMR of DMPC (Dufourc et al., 1992)), choline segment reorientation (τ ∼ 70–200 ps from molecular dynamics (MD) simulation of dioleoylphosphatidlcholine (Mashl et al., 2001)), acyl chain isomerization (τ ∼ 7–48 ps from MD of DMPC and dipalmitoylphosphatidylcholine (DPPC) (Venable et al., 1993; Lindahl and Edholm, 2001); ∼10 ps from ²H and ¹³C NMR of DPPC (Brown et al., 1983; Weisz et al., 1992)). In addition, the rotation of lipids about its long axis (τ = 2.6 ns from MD of DPPC (Lindahl and Edholm, 2001); τ ∼ 1–2 ns from ²H and ³¹P NMR of DMPC (Weisz et al., 1992; Dufourc et al., 1992; Nevzorov et al., 1998)) seems to be responsible for the observed 2-ns component of the compressional relaxation.

Responses to oscillatory strain

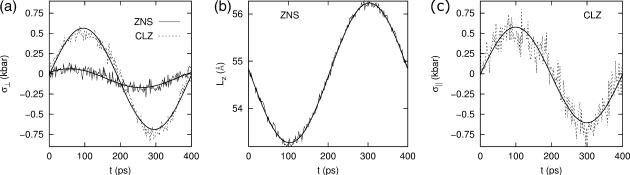
We have carried out NEMD simulations applying the oscillatory lateral strain of Eq. 20 with different 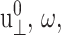and boundary conditions in the normal direction (ZNP and CLZ). The resulting stress responses σ_⊥(t) and σ_‖(t), and the system size variation L_z(t), give us full information on the relevant viscoelastic moduli as described in the section, “Oscillatory strain”. Fig. 2 shows responses from the reference DMPC system (D1) with 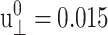and the period of oscillation T = 2π/ω = 400 ps. σ_⊥(t) obtained with two different boundary conditions are compared in Fig. 2 a. We observe the lateral stresses generally following the applied strain but with a phase shift, as expected from a viscoelastic material. However, the two boundary conditions yield quite different responses in terms of the magnitudes of the amplitude and phase shift. The ZNS data provide the apparent 2D moduli G_2D*(ω) via fitting to Eq. 25. The CLZ data, on the other hand, give G_⊥*(ω) after fitting to the first identity of Eq. 21. The fit results are shown in the figure as thick solid lines. As mentioned in the section “Oscillatory strain”, the steady state is established quickly and the agreement of the fit with the data is already excellent in the first cycle. The variation of L_z under the ZNS condition is shown in Fig. 2 b, together with its numerical fit to the following expression obtained from Eqs. 15 and 22:

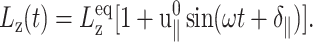(27)

As noted in the section “Stepwise strain”, the fit produced a negative phase shift δ_‖ and, thus, negative imaginary part Im[ν*] of the biaxial Poisson's ratio (cf. Table 2). The excellent agreement between the data and fit justifies the ansatz of Eq. 22. Fig. 2 c shows the normal stress response under the CLZ condition. A numerical fit of the data to the second member of Eq. 21 (solid line) determines G₁₃*(ω). This, together with 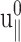and δ_‖, yields G_‖*(ω) according to Eqs. 23 and 24.

FIGURE 2.

Responses of the reference DMPC system to the sine strain (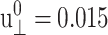) with period T = 400 ps. (a) The lateral stresses under the ZNS (thin solid line) and CLZ conditions (short-dashed line). (b) The system size in the normal direction under the ZNS condition. (c) The normal stress under the CLZ condition. The raw data were obtained by averaging results of 16 independent trajectories. The smooth solid lines in each plot are numerical fits to phase-shifted sine functions. See text for details.

TABLE 2.

Three-dimensional viscoelastic moduli and biaxial Poisson's ratio of the water, DMPC, and gA systems from NEMD simulations with oscillatory strain ( and varying period T)

T	G′⊥	G″⊥	G′13	G″13	G′‖	G″‖	Re[ν*]	Im[ν*]
Water
25	16.55 (0.73)	1.43 (0.97)	16.68 (1.23)	1.01 (1.29)	16.05 (0.74)	2.50 (1.30)	2.037 (0.104)	−0.192 (0.163)
100	16.77 (0.41)	0.29 (0.61)	17.18 (0.93)	− 0.04 (0.39)	17.01 (0.88)	0.40 (0.20)	2.020 (0.045)	−0.052 (0.019)
400	16.75 (0.56)	0.14 (0.25)	16.89 (0.69)	− 0.08 (0.05)	16.86 (0.79)	− 0.05 (0.13)	2.005 (0.025)	−0.003 (0.014)
DMPC
25	26.17 (1.59)	5.06 (1.29)	21.78 (1.75)	3.23 (2.11)	27.39 (2.79)	8.50 (2.79)	1.515 (0.088)	−0.239 (0.108)
100	23.10 (1.32)	2.96 (0.85)	20.69 (1.76)	1.86 (0.94)	24.10 (2.34)	4.89 (1.85)	1.676 (0.083)	−0.185 (0.106)
400	20.83 (1.30)	1.55 (0.63)	19.72 (1.66)	0.18 (0.55)	21.86 (1.82)	1.43 (1.34)	1.797 (0.090)	−0.100 (0.072)
1600	19.93 (1.27)	0.88 (0.34)	19.64 (0.98)	0.33 (0.51)	20.67 (1.46)	1.24 (0.66)	1.898 (0.063)	−0.080 (0.047)
gA
25	24.65 (1.07)	4.80 (0.75)	21.92 (2.05)	1.78 (1.42)	27.43 (2.80)	5.82 (2.42)	1.553 (0.043)	−0.201 (0.060)
100	21.34 (1.19)	2.64 (0.73)	19.98 (1.14)	1.32 (0.90)	22.84 (1.46)	3.71 (1.48)	1.722 (0.075)	−0.163 (0.072)
400	20.11 (0.90)	0.99 (0.45)	19.31 (1.07)	0.49 (0.62)	21.05 (1.28)	1.66 (0.85)	1.828 (0.068)	−0.099 (0.059)
1600	19.23 (0.95)	0.79 (0.27)	18.98 (0.98)	0.23 (0.49)	20.27 (1.01)	0.75 (0.82)	1.870 (0.053)	−0.048 (0.058)

The averages of data from multiple trajectories (4 for water, 16 for DMPC, and 8–19 for gA) are shown. The SD are indicated in parentheses. Units: T in picoseconds and G in kilobars.

The results of the analyses are summarized in Tables 2 and 3 and Figs. 3–5 for the water, DMPC (D1), and gA (g1) systems. From the 3D moduli in Table 2, we first note that each 3D storage modulus is about an order of magnitude larger than the corresponding loss modulus. Also, the membrane systems show a substantial frequency dispersion unlike the water system (cf. Fig. 3). The 3D moduli in Table 2 can be tested against various stability conditions: i), elastic stability requires G′_⊥ ≥ 0 and G′_⊥G′_‖ ≥ (G′₁₃)², (Nye, 1985); ii), hydrodynamic stability requires 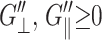and 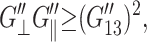(Martin et al., 1972); and iii), from the fact that the normal strain would lag the applied lateral strain (cf. section “Stepwise strain”) and vice versa, G″₁₃/G′₁₃ < G″_‖/G′_‖ and G″₁₃/G′₁₃ < 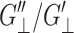(Tschoegl, 1989). These conditions are satisfied for all entries in Table 2 except for the water system. We note that, for liquid water, the shear elasticity G′_S is expected to be very small and thus all 3 3D elastic moduli will become identical to each other according to Eqs. 3 and 6. The small differences among the three elastic moduli can then be regarded as numerical errors, leading to the violation of the above conditions. This, together with the weak frequency dependence of water elastic moduli, suggests that the static limit of water bulk modulus G′_B is ∼17 kbar. Thus, the TIP3P water model seems to underestimate the static bulk storage modulus compared to the experimental value of 22.3 kbar at 303 K (Lide, 2002). Similarly, the loss moduli of water are estimated as G″_B ∼ 0.2 and 0.7 kbar and G″_S ∼ 0.2 and 1.9 kbar at 15.7 and 251 GHz, respectively (cf. Eq. 3). Although these are less reliable than the elastic moduli, the loss moduli at 15.7GHz yield viscosities of the same order of magnitude as the experimental static bulk (2.13 × 10⁻³ Pa s) and shear (7.97 × 10⁻⁴ Pa s) viscosities (Guo and Zhang, 2001).

TABLE 3.

Apparent 2D viscoelastic moduli determined directly from the lateral stress response under the ZNS condition (entry A) and the predicted values from the 3D moduli according to Eq. 10 (entry B)

	A		B
T	G′2D	G″2D	G′2D	G″2D
Water
25	0.40 (0.64)	2.19 (0.47)	−0.54 (1.95)	1.90 (2.44)
100	0.06 (0.59)	0.54 (0.39)	−0.58 (1.11)	0.77 (0.20)
200	−0.40 (0.14)	0.25 (0.26)	-	-
400	−0.04 (0.26)	0.22 (0.24)	−0.18 (0.38)	0.25 (0.32)
800	−0.02 (0.00)	0.17 (0.16)	-	-
DMPC
25	9.84 (1.32)	6.29 (1.26)	9.29 (2.39)	5.16 (1.88)
100	5.37 (1.07)	3.92 (1.19)	5.59 (1.33)	3.30 (1.94)
200	3.73 (0.65)	3.40 (0.70)	-	-
400	3.07 (0.82)	2.36 (0.77)	3.09 (1.35)	2.42 (0.96)
800	2.48 (0.78)	1.89 (0.82)	-	-
1600	1.11 (0.64)	1.59 (0.41)	1.29 (1.10)	1.36 (0.62)
gA
25	8.04 (1.13)	5.95 (1.28)	7.43 (0.90)	5.58 (1.17)
100	4.25 (0.73)	3.28 (0.84)	4.01 (1.21)	3.14 (0.93)
200	3.35 (0.70)	2.80 (0.74)	-	-
400	2.29 (0.47)	1.92 (0.51)	2.43 (1.14)	1.49 (0.73)
800	1.43 (0.61)	1.37 (0.38)	-	-
1600	1.18 (0.53)	1.04 (0.42)	1.46 (0.68)	1.02 (0.68)

The amplitude of lateral strain 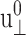was 0.015 in all cases. All entries are averages of data from multiple trajectories. SD are indicated in parentheses. 8–19 independent trajectories were used in all entries except for T = 200 and 800ps, where 2–4 trajectories are used. Units: T in picoseconds and G in kilobars.

FIGURE 3.

Frequency dependence of 3D viscoelastic moduli of the water (solid line), DMPC (long-dashed line), and gA (short-dashed line) systems. The data are from Table 2, and the SD there are shown as error bars.

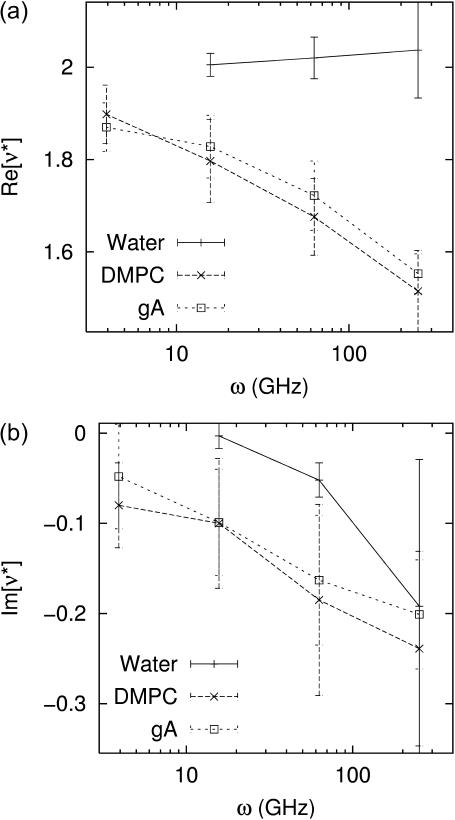
FIGURE 4.

Frequency dependence of the biaxial Poisson's ratio of the water (solid line), DMPC (long-dashed line), and gA (short-dashed line) systems. (a) The real part and (b) the imaginary part are shown. The data are from Table 2.

FIGURE 5.

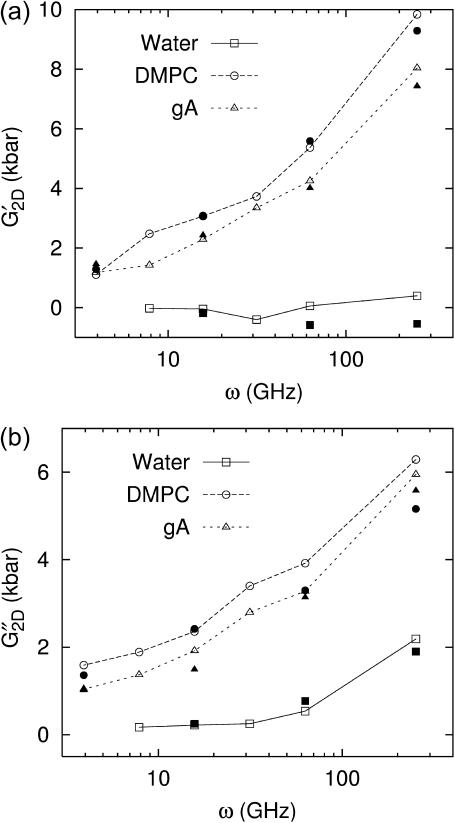
Frequency dependence of the apparent 2D (a) storage and (b) loss moduli of the water (solid line), DMPC (long-dashed line), and gA (short-dashed line) systems. The open symbols connected with lines are direct fit results (entry A of Table 3). The prediction from 3D moduli (entry B of Table 3) is shown as solid symbols with the same shape.

The DMPC and gA systems exhibit a quite different viscoelastic behavior (Fig. 3): both the storage and loss moduli are significantly larger and the frequency dispersion is stronger than those for liquid water. According to Eqs. 3 and 6, the criterion for anisotropy is 2(G′_⊥ − G′₁₃)/(G′_‖ − G′₁₃) ≠ 1 and similarly for the loss modulus. For the elastic modulus, this ratio decreases with increasing period—the membranes become more compressible laterally than normally in the static limit. On the other hand, the ratio for the loss modulus did not show any consistent behavior as a function of frequency. Fig. 3 also shows that the gA system exhibits consistently smaller moduli than the DMPC system. However, this difference cannot be simply attributed to the presence of gramicidin A because the gA system has ∼5 Å thicker water layer than the DMPC system. This point will be further discussed below in relation with the system-size dependence. The biaxial Poisson's ratio in Table 2 and Fig. 4 also reflects the different responses between the water and lipid systems. For water, the real part Re[ν*] exhibits the asymptotic value ν₀ = 2 already at the highest frequency studied (ω = 251 GHz). On the other hand, for the DMPC and gA systems, this limiting value is not achieved even at the lowest frequency of 3.93 GHz. This is consistent with the time-domain results in the section “Responses to stepwise strain”. As expected, the negative Im[ν*], which represents the delay of the L_z response to the lateral strain, tends to zero as ω decreases.

The apparent 2D moduli in Table 3 and Fig. 5 reveal quite different aspects of the water and membrane systems. First, assuming that the shear elastic modulus G′_S is negligible for water, it can be shown that G′_2D ∼ 4(G″_S)²/G′_B ∼ 0 and G″_2D ∼ 3G″_S—the bulk viscosity of water does not come into effect under the ZNS condition. Therefore, the small negative G′_2D values for water in Table 3 are likely due to numerical errors. On the other hand, G″_2D for water directly yields the shear viscosity of water. At the largest period of T = 800 ps, we obtain the shear viscosity η_S ∼ G″_2D/(3ω) ∼ 7.2 × 10⁻⁴ Pa s, in excellent agreement with the static experimental value mentioned previously. For the membrane systems, the 2D moduli are much larger than the water values. Also, G′_2D are at least several times smaller than the 3D storage moduli and G″_2D are somewhat larger than any of the 3D loss moduli. As a result, G′_2D and G″_2D are now of comparable magnitude. Therefore, the lateral stress response of the membrane system becomes about as equally viscous as it is elastic, if we allow the normal system size to adjust to lateral area change (the ZNS condition). However, we note that this does not change the validity of the previous elastic modulus calculations (Ayton et al., 2002) thanks to the linear independence of the viscous and elastic responses to the oscillatory strain.

Turning to the frequency dependence of apparent 2D moduli in Fig. 5, the good agreement between the predicted 2D moduli from Eq. 10 (entry B in Table 3 and solid symbols in Fig. 5) and the direct values (entry A in Table 3 and open symbols in Fig. 5) show that the anisotropic linear viscoelastic model employed here is internally consistent. This can be better understood by the following analysis: since the 3D loss moduli are about an order of magnitude smaller than the storage moduli, we can ignore the terms with the highest order in loss moduli in the right-hand side of Eq. 10 and obtain

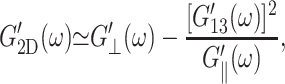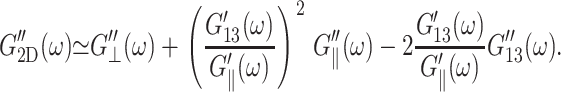(28)

Thus, G′_2D, given as the difference between two terms of similar magnitude, is much smaller than the 3D storage moduli. On the other hand, G″_2D is determined from three terms of similar magnitude. In both cases, the anisotropy of three storage and loss moduli plays a crucial role in determining the 2D moduli. The stability conditions mentioned above guarantee that G′_2D and G″_2D are finite and positive, as can be seen in Table 3. Conversely, the good prediction of G″_2D in Table 3 and Fig. 5 indicates that the loss moduli in Table 2 are more reliable than their large SD suggests. One important consequence of the large 2D viscous effect is that the energy loss due to dissipation is of comparable magnitude to the elastic energy stored during area change since the ratio of the two is given by 4πG″_2D/G′_2D (Goodwin and Hughes, 2000).

In principle, the response to the oscillatory strain gives the same information as that to the stepwise strain. However, as mentioned above, the latter response is quite different between compression and expansion, whereas the former is an average over the two. This is highlighted in Fig. 6: at a given frequency, the elastic moduli from oscillatory NEMD (solid circles) are bounded by the compressional and expansional moduli determined from stepwise NEMD. On the other hand, the viscous moduli from the oscillatory NEMD are much closer to both the stepwise NEMD results.

We can compare the computed moduli of the membranes with a few existing experimental results. First, from the Brillouin scattering measurement of sound velocity, LePesant et al. (1978) reported G′_⊥ ∼ G′_‖ = 22 kbar and G′_2D below their detection limit of 5 kbar at T ∼ 100 ps for a multilamellar DPPC at 25 wt % water in the liquid crystalline phase. Second, El-Sayed et al. (1986) used the laser-induced phonon spectroscopy to obtain G′_⊥ = 22 kbar and η₁₁ ≡ G″₁₁/ω = 0.016 Pa s (cf. Eq. 1) at T ∼ 1 ns for a fully hydrated multilamellar DPPC system at 47.5°C. We note that DPPC bilayer has a gel-to-liquid-crystal phase transition temperature of 41°C, compared to 24°C for DMPC. Thus, the good agreement of these results with our DMPC moduli at 35°C is encouraging. Also, Yamamoto et al. (1992) report the thickness compressibility modulus 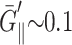kbar (cf. Eq. 12) in the static limit for multilamellar hydrated DMPC in the liquid-crystalline L_α phase at 39.5°C and relative humidity of 82%. This value is about an order of magnitude smaller than our result of 1.3 kbar at T = 1600 ps calculated from data in Table 2. Incidentally, Yamamoto et al.'s result at lower humidity (∼1 kbar at 40.7°C and relative humidity of 54%), which they attributed to the more ordered L_β′ phase, is much closer to our result. We believe that this agreement is fortuitous and our approach will yield closer to 0.1 kbar at lower frequencies once the slower relaxation modes are taken into account. See the “Discussion” section for further discussions on the possible relaxation modes not captured in this study and the static limits of the viscoelastic moduli.

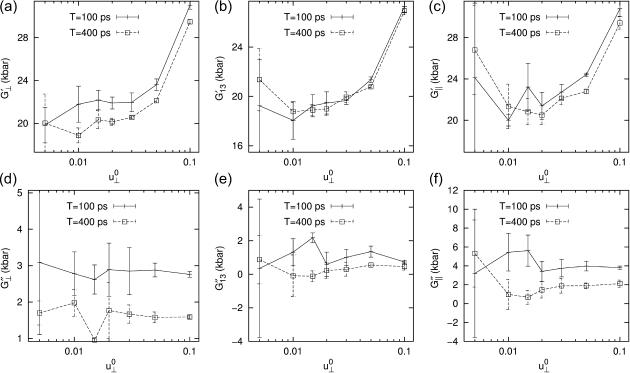
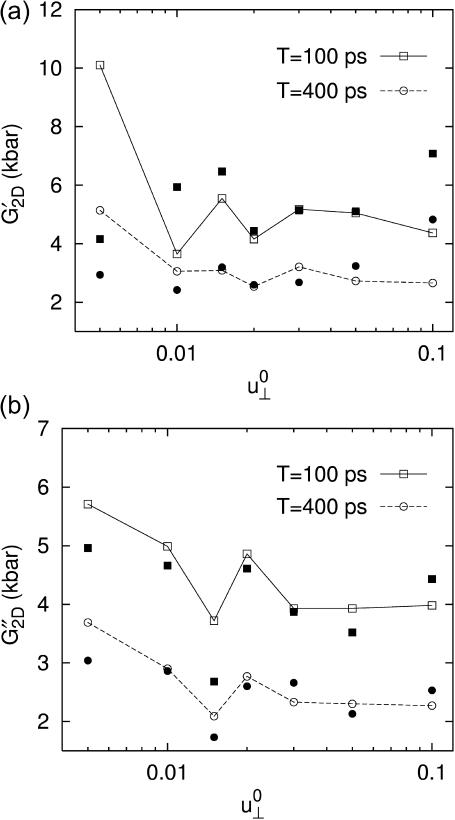
The results presented above show that, under the applied lateral strain, the membrane system behaves as a linear viscoelastic material with anisotropy and frequency dispersion. To understand the extent to which the linear model is valid, we have repeated the calculations for a smaller set of configurations and frequencies with varying strain amplitude (see Figs. 7 and 8 for the results from the DMPC system D1.). We first note that the smallest amplitude employed (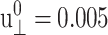) suffers from noise, as indicated by its large SD, and will be disregarded. With this provision, the 3D storage moduli for the DMPC system in Fig. 7 remain fairly constant up to 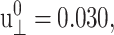corresponding to area change of ∼6%, and then begin to increase at larger amplitudes. That figure also shows the SD decreasing with increasing amplitude. On the other hand, the 3D loss moduli are largely independent of the amplitude in its entire range. We therefore conclude that the 3D elastic and viscous behaviors are linear up to 6% and 20% changes in area, respectively. The apparent 2D moduli from system D1 in Fig. 8 are even less sensitive to 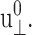This indicates that the effects of large lateral strain perturbations are relieved by the interplay of the lateral and normal motions and, as a result, the lateral stress response remains linear at higher amplitude. In this context, the large difference between the direct and predicted G′_2D of the DMPC system at 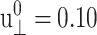(the right-most data points in Fig. 8 a) probably signals the breakdown of the linear model for the full 3D response. We mention here that the gA system (g1) exhibits a similar behavior (not shown).

FIGURE 7.

Strain amplitude dependence of the frequency-domain 3D moduli of the DMPC system. Results with two different periods, T = 100 ps (solid line) and 400 ps (dashed line), are shown. The averages of data from four independent trajectories are shown.

FIGURE 8.

Strain amplitude dependence of the apparent 2D (a) storage and (b) loss moduli of the DMPC system. Results with two different periods, T = 100 ps (solid line) and 400 ps (dashed line), are shown. The open symbols connected with lines are direct fit results. The prediction from 3D moduli is shown as solid symbols with the same shape. All entries are averages of data from four independent trajectories.

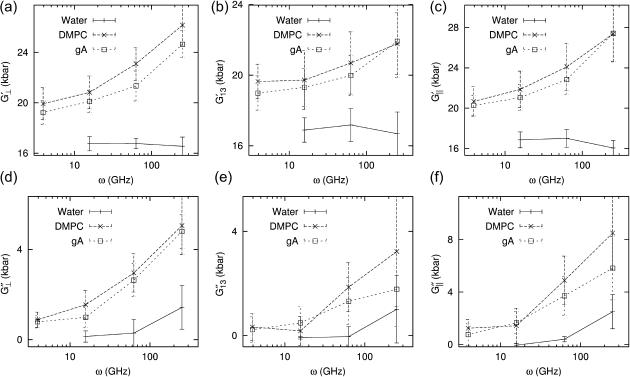
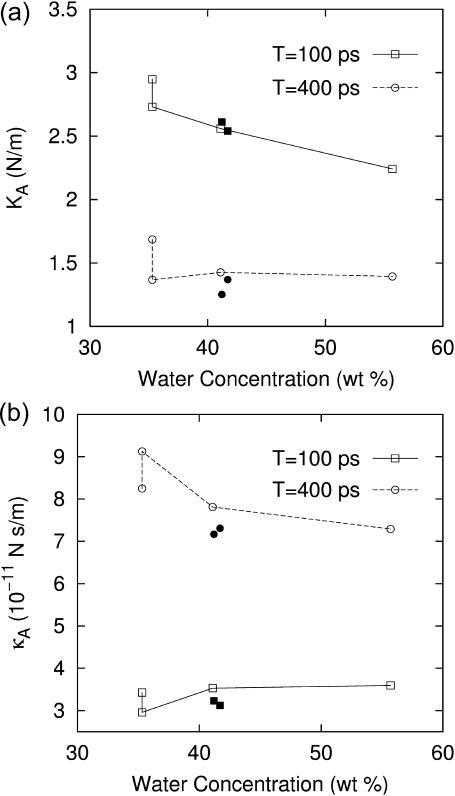
We next turn to the system size dependence of the viscoelastic properties. First, Table 4 shows that the systems with larger area but with the same L_z (D2 and g2) produce 2D moduli comparable to their reference values (D1 and g1). On the other hand, the DMPC systems with larger L_z (D3 and D4) produce significantly smaller moduli. This difference can be attributed to the stoichiometric effect arising from the thicker water layer of systems D3, D4, and g2. However, we cannot rule out the effects arising from the modified lipid structure and interaction due to higher hydration. To resolve this, we consider the area compressibility modulus K_A and surface viscosity κ_A (cf. Eq. 11). Because these quantities are defined in terms of the lateral tension, the direct effect of isotropic water layer is largely eliminated, and any observed dependence on water concentration can be attributed to the structural modification of the bilayer region. They are plotted in Fig. 9 for all systems studied as a function of the water concentration. First of all, we note that K_A and κ_A show much weaker dependence on water concentration than G*_2D in Table 4. The 4 DMPC systems in Fig. 9 (open symbols connected with lines) show a sign of decreasing modulus with increasing water content, especially for K_A at T = 100 ps and κ_A at T = 400 ps. However, κ_A at T = 100 ps is virtually independent of water concentration. Overall, the increase in water concentration from 35% (D1) to 56% (D4) seems to reduce the elasticity of bilayers by ∼20% and the viscosity by <10%. Also included in Fig. 9 are values for the two gA systems (g1 and g2) with almost identical water content (solid symbols). For K_A, they show slightly smaller values than the DMPC system at T = 400 ps but no difference at T = 100 ps. In contrast, κ_A for the gA systems are distinctly smaller by ∼10% at both T. Thus, we conclude that the inclusion of gramicidin A at the mole fraction of 0.5–1% reduces the area viscosity by a small degree (≲10%) and has a negligible effect on the bilayer elasticity.

TABLE 4.

System size dependence of the apparent 2D viscoelastic moduli ()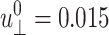

			T = 100 ps		T = 400 ps
System		fw	G′2D	G″2D	G′2D	G″2D
DMPC
D1	54.9	35.3	5.37 (1.07)	3.92 (1.19)	3.07 (0.82)	2.36 (0.77)
D2	54.5	35.3	5.01 (0.48)	3.41 (0.49)	2.51 (0.41)	2.63 (0.15)
D3	58.7	41.1	4.36 (1.37)	3.78 (0.58)	2.43 (0.25)	2.09 (0.28)
D4	83.0	55.7	2.70 (0.33)	2.72 (0.39)	1.68 (0.27)	1.38 (0.40)
gA
g1	59.8	41.7	4.25 (0.73)	3.28 (0.84)	2.29 (0.47)	1.92 (0.51)
g2	59.9	41.2	4.36 (0.62)	3.39 (1.36)	2.09 (0.36)	1.88 (0.20)

The systems are: the reference DMPC (D1), four times the area (D2), 7% larger L_z (D3), 51% larger L_z (D4), the reference gA (g1), and twice the area (g2). f_w is the water concentration in wt %. The reference system data (D1 and g1) are averages over 16–19 independent trajectories from Table 3. For the larger systems, averages of data from four independent trajectories are shown. SD are indicated in parentheses. Units: L_z in angstroms, f_w in weight percent, and G in kilobars.

FIGURE 9.

Plots of (a) the area compressibility modulus K_A and (b) the surface viscosity for area change κ_A as a function of water concentration of the system. Results with two different periods, T = 100 ps (solid line) and 400 ps (dashed line), are shown. The four connected open symbols correspond to the DMPC systems D1–D4, from left to right. The solid symbols of the same shape represent the gA systems g1 and g2. The data were obtained from Table 4 using Eq. 11.

To assess the effects of the thermostat and barostat on the calculated viscoelastic properties, we have carried out additional NEMD simulations with four independent trajectories using different extended system parameters. First, adiabatic simulations with τ_T ≥ 10 ns yield G′_2D and G″_2D that are 27 and 6% smaller, respectively, than the corresponding isothermal values at period T = 100 ps, and 8 and 13% smaller at T = 400 ps. Thus, it seems that the Nose-Hoover thermostat somewhat increases the viscoelastic moduli. This is apparently at odds with Evans and Holian (1985), who show that Nose-Hoover thermostated NEMD produces the linear susceptibilities identical to the adiabatic ones in the thermodynamic limit. It is possible that the number of adiabatic trajectories (four) is not sufficient and its full resolution requires a further study. However, the observed differences are within SD of the average values and does not change the semiquantitave and qualitative pictures presented above. Similarly, the change in barostat relaxation time does not affect the response significantly in the studied frequency range: with τ_P = 1 ps instead of 0.25 ps, G′_2D and G″_2D were <10% different from the standard results at T = 25 ps and the difference was even smaller at T = 100 ps.

Major findings of this study can be summarized as follows:

1. The lipid bilayer membranes behave as a viscoelastic material with anisotropy when stretched or compressed laterally on the nanosecond timescale.

2. The stress response is significantly larger under the compression of membrane area than under expansion. Also, the membrane response is much larger and slower than the response of liquid water.

3. Membranes behave as an incompressible system on the nanosecond timescale, adjusting their thickness in response to the area change. However, the thickness readjustment takes 100–200 ps, and this delay produces a large viscous modulus comparable in magnitude to the elastic modulus.

4. The timescales of the membrane response correlate well with those of the internal or individual motions of lipid molecules determined experimentally or from simulations.

5. The membrane stress response is linear up to 20% change in the area, if the membrane thickness is allowed to readjust accordingly.

6. The multi-exponential model (generalized Maxwell model) provides an excellent description of the membrane viscoelastic behavior. It produces a good fit of the time-dependent stress responses, and the viscoelastic moduli thus obtained are consistent with the direct frequency-domain simulation results.

DISCUSSION

Since our NEMD study captures stress relaxation in the nanosecond or shorter timescales, the question may arise as to the existence of slower relaxation mechanisms. A recent dielectric spectrum study on the DMPC vesicle solution (Schrader and Kaatze, 2001) shows that the dielectric relaxation in the microsecond to nanosecond range is mainly due to the headgroup rotation with timescale τ = 2.6 ns at 31°C, similar to that of the rotational diffusion (see the section “Responses to stepwise strain”). A similar decay mode was also identified as solely responsible for the ultrasonic attenuation in the microsecond to nanosecond range (τ ∼ 2.4 ns at 32°C) (Schrader et al., 2003). Since the slowest relaxation mode of G_2D(t) is ∼200 ps for the expansion and ∼2 ns for the compression (Table 1), it is very likely that the lipid overall and headgroup rotations are the only significant stress relaxation mechanism under a microsecond timescale that is not fully captured in this study. As mentioned above, the compressional relaxation component with τ ∼ 2 ns will be closely related to this mode. We also note that the apparent 2D moduli in Figs. 5 and 6 still exhibit a frequency dispersion near the period of 1 ns, and the data in Table 3 yield an apparent divergent behavior of the 2D viscosity η_2D(ω) = G″_2D(ω)/ω with decreasing ω in the studied frequency range (not shown). This apparent divergence will disappear at a smaller frequency than is covered in our simulation, once the slower relaxation mechanisms mentioned above are taken into account. Assuming that the missing relaxation mechanisms have timescales τ ∼ 2–3 ns as discussed above, we expect the static limit to be reached at ω ≲ 1/τ ∼ 0.4 GHz or T ≳ 16 ns.

The apparent 2D elastic modulus can be translated to the area compressibility modulus K_A via Eq. 11. We have used it in Fig. 9 to eliminate the direct water layer effect. K_A is also one of the key quantities characterizing membrane elasticity and has been extensively studied. The currently accepted value of K_A (Nagle and Tristram-Nagle, 2000) for a DMPC bilayer is 0.234 N/m (Rawicz et al., 2000) obtained from micropipette aspiration of vesicles. This represents the elastic response to local area expansion after the thermal bending undulation effects are separated, and thus is about twice larger than the apparent modulus, which is not corrected for the undulation effect. (A recent reexamination of this method (Henriksen and Ipsen, 2004) resulted in a smaller bending modulus but a similar area compressibility modulus compared to the values in Rawicz et al., 2000.) Still, this is ∼2.6 times smaller than our result (K_A = 0.609 N/m for system D1 at period T = 1.6 ns (ω = 3.93 GHz)). This difference is partly attributed to the different responses to compression and expansion: the micropipette aspiration experiment measures only the expansional response, which is softer than the response to compression, whereas our NEMD results from oscillatory strains are averages of the two. In addition, the value of K_A in the static limit, as discussed above, would be considerably smaller than at T = 1.6 ns.

In conclusion, we have presented a unified formulation of the phenomenological linear viscoelastic properties of a planar biomembranes. The relevant viscoelastic moduli were quantified with NEMD simulations of the area change process. We have found a close coupling between the area and thickness variations, and it plays a critical role in the apparent in-plane viscoelastic behavior, which is surprisingly linear up to 20% area change. In addition, this coupling results in large in-plane viscous moduli of membranes comparable in magnitude to the corresponding elastic moduli. This will have a significant influence on many dynamic and relaxation processes occurring in lipid bilayer membranes. The quantitative information on the membrane viscoelastic properties obtained in this study is also expected to be useful in various efforts to model meso- to macroscale biomembrane systems (Ayton and Voth, 2002).

APPENDIX: THE NEMD SIMULATION METHOD

In the NEMD simulation method, the external perturbation is homogeneously reflected in the equations of motion of the individual atoms in a way consistent with the concomitant change in the boundary conditions. For the simulation of lateral area change, which incurs the system size change in the x and y directions, Ayton et al. (2002) devised the following equations of motion:

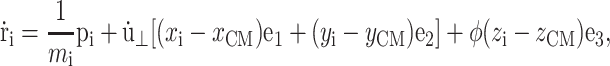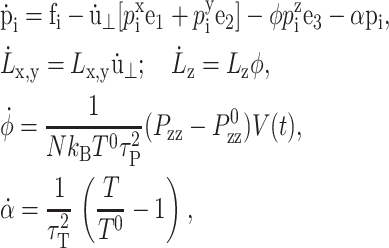(29)

where m_i, r_i, p_i, and f_i are, respectively, the mass, position, peculiar momentum (difference between the lab-frame and streaming momenta), and force of particle i; r_CM is the center of mass of the particles in the simulation box; L_α (α = x, y, z) is the box size in the α direction; P_zz and T are instantaneous normal pressure and temperature of the system determined from the peculiar momentum; e_i (i = 1, 2, 3) is the unit vector in each Cartesian direction; N is the number of particles; k_B is the Boltzmann constant; and φ and α are the barostat and Nose-Hoover thermostat variables, respectively. The time evolutions of φ and α are controlled by the imposed normal pressure 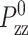and temperature T⁰, and by the relaxation times τ_P and τ_T of the barostat and thermostat, respectively. Finally, 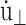is the rate of the lateral strain given by Eq. 13 or 20. In the former, the jump in u_⊥ at t = t₀ was approximated by a linear function of short duration (0.05 ps). Although Eq. 29 is not a unique representation of microscopic motions under the given strain and boundary conditions, it has the major advantage of simplicity and intuitive appeal. In addition, it is closely related to equations of motion for many equilibrium isobaric ensembles as shown below. Moreover, on theoretical grounds (Evans and Holian, 1985), the linear susceptibilities obtained from the above equations of motion are expected to be free from uncertainties related to thermostat. For these reasons, its variants have been used extensively to study the viscoelastic behavior of fluids (Hoover et al., 1980b,a; Evans and Morriss, 1990).

We have implemented Eq. 29 in the DL_POLY molecular dynamics simulation package version 2.12 (Smith and Forester, 1999). In the ZNS condition simulations, the normal stress was maintained close to zero by setting 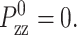In the CLZ condition simulations, we simply used a very large value of τ_P with the initial condition φ(t = 0) = 0 to suppress the change in L_z. By proper choice of 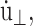Eq. 29 also generates several equilibrium isobaric ensembles. First, when 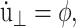we obtain the NPT ensemble with isotropic volume fluctuation (i-NPT, Melchionna et al., 1993). If, instead of φ, three independent variables are used for each Cartesian components, we have the NPT ensemble with anisotropic system size variations (a-NPT, Melchionna et al., 1993). Another useful equilibrium ensemble derived from Eq. 29 is that of constant lateral area and normal stress, usually referred to as the NP_nAT ensemble (Zhang et al., 1995). This ensemble is obtained by setting 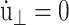in Eq. 29.