Exonuclease I Hydrolyzes DNA with a Distribution of Rates

Abstract

We report heterogeneity in the time necessary for Exonuclease I to hydrolyze identical DNA fragments. A real-time fluorescence method measured the time required by molecules of Exonuclease I to hydrolyze single-stranded DNA that was synthesized to have two fluorescently labeled nucleotides. One fluorescently labeled nucleotide was located near the 3′ end of the DNA and the other near the 5′ end. Heterogeneity in the hydrolysis rate of the exonuclease population was inferred from the distribution of times necessary to cleave these DNA fragments. In particular, we found simple first-order kinetics, using a single hydrolysis rate, did not result in a good fit to the data. Better fits to the data were obtained if one assumed a distribution of hydrolysis rates for the exonuclease population. Under our experimental conditions, this broad distribution of rates was centered near 100 nt/s.

INTRODUCTION

Exonuclease hydrolysis of DNA is seldom observed in real-time. To measure a hydrolysis rate, typically a known amount of exonuclease digests an excess of radioactively labeled DNA and the amount of acid-soluble free nucleotides released during a given reaction time period is measured (Weiss, 1981). If more information than the hydrolysis rate is desired, the products of the hydrolysis may be assayed by gel electrophoresis (Brody et al., 1986). Monitoring exonuclease hydrolysis of DNA in real-time has the potential to be both more informative and more rapid.

We report a method to monitor exonuclease hydrolysis of DNA in real-time that makes the extraction of an average hydrolysis rate straightforward. In addition to offering a means to simply and accurately measure the average hydrolysis rate, these experiments revealed heterogeneous behavior in the enzymatic activity of Exonuclease I (Exo I). We note that other studies of enzymes have revealed heterogeneity in enzyme activity or catalytic rate, with examples including: the non-exponential binding of CO to myoglobin (Austin et al., 1975), the non-Michaelis-Menten kinetics of phosphofructokinase (Neet and Ainslie, 1980), the history-dependent turnover dynamics of cholesterol oxidase (Lu et al., 1998), the capture of antigens to surface-immobilized monoclonal antibodies (Vijayendran and Leckband, 2001), and the hydrolysis of DNA by λ-exonuclease (Perkins et al., 2003; van Oijen et al., 2003). Although the hydrolysis kinetics (Brody, 1991; Brody and Doherty, 1985; Brody et al., 1986; Lehman, 1960; Lehman and Nussbaum, 1964) and structure (Breyer and Matthews, 2000) of Exo I have been studied in a series of works, there is no evidence to date that would suggest any heterogeneity in the structure or function of this particular protein. We observed, and herein report, heterogeneity in the time required for Exo I hydrolysis of short, identical strands of DNA.

Briefly, our technique for monitoring exonuclease hydrolysis is as follows:

1. DNA strands are synthesized to have a 5′ biotin and fluorescently labeled nucleotides toward both the 3′ and 5′ ends of the strand.

2. These DNA strands are attached to streptavidin-coated polystyrene beads.

3. The DNA-laden beads are incubated with Exo I in a buffer that allows attachment of the enzyme to the 3′ end of the DNA strands, but lacks the necessary Mg²⁺ cofactor needed by the exonuclease for hydrolysis of the DNA.

4. A single polystyrene bead, laden with fluorescently labeled DNA and Exo I, is anchored by an optical trap (Machara et al., 1998; Wang et al., 1995) in a flow stream of an ultrasensitive flow cytometer (see Fig. 1).

5. The Mg²⁺ cofactor is introduced to the exonuclease-DNA complexes on the microsphere using rapid (∼ms) laminar mixing techniques (Knight et al., 1998) and hydrolysis of the DNA begins.

6. The cleaved, labeled nucleotides are carried by the flow downstream and detected by laser-induced fluorescence.

FIGURE 1.

Cartoon depicting the experimental procedure. In A, DNA-laden microspheres are discharged from the capillary and flow through the IR trapping laser and fluorescence excitation probe volume. The laser beam for fluorescence excitation travels out of the page in this view. In B, a DNA laden microsphere is optically trapped. In C, the sample delivery capillary, is turned off (a vacuum is applied), the Mg²⁺ cofactor diffuses to the microsphere, and Exo I hydrolysis begins. Hydrolyzed nucleotides enter the flow stream and are detected downstream by the excitation laser beam. The same objective used for IR trapping is used to collect the fluorescence.

The passage of the liberated, labeled bases through the laser probe volume leads to an increase in the measured fluorescence intensity. The average hydrolysis rate is determined by the time elapsed between the recorded fluorescence intensity maxima while the shapes of the fluorescence maxima are used to measure the distribution of hydrolysis rates.

Conceivably, the same information (the average hydrolysis rate and the distribution of rates) can be found from more conventional measurements. One could use rapid mixing to both start and quench an exonuclease hydrolysis reaction before completion and measure the distribution of DNA lengths produced from the digestion via gel electrophoresis. The distribution of fragment lengths could be turned into a distribution of hydrolysis rates. Studies such as this seem to be lacking in the literature. However, similar methods have been used to assay the distribution and heterogeneity of primer extension products (Tombline et al., 1996). Moreover, using a different method, namely atomic force microscopy, Hori et al. (1998) examined the distribution of DNA fragments lengths produced by BAL 31 nuclease digestion. However, this data was not analyzed with an eye toward observing or quantifying heterogeneity in the nuclease population.

The technique described herein offers several advantages to quantifying exonuclease hydrolysis kinetics and enzyme heterogeneity. This method monitors the hydrolysis reaction in real-time, which has the potential to be more informative than studies that examine the distribution of products. Moreover, this technique is quite rapid, as there is no need to assay products of the reaction using gel electrophoresis. It is a simple and fast means to measure both an average hydrolysis rate and observe the distribution of rates.

MATERIALS AND METHODS

Preparation of a biotinylated 56-mer with a fluorescent label near each end

Biotinylated, single-stranded biotinylated 56-mers were synthesized (Operon, Technologies, Alameda, CA) to have the sequence (Sequence No. 1)

where the symbol B denotes the biotin 5′ head of this sequence (Glen Research, Sterling, VA, catalog No. 10-5950-xx) and the two bold Ts in the sequence denote dTMPs fluorescently labeled with tetramethyl rhodamine (TMR), synthesized using a dT-TMR precursor (Glen Research, catalog No. 10-1057-xx, Fig. 2). The synthesized biotinylated 56-mer DNA was de-protected by an optimized protocol provided by the manufacturer and purified by gel-electrophoresis.

FIGURE 2.

Structure of the TMR-labeled nucleotide (5′-di-methoxytrityloxy-5-[n-((tetra-methylrhodaminyl)-aminohexyl)-3-acrylimido]-2′-de-oxyuridine-3′-[(2-cyanoethyl)-(n,n-di-isopropyl)]-phosphoramide) precursor used in the synthesis of DNA Sequence No. 1.

Preparation of a biotinylated 56-mer with one fluorescent label near the 3′ end

A native 20-mer, complimentary to the last 20 bases of the 3′ end of Sequence No. 1, was synthesized (Operon Technologies, Alameda, CA) and annealed to a sample of the fluorescently labeled biotinylated 56-mers (Sequence No. 1), at a ratio of approximately one 20-mer per biotinylated 56-mer. Exonuclease III (New England Biolabs, Beverly, MA) was used to remove bases from the 3′ end of the labeled strand of the double-stranded DNA. This hydrolysis liberated the labeled dT nearest the 3′ end. After exonuclease hydrolysis, another synthetic oligomer, 56 bases long, complimentary to Sequence No. 1 (Operon Technologies, Alameda, CA), was annealed to the biotinylated single-stranded DNA produced from the Exo III digestion. This 56-mer was complimentary to the entire length of Sequence No. 1. Polymerization (Deep Vent Exo⁻, New England Biolabs, Beverly, MA) with unmodified nucleotides extended this primer-template combination. The resulting biotinylated double-stranded DNA was converted into a single-stranded form by a PCR competition assay, similar to that described in Werner et al. (2003). After the above procedures, the majority of the DNA species attached to the microsphere were single-stranded and of the sequence (Sequence No. 2)

where, again, B denotes biotin and T denotes TMR-labeled dTMP. A small fraction (∼15%) of the biotinylated, single-stranded DNA present on the microspheres after this procedure was the original two-TMR-labeled sequence (Sequence No. 1). We believe the reason for this two-label DNA contamination in the one-label sample was due to having an insufficient amount of 20-mer for complete hybridization to Sequence No. 1.

Preparation of microspheres for exonuclease studies

The labeled, biotinylated DNA was attached to streptavidin-coated microspheres (3.2-μm-diameter, Spherotek, Libertyville, IL) under incubation conditions (∼1 μM DNA) such that ∼30,000 DNA fragments were attached to each microsphere. These DNA-laden microspheres were incubated with a solution containing Exo I at 1.0 nM concentration, 1 mM Glycine-KOH (pH 9.5), and 1 mM EDTA buffer for ∼30 min before the exonuclease hydrolysis experiments. In this buffer, the Exo I binds to the DNA strands, but lacks the Mg²⁺ cofactor necessary for DNA hydrolysis.

The Exonuclease I used in these experiments was purchased from Amersham Pharmacia (Piscataway, NJ) and used without any further purification. Once the Exo I was bound to the DNA present on the microspheres, the Exo-DNA complex was quite stable, even in the absence of magnesium.

We performed experiments to explicitly test if the Exo-DNA complex could be in any sort of dynamic binding equilibrium during the hydrolysis experiments (i.e., could the Exo I become dissociated from the DNA during the time course of these experiments). In these experiments, several hundred-thousand strands of fluorescently labeled, biotinylated single-stranded DNA were attached to 6-μm-diameter streptavidin-coated microspheres. Exo I was attached to the DNA strands. The beads were purified from free Exo I by centrifugation. This wash procedure was performed twice. These beads were subsequently measured in a commercial flow cytometer (FACSCalibur, Beckton-Dickinson, San Jose, CA). In the absence of Mg²⁺, the beads were very fluorescent and easily detected, via fluorescence, in the flow cytometer. Mg²⁺ was added to an aliquot of the washed beads in intervals of 0, 10, 20, 30, and 40 min after washing off unbound Exo I. At all timepoints in this series, upon addition of Mg²⁺, the fluorescence intensity of the beads was lost (fluorescence intensity near baseline levels), due to exonuclease hydrolysis of the fluorescent tag. These experiments demonstrate that the Exo-DNA complex is stable and that dissociation of the Exo from the DNA must take place on a timescale >40 min, which is significantly longer than the time-ranges sampled during the hydrolysis measurements.

Experimental apparatus

The apparatus is an ultrasensitive flow cytometer described in detail elsewhere (Machara et al., 1998; Werner et al., 1999) that combines sensitive fluorescence detection with optical trapping (Machara et al., 1998; Wang et al., 1995). Fig. 1 is a cartoon of the flow channel that depicts how exonuclease hydrolysis experiments were performed. The flow in Fig. 1 is from top to bottom. For the experiments depicted in Figs. 3 and 4, the volumetric flow rate of the sheath stream was 10 μl/min, yielding a linear flow velocity of ∼0.53 cm/s in the center of the flow channel. For the data taken at a lower trapping power, the volumetric flow rate was 5 μl/min, yielding a linear flow velocity of ∼0.26 cm/s in the center of the flow channel. The sheath stream in these experiments consisted of 1 mM Glycine-KOH (pH 9.5) and 5 mM MgCl₂. The square-bore channel is 250 μm across and the sample introduction capillary seen at the top of the figure has an inner diameter of 20 μm and an outer diameter of 90 μm. This capillary leads to a sample reservoir of polystyrene beads laden with the exonuclease-DNA complexes in a solution of 1 mM Glycine-KOH (pH 9.5) and 1 mM EDTA. By applying pressure to this reservoir, a sample stream containing the beads was discharged from the capillary. A single microsphere in this sample stream was suspended in flow by an optical trap, as previously described (Machara et al., 1998). Optical trapping was performed by 1.06 μm light from a continuous-wave Nd:YAG laser focused by a 1.2 NA 60× water immersion microscope objective (CFN plan Apochromat, Nikon, New York) to a nearly diffraction-limited spot in the center of the flow channel. For the data depicted in Figs. 3 and 5, 800 mW of near-infrared light impinged on the back of the objective, although for some of the data, 180 mW was employed. When a DNA-laden microsphere was optically trapped in the flow channel, the delivery capillary was turned off (a vacuum was applied to the delivery capillary), Mg²⁺ was rapidly carried by diffusion to the microsphere, and cleavage began. Cleaved nucleotides were entrained in the sheath flow and crossed a laser beam located ∼20 μm downstream from the optically trapped microsphere. This probe laser beam intersected the flow stream orthogonal to both the flow stream and the near-infrared trapping laser beam. An average power of 10 mW at 514.5 nm from a mode-locked Argon ion laser (82 MHz pulse repetition rate, ∼100 ps pulse width), focused to an ∼12-μm 1/e² diameter spot, was used for fluorescence excitation. Fluorescence from the labeled nucleotides was collected and imaged by the same objective used to trap the microsphere. The collected fluorescence passed through a spatial filter in the image plane of the objective (a slit of dimensions 1 mm × 0.5 mm, long axis oriented parallel to the flow) and a 50-nm bandpass spectral filter centered at 580 nm (580df50, Omega Optical, Brattleboro, VT) before impinging on a single-photon-counting avalanche photodiode (SPCM-200-PQ, Perkin-Elmer Optoelectronics, Vaudreville, Quebec, Canada). The apparatus is sensitive enough to detect the fluorescence from a single TMR-dTMP (Machara et al., 1998; Werner et al., 1999). For this work, this level of sensitivity was not needed and neutral density filters were used to attenuate the fluorescence to match the optimal dynamic range of the avalanche photodiodes. Filters of optical density 2.6 were used to attenuate the fluorescence emission for the data shown for DNA Sequence No. 1 and filters of an optical density of 1.6 were used for the data taken on the mixture of DNA of Sequences No. 1 and No. 2. We used the total integrated fluorescence signal and the fact that a single TMR-dTMP yields ∼70 detected photoelectrons in our apparatus (Werner et al., 2003) to estimate the number of TMR-dTMPs cleaved and hence the number of DNA fragments present on each microsphere. These estimates gave ∼30,000 DNA fragments per microsphere for the data presented on Sequence No. 1 and ∼4000 DNA fragments per microsphere for the data collected on the mixture of Sequences No. 1 and No. 2.

FIGURE 3.

Fluorescence measured as a function of time for cleavage experiments performed on four different microspheres (A–D, solid lines). Two peaks in the fluorescence count rate are seen in the experimental data. The first peak, centered near 0.4 s, is due to the cleavage of the first labeled nucleotide (in the fifth position of the DNA sequence) and the transit of these fluorescent nucleotides through the excitation laser beam. The second, less pronounced peak seen at ∼0.6 s is due to the cleavage of the second fluorescent nucleotide, at the 38th position of the DNA sequence (see text). The open circles in A denote the fluorescence time history expected if Exo I hydrolysis were described by first-order kinetics with a single rate (Eq. 1) The dashed line in each panel is a fit of the data to a model that assumes that the exonuclease population hydrolyzes DNA with a distribution of cleavage rates.

FIGURE 4.

Distribution of cleavage rates derived from the fits to the fluorescence transients. The solid line represents the average distribution from the four fits shown in Fig. 3.

FIGURE 5.

Fluorescence intensity measured as a function of time for Exo I hydrolysis experiments on microspheres laden with a mixture of DNA populations (Sequence No. 1 ∼15% and Sequence No. 2, ∼85%, solid line) overlaid with the fluorescence time history for a microsphere only laden with DNA Sequence No. 1 (dotted line). Two peaks in the fluorescence intensity are still visible for the data taken on a mixture of DNA, but the second peak is noticeably larger. The shifting of the relative fluorescence intensity to the second peak validates the interpretation that each peak comes from the cleavage of the 5th and 38th fluorescently labeled nucleotides in the DNA sequence. The time between the two peaks is roughly the same for the two data sets (see text).

To ensure that crowding on the microsphere did not affect the hydrolysis kinetics, experiments were also performed for DNA Sequence No. 1 where the DNA content was ∼3000 strands per microsphere (data not shown). The hydrolysis data from this sample was identical to that depicted at higher DNA concentrations shown in Fig. 3.

Fitting fluorescence time histories assuming first-order kinetics

The published kinetic scheme (Brody et al., 1986) for Exo I assumes that after Exo I attaches to a DNA strand, first-order kinetics describe the subsequent hydrolysis of the DNA. In such a first-order kinetic scheme, the expected fluorescence time history should be well fit to the expression (see Appendix 1)

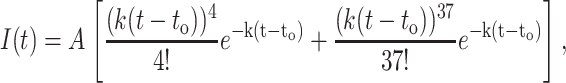(1)

where I(t) is the fluorescence intensity as a function of time, A is the amplitude of the fit function, t_o is the time cleavage begins, and k is the hydrolysis rate. This function is valid only for times >t_o. For this function, the standard deviation in time, or width, of the first peak is the square-root of 5 divided by k, whereas the width of the second peak is the square-root of 38 divided by k.

Fitting fluorescence time histories to a distribution of rates

We desired a description of the hydrolysis kinetics that allowed for heterogeneity in the hydrolysis rate. Equation 1 was used to yield the shape of the fluorescence time history for a particular value of k, wherein the probability of obtaining this k was assumed to be Gaussian-distributed about some central value, k_o, with a standard deviation of σ_k. Values of k ≤ 10 nt/s were ignored during the fit. The centroid of the rate distribution (k_o), and the standard deviation of the rate distribution (σ_k), as well as the fluorescence amplitude (A) and the time offset (t_o) of the data, were varied for each fluorescence time history to produce the best fit (χ² minimization, data fitting performed with Igor Pro Version 4.06, Wavemetrics, Lake Oswego, OR).

In addition to a truncated Gaussian distribution, we tried fitting the data using rate distributions that, by their nature, had no members with a zero hydrolysis rate. In particular, log-normal distributions of the hydrolysis rate were attempted. Although the data could be fit using these models, the fits were poorer, based upon the χ² value, than the fits provided by the truncated Gaussian distributions described above. In general, the log-normal distributions had much lower probabilities of generating slow (10–20 nt/s) hydrolysis rates than did the truncated Gaussian distributions and fit the experimental data poorly at long timescales. The hydrolysis rate distributions need a substantial population of slow members to fit the observed data, and as such, a truncated Gaussian distribution was used.

Fitting fluorescence time histories using a sum of two Gaussians

For a quantitative comparison of exonuclease hydrolysis data taken on different microspheres, different sequence mixtures of DNA, and different optical trapping powers, the fluorescence time histories were fit to a sum of two independent Gaussians. The difference in time between the peak positions can be used to estimate the hydrolysis rate, since the number of nucleotides separating fluorescently labeled bases is known. These times are listed in Table 1. The errors on the values reported for the different microspheres represent the standard deviation for that value (χ² minimization) reported by the fitting software (Igor Pro Version 4.06). The errors on the average values in this table represent the standard deviation of the values determined for the individual experiments listed.

TABLE 1.

Time elapsed between fluorescence maxima

DNA sequence	Bead No.	Optical trapping power (mW)	Position of 1st fluorescence maximum (s)	Position of 2nd fluorescence maximum (s)	Δt (s)
1	1	800	0.435 ± 0.001	0.624 ± 0.02	0.19 ± 0.02
1	2	800	0.437 ± 0.002	0.625 ± 0.02	0.19 ± 0.02
1	3	800	0.437 ± 0.002	0.625 ± 0.02	0.19 ± 0.02
1	4	800	0.437 ± 0.002	0.625 ± 0.02	0.19 ± 0.02
Average					0.19 ± 0.01
Mix 1&2	1	800	0.381 ± 0.004	0.553 ± 0.004	0.172 ± 0.006
Mix 1&2	2	800	0.386 ± 0.005	0.554 ± 0.004	0.168 ± 0.006
Mix 1&2	3	800	0.382 ± 0.005	0.551 ± 0.004	0.169 ± 0.006
Average					0.170 ± 0.003
1	1	180	0.413 ± 0.002	0.66 ± 0.02	0.25 ± 0.02

RESULTS

The laser-induced fluorescence measured as a function of time for a cleavage experiment of the DNA given by Sequence No. 1 is shown in Fig. 3 (solid lines) for four different microspheres. Each panel displays 2 s of data, with the fluorescence counts binned into 10-ms intervals. The data from different microspheres are aligned in time to ease comparison. After introducing Mg²⁺ to the exonuclease-DNA complexes, hydrolysis begins at some undetermined time. After the exonucleases hydrolyze their way through four native bases, they liberate the first TMR-dTMP present on the labeled DNA strands. The passage of these TMR-dTMPs through the interrogation laser beam gives rise to the first sharp fluorescence peak observed in the data, seen near 0.4 s. The exonuclease molecules continue to processively hydrolyze the DNA, releasing native (unlabeled) nucleotides and the fluorescence falls to a minimum ∼0.1 s after this first peak. After hydrolyzing the 33 native nucleotides separating the fluorescently labeled bases, the second TMR-dTMP present on the DNA strands is liberated. The passage of these TMR-dTMPs through the interrogation laser beam gives rise to the second broader fluorescence maximum seen at ∼0.6 s. We show the data from four different microspheres to illustrate the reproducibility of these experiments.

The trace depicted by the open circles in the top-left of Fig. 3 was produced by a fit (Eq. 1) that assumed simple first-order kinetics described the hydrolysis of the DNA by Exo I. A first-order kinetic scheme fails to describe the measured fluorescence time history. In particular, the measured fluorescence time histories have much broader widths than those predicted by first-order kinetics. Because recent single-molecule studies that examined λ-exonuclease digestion of DNA reported a distribution of hydrolysis rates (Perkins et al., 2003; van Oijen et al., 2003), we tested to see if we could achieve a better fit to the experimental data by assuming that Exonuclease I hydrolyzed DNA with a distribution of hydrolysis rates. Equation 1 was used to generate the fluorescence time history for a single hydrolysis rate, wherein the distribution of rates was assumed to be Gaussian-distributed about some central value k_o. The dotted lines in Fig. 3 represent the results of the fitting procedure. As can be seen, this model describes the data much better than a model that has a single hydrolysis rate. The centroid (k_o) and standard deviation (σ_k) of the distribution of rates are, for Fig. 3 A (96, 61); Fig. 3 B (97, 64); Fig. 3 C (88, 62); and Fig. 3 D (108, 66). Combining these fits, the average distribution of rates for these data sets is centered at 97 ± 8 nt/s, with a standard deviation about this centroid of 63 ± 2 nt/s. The distribution of rates, determined by the average of the fits to the data, is shown in Fig. 4 (solid lines). This distribution is comparable in character to other hydrolysis rate distributions measured from single-molecule hydrolysis experiments on λ-exonuclease (Perkins et al., 2003; van Oijen et al., 2003) in that it is quite broad, with a width comparable to the mean.

To ensure that the two fluorescence peaks seen in the data were due to the cleavage of the two sets of labeled nucleotides and not some experimental artifact, a control experiment was performed. Fig. 5 shows a similar cleavage experiment performed on a microsphere that contained two populations of labeled DNA (solid line), overlaid with data taken on a pure population of Sequence No. 1 DNA (this trace is the same as that shown in Fig. 3 D). For the data depicted by the solid line, the majority (∼85%) of the DNA contained only a single label (TMR-dTMP) in the 38th position (Sequence No. 2) and a minority of the labeled DNA (∼15%) contained TMR-dTMPs in both the 5th and 38th positions of the DNA (Sequence No. 1). One can see that two peaks are still clearly visible, but that the second peak is now much larger than the first fluorescence peak. This change of the relative peak intensity validates the interpretation of the two observed fluorescence maximums observed in our cleavage experiments of Sequence #1 as being due to the cleavage of the 5th- and 38th-labeled nucleotides of the DNA. Moreover, we have fit these fluorescence time histories to a sum of two Gaussians to measure the time delay between the peak positions. For the data taken on a mixture of DNA sequences (the solid line in Fig. 5), the delay between peaks is ∼0.170 ± 0.003 s (see Table 1, error reported here is the standard deviation of the Δt values listed in the table). For the data taken on DNA Sequence No. 1, the delay between the fluorescence peaks was 0.19 ± 0.01 (see Table 1). As the time delays between the fluorescence maxima are within 2σ of each other, we infer that the Exo I is not significantly perturbed or stalled when cleaving the first TMR-labeled nucleotide. We have previously reported the ability of Exo I to hydrolyze fluorescently labeled DNA that was labeled with TMR-dTMPs possessing a 12-carbon spacer between the nucleotide and the dye (Werner et al., 2003).

The number of nucleotides between the fluorescent bases, divided by the time elapsed between fluorescence maxima, is a simple way to estimate an average hydrolysis rate. For the data depicted in Fig. 3 and listed in Table 1, this estimate yields an average hydrolysis rate of 174 ± 9 nt/s. This value is significantly higher than the central hydrolysis rate determined by fitting the fluorescence time history to a distribution of hydrolysis rates (∼100 nt/s). This can be explained by the fact that the fluorescence time history is asymmetric and that a Gaussian function fails to reproduce the tail of these time histories accurately. Since the lagging tail of the fluorescence time history reflects slower hydrolysis rates, the Gaussian fits tend to give an artificially fast value for the hydrolysis rate. However, we have still decided to make use of Gaussian fits to the data, as this allows simple and direct comparisons between data sets acquired on different experimental conditions or DNA sequences, as shown in Table 1.

The measured Exo I hydrolysis rate estimated from Gaussian fits to the fluorescence data (174 ± 9 nt/s), as well as the centroid of the distribution of hydrolysis rates shown in Fig. 4 (103 nt/s), are significantly slower than the hydrolysis rate reported by Brody et al. ( 1986) (275 nt/s at 37°C). We attribute this discrepancy to the different temperatures of the two experiments. The temperature of the sheath stream in our flow cytometer in the absence of laser heating is ∼22°C. However, the laser fluences necessary for optical trapping a 3-μm-diameter polystyrene microsphere in a 0.5-cm/s velocity flow stream can heat the microsphere (Liu et al., 1995; Neuman et al., 1999; Peterman et al., 2003). We estimate our microscope objective to have a transmission of ∼50% in the near-infrared, based upon measurements taken on similar objectives (Neuman et al., 1999). With this transmission efficiency, ∼400 mW of power comprised the optical trap used for the data presented in Fig. 3. According to the models of Peterman et al. (2003), for a microsphere optically trapped ∼100 μm from the surface of a coverslip, the temperature increase should be ∼8°C (∼21°K per Watt of trapping power; Peterman et al., 2003). This would put the temperature of the exonuclease hydrolysis experiments at 31°C. As the flow stream in these experiments convectively cools the microsphere, the 31°C estimate is an upper limit of the temperature.

Absolute calibration of the temperature of the optically trapped microsphere is difficult. However, to see if heating was occurring to any extent, and if this heating was affecting the Exo I hydrolysis kinetics, experiments were performed at lower trapping power. It was necessary to lower the flow speed to 5 μl/min (from 10 μl/min) to perform Exo I hydrolysis experiments reliably with less trapping power. Table 1 lists the peak separation for an exonuclease hydrolysis experiment taken at a lower trapping power. The average hydrolysis rate from this time delay is 130 ± 10 nt/s. The hydrolysis kinetics are measurably slower for the data taken at lower trapping power, indicating that the trapping laser beam is locally heating the environment around the DNA-laden microsphere and affecting the hydrolysis kinetics.

DISCUSSION

The fluorescence time histories of Fig. 3 contain a wealth of kinetic information. First, the observation of two fluorescence peaks is conclusive proof of processivity. If Exonuclease I became detached from the DNA, it would be washed downstream and the second fluorescence peak would not be seen. Second, as mentioned previously, the time between the two fluorescence peaks can be used to directly measure the hydrolysis rate of the enzyme, as the number of nucleotides separating the fluorescently labeled nucleotides is known. Third, the rapid rise of the first fluorescence maximum puts a strict upper bound on the timescale of magnesium binding to the exonuclease and of the subsequent activation of this enzyme. Fig. 6 is an expansion of the first fluorescence rise of Fig. 3 A. The fluorescence rise in this figure has a 1/e rise time of 0.024 s (Gaussian fit shown). Hence, magnesium binding and any sort of conformational change that occurs in the exonuclease upon binding must take place in <∼20 ms. Lastly, it appears the hydrolysis of DNA by Exo I is more complicated than a first-order kinetic mechanism, given the poor fits of a first-order kinetic scheme (Eq. 3) to the data (Fig. 3 A, open circles). The observed arrival time distribution of liberated nucleotides is significantly broader than that which can be ascribed to first-order kinetics.

FIGURE 6.

Expansion of the first fluorescence rise of Fig 3 A (open circles). Data points are at 10-ms intervals. The dashed line is a Gaussian fit to the fluorescence rise, yielding a 1/e rise-time of 24 ms. The solid line in this figure is the arrival time distribution calculated from Monte Carlo simulations for molecules eluting from a uniformly covered 3.2-μm-diameter microsphere. The flow velocity in this simulation was 0.53 cm/s and the detection region is 20-μm downstream of the trapped bead. Ten-thousand starting points on a microsphere were chosen at random to build this simulated arrival time distribution. The measured distribution is significantly broader than the anticipated broadening due to diffusion.

We attribute the widths of the fluorescence maxima as representing a distribution of hydrolysis rates present in the exonuclease population. However, several other experimental artifacts or other sources of heterogeneity in the experiment could contribute to the observed widths of the fluorescence maxima. We considered and eliminated the major anticipated experimental artifacts. First, there could be heterogeneity in the DNA microenvironment. It is conceivable that if a streptavidin held two DNA strands, these DNA strands would be digested differently than a streptavidin that contained a single strand, due to steric hindrance of the two exonuclease molecules. To eliminate this possibility, experiments were performed with an order-of-magnitude less DNA per microsphere, which ensures each streptavidin only holds a single DNA strand. The fluorescence time history under these conditions was indistinguishable from the data shown in Fig. 3. Second, if the binding/unbinding of the exonucleases to the DNA strands occurs during the timescale of these experiments, this could contribute to the observed fluorescence widths. We performed experiments to test the stability of the Exo I–DNA complex in the absence of magnesium. These experiments indicated that the Exo I-DNA complex in the absence of magnesium and Exo was stable over the course of half an hour and that association-dissociation of the Exo with the DNA strand was not occurring during these measurements. Third, there is a distribution of starting times for the exonucleases and fourth, there is a distribution of arrival times for the fluorescent nucleotides at the excitation laser probe volume, due to both the different locations of the DNA on the microsphere and to the finite transit time of the fluorescent nucleotides through the probe volume. However, these experimental contributions to the widths of the fluorescence maxima should occur on a timescale <10 ms. For example, the transit of fluorescent nucleotides through the laser is ∼2 ms and does not contribute significantly to the observed fluorescence widths. In addition, we have used Monte Carlo simulations, such as those reported in Machara et al. (1998), to estimate the distribution of arrival times of liberated nucleotides reaching the probe volume, assuming that the DNA is uniformly distributed over the optically trapped microsphere. The anticipated arrival time distribution from these simulations is shown as a solid line in Fig. 6. The width of this distribution results from the diffusion of nucleotides in the flowstream (Pratt and Keller, 1993), the differing DNA positions on the optically trapped microsphere (Machara et al., 1998), and the perturbation from a linear flow profile that results from the presence of the microsphere (Machara et al., 1998). The primary point of these simulations is to show that the measured fluorescence time histories are significantly broader than any anticipated experimental artifacts.

The most convincing argument against the widths of the observed fluorescence maxima being an experimental artifact is that this source of noise will affect both fluorescence maxima equally. As can be seen in the data in Fig. 3, the second fluorescence maximum is significantly broader than the first. Most technical sources of noise would affect both fluorescence maxima equally. For example, if the cleaved TMR-dTMPs interacted with or stuck to the microsphere before being entrained in the flow, then the first and second peaks in the fluorescence time history would be equally affected by this broadening mechanism. From the observation that the second fluorescence peak is significantly broader than the first, we have inferred that the technical broadening mechanisms present in this experiment are narrower than the kinetics under study.

As a first-order kinetic scheme fails to describe the fluorescence time histories, one might imagine more complicated mechanisms capable of describing the observed data. In particular, the simplest deviation from a first-order kinetic scheme would involve multiple kinetic steps per hydrolysis cycle. It is easy to envision multiple, sequential steps necessary for processive digestion of DNA. For example, after the hydrolysis of the last nucleotide, the exonuclease needs to inch its way up the DNA; the exonuclease may then need to attain a specific conformation to hydrolyze the next base, this base is hydrolyzed by the exonuclease, and finally, the liberated base is carried away by diffusion into the flow stream. However, the presence of multiple, sequential kinetic steps will make the standard deviation of the average time necessary to cleave a single base smaller than the standard deviation about the average cleavage time for a one-step mechanism (see Appendix 2). Briefly, the reason for this narrowing of the distribution is that instead of pulling an average hydrolysis time from a single exponential distribution, one is pulling two times from two exponential distributions of faster decay rates and is, in essence, averaging the total hydrolysis time over these distributions. As our data shows distributions broader than can be ascribed to first-order kinetics with a one-step mechanism, multiple step mechanisms will provide poorer fits to the data. One discovers (see Appendix 2), in the context of a first-order kinetic mechanism, the standard deviation per kinetic cycle is maximized in a one-step mechanism, or in a pseudo-one-step mechanism, where the slowest kinetic step is rate-limiting.

We attribute the distribution in arrival times to the exonuclease molecules sampling a distribution of hydrolysis rates and presumably, conformations. Our data is an ensemble measure of heterogeneity of the enzymatic activity of an exonuclease population, similar to the heterogeneity reported by other ensemble studies of proteins, such as Austin et al. (1975), Neet and Ainslie (1980), and Vijayendran and Leckband (2001). Although we can observe and quantify molecular heterogeneity, our measurements cannot distinguish between static and dynamic disorder (Lu et al., 1998; Xie and Lu, 1999). In static disorder, each exonuclease molecule is locked into a specific conformation or catalytic activity and there would be no interconversion of protein conformation. We have modeled our data assuming static disorder. A given exonuclease hydrolyzes DNA at a fixed rate, but there exist a distribution of conformations and a distribution of hydrolysis rates. An alternative explanation of the heterogeneity observed in our fluorescence time history could be provided by the concept of dynamic disorder (Lu et al., 1998). In this scenario, each exonuclease molecule would be fluctuating between conformational substates and each protein would sample a distribution of hydrolysis rates. We tried using dynamic disorder models to fit our data in addition to the static fits shown in Fig. 3. Even the most extreme case of dynamic disorder, wherein the exonuclease molecules change conformation and hydrolysis rate after each hydrolysis step, can be made to look like our data. Both static disorder and dynamic disorder models can fit our data and both models point to a broad distribution of hydrolysis rates. These distributions of hydrolysis rates are similar in character, but are not identical. In brief, our experiments cannot distinguish between whether static or dynamic disorder is responsible for the observed heterogeneity. Measurements that explore enzyme dynamics on the single molecule level can, however, make this distinction. In particular, single-molecule investigations of λ-exonuclease have revealed a distribution of hydrolysis rates (Perkins et al., 2003; van Oijen et al., 2003), dynamic disorder in the hydrolysis kinetics (van Oijen et al., 2003), and pauses at sequence-specific sites on the DNA substrate (Perkins et al., 2003).

Although the data reported herein cannot discern exonuclease pauses or the presence of dynamic disorder, the technique is a means of discerning and quantifying heterogeneity and points to other experiments that may be of interest. For example, this method could investigate whether the distribution of hydrolysis rates or distribution of digestion times depends upon the DNA sequence. In addition to such sequence-dependence studies, one could study the effect of cofactors upon exonuclease hydrolysis. For example, single-stranded binding protein is known to interact with (Genschel et al., 2000; Molineux and Gefter, 1975) and enhance (Molineux and Gefter, 1975; Sandigursky and Franklin, 1994) the activity of Exo I. One could investigate if single-stranded binding protein just affects the average hydrolysis rate, or whether the distribution of hydrolysis rates becomes narrower, due to the cofactor perhaps locking the exonuclease in a highly active conformation. Finally, while this study used short pieces of DNA and a highly processive exonuclease, the technique is not limited to these constraints. By adding exonuclease to the sheath stream of the flow cytometer in saturating concentrations, one could explore the kinetics of nonprocessive exonucleases. Similarly, longer pieces of fluorescently labeled DNA could be fabricated and the hydrolysis kinetics of these fragments studied to observe enzyme behavior over longer time spans.

APPENDIX 1: FLUORESCENCE TIME HISTORY EXPECTED FROM FIRST-ORDER KINETICS

For hydrolysis that occurs via a single first-order kinetic process that commences at t = 0, the probability a base is hydrolyzed between time t and time t + dt is

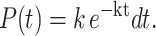(2)

The probability that two bases are hydrolyzed between time t and t + dt is the product of the probability that the first base was hydrolyzed at some intermediate time t′ whereas the second step occurred in a time of t–t′, integrated over × all intermediate times t′,

(3)

One can similarly calculate the probability that three bases are hydrolyzed between time t and t + dt, as this is the product of the probability that two bases were hydrolyzed at time t′ whereas the third step occurred with a time of t–t′, again integrated over all intermediate times,

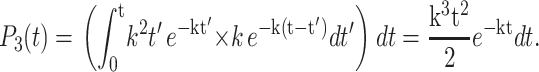(4)

One can prove by induction that in the context of a first-order kinetic mechanism the probability to cleave m nucleotides between time t and t + dt is given by

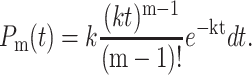(5)

The probability to hydrolyze m nucleotides in time t is Poisson-distributed. From this probability distribution, one can calculate the average time necessary to cleave m bases as

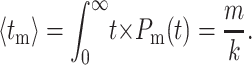(6)

As expected, the average time to hydrolyze m bases is simply the number of bases, m, divided by the rate to cleave a single base, k. The standard deviation around this time can be similarly calculated as

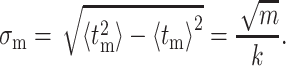(7)

The standard deviation in time necessary to hydrolyze a base scales with the square-root of the number of hydrolysis steps involved.

The measured fluorescence time histories shown in Fig. 3 reflect the time necessary to hydrolyze the 5th and 38th nucleotides, respectively. Hence, a first-order kinetic fit to the data is the sum of the probability to cleave 5 and 38 bases, respectively, as a function of time, as

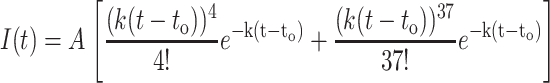(8)

The term t_o has been introduced to account for the time at which hydrolysis commences. This functional form is valid only for times t > t_o.

APPENDIX 2: FLUORESCENCE TIME HISTORY EXPECTED IF THE HYDROLYSIS OCCURS VIA A TWO-STEP MECHANISM

We consider the fluorescence time history expected if Exo I hydrolysis of a single base occurs via a two-step mechanism, with the kinetic steps possessing a rate of k₁ and k₂. For example, the first step (k₁) could reflect the exonuclease translocation along the DNA to the current base whereas the second step (k₂) could reflect the rate to hydrolyze this base. The probability that these two steps happen between time t and t + dt is the product of the probabilities that the first step occurred at time t′ whereas the second step occurred in a time of t–t′, integrated over all intermediate times t′,

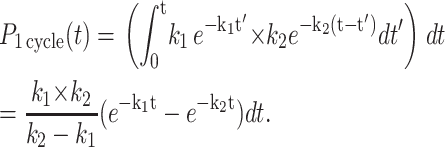(9)

We refer to the probability of both steps occurring as a single kinetic cycle. Given this probability distribution, one can calculate the average time necessary to complete a cycle,

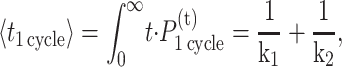(10)

as well as the standard deviation around this average time,

(11)

If m nucleotides are hydrolyzed, m complete cycles need to occur. The average time necessary for this to occur is m times the result of Eq. 10, whereas the standard deviation about this average time is the square-root of m times the result of Eq. 11, or

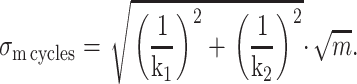(12)

We wish to compare the standard deviation about the average time necessary to hydrolyze m nucleotides that would result from such a two-step mechanism (Eq. 12) to the width anticipated from a single-step mechanism (Eq. 7). To compare a one-step mechanism with a two-step mechanism that occurs at the same observable average time, we are constrained to 1/k₁ + 1/k₂ = 1/k. Under this constraint, one finds the standard deviation of a cleavage process that involves two sequential steps (Eq. 12) is minimized at k₁ = k₂ = 2k, yielding a standard deviation that is a factor of 1/√2 times that of a one-step kinetic mechanism. The standard deviation in time for a two-step mechanism increases monotonically from this minimum and is maximized at the extremes (k₁ = k, k₂ = ∞) and at (k₁ = ∞ and k₂ = k). These extreme points are the limit where a two-step process is essentially a one-step kinetic mechanism, as one of the steps is infinitely fast. These extreme points have a standard deviation per complete kinetic cycle of (√m)/k. For any two-step kinetic mechanism bound to the constraint 1/k₁ + 1/k₂ = 1/k, the standard deviation in time per kinetic cycle always lies between (1/√2 × 1/k) and 1/k.

In summary, the standard deviation per kinetic cycle (hydrolysis step) is maximized in a one-step kinetic process and is smaller than this for any two-step mechanism. This argument can be extended from a two-step mechanism to any multistep mechanism. One finds that the standard deviation about the average time necessary to perform a complete kinetic cycle is maximized in a one-step kinetic mechanism, or in a pseudo-one-step mechanism wherein the slowest step is rate-limiting.