Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Dec 1;88(2):1423–1431. doi: 10.1529/biophysj.104.052746

Molecular Force Modulation Spectroscopy Revealing the Dynamic Response of Single Bacteriorhodopsins

Harald Janovjak *, Daniel J Müller *, Andrew D L Humphris †
PMCID: PMC1305144  PMID: 15574708

Abstract

Recent advances in atomic force microscopy allowed globular and membrane proteins to be mechanically unfolded on a single-molecule level. Presented is an extension to the existing force spectroscopy experiments. While unfolding single bacteriorhodopsins from native purple membranes, small oscillation amplitudes (6–9 nm) were supplied to the vertical displacement of the cantilever at a frequency of 3 kHz. The phase and amplitude response of the cantilever-protein system was converted to reveal the elastic (conservative) and viscous (dissipative) contributions to the unfolding process. The elastic response (stiffness) of the extended parts of the protein were in the range of a few tens pN/nm and could be well described by the derivative of the wormlike chain model. Discrete events in the viscous response coincided with the unfolding of single secondary structure elements and were in the range of 1 μNs/m. In addition, these force modulation spectroscopy experiments revealed novel mechanical unfolding intermediates of bacteriorhodopsin. We found that kinks result in a loss of unfolding cooperativity in transmembrane helices. Reconstructing force-distance spectra by the integration of amplitude-distance spectra verified their position, offering a novel approach to detect intermediates during the forced unfolding of single proteins.

INTRODUCTION

The protein-folding problem is one of the most challenging areas of inquiry in today's biological research. Its key questions, e.g., how an unfolded polypeptide chain acquires the conformation of the native protein based on the amino acid (aa) sequence, still remain unanswered (Booth et al., 2001). The trapping and characterization of folding intermediates of small globular proteins like lysozyme and bovine pancreatic trypsin inhibitor revealed that protein folding is guided by the same interactions that stabilize the final folded state (Radford et al., 1992; Weissman and Kim, 1991). Therefore, considerable effort has been devoted to the study of the stability and unfolding of proteins under different physiological conditions or in different functional states, most commonly in thermal or chemical denaturation experiments. However, such ensemble measurements only probe the average behavior of large numbers of molecules. Therefore, these techniques cannot resolve simultaneously occurring (un)folding pathways or nonaccumulative folding intermediates. Perceptions of protein (un)folding, such as described by multidimensional landscapes or folding funnels, can be seen as a result of the complexity of inter- and intramolecular interactions (Radford, 2000). Thus, different unfolding pathways may be populated depending on the physiological environment requiring novel investigative approaches to observe coexisting minor and major pathways.

The atomic force microscope (AFM; Binnig et al., 1986) is increasingly used as a novel tool to study the molecular interactions determining the stability of single proteins. In experiments termed force spectroscopy, an external mechanical force plays the role of the denaturant and leads to sequential unfolding of the three-dimensional structure of individual proteins (Mitsui et al., 1996; Rief et al., 1997). To this state, a single protein is tethered between the tip of the micromachined AFM cantilever and a supporting surface. The tip-surface separation is then continuously increased using a piezoelectric actuator while the forces applied to the molecule by the cantilever are detected with an accuracy of a few pN. In initial experiments, Rief and others applied force spectroscopy to the giant muscle protein titin, which consists of repeats of globular immunoglobulin and tenascin domains (Marszalek et al., 1999; Rief et al., 1997; Williams et al., 2003). The continuous extension of an individual titin molecule resulted in subsequent unfolding of the protein domains. Plotting force against tip-surface separation produced a characteristic force-distance (F-D) curve from which the unfolding force as well as the unfolding pathway of a single protein domain is derived (Marszalek et al., 1999; Rief et al., 1997; Williams et al., 2003). In contrast to many forced unfolding experiments on globular proteins, the combination of single-molecule force microscopy and force spectroscopy revealed surprisingly detailed insights into the stability of membrane proteins like bacteriorhodopsin (BR) or the Na+/H+ antiporter NhaA (Kedrov et al., 2004; Oesterhelt et al., 2000). It has been shown that the secondary structure elements of BR and NhaA unfold sequentially and that their stability depends on the physiological environment of the protein (Janovjak et al., 2003; Müller et al., 2002).

Over the past few years, AFM force spectroscopy measurements were extended to also probe the dynamical properties of a wide class of single (bio)molecules, including polysaccharides (Humphris et al., 2000), synthetic polymers (Kienberger et al., 2000), nucleic acids (Liu et al., 1999), receptor-ligand complexes (Chtcheglova et al., 2004), and proteins (Mitsui et al., 2000; Okajima et al., 2004). In these experiments, either the sample stage or the AFM cantilever was sinusoidally oscillated and the dynamics of the molecule attached to the cantilever inferred from changes in oscillation amplitude and phase. This approach enabled the separation of the elastic and dissipative contributions to the chair-boat transition of single dextran molecules (Humphris et al., 2000). In apparent contrast, the extension of nucleic acids and poly(ethyleneglycol) was found to be dominated by purely elastic interactions (Kienberger et al., 2000; Liu et al., 1999), and the stretching elasticity of single antibody-antigen bonds could be determined (Chtcheglova et al., 2004). Okajima and co-workers constructed an oscillated sample stage to study the dynamical behavior of bovine carbonic anhydrase II in the millisecond domain (Mitsui et al., 2000; Okajima et al., 2004). An out-of-phase response of the partially unfolded molecule was observed and correlated to refolding of the hydrophobic protein core (Okajima et al., 2004).

In our study, we probed the complex elastic and viscous properties of the membrane protein BR by oscillating the AFM cantilever during mechanical unfolding (force modulation spectroscopy, Fig. 1). BR was chosen as a model system for this study because it represents one of the most extensively studied transmembrane proteins. The structural analysis has revealed the photoactive retinal to be embedded in seven closely packed transmembrane α-helices lettered A–G, a common structural motif among a large class of related G-protein coupled receptors (Baldwin, 1993; Kolbe et al., 2000; Mitsuoka et al., 1999). The purple chromophore and the proton-pumping activity of BR provide convenient biochemical and functional assays for the correct folding of BR. Therefore, and as BR renatures efficiently from a denatured state into the functional protein (Huang et al., 1981), BR has become a paradigm for the folding of α-helical membrane proteins (Booth, 1997).

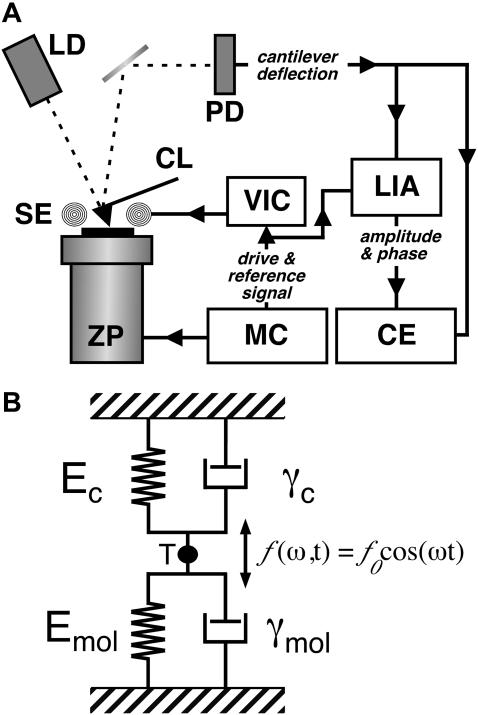
FIGURE 1.

FIGURE 1

Open in a new tab

Illustration of the experimental setup. (A) A commercial AFM with an optical detection system (laser diode (LD) and photodetector (PD)) was equipped with magnetically coated cantilevers (CL) and a magnetic excitation system consisting of a solenoid (SE). The solenoid was driven by a voltage-current converter (VIC) connected to the sinusoidal drive signal from the microscope controller (MC). While controlling the z-position of the piezoelectric actuator (ZP), the cantilever deflection was analyzed in a lock-in amplifier (LIA) to separate amplitude and phase of the oscillation. Amplitude and phase were recorded together with the quasi-static deflection of the cantilever in external capture electronics (CE). (B) The cantilever-molecule system was considered as two VK elements (i.e., a spring and dashpot) acting in parallel, as the motion of the cantilever is detected at its tip (T).

METHODS

Preparation of native BR membranes

Native purple membranes (whose only protein content is BR) were extracted from Halobacterium salinarum as described previously (Oesterhelt and Stoeckenius, 1974) and adsorbed onto freshly cleaved mica from buffer solution (300 mM KCl, 20 mM Tris, pH 7.8) (Müller et al., 1997). All buffer solutions were prepared with nanopure water and pro analysi grade chemicals from Sigma/Merck (St. Louis, MO).

Attachment of BR to the AFM cantilever

In earlier work, we developed two different strategies to attach the C-terminus of BR to the tip of the AFM cantilever. We showed that the thiol group of cysteine-241 of the G241C mutant binds with a likelihood of ≈90% to a gold-coated tip when brought into contact with the cytoplasmic purple membrane surface at forces below 200 pN (Oesterhelt et al., 2000). Although this procedure allows a well-defined attachment, it requires replacement of the AFM cantilever after a few experiments since the tip is covered with bound proteins. An alternative method, nonspecific attachment to a silicon nitride cantilever at slightly higher contact forces, was shown to provide equivalent results and allows a much higher throughput (Müller et al., 2002). We chose the nonspecific attachment as described below.

Single-molecule force modulation spectroscopy

A commercial AFM (Multimode Nanoscope III, Veeco Metrology, Santa Barbara, CA) was equipped with a magnetic cantilever actuation system (Veeco Metrology) and 100 μm long magnetically coated silicon nitride cantilevers (Olympus MAD-OTR4, Veeco Metrology; nominal spring constant ≈0.08 N/m, nominal resonance frequency in buffer ≈7 kHz). The spring constants of the cantilevers were calibrated in solution using thermal fluctuation analysis (Butt and Jaschke, 1995; Florin et al., 1995). To perform force-spectroscopy experiments, we recorded AFM topographs of the cytoplasmic purple membrane surface in 300 mM KCl, 20 mM Tris, and pH 7.8 (Müller et al., 1995). The AFM stylus was then approached to the cytoplasmic membrane surface, kept in contact with the proteins for ≈1 s while applying a force of between 300 and 1000 pN, and then retracted with a velocity of 91 nm/s. In ≈15% of all retraction curves, we detected one or more adhesive peaks. One should note that the experiments were performed at relatively low pulling velocities (compared to many other AFM force measurement studies) due to the measurement bandwidth of the dynamic response of the cantilever. During the force measurements, the cantilever was oscillated at a frequency of 3 kHz with free peak-to-peak amplitudes between 6 and 9 nm. The response of the cantilever was analyzed with a lock-in amplifier (SR830DSP, Stanford Research Systems, Sunnyvale, CA; 1 ms time constant). The in and out of phase motion and deflection of the cantilever were recorded using external data-acquisition electronics (6052E, National Instruments, Munich, Germany) and LABVIEW software at a sampling rate of 11.6 kHz with 16-bit resolution. Except for the quasi-static F-D curves and the superimpositions (see Fig. 3), no smoothing was applied.

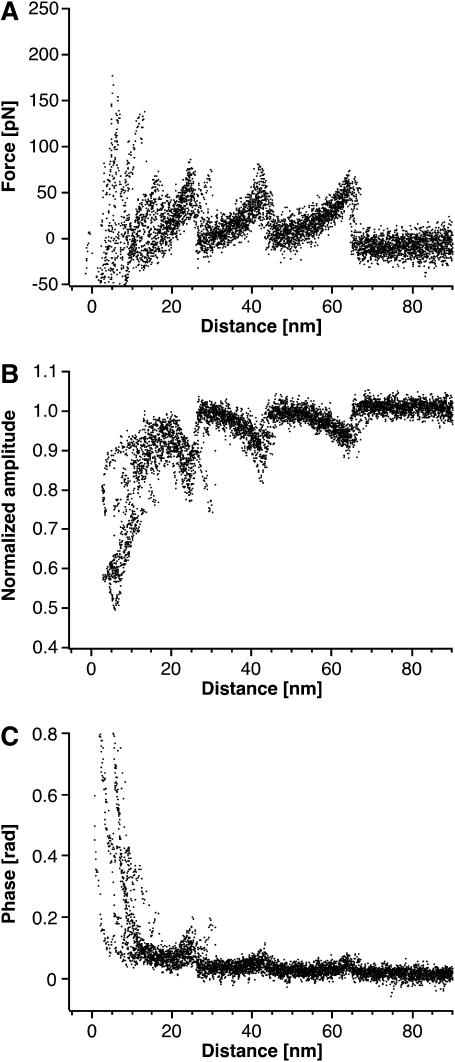
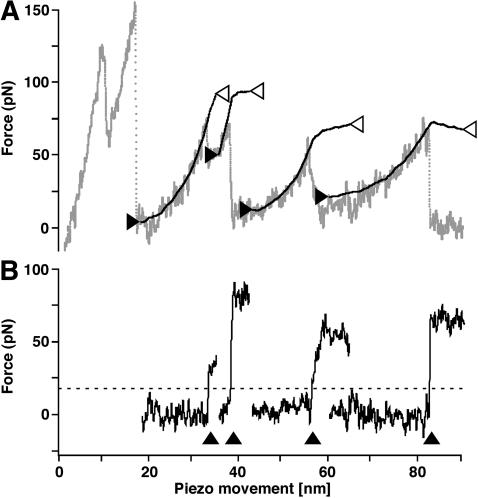
FIGURE 3.

FIGURE 3

Open in a new tab

Force modulation spectroscopy of single BRs. (A) A superimposition of 15 F-D curves each recorded while unfolding a single BR molecule. The overlaid curves show a reproducible unfolding pattern similar to that observed in conventional unfolding experiments of BR (Fig. 2 A). (B and C) Application of a small oscillation to the cantilever allows the measurement of the amplitude (B) and phase (C) response of single proteins. The A-D and phase-distance curves were superimposed with the same distance offsets as the corresponding F-D curves. The amplitude of the cantilever oscillation decreased by up to ≈50% during the force curve, whereas the phase response showed less clear events.

Force curve analysis

A clear criterion is required to distinguish unfolding curves where BR molecules attached to the AFM tip with different regions of their polypeptide backbone. One suitable criterion is the overall length of the F-D curve, i.e., the tip-sample distance at which the last force peak occurs (Oesterhelt et al., 2000). It is evident that a molecule attached to the cantilever by one of its loops results in a F-D curve of smaller overall length than a molecule attached by one of its termini. We have previously shown that F-D curves exhibiting an overall length between 60 and 70 nm result from completely unfolded and extended BR molecules attached with their C-terminus to the AFM tip (Müller et al., 2002; Oesterhelt et al., 2000). To assign events in the F-D spectra to the unfolding of secondary structure elements, every peak of the curves was fitted using the wormlike chain (WLC) model (solid lines in Figs. 2 and 5) with a persistence length (lp) of 4 Å (Müller et al., 2002; Rief et al., 1997). The WLC model describes the force-extension relationship F(x) of an unfolded polypeptide according to (Rief et al., 1997):

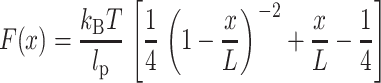graphic file with name M1.gif

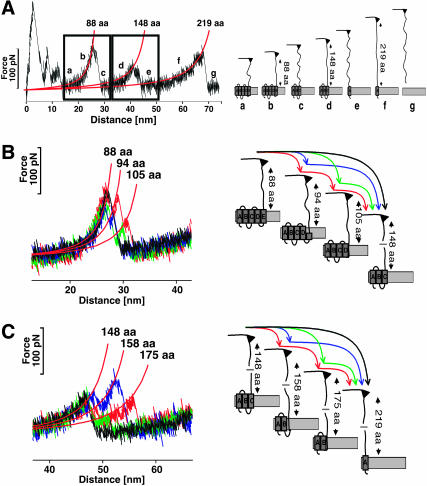
FIGURE 2.

FIGURE 2

Open in a new tab

Unfolding pathways of individual BRs. (A) Conventional F-D curve (left) showing a typical unfolding spectrum of a single BR together with the schematic unfolding pathway (right). The first peaks detected at tip-sample separations below 15 nm indicate the unfolding of helices F and G. However, nonspecific interactions between the membrane surface and AFM tip make a detailed analysis of the first peaks difficult. After unfolding these elements, 88 aa are tethered between the tip and the surface (a). Separating the tip further from the surface stretches the polypeptide (b), thereby exerting force to helices E and D. At a certain critical load, helices E and D unfold in one event. As the number of aa linking the tip and the surface is now increased to 148, the cantilever relaxes (c). In a next step, 148 aa are extended, thereby pulling on helix C (d). After unfolding helices B and C in a single step, the molecular bridge is lengthened to 219 aa (e). By further separating tip and membrane, helix A unfolds (f) and the polypeptide is completely extracted from the membrane (g). (B and C) Unfolding individual secondary structure elements. (B) Occasionally the first unfolding peak (88 aa) shows two shoulder peaks, which indicate the stepwise unfolding of the helical pair. If both shoulders occur, the peak at 88 aa indicates the unfolding of helix E, the peak at 94 aa of loop D-E, and the peak at 105 aa corresponds unfolding of helix D. (C) The shoulder peaks of the second peak indicate the stepwise unfolding of helices C and B and loop B-C. The peak at 148 aa indicates the unfolding of helix C, the peak at 158 aa of the loop BC, and the peak at 175 aa represents unfolding of helix B.

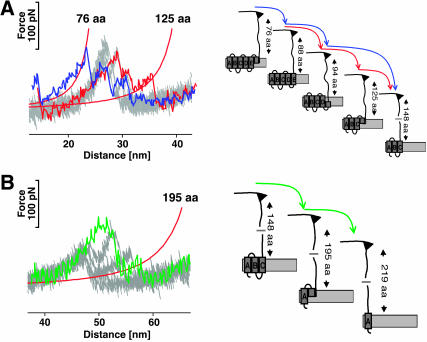
FIGURE 5.

FIGURE 5

Open in a new tab

Force modulation spectroscopy reveals new unfolding intermediates. Additional unfolding events were observed during forced modulation unfolding of BR indicating the presence of novel unfolding intermediates. In the left frames, the curves from the conventional pulling experiment (Fig. 2, B and C) are shown in gray, whereas individual force modulation F-D curves are overlaid. The selected curves show the three new unfolding peaks, each of which was detected in ≈50% of all curves. Fitting these peaks with the WLC model revealed that they correspond to the extension of 76, 125 (A), and 195 (B) aas. As for any of the other force events, the positions of the peaks allow localizing the corresponding unfolding barriers and unfolding intermediates in the structure of the protein (right frames).

The number of aa extended at each unfolding step was calculated using the contour length (L) obtained from the WLC fit curves and a monomer length of 3.6 Å (Müller et al., 2002; Rief et al., 1997). To correlate these polypeptide lengths with the BR structure, the atomic models of Mitsuoka et al. (1999) and Essen et al. (1998) were chosen. To derive the unfolding forces and probabilities, every event of each curve was analyzed.

Reconstruction of F-D curves

Each F-D curve was reconstructed by integrating the corresponding amplitude-distance (A-D) curve according to Eq. 10 using Igor Pro (Wavemetrics, Lake Oswego, OR). Except for the exemplary curves shown in Fig. 6 A, the A-D curves were integrated in a 4 nm window sliding over the curves with 0.4 nm steps. By subtracting the measured F-D data (Fig. 6 A, shaded line) from the reconstructed F-D data (Fig. 6 A, solid lines), a difference curve was calculated for each step (Fig. 6 B, solid lines). From Fig. 6 A, it becomes clear that, in cases where the reconstruction was performed over a force peak, the reconstructed and measured curves poorly overlap in areas after the force peak. Consequently, a sudden increase in the difference curve is observed at the force peaks (Fig. 6 B, arrowheads), and we have used a difference threshold of 20 pN (Fig. 6 B, dashed line) to identify and localize force events.

FIGURE 6.

FIGURE 6

Open in a new tab

Reconstruction of a F-D curve. (A) Experimental F-D curve (shaded line) was reconstructed from the corresponding A-D curve in several segments (solid black lines flanked by two arrowheads). The x-position of the arrowheads corresponds to the point where the integration of each segment was started (solid arrowheads) or stopped (open arrowheads). Consequently, the y-positions of the solid arrowheads correspond to the constant C in Eq. 10 for each segment. Excellent agreement between reconstructed and measured data is obtained for areas of elastic polypeptide extension, whereas no agreement was observed if the reconstruction was performed over force peaks. (B) For each segment,a difference curve was calculated by subtracting the measured data from the reconstructed data. As the poor overlap between reconstructed and measured data leads to a sudden increase in the difference curve (arrowheads), this approach can be used to detect unfolding events in F-D curves. For the detection routine, we have used a threshold of 20 pN (dashed line).

RESULTS AND DISCUSSION

Mechanical unfolding of single-membrane proteins

Recently, the combination of force microscopy imaging and single-molecule force spectroscopy allowed the measurement of the forces stabilizing single-membrane proteins such as BR (Müller et al., 2002; Oesterhelt et al., 2000) and halorhodopsin (Cisneros et al., 2005) from H. salinarum, human aquaporin-1 from red blood cells (Möller et al., 2003), and the Na+/H+ antiporter NhaA from Escherichia coli (Kedrov et al., 2004). To this end, one of the termini of the protein is attached to the tip of the AFM cantilever either by a covalent bond or, more commonly, by nonspecific attachment (Müller et al., 2002; Oesterhelt et al., 2000). Individual proteins are then unfolded and extracted from the membrane bilayer using the AFM cantilever as a force transducer applying an external pulling force (Fig. 2 A). Attachment of the polypeptide loops connecting the helices is excluded by limiting the analysis to F-D traces that show the length of a fully unfolded molecule (see “Methods”).

In contrast to most globular proteins (Best et al., 2001; Rief et al., 1997), the secondary structure elements of BR unfold in a well-defined sequence, thereby allowing the detection of mechanical unfolding intermediates and different unfolding pathways (Müller et al., 2002). Consequently, the extension of already unfolded elements results in F-D spectra with a characteristic saw-toothlike pattern (Fig. 2). Analyzing the extension pattern with the WLC model (Fig. 2, A–C, red lines) and correlating it to the three-dimensional structure of BR allowed the assignment of the discrete peaks in the F-D spectra to the unfolding of individual secondary structure elements, such as transmembrane α-helices or polypeptide loops (Müller et al., 2002) (Fig. 2, A–C). The inter- and intramolecular interactions stabilizing these structural elements were quantified in terms of the unfolding forces and the underlying energy landscape (Janovjak et al., 2004; Müller et al., 2002). It was shown that each folded secondary structure element exhibits a free-energy minimum confined by a single potential barrier (Janovjak et al., 2004). Although single helices were sufficiently stable to unfold individually, they at the same time exhibited a distinct probability to unfold pairwise, thereby forming a collective potential barrier (Janovjak et al., 2004; Müller et al., 2002).

Probing the dynamic properties of BR

To investigate the viscous and elastic contributions to the mechanical unfolding of a single-membrane protein, a sinusoidal drive signal was supplied to the AFM cantilever. Avoiding contributions of 1/frequency noise and allowing sufficient oscillations per sampling period, an off-resonance modulation frequency of 3 kHz was chosen. A direct cantilever excitation method based on an alternating magnetic field and magnetically coated cantilevers was used to oscillate the cantilever with free peak-to-peak amplitudes ranging between 6 and 9 nm. Magnetic excitation (Han et al., 1996; Lindsay et al., 1993), as well as other direct excitation methods (Enders et al., 2004; Rogers et al., 2002), enable the drive signal to be directly related to the drive force and thus to the response of the cantilever. In addition, a substantial signal/noise advantage may be obtained if the tip is directly oscillated (Han et al., 1996; Lindsay et al., 1993) as opposed to indirect mechanical excitation with an acoustic transducer (Putman et al., 1994; Schäffer et al., 1996). Finally, the application of a lock-in technique enabled the measurement of the A-D and phase-distance curves during the mechanical unfolding of single BR molecules. A schematic of the AFM used is shown in Fig. 1.

A superimposition of 15 F-D curves each recorded while unfolding a single BR and the corresponding dynamic responses are shown in Fig. 3. As in conventional force spectroscopy experiments, the F-D curves in Fig. 3 A were obtained from the quasi-static deflection of a cantilever with a known spring constant. Overlaying the curves according to their last peak reveals the typical, highly reproducible unfolding pattern of BR (compare to Fig. 2 A). The amplitude and phase signals were overlaid using the distance-offsets determined by the superimposition the corresponding F-D curve (Fig. 3, B and C). To compare the A-D curves, each one was normalized with the free oscillation amplitude displaying a reproducible pattern among the A-D curves. During the extension of unfolded elements, the oscillation amplitude of the cantilever decreased to ≈50% of the initial value (Fig. 3 B). In contrast, the phase response of individual unfolding events was only slightly above the experimental noise (Fig. 3 C). It is important to note that events observed in the phase and amplitude channels coincided with the unfolding peaks observed in the F-D curve (also see Fig. 4).

FIGURE 4.

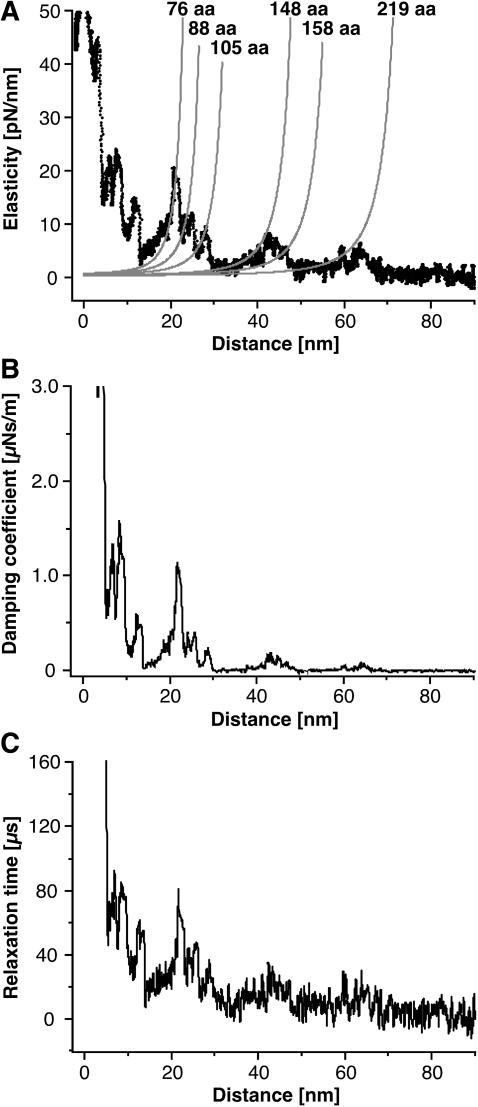
FIGURE 4

Open in a new tab

Elastic and dissipative response of BR. The elasticity of the extended parts of BR as well as the relaxation time and the damping coefficient corresponding to unfolding events are derived from the amplitude and phase response. (A) Fitting the elasticity curves with the derivative of the WLC model (Eq. 8) indicates the characteristic unfolding spectrum of BR to consist of purely elastic polypeptide extension. (B and C) Discrete events are observed in the damping coefficient and the relaxation time of the molecules.

Elastic and dissipative response while unfolding a single molecule

To examine the elastic and viscous contributions to the unfolding of single BRs, we converted the amplitude and phase response to obtain elasticity and damping curves. Our analysis assumes that the drive frequency (ω) is significantly below the resonance frequency of the cantilever, and therefore the inertia of the cantilever can be neglected. In this off-resonance approach, an increased sensitivity is achieved by excluding the thermal fluctuations of the cantilever at all frequencies apart from the bandwidth of the measurement centered at the modulation frequency (Hoffmann et al., 2001).

For our analysis we have considered the molecule and cantilever as two single Voigt-Kelvin (VK) elements acting in parallel (Fig. 1 B) as suggested by Pethica and Oliver (1987). As both VK elements are directly connected to the tip (and not one via the other), the experimental situation (as shown in Fig. 1 B) is equivalent to a more classical parallel assembly where both VK elements are connected to the same surface (Pethica and Oliver, 1987). Consequently, the system can be described by the following equation of motion:

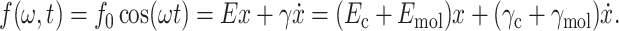graphic file with name M2.gif (1)

Here, E is the elasticity and γ is the damping of the cantilever-molecule system, Ec and Emol are the elasticity, γc and γmol are the damping of the free cantilever and molecule, respectively, and 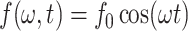Inline graphic denotes the sinusoidal drive force supplied to the cantilever. Thus, the viscoelastic properties of the molecule attached between the tip and surface can be related to E and γ. Assuming higher harmonics are small and negligible, the response of the cantilever has the form 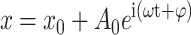Inline graphic and Eq. 1 has a solution of the form

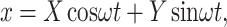graphic file with name M5.gif (2)

where X and Y can be directly measured with a lock-in amplifier. Equation 2 has a proper solution,

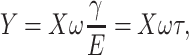graphic file with name M6.gif (3)

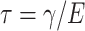where Inline graphic is called the relaxation time of the system. The observed amplitude (A) and phase (ϕ) response of the cantilever can be expressed as (Schultz, 1974)

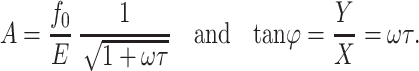graphic file with name M8.gif (4) and (5)

Thus, the phase response of the cantilever can be used to calculate the relaxation time of the system using Eq. 5. Substituting Eq. 5 into Eq. 4 produces

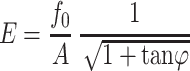graphic file with name M9.gif (6)

from which γ can be derived using τ. In the above equations, 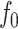Inline graphic denotes the peak sinusoidal drive force. By defining the phase response of the system as zero when the cantilever is oscillating freely above the surface, the peak drive force is

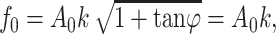graphic file with name M11.gif (7)

where A0 denotes the free peak amplitude and k the quasi-static spring constant of the cantilever. Following Eqs. 4, 5, 6, and 7, the elastic and viscous response of a single molecule can be calculated from the dynamic response of the cantilever.

Elastic polypeptide extension and dissipative unfolding events

The molecular elasticity, damping coefficient, and relaxation time of a single BR molecule are shown in Fig. 4. As discussed above, the characteristic saw-toothlike unfolding pattern of BR stems from the extension of already unfolded secondary structure elements, whereas other elements remain anchored in the membrane. As the F-D curves can be well described using the WLC model, the elasticity curve should obey the derivative of the WLC F-D relationship, 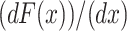Inline graphic, according to (Kienberger et al., 2000; Marko and Siggia, 1995),

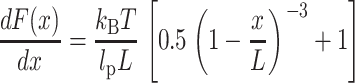graphic file with name M13.gif (8)

Fig. 4 A clearly shows, that the peaks in the elasticity curve are well-described by Eq. 8 using the indicated number of aas and the same persistence and monomer length as in Fig. 2 (lp = 4 Å, monomer length = 3.6 Å). The good agreement between the experimental curve and the predicted elasticity pattern shows that such a typical unfolding spectrum consists of the purely elastic extension of unfolded polypeptides (also see Fig. 6). As expected from an estimation of the slopes of the F-D curves, the stiffness of the extended polypeptide fragments was of the order of a few ten pN/nm.

As for the elasticity, discrete events were observed in the dissipative response of the molecules (Fig. 4, B and C). The positions of the peaks, and as we could show that the extension of the unfolded polypeptide fragments is mostly elastic, suggest that these interactions are associated with the unfolding of secondary structure elements. Surprisingly, the dissipative interactions decrease strongly after the first force peak occurring at a tip-sample distance of 25 nm (Fig. 4 B). This indicates, that the unfolding of the first few helices disrupts the tertiary structure of the protein and therefore lowers the dissipative contribution to the unfolding of the remaining helices. However, dissipation is measured for all helices of BR in agreement with experimental observations that individual helices are folded in the membrane bilayer (Popot et al., 1987). Therefore our measurements provide novel means to quantify the stability of the secondary structure elements of single proteins. However, additional experiments with an improved signal/noise ratio will be required to exclude effects such as solvent damping to provide a more precise picture of the energy dissipated during protein unfolding events.

At this very point, we recognize that the possibility to detect dissipative and elastic contributions during protein unfolding builds one important step toward unraveling the different interactions that establish the structure-function relationship of proteins. Although BR represents one of the most extensively studied membrane proteins, it is not clear which forces kink helices or to which extent hydrophobic or packing interactions contribute to the stability of the transmembrane helices (Faham et al., 2004). In the near future, more advanced force measurement techniques will not only allow separating dissipative and elastic contributions but provide an exact time-resolved picture at which instances individual interactions contribute to the complex mechanisms of protein folding, unfolding, and misfolding.

New force events observed in force modulation spectroscopy

Surprisingly, the F-D curves obtained in the force modulation experiments locally differed from F-D curves collected in conventional force spectroscopy experiments. To compare the F-D traces from the two types of experiment, we first applied a peak finding algorithm. This analysis revealed the appearance of three new force peaks in the oscillatory F-D curves. These events are located at 76 aa, 125 aa, and 195 aa extension lengths, observed in 53.3% (75 aa), 43.3% (125 aa), and 45% (195 aa) of the curves (n = 60) and of comparable intensity as the other peaks (50–80 pN) (Fig. 5).

Additional evidence for the presence of these events in F-D curves was obtained from the corresponding A-D curves as, in regimes of purely elastic extension (see above), F-D curves can be reconstructed by integrating A-D curves (Liu et al., 1999; Pethica and Oliver, 1987). In the absence of dissipation, a change in stiffness S(z) is detected by the cantilever as a change in oscillation amplitude. Under the assumption the oscillation amplitude is small, S(z) can be written as

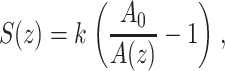graphic file with name M14.gif (9)

where A0 denotes the free oscillation amplitude and, as introduced above, A(z) is the amplitude as a function of tip-surface distance (Liu et al., 1999; Pethica and Oliver, 1987). Integrating Eq. 9 yields Eq. 10 and thus the possibility to recalculate F-D curves from A-D curves, often even with an increased signal/noise ratio (Kienberger et al., 2000):

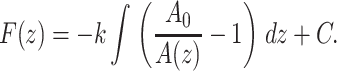graphic file with name M15.gif (10)

In Eq. 10, C denotes the force at the point where the integration was started. Fig. 6 shows a reconstructed F-D curve in excellent agreement with the measured curve in the regions of elastic polypeptide extension (see above). From Fig. 6 A and Eq. 10, it is also apparent that the reconstruction will not be successful in regimes where the slope of the F-D curves is negative as the integral of the amplitude is always positive (Liu et al., 1999; Pethica and Oliver, 1987). Thus, a disagreement between measured and reconstructed data can be used to identify unfolding events as, in these cases, the force always decreases with displacement. Following this approach, we verified the position of all previously found and the three new force peaks (data not shown).

Stepwise unfolding or refolding of transmembrane α-helices?

We suggest two possible explanations for the appearance of new force peaks in the force modulation F-D curves. First, these events could correspond to additional unfolding intermediates during the mechanical manipulation of BR (Fig. 5). It should be noted that in the experiments described here, the pulling speed and therefore the loading rate applied to the transmembrane helices is not comparable to quasi-static force spectroscopy experiments. Due to the oscillatory movement of the cantilever, tip velocities as high as ≈15 μm/s are reached both toward and away from the direction of the quasi-static pulling force. However, the tip velocity will decrease and eventually reach zero as the tip approaches the maximum deflection during each oscillation. In a recent study, we showed that the detection of unfolding intermediates in BR depends on the pulling velocity and an increased velocity lead to the observation of a greater number of intermediates (Janovjak et al., 2004). Therefore, one could conclude that the oscillatory movement of the cantilever reveals new mechanical unfolding pathways in the energy landscape of the protein. In this scenario, the data suggest that stable intermediates are formed by the upper halves of helices F, D, and B, which remain folded even after the lower halves of these helices were unfolded (Fig. 5, A and B, right frames). As proposed earlier for helices E and G (Müller et al., 2002) and helix E of Halorhodopsin (Cisneros et al., 2005), helices F, D, and B obviously can follow two different unfolding pathways, in one of which they do not undergo cooperative unfolding.

For a different interpretation, it is important to consider that the quasi-static deflection of the cantilever (≈1 nm) is relatively small compared to the cantilever oscillation amplitude (≈3–5 nm peak-to-peak during polypeptide extension). Thus, ≈11 aa (≈4 nm) long unfolded polypeptide segments will be periodically relaxed toward the surface during the cantilever oscillation and thereby eventually refold or aggregate. This scenario seems to be less probable than the first one, as new force peaks are only and reproducibly detected at three well-defined positions. In addition, the cantilever often does not fully relax after an unfolding event. This results in a small but maintained force applied to the polypeptide, which may prohibit recoiling or refolding. However, one should note that we recently refolded single-membrane proteins into the membrane bilayer by relaxing unfolded and fully stretched polypeptides (Kedrov et al., 2004).

Structural origin of the unfolding intermediates

Finding a structural explanation for the unfolding intermediate observed in helix D is not straightforward, especially as molecular dynamics simulations of the forced unfolding of BR are currently not available. However, the positions of the intermediate detected in helices B and F (Fig. 5) correlate very well with the center of the kinks of these helices. Like many transmembrane helices of other membrane proteins, helices B and F are tilted and exhibit kinks centered at proline residues 50 and 186, respectively. To learn about the structural importance of these residues, the group of James Bowie replaced them with alanines (Faham et al., 2004; Yohannan et al., 2003). Surprisingly, the thermal stability of BR was not altered by these mutations, nor was the proteins' structure significantly affected. Thus, it was concluded that the kink of wild-type and mutant helices originates from cumulative interactions of surrounding residues rather than the presence of prolines. In addition, our data indicate that the kinks are responsible for the detection of two unfolding intermediates for each of these two helices. It may be assumed that further developments of single-molecule force spectroscopy will allow detecting the contributions of individual aa residues stabilizing such unfolding intermediates.

CONCLUSIONS

Here, we present an extension to the existing AFM forced unfolding experiments of single proteins. In addition to monitoring the deflection of the cantilever, a small vertical oscillatory motion was supplied to the tip of the cantilever. Considering the cantilever-molecule system as two VK elements acting in parallel, we determined the complex viscoelastic response of single-membrane proteins. We were able to measure the damping associated with the unfolding of single transmembrane helices and provide a direct and continuous measurement of the elasticity of single polypeptide strands. We also showed that such force modulation spectroscopy experiments can uncover novel mechanical unfolding intermediates of a single protein. In particular, we found that transmembrane helices do now always follow a cooperative unfolding pathway and that kinks result in a loss of unfolding cooperativity of transmembrane helices. This highlights that our method provides a more detailed picture of a protein's mechanical energy landscape.

Acknowledgments

The authors thank J. Hobbs, D. Cisneros, A. Kedrov, M. Stark, and M. Miles for stimulating discussions.

A.D.L.H. is thankful to the Royal Commission for the Exhibition of 1851.

The Deutsche Volkwagenstiftung, European Union, and Free State of Saxony supported H.J. and D.J.M.

References

  1. Baldwin, J. M. 1993. The probable arrangement of the helices in G protein-coupled receptors. EMBO J. 12:1693–1703. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Best, R. B., B. Li, A. Steward, V. Daggett, and J. Clarke. 2001. Can nonmechanical proteins withstand force? Stretching barnase by atomic force microscopy and molecular dynamics simulation. Biophys. J. 81:2344–2356. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Binnig, G., C. F. Quate, and C. Gerber. 1986. Atomic force microscope. Phys. Rev. Lett. 56:930–933. [DOI] [PubMed] [Google Scholar]
  4. Booth, P. J. 1997. Folding alpha-helical membrane proteins: kinetic studies on bacteriorhodopsin. Fold. Des. 2:R85–R92. [DOI] [PubMed] [Google Scholar]
  5. Booth, P. J., R. H. Templer, A. R. Curran, and S. J. Allen. 2001. Can we identify the forces that drive the folding of integral membrane proteins? Biochem. Soc. T. 29:408–413. [DOI] [PubMed] [Google Scholar]
  6. Butt, H. J., and M. Jaschke. 1995. Calculation of thermal noise in atomic force microscopy. Nanotechnology. 6:1–7. [Google Scholar]
  7. Chtcheglova, L. A., G. T. Shubeita, S. K. Sekatskii, and G. Dietler. 2004. Force spectroscopy with a small dithering of AFM tip: a method of direct and continuous measurement of the spring constant of single molecules and molecular complexes. Biophys. J. 86:1177–1184. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Cisneros, D., D. Oesterhelt, and D. J. Müller. 2005. Probing origins of nolecular interactions stabilizing the membrane proteins halorhodopsin and bacteriorhodopsin. Structure. In press. [DOI] [PubMed]
  9. Enders, O., F. Korte, and H. A. Kolb. 2004. Lorentz-force-induced excitation of cantilevers for oscillation-mode scanning probe microscopy. Surf. Int. Anal. 36:119–123. [Google Scholar]
  10. Essen, L., R. Siegert, W. D. Lehmann, and D. Oesterhelt. 1998. Lipid patches in membrane protein oligomers: crystal structure of the bacteriorhodopsin-lipid complex. Proc. Natl. Acad. Sci. USA. 95:11673–11678. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Faham, S., D. Yang, E. Bare, S. Yohannan, J. P. Whitelegge, and J. U. Bowie. 2004. Side-chain contributions to membrane protein structure and stability. J. Mol. Biol. 335:297–305. [DOI] [PubMed] [Google Scholar]
  12. Florin, E. L., M. Rief, H. Lehmann, M. Ludwig, C. Dornmair, V. T. Moy, and H. E. Gaub. 1995. Sensing specific molecular-interactions with the atomic force microscope. Biosensors. Bioelectr. 10:895–901. [Google Scholar]
  13. Han, W. H., S. M. Lindsay, and T. W. Jing. 1996. A magnetically driven oscillating probe microscope for operation in liquids. Appl. Phys. Lett. 69:4111–4113. [Google Scholar]
  14. Hoffmann, P. M., S. Jeffery, J. B. Pethica, H. O. Ozer, and A. Oral. 2001. Energy dissipation in atomic force microscopy and atomic loss processes. Phys. Rev. Lett. 87:265502–265504. [DOI] [PubMed] [Google Scholar]
  15. Huang, K. S., H. Bayley, M. J. Liao, E. London, and H. G. Khorana. 1981. Refolding of an integral membrane protein. Denaturation, renaturation, and reconstitution of intact bacteriorhodopsin and two proteolytic fragments. J. Biol. Chem. 256:3802–3809. [PubMed] [Google Scholar]
  16. Humphris, A. D. L., J. Tamayo, and M. J. Miles. 2000. Active quality factor control in liquids for force spectroscopy. Langmuir. 16:7891–7894. [Google Scholar]
  17. Janovjak, H., M. Kessler, D. Oesterhelt, H. E. Gaub, and D. J. Müller. 2003. Unfolding pathways of native bacteriorhodopsin depend on temperature. EMBO J. 22:5220–5229. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Janovjak, H., J. Struckmeier, M. Hubain, A. Kedrov, M. Kessler, and D. J. Müller. 2004. Probing the energy landscape of the membrane protein bacteriorhodopsin. Structure. 12:871–879. [DOI] [PubMed] [Google Scholar]
  19. Kedrov, A., C. Ziegler, H. Janovjak, W. Kühlbrandt, and D. J. Müller. 2004. Controlled unfolding and refolding of a single sodium-proton antiporter using atomic force microscopy. J. Mol. Biol. 340:1143–1152. [DOI] [PubMed] [Google Scholar]
  20. Kienberger, F., V. P. Pastushenko, G. Kada, H. J. Gruber, C. Riener, H. Schindler, and P. Hinterdorfer. 2000. Static and dynamical properties of single poly(ethylene glycol) molecules investigated by force spectroscopy. Single Mol. 1:123–128. [Google Scholar]
  21. Kolbe, M., H. Besir, L. O. Essen, and D. Oesterhelt. 2000. Structure of the light-driven chloride pump halorhodopsin at 1.8 A resolution. Science. 288:1390–1396. [DOI] [PubMed] [Google Scholar]
  22. Lindsay, S. M., Y. L. Lyubchenko, N. J. Tao, Y. Q. Li, P. I. Oden, J. A. DeRose, and J. Pan. 1993. Scanning tunneling microscopy and atomic force microscopy studies of biomaterials at a liquid-solid interface. J. Vac. Sci. Technol. A. 11:808–815. [Google Scholar]
  23. Liu, Y. Z., S. H. Leuba, and S. M. Lindsay. 1999. Relationship between stiffness and force in single molecule pulling experiments. Langmuir. 14:8547–8548. [Google Scholar]
  24. Marko, J. F., and E. D. Siggia. 1995. Stretching DNA. Macromolecules. 28:8759–8770. [Google Scholar]
  25. Marszalek, P. E., H. Lu, H. Li, M. Carrion-Vazquez, A. F. Oberhauser, K. Schulten, and J. M. Fernandez. 1999. Mechanical unfolding intermediates in titin modules. Nature. 402:100–103. [DOI] [PubMed] [Google Scholar]
  26. Mitsui, K., M. Hara, and A. Ikai. 1996. Mechanical unfolding of alpha(2)-macroglobulin molecules with atomic force microscope. FEBS Lett. 385:29–33. [DOI] [PubMed] [Google Scholar]
  27. Mitsui, K., K. Nakajima, H. Arakawa, M. Hara, and A. Ikai. 2000. Dynamic measurement of single protein's mechanical properties. Biochem. Biophys. Res. Commun. 272:55–63. [DOI] [PubMed] [Google Scholar]
  28. Mitsuoka, K., T. Hirai, K. Murata, A. Miyazawa, A. Kidera, Y. Kimura, and Y. Fujiyoshi. 1999. The structure of bacteriorhodopsin at 3.0 A resolution based on electron crystallography: implication of the charge distribution. J. Mol. Biol. 286:861–882. [DOI] [PubMed] [Google Scholar]
  29. Möller, C., D. Fotiadis, K. Suda, A. Engel, M. Kessler, and D. J. Müller. 2003. Determining molecular forces that stabilize human aquaporin-1. J. Struct. Biol. 142:369–378. [DOI] [PubMed] [Google Scholar]
  30. Müller, D. J., M. Amrein, and A. Engel. 1997. Adsorption of biological molecules to a solid support for scanning probe microscopy. J. Struct. Biol. 119:172–188. [DOI] [PubMed] [Google Scholar]
  31. Müller, D. J., M. Kessler, F. Oesterhelt, C. Möller, D. Oesterhelt, and H. Gaub. 2002. Stability of bacteriorhodopsin alpha-helices and loops analyzed by single-molecule force spectroscopy. Biophys. J. 83:3578–3588. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Müller, D. J., F. A. Schabert, G. Büldt, and A. Engel. 1995. Imaging purple membranes in aqueous solutions at sub-nanometer resolution by atomic force microscopy. Biophys. J. 68:1681–1686. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Oesterhelt, D., and W. Stoeckenius. 1974. Isolation of the cell membrane of Halobacterium halobium and its fractionation into red and purple membrane. Methods Enzymol. 31:667–678. [DOI] [PubMed] [Google Scholar]
  34. Oesterhelt, F., D. Oesterhelt, M. Pfeiffer, A. Engel, H. E. Gaub, and D. J. Müller. 2000. Unfolding pathways of individual bacteriorhodopsins. Science. 288:143–146. [DOI] [PubMed] [Google Scholar]
  35. Okajima, T., H. Arakawa, M. T. Alam, H. Sekiguchi, and A. Ikai. 2004. Dynamics of a partially stretched protein molecule studied using an atomic force microscope. Biophys. Chem. 107:51–61. [DOI] [PubMed] [Google Scholar]
  36. Pethica, J. B., and W. C. Oliver. 1987. Tip surface interactions in STM and AFM. Phys. Scripta. T19 A:61–66. [Google Scholar]
  37. Popot, J. L., S. E. Gerchman, and D. M. Engelman. 1987. Refolding of bacteriorhodopsin in lipid bilayers. A thermodynamically controlled two-stage process. J. Mol. Biol. 198:655–676. [DOI] [PubMed] [Google Scholar]
  38. Putman, C. A. J., K. O. Van der Werf, B. G. De Grooth, N. F. Van Hulst, and J. Greve. 1994. Tapping mode atomic-foce microscopy in liquid. Appl. Phys. Lett. 64:2454–2456. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Radford, S. E. 2000. Protein folding: progress made and promises ahead. Trends Biochem. Sci. 25:611–618. [DOI] [PubMed] [Google Scholar]
  40. Radford, S. E., C. M. Dobson, and P. A. Evans. 1992. The folding of hen lysozyme involves partially structured intermediates and multiple pathways. Nature. 358:302–307. [DOI] [PubMed] [Google Scholar]
  41. Rief, M., M. Gautel, F. Oesterhelt, J. M. Fernandez, and H. E. Gaub. 1997. Reversible unfolding of individual titin immunoglobulin domains by AFM. Science. 276:1109–1112. [DOI] [PubMed] [Google Scholar]
  42. Rogers, B., D. York, N. Whisman, M. Jones, K. Murray, J. D. Adams, T. Sulchek, and S. C. Minne. 2002. Tapping mode atomic force microscopy in liquid with an insulated piezoelectric microactuator. Rev. Sci. Ins. 73:3242–3244. [Google Scholar]
  43. Schäffer, T. E., J. P. Cleveland, F. Ohnesorge, D. A. Walters, and P. K. Hansma. 1996. Studies of vibrating atomic force microscope cantilevers in liquid. J. Appl. Phys. 80:3622–3627. [Google Scholar]
  44. Schultz, J. M. 1974. Sinusoidal loading and the mechanical loss measurement. In Polymer Materials Science. N. R. Amundson, editor. Prentice Hall, Englewood Cliffs, NJ. 371–379.
  45. Weissman, J. S., and P. S. Kim. 1991. Reexamination of the folding of BPTI: predominance of native intermediates. Science. 253:1386–1393. [DOI] [PubMed] [Google Scholar]
  46. Williams, P. M., S. B. Fowler, R. B. Best, J. L. Toca-Herrera, K. A. Scott, A. Steward, and J. Clarke. 2003. Hidden complexity in the mechanical properties of titin. Nature. 422:446–449. [DOI] [PubMed] [Google Scholar]
  47. Yohannan, S., S. Faham, D. Yang, J. P. Whitelegge, and J. U. Bowie. 2003. The evolution of transmembrane helix kinks and the structural diversity of G protein-coupled receptors. Proc. Natl. Acad. Sci. USA. 101:959–963. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES