Abstract
Continuum constitutive laws are needed to ensure that bio-artificial tissue constructs replicate the mechanical response of the tissues they replace, and to understand how the constituents of these constructs contribute to their overall mechanical response. One model designed to achieve both of these aims is the Zahalak model, which was modified by Marquez and co-workers to incorporate inhomogeneous strain fields within very thin tissues. When applied to reinterpret previous measurements, the modified Zahalak model predicted higher values of the continuum stiffness of fibroblasts than earlier estimates. In this work, we further modify the Zahalak model to account for inhomogeneous strain fields in constructs whose cell orientations have a significant out-of-plane component. When applied to reinterpret results from the literature, the new model shows that estimates of continuum cell stiffness might need to be revised upward. As in this article's companion, we updated the average cell strain by defining a correction factor (“strain factor”), based upon the elastic response. Three different cell orientation distributions were studied. We derived an approximate scaling model for the strain factor, and validated it against exact and self-consistent (mean-field) solutions from the literature for dilute cell concentrations, and Monte Carlo simulations involving three-dimensional finite element analyses for high cell concentrations.
INTRODUCTION
The Zahalak (Zahalak et al., 2000) model is a constitutive law that relates the active and passive mechanical response of cells and collagen to the overall response of a bio-artificial tissue construct. Such models are important for ensuring that tissue constructs adequately replicate the mechanical properties of the tissues they replace, and for interpreting experiments designed to probe the mechanical properties of cells and collagen in these constructs.
Zahalak's first-order approximation that cells and matrix deform in registry with one another provides a lower bound on cell stiffness when the Zahalak model is used to interpret cell stiffness from tests on a tissue construct. Except in cases in which cell concentration is sufficiently high that a continuous, “percolated” network of cells forms, cells and matrix experience different average strains even in a uniformly stretched tissue construct. The actual distribution of strain in a construct depends on the details of the cell orientations, and on the relative properties of cells and matrix (e.g., Marquez et al., 2005). This article's companion (Marquez et al., 2005) developed a framework for incorporating into the Zahalak model the average strain field, as predicted by linear elasticity and simple network statistics, for a planar distribution of cells. When reinterpreting results from the literature using this framework, Marquez et al. (2005) found that accounting for the statistical connectivity of a cell network caused estimates of instantaneous continuum cell stiffness to be nearly doubled to 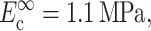 and estimates of fully relaxed cell stiffness to be nearly doubled to
and estimates of fully relaxed cell stiffness to be nearly doubled to 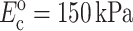 (Table 1).
(Table 1).
TABLE 1.
Cell and matrix stiffness
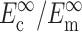 |
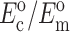 |
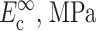 |
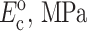 |
|
|---|---|---|---|---|
| Zahalak model (Zahalak, 2000) | 21 ± 15 | 73 ± 32 | 0.09 ± 0.054 | 0.62 ± 0.22 |
| 2D uniform cell distribution (Marquez et al., 2005) | 35 ± 26 | 124 ± 54 | 0.15 ± 0.09 | 1.06 ± 0.37 |
| 3D uniform cell distribution (this article) | 40 ± 30 | 372 ± 163 | 0.17 ± 0.102 | 3.18 ± 1.11 |
Cell stiffness calculated using the unmodified Zahalak model, compared to those calculated using the theory modified for 2D membranes (Marquez et al., 2005) and for 3D cell distributions.
This article addresses the question of how an out-of-plane component to the distribution of cell orientations affects estimates of cell stiffness in tissue constructs. The results show that a tissue with a uniform planar orientation distribution of relatively stiff cells, as in Marquez et al. (2005), will have a greater stiffness than an otherwise identical tissue in which cells are oriented randomly. When interpreting the stiffness of cells from tests on bio-artificial tissue constructs, the assumption of a uniform planar cell distribution and a three-dimensional (3D) uniform cell distribution can be viewed as opposite extremes, which, as we show, may bound the actual cell moduli.
We arrived at these conclusions by developing a model to account for the average strain in cells in a tissue construct. Three specific 3D cell orientation distributions were studied (fully aligned, 3D planar and 3D uniform distributions). Modified estimates of average cell strain were incorporated into the Zahalak model through a scaling term called a “strain factor”, and a framework was developed for backing out cell stiffness from the results of tests on tissue constructs.
The focus in this work is tissue constructs consisting of fibroblasts in a reconstituted collagen matrix. In these constructs, the fibroblasts are stiffer than the matrix, except at very high strains (Wakatsuki et al., 2000). Linear elasticity and small strain theory were employed as first-order approximations; limitations of these approximations are addressed in this article's companion (Marquez et al., 2005), and discussed in detail by Prager (1969). We approximated cells as being cylindrical and perfectly bonded to the matrix, and found strain factors for different cell and matrix parameters when these idealized constructs were subjected to uniaxial stretching.
Background
Strain factors, and their incorporation into the Zahalak model
In this article's companion (Marquez et al., 2005), a two-dimensional (2D) model for the strain factor was developed, and incorporated into the Zahalak constitutive law. This model was a scaling model that was calibrated and validated against exact solutions and Monte Carlo simulations for idealized tissues with low cell concentration. A “percolation model” extended this scaling model to constructs with very high cell densities, including cell densities at which cells overlap, through application of network statistics. The percolation model was validated against Monte Carlo simulations involving finite element (FE) estimates of exact linear elasticity solutions for strain factors in idealized tissues.
Marquez et al. (2005) showed that the average strain tensor 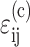 in cells embedded in a thin membrane is related to the average strain tensor ɛij in the entire membrane by a scalar called the “strain factor”, S, so that
in cells embedded in a thin membrane is related to the average strain tensor ɛij in the entire membrane by a scalar called the “strain factor”, S, so that 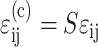 to within a reasonable approximation. When incorporated into the Zahalak model, the general equation governing the response of the cells to a remote strain field ɛij is given as
to within a reasonable approximation. When incorporated into the Zahalak model, the general equation governing the response of the cells to a remote strain field ɛij is given as
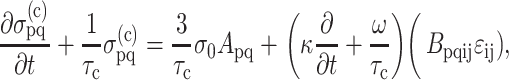 |
(1) |
where, σo = 1/3 N l Fo, N is the cell concentration (number of cells per unit volume), l is the cell length, Fo is the active axial cell force, A and B are “anisotropy tensors” that account for the cell orientation distribution, τc is the cell time constant, κ and ω are constants to be determined experimentally, and repeated indices imply summation. (Zahalak et al., 2000). The instantaneous and long-term mechanical responses of cells are linear. κ and ω can be related to the instantaneous elastic modulus 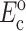 and long-term elastic modulus
and long-term elastic modulus 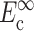 of the cells by
of the cells by
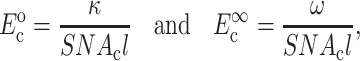 |
(2) |
or
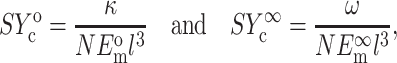 |
(3) |
where Ac is the cross-sectional area of a cell, 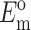 and
and 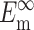 are the instantaneous and long-term elastic moduli of the matrix, and the “normalized stiffnesses” of the cell are defined by
are the instantaneous and long-term elastic moduli of the matrix, and the “normalized stiffnesses” of the cell are defined by
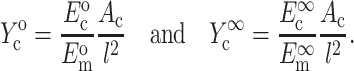 |
(4) |
The anisotropy tensors are defined as the integrals of the cell orientation unit vector n in all directions Ω, as follows:
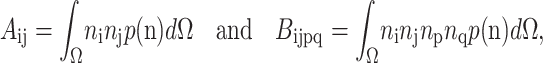 |
(5) |
where p(n)dΩ is the probability that a cell in the volume dΩ points in the direction of n.
The full tissue constitutive relation has the form
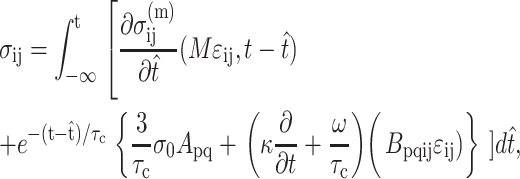 |
(6) |
where 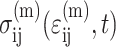 is the average matrix stress at time t, and M is the factor relating the average matrix stain
is the average matrix stress at time t, and M is the factor relating the average matrix stain 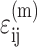 to the remote strain field
to the remote strain field 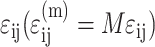 :
:
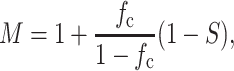 |
(7) |
in which fc is the volume fraction of cells in the tissue. The instantaneous and long-term responses of the matrix were approximated to first order as linear elastic in this work.
This model applies to the 3D cellular distributions of interest in this article. The missing ingredient is the correct functional form of the 3D strain factor, S, for 3D cell distributions.
Micromechanical models used to estimate strain factors
The micromechanical models we employed to estimate the strain factor fall into two groups: models based on Eshelby's (Eshelby, 1957) solution, and models based upon numerical simulation of repeating microstructures (“unit cells”). The following summarizes the models we used, and their specific implementation in this article.
Eshelby-based approaches
Methods based upon Eshelby's solution describe the microgeometries of inhomogeneous materials with statistical “self-consistent” (“mean-field”) approaches (Budiansky, 1965; Hill, 1965), in which elastic fields within each constituent are approximated by their averages. Such descriptions can use information about the microscale geometry, the cell shape and orientation, and, to a limited extent, the statistics of the cell distribution. The three approaches we employed were Eshelby's exact solution (Eshelby, 1957, 1959), the Mori-Tanaka method (Mori and Tanaka, 1973), and a very important recent extension to the Mori-Tanaka approach by Chen and Cheng (1996). These are valid for low and moderate concentrations of cells. We used these models to validate the continuum predictions of the approximate scaling model at very low cell concentrations.
Strain factor for dilute cell populations: Eshelby's solution
Eshelby's equivalent inclusion approach (Eshelby, 1957, 1959) provides an exact solution for the uniform strain field inside an isolated, ellipsoidal, linear elastic cell in a linear elastic matrix as a function of the remote strain. This was specialized to the case of long, slender, isotropic, relatively stiff, aligned ellipsoidal cells in Appendix A to obtain an analytical estimate of the strain factor at very low cell concentrations. For the case of νm = νc = 0.5, this expression can be written as
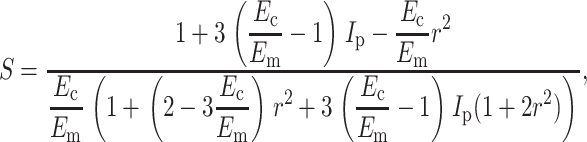 |
(8) |
where
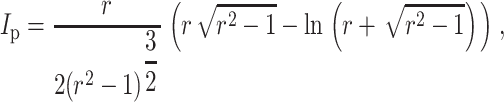 |
(9) |
in which r = l/d is the aspect ratio of the cells (long axis/short axis), Ec and νc are the elastic modulus and Poisson's ratio of the cells, and Em and νm are those of the matrix (e.g., Jones, 1998).
Extension to moderately dilute cell populations
We extended these estimates to slightly higher cell concentrations, with the aim of validating the trends predicted by our statistical model for cell interactions. We used two results from the literature for this purpose. The first was that of Mori and Tanaka (1973), who extended the Eshelby solution to include moderate concentrations of cells by modifying the average matrix stress to approximately account for the perturbation caused by the presence of identical neighboring cells. Mori and Tanaka assumed that when many identical cells are introduced in the tissue, the average cell strain is given by 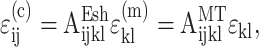 where AEsh is defined in Appendix A, and
where AEsh is defined in Appendix A, and
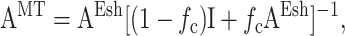 |
in which fc is the cell volume fraction and I is the fourth-rank unit tensor. The strain factor for an aligned cell distribution may be found from this by replacing AEsh with AMT in Eq. A1.
The second result we employed was that of Chen and Cheng (1996), who extended the Mori-Tanaka approach to short-fiber composites with random orientation distributions. In the Mori-Tanaka approach, the average tissue stiffness, CMT, is
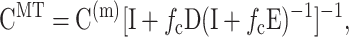 |
where
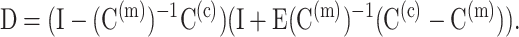 |
Chen and Cheng replace D and E with their volumetric averages, 〈D〉 and 〈E〉, over all possible cell orientations n:
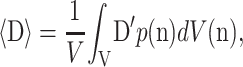 |
(10) |
where V is a statistically representative volume of tissue, and D′ represents the values of D for a cell pointing in the direction of n. Then,
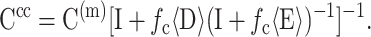 |
(11) |
We approximated strain factors from this generalization by using an approach motivated by the result derived in Appendix B, indicating a linear relationship between the strain factor and the effective modulus of the material surrounding a cell: we assumed that the strain factor in both the Mori-Tanaka and Chen-Cheng models were the same when the environment of each individual cell is similar; that is, when 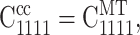 where the 1-direction lies parallel to a cell.
where the 1-direction lies parallel to a cell.
Unit cell approaches
The second group of models is based on numerical analysis of discrete repeating microstructures, and includes “periodic microfield” approaches and “unit cell” methods (e.g., Wu et al., 1989, Bohm and Han, 2001). These approaches can provide numerical approximations to exact solutions for tissues in which the cellular orientations and spacing have a periodic pattern, and were used in our work to 1), calibrate the scaling model for tissues with low cell densities, and 2), validate the statistical extension of the scaling model to tissues with higher cell densities. Applying these approaches to random cellular distributions is a challenge, especially in cases of high cell concentration, but Monte Carlo simulations involving finite element analyses of representative tissue structures can be used as a homogenization procedure.
Overlap in dense cell populations
The scaling model for the strain factor in tissues with low cell densities was extended to tissues with higher cell densities by incorporating the statistically expected overlap of random networks of straight, identical cylindrical cells. Kallmes and Corte (1960) address percolation in fibrous networks through a statistical relationship for the number of cells, Ni, that each cell would expect to intersect in a tissue containing cylindrical cells of length l and diameter d. For tissues in which cells follow a 3D random orientation distribution,
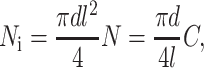 |
(12) |
where N is the number of cells per unit volume in the tissue, and C ≡ Nl3 is the dimensionless cell concentration. This can be written in terms of average cell spacing, b, by noting that C = (l/b)3, and in terms of cell volume fraction fc and cell volume Vc by noting that C = fcl3/Vc. This result is applied in the “Numerical models” section to arrive at an effective cell length in cases when cells overlap.
Overview
We developed a simple scaling model for the strain factor in tissues containing three different models of cell distribution. This model, described in the next section, was calibrated to the results of numerical analyses (the section “Strain factors in 3D tissues), and compared for accuracy with the established composite material models for special cases (the section “Strain factors in dense cell populations”), described above. We extended the scaling model to higher cellular concentrations (the section “Physical models and boundary conditions”) using the Kallmes-Corte statistical model (the section “Overlap in dense cell populations”), and validated the resulting predictions against Monte Carlo predictions involving repeated finite element calculations (the section “Strain factors in dense cell populations”).
We incorporated the strain factor model into the Zahalak model, and reevaluated data presented by Zahalak et al. (2000) to assess the effect of three-dimensionality in cell orientation distribution on the estimates of cell stiffness from experiments on tissue constructs found in the literature (the “Discussion” section).
METHODS
This section describes the approaches used to evaluate 3D strain factors in elastic, isotropic tissues, and the way that 3D strain factors were used to evaluate the effect of 3D orientation distributions on the predictions of cell stiffness from experiments on tissue constructs. The next section describes the scaling model for the strain factor, and its extension to tissues containing dense cell populations (a “percolation model”), and the “Numerical models” section describes numerical estimates used to calibrate and validate these models, in conjunction with the micromechanical models described in the section “Micromechanical models used to estimate strain factors”. The final section describes the way that strain factors incorporated into the Zahalak model can be used to study tissues.
Scaling model
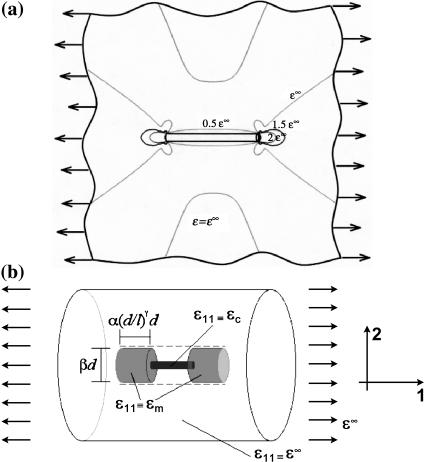
We developed a scaling law for strain factors in low cell concentration tissues, where cells are spaced sufficiently far apart that the strain fields surrounding them do not interact appreciably. The scaling law is a simple approximation, motivated by the strain field illustrated in Fig. 1 a. When a remote uniaxial strain, ɛ∞, is applied to the tissue, with all other components of the strain tensor zero, the strains in the matrix surrounding the ends of the cell are elevated and reduced within the cell itself. The scaling model depicted in Fig. 1 b is obtained by assuming a constant strain field in the cell and smoothing the matrix strain concentrations in Fig. 1 a over two cylindrical regions of matrix material of length βd and diameter (α(d/l)γ)d, where d and l are the cell diameter and length, and α, β, and γ are scaling parameters. The elevated axial matrix strain, ɛm, in this region and the axial strain, ɛc, in the cell are both taken as uniform. ɛc will be slightly smaller than ɛ∞, so ɛm must be slightly greater than ɛ∞ for the ends of this “region of influence” to deform in registry with the matrix material far from the cell.
FIGURE 1.
Schematic of the scaling model. Panel a shows the matrix strain contours around a cell. The scaling model depicted in b is obtained by assuming a constant strain field in the cell and smoothing the matrix strain concentrations in over two cylindrical regions of matrix material of length βd and diameter (α(d/l)γ)d, where d and l are the cell diameter and length, and α, β, and γ are scaling parameters. The elevated axial matrix strain ɛm in this region and the axial strain ɛc in the cell are both taken as uniform.
The scaling law is obtained by enforcing equilibrium, but allowing this kinematically inadmissible strain field. The force on the central linkage in Fig. 1 b will be the same for the cell and the (shaded) regions of influence in the matrix. Using straightforward mechanics (e.g., Gere and Timoshenko, 1984), the longitudinal force F (in the cell) can be written
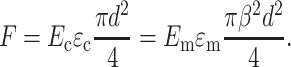 |
(13) |
The condition that the total displacement Δ of this linkage must be in registry with that of the surrounding matrix with a constant strain ɛ∞ may be written
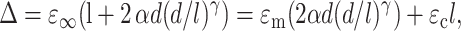 |
(14) |
where α and γ account the size of the “region of influence” surrounding a cell. Equations 13 and 14 may be solved to obtain an expression for ɛc in terms of ɛ∞. Then, the strain factor may be written as:
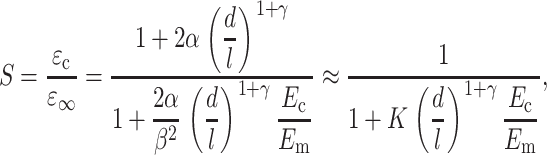 |
(15) |
where the second term expression is a good approximation for tissues whose cells have very high aspect (d/l ≪ 1). Since S = 1 when the cell-matrix modulus ratio is unity, β = 1. This scaling relationship suggests the governing dimensionless parameters m = Ec/Em and r = l/d, which we call the Young's modulus ratio and the cell aspect ratio, respectively.
Extension to high cell concentrations
The scaling and Eshelby models for strain factor in Eqs. 9 and 10 were derived for isolated cells. As in this article's companion, the expressions were extended to higher cell concentrations by 1), incorporating an “effective cell length” that accounts for cell overlap and bonding, and 2), modifying the elastic properties of the medium directly surrounding the cell.
Effective matrix modulus
As the cell concentration increases, the average stiffness of the material near each cell rises due to contributions from neighboring cells. Using a self-consistent type approach (Budiansky, 1965; Hill, 1965), we modified the models for predicting the strain factor by replacing the elastic properties of the matrix surrounding each cell with the effective elastic properties of the tissue as a whole. We used a “parallel” estimate for the effective modulus E11 in the direction of macroscopic tissue straining:
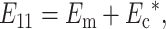 |
(16) |
where Ec* is the contribution of the randomly oriented cells to the overall modulus. An expression for this is derived in Appendix B. In the case of an isotropic distribution of cells,
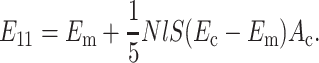 |
(17) |
Effective cell length
The average effective length for all cells was assumed to be proportional to the average number of intersections per cell, which can be calculated using the Kallmes-Corte network model (Eq. 12). However, not every cell intersection increases the “effective cell length”: globular cell clusters can form. If a cell pointing in an arbitrary direction n intersects a cell of length l oriented at random Euler angles θ and φ (e.g., Ginsberg and Genin, 1983) relative to n, the average increase in effective cell length in the n-direction is
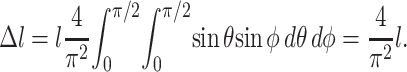 |
(18) |
Since this is shared between two cells,
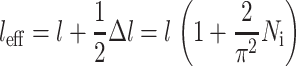 |
(19) |
This effective length defines an effective aspect ratio, 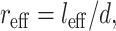 which can be incorporated into the scaling model along with the effective matrix modulus (Eq. 15):
which can be incorporated into the scaling model along with the effective matrix modulus (Eq. 15):
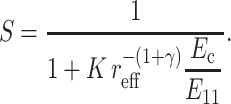 |
(20) |
Numerical models
For validation and calibration of the scaling and percolation strain factor over a broad range of material parameters and cell concentrations, we performed Monte Carlo simulations involving repeated use of the FE method implemented in a commercial software package (ADINA v.7.5.2). Since random distributions of cells required extensive statistical analysis, many finite element meshes with different values for the variables were needed. We describe these analyses in the following sections.
Physical models and boundary conditions
The overall FE model involved a representation of a cube-shaped region of a linear elastic tissue composed of collagen and cylindrical cells. A uniform displacement was applied to the face of the cube that was arbitrarily called the positive x-face. The negative x-face was constrained from displacing in the x direction, the y-faces were constrained from displacing in the y direction, and one z-face was constrained from displacing in the z direction. The remaining face was unconstrained to simulate a specimen that was relatively thinner in one of its dimensions. All faces were free of shear tractions. These boundary conditions provided mirror symmetry on five faces of the cube, and thus simulated an infinitely long and infinitely wide repeating structure that was constrained from contracting in one direction perpendicular to an applied stretch. In a few simulations in which a shear strain was applied, similar periodic boundary conditions were used.
Models of cell distributions
We studied three different cell orientation distributions: 1), isotropic (uniform), 2), planar-isotropic, and 3), uniaxial. We adopted these three distributions motivated by cell distributions observed in bio-artificial tissue specimens. Wakatsuki et al. (2000) observed that unconstrained bio-artificial tissue samples exhibited 3D isotropic distributions on their interiors, and a “planar isotropic” distribution nearer their external surfaces. Wagenseil et al. (2004) observed a degree of uniaxial alignment in the orientation distribution of cells in tissue constructs that were physically constrained as the cells remodeled the matrix. All of these cell distributions led to a nearly constant strain factor for any cell orientation, as will be shown.
3D isotropic distributions. FE models containing 3 × 3 × 3 arrays of cells were studied. To avoid any irregularities near the boundaries, attention was focused on a cell centered in the mesh; the remaining cells served as a quasi-random environment for this central cell. Surrounding cell centers were assigned to fall within one “unit cell” of a uniform 3 × 3 × 3 cubic grid. The cell orientations and the locations of the cells' center-points within their unit cells were assigned according to an isotropic distribution. A typical 3D isotropic cell distribution is shown in Fig. 2 a. A range of cell concentrations was studied; the maximum cell concentration considered was that reached when the cell whose center lay at the center of the 3 × 3 × 3 array of cells stretched from one boundary of the model to the other.
Planar isotropic distributions. Planar isotropic distributions were assigned in the same way as the 3D isotropic distributions, with the exception that cell orientations were prohibited from having a component in the z direction, perpendicular to the direction of macroscopic straining (Fig. 2 b).
Uniaxial distributions FE models that investigate strain factors in unidirectional distributions of cells involve simple unit cells containing a single cell, with boundary conditions as described above.
FIGURE 2.
Sample finite element discretizations of cells. (a) The 3 × 3 × 3 array of cells in an isotropic distribution appears to be randomly distributed from all vantage points. (b) The cells in a planar isotropic distribution are centered randomly, but have no x-component to their orientations.
Material properties of the cells and matrix
In all simulations, the cells and matrix were assigned linear elastic, isotropic material properties. The matrix and cells were taken to be nearly incompressible, with a Poisson's ratio of ν = 0.49.
Finite element discretization
FE discretizations were refined to ensure accuracy in calculating the strain factors. Meshes were finest in the vicinity of the largest gradients of strain, which occurred near the ends of the cells. Both the matrix and cells were modeled with 3D parabolic-interpolation tetrahedral elements to prevent the Poisson's ratio locking effect (e.g., Szabo and Babuska, 1991). Sample discretizations of the cells are shown in Fig. 2, a and b (the mesh for the matrix is not shown).
Statistics
The Monte Carlo simulations involved repeated finite element analyses of random distributions of cells. These cell distributions were all based upon either isotropic or planar isotropic probability density functions for cell orientations.
Statistical uniformity was checked by calculating the anisotropy tensors A and B (Eq. 5). All components of the discrete anisotropy tensors calculated for all uniform and planar isotropic cell orientation distributions studied were within 15% of the values calculated for an infinite tissue containing perfect uniform and planar isotropic cell orientation distributions, respectively.
Interpretation of mechanical parameters using the modified Zahalak model
The companion article (Marquez et al., 2005) adjusted the Zahalak model to incorporate a strain factor for thin tissue constructs, and described an algorithm for using this “modified Zahalak model” to back out the long-term and short-term elastic responses of cells. The procedure detailed in this section differs from that of Marquez et al. (2005) because a more complicated geometric description of cells and cell concentration is required in 3D.
N, l, d, 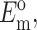 and
and 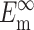 can be found from calibration experiments; the parameters κ and ω are obtained from direct measurements on a tissue. The procedure for finding the instantaneous elastic response
can be found from calibration experiments; the parameters κ and ω are obtained from direct measurements on a tissue. The procedure for finding the instantaneous elastic response 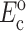 and the long-term elastic response
and the long-term elastic response 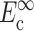 involves 1), calculating C from Eq. 12; 2), using procedures described in Zahalak et al. (2000) to find κ and ω; 3), using Eq. 3 to calculate
involves 1), calculating C from Eq. 12; 2), using procedures described in Zahalak et al. (2000) to find κ and ω; 3), using Eq. 3 to calculate 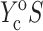 and
and 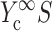 ; 4), determining
; 4), determining 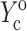 and
and 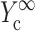 from the appropriate graph of log(YcS) versus log(Yc) described in the section “Strain factors in 3D tissues”, and 5), using Eq. 4 to calculate the cell modulus
from the appropriate graph of log(YcS) versus log(Yc) described in the section “Strain factors in 3D tissues”, and 5), using Eq. 4 to calculate the cell modulus 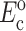 and
and 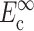 from
from 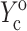 and
and 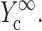 Knowing Yc, one can compute the cell modulus Ec using Eq. 22.
Knowing Yc, one can compute the cell modulus Ec using Eq. 22.
RESULTS
The computations served to establish strain factors as a means of assessing the average strain fields in cells in 3D tissues, to characterize strain factors as a function of tissue parameters, and to fit the scaling model's two free parameters using a Monte Carlo approach. Section 3.1 describes strain factors in idealized tissues made of periodic arrays of cells, and parametric analyses of different periodic unit cell models. The section “Strain factors in dense cell populations” explores strain factors in uniaxial and random cell distributions. The section “Charts for deriving cell properties from mechanical measurements on tissues” assesses the effect of an out-of-plane component of the cell orientation distribution on predictions of cell stiffness from tests on tissue constructs.
Strain factors in 3D tissues
Strain factors provide a reasonable representation of average cell strain in 3D
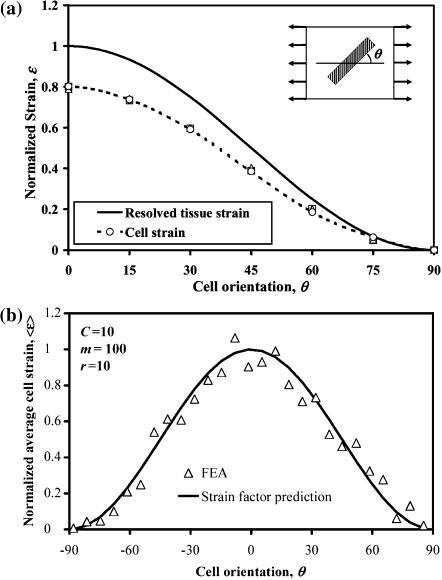
Periodic arrays of identical cells with identical orientations were strained as shown in Fig. 3 a. The solid curve in Fig. 3 a represents the normalized macrostrain, resolved in the direction of a cell. The symbols represent the normalized average longitudinal strain calculated for cells with differing orientation angles θ = {0,15,30,45,60,75,90}, each having an elastic modulus 10 times that of the matrix. The key result is that, as in the 2D case (Marquez et al., 2005), the two curves are proportional regardless of the angle at which the cell is oriented, meaning that cell axial strain is related to resolved tissue strain by a scalar. Fig. 3 b shows that this is true for randomly oriented cells in a 3 × 3 × 3 array as well. The solid curve in Fig. 3 b is the average strain calculated for all the 27 cells in the mesh, multiplied by cos2θ. Further analyses showed the average strain factor to be invariant for both uniaxial and shear stretching for any prescribed cell concentration C, modulus ratio m, and cell aspect ratio r = l/d.
FIGURE 3.
Average strain in cylindrical cells scales with the “nutation” angle θ of a cell according to a cos2θ distribution. The data shown is for (a) the central cell in a 3 × 3 × 3 array of aligned cells (C = 1) and (b) all 27 cells in a 3 × 3 × 3 array of randomly distributed cells.
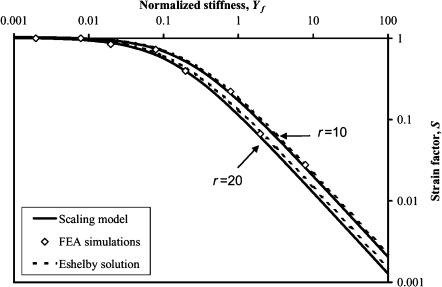
Strain factors scale with Yc and follow the Eshelby solution
As expected from the scaling analysis in the “Scaling model” section, all data for strain factors of a particular aspect ratio collapse to a single curve when plotted against Yc, as shown in Fig. 4, which shows the FE estimates for strain factors in periodic arrays of sparsely concentrated cells. The results shown with diamonds are for C = 0.02, r = {10,20}, and m = {10,100,1000,10000}. The scaling model (Eq. 15) fits the data best with K = 0.89 and γ = 0.35. Also shown in Fig. 4 is the Eshelby solution (Eq. 20), which follows the FE data fairly well, but very slightly overpredicts the strain factor.
FIGURE 4.
Scaling of the strain factor as a function of normalized stiffness Yc for two different cell aspect ratios in a tissue with a sparse cell concentration. The FE simulations of sparse cell distributions are qualitatively modeled by both the Eshelby solution and the scaling model.
Strain factors in dense cell populations
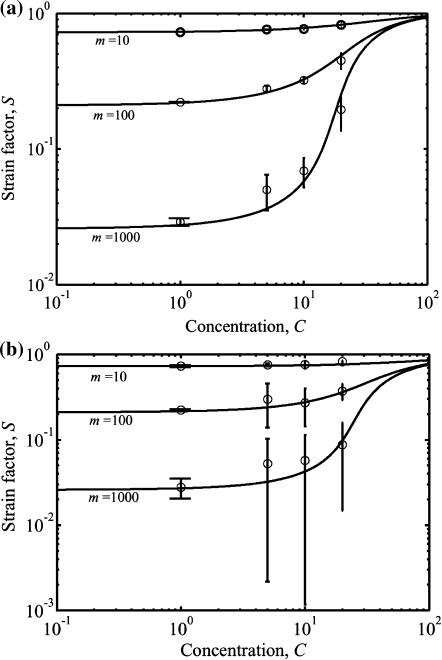
Monte Carlo simulations
FE analyses were run to establish variations of strain factors with higher cell concentrations. These analyses required 3 × 3 × 3 arrays of cells (Fig. 2), since, with larger cell concentrations, cells spanned multiple unit cells and could overlap one another.
Results are shown in Fig. 5, a and b, for isotropic and planar isotropic distributions of cells, respectively. Both plots show results for cells of aspect ratio r = 12.5 with dimensionless concentrations C ranging from 1 to 20, and for values of Yc ranging from 0.05 to 50; results for the four other aspect ratios considered (r = {10,15,20,30}) showed similar trends. Each point in Fig. 5, a and b, for C < 1 corresponds to an average of finite element predictions using two different but statistically identical cell distributions; since the cells were nearly isolated, the scatter was extremely small. The remaining points each represent the average of finite element predictions using 10 different but statistically identical cell distributions. Scatter increases dramatically near the sharp rise in strain factor at the cell concentration corresponding to formation of a continuous, “percolated” cellular network. This scatter is analogous to critical fluctuations near a phase transition. The scatter increased with increasing Yc.
FIGURE 5.
Percolation model and results of Monte Carlo simulations. The solid lines are the predictions of the model (Eq. 20); the symbols are the averages from simulations. (a) A fully isotropic cell orientation distribution and (b) a planar isotropic distribution.
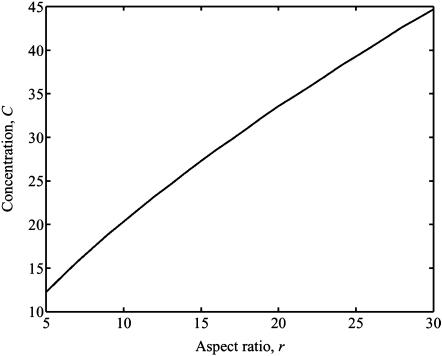
The trend lines in both plots correspond to the percolation model (Eq. 20), which matches the Monte Carlo simulations over all cell concentrations evaluated. For uniform and planar isotropic cellular distributions, the percolation points and variation in strain factor with respect to Yc are statistically indistinguishable. As predicted by Eq. 20, the strain factor exhibits high dependence on the aspect ratio at lower values of aspect ratio; however, for aspect ratios >30, the dependence is weak.
Percolation
Formation of a continuous, “percolated” cellular network requires a higher cell density in tissues with a 3D cell architecture than in the 2D membranes studied in the companion article. An additional feature of percolation in 3D cell networks that does not occur with 2D networks is that the percolation threshold is a strong function of the cell aspect ratio in 3D, as illustrated in Fig. 6. As in 2D tissues, the magnitude of the jump in the strain factor that occurs at the percolation point increases as Yc increases.
FIGURE 6.
Values of dimensionless cell concentration C at which percolation occurs as a function of the aspect ratio r.
Analytical verification of observed trends
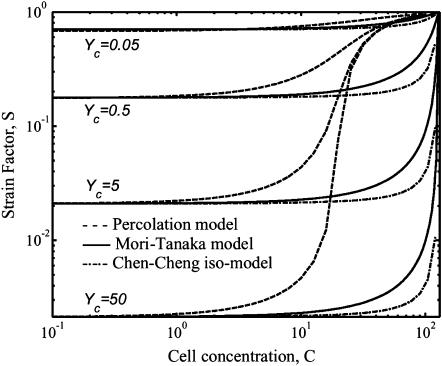
As shown in Fig. 7, the Eshelby solution predicts strain factors in ellipsoidal cells to within a few percent in very sparsely populated tissues, but is valid only for these extremely low cell concentrations. The Chen-Cheng model predicts a rise in the strain factor with increasing cell concentration as was observed in the Monte Carlo simulations, but underestimates the strain factor at all except low cell concentrations. As a consequence, the percolation model was used as a tool for incorporating strain factors into the Zahalak model across the entire range of cell concentrations.
FIGURE 7.
Predictions of the strain factor as a function of dimensionless cell concentration and normalized stiffness. The Eshelby model predicts the lower asymptotes of the percolation model (Eq. 20) as fit to the Monte Carlo simulations. The Chen-Cheng model (Chen and Cheng, 1996) predicts a rise in strain factor with increasing cell concentration.
Charts for deriving cell properties from mechanical measurements on tissues
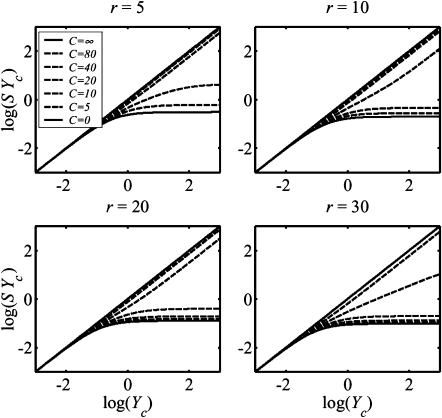
The central result of this article, needed for interpretation of experiments on tissues with uniform and planar isotropic cell orientation distributions, is the relation between log(YcS) and log(Yc), shown in Fig. 8. The charts shown in Fig. 8 allow one to determine the normalized stiffness Yc from the product YcS, which can be found from experimentally determined values of κ and ω (Eq. 3). If the aspect ratio of the cells and the elastic modulus of the matrix are also known, the elastic modulus Ec of the cells may be derived from Yc. These curves were derived from the percolation model.
FIGURE 8.
Relationship between and the product SYc, which can be found from experimental measurements, and the normalized stiffness, Yc, for several values of cell aspect ratio r. These plots are needed to derive in situ cell stiffness from macroscopic tissue measurements. The Zahalak model (Zahalak, 2000) corresponds to the upper limit in each case.
As the cell concentration grows, the strain factor S of the contiguous cell network approaches 1, and log(YcS) approaches log(Yc). Therefore, all these curves must lie beneath the solid lines labeled C = ∞. The lower limits were established by looking at the low-cell concentration scaling law for S (Eq. 15): at very large Yc values (Yc/K ≫ 1), log(YcS) approaches a constant equal to log(r−1.63/K). Consequently, the curves all lie above the solid lines labeled C = 0.
The charts in Fig. 8 were derived assuming incompressible cells. However, a variation in the strain factor of only 10% was seen in analyses varying the cell Poisson's ratio from 0 to 0.49. Therefore, the charts shown in Fig. 8 also provide a reasonable approximation for strain factors in cells that are not incompressible.
Accounting for the 3D architecture of a cellular network forces cell stiffness estimates to be revised upwards
We reinterpreted experiments from Zahalak et al. (2000), assuming that cells exhibited a 3D orientation distribution that was either planar isotropic or uniform. The results were nearly identical for both of these assumptions. The results are compared in Table 1 to the interpretations of these data by Zahalak et al. (2000) and in the companion article, for both the instantaneous and long-term elastic moduli of the cells.
The predictions of cell stiffness that result from an assumption of a 3D uniform cell orientation distribution are 2–5 times higher than those predicted by Zahalak, and modestly higher than those predicted by assuming a 2D cell distribution.
DISCUSSION
Marquez et al. (2005) extended the Zahalak constitutive model to overcome one of its fundamental limitations by incorporating a more accurate assessment of the average strain of cells within a strained thin tissue. The work presented in this article establishes how the ratio between the remote strain tensor and the average axial strain in cells varies as a function of tissue parameters in a 3D tissue that is strained in one direction. The strain factor was shown to follow the percolation model (Eq. 20).
By incorporating this model for the three-dimensional strain factor into the Zahalak constitutive law, cell stiffnesses could be calculated from measurements of the cell concentration, Young's modulus of the matrix, aspect ratio of cells, and mechanical properties of a tissue.
Predictions of strain factors
The model for the strain factor that was incorporated into the Zahalak model was based upon several idealizations, including linear elasticity, matrix homogeneity, isotropy, idealized cell shapes, perfect cell-to-matrix bonding, and steric cell-to-cell interactions. Significant material nonlinearity, matrix inhomogeneity, and matrix anisotropy could lead to increases or decreases in strain factors in constructs with low cell concentrations, which could either lower or raise estimates of cell stiffness. These effects would be less pronounced at cell concentrations above the percolation point, as they would not cause the strain factor to differ from 1 significantly. Since differences between the Eshelby solution for ellipsoids and the Monte Carlo predictions for cylinders were small, the effect of cell shape might also be expected to be small. Preliminary simulations of ellipsoidal cells not bonded to the matrix indicate that cell-matrix bonding might also be a less critical factor. Nonsteric cell-to-cell bonding could move the percolation point to a lower cell concentration, and affect estimates of the strain factor near the percolation point.
Within the context of these idealizations, discussed at length in the companion article, the approximate percolation model (Eq. 20) is accurate in that it qualitatively follows the exact Eshelby solution for very low cell concentrations, and the Chen-Cheng model for slightly higher cell concentrations. When fit to Monte Carlo simulations of very sparse populations of cylindrical cells, the percolation model predicts slightly lower strain factors than the Eshelby solution or the Chen-Cheng method. This is because the ellipsoids modeled by the Eshelby and Chen-Cheng methods have a smaller average cross-sectional area (and hence smaller stiffness) than cylinders of equivalent thickness. Differences between ellipsoidal and cylindrical cell idealizations faded with increasing cellular length/diameter ratio.
The percolation model was fit only to simulations of constructs containing very low cell concentrations, and extended to higher cell concentrations through a statistical model with no “fitting parameters”. The 3D percolation phenomenon differed from the thin membrane case described by Marquez et al. (2005). The primary difference between this percolation phenomenon in thin membranes and that in 3D tissues is that the percolation point is a strong function of the cell aspect ratio in 3D (Fig. 6). As with 2D constructs, the magnitude of the percolation jump increases as Yc increases, leading to a relatively sharper percolation threshold.
Reinterpretation of published cell stiffness estimates
The methods of this article were used to reinterpret experiments reported by Zahalak et al. (2000), who derived mechanical properties of cells from tissue measurements based upon the following two assumptions: 1), they assumed that the strain factor in their tissues was 1, and 2), they assumed a planar isotropic distribution of fibroblasts. Marquez et al. (2005) reinterpreted these experiments by treating the specimens like thin membranes, and incorporating the correct strain factor. In the current work, we treated the tissue as having a planar isotropic or 3D isotropic, and applied the appropriate strain factor.
The linear elastic cell stiffnesses estimated in this article and its companion (Table 1) are slightly higher than the highest estimates reported in the literature for the long-term cell modulus, and an order of magnitude higher than those reported for the instantaneous modulus (see the companion article for a table containing a comparison). The upper bound instantaneous linear elastic stiffness estimate in this article is three times that estimated by assuming a 2D uniform cell distribution; the long-term modulus is 10% higher.
Studies by Wagenseil et al. (2003) of tissue constructs similar to those considered by Zahalak et al. (2000) indicate that these constructs are best modeled as having cell orientation distributions like those in thin membranes near their outer surfaces, and as having more isotropic distributions nearer their centers. In light of this, the actual cell properties are most likely bounded by the current estimates of cell properties and those of Marquez et al. (2005).
That the cell stiffnesses estimated within a tissue construct are significantly higher than those estimated by techniques such as cell poking and micropipette aspiration that rely on localized stretching of the membrane is not surprising. The results of Guilak et al. (2002) indicate that cell membranes must stretch significantly before resisting stretch appreciably. The application of a uniform strain to a cell through its connections to the collagen matrix could certainly be expected to engage more of a cell's structural elements. The contribution of activated cells to the continuum stiffness of a bio-artificial tissue construct appears to be far greater than experiments on isolated cells suggest, since the stiffness of a cell in response to a localized probing of its membrane differs from the stiffness of a cell strained uniformly in a collagen matrix.
CONCLUSION
The Zahalak constitutive model for bio-artificial tissues was adapted to model the short- and long-term response of tissue constructs with 3D isotropic and 3D planar isotropic cellular architectures. This was achieved using the strain factor approach introduced by Marquez et al. (2005). This work modeled 3D strain factors, and established how strain factors depend upon the 3D architecture of an idealized tissue. For the experimental data that was reevaluated in this article, the updated model allows for an upper bound on linear elastic cell stiffness to be established.
As with our earlier work, the approach presented in this article has some limitations that need to be addressed. The strain factor was calibrated in this article for 3D distributions of linear elastic cells embedded in a linear elastic matrix. However, the actual response of most living cells is viscoelastic and nonlinear. The consequence of this is that the model in this article is applicable only to short-term and long-term tissue response; the time variation of strain factor over the time scales associated with tissue relaxation (e.g., Zahalak et al., 2000) requires further investigation. Cell-cell interactions that occur when neighboring cells are near one another may affect strain factors in a way that is not represented by our formulation. Local variations in matrix properties may also influence strain factors. This must be considered in future work.
Acknowledgments
The authors thank Ali Nekouzadeh, Tony Pryse, and Jessica Wagenseil for many insightful discussions.
This work was supported in part by the National Institutes of Health through grants AR47591 and GM38838.
APPENDIX A: EXPRESSIONS FOR THE STRAIN FACTOR USING ESHELBY'S SOLUTION
Eshelby's solution (Eshelby, 1957, 1959) can provide an analytical estimate of the strain factor in idealized tissues with sparse cell populations. We model the cells as ellipsoidal inclusions, with the dimensions of the major axes matching those of the cells. The key ingredient is Eshelby's strain concentration tensor, AEsh = [I + E(C(m))−1(C(c) − C(m))]−1, where C(c) and C(m) are the fourth-rank cell and matrix stiffness tensors, I is the fourth-rank unit tensor, and E is called the “Eshelby tensor”, which describes the geometry of the cells. For isotropic materials, C(c) and C(m) can be found in many sources in terms of the elastic modulus and Poisson's ratio Ec and ν for the cells, and Em and μ for the matrix (e.g., Jones, 1998). Expressions for Eshelby's tensor, E, in terms of μ and the cell dimensions d and l may be found in Mura (1982).
The strain tensor 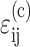 within the cells is related to the remote strain tensor
within the cells is related to the remote strain tensor 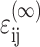 by
by 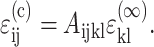 Then, for the case of a unidirectional stretch (
Then, for the case of a unidirectional stretch (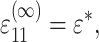 with all other components of the strain tensor zero), the strain factor in a cell point in the direction of n is
with all other components of the strain tensor zero), the strain factor in a cell point in the direction of n is
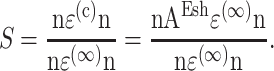 |
(A1) |
Solving, the general expression for the strain factor S in an idealized tissue can be written
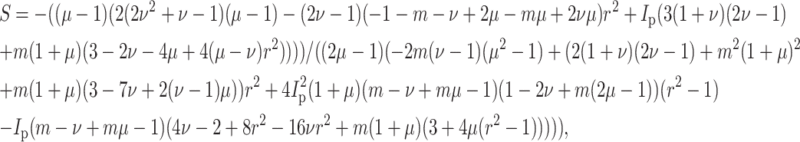 |
(A2) |
where r is the aspect ratio of the cells (long axis/short axis), and Ip is given in Eq. 9, and m = Ec/Em. For ν = μ, the expression becomes
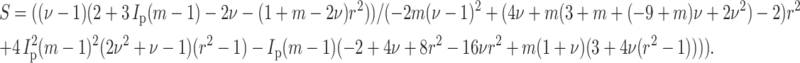 |
(A3) |
When ν = 0, strain factor may be written
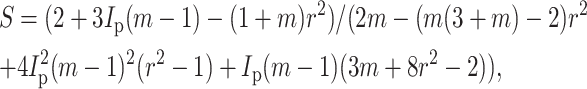 |
(A4) |
and, when ν = 0.5, the strain factor simplifies to
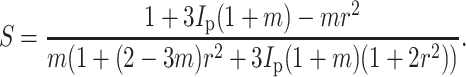 |
(A5) |
APPENDIX B: RELATION BETWEEN THE STRAIN FACTOR AND EFFECTIVE YOUNG'S MODULUS
The Zahalak model is based on a polymer rheology result (Bird et al., 1987), which establishes the contribution to the continuum stress of a distribution of contractile rods. The cells are superimposed upon a uniform matrix by adding a term 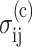 that accounts for the perturbation to the stress field:
that accounts for the perturbation to the stress field:
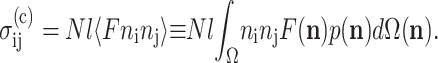 |
(B1) |
The probability density function p for a uniform orientation distribution is p = 1/4π, the cell orientation vector in the 1-direction is n1 = cosθ, and the differential of area of the unit sphere is dΩ = sinθ dθ dφ. Noting that the additional force due to the cells is related to the cell strain 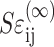 and the additional stiffness due to the cell is (Ec − Em), the average force along the cell can be expressed as
and the additional stiffness due to the cell is (Ec − Em), the average force along the cell can be expressed as
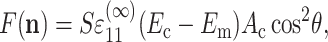 |
(B2) |
where Ac is the cross-sectional area of a cell. Then, the 11-stress is given by
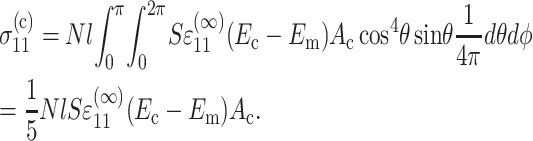 |
(B3) |
Therefore, the contribution of the cells to the Young's modulus of the tissue can be written
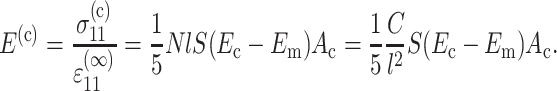 |
(B4) |
The contribution of the cells to the Young's modulus of the tissue for planar-isotropic and uniaxial distribution can be computed using the same procedure. The effective moduli for the three different cell orientation distributions of interest can be written as follows.
For an isotropic distribution,
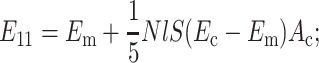 |
(B5) |
for a planar-isotropic distribution,
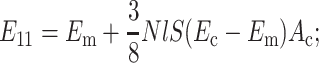 |
(B6) |
and, for a uniaxial distribution,
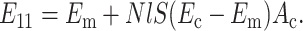 |
(B7) |
This article and its companion are dedicated to the memory of George I. Zahalak.
References
- Bird, B. R., C. F. Curtiss, R. C. Armstrong, and O. Hassager. 1987. Dynamics of Polymeric Liquids, Vol. 2. Kinetic Theory. Wiley, New York.
- Bohm, H. J., and W. Han. 2001. Comparison between three-dimensional and two-dimensional multi-particle unit cell models for particle reinforced metal matrix composites. Mod. Simul. Mater. Sci. Eng. 9:47–65. [Google Scholar]
- Budiansky, B. 1965. On the elastic moduli of some heterogeneous materials. J. Mech. Phys. Solids. 13:223–227. [Google Scholar]
- Chen, C. H., and C. H. Cheng. 1996. Effective elastic moduli of misoriented short-fiber composites. Int. J. Solids Structures. 33:2519–2539. [Google Scholar]
- Eshelby, J. D. 1957. The determination of the elastic field outside an ellipsoidal inclusion, and related problems. Proc. Roy. Soc. A. 241:376–396. [Google Scholar]
- Eshelby, J. D. 1959. The elastic field outside an ellipsoidal inclusion. Proc. Roy. Soc. A. 252:561–569. [Google Scholar]
- Gere, J. M., and S. P. Timoshenko. 1984. Mechanics of Materials, 2nd ed. PWS Publishers, Boston.
- Ginsberg, J. H., and J. Genin. 1983. Dynamics, 2nd ed. John Wiley and Sons, New York.
- Guilak, F., G. R. Erickson, and H. P. Ting-Beall. 2002. The effects of osmotic stress on the viscoelastic and physical properties of articular chondrocytes. Biophys. J. 82:720–727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill, R. 1965. A self-consistent mechanics of composite materials. Mech. Phys. Solids. 13:213–222. [Google Scholar]
- Kallmes, O., and H. Corte. 1960. The structure of paper: the statistical geometry of an ideal two-dimensional fiber network. Tappi. 43:737–752. [Google Scholar]
- Jones, R. M. 1998. Mechanics of Composite Materials. Taylor & Francis, London.
- Marquez, J. P., G. M. Genin, G. I. Zahalak, and E. L. Elson. 2005. Thin bio-artificial tissues in plane stress: the relationship between cell and tissue strain, and an improved constitutive model. Biophys. J. 88:765–777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mori, T., and K. Tanaka. 1973. Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metall. 21:571–574. [Google Scholar]
- Mura, T. 1982. Micromechanics of Defects in Solids. Martinus Nijhoff, The Hague, The Netherlands.
- Prager, W. 1969. On the formulation of constitutive equations for living soft tissues. Q. Appl. Math. 27:128–132. [Google Scholar]
- Szabo, B. A., and I. Babuska. 1991. The Finite Element Method. John Wiley & Sons, New York.
- Wagenseil, J. E., E. L. Elson, and R. J. Okamoto. 2004. Cell orientation influences the biaxial mechanical properties of fibroblast populated collagen vessels. Ann. Biomed. Eng. 32:720–731. [DOI] [PubMed] [Google Scholar]
- Wagenseil, J. E., T. Wakatsuki, R. J. Okamoto, G. I. Zahalak, and E. L. Elson. 2003. One-dimensional viscoelastic behavior of fibroblast populated collagen matrices. J. Biomech. Eng. 125:719–725. [DOI] [PubMed] [Google Scholar]
- Wakatsuki, T., M. S. Kolodney, G. I. Zahalak, and E. L. Elson. 2000. Cell mechanics studied by a reconstituted model tissue. Biophys. J. 79:2353–2368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu, J. F., M. S. Shephard, G. J. Dvorak, and Y. A. Bahei-El-Din. 1989. A material model for the finite element analysis of metal matrix composites. Compos. Sci. Technol. 35:347–366. [Google Scholar]
- Zahalak, G. I., J. E. Wagenseil, T. Wakatsuki, and L. E. Elson. 2000. A cell-based constitutive relation for bio-artificial tissues. Biophys. J. 79:2369–2381. [DOI] [PMC free article] [PubMed] [Google Scholar]