Distance-Restrained Docking of Rifampicin and Rifamycin SV to RNA Polymerase Using Systematic FRET Measurements: Developing Benchmarks of Model Quality and Reliability

Abstract

We are developing distance-restrained docking strategies for modeling macromolecular complexes that combine available high-resolution structures of the components and intercomponent distance restraints derived from systematic fluorescence resonance energy transfer (FRET) measurements. In this article, we consider the problem of docking small-molecule ligands within macromolecular complexes. Using simulated FRET data, we have generated a series of benchmarks that permit estimation of model accuracy based on the quantity and quality of FRET-derived distance restraints, including the number, random error, systematic error, distance distribution, and radial distribution of FRET-derived distance restraints. We find that expected model accuracy is 10 Å or better for models based on: i), ≥20 restraints with up to 15% random error and no systematic error, or ii), ≥20 restraints with up to 15% random error, up to 10% systematic error, and a symmetric radial distribution of restraints. Model accuracies can be improved to 5 Å or better by increasing the number of restraints to ≥40 and/or by optimizing the distance distribution of restraints. Using experimental FRET data, we have defined the positions of the binding sites within bacterial RNA polymerase of the small-molecule inhibitors rifampicin (Rif) and rifamycin SV (Rif SV). The inferred binding sites for Rif and Rif SV were located with accuracies of, respectively, 7 and 10 Å relative to the crystallographically defined binding site for Rif. These accuracies agree with expectations from the benchmark simulations and suffice to indicate that the binding sites for Rif and Rif SV are located within the RNA polymerase active-center cleft, overlapping the binding site for the RNA-DNA hybrid.

INTRODUCTION

Key insights into the biological function of “macromolecular machines” (Alberts, 1998) may be gained by elucidating their structure at different stages along their mechanistic pathway. These large assemblies are often composed of multiple individual proteins and/or nucleic acids, and the size of these complexes (often >1 MDa) complicates routine high-resolution structure determination by standard x-ray crystallographic and nuclear magnetic resonance spectroscopic methods. Thus, there is a need to develop modeling strategies that combine different sources of structural information to build up a description of these macromolecular assemblies (Baker and Johnson, 1996; Baumeister and Steven, 2000; Nogales and Grigorieff, 2001; Wriggers and Chacón, 2001; Crowther and Prasad, 2004; Ma, 2004).

Hybrid structure determination methods seek to combine high-resolution structures of the components of a complex in a manner that is consistent with lower-resolution structural restraints. The cryo-electron microscopy (cryo-EM) community has taken advantage of this hybrid method and has modeled several different biological assemblies, including actin complexes, ribosome complexes, and viruses (Wriggers et al., 2000; Frank, 2002; Tang and Johnson, 2002; Orlova and Saibil, 2004). In this strategy, the high-resolution structures of components are treated as rigid bodies and the relative positions and orientations of the high-resolution structures of components are optimized to fit within a low-resolution electron density map of the intact complex. This procedure can be performed manually; however, several research groups have developed computational techniques to generate models of assemblies (Rossmann et al., 2001; Unger, 2001; Chacón and Wriggers, 2002). Hybrid methods in which components are treated as rigid bodies demand that conformational changes of the components induced by or required for complex formation be minimal. However, this restraint may be relaxed by identifying flexible domains in the subunits (Gerstein et al., 1994; Gerstein and Krebs, 1998; Hayward and Berendsen, 1998; Ma et al., 2002), and introducing conformational flexibility into models of components as has been explored in cryo-EM hybrid modeling (Wriggers and Schulten, 1997; Wriggers et al., 2000; Wriggers and Birmanns, 2001; Tama et al., 2002, 2003; Beuron et al., 2003; Chacón et al., 2003; Kim et al., 2003).

It is important to emphasize that, with hybrid structure-determination methods, the objective is not to generate high-resolution structures, but, rather, to position a component relative to the overall size of the complex with accuracy sufficient to draw biological conclusions. Taken in the context of a macromolecular assembly, well-defined models should, for example, be able to identify the correct binding surface or pocket.

In previous work, we have developed a method to construct structural models of macromolecular complexes using available high-resolution structures of individual components in conjunction with intercomponent distance restraints derived from systematic fluorescence resonance energy transfer (FRET) measurements (Mekler et al., 2002; Mukhopadhyay et al., 2004). FRET has the distinct advantage of providing long-range distance information (∼10–100 Å) under physiological conditions (Lilley and Wilson, 2000; Selvin, 2000; Hillisch et al., 2001). We have used tens to hundreds of FRET-derived distance restraints to construct structural models of bacterial RNA polymerase (RNAP) holoenzyme and the RNAP-promoter open complex in solution (Mekler et al., 2002) and to define the binding site within RNAP of the small-molecule inhibitor microcin J25 (Mukhopadhyay et al., 2004).

Here, we have developed an appropriate functional form of FRET-derived distance restraints to account explicitly for random error in restraints. In addition, we have used simulated FRET-derived distance restraints and simulated target macromolecular assemblies to establish benchmarks that permit estimation of model accuracy based on the number, random error, systematic error, distance distribution, and radial distribution of FRET-derived distance restraints. Finally, we have used experimental FRET-derived distance restraints to define the positions of the binding sites within RNAP of the small-molecule inhibitors rifampicin (Rif) and rifamycin SV (Rif SV) and, by comparison to benchmark simulations and to the crystallographic structure of an RNAP-Rif complex (Campbell et al., 2001), to evaluate expected and observed model accuracies.

In this study, we also explored how the RNAP reference model affects modeling results using experimental FRET data. This course was motivated for two reasons. First, our FRET measurements were obtained for the Escherichia coli RNAP holo-Rif complex whereas the reference model for RNAP is based on the Thermus aquaticus RNAP-Rif complex. Although there is a high degree of sequence and structural similarity across bacterial and eukaryotic RNAP (Ebright, 2000), differences in the positions of the chromophore attachment sites between species may impact model quality. Second, and more significantly, whereas the FRET measurements are taken in solution, the RNAP reference was modeled using the static crystallographic structure of T. aquaticus RNAP holoenzyme (Murakami et al., 2002). Crystallographic and cryo-EM structures of RNAP and RNAP complexes indicate that the RNAP β′-pincer (one of the two pincers that define the downstream DNA channel and active center cleft) is flexible and may adopt a range of conformational states—from a fully “open” state that permits unimpeded entry and exit of DNA, to a fully “closed” state that prevents entry and exit of DNA (Darst et al., 1998, 2000; Zhang et al., 1999; Cramer et al., 2000, 2001; Gnatt et al., 2001; Minakhin et al., 2001; Vassylyev et al., 2002; Armache et al., 2003; Bushnell and Kornberg, 2003; Kettenberger et al., 2003; Bushnell et al., 2004; Westover et al., 2004). This implied flexibility can potentially affect our modeling because approximately one-third of the chromophore sites in this work are located on a domain of the σ⁷⁰ transcription initiation factor that interacts and moves with the β′-pincer.

METHODS AND MATERIALS

Reference models: benchmarking targets

Benchmark targets were designed to simulate a macromolecular assembly containing multiple flexibly tethered probes (e.g., multiple flexibly tethered donor chromophore on a receptor) and a single fixed probe (e.g., an intrinsic acceptor chromophore on a receptor-bound small-molecule ligand). Benchmark targets consisted of multiple flexibly tethered probes—each modeled as an ensemble of 500 probes clustered within a hemisphere of radius ∼10 Å—surrounding a single fixed complementary probe site. Effects of the distance distribution of FRET-derived distance restraints were explored by distributing flexibly tethered probe sites at a series of mean relative distances, μ(R/R_o), spanning the range 0.5 ≤ μ(R/R_o) ≤ 1.75. Effects of the radial distribution of restraints were explored by symmetrically distributing flexibly tethered probe sites about the single fixed complementary probe site and by constraining flexibly tethered probe sites to one hemisphere, one quadrant, or one octant about the fixed complementary probe site.

Reference models: RNAP

A reference model of T. aquaticus RNAP holoenzyme in complex with Rif was prepared by superimposition of the crystallographic structure of T. aquaticus RNAP holoenzyme (Murakami et al., 2002; protein data bank (PDB) accession 1L9U) on the crystallographic structure of T. aquaticus RNAP core in complex with Rif (Campbell et al., 2001; PDB accession 1I6V) using RNAP core Cα atoms not located in the β′-pincer (β′-pincer defined as β′-residues 3–157, 453–621, 1441–1455, and β-residues 1080–1116). Probes and linkers were modeled into the reference structure using the molecular modeling program IMPACT (Schrödinger, Portland, OR). At each probe site, all linker torsional angles were sampled in 30° increments, and all sterically allowed conformations as determined by the van der Waals energy in the OPLS-AA all-atom force field (Jorgenson et al., 1996) were accepted. For each sterically allowed conformation, a probe pseudoatom corresponding to the center of the probe chromophore was defined, and thus each probe was represented as an ensemble of pseudoatoms positioned about the attachment site. Rif and Rif SV were modeled as pseudoatoms corresponding to the center of the Rif and Rif SV chromophore naphthol ring.

Two sets of additional reference models were generated to mimic conformational flexibility of RNAP in solution (Cramer et al., 2000, 2001; Gnatt et al., 2001; Darst et al., 2002). The first set of additional reference models (“β′-pincer rotation model”; Mekler et al., 2002) was constructed by rigid-body rotation of the β′-pincer about an axis defined based on a comparison of crystallographic structures of bacterial RNAP and eukaryotic RNAP II. Twenty models were generated by rotating the β′-pincer in 2° increments about the line joining Cα atoms of β′-residues 621 and 1398; in 12 models, the β′-pincer was in a more “closed” position than the T. aquaticus RNAP holoenzyme structure, whereas in eight models, the β′-pincer was in a more “open” position. The second set of additional reference models (“RNAP flexed model”; Darst et al., 2002) was generated by interpolation and extrapolation using a crystallographic structure of T. aquaticus RNAP and the cryo-EM structure of E. coli RNAP. Twenty models were generated by interpolation between crystallographic and cryo-EM structures; 14 models were generated by extrapolating β′-pincer conformations to those that were even more “closed” than the T. aquaticus crystal structure. These “open” and “closed” models of the β′-pincer reflect plausible conformations along a functionally relevant pathway leading to binding of RNAP to DNA followed by transcription initiation. A series of models with Rif bound to RNAP were constructed using each of these perturbed reference models in turn.

Simulated FRET-derived distance restraints

Simulated restraint sets were generated by randomly selecting R/R_o values from normal distributions with mean values from 0.5 through 1.75 and variance of 0.25. From the set of simulated R/R_o values and given R_o = 40 Å, the set of corresponding distance restraints was simulated. Random errors in FRET measurements were simulated by incorporating 15% Gaussian noise into each exact target distance. Systematic errors were modeled by lengthening or shortening all distances within a restraint set by ∼10%.

Systematic errors are likely to be present in the overall distances because some parameter terms contributing to R and R_o are only measured or estimated once and then applied to each interchromophore FRET intensity measurement. The donor-acceptor distance (R) is defined by the equation (Förster, 1948) (Fig. 1):

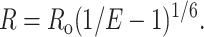(1)

FIGURE 1.

Distance-restrained docking using FRET. (Top) Relationship between efficiency of donor-acceptor energy transfer (E), donor-acceptor distance (R), and the Förster parameter (R_o). Representative penalty functions for three classes of FRET-derived distance restraints: (bottom left) R < 0.5R_o, (bottom middle) 0.5R_o < R < 1.75R_o; and (bottom right) R > 1.75R_o with σ_i = 0.15R_i.

The efficiency of energy transfer (E) is calculated by:

(2)

where I^FRET is the FRET intensity measured in the presence of both donor and acceptor, I^A is the FRET intensity measured in the presence of only the acceptor, and ɛ^D and ɛ^A are the measured extinction coefficients of the donor and acceptor, respectively, at the wavelengths analyzed. The Förster parameter, R_o, is calculated by:

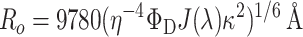(3)

where η is the refractive index of the medium, Φ_D is the quantum yield of the donor in the absence of the acceptor, J(λ) is the spectral overlap integral of the donor emission spectrum and the acceptor absorption spectrum, and κ² is the orientation factor relating the donor emission dipole and the acceptor absorption dipole.

Experimental FRET-derived distance restraints

Fluorescein was incorporated into σ⁷⁰ at positions 95, 132, 366, 376, 396, 440, 442, 459, 496, 517, 527, 557, 569, 578, 583, and 596, using Cys-specific chemical modification (procedures as described for preparation of tetramethylrhodamine-labeled σ⁷⁰ derivatives in Mukhopadhyay et al., 2003, except that fluorescein maleimide (Molecular Probes, Eugene, OR) was used in place of tetramethylrhodamine maleimide). Fluorescein was incorporated into RNAP core at position 235 of α^II, position 643 of β, position 937 of β, and position 1377 of β, using intein-mediated C-terminal labeling (procedures as in Mekler et al., 2002 and Mukhopadhyay et al., 2003). Fluorescein-labeled RNAP holoenzyme derivatives were prepared from labeled σ⁷⁰ and unlabeled RNAP core, or from unlabeled σ⁷⁰ and labeled RNAP core (procedures as in Mukhopadhyay et al., 2003).

For FRET distance measurements, assay mixtures (750 μl) contained 20 nM fluorescein-labeled RNAP holoenzyme derivative in 50 mM Tris-HCl, pH 8.0, 800 mM NaCl, 10 mM MgCl₂, 1 mM DTT, and 0.1% Tween 20 at 25°C. Fluorescence emission intensities were measured before and 6 min after addition of 2 μl of 100 μM Rif or Rif SV (Sigma, St. Louis, MO) (excitation wavelength = 482 nm; emission wavelength = 520 nm; excitation and emission slit widths = 5 nm; QuantaMaster QM1 spectrofluorimeter (PTI, Lawrenceville, NJ)).

For FRET distance measurements with fluorescein-labeled RNAP holoenzyme derivatives containing a probe at position 643 of β or position 937 of β—derivatives insufficiently homogeneous and stable for analysis without further purification—samples (20 μl; 200 nM in 50 mM Tris-HCl, pH 8.0, 100 mM NaCl, 10 mM MgCl₂, 1 mM DTT, 10 μg/ml bovine serum albumin, and 5% glycerol) were applied to 5% polyacrylamide slab gels (30:1 acrylamide/bisacrylamide; 6 × 9 × 0.1 cm) and electrophoresced in 90 mM Tris-borate, pH 8.0, and 0.2 mM EDTA (5 V/cm; 2 h at 4°C). Gel regions containing fluorescein-labeled RNAP holoenzyme derivatives were identified using an x/y fluorescence scanner (FluorImager 595; Molecular Dynamics, Sunnyvale, CA), excised, and mounted in submicro fluorometer cuvettes (Starna, Atascadero, CA) containing 100 μl 50 mM Tris-HCl, pH 8.0, 800 mM NaCl, 10 mM MgCl₂, 1 mM DTT, 10 μg/ml bovine serum albumin, and 5% glycerol at 25°C. For each gel slice, fluorescence emission intensities (excitation wavelengths = 482 nm; emission wavelengths = 515 nm; excitation and emission slit widths = 5 nm) were measured before and 10 min after addition of 2.5 μl 100 μM Rif or Rif SV. Concentrations of Rif and Rif SV were determined spectrophotometrically using ɛ₃₃₄ = 28,000 and ɛ₃₁₄ = 32,300, respectively (Maggi et al., 1966). FRET efficiencies (E) were calculated as:

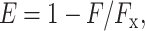(4)

where F and F_x are emission intensities before and after addition of Rif or Rif SV. Donor-acceptor distances (R) were calculated as in Eq. 1 where R_o is the Förster parameter (36.5–39.7 Å for Rif and 33.5–33.6 Å for Rif SV in this study; calculated essentially as in Mekler et al., 2002).

Distance-restrained docking using FRET-derived distance restraints

In our FRET-based modeling strategy, structural components were treated as rigid bodies, the donor was modeled as an ensemble of sterically allowed donor chromophore positions, and the acceptor was modeled as a single fixed acceptor chromophore position. Assuming that κ² = 2/3, the FRET efficiency for each pair of modeled donor chromophore position, j, and acceptor chromophore position, k, was given by:

(5)

For each trial configuration, Y, the apparent donor-acceptor distance corresponding to the i^th FRET restraint is defined to be:

(6)

where M is the number of individual donor chromophore positions, j, in the donor ensemble.

Each FRET-derived target distance, R_i, was computed from the corresponding measured FRET efficiency and R_o using Eq. 1; trial configurations of the components could then be evaluated by comparing target and modeled donor-acceptor distances. Specifically, each FRET-derived distance restraint was approximated by a Gaussian probability density function:

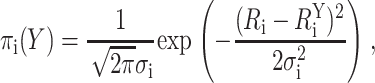(7)

where 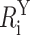is the i^th modeled donor-acceptor distance in configuration Y, R_i is the i^th target distance, and σ_i is the uncertainty associated with the target distance restraint. Thus, π_i(Y) is the probability density that the modeled donor-acceptor distance in configuration Y fits the i^th target distance restraint. The argument of the exponential term contains the penalty function for a given FRET restraint:

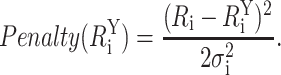(8)

Distances that are smaller than 0.5R_o are virtually indistinguishable from one another as the efficiency of the Förster transfer approaches 1 (Fig. 1) and thus were treated as upper bounds with R = 0.5R_o; the corresponding probability density function was defined as:

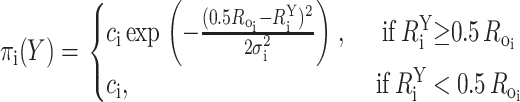(9)

Similarly, large donor-acceptor distances, for which the FRET efficiency is close to 0, also are indistinguishable; therefore, distances >1.75R_o were treated as lower bounds with a probability density function described by:

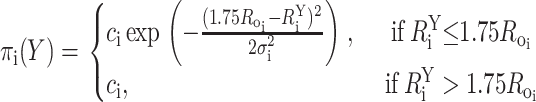(10)

Fig. 1 depicts representative penalty functions for the three classes of FRET-derived distance restraints. In all modeling presented in this article σ_i = 0.15R_i. The overall likelihood of a given configuration was computed as a product of the N individual chromophore pair probabilities:

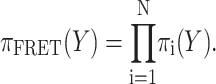(11)

With this strategy, the likelihood that a given docking model fit the experimental restraints could be assessed and potential models could be compared to one another.

Finally, sampling of configurational space was performed to find models that best fit the FRET-derived distance restraints. Through Markov chain Monte Carlo (MC) searches, 10,000 different trial configurations were sampled and the maximum-likelihood model was identified. A trial configuration, Y, was accepted with a probability α(X,Y) (Metropolis et al., 1953; Hastings, 1970):

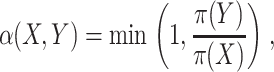(12)

where X was the previously accepted configuration. Translational sampling parameters were optimized to achieve acceptance rates of 35–65%. Results for analysis of Rif and Rif SV were postprocessed to eliminate sterically implausible solutions (solutions with Rif or Rif SV pseudoatom <3.4 Å, or >13 Å, from the closest RNAP Cα atom).

Model quality statistics

For each benchmark simulation, the most-probable model was identified (i.e., the configuration with the lowest penalty) given the structure of the components and chromophore positions as well as the FRET-derived distance restraints and their corresponding probability density functions. The accuracy of the model was defined as the distance between the maximum-likelihood configuration and the target structure whereas the precision was defined as the mean distance between the maximum-likelihood configuration and each accepted trial configuration.

For each model, the accuracy, precision, mean FRET penalty (Eq. 8) per restraint and distance violations, i.e. 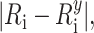were calculated. For each experimental data set or combination of benchmark parameters, 10 independent simulations were performed and the means and standard deviations of the 10 runs were reported.

RESULTS AND DISCUSSION

Distance-restrained docking: penalty function development

Distance-restrained docking requires a penalty function to describe the fit of the docked components given FRET-derived restraints. To use the probability density functions described in Eqs. 7, 9, and 10 (which are the bases of the penalty function), it was necessary to estimate the uncertainty, σ_i in distance restraints, R_i. In this section, we explain the basis for estimating the uncertainty in target distances used throughout this work as σ_i = 0.15R_i, where the uncertainty arises from error in the FRET efficiency, E, and random error in the Förster parameter, R_o (Eq. 1).

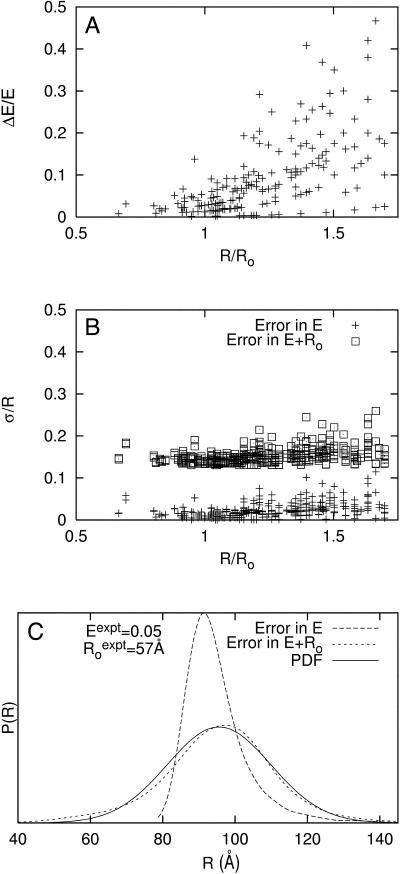
Error in E represents experimental error in the measurement of E. Fig. 2 A shows observed relative errors, ΔE_i/E_i, from multiple independent measurements of E for each of 242 donor-acceptor pairs in RNAP complexes. The observed relative errors in E range from 0 to 50%. Fig. 2 B (data points marked “+”) shows the corresponding relative uncertainties, σ_i/R_i in distance. Despite the relatively large errors in E, the corresponding relative uncertainties in distance range only from 0 to 10%, due to the “switching-function”-like behavior of Eq. 1 for 0.5 < R/R_o < 1.75.

FIGURE 2.

Distance-restrained docking: penalty function development. (A) Observed relative random errors in E, ΔE_i/E_i, from means and standard deviations of multiple independent measurements of E for each of 242 donor-acceptor pairs in RNAP complexes (including 171 RNAP-σ FRET measurements from Mekler et al., 2002; 12 RNAP-MccJ25 FRET measurements from Mukhopadhyay et al., 2004; and 42 RNAP-Rif and RNAP-Rif SV measurements from this work). (B) Simulated relative uncertainty in R, σ_i/R_i, for data in panel A. (+) relative distance uncertainties estimated using random error in E from panel A and assuming absence of random error in R_o; (□) relative distance uncertainty estimated using random error in E from panel A, 100% random error in κ², and 10% random error in non-κ² parameters of R_o. Relative distance uncertainties were obtained by: i), randomly generating many E values from a normal distribution given an experimental mean and standard deviation; ii), generating many R_o values from randomly generated κ² and non-κ² terms from normal distributions given their experimental means and estimated standard deviations; and iii), computing the corresponding set of distances as well as the mean and standard deviation. (C) Representative simulated distance distributions given uncertainties in E only, in both E and R_o, and the best-fit Gaussian distribution (PDF) of the latter distribution: E^expt = 0.05; σ(E^expt) = 0.021; 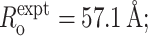σ(non-κ² in R_o) = 10%; σ(κ²) = 100%, R/R_o = 1.63.

The primary source of error in R_o is the parameter κ², which encapsulates information about the relative orientation of the donor and acceptor transition dipoles. For an assembly having donor and acceptor probes that rotationally reorient on the timescale of the donor excited-state lifetime, κ² is equal to 2/3 (Dale and Eisinger, 1974; Dale et al., 1979). However, for an assembly having a donor or an acceptor that does not rotationally reorient on the timescale of the donor excited-state lifetime—such as the complexes of RNAP with Rif or Rif SV, which contain rotationally fixed intrinsic chromophores, analyzed in this work—κ² ranges from 1/3 to 4/3, with the distribution skewed to smaller κ² values (van der Meer et al., 1994), and, thus, uncertainty in the assumption that κ² = 2/3 may be as large as ∼100%. Fortunately, because R_o scales as κ^2(1/6) (Eq. 3), large errors in κ² translate into modest errors in R_o and thus modest relative uncertainties in distance, σ_i/R_i; errors of 25%, 50%, and 100% in κ² correspond to errors of ∼5%, ∼10%, and ∼15%, respectively, in R_o and σ_i/R_i. Errors in the non-κ² terms of R_o—J(λ), Φ_D, and η (Eq. 3)—are modest, comprising ∼2.5% in J(λ), ∼5% in Φ_D, and ∼10% in η (Clegg, 1992); the estimated combined contribution of random error in non-κ² terms of R_o is ∼10%.

We used numerical simulations to determine relative uncertainties in distance that result from simultaneously and explicitly accounting for both i), experimentally determined error in E and ii), estimated random error in R_o. Fig. 2 B (data points marked with open squares) shows that with experimentally determined error in E, 100% random error in κ², and 10% random error in non-κ² parameters of R_o, the relative distance uncertainties, σ_i/R_i, range from ∼11–25%, with a mean of ∼15%. These results indicate that the uncertainties in distance are dominated by the random error in R_o. We conclude that, for an assembly having a donor or an acceptor that does not rotationally reorient on the timescale of the donor excited-state lifetime—such as the RNAP-Rif and RNAP-Rif SV complexes analyzed in this work—a distance uncertainty of σ_i = 0.15R_i should be used in the penalty function.

Similarly, we determined that estimated uncertainties of 25%, 50%, and 200% in κ² correspond to mean relative distance uncertainties of ∼5%, ∼10%, and ∼20%, respectively (data not shown). Thus, we conclude that for chromophores that are attached to macromolecules via long, flexible linkers, in which a small uncertainty in κ² (e.g., 10–25%) is reasonable (Haas et al., 1978; Clegg, 1992; dos Remedios and Moens, 1995; van der Meer, 2002), an uncertainty of σ_i = 0.05R_i should be used in the respective penalty functions.

Fig. 2 C provides an example of distance distributions generated for a specific data point considering: i), experimental error in E only, and ii), experimental error in E as well as random error in R_o. It is clear that explicitly accounting for random error in R_o substantially broadens the distance distribution. This distance distribution, however, is well approximated by a Gaussian distribution that corresponds to the probability density function in Eq. 7, where mean distances are equal to target distances and σ = 0.15R. Because the width of the distance distribution is strongly dependent on random error in R_o, a realistic estimate of random error in R_o is critical when estimating the distance uncertainties used to construct restraints in subsequent modeling. Simulations in this article use σ_i = 0.15R_i.

Distance-restrained docking: benchmarking

We have developed benchmarks of the quality of structural models by systematically examining how their accuracy and precision are affected by parameters that are relevant to modeling with FRET data, including: the number of distance restraints, distance distributions of restraints, radial distribution of restraint sites, and random and systematic errors. In each simulation, we: i), generated a target macromolecular assembly, probe sites, and simulated FRET data consistent with a given combination of parameters and with R_o = 40 Å; ii), through MC searches, identified a model that best fit the simulated FRET data given the data and probe sites; and iii), calculated the accuracy, precision, and other measures of quality of the resulting model. For every combination of parameters examined, we report means and standard deviations over 10 independent simulations.

Sensitivity to number of restraints (N)

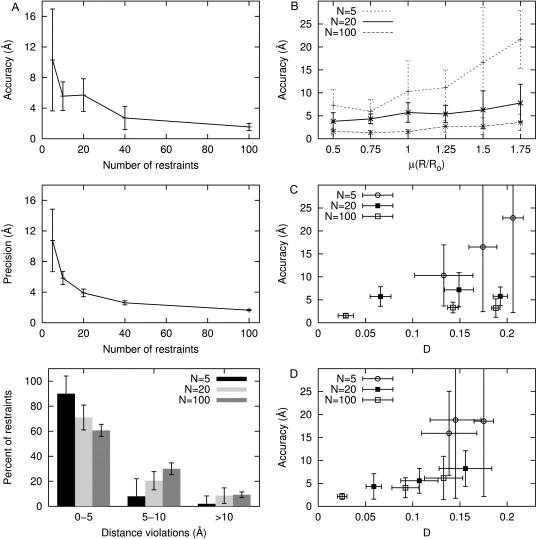
When flexibly tethered probes are symmetrically distributed about the target containing a fixed complementary probe, distance restraints are distributed with a mean R/R_o value of 1.0 and variance of 0.25, and assuming 15% Gaussian random error in each restraint, the model accuracy improves as the number of restraints increases in the following manner: with 5, 20, and 40 restraints, the accuracy is 10 ± 7, 6 ± 2, and 3 ± 2 Å, respectively (Fig. 3 A, top). Although there is substantial variability in the accuracy for models with only five restraints, it is greatly reduced for models with 40–100 restraints. The precision of the models improves from 10 ± 4 to 3.9 ± 0.5 to 2.6 ± 0.3 Å as the number of restraints increases from 5 to 20 to 40, respectively (Fig. 3 A, middle). Models that are generated from small data sets tend to fit the data better (i.e., have both smaller distance violations and smaller mean penalties per restraint), but are more susceptible to errors in the restraints and thus, are less accurate than models that are generated from large noisy data sets. Specifically, in models generated using five restraints and random error of 15%, 4–5 of the restraints are violated by <5 Å whereas virtually no restraints are violated by >10 Å. By contrast, with ≥10 restraints and random error of 15%, only ∼65% of the restraints are violated by <5 Å, and ∼10% are violated by >10 Å (Fig. 3 A, bottom). Even so, larger numbers of restraints with chromophore sites more symmetrically distributed throughout the macromolecular assembly are able to compensate for the presence of random error in FRET data and yield well-defined models of the docked components.

FIGURE 3.

Distance-restrained docking: benchmarking. (A) Sensitivity to number of restraints: (top) accuracy (defined as the distance between the maximum likelihood model and the target), (middle) precision (defined as the mean distance between the maximum likelihood model and all other accepted models), and (bottom) distribution of distance violations for models generated from simulated FRET data with flexibly tethered probe sites uniformly distributed about the fixed chromophore target, μ(R/R_o) = 1 and 15% random error. (B) Sensitivity to distance distribution of restraints. Models generated from simulated FRET data with flexibly tethered probe sites symmetrically distributed about the fixed target and 15% random error while varying μ(R/R_o). (C) Sensitivity radial distribution of restraints. Models generated from simulated FRET data with μ(R/R_o) = 1, 15% random error, and flexibly tethered probe sites located in one octant (large D), located in one quadrant (intermediate D), or distributed symmetrically (small D) about the fixed target. (Because results for models with chromophore sites located in one hemisphere or distributed symmetrically are similar to one another, the latter are omitted for clarity.) (D) Sensitivity to systematic error in restraints. Models generated from simulated FRET data with μ(R/R_o) = 1.0, 15% random error, 10% systematic error, and flexibly tethered probe sites located in one quadrant (large D), located in one hemisphere (intermediate D), or distributed symmetrically (small D) about the fixed target. (Because results for models with chromophore sites located in one octant or one quadrant are similar, the latter are omitted for clarity.)

Sensitivity to distance distribution of restraints (μ(R/R_o))

We also examined how the distribution of distances in the restraint set affect model quality. Fig. 3 B illustrates how decreasing the mean R/R_o value, μ(R/R_o), in the restraint set enhances model quality; the distance distribution is a more critical determinant of model quality with few restraints than with many. For example, with five restraints and random error of 15%, the mean accuracy degrades from 6 ± 3 to 17 ± 12 Å as μ(R/R_o) increases from 0.75 to 1.5 whereas with 40 restraints the mean accuracy is 3 ± 1 and 3 ± 2 Å, respectively. With μ(R/R_o) = 1.75, 50% of the restraints are treated as lower bounds; thus, these data sets contain proportionally less information than the same-sized data sets with smaller μ(R/R_o) values; in fact, data sets with μ(R/R_o) = 1.75 require twice as many restraints as data sets with μ(R/R_o) = 1.25 to obtain a comparable mean accuracy. In contrast, with μ(R/R_o) = 0.5, 50% of the restraints are treated as upper bounds, yet resulting models are comparable in quality to models generated from restraint sets with μ(R/R_o) = 0.75 regardless of the number of restraints. Because an upper-bound restraint (R < 0.5R_o) has fewer possible solutions than a lower-bound restraint (R > 1.75R_o), the former can enhance model quality more significantly than the latter.

Sensitivity to radial distribution of restraints (D)

In cases where a ligand is located centrally within the assembly (as in the case of the RNAP-Rif and RNAP-Rif SV complexes analyzed in this work; see below), chromophore sites can be symmetrically distributed about the target. In contrast, in cases where a ligand is located at the periphery of the assembly (as in the case of the RNAP-MccJ25 complex; see Mukhopadhyay et al., 2004), chromophore sites may be limited to a single hemisphere or single octant about the target. We have explored how the extent of symmetry of the radial distribution of the flexibly tethered probe sites affects model quality. The parameter D is employed to characterize the extent of symmetry of the radial distribution, where D is the “generalized discrepancy” used in numerical analysis and is defined as (Cui and Freeden (1995)):

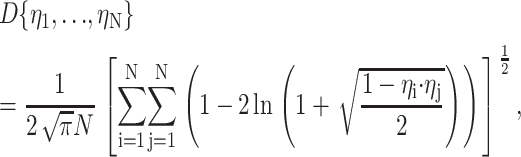(13)

where η_i is the unit vector between the final model and the i^th chromophore. If the chromophore sites are clustered tightly together, the value of D approaches its upper limit of (4π)^−0.5 ≈ 0.28. At its lower limit, with symmetrically distributed chromophore sites, as N → ∞, D → 0.

In Fig. 3 C we show that in the presence of random errors, the radial distribution of chromophore sites affects model accuracy when only a few restraints are used, but is not an important factor when many restraints are used. Thus, with five donor chromophore sites localized in one octant of the macromolecular assembly (D = 0.21 ± 0.01) and random error of 15%, the model accuracy is 23 ± 20 Å; and with five donor chromophore sites more symmetrically distributed about the target (D = 0.13 ± 0.03), the model accuracy improves to 10 ± 7 Å. In contrast, with large numbers of restraints (≥40 restraints), model accuracies are ∼3–4 Å, irrespective of the radial distribution. Furthermore, neither the precision, nor the distance violations, nor the mean penalty per restraint is affected by the radial distribution; these parameters depend primarily on the number of restraints.

Sensitivity to systematic error in restraints

In the simulations we have considered thus far, only random error has been incorporated into the simulated FRET-derived restraints. However, it is likely that systematic errors also may be present in the restraint set because several parameters in E and R_o are estimated (i.e., η in Eq. 3) or are measured (i.e., ɛ^D and ɛ^A in Eq. 2) and then applied to all the data. Literature values of η range from 1.3 to 1.6, and the most commonly reported values are between 1.33 and 1.4 (Clegg, 1992; van der Meer et al., 1994). Because we use a value of 1.4 for η, we estimate the error in η to be ∼10%. Reasonable estimates of systematic error in ɛ^D and ɛ^A are ∼2.5%. In some cases—for example, by overestimating both ɛ^D and ɛ^A in Eq. 2—systematic errors may cancel. However, even compounded systematic errors should result in only relatively small systematic error in R_o, 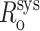(systematic errors in the range 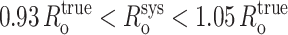), and relatively small systematic error in E, E^sys (systematic errors in the range 0.95 E^true < E^sys < 1.09 E^true). For R/R_o values >0.85—for all R/R_o values with RNAP-Rif and RNAP-Rif SV complexes in this work; see below—compounded systematic errors should contribute up to ∼10% systematic error in R. For R/R_o values <0.85, the compounded systematic errors may contribute up to ∼50% systematic error in R. Systematic error in distance-restrained docking also can arise from errors in the reference model used (see below).

We have explored how systematic error affects model quality by performing simulations in which we systematically shortened or lengthened all target distances by ∼10% within a restraint set before adding random noise. Results from these simulations are summarized in Fig. 3 D and confirm that with chromophores symmetrically distributed (smaller D values), many restraints may compensate for the presence of systematic errors in FRET data. With 5, 20, and 100 restraints from flexibly tethered probes restricted to one quadrant of the assembly (D = 0.18 ± 0.01, 0.16 ± 0.03, and 0.13 ± 0.02, respectively), the addition of systematic error yields model accuracies of 19 ± 16, 8 ± 4, and 6 ± 5 Å, respectively. The respective model accuracies improve to 16 ± 9, 4 ± 3, and 2 ± 1 Å when flexibly tethered probes are symmetrically distributed in the assembly (D = 0.14 ± 0.03, 0.06 ± 0.01, and 0.02 ± 0.01, respectively). These results are reasonable, because, in cases where chromophore sites are located only in a single quadrant, systematically shorter target distances will “pull” the model toward the chromophore sites, and systematically longer target distances will “push” the model away from the chromophore sites. In contrast, in cases where many chromophore sites are symmetrically distributed about the target, systematic errors in distance restraints effectively cancel.

In summary, results of benchmarking with simulated FRET data indicate that model accuracy is 10 Å or better for models based on: i), ≥20 restraints with up to 15% random error and no systematic error, or ii), ≥20 restraints with up to 15% random error, up to 10% systematic error, and a symmetric radial distribution. Model accuracies can be improved to 5 Å or better by increasing the number of restraints to ≥40 and/or by optimizing the distance distribution of restraints. In the context of a macromolecular assembly with dimensions of ∼100 × ∼100 × ∼100 Å, such as RNAP (see below), this accuracy is sufficient to position a probe site within ∼10% of each dimension of the assembly and within ∼0.1% of the volume of the assembly, which, in general, is more than sufficient to identify a binding site, suggest a function, and suggest subsequent experiments.

Distance-restrained docking: applications to RNAP

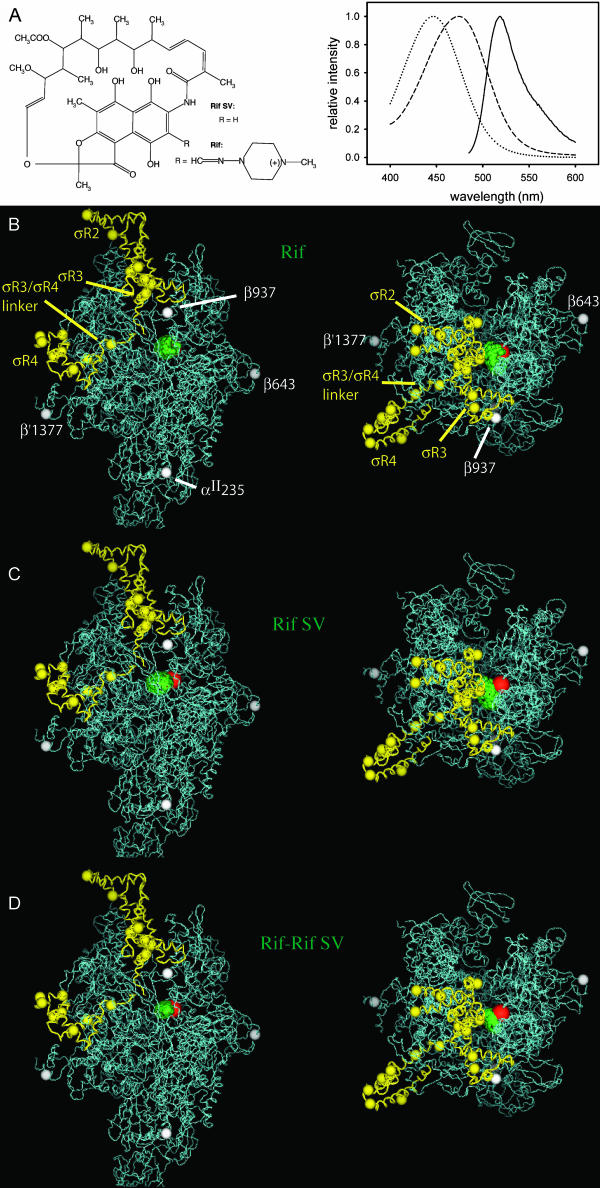
Ansamycin antibiotics, including Rif and Rif derivatives, are macrocyclic compounds that exhibit bacteriocidal activity against a broad spectrum of Gram-positive and Gram-negative bacteria (Sande, 1983; Sensi, 1983; Parenti and Lancini, 1997). The bacteriocidal activity of Rif and Rif derivatives is due to their ability to bind to bacterial RNAP and inhibit transcription (Chopra et al., 2002). Rif and Rif derivatives interact within a binding site, the “Rif pocket”, located within the RNAP active-center cleft, overlapping the binding site for the RNA-DNA hybrid, and inhibit transcription by sterically preventing synthesis of RNA products >3–4 nt in length (McClure and Cech, 1978; Campbell et al., 2001). The crystallographic structure of an RNAP-Rif complex has been determined at 3.3 Å (Campbell et al., 2001). Rif and Rif derivatives contain intrinsic chromophores and thus can be used as acceptors in FRET without modification (Wu and Goldthwait, 1969; Hillel and Wu, 1976; Wu et al., 1976; Yarbrough et al., 1976; Fig. 4 A). Rif derivatives having identical binding and functional properties, but having different chromophore absorption spectra (Fig. 4 A), and thus different spectral overlap and different R_o values when used as acceptors in FRET, are available, permitting straightforward engineering of R_o by choice of appropriate Rif derivatives.

FIGURE 4.

Distance-restrained docking: applications to RNAP. (A) (left) Structures of Rif and Rif SV. (right) Fluorescein emission spectrum (solid line), Rif absorption spectrum (dashed line), and Rif SV absorption spectrum (dotted line). (B) Model of RNAP-Rif and RNAP-Rif SV complexes generated using experimental FRET-derived distance restraints for Rif (Table 1) and distance-restrained docking (two orthogonal views: view of upstream face of RNAP, left; view into the RNAP active-center cleft, right). Green spheres, possible positions of Rif chromophore (top 50% of solutions); red sphere, crystallographically defined position of Rif chromophore (Campbell et al., 2001); white and yellow spheres, attachment sites of donor chromophores on RNAP core and σ⁷⁰, respectively. (C) The same as for panel B, but model generated using experimental FRET-derived distance restraints for Rif SV (Table 1). (D) The same as for panel B, but model generated using combined experimental FRET-derived distance restraints for Rif and Rif SV (Table 1). Figures were prepared using PyMOL (DeLano, 2002).

Here, we have used systematic FRET and distance-restrained docking to define the position of the Rif pocket within RNAP, and have compared the results to those expected based on the crystallographic structure of the RNAP-Rif complex (Campbell et al., 2001). We performed experiments, in parallel, with Rif and with Rif SV, which exhibit R_o values of ∼38 and ∼32 Å, respectively, when used with fluorescein as acceptors in FRET (Fig. 4 A; Table 1). We measured FRET between fluorescein incorporated at each of 21 sites within RNAP holoenzyme (four sites in core subunits; 17 sites in σ⁷⁰ subunit) and Rif or Rif SV (Table 1). We then performed distance-restrained docking using, in parallel, experimental and simulated FRET-derived distance restraints for Rif, Rif SV, and the combined Rif/Rif SV data set (Fig. 4 B; Table 2).

TABLE 1.

Distance-restrained docking: application to RNAP

		Rifampicin			Rifamycin SV
Region	Residue	E	Ro (Å)	R (Å)	E	Ro (Å)	R (Å)
RNAP	αII235	<0.03	39.4	>70.0	<0.03	31.5	>56.0
	β643	0.32	37.6	42.6	0.19	31.9	40.6
	β937	0.43	38.1	39.9	0.27	32.3	38.1
	β′1377	0.06	38.9	60.8	0.04	31.0	53.6
σR2	95	0.34	36.6	40.9	0.18	31.0	39.9
	132	0.03	38.6	68.9	0.01	32.7	70.3
	366	0.04	38.8	65.9	0.01	32.9	70.8
	376	0.09	36.5	53.7	0.05	30.9	51.4
	396	0.12	37.3	52.0	0.06	31.6	50.0
	440	0.20	38.0	47.9	0.08	32.2	48.4
	442	0.05	38.0	62.1	0.05	32.2	53.6
σR3	459	0.43	37.4	39.2	0.18	31.7	40.8
	496	0.20	37.1	46.7	0.09	31.4	46.2
σR3/σR4 Linker	527	0.24	38.3	46.4	0.12	32.5	45.7
	537	0.05	37.8	61.7	0.01	32.0	65.8
σR4	557	0.03	39.5	70.5	0.01	33.5	68.9
	560	0.03	38.5	68.7	0.03	32.6	58.9
	569	0.06	38.8	61.4	0.03	32.9	60.6
	578	0.09	38.9	57.2	0.09	33.0	48.2
	583	0.03	39.5	70.5	0.01	33.5	72.1
		596	0.02	39.7	75.9	0.02	33.6	65.4

Experimental FRET measurements.

TABLE 2.

Distance-restrained docking: application to RNAP

	Experimental FRET data			Simulated FRET data
	Rif	Rif SV	Rif+Rif SV	Rif	Rif SV	Rif+Rif SV
Number of restraints	21	21	42	21	21	42
Accuracy (Å)	7.1	10.1	7.1	11±4	13 ± 3	8 ± 2
Precision (Å)	7.4	9.3	6.6	12 ± 7	12 ± 4	9 ± 4
Mean FRET penalty (Å)	0.9	1.1	1.0	0.4 ± 0.3	0.2 ± 0.1	0.4 ± 0.2
% FRET violation (0–5 Å)	48	57	36	65 ± 14	80 ± 7	72 ± 8
% FRET violation (5–10 Å)	9	10	17	24 ± 8	16 ± 7	18 ± 7
% FRET violation (>10 Å)	43	33	47	11 ± 12	4 ± 5	10 ± 5

Comparison of model quality for models of antibiotics generated with experimental and simulated FRET data. Simulated FRET efficiency data were generated by back-calculating exact donor-acceptor distances in the RNAP holoenzyme reference model and incorporating 10% systematic error as well as 15% random error into the restraints. Results are postprocessed to eliminate all sterically impossible solutions given the RNAP reference model.

Each set of experimental FRET-derived distance restraints yields models that are well defined and that place the binding site for Rif and Rif SV within the RNAP active-center cleft, overlapping the binding site for the RNA-DNA hybrid (Fig. 4, B–D). The Rif, Rif SV, and combined Rif/Rif SV data sets yield models with accuracies of 7.1, 10.1, and 7.1 Å, respectively, as compared to the crystallographically defined binding site for Rif (Campbell et al., 2001; green and red spheres in Fig. 4, B–D; Table 2), and with precisions of 7.4, 9.3, and 6.6 Å, respectively (Table 2). (Because the donor chromophore sites are not symmetrically distributed around Rif (white and yellow spheres in Fig. 4, B–D), the systematically shorter RNAP holo-Rif SV distance restraints (five out of 21 distance restraints are at least 10% shorter than the corresponding RNAP holo-Rif restraints) “pull” the Rif SV model toward the quadrant of RNAP containing the majority of chromophore sites relative to the Rif model.) Not surprisingly, the model generated from the combined Rif/Rif SV data sets overlaps the models generated from each of the single data sets.

To provide a comparison with the benchmark results, we generated simulated FRET-derived data mimicking: i), Rif data, ii), Rif SV data, and iii), combined Rif/Rif SV data, using the corresponding experimental R_o values and the RNAP-Rif reference model and experimental probe sites as the target assembly. We then generated noisy restraint sets, with and without 10% systematic error, and constructed models for Rif. Based on 10 runs (including postprocessing for eliminating all sterically impossible solutions given the reference model, exactly as with the experimental FRET-derived distance restraints), model accuracy is 11 ± 4 and 9 ± 4 Å for models with and without systematic error, and model precision is 12 ± 7 and 8 ± 2 Å for models with and without systematic error. All descriptors of model quality are within the ranges anticipated by benchmark simulations with 20 flexibly tethered probes limited to one quadrant of the assembly. (From Fig. 4, B–D, it is clear that a single quadrant of RNAP contains the majority of donor chromophore sites, represented by white and yellow spheres.)

Results for model accuracy and precision based on experimental FRET restraints are well within the range anticipated from our benchmark simulations and suggest that the reference model based on the T. aquaticus RNAP crystallographic structure is consistent with the experimental FRET data. However, there are differences in the mean FRET penalty per restraint and the distance distribution of violations between models generated using experimental FRET restraints and those generated from benchmark simulations (Table 2). For example, in the model generated using experimental FRET restraints for Rif, the mean FRET penalty per restraint is 0.9, and the distribution of distance violations is bimodal, with 47% of the restraints being violated by 0–5 Å and 43% of the restraints being violated by >10 Å. In contrast, in the models generated in the benchmark simulations, the mean FRET penalty per restraint is only ∼0.4, and only ∼10% of the restraints are violated by >10 Å. These results indicate that there may be additional sources of error in the experimental FRET restraints (e.g., larger errors in E or R_o than anticipated) or reference model (e.g., conformational difference between RNAP derivative in experiments and RNAP reference model and/or incorrect modeling of probe and linker conformations) that are not completely reflected in the simulated data used in the benchmark simulations.

Crystallographic and cryo-EM structures of RNAP and RNAP complexes establish that the RNAP β′-pincer can exist in a range of distinct conformational states—from a fully “open” state that permits unimpeded entry and exit of DNA (β′-pincer perpendicular to floor of active-center cleft), to a fully “closed” state that prevents entry and exit of DNA (β′-pincer rotated into active-center cleft) (Cramer et al., 2000, 2001; Gnatt et al., 2001; Armache et al., 2003; Bushnell and Kornberg, 2003; Kettenberger et al., 2003; Bushnell et al., 2004; Westover et al., 2004; Yildirim and Doruker, 2004). The transition between the fully open and fully closed states involves a swinging motion of the β′-pincer, with rotation by ∼30° about a hinge region at the base of the β′-pincer, and with displacement by ∼30 Å of residues at the distal tip of the β′-pincer. Because approximately one-third of donor chromophore sites in this work are located on a domain of σ⁷⁰ that interacts and moves with the β′-pincer, the conformational state of the β′-pincer used in the reference structure for distance-restrained docking potentially can be important (see Mekler et al., 2002). In this work, to assess the possibility that differences in the conformational state of the β′-pincer are responsible for the unassigned error, we constructed two sets of additional reference models with differing states of the β′-pincer, from fully open through fully closed, and evaluated the impact on model quality. We constructed the first set of additional reference models by rigid-body rotation of the β′-pincer about an axis defined by comparison of crystallographic structures of bacterial RNAP and eukaryotic RNAP II (“β′-pincer rotation model”; Mekler et al., 2002). We constructed the second set of additional reference models by interpolation and extrapolation—with nonrigid body motions—using a crystallographic structure of T. aquaticus RNAP and the cryo-EM structure of E. coli RNAP (“RNAP flexed model”; Darst et al., 2002).

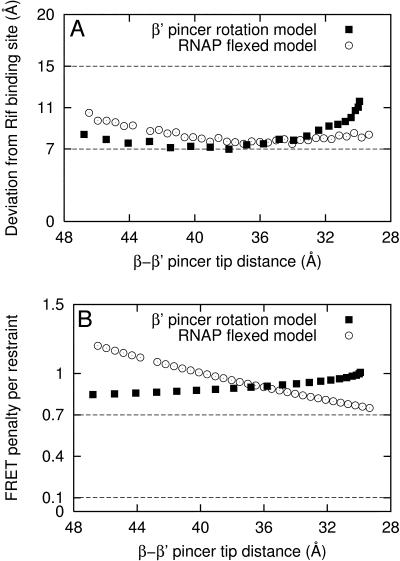
Using each of the set of alternative reference models, in turn, we generated a series of models of the RNAP-Rif complex using the experimental FRET-derived distance restraints for Rif (Fig. 5). The alternative reference models yield model accuracies (as compared to the crystallographically defined binding site for Rif (Campbell et al., 2001)) of 7–12 Å, comparable to that with the default reference model and comparable to benchmark simulations (Fig. 5 A). The additional reference models yield mean FRET penalties per restraint from 0.75 to 1.25, comparable to that with the default reference model, but higher than that in the benchmark simulations, 0.4 ± 0.3 (Fig. 5 B). Based on the higher mean FRET penalty per restraint in models generated using experimental FRET-derived distance restraints relative to the benchmark simulations, there appear to be additional sources of systematic error present in the experimental FRET-derived distance restraints or reference model, possibly including other modes of motion of the β′-pincer, species differences between experimental system (E. coli RNAP) and reference model (T. aquaticus RNAP) and/or errors in modeling of probe and linker conformations. (For the set of alternative reference models generated by rigid-body rotation of the β′-pincer, reference models with highly closed states of the β′-pincer yield models that are located further from the crystallographic Rif binding site and have higher mean FRET penalties per restraint (Fig. 5). In contrast, for the set of alternative reference models generated by interpolation and extrapolation based on the crystallographic structure of T. aquaticus RNAP and the cryo-EM structure of E. coli RNAP, reference models with highly closed states of the β′-pincer closed yield models that are closer to the crystallographic Rif binding site and have lower mean FRET penalties per restraint (Fig. 5). Thus, we cannot say in general that a more highly closed, or more highly open, state of the β′-pincer is more consistent with the experimental RNAP holo-Rif FRET data.)

FIGURE 5.

Distance-restrained docking: applications to RNAP. Results using experimental FRET measurements and alternative sets of reference models. (A) Distance deviation between the crystallographic Rif binding site (Campbell et al., 2001) and model generated from a given RNAP reference model. (B) Mean FRET penalty per restraint. The dashed lines indicate one standard deviation about the corresponding mean values determined from benchmark simulations using the default reference model (Table 2; Fig. 4, B–D), and simulated FRET data with 15% random error and 10% systematic error. The “β′-pincer rotation model” (▪) was constructed by rigid-body rotation of the β′-pincer (Mekler et al., 2002). The “RNAP flexed model” (○) was generated by interpolation and extrapolation based on the crystallographic structure of T. aquaticus RNAP and the cryo-EM structure of E. coli RNAP holoenzyme (Darst et al., 2002). The β′–β pincer tip distance was defined as the distance between the Cα atoms of residues β′-561 and β-363 (numbered as in PDB accession 1L9U). For comparison, the default reference model has β′–β pincer tip distance of 36 Å.

All resulting models place Rif in the RNAP active-center cleft, near the crystallographic Rif binding pocket. Although we have not exhaustively explored all possible states of the β′-pincer, we consider that the range of solutions provided by the different reference models analyzed represents an approximate upper limit on the range of possible solutions. Using the reference models analyzed, the range of possible solutions is a sphere of ∼10 Å radius—or ∼0.1% of the volume of RNAP—which overlaps the crystallographic Rif binding site. In the context of a macromolecular assembly the size of RNAP (∼100 × ∼100 × ∼150 Å; Ebright, 2000), this is a sufficiently well-defined solution to identify correctly the binding surface and to begin to apply molecular-modeling and/or site-directed-mutagenesis approaches to study details of interactions.

CONCLUSIONS

FRET measurements provide long-range distance information (10–100 Å) and thus are capable of spanning the dimensions of many biologically important complexes. By combining FRET-derived distance restraints with other structural information (e.g., x-ray or cryo-EM structures), models of large macromolecular assemblies may be constructed (Mekler et al., 2002; Mukhopadhyay et al., 2004; Fig. 5). Using simulated FRET data and target macromolecular assemblies, we have generated a series of benchmarks that permit estimation of the quality of models given the quality and quantity of FRET-derived restraints. We have shown how model quality primarily depends on the number of restraints and that the symmetry of chromophore sites becomes important in the presence of systematic errors in FRET measurements. However, with only a few restraints, the symmetry of chromophore positions and the distribution of distances in the restraint set are important indicators of model quality.

We also have determined the positions of Rif and Rif SV bound to RNAP using experimental FRET measurements. The accuracies of the resulting models were 7–10 Å, and corresponding precisions were 7 and 9 Å. The accuracy and precision using experimental data were comparable to those of benchmark simulations using simulated data. However, other measures of model quality (e.g., mean FRET penalties and distribution of distance violations) were underestimated by the benchmark simulations suggesting that there are additional sources of error that are not reflected in the simulated FRET data.

Finally, in FRET-based modeling, flexible regions of components that contain chromophore sites are most likely to produce problematic “structural errors” if treated as static structures because they introduce additional uncertainty when fitting the distance restraints. In this study, we have explored how the use of alternative RNAP reference models, reflecting motions of the RNAP β′-pincer, affects model quality. The results indicated that none of the alternative reference models were consistent with the benchmark simulations in all measures of model quality, suggesting that there may be additional sources of systematic error beyond uncertainties in the reference model that are not reflected in the simulated data. Multiple alternative reference models were used to define a range of possible solutions that satisfied experimental FRET restraints; these define a Rif binding site that occupies a sphere of ∼10 Å radius overlapping the crystallographically defined Rif binding site (Campbell et al., 2001).

Future work will lead to a comprehensive set of benchmarks in which the quality of models—from the most simple to the most complex—may be estimated from the quality and quantity of the FRET-derived distance restraints. We will move from the current benchmark simulations with a docking target with single fixed probe to benchmark simulations with a docking target with a single flexibly tethered probe (e.g., as in the analysis of the RNAP-MccJ25 complex in Mukhopadhyay et al., 2004) and docking targets with multiple flexibly tethered probes (as in the analysis of the RNAP-σ in Mekler et al., 2002). In addition, we will assess the improvements to model quality upon integrating additional structural, biochemical, and genetic experimental restraints into FRET-based modeling. One challenge in incorporating different types of structural restraints lies in appropriately adjusting the relative weighting of restraints in probability density functions. (In NMR and x-ray crystallographic studies, the R^free factor has been used to optimize the relative weighting of the nuclear Overhauser enhancement and energetic terms; Brünger, 1992, 1993; Brünger et al., 1993; Kleywegt and Brünger, 1996; however, this strategy relies on one to two orders of magnitude more data points than are currently employed in FRET modeling.) Finally, because a single structure is incapable of depicting the inherent flexibility of a macromolecule, we will integrate conformational flexibility into the modeling and use the resulting modeling procedures to develop models of RNAP assemblies corresponding to distinct states along the pathway of transcription.