Models for Excluded Volume Interaction between an Unfolded Protein and Rigid Macromolecular Cosolutes: Macromolecular Crowding and Protein Stability Revisited

Abstract

Statistical-thermodynamic models for the excluded volume interaction between an unfolded polypeptide chain and a hard sphere or hard rod cosolute are presented, permitting estimation of the free energy of transfer of a polypeptide chain with fixed radius of gyration from a dilute (ideal) solution to a solution containing volume fraction φ of either cosolute. Also presented is a general thermodynamic description of the equilibrium between a unique native state and a manifold of unfolded or partially unfolded states of a protein distinguished by their respective radii of gyration. Together with results of a Monte Carlo calculation of the distribution of radii of gyration of four different unfolded proteins published by Goldenberg in 2003, these models are used to estimate the effect of intermolecular excluded volume upon an experimentally measurable apparent two-state constant for equilibrium between native and nonnative conformations of each of the four proteins, and upon the experimentally measurable root mean-square radius of gyration of the unfolded protein. Model calculations predict that addition of inert cosolutes at volume fractions exceeding 0.1 stabilizes the native state relative to unfolded states by an amount that increases strongly with φ and with the size of the native protein relative to the size of inert cosolute, and results in significant compaction of the manifold of unfolded states. Predicted effects are in qualitative and/or semiquantitative accord with the results of several published experimental studies.

INTRODUCTION

Recognition of the highly volume-occupied nature of most if not all biological fluid media has stimulated numerous experimental and theoretical studies of the effect of steric exclusion by “inert” macromolecular cosolutes, termed “macromolecular crowding” (Minton and Wilf, 1981) upon the rates and equilibria of macromolecular reactions (Zimmerman and Minton, 1993; Hall and Minton, 2003). Such studies have included the effect of crowding upon the transition between conformational states of proteins (Minton, 2000; Sasahara et al., 2003; Tokuriki et al., 2004). It is generally agreed that for the purposes of estimating the free energy of excluded volume interaction between the native state of a compact globular protein and a macromolecular cosolute, the protein may be modeled by an equivalent hard convex hard particle (Wills et al., 1995; Minton, 1998). However, calculation of the free energy of steric interaction between a nonnative protein and a macromolecular cosolute is considerably more challenging, as the nonnative protein exists in a manifold of conformational states rather than in a single conformation.

We previously proposed an effective two-state model for the native-denatured transition of a protein (Minton, 2000), in which the properties of the denatured “state” were calculated as an average over the distribution of nonnative conformational states, as recapitulated in the next section. The effect of steric exclusion by a rigid cosolute upon the distribution of nonnative states, and upon the average free energy of this distribution, was then obtained by calculating the free energy of transfer of each individual conformational state from a dilute solution to a solution containing a given volume fraction of inert cosolute, or “crowding agent”.

Recently, an alternative model for the calculation of the excess free energy of an unfolded protein has been proposed (Zhou, 2004a,b), according to which the free energy of excluded volume interaction between an unfolded protein and a rigid spherical cosolute is calculated to be substantially smaller than obtained in our previous calculation. We therefore reexamine this problem and propose a modified model for calculation of the excluded volume interaction between an unfolded protein and a rigid hard spherical cosolute, which is based upon a treatment of chain conformation that we feel is significantly more realistic than that employed previously, and takes into account intramolecular excluded volume interaction between different segments of the unfolded polypeptide chain. The model is then extended to calculate the excluded volume interaction between an unfolded protein and a polymer modeled as a long rigid rod. Using the results, the effect of volume exclusion by both spherical and rodlike cosolutes on the equilibrium between native and unfolded conformations of four test proteins is calculated and compared with previous theoretical results and recently published experimental data.

EFFECTIVE TWO-STATE MODEL FOR PROTEIN DENATURATION

The treatment to follow is a modification and extension of that presented previously (Minton, 2000). A unique native state is postulated to exist in equilibrium with a manifold of denatured or unfolded states. The native state of the protein is denoted by N, and the ith nonnative conformational state by D_i. In this model, nonnative conformational states are distinguished by their respective radii of gyration, so each nonnative state represents an average of all substates with the same radius of gyration, denoted by R_G,i. The chemical potential of N is given by

(1)

where denotes the chemical potential of N at unit concentration in ideal solution (no solute-solute interaction), c_N the molar concentration of N, γ_N the thermodynamic activity coefficient of N in real solution, R the molar gas constant, and T the absolute temperature. We select as a reference nonnative state that state which is most abundant in the absence of solute-solute interaction under the selected environmental conditions, and denote this state by D₀. The chemical potential of D_i is then given by

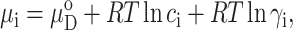(2)

where denotes the chemical potential of D₀ at unit concentration in ideal solution, and c_i and γ_I, respectively, denote the concentration and thermodynamic activity coefficient of state D_i in real solution. The assignment of a single standard state chemical potential to all nonnative conformations is equivalent to the statement that differences between the chemical potential of any two nonnative states at equal concentration shall be manifested as differences in the activity coefficients, e.g., when c_i = c_j = c:

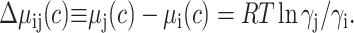(3)

At equilibrium, the chemical potential of all species is equal, and it follows from Eq. 2 that for any two species,

(4)

The fractional abundance of state i within the manifold of denatured states at equilibrium is then calculated to be

(5)

Since the mean value of any state property X is given by 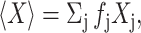it follows from Eq. 5 that the mean activity coefficient of all denatured states is

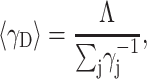(6)

where λ denotes the total number of denatured states.

The difference between the chemical potential of the two standard states N and D₀ is a constant at constant temperature, pressure, and solvent conditions. We may thus define a thermodynamic constant relating the concentrations of these two species:

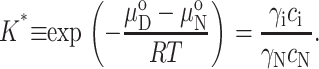(7)

Let us postulate that there exists an experimental measurement that permits one to measure the fraction of protein in the native state, denoted by f_N. The fraction of “denatured” protein, denoted by f_D, is then 1 − f_N. We may then define an experimentally measurable apparent two-state equilibrium constant for unfolding of the native state,

(8)

and a root mean-square radius of gyration of the denatured state

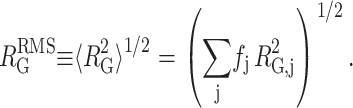(9)

Note that K_ND is an apparent rather than true thermodynamic equilibrium constant, because even when the protein itself is highly dilute, γ_N and 〈γ_D〉 may depend in principle upon the concentration of other nominally inert (i.e., unreactive) cosolutes.

We indicate the value of any variable in the dilute (ideal) limit with a superscript “o”, e.g., 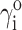or 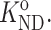Since the value of 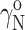is by definition 1, it follows from Eqs. 6 and 8 that

(10)

CONFORMATIONAL STATISTICS OF A DENATURED PROTEIN CHAIN; CONTRIBUTION OF INTRAMOLECULAR INTERACTION TO THE CHEMICAL POTENTIAL

The simplest model of a denatured protein is the random coil or freely jointed chain (Tanford, 1961). The conformational statistics of this model have been intensively studied and are known in some detail (see, for example, Flory, 1969). It is understood that the random coil model is unrealistic due to neglect of steric repulsion between different segments of the same chain, but it has been commonly argued that intramolecular steric repulsion may be taken into account by introduction of an empirical expansion factor (Flory, 1969). More recently, advances in computer processing speed and simulation algorithms have enabled intensive Monte Carlo calculations of the conformational statistics of both on-lattice and off-lattice self-avoiding walks (Victor et al., 1994; Dautenhahn and Hall, 1994; Bishop and Saltiel, 1991). Very recently, Goldenberg (2003) has reported off-lattice Monte Carlo simulations of the distribution of radii of gyration of models of four actual protein chains, taking into account local steric interactions between adjacent amino acid residues (i.e., restricted φ-ψ angles). Two sets of calculations were performed: in the first, long-range steric interactions (i.e., between nonadjacent residues) were ignored, and in the second, they were taken into account. Goldenberg found that when long-range steric interaction was taken into account—and only when it was taken into account—dependence of the calculated root mean-square radius of gyration upon chain length for all four proteins agreed well with experimental values obtained for a large set of denatured proteins.

According to Flory and Fisk (1966), the distribution of the radius of gyration of a freely jointed chain is given approximately by

(11)

where P is the relative abundance of a conformation with a given value of R_G, is the mean-squared radius of gyration, and A is a normalization constant. More recently, on the basis of scaling arguments, Lhuillier (1988) proposed the following distribution of the radius of gyration of a nonself-intersecting polymer chain in three dimensions:

(12)

where R_G* is the value of R_G corresponding to the maximum value of P, r ≡ R_G/R_G*, and B is an undetermined scaling parameter. Both of these functions were fit by nonlinear least squares to the eight distributions of R_G calculated by Goldenberg (four with long-range intramolecular steric interaction, four without). The best-fit functions are plotted together with the data in Fig. 1, and the best-fit parameters are given in Table 1.

FIGURE 1.

Distributions of the radius of gyration for four proteins. The relative abundance of conformations having a given value of R_G is plotted as a function of the value of R_G. Symbols indicate the results of Monte Carlo simulations of Goldenberg (2003), taking into account long-range steric interactions between nonadjacent chain segments (circles) and with neglect of long-range steric interactions (squares). Also plotted are the best-fit distributions of Lhullier (solid curves) and Flory and & Fisk (dotted curves), calculated using the parameter values given in Table 1.

TABLE 1.

Best-fit parameter values obtained by fitting Eqs. 1 and 2 to distributions of radius of gyration obtained by Goldenberg (2003); R_G,native taken from Goldenberg (2003)

		Long-range steric interaction included	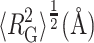(Monte Carlo result)	Best-fit parameters for Flory-Fisk distribution (Eq. 9)		Best-fit parameters for Lhuillier distribution (Eq. 10)
Protein	RG,native (Å)			A		RG* (Å)	P(RG*)	B
α-TS (268 aa)	16	n	38.4	2647	36.7	32.6	89.7	0.80
		y	56.3	1953	52.8	48.1	73.9	1.23
RNase (124 aa)	13	n	25.8	4091	24.8	21.9	136	0.74
		y	36.0	3112	35.4	32.0	112	1.04
BPTI (58 aa)	10.2	n	17.3	6019	16.6	14.7	201	0.75
		y	23.2	4778	23.1	21.0	178	1.15
ω-MVII-Gly (26 aa)	4.45	n	11.4	9433	10.6	9.31	314	0.73
		y	14.6	8250	13.8	12.8	321	1.43

It is evident that the Lhullier distribution function provides a satisfactory semiempirical description of the calculated distributions, both with and without included long-range steric interaction, whereas the Flory-Fisk distribution does not. This result implies that the freely jointed chain model does not provide a satisfactory description of conformational statistics of a real nonself-intersecting chain, even when only short-range steric interactions only are taken into account.

Since all denatured states are in equilibrium, and since 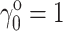by definition, it follows from Eq. 4 that

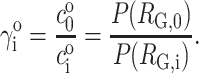(13)

Combining Eqs. 12 and 13, we obtain

(14)

where r_i ≡ R_G,i/R_G,0. The calculated dependence of 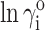on R_G,i for each of the four test proteins, calculated according to Eq. 14, is plotted in Fig. 2.

FIGURE 2.

Contribution of intramolecular excluded volume to the total chemical potential of a protein chain, calculated as a function of the radius of gyration according to Eq. 12 for α-TS (solid), RNase (dashed), BPTI (dot-dashed) and ω-MVII-Gly (dotted lines).

EXCLUDED VOLUME INTERACTION BETWEEN AN UNFOLDED POLYPEPTIDE CHAIN AND A HARD PARTICLE COSOLUTE

It follows from Eq. 3 that

(15)

Δμ_i (φ) is the free energy of transfer of an isolated polypeptide chain with a (fixed) radius of gyration R_G,i from a bath of solvent to a solution containing a volume fraction φ of inert macromolecular cosolute. We shall make two estimates of the contribution of excluded volume to the free energy of transfer (referred to as the excluded volume interaction), using two different models for the polypeptide chain.

Model 1: The “Gaussian cloud”

The polypeptide chain with a given value of R_G is treated as a time-averaged spherically symmetric cloud of residues. The average number density of residues, specified as a function of distance r_p from the center of mass of a polymer chain, is given by the Gaussian function (Tanford, 1961)

(16)

where 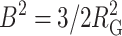and 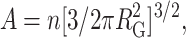and n denotes the total number of residues in the chain. This semiempirical function has been shown to provide a fairly accurate description of the density for polymer chains that are in a good solvent, and hence may be reasonably well represented by a freely jointed chain model (Debye and Bueche, 1952). A plot of ρ against r when 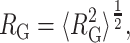calculated for each test protein using Eq. 13, is presented in Fig. 3. The probability that a rigid cosolute can penetrate to within a certain distance of the center of mass of the cloud without intersecting any residue is calculated as described below, and this probability is integrated over all intercenter distances to obtain the covolume of the polypeptide chain and rigid cosolute.

FIGURE 3.

Density of residues (No. residues/ų) plotted as a function of distance from the center of mass. Curves calculated according to Eq. 13 in the absence of intermolecular interaction for α-TS (solid), RNase (dashed), BPTI (dot-dashed) and ω-MVII-Gly (dotted lines).

Model 2: The equivalent hard sphere

The polypeptide chain is treated as an equivalent rigid sphere having the corresponding radius of gyration, and the covolume of this rigid sphere and the hard particle cosolute are calculated in the conventional manner (Minton, 1998).

It is emphasized at the outset that we recognize that neither of these models is expected to provide a realistic picture of the excluded volume interaction between the polypeptide chain and the rigid cosolute over the entire range of accessible radii of gyration. However, as will be discussed more fully in the concluding section of this article, we do expect the Gaussian cloud model to provide a more realistic picture of excluded volume interaction in the limit of large radii of gyration, and the equivalent hard sphere model to provide a more realistic picture in the limit of small radii of gyration (i.e., approaching that of the native protein). We thus expect the two models to yield limiting estimates of the magnitude of the excluded volume interaction, and that the true free energy of intermolecular excluded volume interaction will be bracketed by these estimates.

Excluded volume interaction between an unfolded polypeptide chain and a hard sphere: Gaussian cloud model

We define the system of spherical polar coordinates illustrated schematically in Fig. 4. The origin is the center of the hard sphere of radius r_S. A position is designated by the coordinates {r,φ,θ}, where r is the distance from the center of the sphere, θ is the angle between r and the polar (z) axis, and φ is a dihedral angle about the polar axis. The center of mass of the protein chain lies at a distance of r_sep along the polar axis. The point {r,θ,φ} is located at a distance r_p from the center of mass of the protein chain, where according to the law of cosines,

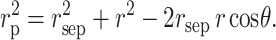(17)

The volume element dV is defined

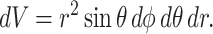(18)

The average number of segments in volume element dV is ρ(r, θ)dV. The probability of there being zero segments within this volume element is given by Poisson's law

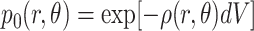(19)

and the logarithm of this probability is

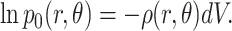(20)

The probability that no chain segments lie anywhere within the volume of an arbitrarily placed hard sphere is the product of the probabilities that a chain segment does not lie in any volume element within the sphere, which is equivalent to integrating ln p₀ over the volume of the sphere

(21)

Combining Eqs. 16–21, we obtain

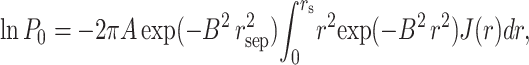(22)

where

(23)

Substituting in the values of A and B corresponding to the ith species, we obtain

(24)

FIGURE 4.

Spherical polar coordinate system for calculating steric interaction between a hard sphere centered at the origin and an unfolded protein chain with center of mass located at a distance of r_sep along the z axis.

We now scale all dimensions to r_S, the hard sphere radius:

(25)

Substituting relations (25) into (24), we obtain the dimensionless relation

(26)

The excess chemical potential of dilute polypeptide in a suspension of hard spheres arising from steric intermolecular interaction is given by (Minton, 1998):

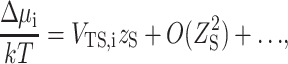(27)

where k is Boltzmann's constant, V_TS,i is the covolume of polypeptide species i and sphere, and z_S is the number density of spheres. In spherical polar coordinates, the covolume is given by

(28)

where P₀ is the probability that a sphere at distance r_sep from the center of mass of the tracer will not intersect any part of the tracer. The fraction of volume occupied by spheres is given by

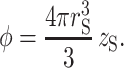(29)

Combination of Eqs. 27–29 yields

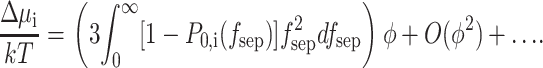(30)

To estimate the contribution of higher order terms not evaluated explicitly in Eq. 30, we shall treat each tracer species as an effective hard sphere of radius r_eff,i, which is a function of N and f_G,i. The covolume of this effective hard sphere and the hard sphere of radius r_S is (see, for example, Minton, 1998)

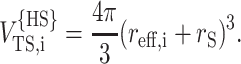(31)

The value of r_eff,i is then obtained by setting 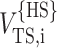equal to V_TS,i calculated according to Eq. 28, yielding

(32)

In the context of the effective hard particle approximation, the free energy of steric interaction between the ith denatured species and a hard sphere fluid may be estimated to all orders of φ using the scaled particle theory of hard sphere mixtures (Lebowitz et al., 1965):

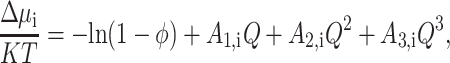(33)

where

For the effective hard particle approximation to be validly used to estimate higher order contributions to the total free energy of excluded volume interaction, the “soft” part of the repulsive potential of mean force acting between the polypeptide chain and the hard sphere must be short-ranged relative to the size of the hard repulsive core (Hall and Minton, 2003). This condition was checked and found to be met for the calculations whose results are presented below.

Excluded volume interaction between an unfolded polypeptide chain and a hard sphere: equivalent hard sphere model

The polypeptide chain with radius of gyration R_G,i is modeled as a hard sphere with an effective radius

(34)

Defining the scaled radius 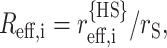the value of Δμ_i is calculated using Eq. 33.

Excluded volume interaction between an unfolded polypeptide chain and a hard rod: Gaussian cloud model

The free energy of steric interaction between a tracer hard convex particle and a polymeric cosolute has been estimated using the model of Ogston (Ogston, 1958; Ogston, 1970) and Giddings et al. (1968), according to which it is assumed that the polymer is sufficiently large that only part of the chain, modeled as a hard rod, can interact with the tracer particle. In this section, we estimate the free energy of steric interaction between a denatured protein with radius of gyration R_G and a polymer modeled as a hard rod of radius r_cyl.

Fig. 5 illustrates the following system of cylindrical coordinates. The origin is defined as the point on the rod axis closest to the center of mass of the protein coil. A position is designated by the coordinates {r,L,θ}, where r is the distance from the cylinder axis, θ is the angle between the vector r and the plane defined by the cylindrical axis and the center of mass of the protein, and L is the distance along the rod axis from the origin. Thus the interior of the rod is defined by all points such that 0 < r ≤ r_cyl, 0 < θ ≤ 2π, −∞ < L < ∞. The volume element dV(r,θ,L) is given by r dθ dr dL. We wish to calculate r_p, the distance between the point {r,θ,L} and the center of mass of the protein coil. From Fig. 4 we see that

(35)

The probability that no part of the denatured protein intersects the hard rod located at a distance r_sep from the center of mass of the protein is

(36)

Combining Eqs. 16, 35, and 36, we obtain

(37)

We now introduce the following scaled (dimensionless) variables:

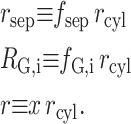(38)

Substituting the scaled variables into Eq. 37, we obtain

(39)

The excess chemical potential of a tracer particle in a polymer solution modeled as a suspension of hard rods, due to intermolecular excluded volume interactions, is well described by the first order term

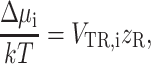(40)

where V_TR,i is the covolume of the ith tracer species and rod, and z_R is the number density of rods (Giddings et al., 1968; Ogston, 1970, 1958). This relation may be generalized to the case where the tracer is a coil rather than a hard sphere. The covolume may be expressed in cylindrical coordinates as

(41)

where l is the length of the rod and P₀ is the probability that a rod at a distance of r_sep from the center of mass of the tracer particle does not intersect any part of the tracer particle. The total fraction of volume occupied by rods is given by

(42)

Combining Eqs. 40–42, we obtain

(43)

The excluded volume contribution to the chemical potential of a hard sphere in a polymer solution modeled as a random array of hard rods is given by (Ogston, 1970; Minton, 1983)

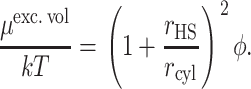(44)

By setting the chemical potentials expressed in Eqs. 43 and 44 equal, we may define an equivalent hard sphere radius corresponding to the ith unfolded species:

(45)

The value of r_eff,i calculated according to Eq. 45 is the radius of an effective hard sphere calculated using the Gaussian cloud model, defined with respect to excluded volume interaction with a hard rod. It is stressed that this value is not equal to the value of r_eff,i calculated according to Eq. 32, i.e., the radius of an effective hard sphere calculated using the Gaussian cloud model, defined with respect to excluded volume interaction with a hard sphere. The difference between the two values will be examined further in the discussion section.

FIGURE 5.

Cylindrical polar coordinate system for calculating steric interaction between a hard cylinder and an unfolded protein with center of mass located at a distance r_sep normal to the cylinder axis.

Intermolecular excluded volume interaction between an unfolded polypeptide chain and a hard rod: equivalent hard sphere model

The radius of the equivalent hard sphere representing the polypeptide chain is calculated according to Eq. 34, and the intermolecular excluded volume potential calculated according to Ogston (1970) and Minton (1983):

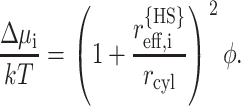(46)

EXCLUDED VOLUME INTERACTION BETWEEN A NATIVE PROTEIN AND A HARD PARTICLE COSOLUTE

It is assumed here that the native state of each of the four proteins treated by Goldenberg may be modeled as a hard sphere with a radius equal to times the radius of gyration of the native state calculated by Goldenberg. The corresponding value of γ_N is then calculated using either the scaled particle theory of Lebowitz et al. (1965) or the available volume theory of Ogston (1958), depending upon whether the inert cosolute is a globular protein modeled as a hard sphere, or a polymer modeled as a matrix of rigid rods.

RESULTS AND DISCUSSION

For each of the four proteins simulated by Goldenberg, calculations of the properties of the ensemble of denatured states were carried out on a set of 30 states with R_G values spaced logarithmically in the range between 0.4 and 1.5 Preliminary test calculations established that increasing the density of states and/or the range of R_G of the ensemble did not significantly alter the final results. Values of 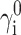were calculated as described in the section, “Conformational statistics of a denatured protein chain; contribution of intramolecular interaction to the chemical potential”. Values of γ_i were then calculated as a function of φ for each of several excluded volume models as described in the prior section. The value of 〈γ_D〉 was then calculated according to Eq. 6 with Λ = 30. The value of γ_N was then calculated as described in Section V. Finally, the values of 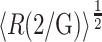and were calculated as functions of φ according to Eqs. 5, 9, and 10.

Denatured protein in a hard sphere fluid

The results of calculations carried out for each of four dilute tracer proteins (native and unfolded) in various volume fractions of a globular protein modeled as a hard sphere, with radius equal to that assumed for native ribonuclease A (r_S = 16.7 Å), are summarized in Fig. 6. The results of the corresponding calculations carried out for each of the four dilute tracer proteins in various volume fractions of polymer modeled as a hard rod cosolute, with cylindrical radius equal to that assumed for dextran (r_cyl = 7 Å) (Laurent and Killander, 1964; Rivas et al., 1999), are summarized in Fig. 7. The following salient points emerge.

1. Results of calculations carried out using unperturbed polypeptide size distributions obtained by Goldenberg that respectively neglect and explicitly take into account long-range intramolecular steric exclusion in the unfolded protein are plotted in Fig. 6. Comparison of these results indicates that neglect of steric exclusion acting between residues that are not adjacent on the peptide chain results in a), a reduction of ∼50% in the calculated difference between the free energies of the (equilibrium average) unfolded and native states at all nonzero volume occupancies, b), a more compact equilibrium average conformation at all degrees of fractional volume occupancy, and consequently, c), a significant underestimate of the free energy of stabilization of the native state relative to the equilibrium average unfolded state at all nonzero degrees of fractional occupancy. An even more dramatic consequence of neglecting long-range intramolecular steric exclusion is shown in Fig. 8, in which is plotted the calculated distribution of the radius of gyration of unfolded BPTI and α-TS at different values of the fractional volume occupancy of hard sphere cosolute. When long-range intramolecular steric exclusion is neglected (panels B and B′), at higher values of fractional volume occupancy a significant fraction of the equilibrium ensemble of unfolded protein is calculated to have a radius of gyration that is close to or even less than that calculated for a sphere consisting of an equal number of close packed residues (Chan and Dill, 1991), hence physically unrealizable. In summary, we find that neglect of intramolecular excluded volume leads to large qualitative errors in the predicted conformation and energetics of unfolded polypeptides in crowded fluids.

2. The Gaussian cloud and equivalent sphere models predict a qualitatively (and in favorable cases quantitatively) similar dependence of the average thermodynamic activity and conformation of unfolded polypeptides upon the fractional volume occupancy of both hard sphere and hard rod cosolutes, and a correspondingly similar dependence of the free energy of stabilization, as reflected in the equilibrium constant for unfolding. Since the two approximate models for intermolecular excluded volume interaction of unfolded polypeptide and hard sphere crowder are rather different, this finding suggests at first glance that the results are insensitive to details of the model for intermolecular excluded volume. As will be discussed subsequently, this is only partially true.

3. Model calculations predict that high concentrations of a stable globular protein, modeled as a hard sphere, or a random coil polymer, modeled as a hard rod, can substantially stabilize the compact native state of a dilute test protein relative to its equilibrium average denatured state. For a given volume fraction of cosolute, the magnitude of the stabilizing effect strongly depends upon the size of the test protein relative to the stable solute, a direct reflection of the highly nonlinear dependence of the free energy of cavity formation in a volume-occupied fluid upon the size of the cavity (Lebowitz et al., 1965). In the particular numerical simulations presented here, the stable globular cosolute protein was selected to be approximately the size of a native ribonuclease A molecule, and the diameter of the hard rod cosolute selected to be approximately that of an individual chain of dextran.

FIGURE 6.

Equilibrium average properties of four simulated proteins, plotted as functions of the volume fraction of hard spherical cosolute. (Top row) Thermodynamic activity coefficients of the native state (squares), the denatured “average state”, calculated using the Gaussian coil model with neglect of long-range intramolecular steric interaction (triangles), taking into account long-range intramolecular steric interaction (circles), and calculated using the equivalent hard sphere model with long-range intramolecular steric interaction (diamonds). (Middle row) Root mean-square radius of gyration of denatured “average state”, calculated using the Gaussian coil model with neglect of long-range intramolecular interaction (triangles), taking into account long-range intramolecular steric interaction (circles), and calculated using the equivalent hard sphere model with long-range intramolecular steric interaction (diamonds). Horizontal dotted line indicates R_G (native). (Bottom row) Change in the apparent two-state equilibrium constant for unfolding. Symbols denote different models as described above for the middle row.

FIGURE 7.

Equilibrium average properties of four simulated proteins, plotted as functions of the volume fraction of hard rod cosolute. (Top row) Thermodynamic activity coefficients of the native state (squares), the denatured “average state”, calculated using the Gaussian coil model taking into account long-range intramolecular steric interaction (circles), and calculated using the equivalent hard sphere model with long-range intramolecular steric interaction (diamonds). (Middle row) Root mean-square radius of gyration of denatured “average state”, calculated using the Gaussian coil model taking into account long-range intramolecular steric interaction (circles), and calculated using the equivalent hard sphere model with long-range intramolecular steric interaction (diamonds). Horizontal dotted line indicates R_G (native). (Bottom row) Change in the apparent two-state equilibrium constant for unfolding. Symbols denote different models as described above for the middle row.

FIGURE 8.

Distribution of the radius of gyration of two simulated proteins, calculated taking into account long-range intramolecular steric interaction (panels A and A′), and neglecting long-range intramolecular steric interaction (panels B and B′). Solid curves with unprimed labels were obtained using the Gaussian cloud model, and dashed curves with primed labels (panels A and A′ only) were obtained using the equivalent hard sphere model. The vertical dotted line corresponds to the radius of gyration of the native state, as reported by Goldenberg (2003). Plotted distributions were calculated for φ = 0, 0.1, 0.2, 0.3, and 0.4 (curves a–e, respectively).

The extent to which excluded volume effects in crowded solutions are predicted by this model to influence the chemical potential and conformation of an unfolded polypeptide chain seems surprisingly large. The increase in chemical potential is several times greater than that estimated by Zhou (2004a,b), and significantly greater than our previous treatment (Minton, 2000). It is therefore necessary to examine each of the assumptions and approximations underlying the model and to inquire whether that approximation might lead to a qualitative error in the resulting numerical estimate.

1. It is assumed that the magnitude of both intra- and intermolecular interactions may be specified as explicit functions of a single variable, namely the radius of gyration of a particular state. Although this is clearly somewhat of an oversimplification, it does not automatically follow that the assumption leads to gross numerical errors. Moreover, the assumption is indisputably more realistic than the naive two-state approximation underlying most current models of protein stability, as it permits variation in chain dimension, and corresponding changes in chain free energy, in response to imposed changes in external conditions or intra- and intermolecular forces. Our analysis of Goldenberg's results yields a well-defined phenomenological correlation, expressed in Eq. 12, between the free energy of chain compression or expansion and the radius of gyration. Whether the intermolecular excluded volume interaction between an unfolded polypeptide and other molecules modeled as hard particles may be adequately described as a function solely of the radius of gyration of the polypeptide is a more complex question. One can envisage conformations of the polypeptide chain with different degrees of anisometricity (deviation from spherical symmetry) that have the same radius of gyration, and these would not be expected, a priori, to have the same excluded volume interactions with hard particle fluids. However, since a sphere is the most compact conformation that can be adopted by a body of fixed volume, to the extent that we are neglecting such conformations, we are underestimating rather than overestimating the intermolecular excluded volume effect attributed to a polypeptide chain with a given radius of gyration.

2. The Gaussian cloud model is based upon a mean-field approximation involving a process of explicit preaveraging over all conformations with the same radius of gyration. In principle, one can test the validity of the preaveraging approximation by Monte Carlo simulations, but such simulations have not yet been performed and are beyond the scope of this work. However, similar approximations have served well in a variety of contexts (e.g., solution and liquid state theories), and in the absence of direct evidence to the contrary should not be rejected out of hand.

3. The number density of residues at distance r_p from the center of mass of the polypeptide is approximated by the Gaussian function, Eq. 16. This approximate function becomes progressively unrealistic as R_G shrinks toward the value characterizing the native protein, as when R_G becomes sufficiently small, the calculated density of residues at small r_p will surpass that of the native protein, which is regarded as a nearly close-packed entity (Richards and Lim, 1993). If the density of the innermost residues is constrained to a value less than or equal to that of the native protein, then as the value of R_G approaches that of the native protein, the density of outermost residues must decay more steeply with radial distance than predicted by a Gaussian function. As a consequence, as the radius of gyration of the unfolded polypeptide chain shrinks toward that of the natively folded chain, the potential of mean force characterizing the excluded volume interaction between the unfolded polypeptide chain and the hard particle crowder will increasingly resemble that between two hard particles. Thus, for values of R_G not much larger than that of the native protein, we may expect that the equivalent hard sphere provides the more realistic estimate of intermolecular excluded volume interactions between the (partially) unfolded polypeptide and the rigid cosolute. As the value of R_G increases and the average number density of residues declines at all radial distances to a small fraction of the close packing density, Eq. 13 is expected to provide an increasingly realistic estimate of the number average density of residues, and the Gaussian cloud model is concomitantly expected to provide an increasingly accurate estimate of the intermolecular excluded volume interaction between an unfolded polypeptide and a hard particle cosolute.

The two-body excluded volume interaction between the Gaussian cloud model of an unfolded polypeptide chain with a rigid cosolute is reflected in the value of r_eff, calculated according to either Eq. 29 or Eq. 42, depending upon whether the cosolute is modeled as a hard sphere or hard rod. These values may be compared with that obtained assuming that the unfolded polypeptide may be treated as an equivalent hard sphere, as in Eq. 31. The values of r_eff for each of the four unfolded test proteins, calculated according to all three equations, are plotted as a function of R_G in Fig. 9. An unexpected result obtained for all four proteins is that as R_G shrinks toward the value characteristic of the native folded protein, the value of r_eff approaches that of the equivalent hard sphere, which we expect to realistically describe the excluded volume interaction in the limit of small R_G (see above). At large values of R_G, the Gaussian cloud model polypeptide excludes less volume to a hard sphere cosolute than does the equivalent sphere (as expected), but, interestingly, the Gaussian cloud model polypeptide excludes as much or more volume to a hard rod cosolute than does the equivalent sphere. For the three smallest test polypeptides, the equivalent hard sphere model appears to provide an extremely simple method for estimating the free energy of excluded volume interaction of an unfolded polypeptide with a polymer modeled as a rigid rod.

FIGURE 9.

Dependence of the effective hard sphere radius for two-body excluded volume interaction upon radius of gyration. Vertical dotted lines in each plot indicate the radius of gyration of the native state of the respective test protein (Goldenberg, 2003). Solid curves are the result of the equivalent hard sphere approximation, in which the effective hard sphere radius is proportional to the radius of gyration. Dashed and dot-dashed curves are the results of Gaussian cloud model calculations of excluded volume interaction of each polypeptide chain with a hard sphere and hard rod cosolute, respectively.

We return to the question of why two quite dissimilar models for the intermolecular excluded volume interaction between an unfolded polypeptide chain and a rigid cosolute predict qualitatively (and sometimes semiquantitatively) similar dependences of the chemical potential of the unfolded chain upon the concentration of cosolute. The answer seems to be that the model predictions are most dissimilar for those chain conformations with large values of R_G. Such conformations are only important when fractional volume occupancy is low, as shown in Fig. 8, and the contribution of intermolecular excluded volume to the total chemical potential of the unfolded chain is relatively low, so the overall discrepancy is not major. As fractional volume occupancy of rigid cosolute, and consequently the contribution of intermolecular excluded volume to the total chemical potential of the chain increases, chain conformations with smaller values of R_G become increasingly important. The results shown in Fig. 9 indicate that as R_G shrinks toward the value characterizing the native state, the free energies of intermolecular excluded volume interaction calculated according to the Gaussian cloud and equivalent hard sphere models tend to converge toward the correct limit and hence each other.

The results presented in this article are deemed to be more realistic than previous estimates of the effect of intermolecular excluded volume on protein stability (Minton, 2000; Zhou, 2004a,b) for the following reasons:

1. The magnitude of the stabilizing effect deriving from excluded volume interaction between a protein and a hard sphere cosolute is somewhat greater than that predicted earlier by Minton (2000). The difference is attributed to a more realistic treatment of the conformational statistics of the unfolded polypeptide chain in the current model. Mutual volume exclusion of different segments of the unfolded polypeptide disfavors more compact conformations, causing the polypeptide to appear larger and to exclude more volume to crowder (compare panels A and A′ to panels B and B′ of Fig. 8), thereby increasing its chemical potential in the presence of a given concentration of crowder, as indicated in Fig. 6.

2. To calculate ΔΔG, the change in the free energy of unfolding arising from intermolecular excluded volume, Zhou (2004a,b) separately calculated the chemical potential of native and unfolded states of the polypeptide in the presence of a given concentration of hard sphere crowder. The formalism Zhou used to calculate the chemical potential of unfolded polypeptide describes the interaction between a random walk and a single trap (crowder molecule) that is correct—within the context of his model—only to first order in crowder concentration, and is equivalent to the first term on the right-hand side of Eq. 27. However, Zhou calculated the chemical potential of native polypeptide using an approximate equation of state that describes the interaction between hard sphere tracer and hard sphere crowder to all orders of crowder concentration. The appearance of an apparent maximum of the crowding effect calculated by Zhou (Fig. 4 b in Zhou et al., 2004b) is an artifact resulting from inappropriate comparison of two chemical potentials calculated to different orders of crowder concentration. A calculation that corrects approximately for this internal inconsistency (available upon request) indicates that the physical model of Zhou (2004a,b) predicts an effect of hard sphere crowding on protein stability that is comparable in magnitude to estimates obtained in the current work.

In the last analysis, the success or failure of a theory must be judged by its ability to account for or to predict experimental observations. In this work, we present a model for the effect of excluded volume by macromolecular cosolutes on protein stability with respect to denaturation. Despite widespread research on the subject of protein stability for many years, the number of experimental results with which this model may be validly compared is very limited. This is because in general, the effect of high concentrations of an added substance or combination of substances upon the stability of a trace protein may be due at least in part to specific and nonspecific interactions between the added substance and the trace protein other than excluded volume. For example, the effect of high concentrations of different size fractions of polyethylene glycol (PEG) on protein stability cannot be attributed solely to excluded volume interactions, as composition-dependent weakly attractive interactions between a variety of proteins and PEG are well documented (Tubio et al., 2004). However, two recent studies offer some reasonable basis for comparison with the current model, as they report effects of added dextran and Ficoll, two polymers that have been found to interact with a variety of native proteins essentially entirely via excluded volume (Laurent, 1963a,b; Laurent and Ogston, 1963). To facilitate comparison of experimental data with experiment, the fractional volume occupancy corresponding to a particular weight concentration is calculated according to

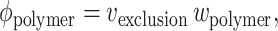(47)

where w is the w/v concentration of polymer, and v_exclusion is the specific volume of exclusion of the polymer with respect to the tracer solute. (Note that this volume is not equal to the partial specific volume of the polymer, which is defined as the volume excluded to solvent. The significance of v_exclusion is discussed in Zimmerman and Minton (1993).)

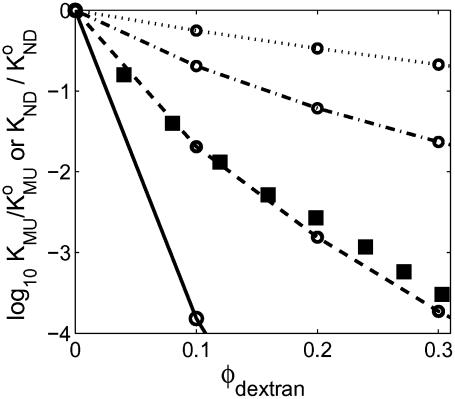
Relative stability of the molten globule and fully unfolded forms of cytochrome c at pH 2.0

At pH 2.0 and low ionic strength, cytochrome c unfolds, but in the presence of high concentrations of either salt or the inert polymer dextran, acquires a compact nonnative structure referred to as molten globule via an apparent two-state process (Goto et al., 1990; Sasahara et al., 2003). Sasahara et al. (2003) measured the fraction of protein present in the fully unfolded form, f_U, at different dextran concentrations via circular dichroism spectroscopy, and these data may be transformed into estimates of the equilibrium constant for unfolding of the molten globule according to

(48)

The value of K_MU in the absence of added dextran is denoted by 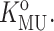The experimentally measured dependence of 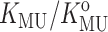upon the fraction of solution volume occupied by dextran is plotted in Fig. 10. Also plotted for comparison are the corresponding dependences of calculated for each of the four test proteins using the Gaussian cloud model with hard rod crowder. The model predicts that the expected degree of stabilization deriving from intermolecular excluded volume is extremely sensitive to the size of the tracer protein relative to the size of the hard particle cosolute. Since the molten globule state of a protein is almost as compact as that of the native state, the near-coincidence of the measured dependence of 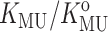upon φ for cytochrome c (molecular weight 12,500) and the predicted dependence of upon φ for the similarly sized RNase A (molecular weight 13,500) lends confidence in the quantitative capability of this model.

FIGURE 10.

Dependence of the equilibrium constant for unfolding upon fractional volume occupancy of dextran. (Solid squares) Calculated from the experimental results of Sasahara et al. (2003) for the two state transition between molten globule and fully unfolded forms of cytochrome c at pH 2.0, with v_exclusion = 0.8 cm³/g (Rivas et al., 1999). (Open symbols) Calculated for each of the four test proteins using the Gaussian cloud model of the unfolded state(s). (Dotted line) ω-MVIIa-gly. (Dot-dashed line) BPTI. (Dashed line) RNase. (Solid line) α-TS.

Stability of native ribonuclease A with respect to urea denaturation

Tokuriki et al. (2004) measured changes in the circular dichroism spectrum of ribonuclease A at 222 and 275 nm at pH 3.0 in the presence of 2.4 M urea and various concentrations of Ficoll 70. These authors estimated that under these conditions, in the absence of Ficoll the protein was ∼75% unfolded. Assuming a linear relationship between ellipticity and fractional folding, one may convert the data presented in Fig. 2, panels C and D, of Tokuriki et al. (2004) into estimates of the fraction of folded protein, which is plotted as a function of Ficoll concentration in Fig. 11. Also plotted in the figure are the best fits to these data of the Gaussian cloud model for RNase with hard sphere and hard rod crowder, calculated as described in the Appendix. The hard sphere crowder model, but not the hard rod crowder model, can satisfactorily fit the observed dependence. This is not surprising, as Ficoll 70 is a highly cross-linked polymer that is much more compact than a random coil polymer, although less compact than a native protein (Table 2). Because the analogy between Ficoll 70 and a hard sphere is only approximate, the significance of the best-fit parameter values given in the figure legend is only qualitative; namely, they are not obviously unphysical.

FIGURE 11.

Fraction of folded ribonuclease A at pH 3.0, plotted as a function of the fractional volume occupancy of Ficoll 70. Points calculated from molar ellipticity data of Tokuriki et al. (2004) at 222 nm (circles) and 275 nm (squares). Curves represent best fits of Eqs. 40) and 42 to the data when the activity coefficients are calculated using expressions given in the text for activity coefficients of folded and unfolded species given by the Gaussian cloud model for hard sphere crowder (solid curve) and hard rod crowder (dashed curve). Best fit parameter values for the hard sphere crowder model are 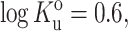r_native/r_crowder = 0.34, v_exclusion = 1.31 cm³/g.

TABLE 2.

Intrinsic viscosity of different classes of macromolecules; intrinsic viscosity is proportional to the ratio of hydrodynamic volume to mass, hence roughly inversely proportional to average molecular “density” (Tanford, 1961)

	Molecular weight	[η] (cm3/g)
Globular proteins	13,000– 250,000	3.3–4.0*
Ficoll 70	70,000 (average)	10†–13‡
Dextran T70	70,000 (average)	280§

^*Tanford (1961).

^†Amersham Biosciences Ficoll PM 70 product data sheet.

^‡Calculated from measurements of Busch et al. (2000).

^§Pharmacia product specification, lot 16108.

Compaction of a random coil polymer chain in concentrated polymer solutions

Tokuriki et al. (2004) measured the tracer diffusion coefficient of fluorescently labeled PEG 11700 via fluorescence correlation spectroscopy in solutions containing various concentrations of Ficoll 70, and interpreted their results in terms of the effective Stokes' radius of the equivalent hydrodynamic particle. Relative values of r_h taken from the cited publication are plotted against the fractional volume occupancy of Ficoll 70 in Fig. 12. For comparison, relative values of 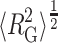of the unfolded “state” of similarly sized RNase (MW 12500) are also plotted as a function of φ_Ficoll. Although the hydrodynamic radius and the radius of gyration reflect different properties of a polymer chain and are hence not strictly comparable, the observation that these two quantities undergo a roughly parallel fractional decrease with increasing Ficoll concentration lends additional confidence in the semiquantitative significance of the calculated result.

FIGURE 12.

Dependence of apparent hydrodynamic radius of PEG 11700 (solid circles) and calculated RMS radius of gyration of unfolded ribonuclease A (open squares) upon fractional volume occupancy by Ficoll 70. Data of Tokuriki et al. (2004), with v_exclusion set equal to that obtained via the fitting procedure described in the Fig. 11 legend. Results of Gaussian coil model calculations scaled from Fig. 7.

Overall, we find that quantitative predictions of the models presented here are in reasonable harmony with the limited experimental data with which they may be properly compared, supporting the claim that the current model represents, at a minimum, a valid first-order picture of the underlying phenomena. Further progress will require additional critical, well-controlled experimental studies, and refinement of the theory, hopefully with the benefit of additional insightful simulations such as those provided by Goldenberg (2003).

APPENDIX: SEMIEMPIRICAL MODEL FOR FRACTIONAL FOLDING AS A FUNCTION OF COSOLUTE CONCENTRATION AND RELATIVE SIZE OF TRACE PROTEIN AND RIGID COSOLUTE

The value of was calculated as a value of φ and where r_C is either the radius of a hard sphere cosolute or the cylindrical radius of a hard rod cosolute, via interpolation between 20 “data points” of the form 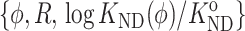calculated from the Gaussian cloud model as described in the text. The “data points” for each model cosolute (hard sphere and hard rod) were calculated for five values of φ, spanning the range 0–0.4, and four values of R, spanning the range 0.3–1.3 for the hard sphere cosolute and 0.8–3.0 for the hard rod cosolute. Each “data set” was fitted by a two dimensional polynomial of the form

(A1)

This function fitted both data sets with root mean-square residuals of <0.02. Once the best-fit values of C_ij—one set for each model cosolute—were determined in this fashion, they were fixed and no longer regarded as adjustable parameters.

Using Eq. A1 with no parameter adjustment together with Eq. 44, K_ND may be calculated as a function of the weight/volume concentration of cosolute together with the following adjustable parameters R, and v_exclusion. Then the fraction of natively folded protein is calculated from the two-state model according to

(A2)