Cooperativity and Kinetics of Phase Transitions in Nanopore-Confined Bilayers Studied by Differential Scanning Calorimetry

Abstract

The first-order nature of the gel-to-liquid crystal phase transition of phospholipid bilayers requires very slow temperature rates in differential scanning calorimetry (DSC) experiments to minimize any rate-dependent distortions. Proportionality of the DSC signal to the rate poses a problem for studies of substrate-supported bilayers that contain very small volumes of the lipid phase. Recently, we described lipid bilayers self-assembled inside nanoporous substrates. The high density of the nanochannels in these structures provides at least a 500-fold increase in the bilayer surface area for the same size of the planar substrate chips. The increased surface area enables the DSC studies. The rate-dependent DSC curves were modeled as a convolution of a conventional van't Hoff shape and a first-order decay curve of the lipid rearrangement. This analysis shows that although confinement of bilayers to the nanopores of ∼177 nm in diameter results in a more than threefold longer characteristic time of the lipid rearrangement and a decrease in the cooperative unit number, the phase transition temperature is unaffected.

Substrate-supported phospholipid bilayers serve as useful models for studying various properties of biological membranes and as a convenient way to biofunctionalize various inorganic substrates (1). Typically, substrates employed for such purposes have a planar geometry. Although these structures are convenient for studying with advanced surface-sensitive and imaging techniques, the small amount of lipids per substrate-supported sample poses a problem for other methods such as electron paramagnetic resonance, nuclear magnetic resonance (NMR), and differential scanning calorimetry (DSC). Recently, we have described substrate-supported bilayers that are formed by lipid self-assembly inside nanoporous substrates (2). These structures—which we call lipid nanotube arrays—have a high density of the nanoporous channels providing at least a 500-fold increase in the bilayer surface area for the same size planar substrate chips. Thus, such arrays could be studied by DSC and other methods. Recent NMR studies of such lipid nanotubes formed from 1,2-dimyristoyl-sn-glycero-3-phospho-choline (DMPC) and confined to anodic aluminum oxide (AAO) substrate with ∼200 nm pore diameter indicated some differences in the gel-to-liquid crystal phase transition when compared with unsupported bilayers (3). Specifically, temperature dependence of the normalized methylene resonance intensity measured in a ¹H magic-angle spinning NMR experiment indicated a substantial broadening of the phase transition and ≈1 K shift of the phase transition to lower temperatures (3).

To study the thermodynamics and the mechanism of the phase transition in substrate-supported lipid nanotubes we employed DSC as the most direct and convenient method. Multilamellar DMPC vesicles (20% lipid by volume) were prepared as in (2) and used as a control sample 1. For sample 2, an AAO disk (Whatman, Middlesex, UK; 20 nm pores) was immersed in a buffer and placed inside an ER-3 extruder (Eastern Scientific, Rockville, MD) that was attached to 0.5-ml Hamilton syringes (Hamilton, Reno, NV) on each end. DMPC vesicles were loaded into one of the syringes and pushed back and forth at least 25 times. Subsequently, an excess of lipids was removed by flushing the nanopores with a buffer to ensure that only a single nanotubular bilayer is left on the surface (5). From examination of this AAO substrate with a JEOL 6400F field Emission scanning electron microscope (JEOL, Tokyo, Japan), the average pore diameter was 177 ± 25 nm for one side and 28 ± 8 nm for the thin (1–2 μm) filtration layer on the other side. After depositing the lipids, two AAO disks of 25-mm diameter were broken into a few pieces and placed into a steel high-volume pan. The pan was filled with 20–30 μl of buffer, sealed with a lid and an O-ring, and loaded into a Q100 calorimeter (TA Instruments, New Castle, DE). Each sample contained ∼1 mg of DMPC.

Fig. 1 shows a series of DSC curves for samples 1 and 2 measured at progressively decreasing rates from β = 1.75–0.1 K/min (from top to bottom). The scans obtained at β > 0.5 K/min are visibly distorted. Decreasing β below 0.1 K/min was impractical because of the low amplitude of the DSC signal. Our minimal rate β was slower than the 0.5 K/min previously employed in the DSC studies of DMPC bilayers formed on mica chips (4) but faster than β = 0.0232 K/min reported for unsupported bilayers (5).

FIGURE 1.

Experimental DSC curves for DMPC bilayers for control sample 1 (A) and AAO-supported nanotubes, sample 2 (B). Temperature rate β is in K/min.

Typically, the DSC curve for the gel-to-liquid crystal bilayer phase transition is modeled as (6):

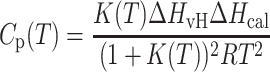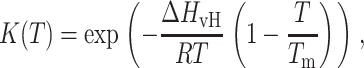where ΔH_vH and ΔH_cal are the van't Hoff and calorimetric enthalpy, respectively, K(T) is the equilibrium constant, and T_m is the phase transition temperature. These equations represent an idealized model of the bilayer phase transition occurring as a quasiequilibrium non-two-step process composed of many A↔B reversible steps.

When the temperature is changing rapidly, the equilibrium for the A↔B process is restored as ([A] − [A₀]) ∝ −(k₁ + k₋₁)t resulting in a proportional time dependence of the heat flow q(t) ∝ −(k₁ + k₋₁)t = −t/τ, where k₁ and k₋₁ are the rate constants for the forward and the reverse processes, respectively, and τ is the effective time constant of the lipid rearrangement. If β = const, then T is proportional to t and the experimental DSC signal E(T) can be approximated by a convolution integral:

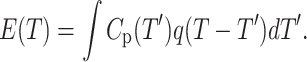We have applied this first-order relaxation model to least-square fit the DSC data using a modification of a convolution-based Levenberg-Marquardt optimization program we developed previously for electron paramagnetic resonance (7). It was found that this model fits the DSC curves exceptionally well (Fig. 2). The results of least-squares simulations of all the DSC data are plotted in Fig. 3. Two parameters of the phase transition, T_m and ΔH_vH, were found to be rate dependent and therefore were determined by extrapolating to β = 0 as shown in Fig. 3, A and B. It was found that although for AAO-confined DMPC bilayer T_m = 23.43 ± 0.05°C was essentially the same as for the control sample T_m = 23.50 ± 0.05°C, the van't Hoff enthalpy was lower (ΔH_vH = 8.9 ± 0.2 vs. 18.8 ± 0.2 MJ/mol).

FIGURE 2.

DSC curve for the control sample 1 measured at 1.5 K/min (open circles) and least-squares simulations as described in text (solid line).

FIGURE 3.

Experimental parameters obtained from fitting DSC curves for the control sample 1 (solid circles) and AAO-supported sample 2 (open circles) as a function of temperature rate β.

Fig. 3 C demonstrates that the time constants, τ, for both samples were essentially independent of the temperature rate β in accord with our model. However, τ for the nanopore-confined DMPC bilayer was significantly longer than for the control (τ = 70 vs. 21 s). Although the finite time-response of the DSC calorimeter could also contribute to τ, we speculate that this contribution is minimal because of the small amount of lipids and very thin samples used for the experiments. Moreover, because of essentially the same lipid amounts in both samples, this contribution is also expected to be the same. Thus, this difference in τ indicates that rearrangement of the lipid in the bilayers confined to nanopores during the phase transition is significantly slower than for the control.

Another effect of nanoscale confinement on the mechanism of the phase transition is a decrease of the cooperative unit number N. By taking ΔH_cal ≈ 22.5 KJ/mol for DMPC (8) we estimate N by dividing ΔH_vH to ΔH_cal as ≈400 for the AAO-confined nanotubular bilayer versus ≈840 for the control sample. It is worthwhile to note here that for AAO-supported nanotubular bilayer the domain size N ≈ 400 is about an order of magnitude greater than N = 35–45 estimated from atomic force microscopy measurements for planar substrate-supported bilayers (9). Thus, the main effect of nanopore confinement appears to be in longer time constants associated with lipid rearrangement during the phase transition but not in the thermodynamics as previously thought (3).