Calcium Mobilization and Spontaneous Transient Outward Current Characteristics upon Agonist Activation of P2Y₂ Receptors in Smooth Muscle Cells

Abstract

A quantitative model is provided that links the process of metabotropic receptor activation and sequestration to the generation of inositol 1,4,5-trisphosphate, the subsequent release of calcium from the central sarcoplasmic reticulum, and the consequent release of calcium from subsarcolemma sarcoplasmic reticulum that acts on large-conductance potassium channels to generate spontaneous transient outward currents (STOCs). This model is applied to the case of STOC generation in vascular A7r5 smooth muscle cells that have been transfected with a chimera of the P2Y₂ metabotropic receptor and green fluorescent protein (P2Y₂-GFP) and exposed to the P2Y₂ receptor agonist uridine 5′-triphosphate. The extent of P2Y₂-GFP sequestration from the membrane on exposure to uridine 5′-triphosphate, the ensuing changes in cytosolic calcium concentration, as well as the interval between STOCs that are subsequently generated, are used to determine parameter values in the model. With these values, the model gives a good quantitative prediction of the dynamic changes in STOC amplitude observed upon activation of metabotropic P2Y₂ receptors in the vascular smooth muscle cell line.

INTRODUCTION

Purine nucleotide receptors have been divided into two classes, P2X (ionotropic ligand-gated) and P2Y (metabotropic G-protein coupled; for a review see Abbracchio and Burnstock, 1994). The subclasses of metabotropic receptors, P2Y₁ and P2Y₂, are especially prominent in arteries, with the mRNA for P2Y₂ receptors found in arterial smooth muscle cells (Harper et al., 1998). P2Y₂ receptors are clearly distinguished from P2Y₁ because of the specific actions on the P2Y₂ receptor of uridine 5′-triphosphate (UTP), ED₅₀ of 1 μM (see Bultmann et al., 1998), which can be released by endothelial cells (Saiag et al., 1998). Activation of P2Y₂ receptors, which like other P2Y receptors are coupled to phospholipase C (von Kugelgen and Wetter, 2000), releases calcium from intracellular stores (Hou et al., 1999), after which receptor phosphorylation appears to regulate desensitization of the P2Y₂ receptor through the action of a protein kinase (Otero et al., 2000).

The wild-type P2Y₂ receptor sequesters in a time-dependent manner, as do other G-protein coupled receptors (Wilkinson et al., 1994; Koenig and Edwardson, 1996). Approximately 60% of the membrane receptor is internalized in 5 min upon exposure to UTP, as indicated using monoclonal antibodies (Garrad et al., 1998). However, this labeling technique does not allow the receptor sequestration to be monitored continuously after exposure to agonist, so it has limited time-resolution. An alternative approach is to use chimeras of green fluorescent protein (GFP) and the receptor of interest, which enables sequestration to be followed in real-time after application of agonist (see, for example, Dutton et al., 2000). In the first part of the present work we have constructed chimeras of GFP and the P2Y₂ receptor (P2Y₂-GFP) and determined, after transfection of cDNA P2Y₂-GFP in the vascular smooth muscle cell line A7r5, the time-course of changes in P2Y₂-GFP at the membrane after exposure to the agonist UTP. In addition, we have shown that exposure of these transfected cells to agonist gives rise to a calcium transient in the cytosol of these cells which has a similar time-course to that of the changes in the P2Y₂-GFP at the membrane. We have recently developed a model that links the process of metabotropic receptor activation and sequestration to the generation of inositol 1,4,5-trisphosphate (IP₃) and the release of calcium from the sarcoplasmic reticulum (SR) (Lemon et al., 2003a,b). Such SR is found throughout A7r5 cells, both in the subsarcolemma as well as deeper in the cytoplasm (Vermassen et al., 2003). We use this model to link the desensitization/sequestration of P2Y₂ receptors at the membrane with changes in cytosolic calcium so as to provide a quantitative account of the experimental observations.

Spontaneous transient outward currents (STOCs) in smooth muscle cells are due to the opening of calcium-activated potassium channels which fall principally into two classes, large conductance (BK) channels and small conductance channels (Benham and Bolton, 1986). They have been reported in smooth muscle cells of a variety of organs, including the gastrointestinal tract (Kong et al., 2000) and particularly blood vessels (Komori and Bolton, 1989; Hume and Leblanc, 1989; Greenwood and Large, 1995; Perez et al., 1999; Smirnov and Aaronson, 1992; Bychkov et al., 1997). Activation of P2Y receptors in some cell types increases the frequency of STOCs, for example in colonic smooth muscle (Kong et al., 2000) and clonal kidney cells (Hafting and Sand, 2000; Bringmann et al., 2002). In others it decreases the frequency, as in cerebral artery smooth muscle (Jagger and Nelson, 2000) and ileal smooth muscle (Gomez et al., 2002). In the second part of the present work we determine the amplitude and temporal characteristics of STOC generation upon agonist activation of P2Y₂ receptors and show that STOCs are elevated over a time-course similar to that of P2Y₂ desensitization/sequestration. Our model has therefore been extended to include the release of calcium from strategically placed SR, located at the periphery of the cells just beneath the sarcolemma; the calcium released into this subsarcolemmal space acts on BK channels to generate STOCs. This model provides a quantitative account of observations and links the rates of desensitization/sequestration of the metabotropic receptors to changes in the cytosolic calcium in the cell, calcium changes in the subsarcolemmal space, and the generation of STOCs.

MATERIALS AND METHODS

Experimental

Plasmid construction

Plasmid construction pCI-P2Y₂-GFP was constructed as follows. The plasmid pBluescript small-conductance (−) containing P2Y₂ cDNA insert from human epithelial cells was obtained (Parr et al., 1994). The P2Y₂ cDNA was amplified from the plasmid by polymerase chain reaction (PCR) using a forward primer that annealed to the T3 promoter region and a reverse primer that annealed directly upstream of and over the stop-codon in P2Y₂. The forward primer (5′ G CGC AAG CTT ATG GCA GCA GAC CTG GGC 3′) incorporated an in-frame Hind III site to ligate upstream of GFP-20 in pBluescript II KS(+). The reverse primer (5′ GAC CAT GGC GCC GCC GCC CAG CCG AAT GTC CTT AGT 3′) eliminated the stop-codon and incorporated an in-frame Nco1 site at the 3′ end of P2Y₂. The PCR product was ligated upstream and in-frame into the 5′ Nco1 site of GFP-20 in pBluescript II KS(+). The P2Y₂-GFP insert was removed and ligated into pCI (Promega, Madison, WI), a CMV promoter-driven mammalian vector. The sequence of the P2Y₂ PCR product of both the coding and noncoding strands and P2Y₂-GFP insert was confirmed using automated fluorescence sequencing.

Transfection of A7r5 smooth muscle cells

Cells were seeded onto glass coverslips in 24-well plates and grown to 50–70% confluence at 37°C in a humidified atmosphere of 5% CO₂ and 95% air. A7r5 cells were cultured in Dulbecco's modified Eagle's medium (Life Technologies, Gaithersburg, MD) with Earle's salts. A total of 0.5 μg pCI-P2Y₂-GFP in 50 μL serum-free media was added to 2.1 μL Lipofectamine reagent (Life Technologies) in 50 μL serum-free media. The DNA and Lipofectamine mixture was incubated at room temperature for 10 min to allow complexes to form before addition of the complexes to the cells. The complexes were removed after incubation at 37°C and 5% CO₂ for 3–6 h. Media containing FCS was added and the cells were further incubated for ∼24 h before visualization.

P2Y₂ receptor antibodies

We have generated rabbit polyclonal antibodies against the P2Y₂ receptor C-terminal 18 residues with an added C-terminal Cys as well as against sequences 226–242 of the receptor. The specificity of antibodies for these P2Y₂ receptors (Ab P2Y₂) has been established (see Methods in Ray et al., 2002).

Immunohistochemistry

Cells were fixed in 4% paraformaldehyde in borate acetate buffer (pH 9.5) for 1 min, washed in 5 mM phosphate-buffed saline (PBS) for 10 min (3×) and placed in 0.1% DMSO in phosphate-buffered horse serum (100 mL PBS, 2 mL normal horse serum, 0.1 mL Triton X-100, 1 g bovine serum albumin) for 10 min to permeabilize the cellular membranes. Cells were washed in 5mM PBS for 10 min (3×) and immersed in 20% normal horse serum in PBS for 1 h to block nonspecific binding sites before incubation with 1:100 of sheep AbP2Y₂ or mouse AbSV2 in PBS. Incubation time varied from 2 h at 20°C to 18 h at 4°C. Slides were rinsed in PBS for 10 min (3×) followed by application of the appropriate secondary antibodies (anti-mouse Cy2 for AbSV2 or anti-sheep Cy3 for AbP2Y₂) for 2–3 h at 20°C. Slides were washed in PBS for 10 min (3×), coverslipped and sealed.

Confocal microscopy of P2Y₂-GFP

Fluorescent images were collected with an inverted Leica four-dimensional laser-scanning confocal microscope using a 40:10 oil immersion objective (Leica, Wetzlar, Germany). Full-frame images (256 pixels × 256 pixels) were taken of an area of interest of cells and a flattened two-stack image of the confocal images of P2Y₂-GFP generated. Sufficient numbers of slices were taken, with an interval of 0.5 μm. Images were transferred to a Power Macintosh 6200/75AV between each slice, to avoid the difficulties that arise due to change in the focal plane of the microscope with respect to the cell interior as the cells rounded up upon exposure to agonist (see Fig. 4 A). Each of the images of the z-stack was then superimposed over the previous one to generate a flattened z-stack. The images were processed using NIH Image 1.60 (available from the US National Institute of Health at http://rsb.info.nih.gov/nih-image/). The mean intensities of the images were used to generate data such as that graphed in Fig. 5.

FIGURE 4.

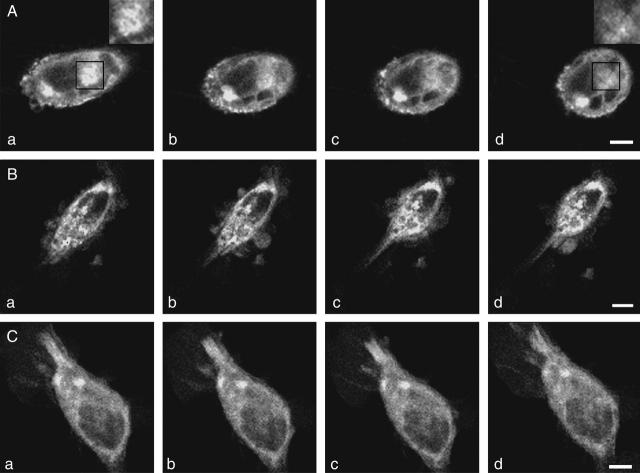
P2Y₂-GFP in A7r5 cells under different experimental conditions. (A) Confocal images of A7r5 cells showing the clustering of P2Y₂-GFP in the membrane 24 h after transfection (a), and then the gradual loss of many of the clusters after exposure of the cells to 10 μM UTP for 1 min (b), 2 min (c), and 5 min (d); higher magnification inserts in a and d are taken from the solid-square regions and show dense clusters of P2Y₂-GFP in a that are largely lost in d. Note that in addition to the loss of many of the clusters, there is a gradual rounding-up of cells in the presence of the agonist. (B) Confocal images of P2Y₂-GFP as in A, but this time in the presence of monensin (5 μM); note no loss of P2Y₂-GFP fluorescence, but the cells still round up. (C) Confocal images of P2Y₂-GFP as in A, but this time in the presence of suramin (10 μM); note again no loss of P2Y₂-GFP fluorescence, and in this case the cells do not round up. Calibration bar is 10 μm.

FIGURE 5.

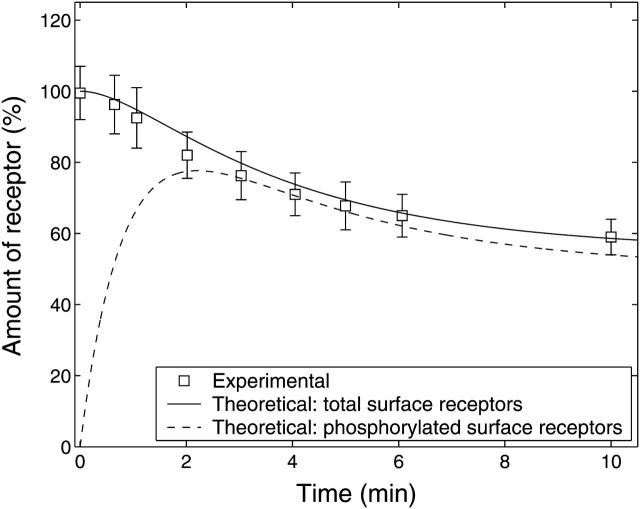
Experimental and theoretical membrane P2Y₂ receptor fraction with respect to time. Experimental data show the time-course of P2Y₂-GFP in A7r5 cells (squares with mean ± SE for six cells) after application of 10 μM UTP at t = 0. The P2Y₂-GFP fluorescence has been taken to be proportional to the number of receptors in the membrane and has been scaled to become a percentage of the amount of receptor relative to that before agonist stimulation. The solid line is the theoretical time-course of the total surface receptor fraction, and the broken line is the time-course of the phosphorylated surface receptor fraction, both obtained by solving Eqs. 1 and 2.

Calcium measurements

Coverslips with cells grown to 50–70% confluence were incubated in culture medium with 5–10 μM Fluo-3 AM (Molecular Probes, Eugene, OR) at 37°C and 5% CO₂ for 30 min to 1 h. Coverslips were mounted in a Perspex holder and mounted on an upright Leica system as described above and fluorescence was recorded at 526 nm. Desensitization experiments were performed by incubating cell suspensions in 10 μM UTP for 8 min at 20°C.

Whole-cell voltage-clamp of cells

Cells were voltage-clamped using the nystatin perforated patch-clamp technique. Whole-cell recordings were made with an Axopatch-1C amplifier (Axon Instruments, Union City, CA) at a holding potential of −60 mV and −30 mV. Patch pipettes between 2 and 4 MΩ were filled with standard pipette solution containing: 130 mM CsCl, 10 mM HEPES, 10 mM EGTA, 1 mM CaCl₂, 2 mM MgCl₂, pH 7.3 adjusted with CsOH. The standard bath solution contained: 140 mM NaCl, 5 mM KCl, 10 mM HEPES, 10 mM glucose, 2 mM CaCl₂, 1 mM MgCl₂, pH 7.3 adjusted with NaOH. ATP was applied with a fast-flow U-tube delivery system. All electrical recordings were carried out at room temperature (20–22°C). Data were acquired and analyzed using a MacLab (AD Instruments, Charlotte, NC).

Materials

All chemicals were obtained from Sigma (St. Louis, MO).

Theoretical model

Overview of model

The model cell contains sarcoplasmic reticulum that is represented by two compartments—a central SR and a peripheral SR (Fig. 1). After application of UTP, the P2Y₂ receptors form five dynamically linked classes: in the sarcolemma they can either be phosphorylated or unphosphorylated and each type can be unbound or bound to ligand; in addition, bound phosphorylated receptors can be internalized and eventually recycled (Fig. 2 a). The ligand-bound unphosphorylated receptors activate a G-protein cascade, leading to the production of IP₃ that diffuses into the cytosol and acts on IP₃ receptors (IP₃Rs) in the central SR (Fig. 1). This results in the release of calcium ions (Ca²⁺) that diffuse throughout the cytosol, are pumped into the peripheral SR by a Ca²⁺-ATPase, and also act on ryanodine receptors (RyRs) in the peripheral SR to release further Ca²⁺ in an oscillatory manner into the subsarcolemmal space between the peripheral SR and the sarcolemma (Fig. 2 b). These calcium sparks act on nearby BK channels in the sarcolemma (Fig. 1), thus generating STOCs.

FIGURE 1.

Schematic diagram of the multicompartment vascular smooth muscle cell model. P2Y₂ receptors are present in the sarcolemma. The cell interior contains three main compartments: the cytosol (1), the central SR (3), and the peripheral SR (2), with the cytosol being divided into a main part and a smaller subsarcolemmal space lying between the peripheral SR and the sarcolemma. The central SR membrane contains IP₃Rs and the peripheral SR membrane contains RyRs; both have Ca²⁺ leaks and pumps. BK channels are in the sarcolemma in close apposition to the RyRs in the peripheral SR. J_ab denotes a Ca²⁺ current from compartment a to compartment b.

FIGURE 2.

(a) Kinetic scheme for receptor-ligand binding, phosphorylation, and internalization. (b) Schematic diagram of the compartments in the model and the Ca²⁺ fluxes between them. (c) Kinetic scheme of the model for the bursting behavior of the ryanodine channels on the peripheral SR membrane. (There are four states: inactive, open, closed, and refractory, denoted by the A, B, C, and D, respectively.)

The diffusion of Ca²⁺ and of IP₃ has not been explicitly treated; its inclusion would require detailed spatial modeling of the SR and is beyond the scope of this investigation. Given that the time interval between individual STOCs is the order of 30 s, diffusion effects would be expected to be small compared to those from other processes in the model. The one place where an inhomogeneity is invoked is in the subsarcolemmal space where the RyRs are assumed to produce a local increase in Ca²⁺ concentration, above that in the rest of the cytosol.

Regulation of receptor activity, G-protein cascade, and IP₃ production

The equations describing the processes involved in P2Y₂ receptor regulation, the G-protein cascade, and the production and regulation of IP₃ are adapted from a previous model (Lemon et al., 2003a). However, the equations have been simplified because some aspects of that model are superfluous for the purposes of this study; these differences are discussed below.

The interaction between ligand (L) and receptors (R) are shown in Fig. 2 a; R_P denotes phosphorylated receptors and R_I denotes internalized receptors. The stimulus applied to the cells is taken to be a step application of agonist of concentration [L] applied at time t = 0. The equations describing the dynamics of the receptors in response to this stimulus are

(1)

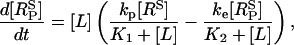(2)

where [R^S] = [R] + [LR] and 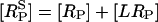are the numbers of unphosphorylated and phosphorylated surface receptors, respectively. The total number of receptors is where is the total number of surface receptors; and k_p, k_e, and k_r are the rates of receptor phosphorylation, endocytosis, and recycling, respectively. 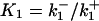and are the dissociation constants for the binding of ligand to the unphosphorylated and phosphorylated receptors, respectively.

The unphosphorylated ligand-bound receptors activate G-protein molecules in the plasma membrane, the amount of active G-protein, [G], satisfying

(3)

where k_a and k_d are the G-protein activation and deactivation rate parameters, [G_T] is the total number of G-protein molecules, δ is the ratio of the activities of the ligand-unbound and -bound receptor species, and ρ_r is the ratio of the number of ligand-bound receptors to the total number of receptors: ρ_r = [L][R^S]/([R_T](K₁ + [L])). This differs from Eq. 17 of Lemon et al. (2003a) in that there is assumed to be no immobile receptor fraction, so ξ = 1. The active G-protein activates phospholipase C (PLC) which hydrolyzes phosphatidylinositol 4,5-bisphosphate (PIP₂) in the plasma membrane to form IP₃. The rate of hydrolysis of PIP₂ is r_h[PIP₂], where [PIP₂] is the number of PIP₂ molecules and r_h = α[G], where α is an effective signal-gain parameter. This differs from Eq. 18 of Lemon et al. (2003a) in that there is assumed to be no Ca²⁺-activated synthesis of IP₃, so K_c = 0. Also, in the present study there is assumed to be no depletion of PIP₂, so [PIP₂] = [(PIP₂)_T] is the total number of PIP₂ molecules in the plasma membrane. Thus Eq. 24 of Lemon et al. (2003a) becomes

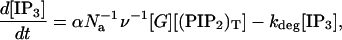(4)

where ν is the volume of the cell, N_a is Avogadro's constant, [IP₃] is the molar concentration of IP₃ in the cytosol, and k_deg is the IP₃ degradation rate.

Cytosolic Ca²⁺ dynamics

The following equations are again adapted from Lemon et al. (2003a), with some simplifications and extensions. Whereas the model in that article had a single interior compartment and a single cytosolic compartment, the present model has three main compartments (Fig. 1). These are a cytosolic compartment, a central SR, and a peripheral SR. In addition, the cytosol is divided into two communicating regions: a central region and a sarcolemmal space lying between the peripheral SR and the sarcolemma. This arrangement of compartments is consistent with current thinking regarding vascular smooth muscle morphology (Laporte and Laher, 1997). The subsarcolemmal space is assumed to be open to the cytosol (Fig. 1), so that over the timescale of receptor desensitization (several minutes), the two compartments form a well-mixed pool.

The Ca²⁺ currents between the different compartments are shown in Fig. 1, where J_ab denotes the current going from compartment a to compartment b. The equations governing the free Ca²⁺ concentration in the cytosol, peripheral SR, and central SR, [(Ca²⁺)_cyt], [(Ca²⁺)_psr], and [(Ca²⁺)_csr], respectively, are

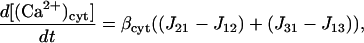(5)

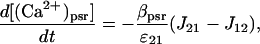(6)

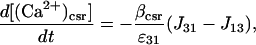(7)

where ɛ_ij is the ratio of the volume of compartment i to compartment j and β_{−} is the buffering function for the indicated compartment. The same Ca²⁺ buffering model used in Lemon et al. (2003a) will be used in this article,

(8)

where [B_e] and K_e are the total concentration and dissociation constant, respectively, of the endogenous buffer, and [B_x] and K_x are the corresponding parameters for the exogenous buffer, in this case fluo3-AM. The other compartments will be assumed to have an excess of rapid, low affinity, stationary endogenous buffer of the same concentration and so β_psr = β_csr are constants. Conservation of the total amount of Ca²⁺, [(Ca²⁺)_T], implies the following relation between the [(Ca²⁺)_{−}]:

(9)

which is the counterpart of Eq. 37 of Lemon et al. (2003a) and where

(10)

is the ratio of free Ca²⁺ to total Ca²⁺ in the cytosol. Eqs. 8 and 10 imply that, for the simplified buffering used here, γ_psr = β_psr and γ_csr = β_csr.

The Ca²⁺ current through the membrane of the central SR is assumed to be due to IP₃ receptors, Ca²⁺ pumps, and Ca²⁺ leaks (Fig. 1). The Ca²⁺ current due to ryanodine receptors in the central SR is neglected. The equations for the currents through the central SR are

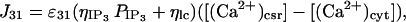(11)

(12)

where η_IP3, η_lc, and η_pc are effective permeability constants for the IP₃ channels, membrane leakage, and Ca²⁺ pumps, respectively; P_IP3 is the open probability for an IP3 channel; and k₃ is the pump dissociation constant. The expression for P_IP3 is derived by further simplification of the Li and Rinzel (1994) model employed in Lemon et al. (2003a). In the experimental data presented in this article, the rise and fall of cytosolic Ca²⁺ concentration occurs over a timescale of minutes, which justifies neglecting the time-dependence of channel behavior since this typically occurs over the timescale of seconds. Thus h = h_∞ in Lemon et al. (2003a) and the equation for 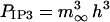is obtained by combining Eqs. 31–33 of that article to give

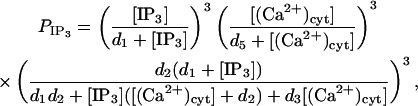(13)

where d₁, d₂, d₃, and d₅ are channel kinetic parameters. The Ca²⁺ exchanged between the cytosol and the peripheral SR is assumed to be due to Ca²⁺ pumps, leaks, and ryanodine channels only. The equations for the currents J₂₁ and J₁₂ are

(14)

(15)

where η_RyR, η_lp, and η_pp are effective permeability constants for the RyRs, membrane leakage, and Ca²⁺ pumps, respectively, and P_RyR is the open probability for a ryanodine receptor, an expression for which is given in the next section.

Model for Ca²⁺ oscillations

The experimental evidence upon which this article is based suggests that Ca²⁺ oscillations occur during stimulation with agonist but are localized in the subsarcolemmal space. Since these oscillations are associated with the bursts of STOCs, it will be assumed that the Ca²⁺ oscillations arise from RyRs located on the surface of the SR facing the sarcolemma (Fig. 1). A four-state quasidynamical model for the collective behavior of the RyRs giving rise to these oscillations is shown in Fig. 2 c. Initially the channels are all in the inactive state A, but in the presence of Ca²⁺ they are rapidly activated at a rate k_bstf([(Ca²⁺)_cyt]), thereby passing into the open state B. The channels are then deactivated rapidly at a rate k_bst and pass into the closed state C. They then enter a phase whereby they pass slowly to a refractory state D at a rate k_ref. The model incorporates a feedback mechanism that returns the RyRs to A at a rate k_retg([C]) where [C] is the number of channels in the closed state and the function g is a decreasing function of [C]. It can be shown that this scheme gives rise to Ca²⁺ oscillations of a spiking nature if the transition rates satisfy k_retg([C]) ≫ k_bst, k_bstf([(Ca²⁺)_cyt]) ≫ k_ref, and threshold kinetics are used for the functions f and g. Under these assumptions it is seen, provided [(Ca²⁺)_cyt] is above the critical threshold of the function f, that the channels pass rapidly through the states A then B during the burst, accumulate in the state C, and then make a slow transition to state D. When the number of channels in state C falls below the threshold level of the function g, the channels in state D are passed rapidly into state A.

Using this scheme, the bursting behavior of the RyRs is described by

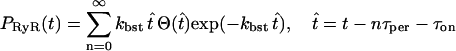(16)

(see the Appendix for details), where 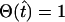for and is zero otherwise, τ_on is the time at which [(Ca²⁺)_cyt] passes through its activation threshold [(Ca²⁺)_cyt]_thr, and τ_per is the period of the bursting.

There is considerable evidence that stochastic transient outward currents (STOCs) in smooth muscle are associated with sparks of Ca²⁺ from RyRs (Jagger et al., 2000). In this article, it will be assumed that the RyRs are located close to the BK channels (Fig. 1). This implies that during an opening of a single RyR, the Ca²⁺ concentration that builds up in the vicinity of the mouth of an apposite BK channel will be greater than the average Ca²⁺ concentration in the subsarcolemmal space, measured over the receptor desensitization timescale. To model this effect the domain Ca²⁺ concentration, being the effective Ca²⁺ concentration which activates the BK channels, will be expressed as a weighted sum of the contributions by the RyR channel current and the cytosolic Ca²⁺ concentration, so

(17)

where [(Ca²⁺)_d] is the domain Ca²⁺ concentration and w_dom > 0 is a constant. An appropriate value for w_dom is determined by fitting the model predictions to the experimental data.

Plasmalemmal ion currents

The principal outward current-carrying channel in the plasmalemma is assumed to be the large conductance Ca²⁺-sensitive K⁺ (BK) channel which gives rise to the STOCs seen in the experiments. The dependence of opening probability of BK channels on Ca²⁺ is modeled using a Hill function; thus the total outward current through the cell membrane is

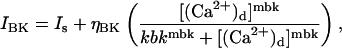(18)

where η_BK is the effective permeability of the BK channels to K⁺ ions, mbk is the Hill coefficient, and kbk is the value of [(Ca²⁺)_d] producing half the maximum activation of the BK channels. The quantity I_s accounts for a small constant outward current observed in the experiments which was apparently Ca²⁺-independent; η_BK = N_BK g_bk φ_K, where N_BK is the number of BK channels in the membrane, g_bk is the conductance of a single BK channel, and φ_K is the Goldman-Hodgkin-Katz driving force for the BK channel. The other significant plasma membrane current that may be of importance in smooth muscle, the inward Ca²⁺ flux, has not been included because, in the in vitro experiments upon which the present work is based, the extracellular space was depleted of Ca²⁺.

Model for Ca²⁺ indicator

The Ca²⁺ indicator used in these experiments is fluo3-AM whose fluorescent efficiency increases when bound to Ca²⁺ (Tsien, 1989). It will be assumed that the whole-cell fluorescence measurement is proportional to the amount of cytosolic Ca²⁺ bound to the buffer, and is therefore

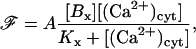(19)

where A is a constant, and so the ratio of fluorescence at a given cytosolic Ca²⁺ concentration to that before agonist stimulation is

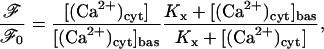(20)

where ℱ₀ and [(Ca²⁺)_cyt]_bas are, respectively, the basal fluorescence and basal cytosolic Ca²⁺ concentrations (see below).

Initial conditions and methods of solution

Equations 1–6, together with the appropriate initial conditions (see Appendix), suffice to determine the time-courses of the principal quantities [R^S], 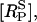[G], [IP₃], [(Ca²⁺)_cyt], and [(Ca²⁺)_psr]. These time-courses are then used to calculate [(Ca²⁺)_csr] using Eq. 9 and the derived quantities [(Ca²⁺)_d] and I_BK, using Eqs. 17 and 18, respectively.

All parameters, together with numerical values, are listed in Table 1. Some parameters' values were taken from Lemon et al. (2003a), which modeled the stimulation of 1321N1 human astrocytoma cells with UTP (Garrad et al., 1998); these values are listed briefly in the table. The assignment of other parameter values is discussed in the Appendix. Equations 1–6 were solved numerically using the MATLAB computer package (The MathWorks, Natick, MA). During the integration it is necessary to test where [(Ca²⁺)_cyt] passes through the RyR activation threshold, [(Ca²⁺)_cyt]_thr, to determine the bursting start time, τ_on.

TABLE 1.

Model parameter values; further details of the selection of the parameter values can be found in the text

Symbol	Definition	Value	Notes
Receptor regulation
kr	Receptor recycling rate	0.0023 s−1	Fit to experiment
ke	Receptor endocytosis rate	0.023 s−1	Fit to experiment
[RT] = 2 × 104, K1 = 5 μM, K2 = 100 μM, and kp = 0.03 s−1			See Lemon et al. (2003a)
G-protein cascade
kdeg	IP3 degradation rate	0.01 s−1	Fit to experiment
δ	G-protein intrinsic activity parameter	0.0040	Fit to experiment
α	Effective signal gain parameter	1.1 × 10−7 s−1	Fit to experiment
ν	Cell volume	4.2 × 10−15 m3	From Fig. 4 A(d)
[GT] = 1 × 105, ka = 0.017 s−1, kd = 0.15 s−1,
[(PIP2)T] = 5 × 107, and Na = 6.02252 × 1023			See Lemon et al. (2003a)
ɛ31	Ratio of central SR to cytosolic volume	0.05	Aortal SM; Devine et al. (1972)
ɛ21	Ratio of peripheral SR to cytosolic volume	0.005	See text
βcsr, βpsr	Calcium buffering constants	0.01	See text
[Bx]	Conc. of cytosolic exogenous buffer (fluo3-AM)	10 μM	Experimental value
Kx	Fluo3-AM dissociation constant	1.1 μM	Harkins et al. (1993)
ηIP3	Permeability of IP3 channels on central SR	1.2 × 104 s−1	Fit to experiment
ηRyR	Permeability of RyRs on peripheral SR	7.2 s−1,	Fit to experiment
ηlc	Permeability of Ca2+ leak of central SR	40 s−1	Fit to experiment
ηpc	Permeability of Ca2+ pumps on central SR	2300 μM s−1	Fit to experiment
ηlp	Permeability of Ca2+ leak of peripheral SR	40 s−1	Fit to experiment
ηpp	Permeability of Ca2+ pumps on peripheral SR	230 μM s−1	Fit to experiment
kbst	Rate of RyR channel activation	1.3 s−1	Fit to experiment
τper	Time between bursts	24.5 s	From Fig. 10 A
τon	Time to start of bursts	9.3 s	See text
[(Ca2+)cyt]thr	Threshold for RyR channel activation	160 nM	See text
wdom	Domain Ca2+ weighting factor	3.1 × 10−3	Fit to experiment
[(Ca2+)T]	Total concentration of Ca2+	533 μM	Fit to experiment
d1 = 0.13 μM, d2 = 1.05 μM, d3 = 0.943 μM, d5 = 0.0823 μM,
[Be] = 150 μM, Ke = 10 μM, and k3 = 0.4 μM			See Lemon et al. (2003a)
Plasmalemmal ion currents
ηBK	Permeability of BK channels on the plasma membrane	40 pA	Fit to experiment.
kbk	Value of [(Ca2+)d] producing half-maximal activation of BK channels	2.8 μM	Canine colonic myocytes; Carl et al. (1996)
mbk	Hill coefficient of BK channels	3.2	Canine colonic myocytes; Carl et al. (1996)
Is	Membrane outward current offset	6.0 pA	From Fig. 9
Basal levels
[(Ca2+)cyt]bas = 121 nM; [(Ca2+)psr]bas = 97 μM; [(Ca2+)csr]bas = 96 μM; [G]bas = 45; and [IP3]bas = 10 nM			See text

RESULTS

P2Y₂ receptors on A7r5 smooth muscle cells and their internalization on exposure to the agonist UTP

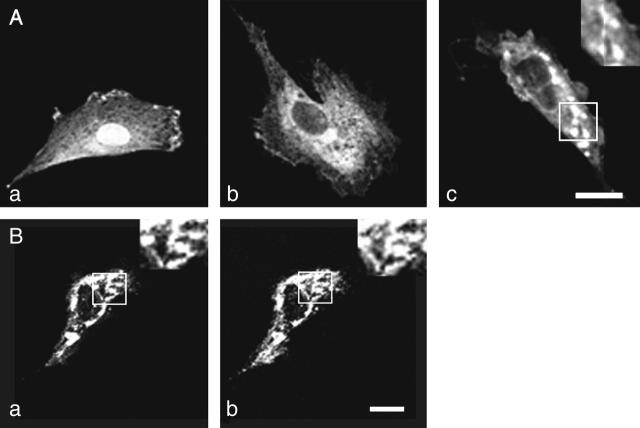
A7r5 cells do not give significant responses to the P2Y₂/P2Y₄ receptor-specific agonist UTP unless high concentrations are used (∼1 mM; Filipeanu et al., 2001). These cells were transfected with cDNA for P2Y₂-GFP, using lipofection. Between 70% and 90% of the A7r5 cells in culture were transfected as indicated by the presence of GFP fluorescence. Within 12 h of transfection, confocal microscopy showed that GFP fluorescence from P2Y₂-GFP was diffusely distributed. There was colocalization of AbP2Y₂ fluorescence with that of the chimera (Fig. 3 B, compare a with b). The overlap in the fluorescence of the AbP2Y₂ and that of the P2Y₂-GFP is consistent with the chimera being inserted in the membrane. There was a gradual emergence of clusters of P2Y₂-GFP over a 24-h period after transfection of A7r5 cells (Fig. 3 A, a–c). These were ∼0.5–1 μm in diameter and were responsible for a large percentage of the entire fluorescence of the membrane of the cells at this time (Fig. 3 A, c, see higher magnification insert).

FIGURE 3.

Transfection of A7r5 cells with P2Y₂-GFP. (A) Confocal images of the membranes of A7r5 cells shortly after transfection with P2Y₂-GFP (a), 12 h after transfection when the P2Y₂-GFP distribution is still diffuse (b), and 24 h after transfection when P2Y₂-GFP has formed clusters of ∼0.5–1 μm in diameter (c); the insert in c shows several clusters of P2Y₂ receptors at higher magnification of the area indicated by the white square. (B) Comparison between the localization of P2Y₂-GFP (a) and of anti-P2Y₂ antibodies (b) on the same A7r5 cell; higher magnification inserts are of the identical areas indicated by the open squares. Calibration bar is 10 μm.

It is known that application of UTP to P2Y₂ receptors at concentrations >10 nM leads to desensitization of the receptor (Garrad et al., 1998). However, the extent to which receptor internalization follows this rate of desensitization in real-time is not known, as it has so far only been possible to ascertain a few time-points in this process (Garrad et al., 1998). We therefore used the chimera to investigate the redistribution of P2Y₂ receptors on exposure to UTP (10 μM).

Fig. 4 A shows the decrease in P2Y₂-GFP fluorescence at the surface of A7r5 cells on exposure to the agonist over 5 min. This decrease is accompanied by a loss of P2Y₂-GFP receptor clusters and a gradual rounding-up of the cells (Fig. 4 A, a–d), as receptor activation continues (see higher magnification inserts in a and d of Fig. 4 A; the clusters overlap extensively in the insert of Fig. 4 A, a, but only one cluster is discernable in Fig. 4 A, d, after agonist exposure). The loss of surface membrane fluorescence from A7r5 cells on exposure to UTP was completely blocked, as was the rounding up of the cells, by their prior incubation in suramin (10 μM; Fig. 4 C). This loss of P2Y₂-GFP fluorescence upon exposure of the cells to agonist suggests an uptake of the chimera into acidic endosomes, as GFP is quenched under acidic conditions (Kneen et al., 1998). To test this, monensin (5 μM) was used to block the pH differential in endosomes (Cremaschi et al., 1996). There was no loss of P2Y₂-GFP fluorescence on exposure to UTP (10 μM) in the presence of monensin in A7r5 cells (Fig. 4 B).

The time-course of loss of fluorescence intensity of the cells was determined. Approximately 30% of the membrane fluorescence is lost over 5 min during exposure to 10 μM of UTP until a steady-state level is reached at ∼10 min (Fig. 5). This is a quantitatively similar loss to that observed at this concentration of UTP, using a monoclonal antibody technique to follow P2Y₂ receptors (Garrad et al., 1998). Solution of Eqs. 1 and 2 for a step application of [L] = 10 μM UTP gives the theoretical transient in the number of receptors at the sarcolemma 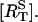The continuous line in Fig. 5 shows a good fit to the experimental results, using the assumption that the P2Y₂-GFP fluorescence is proportional to the number of receptors in the sarcolemma. Also shown in Fig. 5 (dashed line) is the time-course of the phosphorylated surface receptor fraction, 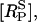as calculated from Eq. 2. Upon application of UTP, 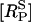rises rapidly to a peak, at which point most of the receptors have been phosphorylated, followed by a slow decline due to internalization. During this decline the difference between the two curves is the unphosphorylated surface receptor, 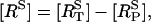and is small due to the receptors being nearly saturated with ligand.

Transient elevation of cytosolic calcium in A7r5 smooth muscle cells after exposure to UTP

Native A7r5 cells did not respond upon exposure to UTP (10 μM) with a detectable increase in calcium concentration using the calcium indicator fluo3-AM. However, exposure of A7r5 cells to UTP, after their transfection with P2Y₂-GFP, did give a transient increase in calcium concentration (Fig. 6, dotted line; the continuous line is the theoretical curve from the model). The calcium remained elevated for only ∼5 min, over the same period in which there is a loss of P2Y₂-GFP clusters from the membrane (compare Figs. 5 and 6). These observations further indicate that the chimera possesses characteristics of the endogenous wild-type receptor.

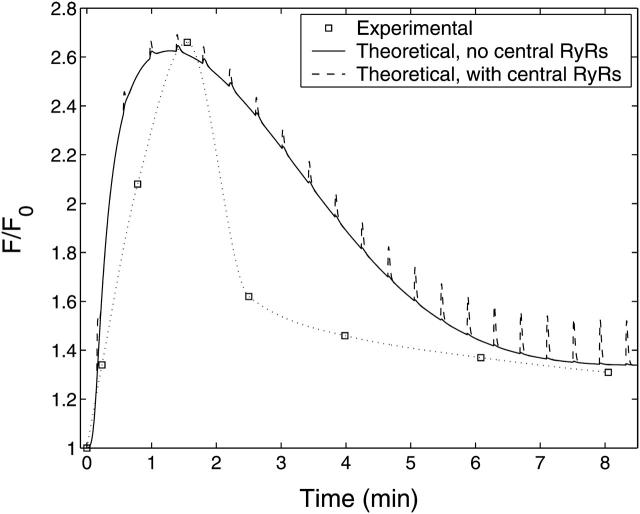
FIGURE 6.

Experimental and theoretical Ca²⁺ fluorescence with respect to time. Experimental data (squares = mean ± SE < size of squares; n = 4 cells) show the time-course of fluo3-AM fluorescence in an A7r5 cell after application of 10 μM UTP at t = 0. The solid line shows the theoretical time-course of the cytosolic Ca²⁺ fluorescence obtained by solving the model equations to determine [(Ca²⁺)_cyt] and calculating the corresponding fluo3-AM fluorescence using Eq. 20. The broken line shows the effect of including RyRs on the central SR.

Comparison between the theoretical and experimental time-courses of fluo3-AM fluorescence after exposure to 10 μM UTP are shown in Fig. 6 for the A7r5 cells. The quantity ℱ/ℱ₀ is the ratio of the whole-cell fluo3-AM fluorescence at a particular time, t, to that before exposure to agonist. Shown in Fig. 6 is the theoretical time-course of ℱ/ℱ₀ for the A7r5 cells calculated using Eq. 20 with the transient in [(Ca²⁺)_cyt] and the basal value of [(Ca²⁺)_cyt], [(Ca²⁺)_cyt]_bas, used as inputs. The overall period of the transient, and its steady-state value reached at ∼8 min, are well predicted by the theory but the experimental transient declines more rapidly than the model predictions.

The model has RyRs only on the peripheral SR and not on the central SR; there is experimental evidence for this distribution of receptors (Ohi et al., 2001; see also the Discussion section below) but it is of interest to see what theoretical effect their inclusion would have. The extension of the theory is given in the Appendix and the result is shown in Fig. 6 (dashed line). Thus the inclusion of RyRs on the central SR leads to Ca²⁺ spikes that are not observed experimentally. Therefore the rest of the theoretical results in this article will be for the case where RyRs are not placed on the central SR.

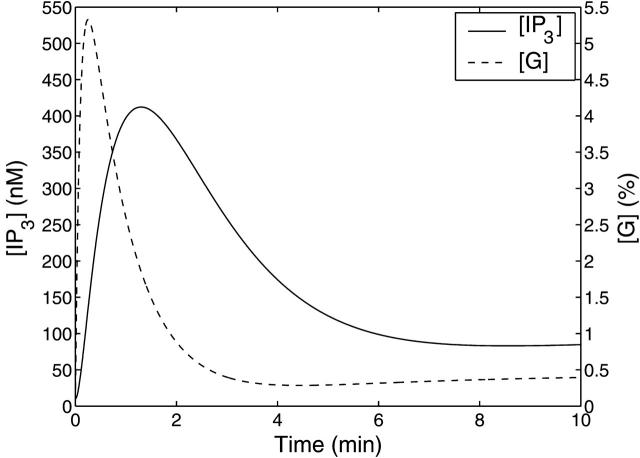
The theoretical transients in IP₃ concentration, [IP₃], and percentage of activated G-protein, [G], for a step application of 10 μM UTP at t = 0, are shown in Fig. 7. The time for [G] to reach its maximum value of 5.3%, ∼15 s, is controlled mainly by the G-protein deactivation rate parameter k_d. Since the value of the IP₃ degradation rate parameter, k_deg, is much smaller than k_d, the [IP₃] transient lags behind that of [G]. [IP₃] peaks at ∼410 nM after 80 s. The sustained levels of activated receptors maintained by receptor recycling causes the raised levels of [IP₃] and [G] seen for long times in these curves.

FIGURE 7.

Theoretical IP₃ concentration, [IP₃] (solid line), and amount of activated G-protein, [G], expressed as a percentage of [G_T] (dashed line), with respect to time for a step application of 10 μM UTP at t = 0.

Comparison between cytosolic calcium and subsarcolemmal calcium transients in A7r5 cells after exposure to UTP

The corresponding theoretical Ca²⁺ transients for the different subcellular compartments are shown in Fig. 8. In Fig. 8 A, the cytosolic Ca²⁺ concentration, [(Ca²⁺)_cyt] (dashed line), and subsarcolemmal domain Ca²⁺ concentration, [(Ca²⁺)_d] (solid line), are plotted with respect to time. The cytosolic Ca²⁺ concentration initially increases due to the opening of IP₃Rs and the resultant release of Ca²⁺ from the central SR. The subsequent time-course of [(Ca²⁺)_cyt] mirrors the time-course of IP₃ shown in Fig. 7, peaking at ∼390 nM after 80 s and declining to a steady-state concentration of ∼170 nM. The time-course of domain Ca²⁺ concentration, [(Ca²⁺)_d], in the peripheral space shows repeated spiking behavior due to the bursting model used for the RyR channels on the outer side of the peripheral SR. [(Ca²⁺)_d] increases rapidly when the channels are open but declines during the refractory period between the bursts, due to the action of the Ca²⁺ pumps. The transient in cytosolic Ca²⁺, [(Ca²⁺)_cyt], together with its basal value, [(Ca²⁺)_cyt]_bas, was used in Eq. 20 to produce the theoretical transient in ℱ/ℱ₀ plotted in Fig. 6. Thus the elevated fluorescence level for long time seen in that figure is due to receptor endocytosis and recycling.

FIGURE 8.

Theoretical Ca²⁺ concentrations with respect to time for a step application of 10 μM UTP at t = 0. The time-course of the Ca²⁺ concentration in the cytosol, [(Ca²⁺)]_cyt (dashed line), and the domain Ca²⁺ in the subsarcolemmal space, [(Ca²⁺)_d] (solid line), are shown in A. Shown in B are the Ca²⁺ concentration in the central SR, [(Ca²⁺)_csr] (dashed line) and peripheral SR [(Ca²⁺)_psr] (solid line). Note the very different vertical axes scales in A.

In Fig. 8 B, the Ca²⁺ concentrations in the peripheral SR Ca²⁺, [(Ca²⁺)_psr] (solid), and central SR, [(Ca²⁺)_csr] (dashed), are plotted with respect to time. Upon stimulation with UTP, [(Ca²⁺)_psr] initially increases because of the initial increase of cytosolic Ca²⁺ concentration, part of which is taken up into the peripheral SR by the pumps located on the inner surface of the store. Likewise the central SR is initially depleted by the release of Ca²⁺ into the cytosol through the IP₃Rs. Like [(Ca²⁺)_cyt], the time-courses of [(Ca²⁺)_psr] and [(Ca²⁺)_csr] are controlled by the concentration of IP₃. When the RyR channels in the peripheral SR are activated, the magnitude of the Ca²⁺ current into the subsarcolemmal space depends mainly on [(Ca²⁺)_psr]. The amplitudes of the peaks in [(Ca²⁺)_d] therefore reflect the time-course of [(Ca²⁺)_psr] and thus are also indicative of the time-course of [IP₃] and hence ultimately of the extent of receptor desensitization. In the time-course of [(Ca²⁺)_d] the contribution by the cytosolic Ca²⁺ is visible as a raised level of Ca²⁺ between each burst. Although small in magnitude compared to the peak of [(Ca²⁺)_d], it is this leakage of Ca²⁺ into the subsarcolemmal space that initiates and sustains the train of bursts.

The value of the RyR channel permeability, η_RyR (see Parameter Value Selection in the Appendix), is too small to allow a current big enough to make significant perturbations to the cytosolic and SR Ca²⁺ concentrations. However, as seen in Fig. 8 a, the effects of constrained diffusion, included implicitly in the model for domain Ca²⁺, result in effective concentrations in the micromolar range near the BK channels.

Subsarcolemma calcium transients and the generation of STOCs in A7r5 cells exposed to UTP

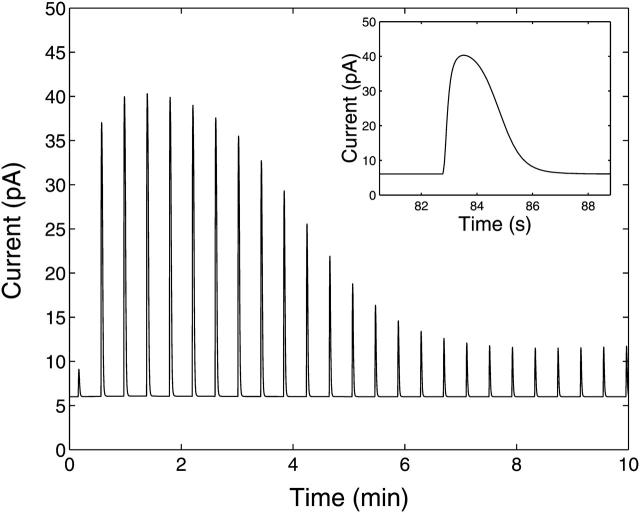
Fig. 9 shows experimental measurements of the whole-cell membrane current of an A7r5 cell, during a patch-clamp at −30 mV, with respect to time after application of 10 μM UTP. This current is the summation of contributions by individual STOCs arising from large-conductance potassium (BK) channels. Individual STOCs are clearly visible in the trace immediately after each burst. The bursts of STOCs seen in Fig. 9 are evidence of the existence of subsarcolemmal Ca²⁺ oscillations that activate the BK channels. In the results of the experiment shown in Fig. 9, the general amplitude of consecutive bursts declines over the first 2 min and thereafter bursts recur indefinitely at approximately the same amplitude. The constant 6-pA outward current visible in the current trace has been included in the model as the membrane outward current offset, I_s.

FIGURE 9.

Experimental membrane current with respect to time showing several bursts of STOCs upon application of 10 μM UTP. These currents are given on a compressed time-base for illustration purposes, and are not those analyzed in Fig. 10.

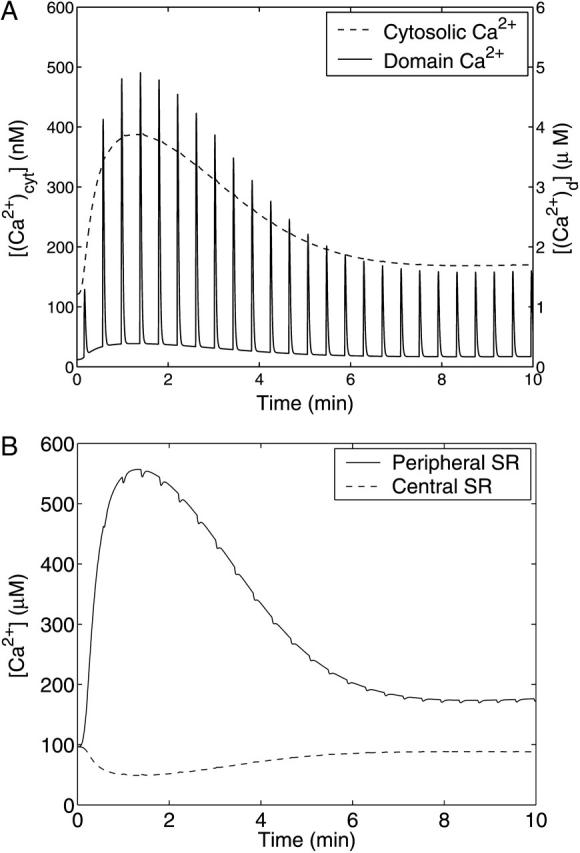
In Fig. 9, the time between each burst remains relatively constant after the first burst. This property of the oscillations in the outward current is evident in Fig. 10 A, where the time between the peaks of the bursts are plotted for one cell, representative of observations on five cells. The dashed line represents the average of the intervals, 25 s, and this has been used as the value for the parameter τ_per in the bursting model of the RyRs in the peripheral SR membrane. The small deviation of the interval from the average value shows that the frequency of the membrane current bursts and hence subsarcolemmal Ca²⁺ oscillations does not strongly depend on the extent of receptor desensitization. The experimental peak amplitudes of the bursts are plotted in Fig. 10 B.

FIGURE 10.

Experimental results (▵) for the time between bursts (A) and amplitudes of bursts (B) of STOCs after application of 10 μM of UTP to an A7r5 cell. In A the dashed line shows the average value of the intervals which is used to specify the bursting interval for the theoretical model. In B the solid line gives the theoretical amplitudes obtained by solving the model equations using the theoretical cytosolic Ca²⁺ fluorescence (Fig. 6, solid curve) as input; the crosses indicate the locations of the peaks. The experimental data-point is not given for burst 1 because of an artifact shortly after the addition of UTP. The broken line in B gives the corresponding theoretical results when the experimental cytosolic Ca²⁺ fluorescence (Fig. 6, dotted curve) is used as input (see the Appendix for modifications to the theory); the remaining parameters are as in Table 1, except that w_dom has been increased to 4 × 10⁻³.

The theoretical membrane current, with respect to time, for a step application of 10 μM of UTP at t = 0 is shown in Fig. 11. The first burst begins at t = τ_on = 9.3 s, when [(Ca²⁺)_cyt] reaches the firing threshold [(Ca²⁺)_cyt]_thr. A closeup of the fourth burst is shown in the inset. This fourth burst has the largest magnitude of all with a maximum outward current of 40 pA. The curve reproduces the general characteristics of the bursts shown in Fig. 9, including the correct rise and fall times of the membrane current during each burst and the constant Ca²⁺-independent outward current. The decline in amplitudes of the bursts over time in Fig. 11 is plotted in Fig. 10 B (solid curve with crosses indicating the position of the peaks). The theoretical data matches approximately the general trend of the experimental data. The theoretical curve in Fig. 10 B was recalculated using the experimental Ca²⁺ fluorescence time-course as given by the dotted curve in Fig. 6, rather than the calculated [Ca_cyt²⁺] (solid curve in Fig. 6). The details of the method are given in the Appendix and the result is shown as the dashed curve in Fig. 10 B. Both curves are equally consistent with the general trend of the experimental data.

FIGURE 11.

Theoretical membrane current, I_BK, with respect to time upon application of 10 μM UTP at t = 0. The insert shows a closeup of the fourth burst of STOCs, this being the burst with the greatest amplitude.

DISCUSSION

The P2Y₂-GFP chimera

The P2Y₂-GFP chimera in A7r5 cells appears to have similar properties to the wild-type P2Y₂ receptor in phaeochromocytoma cells. There is a similar release of calcium from intracellular stores as with the native P2Y₂ (compare Fig. 6 with Fig. 3 a in Koizumi et al., 1995). Furthermore, there is approximately the same loss of P2Y₂-GFP fluorescence as there is loss of the native P2Y₂ after prolonged exposure to agonist in 1321N1 cells (compare Fig. 5 with Fig. 4 in Garrad et al., 1998). Together, these observations indicate that the C-terminal fusion of P2Y₂ with GFP does not seem to affect the functional properties of P2Y₂.

Time-course of desensitization of the P2Y₂ purinergic receptor

Desensitization of metabotropic receptors has been most extensively studied for the β₂ adrenergic receptor (β₂-AR; Kallal et al., 1998) and to a lesser extent for the α₁ and α₂ adrenergic receptors (α₁-AR and α₂-AR) as well as the mGluR1 glutamate receptors (Wang and Linden, 2000; Sallese et al., 2000). The rates of desensitization of these receptors in the presence of agonist are similar to their rates of internalization (Fonseca et al., 1995; Heck and Bylund, 1998). All these receptors conform to the accepted paradigm for G-protein coupled receptor kinase-mediated desensitization of the receptor: G-protein coupled receptor kinase-mediated receptor phosphorylation is followed by the binding of arrestin proteins; internalization of the receptors is then mediated by β-arrestin and dynamin-dependent, clathrin-coated, vesicle-dependent endocytosis (for the mGluR receptors see, for example, Dale et al., 2002) with the receptor directed to endosomes (Mundell et al., 2001). It has recently been shown that some ionotropic purinergic receptors are also internalized upon binding ligand, such as the P2X₁ and P2X₄ receptors, and this also involves a dynamin-dependent endocytosis to endosomes followed by subsequent reinsertion in the membrane (Dutton et al., 2000; Ennion and Evans, 2001; Bobanovic et al., 2002). Desensitization of the P2Y₂ receptors is not contingent on internalization any more than is desensitization of other metabotropic receptors (Sromek and Harden, 1998), so the loss of IP₃ production in the presence of a P2Y₂ receptor agonist is not due to internalization of P2Y₂ but to its phosphorylation which is closely followed in time by sequestration (Sromek and Harden, 1998). Our model of this process follows that of Lemon et al., (2003a) and gives an account of the changes in P2Y₂-GFP at the sarcolemma after exposure of the receptors to agonist (see Fig. 5). However, the quantitative description of the data in Fig. 5 is given by the curve derived from Eqs. 1–6 in the model. Although this is a good fit, it is not an independent prediction of the model inasmuch as the steady state reached at 10 s is used in the model to ascertain the values of parameters (see Parameter Value Selection in the Appendix).

After activation of metabotropic receptors, the generation of IP₃, and activation of IP₃Rs, there is release of Ca²⁺ into the cytosol from the central SR. Desensitization of the P2Y₂ receptors thereby modulates the concentration of cytosolic Ca²⁺. In Fig. 6 the theoretical Ca²⁺ fluorescence transient shows the correct overall timescale for the decay after the peak (∼5 min), but the experimental curve shows a biphasic decay which results in an underestimate of the extent of receptor desensitization in the theoretical curve. This biphasic response cannot be modeled using a receptor desensitization mechanism characterized by a single rate constant, but a more detailed model for this effect is beyond the scope of the present work.

Subsarcolemma calcium transients

The present experiments show that the time-course of both the transient increase in calcium concentration and in the amplitude of STOCs is qualitatively similar to that of the internalization of P2Y₂-GFP. Given that the latter follows phosphorylation of the receptor, it appears likely that both the decline in calcium concentration and in STOC amplitude is consequent upon desensitization of the receptor. However, a model is required to provide a quantitative assessment of the possibility that the changes in cytosolic calcium concentration and STOC characteristics, after agonist application to the metabotropic receptors, are governed by the desensitization of the receptors.

In this article a new model is proposed for Ca²⁺ oscillations due to the collective behavior of ryanodine channels. Existing models for Ca²⁺ oscillations due to the RyRs alone (Keizer and Levine, 1996; Tang and Othmer, 1994) or combinations of IP₃Rs and RyRs (Sneyd et al., 2003) do not satisfactorily reproduce the bursting characteristics seen in the experiments. Thus a simple quasidynamical model for calcium oscillations was developed which features plausible mechanisms, these being Ca²⁺-dependent activation, Ca²⁺-independent deactivation, and recovery after a slow refractory phase.

Our model takes into account the fact that the SR is not uniformly distributed. The SR of smooth muscle cells varies between 2 and 6% of the cell volume (Devine et al., 1972). The peripheral SR, immediately beneath the sarcolemma, amounts to ∼2% of the total SR volume (Bazzazi et al., 2003) and is a potential source of calcium to raise the concentration of this ion in the subsarcolemmal space to open BK channels (for an analogous situation, see Coop et al., 1998). This SR, like that throughout the cells, appears to possess both RyR as well as IP₃ receptor calcium channels (Nixon et al., 1994) but, at least in A7r5 cells, the peripheral SR does not possess the class of IP₃ receptors that are mainly responsible for IP₃-induced Ca²⁺ release, whereas the central SR does possess these receptors (Vermassen et al., 2003). In the model we do not have IP₃Rs in the peripheral SR, but only RyRs. There is evidence that RyRs are preferentially located in the peripheral SR in smooth muscle cells (Ohi et al., 2001). Furthermore, including RyRs on the central SR in the model gave unrealistic results (Fig. 6). All the SRs possess calcium pumps and calcium leaks, with no evidence that these are differentially distributed between central and more peripheral SR (Bazzazi et al., 2003).

Calcium release through RyRs in the SR of smooth muscles gives rise to calcium sparks. These are associated with the activation of STOCs due to the opening of BK channels (Perez et al., 1999). There appears to be a close association between the peripheral SR calcium release sites in the smooth muscle cells and the BK channels in the sarcolemma responsible for the STOCs (Zhu-Ge et al., 1999). The BK channels are at highest density in the sarcolemma at sites of spark generation (Zhu-Ge et al., 2002). The amplitude of STOCs can vary more than threefold, and part of this variability may be attributed to differences in the coupling ratio of RyRs to BK channels in the spark microdomain (Zhu-Ge et al., 2000) rather than just to changes in desensitization/sequestration of sarcolemma receptors. Such microdomains consist of colocalization of BK channels in the plasma membrane and RyRs in the peripheral SR where calcium sparks elicit STOCs (Ohi et al., 2001; Lohn et al., 2001; McCarron et al., 2002). Recent modeling has provided estimates of 10 μM for the spark calcium concentration in the microdomain of apposed peripheral SR membrane and sarcolemma, which are separated by ∼25 nm (Zhu-Ge et al., 2002). Our results and modeling indicate a concentration of ∼5 μM (see Fig. 8 a). Bazzazi et al. (2003) suggest that the peripheral SR calcium uptake is primarily from the cytosolic calcium and not as a result of the opening of sarcolemma calcium channels, which is consistent with our model.

In our model we have not allowed for a contribution from IP₃ receptors in the peripheral SR to the generation of STOCs as evidence suggests that such receptors are only to be found on central SR in A7r5 cells (Vermassen et al, 2003). This has allowed for a reasonably simple model of the interaction between cytosolic Ca²⁺ and that in the subsarcolemmal space. The extent to which IP₃ releases calcium from SR throughout the smooth muscle cells which then leads to the release of Ca²⁺ through RyRs channels appears to be variable between different smooth muscle cell types (Guerrero-Hernandez et al., 2002). The present model faithfully reproduces the shape, length, and period of the bursts but cannot explain irregularities seen near the start of the current traces in some experiments (Fig. 9). The reasons for the initial irregular rate of bursting seen in that figure remain obscure.

The present theory indicates that the contribution of the RyR current to the cytosolic Ca²⁺ concentration transient is small (see Fig. 6). The bursting effects are most visible near the peak of the curve in Fig. 6 because this is where the peripheral SR concentration is largest and hence the maximum RyR channel current is also largest. The appearance of these bursts suggests that the theoretically determined ratio of η_RyR:η_IP3 (see Parameter Value Selection in the Appendix) is an overestimate. Although the magnitude of these perturbations could be reduced by lowering η_RyR, this is a somewhat arbitrary step—so it was decided to retain the theoretical estimate for η_RyR:η_IP3 for the simulations.

That the RyRs are insensitive to IP₃ suggests that the heights of the bursts are determined by the amount of Ca²⁺ in the peripheral SR which is, in turn, modulated by the cytosolic Ca²⁺ concentration, due to there being pumps and leaks on the inner side of that store. Thus IP₃Rs control RyRs indirectly by liberating intracellular Ca²⁺ which both switches on the RyRs and modulates the Ca²⁺ current through them. According to this theory, the current from IP₃Rs in the peripheral SR must be negligible since this current would have a tendency to decrease the heights of the bursts. Thus the modeling suggests that IP₃Rs dominate on central SR and RyRs dominate on peripheral SR.

Values for the parameters kbk and mbk vary widely for different smooth muscle types (Carl et al., 1996). For example the Hill coefficient mbk can lie in the range 1–2 for guinea pig mesenteric artery (Benham and Bolton, 1986) but the value of mbk = 3.2 for canine colonic myocytes (Carl et al., 1996) used in this study seems more appropriate. This is because the resultant high degree of nonlinearity in the relation between Ca²⁺ and BK channel current, defined by Eq. 18, tends to suppress the appearance of submicromolar Ca²⁺ artifacts in the membrane current trace. This effect is essential for the bursting appearance in the time-course of I_BK shown in Fig. 11, where the cytosolic Ca²⁺ component of the domain Ca²⁺, [(Ca²⁺)_d], is not visible between the bursts. It is likely that this nonlinear effect also shapes the bursts in the experimental membrane current trace shown in Fig. 9.

APPENDIX

Model for Ca²⁺ oscillations

An expression for the open probability of a RyR, P_RyR(t), during bursting can be derived from the equations defining the model as follows. Let the functions f and g be defined by

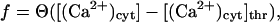(21)

(22)

where Θ is the Heaviside step function, and [(Ca²⁺)_cyt]_thr and [C]_thr are the threshold activation levels of [(Ca²⁺)_cyt] and [C], respectively. Suppose that before stimulation of the cell with agonist, [(Ca²⁺)_cyt] = [(Ca²⁺)_cyt]_bas < [(Ca²⁺)_cyt]_thr and all the RyRs are in the inactive state. When agonist is applied, [(Ca²⁺)_cyt] increases and at some time, τ_on, [(Ca²⁺)_cyt] increases through [(Ca²⁺)_cyt]_thr. The equations for the fraction of channels in each of states A, B, and C are therefore

(23)

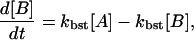(24)

(25)

with [A(τ_on)] = 1, [B(τ_on)] = 0, and [C(τ_on)] = 0. The solution is

(26)

(27)

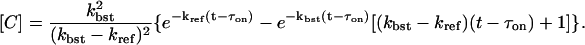(28)

The fraction of RyRs in state D is then [D] = 1 – [A] – [B] – [C]. With the assumption that k_bst ≫ k_ref, the following approximation for [C] can be used for a large time as

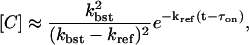(29)

which leads to an approximation for the time delay until the transition of the channels back to the inactive state, which is

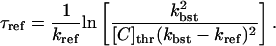(30)

Since k_retg([C]) ≫ k_bst all the RyRs are recycled before the next burst and so τ_on + τ_ref is approximately the starting time of the next burst. Before the second and subsequent bursts only a fraction of ∼1 − [C]_thr of the RyRs will be returned to A with a proportion of ∼[C]_thr receptors remaining in C. For simplicity it will be assumed that [C]_thr ≪ 1, so that approximately all the RyRs are recycled before a burst. Under this assumption the solutions defined by Eqs. 26–28 are still valid, but with τ_on replaced with the starting time of the burst. It follows that, provided [(Ca²⁺)_cyt] remains above [(Ca²⁺)_cyt]_thr, the bursting behavior of the RyRs can be characterized by the piecewise function

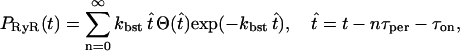(31)

where τ_per is the period of the ursting. Because τ_per ≈ τ_ref, τ_per can be calculated in terms of the model parameters using Eq. 30. However, in practice it is chosen directly along with k_bst so that the bursting characteristics of the theoretical model, through Eq. 31, match the experimental data.

Inclusion of RyRs on the central SR

To allow for RyRs on the central SR, Eq. 11 is to be modified to

(32)

where η′_RyR and P′_RyR are the permeability and open probability, respectively, of the RyRs in the central SR. The permeabilities are proportional to the number of receptors and assuming these have the same surface density on the central and peripheral SR, then η′_RyR/η_RyR = ɛ₃₁/ɛ₂₁, where η_RyR is the permeability of RyRs on the peripheral SR. It is assumed that the RyRs on both central and peripheral SR have the same oscillatory characteristics and since they are both triggered by cytosolic Ca²⁺, it follows that P′_RyR is also given by Eq. 31.

Theoretical bursts of STOCs driven by experimental [(Ca²⁺)_cyt]

Instead of using [(Ca²⁺)_cyt](t) as calculated theoretically the experimental fluorescence time-course, as shown in Fig. 6, can be used. The first step is to invert Eq. 20 to obtain

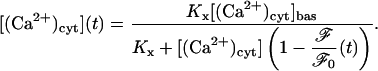The function ℱ/ℱ₀(t) which appears as the dotted line in Fig. 6, is a cubic spline fit to the data points (squares) shown in that figure. Equation 6 can now be integrated to determine [(Ca²⁺)_psr] and Eq. 9 then gives [(Ca²⁺)_csr]; [(Ca²⁺)_d] and I_BK then follow from Eqs. 17 and 18, respectively.

Initial conditions

The basal levels of the modeled quantities were determined by numerically integrating the equations for a sufficiently long time in the absence of ligand ([L] = 0); then, in the steady state, [R^S] = [R_T] and The appropriate initial conditions for the model equations in the presence of ligand are thus

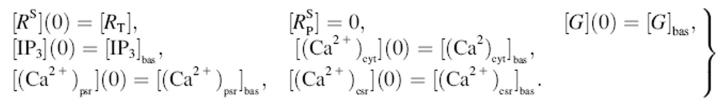(33)

As in Lemon et al. (2003a), the expression for [G]_bas can be solved by putting d[G]/dt = 0 in Eq. 3 with ρ_r = 0 to obtain

(34)

The expression for [IP₃]_bas is obtained by putting d[IP₃]/dt = 0 in Eq. 4 to obtain

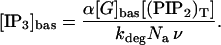(35)

An approximate expression for [(Ca²⁺)_cyt]_bas can be obtained using the following assumptions. For the parameter values used in this article it holds that in the absence of ligand the amount of Ca²⁺ taken up into the peripheral compartments is small compared to that taken up by the central SR. Also the Ca²⁺ current across the SR membrane due to IP₃Rs is small compared to that due to Ca²⁺ pumps and leaks. Then the derivation given by Lemon et al. (2003a) to obtain Eq. 42 of that article for the basal concentration of Ca²⁺ is still valid, so

(36)

Using Eqs. 34 and 35, the parameter δ can be chosen to set exactly the desired basal level of [IP₃]. Equation 36 can be used as an aid to set the basal level of [Ca²⁺] for the simulations by adjusting the parameters in that equation.

Parameter value selection

It is appropriate to use many of the parameter values from a previous modeling study (Lemon et al., 2003a) of the stimulation of P2Y₂ receptors with UTP for the case of 1321N1 human astrocytoma cells (Garrad et al., 1998). In particular, the total number of P2Y₂ receptors was taken to be [R_T] = 2 × 10⁴, in line with the value of 22,767 ± 9753 found for 1321N1 cells by Garrad et al. (1998). For other parameters new values were obtained as follows.

Regulation of receptor activity, G-protein cascade, and IP₃ production

The IP₃ degradation rate parameter, k_deg, was set to obtain approximately the correct rise-time of Ca²⁺ concentration, with the parameter α used to set the peak Ca²⁺ concentration (see Fig. 6). The receptor internalization and recycling parameters, k_e and k_r, were then adjusted to obtain the correct equilibration time and steady-state levels of surface receptor fraction, 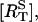and cytosolic calcium, [(Ca²⁺)_cyt], seen in Figs. 5 and 6, respectively. The parameter δ was adjusted so that [IP₃]_bas = 10 nM. The value of ν = 4.2 pL = 4.2 × 10⁻¹⁵ m³ used for the A7r5 cell volume is based on the image in Fig. 4 A (d), which shows the cell to have a diameter of ∼20 μm.

Cytosolic Ca²⁺ dynamics

A precise value for the ratio of the peripheral and central SR volumes for the A7r5 cell is not known, but being a tonic smooth muscle type, is likely to be small (Laporte and Laher, 1997), and a value ɛ₂₃ = 0.1 has been used. Thus ɛ₂₁ = ɛ₂₃ɛ₃₁ = 5 × 10⁻³ as shown in Table 1. The Ca²⁺ buffering parameters β_csr and β_psr were all given the same value, 0.01, which was the value used for the buffering factor in the endoplasmic reticulum (ER) in Lemon et al. (2003a), this being equal to the ratio K_ER/[B_ER] in that article. The intracellular concentration of fluo3-AM, [B_x] = 10 μM, was assumed to be the same as that of the culture medium in which the cells were incubated.

The Ca²⁺ leak and pump permeabilities of the central SR, η_lc, and η_pc, respectively, were adjusted so as to give a basal cytosolic Ca²⁺ concentration near 100 nM and basal central SR Ca²⁺ concentration near 100 μM. This latter value is consistent with the experimentally determined resting levels of SR Ca²⁺ concentration in Bufo marinus stomach smooth muscle (Zhu-Ge et al., 1999) and rat arterial smooth muscle (Golovina and Blaustein, 1997). The IP₃R permeability, η_IP3, was adjusted in conjunction with the value of α to achieve an IP₃ concentration during agonist stimulation in the hundreds of nM-range, typical of experimentally determined estimates for IP₃ levels in vascular smooth muscle cells. The permeabilities of the peripheral SR, η_lp, and η_pp, as well as the total concentration of Ca²⁺, [(Ca²⁺)_T], were chosen to give a basal peripheral SR Ca²⁺ concentration near 100 μM. If the surface area/volume ratios and channel/leak surface densities are the same for the peripheral and central SR, it follows that the ratio of the permeabilities will be the same as the ratio of the volumes of the two compartments, that is, ɛ₂₃ = 0.1. Indeed the value of η_pp was chosen in order that η_pp = 0.1 η_pc (see Table 1) but a value >0.1 η_lc was required for η_lp (η_lp = η_lc) to achieve the constraint on the basal Ca²⁺ concentration. This higher value for η_lp was also required so that there was negligible delay of the time-course of the peripheral SR Ca²⁺ concentration behind that of the cytosolic Ca²⁺ concentration during stimulation with agonist.

The value for the RyR channel activation rate, k_bst, was estimated from the experimental time-course of the bursts of STOCs shown in Fig. 9. This was done by making the difference between the times at which the bursting current was halfway between basal and maximum the same for the theoretical and experimental curves. This time difference was determined to be ∼1.9 s, which required the value k_bst = 1.3. A precise value of the RyR firing threshold, [(Ca²⁺)_cyt]_thr, is not known but was given the value of 160 nM so that [(Ca²⁺)_cyt] never fell back below [(Ca²⁺)_cytthr] during agonist stimulation.

An estimate for the value of η_RyR was obtained by the derivation of a plausible estimate for the ratio η_RyR:η_IP3. It is assumed that this ratio is such that the channel currents in Eqs. 11 and 14 would result in the same Ca²⁺ concentrations in the cytosol and subsarcolemmal space, respectively, for the same [Ca²⁺] difference across the SR membrane. It can be shown that this implies

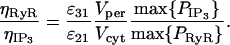(37)

The volume of the subsarcolemmal space, V_per, is calculated based on a cell which has 10% of its sarcolemma in apposition to its peripheral SR, with a subsarcolemmal gap of 20 nm (Lee et al., 2002). The cytosolic volume V_cyt may be approximated adequately by the whole-cell volume. Thus V_per/V_cyt ≈ (0.1 × 20 × 10⁻⁹ × 4π × (10 × 10⁻⁶)²)/4.2 × 10⁻¹⁵ ≈ 6 × 10⁻⁴. The quantity is determined from the simulations, and which is determined by maximizing [B](t) in Eq. 27. Thus η_RyR/η_IP3 = 5.7 × 10⁻⁴ from Eq. 37.

Plasmalemmal ion currents

The parameters kbk and mbk, characterizing the dependence of BK channel opening probability on Ca²⁺ concentration, were determined from the data of Fig. 4 B of Carl et al. (1996) for canine colonic myocytes. At the different Ca²⁺ concentrations used for that figure, a least-squares fit of the Boltzmann function for the dependence of channel open probability on voltage, P_o = 1/(1 + exp [ − (V − V_1/2)/V_s]), was performed to determine the voltage for half-maximal channel activation, V_1/2, and slope factor V_s. This allowed determination of P_o at the different Ca²⁺ concentrations for the case V = −30 mV, which was the voltage used in the whole-cell patch-clamp procedure in the present study. A least-squares fit of Eq. 18 to this transformed data yielded the values of the parameters kbk and mbk. Further explanation of these techniques is given by Carl et al. (1996).

The values of the BK channel permeability, η_BK, and the domain Ca²⁺ weighting factor, w_dom, were determined by fitting the amplitudes of the peaks of the time-course of I_BK to the data of the first experiment in Fig. 10 b. To get an adequate fit to the data for large times it was found necessary to have these parameters such that the heights of the peaks of [(Ca²⁺)_d] were comparable to the value of kbk = 2.8 μM (see Fig. 8 a). This then implied that the BK channels are saturated by subsarcolemmal Ca²⁺ during the bursts at earlier times when IP₃ and cytosolic Ca²⁺ reach their maximum. Thus a value of 40 pA was used for η_BK, and a value w_dom = 0.0031 was chosen to give the correct decline and steady-state bursting characteristics of the data in Fig. 10 b.