Folding Thermodynamics of Peptides

Abstract

A simplified interaction potential for protein folding studies at the atomic level is discussed and tested on a set of peptides with ∼20 residues each. The test set contains both α-helical (Trp cage, F_s) and β-sheet (GB1p, GB1m2, GB1m3, Betanova, LLM) peptides. The model, which is entirely sequence-based, is able to fold these different peptides for one and the same choice of model parameters. Furthermore, the melting behavior of the peptides is in good quantitative agreement with experimental data. Apparent folded populations obtained using different observables are compared, and are found to be very different for some of the peptides (e.g., Betanova). In other cases (in particular, GB1m2 and GB1m3), the different estimates agree reasonably well, indicating a more two-state-like melting behavior.

INTRODUCTION

The function of peptides and proteins is inextricably connected to their folding behavior, as is underlined by the facts that many neurodegenerative disorders are being linked to misfolding and aggregation (Dobson, 2003), and that coupled folding and binding seems to be a more common phenomenon than previously thought (Dyson and Wright, 2002). It is therefore an important development that folding simulations at the atomic level are now becoming feasible for short polypeptide chains (Gnanakaran et al., 2003), thanks to faster computers, more efficient algorithms, and improved force fields.

There are, however, questions about the interaction potentials used in the simulations that need further investigation. One difficulty is that different potentials give very different relative weights to the α-helix and β-strand regions of the Ramachandran space (Zaman et al., 2003). A potential that successfully folds an α-helical peptide might therefore have problems with β-sheet peptides, and vice versa. Another difficulty is with the temperature-dependence of observable quantities. As pointed out by Zhou et al. (2001), it seems that most current models need further calibration to give a temperature-dependence that is not too weak; as a result, calculated melting temperatures are often unrealistically high. A systematic study of these thermodynamic questions requires extensive conformational sampling and is a challenge, especially in models with explicit water.

Here we study a model that contains all atoms of the polypeptide chains but no explicit solvent molecules. Formally, such a model is obtained by integrating out the solvent degrees of freedom. Finding an accurate and computationally tractable approximation of the resulting effective potential is, however, a highly nontrivial problem. Examples of implicit solvent models that have been used in folding studies with some success include the generalized Born approach (Still et al., 1990), the method based on screened Coulomb potentials by Hassan et al. (2003), and the method based on solvent-accessible surface areas by Ferrara et al. (2002). In this article, we study a minimalistic model in which the effects of the solvent are represented by an effective attraction between nonpolar side chains. Our study focuses on the thermodynamic behavior of this model, which we investigate using efficient Monte Carlo methods rather than molecular dynamics. This choice is made for computational convenience; with some minor modifications, it would be possible to study the same model using molecular dynamics. Promising computational techniques have recently been proposed by Hansmann and Wille (2002) and Schug et al. (2003), but these methods are for energy-minimization, which is insufficient for our purposes.

In addition to effective hydrophobic attraction, the interaction potential of our model contains two major terms, representing excluded-volume effects and hydrogen bonding. The potential is deliberately kept simple, partly for the sake of clarity but also for practical reasons; any potential requires careful calibration, and this task is easier with a simple potential like ours with fewer parameters to tune. In the future, the potential may be further developed with the inclusion of new terms such as Coulomb interactions between side-chain charges, but not before it becomes clear that they are needed. The different terms of the potential represent either the interaction between two individual atoms (excluded volume), or two pairs of atoms (e.g., hydrogen bonds), or an effective interaction between a pair of side chains (hydrophobicity). The largest units playing a role in the potential are the amino acids, and no information about the sequence as a whole or its native structure is used in the potential.

Our approach toward the problem of determining the interaction potential is phenomenological. The shape of individual terms is inspired by intuitive notions rather than being rigorously derived from a microscopic picture. Their exact functional forms and relative sizes are constrained by the effectiveness of the model in describing the folding behavior of more and more sequences. When such a potential evolves to a point where it can successfully fold a significant number of peptides of different native geometries, and capture the thermodynamic behavior of all those peptides, it would be useful on its own as a working potential for thermodynamic studies of new sequences, and also provide hints about the relative importance of different physical effects in protein folding.

We have previously shown that earlier versions of this model are able to fold both α-helix and β-sheet peptides (Irbäck et al., 2003; Irbäck and Sjunnesson, 2004). In this article we present a further development of this model. We test the new model on the following set of peptides (see Fig. 1): the α-helical Trp cage (Neidigh et al., 2002) and F_s (Lockhart and Kim, 1992, 1993), and the β-sheet peptides GB1p (Kobayashi et al., 1993; Blanco et al., 1994), GB1m2 and GB1m3 (Fesinmeyer et al., 2004), Betanova (Kortemme et al., 1998), and LLM (López de la Paz et al., 2001). Here GB1p denotes the C-terminal β-hairpin from the protein G B1 domain, whereas Betanova is a designed three-stranded β-sheet peptide. GB1m2 and GB1m3 are mutants of GB1p, whereas LLM is a mutant of Betanova, with enhanced stabilities. We find that our model provides a good description of the thermodynamic behavior of all these peptides. The same model was furthermore used in a recent study of the oligomerization properties of the amyloid Aβ_16–22 peptide (Favrin et al., 2004), with very promising results.

FIGURE 1.

Schematic illustration of the different geometries of the peptides studied. Shown from left to right are the reference structures (see below) used for the Trp cage, F_s, GB1m3, and Betanova. Drawn with the program RasMol (Sayle and Milner-White, 1995).

MODEL AND METHODS

Model

Our model contains all atoms of the polypeptide chains, including hydrogen atoms. The model assumes fixed bond lengths, bond angles, and peptide torsion angles (180°), so that each amino acid only has the Ramachandran torsion angles φ, ψ and a number of side-chain torsion angles as its degrees of freedom. Numerical values of the geometrical parameters held constant can be found elsewhere (Irbäck et al., 2003).

In the simulations we internally use a dimensionless energy scale. The correspondence (constant factor) of this scale to the physical energy scale is determined by using the model prediction of the dimensionless energy value for an observable and the experimental value for the same. We use the melting temperature T_m = 315 K of the Trp cage (Neidigh et al., 2002) for this purpose (see below), which is found to correspond to a dimensionless energy kT_m of 0.470 in the model (k is Boltzmann's constant). Energy parameters of the model (such as the κ_ev, κ_loc, 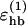, etc., below) are given in our internal energy scale. It must be emphasized that this energy scale is left unchanged when analyzing the other peptides.

The interaction potential,

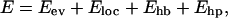(1)

is composed of four terms. The first term in Eq. 1, E_ev, represents excluded-volume effects and has the form

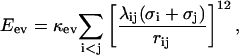(2)

where the summation is over pairs of atoms (i,j), κ_ev = 0.10, and σ_i = 1.77, 1.75, 1.55, 1.42, and 1.00 Å for S, C, N, O, and H atoms, respectively. The values of the radii σ_i agree reasonably well with the statistical analysis of Tsai et al. (1999). The σ_i values for C, N, and O strongly influence the shape of the Ramachandran φ,ψ distribution, and must therefore be carefully chosen. The parameter λ_ij in Eq. 2 has the value 0.75 for all pairs except those connected by three covalent bonds, for which λ_ij = 1. The reason why we use a reduction factor λ_ij < 1 for all nonlocal pairs is both computational efficiency and the restricted flexibility of a chain with only torsional degrees of freedom, which could create artificial traps. To speed up the calculations, Eq. 2 is evaluated using a cutoff of 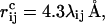and pairs with fixed separation are omitted.

The second energy term, E _loc, has the form

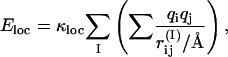(3)

where the inner sum represents the interactions between the partial charges of the backbone NH and C′O groups in one amino acid, I. This potential is not used for Pro which lacks the NH group, or Gly which tends to be more exposed to water than other amino acids, due to the missing side chain. Neither is it used for the two end-amino acids, unless these are protected by capping groups. The inner sum in Eq. 3 has four terms (NO, NC′, HC′, and HO) which depend only on the φ- and ψ-angles for amino acid I. The partial charges are taken as q_i = ±0.20 for H and N and q_i = ±0.42 for C′ and O (Brändén and Tooze, 1991), and we put κ_loc = 100, corresponding to a dielectric constant of ɛ_r ≈ 2.5.

The third term of the energy function is the hydrogen-bond energy E_hb, which has the form

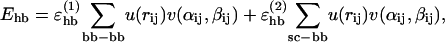(4)

where the two functions u(r) and v(α, β) are given by

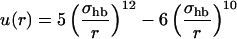(5)

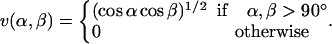(6)

We consider only hydrogen bonds between NH and CO groups, and r_ij denotes the HO distance, α_ij the NHO angle, and β_ij the HOC angle. The parameters 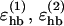, and σ_hb are taken as 3.1, 2.0, and 2.0 Å, respectively. The function u(r) is calculated using a cutoff of r_c = 4.5 Å. The first sum in Eq. 4 contains backbone-backbone interactions, whereas the second sum contains interactions between charged side chains (Asp, Glu, Lys, and Arg) and the backbone. The latter type of interaction is taken to be effectively weak (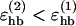), because there are competing interactions between the side-chain charges and the surrounding water that are omitted in the model. For the same reason, we do not include any term in E_hb corresponding to side chain-side chain interactions. It is possible that the effective strength 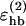should be made stronger in case the side-chain charge gets shielded from the water. This context dependence is ignored in the model, which should be a reasonable approximation for small peptides. Hydrogen bonds between parts that are very close in sequence are rare in protein structures and therefore disregarded in the model; specifically, we disallow backbone NH (C′ O) groups to make hydrogen bonds with the two nearest backbone C′ O (NH) groups on each side of them, and we also forbid hydrogen bonds between the side chain of one amino acid with the nearest donor or acceptor on either side of its C_α. As a simple form of context dependence, we assign a reduced strength to hydrogen bonds involving chain ends, which tend to be exposed to water. A hydrogen bond involving one or two end groups is reduced in strength by factors of 2 and 4, respectively. If there are capping groups, these groups are taken to be the end groups; otherwise, the two end-amino acids take this role.

The fourth energy term, E_hp, represents an effective hydrophobic attraction between nonpolar side chains. It has the pairwise additive form

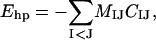(7)

where C_IJ is a measure of the degree of contact between side chains I and J, and M_IJ sets the energy that a pair in full contact gets. The matrix M_IJ is defined in Table 1. To calculate C_IJ we use a predetermined set of atoms, A_I, for each side chain I. We define C_IJ as

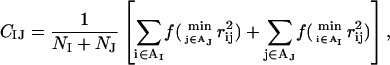(8)

where the function f(x) is given by f(x) = 1 if x < A, f(x) = 0 if x > B, and f(x) = (B − x)/(B − A) if A < x < B [A = (3.5 Å)² and B = (4.5 Å)²]. Roughly speaking, C_IJ is the fraction of atoms in A_I or A_J that are in contact with some atom from the other side chain. For Pro, the set A_I consists of the C_β, C_γ, and C_δ atoms. The definition of A_I for the other hydrophobic side chains has been given elsewhere (Irbäck et al., 2003). We expect the gain in forming a hydrophobic contact to be smaller if the two side chains are close in sequence, because such a pair is partly protected by the backbone. Therefore, we reduce the strength of the hydrophobic attraction for pairs that are nearest or next-nearest neighbors along the sequence; M_IJ is reduced by a factor of 2 for next-nearest neighbors, and taken to be 0 for nearest neighbors.

TABLE 1.

The hydrophobicity matrix M_IJ

		I	II	III
I	Ala	0.0	0.1	0.1
II	Ile, Leu, Met, Pro, Val		0.9	2.8
III	Phe, Trp, Tyr			3.2

Hydrophobic amino acids are divided into three categories. The matrix M_IJ represents the size of hydrophobicity interaction when an amino acid of type I is in contact with an amino acid of type J.

The parameters of this potential were essentially determined by a somewhat tedious trial and error procedure, involving parallel simulations of the different peptides. The target was to have nativelike free-energy minima for all the peptides at low temperature, whereas the temperature dependence was not considered at all. It is interesting to note that this criterion alone was sufficiently discriminating to yield parameter values that appear physically reasonable, as well as a realistic temperature-dependence (see below). Some parameters, such as 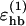, strongly influence the folding properties of the model, and are therefore well determined. Others, such as 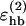, are less important and, as a result of this, quite poorly determined.

The new version of the model differs from earlier versions in the precise form of the simple context-dependence of E_loc and E_hb. Also, the reduction factor for the hydrophobic attraction between next-nearest neighbors along the chain has been changed. Furthermore, we have added Pro, which does not occur in any of our previously studied sequences, to the list of hydrophobic amino acids. All other parameters of the potential are the same as in the last version of the model, except for a slight reduction in strength of the local potential (κ_loc).

It should be stressed that this potential is not expected to provide a good description of general amino acid sequences. For example, it is likely that the pairwise additive hydrophobicity potential is inadequate for long chains, due to double-counting effects. For long chains, anticooperative multibody effects might play a significant role (Shimizu and Chan, 2001). By extending the present calculations in the future to new and longer sequences, we hope that it will be possible to refine the potential and thereby make it more general.

Computational methods

To study the thermodynamic behavior of this model, we use simulated tempering (Lyubartsev et al., 1992; Marinari and Parisi, 1992; Irbäck and Potthast, 1995), in which the temperature is a dynamical variable. For a review of simulated tempering and other generalized-ensemble techniques for protein folding, see Hansmann and Okamoto (1999). We study eight different temperatures T_k, which range from T_min = 275 K to T_max = 369 K and are given by 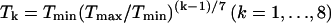. The average acceptance rate for the temperature jumps is ∼70%.

Our simulations are carried out using two different elementary moves for the backbone degrees of freedom: first, the highly nonlocal pivot move in which a single backbone torsion angle is turned; and second, a semilocal method (Favrin et al., 2001) that works with up to eight adjacent backbone degrees of freedom, which are turned in a coordinated manner. Side-chain angles are updated one by one. Every update involves a Metropolis accept/reject step, thus ensuring detailed balance. All our simulations are started from random configurations. All statistical errors quoted are 1σ errors obtained from the variation between independent runs. For each peptide, we performed ∼10 independent runs. Each run contained 10⁹ elementary Monte Carlo steps (1.5 × 10⁹ steps for GB1p) and required 1–2 CPU days on a 1.6-GHz computer.

To characterize the folding behavior of the different peptides, we monitor several quantities. For a peptide with N amino acids, we define the α-helix content H as the fraction of the N–2 inner amino acids with their Ramachandran (φ,ψ) pair in the region −90° < φ < −30°, −77° < ψ < −17°. We calculate the radius of gyration, R_g, over the backbone atoms, with unit mass for all atoms. We also study root mean-square deviations (RMSD) from folded reference structures, calculated over either the backbone atoms or all heavy atoms. A backbone RMSD is denoted by Δ_b and a heavy-atom RMSD by Δ. For the β-sheet peptides, there exist topologically distinct states that the backbone RMSD cannot discriminate between, which makes it necessary to use the heavy-atom RMSD.

In our analysis of the results from the simulations, it turns out that the temperature-dependence of a quantity X in many cases can be well described by the simple two-state expression

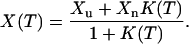(9)

Our fits to this equation are carried out by using a Levenberg-Marquardt procedure (Press et al., 1992). Throughout this article, the baselines X_u and X_n are taken to be temperature-independent, whereas the effective equilibrium constant K(T) is assumed to have the first-order form K(T) = exp [(1/kT − 1/kT_m)ΔE], where T_m is the midpoint temperature and ΔE = E_u–E_n is the energy difference between the unfolded and native states. With these assumptions, a fit to Eq. 9 has four parameters: ΔE, T_m, X_u, and X_n.

RESULTS AND DISCUSSION

Using the model and the methods described in the previous section, we performed high-statistics thermodynamic simulations of the peptides mentioned in the Introduction—namely the Trp cage, F_s, GB1p, GB1m2, GB1m3, Betanova, and LLM. In this section we present the results of these calculations.

Trp cage

The optimized 20-residue Trp cage (NLYIQWLKDGGPSSGRPPPS) is a miniprotein with a compact folded state and a melting temperature of 315 K, as determined by circular dichroism (CD) and nuclear magnetic resonance (NMR) measurements (Neidigh et al., 2002). The NMR-derived native structure (Neidigh et al., 2002) contains a short α-helix (residues 2–8), a single turn of 3₁₀-helix (residues 11–14), and a hydrophobic core consisting of three proline residues (Pro¹², Pro¹⁸, Pro¹⁹) and two aromatic residues (Tyr³, Trp⁶). The folding time is a few microseconds at room temperature (Qiu et al., 2002). Its small size, fast folding, and relative stability makes the Trp cage an ideal testbed for computational methods, and folding simulations of this peptide were reported by several groups (Snow et al., 2002; Simmerling et al., 2002; Schug et al., 2003; Pitera and Swope, 2003; Zhou, 2003a). Two of these groups performed thermodynamic studies (Pitera and Swope, 2003; Zhou, 2003a). Both groups made detailed comparisons with raw NMR data with very good results, but the calculated melting temperatures were too high (≳400 K).

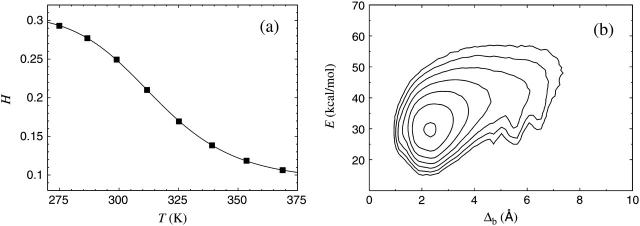
In our model the melting temperature of the Trp cage is, by definition, equal to its experimental value, since we use this quantity to set the energy scale of the model. For this purpose, we consider the helix content H, as defined in the previous section, which should be strongly correlated with the CD signal studied experimentally. Fig. 2 a shows our results for H against temperature. A fit to the data with the two-state expression in Eq. 9 is also shown. As can be seen in the figure, the two-state fit provides an excellent description of the data. The midpoint temperature from this fit, T_m, is set to 315 K, the experimental melting temperature. Having done that, there is no free parameter left in the model. The fitted value of the parameter ΔE = 11.5 ± 0.2 kcal/mol is, in contrast to that of T_m, not used for calibration, but is rather a prediction of the model.

FIGURE 2.

The Trp cage. (a) Helix content against temperature. The line is a fit to Eq. 9 (T_m = 315 K, ΔE = 11.5 ± 0.2 kcal/mol). Statistical errors are smaller than the plot symbols. (b) Contour plot of the free energy F(Δ_b, E) at 275 K. The contours are spaced at intervals of 1 kT. Contours more than 6 kT above the minimum free energy are not shown. The free energy F(Δ_b, E) is defined by exp [ − F(Δ_b, E)/kT] ∝ P(Δ_b, E), where P(Δ_b, E) denotes the joint probability distribution of Δ_b and E at temperature T.

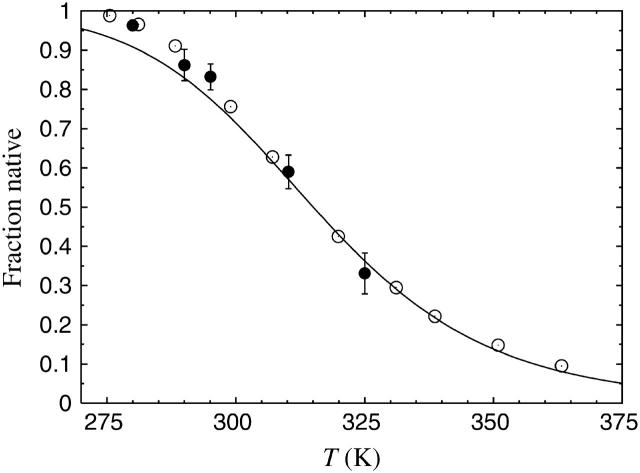
In the two-state picture (Eq. 9), the native population at temperature T is given by 1/{1 + exp[ − (1/kT − 1/kT _m)ΔE]}. Fig. 3 shows the native population obtained using the above mentioned ΔE and T_m, against temperature, along with experimental values based on CD and NMR (Neidigh et al. 2002). We see that the results obtained from the model are in good agreement with the experimental data over the entire temperature range, with a maximum deviation of ∼5% at the lowest temperatures. With the overall energy scale properly determined, we thus find that the melting behavior of this peptide is well described by the model.

FIGURE 3.

Native population against temperature for the Trp cage. The line is the result obtained from the model, through the fit shown in Fig. 2 a. Plot symbols show experimental results (Neidigh et al., 2002) based on CD (○) and NMR (•), respectively.

At low temperatures, we find a helix content similar to that of the NMR structure, ∼30% (see Fig. 2 a). An RMSD analysis confirms that the typical low-temperature structure is similar to the NMR structure (PDB code 1L2Y, first model), as illustrated in Fig. 2 b. This figure shows the free energy F(Δ_b, E) calculated as a function of the backbone RMSD Δ_b (residues 2–19) and the energy E, at 275 K. We see that F(Δ_b, E) has a simple shape with one dominating minimum, which is located at Δ_b ≈ 2.3 Å.

F_s

The designed 21-residue F_s peptide is given by Suc-A₅(AAARA)₃A-NH₂, (where Suc is succinylic acid) and makes an α-helix (Lockhart and Kim, 1992, 1993). Other N-capping groups than Suc have also been used in the experiments on this peptide. The melting behavior of F_s was studied using CD as well as infrared (IR) spectroscopy. The melting temperature measured by IR was 334 K (Williams et al., 1996), whereas the CD-based studies obtained T_m = 308 K (Lockhart and Kim, 1993) and T_m = 303 K (Thompson et al., 1997). Computational studies of F_s have also been reported (Vila et al., 2000; García and Sanbonmatsu, 2002; Nymeyer and García, 2003). By explicit water simulations, García and Sanbonmatsu (2002) obtained a T_m of 345 K, which is in reasonable agreement with the IR-based value. Using an earlier version of our model and ignoring the capping groups, a T_m of 310 K was obtained (Irbäck et al., 2003). In the present calculations, we include the Suc and NH₂ groups.

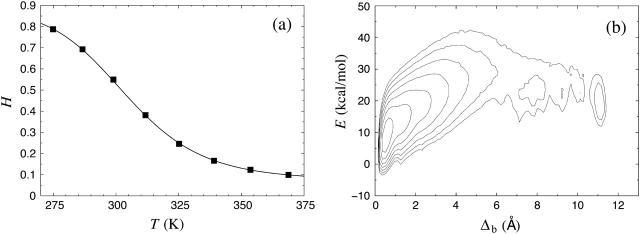
Fig. 4 a shows the helix content versus temperature as obtained from our F_s calculations. A two-state fit of the data gives T_m = 304 ± 1 K, which is significantly lower than the IR-based result mentioned above but in perfect agreement with the CD studies, especially that of Thompson et al. (1997). For the energy difference, we obtain ΔE = 11.9 ± 0.3 kcal/mol, which also agrees with what Thompson and co-workers found, namely ΔE = 12 ± 2 kcal/mol. It may be worth noting that the experimental data that we compared with in the Trp cage case were based on CD rather than IR.

FIGURE 4.

Same as Fig. 2 for the F_s peptide (T_m = 304 ± 1 K, ΔE = 11.9 ± 0.3 kcal/mol).

In Fig. 4 b we show the free energy F(Δ_b, E) at 275 K. In the absence of a precise experimental structure for F_s, we define Δ_b as the (backbone) RMSD from an ideal α-helix (all residues). From the figure we see that the free energy has its global minimum at Δ_b ≈ 0.5 Å, which indeed corresponds to the α-helix. There are also two local minima at Δ_b ≈ 7 Å and Δ_b ≈ 11 Å, both of which correspond to β-sheet structures. These two minima are very weakly populated compared to the α-helix minimum.

GB1p and GB1m2/GB1m3

Using exactly the same model, we now turn to β-sheet peptides. That GB1p (GEWTYDDATKTFTVTE), the 41–56-residue fragment from the protein G B1 domain, makes a β-hairpin on its own, was a breakthrough discovery (Blanco et al., 1994) that has been followed by numerous atomic simulations of this particular sequence (Roccatano et al., 1999; Pande and Rokhsar, 1999; Dinner et al., 1999; García and Sanbonmatsu, 2001; Zhou et al., 2001; Zhou, 2003b; Zagrovic et al., 2001; Kussell et al., 2002; Bolhuis, 2003; Wei et al., 2004). Recently, two mutants of GB1p with enhanced stability were designed (Fesinmeyer et al., 2004), GB1m2 and GB1m3, by replacing the turn segment DDATKT by NPATGK. The mutant GB1m2 (GEWTYNPATGKFTVTE) is identical to GB1p except for this change, whereas GB1m3 (KKWTYNPATGKFTVQE) differs from GB1p at the chain ends as well. By CD and NMR, GB1m3 was estimated to be 86 ± 3% folded at 298 K and to have a T_m of 333 ± 2 K, whereas GB1m2 was found to have a slightly lower folded population, 74 ± 5% at 298 K, and a T_m of 320 ± 2 K (Fesinmeyer et al., 2004). In the same study, GB1p was estimated to be ∼30% folded at 298 K. An earlier NMR study found GB1p to be 42% folded at 278 K (Blanco et al., 1994). Both these estimates of native population for GB1p are low compared to the result of a Trp fluorescence study (Muñoz et al., 1997); a two-state analysis of these data gave T_m = 297 K and ΔE = 11.6 kcal/mol (Muñoz et al., 1997).

It turns out that our model fails to reproduce the experimental difference in stability between GB1m2 and GB1m3. In fact, GB1m2 and GB1m3 show nearly identical behavior in our model. For clarity, we therefore show results only for one of these peptides, GB1m3, in the figures below.

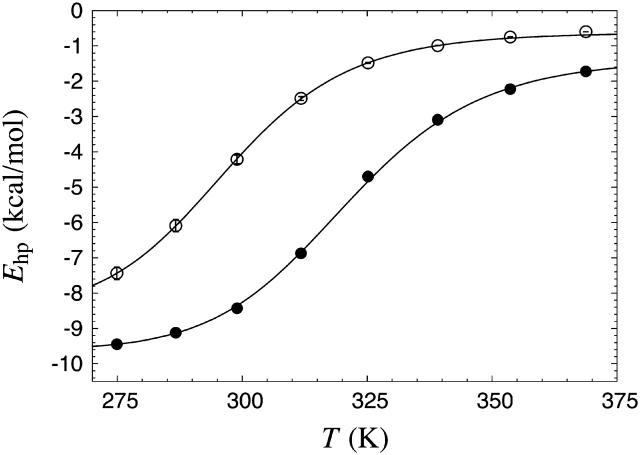
Fig. 5 shows the hydrophobicity energy E_hp against temperature for GB1p and GB1m3 in the model. We expect E_hp to be strongly correlated with Trp fluorescence for these peptides, as Trp⁴³ forms a hydrophobic cluster together with Tyr⁴⁵, Phe⁵², and Val⁵⁴. A two-state fit to our data for GB1p gives T_m = 297 ± 1 K and ΔE = 14.2 ± 0.2 kcal/mol, which indeed is in good agreement with the Trp fluorescence results for this peptide (T_m = 297 K, ΔE = 11.6 kcal/mol). The same type of fit gives T_m = 321 ± 1 K and ΔE = 15.0 ± 0.4 kcal/mol for GB1m3, and T_m = 322 ± 2 K and ΔE = 15.1 ± 0.4 kcal/mol for GB1m2. These two very similar T_m estimates lie close to the experimental result for GB1m2 (320 ± 2 K) and somewhat below that for GB1m3 (333 ± 2 K). Our E_hp data indicate that GB1m2 and GB1m3 indeed are markedly more stable than GB1p in the model, which is confirmed by the results discussed next.

FIGURE 5.

The hydrophobicity energy E_hp against temperature for GB1p (○) and GB1m3 (•). The lines are fits to Eq. 9 (T_m = 297 ± 1 K, ΔE = 14.2 ± 0.2 kcal/mol for GB1p; T_m = 321 ± 1 K, ΔE = 15.0 ± 0.4 kcal/mol for GB1m3). The points corresponding to the two highest temperatures were omitted for GB1p, as removing them resulted in a significantly better fit in terms of χ² per degree of freedom.

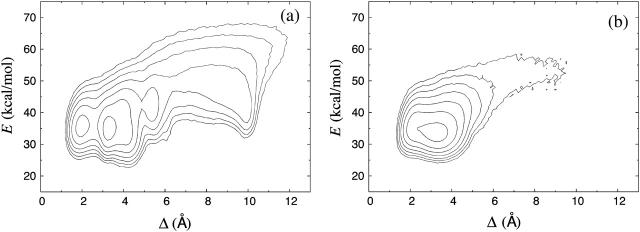
Fig. 6 a shows our data for the free energy F(Δ,E) for GB1p, at 275 K. On its own the GB1p fragment is believed to adopt a folded structure similar to that it has as part of the native protein G B1 domain, although the NMR restraints were insufficient to determine a unique structure for the excised fragment. As reference structure in the calculation of Δ, we therefore use the corresponding fragment of the NMR structure for the full protein G B1 domain (PDB code 1GB1, residues 41–56, first model; see Gronenborn et al., 1991). The heavy-atom RMSD Δ is used instead of the backbone RMSD Δ_b, because Δ_b cannot distinguish between the two possible β-hairpin topologies (with similar backbone folds but oppositely oriented side chains). We find that the two lowest minima of F(Δ,E), at Δ ≈ 2.0 Å and Δ ≈ 3.2 Å, both correspond to a β-hairpin with the same topology and the same set of backbone hydrogen bonds as the reference structure. The main difference between these two minima lies in the shape of the turn region. In addition to these minima, there are two weakly populated local minima at Δ ≈ 5.3 Å and Δ ≈ 8–10 Å, which correspond to a β-hairpin with the opposite topology and α-helix, respectively. The shape of F(Δ, E) for GB1p was also studied using earlier versions of our model (Irbäck et al., 2003; Irbäck and Sjunnesson, 2004). The present model yields very similar results, with a minor enhancement of the two nativelike minima at the expense of the two other local minima mentioned above.

FIGURE 6.

Contour plot of the free energy F(Δ,E) for (a) GB1p and (b) GB1m3, at 275 K. Contour levels are as in Fig. 2 b.

Fig. 6 b shows the corresponding free-energy plot for GB1m3. As reference structure for GB1m3, we use a mutated and relaxed version of the GB1p reference structure. We see that F(Δ,E) has a simpler shape for GB1m3 than for GB1p. There is only one detectable free-energy minimum for GB1m3, and this minimum corresponds to a structure similar to that favored for GB1p.

Different experiments on GB1p have, as mentioned above, obtained different β-hairpin populations. One way of estimating folded populations in the model is by two-state fits like those in Fig. 5. An independent and more direct estimate can be obtained by counting native backbone hydrogen bonds. To this end, we consider a hydrogen bond formed if its energy is 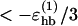. The number of native backbone hydrogen bonds in a given conformation is denoted by 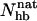. Fig. 7 shows the probability distribution of 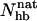for GB1p and GB1m3 at 299 K, which is very close to the temperature (298 K) at which the folded populations of these two peptides were compared by CD and NMR (Fesinmeyer et al., 2004). We find that the probability distribution 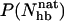has a clear bimodal shape for both peptides, with one native and one unfolded peak. The native peak is, as expected from the results above, significantly larger for the mutant GB1m3 than for GB1p. Taking conformations with 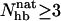as native and those with 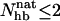as unfolded, we obtain native populations of 82 ± 1% for GB1m3, 84 ± 1% for GB1m2, and 27 ± 2% for GB1p. The overall agreement between these results and the experimental data (86 ± 3% for GB1m3, 74 ± 5% for GB1m2, ∼30% for GB1p) is very good, although the model slightly overestimates the folded fraction for GB1m2. Note that the native populations estimated from 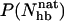, thanks to the bimodality, are quite well determined, despite that the precise definition of native in terms of 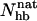is somewhat arbitrary.

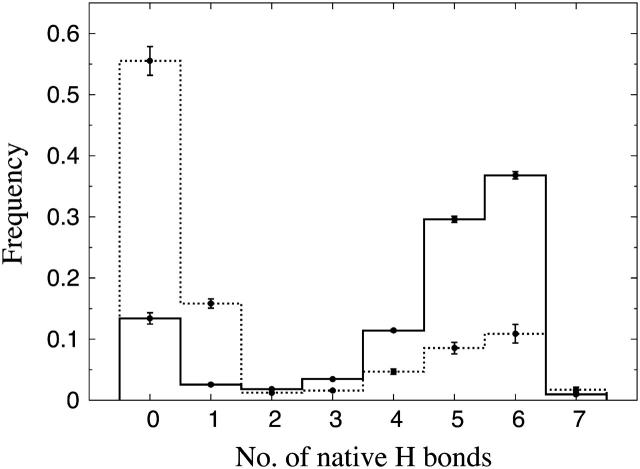
FIGURE 7.

Probability distribution of the number of native hydrogen bonds, 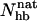, for GB1m3 (solid line) and GB1p (dotted line) at 299 K. The hydrogen bonds taken as native are the same for both peptides. In GB1p notation, the native hydrogen bonds are Glu⁴²(N)-Thr⁵⁵(O), Glu⁴²(O)-Thr⁵⁵(N), Thr⁴⁴(N)-Thr⁵³(O), Thr⁴⁴(O)-Thr⁵³(N), Asp⁴⁶(N)-Thr⁵¹(O), Asp⁴⁶(O)-Thr⁵¹(N), and Asp⁴⁷(O)-Lys⁵⁰(N).

For GB1m3, we find that one of the hydrogen bonds taken as native is very unlikely to form in our model, namely Pro⁴⁷(O)-Gly⁵⁰(N). As a result, conformations with 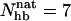are very rare (see Fig. 7).

Our E_hp- and 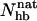-based native populations for GB1p are different; from the E_hp data we obtain a native population of 46% at 299 K, where the 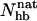analysis gives 27%. The magnitude of this difference is similar to that between different experiments. The 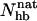-based result is in good agreement with CD and NMR data, whereas the E_hp-based result agrees with Trp fluorescence data. For GB1m3 (and GB1m2), we do not know of any Trp fluorescence study. Our model suggests that the difference between different methods would be smaller in this case. Our E_hp-based folded population at 299 K is 85% for GB1m3, which is close to our 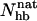-based result of 82%.

Betanova and LLM

Betanova is a designed antiparallel three-stranded β-sheet peptide with 20 residues (RGWSVQNGKYTNNGKTTEGR) (Kortemme et al., 1998), which is only marginally stable (López de la Paz et al., 2001). Recently, Betanova mutants with higher stability were developed (López de la Paz et al., 2001), such as the triple mutant LLM (Val⁵Leu, Asn¹²Leu, Thr¹⁷Met). The NMR-based native populations of LLM and Betanova are 36% and 9%, respectively, at 283 K (López de la Paz et al., 2001). Results in good agreement with these estimates were obtained when testing an earlier version of our model on these two peptides (Irbäck and Sjunnesson, 2004). Folding simulations of Betanova have also been performed by other groups, using coarse-grained (Kim et al., 2004) and atomic (Bursulaya and Brooks, 1999; Colombo et al., 2002) models.

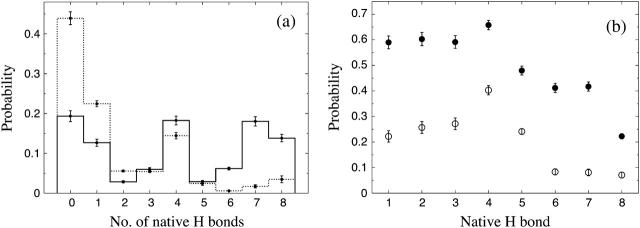
The folded structure of Betanova and LLM contains eight backbone hydrogen bonds, four in each of the two β-hairpins. Fig. 8 a shows the probability distribution of the number of native backbone hydrogen bonds, 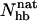, in our model for LLM and Betanova, at 287 K. The distributions have three peaks. In addition to the folded and unfolded peaks at high and low 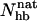, there is also a peak at 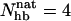. Visual inspection of snapshots from the simulations reveals that conformations at this peak tend to contain the first (N-terminal) β-hairpin but not the second (C-terminal) one. This conclusion, which is in agreement with experimental data (López de la Paz et al., 2001), is confirmed by the frequencies of occurrence of the individual hydrogen bonds, shown in Fig. 8 b. We see that the hydrogen bonds of the first β-hairpin (1–4) occur more frequently than those of the second β-hairpin (5–8), especially for Betanova. For a conformation to be counted as folded, we require that 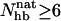. With this definition, we find that Betanova and LLM are 6 ± 1% and 38 ± 2% folded, respectively, at 287 K, which is in good agreement with the experimental results (9% and 36% at 283 K).

FIGURE 8.

(a) Probability distribution of the number of native backbone hydrogen bonds, 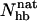, for LLM (solid line) and Betanova (dotted line) at 287 K. (b) Frequencies of occurrence for the different native hydrogen bonds for Betanova (○) and LLM (•) at 287 K. In Betanova notation, the native hydrogen bonds are 1, Ser⁴(N)-Thr¹¹(O); 2, Ser⁴(O)-Thr¹¹(N); 3, Gln⁶(N)-Lys⁹(O); 4, Gln⁶(O)-Lys⁹(N); 5, Tyr¹⁰(N)-Thr¹⁷(O); 6, Tyr¹⁰(O)-Thr¹⁷(N); 7, Asn¹²(N)-Lys¹⁵(O); and 8, Asn¹²(O)-Lys¹⁵(N).

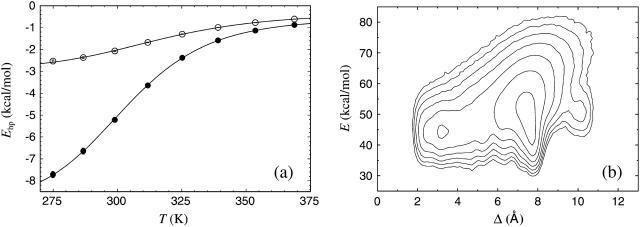
The melting behavior has, as far as we know, not been studied experimentally for Betanova or LLM. In Fig. 9 a we show melting curves for these peptides in our model. As in the β-hairpin case, we consider the hydrophobicity energy E_hp. Betanova has fewer hydrophobic residues than LLM, and we see that E_hp is much lower in absolute value for Betanova than for LLM. In our model, the difference in hydrophobicity is the main reason why LLM is more stable than Betanova. A two-state analysis of our E_hp data gives T_m = 314 ± 1 and ΔE = 8.9 ± 0.1 kcal/mol for Betanova, and T_m = 302 ± 1 K and ΔE = 10.9 ± 0.2 kcal/mol for LLM. These fitted two-state parameters contrast sharply with the results of the 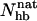analysis above, especially for Betanova. In fact, for Betanova, the fitted two-state parameters correspond to a native population of 80% at the temperature 287 K, at which Betanova was estimated above to be only 6% folded. This discrepancy between the native populations obtained using E_hp and 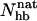data clearly show that, in our model, these two peptides do not behave as ideal two-state systems. It is worth noting that the quality of the two-state fits in Fig. 9 a, nevertheless, is very good, which illustrates that deviations from the simple two-state picture can be very hard to detect from the temperature-dependence of a single quantity (Favrin et al., 2003).

FIGURE 9.

(a) The hydrophobicity energy E_hp against temperature for Betanova (○) and LLM (•). The lines are fits to Eq. 9 (T_m = 314 ± 1, ΔE = 8.9 ± 0.1 kcal/mol for Betanova; T_m = 302 ± 1 K, ΔE = 10.9 ± 0.2 kcal/mol for LLM). (b) Free energy F(Δ,E) for Betanova at 275 K. Contour levels are as in Fig. 2 b.

Fig. 9 b shows the free energy F(Δ,E) for Betanova at 275 K. Like for the β-hairpins, we use all the heavy atoms in the RMSD, but limit the comparison to the residues 3–18. The residues 1, 2, 19, and 20 do not participate in the β-sheet structure. There is a local minimum at Δ ≈ 3.2 Å representing the state obtained in our model that most resembles the NMR structure. That this state is not the most probable state in the model is consistent with the low native population found experimentally for this peptide. The corresponding graph for LLM shows a much more prominent minimum representing the native conformation.

The character of the melting transition

For GB1p, Betanova, and LLM, we saw above that the apparent native population depends on which quantity we study. This dependence reflects the fact that these peptides do not show ideal two-state behavior in the model. A quantity for which we obtain a relatively high apparent melting temperature not only for these three peptides but for all the peptides studied, is the radius of gyration, R_g. The T_m values obtained from our R_g data for F_s and the Trp cage are 29 K and 9 K higher, respectively, than what we found above using the helix content. For GB1m3, our R_g data gives a T_m that is 6 K higher than that obtained above using the hydrophobicity energy. These comparisons show that none of the peptides studied behaves as a perfect two-state system in our model, although the deviations from this behavior might be relatively small for some of them, such as GB1m3.

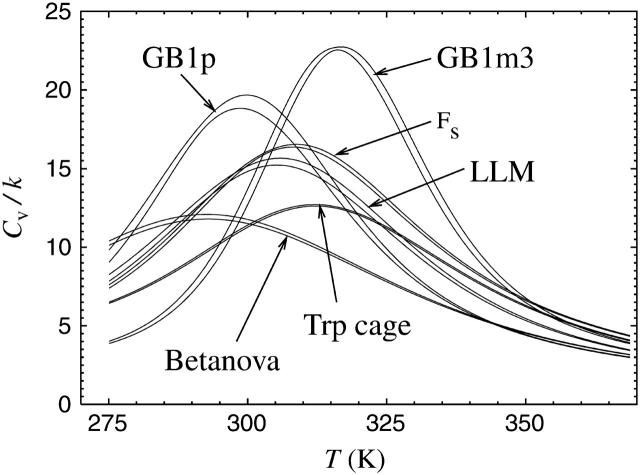
One measure of the sharpness of the melting transition is the height of the peak in the specific heat, C_v. In Fig. 10, we show specific heat curves for the different peptides studied. The results for GB1m2 are again very similar to those for GB1m3 and therefore omitted. The specific heat exhibits a clear peak for all the peptides studied, but the height of the peak varies. The peak is highest for GB1m3, indicating that the melting transition is most two-state-like for this peptide. A comparison of the energy distributions of the different peptides (not shown) supports this conclusion. For GB1m3, we find that the energy distribution has a bimodal shape, although not very pronounced. The other peptides all have wide but single-peaked distributions. The distribution is particularly wide, virtually flat, for GB1p, which has the next highest peak in C_v.

FIGURE 10.

The specific heat C_v against temperature for the different peptides, as obtained using histogram reweighting techniques (Ferrenberg and Swendsen, 1988). For each peptide, a band is shown. The band is centered around the expected value and shows statistical 1σ errors. C_v is defined as C_v = N⁻¹d〈E〉/dT = (NkT²)⁻¹(〈E²〉 − 〈E〉²), where N is the number of amino acids and 〈O〉 denotes a Boltzmann average of variable O.

For the peptide with the sharpest transition, GB1m3, we find that the specific heat maximum, 316 K, is located near the temperature at which its folded population is 50%. The other peptides are <50% folded at their specific heat maxima, especially Betanova. Betanova was estimated above to be 6% folded at 287 K in the model, and has its specific heat maximum at a temperature higher than that, 293 K.

CONCLUSION

We have developed an atomic model with a simplified phenomenological potential for folding studies of polypeptide chains, which was tested on a set of peptides with ∼20 amino acids each, namely the Trp cage, F_s, GB1p, GB1m2, GB1m3, Betanova, and LLM. First of all, our study shows that the model folds these different sequences to structures similar to their experimental structures, for one and the same choice of model parameters. In addition, we investigated the stability and melting behavior of the peptides. The following list is a brief summary of these calculations, focusing on the observables expected to be correlated with the corresponding experimental probes.

1. The helix content of the Trp cage shows a temperature-dependence that is in good agreement with experimental data based on CD and NMR (see Fig. 3).

2. A two-state analysis of the helix content of F_s gives T_m and ΔE values that are in good agreement with CD data, whereas the T_m value is somewhat low compared to its IR-based value.

3. Estimates of folded populations based on native hydrogen bond data for the β-sheet peptides GB1p, GB1m2, GB1m3, Betanova, and LLM are in good agreement with CD- and NMR-based experimental results, as is summarized in Table 2. Recall that the energy scale was set using the α-helical Trp cage.

4. Experimentally, GB1p has been studied using Trp fluorescence as well, which gave a folded population higher than that in Table 2. Our results based on hydrophobicity energy data are in good agreement with those from the Trp fluorescence study.

TABLE 2.

Folded populations of the different β-sheet peptides in the model, along with experimental results

	Exp.	Model
GB1p	∼30% (298 K)	27 ± 2% (299 K)
GB1m2	74 ± 5% (298 K)	84 ± 1% (299 K)
GB1m3	86 ± 3% (298 K)	82 ± 1% (299 K)
Betanova	9% (283 K)	6 ± 1% (287 K)
LLM	36% (283 K)	38 ± 2% (287 K)

The experimental data on GB1p, GB1m2, and GB1m3 are from Fesinmeyer et al. (2004), whereas those on Betanova and LLM are from López de la Paz et al. (2001).

The model fails to reproduce the difference in folded population between the two stable mutants of GB1p (see Table 2), which in part may be due to the fact that Coulomb interactions between side-chain charges are ignored; GB1m3 contains some charged residues that are missing in GB1m2. The overall quantitative agreement with experimental data is, nevertheless, excellent. This agreement indicates that factors such as Coulomb interactions between charged residues play a quite limited role in the folding thermodynamics of these peptides, compared to hydrogen bonding and hydrophobic attraction, which are the main driving forces of the model.

The temperature-dependence of the model is, to us, surprisingly good, for two reasons. First, the temperature-dependence was not considered at all when calibrating the model, except in the determination of the energy scale. A considerable amount of fine-tuning was required to obtain proper folded structures, but no further fine-tuning was performed once that goal had been achieved. Second, our calculations do not involve any reparameterization of the energy function. In other words, the parameters of the energy function are temperature-independent, which is a simplifying assumption rather than a controlled approximation. On the other hand, it should be noted that the melting transition is not triggered by a sudden change in, for example, the strength of the hydrophobic attraction.

In the development of this model, we have taken a purely phenomenological approach. The model will be further developed by studying new amino acid sequences, which will impose new conditions on the interaction potential. As before, the challenge will be to do this in a backward-compatible manner; the model must not lose its ability to fold previously studied sequences. As to limitations of the current version of the model, we know that it is unable to properly fold the so-called Trp-zip β-hairpins (Cochran et al., 2001), which make β-hairpins in the model but with the wrong topology. We also expect that refinement of the model will be needed as the chains get larger. For example, as mentioned earlier, it is likely that our pairwise additive hydrophobicity potential will have to be supplemented with multibody terms for large chains. Finding out how to change the model to make it more general without losing computational efficiency will not be an easy task, but the results obtained so far makes it tempting to try.