A Model for the Mediation of Processivity of DNA-Targeting Proteins by Nonspecific Binding: Dependence on DNA Length and Presence of Obstacles

Abstract

A physical and mathematical model is presented to explain processivity of proteins on DNA. In this model, a DNA-targeting protein such as a restriction enzyme can diffuse to the DNA surface and nonspecifically bind to it. Once on the DNA surface it will either move along the DNA or equilibrate with the surrounding region. Owing to the nonspecific binding, the search for a specific site on the DNA occurs in a reduced dimensionality, and the protein appears processive when moving from one specific site to another. The simplest version of this nonspecific-binding-facilitated diffusion model is solved and the results quantitatively explain experimentally observed dependence of the processivity ratio on the intervening DNA length between two specific sites.

INTRODUCTION

Processivity—the interaction of a protein with two or more specific sites on the same DNA—is essential for the proper functioning of many DNA-targeting proteins (Ptashne and Gann, 2001; Halford and Marko, 2004). To hold on to their DNA templates, replicative DNA polymerases require cognate processivity factors, which have been shown to have distinctive DNA-binding architectures such as circular clamps (Zuccola et al., 2000; Appleton et al., 2004; Bowman et al., 2004). Other DNA-targeting proteins such as restriction enzymes can bind to DNA nonspecifically. Here I present a model to demonstrate that nonspecific binding can mediate processivity and to quantitatively explain experimental data (Terry et al., 1985; Stanford et al., 2000) on the dependence of the processivity ratio on the intervening DNA length between two specific sites.

Adam and Delbruck (1968) originated the idea that nonspecific binding can reduce the dimensionality of the search space for a specific site. This idea has been subsequently appreciated by others (Riggs et al., 1970; Richter and Eigen, 1974; Berg et al., 1981; Berg and Ehrenberg, 1982). In particular, Berg et al. (1981) phenomenologically described three modes of nonspecific-binding facilitated translocation along the DNA (a fourth mode—intersegment transfer—applies to bidentate proteins and is not considered here). Berg and Ehrenberg (1982) empirically incorporated surface diffusion into the Smoluchowski theory (Smoluchowski, 1917) for diffusion-influenced reactions. Recently we introduced a more fundamental and realistic approach, in which nonspecific binding is accounted for by a short-range attractive potential around the DNA surface (Zhou and Szabo, 2004). All the three modes described by Berg et al. (1981) are encompassed in this approach and there is no need (and rigorously it is impossible) to distinguish them. When a DNA is treated as an infinite cylinder (with radius R) and association with a specific site treated as absorbing on a reactive patch (with length 2h) on the DNA surface, the diffusion-limited association rate constant is found to be

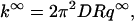(1a)

with

(1b)

In these expressions x₁ = xh/R, K₀(x) and K₁(x) are modified Bessel functions, and K′_ns = D_∥K_ns/D with D the relative diffusion constant of the DNA-targeting protein in bulk solution and D_∥ the counterpart along the DNA surface, and K_ns the nonspecific binding constant per unit surface area given by

(1c)

where β = (k_BT)⁻¹, ρ is the distance to the DNA axis, and U(ρ) is the surface potential.

THEORETICAL METHODS

Nonspecific-binding-facilitated diffusion model

The Smoluchowski theory incorporating a surface potential is physically and mathematically equivalent to what I will call the nonspecific-binding-facilitated diffusion model (see Fig. 1). In this model, a DNA-targeting protein can diffuse to the DNA surface and nonspecifically bind to it. Once on the DNA surface it will either move along the DNA or equilibrate with the surrounding region, and the process repeats itself. There is no need to differentiate among different possible modes (e.g., sliding, hopping, and jumping) of translocation from one site on the DNA to another site. All these events can take place and the model is all-encompassing. The model can be used to treat a number of important biological situations, such as finite DNA lengths, multiple specific sites, and presence of obstacles on the DNA surface. Exact solutions can be found, allowing for direct comparison with experimental data.

FIGURE 1.

The nonspecific-binding-facilitated diffusion model. Here the DNA is modeled as a cylinder and the protein is modeled as a sphere. A surface potential is present (in the hatched region). Upon nonspecifically binding to the DNA, the protein may spend a period of time in the surface phase and then transiently diffuse to the bulk phase. Nonspecific binding recurs and the process is repeated. Key: z, coordinate along the central axis of the DNA; ρ, distance to the central axis; and 2h, height of the reactive patch (assumed to be absorbing) that models a specific site.

As before, the DNA will be modeled as a cylinder. Let z be the coordinate along the DNA axis and C(ρ, z, t) be the probability per unit volume for finding the protein at time t. In the presence of an interaction potential U(ρ), the diffusion equation is

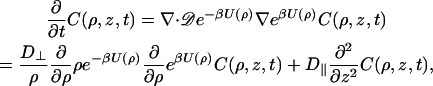(2)

where D_⊥ is the diffusion constant perpendicular to the DNA axis. The DNA surface is reflecting except for the reactive patch, which is absorbing. Therefore

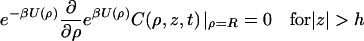(3a)

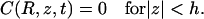(3b)

The distribution function C(ρ, z, t) is normalized such that its value at infinity is 1.

If the potential is restricted to a short range (of magnitude ɛ) around the DNA surface, then it is convenient to divide the space outside the DNA into the surface phase and the bulk phase. It is assumed that in the bulk phase D_⊥ = D_∥ = D. Only motion in the surface phase is under the influence of the potential. The probability per unit surface area for finding the protein in the surface phase is

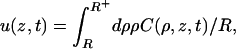(4)

where R⁺ = R + ɛ. The surface and bulk phases equilibrate, thus

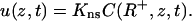(5)

The interaction potential between the protein and the DNA will probably have electrostatic as well as hydrophobic and van der Waals contributions that are of much shorter range. For purely electrostatic interactions, if the DNA is modeled as a cylinder with a smeared surface charge distribution and the protein is treated as a test charge, the interaction potential obtained from the Poisson-Boltzmann equation has the form U(ρ) = −U₀K₀(ρ/λ). The Debye-Hückel screening length λ at physiological ionic strength (∼0.15 M) is ∼8 Å. As ionic strength increases, the electrostatic contribution to the interaction potential is expected to decrease in magnitude. In the present model, all the effects of the interaction potential are captured by the nonspecific binding constant K_ns, which can be directly measured experimentally.

What is the mathematical advantage of introducing a surface phase? Integrating Eq. 2 over ρ from R to R⁺ and using Eq. 3a, one finds

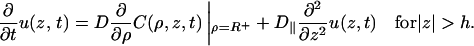(6)

All the effect of the surface potential is now incorporated in this equation, which serves as a boundary condition for the free diffusion equation in the bulk phase. The full boundary conditions are of a mixed type, involving the distribution function itself on one region of the surface (Eq. 3b) and its flux on another (Eq. 6). As shown in the Appendix, the mixed boundary conditions can be dealt with by a constant-flux approximation (Shoup et al., 1981), which is used in obtaining the result in Eq. 1a (Zhou and Szabo, 2004). Exactly the same result for the rate constant is obtained with the boundary conditions of Eqs. 3b and 6.

Capture probability and processivity

The distribution function C(ρ, z, t) is numerically identical to the survival probability S(t|ρ, z), i.e., the probability that a protein molecule started at position (ρ, z) at time 0 has not been absorbed at time t. The complement of S(t|ρ, z) is the capture probability p_c(t|ρ, z), i.e., the probability that the protein molecule has been absorbed by time t:

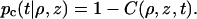(7)

Of particular interest is p_c(∞|R⁺, z), the steady-state (t → ∞) capture probability of a protein molecule started from a point on the DNA surface. This can be viewed as the processivity ratio f_p(z), i.e., the probability a protein that encountered a site at z will eventually encounter a second site at z = 0. From now on I will specialize to the steady state and the DNA surface (i.e., ρ = R⁺) and drop explicit reference to t and ρ.

For an infinitely long DNA, the capture probability is

(8)

Finite DNA length

A DNA with a finite contour length 2L can be treated by fictitiously continuing the cylindrical surface ρ = R beyond z = ±L to infinity but restricting the surface potential to only the physical length of the DNA (Berg and Ehrenberg, 1982). Therefore the surface distribution function u(z) is only defined for |z| < L. The physical ends at z = ±L are reflecting for u(z):

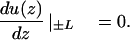(9)

The solution of the distribution function C from Eq. 2 subjected to the boundary conditions of Eqs. 3b, 6, and 9 is given in the Appendix. The result for the capture probability is given by

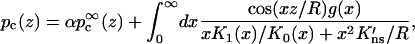(10a)

in which

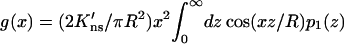(10b)

and

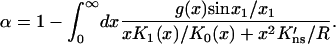(10c)

The association rate constant is given by

(11)

The function p₁(z) introduced in Eq. 10b is

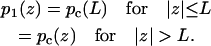(12)

Equation 10a is thus an implicit equation for the capture probability since the right-hand side contains p_c(z) itself. The coupled Eqs. 10a–c can be solved by iteration, starting with α = 1 and g(x) = 0. Note that the model has only a single adjustable parameter, i.e., K′_ns ≡ D_∥K_ns/D. Although K_ns can be determined experimentally from the binding constant per basepair (bp) of nonspecific DNA (Terry et al., 1983; Kim et al., 1987; Jeltsch and Pingoud, 1998), there is uncertainty regarding the surface diffusion constant D_∥, although single-molecule techniques have now opened the possibility for its direct determination (Harada et al., 1999; Guthold et al., 1999). It is generally accepted that D_∥ is orders-of-magnitude smaller than D (Schurr, 1979; Winter et al., 1981; Jack et al., 1982).

RESULTS AND DISCUSSION

Comparison with experimental data

The processivity ratios of the restriction enzymes EcoRI and EcoRV have been measured by Terry et al. (1985) and by Stanford et al. (2000), respectively. Both groups engineered DNA substrates with two specific sites and unequivocally showed that some of the enzyme molecules, after cleaving the first site, could go on to cleave the second site. The experiments were done at large excess of DNA substrate over enzyme, so that the appearance of the cleavage product corresponding to the fragment between the two specific sites could only be attributed to processive events. The processivity ratio f_p was obtained as the fraction, among the population of DNA molecules with cleavage at at least one site, which are cleaved by the same enzyme at both sites. Terry et al. (1985) observed a doubling of the processivity ratio at low salt when a linear DNA with two specific sites is circularized. In the study of Stanford et al. (2000), the two specific sites on linear DNA substrates were separated by various lengths. The probability for cleaving the second site decreased as the intervening DNA length increased, but processive cleavage could be detected even when the two sites were separated by as much as 764 bp (measured at 0 NaCl).

Theoretical predictions for the capture probability can be directly compared with the experimental data for f_p. A relevant detail is that, upon cleavage at the first site, the DNA is broken. Assuming that the enzyme has equal chance of starting at the new ends, that chance is at best 50% (Terry et al., 1985). The actual chance, η, is perhaps smaller than 50% since an overhanging enzyme may be released to the solution. For a linear DNA, only an enzyme starting at the end of the new fragment containing the second site is viable for processive cleavage. Thus the measured processive ratio f_p is comparable to ηp_c(L), where L is the DNA length separating the two sites. For a circular DNA, an enzyme starting at either of the new ends is viable for processive cleavage, thus in this case f_p is comparable to η[p_c(L₁) + p_c(L₂)], where L₁ and L₂ are the DNA contour lengths separating the two sites on the circular DNA.

Terry et al. (1985) found that at 25 mM NaCl the processivity ratios for a circular DNA, with two specific sites separated by 51 and 337 bp, and its linear counterpart were 0.77 ± 0.02 and 0.46 ± 0.04, respectively. Using a value for K′_ns ≡ D_∥K_ns/D that is equivalent to 3.5 × 10⁴ M⁻¹ per bp, p_c(51 bp) and p_c(337 bp) are calculated to be 0.997 and 0.938, respectively. The predicted values for f_p are thus 0.77 and 0.40, respectively, for the circular and linear DNA when η is set to 40%. The experimental data can be explained within a relatively large range of 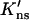values. The particular value for 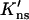used above also gives good fit (see Fig. 2) to the dependence of the dissociation rate constant of EcoRI on DNA length (Jack et al., 1982). For comparison, the experimental value for K_ns is ∼7.4 × 10⁵ M⁻¹ per bp (Terry et al., 1983), suggesting D_∥/D ∼0.05. It should be noted, however, that the buffer conditions for measuring the processivity ratio (Terry et al., 1985) were somewhat different from those for measuring the nonspecific binding constant (Terry et al., 1983) and the dissociation rate (Jack et al., 1982).

FIGURE 2.

The length-dependence of the association rate constant. The ordinate of the plot is the ratio between the association rate constant, k, at a DNA length of 2L bp and the value of k at a reference DNA length. The calculations assumed a centrally located absorbing patch (with length set to 6 Å). The length of each bp was set to 3.4 Å, and the contact distance (R) between the protein and the DNA was taken as 30 Å. The forward and inverse cosine transforms involved in the iteration of Eqs. 10a–c were implemented by fast Fourier transform (Swarztrauber, 1982). Circles are experimental data of Jack et al. (1982) for the dissociation rate of EcoRI. Their comparison with calculation is based on the experimental result (Jack et al., 1982) that the specific binding constant (equal to the ratio of the association and dissociation rate constants) is length-independent, so that the dissociation rate should have the same length-dependence as the association rate. Diamonds and triangles are experimental data of Jeltsch and Pingoud (1998) for the cleavage rates of EcoRV at 1 and 10 mM MgCl₂, respectively. Their comparison with calculation assumes that EcoRV cleavage is diffusion-controlled (Wright et al., 1999 found experimental evidence for diffusion control in EcoRI cleavage). The specific site was centrally located in the study of Jack et al. (1982) but was near one end of the DNA in the study of Jeltsch and Pingoud (1998).

More discriminatory experimental data are provided by the study of Stanford et al. (2000), who varied the intervening DNA length between two specific sites for EcoRV. In Fig. 3 their data for f_p at 0 NaCl are compared with ηp_c(L) calculated with K′_ns = 5.2 × 10³ M⁻¹ per bp and η = 37%. Good agreement is obtained. The K′_ns value used also yields a length-dependence of the association rate that is consistent (see Fig. 2) with experimental data for the cleavage rate of EcoRV (Jeltsch and Pingoud, 1998). The experimental value for K_ns is ∼2 × 10⁵ M⁻¹ per bp (Jeltsch and Pingoud, 1998), leading to D_∥/D ∼0.03.

FIGURE 3.

Comparison of theoretical (curve) and experimental (circles) results (Stanford et al., 2000) for the processivity ratio of EcoRV. The calculations assumed a DNA with 2L bp containing a centrally located absorbing site (other details are given in the caption of Fig. 2; K′_ns = 5.2 × 10³ M⁻¹ per bp). The protein molecule was initially located at one end of the DNA.

At higher NaCl concentrations, the nonspecific binding (assumed to have a major electrostatic component) is expected to be weakened, resulting in reduced values for K′_ns (Lohman, 1986). With K′_ns reduced to 1.2 × 10³ and 60 M⁻¹ per bp, the experimental data at 25 and 100 mM NaCl can also be reproduced well by the theoretical model. Specifically, at 25 mM NaCl, the experimental results for f_p were 0.29 ± 0.02, 0.18 ± 0.01, and 0.14 ± 0.03, respectively, for L = 54, 200, and 387 bp. The corresponding theoretical values for ηp_c(L) are 0.34, 0.20, and 0.10. A small underestimate for a long DNA substrate is expected, since the DNA is treated as straight in the theoretical model whereas a long DNA in the presence of NaCl will be curved. The curving reduces the distance between the two specific sites and thus may increase f_p.

To obtain exact solutions of the nonspecific-binding-facilitated diffusion model, the DNA and protein molecules are represented by the simplest geometrical shapes—cylinder and sphere, respectively. The reproduction of the experimental data is thus very satisfying. Yet what is worth emphasizing is the physical aspect of the model. Equilibration between the surface and bulk phases is explicitly introduced; a processive protein thus can transiently dissociate from the DNA and then rebind (Fig. 1). In contrast, in a recent theoretical work a dissociated protein molecule was assumed to be permanently lost and dissociation was assumed to occur just at the DNA ends (Belotserkovskii and Zarling, 2004). Another recent theoretical work (Coppey et al., 2004) specifically considered rebinding after dissociation in an empirical fashion. There is now mounting experimental evidence for such dissociation-rebinding events as proposed in the nonspecific-binding-facilitated diffusion model (Halford and Marko, 2004; Hannon et al., 1986; Houtsmuller et al., 1999; Phair and Misteli, 2000; Lever et al., 2000; Misteli et al., 2000; Gowers and Halford, 2003). Even the archetypical processive proteins, replicative DNA polymerases, have now been shown to undergo rapid exchange during replisome-mediated DNA replication (Yang et al., 2004; Joyce, 2004). In addition, Jeltsch and Pingoud (1998) presented experimental evidence that DNA ends are reflecting to EcoRV, supporting the assumption (Eq. 9) built into the nonspecific-binding-facilitated diffusion model.

Presence of obstacles on DNA surface

The idea of dissociation and rebinding can be critically tested if there is an obstacle on the nonspecific DNA. As proposed in the nonspecific-binding-facilitated diffusion model, a protein molecule upon encountering an obstacle on the DNA surface can dissociate to the surrounding region and rebind to the DNA in front of the obstacle. On the other hand, if surface sliding is the only route to a specific site, the protein will be blocked in its track and will not be able to reach the specific site. There appear to be many ways that obstacles can form. When protein concentration is in excess so that two or more protein molecules may be nonspecifically bound to the same DNA, they will serve as obstacles to each other for motion along the DNA surface. Jeltsch et al. (1994) and recently Kampmann (2004) have studied the effects on the cleavage rate of EcoRI by different obstacles, such as triple helix, specific DNA-binding proteins, DNA bend, and Holiday junction. It should be noted that cellular DNA is heavily covered by proteins (Hildebrandt and Cozzarelli, 1995).

An obstacle on a DNA can be treated as a stretch of DNA with an altered nonspecific binding constant, K_ns*, and an altered surface diffusion constant, D_∥*. A reduced D_∥* models an obstacle that stalls the movement of a protein, and D_∥* = 0 means that the movement is completely blocked. Suppose that an obstacle is located between z = L₁ and z = L₂. Over the obstacle, the equilibration between the surface and bulk phases becomes (see Eq. 5)

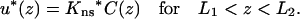(13a)

At the borders of the obstacle, the flux in the surface phase is continuous:

(13b)

Note that for a complete blocker (i.e., D_∥* = 0), the right-hand side is zero and one recovers the reflecting boundary condition in Eq. 9.

For a pair of obstacles symmetrically located between L₁ and L₂ and between −L₁ and −L₂ on an infinite DNA, the capture probability is again given by Eqs. 10a–c. Here the function p₁(z) is given by

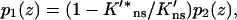(14a)

where

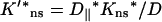and

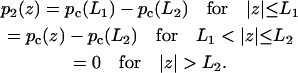(14b)

Note that Eq. 14b becomes Eq. 12 when L₁ = L and L₂ → ∞, thus a DNA with a finite length 2L in the present treatment is equivalent to the presence of completely-blocking obstacles (with ) occupying the regions z = L to ∞ and z = −L to −∞.

Similar to finite DNA length, obstacles serve to reduce the association rate. Jeltsch et al. (1994) observed up to fourfold reduction in the cleavage rate of EcoRI when obstacles are introduced at a location near the specific site on a 912-bp DNA. Such rate reductions can be obtained with reasonable choices of model parameters. For example, at K′_ns = 5.2 × 10³ M⁻¹ per bp, k(456 bp)/k^∞ = 0.87 for the finite DNA and k*/k^∞ = 0.11 in the presence of two completely-blocking obstacles occupying basepairs 9–25 on both sides of the specific site. As the obstacles are moved away from the specific site, the effect on the association rate constant k is reduced. Similarly, for longer DNA, the difference between k and k^∞ diminishes.

The effects of obstacles on the capture probability are also interesting. As Fig. 4 shows, a protein molecule experiences a significant drop in the capture probability behind an obstacle. For example, when an obstacle occupies basepairs 100–110 (measured from the specific site), p_c decreases from 0.94 in front of the obstacle to 0.17 behind the obstacle. The effects of the obstacle on p_c are moderated as it is moved away from the specific site. When the obstacle occupies basepairs 500–510, p_c decreases from 0.51 to 0.15. Kampmann (2004) has indeed obtained a significant lower but measurable processivity factor when two specific sites are located on different arms of a Holiday junction.

FIGURE 4.

The capture probabilities for an infinite DNA free of obstacles, a finite DNA with 2L bp, and an infinite DNA with an obstacle occupying z = L₁ to L₂. All the DNA molecules were symmetric with respect to z = 0, which means that there was also an image obstacle occupying z = −L₁ to −L₂. K′_ns = 5.2 × 10³ M⁻¹ per bp; other details are given in the caption of Fig. 2.

It is noteworthy that, relative to the capture probability for an infinitely long DNA free of obstacles, p_c is lowered behind the obstacle but actually raised in front of it. The latter result can be rationalized by the fact that the obstacle impedes the motion of the protein in both directions, both toward and away from the specific site. In the second case, the protein has less chance of dissociating from the DNA and thus more chance to be captured at the specific site. Terminating the DNA has the same effect of raising p_c for a protein that is initially in front of the termination point. As Fig. 4 shows, the capture probabilities for a finite DNA and for a DNA with an obstacle starting at the termination point are very close before the termination point. It is intriguing that, on a DNA with two specific sites, cleavage of the first site (resulting shortening of the DNA) actually has the consequence of increasing the capture probability for the second site!

Other applications

Treatments of other situations by the theoretical model may also be of interest. For example, a different question regarding a DNA with two specific sites is which site is cleaved first. A number of studies (Terry et al., 1985; Stanford et al., 2000; Jeltsch and Pingoud, 1998; Jeltsch et al., 1994) have produced such data, indicating that the site flanked by a longer DNA length is preferred. Qualitatively, this result can be rationalized by the increase in the rate constant k with DNA length, but a more careful treatment will require explicit consideration of both specific sites and will be presented in the future.

The case of a DNA with multiple obstacles may be adapted to study specific binding by a protein that is in excess (Shanblatt and Revzin, 1984). In this case multiple protein molecules may nonspecifically bind to the same DNA. Although each of these protein molecules can potentially reach the specific site, they interfere with each other as obstacles.

Another type of experiment that can be treated by the theoretical model is preferential cleavage assay (Taylor et al., 1991), in which a DNA substrate pre-bound with a restriction enzyme is mixed with a competitor DNA. Cleavage of the pre-bound DNA is described by the capture probability p_c, whereas cleavage of the competitor is described by the bimolecular rate constant k. In this context, processivity is similar in spirit to substrate channeling in bifunctional enzymes.

In the present study the DNA is modeled as a rigid straight cylinder. As already noted, a long DNA in the presence of salt will be curved. The curving will reduce the distance between two sites on the DNA and likely increase the association rate and the processivity ratio. Supercoiling also has the effect of reducing the distance between two sites on a DNA, and indeed Gowers and Halford (2003) found that supercoiling leads to higher catalytic rates. It will be of interest to specifically model the effects of DNA curvature and supercoiling.

Enzymatic cleavage has been assumed to be diffusion-controlled. For EcoRI Wright et al (1999) found experimental evidence for diffusion control. If the reactive patch is treated as partially absorbing (with a radiation boundary condition), the present model can still be solved. The association rate constant k will be reduced by

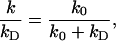(15)

where k_D is the diffusion-controlled rate constant as calculated earlier and k₀ is the reaction-controlled rate constant. The capture probability and processivity ratio are reduced by the same factor. If a catalytic reaction is not found to be rate-limited by binding to the specific site, Eq. 15 provides a possible solution for analyzing experimental data.

In summary, I have presented a physically appealing model for nonspecific-binding-mediated processivity that allows for exact solutions. The results quantitatively explain experimental data for the processivity ratio. Other applications providing additional critical tests of the model have been proposed.

APPENDIX

Here the solution for the steady-state distribution function C(ρ, z) is presented. In the bulk phase, C(ρ, z) satisfies the free diffusion equation (Eq. 2),

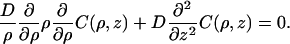(A1)

The equilibration between the surface and bulk phases is described by (Eq. 13a),

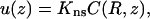(A2a)

except when obstacles are present. Here two obstacles are assumed to be present symmetrically in z = L₁ to L₂ and z = −L₁ and −L₂. In these regions

(A2b)

At the borders of the obstacles, the continuity conditions are (Eq. 13b)

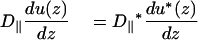(A3)

and C(R, z) continuous. The specific site is modeled as an absorbing patch (Eq. 3b):

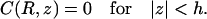(A4b)

For the rest of the DNA surface, the boundary conditions are (Eq. 6)

(A5a)

outside the obstacles and

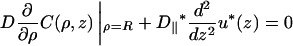(A5b)

within the obstacles.The solution of Eq. A1 has the form

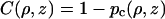(A6a)

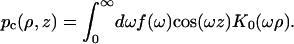(A6b)

To prepare for the determination of the coefficient f(ω), let us first consider the case where no obstacles are present. For specificity, variables for this case will bear a superscript ∞. Since the boundary conditions, Eqs. A4b and A5a, are of a mixed type, the constant-flux approximation (Shoup et al., 1981) will be adapted. In the present context, the approximation takes the form

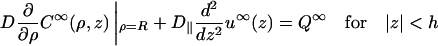(A7a)

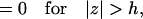(A7b)

where the constant Q^∞ is to be determined. Using Eqs. A2a and A6a, Eqs. A7a and A7b become

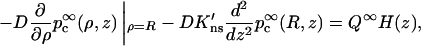(A7c)

in which H(z) = 1 for |z| < h and 0 otherwise. Taking the cosine transform and using Eq. A6b, one finds

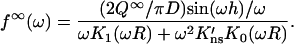(A8)

The constant Q^∞ is determined by requiring that the absorbing boundary condition (Eq. A4b) is satisfied on average by

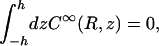leading to

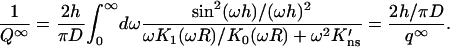(A9)

The explicit expression for q^∞ is given in Eq. 1b with x = ωR. The rate constant is the integration of Q^∞ over the reactive patch,

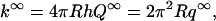(A10)

which is Eq. 1a.

In the presence of the obstacles, Eq. A7c becomes

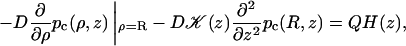(A11a)

where

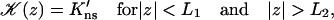(A11b)

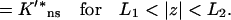(A11c)

To deal with the discontinuity of 𝒦(z) and account for the continuity of C(R, z) and 𝒦(z)∂C(R, z)/∂z at z = ±L₁ and z = ±L₂, consider the equation

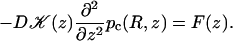(A12a)

Comparison of Eqs. A11a and A12a leads to

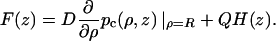(A12b)

It can be easily verified that the solution

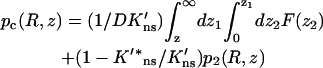(A13)

satisfies the continuity conditions. The function p₂(R, z) is related to the capture probability p_c(R, z) via Eq. 14b. After taking the cosine transform and using Eq. A12b, Eq. A13 takes the form

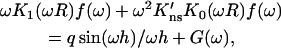(A14)

where

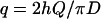and

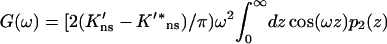corresponds to g(x) given in Eq. 10b. With f(ω) given by Eq. A14, the capture probability on the DNA surface is found to be

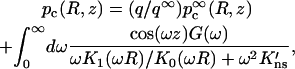(A15)

which is just the result given in Eq. 10a. Requiring that the absorbing boundary condition (Eq. A4b) is satisfied on average leads to Eq. 10c, with α = q/q^∞. Finally, the rate constant is (Eq. A10)

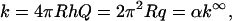(A16)

which is just Eq. 11.