Disruption of Protein-Mediated DNA Looping by Tension in the Substrate DNA

Abstract

Protein-mediated DNA looping is important in a variety of biological processes, including gene regulation and genetic transformation. Although the biochemistry of loop formation is well established, the mechanics of loop closure in a constrained cellular environment has received less attention. Recent single molecule measurements show that mechanical constraints have a significant impact on DNA looping and motivate the need for a more comprehensive characterization of the effects of tension. By modeling DNA as a wormlike chain, we calculate how continuous stretching of the substrate DNA affects the loop formation probability. We find that when the loop size is >100 bp, a tension of 500 fN can increase the time required for loop closure by two orders of magnitude. This force is small compared to the piconewton forces that are associated with RNA polymerases and other molecular motors, indicating that intracellular mechanical forces might affect transcriptional regulation. In contrast to existing theory, we find that for loops <200 bp, the effect of tension is partly dependent on the relative orientation of the DNA-binding domains in the linker protein. Our results provide perspective on recent DNA looping experiments and suggestions for future micromechanical studies.

INTRODUCTION

Protein-mediated DNA loops occur when two operator sites on a single DNA molecule are connected via a linker protein or multi-protein complex (Fig. 1). DNA looping is typically associated with gene regulation and genetic transformation (Schleif, 1992). A number of prokaryotic operons have been studied in the context of DNA looping including ara, Gal, Lac, and λ-phage (Ptashne, 1992; Schleif, 1992). Many eukaryotic looping proteins have also been identified—examples include the progesterone receptor (Theveny et al., 1987), P53 (Stenger et al., 1994), and SP1 (Su et al., 1991). Loops may be relatively stable as in the Lac operon or transient as in eukaryotic transcription initiation complexes. Because DNA can be thought of as an inextensible polymer, tension, torsion, and other mechanical constraints acting on the substrate DNA will affect the loop formation process. This article focuses on how a continuous tensile load on the substrate DNA affects the loop formation time.

FIGURE 1.

Statistical mechanics of protein-mediated DNA looping. (A) DNA looping as a two-state system. Three free energies determine the lifetimes of the looped and unlooped states: the energy of unlooped DNA, the loop energy, and the kink energy. The loop energy includes contributions from protein-DNA interactions and DNA bending. The kink energy is associated with the deformation of DNA exterior to the loop. (B) The kink angle specifies different looping geometries. Maximum kinking occurs in the hairpin loop (θ = 0°). Parallel alignment of operators results in no kinking (θ = 180°).

Initial evidence of loop formation was provided by gel shift assays (Dunn et al., 1984). Since then, many experiments have focused on the peculiarities of the DNA-protein interactions involved in looping. Using Lac repressor (LacR) as an example, kinetic studies have elucidated equilibrium constants (Oehler et al., 1990) and crystallographic data have provided details of the molecular interactions (Friedman et al., 1995; Lewis et al., 1996). Coarse-grain simulations have determined the zero-temperature structure of a protein-mediated loop (Balaeff et al., 1999), which can be extended into full-atom models of the binding complex (Balaeff et al., 2004). Cyclization experiments (Shore et al., 1981; Zhang and Crothers, 2003a), and theory (Levene and Crothers, 1986; Rippe et al., 1995; Shimada and Yamakawa, 1984; Zhang and Crothers, 2003b) have investigated the effects of loop size and intrinsic curvature on looping in the absence of linker protein(s). Other studies on the mechanics of protein-mediated looping measure the effect of helical-operator alignment (Dunn et al., 1984; Muller et al., 1996), operator separation (Hsieh et al., 1987; Muller et al., 1996; Ringrose et al., 1999), and superhelical organization (Bussiek et al., 2002; Huang et al., 2001; Klenin and Langowski, 2001). Single-molecule experiments now permit the direct observation of individual looping events (Finzi and Gelles, 1995). In addition, recent single-molecule experiments demonstrate the sensitivity of looping to mechanical constraints, suggesting that tension or torsion may play an important role in gene regulation (Lia et al., 2003).

Our analysis of the effect of tension on protein-mediated DNA loop formation is based on a wealth of research concerning the elasticity of ds-DNA. In particular, micromechanical force-extension experiments have verified the applicability of Kratky and Porod's wormlike chain (WLC) model of DNA (Bustamante et al., 1994; Kratky and Porod, 1949; Smith et al., 1992). Our theory is based on the WLC model and employs an approach that is an extension of Marko and Siggia's analysis of how tension affects protein binding (Marko and Siggia, 1997). Our analysis differs from Marko and Siggia's in that in addition to considering the free energy of a wormlike chain, we quantify the relationship between tension and DNA alignment constraints imposed by protein binding. These additional considerations have implications for the interpretation of micromechanical experiments and for our understanding of the relationship between DNA structure and function. Since our analysis describes the formation of loops within longer DNA segments, it can be applied to loops of any size, provided that the adjacent DNA outside of the loop is longer than a persistence length.

The next section describes a statistical mechanical treatment of DNA looping. In the Results section, specific numerical results are presented for how tension, operator spacing, and DNA alignment affects the time required for loop formation to occur. The Discussion section provides perspective on the biological significance of our findings, particular with regard to micromechanical experiments.

THEORY

Loop formation depends on thermal fluctuations. In an unconstrained environment, DNA forms an entropically favorable Gaussian coil (Boal, 2002; Doi and Edwards, 1988). The conformation of the coil and with it the spatial location of the operators fluctuate thermally. This fluidity allows the operators to align for looping. However, as the DNA is stretched, it transitions from an isotropic coil to an extended form. Because tension restricts the ability of DNA operator sites to diffuse randomly, it decreases looping probability. If DNA is stretched with enough tension, looping will be prevented. Given that thermal energy can bend DNA that is a persistence length long, the force scale over which DNA is extended is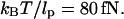

To determine how much tension is necessary to prevent the formation of protein-mediated DNA loops, we treat the interaction of linker protein and DNA as a two-state “looped” or “unlooped” system. In this representation, “looped” DNA refers to the instance in which one linker protein (or protein complex) forms a bridge between two specific sites on the same DNA molecule. Meanwhile, “unlooped” DNA refers to the case in which some protein may be bound to DNA (possibly at multiple sites), but no protein bridges exist (Fig. 1). As explained below, our two-state model addresses the effects of different loop sizes and binding geometries of the DNA substrate. As such, our analysis is applicable to recent DNA looping experiments. Torsional constraints are initially ignored, but will be revisited in the Discussion section.

Our analysis rests on computing the difference in free energy, ΔF, between looped and unlooped DNA, whereby we can account for the thermal fluctuations of the substrate DNA. The relationship between looped lifetime τ_l and unlooped lifetime τ is given by the thermodynamic expression for detailed balance,

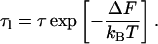(1)

As sketched in Fig. 1, there are three contributions to ΔF:

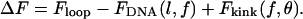(2)

F_loop represents the intrinsic energy of the DNA loop. It includes the free energy of protein-DNA interactions and the energetic cost of bending DNA into a loop. As explained below, the specific value of F_loop is not relevant for our analysis of the effect of tension. Meanwhile, F_DNA represents the intrinsic free energy of DNA that has no mechanical constraints other than tension. This energy is subtracted from ΔF because loop formation effectively reduces the length of DNA exposed to tension. F_DNA is a function of the loop length, l, and the applied tension, f. Lastly, the need for the protein-binding operators to orient themselves in a manner compatible with loop formation imposes internal and external geometrical constraints on the DNA. Whereas the interior geometric constraint affects the overall topology of the loop structure (Geanacopoulos et al., 2001), it is not included in our analysis because it is uncoupled to external tension. In contrast, the exterior angular orientation is coupled to externally applied tension. F_kink is the energy associated with this external coupling constraint. In addition to tension, F_kink is a function of the angle, θ, that is created between the two pieces of DNA entering the loop (Fig. 1). If the loop causes an antiparallel “hairpin” orientation between the two operators, then θ will be 0°. Conversely, if there is a parallel relationship between the operators, then θ will be 180°.

An accurate determination of the intrinsic free energy of the protein-mediated loop, F_loop is the subject of much recent research (Balaeff et al., 2004; Cloutier and Widom, 2004; Zhang and Crothers, 2003b). Because the WLC model assumes isotropic flexibility of DNA and ignores the possibility of sequence-dependent curvature, it cannot be used to accurately determine the bending energy within a loop. In addition, the specific contribution attributable to the protein-DNA interactions can vary substantially depending on the operator sequence and linker protein(s). Thus, it is beyond the scope of this article to explicitly determine F_loop. Instead, in our theory we assume that tension in the external DNA does not alter the DNA-protein contacts associated with the linker protein. Under this assumption, F_loop is independent of tension.

To compute the free energy of stretched DNA, F_DNA, we use the wormlike chain model, which is characterized by isotropic elasticity and smooth transitions in the chain's curvature. For a WLC, the only intrinsic parameter that needs to be specified is the persistence length, l_p. This length is the characteristic length over which a WLC bends in response to thermal forces. For DNA in typical ionic conditions, l_p is ∼53 nm or 156 bp (Bustamante et al., 1994). If x denotes the end-to-end extension of a DNA strand relative to its contour length, then the force-extension relationship for a WLC is (Marko and Siggia, 1995)

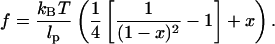(3)

F_DNA is the difference between the potential energy of a WLC and the work done by the tension, f, to stretch the chain. Thus,

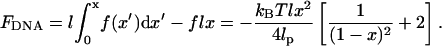(4)

It is important to recognize that F_DNA represents the relative change of free energy of the substrate DNA when it is shortened by looping. So in the context of DNA looping, Eq. 4 is valid for loop sizes that are both larger and smaller than the persistence length. The only constraint is that a small loop must exist in the context of a larger DNA strand so that tension is applied over a region that is longer than the persistence length.

It is harder to construct an exact expression for F_kink, the free energy associated with the orientational localization of the operator sites around the protein. Therefore, we construct an interpolated formula that matches the high and low force asymptotic solutions. The relevant force scale for deciding whether a given tension is small or large is 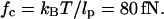At this critical tension, a wormlike chain extends 45% of its contour length. As explained below, for applied tensions much smaller than f_c, entropic effects dominate and the kink energy can be calculated by a second-order expansion of force-free equations. Meanwhile, for tensions much larger than f_c, the kink energy is primarily determined by the enthalpic cost of bending a wormlike chain into its kinked shape.

In the low force limit, DNA is an entropic spring and F_kink is equal to the loss of entropy created by the kink. Specifically, let 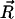denote the end-to-end vector of a wormlike chain and L denote its overall contour length. (Note that L is not the same as intraoperator distance and will drop out of the final expression for F_kink.) There are three degrees of freedom for the end-to-end vector of the chain, corresponding to a free energy of 3/2 k_BT in the thermodynamic limit. To second order, the free energy of an extended state is then

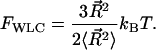(5)

The entropic relationship between tension and free energy gives

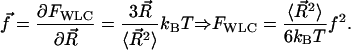(6)

The kink energy at low force, 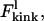is the difference in F_WLC for a nonkinked and kinked chain. Therefore,

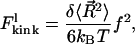(7)

where 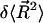represents the correction to the mean square end-to-end distance that is attributable to the kink.

To evaluate 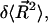note that 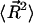can be written as

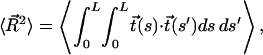(8)

where 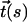represents the tangent vector as a function of contour length. In the absence of externally applied tension, wormlike chains are characterized by an exponential decay in the correlation of tangent vectors as a function of intervening contour length. Thus, in the presence of a single kink of angle θ (see Fig. 1), the correlation is described by

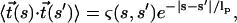(9)

where 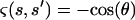if the segment between s and s′ contains the kink and 1 otherwise. If the kink is located at s = s₀,

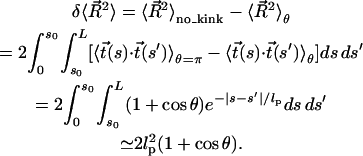(10)

In the last step, the approximation 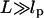is made, which is justified provided that tension on the DNA is applied at a point >53 nm (i.e., 156 bp) from the protein binding sites. Substitution of Eq. 10 into Eq. 7 yields

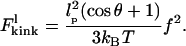(11)

Meanwhile, in the high force limit, we can ignore the effects of thermal fluctuations. (An unpublished variational approach confirms that the entropic contribution is not important for our analysis, because it is essentially independent of tension.) Thus in the high force limit, F_kink is simply the bending energy of two rigid rods that are anchored at the origin, make an angle of θ/2 with respect to the y axis and are pulled apart by tension that is directed along the x axis. With this model, equilibrium rod theory can be used to calculate the energy for each half of the kink. Specifically, for a curved rod, the bending energy per unit length is inversely proportional to the square of the radius of curvature. For a rigid rod to have the same bending modulus as a WLC, the constant of proportionality is such that a section of length l_p will contribute 1/2 k_BT to the bending energy if its radius of curvature is also l_p. Thus the infinitesimal kink energy is

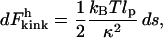(12)

where the radius of curvature, κ, is a function of the arc length. Conservation of energy requires that the capacity of tension to do work on the rod must equal the actual amount of work done plus the energy of bending the rod. Thus

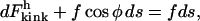(13)

where φ is the angle the tangent vector makes with respect to the x axis. Since κ is 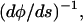Eqs. 12 and 13 yield

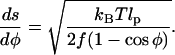(14)

Integrating Eq. 12 for the two sides of the kink and substituting Eq. 13 and then Eq. 14 gives

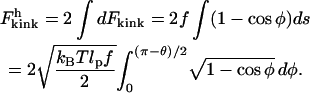(15)

Evaluation of the integral yields

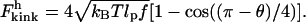(16)

Equation 16 shows that in the high force limit, the kink energy is proportional to the square root of tension. This relation arises because of a balance between two conflicting constraints associated with bending a rod. On the one hand, a gradual bend is preferable because the energy of bending is inversely proportional to the bending radius. On the other hand, a smaller bending radius is favorable, because it allows the external DNA to be stretched farther and thus increases the work that is done by the applied tension.

A standard interpolative formula that maintains the asymptotic limits is

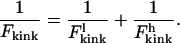(17)

By defining a dimensionless force, 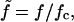and setting 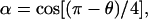trigonometric manipulations allows us to write our closed-form expression for F_kink,

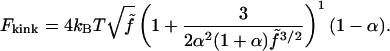(18)

Equation 18 has a relative error of <10% when compared to a more sophisticated variational approach (A. V. Tkachenko, unpublished).

RESULTS

Quantifying the disruptive effect of tension on looping time

For Eq. 1, we defined the loop lifetime, τ_l, and unlooped lifetime, τ. Since our focus is on the effects of tension, we choose to calculate the normalized time of loop formation, which we define as

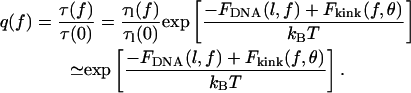(19)

In this expression, we utilize our prior assumption that F_loop is independent of tension and note that our values for F_DNA and F_kink are zero when the substrate tension is zero.

Both 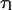and τ can be considered to be a function of the substrate tension, f. However, in the last equality of Eq. 19, we make the assumption that the loop lifetime is unaffected by tension. From a theoretical standpoint, for protein-DNA binding to be stable, the associated binding energy must be greater than k_BT (4.1 pN-nm). In addition, the protein-operator separation required for disassociation is unlikely to be much more than a nanometer. Thus the force needed to disrupt the lifetime of an existing protein-mediated loop is at least k_BT per nanometer. This means that >4 pN of tension is necessary to see an effect on 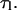Meanwhile, experiments show that 5–200 pN forces are necessary to disrupt existing biotin-avidin linkages (Florin et al., 1994; Merkel et al., 1999). Since all these forces are much larger than the forces we will be considering in our analysis of loop formation time, our assumption that is independent of tension is justified.

Our definition of normalized looping time provides a convenient statistic for measuring the effect of tension on protein-mediated DNA looping. Although the absolute rate of loop formation is dependent on the biochemical and structural details of the protein bridge, our calculation of normalized looping time just requires knowledge of the loop length, the angular orientation of the operators, and the tension applied to the substrate DNA. In the absence of tension, the normalized looping time is unity and it increases as tension is applied.

As explained in the previous section, tension has two effects on the energetics of loop formation. First, tension affects the free energy of the unlooped state (Eq. 4). Second, tension impacts the kink energy associated with spatial positioning of the binding sites in looped DNA (Eq. 18). Fig. 2 graphs the dependence of these two energies on applied tension as calculated from the WLC model.

FIGURE 2.

Free energies. (A) Free energy of unlooped DNA versus applied tension for DNA of varying length (Eq. 4). (B) Free energy of DNA kink versus applied tension for different kink angles (Eq. 18). The free energies were calculated using the wormlike chain model.

Fig. 2 A plots F_DNA versus tension. F_DNA represents the reduction in free energy of looped DNA caused by decreasing the length of DNA over which tension can be applied. For low tension (i.e., f < 80 fN), F_DNA is proportional to the square of the applied force. This is attributable to the entropically driven linear relation between tension and extension. However, for high tension (i.e., f > 80 fN), the entropic contribution to F_DNA is negligible and the force-energy relation becomes linear. For all values of tension, the free energy increases linearly with chain length, because tension specifies the relative extension of DNA rather than the absolute extension. For a 100 bp segment of DNA, the free energy is k_BT when the tension is 240 fN. The corresponding values for 200 bp and 500 bp DNA segments are 150 and 87 fN, respectively.

In Fig. 2 B, the kink energy, F_kink, is plotted as a function of tension for a variety of kink angles. As illustrated in Fig. 1, a kink angle of 0° is equivalent to a hairpin loop and imposes the most severe constraint on the DNA contour line. Thus it is associated with maximum kink energy. For a given tension, the kink energy decreases as the kink angle increases. Parallel-oriented operators produce the maximum kink angle of 180°. In this case, 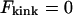because the operators provide a seamless transition in the contour of the DNA that is external to the loop. For kink angles of 0, 45, and 90°, the tensions that yield a kink energy of 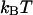are 150, 250, and 875 fN, respectively.

From Eqs. 4, 18, and 19, we can determine how the normalized looping time, q, is affected by tension. Fig. 3 shows plots of q versus tension for DNA loops ranging in size from 100 bp to 1 kbp. Fig. 3 A displays the results when there is no protein-induced kink in the looped DNA (θ = 180°), whereas Fig. 3 B shows the results for a hairpin orientation of the operators (θ = 0°). Fig. 3, A and B, show three significant trends. Both sets of graphs show that the time for loop formation increases dramatically with tensions of a few hundred femtonewtons. Since tension explicitly determines the relative extension of a WLC, all the graphs show that long loops are more sensitive to tension than short loops. Lastly, Fig. 3 B shows the hairpin loop configuration is more sensitive to tension than its nonkinked counterpart. This latter effect is especially pronounced for small loops demonstrating that kink energy can make a substantial contribution to looping rates. However, when the kink angle is >90° or the loop size is >500 bp, Fig. 2 shows that the kink energy will not make a prominent contribution to the energetics of loop formation.

FIGURE 3.

Loop formation time. (A) Normalized loop formation time versus tension for parallel configuration of operators (θ = 180°, Eqs. 4, 18, and 19). The legend indicates loop sizes. The normalized loop formation time is defined so that it is unity when tension is zero. In this way, the specific effects of tension are isolated. (B) Normalized loop formation time versus tension for hairpin looping configuration (θ = 0°).

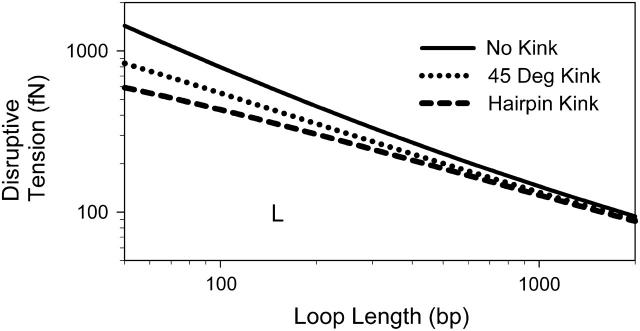
Fig. 4 summarizes the effect of tension on looping. It plots the tension that is needed to increase the loop formation time by a factor of 100. This 100-fold increase in looping time occurs when the sum of 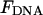and F_kink equals 4.6 k_BT. The graph reflects the key dependencies discussed above. Namely, the formation of large loops is disrupted with small force and the formation of small loops is sensitive to the kink energy. For loops 100 bp long, a 100-fold increase in looping time occurs with a tension of 800 fN for nonkinked DNA (θ = 180°), 550 fN for partially kinked DNA (θ = 45°), and 430 fN for hairpin conformations (θ = 0°). The corresponding tension for 1 kbp loops are 145, 133, and 128 fN, respectively. By focusing on the tension required to increase the loop formation time by a factor of 100, we imply that a reduction in looping probability to 1% of the wild-type value is biologically relevant. To justify this sentiment, we note that Lac repressor has 1–2% functionality when LacR-mediated looping is prevented by removing both auxiliary operators from the Lac operon (Oehler et al., 1990). Yet it is widely accepted that removal of these operators is tantamount to eliminating the regulatory ability of LacR. In addition, it should be noted that because of the exponential relationship between the loop formation time and ΔF, a plot of the force required to increase the loop formation time by 1000 would not differ significantly from Fig. 4.

FIGURE 4.

Disruptive tension, defined as the tension that increases looping time by a factor of 100 (calculated by solving Eq. 19 for q = 100). Each line represents a different kink angle as indicated by the legend.

The effect of loop size on the static and dynamic stability of loop formation

Until now, we have ignored how the intrinsic loop energy, 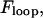is affected by loop size. To gain a more comprehensive understanding of the mechanics of loop formation, it is instructive to combine our equations with prior research on the relationships between loop size, loop energy, and the absolute rate of loop formation. In particular, there is an ideal loop size, 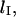that maximizes the rate of loop formation. For loops smaller than 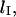the energetic cost of bending DNA constrains the looping rate. Meanwhile, for large loops, the huge number of possible DNA conformations decreases the likelihood of loop formation. Thus 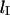represents a balance between the enthalpic and entropic energies of loop formation. The notion of effective concentration, j_M, helps to formalize the concept of ideal loop size. j_M is a measurement of the likelihood that two operators, O₁ and O₂, on the same strand of DNA will make contact (Rippe et al., 1995). j_M is a function of the distance between O₁ and O₂ and is maximized when the operator separation equals l_I.

An approximation for j_M that is based on the wormlike chain can be used to estimate l_I. For wormlike chains with intraoperator distances <1000 bp, Shimada and Yamakawa (1984) derive

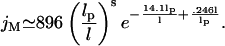(20)

To determine how the effective operator concentration is affected by tension, the prior expression for j_M is divided by the normalized looping time. The results are shown in Fig. 5 A. To maintain consistency with the derivations of Eq. 20, θ is chosen to be 81°, which is the kink angle that minimizes the bending energy of a homogenous WLC (Yamakawa and Stockmayer, 1972). As the tension is increased, the effective concentration decreases because it becomes harder for the operator sites to make contact. Moreover, tension causes the effective concentration peak to shift to the left and therefore decreases the ideal loop size. This latter trend is quantified in Fig. 5 B, which shows that the ideal loop size is 530, 320, 210, and 160 bp for tensions of 0, 200, 500, and 1000 fN respectively. Equation 20 applies for idealized WLC that have a uniform, isotropic bending modulus and no intrinsic curvature. In addition, Eq. 20 ignores the 10.5 bp periodicity seen in looping probability for small loops that is due to helical operator alignment (Dunn et al., 1984; Muller et al., 1996). However, alternate models for effective concentration that take into account deviations from the wormlike chain approximation do not change the premise that ideal loop size is determined by balancing the effects of entropy and enthalpy. Thus our key result that ideal loop size decreases as continuous tension is applied still holds.

FIGURE 5.

Ideal loop size. (A) Effective concentration versus loop size for different values of applied tension (j_M/q, where j_M is given by Eq. 20 and q by Eq. 19. A kink angle of 81° is assumed). The effective concentration is a measurement of the likelihood for two unlooped operators to come into contact. Short loops have enthalpic limitations, whereas long loops have significant entropic costs. (B) Ideal loop size as a function of tension. The ideal loop size is the loop length that maximizes the effective concentration.

Although the preceding analysis focuses on the effect of applying a constant tension, RNA polymerase and other motor proteins associated with DNA are likely to impose transient forces on their DNA substrates. Given the stochastic nature of intracellular mechanics, it is illustrative to consider the stability of looping rate in response to fluctuations in applied tension. For this purpose, we define the looping sensitivity, S, as the normalized rate of change of looping time with force

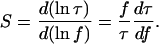(21)

In Fig. 6, S is plotted for loop lengths ranging from 100 bp to 1 kbp with θ equal to 81°. Fig. 6 demonstrates that S increases as the tension or loop size increases. Thus, just as small loops are favorable when there is a constant applied tension in the substrate DNA, the creation of small loops is also less affected by transient changes in tension.

FIGURE 6.

Looping sensitivity. Sensitivity of looping to fluctuations in applied tension, defined as the relative change in looping time per relative change in applied tension (Eq. 21). The kink angle is 81°. Each line represents a different loop length.

DISCUSSION

The theory of wormlike chains has proved remarkably useful for understanding DNA mechanics. Force-extension curves closely match theoretical predictions. Furthermore, the Brownian motion predicted by the WLC model can be used to infer the length of immobilized DNA constructs. In this article, we have extended the WLC model to the case where protein-mediated looping can dynamically change the effective length of a DNA molecule. Our results indicate that the formation of protein-mediated DNA loops is particularly sensitive to tension in the substrate DNA. For loops >100 bp, we predict that less than a piconewton of tension is needed to disrupt loop formation.

The validity of our model

Our model is based on the premise that DNA loops can be characterized by a two-state “looped” or “unlooped” system. The possibility for dynamic changes in loop structure challenges this assumption. One example of a dynamic change is the possibility of partial disassociation of protein-DNA contacts as tension is applied to the substrate DNA. In the case of nucleosomes, 10 pN of tension results in reversible unraveling of DNA from the histone core (Brower-Toland et al., 2002). Another possibility for a dynamic change is that the linker protein may bend in response to externally applied tension, thereby altering the kink angle and the width of the protein bridge. By adding an additional variable for the force dependence of the protein bridge width and allowing the kink angle to be a function of tension, our theory can be modified to account for partial protein-DNA disassociation and protein flexibility. However, since our results indicate that subpiconewton tension is typically sufficient to disrupt loop formation, adjustments to our theory are meaningful only if they relate to a change in the response to subpiconewton tension. With this in mind, a consideration of the data on nucleosome unraveling suggests it is not necessary to compensate for the partial disassociation of protein-DNA contacts. It is also quite possible that protein flexibility can be ignored because the internal strain of the loop prestresses the protein bridge. In the case of the lactose repressor, this stress is estimated to be 15 pN (Balaeff et al., 1999). Prestressing the flexible portions of the linker protein limits additional distortions due to externally applied subpiconewton tension.

A shortcoming of our model is that we do not explicitly consider the effect of torsional strain. The extent to which torsion affects looping depends on the helical flexibility of the linker protein, sequence-dependent curvature between operator sites, and twist-induced conformational changes of the substrate DNA. Given the complex response of DNA to torsion, a quantitative prediction on its effect on looping is beyond the scope of this study. However, a few qualitative statements can be made. For instance, loop formation rates are known to depend on the helical alignment of the two operators (Dunn et al., 1984; Muller et al., 1996). Because of DNA's 10.5 bp helical periodicity, proper phasing of operators improves the capacity for simultaneous binding of a linker protein. One might imagine that as torsional stress is applied, the helical alignment of operators could be rotated in a way that either favors or disrupts loop formation. Indeed, for small torsional loads, energy is transferred entirely into twist. However, micromechanical measurements show that as the excess linking number, s, increases beyond .01, torsional stress is partly converted into writhe (Strick et al., 1996). That is, once DNA is twisted more than one turn per kilobase, the DNA backbone starts to twist around itself, forming supercoiled DNA. Since the rotational persistence length of DNA is ∼220 bp, a linking deficit of .01 would correspond to &1t;1/4 of a helix turn per rotational persistence length. Thus, it is unlikely that torsion can meaningfully affect the helical operator alignment by twist alone. Rather, the combined effects of twist and writhe need to be considered.

Twist and write are not the only mechanisms whereby torsion might affect looping. Interestingly, it appears torsion alters the apparent persistence length of DNA. For s = ±.01, Strick et al. (1996) report the apparent persistence length of DNA is 35 nm. This suggests torsion may affect looping by changing DNA's response to bending forces and thermal fluctuations. In the context of our theory, a smaller persistence length would increase the force needed to extend DNA and therefore make looping less sensitive to tension.

A final consideration of our use of the WLC model is that we ignore the way in which tension can affect the microscopic structure of DNA. Stretching DNA tends to unwind the double helix (Marko, 1997) and can induce conformational changes in the basepairing architecture (Cluzel et al., 1996; Smith et al., 1996). However, 10 pN of tension are needed to see a change in the contour length of DNA associated with DNA unwinding, and 65 pN is necessary to induce a major structural transformation. Therefore, tension-induced microscopic structural change can be ignored for the subpiconewtron range of tension we believe will typically prevent loop formation.

Micromechanical experiments

Single-molecule micromanipulation experiments provide an ideal platform for testing our theoretical predictions. Finzi and Gelles (1995) were the first to observe looping of single DNA molecules. However, their observations focused on DNA looping in the absence of tension. In recent years, a number of optical and magnetic techniques have been developed for applying force and torsion on single molecules (Bryant et al., 2003; Strick et al., 2000). These advances will likely permit an experimental determination of the relationship between loop formation rate and mechanical tension.

Although there is currently not enough published experimental data to make a complete quantitative comparison to our theory, recent experiments with Gal repressor (GalR) provide evidence that mechanical constraints affect looping rates (Lia et al., 2003). Lia et al. find that in the presence of heat-unstable nucleoid proteins (HU), looping occurs when a tension of .88 pN and a linking deficit of s = −.03 is applied to the substrate DNA. Because they were unable to observe looping in the absence of HU, Lia et al. assert that HU is required for looping. Since looping results in a reduction of the tether length by 55 nm rather than the 38 nm intraoperator distance, Lia et al. propose an antiparallel (hairpin) structure for the loop. In addition, Lia et al. use the 55 nm length reduction to extrapolate a force-free loop formation time of 0.1 ms. Lastly, Lia et al. present conflicting results concerning the inhibitory activity of single-stranded binding protein (SSB). SSB inhibits looping in their single molecule experiments, but does not appear to affect bulk measurements of looping in force-free constructs.

Our theory supports some of Lia et al.'s conclusions, but questions others. With regard to whether or not a hairpin loop is formed, Eq. 18 can be used to determine the excess shortening of the construct attributable to a hairpin kink (θ = 0°). If we take the effective persistence length to be 35 nm (as experimentally determined for torsionally stressed molecules (Strick et al., 1996)) we find that the excess shortening is 14 nm. This agrees well with the measured value of 17 nm, especially when the width of the protein bridge is considered. On the other hand, our theory predicts that a tension of .88 pN essentially eliminates looping for Lia et al.'s intraoperator spacing of 113 bp. Indeed, their 0.1 ms extrapolated looping time for unstretched DNA is at odds with Finzi and Gelles' (1995) determination that Lac repressor forms 305 bp loops within unstretched DNA in ∼80 s. To explain this discrepancy, our theory suggests another factor is needed that shortens the effective distance between operator sites. Lia et al.'s (2003) proposal that HU bends the DNA in between the operator sites provides an explanation for how the effective intraoperator distance can be shortened. According to our theory, if we take the effective intraoperator spacing to be 50 bp after HU binding and again use 35 nm as the effective persistence length, then Lia et al.'s determination that the looping time at .88 pN is 17.7 s translates into a force-free looping time of 100 ms. This is in much closer agreement to Finzi and Gelles' work, but is still off by more than two orders of magnitude. It may be that an even smaller value should be chosen for the effective intraoperator spacing. Other factors that may contribute to the apparent discrepancy in looping rate between the two experiments include dissimilar intraoperator sequences having different tension-free j factors and LacR having different kinetic properties than GalR.

Besides providing an alternate value for the force-free looping rate of GalR, our theory offers a new explanation for why SSB does not affect Lia et al.'s (2003) bulk measurement of looping in force-free constructs. In contrast to Lia et al.'s explanation that SSB cannot competitively inhibit HU binding at zero tension, we wonder whether HU binding is necessary for looping of tension-free substrate DNA. It could be that although SSB and HU compete equally well for binding sites in stretched and unstretched DNA, competitive binding by SSB is only detectable when the tension in the substrate DNA is sufficient to prevent looping of an unbent DNA construct. To distinguish between these two hypotheses, a transcription assay that considers looping in supercoiled constructs in the absence of HU and SSB would be helpful (transcription assay results for other conditions are displayed in Lia et al.'s Fig. 5).

Lia et al.'s pioneering experiments provoke many questions about the role of mechanical constraints in DNA looping and motivate future experiments. Combining single-molecule analysis of tension with molecular manipulation of intraoperator sequence would permit insight into overall loop structure in cases where other structural techniques may be problematic. For instance, additional data quantifying the rate of GalR looping for a variety of tensions and intraoperator spacing would help to resolve whether HU alters the effective intraoperator distance by bending the intervening DNA. Meanwhile, bulk experiments with LacR (Mehta and Kahn, 1999) and SfiI (Watson et al., 2000) have demonstrated that by varying the intraoperator sequence, multiple looping geometries are possible for the same linker protein. Our analysis of the kink energy and its response to tension provides the theoretical framework for distinguishing the sequence-dependent orientation of looping operators in micromanipulation experiments. These experiments would complement other genetic, simulation, and atomic force microscopy visualization techniques for studying looping geometry (Geanacopoulos et al., 2001; Virnik et al., 2003).

Tension could act as a genetic switch

In a number of prokaryotic systems, such as the Lac operon, experimental evidence suggests that DNA looping prevents RNA polymerase from transcribing DNA that is within and downstream of the loop (Oehler et al., 1990). Meanwhile, in eukaryotes transient looping between the promoter and upstream activators is often needed to initiate transcription (Ptashne and Gann, 2002). Therefore, any mechanical constraint that disrupts loop formation can play a significant role in gene regulation. In particular, since we have shown that less than a piconewton of force may be sufficient to prevent the formation of loops, it appears that tension could act as a molecular switch that controls the much larger forces associated with the processive motion of RNA polymerase. Since RNA polymerase can exert forces >25 pN before it stalls (Wang et al., 1998), a “substrate tension switch” would offer a mechanical advantage of a couple orders of magnitude. By providing a molecular mechanism for mechanotransduction, DNA looping might play a role in converting extracellular mechanical stress into gene regulatory signals (Liu et al., 1999). This possibility is supported by the experiments of Maniotis et al. (1997), which show that mechanical stress can be transferred into the nucleus. Given the complex geometry of a living cell and the continuous regulation of DNA conformation, the possibility that tension may play an important role in gene regulation should not be ignored.

CONCLUSION

We have shown with a free-energy calculation based on the wormlike chain model for dsDNA that tension in the substrate DNA can significantly disrupt the formation of protein-mediated loops. Generally, forces of the order of 200 fN have significant effects, possibly providing a mechanical mechanism for the control of gene expression. Based on our analysis of recent micromechanical experiments, we have suggested future experiments that relate biological function to mechanical constraints and probe the structure of protein-DNA complexes.