Domain Formation Induced by the Adsorption of Charged Proteins on Mixed Lipid Membranes

Abstract

Peripheral proteins can trigger the formation of domains in mixed fluid-like lipid membranes. We analyze the mechanism underlying this process for proteins that bind electrostatically onto a flat two-component membrane, composed of charged and neutral lipid species. Of particular interest are membranes in which the hydrocarbon lipid tails tend to segregate owing to nonideal chain mixing, but the (protein-free) lipid membrane is nevertheless stable due to the electrostatic repulsion between the charged lipid headgroups. The adsorption of charged, say basic, proteins onto a membrane containing anionic lipids induces local lipid demixing, whereby charged lipids migrate toward (or away from) the adsorption site, so as to minimize the electrostatic binding free energy. Apart from reducing lipid headgroup repulsion, this process creates a gradient in lipid composition around the adsorption zone, and hence a line energy whose magnitude depends on the protein's size and charge and the extent of lipid chain nonideality. Above a certain critical lipid nonideality, the line energy is large enough to induce domain formation, i.e., protein aggregation and, concomitantly, macroscopic lipid phase separation. We quantitatively analyze the thermodynamic stability of the dressed membrane based on nonlinear Poisson-Boltzmann theory, accounting for both the microscopic characteristics of the proteins and lipid composition modulations at and around the adsorption zone. Spinodal surfaces and critical points of the dressed membranes are calculated for several different model proteins of spherical and disk-like shapes. Among the models studied we find the most substantial protein-induced membrane destabilization for disk-like proteins whose charges are concentrated in the membrane-facing surface. If additional charges reside on the side faces of the proteins, direct protein-protein repulsion diminishes considerably the propensity for domain formation. Generally, a highly charged flat face of a macroion appears most efficient in inducing large compositional gradients, hence a large and unfavorable line energy and consequently lateral macroion aggregation and, concomitantly, macroscopic lipid phase separation.

INTRODUCTION

The binding of water soluble proteins to lipid membranes is often mediated by electrostatic interactions between the proteins' basic domains and acidic lipids. Upon adsorption onto a mixed membrane, consisting of negatively charged and neutral lipids, a peripheral protein may induce local changes in lipid composition at the binding site. This protein-induced lipid “demixing” is due to the lateral fluidity of the membrane, and hence the ability of charged lipids to migrate and adjust their concentration at the adsorption site, so as to optimize the electrostatic interaction strength between the protein and the membrane. Experimental evidence for this kind of lipid segregation has been reported for various systems; e.g., the binding of polylysine (Franzin and Macdonald, 2001; Roux et al., 1988), cardiotoxin II (Carbone and Macdonald, 1996), cytochrome c (Heimburg et al., 1999), and model peptides (Gawrisch et al., 1995) onto monovalently charged membranes, as well as membranes containing multivalent lipids (Gambhir et al., 2004; Rauch et al., 2002).

Segregation of lipids in mixed fluid membranes can also occur spontaneously, in the absence of bound proteins, as a result of direct lipid-lipid interactions, i.e., due to stronger attraction between like species as compared to that between different lipid molecules. If one of the lipid components in the mixture carries electrically charged headgroups, then electrostatic repulsion between these headgroups will oppose lipid demixing. In this case lipid segregation is only possible if the nonelectrostatic interlipid forces between like species are strongly attractive, strong enough to overcome the electrostatic repulsion. Nonelectrostatic attraction between lipids could arise, for example, from a length mismatch (or structural difference) of the lipid tails of the different species (Lehtonen et al., 1996), or from distinct intermolecular headgroup interactions, as found, for instance, by Garidel and Blume (2000a,b). As in any nonideal mixture, if the net average attraction between like lipids is strong enough, the membrane may undergo a thermodynamic phase separation, whereby the membrane splits up into lateral domains of different lipid compositions, as is the case, for instance, in raft-forming systems (Brown and London, 1998).

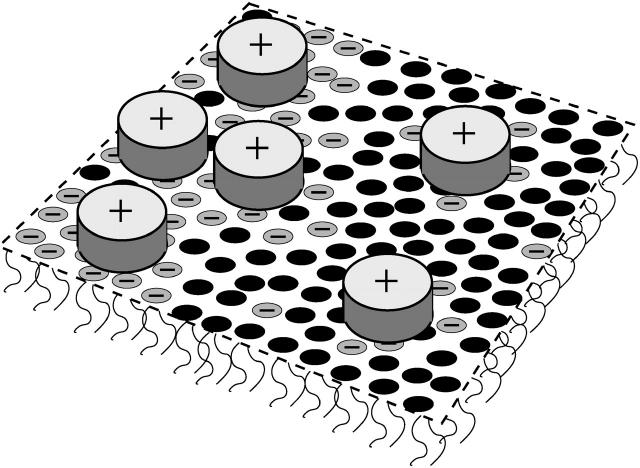
Consider again a binary lipid membrane, composed of charged and neutral lipids, in which the nonelectrostatic interactions between like species favor lipid demixing. The demixing tendency of this system can be enhanced by increasing the salt concentration in solution, or (in the case of acidic lipids) by lowering the pH, so as to screen the electrostatic repulsion between charged lipids, thus amplifying the net average attraction between like lipid species. Similar electrostatic screening can be provided by, say, positively charged peripheral proteins that electrostatically adhere and sequester the negatively charged lipids of a mixed membrane. In fact, multivalent proteins are expected to provide efficient electrostatic screening, possibly inducing phase separation in the protein-dressed membrane, i.e., the appearance of membrane domains that are rich in proteins and oppositely charged lipids, coexisting with protein-poor domains containing a smaller fraction of charged lipids, as schematically illustrated in Fig. 1. This qualitative scenario appears consistent with the experimental results reported by Hinderliter et al. (2001), pertaining to the binding of the charged peripheral protein, synaptotagmin I C2A motif, to a mixed phosphatidylcholine/phosphatidylserine bilayer. It was also found that minor chemical variations of the uncharged lipid, such as changing the acyl chain length or the degree of unsaturation, have pronounced effects on the protein-induced tendency for domain formation (Hinderliter et al., 2004). Notably, the modifications of the lipid structure involved nonelectrostatic properties, suggesting that the ability of the adsorbed proteins to induce membrane domains is an indirect, membrane-mediated, effect.

FIGURE 1.

Schematic illustration of a charged, two-component lipid membrane, consisting of neutral and negatively charged lipids. Binding of oppositely charged proteins via electrostatic interactions induces domain formation. Highly charged membrane regions are also enriched in adsorbed proteins. The shape of the proteins is depicted as disk-like.

Several theoretical studies have addressed the phenomenon of protein-induced domain formation in membranes. These include lattice models that do not explicitly account for electrostatic interactions (Netz, 1996), and mean-field models that describe electrostatic interactions in an approximate fashion (Heimburg et al., 1999; Denisov et al., 1998). None of these studies, however, has considered the role of lipid nonideality, which, as explained below, plays a central role in the phase behavior of the dressed membrane. More relevant in this context are the Monte Carlo lattice simulations of Hinderliter at al. (2001, 2004). Although electrostatic interactions do not appear explicitly in this model (but are rather lumped into the lipid-lipid and lipid-protein interaction constants), the simulations clearly indicate that protein adsorption indeed enhances domain formation. Of particular interest here is that the lipid-lipid interaction parameters used to fit the experimental results reported in this work correspond to effectively attractive interaction between lipids of the same kind. In other words, domain formation was found to take place provided lipid demixing is nonideal (with interlipid interactions favoring demixing). Below we argue that nonideal lipid mixing (or, more precisely, “positive deviations” from ideality) is a necessary condition for thermodynamic instability, i.e., for lateral phase separation of the protein-dressed membrane.

As noted above, a key feature associated with the adsorption of a large and highly charged protein onto a mixed, oppositely charged, membrane, is its ability to sequester and thus simultaneously neutralize a large number (depending on the macroion's charge and size) of charged lipids. In a membrane containing initially a small fraction of charged lipids this process will result in a significantly higher concentration of these lipids within the protein's interaction zone, concomitantly generating a concentration gradient across its circumference. In other words, the adsorption of an isolated protein induces local demixing in the membrane whereby the lipid composition within the protein's interaction region is different from the lipid composition around this region. Attractive (nonelectrostatic) interactions between charged lipids facilitate this local demixing process but are not essential for its occurrence. Note also that this local demixing is very different from lateral phase separation (often referred to as “domain formation”) of the dressed membrane, as this later process is, in fact, a thermodynamic two-dimensional (2D) condensation transition involving the protein-lipid clusters. (The term “cluster” is used here for the adsorbed protein together with its “favorite lipid patch”). This condensation transition will only take place if the effective interaction between these clusters is attractive, and strong enough to overcome the concomitant loss of 2D translational entropy. Direct, nonpolar forces between the adsorbed proteins could perhaps provide such attraction in certain systems, but seem quite unlikely in the case of similarly charged proteins. Of special interest in this work and of special relevance to mixed, charged, membranes is another mechanism, namely, the membrane-mediated interaction between the adsorbed proteins.

The concentration gradient across the boundary of the protein adsorption site is associated with a line energy, proportional to the circumference length of interaction zone. Positive line energy will favor protein aggregation, because the circumference of two adjoining proteins is smaller than that of two isolated ones. (Ideal mixing obviously implies vanishing line energy.) It is not difficult to show that a necessary condition for positive line energy is that the net average interaction between like species is attractive, and that the magnitude of this energy is proportional to the square of the concentration gradient across the boundary of the adsorption zone and the extent of lipid nonideality; see May et al. (2002) and the Appendix. Qualitatively then, large and highly charged proteins can more easily induce domain formation in the dressed membrane, provided the lipid substrate exhibits a nonzero demixing propensity. It should be emphasized that under these conditions protein adsorption can induce domain formation even if the bare lipid membrane is uni-phasic. That is, lipid nonideality need not be strong enough to warrant phase separation in the protein-free membrane; protein adsorption can significantly amplify the demixing tendency.

These qualitative notions were mentioned in a recent study, which has also reported an approximate evaluation of the critical constants characterizing lateral phase separation in the dressed membrane (May et al., 2002). The thermodynamic stability of the lipid-protein membrane was characterized in terms of the spinodal equation for macroion-decorated binary membranes. The spinodal formalism has been applied to one specific (thin disk-like) protein model, using a simple two-state cell model scheme for calculating the electrostatic interaction free energy. More specifically, each protein has been associated with a membrane cell (whose size is inversely proportional to the surface concentration of proteins), with each cell divided into a central, “protein shaded” region, surrounded by an annular region of bare membrane. A step-function change has been assumed for the variation in lipid composition between the two regions. Despite its simplicity, this two-state model provides instructive qualitative insights concerning the role of the line tension associated with the boundary of the adsorption zone, the stability of the dressed membrane, and reasonable estimates of the critical constants for the particular protein model considered (see below).

Our main goal in this work is to demonstrate that protein-induced domain formation in lipid membranes depends sensitively on the structural characteristics of the adsorbed proteins. To this end we shall analyze the thermodynamic stability of mixed membranes covered by several different types of model proteins, distinguished by their overall shape (sphere versus disks) and the charge distributions over their membrane-facing surfaces. As we shall see, these protein shape characteristics have a pronounced effect on the stability of the dressed membrane. The nonelectrostatic lipid-lipid interactions within the membrane plane, as well as the electrostatic interactions involving the charged species, namely the charged lipids and the adsorbed (oppositely charged) proteins, are taken into account in a mean-field level. For the nonelectrostatic lateral interlipid interactions we use the random mixing approximation of regular solution (Bragg-Williams) theory (Evans and Wennerström, 1994). Electrostatic interactions are treated on the basis of nonlinear Poisson-Boltzmann theory. The separation of electrostatic and nonelectrostatic interactions allows us to study the influence of electrostatically mediated protein adsorption on membrane stability.

Our calculations are carried out for a microscopic-level cell model for the protein-membrane complex, similar to the model used by May et al. (2000) to calculate the electrostatic binding energy of a simple model (spherical) protein to a binary membrane composed of lipids lacking any nonelectrostatic interactions. Using the cell model for the protein-membrane complex we evaluate the free energy of the protein-dressed membrane as a function of membrane composition and protein coverage. The free energy is then used to calculate, numerically, the spinodal surfaces, defining the stability limits of the dressed membrane, including, in particular, the critical constants (interlipid interaction strength, as well as lipid composition and protein coverage) corresponding to the different protein geometries. The thermodynamic spinodal analysis used to this end is the same as in May et al. (2002).

Lipid-mediated attraction between electrostatically adsorbed proteins (or other peripheral macromolecules) is not the only possible mechanism for protein aggregation or domain formation in dressed lipid membranes. Another possibility, for example, is that direct nonpolar forces between the adsorbed proteins will favor their attraction, especially if no charges reside on their apposed surfaces. Peripheral proteins, though perhaps not to the extent of integral proteins, may also inflict elastic deformations to the underlying lipid membrane, whose magnitude is roughly proportional to the length of their circumference. Thus, protein-induced elastic perturbations of the lipid substrate may serve as yet another mechanism of protein lateral segregation. We have chosen to focus here on the lipid-mediated interaction between electrostatically bound proteins, because electrostatic binding of proteins to mixed-fluid lipid membranes is common to many biological systems and processes. Clearly, owing to the complex nature of both proteins and multicomponent lipid membranes, several interaction mechanisms may be simultaneously operative in a given system, possibly acting in different directions. Furthermore, the few model proteins considered in this study represent highly idealized structures, which hopefully provide an approximate realistic description of certain protein geometries. Thus, although the predictions of our analysis may help explain certain experimental findings, our goal here is not to describe the observed behavior of a specific experimental system but, rather, to emphasize the nontrivial coupling between the local compositional changes induced by electrostatic binding of proteins (of different structural characteristics) onto mixed lipid membranes and the thermodynamic phase behavior of the composite membrane.

THEORY

Free energy

Consider a flat, two-component, lipid layer in equilibrium with an adlayer of electrostatically bound proteins. For concreteness, suppose that the proteins are positively charged, and that one of the two lipid species carries a monovalent anionic headgroup while the other is electrically neutral. For simplicity we also assume that both lipids occupy the same cross-sectional area at the membrane plane, a_l per headgroup. At given temperature and solvent conditions, the thermodynamic state of the membrane is specified by two concentration variables. One is the mol fraction of charged lipids or, simply, the lipid composition φ; i.e., for φ = 0 the lipid layer is electrically neutral and for φ = 1 it is fully charged. The other variable is the (dimensionless) protein coverage, θ, expressing the ratio between the actual number of adsorbed proteins and their number at maximal membrane coverage. For θ = 0 no proteins are adsorbed, and for θ = 1 the membrane is completely covered with proteins.

The free energy of the protein-dressed lipid layer, f = f(φ, θ), measured per lipid molecule, depends on the membrane composition (φ) and protein coverage (θ). In the following, we express all energies in units of k_BT where k_B is the Boltzmann constant and T is the absolute temperature. We decompose the free energy of the dressed membrane into a sum of three contributions, which in the mean-field scheme adopted here reads

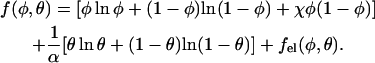(1)

The three terms within the square brackets account for the nonelectrostatic free energy of the mixed lipid layer, within the familiar random mixing approximation of regular solution theory for an incompressible binary fluid (here 2D) mixture with nearest-neighbor interactions. This mean-field level approach is widely used to describe thermodynamic properties, stability, and phase behavior of surfactant systems, polymer solutions, emulsions, and colloids (Evans and Wennerström, 1994). The first two terms here account for the translational (“mixing”) entropy of the mixture, whereas the third term accounts for the interaction energy associated with nonideal lipid mixing. The extent of nonideality is measured by χ, reflecting the different interaction potentials associated with like and unlike lipid species (see Appendix). Attractive interactions between lipids of the same species dominate for χ > 0, which for χ > χ_c become strong enough to drive lateral phase separation of the lipid layer. Calculation of the critical interaction strength, χ_c, is one of the main concerns of this work. Note that χ only accounts for next-neighbor nonelectrostatic interactions between the lipid molecules. The electrostatic interactions are long ranged; they are included in the last term of Eq. 1 and will be treated separately and in detail below. It should thus be noted that even if χ > 0, implying that the nonelectrostatic (e.g., intertail) interactions favor lipid demixing, the overall interaction potential, which is the sum of electrostatic and nonelectrostatic contributions, will be repulsive if the electrostatic repulsion between the charged lipid headgroups is sufficiently strong.

For a bare membrane with no (or fully screened) electrostatic interactions between lipids only the first contribution (in square brackets) in Eq. 1 is relevant, predicting the critical constant χ_c = 2, and the corresponding critical composition φ_c = 0.5 (Evans and Wennerström, 1994). This will be the only relevant contribution in the limit of high salt concentration where all electrostatic interactions are safely screened, no proteins are adsorbed, and the mixed lipid layer effectively behaves as an electrically neutral mixture.

The second contribution in Eq. 1 represents the ideal mixing entropy of the adsorbed protein layer, weighted by the protein/lipid size mismatch α = a_p/a_l where a_p denotes the (fixed) projected cross-sectional area per protein. Finally, the last contribution, f_el(φ, θ), accounts for all electrostatic interactions in the system, including lipid headgroup repulsion, lipid-protein interaction, and interprotein interaction. Our model for f_el(φ, θ), which we base on a detailed microscopic-level Poisson-Boltzmann approach, will be outlined after introducing our criterion for the thermodynamic stability of the membrane.

Thermodynamic stability

We use here the term “stable membrane” to describe a monophasic lipid-protein membrane. The critical point of the dressed membrane is characterized by the triade φ_c, θ_c, χ_c, marking the common minimum of the so-called binodal (χ_b(φ, θ)), and spinodal (χ_s(φ, θ)) surfaces. Within the χ ≥ χ_c region bounded by the binodal surface, the membrane is globally unstable, decomposing into two coexisting phases of different (lipid and protein) compositions. The spinodal surface, embedded within the global instability region (i.e., “surrounded” by the binodal surface) defines the limits of metastability. Between the two surfaces the membrane is metastable with only local stability. That is, upon an increase in χ at given φ and θ, the system first passes through the binodal and then through the spinodal surface, thereby proceeding from a stable via a metastable to an unstable region. Crossing the binodal surface marks the loss of global stability, whereas beyond the spinodal line local stability is lost as well. At the critical point, which corresponds to the smallest χ leading to an instability, the two surfaces coincide: χ_b(φ_c, θ_c) = χ_s(φ_c, θ_c) = χ_c (Safran, 1994).

Mathematically it is often more convenient to calculate the spinodal surface rather than the coexistence conditions determining the binodal surface. Because our main interest in this work is in the role of protein size and shape on the critical constants, most of our calculations will involve local stability (i.e., spinodal) analysis. Clearly, local stability requires the inequality

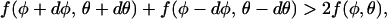(2)

to be fulfilled for any (small) changes dφ and dθ. At the spinodal, local stability breaks down, and Eq. 2 gives us the criterion (Landau and Lifshitz, 1976)

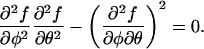(3)

Inserting into Eq. 3 the expression of the free energy per lipid, f(φ, θ) according to Eq. 1, we find for the spinodal

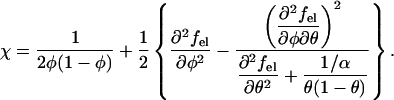(4)

Note that the second contribution to χ in Eq. 4 accounts for the electrostatic interactions of the system. In their absence (that is, for f_el(φ, θ) ≡ 0), Eq. 4 predicts the critical point χ_c = 2 and critical composition φ_c = 0.5, as noted earlier for an electrically neutral lipid membrane. Note also that in this case there is no coupling between the φ and θ dependent terms in Eq. 1, and the membrane is stable for all θ, in agreement with the stability condition ∂²f/∂θ² > 0.

Electrostatic free energy of the complex

Calculation of the spinodal according to Eq. 4 requires a model for the electrostatic free energy f_el(φ, θ) of a protein-dressed membrane. We use Poisson-Boltzmann theory for a symmetric 1:1 electrolyte to calculate this free energy, explicitly taking into account the microscopic structure of the protein and the lateral fluidity of the mixed lipid layer.

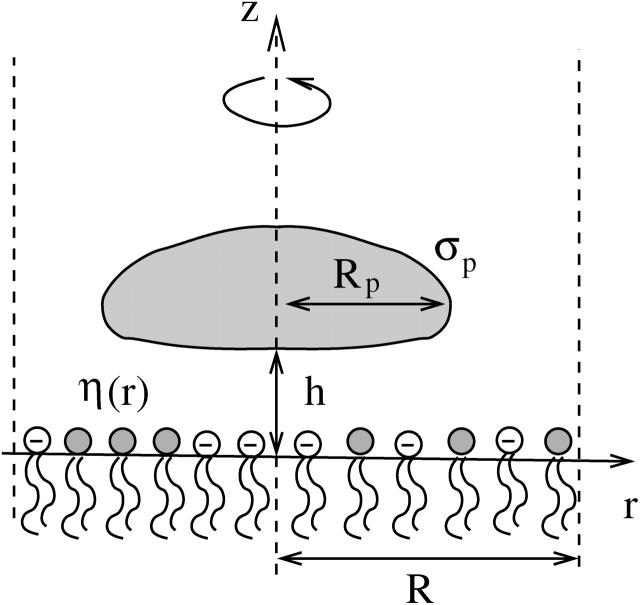
Consider a single, cylindrically symmetric protein, of maximal radial extension R_p, and hence of projected cross-sectional area 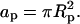On average, the distribution of lipids and proteins in the vicinity of the protein under consideration is radially symmetric. Within the mean-field level of our treatment it is thus appropriate to adopt a cell model, whereby each adsorbed protein is associated with a cylindrically symmetric cell of radius R > R_p and a corresponding membrane area A_c = πR². The cell radius is inversely proportional to the protein coverage θ = a_p/A_c = (R_p/R)², thus accounting (approximately) for interprotein interactions and the effects of protein concentration on lipid composition profiles. Note that the number of lipids in the unit cell is N = A_c/a_l = α/θ. A cross section through the unit cell of the protein-decorated lipid layer is depicted in Fig. 2.

FIGURE 2.

Cross section through the cylindrical unit cell of a protein-dressed lipid layer. The protein (shaded region) is assumed cylindrically symmetric around the z axis with projected radius R_p, local surface charge density σ_p, and minimal distance h to the membrane. The cell radius, R, determines the protein coverage through θ = (R_p/R)². The local mol fraction of negatively charged lipids within the mixed lipid layer is denoted by η(r).

Because of the fluid nature of the mixed lipid layer, charged lipids migrate toward the protein if this is energetically favorable. In other words, the composition of the lipid layer may locally adjust. To account for this possibility we introduce the local composition η = η(r), corresponding to the local fraction of charged lipids at distance r away from the axis of rotational symmetry. Recall that in our expression for f_el(φ, θ) the average composition, φ, is fixed. Thus, the local compositional profile, η, must fulfill the condition of charge conservation

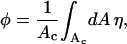(5)

where the integration is performed over the membrane area, A_c = πR², of the unit cell.

Our expression for the electrostatic free energy per unit cell, F_el(φ, θ) = Nf_el(φ, θ) = αf_el(φ, θ)/θ, is a straightforward extension of the Poisson-Boltzmann free energy, and consists of five contributions

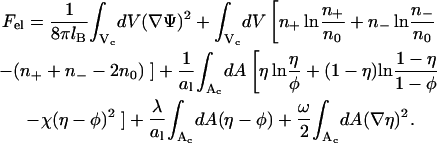(6)

The first term is the energy stored in the electrostatic field, expressed in terms of the dimensionless electrostatic potential Ψ = eΦ/k_BT (or, equivalently, Ψ = eΦ because in this work we express energies in units of k_BT; the elementary charge is denoted by e). The integral extends over the entire aqueous volume V_c of the cylindrical cell. The Bjerrum length, l_B = e²/4πɛ_w = 7.14 Å, describes the strength of the bare Coulomb interactions in water (with dielectric constant ɛ_w = 80). The second contribution accounts for the (ideal) mixing entropy of the mobile salt ions within the aqueous region of the unit cell where n₊ and n₋ denote the local concentrations of positively and negatively charged salt ions, respectively, and n₀ is their corresponding concentration in the bulk. Similarly, the third term is the (nonideal) demixing free energy of the lipids within the membrane, measured with respect to the uniform distribution η(r) ≡ φ; it includes (for χ ≠ 0) nearest-neighbor interactions between the lipids. The fourth term ensures the conservation of the number of charged lipids in the cell; see Eq. 5. The Lagrange multiplier, λ, enforces this constraint. Finally, the last term in Eq. 6 is the line tension contribution, resulting from compositional gradients within the lipid layer due to protein adsorption. The quantity ω, which measures the strength of the line tension contribution, is directly related to the lipid nonideality constant χ = Cω; with C = 3 if the lipid molecules organize as a triangular lattice and C = 2 for a square lattice configuration. The derivation of the relation χ = Cω is outlined in the Appendix. The value C = 3 will be used in this work. Note that the line tension contribution is expected (as we shall show in the Results section) to depend on the size, shape, and charge distribution over the protein surface, as well as on θ and φ.

It is worth mentioning at this point that the free energy, Eq. 6, does not include contributions from the inner hydrophobic regions (of dielectric constant ɛ_l ≈ 2) of the membrane and the protein. This is justified because the dielectric mismatch between these regions and the aqueous environment, ɛ_l/ɛ_w, is generally much smaller than d/l_D where d is the linear extension of the involved macroions—the membrane thickness or the protein radius—and l_D = (8 πn₀l_B)^−1/2 = 10 Å is the Debye screening length at physiological conditions.

At equilibrium, the free energy f_el(φ, θ) = F_el/N (see Eq. 6) is at its minimum with respect to the local ion concentrations, n₊ and n₋, and the local membrane composition, η(r). The minimization is subject to four boundary conditions. The first two,

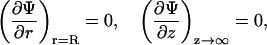(7)

express the symmetry at the rim of the unit cell (where the limit corresponds to modeling a single protein-dressed membrane). The other two,

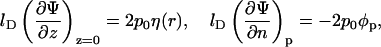(8)

relate the electric field to the local two-dimensional charge density at the membrane and protein surfaces. Specifically, at the lipid layer (z = 0) ɛ_w∂Φ/∂z = σ_l where σ_l = −ηe/a_l is the local surface charge density of the lipid molecules. Then, the first boundary condition in Eq. 8 follows from the definition of the dimensionless constant p₀ = 2πl_Bl_D/a_l. Similarly, the second boundary condition in Eq. 8 expresses the local (positive) surface charge density, σ_p = φ_pe/a_l, at the protein surface; we shall refer to φ_p as the effective composition of the protein; for φ_p = φ the average charge density of the membrane and of the protein have equal magnitude but opposite sign. Note also that ∂Ψ/∂n denotes the derivative of the electrostatic potential along the local normal to the surface of the protein, pointing into the aqueous environment. It should finally be mentioned that the two boundary conditions in Eq. 8 account for the low dielectric constants inside the membrane and protein, respectively. That is, terms proportional to ɛ_l/ɛ_w are neglected.

Minimization (in fact, functional minimization) of f_el(φ, θ) with respect to n₊, n₋, and η gives rise to the familiar Poisson-Boltzmann equation

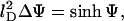(9)

which is a two-dimensional nonlinear partial differential equation for the (dimensionless) potential Ψ = Ψ(r, z)—note that Δ denotes the Laplacian in cylindrical coordinates Δ = ∂²/∂r² + (1/r)∂/∂r + ∂²/∂z²—that must be solved within the aqueous region, subject to the boundary conditions, Eqs. 7 and 8. In addition, the minimization leads to another differential equation, namely

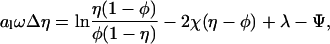(10)

whose solution determines the local composition η = η(r). For ω = χ/C = 0 it reduces to an algebraic relation previously derived by Harries et al. (1998). Generally, for ω ≠ 0, Eq. 10 constitutes a partial differential equation that must be solved at the lipid layer. Yet, because of the cylindrical symmetry of the unit cell Δη = η″ + η′/r where the prime denotes the derivative of η(r), and Eq. 10 reduces to an ordinary nonlinear differential equation for η(r). The two equations, Eqs. 9 and 10, are not independent from each other. Solution of the Poisson-Boltzmann equation, Eq. 9, requires to know η through the boundary condition on the lipid layer. Conversely, Eq. 10 contains the reduced potential Ψ. Hence, both equations must be solved self-consistently, including the determination of the Lagrange parameter, λ, that ensures Eq. 5 to be satisfied. The practical procedure to solve Eqs. 9 and 10 proceeds via a Newton-Raphson iteration scheme; that is, employing a linearization method upon which both equations transform into an iterative sequence of (coupled) linear equations (Houstis et al., 1985).

Isolated, protein-free membrane

Let us shortly discuss the case of a bare, protein-free lipid layer, where θ = 0. In this case the electrostatic free energy, Eq. 6, is given by the charging free energy of an isolated planar surface that can be calculated analytically within Poisson-Boltzmann theory (Evans and Wennerström, 1994). It is given by

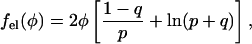(11)

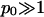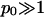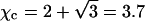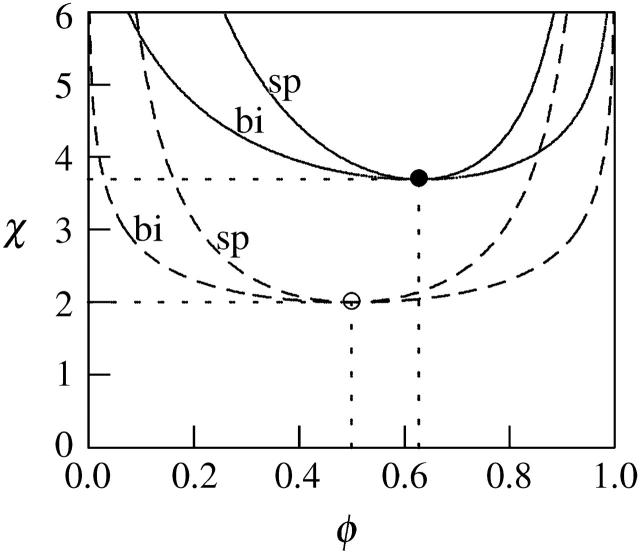
with q² = p² + 1 and p = φp₀. Recalling the definition p₀ = 2πl_Bl_D/a_l we note that typically (For example, for double-chained lipids a_l = 65 Ų and under physiological conditions l_D = 10 Å, implying p₀ = 6.9.) In the limit we find f″_el(φ) = 2p₀/q = 2/φ and the spinodal line, χ(φ) = 1/[2φ(1 − φ)] + 1/φ gives rise to the critical point and 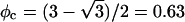(Gelbart and Bruinsma, 1997; May et al., 2002). In Fig. 3 we show both the spinodal and binodal for a charged lipid layer; calculated for a_l = 65 Ų and l_D = 10 Å, implying p₀ = 6.9. Also shown are the binodal and spinodal curves for a fully screened (effectively uncharged, corresponding to the limit 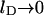) lipid layer. Several conclusions are worth mentioning. First, for any given φ both the binodal and spinodal move to higher χ, indicating increased stability for the charged compared to the (effectively) uncharged membrane. Hence, the electrostatic repulsions between the charged lipids increase the stability of the lipid layer. Second, the upshift of the critical point 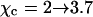is independent of p₀ if 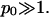And finally, the shift of the critical composition φ_c reflects the negligible size of the mobile salt ions compared to the cross-sectional area a_l of the lipids.

FIGURE 3.

The spinodal (“sp”) and binodal (“bi”) for a charged (solid lines) and for an uncharged (dashed lines) lipid layer. For the charged layer a_l = 65 Ų and l_D = 10 Å, implying p₀ = 6.9. The uncharged lipid layer corresponds to the limit of vanishingly small Debye length; l_D = 0. Upon charging the lipid layer the critical point upshifts from χ_c = 2, φ_c = 0.5 (○) to χ_c = 3.7, φ_c = 0.63 (•).

Regarding the experimental relevance of the predicted upshift in the critical point χ_c we note a recent work of Garidel et al. (1997) who studied various phosphatidylcholine/phosphatidylglycerol (PC/PG) mixtures at different pH. Specifically, upon increasing the pH from 2 to 7 (and hence deprotonating PG) they found the actual nonideality parameter (which includes electrostatic interactions) to decrease roughly from 1.3 to 0. Hence, the charging shifted the membrane toward a more uniform distribution of the lipids. Remarkably, even the numerical value of the difference in the demixing parameters (1.3) is not far away from the theoretical Poisson-Boltzmann prediction (1.7). Note that the ideal mixing properties of the PC/PG mixture at pH 7 reflect two competing (and compensating) tendencies: electrostatic repulsion between the charged headgroups and nonelectrostatic attraction.

RESULTS AND DISCUSSION

We have solved the Poisson-Boltzmann equation, Eq. 9, numerically subject to the boundary conditions, Eqs. 7 and 8. The local composition of charged lipids, η(r), was determined self-consistently according to Eq. 10. For any given average membrane composition φ, protein coverage θ, and nonideality parameter χ, we have subsequently obtained the electrostatic free energy per lipid, f_el = F_el/N, of the protein-dressed membrane (see Eq. 6). The calculation of f_el(φ, θ) as a function of φ and θ allowed us to numerically obtain the second derivatives ∂²f_el/∂φ², ∂²φ_el/∂f∂θ, and ∂²θ_el/∂q², needed to compute a conveniently defined stability function

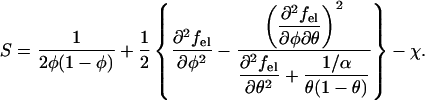(12)

The two cases, stability of the membrane for S > 0 and instability for S < 0, are separated by the spinodal surface, S(φ, θ, χ) = 0; see Eq. 4. The minimum of the spinodal surface, χ_c = χ(φ_c, θ_c), yields the critical point.

In all our calculations we have used a_l = 65 Ų for the cross-sectional area per lipid molecule (the same for both lipid species) and a Debye screening length of l_D = 10 Å. Recall that in this case, 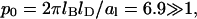and hence the critical point for an isolated, protein-free (θ = 0) membrane is χ_c = 3.7 (with corresponding critical composition φ_c = 0.63). The decisive question is thus if upon binding of proteins (θ > 0) the critical point can be reduced below 3.7.

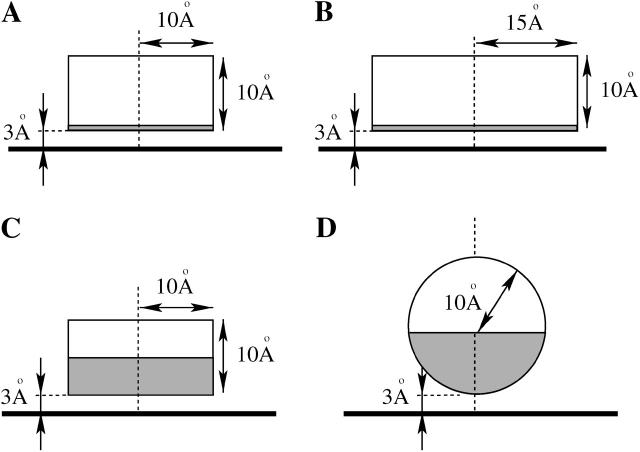
We have analyzed four representative model proteins that are displayed in Fig. 4. These macroions, denoted by the letters A, B, C, and D, represent model proteins of different size, shape, and surface charge distribution, as follows: A), The protein is a cylindrical disk of radius R_p = 10 Å and height h_p = 10 Å. Its charges are distributed only over the bottom face of the disk. B), This protein is of the same shape as A, except that its radius is increased to R_p = 15 Å. C), Again, the protein is of size and shape equivalent to A, but charges are distributed not only on the bottom face of the cylinder, but also on the lower half of its rim. D), This protein is modeled as a sphere of radius R_p = 10 Å. The charges are distributed only over the lower—membrane facing—half of the sphere.

FIGURE 4.

We consider four representative generic model proteins. Cases A, B, and C are disk-like proteins of height h_p = 10 Å and radius R_p = 10 Å. Case D is a sphere of radius R_p = 10 Å. The shaded regions represent charged areas: in A and B only the membrane-facing bottom is charged whereas in C and D it is also the lower half of the protein. The dashed lines coincide with the axis of cylindrical symmetry, the horizontal thick solid lines mark the charged membrane. In all cases, the surface charge density corresponds to an effective composition of φ_p = 0.6 (recall σ_p = φ_pe/a_l), and the minimal membrane-protein distance is set to h = 3 Å.

All remaining structural parameters concerning the proteins are kept constant. Specifically, the minimal distance between the protein and the membrane is fixed at h = 3 Å, and the charge density of the protein corresponds to an effective composition φ_p = 0.6 (recall σ_p = φ_pe/a_l). Finally, the interior of each protein has low dielectric constant so that we can safely neglect the electrostatic field inside the protein bodies (as we also do within the hydrocarbon core of the membrane).

Disk-like protein, case A

We first analyze the small disk-like protein, A, charged only at the bottom face. The charge density σ_p = φ_pe/a_l corresponds to 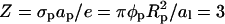positive charges on the membrane-facing side of the protein. Because the mantle of the cylindrical disk is uncharged, we expect electrostatic protein-protein repulsion to be negligible.

In Fig. 5, we plot the stability function, S, as defined in Eq. 12, versus the membrane composition, φ, for various values of θ, ranging from θ = 0.05 (the thinnest solid line) to θ = 0.85 (the thickest solid line) . The dashed line is the spinodal curve of the protein-free membrane (θ = 0). Fig. 5 shows that in panel a, where χ = 3.0, there is no solution for S ≤ 0, i.e., the membrane consists of a single, stable, phase. In diagram b, where χ = 3.4, there exist solutions of S < 0 for some combinations of φ and θ, indicating an unstable membrane. Most notably, the instability occurs for such values of χ where the bare membrane (see the dashed line in Fig. 5 b) is still stable. That is, protein adsorption can indeed trigger domain formation in the membrane; the domains differ in both their lipid composition φ and protein concentration θ. Clearly, the extent of the unstable regions (S < 0) increases with χ.

FIGURE 5.

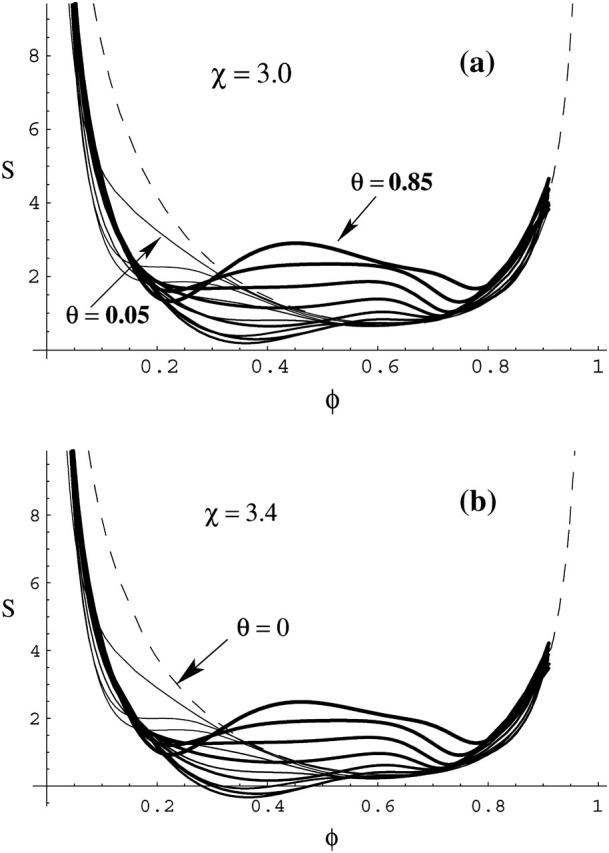
The stability function, S, defined in Eq. 12, versus composition φ for several different protein coverages, θ; varying in steps of 1/15 from θ = 0.05 (the thinnest solid line) to θ = 0.85 (the thickest solid line). For χ = 3.0 (a) S > 0 for all φ, indicating stable monophasic membrane. For χ = 3.4 (b) the membrane is unstable for those combinations of φ and θ for which S < 0. The spinodal fulfills the equation S = 0.

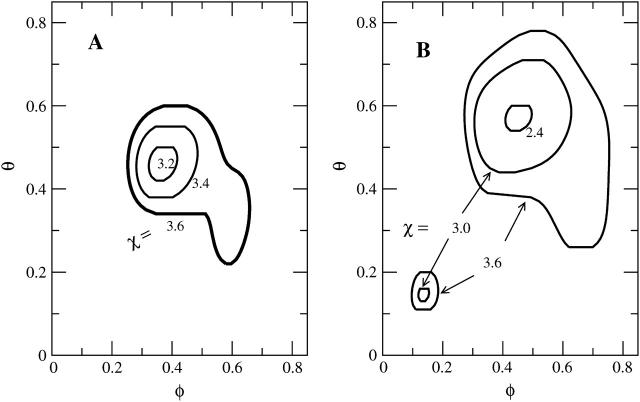
Computing solutions of the equation S(φ, θ) = 0 for different choices of the nonideality parameter χ allows us to obtain the spinodal surface χ = χ(φ, θ). Contours of this surface are plotted in the left diagram of Fig. 6 for protein A (the right diagram shows protein B). Because we see a spinodal line for χ = 3.2 but none for χ = 3.0 (see Fig. 5 a) we conclude that the critical point must be in the range 3 < χ_c < 3.2. Hence, the binding of the disk-like proteins of radius R_p = 10 Å lowers the critical lipid nonideality from χ_c = 3.7 to about χ_c = 3.1.

FIGURE 6.

Calculated spinodal surface χ = χ(φ, θ) for protein A (left panel) and protein B (right panel). Shown are the contours at several indicated values of χ. Proteins A and B are introduced in Fig. 4. Note that in the right diagram the spinodal has two branches.

The numerical results above may be compared to those predicted by the simple two-state model mentioned earlier (May et al., 2002), which yields

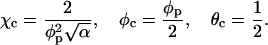(13)

A simplified and instructive derivation of these results can be obtained as follows. Assume that every adsorbed protein recruits to within its interaction zone exactly the number of charged lipids necessary to neutralize the total charge on its membrane-facing surface. Assume further that protein adsorption saturates once all charged lipids have migrated into protein binding sites, implying η(r) = φ_p within the interaction zones and η(r) = 0 in the uncovered membrane area, and hence, assuming a sharp boundary between these regions ∇η = φ_p. As shown in the Appendix, the line energy corresponding to a singly adsorbed protein is proportional to the product of three factors (see the second term in Eq. 24): the protein's circumference length (2πR_p), the lipid nonideality strength (χ), and the square of the concentration gradient across the boundary of the interaction zone, which in this limit of “strong adsorption” is simply 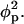When two, initially isolated proteins (including their “associated patches of lipids”) are brought into contact, the total line energy is reduced by an amount proportional to the contact length between the two patches, implying an attractive (membrane-mediated) pairwise interaction between proteins, W, whose magnitude equals the gain in line energy. Based on this simple picture the protein-dressed membrane can now be regarded as an interacting 2D gas of proteins. Adopting a lattice gas scheme, the free energy per protein is now given by

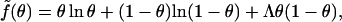(14)

with Λ ∝ W denoting (in analogy to χ for the lipid mixture) the interaction parameter for the gas of adsorbed proteins. For a triangular 2D lattice one finds 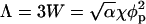where 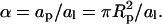From Eq. 14 we find that for Λ > Λ_c = 2 the 2D lattice gas undergoes a condensation transition, or, in other words, the protein-covered membrane exhibits domain formation. The critical protein coverage is θ = 1/2 implying also φ_c = φ_p/2 because (in the two-state model) charged lipids are only present in the protein covered patches, where their concentration is φ_p. The first equality in Eq. 13 follows from 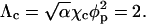Finally we note that, formally, Eq. 14 could also be derived from Eq. 1. That is, noting that all local variation in lipid composition are actually included in the electrostatic free energy, Eq. 6, then for a membrane of given total composition φ the first two terms in Eq. 14 are constants. Furthermore, following the assumption of exact charge neutralization of adsorbed proteins by membrane lipids eliminates all terms in Eq. 1 but the last one. And this last term becomes simply the last term in Eq. 14.

Returning to Eq. 13 we reiterate that these critical constants are approximate because the two-state model assumes a stepwise variation of the lipid composition across the boundary of the protein adsorption zone, and that all charged lipids enter (and are uniformly distributed within) this zone, the membrane-protein adsorption zone so as to ensure iso-electricity of the bound complex. Alternatively stated, the number of membrane-bound proteins is determined by the requirement for electrical neutrality. This assumption is valid only in the limit of strong adsorption (large p₀). Finally, the two-state model ignores direct electrostatic protein-protein repulsions. Not surprisingly then, substituting a_l = 65 Ų, R_p = 10 Å, and φ_p = 0.6 in Eq. 13 we find χ_c = 2.5, considerably smaller than our present, more accurate estimate, χ_c ≈ 3.1. Note, however, that had we allowed the lipid composition around the interaction zone to be nonzero or, equivalently, allowing for η(r) < φ_p (thus reducing the composition gradient across the boundary of the interaction zone), the two-state model would yield a better estimate. For example, the choice η(r) ≡ 0.54 (instead of η(r) = φ_P = 0.6) recovers the numerically calculated value χ_c = 3.1. Note also that the critical composition, φ_c, and critical protein coverage, θ_c, are both quite well predicted by Eq. 13. Clearly, the main advantage of the analytical expressions in Eq. 12 is their ability to predict (at least qualitatively) how the critical point behaves as a function of the system parameters such as the protein charge density and size.

Effect of protein size, case B

Protein B has radius R_p = 15 Å and is otherwise identical to protein A; see Fig. 4. Its circular bottom face accommodates 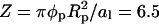charges (recall a_l = 65 Ų and φ_p = 0.6). The corresponding spinodal surface χ = χ(φ, θ) is displayed in the right diagram of Fig. 6. The most apparent feature is the much smaller magnitude of the critical nonideality; χ_c ≈ 2.35. A similar decrease is predicted by Eq. 13 according to which 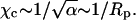Thus, changing the protein radius from R_p = 10 Å (case A) to R_p = 15 Å (case B) should downshift the critical nonideality from χ_c = 3.1 to χ_c = 3.1 × 2/3 = 2.1, in reasonable agreement with the numerically computed value χ_c ≈ 2.35. The reason for the decrease of χ_c with increasing protein radius, R_p, is a direct consequence of the fact that the energetically unfavorable line tension term in the free energy per adsorbed protein, F_el in Eq. 6, is the only incentive for phase separation. This contribution, which increases linearly with the protein's circumference, gives rise to an effective, membrane-mediated, attraction between the adsorbed macroions (May et al., 2002), and thus acts toward membrane destabilization (see Appendix).

Two other features are worth mentioning. First, the critical protein coverage increases somewhat from θ_c = 0.46 for R_p = 10 Å to θ_c = 0.57 for R_p = 15 Å. Yet, this increase translates into virtually the same average protein-protein distance, 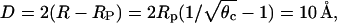in both cases. The other feature is a second branch of the spinodal that appears for higher χ (higher than χ = 3) in the low φ and θ region. We do not have a simple qualitative explanation for this behavior but it shows that the adsorption of relatively few (but sufficiently large) proteins on a weakly charged membrane can cause an instability.

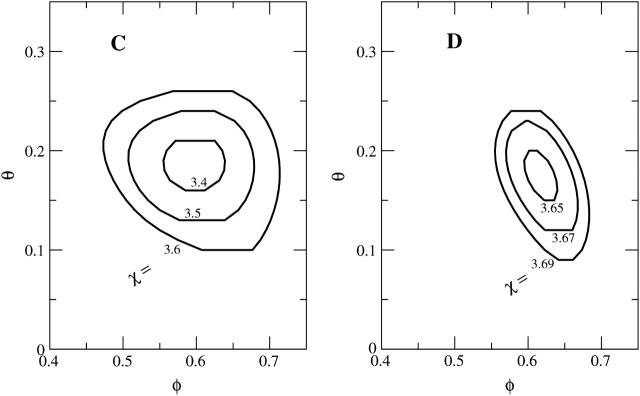
Effect of protein-protein repulsion, case C

To investigate the influence of direct electrostatic protein-protein repulsion, we have analyzed the adsorption characteristics of a disk-like model protein, where charges are present not only on its bottom face, but also on (the lower half of) its mantle surface (protein C in Fig. 4). Specifically, in addition to the Z = 3 charges on the bottom surface this protein carries πR_ph_pφ_p/a_l = 3 additional charges on its side face. Due to their location these charges are expected to mainly cause direct electrostatic protein-protein repulsion rather than to interact with the membrane. The spinodal surface for this system, shown in the left diagram of Fig. 7, reveals a critical nonideality χ_c = 3.38, critical composition φ_c = 0.60, and critical protein coverage θ_c = 0.18. Hence, compared to protein A (where χ_c = 3.1), protein C is notably less potent to destabilize the membrane. The reason, direct electrostatic protein-protein repulsion, also leads to a drastic downshift of θ_c. This downshift corresponds to an increased average protein-protein distance of 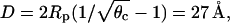considerably larger than the electrostatic screening length l_D = 10 Å. Because of the small critical protein coverage, the critical membrane composition can be expected to be close to that of a bare membrane (for which we recall φ_c = 0.63); this is indeed seen in Fig. 7.

FIGURE 7.

Calculated spinodal surface χ = χ(φ, θ) for protein C (left panel) and protein D (right panel). Shown are the contours at several indicated values of χ. Proteins C and D are introduced in Fig. 4.

Effect of protein shape, case D

The lower half of the spherical protein (case D in Fig. 4) is charged, its effective composition φ_p = 0.6 amounts to 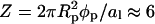charges, comparable to both cases B and C. The corresponding spinodal surface χ = χ(φ, θ) is displayed in the right diagram of Fig. 7. It shows, somewhat unexpectedly perhaps, that the spherical protein has practically no influence on membrane stability; the critical point χ_c = 3.645 is close to that of a bare membrane (χ_c = 3.7). The critical membrane composition, φ_c = 0.63, and protein coverage, θ_c = 0.18, are close to those in case C; the reason is the same: direct protein-protein repulsion.

Both proteins C and D have the same projected area a_p, surface charge density σ_p and overall charge Z. They both carry charges on their side faces, so that direct protein-protein repulsion should play a similar role. Nevertheless, the spherical protein appears considerably less potent to induce membrane domains as compared to protein C. Qualitatively it is quite clear that the reason for this difference is the weaker ability of the spherical protein to create compositional gradients in the membrane. The correspondingly lower line tension contribution to the free energy accounts for the increased membrane stability, as discussed in more detail in the next section.

The line tension

There is no attraction between like-charged objects within Poisson-Boltzmann theory (Neu, 1999). Yet, such an attraction is necessary to mediate the phase splitting of the membrane-bound proteins. Any reduction of the critical point beyond that of the bare membrane requires either direct or membrane-mediated attractive forces between the like-charged proteins. Because our model does not contain any direct protein-protein attraction, attraction must be mediated by the membrane substrate. Inspection of the free energy per unit cell, F_el (see Eq. 6), reveals that only one contribution can give rise to attractive (membrane-mediated) interactions, namely, the line tension contribution

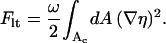(15)

Recall that ω = χ/C where C is a numerical prefactor depending on the number of neighbors surrounding a lipid molecule (we have used C = 3 as appropriate for a triangular lattice). It can be shown that ignoring F_lt by setting ω = 0 leads to a critical point of χ_c ≥ 3.7 for the protein-dressed membrane (where the equality sign is adopted in the complete absence of direct electrostatic protein-protein repulsion). Hence, for χ = 0 (implying ω = 0 and thus F_lt = 0) there would be no protein-induced membrane domain formation. We conclude that within the limits of this approach (below, in the final section we provide a short discussion of these limits) some degree of effective lipid-lipid attraction within the membrane (that is, χ > 0) is a necessary condition for protein-induced membrane destabilization.

For χ > 0 the membrane would tend to minimize the unfavorable line tension contribution, F_lt > 0, by reducing the compositional gradients within, and especially at the boundaries of, the protein-lipid interaction zone. Lateral aggregation of the adsorbed proteins, whereby their lipid interaction zones overlap each other, is an efficient way to reduce lipid composition gradients (as illustrated very schematically in Fig. 1). If this aggregation tendency of the protein-lipid “complexes” (i.e., the adsorbed proteins together with their “associated” charged lipids) is strong enough to overcome the loss of translational entropy of these complexes (the last term in Eq. 1) and, if present, the direct electrostatic repulsion between proteins, then the dressed membrane will become unstable. That is, phase separation will take place whereby “domains” composed of densely packed proteins and a high mol fraction of charged lipid coexist with a dilute phase of proteins and fewer charged lipids.

The origin of the gradients in lipid composition upon protein adsorption is, of course, the favorable electrostatic interaction between the protein and the oppositely charged lipids. The magnitude of these gradients depends on the protein's geometry and charge distribution. For example, flat and highly charged proteins will induce larger gradients than, e.g., smoothly curved proteins. The line tension energy, per protein, will scale linearly with its circumference. Lipid nonideality, or more precisely χ > 0 (“positive deviation” from ideal mixing), is a necessary condition for large positive F_lt. As we have seen, however, a smaller χ than χ_c of the bare membrane may suffice for phase separation of the dressed membrane, provided the lipid composition gradients and/or the protein size are large enough.

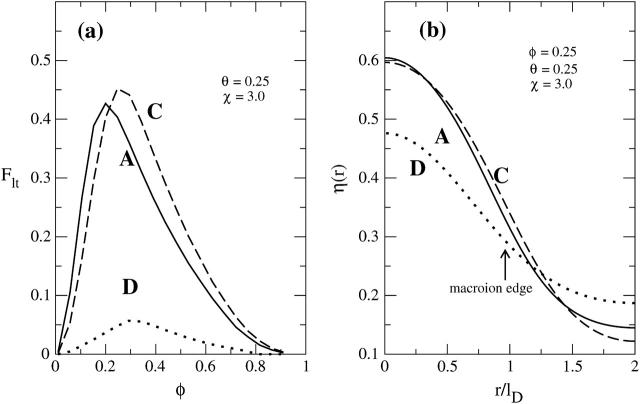
To test the qualitative notions above let us analyze the line tension contribution for the different protein shapes that we have considered in this work. Fig. 8 a compares F_lt, for proteins A, C, and D, as a function of the membrane composition φ, calculated for protein coverage θ = 0.25 and nonideality parameter χ = 3.0. Fig. 8 b displays for φ = 0.25 the corresponding compositional profiles, η(r). Generally, the line tension vanishes at φ = 0 and φ = 1, adopting a maximum at intermediate compositions. The magnitude of F_lt depends on the protein characteristics. Specifically, the equal shaped proteins A and C show similar line tension. The charged mantle face of protein C appears to have a marginal effect on the lipid composition at the protein binding site. Even at φ = 0.3, where the additional local lipid demixing is maximal, the corresponding increase of the line tension is small. This observation supports our notion regarding the increase in χ_c and decrease in θ_c due to direct (in contrast to “indirect,” membrane-mediated) interprotein repulsion for protein C, as compared to protein A. Much more dramatic is the influence of the protein shape on the line tension; compare the spherical protein D to either A or C in Fig. 8. The spherical protein is smoothly curved, inducing comparatively mild variations in the membrane composition η(r). The corresponding line tension is small, providing only weak attractive forces between membrane-adsorbed proteins.

FIGURE 8.

(a) Displays the line tension contribution to the total free energy, F_lt, versus φ, calculated at χ = 3.0 and θ = 0.25 for systems A, C, and D; (b) shows at φ = 0.25 the corresponding local composition η(r) of charged lipids.

Our final comment concerns the assumption of a step-like profile for η(r) as has been employed in previous work (May et al., 2002; Haleva et al., 2004). Fig. 8 b indicates strong, yet not step-like, variations in the compositional profile, η(r). Clearly then, Eq. 13, which was derived on the basis of a step-like profile for η(r) (the so-called two-state model), generally underestimates χ_c.

SUMMARY AND CONCLUSIONS

In this work we have analyzed the influence of electrostatically adsorbed proteins on the stability of a mixed, two-component fluid lipid membrane, treating both electrostatic and nonelectrostatic interactions in a mean-field level. The electrostatic free energy was calculated using nonlinear Poisson-Boltzmann theory, allowing for lipid lateral reorganization in response to the interaction with the peripheral macroion. Regular solution theory has been used to account for the nonideal mixing properties associated with (the nonelectrostatic) interlipid interactions. We have treated the membrane as a binary fluid mixture of anionic and neutral lipids with mol fractions φ and 1 − φ, respectively. The lipid molecules interact nonideally with strength χ > 0, favoring attraction of lipids of the same species. The protein is characterized by its shape, which we have modeled as disk-like or spherical, the distribution of charges on its surface, and its two-dimensional membrane concentration θ. We determined the stability limits and the critical constants of the protein-dressed membrane using the spinodal equation as a function of χ, φ, and θ.

Table 1 summarizes our findings for the critical points of the four model proteins A–D, as well as that of the protein-free membrane M. Our main conclusion is that electrostatically adsorbed proteins are indeed able to induce lateral phase separation of the dressed membrane. A necessary condition for this phenomenon is (positive deviations from) nonideality due to the nonelectrostatic interactions between lipids of the same species; that is, χ > 0 in the mean-field treatment. This result is in qualitative agreement with the interpretation of recent experimental studies on protein-induced domain formation in terms of attractive lipid-lipid interactions (Hinderliter et al., 2001, 2004).

TABLE 1.

A summary of the critical points (the critical nonideality parameter, χ_c, the critical membrane composition, φ_c, and the critical protein coverage, θ_c) for the different protein types, A, B, C, and D (see Fig. 4) that we have considered

	A	B	C	D	M
χc	3.1	2.35	3.38	3.65	3.7
φc	0.38	0.44	0.60	0.63	0.63
θc	0.46	0.57	0.18	0.18	–

The last row (M) refers to the bare (protein-free) membrane.

We have also shown that the extent to which the critical point, χ_c, is lowered below that of a bare (protein-free) membrane (where χ_c = 3.7) depends sensitively on the shape of the proteins and the charge distribution on their surface. Proteins with high potential for domain formation have their charges distributed on a (preferably flat) bottom face, rather than on their side faces where they would give rise to direct electrostatic interprotein repulsion. In general, when far apart, domain-inducing proteins create a strongly varying compositional profile of the membrane lipids, and thus large positive line energy, providing a major driving force for lateral phase separation of the composite membrane.

Modeling a macroscopically large, nonhomogeneous, protein-dressed membrane necessarily requires approximations. Apart from treating all interactions in a mean-field level and modeling the proteins as simple generic shapes, we have adopted the continuum limit in considering the distribution of charges in the membrane and the aqueous environment, thus neglecting the discrete size of the lipid headgroups, salt ions, and the molecular structure of water. Another significant assumption of this work is to treat the lipid membrane as being perfectly flat. Hence, any possible protein-induced curvature changes are entirely suppressed. In this connection it should be noted that theory predicts (see, for example, Weikl, 2003 and Schiller et al., 2004) that elastic membrane deformations can mediate either attractive or repulsive interactions between membrane-adsorbed colloidal particles, depending on membrane elasticity and particle shape. We have not included the possibility of elastic membrane deformations in this work because their action is not necessarily coupled to the demixing of the underlying lipid layer (in fact, a two-component membrane is not even required). Similarly, we have not included here the possible role of direct (as distinguished from membrane-mediated) nonelectrostatic protein-protein interactions, because they obviously depend on the size, shape, and chemical composition of the protein in question. The influence of such interactions on the critical behavior of the dressed membrane can be estimated by adding their contribution to that of the membrane-mediated forces, as given for instance by the two-state model.

Notwithstanding the various approximations and assumptions inherent to our theoretical analysis, we believe that its general conclusions are valid and helpful in terms of understanding the physical origin of protein-induced domain formation in mixed membranes, and their dependence upon the major structural characteristics of the adsorbed macroions.

APPENDIX

We shall derive the relation χ = Cω for a square lattice. The lattice points are located at positions 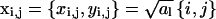with 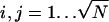and a_l being the cross-sectional area per lipid. Each of the N lattice points represents one lipid within the unit cell; the lateral area of the unit cell is A = Na_l. The composition at position x_i,j is η_i,j.

Denote by ɛ₁₁, ɛ₂₂, ɛ₁₂ the interlipid, nearest-neighbor interaction energies (subscript “1” refers to the charged and “2” to the uncharged lipid species). In random mixing approximation the overall nonelectrostatic interaction energy between charged lipids is

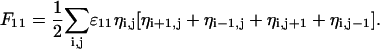(16)

The sum runs over the whole lattice (that is, over all N lattice points), and the factor of 1/2 avoids double counting of the interaction energies. Note that the four terms in the brackets refer to the z = 4 nearest neighbors of a square lattice (more generally, z is the coordination number of the lattice). We reexpress F₁₁ as

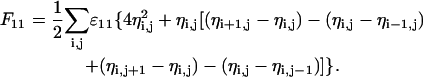(17)

In the continuum limit, we identify 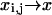and 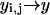with continuous coordinates of the lattice. The sum, 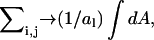transforms into an integration over the area A of the lattice, and

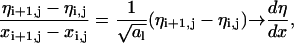(18)

becomes the derivative along the x-direction. Similarly for the derivative along the y-direction, 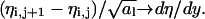Hence, in the continuum limit F₁₁ is given by

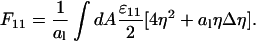(19)

Using the identity ηΔη = ∇(η∇η) − (∇η)², applying Gauss law, and assuming that the derivative of η in normal direction to the cell boundary vanishes, we obtain

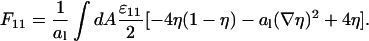(20)

Analogously, we obtain for the interaction energy between the uncharged lipids

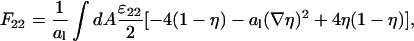(21)

and, finally, for the interaction energy between charged and uncharged lipids

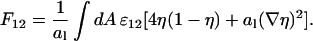(22)

A convenient reference state is that of a completely phase separated lipid layer. The corresponding interaction energy in the reference state is

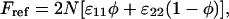(23)

where 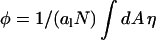is the average composition of the lipid layer (see also Eq. 5). The overall interaction energy, F_int = F₁₁ + F₂₂ + F₁₂ − F_ref, measured with respect to the reference state, is then

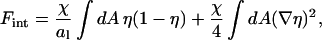(24)

where the nonideality parameter is χ = z[ɛ₁₂ − (ɛ₁₁ + ɛ₂₂)/2] (recall the coordination number z = 4). Comparison with Eq. 6 shows that ω = χ/C with C = 2. The calculation for a triangular lattice proceeds analogously (with coordination number z = 6). It leads to C = 3, which is used in this work.