Functional Interaction of Ca_V Channel Isoforms with Ryanodine Receptors Studied in Dysgenic Myotubes

Abstract

The L-type Ca²⁺ channels Ca_V1.1 (α_1S) and Ca_V1.2 (α_1C) share properties of targeting but differ by their mode of coupling to ryanodine receptors in muscle cells. The brain isoform Ca_V2.1 (α_1A) lacks ryanodine receptor targeting. We studied these three isoforms in myotubes of the α_1S-deficient skeletal muscle cell line GLT under voltage-clamp conditions and estimated the flux of Ca²⁺ (Ca²⁺ input flux) resulting from Ca²⁺ entry and release. Surprisingly, amplitude and kinetics of the input flux were similar for α_1C and α_1A despite a previously reported strong difference in responsiveness to extracellular stimulation. The kinetic flux characteristics of α_1C and α_1A resembled those in α_1S-expressing cells but the contribution of Ca²⁺ entry was much larger. α_1C but not α_1A-expressing cells revealed a distinct transient flux component sensitive to sarcoplasmic reticulum depletion by 30 μM cyclopiazonic acid and 10 mM caffeine. This component likely results from synchronized Ca²⁺-induced Ca²⁺ release that is absent in α_1A-expressing myotubes. In cells expressing an α_1A-derivative (α₁Aas(1592-clip)) containing the putative targeting sequence of α_1S, a similar transient component was noticeable. Yet, it was considerably smaller than in α_1C, indicating that the local Ca²⁺ entry produced by the chimera is less effective in triggering Ca²⁺ release despite similar global Ca²⁺ inward current density.

INTRODUCTION

The mobilization of Ca²⁺ for force activation in muscle cells involves the rapid communication of voltage-dependent Ca²⁺ channels with the ryanodine receptors of the sarcoplasmic reticulum (SR) (Rüegg, 1986; Melzer et al., 1995; Bers, 2001; Dirksen, 2002; Beam and Horrowitz, 2004). In cardiac cells, a Ca²⁺ inward flux mediated by voltage-operated L-type Ca²⁺ channels triggers a larger secondary Ca²⁺ efflux from the SR (DelPrincipe et al., 1999; Cheng and Wang, 2002). This mechanism requires the close proximity of the pore-forming subunit α_1C of the cardiac L-type channel (Ca_V1.2) with the Ca²⁺ release channel of the SR (ryanodine receptor RyR2) (Franzini-Armstrong et al., 1999; Bers, 2001). In contrast, the skeletal muscle L-type Ca²⁺ channel (α_1S = Ca_V1.1) interacts with the ryanodine receptor (RyR1) via a direct physical link (Dirksen, 2002; Beam and Horrowitz, 2004). The protein-protein interaction is reflected in a regular tetrameric pattern (junctional tetrads) formed by the Ca_v1.1 in the transverse tubular (TT) membrane opposite the RyR1 clusters (Franzini-Armstrong et al., 1998, 2004). The correct targeting to the TT-SR junction that is essential for both types of interaction mechanisms seems to depend on amino acid sequences in the C-terminal regions of α_1C and α_1S (Flucher et al., 2000; Proenza et al., 2000). The skeletal muscle-specific type of direct interaction with the ryanodine receptor, on the other hand, has been attributed to specific sequences in the II–III loop of the α_1S isoform (Nakai et al., 1998; Grabner et al., 1999; Dirksen, 2002) and may involve further cytoplasmic regions of this protein (Ahern et al., 2001) as well as the participation of the auxiliary β_1a subunit (Beurg et al., 1999a,b).

The α_1A-subunit (Ca_V2.1) of neuronal P/Q-type Ca²⁺ channels is thought to lack both a specific junctional targeting sequence as well as a RyR interaction domain (Flucher et al., 2000). Immunolabeling after heterologous expression in α_1S-deficient dysgenic myotubes showed colocalization with RyR1 for α_1S and α_1C but not for α_1A. However, a chimeric construct consisting of a truncated form of α_1A fused with the distal half of the C-terminal α_1S sequence, α₁Aas(1592-clip), restored targeting to the ryanodine receptor based on the immunostaining results (Flucher et al., 2000).

The scheme of Fig. 1 summarizes putative functional properties of the four α₁ variants in dysgenic myotubes: All constructs except α_1S should lead to intracellular Ca²⁺ signals that depend on the size of the voltage-activated Ca²⁺ inward current rather than on membrane voltage alone. Because of the lack of specific junctional targeting, α_1A should be least effective in triggering secondary Ca²⁺ release and may even not be able to cause Ca²⁺ release at all. Finally, α₁Aas(1592-clip), like α_1C, would be expected to restore cardiac-type EC coupling exhibiting a significant secondary Ca²⁺ release component.

FIGURE 1.

Expression of different Ca²⁺ channel α₁-subunits in dysgenic (GLT) myotubes. The four Ca²⁺ channel α₁-subunits that were expressed in the α₁-deficient GLT myotubes are known to differ in their location (specific targeting to the TT-SR junction or not) and their mode of interaction with the ryanodine receptor (direct mechanical coupling or not). Based on previous structural and functional investigations, α_1S controls release from the SR without the participation of a Ca²⁺ inward flux. α_1C and α₁Aas(1592-clip) which are colocalized with RyR1 should support Ca²⁺ inward current-induced Ca²⁺ release whereas α_1A which was reported not to be targeted to the junction should not be able to functionally interact with the junctional ryanodine receptors.

The functional data presently available can be summarized as follows: Only for α_1S, Ca²⁺ transients were relatively independent of the Ca²⁺ inward current (García et al., 1994; Flucher et al., 2000), consistent with the particular type of coupling mechanism. Compared with α_1C-expressing dysgenic myotubes, α_1A-expressing myotubes showed considerably lower contractile activity when subjected to extracellular electrical stimulation (Adams et al., 1994; Grabner et al., 1998). This was attributed to the lack of junctional targeting of α_1A (Flucher et al., 2000). The expression of the chimera α₁Aas(1592-clip), which exhibited junctional targeting (Flucher et al., 2000), produced larger Ca²⁺ current densities than α_1A and more frequently intracellular Ca²⁺ transients in response to extracellular stimulation. On the other hand, α₁Aas(1592-clip) showed considerably lower responsiveness than α_1S and α_1C under these conditions: the number of myotubes responding with a Ca²⁺ transient per investigated culture dish increased in the order α_1A < α₁Aas(1592-clip) < α_1S < α_1C with relative values of 1, 9, 133, and 140 (Flucher et al., 2000). Because the resting potential and the shape of the action potential may vary with the type of Ca²⁺ channel expressed, the different responsiveness might also result from differences in the excitation process. We therefore investigated myotubes of the dysgenic cell line GLT (Powell et al., 1996) expressing these four Ca²⁺ channel isoforms (Fig. 1) under identical voltage-clamp conditions. In a search for differences in their gating properties, we simultaneously measured transmembrane Ca²⁺ inward currents and intracellular Ca²⁺ signals to determine their time course and voltage-dependence. For skeletal and cardiac cells, methods have been developed to estimate the flux of Ca²⁺ mobilization (termed Ca²⁺ input flux, i.e., the sum of Ca²⁺ release flux from the SR and Ca²⁺ entry flux from the extracellular space) from optical recordings of Ca²⁺ transients (for references, see Bers, 2001; Schuhmeier and Melzer, 2004). Here, we applied this approach for the first time to transfected cells. We estimated the gain of EC coupling, i.e., the ratio of Ca²⁺ input to Ca²⁺ entry flux during step depolarization (for references, see Bers, 2001; Cheng and Wang, 2002). We further depleted the SR to estimate the relative contributions of Ca²⁺ release and Ca²⁺ entry flux to the measured Ca²⁺ signals.

MATERIALS AND METHODS

Solutions and media

The following solutions were used in the cell culture:

• Growth medium—Dulbecco's Modified Eagle Medium (DMEM) with 1% glutamine (200 mM), 10% fetal calf serum (FCS), and 10% horse serum (HS).

• Trypsin solution—Trypsin-EDTA (0.05–0.53 μM) in Ca²⁺- and Mg²⁺-free phosphate-buffered saline (PBS).

• Fusion medium—DMEM with 1% glutamine (200 mM) and 2% HS.

• Transfection medium—100 μl per 35-mm dish, containing 94 μl serum-free DMEM, 6 μl Fugene 6 (see below), and 2 μg DNA.

The experimental recording solutions had the following compositions:

• External solution—130 mM tetraethylammonium hydroxide, 127 mM HCl, 10 mM CaCl₂, 1 mM MgCl₂, 2.5 mM 4-aminopyridine, 0.00125 mM tetrodotoxin, and 10 mM HEPES, pH-adjusted to 7.4 with HCl.

• Internal (pipette) solution—145 mM CsOH, 145 mM aspartic acid, 0.1 mM EGTA, 0.01 mM CaCl₂ (free Ca²⁺, 10⁻⁵ mM), 1.14 mM Na₂ATP, 3.86 mM MgATP (Mg/ATP ratio according to supplier, 1.4; free Mg²⁺, 1 mM), 5 mM Na creatine phosphate, 0.2 mM K₅-Fura-2, and 10 mM HEPES, pH-adjusted to 7.4 with CsOH.

DMEM, HS, and Trypsin-EDTA were purchased from Gibco (Karlsruhe, Germany), FCS, and PBS from PAA Laboratories (Cölbe, Germany), rat tail collagen (Typ 1, C 7661), EGTA, ATP, caffeine, cyclopiazonic acid, and CsOH from Sigma-Aldrich (Taufkirchen, Germany), Fugene 6 from Roche Biochemicals (Mannheim, Germany), TEA and HEPES from Merck (Darmstadt, Germany), tetrodotoxin and Fura-2 from Molecular Probes (Leiden, Netherlands), creatine phosphate from Boehringer (Mannheim, Germany), 4-aminopyridine from Fluka (Neu-Ulm, Germany), and L-glutamine from Biochrom (Berlin, Germany).

Cell culture and transfection

For heterologous expression of the Ca²⁺ channel α₁-subunits, we used myotubes of the homozygous dysgenic (mdg/mdg) cell line GLT that was originally generated by transfection of mdg myoblasts with a plasmid-encoding Large-T Antigen (Powell et al., 1996). GLT myoblasts were expanded in growth medium at 10% CO₂ and 37°C and passaged before reaching 80% confluence using trypsin detachment. To obtain myotubes, cells were plated onto carbon- and gelatin-coated coverslips in 35-mm dishes. After reaching confluence, growth medium was exchanged for fusion medium. We used mammalian expression plasmids coding for N-terminally GFP-tagged fusion proteins of the Ca²⁺ channel pore-forming subunits α_1S, α_1C, α_1A, and α₁Aas(1592-clip), respectively, as described by Flucher et al. (2000). Cells were transfected at the onset of fusion. Measurements were made from the myotubes four days later.

Electrophysiology and fluorimetry

Whole-cell patch-clamp experiments and microfluorimetric recordings were performed at room temperature (20–23°C) as described by Schuhmeier et al. (2003) and Schuhmeier and Melzer (2004). Briefly, myotubes were loaded with Fura-2 by diffusion from a patch-pipette containing internal solution (see above). Leak-resistance and capacitance were determined by using small positive and negative pulse excursions (10 mV amplitude, 25 ms duration) from the holding potential. Linear leak correction of current recordings was performed by a standard p/n method (n = 4 or 8). Ca²⁺-dependent fluorescence changes were recorded at 515 nm while exciting at 380 nm (F₃₈₀). After background correction, the F₃₈₀ recordings were normalized either by F₃₈₀ measurements preceding each voltage-clamp activation (Figs. 2–4, displayed as −ΔF/F₀), or by F₃₆₀ (Figs. 5–8), as described in Schuhmeier et al. (2003).

FIGURE 2.

Simultaneously recorded Ca²⁺ inward currents and intracellular Ca²⁺ signals in GLT myotubes. (A) Recordings of leak-corrected Ca²⁺ inward currents (a and c) and fluorescence changes (b and d) in GLT myotubes transfected with expression plasmids carrying cDNA encoding α_1S and α_1C, respectively. (B) Peak Ca²⁺ current densities (a and c) and Ca²⁺ transients (b and d) as functions of voltage. Continuous lines are least-squares fits with Eqs. 1 and 2, i.e., formally the same functions were used to describe the voltage-dependence of transmembrane Ca²⁺ current density and intracellular Ca²⁺ transient.

FIGURE 3.

Voltage-dependence of Ca²⁺ inward current density and intracellular Ca²⁺ transient. Mean data obtained from recordings in transfected GLT myotubes. (A) α_1S (n = 6), (B) α_1C (n = 5), (C) α_1A (n = 5), and (D) α₁Aas(1592-clip) (n = 10). The continuous curves show least-squares fits according to Eqs. 1 and 2 (see also Fig. 2).

FIGURE 4.

Voltage-dependence of activation. The inward current data of Fig. 3 were converted to fractional conductance using Eq. 1 and solving for f(V) (solid symbols). A formally equivalent conversion was performed using the optically recorded Ca²⁺ signal data of Fig. 3 (open symbols). The two types of activation curves differ clearly for α_1S (A) and to a lesser degree for α_1C (B), whereas for α_1A (C) and α₁Aas(1592-clip) (D), the difference is below 5 mV.

FIGURE 5.

Comparison of Ca²⁺ input flux and Ca²⁺ entry flux. (A) Averaged Ca²⁺ input flux calculations for the constructs shown in Fig. 1 during 100 ms depolarizations to +30 mV. (B) Averaged Ca²⁺ inward current densities for the same pulses that elicited the records in A. Number of experiments from left to right: n = 17, 16, 16, and 15. Thick lines indicate mean values; shaded areas indicate mean ± SE.

FIGURE 6.

Effect of SR depletion on EC coupling gain. (A) 30 μM CPA and 10 mM caffeine were applied to deplete the SR of stored Ca²⁺ to study the effect on Ca²⁺ fluxes and gain in a number of myotubes expressing the four α₁-subunits of Fig. 1. (B) Time-dependent changes in mean baseline free Ca²⁺ concentration indicating comparable Ca²⁺ release in all cases. (C) Mean Ca²⁺ input flux and Ca²⁺ entry flux (average from 25 to 75 ms during the voltage pulse) for each of the three intervals, labeled a, before drug application; b, after CPA application; and c, after caffeine application. Entry flux plotted in opposite direction of input flux. (D) A gain factor was calculated representing the ratio of Ca²⁺ input flux (derived from the optical signals) and Ca²⁺ entry flux (derived from the inward current density) using the data of C. Because small current amplitudes produced large variances, current density amplitudes <0.5 A/F were excluded for the gain calculation of α_1S in D. From left to right, the numbers of cells were 7, 4, 5, and 8, respectively.

FIGURE 7.

Time course of Ca²⁺ input and entry flux during SR depletion. Time course of calculated Ca²⁺ fluxes (Ca²⁺ input flux drawn upward, Ca²⁺ entry flux downward). Columns (a), (b), and (c) show the averaged responses to pulse depolarization (100 ms, +30 mV) in the correspondingly labeled intervals of Fig. 6 B, respectively. Column (d) shows the depletion-sensitive flux components. After scaling with a factor f to correct for a rundown in the current traces, the depolarization-induced responses persisting after CPA and caffeine application (column c) were subtracted from the responses before drug application (column a). The subtraction was performed for each individual experiment and the differences were averaged. Shaded areas indicate point by point SE.

FIGURE 8.

Correlation between Ca²⁺ entry flux and Ca²⁺ input flux. Mean values of Ca²⁺ input flux plotted versus corresponding means of Ca²⁺ entry flux, evaluated at the input flux peak (A) and near the end of the pulse (95 ms) (B). Each connected data points correspond to Fig. 7, a, b, and c.

Data analysis

General analysis and nonlinear curve fitting were carried out using Excel (MicroSoft, Seattle, WA) and Origin (OriginLab, Northampton, MA). The program CalcV22 (Föhr et al., 1993) was used to calculate the free ion concentrations in the internal solution.

The leak-corrected ionic currents I(V) were normalized by the linear capacitance to obtain current densities i(V). The voltage-dependence of the Ca²⁺ current density i_Ca(V) was least-squares-fitted with Eq. 1:

(1)

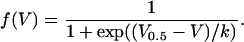(2)

The values g_Ca,max and V_Ca are maximal normalized conductance and reversal potential, respectively, of the L-type Ca²⁺ current; f(V), voltage-dependence of activation; and V_0.5 and k, voltage of half-maximal activation and voltage sensitivity parameter, respectively. The fit also included correction for a small offset resulting from noise effects in the minimum detection.

Ca²⁺ current densities i_Ca were converted to Ca²⁺ entry flux using Eq. 3:

(3)

Here, z is the valence of the Ca²⁺ ion, F is the Faraday's constant, V_C is the intracellular volume per membrane capacitance, and f_V is the fraction of the total volume that is immediately accessible to Ca²⁺.

Free Ca²⁺ concentration was determined using background- and bleaching-corrected fluorescence ratio signals (R = F₃₈₀/F₃₆₀) according to Eq. 4 (Klein et al., 1988):

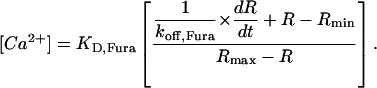(4)

The following values were used for R_min (fluorescence ratio at zero dye saturation), R_max (ratio at full dye saturation), and K_D,Fura (dissociation constant of the dye): 2.84, 0.68, and 276 nM, respectively (see Schuhmeier et al., 2003). For the Fura-2 dissociation rate constant k_off,Fura we used the value of 46.4 s⁻¹ (Schuhmeier and Melzer, 2004).

An estimate of the flux of Ca²⁺ mobilization in the myoplasm (called Ca²⁺ input flux) during strong depolarizations was calculated with a Ca²⁺ binding model using the general method of Baylor et al. (1983). The free Ca²⁺ transient (Eq. 4), averaged for three sequential voltage pulses (+30 mV) of 100-ms duration, applied at 30-s intervals, was used to calculate the Ca²⁺ occupancies of the model components. Free Ca²⁺ and the estimated occupancies were summed and the time derivative calculated. Differential equations were solved using Euler's method. The calculation employed a digital filter that adjusted its bandwidth automatically to the signal dynamics (Schuhmeier et al., 2003). In the model we used troponin C with concentration (120 μM) and kinetic properties as reported for skeletal muscle fibers (Baylor and Hollingworth, 1998). Each molecule of troponin C has two fast, Ca²⁺-specific binding sites (T-sites) and two slow Ca²⁺-Mg²⁺-binding sites (P-sites) with rate constants k_on,T,Ca = 88.5 μM⁻¹ s⁻¹, k_off,T,Ca = 115 s⁻¹, k_on,P,Ca = 41.7 μM⁻¹ s⁻¹, k_off,P,Ca = 0.5 s⁻¹, k_on,P,Mg = 0.033 μM⁻¹ s⁻¹, and k_off,P,Mg = 3 s⁻¹. In contrast to mature muscle fibers, there is no evidence for the presence of parvalbumin in developing muscle (Leberer and Pette, 1986). EGTA (0.1 mM) in the myoplasm was described by using the means of in situ rate constants (k_on,S = 20 μM⁻¹ s⁻¹ and k_off,S = 2.71 s⁻¹) determined empirically in C2C12 myotubes loaded with large excess of EGTA (Schuhmeier and Melzer, 2004). Because SR uptake rates in myotubes seem to be small compared to release rates during depolarization (García and Beam, 1994), a component simulating the SERCA pump was not included in the model.

Statistics

Data are presented as means ± SE (n = number of experiments) for averaged values, and as parameter ± SE for best-fit parameters.

RESULTS

To determine the voltage-dependence of both Ca²⁺ inward currents and Ca²⁺ transients, the pulse paradigm described in Fig. 2 was used. The recordings in Fig. 2 A were obtained from one GLT cell expressing α_1S (a and b) and another one expressing α_1C (c and d). The length of the voltage-clamp pulse was 200 ms in all cases (horizontal bar). Leak-corrected Ca²⁺ inward current (I_Ca) and normalized change in fluorescence (−ΔF/F₀) are displayed next to each other for a series of pulses from −20 mV to +70 mV.

Fig. 2 B depicts the voltage-dependence obtained from each series of recordings, upon taking the signal peak for the inward current (solid symbols) and the average of the last 10 ms during the pulse for the fluorescence (open symbols). Clearly, in the case of α_1S the threshold for activation of Ca²⁺ transients (b) is considerably more negative than for the activation of inward current (a) and Ca²⁺ transients are of almost equal amplitude between +50 and +80 mV. In contrast, in the case of α_1C, Ca²⁺ current (c) and Ca²⁺ transient (d) start at a similar potential and show a similar decline in amplitude at large depolarizing potentials.

Fig. 3 compares voltage-dependence of Ca²⁺ current (solid symbols) and Ca²⁺ transient (open symbols) for each of the α₁-subunit types of Fig. 1 using averaged data of individual experiments. α_1S produced the smallest Ca²⁺ current densities but the largest Ca²⁺ transients (Fig. 3 A). The α_1S-transients show only a small decrease in amplitude at large voltages whereas the decrease is substantial in the three other cases (Fig. 3, B–D). The bell-shaped fluorescence-voltage relations for α_1C, α_1A, and α₁Aas(1592-clip) indicate a close relation between inward current and Ca²⁺ signal. The maximal mean Ca²⁺ signal of α_1S was significantly larger than that of α_1C and α_1A (but not α₁Aas(1592-clip)). The putative junctionally targeted α₁Aas(1592-clip) showed a significantly larger maximal current density than the nontargeted α_1A channel. On the other hand, the amplitude of the α₁Aas(1592-clip) Ca²⁺ signal was not found to be significantly larger than that of α_1A.

To better compare the voltage-dependence of activation of Ca²⁺ current and intracellular Ca²⁺ transients we formally fitted both leak-corrected current and fluorescence data in Fig. 3 with Eq. 1. The best-fit functions are superimposed on the data points as continuous lines using the means of the individual best-fit parameters.

Fig. 4 displays the data of Fig. 3 after conversion to f(V) to show the voltage-dependence of fractional activation according to Eq. 2. If the Ca²⁺ transient is the immediate result of the Ca²⁺ entry flux, the two activation curves are expected to be similar. As can be seen from these plots, for the skeletal muscle α₁-subunit (α_1S), the optically recorded Ca²⁺ transient reaches its half-maximal value at a considerably more negative potential than the Ca²⁺ conductance activation (Fig. 4 A, open and solid circles, respectively). The midpoint voltages of activation are separated by 29.9 mV. In the case of the cardiac α₁-subunit (α_1C) the activation curves are closer together, but still separated by a gap of ∼8.6 mV (Fig. 4 B). In contrast, the two activation curves show much smaller differences for α_1A and its chimeric construct, 3.3 and 4.1 mV, respectively (Fig. 4, C and D).

Table 1 summarizes the parameters describing the voltage-dependence obtained from the data of Figs. 3 and 4. The two L-type channels can be easily distinguished from α_1A and its chimeric derivative by the lower steepness of activation (larger k). Within each group, steepness of activation of Ca²⁺ entry and intracellular Ca²⁺ signals were similar.

TABLE 1.

Parameters of voltage-dependent activation of Ca²⁺ inward currents and intracellular Ca²⁺ transients

	Ca2+ current				Ca2+ transient
	α1S	α1C	α1A	α1Aas(1592-clip)	α1S	α1C	α1A	α1Aas(1592-clip)
V0.5 (mV)	33.9 ± 2.7	22.8 ± 2.5	17.8 ± 0.9	15.0 ± 2.5	4.0 ± 2.1	14.2 ± 3.4	14.5 ± 0.9	10.9 ± 2.5
k (mV)	8.3 ± 0.4	7.3 ± 0.3	4.7 ± 0.5	4.1 ± 0.3	8.6 ± 0.2	7.2 ± 0.6	4.4 ± 0.3	4.2 ± 0.1
gCa.max (pS/pF)	45 ± 5	169 ± 40	90 ± 21	252 ± 76
VCa (mV)	74.6 ± 3.5	87.8 ± 4.8	80.6 ± 12.0	84.9 ± 4.3
n	6	5	5	10	6	5	5	10

Current-voltage relations and fractional changes in the fluorescence ratio signals were fitted with Eqs. 1 and 2 as described in Materials and Methods. n = number of cells.

Estimating voltage-dependent Ca²⁺ fluxes

The different modes of EC coupling and different targeting properties of the four types of channels (Fig. 1) might result in detectable differences in kinetic features of the SR Ca²⁺ release flux. Therefore, we converted fluorescence ratio signals measured in a further set of experiments to estimates of the total flux of Ca²⁺ into the myoplasmic water space (Ca²⁺ input flux), i.e., the sum of the two voltage-activated flux components (Ca²⁺ entry and Ca²⁺ release) underlying the recorded Ca²⁺ transients. To obtain sufficiently high signal/noise ratios we performed these experiments at a voltage close to the maximum of inward current and Ca²⁺ transient amplitude. Three pulses of 100-ms duration depolarizing the membrane to +30 mV were applied at 30-s intervals and the recorded signals were averaged. To calculate the dynamics of intracellular Ca²⁺ binding and to estimate the Ca²⁺ input flux from the optical measurements, we used a model-based approach similar to that originally described by Baylor et al. (1983) and previously used for skeletal myotubes (Dietze et al., 1998, 2000; Ursu et al., 2001; Schuhmeier et al., 2003). A set of kinetic constants describing the intracellular binding sites that likely predominate under our conditions was taken from the literature and from our own experimental results obtained in C2C12 myotubes, and was used for the model calculations (Schuhmeier and Melzer, 2004; for more details, see Materials and Methods).

In some experiments with α_1S-expressing myotubes, we also applied the approach described recently to determine Ca²⁺ input flux in C2C12 myotubes equilibrated with a high concentration (15 mM) of EGTA in the pipette solution (Schuhmeier and Melzer, 2004). In this method, removal model parameters were determined by a least-squares fitting of model-calculated to measured Ca²⁺ transients in the time intervals after depolarizing pulses. This method was not generally used in the present investigation, because of low signal/noise ratios that made the numerical calculations difficult and because of possible suppression of Ca²⁺-induced Ca²⁺ release by the strong EGTA buffering. Two α_1S-expressing cells that were analyzed in this way showed removal parameter results and a time course of Ca²⁺ input flux comparable to those determined in C2C12 cells (Schuhmeier and Melzer, 2004). They also showed a phasic-tonic time course similar to that estimated for the α_1S-expressing cells in the present experiments with 0.1 mM EGTA in the pipette solution.

In addition to the Ca²⁺ input flux derived from the optical indicator signal, the flux of Ca²⁺ entry was determined from the electrically measured Ca²⁺ inward current. The transmembrane Ca²⁺ inward current density was converted to flux according to Eq. 3. The necessary volume/capacitance ratios (V_C) were measured by scanning dye-loaded and whole-cell patch-clamped GLT myotubes with a confocal microscope as described by Schuhmeier et al. (2003). Volume (corrected for the space occupied by nuclei) was approximately proportional to capacitance in the range 200–800 pF, with a best-fit proportionality factor of V_C = 0.26 l/F that was used for the calculation. The factor f_V was arbitrarily set to 1 (the upper bound of this value).

Fig. 5 A shows the averaged Ca²⁺ input flux records obtained at +30 mV in a number of cells expressing the four different α₁-subunits shown in Fig. 1. Mean values are displayed as thick lines and their standard errors as shaded areas. The corresponding Ca²⁺ entry flux traces derived from the Ca²⁺ inward currents are plotted in Fig. 5 B with the same scale (for comparison of flux amplitudes) but opposite in sign.

Even though the calculated absolute flux amplitudes are somewhat questionable because of uncertainties in the model parameters, a relative comparison shows some interesting details. Consistent with Fig. 3, the Ca²⁺ input flux was found to be largest in the α_1S-expressing myotubes whereas the Ca²⁺ entry flux was very small, indicating that essentially all the Ca²⁺ input flux resulted from SR Ca²⁺ release. α₁Aas(1592-clip), the brain α₁-subunit carrying the putative signal sequence for SR-TT junctional targeting, showed the second-largest flux amplitude. Here, however, the Ca²⁺ entry flux from the extracellular space was many times larger than in the case of α_1S. Therefore, a much larger part of the total estimated Ca²⁺ input flux resulted from Ca²⁺ entry and it appears difficult to determine which component of the Ca²⁺ input flux results from SR Ca²⁺ release and which from Ca²⁺ entry. A similar situation exists for α_1A and α_1C.

Based on previous physiological data, one should expect clear differences between the junctionally targeted and nontargeted channels in their effectiveness to elicit intracellular Ca²⁺ transients. When activated by extracellular electrical stimulation, α_1A-expressing myotubes had been reported to show much weaker force and Ca²⁺ responses than α_1C-expressing myotubes which was attributed to the lack of specific junctional targeting (Flucher et al., 2000). In contrast to this, under voltage-clamp conditions in the present experiments, both channel types produced approximately equal input flux amplitudes.

Estimating EC coupling gain

The ratio of Ca²⁺ transient amplitude to Ca²⁺ inward current has frequently been used as a measure of EC coupling gain (for references, see Bers, 2001). On the other hand, the ratio between total Ca²⁺ input flux, which includes Ca²⁺ release, and the flux of Ca²⁺ entry, defines a physically more meaningful gain (Wier et al., 1994). Using the flux determinations of Fig. 5, we determined average EC coupling gain factors by calculating the mean ratio between total Ca²⁺ input flux and Ca²⁺ entry flux in a broad time interval during the pulse (from 25 ms to 75 ms) excluding the rapid phases of activation and deactivation. If the absolute amplitudes of the fluxes were correctly determined, a value of 1 of the gain factor would mean that no secondary release of Ca²⁺ from intracellular stores is present, i.e., all measured Ca²⁺ changes result from Ca²⁺ entering from the extracellular space. For the α_1S-subunit, this gain factor was many times >1 (mean value 31.5 ± 4.4), consistent with the major contribution of the SR Ca²⁺ release to the Ca²⁺ transient and the negligible role of the Ca²⁺ current. For the three subunits that show no skeletal-type conformational coupling, the ratios were 3.2 ± 0.5 (α_1C), 3.9 ± 0.4 (α_1A), and 2.0 ± 0.3 (α₁Aas(1592-clip)). That is, quite consistent with the experiments of Fig. 3, there were no large differences between the three non-skeletal-type channels in their mean EC coupling gain.

Effects of SR depletion

These results indicate that Ca²⁺ entry makes a substantial contribution to the total Ca²⁺ input flux, with the exception of α_1S. However, considering the uncertainties in determining the absolute flux amplitudes (see above), it seems difficult to quantify the true fractional contribution. In particular, the value larger than unity for the gain factor of the non-junctionally targeted α_1A-subunit may result from a Ca²⁺ release component in addition to Ca²⁺ entry or from false assumptions in the calculation of the absolute flux amplitudes leading to overestimation of Ca²⁺ input flux, underestimation of Ca²⁺ entry flux, or both. We therefore performed experiments in which the SR was depleted of its stored Ca²⁺ by applying 30 μM cyclopiazonic acid (CPA), a blocker of the SERCA Ca²⁺ pump (Schuhmeier and Melzer, 2004), and 10 mM of the ryanodine receptor agonist caffeine (Herrmann-Frank et al., 1999). This procedure has been shown to drastically reduce the flux component resulting from SR Ca²⁺ release in C2C12 myotubes and should reveal the component that consists only of the Ca²⁺ entry through the voltage-activated Ca²⁺ channels (Schuhmeier and Melzer, 2004).

Fig. 6, A and B, demonstrates the depletion protocol. The measurements shown covered a time interval of 10 min. Application of CPA and caffeine (as indicated by the bars in Fig. 6 A) caused changes in baseline free [Ca²⁺] values calculated from the fluorescence ratio immediately before each voltage pulse that was applied (Fig. 6 B). The mean values for each group of cells are shown. In all cases a similar increase in baseline Ca²⁺ concentration occurred when CPA was applied, indicating that a discharge of similar amounts of Ca²⁺ from the SR took place and that the loading state of the SR had not been considerably different before the application of CPA.

Fig. 6, C and D, summarize the mean results for fluxes and gains for all four α₁ isoforms. Fig. 6 C shows the means of Ca²⁺ input flux and Ca²⁺ entry flux (plotted upward and downward, respectively), obtained in the three regions labeled a, b, and c (i.e., before and after CPA application and after caffeine application). Fig. 6 D displays the means of the individually calculated gains from the data in C. The initial gains were very similar to those determined in the previous series of experiments (Fig. 5). In the α_1S case (left column), the input flux amplitude dropped substantially after application of CPA, whereas the entry flux (L-type current) amplitude changed only a little. Little further change was observed when applying caffeine in addition to CPA, indicating that the CPA treatment had already released most of the Ca²⁺ stored in the SR, consistent with results in C2C12 myotubes (Schuhmeier and Melzer, 2004). In the other cases (columns 2–4), the relative change in input flux was considerably smaller on CPA application and showed only small further changes on application of caffeine. The fractions of the initial gain that remained after CPA application showed mean values of 12%, 58%, 54%, and 65% for α_1S, α_1C, α_1A, and α₁Aas(1592-clip), respectively. After caffeine application the fractional values were 8.7%, 64%, 56%, and 60%, respectively.

Fig. 7 presents the mean time course of Ca²⁺ input flux and Ca²⁺ entry flux induced by the +30 mV step depolarizations averaged over the intervals a, b, and c indicated in Fig. 6 B, respectively. During depletion, Ca²⁺ input flux remained phasic (i.e., exhibits a peak) in α_1C, α_1A, and α₁Aas(1592-clip) but loses the peak in α_1S (see inset). Fig. 8 evaluates both peaks (A) and end level (values at 95 ms, B) by plotting Ca²⁺ input flux versus Ca²⁺ entry flux. The dotted lines indicate a ratio (i.e., gain) of 1. In all four cases, the gain at the pulse end approaches unity after the CPA/caffeine treatment, as would be expected for full SR depletion and a correct description of cytoplasmic Ca²⁺ binding by the model. The reason for the larger deviation from unity gain in CPA/caffeine observed at the peak (Fig. 8 A) is unclear, but might be a remaining small reuptake activity of the SR that permits a transient residual Ca²⁺ release at the onset of the depolarization.

The records in Fig. 7, column 3 (c), represent, for each series of experiments, the maximum of depletion that could be obtained under these conditions. By subtracting this component from the record in column 1 (a) we calculated the fraction of the control flux that is eliminated by CPA and caffeine (Fig. 7, column 4 (d)). Before subtracting the full-depletion response (c), we compensated for the rundown in Ca²⁺ entry flux by multiplying entry and input flux with scaling factors to obtain equal entry flux amplitudes for each row. The depletion-sensitive component showed two phases, a rapidly and a slowly declining one. The rapidly declining phase, i.e., the peak above the dashed line in Fig. 7, column 4 (d), was largest in α_1S (A), intermediate in α_1C (B), and small in α₁Aas(1592-clip) (D). It was absent in α_1A (C). The slow component (indicated by the dashed lines) was similar in size for α_1C, α_1A, and α₁Aas(1592-clip), but considerably larger for α_1S. A tentative interpretation for these observations will be given in the Discussion in conjunction with Fig. 9.

FIGURE 9.

Ca²⁺ mobilization from extra- and intracellular sources by voltage-dependent Ca²⁺ channels of different properties. The scheme summarizes the interpretation of experimental data obtained in this study. (A) The skeletal muscle-type α_1S responds to depolarization with an intramolecular charge movement that initiates direct conformational coupling to the RyR1 causing voltage-dependent Ca²⁺ release (VDCR). This leads to a primary Ca²⁺ signal in the junctional gap. The small and slow Ca²⁺ inward current plays a negligible role in Ca²⁺ mobilization and is omitted in the scheme. The released Ca²⁺ enhances further Ca²⁺ release leading to a secondary Ca²⁺-induced Ca²⁺ release flux component (CICR) that has phasic and tonic components. VDCR and CICR together make up the Ca²⁺ input flux. (B) The cardiac muscle-type DHPR likewise responds to depolarization with an intramolecular charge movement that also results in a primary Ca²⁺ signal but by voltage-induced Ca²⁺ inward current (Ca²⁺ entry) instead of VDCR. This also leads to CICR, which, together with the Ca²⁺ entry flux, makes up total Ca²⁺ input flux. (C) The brain α_1A-subunit, which is not positioned close to the ryanodine receptors, generates a rapid global Ca²⁺ entry flux signal, although probably a much slower and smaller primary junctional Ca²⁺ signal than α_1S or α_1C, leading to ineffective CICR (lacking the phasic component). α₁Aas(1592-clip) shows a phasic component unlike α_1A but not as large as in α_1S or α_1C, probably because not enough α₁Aas(1592-clip) subunits become positioned close to the RyRs. See Discussion for further explanations.

DISCUSSION

In this study, four types of Ca_V-channels were expressed and investigated in dysgenic GLT myotubes (Powell et al., 1996). These channels differ in their reported cellular targeting and in their putative way of communication with the SR Ca²⁺ release channels (see Fig. 1). By studying Ca²⁺ currents and Ca²⁺ transients under voltage-clamp conditions, we identified characteristics of Ca²⁺ signaling corresponding to these differences. In contrast to previous studies on reconstituted channels in dysgenic myotubes (e.g., García et al., 1994; Jurkat-Rott et al., 1998; Ahern et al., 2001), we applied a more rigorous kinetic analysis and estimated the flux of Ca²⁺ mobilization whose time course is concealed in the Ca²⁺ transients by the kinetics of Ca²⁺ binding to the indicator dye and to intrinsic sites. Further, we quantified the gain of Ca²⁺ mobilization by determining the ratio of the total Ca²⁺ input flux to the flux of Ca²⁺ entry from the extracellular space.

Comparison between α_1S and α_1C

The α_1S channels generated Ca²⁺ input flux with a time course similar to that found in normal mammalian myotubes (Dietze et al., 1998; Ursu et al., 2001; Schuhmeier et al., 2003; Schuhmeier and Melzer, 2004) and mature muscle fibers (Delbono and Stefani, 1993; García and Schneider, 1993; Shirokova et al., 1996; Csernoch et al., 1999a,b; Ursu et al., 2004), providing evidence that the rescued Ca²⁺ release in this expression system shows the typical kinetic hallmarks of skeletal muscle type EC coupling, including the rapid partial inactivation (Melzer et al., 1984).

Despite the fundamentally different mechanisms of EC coupling in α_1S- and α_1C-expressing cells, the time courses of Ca²⁺ input flux were surprisingly similar (Fig. 7). As a major difference, depletion of the SR reduced primarily the phasic component in α_1C, whereas it eliminated both phasic and tonic components in α_1S (Fig. 7, (d), B and A, respectively). The reason is that the tonic component of α_1C-expressing cells results largely from the Ca²⁺ inward current, whereas in α_1S-expressing cells it is a flux from the SR, controlled by the DHPR voltage sensor (Csernoch et al., 1993). This is depicted in the idealized scheme of Fig. 9 (A and B). In both α_1S- and α_1C-expressing GLT myotubes, a pedestal flux of Ca²⁺ is activated by the membrane depolarization. Yet, in the α_1C case this flux component enters the myoplasm from the extracellular space (Fig. 9 B), whereas in the case of α_1S it originates from the sarcoplasmic reticulum (Fig. 9 A, VDCR).

Both rapid synchronous activation by conformational coupling in α_1S-expressing cells and rapid voltage activation of Ca²⁺ entry in α_1C-expressing cells likely cause similar fast primary Ca²⁺ signals in the junctional gap that probably lead to similar phasic components of CICR (Fig. 7).

Comparison between α_1C- and α_1A-controlled Ca²⁺ fluxes

Strong differences had been found between α_1C- and α_1A-expressing dysgenic myotubes in their responsiveness to extracellular electrical stimulation: Whereas α_1C-expressing cells responded frequently with a Ca²⁺ transient or contraction, α_1A-expressing cells responded only rarely (Adams et al., 1994; Flucher et al., 2000). The similar size of the fluxes obtained in the two groups of cells in our voltage-clamp experiments seemed, therefore, surprising (Fig. 5). At closer look, however, differences could be detected. The Ca²⁺ input flux component in α_1A cells that is sensitive to SR depletion by CPA and caffeine (Fig. 7 C, d) lacks the pronounced peak seen in the corresponding component of α_1C cells (Fig. 7 B, d). In addition, the voltage-dependence of the Ca²⁺ signals in α_1C cells was different. It was shifted to more negative potentials, with respect to the voltage-dependence of Ca²⁺ inward current activation (Fig. 4 B). This is a characteristic also found in heart cells and has been attributed to the stronger driving force for Ca²⁺ entry at more negative potentials leading to a higher gain of Ca²⁺-induced-Ca²⁺ release (Wier et al., 1994). It is a consequence of the local control of Ca²⁺-induced Ca²⁺ release that depends on local single-channel currents rather than on global Ca²⁺-current amplitudes (Cheng and Wang, 2002). In contrast, in α_1A-expressing cells the voltage-dependence of Ca²⁺ signal and Ca²⁺ current was more similar (Figs. 3 and 4 C). These results point to the presence of a more efficient Ca²⁺-induced Ca²⁺-release component in α_1C-expressing cells compared to α_1A-expressing cells.

Because the transient CPA- and caffeine-sensitive flux component present in α_1C but not in α_1A cells occurs at the beginning of the depolarizing voltage step, it may be responsible for the much more frequent appearance of Ca²⁺ signals upon short extracellular stimuli in α_1C-expressing myotubes (Flucher et al., 2000). As suggested by Flucher et al. (2000), a plausible reason is the specific targeting of α_1C to the sarcolemma-SR junctions. Another possibility for the lower responsiveness of α_1A-expressing myotubes would be a higher failure rate to elicit all-or-none action potentials, even though it is difficult to see how such a failure would come about.

Gain determinations

The amplification process in Ca²⁺-induced Ca²⁺ release has been studied in detail in cardiac myocytes and is usually quantified by calculating an EC coupling gain factor (for review, see Bers, 2001). Previous determinations of global gain derived from whole-cell measurements in heart cells were based on estimates of integral (total) Ca²⁺ (e.g., Shannon et al., 2000) or of the corresponding Ca²⁺ fluxes (e.g., Wier et al., 1994). The latter approach was also used in the present study and allowed a quantitative comparison of Ca²⁺ entry flux and total Ca²⁺ input flux to the myoplasm.

As a second approach to estimating amplification by Ca²⁺ release, we compared the change in intracellular Ca²⁺ caused by identical trigger pulses before and after depleting the SR of its stored Ca²⁺. In our experiments, the Ca²⁺ input flux controlled by the α_1S-subunit was almost completely suppressed by the depletion procedure, demonstrating that it originated almost exclusively from SR Ca²⁺ release. In the presence of the other Ca_V channels tested, the Ca²⁺ current itself made a relatively large contribution to the total Ca²⁺ input flux, but not even in the case of α_1A was secondary Ca²⁺ release completely absent.

Our experiments indicated a lower gain in α_1C-transfected GLT cells (+30 mV) than in mature heart cells, for which values close to 10 have been estimated in a voltage range of comparable fractional activation (Wier et al., 1994). Reasons might be a higher coupling fidelity of RyR2 in cardiac myocytes compared to RyR1 in skeletal myotubes or a steeper Ca²⁺ gradient produced by the SERCA pump. In heart cells, gain was shown to exhibit a strong dependence on the concentration of Ca²⁺ in the SR lumen (Shannon et al., 2000). In the myotubes, a rather low rate of uptake, likely associated with establishing a smaller gradient, is indicated by the slow change of the signal at the end of a depolarization, which has been observed by us and others (García and Beam, 1994). However, strong differences in SR loading between the four constructs tested is unlikely, since a similar response on application of CPA/caffeine could be observed (see Fig. 6 B).

α₁Aas(1592-clip) characteristics

Surprisingly, α₁Aas(1592-clip)-expressing cells did not show a fundamentally different pattern than α_1A-type cells despite the observed differences in junctional targeting. Both Ca²⁺ inward current and Ca²⁺ input flux were larger than for α_1A, but regarding gain they can at best be described as intermediate between α_1A and α_1C cells. The smaller gain at larger current density is reminiscent of the situation in heart cells where β-adrenergic up-regulation of Ca²⁺ inward current does not increase the Ca²⁺ signal proportionally (Song et al., 2001). A fast CPA/caffeine-sensitive component was detectable in α₁Aas(1592-clip) (Fig. 7 D, d), but its amplitude was smaller than in α_1C. Also, the voltage-dependence of Ca²⁺ inward current and Ca²⁺ signal (Figs. 3 and 4) resembled more α_1A than α_1C. The significantly larger Ca²⁺ input flux in α₁Aas(1592-clip) compared to α_1A resulted mainly from the larger Ca²⁺ entry flux, not from an increase in gain.

From the present and previous results it seems that the C-terminal signal sequence of the L-type channel introduced into α₁Aas(1592-clip) improves the level of expression but may not establish full α_1C-type Ca²⁺-induced Ca²⁺ release despite the junctional targeting. In dual immunostaining experiments for the localization of α₁-subunits and RyRs, a cell is labeled colocalized if regions of colocalization are detectable (Flucher et al., 2000). This criterion makes a quantitative comparison with electrophysiological measurements difficult, because an uncertain percentage of the Ca_V channels that participate in the functional signals may not be colocalized with RyR1. Moreover, the density of channels in the junction, a crucial determinant for establishing efficient cardiac type EC coupling, may well be considerably smaller in α₁Aas(1592-clip)-expressing cells than in α_1C cells. The global Ca²⁺ current density was comparable, but the open probability of α_1A in dysgenic myotubes is thought to be higher than that of α_1C. This follows from the much larger whole-cell current measured per voltage-sensor charge movements (Adams et al., 1994). Longer openings provide more local Ca²⁺ per channel. However, it appears to be the amount of Ca²⁺ supplied immediately on opening of a Ca_V1.2 channel that triggers Ca²⁺ release (Song et al., 2001). Therefore, longer openings are not necessarily more effective than short openings and are unlikely to compensate for a lower channel density in the junction. Ca²⁺ channels that are not specifically targeted, such as the α_1A channels, may generate a slowly rising junctional Ca²⁺ transient from diffusional delays, which may still cause a secondary efflux of Ca²⁺ from the SR (CICR in Fig. 7 C). However, this release is less synchronized, explaining the different shape of the CPA/caffeine-sensitive component in Fig. 7 C (d), which lacks a peak. α₁Aas(1592-clip) which is targeted to the junction may not reach a sufficient density there to provide the same local trigger flux of Ca²⁺ as α_1C. This may be the reason why cells expressing this isoform show a behavior intermediate between Fig. 9, B and C.

CONCLUSION

In summary, we compared, in the same cellular expression system, properties of interaction of different Ca_V channel α₁-subunits with the ryanodine receptor RyR1. The observations made here in voltage-clamped myotubes helped us to reconcile previous results from immunocytochemical localization studies and measurements of action-potential stimulated Ca²⁺ transients. In these studies, introducing the putative junctional targeting sequence into α_1A had been shown to increase the response frequency approximately ninefold, but not nearly to the level of α_1C-expressing cells (140-fold; see Flucher et al., 2000). We conclude that these differences result from different junctional channel densities and single-channel gating properties leading to characteristic local Ca²⁺ signals near the RyRs. To investigate the local functional properties of Ca²⁺ signaling of heterologously expressed channels in further detail will require more refined methods. A promising recent approach has been the recording of Ca²⁺ currents, i.e., sparklets and sparks from small junctional regions of patch-clamped cardiac myocytes (Wang et al., 2001).