Strong Binding of Myosin Heads Stretches and Twists the Actin Helix

Abstract

Calculation of the size of the power stroke of the myosin motor in contracting muscle requires knowledge of the compliance of the myofilaments. Current estimates of actin compliance vary significantly introducing uncertainty in the mechanical parameters of the motor. Using x-ray diffraction on small bundles of permeabilized fibers from rabbit muscle we show that strong binding of myosin heads changes directly the actin helix. The spacing of the 2.73-nm meridional x-ray reflection increased by 0.22% when relaxed fibers were put into low-tension rigor (<10 kN/m²) demonstrating that strongly bound myosin heads elongate the actin filaments even in the absence of external tension. The pitch of the 5.9-nm actin layer line increased by ∼0.62% and that of the 5.1-nm layer line decreased by ∼0.26%, suggesting that the elongation is accompanied by a decrease in its helical angle (∼166°) by ∼0.8°. This effect explains the difference between actin compliance revealed from mechanical experiments with single fibers and from x-ray diffraction on whole muscles. Our measurement of actin compliance obtained by applying tension to fibers in rigor is consistent with the results of mechanical measurements.

INTRODUCTION

In the first kinetic model of muscle contraction (A. F. Huxley, 1957), the compliance of the actin and myosin filaments was assumed to be negligible compared to that of the actin-myosin cross-bridges, which produce active tension and/or sarcomere shortening. The assumption is critical for the estimation of the size of the power stroke in isometrically contracting muscle fibers, and has implications in calculations of muscle energetics and contraction efficiency. The results of mechanical experiments with single intact muscle fibers (A. F. Huxley and Simmons, 1973; Ford et al., 1981) were consistent with this hypothesis, suggesting that compliance of the thin and thick filaments is <20% of sarcomere compliance which is ∼4 nm/T₀ per half-sarcomere, or ∼0.4%/T₀, where T₀ is isometric tension. Other experiments led to higher estimates of actin compliance, up to 20–30% of sarcomere compliance (Julian and Morgan, 1981; Bagni et al., 1990). More recently, in x-ray diffraction experiments with whole frog muscles the compliance of actin and myosin filaments was found to be comparable to that of the cross-bridges, 0.2–0.3%/T₀ (H. E. Huxley et al., 1994; Wakabayashi et al., 1994). This finding was later confirmed by mechanical experiments with single permeabilized (Higuchi et al., 1995) and intact (Linari et al., 1998) muscle fibers. Linari and colleagues measured stiffness of contracting and rigor frog muscle fibers as a function of the sarcomere length between 2.05 μm and 2.15 μm. In this range, the length of the overlap zone between the thin and thick filaments is maximal and active tension is constant, so that the slope of the relationship between instantaneous fiber compliance and sarcomere length is a direct mechanical measure of actin compliance in the I-band of a sarcomere. A 0.15–0.2%/T₀ compliance of the actin filaments obtained by Linari et al. (1998) was somewhat lower than that found in the x-ray experiments. More recent x-ray diffraction experiments with whole intact frog muscles performed using highly collimated and very bright synchrotron x-ray sources gave even higher figures for actin compliance than the earlier x-ray experiments (Takezawa et al., 1998; Bordas et al., 1999; 0.38%/T₀ and 0.42%/T₀, respectively), i.e., about twice that found in the mechanical experiments of Linari et al. (1998). These figures look puzzling because the total compliance of a half-sarcomere in a contracting intact frog muscle fiber is of the same order, 0.35–0.4%/T₀ (Ford et al., 1977; Linari et al., 1998); although in addition to the actin compliance it contains compliances of the cross-bridges, myosin filaments, and the Z-lines.

A possible explanation for the difference between the mechanical and the x-ray estimations of actin compliance is that the strong binding of the myosin heads leads to an elongation of the actin filaments even without external load. If this is the case, a change in the number of myosin heads strongly bound to actin after a release or a stretch of a contracting muscle can contribute to the observed change in the spacing of the actin-based x-ray reflections leading to an over- or underestimation of actin compliance. Here, we verified this hypothesis by comparison of the spacing of the actin-based x-ray reflections in the diffraction patterns collected from small bundles of rabbit muscle fibers in the relaxed state, where myosin heads are detached from actin, and in rigor, where all heads are strongly bound to actin. Special efforts were made to keep rigor tension below 10 kN/m² so that the changes in spacing of the actin reflections were induced by binding of myosin heads per se, not by tension produced by rigor cross-bridges. We also measured the change in the spacing of the actin-based reflections induced by stretches of bundles of muscle fibers in rigor where the number of myosin heads bound to actin is constant and maximal.

The experiments were carried out on bundles of three to five permeabilized fibers from rabbit skeletal muscle. This preparation has an advantage compared to whole muscle used by H. E. Huxley et al. (1994), Wakabayashi et al. (1994), Takezawa et al. (1998), and Bordas et al. (1999), as homogeneity of sarcomere length can be achieved and the chemical environment of contractile proteins is controlled. An obvious disadvantage of small bundles of muscle fibers compared to whole muscles is a smaller diffracting mass and, in consequence, lower intensity of the x-ray reflections.

Although changes in length of actin filaments are <0.5%, precise knowledge of the origin and value of actin compliance is important for the interpretation of mechanical and structural experiments with contracting muscle fibers and for calculating the elementary mechanical parameters of the myosin motor in muscle (Goldman and H. E. Huxley, 1994; A. F. Huxley and Tideswell, 1996, 1997).

METHODS

Muscle fibers

Bundles of fibers from rabbit psoas muscle were prepared, glycerinated, and stored as described previously (Thirlwell et al., 1994). Small bundles of 3–5 single fibers were dissected under a microscope. The ends of the bundles were tied together either by a knot or by a hair segment to improve their mechanical stability and to maintain the same sarcomere length in all fibers in the bundle. Before mounting in the experimental trough, the bundles were additionally treated by soaking in relaxing solution with 0.5% Triton X-100 for 15–30 min. One end of a 3.1–3.6 mm long bundle was glued with shellac dissolved in ethanol (50/50% v/v) to the force transducer and another end to the motor, as described by Bershitsky and Tsaturyan (2002); the bundle was mounted horizontally and aligned and sarcomere length was adjusted to 2.4 μm by monitoring the position of the first-order diffraction lines from a He-Ne laser beam (Bershitsky et al., 1996). The bundles were put in rigor at 0°C in the presence of 10 mM 2,3-butanedione-monoxime (BDM) to maintain low rigor tension (<10 kN/m²) and uniform sarcomere length (Bershitsky et al., 1996). Relaxing solution contained (in mM) 100 MOPS (3-[N-morpholino]-propanesulfonic acid), 5 EGTA (ethylene glycol bis-(β-aminoethyl ether)N,N,N′,N′ tetraacetic acid), 5 MgATP, 2 Mg²⁺, 80 potassium propionate, 5 DTT (dithiothreitol); rigor solution had the same composition, except no ATP was added and potassium propionate concentration was increased to 100 mM. The ionic strength was 150 mM, pH 7.1, at 20°C.

X-ray diffraction

Data were collected at station ID02 at ESRF (European Synchrotron Radiation Facility, Grenoble, France, wave length 0.0995 nm, flux 10¹³ photons·s⁻¹) using FReLoN CCD detector operating at 1024 × 1024 pixel mode with a sample-to-detector distance of 2.4 m; pixel size corresponded to 6.94 × 10⁻⁴ nm⁻¹ in reciprocal space. The beam size on the sample was 240 μm vertically and 400 μm horizontally (full width at half-maximal intensity). The diffraction patterns were collected when the bundle was suspended in air for 2–3 s in a water-saturated atmosphere at ∼5°C. Between exposures the set-up was moved along the bundle axis to spread x-ray radiation uniformly along the whole length of the bundle and thus minimize local radiation damage. The detector was off-set horizontally so that the 5.9-nm and 5.1-nm actin layer lines were seen on both sides of the detector and the 2.73-nm actin meridional reflection was seen only on one side. The diffraction patterns collected during 100 ms long exposures were corrected for dark noise, read-out noise, and the spatial distortion of the detector using software provided by ESRF. Bundle exposures to the x-rays in relaxed and rigor states were alternated so that the total exposure of each bundle was up to 1 s. To obtain more photons in the 2.73-nm reflection in the relaxed state the exposure of each bundle in this state was 30–50% longer than in rigor, where the intensity of the 2.73-nm reflection was higher. Data collected from 17 different bundles in the same states were added together to improve the signal-to-noise ratio.

In the experiments to measure actin compliance in rigor the following protocol was used. A bundle of muscle fibers in the rigor state was suspended in air for ∼1 s, then exposed to the x-rays for 50 ms at low (5–10 kN/m²) tension, then stretched with the motor by ∼2% of their length (change in sarcomere length 1–2 nm per half-sarcomere) and subjected to another 50 ms long exposure at the elevated tension (65–70 kN/m²) 0.5 s after the first exposure (see Fig. 4). Then the bundle was released to its initial length and returned to the rigor solution. The protocol was repeated 10–14 times in each of four bundles, exposing different segments of the bundle. Data collected during the low-tension and high-tension exposures in all bundles were added together to improve the signal-to-noise ratio.

FIGURE 4.

Protocol used for measurement of actin compliance in rigor. From top to bottom: an example of records of change in the length of the bundle of muscle fibers, rigor tension, and signal from a pin photodiode showing times of opening of the x-ray shutter.

Data analysis

Upper and lower halves of each diffraction pattern were averaged to improve the signal-to-noise ratio. The intensity of a peak was obtained by integration of a diffraction pattern in the radial direction, which was then plotted against the meridional spacing. The background under a peak was subtracted using a cubic polynomial spline. Then the position of the peaks of a reflection was determined either using a fit of the upper half of the peak with a Gaussian of appropriate width and spacing or by measuring the center of gravity of the upper half of the peak (H. E. Huxley et al., 1994). Both methods gave the same result within 0.03% for the peak position normalized for the distance between the peak and the center of the pattern. In the first series of experiments the total exposure time was 9.5 s in the relaxed state and 6.7 s in low-tension rigor. In the experiments with stretches and releases of rigor muscles the exposure was 2.3 s in each state. The noise in the data collected from a single bundle of muscle fibers was too big for determination of the peak position with reasonable accuracy. For this reason we were unable to perform sample to sample statistical analysis as it was done previously by groups working with whole muscles. The standard error of the peak position in the summed patterns was estimated from the deviation between the data points and the Gaussian fit using a procedure described by Richter (1995).

RESULTS

Changes in the spacing of the actin-based reflections during transition from the relaxed state to low-tension rigor

Fig. 1 shows the two-dimensional diffraction patterns collected from 17 bundles of muscle fibers in the relaxed (upper half) and low-tension rigor (lower half) states. The spacing of the 2.73-nm actin meridional reflection on the right side of the pattern and the spacing of the 5.9-nm and 5.1-nm layer lines on both sides were used for measuring the changes in the geometry of the actin helix.

FIGURE 1.

X-ray diffraction patterns collected in relaxed (upper half) and low-tension rigor (lower half) states from 17 muscle fiber bundles. The equator is vertical. White corresponds to higher intensity and a logarithmic gray scale is used. The center of the patterns appears overexposed to bring out the weaker features toward the edge of the patterns. The black rectangle in the center of the pattern is a metal beam stop to shield the detector from the direct x-ray beam. For each state only one-half of the averaged pattern is shown. The 5.9-nm, 5.1-nm, and 2.73-nm actin reflections are marked by arrows. White rectangles show the area of integration along the reciprocal radius used for calculation of the spacing of the reflections (Figs. 2 and 3). The total exposure of the bundles was 9.5 s in the relaxed state and 6.7 s in rigor. Rigor tension was <10 kN/m².

The meridional intensity profiles of the 2.73-nm actin meridional reflection is shown in Fig. 2. To minimize the effect of arching of the reflections arising from imperfect alignment of actin filaments in the fibers, the intensities were integrated in a narrow, near-meridional region of ±0.014 nm⁻¹ (Fig. 1). When relaxed fibers were transferred to rigor solution, the intensity of the ∼2.73 nm reflection increased ∼4.5 times (note that exposure in the relaxed state in Figs. 1 and 2 was ∼1.5 times longer than in rigor) and its position moved toward the center of the pattern. As this reflection originates from the ∼2.73-nm true axial repeat of the actin monomers in the thin filaments, it can be used as a model-independent measure of the distance between neighbor actin monomers. There is a high-angle shoulder on the 2.73-nm reflection that is especially pronounced in the relaxed pattern (Fig. 2), probably originating from a myosin layer line. To avoid any possible influence of this shoulder on our estimation of the spacing of the 2.73-nm reflection, only the upper half of the peak was used for measuring the position of the reflection (Fig. 2). The shift of the peak position of the 2.73-nm reflection toward the center suggests that the average axial distance between neighboring actin monomers increases by 0.22 ± 0.02% in low-tension rigor compared to the relaxed state (Fig. 2).

FIGURE 2.

Meridional profile in the region of the 2.73-nm meridional reflection in the relaxed state (thin line) and in rigor (thick line). (A) Same data as in Fig. 1 integrated along the reciprocal radius from −0.013 nm⁻¹ to +0.013 nm⁻¹ (Fig. 1), background subtracted. (B) Same profiles as in A normalized for the peak intensity of the 2.73-nm reflection. Black dotted lines in B show the Gaussian fits of the upper halves of the peaks.

Fig. 3 shows the intensity profiles of the 5.9-nm and 5.1-nm actin layer lines in the relaxed state and low-tension rigor in both left and right sides of the diffraction patterns (see Fig. 1). As the spacing of the meridional spot on the 5.9-nm layer lines is different from that of the rest of the layer line and probably originates from structures different from the actin helix (H. E. Huxley and Brown, 1967; H. E. Huxley et al., 1994; Wakabayashi et al., 1994; Bordas et al., 1999), the spacing of the actin layer lines was measured in the off-meridional region of reciprocal radii R between 0.02 nm⁻¹ and 0.04 nm⁻¹, avoiding the meridional spot as marked by rectangles in Fig. 1. A relatively low upper limit was chosen to minimize the effect of arching of the layer lines. There is a high-angle shoulder on the 5.1-nm layer lines and a hint of a shoulder on the 5.9-nm layer line, which probably originate from myosin-based reflections (Figs. 1 and 3). To avoid any possible influence of these reflections on the results of our analysis, only the top halves of the peaks were used for spacing measurements. The transition from relaxed state to rigor induced opposite changes in the positions of the peaks on the 5.9-nm and 5.1-nm layer lines: the 5.9-nm peaks moved toward the meridian whereas the 5.1-nm layer line moved away (Fig. 3). The intensity profiles in the left and right halves of the pattern were very similar (Fig. 3), suggesting that the difference between them can be attributed to photon noise and heterogeneous response of the detector, so that the difference between the measurements of the spacing change in the left and right halves of the pattern can be used as an estimate of absolute experimental error. The spacing of the 5.9-nm layer line increased by 0.61 ± 0.07% and 0.64 ± 0.06% in the left (L) and right (R) sides of the pattern, respectively, whereas the spacing of the 5.1-nm layer line decreased by 0.22 ± 0.08% (L) and 0.29 ± 0.1% (R).

FIGURE 3.

Meridional profiles of the 5.1-nm and 5.9-nm actin layer lines in the relaxed state (thin line) and in rigor (thick line). Panels A and C and B and D correspond to the left and right sides of the pattern (Fig. 1), respectively. (A and B) Same data as in Fig. 1 integrated along the reciprocal radius R from 0.02 nm⁻¹ to 0.04 nm⁻¹, background intensity subtracted. (C and D) Same profiles as in A and B normalized for the intensity of the peaks of the 5.1-nm and 5.9-nm layer lines, respectively. Open and closed symbols in C and D represent data points for relaxed and rigor states, correspondingly; solid lines are the Gaussian fits to the upper halves of the peaks.

These changes in the spacing of the 5.1- and 5.9-nm actin layer lines suggest that the ∼5.1-nm pitch of the right-handed generic actin helix decreases whereas the ∼5.9-nm pitch of the left-handed actin helix increases. At a given axial repeat d and helical angle θ, the pitches of the 5.9-nm and 5.1-nm helices, d_5.9 and d_5.1, and of the long (∼36-nm) helix, D, can be determined using formulas d_5.9 = 2πd/θ, d_5.1 = 2πd/(2π − θ), and D = dπ/(π − θ). By converting the first and the second formulas, estimates of the actin helix parameters d and θ are obtained from the measured pitches of the 5.9- and 5.1-nm layer lines, d_5.9 and d_5.1:

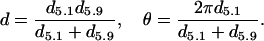The results of estimations of changes in d (Δd/d) and in θ (Δq) during the transition from relaxed state to rigor derived from our measurement of d_5.9 and d_5.1 using these formulas, as well as the results of measurements of Δd/d from the position of the 2.73-nm reflection, are presented in Table 1. The helical angle θ was 166.76 ± 0.15° (L) and 166.92 ± 0.13° (R) in the relaxed state and decreased to 166.02 ± 0.06° (L) and 166.08 ± 0.07° (R) when bundles of muscle fibers were transferred to low-tension rigor. The estimated pitch of the long actin helix D was 37.12 ± 0.42 nm (L) and 37.55 ± 0.37 nm (R) for the relaxed state and 35.15 ± 0.15 nm (L) and 35.31 ± 0.19 nm (R) in rigor.

TABLE 1.

Estimated changes in length d and helical angle θ of the actin helix in low-tension rigor with respect to their values in the relaxed state

Reflections used	Δd/d, %	Δθ, °
2.73-nm, right side	0.22 ± 0.02
5.9-nm and 5.1-nm, left/right side	0.17 ± 0.07/0.14 ± 0.06	−0.74 ± 0.16/−0.84 ± 0.15

Wakabayashi et al. (1994) and Bordas et al. (1999) reported that in intact frog muscle activation itself induces shortening of actin filaments by ∼0.1%. To estimate a possible effect of activation on the length of the thin filaments in our preparations of permeabilized rabbit muscle fibers, we compared the spacing of the 2.73-nm meridional reflection in the relaxed state with that in the presence of Ca²⁺ (5 mM CaEGTA) in the conditions where force generation by myosin heads was depressed by adding 50 mM BDM and 30 mM inorganic phosphate. The solution also contained 5 mM MgATP, 1 mM Mg²⁺, pH 7.0, the ionic strength 0.15 M. Tension produced by muscle bundles in this solution was <10 kN/m² and stiffness measured by tension responses to step stretches by ∼2 nm per half-sarcomere completed in 0.15 ms was <5% of that in rigor. The total x-ray exposure of 17 muscle bundles in this solution was 9.5 s, the same as that in relaxing solution. The difference in the spacing of the 2.73-nm meridional reflection between the relaxed state and the low-tension low-stiffness contraction in the presence of BDM and phosphate was within ∼0.03% error of our measurements (data not shown).

Changes in the spacing of actin-based reflections due to stretch of muscle in rigor

The data presented in Figs. 2 and 3 and in Table 1 suggest that strong binding of myosin heads elongates the actin filaments even in the absence of external force. When contracting muscle is stretched or allowed to shorten at a moderate speed, the number of myosin heads strongly bound to actin increases or decreases, respectively (Lombardi and Piazzesi, 1990; Stehle and Brenner, 2000). This change should directly affect the length of the actin filaments. For this reason the observed changes in the spacing of the actin-based x-ray reflections in the experiments with relatively slow changes in length of contracting muscles reflect not only a true compliance of the actin filaments but also a change in the actin helix due to a change in the number of myosin heads strongly bound to actin.

To measure actin compliance in conditions where the number of myosin heads strongly bound to actin remains constant, we compared the spacing of actin-based reflections from fiber bundles in low- and high-tension rigor. For this, a ramp stretch was applied to a bundle of muscle fibers in rigor and the diffraction patterns were recorded during 50 ms long periods before and after the stretch (Fig. 4). Tension level before the stretch was always <10 kN/m² (full range 5–10 kN/m²) whereas “high-tension” level was between 65 kN/m² and 70 kN/m² at the time of x-ray exposure. The patterns in low- and high-tension rigor collected from four bundles are shown in Fig. 5. The changes in spacing of the 2.73-nm, 5.1-nm, and 5.9-nm actin-based layer lines were measured using the same procedure as described above for relaxed state and rigor.

FIGURE 5.

X-ray diffraction patterns collected from four bundles of muscle fibers in rigor using the protocol shown in Fig. 4. Upper and lower halves of the patterns correspond to low- and high-tension rigor, respectively. Total exposure in each state was 2.3 s.

The meridional profiles of the 2.73-nm meridional reflection in low- and high-tension rigor are shown in Fig. 6. Stretch of rigor muscle led to a decrease in the width of the reflection, to an increase in its intensity, and to a movement of the peak toward the center (Fig. 6). The normalized decrease in the spacing of the 2.73-nm meridional reflection, Δd/d, due to applied tension was 0.14 ± 0.01% (see also Table 2). The meridional profiles of the 5.1-nm and 5.9-nm actin layer lines in low- and high-tension rigor are shown Fig. 7. The intensity profiles in the two halves of the pattern were similar, differing only because of experimental noise. Both the 5.1-nm and 5.9-nm peaks moved toward the center after the stretch demonstrating elongation of both 5.1-nm and 5.9-nm generic actin helices upon the applied load. Change in the spacing of the 5.1-nm reflection (0.31 ± 0.07%, L, and 0.34 ± 0.11%, R) was more than twice that of the 5.9-nm layer line (0.1 ± 0.03%, L, and 0.15 ± 0.06%, R). This means that the changes in the pitch of the 5.9-nm actin generic helix were smaller than those of the 5.1-nm helix, and the helical angle θ increased by 0.18 ± 0.05° (L) and 0.19 ± 0.1°(R) when the thin filaments were stretched by applied tension (Table 2). Calculations of the changes in the axial distance d and helical angle θ between neighbor monomers in the actin helix from the spacings of the 5.1-nm and 5.9-nm layer lines are shown in Table 2.

FIGURE 6.

Meridional profiles of the 2.73-nm actin meridional reflection in low- and high-tension rigor (thin and thick lines, respectively). (A) Same data as in Fig. 5, same integration range as in Fig. 2. (B) Profiles of the peaks normalized for maximal intensity; dotted lines show the Gaussian fits to the upper halves of the peaks.

TABLE 2.

Estimated changes in length d and helical angle θ of the actin helix in high-tension rigor compared to low-tension rigor

Reflections used	Δd/d, %	Δθ, °
2.73-nm, right side	0.14 ± 0.01
5.9-nm and 5.1-nm, left/right side	0.21 ± 0.07/0.25 ± 0.13	+0.18 ± 0.05/+0.19 ± 0.1

FIGURE 7.

Meridional profiles of the 5.1-nm and 5.9-nm actin layer lines in low- and high-tension rigor (thin and thick lines, respectively). Panels A and C and B and D correspond to the left and right sides of the pattern (Fig. 5), respectively. (A and B) Same data as in Fig. 5, integrated along the reciprocal radius R from 0.02 nm⁻¹ to 0.04 nm⁻¹, background intensity subtracted. (C and D) Same profiles as in A and B normalized for the intensity of the peaks of the 5.1-nm and 5.9-nm layer lines, respectively. Open and closed symbols in C and D represent data points for low- and high-tension rigor, correspondingly; solid lines are the Gaussian fits to the upper halves of the peaks.

DISCUSSION

Changes in the length of actin filaments due to strong binding of myosin heads

Here we report that binding of rigor myosin heads per se induces an elongation of the axial repeat between neighbor actin monomers in the thin filaments. A myosin-induced rearrangement of actin filaments was detected by fluorescent measurements that revealed a change in radial position of a probe on Cys374 (Moens and dos Remedios, 1997) and reorientation of several probes attached to different amino acids or to nucleotide in actin (Borovikov et al., 2004). The ∼0.006 nm (0.0022 × 2.73 nm) change in axial repeat d reported here is too small to be detectable using fluorescent probes although it may be a part of the same rearrangement. A plausible assumption, which we use in calculations below, is that this rearrangement involves only those actin monomers that are involved in binding of myosin heads and does not propagate to neighbor monomers.

The intensity of the 2.73-nm reflection increased 4.5 times during the transition from the relaxed state to rigor (Fig. 2). This means that in rigor the main contribution to this reflection comes from myosin heads bound to actin, not from actin monomers themselves. Although in rabbit muscle fibers in rigor all myosin heads are bound to actin (Cooke and Franks, 1980) the fraction of occupied actin monomers in the A-band of sarcomeres is only 57%, as there are more actin monomers than myosin heads. The 0.22% increase in average axial repeat d in the overlap zone corresponds to a ∼0.4% (0.22%/0.57) increase in d for actin monomers bound to myosin heads. On the other hand, at a sarcomere length of 2.4 μm in rabbit muscle fibers, only 0.65 of the length of the actin filament overlaps with the myosin filaments (0.735/1.12 μm, where 0.735 μm and 1.12 μm are the length of the overlap zone and of an actin filament, respectively; Higuchi et al., 1995). Therefore a 0.22% increase in the length of the actin filaments in the A-band of sarcomeres due to binding of rigor myosin heads corresponds to a 0.14% (0.65×0.22%) increase in the total length of the actin filaments. This figure gives an upper estimate of the elongation of the thin filaments when all myosin heads are bound.

An interesting question to address is how significant is the myosin-induced actin elongation during active muscle contraction. The answer, however, is not straightforward and depends on several unknown or uncertain values. Estimates of the fraction of myosin heads bound to actin vary from 20% or less (Cooke et al., 1982) to 50% or higher (Linari et al., 1998). Also, strongly bound heads, which generate active isometric force, may produce a different change in actin length from that produced by rigor heads. Besides, our data provide no evidence for or against the possible change in the length and helical angle of actin filaments induced by weakly bound myosin heads, which are also present during active contraction. However, a reasonable estimate of actin elongation during isometric contraction can be made assuming that either 50% or 20% of the total number of myosin heads produce the same effect as rigor heads. If 50% of myosin heads are bound to actin and elongate it, then they should induce a 0.07% (0.5 × 0.14%) increase in length of actin filaments. Alternatively, if only 20% of the heads are bound, the elongation should be 0.03% (0.2 × 0.14%).

Changes in helical angle of actin filaments due to strong binding of myosin heads

The measurement of spacing of the 5.1-nm and 5.9-nm actin layer lines is less precise than that of the 2.73-nm meridional reflection because the intensity peaks on these layer lines are off-meridional, and arching of the layer lines due to misalignment of the filaments spreads the intensity both radially and axially. This shift in apparent axial position of the layer line is more pronounced at higher reciprocal radii. For this reason we measured the spacing of the 5.1-nm and 5.9-nm layer lines as close to meridian as possible, avoiding its meridional part, which has different spacing (Fig. 1). This procedure minimizes the error but probably does not completely eliminate it. The changes in d upon myosin binding calculated from the spacing of these layer lines was slightly less than that measured from the 2.73-nm reflection (Table 1), although the difference did exceed the experimental error of our measurements. This difference can be explained by the fact that the contribution to the intensity of the 5.9-nm, and especially the 5.1-nm, layer line from the actin monomers not bound to myosin heads and not affected by myosin binding was higher than that for the 2.73-nm reflection. The intensities of the 5.9-nm and 5.1-nm actin layer lines in low-tension rigor in the inner off-meridional region of integration (0.02–0.04 nm⁻¹) were, respectively, ∼3.5 times and 1.3 times higher than in the relaxed state (Fig. 3), whereas the intensity of the 2.73-nm reflections increased 4.5 times.

The myosin-induced changes in the apparent spacing of the 5.1-nm and 5.9-nm layer lines were in opposite directions, suggesting an ∼0.8° decrease in average helical angle of the actin helix. As the arching of these two layer lines is expected to be similar, the change in θ calculated from our measurements probably was not much affected by this artifact. The ∼0.8° decrease in average helical angle θ in rigor compared to relaxed state corresponds to a 1.4° = 0.8°/0.57 decrease in θ for those actin monomers that are bound to myosin heads. Because the estimate of the change in θ was obtained from the positions of the 5.1-nm and 5.9-nm actin layer lines, which contain a significant contribution from actin monomers from nonoverlap zone of sarcomeres, the actual change in θ for bound actin monomers can be even higher, up to 2°.

Extensibility of actin filaments in rigor

Estimating the elongation of the actin filaments induced by external tension from x-ray diffraction data is not simple. First, strain distribution along the actin filament is not uniform. It is maximal in the I-band and decreases to zero at the free end of the actin filament. Second, the relative contribution of myosin heads and actin monomers to the intensity of different actin-based reflections is not equal and also depends on strain-induced change in the shape of a myosin head. Third, the observation that the width of the peaks of the 2.73-nm, 5.1-nm, and 5.9-nm reflections in the meridional direction decreases in low-tension rigor compared to the relaxed state (Figs. 2 and 3) suggests that strongly bound myosin heads stabilize the actin filaments, possibly by increasing their longitudinal or/and bending stiffness.

As most of the intensity of the 2.73-nm reflection comes from myosin heads bound to actin, the 0.14% change in the spacing of this reflection in high-tension rigor (Fig. 6, Table 2) corresponds to an average elongation of the actin filaments in the overlap zone of sarcomeres. The strain distribution in the overlap zone induced by a stretch of sarcomeres is expected to be near linear (Ford et al., 1981), and therefore actin elongation in the I-band is twice this value or 0.28%. Normalized elongation of a whole actin filament can be estimated as 0.19% = 0.65 × 0.14% + 0.35 × 0.28%. This figure is still lower than those derived from the changes in the positions of the 5.1-nm and 5.9-nm layer lines, although the difference is within the experimental error (Table 2).

Contribution from myosin to actin spacing

An increase in the intensities of the 2.73-nm, 5.1-nm, and 5.9-nm actin reflections after a stretch of rigor muscle fibers (Figs. 6 and 7) indicates that the stretch causes a change in the shape of myosin heads bound to actin, probably by the elastic bending of the light chain domain of the heads to a position more perpendicular to the filament axis, also leading to an increase in the intensity of the M3 myosin meridional reflection (Fig. 5, Bershitsky et al., 1996; Dobbie et al., 1998; Reconditi et al., 2003). As the near meridional intensity of the 5.1-nm and 5.9-nm layer lines mainly comes from the light chain domains of myosin heads (Kraft et al., 2002), the change in the spacing of these layer lines induced by a stretch of rigor muscle depends not only on the compliance of actin filaments, but also on that of the myosin filaments. The distal ends of the light chain domains are connected to the myosin filaments via stiff coiled-coil subfragment 2 of myosin molecules. Therefore an elongation of the myosin filaments should increase the spacing of the actin-based reflections in the inner part of the 5.1-nm and 5.9-nm layer lines where the contribution of the light chain domains is essential. This leads to an overestimation of compliance of the actin filaments deduced from the measurements of spacing of these layer lines. With the corrections listed above our data suggest that elongation of the thin filaments due to stretch of rigor muscle in our experiments was <0.2% or ∼2 nm.

Implication for the measurements of actin compliance

There is a discrepancy between estimations of actin compliance obtained from mechanical and x-ray diffraction experiments. Measurements of stiffness of intact frog muscle fibers during tetanus contraction at different sarcomere lengths at full overlap between the thin and thick filaments (Bagni et al., 1990; Linari et al., 1998) gave an estimate of actin compliance of <0.2%/T₀. These experiments provide a measure of compliance of the thin filaments in the nonoverlap region of sarcomeres (i.e., in the I-bands) in the conditions where the number of myosin heads attached to the thin filament in the A-bands and the tension they produce are constant. X-ray diffraction experiments on whole frog muscles subjected to slow stretches and releases (H. E. Huxley et al., 1994) or activated at different sarcomere lengths (Wakabayashi et al., 1994) gave a higher figure for actin compliance, between 0.2%/T₀ and 0.3%/T₀, estimated from the changes in the spacing of the 2.73-nm, 5.1-nm, and 5.9-nm actin reflections. Even higher values of 0.38%/T₀ and 0.42%/T₀ were derived from more recent x-ray experiments by Takezawa et al. (1998) and Bordas et al. (1999), respectively.

The possible contribution of myosin-induced actin elongation to the increase in length of the thin filaments during isometric contraction was estimated above to be between 0.03% and 0.07%. During stretch of a muscle fiber its stiffness and probably the fraction of strongly bound myosin heads increase to approach rigor values (Lombardi and Piazzesi, 1990). Conversely, during shortening of a contracting muscle under near-zero load the fraction of strongly bound myosin heads decreases to a negligibly low value (Stehle and Brenner, 2000). Therefore one can expect that contribution of direct elongation of actin filaments due to strong binding of myosin heads scales with tension from 0.14% to zero if the change in tension is achieved by a relatively slow stretch or release of muscle. This should lead to an overestimation of the apparent compliance of actin filaments in contracting muscle revealed from x-ray experiments.

CONCLUSIONS

Our data suggest that the extensibility of actin filaments has two components. One is a direct effect of strong binding of myosin heads on the structure of actin helix, namely its elongation and a decrease in the helical angle θ between neighbor actin monomers. Another component is true compliance, i.e., elongation due to applied force.

When actin compliance is estimated from x-ray diffraction experiments with relatively slow releases or stretches of muscle, the actin-induced elongation also changes with the number of myosin heads strongly bound to actin, namely decreases during shortening and increases during stretching. This leads to an overestimation of the true compliance. Taken together our data are consistent with the results of the mechanical experiments of Linari et al. (1998) showing a moderate value of actin compliance of not more than 0.2%/T₀.