Modulation of Mg²⁺ Efflux from Rat Ventricular Myocytes Studied with the Fluorescent Indicator Furaptra

Abstract

The fluorescent Mg²⁺ indicator furaptra (mag-fura-2) was introduced into single ventricular myocytes by incubation with its acetoxy-methyl ester form. The ratio of furaptra's fluorescence intensity at 382 and 350 nm was used to estimate the apparent cytoplasmic [Mg²⁺] ([Mg²⁺]_i). In Ca²⁺-free extracellular conditions (0.1 mM EGTA) at 25°C, [Mg²⁺]_i averaged 0.842 ± 0.019 mM. After the cells were loaded with Mg²⁺ by exposure to high extracellular [Mg²⁺] ([Mg²⁺]_o), reduction of [Mg²⁺]_o to 1 mM (in the presence of extracellular Na⁺) induced a decrease in [Mg²⁺]_i. The rate of decrease in [Mg²⁺]_i was higher at higher [Mg²⁺]_i, whereas raising [Mg²⁺]_o slowed the decrease in [Mg²⁺]_i with 50% reduction of the rate at ∼10 mM [Mg²⁺]_o. Because a part of the furaptra molecules were likely trapped inside intracellular organelles, we assessed possible contribution of the indicator fluorescence emitted from the organelles. When the cell membranes of furaptra-loaded myocytes were permeabilized with saponin (25 μg/ml for 5 min), furaptra fluorescence intensity at 350-nm excitation decreased to 22%; thus ∼78% of furaptra fluorescence appeared to represent cytoplasmic [Mg²⁺] ([Mg²⁺]_c), whereas the residual 22% likely represented [Mg²⁺] in organelles (primarily mitochondria as revealed by fluorescence imaging). [Mg²⁺] calibrated from the residual furaptra fluorescence ([Mg²⁺]_r) was 0.6–0.7 mM in bathing solution [Mg²⁺] (i.e., [Mg²⁺]_c of the skinned myocytes) of either 0.8 mM or 4.0 mM, suggesting that [Mg²⁺]_r was lower than and virtually insensitive to [Mg²⁺]_c. We therefore corrected furaptra fluorescence signals measured in intact myocytes for this insensitive fraction of fluorescence to estimate [Mg²⁺]_c. In addition, by utilizing concentration and dissociation constant values of known cytoplasmic Mg²⁺ buffers, we calculated changes in total Mg concentration to obtain quantitative information on Mg²⁺ flux across the cell membrane. The calculations indicate that, in the presence of extracellular Na⁺, Mg²⁺ efflux is markedly activated by [Mg²⁺]_c above the normal basal level (∼0.9 mM), with a half-maximal activation of ∼1.9 mM [Mg²⁺]_c. We conclude that [Mg²⁺]_c is tightly regulated by an Mg²⁺ efflux that is dependent on extracellular [Na⁺].

INTRODUCTION

Mg²⁺ regulates numerous cellular functions, serving as a cofactor in many different enzymatic pathways. It is therefore important to maintain cytoplasmic [Mg²⁺] ([Mg²⁺]_c) at the level necessary for cellular function. [Mg²⁺]_c is regulated by both passive and active transport (i.e., influx driven by the electrochemical gradient of this ion and active efflux), cytoplasmic Mg²⁺ buffering, and possibly exchange between cytoplasm and intracellular compartments (see Flatman, 1991). The Na⁺-Mg²⁺ exchange, which extrudes Mg²⁺ in exchange with Na⁺, has been postulated in many types of cells, including squid giant axons (Baker and Crawford, 1972; Gonzalez-Serratos and Rasgado-Flores, 1990), erythrocytes (Günther et al., 1984; Flatman and Smith, 1990), neurons (Brocard et al., 1993; Günzel and Schlue, 1996), thymocytes (Günther and Vormann, 1992a), sublingual acini cells (Zhang and Melvin, 1995), smooth muscle cells (Palaty, 1974; Nakayama et al., 1994; Tashiro and Konishi, 1997), and hepatocytes (Cefaratti et al., 1998). In cardiac myocytes, however, evidence for the Na⁺-Mg²⁺ exchange has been obtained only relatively recently; the Mg²⁺ transport is activated only in the presence of extracellular Na⁺ (Günther and Vormann, 1992b; Romani et al., 1993), is inhibited by imipramine (Handy et al., 1996; Tashiro and Konishi, 2000), and is slightly accelerated by a large depolarization of the cell membrane (Tashiro et al., 2002). However, detailed characteristics of the transport are only poorly understood (see McGuigan et al., 2002).

In the present study, we have studied modulation of the Na⁺-Mg²⁺ exchange by intracellular and extracellular concentrations of Mg²⁺. We used the fluorescent Mg²⁺ indicator furaptra in isolated ventricular myocytes, and the fluorescent ratio signal of furaptra was converted to the apparent cytoplasmic [Mg²⁺] ([Mg²⁺]_i) using calibration parameters previously estimated in myocytes (Watanabe and Konishi, 2001). Mg²⁺ efflux from Mg²⁺-loaded cells was initiated by addition of extracellular Na⁺, and the Mg²⁺ transport rate was evaluated by monitoring the rate of changes in [Mg²⁺]_i. Analysis also included correction for indicator molecules contained within intracellular organelles and for Mg²⁺ binding by known buffers in the cytoplasm (to estimate total Mg concentration, [Mg_tot]). The results show that Mg²⁺ efflux by the putative Na⁺-Mg²⁺ exchange is strongly activated by elevation of [Mg²⁺]_c above the resting level, whereas it is inhibited by elevation of extracellular [Mg²⁺] ([Mg²⁺]_o). Some of these results have been published previously in abstract form (Tursun et al., 2004; Konishi et al., 2004).

METHODS

Cell preparation

Hearts were excised from male Wistar rats (9–12 wks) under deep anesthesia with pentobarbital, and single ventricular myocytes were isolated enzymatically as previously described (Konishi and Berlin, 1993, Tashiro and Konishi, 2000). Cells were placed in a chamber mounted on the stage of an inverted microscope (TE300; Nikon, Tokyo, Japan), and were superfused with normal Tyrode's solution (Table 1). After the background fluorescence (cell autofluorescence plus instrumental stray fluorescence) was measured, the cells were loaded with furaptra by incubation with 5 μM furaptra AM (0.5% DMSO) for 13–15 min at room temperature. The AM ester was then washed out for at least 10 min with Ca²⁺-free Tyrode's solution that contained 0.1 mM K₂EGTA in place of the 1.0 mM CaCl₂ of normal Tyrode's solution (Table 1). The fluorescence measurements described in the next two sections were carried out at 25°C in Ca²⁺-free conditions to minimize any potential interference in furaptra's fluorescence signal by changes in cytoplasmic [Ca²⁺] ([Ca²⁺]_c). For the experiments with skinned myocytes, saponin-treated cells were placed in the chamber as described above for the intact myocytes, and the fluorescence measurements were carried out at 25°C.

TABLE 1.

Composition of solutions

(A) Extracellular solutions
(mM)	NaCl	KCl	NMDG-Cl	MgCl2	MgMs2	CaCl2	K2EGTA	NaH2PO4	HEPES	Glucose
Normal Tyrode's	135	5.4	0	1.0	0	1.0	0	0.33	10	5.0
Ca2+-free Tyrode's	135	5.4	0	1.0	0	0	0.1	0.33	10	5.0
NMDG Tyrode's	0	5.4	135	1.0	0	0	0.1	0.33	10	5.0
93 mM-Mg2+	0	5.4	0	68.5	24	0	0.1	0.33	10	5.0
(B) Intracellular solutions
(mM)	KMs	NaMs	MgMs2	Na2ATP	K2ATP	K2EGTA	MOPS	[Mg2+]	[Na+]	[K+]
Sol 0.8 Mg/10 Na	120	0	5.13	5.0	0	2.5	10	0.8	10	140
Sol 4.0 Mg/10 Na	110	0	9.31	5.0	0	2.5	10	4.0	10	130
Sol 0.8 Mg/50 Na	80	40	5.09	5.0	0	2.5	10	0.8	50	100
Sol 4.0 Mg/50 Na	70	40	9.30	5.0	0	2.5	10	4.0	50	90
Sol 0.8 Mg/0 Na	120	0	5.13	0	5.0	2.5	10	0.8	0	150
Sol 4.0 Mg/0 Na	110	0	9.31	0	5.0	2.5	10	4.0	0	140

The pH of the Extracellular solutions was adjusted to 7.40 by adding NaOH or HCl. Final Na⁺ concentrations were 140 mM (normal Tyrode's solution and Ca²⁺-free Tyrodes's solution), 0.33 mM (NMDG Tyrode's solution), and 5.2 mM (93 mM-Mg solution). The pH of the Intracellular solutions for skinned cells was adjusted to 7.10 by addition of 15 mM KOH. The rightmost three columns of B give final free concentrations of Mg²⁺, Na⁺, and K⁺.

Time-resolved fluorescence measurements

The apparatus and methods for time-resolved fluorescence measurements and analysis have been described previously (Tashiro and Konishi, 2000; Watanabe and Konishi, 2001; Tashiro et al., 2002). Briefly, fluorescence intensity at 500 nm (25 nm FWHM) was measured from the 150-μm diameter field of a 40× objective (CFI S Fluor 40×, Nikon) with excitation wavelengths of 350 nm and 382 nm switched at 100 Hz (CAM230, JASCO, Tokyo, Japan). For data obtained with the intermittent illumination (Figs. 6–8), fluorescence signals were low-pass filtered at 1.7 Hz, digitized at 20 Hz, and were averaged over a 7-s period. For continuous monitoring of the fluorescence (Figs. 1, 2, and 4), signals were low-pass filtered at 1.7 Hz, digitized at 5 Hz, and were smoothed with adjacent averaging of 51 data points (10 s) to reduce noise.

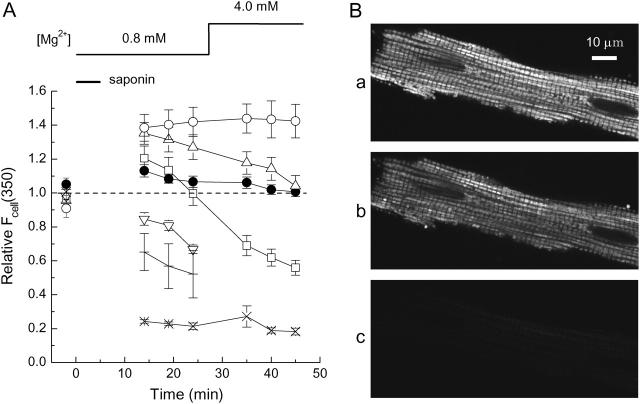
FIGURE 6.

(A) Changes in cell autofluorescence at 350-nm excitation, F_cell(350), were monitored without furaptra loading during the solution protocol as employed in the [Mg²⁺]_r measurement runs (see Fig. 7). In each cell, F_cell(350) was first measured in normal Tyrode's solution, and all values of F_cell(350) subsequently obtained in the same cell were expressed relative to the initial value (ordinate), and means ± SE values from 4 to 7 cells were plotted as a function of time after saponin application (abscissa). After the autofluorescence measurement in Ca²⁺-free Tyrode's solution (first data points), saponin was applied for 5 min in the intracellular solution of 10 mM [Na⁺] and 0.8 mM [Mg²⁺] (Sol 0.8 Mg/10 Na) as indicated by a horizontal bar. Subsequent autofluorescence measurements were carried out in the intracellular solution with [Mg²⁺] set at either 0.8 mM (Sol 0.8 Mg/10 Na) or 4.0 mM (Sol 4.0 Mg/10 Na), as indicated at the top. The intracellular solutions contained: no substrate (crosses), 0.1 mM pyruvate (solid circles), 0.5 mM pyruvate (triangles), 1 mM pyruvate (squares), 2 mM pyruvate (inverted triangles), 0.1 mM pyruvate plus 1 mM KCN (open circles), or 1 μM FCCP (x symbols) throughout saponin treatment and the subsequent measurements. (B) Confocal images of TMRM fluorescence taken from a skinned myocyte. After saponin treatment (25 μg/ml) for 5 min in Sol 0.8 Mg/10 Na plus 0.1 mM pyruvate, the myocyte was incubated in the solution free of saponin for 10 min. Images of a–c were then sequentially recorded in the presence of 0.1 mM pyruvate (a), 10 min after washout of pyruvate (b), and 10 min after addition of 1 μM FCCP (c). Cell 070104-1.

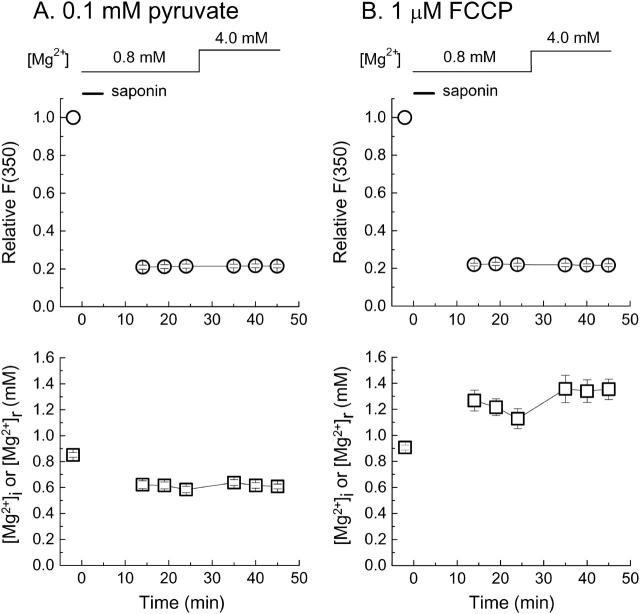
FIGURE 7.

Measurement runs of furaptra fluorescence from skinned cells in the intracellular solutions containing 0.1 mM pyruvate (A) or 1 μM FCCP (B). After the fluorescence measurement in Ca²⁺-free Tyrode's solution (first data points), saponin was applied for 5 min in the intracellular solution of 10 mM [Na⁺] and 0.8 mM [Mg²⁺] (Sol 0.8 Mg/10 Na) as indicated by a horizontal bar. Subsequent fluorescence measurements were carried out in the intracellular solution with [Mg²⁺] set at either 0.8 mM (Sol 0.8 Mg/10 Na) or 4.0 mM (Sol 4.0 Mg/10 Na), as indicated at the top. The intracellular solutions contained either 0.1 mM pyruvate (A) or 1 μM FCCP (B) throughout saponin treatment and the subsequent measurements. In A and B, upper panels show changes in F(350) of furaptra. In each cell, all values of F(350) are normalized to that initially measured in Ca²⁺-free Tyrode's solution (ordinate), and means ± SE values are plotted as a function of time after saponin treatment (ordinate). Lower panels in A and B plot, as a function of time, means ± SE values of [Mg²⁺]_i measured before saponin treatment and [Mg²⁺]_r measured after saponin treatment. Number of cells: 19 for A, 6 for B.

FIGURE 8.

(A) Measurement of furaptra fluorescence in a Mg²⁺-loaded cell carried out as a function of time after saponin treatment. The cell had been loaded with Mg²⁺ in 93 mM-Mg²⁺ solution for 3 h before saponin (25 μg/ml) was applied in the intracellular solution for the period indicated by a horizontal bar (5 min). [Mg²⁺] of the intracellular solution was initially 4.0 mM (Sol 4.0 Mg/10 Na) and then decreased to 0.8 mM (Sol 0.8 Mg/10 Na) as indicated at the top; the solution also contained 0.1 mM pyruvate throughout. (Upper) Furaptra F(350) normalized to that initially measured in 93 mM-Mg²⁺ solution before saponin treatment. (Lower) [Mg²⁺]_i measured before saponin treatment and [Mg²⁺]_r measured after saponin treatment. Cell 031304-9. (B) The relation between [Mg²⁺]_r (ordinate) and [Mg²⁺]_i (abscissa) obtained from 12 cells in the experiments of the type shown in A. For each cell, a mean value of [Mg²⁺]_r obtained at 4–6 min after washout of saponin (9–11 min on the abscissa in A) is plotted against a [Mg²⁺]_i value measured just before saponin treatment in 93 mM-Mg²⁺ solution. A solid line indicates a linear regression for the data points of the form indicated in the panel.

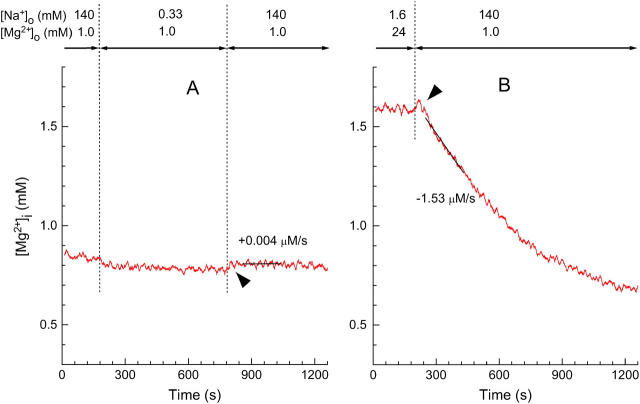
FIGURE 1.

Effects of [Na⁺]_i on the [Mg²⁺]_i measurements with furaptra. Records from two separate runs in which [Na⁺]_o and [Mg²⁺]_o were changed as indicated above at the times shown by vertical dotted lines. (A) The initial perfusion with Ca²⁺-free Tyrode's solution was followed by withdrawal and reintroduction of Na⁺. Cell 052203-4. (B) After the myocyte was loaded with Mg²⁺ by incubation in the high-Mg²⁺ and low Na⁺ solution, Ca²⁺-free Tyrode's solution was introduced to induce Mg²⁺ efflux. Cell 072502. In A and B, values of [Mg²⁺]_i (ordinate) were calculated under the assumption that fluorescence ratio signals of furaptra exclusively reflected Mg²⁺ concentration. Arrowheads indicate small upward deflections of [Mg²⁺]_i seen on introduction of Ca²⁺-free Tyrode's solution that contained 140 mM Na⁺. For this and subsequent figures, a solid line was drawn by linear regression to data points for 180 s of each trace, and the initial rate of change in [Mg²⁺]_i (initial Δ[Mg²⁺]_i/Δt) estimated from the slope is indicated (μM/s) nearby.

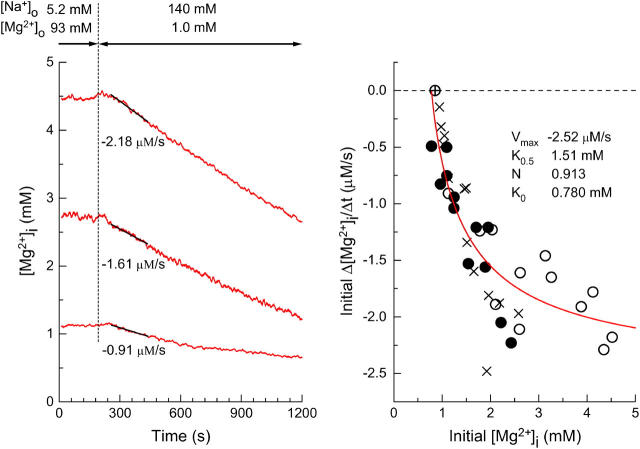
FIGURE 2.

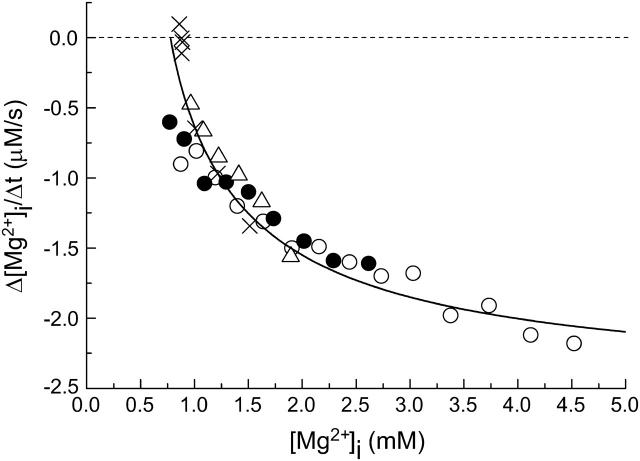
(Left) Estimation of the initial rates of decrease in [Mg²⁺]_i in three myocytes which were loaded with Mg²⁺ to different levels of [Mg²⁺]_i. After the Mg²⁺ loading in the high-Mg²⁺ and low Na⁺ solution, Ca²⁺-free Tyrode's solution was introduced to induce Mg²⁺ efflux, as indicated at the top. Cells 051203 (top), 060303 (middle), and 062403 (bottom). (Right) Values of the initial Δ[Mg²⁺]_i/Δt estimated as shown in the left panel are plotted as a function of initial [Mg²⁺]_i (defined as [Mg²⁺]_i at the first point of the fitted line). The myocytes were loaded with Mg²⁺ in solutions containing either 93 mM Mg²⁺ (open circles) or 24 mM Mg²⁺ (solid circles) for 2–5 h. Mean basal [Mg²⁺]_i measured before Mg²⁺-loading in these myocytes was 0.855 mM (n = 23), and is plotted at zero initial Δ[Mg²⁺]_i/Δt (⊕). Also shown (x symbols) are data taken from Figs. 4 and 6 of Tashiro et al. (2002); the myocytes were loaded with Mg²⁺ in the 93 mM Mg²⁺-containing solution, and the initial Δ[Mg²⁺]_i/Δt values were estimated under voltage-clamp at the holding potential of −80 mV. A solid curve indicates the least-squares fit to the data points (open circles and solid circles) by the Hill-type curve (Eq. 2) with the parameters shown in the panel.

FIGURE 4.

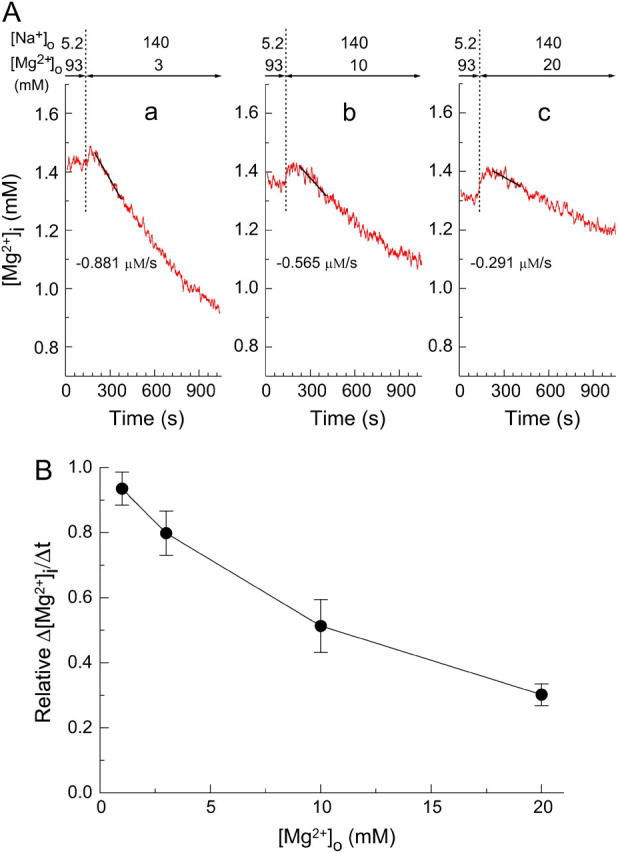
Extracellular Mg²⁺-dependence of the initial Δ[Mg²⁺]_i/Δt in the Mg²⁺-loaded myocytes. (A) Records from three separate experiments in which the [Mg²⁺]_i decrease was induced at 3 mM (a), 10 mM (b), or 20 mM (c) [Mg²⁺]_o as indicated above. The initial Δ[Mg²⁺]_i/Δt values (the slopes of solid lines) are indicated below the traces. Cells 101003 (a), 072203 (b), and 092203 (c). (B) Solid circles show the relation between [Mg²⁺]_o and relative Δ[Mg²⁺]_i/Δt (Δ[Mg²⁺]_i/Δt relative to the value expected for the initial [Mg²⁺]_i; see text for details) obtained from the type of experiments shown in A. Each symbol represents a mean ± SE from 5 to 10 cells.

The ratio (R) of the fluorescence intensities at 382-nm excitation, F(382), and at 350-nm excitation, F(350), was used as an Mg²⁺-related signal [R = F(382)/F(350)]. Because instability of the lamp, and possibly other optical components, caused small drifts during the course of the study, we occasionally measured R in a Ca²⁺-Mg²⁺-free buffer solution (140 mM KCl, 10 mM NaCl, 1 mM EDTA, 1 mM EGTA, 0.05 mM furaptra, and 10 mM PIPES, pH 7.1) as a standard; thin-wall quartz capillaries (internal diameter ∼50 μm) that contained the buffer solution were placed in the chamber and the standard R was measured. All values of R measured from cells were normalized to the standard R-value taken close in time (i.e., within a week), and the normalized R was converted to [Mg²⁺] with

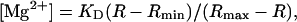(1)

where R_min and R_max are the normalized R-values at zero [Mg²⁺] and saturating [Mg²⁺], respectively, and K_D is the dissociation constant of furaptra for Mg²⁺. For these parameters, we used the values previously estimated in rat ventricular myocytes at 25°C: R_min = 0.969, R_max = 0.223, and K_D = 5.30 mM (Watanabe and Konishi, 2001).

For each cell, the measured background fluorescence at each wavelength was subtracted from the total fluorescence measurements from the furaptra-loaded myocyte to calculate indicator-related fluorescence intensities. [Mg²⁺]_i was calculated as described above with the fluorescence R measured in the myocytes and normalized to the standard R. In this article, [Mg²⁺]_i (i.e., apparent cytoplasmic [Mg²⁺]) refers to the spatially averaged Mg²⁺ concentration in the entire cell volume, which may not reflect [Mg²⁺]_c only. For cell autofluorescence measurements, the cell was removed from the optical field at the end of each experiment and the instrumental stray fluorescence was measured from the cell-free field. The cellular autofluorescence intensity was calculated by subtraction of the instrumental stray fluorescence from the background fluorescence.

Fluorescence imaging

In some experiments, fluorescence images were acquired with a CCD camera system (Aquacosmos, Hamamatsu Photonics, Shizuoka, Japan) with an oil immersion 100× objective (S Fluor 100×, Nikon). Wavelength pairs of excitation/emission were 350 nm (FWHM 15 nm)/510 nm (FWHM 10 nm) for furaptra and 490 nm (FWHM 15 nm)/535 nm (FWHM 30 nm) for mitotracker green FN. The myocytes were first loaded with furaptra by incubation with 5 μM furaptra AM for 14 min. After washout of furaptra AM with Ca²⁺-free Tyrode's solution for 10 min, the cells were incubated with 0.2 μM mitotracker green FN (0.02% DMSO) in Ca²⁺-free Tyrode's solution for 30 min.

For the measurements of mitochondrial membrane potential in skinned myocytes, we recorded fluorescence images of tetramethylrhodamine methyl ester perchlorate (TMRM) using a laser-scanning confocal microscope (C-1, Nikon) with a high numerical aperture objective (NA 1.4, Plan Apo 60×A, Nikon). Images of TMRM fluorescence were obtained at 432-nm excitation (He-Ne laser) and >575-nm emission from saponin-treated myocytes in the intracellular solution that contained 0.5 μM TMRM (0.01% DMSO).

Experimental protocol and solutions

The extracellular solutions used for superfusion of the intact myocytes are listed in Table 1. The essentially Na⁺-free solution (NMDG Tyrode's, Table 1) was made by isosmotic replacement of NaCl of the Ca²⁺-free Tyrode's solution by NMDG-Cl (n-methyl-D-glucamine titrated by HCl to adjust pH to 7.40) to give final [Na⁺] of 0.33 mM. The 93 mM-Mg²⁺ solution was prepared by substitution of 135 mM NaCl of the Ca²⁺-free solution with 68.5 mM MgCl₂ plus 24 mM Mg-methanesulfonate (MgMs₂): final [Mg²⁺] = 92.5 mM and [Na⁺] = 5.2 mM. These solutions were designed to maintain a [K⁺]×[Cl⁻] product constant at ∼800 mM² and osmolality at ∼290 mOsm/kg H₂O.

For observation of Mg²⁺ efflux, the myocytes were first loaded with Mg²⁺ by incubation in the solution containing high Mg²⁺ and low Na⁺ concentrations (Mg²⁺-loading). Mg²⁺ concentration of the Mg²⁺-loading solution was either 93 mM (93 mM-Mg²⁺ solution in Table 1) or 24 mM (1:3 mixture of 93 mM-Mg²⁺ solution and NMDG Tyrode's solution, Table 1). After [Mg²⁺]_i was significantly elevated from the resting level by Mg²⁺-loading for 2–5 h, Mg²⁺ efflux was induced by changing the extracellular solution back to Ca²⁺-free Tyrode's solution, which contained 1 mM Mg²⁺ and 140 mM Na⁺ (Table 1), and the rate of change in [Mg²⁺]_i (Δ[Mg²⁺]_i/Δt) was analyzed as an index of the rate of Mg²⁺ efflux. We primarily estimated the initial Δ[Mg²⁺]_i/Δt by linear regression of data points spanning for 180 s (60–240 s after solution exchange, unless otherwise stated; solid lines in Figs. 1 and 2). Note that NMDG Tyrode's solution that contained little Na⁺ did not cause significant decrease in [Mg²⁺]_i, indicating that Mg²⁺ efflux was extracellular Na⁺-dependent (Tashiro et al., 2002).

For permeabilization of the cell membrane (i.e., skinning of the cells), the myocytes were exposed to one of the intracellular solutions (Table 1) containing saponin (25 μg/ml) for 5 min, followed by a through-perfusion with saponin-free intracellular solution. Although similar results were obtained with a higher concentration of saponin (50 μg/ml) and longer exposure (10 min) in the initial experiments, we somewhat arbitrarily chose the lower concentration and shorter treatment time to minimize possible cell damage. The solutions used for skinned cells are listed in Table 1. All intracellular solutions contained 5 mM ATP and 2.5 mM K₂EGTA, and pH was adjusted to 7.10 by MOPS/KOH (25°C). Ionic strength was set to 0.16 M by adjusting the K-methanesulfonate (KMs) concentration. Free Mg²⁺ concentration was calculated and adjusted by solving simultaneous equations with the apparent dissociation constants assumed for the Mg²⁺-EGTA reaction, 16.5 mM at a pH of 7.1 and 25°C (Martell and Smith, 1974; Fabiato and Fabiato, 1979), and metal-ATP reactions given in Table 3 (Fabiato and Fabiato, 1979).

TABLE 3.

Intracellular Mg²⁺/Ca²⁺ buffers (in μM)

		KD
Species	Concentration	Mg2+	Ca2+	K+	Na+
Troponin	70 × 2	1100	0.013	—	—
Myosin	70 × 2	3.6	0.033	—	—
ATP	5000	90	200	230,000	150,000
ADP	50*	1500	2300	—	—
PCr	12,000	50,000	71,000	—	—
Pi	1000	20,000	31,000	500,000	390,000
Citrate	220†	370§	370§	270,000§	210,000§
Furaptra	220‡	5300¶	100‖	—	—

The values for total concentrations of major cytoplasmic buffers and equilibrium dissociation constants (K_D) for Mg²⁺, Ca²⁺, K⁺, and Na⁺ are expressed as μM, micromole per liter cytoplasm (pH 7.1, ionic strength 0.16 M and 25°C). PCr, creatine phosphate; P_i, inorganic phosphate. Except as footnoted, values are taken from Fabiato and Fabiato (1979) and Bers (2001).

^*Adjusted to set [MgADP]/[MgATP] ratio to 0.0044, the value reported for rat hearts by Jelicks and Gupta (1991).

^†Kauppinen et al. (1982).

^‡Calculated with the loading rate of 312 μM/h reported by Zhao et al. (1997) for frog skeletal muscles at 16°C and a factor-of-3 correction for the temperature difference (see text for details).

^§Martell and Smith (1974).

^¶Estimated in rat myocytes by Watanabe and Konishi (2001).

^‖Assumed for intracellular K_D after Konishi et al. (1991).

Tetra-potassium salt of mag-fura-2 (furaptra) and mag-fura-2 AM (furaptra AM), mitotracker green FN, 3,3′-dihexyloxacarbocyanine iodide (DiOC₆), and TMRM were purchased from Molecular Probes (Eugene, OR). EGTA, Na pyruvate, carbonyl cyanide p-(trifluoromethoxy)phenylhydrazone (FCCP), and saponin (from Quillaja bark) were from Sigma (St. Louis, MO). KCN was from Wako Pure Chemical Industries (Osaka, Japan). Na₂ATP was from Roche Diagnostics (Indianapolis, IN). K₂ATP was from ICN Biomedicals (Aurora, OH). All other chemicals were re-agent grade. When required, organic solvents were present during fluorescence measurements (0.1% ethanol for FCCP and 0.01% DMSO for TMRM), which did not affect the measurements.

Data analysis

Linear and nonlinear least-square fittings were carried out with the program Origin (Ver. 7.0, OriginLab, Northampton, MA). For model calculations, Excel spreadsheets (Microsoft, Redmond, WA) were used. Data are expressed as means ± SE for the number of cells indicated. The statistical significance of a difference between means was evaluated with the Student's two-tailed t-test, with the significance level set at P < 0.05.

RESULTS

Effects of Na⁺ on the Mg²⁺ measurements

The average value of basal [Mg²⁺]_i measured at the beginning of the experiments in Ca²⁺-free Tyrode's solution was 0.842 ± 0.019 mM (n = 43), which was not significantly different from that reported previously (Watanabe and Konishi, 2001; Tashiro et al., 2002). Lowering extracellular [Na⁺] ([Na⁺]_o) to 0.33 mM caused a small increase in furaptra R, which corresponded to an average reduction of 0.039 ± 0.003 mM [Mg²⁺]_i (n = 4) when calibrated under the assumption that R signals exclusively reflected Mg²⁺ concentration with no interference from intracellular [Na⁺] ([Na⁺]_i) (Fig. 1 A). The change in R was reversed by reintroduction of 140 mM extracellular Na⁺ (see arrowhead in Fig. 1 A). These small but significant changes in [Mg²⁺]_i are likely caused by changes in [Na⁺]_i rather than [Mg²⁺]_i, because 1), [Na⁺]_i should quickly fall from 12 mM (an average [Na⁺]_i at 140 mM [Na⁺]_o; Tashiro and Konishi, 2003) to much lower levels on removal of extracellular Na⁺, and vice versa; and 2), the in vitro fluorescence measurements indicate that reduction of [Na⁺] from 10 mM to 0 mM with [Mg²⁺] kept constant at 0.8 mM induces an upward shift of furaptra R, which corresponds to a decrease in [Mg²⁺] of ∼0.03 mM (not shown). Thus, changes in [Mg²⁺]_i calibrated from furaptra R appear to include small effects due to changes in [Na⁺]_i just after removal and reintroduction of extracellular Na⁺.

Fig. 1 B shows an example of [Mg²⁺]_i measurements during Mg²⁺ efflux from a Mg²⁺-loaded myocyte. When 140 mM extracellular Na⁺ was introduced (with reduction of [Mg²⁺]_o to 1 mM) to induce extracellular Na⁺-dependent Mg²⁺ extrusion, we often observed a small upward hump (indicated by an arrowhead) before [Mg²⁺]_i started to decrease. The amplitude of the hump was, on average, 0.031 ± 0.003 mM (n = 24), and could be attributed to the small increase in [Na⁺]_i. Because the effect of [Na⁺]_i was small, and appears to occur within 1 min after solution exchange in the present experimental conditions, the initial rates of fall in [Mg²⁺]_i estimated between 60 s and 240 s after solution exchange should be little influenced by this interference. Although the effect of [Na⁺]_i was considered inconsequential in this article, it should be noted that corrections for the influence of Na⁺ on furaptra fluorescence may be required in the analyses for experimental conditions in which [Na⁺]_i is markedly elevated.

Relation between [Mg²⁺]_i and the rate of Mg²⁺ efflux

The results shown in Fig. 1 indicate that Mg²⁺ efflux after introduction of 140 mM Na⁺ is induced only in the Mg²⁺-loaded cells; the initial Δ[Mg²⁺]_i/Δt was clearly negative (i.e., a decrease in [Mg²⁺]_i) at [Mg²⁺]_i elevated above the basal level, but was close to zero at basal [Mg²⁺]_i. The [Mg²⁺]_i-dependence of Mg²⁺ efflux was further examined in a series of experiments shown in Fig. 2. Myocytes were loaded with Mg²⁺ to achieve various levels of [Mg²⁺]_i (between 0.8 mM and 4.5 mM), and the rate of fall in [Mg²⁺]_i was estimated in each cell (illustrated for three cells in Fig. 2, left). The wide range of Mg²⁺ loading (i.e., elevated levels of [Mg²⁺]_i) was produced not only by natural cell-to-cell variation, but also by differences in [Mg²⁺] in the Mg²⁺-loading solution (24 mM or 93 mM) and differences in loading time (2–5 h). The relation between the initial Δ[Mg²⁺]_i/Δt and the initial [Mg²⁺]_i (symbols in Fig. 2, right) did not seem to depend on [Mg²⁺] of the Mg²⁺ loading solution (24 mM or 93 mM; solid and open circles, respectively) or on the experimental protocol employed (with or without voltage-clamp at −80 mV). It has been reported that changes in membrane potential between −40 mV and −80 mV little-influence the initial Δ[Mg²⁺]_i/Δt (Tashiro et al., 2002). The relation was steep near the basal [Mg²⁺]_i levels and became shallower in the high [Mg²⁺]_i range and could be reasonably described by a Hill-type curve under the assumption that the Mg²⁺ efflux was activated only above a threshold [Mg²⁺]_i,

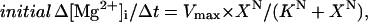(2)

where X = initial [Mg²⁺]_i − K₀, K = K_0.5 − K₀. K₀ is the threshold [Mg²⁺]_i at which initial Δ[Mg²⁺]_i/Δt is zero (fitted value, 0.780 mM) and K_0.5 is [Mg²⁺]_i, which gives the half-maximal value of initial Δ[Mg²⁺]_i/Δt (fitted value, 1.51 mM). V_max denotes the maximum value of initial Δ[Mg²⁺]_i/Δt (fitted value, −2.52 μM/s). N is the Hill coefficient (fitted value, 0.913). The fitted curve suggests that the Mg²⁺ efflux was activated above 0.8 mM [Mg²⁺]_i, and half-maximal activation occurs at 1.5 mM [Mg²⁺]_i.

Fig. 3 shows Δ[Mg²⁺]_i/Δt versus [Mg²⁺]_i relations estimated at different times during Mg²⁺ efflux in single myocytes. Values of Δ[Mg²⁺]_i/Δt approached zero as [Mg²⁺]_i decreased toward the basal level (which corresponds to later times), approximately following the Hill-type curve fitted to pooled data of the initial Δ[Mg²⁺]_i/Δt from many cells (the fitted curve in Fig. 2, right). The results imply that the Mg²⁺ efflux is primarily regulated by [Mg²⁺]_i during the entire course of the [Mg²⁺]_i decay, even though other factors including slow changes in intracellular pH and [Na⁺]_i may also come into play during prolonged measurement runs.

FIGURE 3.

The relation between Δ[Mg²⁺]_i/Δt and [Mg²⁺]_i was analyzed as a function of time during the [Mg²⁺]_i decrease at 140 mM [Na⁺]_o. Each symbol represents data from a different myocyte. The myocytes were loaded with Mg²⁺ in the solution containing either 93 mM Mg²⁺ (open circles, open triangles, and x symbols) or 24 mM Mg²⁺ (solid circles). The rates of decrease in [Mg²⁺]_i (Δ[Mg²⁺]_i/Δt) were estimated at 180-s intervals, and are plotted against [Mg²⁺]_i at the first point of the fitted line. In one myocyte (x symbols), [Mg²⁺]_i measurements were carried out under voltage-clamp at the holding potential of −80 mV (taken from Tashiro et al., 2002). Cells 051203 (open circles), 060303 (open triangles), 082302 (solid circles), and 071101 (x symbols). A solid curve represents the best-fitted curve of the relation between the initial Δ[Mg²⁺]_i/Δt and initial [Mg²⁺]_i shown in the right panel of Fig. 2.

Effects of [Mg²⁺]_o on the Mg²⁺ efflux

Figs. 2 and 3 show that the Δ[Mg²⁺]_i/Δt values depend strongly on [Mg²⁺]_i. Since further comparisons of the initial Δ[Mg²⁺]_i/Δt values must be adjusted for variations in initial [Mg²⁺]_i, we used the fitted Hill-type curve (the curve in Fig. 2, right) as a standard; the initial Δ[Mg²⁺]_i/Δt value was normalized to the value on the curve at a given initial [Mg²⁺]_i to yield relative Δ[Mg²⁺]_i/Δt.

Fig. 4 shows the [Mg²⁺]_i measurements from the Mg²⁺-loaded myocytes at different [Mg²⁺]_o. The myocytes were loaded with Mg²⁺ to reach 1.0–2.0 mM [Mg²⁺]_i, and then were perfused with the solution of 140 mM [Na⁺]_o plus 3, 10, and 20 mM [Mg²⁺]_o. For preparation of these high-Mg²⁺ solutions, an appropriate amount of MgCl₂ was added to Ca²⁺-free Tyrode's solution without osmotic compensation to keep [Na⁺]_o constant at 140 mM, as [Na⁺]_o profoundly influenced the rate of changes in [Mg²⁺]_i in the previous studies (Tashiro and Konishi, 2000; Tashiro et al., 2002).

As shown in Fig. 4 A, the Mg²⁺ efflux was slower at higher [Mg²⁺]_o, when compared at similar initial [Mg²⁺]_i levels. We also noted a hump, expressed in Δ[Mg²⁺]_i units, on the [Mg²⁺]_i traces just after solution exchange that increased with the level of [Mg²⁺]_o. The amplitude of the hump was, on average, 0.044 ± 0.014 mM at 3 mM [Mg²⁺]_o (n = 8), 0.067 ± 0.021 mM at 10 mM [Mg²⁺]_o (n = 5), and 0.13 ± 0.02 mM at 20 mM [Mg²⁺]_o (n = 5), which may be compared with 0.040 ± 0.009 mM observed at 1 mM [Mg²⁺]_o (n = 10). Because the solutions with higher [Mg²⁺]_o also had a higher osmolality, we considered it likely that the hump was due to osmotic shrinkage of the cells and the associated increase in [Mg²⁺]_i (and the exaggerated increase in [Na⁺]_i). To minimize the effect of the hump, we estimated the initial Δ[Mg²⁺]_i/Δt with data points at 90–270 s after solution exchange, a time-range slightly later than the standard (60–240 s; see above).

For 1 mM, 3 mM, 10 mM, and 20 mM [Mg²⁺]_o, the initial Δ[Mg²⁺]_i/Δt averaged, respectively, −1.09 ± 0.11 μM/s (n = 10), −0.95 ± 0.09 μM/s (n = 8), −0.58 ± 0.06 μM/s (n = 5), and −0.38 ± 0.04 μM/s (n = 5). The average value of initial [Mg²⁺]_i for these determinations was 1.47 ± 0.11 mM, 1.46 ± 0.07 mM, 1.44 ± 0.10 mM, and 1.55 ± 0.08 mM, respectively. For more precise comparison (Fig. 4 A), we calculated relative initial Δ[Mg²⁺]_i/Δt using the standard relation between the initial Δ[Mg²⁺]_i/Δt and the initial [Mg²⁺]_i (solid curve in Fig. 2, right), as described above. It is clear in Fig. 4 B that relative Δ[Mg²⁺]_i/Δt values progressively decrease at higher [Mg²⁺]_o with 50% inhibition at ∼10 mM.

To check if osmotic cell shrinkage caused any change in the Mg²⁺ efflux, we measured the initial Δ[Mg²⁺]_i/Δt in a hypertonic solution containing 140 mM Na⁺ and 1 mM Mg²⁺ prepared by addition of 30 mM NMDG-Cl to Ca²⁺-free Tyrode's solution (data not shown). In three myocytes, the average amplitude of the hump observed upon perfusion of the solution of high osmolality was 0.12 ± 0.01 mM, which was similar to that observed at 20 mM [Mg²⁺]_o (above). The initial Δ[Mg²⁺]_i/Δt was, on average, −1.15 ± 0.10 μM/s with the average value of initial [Mg²⁺]_i at 1.55 ± 0.03 mM. Relative Δ[Mg²⁺]_i/Δt values calculated as described above averaged 0.90 ± 0.06, which was significantly higher than that obtained at 20 mM [Mg²⁺]_o (0.30 ± 0.03, n = 5), and was not significantly different from that obtained in the isotonic solution at 1 mM [Mg²⁺]_o (0.94 ± 0.05, n = 10). Thus, the effect of osmotic shrinkage is, if any, minor, and extracellular Mg²⁺ appears to inhibit Mg²⁺ efflux in a concentration-dependent manner.

Measurements of furaptra fluorescence emitted from intracellular organelles

Because we used AM-loading of the indicator, some fraction of furaptra molecules might have been trapped inside organelles (e.g., Miyata et al., 1991). We therefore examined the possible contribution of the fluorescence signals from intracellular organelles. Fig. 5 shows images taken from an intact cell and a permeabilized- or skinned-cell. In the intact cell (Ac), furaptra fluorescence did not show any particular pattern of distribution (Aa), whereas the fluorescence of mitotracker green FN, a mitochondria-staining dye, showed sarcomeric periodicity (Ab). After saponin treatment, however, both furaptra (Ba) and mitotracker green FN (Bb) showed a similar sarcomeric periodicity, suggesting that a part of furaptra fluorescence (∼22%, see below) in intact cells was localized in mitochondria. Fluorescence of other mitochondria-staining dyes, such as DiOC₆ (not shown) and TMRM (Fig. 6), showed very similar distribution patterns. However, we cannot exclude the possibility that fraction of organellar furaptra fluorescence might come from intracellular organelles other than mitochondria.

FIGURE 5.

(A) Panels a–c compare fluorescence images of furaptra (a) and mitotracker green FN (b) and a transmitted light image (c) obtained from an intact myocyte in Ca²⁺-free Tyrode's solution. Times of illumination were 4.2 s (a), 3.1 s (b), and 1.0 s (c). Cell 040204-1. (B) Fluorescence images of furaptra (a) and mitotracker green FN (b) obtained from a skinned myocyte are shown. After saponin treatment (25 μg/ml) for 5 min in the intracellular solution containing 0.8 mM Mg²⁺ and 10 mM Na⁺ (Sol 0.8 Mg/10 Na), the myocyte was incubated in Sol 0.8 Mg/10 Na. The intracellular solution also contained pyruvate (0.1 mM) throughout saponin treatment and fluorescence measurements. Times of illumination were 30.2 s (a) and 6.2 s (b). Cell 061004-10.

If furaptra fluorescence R in mitochondria (and possibly other organelles) behaves differently from that in the cytoplasm, [Mg²⁺]_i calibrated from R in intact cells would not reflect [Mg²⁺]_c only. To test this possibility, we measured furaptra R in skinned myocytes. After skinning the myocytes with saponin, mitochondrial respiration could become inhibited owing to inevitable loss of substrates from cytoplasm. Because transport of Mg²⁺ across the inner membrane of mitochondria appears to depend on respiration (and membrane potential) of mitochondria (e.g., Crompton et al., 1976; Brierley et al., 1987), maintenance of mitochondrial respiration and membrane potential is essential to study Mg²⁺-related furaptra fluorescence from mitochondria. As an index of mitochondrial metabolism, we used cell autofluorescence excited at 350 nm and detected at 500 nm. It was shown that the UV-induced cellular autofluorescence primarily indicated the NADH redox state (Mojet et al., 2001). Although NADH is present in both mitochondria and cytosolic compartments, we assumed that the major fraction of NADH fluorescence is emitted from mitochondria in cardiac myocytes for several reasons: 1), the binding of NADH to membranes enhances its fluorescence, whereas its binding to the cytosolic fraction tends to quench fluorescence, which tends to favor the mitochondrial signal (Chance and Baltscheffsky, 1958); 2), mitochondria occupy a large fraction (∼30%) of the cell volume of cardiac myocytes (Bers, 2001), which makes contribution of mitochondrial NADH greater; and 3), imaging of intact cells without introducing the indicators revealed the sarcomeric periodicity of autofluorescence (not shown) as observed for fluorescence of mitochondria-staining dyes (see above).

Fig. 6 A shows results of experiments carried out to seek solution conditions that support mitochondrial respiration. When the myocytes were skinned in the intracellular solution that contained no substrate, the UV-induced autofluorescence (reflective of the NADH/NAD⁺ ratio) decreased, on average, by 35% in 14 min and by 48% in 24 min (crosses); this inhibition of mitochondrial metabolism could be attributed to loss of substrates. Supply of a substrate, such as pyruvate, should accelerate production of NADH and prevent the reduction of the autofluorescence. In the presence of 0.1 mM pyruvate, the autofluorescence was not reduced and was well maintained even for 45 min after skinning (solid circles). Higher concentrations of pyruvate (0.5–1.0 mM) initially potentiated the autofluorescence with substantial decay in the later periods (triangles and squares). In the presence of 2 mM pyruvate, the autofluorescence decreased without initial potentiation (inverted triangles). The decay of the autofluorescence might have been due to depletion of one or more of the substances required for NADH production. Although we did not further explore the precise mechanisms of the changes in the autofluorescence, we employed 0.1 mM pyruvate as a substrate for most of the following experiments with skinned myocytes. To obtain maximum and minimum values of NADH/NAD⁺ ratio, we applied, respectively, CN⁻, an inhibitor of oxidative phosphorylation, and FCCP, an uncoupler that depolarizes mitochondrial membrane potential. Application of CN⁻ potentiated the autofluorescence by ∼40% (open circles), whereas FCCP caused marked reduction of the autofluorescence to ∼20% (x symbols in Fig. 6 A).

We also assessed membrane potential of mitochondria using TMRM fluorescence. It has been shown that TMRM is concentrated in the mitochondria relative to cytoplasm as expected for a cation under a physiological membrane potential of −150 mV to −200 mV (inside negative to the cytoplasm; Scaduto and Grotyohann, 1999); mitochondrial depolarization caused release of the dye from mitochondria to cytoplasm, and loss of its fluorescence. When the skinned myocytes were incubated in the intracellular solution containing 0.1 mM pyruvate, TMRM fluorescence could be clearly detected with the expected sarcomeric periodicity (Fig. 6 Ba), as observed with other mitochondria-staining dyes (see above). Washout of pyruvate slightly but significantly attenuated intensity of TMRM fluorescence (Fig. 6 Bb) by ∼35%; in three myocytes the average reduction was 24.8 ± 7.9%. This reduction of fluorescence intensity was not due to photobleaching of the dye, because TMRM fluorescence was essentially unchanged if the measurement was repeated in the presence of 0.1 mM pyruvate (data not shown); average intensity obtained from the second measurements was 98.5 ± 3.9% of the first measurements (n = 4). Application of FCCP to depolarize mitochondrial membrane potential markedly diminished the intensity of TMRM fluorescence (Fig. 6 Bc), on average, to 11.6 ± 4.0% in 5 min (n = 3) and to 5.6 ± 1.0% in 10 min (n = 5) of the values initially measured in the presence of 0.1 mM pyruvate. The increase in NADH fluorescence by CN⁻ and the loss of TMRM fluorescence with loss of membrane potential shown in Fig. 6 imply that mitochondria in skinned myocytes incubated with 0.1 mM pyruvate retain respiration and well-polarized membrane potential.

We measured furaptra fluorescence from myocytes loaded with furaptra and then skinned with saponin (Fig. 7). The background fluorescence was corrected for average changes in autofluorescence separately measured for each solution condition (Fig. 6), and was subtracted from the total fluorescence intensities to calculate furaptra fluorescence. After saponin treatment, F(350) decreased to 22.0 ± 0.5% (n = 51), irrespective of the intracellular solutions used (Table 1) or inclusion of pyruvate and FCCP. Since saponin, at low concentrations, selectively permeabilizes the cell membrane (Endo and Kitazawa, 1978), this result suggests that ∼78% of furaptra fluorescence reports [Mg²⁺]_c, whereas the residual fluorescence (∼22%) may represent [Mg²⁺] in organelles, primarily mitochondria (see above). After the initial drop, furaptra F(350) stayed nearly constant during the measurement runs (Fig. 7), indicating that leakage and photobleaching of furaptra in the organelles were negligible. Fig. 7 A shows the results of experiments carried out in the presence of 0.1 mM pyruvate. If the ratio of residual furaptra fluorescence after saponin treatment was calibrated in terms of [Mg²⁺] (residual [Mg²⁺] or [Mg²⁺]_r) with Eq. 1 and parameter values described in Methods, [Mg²⁺]_r averaged 0.601 ± 0.025 mM (n = 19) at 14–19 min after washout of saponin (Table 2). When [Mg²⁺] of the intracellular solution was raised to 4.0 mM, [Mg²⁺]_r increased only slightly, on average, by 0.054 ± 0.018 mM, and [Mg²⁺]_r values at 13–18 min after solution exchange averaged 0.612 ± 0.019 mM (Table 2); two average values obtained at 0.8 mM [Mg²⁺] and 4.0 mM [Mg²⁺] were not significantly different. On the contrary, when mitochondria were uncoupled by FCCP (n = 6), [Mg²⁺]_r values were 1.172 ± 0.070 mM at 0.8 mM solution [Mg²⁺], and increased to 1.347 ± 0.070 mM at 4.0 mM solution [Mg²⁺] (lower panel of Fig. 7 B; also see Table 2).

TABLE 2.

Residual [Mg²⁺] ([Mg²⁺]_r) measured in skinned cells

Experimental conditions	N	[Mg2+]r at 0.8 mM [Mg2+] (mM)	[Mg2+]r at 4.0 mM [Mg2+] (mM)	Δ[Mg2+]r (mM)
No substrate	4	0.612 ± 0.075	—	—
0.1 mM Pyruvate	19	0.601 ± 0.025	0.612 ± 0.019	+0.054 ± 0.018
0.1 mM Pyruvate (0 mM [Na+])	7	0.688 ± 0.052	0.653 ± 0.039	−0.008 ± 0.020
0.1 mM Pyruvate (50 mM [Na+])	9	0.798 ± 0.073*	0.818 ± 0.055*	+0.058 ± 0.018
1 mM Pyruvate	7	0.604 ± 0.055	0.475 ± 0.032*	−0.138 ± 0.076
2 mM Pyruvate	5	0.659 ± 0.055	—	—
1 μM FCCP	6	1.172 ± 0.070*	1.347 ± 0.083*	+0.229 ± 0.044

Summary of [Mg²⁺]_r in various intracellular solutions measured as shown in Fig. 7. The intracellular solutions contain 10 mM Na⁺, unless otherwise stated. Column 1 indicates inclusion of pyruvate or FCCP in the solutions. Pyruvate or FCCP was present (when included) in the solutions throughout saponin treatment and the fluorescence measurement runs, in which [Mg²⁺] of the intracellular solution was initially 0.8 mM and then increased to 4.0 mM. Means ± SE values measured from n cells (indicated in column 2) are shown in columns 3–5. Column 3 gives [Mg²⁺]_r values at 0.8 mM [Mg²⁺] averaged over 14–19 min after washout of saponin (data points at times 19 min and 24 min in the lower panels of Fig. 7). Column 4 gives [Mg²⁺]_r values at 4.0 mM [Mg²⁺] averaged over 13–18 min after solution exchange (data points at times 39 min and 44 min in the lower panels of Fig. 7). Column 5 gives values of Δ[Mg²⁺]_r calculated as the difference of [Mg²⁺]_r between the last measurement at 0.8 mM [Mg²⁺] and the first measurement at 4.0 mM [Mg²⁺] made 8 min after solution exchange.

^*P < 0.01 vs. 0.1 mM pyruvate.

Table 2 summarizes [Mg²⁺]_r measurements in the various solution conditions. In the solutions containing 0.1 mM pyruvate, 0–10 mM Na⁺, and 0.8 mM Mg²⁺, average [Mg²⁺]_r values were in the range of 0.6–0.7 mM, and did not change markedly even when [Mg²⁺] of the intracellular solution was raised to 4.0 mM. When 50 mM Na⁺ was present in the intracellular solution, average [Mg²⁺]_r values were ∼0.8 mM at either 0.8 mM or 4.0 mM solution [Mg²⁺]. The somewhat higher values of [Mg²⁺]_r observed in the presence of the high concentration of Na⁺ could be due to the direct effect of Na⁺ on furaptra fluorescence (Fig. 1).

Although the regulatory mechanisms of [Mg²⁺]_r is still unknown, results shown in Fig. 7 and Table 2 suggest that [Mg²⁺]_r values are well maintained in the 0.6–0.7-mM range independent of [Mg²⁺]_c within the time-range of ∼20 min, unless mitochondrial membrane potential is disrupted. However, long-term elevation of [Mg²⁺]_c during the Mg²⁺-loading procedure employed in the present study might lead to significant changes in [Mg²⁺]_r. To test this possibility, we first loaded the cells with Mg²⁺ for 3 h, and then saponin was applied to estimate [Mg²⁺]_r (Fig. 8). During saponin treatment and subsequent measurements of [Mg²⁺]_r the intracellular solution contained 4 mM Mg²⁺ to minimize possible leakage of Mg²⁺ out of organelles. In the cell shown in Fig. 8 A, [Mg²⁺]_i increased to 1.73 mM after Mg²⁺-loading for 3 h. Immediately after washout of saponin, F(350) decreased to 24% (upper), and [Mg²⁺]_r was 0.71 mM (lower); these values remained relatively constant independent of time after saponin treatment and the solution [Mg²⁺]. The relation between [Mg²⁺]_i before saponin treatment and [Mg²⁺]_r obtained from 12 similar experiments showed little dependence of [Mg²⁺]_r on [Mg²⁺]_i with mean [Mg²⁺]_r of 0.70 ± 0.11 mM (Fig. 8 B). Thus, a large increase in [Mg²⁺]_r appeared unlikely even during prolonged periods of Mg²⁺ loading.

Estimation of cytoplasmic free Mg²⁺ concentration

R-values of residual furaptra fluorescence were found to be virtually insensitive to and consistently higher (i.e., lower in [Mg²⁺]) than those in the cytoplasm. Consequently, [Mg²⁺]_i obtained in intact myocytes appears to underestimate [Mg²⁺]_c. We therefore corrected [Mg²⁺]_i values measured in intact myocytes for this insensitive fraction of fluorescence to estimate [Mg²⁺]_c. If 78% of the indicator molecules are localized in the cytoplasm with the rest being localized in organelles, the fluorescence R measured in intact myocytes (R_i) could be expressed as the linear combination of R in the cytoplasm (R_c) and R of residual fluorescence (R_r): R_i = 0.78 × R_c + 0.22 × R_r. The value of R_c could be obtained as

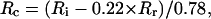(3)

where the R_r-value was set to 0.8875, which corresponded to 0.65 mM [Mg²⁺]_r, a median value of the 0.6–0.7-mM range. [Mg²⁺]_c was then calculated with Eq. 1 and parameter values described in Methods. With [Mg²⁺]_i values of 0.842 ± 0.019 mM obtained from 43 cells in the present study (see above), mean [Mg²⁺]_c was estimated to be 0.900 ± 0.024 mM. Based on the relation between initial [Mg²⁺]_i and initial Δ[Mg²⁺]_i/Δt shown in Fig. 2 (solid curve in the right panel), the relation between initial [Mg²⁺]_c and the initial rate of decrease in [Mg²⁺]_c (initial Δ[Mg²⁺]_c/Δt) was obtained as shown in Fig. 9 (solid circles in the right panel). Comparison of initial Δ[Mg²⁺]_i/Δt (solid curve in the right panel of Fig. 2) and initial Δ[Mg²⁺]_c/Δt (solid circles in the right panel of Fig. 9) clearly indicates that correction for the fluorescence emitted from organelles is rather small near the basal [Mg²⁺]_c level, but becomes progressively greater as [Mg²⁺]_c rises to higher levels.

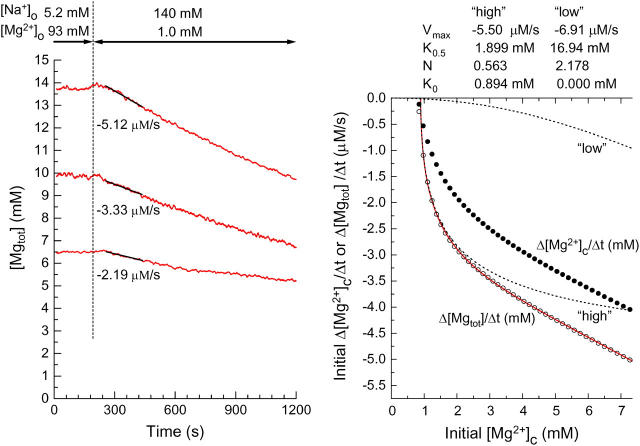
FIGURE 9.

The left panel shows analysis of the initial rates of decrease in [Mg_tot] (initial Δ[Mg_tot]/Δt) in three myocytes which were loaded with Mg²⁺ to different levels of [Mg²⁺]_c (the same cells as used for the analysis in the left panel of Fig. 2). The initial Δ[Mg_tot]/Δt (the slopes of solid lines) estimated by linear regression to [Mg_tot] traces for 180 s (60–240 s after solution exchange) are indicated below the traces. The right panel compares initial Δ[Mg_tot]/Δt (open circles) and initial Δ[Mg²⁺]_c/Δt (solid circles) calculated through Steps 1–7 (see Appendix for details). A solid curve indicates the least-squares-fit to open circles by sum of the two Hill-type curves (see Eq. 2): two dotted curves marked “high” and “low” with the best-fitted parameter values are shown at the top of the panel.

Estimation of cytoplasmic total Mg concentration

Because there are numerous Mg²⁺ binding sites in the cells, changes in [Mg²⁺]_c only partially reflect changes in total Mg concentration in the cytoplasm, [Mg_tot]. To obtain quantitative information on Mg²⁺ flux across the cell membrane, we therefore calculated changes in [Mg_tot] by utilizing concentration and dissociation constant values of known cytoplasmic Mg²⁺ buffers. The model assumed the cytoplasmic space consisted of a single compartment containing furaptra and other Mg²⁺ binding sites (Table 3). Metal binding to the sites were calculated by simultaneous equations for the steady-state 1:1 (metal:site) binding. The concentration and dissociation constant values were taken from Fabiato and Fabiato (1979) and Bers (2001), unless otherwise stated in the legend of Table 3. Zhao et al. (1997) estimated that the AM-loading rate of furaptra was 312 μM/h (or 5.2 μM/min) in frog skeletal muscle fibers at 16°C. They also reported that AM-loading rate of fura-2 was, on average, three times greater at 25°C than at 16°C. Under the assumption that the same temperature-dependence applies to furaptra, we estimated the cellular furaptra loading during a 14-min period (median of 13–15 min) to be 220 μM (∼5.2 μM × 3 × 14). Cytoplasmic concentrations of Na⁺ and K⁺ were assumed to be 10 mM and 140 mM, respectively. Because cells were in extracellular Ca²⁺-free conditions in the present study, [Ca²⁺]_c was somewhat arbitrarily assumed to be 10 nM, which was lower than the 100 nM generally assumed for the resting [Ca²⁺]_c.

Fig. 9 (left panel) shows sample traces of [Mg_tot] calculated based on the fluorescence R data, from which the [Mg²⁺]_i traces shown in the left panel of Fig. 2 were obtained. For each data point, the [Mg²⁺]_c value was calculated as described above, and [Mg_tot] value was calculated, according to

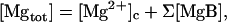(4)

where [MgB] denotes the concentration of the Mg-bound buffer listed in Table 3. Note that [Mg_tot] values on the ordinate are much greater than [Mg²⁺]_i values in Fig. 2. The relation between initial [Mg²⁺]_i and initial Δ[Mg²⁺]_i/Δt shown in Fig. 2 (solid curve in the right panel) was reanalyzed, and the results are shown in the right panel of Fig. 9; open circles are the relation between initial [Mg²⁺]_c and initial rates of changes in [Mg_tot] (initial Δ[Mg_tot]/Δt) calculated by taking cytoplasmic Mg²⁺ binding into account. The relation between initial [Mg²⁺]_c and initial Δ[Mg_tot]/Δt could not be explained by a Hill-type curve (Eq. 2), but was well described by the sum of the two Hill-type curves (a solid curve in the right panel of Fig. 9): one that appears in low [Mg²⁺]_c range around the basal level (a high-affinity component, dotted curve marked “high”) and the other that was significant only in the high [Mg²⁺]_c range (a low-affinity component, dotted curve marked “low”). Because [Mg²⁺]_c reached at the end of Mg²⁺ loading in most of the present study was in the 1.1–2.5-mM range (i.e., 1.0–2.0 mM [Mg²⁺]_i), the Mg²⁺ transport we observed is thought to predominantly represent the high-affinity component, which is activated by [Mg²⁺]_c above 0.9 mM with half-maximal activity at 1.9 mM [Mg²⁺]_c. Little information is currently available on the low-affinity component.

DISCUSSION

The previous study from this laboratory (Tashiro et al., 2002) assumed that initial Δ[Mg²⁺]_i/Δt values were linearly related to initial [Mg²⁺]_i in the 1.0–2.0-mM range. The present results evaluated the relation over a more extended range, and showed that the values of initial Δ[Mg²⁺]_i/Δt tend to saturate at high initial [Mg²⁺]_i (2–5 mM). Thus, it was possible to estimate important parameter values (i.e., K_0.5 and V_max) for the Mg²⁺ transport (Fig. 2).

Estimation of [Mg²⁺]_c

The results of the present study (Fig. 2) strongly suggest that [Mg²⁺]_i is tightly regulated by a Mg²⁺ efflux that is activated by a rise of [Mg²⁺]_i above the basal level. However, a quantitative interpretation of the results is complicated by the fact that ∼22% of furaptra molecules appears to be trapped inside organelles after AM-loading. Trapped furaptra fluorescence was found to be primarily localized in mitochondria. It was thus important to estimate the contribution of the fluorescence signals from mitochondria. In search of the optimum solution conditions for skinned myocytes, we found that 0.1-mM pyruvate as a substrate could well retain respiration and membrane potential of mitochondria (Ca²⁺-free conditions, 25°C). In experiments with isolated mitochondria, respiration has usually been induced by addition of a substrate (or combination of substrates) in millimolar concentrations (e.g., Brierley et al., 1987; Rutter et al., 1990; Jung et al., 1990). We also observed that 0.5–1.0-mM pyruvate induced a transient increase in cellular autofluorescence at 350-nm excitation followed by a slow decay, which could be attributed to a facilitated turnover of NADH. Instead, mitochondrial respiration was kept stable in the presence of 0.1 mM pyruvate probably with slow turnover of NADH. Cytoplasmic concentrations of pyruvate at or below 0.1 mM have been reported in intact cardiac myocytes (see Mallet, 2000).

[Mg²⁺]_r calibrated from ratio values of residual furaptra fluorescence after saponin treatment was 0.6–0.7 mM at bathing solution [Mg²⁺] (i.e., [Mg²⁺]_c of the skinned myocytes) of either 0.8 mM or 4.0 mM. This could mean that mitochondrial Mg²⁺ transport (uptake/release) is unaffected by a large increase in [Mg²⁺]_c. Alternatively, the estimates of [Mg²⁺]_r may not accurately represent [Mg²⁺] in mitochondria, because 1), distribution of furaptra in organelles other than mitochondria cannot be excluded; and 2), calibration of furaptra R in terms of [Mg²⁺] may be altered in mitochondria where ionic composition is very different from that in the cytoplasm. Despite these uncertainties, the virtually constant R-values of residual furaptra fluorescence at 0.8–4.0 mM [Mg²⁺]_c of the skinned myocytes provided us with means to estimate [Mg²⁺]_c in intact myocytes. Average basal [Mg²⁺]_c estimated by the present procedure was only slightly (7%) higher than basal [Mg²⁺]_i, but the difference was greater at higher [Mg²⁺]_c levels.

Our results do not provide evidence for uptake or release of Mg²⁺ by intracellular organelles in the present experimental conditions (Ca²⁺-free, 25°C). However, we do not exclude the possibility that intracellular Mg²⁺ mobilization is important in conditions that activate intracellular signaling pathways, for example, hormonal stimulation (Romani et al., 1993; Fatholahi et al., 2000) and dynamic changes in [Ca²⁺]_c (Bond et al., 1984).

Mg²⁺ flux across the cell membrane

The changes in [Mg_tot] can be experimentally determined by atomic absorption spectroscopy from cell extracts (Romani et al., 1993). One disadvantage of this method is, however, that it is not possible to repeat the measurements as a function of time in the same cells. Alternatively, Romani and Scarpa (1990) and Romani et al. (1993) measured [Mg²⁺] of the extracellular medium to detect Mg²⁺ efflux from the myocytes. Although this method is useful for time-resolved measurements of Mg²⁺ flux, conversion from [Mg²⁺] in the extracellular medium to cellular [Mg_tot] seems difficult. On the other hand, [Mg_tot] measurements by ²⁸Mg is hampered by availability and a short half-life of the isotope (Rasgado-Flores and Gonzalez-Serratos, 2000).

These difficulties led us to develop a computer model to estimate what changes in [Mg_tot] accompany changes in [Mg²⁺]_c. The calculated cytoplasmic buffering power β (defined as d[Mg_tot]/d[Mg²⁺]_c) was 2.09 at 0.9 mM [Mg²⁺]_c. A similar value of ∼2 has been estimated by Westerblad and Allen (1992) for mouse skeletal muscle. Among the buffer species, ATP had the greatest buffering power (∼67% of β), and the contribution of furaptra was small (∼1.5%). The minor contribution of furaptra to cellular Mg²⁺ buffering suggests little influence of furaptra loading on the [Mg²⁺] measurements. For modeling, we somewhat arbitrarily assumed 10 nM [Ca²⁺]_c. However, use of 100 nM [Ca²⁺]_c, instead of 10 nM, caused only 0.9% reduction of β, and did not change the general conclusion of the present study.

Some cytoplasmic buffers that are not included in the model (e.g., Mg²⁺ binding to membrane phospholipids) may have significant effects on cytoplasmic Mg²⁺ buffering power. Also, release/uptake of Mg²⁺ by intracellular organelles which cannot be detected by the residual furaptra fluorescence may act as additional buffers. Thus, the values of Δ[Mg_tot]/Δt calculated with the model should be regarded as lower-end estimates of the Mg²⁺ flux across the cell membrane.

The relation between [Mg²⁺]_o and Δ[Mg_tot]/Δt

Fig. 4 compares the values of Δ[Mg²⁺]_i/Δt as a function of [Mg²⁺]_o. Because conversion from [Mg²⁺]_i to [Mg_tot] is nonlinear, the relation between [Mg²⁺]_o and Δ[Mg_tot]/Δt may be somewhat different from that between [Mg²⁺]_o and Δ[Mg²⁺]_i/Δt shown in Fig. 4 B. When we reanalyzed these data as described in the legend of Fig. 9, average values of the initial Δ[Mg_tot]/Δt for 1 mM, 3 mM, 10 mM, and 20 mM [Mg²⁺]_o were, respectively, −2.56 ± 0.20 μM/s (n = 10), −2.08 ± 0.18 μM/s (n = 8), −1.29 ± 0.15 μM/s (n = 5), and −0.82 ± 0.08 μM/s (n = 5). We also calculated relative Δ[Mg_tot]/Δt using the standard relation between the initial Δ[Mg_tot]/Δt and the initial [Mg²⁺]_c (solid curve in Fig. 9, right). The calculated values of relative Δ[Mg_tot]/Δt were very similar to those of relative Δ[Mg²⁺]_i/Δt; average difference at any given [Mg²⁺]_o was in the range of −0.001 to +0.003 and the relation between [Mg²⁺]_o and relative Δ[Mg_tot]/Δt (not shown) was indistinguishably different from the relation between [Mg²⁺]_o and relative Δ[Mg²⁺]_i/Δt (Fig. 4 B). The excellent agreement between relative Δ[Mg_tot]/Δt and relative Δ[Mg²⁺]_i/Δt probably resulted from the fact that the measurements were carried out at similar initial [Mg²⁺]_i levels (on average, 1.44–1.55 mM). Thus, for data obtained at similar initial [Mg²⁺]_i, comparison of relative Δ[Mg²⁺]_i/Δt should provide valid and meaningful information on the Mg²⁺ flux.

As for the molecular mechanism of extracellular Mg²⁺ effects, the present results do not distinguish competition with extracellular Na⁺ from an allosteric transinhibition. The double reciprocal plot of the Δ[Mg²⁺]_i/Δt amplitude and [Mg²⁺]_o at different [Na⁺]_o will provide useful information, as reported for the Na⁺-Ca²⁺ exchange (Miura and Kimura, 1989).

CONCLUSIONS

[Mg²⁺]_c of rat ventricular myocytes appears to be tightly regulated by extracellular Na⁺-dependent Mg²⁺ efflux. The transport rate is half-maximum at 1.5 mM [Mg²⁺]_i (estimated from raw data) or 1.9 mM [Mg²⁺]_c (estimated after correction for the trapped indicator and model calculations). In any event, the net transport is negligible at the basal [Mg²⁺]_c level, and is strongly activated by small elevations of [Mg²⁺]_c. The transport is 50% inhibited by raising [Mg²⁺]_o from 1 mM to 10 mM. The present method should be useful to characterize the Mg²⁺ transport across the cell membrane in other cell types as well.

APPENDIX

Initial Δ[Mg²⁺]_c/Δt and initial Δ[Mg_tot]/Δt (Fig. 9) were calculated through the following steps, 1–7.

• Step 1. From the least-squares fitted relation between initial Δ[Mg²⁺]_i/Δt and initial [Mg²⁺]_i (a solid curve in the right panel of Fig. 2), the values of Δ[Mg²⁺]_i/Δt were sampled for initial [Mg²⁺]_i ([Mg²⁺]_i at the beginning of a 180-s period, [Mg²⁺]_i(t=0)) between 0.8 mM and 5.0 mM at 0.1-mM intervals.

• Step 2. For each sampled point, [Mg²⁺]_i at the end of a 180-s period, [Mg²⁺]_i(t=180) was calculated as

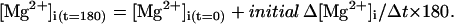
  (5)
• Step 3. Values of [Mg²⁺]_i(t=0) and [Mg²⁺]_i(t=180) were converted to R_i(t=0) and R_i(t=180), respectively,

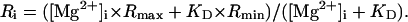
  (6)

• Step 4. R_c(t=0) and R_c(t=180), were calculated from R_i(t=0) and R_i(t=180), respectively, with Eq. 3.

• Step 5. Values of [Mg²⁺]_c at t = 0 ([Mg²⁺]_c(t=0)) and t = 180 s ([Mg²⁺]_c(t=180)) were calculated with Eq. 1.

• Step 6. [Mg_tot] values at t = 0 ([Mg_tot]_(t=0)) and t = 180 s ([Mg_tot]_(t=180)) were subsequently obtained with Eq. 4 as described in the text.

• Step 7. Initial Δ[Mg²⁺]_c/Δt (solid circles) and initial Δ[Mg_tot]/Δt (open circles) for 180 s were calculated by

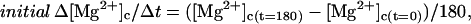
  (7)

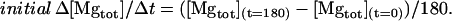
  (8)