Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Dec 21;88(3):2193–2205. doi: 10.1529/biophysj.104.049684

Dielectrophoretic Traps for Single-Particle Patterning

Adam Rosenthal *,†, Joel Voldman *
PMCID: PMC1305270  PMID: 15613624

Abstract

We present a novel microfabricated dielectrophoretic trap designed to pattern large arrays of single cells. Because flowing away untrapped cells is often the rate-limiting step during cell patterning, we designed the trap to be strong enough to hold particles against practical flow rates. We experimentally validated the trap strength by measuring the maximum flow rate that polystyrene beads could withstand while remaining trapped. These bead experiments have shown excellent agreement with our model predictions, without the use of fitting parameters. The model was able to provide us with a fundamental understanding of how the traps work, and additionally allowed us to establish a set of design rules for optimizing the traps for a wide range of cell sizes. We provide the foundations for an enabling technology that can be used to pattern cells in unique ways, allowing us to do novel cell biology experiments at the microscale.

INTRODUCTION

Cell patterning—the ability to place cells in a desired location—has become an increasingly important tool for control of the cellular microenvironment. The cellular microenvironment is influenced by several factors, including cell-media, cell-matrix, and cell-cell interactions. Cell patterning can be used to manipulate cell-cell interactions, varying the contact area between two cell types in coculture (Bhatia et al., 1998). Cell patterning can also be used to direct cell-matrix interactions, controlling the amount of contact area with the extracellular matrix (ECM) (Chen et al., 1997) or the type of ECM that the cell sits on (Folch and Toner, 1998). Techniques have even been developed to extend these planar interactions into a three-dimensional cellular matrix (Tan and Desai, 2003). Cell patterning also has the potential to improve devices like cell-based biosensors—using living cells as sensing elements for applications like toxin detection (Tempelman et al., 1996) and defense monitoring (Paddle, 1996). Cells have successfully been interfaced to sensing elements to form cell-based biosensors and recent advances in cell patterning may enable reproducible and manufacturable biosensor devices (Pancrazio et al., 1999).

Several techniques exist for patterning cells. Microfluidic patterning takes advantage of the laminar flows in microfluidic devices to pattern the cell-culture substrate, cells, or cell-culture media (Takayama et al., 1999). Other methods use physical barriers to place cells, either using microwells (Revzin et al., 2003) or removable elastomeric stencils (Folch et al., 2000). The substrate that the cells sit on can also be modified to selectively pattern cells. Microcontact stamping uses a polydimethylsiloxane (PDMS) stamp to pattern matrix proteins onto a substrate (Xia and Whitesides, 1998), whereas electroactive substrates use an applied voltage to switch the surface properties of a substrate, both allowing cells to selectively attach in specific areas (Lahann et al., 2003; Yeo et al., 2003). Electromagnetic forces can also be used to pattern cells. Electrophoresis utilizes the negative charges of cell-membrane proteins to exert forces on cells in a constant (DC) electric field, creating patterned cellular arrays (Ozkan et al., 2003). Optical tweezers use optical frequency nonuniform electromagnetic fields to manipulate cells (Birkbeck et al., 2003; Dufresne and Grier, 1998), whereas dielectrophoresis (DEP) uses nonuniform AC electric fields in the range from 10 kHz to 100 MHz to position cells on or between electrodes (Gray et al., 2004).

DEP offers many advantages as a cell-patterning technique. Because DEP traps consist of scalable electrode arrays, they can be designed to pattern thousands of cells on a single glass slide and be made small enough to ensure single-cell resolution (Gray et al., 2004). In addition, DEP can be used to place cells without the need for patterning the substrate (Prasad et al., 2004) or, when used in combination with ECM patterning can yield dramatic improvements in patterning efficiency compared to patterning with ECM alone (Gray et al., 2004). Several applications such as cell development studies, cell-based biosensors, and tissue engineering would benefit from the numerous features that DEP provides.

DEP traps can use either negative dielectrophoresis (nDEP)—pushing cells away from the electrodes—or positive dielectrophoresis (pDEP)—pulling cells toward the electrodes. Prior single-cell DEP traps include nDEP octopoles (Schnelle et al., 1993), nDEP cages (Manaresi et al., 2003), nDEP posts (Voldman et al., 2003), pDEP circles (Prasad et al., 2004), and a pDEP points-and-lid geometry (Gray et al., 2004). The nDEP octopole and nDEP cages are created using electrodes on the top and bottom of the chamber and are designed for cell sorting. They both trap cells in the center of the channel, rather than on the surface, making them inappropriate for patterning cells. In addition, the nDEP octopole (Schnelle et al., 1993) has strict packaging needs, requiring alignment of the quadrupoles on the top and bottom of the channel. The nDEP posts (Voldman et al., 2003) use an extruded quadrupole geometry that traps the cells above the substrate, which is also inappropriate for cell patterning. In addition, the 50-μm-high electrode posts make the fabrication difficult and would not allow unobstructed cell proliferation. The pDEP geometries (Gray et al., 2004; Prasad et al., 2004) were designed to pattern cells and can do so effectively. However, to create the necessary conditions for pDEP, the cells need to be immersed in an artificial low-conductivity media that could affect cell physiology, especially for sensitive cells. nDEP traps allow the use of normal cell media.

When patterning cells using DEP, the strength of the DEP trap is another important consideration because flowing away untrapped cells is often the rate-limiting step. Previous nDEP traps that are appropriate for single-cell patterning are too weak for practical experimental times (Voldman et al., 2001). Here we present a single-cell nDEP trap that is strong enough for useful operation. We demonstrated this strength by measuring the maximum flow rate that test particles could withstand while remaining trapped, and matched this to a quantitative predictive model with excellent agreement. The model was able to provide us with a clear understanding of how our traps work, and additionally allowed us to establish a set of design rules for optimizing the traps for a wide range of cell sizes. Overall, we wish to present a fundamental approach to cell patterning that can be utilized by engineers and biologists to do novel cell biology experiments at the microscale.

THEORY

In the traps, the particles experience several forces: the DEP force, the hydrodynamic drag (HD) force, the hydrodynamic lift (HL) force, and gravity. When designing a trap, we use these forces to determine the maximum flow rate the particle can withstand while remaining trapped.

DEP traps use the interaction of an induced multipole in a nonuniform electric field to create forces that will stably position particles. The dipole component of the DEP force is:

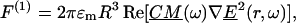graphic file with name M1.gif (1)

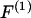where Inline graphic refers to the dipole approximation to the DEP force, 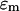Inline graphic is the electrical permittivity of the surrounding media, R is the radius of the particle, and 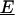Inline graphic is the complex applied electric field, where ω is the frequency of the applied field in radians and r is the spatial coordinate of the particle. 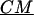Inline graphic is the Clasius-Mossotti (CM) factor, which for a lossy dielectric uniform sphere, such as a bead, is given by:

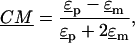graphic file with name M6.gif (2)

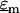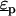where Inline graphic and Inline graphic are the complex permittivities of the medium and particle, respectively, and are each given by 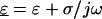Inline graphic where ɛ is the permittivity of the medium or particle, σ is the conductivity of the medium or particle, and j is 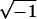Inline graphic. A positive CM factor indicates that the DEP force pushes particles toward the electrodes to the electric-field maxima (pDEP) whereas a negative CM factor indicates that the DEP force pushes particles away from the electrodes to the electric-field minima (nDEP). Equation 1 is the simplest approximation to the DEP force, and only includes the dipole contribution to the DEP force. For electric fields with higher nonuniformities, higher-order moments will be induced in the particle, requiring the addition of multipole DEP forces (Jones and Washizu, 1996; Washizu and Jones, 1996).

The HD force is caused by the flow of a viscous fluid around an object. The trapped particles are stationary and rest on a bottom substrate. The HD force is then similar to Stokes' drag on a sphere, with a correction for the effects of the wall (Goldman et al., 1967), and is given by:

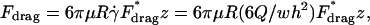graphic file with name M11.gif (3)

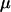where Inline graphic is the viscosity of the liquid, 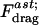Inline graphic is a nondimensional factor incorporating the wall effects, z is the distance from the particle center to the substrate, and 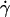Inline graphic is the shear rate at the wall in a parallel plate flow chamber, where Q is the flow rate, w is the chamber width, and h is the chamber height (Deen, 1998).

The gravitational force on the bead is:

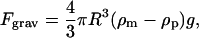graphic file with name M15.gif (4)

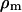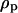where Inline graphic and Inline graphic are the densities of the medium and particle, respectively, and g is the gravitational acceleration constant.

The HL force is caused by low Reynolds-number viscous flow over an object near a solid plane, which tries to levitate the particle. For a stationary sphere in contact with the plane, the lift force becomes (Cherukat and McLaughlin, 1994; Leighton and Acrivos, 1985):

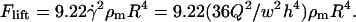graphic file with name M18.gif (5)

MATERIALS AND METHODS

Stock solutions

Bead stock solutions were made with conductivity of 0.01 S/m by combining appropriate volumes of 18.2-MΩ-cm deionized water and Dulbecco's phosphate buffered saline (Gibco, Carlsbad, CA), both containing 0.1% Triton X-100 (Sigma, St. Louis, MO). Conductivities were measured using a Thermo Orion model 555A conductivity meter (VWR, Cambridge, MA).

Beads

Polystyrene beads, with density of 1.062 g/cm3, at five different bead diameters were used. Beads (4.2- and 8.2-μm diameter) (Polysciences, Warrington, PA) with ± SD 0.33 and 0.17 μm, respectively, were packaged as 1% solids in water. A 2.0-mL aliquot of these bead solutions was washed in 1.0 mL of stock solution and resuspended in 1.0 mL of stock solution. Polystyrene beads (incorporating 2% divinyl benzene) with diameters of 9.7, 14.2, and 19.5 μm (Bangs Laboratories, Fishers, IN) with ± SD 0.10, 0.72, and 0.31 μm, respectively, were packaged as 10% solids in water. A 0.5-mL aliquot of these bead solutions was washed in 0.5 mL of stock solution and resuspended in 1.0 mL of stock solution.

Electrode traps

The DEP traps were formed by patterning gold onto glass slides. Standard microscope slides of 38 × 75 mm were cleaned for 10 min in a Piranha solution (3:1 H2SO4:H2O2), blow dried with N2, and then dehydrated for 30 min at 225°C. Photolithography was then performed using the image-reversal photoresist Hoechst AZ-5214 (Somerville, NJ) to define the electrode patterns. Then, 250 Å of titanium and 2500 Å of gold were evaporated onto the slides followed by resist dissolution and metal liftoff in acetone. The traps were designed as one square electrode with inner square side length of 25 μm and another line electrode spaced 10 μm away. All electrode widths were 10 μm (Fig. 1 A).

FIGURE 1.

FIGURE 1

Open in a new tab

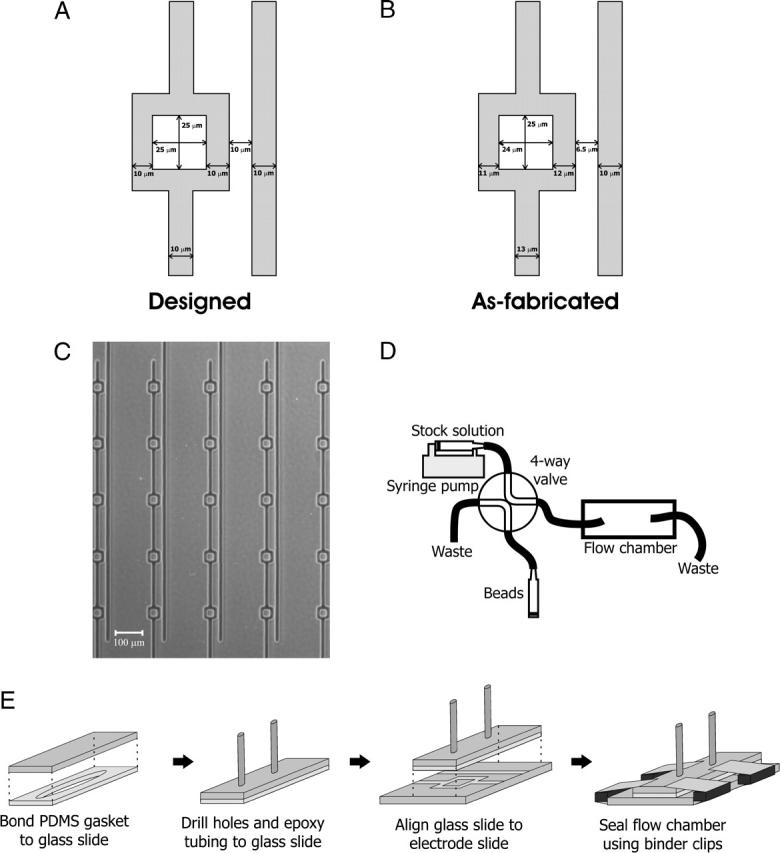
Overview of the DEP trap and trap array, flow chamber packaging, and fluidics. The DEP geometry consists of a square electrode and a line electrode. (A) The designed trap dimensions. (B) The as-fabricated trap dimensions. (C) A micrograph of the fabricated 5 × 5 trap array. (D) The fluidics consisted of one free syringe and one syringe powered by a syringe pump, connected to a four-way valve, with valve output connected to the flow chamber. The flow chamber output was connected to waste. (E) Flow chamber packaging involved bonding a glass slide to a PDMS gasket, drilling holes into the top chamber and epoxying tubing, and aligning and sealing to the electrode slide using four binder clips.

The as-fabricated trap dimensions differed from the designed dimensions submitted to the transparency mask manufacturer (Fig. 1 B). This is because our minimum feature size of 10 μm is also the minimum allowed by the mask manufacturer, and the variance at this feature size is 3.2 μm. In addition, variations in photolithography exposure times significantly changed the trap dimensions and our exposure times were chosen to yield as-fabricated dimensions that were closest to the designed dimensions. However, this discrepancy in designed and as-fabricated trap dimensions did not significantly affect the predicted maximum flow rates (data not shown). All the predictions shown in Figs. 3, 4, and 5 use the as-fabricated geometry and all the predictions shown in Figs. 6, 7, and 8 use the designed geometry.

FIGURE 3.

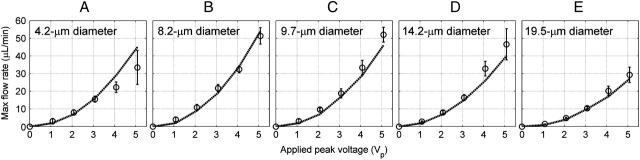
FIGURE 3

Open in a new tab

Experimental and simulated results for five different diameter beads. We vary the applied voltage from 0 to 5 Vp and measured the maximum flow rate at which the beads are still trapped. Bead diameters are (A) 4.2 μm, (B) 8.2 μm, (C) 9.7 μm, (D) 14.2 μm, and (E) 19.5 μm. Shown are the predicted values (dashed line), mean (circles), and standard deviation (solid line) (n ≥ 3; at least three of the 25 traps were filled at each voltage). Model and experiment differ by ≤16% in all cases, except for the 4.2-μm beads that had a difference of 26%.

FIGURE 4.

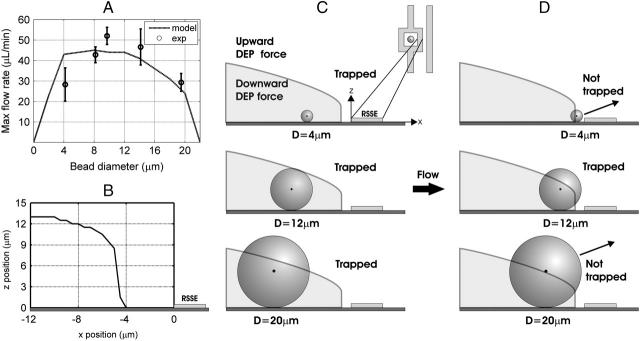
FIGURE 4

Open in a new tab

Size-selectivity behavior. (A) Experimental and simulated results for all bead diameters at a 5 Vp, 5 MHz applied signal. Shown are the predicted values (dashed line), mean (circles), and standard deviation (solid line) (n ≥ 3 at each voltage). Experimental results were normalized for flow chamber height variations between experiments. (B) The stability transition line was determined from the modeling software. (C) Low flow rates. All bead centers are in the stable region such that the bead is being pushed down by the downward DEP force. Importantly, larger beads are trapped further away from the right side of the square electrode. (D) High flow rates. Upon starting flow, the beads are pushed to the right. Both smallest and largest bead centers leave the stable region and are pushed out of the trap by the upward DEP force, whereas the medium-sized beads do not leave the stable region until higher flow rates are reached.

FIGURE 5.

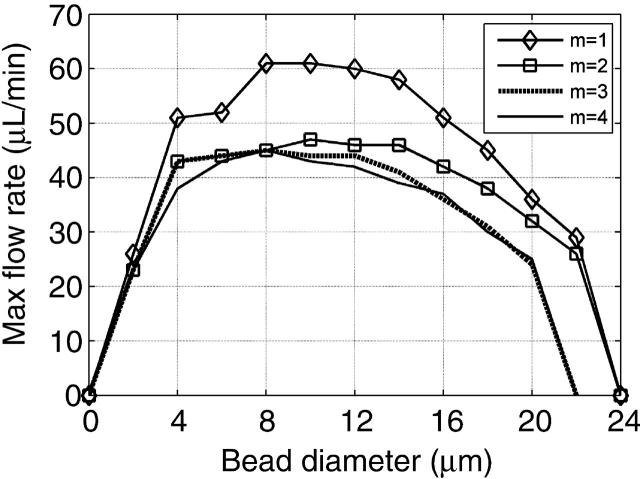
FIGURE 5

Open in a new tab

Multipole contributions to the DEP force. Contributions from the dipole force alone (m = 1), dipole-quadrupole force (m = 2), dipole-quadrupole-octopole force (m = 3), and dipole-quadrupole-octopole-hexadecapole force (m = 4).

FIGURE 6.

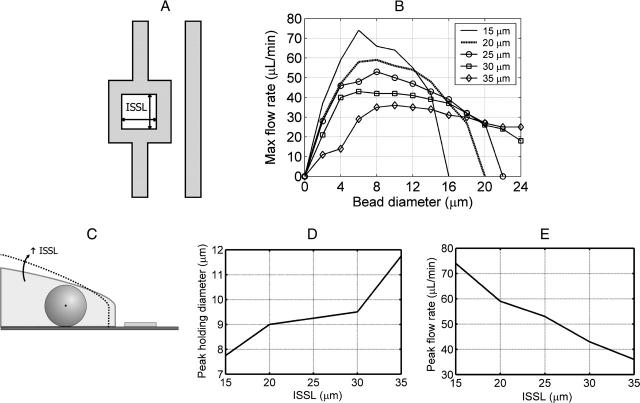
FIGURE 6

Open in a new tab

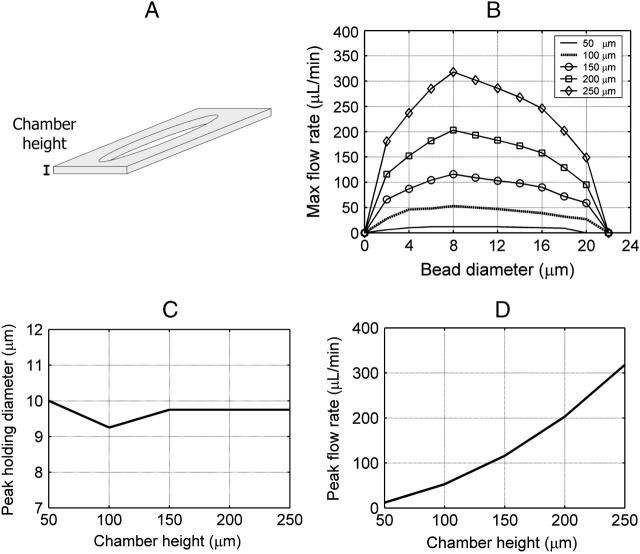
Size-selectivity behavior due to changing inner square side length (ISSL). All other dimensions were held constant. (A) The ISSL was varied from 15 to 35 μm to determine the effects on size-selectivity behavior. (B) The maximum flow rate was calculated at 5 Vp as a function of bead diameter for a given ISSL. (C) Increasing the ISSL increases the slope of the stability transition line and shifts it further away from the RSSE. (D) As the ISSL increases, the peak holding diameter increases. The peak holding diameter was determined by cubically fitting the size-selectivity curves. (E) As the ISSL increases, the maximum flow rate magnitude decreases.

FIGURE 7.

FIGURE 7

Open in a new tab

Size-selectivity behavior due to changing spacing between electrodes (SBE). All other dimensions were held constant. (A) The SBE was varied from 5 to 25 μm to determine the effects on size-selectivity behavior. (B) The maximum flow rate was calculated at 5 Vp as a function of bead diameter for a given SBE. (C) As the SBE increases, the peak holding diameter stays roughly the same. The peak holding diameter was determined by cubically fitting the size-selectivity curves. (D) As the SBE increases, the maximum flow rate magnitude decreases.

FIGURE 8.

FIGURE 8

Open in a new tab

Size-selectivity behavior due to changing the flow chamber height. All other dimensions were held constant. (A) The chamber height was varied from 50 to 250 μm to determine the effects on size-selectivity behavior. (B) The maximum flow rate was calculated at 5 Vp as a function of bead diameter for a given chamber height. (C) As the chamber height increases, the peak holding diameter stays roughly the same. The peak holding diameter was determined by cubically fitting the size-selectivity curves. (D) As the chamber height increases, the maximum flow rate magnitude increases.

The DEP traps were in a 5 × 5 square array, with a trap-to-trap distance of 200 μm (Fig. 1 C). The minimum feature size of the traps is ≥10 μm, which allows the use of inexpensive transparency masks for photolithography (CAD Art Services, Poway, CA).

Flow chamber and packaging

The flow chambers were made using a Si master wafer to mold the PDMS gasket. The Si wafers were cleaned for 10 min using the same Piranha solution described above, blow dried with N2, and dehydrated for 10 min at 130°C. Photolithography was then performed using SU8-50 (Microchem, Newton, MA) to define the flow chamber patterns. The wafers were developed for 10 min using PM acetate (Doe and Ingalls, Boston, MA) and then silanized for 30 min using hexamethyldisiloxane (Shin-Etsu MicroSi, Phoenix, AZ). PDMS (Sylgard 184, Dow Corning, Midland, MI) was then poured over the master Si wafer to form a gasket, using the “sandwich molding process” (Jo et al., 2000). The PDMS gasket was then plasma oxidized and bonded to a standard (25 × 75 mm) microscope slide and two holes were drilled to define inlet and outlet ports for the tubing. The tubing was epoxied (Radioshack quick-setting epoxy) to this chamber top. The chamber top was then clamped to the bottom electrode slide using four binder clips for easy assembling and disassembling. Wires were electrically connected to the electrodes using conductive epoxy (Circuit Specialists, Mesa, AZ). An overview of the packaging is shown in Fig. 1 E.

Fluidics

The two inputs of a four-way valve (V-101D, Upchurch Scientific, Oak Harbor, WA) were connected to a 5-mL syringe filled with beads and a 10-mL syringe filled with stock solution. The 10-mL syringe was controlled using a syringe pump (KD Scientific 210C, Holliston, MA). One output on the four-way valve was connected to 1/16-inch–outer-diameter (OD) PEEK tubing (1536, Upchurch Scientific, Oak Harbor, WA) and the other was connected to waste. The 1/16-inch-OD tubing was then adapted to the 1/32-inch-OD PEEK tubing (1575, Upchurch Scientific, Oak Harbor, WA) at the inlet on the flow chamber top. The 1/32-inch-OD tubing connected to the outlet on the flow chamber top was connected to waste. The fluidics setup is shown in Fig. 1 D.

Optics

An automated upright microscope (Zeiss Axioplan 2 imaging, Thornwood, NY) was used in the bead experiments and an inverted microscope (Zeiss Axiovert 200, Thornwood, NY), along with a SPOT digital camera (Diagnostic Instruments, Burlingame, CA), was used to take pictures of the trap geometries to determine as-fabricated trap dimensions.

Measuring chamber height

We measured the flow chamber height with an automated microscope by focusing on the electrodes on the bottom glass slide and then focusing on the top of the PDMS gasket. The difference between the two focus points was called the chamber height. The microscope has a motorized focus, allowing a minimum step resolution of 25 nm.

Because the device flow chamber is sealed using binder clips, the height of the flow chamber varied depending on how the slides were clipped together. Because the HD force is very sensitive to the flow chamber height (Eq. 3), the flow-chamber height was measured at the same location in the flow chamber, twice before the experiment and once after the experiment. These three values were averaged together to give the height used in the model. The two chamber heights measured before the experiment differed by up to ∼5 μm, due to the variability in focusing on the substrate. The chamber height after the experiment never varied by >∼2 μm from the before measurements, suggesting that the chamber height did not significantly drift over the course of the experiment. Bead experiments for bead diameters 4.2 and 8.2 μm were performed sequentially with the same experimental setup at a flow chamber height of 103 μm and bead diameters 9.7, 14.2, and 19.5 μm were performed sequentially with the same experimental setup at a flow chamber height of 95 μm.

Determining peak holding diameter

To be objective in choosing the peak holding diameter from the size-selectivity curves, the curves were cubically fit using MATLAB (Mathworks, Natick, MA) and the peak holding diameter was chosen as the diameter at the peak maximum flow rate.

Electrical excitation

Sine wave excitation at 5 MHz was generated by an Agilent 33250A signal generator (Agilent, Palo Alto, CA). One trap electrode was set to ground whereas the other trap electrode was set to either 0, 1, 2, 3, 4, or 5 Vp (peak voltage), while the signal was measured using a digital oscilloscope (Tektronix TDS 2024, Beaverton, OR) and found to be 0, 1.08, 2.08, 3.08, 4.08, and 5.08 Vp.

Bead experiments

The flow chamber was initially primed with ethanol to remove any bubbles and then flushed with stock solution to remove the ethanol from the chamber. The bead solution was then injected into the flow chamber so the maximum number of traps in the 5 × 5 array had beads in them (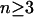Inline graphic). The signal generator was turned on to 5 Vp, trapping beads that were already inside the square electrode. The syringe pump was then turned on and stock solution was flowed through the chamber at 20 μL/min to clear all the untrapped beads from the field. The flow rate was then set to 1 μL/min so the signal could be set to the desired voltage without losing any of the trapped beads. The flow rate was then stepped up, at 1 μL/min intervals, until the maximum flow rate was reached. The maximum flow rate was determined to be the highest flow rate at which the beads would remain trapped for 1 min, observed through the microscope. This time was chosen empirically by observing that beads held for 1 min, if the flow was continued, would usually (>90%) be held indefinitely. The maximum flow rate was recorded for all the trapped beads in the array. Then the procedure was repeated at a different applied voltage. For each bead diameter, maximum flow rate measurements were made every 1 Vp from 0 to 5 Vp.

Modeling

Modeling was performed using an updated version of previous software (Voldman et al., 2001) written in MATLAB (Mathworks). The model takes as inputs electrical field data (Fig. 2) obtained using FEMLAB 3.0 (Comsol, Burlington, MA) and other experimental parameters to compute the total force everywhere in space, consisting of the multiorder DEP force (x-, y-, z-direction), the HD force (x-direction), gravity (z-direction), and the HL force (z-direction). The lift force was found to be negligible compared to the z-directed DEP force and gravity. When included in the total force calculations, the lift force did not affect the maximum flow rate (data not shown). 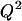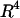However, because the lift is proportional to Inline graphic and Inline graphic (Eq. 5), the lift force could become significant for higher flow rates and larger bead diameters.

FIGURE 2.

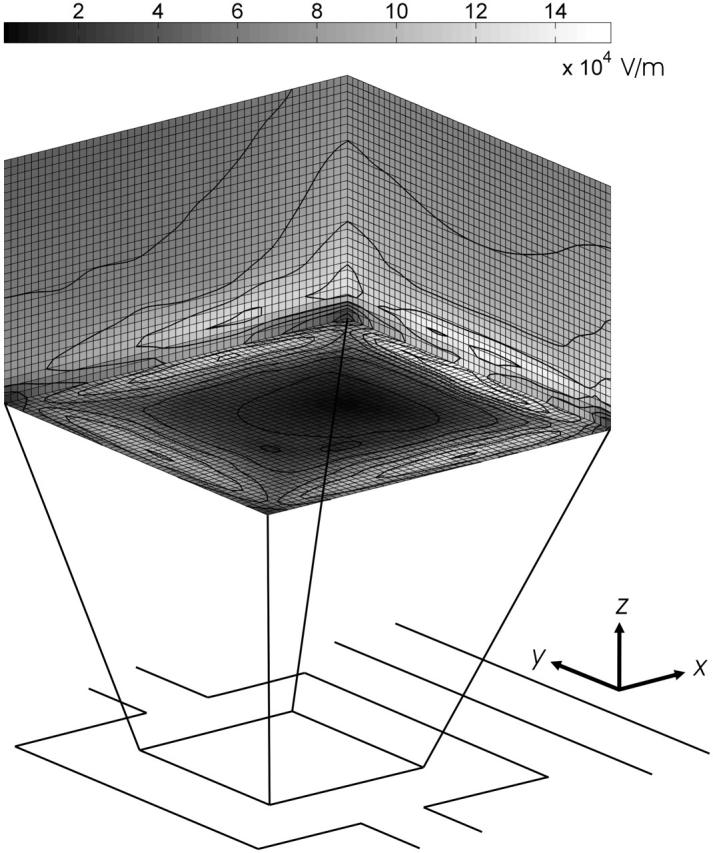
FIGURE 2

Open in a new tab

Electric-field magnitude (in V/m) inside the DEP trap at an applied voltage of 5 Vp. The contour lines show the lines of equal electric-field magnitude.

These forces are used to create streamlines of where the particle will travel, determining if the particle is stably held in the trap or is pushed out of the trap by the flow. By varying the flow rate for a given experimental condition, the modeling software can determine the maximum flow rate at which the particle is still held within the trap. The geometry simulated in FEMLAB is representative of the true experimental conditions, with a 100-μm-high flow chamber sandwiched between two 1-mm-thick glass slides. The boundary conditions were electric potential on the electrodes, electric insulation on the outer surfaces, and continuity everywhere else.

The simulations were performed on polystyrene beads with a bead density of 1062 kg/m3, medium density of 1000 kg/m3, bead conductivity of 2 × 10−4 S/m, and relative permittivity of 2.5, in media with a conductivity of 0.01 S/m and relative permittivity of 80. The applied signal was always a sine wave at 5 MHz. For the bead experiment simulations, the maximum flow rate was determined for each of the bead diameters as a function of the measured voltages of 0, 1.08, 2.08, 3.08, 4.08, or 5.08 Vp. The chamber geometry was 3-mm wide and either 95- or 103-μm high, depending on the experiment. For the size selectivity and design rule simulations, the maximum flow rate was determined at a fixed voltage of 5.08 Vp, as a function of bead diameter that ranged from 2 to 24 μm, with 2-μm resolution. The chamber geometry was 3-mm wide. The chamber height was 95 μm for the size-selectivity simulation, 100 μm for the design rule simulations that varied electrode dimensions, and 50–250 μm for the design rule simulation that varied chamber height. All simulations used a flow-rate resolution of 1.0 μL/min.

RESULTS

Because flowing away untrapped cells is often the rate-limiting step during cell patterning, the DEP traps need to be strong. To demonstrate the strength of our DEP traps, we used beads as model particles to measure the flow rate that test particles could withstand while remaining trapped. Compared to cells, beads are simpler to model and have less variability in size, making them an ideal particle for trap proof-of-concept (Fiedler et al., 1998; Frenea et al., 2003; Medoro et al., 2003; Schnelle et al., 1993; Voldman et al., 2001, 2003). The measurements were in excellent agreement with our modeling predictions. By modeling the maximum flow rate as a function of bead diameter, we were able to determine that the trap displayed a size-selectivity behavior, being optimized to hold ∼9-μm-diameter beads. We then used our model to generate a set of design rules to tune the size-selectivity behavior, allowing us to design DEP traps that are optimized to trap a wide range of cell sizes.

Bead experiments

For each bead diameter of 4.2, 8.2, 9.7, 14.2, and 19.5 μm, maximum flow-rate measurements were made every 1 Vp from 0 to 5 Vp, allowing us to generate the holding characteristic for the trap (Fig. 3). We then compared these measurements to predictions generated by our modeling software. Each subfigure represents a different bead diameter and plots the predicted and experimental maximum flow rate versus the applied voltage. The maximum flow rate always increased as the applied voltage increased. In addition, at 0 Vp the maximum flow rate was always zero, suggesting that the beads did not stick to the glass slide. The difference between the predictions and experimental mean was found to be ≤16% in all cases, except for the 4.2-μm beads that had a difference of 26%. The difference was calculated as:

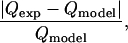graphic file with name M22.gif (6)

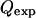where Inline graphic is the experimental mean maximum flow rate at a given voltage and 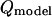Inline graphic is the predicted maximum flow rate at a given voltage. In addition, in other experiments with these traps, the maximum flow rate measurements were shown to be repeatable over different days (data not shown).

Over the course of all the experiments, certain traps in the 5 × 5 array were repeatedly stronger whereas others were repeatedly weaker, which we believe is the major contributor to the standard deviation in the experiments. To understand this observed behavior, we analyzed the differences in maximum flow rate caused by variations in the most sensitive parameters in the system—the trap geometry, the bead size, and the flow chamber height. The upper and lower limits for these parameters were used to calculate the upper and lower limits for the maximum flow rate. By taking the difference of these flow rates and dividing by the average, we were able to calculate a contribution to the variability. There were variations in trap geometry due to fabrication heterogeneity, so we measured the dimensions of both the strongest and weakest DEP trap and used our modeling software to determine how it affected the maximum flow rate. Most dimensions differed by <1 μm, with maximum flow rates that yielded an ∼7% contribution to variability. Although the standard deviations in bead sizes were all <1 μm, we looked at how differences in bead diameter of ±1 μm affected the maximum flow rate. Our model predicted that these bead variations caused a contribution to variability of ∼13%. Finally, we looked at variations in flow chamber height because we noticed that the stronger and weaker traps were located on different sides of the 5 × 5 array, suggesting that the flow chamber height was nonuniform across the array. We measured the flow chamber height three times at both sides of the array and found a height difference of ∼7 μm, which caused differences in maximum flow rates that yielded a contribution to variability of ∼13%. This variation in flow chamber height is probably due to differences in clamping force for the four binder clips or nonuniform height of the PDMS gasket.

Size-selectivity behavior

Using the 5 Vp data of each bead diameter from Fig. 3, we can plot the maximum flow rate as a function of bead diameter (Fig. 4 A). Because the 4.2- and 8.2-μm bead diameter experiments were performed at a different flow chamber height than the other three bead diameter experiments, we normalized the experimental maximum flow rate for these two smaller bead sizes. Because the maximum flow rate is determined by the detailed interactions between the DEP, drag, and gravitational forces, we chose to normalize the experimental maximum flow rate numerically by using the ratio of the simulated maximum flow rates at both chamber heights.

Because the DEP force increases with 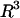Inline graphic (Eq. 1), we would expect the maximum flow rate to increase with bead size for a given DEP trap. However, in our trap, the maximum flow rate increases and then decreases with bead diameter, creating a size-selectivity behavior that is optimized for ∼9-μm particles. The trapped bead experiences x-, y-, and z-directed electric fields and is pushed out of the trap when its center of mass sees upward z-directed electric fields, pushing it up into higher shear flows and therefore out of the trap. The bead remains trapped when the bead center of mass experiences the downward z-directed electric fields. The line defining the transition from upwards to downwards z-directed electric fields—the stability transition line—was determined from the modeling software to have the shape in Fig. 4 B. Although the trap has strong enough x-directed electric fields to resist flow rates >100 μL/min, it is the upward z-directed fields that push the beads out of the trap at lower flow rates. Therefore, this stability transition line is the critical determinant of the size-selectivity behavior.

The size-selectivity behavior occurs because of two effects. First, at low flow rates, the geometry of the electric fields pushes larger beads further away from the right side of the square electrode (RSSE), allowing them to travel a greater distance in the +x-direction (to the right) before they get to the upward z-directed electric fields near this electrode (Fig. 4 C). Second, at higher flow rates the beads are pushed to the right, toward the upward z-directed fields near the RSSE. The smaller-diameter beads started out closer to the RSSE, so with flow they get pushed near this electrode and experience the upward z-directed fields there (Fig. 4 D, top). The larger-diameter beads have centers of mass that are high enough to experience the upward z-directed fields further away from the RSSE (Fig. 4 D, bottom). The medium-sized beads do not experience the upward z-directed fields until higher flow rates, making the trap optimized for these bead sizes (Fig. 4 D, middle).

Multipole contributions to DEP force

Previous nDEP traps typically have been much larger than the particle being trapped and position the particle away from the higher-order electric-field gradients near the electrodes, yielding only significant lower-order pole contributions to the multipole DEP force. For instance, the extruded quadrupole geometry has only significant dipole and quadrupole contributions to the multipole DEP force (Voldman et al., 2001). Our DEP trap geometry is designed to be only slightly bigger than the particle being trapped to minimize trapping of more than one particle. In addition, the trapped particle sits inside the inner square area, right next to the electrodes, and experiences higher-order electric field gradients. Therefore, the multipole DEP force for our trap ends up having significant dipole, quadrupole, and octopole contributions (Fig. 5). Higher-order multipole contributions do not significantly affect the maximum flow rate, and thus all our modeling predictions include only up to octopole contributions.

According to the dipole component of the multipole DEP force (Eq. 1), with a negative CM factor, the 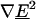Inline graphic must be positive for our traps to operate in the nDEP regime. In Fig. 5, we see that the contribution of higher-order poles lowers the maximum flow rate and therefore the total multipole DEP force. This means that higher-order poles have higher-order field gradients that are negative, weakening the positive 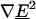Inline graphic from the dipole force.

Design rules

Because the bead-holding experiments show excellent agreement with our predictions, we can use the model to extend beyond the experimental space to develop a set of design rules to tune the size-selectivity behavior shown in Fig. 4 A. This allows us to design traps optimized for placing cells of various sizes. We show that changing the electrode inner square area and spacing between both electrodes grants the freedom to optimize the traps for a specific particle size.

Because it is the z-directed electric fields that determine the stability of the trap, this stability transition line is the critical determinant of the size-selectivity behavior. Therefore, when analyzing how changing the trap dimensions affects the size-selectivity behavior, we only needed to look at the stability transition line. For instance, increasing the slope of the stability transition line allows larger particles to remain in the downward z-directed electric fields, and therefore increases the peak holding diameter, the bead diameter where peak holding occurs. Shifting the stability transition line further from the RSSE decreases the magnitude of the maximum flow rate because it takes less flow to push the particles into the upwards z-directed electric fields, but with the slope unchanged, will not change the peak holding diameter.

We simulated varying the electrode inner square side length (ISSL) from 15 to 35 μm (Fig. 6 A). The maximum flow rate was calculated at 5 Vp as a function of bead diameter for a given ISSL (Fig. 6 B). As the ISSL increases, the stability transition line increases in slope (Fig. 6 C), causing the peak holding diameter to increase (Fig. 6 D). As the ISSL increases, the stability transition line also shifts further from the RSSE (Fig. 6 C), causing a decrease in the maximum flow rate magnitude (Fig. 6 E). Notice that for the smaller ISSL traps, the size-selectivity curve ends before 24 μm. This is because these larger beads experience the upward z-directed electric fields no matter where they are in the smaller inner square area traps, causing them to be pushed out of the trap even at zero flow. Therefore, as the ISSL decreases, the size-selectivity curve ends at smaller bead diameters with larger peak maximum flow rates, making the degree of size selectivity more pronounced. The converse is also true: as the ISSL increases, the degree of size selectivity becomes less pronounced.

Varying the ISSL was designed to allow control over the peak holding diameter, but additionally affected the maximum flow-rate magnitude. Therefore, we wanted to find a way to independently control the maximum flow-rate magnitude. We did this by varying the spacing between the electrodes (SBE) from 5 to 25 μm (Fig. 7 A) and calculated the maximum flow rate at 5 Vp as a function of bead diameter (Fig. 7 B). As SBE was varied, the stability transition line did not significantly change, so the bead peak holding diameter stayed roughly the same (Fig. 7 C). However, as the SBE increases the electric fields become weaker, causing the maximum flow rate magnitude to decrease (Fig. 7 D).

In addition to varying the electrode dimensions, we also simulated how changing the flow chamber height affects the peak holding diameter and maximum flow rate magnitude. We varied the flow chamber height from 50 to 250 μm (Fig. 8 A) and calculated the maximum flow rate at 5 Vp as a function of bead diameter (Fig. 8 B). As flow chamber height increased, the stability transition line did not significantly change, so the peak holding diameter stayed roughly the same (Fig. 8 C). As the flow chamber height increased, the maximum flow rate magnitude increased (Fig. 8 D). This is because the shear rate and thus the drag force are proportional to 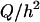Inline graphic (Eq. 3), whereas the DEP force is independent of Q and h. Because the x-directed DEP force and drag force are equal in magnitude for a trapped particle, increasing the chamber height allows an increase in the maximum flow rate. Therefore, making the chamber height as large as possible allows significantly higher maximum flow rates. This would be limited by practical concerns such as the microscope objective working distance (if looking from the top), chamber volume restrictions, or O2 transport issues. Decreasing the chamber height would decrease the maximum flow rate. The lower limit of chamber height is determined either by the size of the cell or practical issues of clogging. Before this limit is reached, the cell would begin to become an appreciable fraction of the chamber height, which would significantly constrict the flow and increase the drag force on the cells faster than predicted from shear rate considerations alone, further decreasing performance.

In addition to varying the ISSL and SBE, we also varied the actual electrode width and the inner square length and width independently. Although these variations produced similar size-selectivity profiles to those generated by varying ISSL and SBE, these variations did not offer any additional ways to tune the profiles—they also only altered the bead diameter where peak holding occurs and the maximum flow rate magnitude (data not shown). We choose to only present the ISSL and SBE variations for design rules because these variations maintain the trap geometry in its simplest form, keeping the inner electrode shape as a square and all electrode widths as 10 μm.

We also looked at other possible shapes for the square electrode (data not shown). Circular geometries were not as strong because the curving electrode splits up the DEP force into x- and y-components, providing less force to counteract the x-directed flow. Rectangular geometries did not significantly affect the trap strength, but do increase the probability of trapping more than one particle in each trap. The square electrode geometry was the best choice for the strongest, single-particle trap.

Multiple- and single-bead trapping

The 4.2-, 8.2-, and 9.7-μm beads were small enough to have multiple beads trapped inside the inner square area, whereas the 14.2- and 19.5-μm diameter beads were large enough that we never observed trapping of more than one bead. When the traps were turned on with two of these larger beads inside, the additional bead would always be pushed out of the trap, leaving one remaining trapped bead. Therefore, one can ensure single-particle trapping using size exclusion. Our 25-μm ISSL trap was shown to ensure single-particle trapping for beads ≥14.2 μm. Even though this trap is optimized for particles of ∼9 μm, the difference in maximum flow rate between 9- and 14.2-μm bead diameters is <5 μL/min (Fig. 4 A), a minimal decrease in trap strength.

Another way to ensure single-particle trapping besides size exclusion is using flow. It was observed during the 4.2-, 8.2-, and 9.7-μm bead experiments that when there were multiple beads trapped inside the inner square, the multiple-particle maximum flow rate was less than the single-particle maximum flow rate. When the flow rate exceeded the multiple-particle maximum flow rate, sometimes all of the beads were removed at once, whereas other times only some of the beads were removed until a single bead remained in the trap. Therefore, another method to ensure single-particle trapping is to operate the flow rate near the single-particle maximum flow rate so multiple particles are unable to remain trapped.

DISCUSSION

Our bead experiments have shown remarkable agreement with our model, without the use of fitting parameters. Our DEP traps have shown a tunable size-selectivity behavior that can be used to optimally pattern particles of a desired size. In addition, we have fabricated a strong, planar, nDEP trap—a combination of features that has not been simultaneously realized to date.

Trap operation for single-particle patterning

The operating scheme for our single-particle traps consists of three steps. First, with the flow on and the traps off, we initially flood the patterning space with a high density of particles, maximizing the number of particles located inside our traps. Second, we turn off the flow and then turn the traps on. Third, with the traps on, we turn the flow on, washing away the untrapped cells and leaving only single particles within each trap. Other DEP trap geometries that pattern particles in localized regions on a substrate, such as interdigitated electrodes that create patterned lines of particles, do not necessarily need to use flow to remove the untrapped particles (Albrecht et al., 2004). However, because our traps do require flow to clear the untrapped particles, we require a strong trap to hold the particles against practical flow rates.

Because particles are only held in the traps if they initially reside within the inner square electrode, we initially flood the patterning space with an excess of particles, thus increasing the probability that at least one particle will be located within the trap. The flooding time is small because the particles can be flowed in at >100 μL/min, being limited by the maximum pressures the flow chamber can withstand. For cells, this flow rate is further limited by the maximum allowable shear stress on the cells. The flooding time will then be a function of the maximum flow rate and the combined chamber and tubing volume. The smaller this combined volume, the less time it takes for flooding. For our traps and fluidics setup, we estimate the flooding time to be <30 s. Once the patterning space is covered with particles, the flow can be turned off for trapping.

With particles inside the inner square electrode, the traps can now be turned on. Our model predicts that there will be only one stable point within the trap at a given flow rate. Although variations in flow, particle size, and fabrication dimensions could change the location of this stable point, we did not observe differences in the trapped particle positions in our bead experiments.

In the absence of flow, the particle is trapped near the center of the square, but the exact location depends on the particle size. The model simulations show that larger particles are trapped within a few microns to the left of the square center whereas the smaller particles are trapped within a few microns to the right of the square center (shown in Fig. 4 C). In addition, we observed experimentally with zero flow that the untrapped particles aligned in between the traps. However, once flow is started, the beads in this region get washed away because of the upwards z-directed electric fields there, leaving particles remaining only in the traps.

The time needed for trapping is negligible for our purposes. We used our modeling software to estimate how long it would take a particle to move the length of the trap using the DEP force on the particle 0.5 μm away from the stable point in the trap (which likely overestimates the average transit time). Using this DEP force, we determined the corresponding velocity of the particle to be ∼20 μm/s. Because particles will be trapped only if they initially reside within the inner square, the maximum distance for them to travel is ∼1/2 ISSL = 12.5 μm, yielding trapping times <1 s, which is consistent with what was experimentally observed in the bead experiments. The DEP force outside the trap is weaker, so it takes longer for the particles outside the inner square to stop moving, observed in the experiments to be <5 s. However, as long as the particles in the inner square are trapped, we could turn on the flow before the particles outside the traps have reached their endpoints, because we will be washing away these particles anyway. Overall, these trapping times are negligible compared to the wash times.

Now that the particles are trapped in the inner square electrode, the flow can be turned back on to wash away the particles outside the traps. This wash step is usually the rate-limiting step in patterning particles because the flow rate cannot exceed the maximum flow rate of the trapped particle. Therefore, we require a strong trap that allows high enough flow rates for practical experimental times. The wash time is also dependent on the combined chamber and tubing volume, so minimizing this volume will help to reduce wash times. For our traps and fluidics setup, we estimate the wash time to be on the order of minutes. Once the particles are washed away, leaving only particles within the traps, the flow and the traps can be turned off.

A strong planar nDEP trap

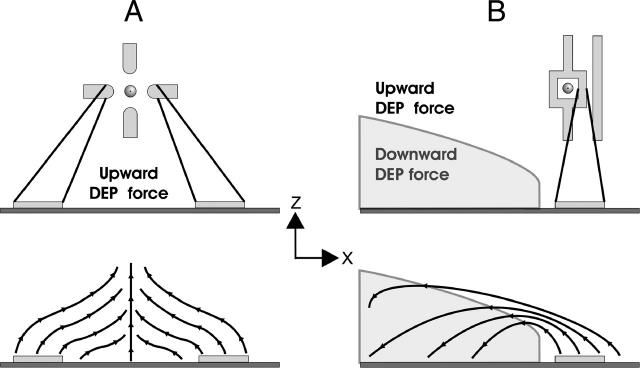
The current methodology for fabricating strong nDEP traps has been to build the trap in three dimensions, either by using electrodes on a top and bottom substrate (Manaresi et al., 2003; Schnelle et al., 1993) or by extruding the actual electrodes (Voldman et al., 2003), making the packaging or fabrication more difficult. In addition, these traps all position the particle away from the bottom substrate, making them inappropriate for patterning cells. Therefore, to be used for cell patterning, the particle needs to be trapped near the substrate, which is more easily accomplished with a planar DEP trap. The limitation of this is that previous planar nDEP traps have not been strong traps (Voldman et al., 2001), and therefore can only be used with lower flow rates, increasing experimental times so significantly that they are inappropriate for patterning cells. To our knowledge, our trap is the strongest planar nDEP trap reported to date. The difference is that typical planar designs, like the planar quadrupole, use nDEP trap geometries that create an upward DEP force everywhere in the trap, shown schematically in Fig. 9 A. Once a certain voltage is reached, the upwards DEP force exceeds the gravitational force, causing the particles to be levitated into higher velocity flows. This causes the maximum flow rate to decrease with increasing voltage (Voldman et al., 2001). Our planar nDEP design, however, traps the particle inside the inner square, where there is an upward DEP force above the stability transition line and a downward DEP force below the line, shown schematically in Fig. 9 B. For the same experimental conditions at 5 Vp, our traps have >200 times the holding force and >2400 times the maximum flow rate as previous planar designs (Voldman et al., 2001). This stabilizing z-directed DEP force is the key feature that makes our traps much stronger than previous planar designs.

FIGURE 9.

FIGURE 9

Open in a new tab

Force fields of a typical planar DEP trap geometry (Voldman et al., 2001) and our nDEP traps. (A) Typical planar nDEP geometries create an upward DEP force everywhere in the trap. (B) Our planar design traps the particle inside the inner square, where there is an upward DEP force above the stability transition line and a downward DEP force below the line.

Previous DEP traps made to pattern single cells use pDEP, which require the cells to be immersed in an artificial low-conductivity media (Gray et al., 2004; Prasad et al., 2004). Although these pDEP traps only need to use this low-conductivity media while trapping, which can be accomplished within minutes, overnight exposure to this media caused cells to detach more frequently and proliferate more slowly than controls (Gray et al., 2004). More sensitive cells might be affected by this artificial media much sooner, within the time needed for trapping. Our nDEP traps should allow single-cell patterning using normal cell media and thus minimize negative cell-media interactions.

Scaling up to arrays of size n × n

Our bead experiments were done in a 5 × 5 array of DEP traps. The fabrication consisted of photolithography, metal evaporation, and liftoff—which is a fairly quick and simple process. It would therefore be very easy to scale up these trap arrays, creating a device that can simultaneously pattern hundreds of thousands of cells on a single microscope slide. The only limiting factor would be the available area for the traps, determined by the size of the slide and the density of the traps, which are both flexible parameters. For a microscope slide of 38 × 75 mm and a trap-to-trap distance of 100 μm, ∼300,000 cells could be patterned on a single chip.

Implications for single-cell patterning

We have created DEP traps that can position beads anywhere on the glass slide, allowing complete control of particle patterning over an entire substrate. Although transitioning from beads to cells has been demonstrated repeatedly in the past (Fiedler et al., 1998; Frenea et al., 2003; Fuhr et al., 1994; Manaresi et al., 2003; Voldman et al., 2002), there are several issues that arise when using nDEP to pattern cells. Cells can be damaged from cell heating, transmembrane loading, and electrochemical effects. In addition, trap operation can be affected due to the large variability in cell size, electrohydrodynamic flows, and electrode fouling.

When electric fields exist in a conductive medium, heating of the medium occurs, which can increase cell temperatures and damage cells. The power generation per unit volume of the media (W) is defined by (Ramos et al., 1998):

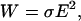graphic file with name M29.gif (7)

where σ is the media conductivity. Because the conductivity of cell-culture media is >100 times greater than that of bead media, the possibility of cell overheating significantly increases. Several approaches exist to mitigate this effect. First, one can pattern the electrodes on a substrate with a high thermal conductivity, such as Si, which helps to minimize the temperature rise (Docoslis et al., 1999). Additionally, minimizing the electric fields by operating at lower applied voltages will also help to keep the temperature rise low (Glasser and Fuhr, 1998), although this also lowers the strength of the traps.

Transmembrane loading occurs when the induced cell membrane voltage exceeds critical values, possibly causing electroporation or disruption of cell-cycle dynamics (Archer et al., 1999; Glasser and Fuhr, 1998). This maximal induced transmembrane potential is given by (Foster and Schwan, 1989):

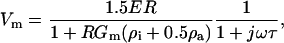graphic file with name M30.gif (8)

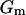where Inline graphic is the membrane conductance, 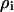Inline graphic is the cytoplasm resistivity, Inline graphic is the media resistivity, and 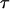Inline graphic is defined as:

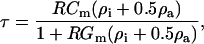graphic file with name M35.gif (9)

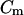where Inline graphic is the membrane capacitance. Because the membrane acts like an electrical high-pass filter, operating at applied signal frequencies in the MHz range and limiting the applied signal voltage will both help to minimize transmembrane loading (Archer et al., 1999; Glasser and Fuhr, 1998).

Electrochemical effects—the production of harmful products caused by interactions between the media and the electrodes—can disrupt cell-cycle dynamics. Wang et al. (1999) found that hydrogen peroxide was produced when sugar-containing media was exposed to electric fields, which inhibited cell growth. This inhibition was exacerbated with higher conductivity media, lower signal frequencies, and higher signal voltages. Minimizing signal voltage and increasing signal frequency helped to remove these effects on cell health. In addition, normal cell growth could be restored by addition of catalase to the medium, breaking down the hydrogen peroxide to oxygen and water.

In addition to cell health, trap operation can also be affected when using nDEP with cells. Along with the absolute temperature rises, temperature gradients can arise that induce gradients in the media permittivity and conductivity. These gradients will force ions to move, dragging the fluid along with it and creating electrohydrodynamic (EHD) flows (Green et al., 2001; Ramos et al., 1998). If these EHD flows are large enough, they can affect cell trapping. Minimizing the absolute temperature rise using the methods mentioned above will limit the effects of EHD flows on trap operation.

Another difference between beads and cells is that the size variability in a cell population is usually quite large, yielding a range of flow rates for each cell diameter. If we wanted to trap all the cells in a population, we would have to operate below the lowest flow rate. However, because the size-selectivity curves are generally flat around the peak holding diameter (Fig. 4 A), the sacrifice in trap strength would be minimal.

Another possible issue when patterning with cells is electrode fouling, caused by reactions between the electrodes and the surrounding cell-culture media. Thoroughly cleaning the electrodes after each experiment should prevent electrode fouling, which is possible with our packaging scheme because it allows us to take apart the flow chamber and thoroughly clean the electrode slide.

Because our validated model can predict the fields and forces everywhere in the patterning space, we can determine the media temperature rise, induced transmembrane voltage, and EHD flows. Thus, we can optimize our geometry and operating conditions to minimize the effects on cell health while maximizing trap strength. In addition, we can take advantage of the high strength of our traps to use high flow rates during the wash step, minimizing our patterning times and exposure of the cells to the electric fields (approximately minutes). Using the trap operation described above, the only cells remaining after the wash step are the cells in the traps. The flow and the traps can then be turned off, allowing the cells to attach to the substrate, grow, and proliferate.

CONCLUSIONS

We have presented a novel DEP trap for single-cell patterning, offering a unique combination of being strong, planar, nDEP, scalable, and size selective. In addition, our devices are easy and inexpensive to fabricate and package. We have elucidated the design rules for making our nDEP trap optimized for a wide range of cell sizes. Thus, we have provided the foundations for an enabling technology with great potential—to be used to pattern single cells in a wide range of configurations—allowing us to do novel cell biology experiments at the microscale that were previously not possible.

Acknowledgments

We thank the Microsystems Technology Laboratory at Massachusetts Institute of Technology (MIT) for fabrication help.

This work was supported by a National Science Foundation graduate Fellowship, a Harvard-MIT Health Sciences and Technology Medical Engineering and Medical Physics Fellowship, the MIT Presidential Fellowship as well as the Department of Electrical Engineering at MIT, and the National Institutes of Health (RR18878).

References

  1. Albrecht, D. R., R. L. Sah, and S. N. Bhatia. 2004. Geometric and material determinants of patterning efficiency by dielectrophoresis. Biophys. J. 87:2131–2147. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Archer, S., T. T. Li, A. T. Evans, S. T. Britland, and H. Morgan. 1999. Cell reactions to dielectrophoretic manipulation. Biochem. Biophys. Res. Commun. 257:687–698. [DOI] [PubMed] [Google Scholar]
  3. Bhatia, S. N., U. J. Balis, M. L. Yarmush, and M. Toner. 1998. Microfabrication of hepatocyte/fibroblast co-cultures: role of homotypic cell interactions. Biotechnol. Prog. 14:378–387. [DOI] [PubMed] [Google Scholar]
  4. Birkbeck, A. L., R. A. Flynn, M. Ozkan, D. Q. Song, M. Gross, and S. C. Esener. 2003. VCSEL arrays as micromanipulators in chip-based biosystems. Biomed. Microdevices. 5:47–54. [Google Scholar]
  5. Chen, C. S., M. Mrksich, S. Huang, G. M. Whitesides, and D. E. Ingber. 1997. Geometric control of cell life and death. Science. 276:1425–1428. [DOI] [PubMed] [Google Scholar]
  6. Cherukat, P., and J. B. McLaughlin. 1994. The inertial lift on a rigid sphere in a linear shear-flow field near a flat wall. J. Fluid Mech. 263:1–18. [Google Scholar]
  7. Deen, W. M. 1998. Analysis of Transport Phenomena. Oxford University Press, New York.
  8. Docoslis, A., N. Kalogerakis, and L. A. Behie. 1999. Dielectrophoretic forces can be safely used to retain viable cells in perfusion cultures of animals cells. Cytotechnology. 30:133–142. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Dufresne, E. R., and D. G. Grier. 1998. Optical tweezer arrays and optical substrates created with diffractive optics. Rev. Sci. Instrum. 69:1974–1977. [Google Scholar]
  10. Fiedler, S., S. G. Shirley, T. Schnelle, and G. Fuhr. 1998. Dielectrophoretic sorting of particles and cells in a microsystem. Anal. Chem. 70:1909–1915. [DOI] [PubMed] [Google Scholar]
  11. Folch, A., B.-H. Jo, O. Hurtado, D. J. Beebe, and M. Tonor. 2000. Microfabricated elastomeric stencils for micropatterning cell cultures. J. Biomed. Mater. Res. 52:346–353. [DOI] [PubMed] [Google Scholar]
  12. Folch, A., and M. Toner. 1998. Cellular micropatterns on biocompatible materials. Biotechnol. Prog. 14:388–392. [DOI] [PubMed] [Google Scholar]
  13. Foster, K. R., and H. P. Schwan. 1989. Dielectric properties of tissues and biological-materials: a critical-review. Crit. Rev. Biomed. Eng. 17:25–104. [PubMed] [Google Scholar]
  14. Frenea, M., S. P. Faure, B. Le Pioufle, P. Coquet, and H. Fujita. 2003. Positioning living cells on a high-density electrode array by negative dielectrophoresis. Materials Science & Engineering C-Biomimetic and Supramolecular Systems. 23:597–603. [Google Scholar]
  15. Fuhr, G., H. Glasser, T. Muller, and T. Schnelle. 1994. Cell manipulation and cultivation under AC electric-field influence in highly conductive culture media. Biochimica Et Biophysica Acta-General Subjects. 1201:353–360. [DOI] [PubMed] [Google Scholar]
  16. Glasser, H., and G. Fuhr. 1998. Cultivation of cells under strong AC-electric field: differentiation between heating and trans-membrane potential effects. Bioelectrochem. Bioenerg. 47:301–310. [Google Scholar]
  17. Goldman, A., R. Cox, and H. Brenner. 1967. Slow viscous motion of a sphere parallel to a plane wall. II. Couette flow. Chem. Eng. Sci. 22:653–660. [Google Scholar]
  18. Gray, D. S., J. L. Tan, J. Voldman, and C. S. Chen. 2004. Dielectrophoretic registration of living cells to a microelectrode array. Biosens. Bioelectron. 19:771–780. [DOI] [PubMed] [Google Scholar]
  19. Green, N. G., A. Ramos, A. Gonzalez, A. Castellanos, and H. Morgan. 2001. Electrothermally induced fluid flow on microelectrodes. Journal of Electrostatics. 53:71–87. [Google Scholar]
  20. Jo, B. H., L. M. Van Lerberghe, K. M. Motsegood, and D. J. Beebe. 2000. Three-dimensional micro-channel fabrication in polydimethylsiloxane (PDMS) elastomer. J. Microelectromech. Syst. 9:76–81. [Google Scholar]
  21. Jones, T. B., and M. Washizu. 1996. Multipolar dielectrophoretic and electrorotation theory. Journal of Electrostatics. 37:121–134. [Google Scholar]
  22. Lahann, J., S. Mitragotri, T. N. Tran, H. Kaido, J. Sundaram, I. S. Choi, S. Hoffer, G. A. Somorjai, and R. Langer. 2003. A reversibly switching surface. Science. 299:371–374. [DOI] [PubMed] [Google Scholar]
  23. Leighton, D., and A. Acrivos. 1985. The lift on a small sphere touching a plane in the presence of a simple shear flow. Journal of Applied Mathematics and Physics. 36:174–178. [Google Scholar]
  24. Manaresi, N., A. Romani, G. Medoro, L. Altomare, A. Leonardi, M. Tartagni, and R. Guerrieri. 2003. A CMOS chip for individual cell manipulation and detection. IEEE Journal of Solid-State Circuits. 38:2297–2305. [Google Scholar]
  25. Medoro, G., N. Manaresi, A. Leonardi, L. Altomare, M. Tartagni, and R. Guerrieri. 2003. A lab-on-a-chip for cell detection and manipulation. IEEE Sensors Journal. 3:317–325. [Google Scholar]
  26. Ozkan, M., T. Pisanic, J. Scheel, C. Barlow, S. Esener, and S. N. Bhatia. 2003. Electro-optical platform for the manipulation of live cells. Langmuir. 19:1532–1538. [Google Scholar]
  27. Paddle, B. M. 1996. Biosensors for chemical and biological agents of defence interest. Biosens. Bioelectron. 11:1079–1113. [DOI] [PubMed] [Google Scholar]
  28. Pancrazio, J. J., J. P. Whelan, D. A. Borkholder, W. Ma, and D. A. Stenger. 1999. Development and application of cell-based biosensors. Ann. Biomed. Eng. 27:697–711. [DOI] [PubMed] [Google Scholar]
  29. Prasad, S., X. Zhang, M. Yang, Y. C. Ni, V. Parpura, C. S. Ozkan, and M. Ozkan. 2004. Separation of individual neurons using dielectrophoretic alternative current fields. J. Neurosci. Methods. 135:79–88. [DOI] [PubMed] [Google Scholar]
  30. Ramos, A., H. Morgan, N. G. Green, and A. Castellanos. 1998. AC electrokinetics: a review of forces in microelectrode structures. J. Phys. D Appl. Phys. 31:2338–2353. [Google Scholar]
  31. Revzin, A., R. G. Tompkins, and M. Toner. 2003. Surface engineering with poly(ethylene glycol) photolithography to create high-density cell arrays on glass. Langmuir. 19:9855–9862. [Google Scholar]
  32. Schnelle, T., R. Hagedorn, G. Fuhr, S. Fiedler, and T. Muller. 1993. 3-Dimensional electric-field traps for manipulation of cells: calculation and experimental verification. Biochim. Biophys. Acta. 1157:127–140. [DOI] [PubMed] [Google Scholar]
  33. Takayama, S., J. C. McDonald, E. Ostuni, M. N. Liang, P. J. A. Kenis, R. F. Ismagilov, and G. M. Whitesides. 1999. Patterning cells and their environments using multiple laminar fluid flows in capillary networks. Proc. Natl. Acad. Sci. USA. 96:5545–5548. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Tan, W., and T. A. Desai. 2003. Microfluidic patterning of cells in extracellular matrix biopolymers: effects of channel size, cell type, and matrix composition on pattern integrity. Tissue Eng. 9:255–267. [DOI] [PubMed] [Google Scholar]
  35. Tempelman, L. A., K. D. King, G. P. Anderson, and F. S. Ligler. 1996. Quantitating staphylococcal enterotoxin B in diverse media using a portable fiber-optic biosensor. Anal. Biochem. 233:50–57. [DOI] [PubMed] [Google Scholar]
  36. Voldman, J., R. A. Braff, M. Toner, M. L. Gray, and M. A. Schmidt. 2001. Holding forces of single-particle dielectrophoretic traps. Biophys. J. 80:531–541. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Voldman, J., M. L. Gray, M. Toner, and M. A. Schmidt. 2002. A microfabrication-based dynamic array cytometer. Anal. Chem. 74:3984–3990. [DOI] [PubMed] [Google Scholar]
  38. Voldman, J., M. Toner, M. L. Gray, and M. A. Schmidt. 2003. Design and analysis of extruded quadrupolar dielectrophoretic traps. Journal of Electrostatics. 57:69–90. [Google Scholar]
  39. Wang, X. J., J. Yang, and P. R. C. Gascoyne. 1999. Role of peroxide in AC electrical field exposure effects on Friend murine erythroleukemia cells during dielectrophoretic manipulations. Biochimica Et Biophysica Acta-General Subjects. 1426:53–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Washizu, M., and T. B. Jones. 1996. Generalized multipolar dielectrophoretic force and electrorotational torque calculation. Journal of Electrostatics. 38:199–211. [Google Scholar]
  41. Xia, Y. N., and G. M. Whitesides. 1998. Soft lithography. Angew. Chem. Int. Ed. Engl. 37:551–575. [DOI] [PubMed] [Google Scholar]
  42. Yeo, W. S., M. N. Yousaf, and M. Mrksich. 2003. Dynamic interfaces between cells and surfaces: electroactive substrates that sequentially release and attach cells. J. Am. Chem. Soc. 125:14994–14995. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES