Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Dec 21;88(3):2257–2265. doi: 10.1529/biophysj.104.050872

Evidence of Piezoelectric Resonance in Isolated Outer Hair Cells

R D Rabbitt *, H E Ayliffe *, D Christensen *, K Pamarthy *, C Durney *, S Clifford *, W E Brownell †
PMCID: PMC1305275  PMID: 15613632

Abstract

Our results demonstrate high-frequency electrical resonances in outer hair cells (OHCs) exhibiting features analogous to classical piezoelectric transducers. The fundamental (first) resonance frequency averaged fn ∼ 13 kHz (Q ∼ 1.7). Higher-order resonances were also observed. To obtain these results, OHCs were positioned in a custom microchamber and subjected to stimulating electric fields along the axis of the cell (1–100 kHz, 4–16 mV/80 μm). Electrodes embedded in the side walls of the microchamber were used in a voltage-divider configuration to estimate the electrical admittance of the top portion of the cell-loaded chamber (containing the electromotile lateral wall) relative to the lower portion (containing the basal plasma membrane). This ratio exhibited resonance-like electrical tuning. Resonance was also detected independently using a secondary 1-MHz radio-frequency interrogation signal applied transversely across the cell diameter. The radio-frequency interrogation revealed changes in the transverse electric impedance modulated by the axial stimulus. Modulation of the transverse electric impedance was particularly pronounced near the resonant frequencies. OHCs used in our study were isolated from the apical region of the guinea pig cochlea, a region that responds exclusively to low-frequency acoustic stimuli. In this sense, electrical resonances we observed in vitro were at least an order of magnitude higher (ultrasonic) than the best physiological frequency of the same OHCs under acoustic stimuli in vivo. These resonance data further support the piezoelectric theory of OHC function, and implicate piezoelectricity in the broad-band electromechanical behavior of OHCs underlying mammalian cochlear function.

INTRODUCTION

The human cochlea can sense sounds over a wide bandwidth from ∼20 Hz to 20 kHz and over a broad dynamic range of sound pressures spanning nearly 12 orders of magnitude. This impressive sensory capability relies to a large extent on the unique properties of outer hair cells (OHCs). These cells are electromotile and undergo robust changes in somatic length when subjected to electric fields (Ashmore, 1987; Brownell et al., 1985; Santos-Sacchi and Dilger, 1988). OHCs shorten when depolarized and lengthen when hyperpolarized. This electromechanical behavior enhances the amplitude of vibration and sharpens the frequency selectivity of the cochlear partition in response to sound. Inactivation of outer hair cells by electrical stimulation of the olivocochlear efferent nerve bundle can attenuate the mechanical response of the cochlea by 35 dB or more (Murugasu and Russell, 1996). Drugs inactivating OHC function also have adverse effects on hearing. Unlike typical motor proteins, the OHC motor is not directly dependent upon ATP (Ashmore, 1987) and is capable of continuous cycling at fast auditory frequencies (Frank et al., 1999). This has led to the suggestion that the fundamental biophysics of the OHC motor might be piezoelectric (Mountain and Hubbard, 1994; Tolomeo and Steele, 1995).

Piezoelectric materials are in common use as actuators for micropositioning, sound delivery, or vibration; and as transducers for sensing displacement, acceleration, or force. The fundamental thermodynamic origin of the piezoelectric effect is well understood, and for small deformations provides the theory of linear piezoelectricity (Tiersten, 1969; Wang and Yang, 2000) (e.g., materials such as lead-zirconate titanate). For thin membranes and plates, the general theory reduces to a hierarchy of specialized forms including curvature-based flexoelectricty (Lee et al., 2002). There is a solid body of work documenting piezoelectric and flexoelectric properties in biological materials ranging from bone to membranes (Aschero et al., 1999; Fukada, 1995; Petrov, 2002). However, in all manifestations of piezoelectricity discovered to date, nowhere is the effect more profound than in somatic electromotility of OHCs. These cells exhibit piezoelectric coefficients orders of magnitude higher than typically encountered in engineering materials (Iwasa, 2001). Furthermore, OHC electromechanical behavior is consistent with thermodynamic Maxwell reciprocity required of piezoelectric materials (Dong et al., 2002; Zhao and Santos-Sacchi, 1999). The remarkable piezoelectric properties of OHCs are tied closely to expression of the membrane-bound protein prestin (Zheng et al., 2000). When this protein is expressed in model cell lines, transfected cells exemplify the essential properties of piezoelectricity (Ludwig et al., 2001; Zheng et al., 2000, 2002). When the gene encoding prestin is deleted in model organisms, piezoelectricity is lost and profound hearing loss occurs (Liberman et al., 2002). This evidence demonstrates the important role of prestin in OHC piezoelectricity, and the important role of piezoelectricity in mammalian hearing.

Some insight into the role of OHC piezoelectricity in the cochlea can be gained by the study of traditional piezoelectric materials. There are two primary regimes where piezoelectric materials are commonly used in applications: low frequencies where a specific voltage-displacement relationship is desired (e.g., 0th-mode microactuators), or at high frequencies where resonance and maximum power transmission are desired (e.g., 1st- and nth-mode ultrasound transducers). In the low-frequency regime, mass is negligible and reciprocal potential energy transfer between electrical and mechanical forms governs behavior. Since kinetic energy increases with increasing frequency, the bandwidth of the low-frequency regime is limited. At the frequency where kinetic energy becomes large and balances potential energy, resonance and maximum power transmission occurs via conversion of electrical power to mechanical or vice versa. Therefore a reasonable hypothesis is that OHCs, if truly piezoelectric, would reveal whole-cell piezoelectric resonance when stimulated at sufficiently high frequencies (Weitzel et al., 2003). Indeed, electrically driven mechanical resonances of the cochlear partition consistent with the piezoelectric hypothesis have been observed in vivo (Grosh et al., 2004). In this work, OHCs were studied in isolation to determine if high-frequency resonances reported in the cochlea might have direct cellular origins.

The ability to observe piezoelectric resonance in isolated OHCs has been stalled in the past partially by technical limitations imposed by the parasitic capacitance and low-pass filtering and mechanical constraints imposed by pipette recording methods. We overcame these limitations by fabricating custom microchambers, using microelectromechanical systems (MEMS) technology, to stimulate and interrogate OHCs using an array of metal electrodes. Even with the high-frequency MEMS-based recording capability, it was not clear at the outset if resonance would be obscured by immersion of the cells in water, a relatively viscous and dissipative media on the microscale. Indeed, low-Q ultrasonic resonances consistent with the piezoelectric prediction were observed. Results further support the piezoelectric theory of OHC somatic electromechanics and have implications regarding OHC physiology and hearing.

METHODS

Microchannels incorporating metal electrodes integrated into the side walls were fabricated using MEMS techniques described previously (Ayliffe et al., 1998), with minor changes noted here. A metal seed layer was sputtered on 3-inch quartz glass wafers (Pyrex 7740, Corning, Corning, NY) and chemically etched to form the eight-electrode pattern shown in Fig. 1. Six of the electrodes were positioned along the length of the microchamber for passive voltage measurements and transverse electric impedance interrogation (black electrodes 1, 1′, 2, 2′, 3, and 3′). Two additional electrodes were positioned on the bottom surface of the microfluidic channel, one downstream and one upstream of the interrogation chamber (arrows denoting electrodes 4 and 4′ are beyond image). Dark regions indicated by the dotted lines are flaws that generated optical interference. An epoxy-based photoresist (SU-8, Microlithography Chemical, Newton, MA) was spun over the metal seed layer and subsequently patterned and etched, using a combination of wet and dry procedures, to form the fluid reservoirs and microchannels. Electrodes were electroplated to the full thickness of the photoresist. The completed wafers included 10–20 useful microchambers of various sizes. The top of the rectangular microchannel was sealed using a thin silicone gasket under mechanical pressure applied using a polycarbonate bulkhead attached to a manual micromanipulator. The bulkhead contained a 2-mm diameter hole (reservoir) overlying one end of the microchannel for delivery of cells, and a second hole overlying the other end of the channel for application of suction pressure (see Supplementary Material for additional details). The entire apparatus was fixed to the stage of an inverted microscope (IM-35, Zeiss, Oberkochen, Germany) for identification and observation of cells. This configuration allowed OHCs to be positioned within the recording chamber by manual aspiration under visual guidance.

FIGURE 1.

FIGURE 1

Open in a new tab

Cell-loaded microchamber. Microchambers were fabricated to include a rectangular channel instrumented with six metal electrodes (1, 1′, 2, 2′, 3, and 3′) embedded in the side walls for transverse interrogation of hair cells, and two electrodes (4 and 4′, off image) for application of axial electric fields. Outer hair cells were visually identified (A) and subsequently positioned between transverse electrodes (B) using manual aspiration. Large images (I, II) show an outer hair cell isolated from the apical turn of the guinea pig cochlea tightly fit between the electrodes. Insets show a different hair cell in a second chamber.

The metal electrode traces were designed to fan out from the recording chamber to form a rectangular pattern of gold contact pads around an ∼1-cm periphery. Electrical contact was made when the bulkhead was lowered using spring-loaded gold pins (contacts indicated in Fig. 1, ⊕ and ⊙). A custom head-stage circuit board, including field-effect transistors and reference impedances, was secured to the top surface of the bulkhead to make direct contact with the spring-loaded gold pins. This configuration allowed us to independently control the voltages on electrodes 1, 2, 3, and 4, and to measure the current in the same electrodes using the voltage-divider circuit shown in Fig. 2. Negative electrodes 1′, 2′, 3′, and 4′ were also independently addressable for voltage stimulation but were not instrumented for current recording. Each electrode was independently excited using arbitrary waveform generators in voltage control mode (AWG 430, Tektronix, Beaverton, OR; 1 kHz to 1 MHz). Voltage measurements were made using digital lock-in amplifiers (SR830 and SR844, Stanford Research Systems, Sunnyvale, CA). Data were downloaded to computer using custom software (G4, Apple Computer, Cupertino, CA; IEEE 488, National Instruments, Austin, TX; Igor Pro, WaveMetrics, Lake Oswego, OR). For calibration, open-circuit measurements of V+ and Vo for each channel were used to determine leak impedance (Zo) of each buffer amplifier. The leak calibration curve was empirical, but consistent with the field-effect transistor amplifier input impedance and instrumentation time delay. This calibration was done on a frequency-by-frequency basis just before each measurement. A short-circuit configuration was used to calibrate the mirror negative source relative to the positive source. Parasitic capacitance was <30 pF. This allowed impedances up to 800 MΩ to be accurately recorded.

FIGURE 2.

FIGURE 2

Open in a new tab

Instrumentation. Eight electrodes were independently addressable by computer for patterning the extracellular voltage stimulation and recording (Vo, ⊕Electrode). and/or interrogation of local electric impedance between pairs of electrodes. A dual-source, voltage-divider configuration was used to determine the chamber impedance Zc from lock-in amplifier measurements of V+, V−, and Vo. Closed-circuit and open-circuit calibrations were used to determine the instrumentation shunt impedance Zo, the reference impedance Zr, and the source calibration for each electrode pair.

Two types of measurements were performed, passive voltage measurements at electrodes 1, 2, and 3 (Fig. 3) and active electric impedance measurements between electrode pair 2-2′ (Fig. 4). For passive voltage-divider experiments, electrodes 4 and 1′ were both wired to the positive source, whereas electrodes 4′ and 3′ were both wired to the negative source (1–100 kHz). Passive voltages were measured along the long axis of the microchannel using electrodes 1, 2, and 3 (see Fig. 4). 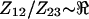In this voltage-divider configuration, the ratio Inline graphic provided a measure of the electrical impedance of material between electrodes 1 and 2 relative to the material in the space between electrodes 2 and 3 (i.e., Inline graphic). One complication was the fact that the microchambers were not perfectly symmetrical, and as a result, 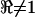Inline graphic even in the control condition when the chamber was filled with homogeneous media. This geometrical asymmetry was corrected post-hoc using data collected in the media-filled control condition. For this, we measured the frequency-dependent voltage ratio 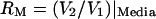Inline graphic in the media-filled condition. 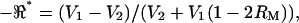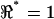A corrected voltage ratio was defined as Inline graphic where the negative and positive sources were balanced, allowing us to eliminate V3 from the denominator (i.e., Inline graphic). Note the voltage ratio Inline graphic for all frequencies in the media-filled control condition. Deviations away from unity indicate a deviation away from the balanced condition and therefore reflect an imbalance of the impedance of the cellular material located between electrodes 1 and 2 relative to the impedance between electrodes 2 and 3. 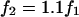The voltage ratio Inline graphic was based on linear voltage-divider theory and was computed using the first-harmonic response at the stimulus frequency f1. The electrode-electrolyte interface and presence of cells both introduced some nonlinearity into the data. To quantify the magnitude of nonlinearity relative to the linear response, we recorded distortion products in the control and cell-loaded conditions using a two-component stimulus with 10% spacing (Inline graphic) and distortion-product measurements at 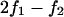Inline graphic and Inline graphic. For active radio-frequency (RF) impedance measurements the positive and negative voltage sources, exciting electrodes 2 and 2′, respectively (Fig. 4), were calibrated to be equal and opposite. This allowed us to compute the impedance across the chamber relative to the on-board reference impedance from two lock-in voltage measurements using Zc = Zr Zo(V+ + Vo)/(Zo (V+ − Vo) − Zr Vo) (see Fig. 2). The transverse RF interrogation (Fig. 4) was superimposed on the axial stimulus (Fig. 3) to assess the influence of the axial stimulus on transverse cell properties. The transverse signal had a random phase relative to the axial stimulus and lock-in recordings were averaged over thousands of cycles of the of the axial waveform. Therefore, the transverse impedance was not modulated by the axial stimulus when the chamber was filled with saline solution or with any structure/cell composed of passive linear dielectric materials.

FIGURE 3.

FIGURE 3

Open in a new tab

Axial stimulation. Cells were stimulated by application of an axial electric field from 1 to 100 kHz between electrodes 4 and 4′. The voltage drop along the length of the cell was used as a voltage divider to estimate the admittance of the apical portion of the cell relative to the basal portion. To facilitate interpretation, the voltage distribution around the cell was estimated by solving the 2D Maxwell equations using the Pamarthy model (Pamarthy, 2004) (results at 1 kHz shown as real part (B) and imaginary part (C)). The nearly isopotential intracellular voltage and controlled membrane potentials at the apical and basal surfaces are notable (B and C). (D) A simplified network model illustrating the major elements: shunt conductance around the cell (Gs), apical transducer impedance (Za), basal impedance (Zb) and lateral wall impedance (Zp).

FIGURE 4.

FIGURE 4

Open in a new tab

Transverse interrogation. (A) Electric impedance (Zd) of the cell-loaded microchamber was measured using a 1-MHz interrogating signal applied between electrodes 2 and 2′. (B and C) To facilitate interpretation, the voltage field generated by this interrogation signal was estimated by solving the 2D Maxwell equations using the Pamarthy model (Pamarthy, 2004) (B, real part; C, imaginary part). A simplified lumped-parameter network illustrating the major current pathways through and around the cell during transverse interrogation is provided in panel D. The electrode-electrolyte interfacial impedance (Zee) and the saline shut impedance (Zss) around the cell contribute significantly to the total chamber impedance (Zc).

Preparation of cells followed the general approach described previously (Brownell et al., 1985). Adult guinea pigs (200–400 g) were exposed to 100% carbon dioxide until completely unconscious, decapitated, and both temporal bones were removed and placed in a balanced phosphate-buffered saline solution (PBS). The bulla was opened to expose the cochlea, the bony capsule was removed, and the apical turn of the organ of Corti was dissected from the modiolus. The tissue containing the OHCs was carefully separated from the organ, under continuous immersion in PBS, and transferred to a 40-μl vial by pipette. OHCs were isolated mechanically under visual observation by repeated manual pipette aspiration. Within 2 h of isolation, cells were transferred to the MEMS and positioned in the microchamber by manual aspiration under visual guidance. Fig. 1 shows examples of two cells outside the microchamber (A) and after positioning between the electrodes (B). Image quality was relatively poor due to the light path through layers of glass, photoresist, silicone, and polycarbonate.

RESULTS

To gain a qualitative understanding of the fields generated within the microchamber, the Maxwell equations were solved for a 2D model approximating the geometry and physical properties of the cell and microchamber (Fig. 3 A; see Supplementary Material (Pamarthy, 2004)). Sample voltage fields predicted by the electromagnetic model are shown in the form of real (Fig. 3 B) and imaginary (Fig. 3 C) components for a 1-kHz, real-valued, source-sink current source located between electrodes (4-1′) and –(4′-3′). Color contour plots show the perturbation from the resting voltage (maximum, black; minimum, white; equally spaced contours). It is significant to note that the intracellular space was predicted to be nearly isopotential during this stimulus. The stimulus generated a voltage pattern around the cell that perturbed the membrane potential on the apical end of the cell at a level nearly equal and opposite to the perturbation on the basal end of the cell. This pattern occurs because of the high impedance of the cell membrane and low impedance of the extracellular saline shunt—a property that allows extracellular voltage stimuli to be used to generate simple patterns of controlled membrane potential around the cell. A lumped-parameter conceptual model capturing the main features of this stimulus is presented in the right panel (Fig. 3 D). During axial electrical stimuli, the hair cell-loaded chamber acts as a voltage divider with the primary current pathways through the apical cell transduction channels (Za), the lateral wall (Zp), the basal membrane (Zb), and around the cell via the extracellular saline shunt conductance (Gs). In the experimental results described below, extracellular voltages were measured along the length of the cell (V1, V2, V3) and used to estimate the admittance of the apical portion of the cell relative to the basal portion using the voltage ratio 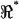Inline graphic.

In a subset of experiments, a 1-MHz electric-impedance interrogating signal was applied between electrodes 2 and 2′ (Fig. 4 A). A 2D solution of the Maxwell equations was again used to provide a qualitative understanding of the fields within the chamber. Voltage patterns predicted by the model for the 1-MHz interrogation are shown as real (Fig. 4 B) and imaginary (Fig. 4 C) components. Note that the fields at 1 MHz were predicted to be localized with a majority of the current passing through the central region of the cell. A lumped-parameter conceptual model is provided in the right panel (Fig. 4 D), including the major elements associated with the transverse impedance: the electrode-electrolyte impedance (Zee), the cell impedance (ZOHC), the saline shunt (Zss), and the microchamber shunt (Zgs). Recognition of the saline shunt (Zss) around the cell is particularly important in interpretation of the experimental results to follow. In the experiments, the RF impedance interrogating field was superimposed on the 1- to 100-kHz axial stimulus to assess the influence of the stimulus on the transverse electrical properties.

When the microchamber was filled with saline, media, or passive cells (erythrocytes, red blood cells; pheochromocytoma cell line, PC12), the transverse impedance was independent of the axial stimulus—as expected for a linear system. This linear independence, however, did not hold for OHCs. Fig. 5 provides sample nonlinear responses observed for OHCs in the form of transverse impedance magnitude (A) and phase (B) as functions of the axial stimulus frequency. Solid curves (Fig. 5, A and B) show the cell-loaded condition where the impedance was only 2–10 times higher than that recorded in the media-filled control condition. When the impedance was low, the phase was nearly equivalent to the media-filled control condition. This low transverse impedance indicates a low shunt impedance and significant current around the cell via the saline shunt path. We term cells in this low-impedance condition “loose-fitting” (e.g., Fig. 1, inset). For the loose-fitting cells, the magnitude of the impedance recorded at 1 MHz shifted at discrete stimulus frequencies (I), with some cells exhibiting multiple peaks in the impedance spectra. Our hypothesis is that changes in magnitude of the transverse impedance occurred due to modulation of the conductive saline shunt pathway around the outside of the cell, presumably caused by electromotility altering the dimensions of the saline shunt. This geometrical interpretation is consistent with the fact that the phase remained near the media-filled control value. In some cases (Fig. 5, A and B, dashed lines), the transverse impedance of the cell-loaded chamber was 10–100 times higher than in the control condition, indicating a highly resistive saline shunt path around the cell and leading to the term “tight-fitting” (e.g., Fig. 1, main image). The transverse impedance recorded when the chamber contained a tight-fitting cell also exhibited frequency dependence, but the nonlinear effects occurred at higher frequencies and included changes in both magnitude and phase. The phase differed from the media-filled chamber indicating significant contributions from the cell membranes and structure. One hypothesis that may explain these data is that electromechanical resonance caused a reconfiguration of the cell and a shift in the current path from one region of the cell to another. It is equally possible that this nonlinear effect has origins in a fundamental nonlinearity of electromotility that might alter charge motility as a function of the stimulus and thereby alter the apparent dielectrics detected by the 1-MHz interrogation. Although results in Fig. 5 clearly show frequency-dependent behavior in the 9–70 kHz range consistent with piezoelectric resonances, interpretation is complex due primarily to mechanically dependent changes in the geometry of the shunt impedance around the cell. As a simplified approach, we used passive measurements of the voltage along the length of the cell to compare frequency-dependent admittance of the apical region of the cell to the basal region.

FIGURE 5.

FIGURE 5

Open in a new tab

Transverse electric impedance during axial stimulation. The overall electric impedance (Zd) of the cell-loaded chamber was recorded transverse to the chamber at 1 MHz (see Fig. 3) in the presence of an axial electric field (see Fig. 4). Example results at 1 MHz are shown in the form of magnitude (A) and phase (B) versus axial stimulus frequency (kHz). Dotted lines provide sample data for PBS and confirm that the magnitude and phase in the absence of a cell were independent of the axial electric field. Outer hair cells responding to this stimulus were divided into two types: cells characterized by a high impedance (e.g., dashed lines, “tight”) and cells characterized by a low impedance and phase near that of PBS (e.g., solid lines, “loose”). Outer hair cells exhibited features akin to resonances evoked by the range of stimulus frequencies, but monitored here by recording impedance at a single interrogation frequency.

During the axial stimulus, passive recordings from electrodes 1 and 3 closely reflected the positive and negative stimuli (Fig. 3) such that the influence of the cell was most easily seen in raw data from the center electrode (Fig. 1, electrode 2). Sample raw voltage data from the center electrode (V2) under axial stimulation is provided in Fig. 6. Thick lines show the raw voltage in the form of magnitude (A) and phase (B) for two different cells, each oriented oppositely in the microchamber. Note the frequency-dependent dips in magnitude and phase present near 10 kHz and 20 kHz. Such dips indicate frequency-dependent changes in the impedance of the apical region of the cell relative to the basal region, and were not present in the media-filled control condition (thin lines). It is notable that the center-electrode voltage was nonzero even in the media-filled control condition (thin curves). This was due to the imperfect symmetry of the microchamber and was accounted for when computing 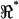Inline graphic (see Methods). We also recorded distortion products (2f2 − f1 and 2f1 − f2), primarily for the purpose of quantifying nonlinearity in the recording system. In both the media-filled control condition and cell-loaded conditions, distortion products were 0.3–10% of the primary. Distortion products in the control condition were due to the inherent nonlinearity of the stimulating electrode-electrolyte interface. When OHCs were placed in the microchamber, cubic distortion products increased relative to the control conditions (Fig. 6, thick versus thin dashed lines). Nonlinear charge movement associated with OHC somatic motility has been shown previously to introduce both quadratic and cubic distortion products (Takahashi and Santos-Sacchi, 1999), and therefore a change in distortion products was expected in these experiments. Distortion products (2f1 − f2, 2f2 − f1) for some cells exhibited a dip in magnitude and shift in phase (Fig. 6 A, arrow) at a frequency near the fundamental f1 resonance (Fig. 6 A, *). This correlation implies that the resonances and distortion products may share biophysical origins.

FIGURE 6.

FIGURE 6

Open in a new tab

Raw voltage and distortion products. Axial electrical stimuli (Fig. 4) were applied to estimate the relative admittance of the apical versus basal regions of the cell. Example raw data recorded at the center electrode (1) are shown in the form of magnitude (A) and phase (B) for two cells (thick lines) and PBS media (thin lines). Characteristic frequency-dependent dips in magnitude and shifts in phase were present when the chamber was loaded with responding hair cells but absent in the control condition. Distortion products in the cell-loaded condition were ∼10–100 times smaller than the primary, depending upon the stimulus frequency.

The admittance of the apical region of the cell was estimated relative to the basal region using the voltage ratio Inline graphic (see Methods), for 67 OHCs. Maintaining the cell in a stationary position between the electrodes posed a serious challenge. Data from 36 cells were rejected because of visually identified gross movement during the recording and associated voltage/impedance artifact. Data from another 17 cells were not included in this summary due to granular visual appearance or because the impedance was so low that the recording was dominated by the saline shunt path around the cell (e.g., Supplementary Material). The admittance ratio for the remaining 14 cells is shown in Fig. 7 in the form of magnitude (A) and phase (B) as functions of frequency ratio. The axial voltage gradient stimulating these cells ranged from 4 to 16 mV applied over the 60–80-μm length of the cell. Average admittance ratios are provided by the thick curves, with error bars denoting one standard error. The peak admittance ratio was used to define the normalizing frequency fn = 13 kHz (8.33–23 kHz) on a cell-specific basis. These curves show similarity to a classical second-order resonator with average quality Q ∼ 1.74 (0.52–3.0). In 36% of the records, cells were observed visually to enter the chamber hair bundle first. As expected, in all cases the admittance ratio for these cells was inverted relative to curves for cells entering basal end first (e.g., Supplementary Material). To account for this, the electrode order was reversed for this subset of cells before averaging in Fig. 7 (V1 interchanged with V3). Although it is not obvious in the average curves, a second resonance peak was identifiable in 45% of the records and occurred at a frequency 3–5 times the fundamental. Thin curves show three sample cells in which a second peak in the admittance ratio was apparent (+). We hypothesize that the second peak is associated with a second resonance mode of vibration, consistent with distributed-parameter piezoelectric models (Weitzel et al., 2003).

FIGURE 7.

FIGURE 7

Open in a new tab

Voltage ratio Inline graphic. The voltages at electrodes 1, 2, and 3 were used to compute Inline graphic, an estimate of the admittance of the apical part of the cell relative to the basal part. Results are shown in the form of magnitude (A) and phase (B) as a function of normalized axial stimulus frequency. The peak admittance corresponding to the average resonance frequency fn was ∼13 kHz, with quality Q ∼ 1.7. Thick curves show the mean and vertical bars denote standard errors. Thin curves show three sample cells; results indicate presence of a second peak (+) occurring at ∼3–6 times the fundamental frequency.

To further interpret the admittance ratio data, we compared results to predictions of two simple piezoelectric models: a single-mode (SM) lumped-parameter model (Fig. 8 A) and a modified length-thickness-extension (LTE) model (Weitzel et al., 2003). For this, the lateral wall admittance Zp in Fig. 3 D was replaced with the single-mode or modified LTE admittance. The physical parameters used in these simplified models were based on OHC geometrical, electrical, and mechanical data (see Supplementary Material). Model predictions for Inline graphic are shown in Fig. 8 in the form of magnitude (B) and phase (C) for comparison to the data in Fig. 7 (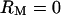Inline graphic in the models). It is notable that both of these models exhibit a fundamental resonance peak and phase shift similar to the average OHC data. The LTE model augments the fundamental resonance with additional peaks (+) and phase shifts occurring at higher frequencies—a feature that is qualitatively consistent with the OHC data.

FIGURE 8.

FIGURE 8

Open in a new tab

Piezoelectric model. Theoretical results showing the voltage ratio Inline graphic treating the lateral wall impedance (Fig. 5) as a simple piezoelectric circuit (A–C, solid lines) or damped LTE resonator (dashed lines). Results are shown in the form of magnitude (B) and phase (C) for comparison to outer hair cell data in Fig. 7. Second peak (+) in the LTE model occurs at a frequency three times the fundamental.

DISCUSSION

Data reported here provide two lines of evidence for piezoelectric resonance in isolated outer hair cells. The first, and most direct, is the voltage ratio (Fig. 7), measured using a voltage-divider configuration (Fig. 3). These data compare favorably to predictions of simple models that treat the lateral wall of the OHC as a piezoelectric element (Figs. 3 D and 8, and Appendix in Supplementary Material). In the second, evidence was obtained by recording the transverse impedance across the cell using a time-averaged 1-MHz interrogation signal in the presence of an axial electric field. The transverse impedance was modulated at discrete axial stimulus frequencies consistent with the electrical resonance observed using the voltage-divider configuration. It is important to note that the 1-MHz interrogation frequency was constant throughout the experiment and therefore was not involved in generating the resonances. We interpret the transverse impedance data as evidence of mechanical resonance altering the electrical shunt pathway around the cell—an expected concomitant with the electrical resonance observed in the voltage-divider configuration. Data for tight-fitting cells indicate that this mechanical effect may be supplemented by nonlinearities in lateral-wall piezoelectricity itself (Fig. 5).

Grosh et al. (2004) previously reported mechanical resonances of the cochlear partition in response to electrical stimulation that occur at ultrasonic frequencies (i.e., above the characteristic best frequency). Resonances in the cochlea showed phase shifts and quality consistent with data from isolated OHCs reported here. This correspondence supports the hypothesis that high-frequency electrically evoked resonances in the cochlea have origins in OHC electromechanical behavior.

High-frequency electromotile responses of isolated OHCs have been investigated previously using the pipette microchamber method at stimulus frequencies up to 100 kHz (Dallos and Evans, 1995a,b; Frank et al., 1999). OHC mechanical responses (displacement and force) were quite flat in these previous experiments and cells exhibiting obvious resonances were not reported. Electrical responses analogous to those reported here were not investigated. We attribute the difference between previous mechanical studies and the electrical voltage-divider data described here to the experimental conditions. It is important to recognize that resonance in piezoelectric structures depends upon the kinetic energy of the vibrating mass. The kinetic energy and the resonance frequency will change if the motion is constrained or the dimensions are altered. Measurements using membrane patches (Gale and Ashmore, 1997) or large pipettes (Dong et al., 2000), designed to investigate intrinsic properties of the membrane motor, clearly limit the total kinetic energy of the vibrating material and therefore would not be expected to reveal the low-frequency whole-cell resonances reported here. Mechanical constraints are also present in the pipette microchamber approach (Dallos and Evans, 1995a), where an isolated OHC is partially inserted into the open tip of a large pipette—like a cork in a bottle. The pipette microchamber introduces a mechanical constraint around the annulus where the pipette tip contacts the plasma membrane. At low frequencies this is not a concern because the ends of the cell are free to displace in the axial direction both inside the pipette and outside of the pipette. The situation is different at high frequencies where the mechanical constraint at the pipette tip would be expected to shift the whole-cell resonance frequency up considerably relative to the unconstrained condition (Meirovitch, 1982; Tiersten, 1969; Weitzel et al., 2003). The situation is analogous to pinning one point of a vibrating guitar string—a manipulation that shifts the resonance frequency up relative to the control condition. Therefore, OHC resonance in a pipette microchamber would be expected to occur at even higher frequencies, where the effect would be much more difficult to observe due to increased viscous dissipation and capacitive roll-off in the excitation. We saw some evidence for this in our experiments as well: “tight-fitting” cells exhibited transverse impedance perturbations at higher frequencies relative to loose-fitting cells (e.g., Fig. 5).

A second important feature distinguishing methods used in this study from earlier work is the use of the voltage ratio 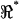Inline graphic to investigate the spatial distribution of properties. The ratio 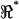Inline graphic (e.g., Fig. 7) maintains sensitivity at high frequencies by comparing the electrical behavior of the apical portion of the cell relative to the basal portion of the cell. The absolute magnitude cancels out, so results are not sensitive to any frequency-dependent roll-off in displacement, force, electrical excitation, or recording impedance. A caveat, of course, is that the resonance shown in Fig. 7 is normalized and electrical; it should not be interpreted directly as a resonance in mechanical displacement or force. Rather, the electrical data shown in this work point to distinct properties of the lateral wall consistent with piezoelectric behavior. Finally, it should be noted that the resonance data summarized in Fig. 7 represent a subset of cells. The conditions under which resonance can be observed are quite specific. OHCs fitting very loosely in the channel would be subject to a large shunt conductance around the cell—a conductance that would mask resonance in the voltage ratio 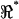Inline graphic. OHCs wedged tightly in the channel would be mechanically constrained, thus shifting the resonance frequency up and sharply attenuating the quality.

There were several key limitations in our experiments that should be noted. First, the low yield was due to the relatively primitive form of the recording technology, cell movement being the primary challenge. Second, it was not possible to alter the extracellular media or apply pharmaceutics during the experiment. New MEMS designed to stabilize the position of the cell within the chamber and to allow wash-in/wash-out application of solutions will be necessary to further advance this research. Third, for loose-fitting cells the saline shunt path around the cell dominated the impedance between the electrode pairs and, in many cases, resulted in 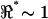Inline graphic, thus precluding observation of resonance using the voltage-divider configuration. Fourth, although nonlinear distortion products were recorded in a subset of experiments, their frequency and amplitude dependence remains to be investigated. Finally, development of alternative recording techniques, such as RF electric-impedance tomography, would be beneficial to overcome limitations of the voltage-divider arrangement.

Even with the limitations of the experimental approach, the data from this study confirm the existence of multimode piezoelectric resonance in isolated OHCs. This finding has three primary physiological implications. First, the existence of multiple resonance peaks shows the existence of multiple eigenmodes, each mode having a distinct spatial distribution of voltage and strain (Meirovitch, 1982). Therefore, our data argue against the common assumption of space-clamp in OHCs and clearly implicate the presence of spatially dependent fields and deformations, at least at high frequencies. It is likely that the electrical constraint imposed by the subsurface cisterna is a key determinant in this behavior (Halter et al., 1997). Second, the fundamental resonance frequency reported here is dependent on size of the cell and increases as the cell is shortened (e.g., LTE model in Supplementary Material). Hence, piezoelectric resonance frequencies for short cells in the basal region of the cochlea are automatically higher than for long cells in the apical region of the cochlea. This distribution generates a piezoelectric frequency map along the length of the cochlea that parallels the passive mechanical tuning. The resonances observed in isolated cells, however, were ultrasonic, and therefore would not be expected to contribute directly to cochlear tuning in this species under physiological conditions. High-frequency specializations, such as echolocation in bats, may be a case where the piezoelectric resonance reported here does contribute directly to tuning. Finally, the 1st (fundamental) natural mode of vibration reported here augments the low-frequency 0th mode, where the OHC mass is negligible and the cell acts as an actuator. It is this 0th mode that is likely to be at work for physiological frequencies below the fundamental OHC resonance. In the low-frequency regime, mammalian cochlear tuning would be expected to result from mechanotransduction (Bozovic and Hudspeth, 2003; Fettiplace and Ricci, 2003) and 0th-mode OHC piezoelectric actuator properties acting in concert with the local mass and stiffness imparted by accessory fluids, cells, and structures in the cochlea.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.

Acknowledgments

The authors thank A. Pungor for electronics design and fabrication, and S. Highstein and R. Boyle for useful discussions and suggestions.

Support was provided by the National Institutes of Health National Institute on Deafness and Other Communication Disorders, grants R01 DC-04928 (R.D.R.) and DC-00354 (W.E.B.).

References

  1. Aschero, G., P. Gizdulich, and F. Mango. 1999. Statistical characterization of piezoelectric coefficient d23 in cow bone. J. Biomech. 32:573–577. [DOI] [PubMed] [Google Scholar]
  2. Ashmore, J. F. 1987. A fast motile response in guinea-pig outer hair cells: the cellular basis of the cochlear amplifier. J. Physiol. 388:323–347. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Ayliffe, H. E., R. D. Rabbitt, and A. B. Frazier. 1998. Electric impedance spectroscopy using microchannels with integrated metal electrodes. IEEE MEMS. 8:50–57. [Google Scholar]
  4. Bozovic, D., and A. J. Hudspeth. 2003. Hair-bundle movements elicited by transepithelial electrical stimulation of hair cells in the sacculus of the bullfrog. Proc. Natl. Acad. Sci. USA. 100:958–963. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Brownell, W. E., C. R. Bader, D. Bertrand, and Y. de Ribaupierre. 1985. Evoked mechanical responses of isolated cochlear outer hair cells. Science. 227:194–196. [DOI] [PubMed] [Google Scholar]
  6. Dallos, P., and B. N. Evans. 1995a. High-frequency motility of outer hair cells and the cochlear amplifier. Science. 267:2006–2009. [DOI] [PubMed] [Google Scholar]
  7. Dallos, P., and B. N. Evans. 1995b. High-frequency outer hair cell motility: corrections and addendum. Science. 258:1420–1421. [PubMed] [Google Scholar]
  8. Dong, X., D. Ehrenstein, and K. H. Iwasa. 2000. Fluctuation of motor charge in the lateral membrane of the cochlear outer hair cell. Biophys. J. 79:1876–1882. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Dong, X.-x., M. Ospeck, and K. H. Iwasa. 2002. Piezoelectric reciprocal relationship of the membrane motor in the cochlear outer hair cell. Biophys. J. 82:1254–1259. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Fettiplace, R., and A. J. Ricci. 2003. Adaptation in auditory hair cells. Curr. Opin. Neurobiol. 13:446–451. [DOI] [PubMed] [Google Scholar]
  11. Frank, G., W. Hemmert, and A. W. Gummer. 1999. Limiting dynamics of high-frequency electromechanical transduction of outer hair cells. Proc. Natl. Acad. Sci. USA. 96:4420–4425. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Fukada, E. 1995. Piezoelectricity of biopolymers. Biorheology. 32:593–609. [DOI] [PubMed] [Google Scholar]
  13. Gale, J. E., and J. F. Ashmore. 1997. The outer hair cell motor in membrane patches. Pflugers Arch. 434:267–271. [DOI] [PubMed] [Google Scholar]
  14. Grosh, K., J. Zheng, Y. Zou, E. de Boer, and A. L. Nuttall. 2004. High-frequency electromotile responses in the cochlea. J. Acoust. Soc. Am. 115:2178–2184. [DOI] [PubMed] [Google Scholar]
  15. Halter, J. A., R. P. Kruger, M. J. Yium, and W. E. Brownell. 1997. The influence of the subsurface cisterna on the electrical properties of the outer hair cell. Neuroreport. 8:2517–2521. [DOI] [PubMed] [Google Scholar]
  16. Iwasa, K. H. 2001. A two-state piezoelectric model for outer hair cell motility. Biophys. J. 81:2495–2506. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Lee, P. C. Y., N. P. Edwards, W.-S. Lin, and S. Syngellakis. 2002. Second-order theories for extensional vibrations of piezoelectric crystal plates and strips. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 49:1497–1506. [DOI] [PubMed] [Google Scholar]
  18. Liberman, M. C., J. Gao, D. Z. Z. He, X. Wu, S. Jia, and J. Zuo. 2002. Prestin is required for electromotility of the outer hair cell and for the cochlear amplifier. Nature. 419:300–304. [DOI] [PubMed] [Google Scholar]
  19. Ludwig, J., D. Oliver, G. Frank, N. Klöcker, A. W. Gummer, and B. Fakler. 2001. Reciprocal electromechanical properties of rat prestin: the motor molecule from rat outer hair cells. Proc. Natl. Acad. Sci. USA. 98:4178–4183. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Meirovitch, L. 1982. Analytical Methods in Vibrations. Macmillan, New York.
  21. Mountain, D. C., and A. E. Hubbard. 1994. A piezoelectric model of outer hair cell function. J. Acoust. Soc. Am. 95:350–354. [DOI] [PubMed] [Google Scholar]
  22. Murugasu, E., and I. J. Russell. 1996. The effect of efferent stimulation on basilar membrane displacement in the basal turn of the guinea pig cochlea. J. Neurosci. 16:325–332. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Pamarthy, K. 2004. Micro-domain electric impedance spectroscopy of outer hair cells using the finite-difference frequency domain technique [M.S.]. University of Utah, Salt Lake City, UT.
  24. Petrov, A. G. 2002. Flexoelectricity of model and living membranes. Biochim. Biophys. Acta. 1561:1–25. [DOI] [PubMed] [Google Scholar]
  25. Santos-Sacchi, J., and J. P. Dilger. 1988. Whole cell currents and mechanical responses of isolated outer hair cells. Hear. Res. 35:143–150. [DOI] [PubMed] [Google Scholar]
  26. Takahashi, S., and J. Santos-Sacchi. 1999. Distortion component analysis of outer hair cell motility-related gating charge. J. Membr. Biol. 169:199–207. [DOI] [PubMed] [Google Scholar]
  27. Tiersten, H. F. 1969. Linear Piezoelectric Plate Vibrations. Plenum, New York.
  28. Tolomeo, J. A., and C. R. Steele. 1995. Orthotropic piezoelectric properties of the cochlear outer hair cell wall. J. Acoust. Soc. Am. 97:3006–3011. [DOI] [PubMed] [Google Scholar]
  29. Wang, J., and J. S. Yang. 2000. Higher-order theories of piezoelectric plates and applications. Appl. Mech. Rev. 53:87–99. [Google Scholar]
  30. Weitzel, E. K., R. Tasker, and W. E. Brownell. 2003. Outer hair cell piezoelectricity: frequency response enhancement and resonance behavior. J. Acoust. Soc. Am. 114:1462–1466. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Zhao, H. B., and J. Santos-Sacchi. 1999. Auditory collusion and a coupled couple of outer hair cells. Nature. 399:359–362. [DOI] [PubMed] [Google Scholar]
  32. Zheng, J., L. D. Madison, D. Oliver, B. Fakler, and P. Dallos. 2002. Prestin, the motor protein of outer hair cells. Audiol. Neurootol. 7:9–12. [DOI] [PubMed] [Google Scholar]
  33. Zheng, J., W. Shen, D. Z. He, K. B. Long, L. D. Madison, and P. Dallos. 2000. Prestin is the motor protein of cochlear outer hair cells. Nature. 405:149–155. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES