Detection of Non-Brownian Diffusion in the Cell Membrane in Single Molecule Tracking

Abstract

Molecules undergo non-Brownian diffusion in the plasma membrane, but the mechanism behind this anomalous diffusion is controversial. To characterize the anomalous diffusion in the complex system of the plasma membrane and to understand its underlying mechanism, single-molecule/particle methods that allow researchers to avoid ensemble averaging have turned out to be highly effective. However, the intrinsic problems of time-averaging (resolution) and the frequency of the observations have not been explored. These would not matter for the observations of simple Brownian particles, but they do strongly affect the observation of molecules undergoing anomalous diffusion. We examined these effects on the apparent motion of molecules undergoing simple, totally confined, or hop diffusion, using Monte Carlo simulations of particles undergoing short-term confined diffusion within a compartment and long-term hop diffusion between these compartments, explicitly including the effects of time-averaging during a single frame of the camera (exposure time) and the frequency of observations (frame rate). The intricate relationships of these time-related experimental parameters with the intrinsic diffusion parameters have been clarified, which indicated that by systematically varying the frame time and rate, the anomalous diffusion can be clearly detected and characterized. Based on these results, single-particle tracking of transferrin receptor in the plasma membrane of live PtK2 cells were carried out, varying the frame time between 0.025 and 33 ms (0.03–40 kHz), which revealed the hop diffusion of the receptor between 47-nm (average) compartments with an average residency time of 1.7 ms, with the aid of single fluorescent-molecule video imaging.

INTRODUCTION

Many cellular processes, such as signaling processes, involve the interaction of several individual molecules that must come together to transmit information across the plasma membrane to the cell interior. Hence, it is of great importance to understand the mechanism by which the motion of transmembrane and membrane-associated molecules is regulated in the cell membrane. However, in the cell, molecular behavior is very inhomogeneous: even molecules of single species interact stochastically with distinct molecules or cellular structures in a variety of local environments. Furthermore, molecular interactions are by nature stochastic. Therefore, bulk-type observations that report on the tendency of molecular behavior averaged over all molecules under observation may not be able to distinguish various stochastic processes occurring in very inhomogeneous environments. Recently, tracking single molecules through single fluorescent-molecule video imaging and single-particle tracking in the membrane of live cells has become available for many researchers (De Brabander et al., 1988; Sheetz et al., 1989; Kusumi and Sako, 1996; Saxton and Jacobson, 1997). These studies have the advantage of being able to view individual characteristics of a membrane molecule that may be washed out in the ensemble averaging inherent in bulk studies.

Specifically, membrane molecules have been shown to undergo anomalous subdiffusion (Kusumi et al., 1993; Ghosh and Webb, 1994; Sako and Kusumi, 1994; Feder et al., 1996; Tomishige et al., 1998; Smith et al., 1999; Fujiwara et al., 2002; Murase et al., 2004). Unlike simple Brownian diffusion, which is isotropic and homogeneous, anomalous diffusion may be anisotropic on some timescales. In the case of anomalous subdiffusion, the timescale of the measurement becomes intimately and nontrivially related to the observed motion. Further, what is easily overlooked is the effect of the finite integration time at the observation device (e.g., a CCD camera attached to the microscope) during each frame of data acquisition.

Anomalous subdiffusion most likely is a result of two main mechanisms that act on the molecules of the membrane simultaneously. Saxton (1994, 1996) has shown that a random distribution of immobilized obstructions (presumably, membrane molecules immobilized on the subsurface scaffolding presented by the actin-based membrane skeleton) is sufficient to produce anomalous subdiffusion at length scales (timescales) shorter than a length characteristic of the average cluster size of obstacles.

As well, much experimental evidence, from both single-particle tracking (Kusumi et al., 1993; Sako and Kusumi, 1994; Tomishige et al., 1998) and optical-tweezers-based molecular dragging studies (Edidin et al., 1994; Sako and Kusumi, 1995; Kusumi et al., 1998; Sako et al., 1998), implies that the cytoplasmic portion of transmembrane proteins nonspecifically collides with the membrane skeleton, causing temporary confinement of the diffusing protein in compartments formed by the membrane skeleton meshwork. This results in so-called hop diffusion, where free diffusion occurs inside these compartments with infrequent intercompartmental transitions. At timescales intermediate to the tracer sensing the compartment boundaries and the average residency time in a compartment, anomalous diffusion is observed. Hop diffusion has also been observed for lipid motion in the outer leaflet of the membrane (Fujiwara et al., 2002; Murase et al., 2004), implying that obstacles are immobilized on the underlying membrane skeleton meshwork and hence reflect its structure in the hindrance of lipid diffusion.

For diffusion of molecules in the membrane, it is most probable that both mechanisms occur with varying degrees of effect. Saxton has presented a detailed study of the effects of a random distribution of obstacles, for both inert and reactive obstacles (Saxton, 1994, 1996). We present in this article a critical examination of the characteristics of hop diffusion. Further, we include the effects of observing diffusion at finite camera exposure times (which sets the fastest rate at which images of the diffusant may be collected) for a molecule diffusing in the membrane of a cell undergoing simple Brownian diffusion, confined diffusion within a compartment, and hop diffusion. From this, we establish the relationship between the observations made at slower rates and those performed at higher rates (which range over three orders of magnitude), and critically assess limitations in the interpretation of the diffusion characteristics of individual particles/molecules as they relate to the frame exposure time and repetition rate at which they are observed.

We systematically consider the relationship between the data acquisition rate and the rate at which biological processes take place, with special attention paid to a transmembrane protein undergoing hop diffusion in the cell membrane. Using a Monte Carlo algorithm, we simulate molecules undergoing simple Brownian, totally confined, and hop diffusion, including the blurring expected at the camera due to finite camera exposure times. Next, the characteristics determined in the first part are experimentally examined. We employed single fluorophore-video imaging at 30 Hz and single-particle tracking at rates up to 40,500 Hz. This led to the finding of very fast hop diffusion (average residency time of 1.7 ms per compartment) of transferrin receptor over a fine membrane skeleton meshwork (compartments ∼47 nm in diameter) in live PtK2 cells. The visualization of these compartments was only possible after a systematic variation of the camera exposure time and frame rate up to rates of 40 kHz.

METHODS

Monte Carlo simulation of protein diffusion in cell membranes

Brownian diffusion was simulated by allowing a point particle to walk randomly on a square lattice. Each timestep consisted of a choice of moving to one of the four nearest-neighbor sites. The scale of the simulation was set such that the spacing between lattice sites was 6 nm and the timestep was 1 μs. As such, the base diffusion coefficient was 9 μm²/s (= (6 nm)²/4/(1 μs)), consistent with the observation of an unsaturated lipid, DOPE, in membrane blebs and unilamellar vesicles (Fujiwara et al., 2002; Murase et al., 2004).

All simulations were performed for 1000 frames per run and 100 runs per case. Free Brownian motion simulations were performed with no barriers to motion. Confined motion simulations were performed in a square of size 42, 120, and 240 nm bounded by impenetrable barriers. Hop diffusion was simulated using a two-dimensional square array of partially permeable barriers (probability of transmission per attempt 0.0008) separated by 42, 120, or 240 nm. The choice of array sizes corresponds roughly to those found experimentally: 240 nm for NRK cells, 120 nm for ECV cells (a sub-line of T24 cells), and 42 nm for FRSK, CHO, and PtK2 cells (Fujiwara et al., 2002; Murase et al., 2004). The average residency time in the compartments reported in these cell types ranges from 1 to 17 ms for DOPE diffusion and was 55 ms for the protein transferrin receptor diffusion in NRK cells (Fujiwara et al., 2002; Murase et al., 2004). Thus, the probability of transmission per each attempt to cross a boundary was chosen to set the average residency time to ∼20 ms.

Video imaging at a data acquisition rate of 0.025, 0.11, 0.2, 2, and 33 ms per frame and a pixel resolution of 40 nm/pixel of the diffusion was simulated by the following method. The particle was represented by a Gaussian intensity profile with a width of 250 nm (approximately one-half the wavelength of light used in video imaging). An image was then developed at every 1-μs timestep by projecting the Gaussian profile of the particle at its current position onto a simulated video camera (CCD array) with each pixel corresponding to 40 nm in the simulated sample plane. Each pixel's intensity was determined through integrating the portion of the particle's intensity profile that overlays each pixel. Each frame of the simulated video at the desired acquisition rate was then built through a sum of the images at the individual 1-μs timesteps (i.e., for 33 ms/frame, the first 33,000 images are summed to make the first frame of the video, the subsequent 33,000 images are summed to make the second frame, and so on), thus incorporating the intrinsic blur of the camera due to particle motion.

The uncertainty in the determination of the particle's position is increased as the frame exposure time is shortened due to the reduction in contrast of the particle in actual experiments (17-nm and 6.9-nm standard deviations for 25-μs and 2-ms frame exposure times, respectively; see High-Speed Video Microscopy, below). The simulations shown in this report do not include this spurious experimental noise so as to show the essential points of the effect of exposure time on the observation of particles undergoing anomalous diffusion. This experimental noise manifests itself as a constant added to all mean-square displacements at all time displacements (Dietrich et al., 2002). A linear regression through the first, second, and third points of the MSD-t plot are used to determine this noise level (the y intercept) which is then subtracted from all MSDs before analysis.

Cell culture

PtK2 kangaroo rat kidney cells were grown in Eagle's Minimum Essential Medium supplemented with 10% fetal bovine serum. Cells were plated on 18 × 18 mm coverslips (for high-speed video imaging) or 12-mm diameter glass-based dishes (for single fluorescent-molecule video imaging) obtained from Matsunami (Kishiwada, Japan) and Iwaki (Funabashi, Japan), respectively, and used 2–3 days later.

Gold probe preparation and fluorescent probe labeling

Colloidal gold particles of 40-nm in diameter (BB International, Cardiff, UK) conjugated with bovine holo transferrin (Wako, Osaka, Japan) were prepared according to Sako and Kusumi (1994). The amount of transferrin mixed with the gold particles was varied to minimize the effect of crosslinking by the gold probe (Fujiwara et al., 2002). For single fluorescent-molecule video imaging, transferrin was labeled with Alexa555-succinimide (Molecular Probes, Eugene, OR). Before observation, cells were incubated in a transferrin-free medium for 15 min at 37°C, washed, and then gold probe or fluorescent probe was applied at 37°C.

Total internal reflection fluorescence microscopy

Single fluorescent-molecule video imaging was performed on a homebuilt objective-lens-type total internal fluorescence microscope using a 1.45 NA TIRF objective (Olympus, Tokyo, Japan) (Iino et al., 2001; Fujiwara et al., 2002). Imaging was performed through an image intensifier (Model # C8600-03, Hamamatsu Photonics, Hamamatsu City, Japan) coupled to a EB-CCD camera (Model # C7190-23, Hamamatsu Photonics). Camera output was stored on DV tape (Model # DSR-20, Sony, Tokyo, Japan) for post-experiment tracking.

High-speed video microscopy

High-speed video microscopy was carried out as described previously (Tomishige et al., 1998; Fujiwara et al., 2002). The precision of the position determination was estimated from the standard deviation of the coordinates of 40-nm diameter gold particles attached to a poly-L-lysine-coated coverslip, further covered with a 10% polyacrylamide gel, and was 17 nm and 6.9 nm at time-resolutions of 25 μs and 2 ms, respectively. On the same instrumental setup, Murase et al. (2004) found the precision to be 13 nm at a time-resolution of 25 μs for gold-labeled fluorescein-DOPE incorporated in large, unilamellar vesicles in the gel phase at 25°C. This result is comparable to that for gold particles attached on the coverslip. Thus, the limiting factor in the position determination in these experiments using immobilized gold particles at the varying exposure times is most likely the signal/noise ratio in the image of the particle. The positional resolution begets a limit on the smallest diffusion coefficient that may be measured. At a time-resolution of 25 μs, the smallest measurable diffusion coefficient was found to be 0.021 μm²/s (Murase et al., 2004).

Quantitative analysis of movement

The apparent position of the particle from video (simulated or experimental) was determined as in Gelles et al. (1988). Briefly, a kernel image of the diffusion probe was taken from the first frame of the video. The kernel is cross-correlated with each subsequent video frame. For each frame, the resulting cross-correlation function is thresholded and the particle position found as the center-of-mass of the thresholded correlation intensity.

The quantitative analysis of molecular movement (both for simulated and experimental data) was carried out based on the MSD methods described previously (Powles et al., 1992; Kusumi et al., 1993; Sako and Kusumi, 1994; Tomishige et al., 1998). For each trajectory, the MSD for every time interval was calculated according to the formula

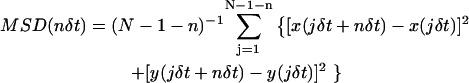(1)

(Qian et al., 1991; Kusumi et al., 1993), where δt is the time-resolution and (x(jδt + nδt), y(jδt + nδt)) describes the particle position following a time interval nδt after starting at position (x(jδt), y(jδt)); N is the total number of frames in the sequence; and n and j are positive integers.

The MSD-versus-time plots (MSD-t plots) are classified into describing simple Brownian, confined or hop diffusion, as described in Fujiwara et al. (2002). The plots determined to represent simple Brownian motion are characterized by the short-term diffusion coefficient, D_2–4 (which is equal to the long-term diffusion coefficient for simple Brownian motion), determined from a linear fit to the MSD-t plot at the second, third, and fourth frames of elapsed time (as defined in Kusumi et al., 1993). The plots determined to represent confined motion are fit with the expected MSD for a particle trapped forever in a square compartment,

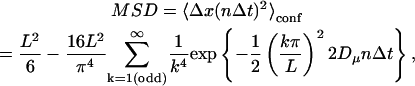(2)

where L is the compartment size, D_μ is a fitting parameter that estimates the microscopic diffusion coefficient, n is the frame number, and Δt is the time for each frame (Kusumi et al., 1993). Confined diffusion is characterized by the compartment size, L, and the short-term diffusion coefficient, D_2–4, is as defined above for simple Brownian diffusion. The plots determined to represent hop diffusion are fit with the result expected for diffusion through an infinite array of partially permeable barriers (Powles et al., 1992), which yields the compartment size, L. For hop diffusion, one expects that at long-times (relative to the average residency time in a compartment), the motion will look like simple Brownian motion with a constant diffusion coefficient, defined as D_MACRO (the macroscopic diffusion coefficient describing the hop diffusion over the compartments). Hop diffusion is characterized by the compartment size, L, the short-term diffusion coefficient, D_2–4, and the average residency time, τ, determined through the average compartment size and average long-term diffusion coefficient as τ = L²/4D_MACRO.

RESULTS AND DISCUSSION

Simulation of the observation of molecular diffusion in membranes

For simplicity, in the following, we have set the exposure time for each frame to the inverse of the frame repetition rate. This equates to running the camera system at the highest data acquisition rate (frame frequency) possible for a given frame exposure time (we neglect the frame download time, but this can be taken into account readily). Of course, one may reduce the open shutter time at the camera so as to reduce the exposure time between frames while maintaining a given frame rate. In what follows, we will highlight when the data acquisition rate becomes an important parameter that must independently be considered. We will not address the added difficulty due to the use of interlaced cameras, where odd and even lines are exposed for equal times but with a time shift between them.

When one is actually carrying out single-molecule tracking experiments, one tends to be intuitively thinking of the experiments in a time domain rather than in the frequency domain. Therefore, in the present report, we present our results in terms of the camera's frame exposure time (frame time) rather than the data acquisition rate (frame rate), and we stick to this convention even where we discuss the frame frequency of the camera.

Simple Brownian diffusion

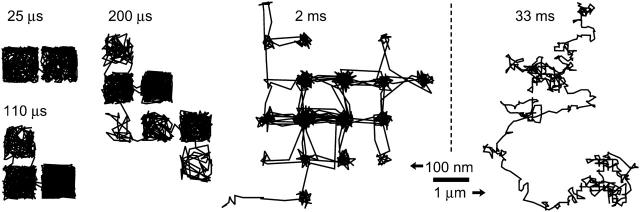
We have simulated trajectories of free diffusion at acquisition rates of every 0.025, 0.11, 0.2, 2, and 33 ms for 1000 frames. Shown in Fig. 1 A are the Monte Carlo trajectories observed at frame rates of 33 ms/frame (data acquisition rate of 30 Hz) and 25 μs/frame (40,500 Hz, trajectory magnified by 36 times []). Note the similarity between the 33-ms trajectory and the expanded 25-μs trajectory, as expected for simple Brownian motion. The MSD-t plots averaged over those for all of the trajectories obtained at 25-μs and 33-ms resolutions are shown in Fig. 1 B. The MSD grows linearly in time as expected for simple Brownian diffusion for both time-resolutions. Shown in Fig. 1 C, the mean microscopic diffusion coefficients, D_2–4, as defined from a linear fit to the MSD in two dimensions at the second, third, and fourth frames of elapsed time (as defined in Kusumi et al., 1993), do not vary significantly regardless of the data acquisition rate used to track the diffusing particle, and is equal to the set value of 9 μm²/s. (Note that although the data point at the 25-μs resolution is lower than expected, this is due to the limited number of trajectories used in the analysis. When 500 trajectories were analyzed at this time-resolution, the average D_2–4 was found to be 8.97 ± 0.03 μm²/s.)

FIGURE 1.

Brownian motion is unaffected by time-averaging at the camera or by the slow repetition of observation by the camera. (A) Typical trajectories of 1000 frames each, from simulation, at frame times of 25 μs (left) and 33 ms (right). The trajectory obtained at a frame time of 25 μs is enlarged by 36 times. (B) MSDs calculated from the trajectories above (single-molecule MSDs) plotted as a function of the time interval. Both MSDs grow linearly with time, indicating that, in both of these very different time-windows, the motion is simple Brownian characterized by similar single diffusion coefficients within the error of the measurement. Note that both x and y axes are expanded by a factor of 1000 in the figure on the right. (C) Average microscopic diffusion coefficient (error bars represent the standard error of the mean) expected to be observed at different frame times (at least 100 simulations for each frame time). The set diffusion coefficient in the simulation was 9 μm²/s (shown by a lateral broken line).

Confined diffusion

In the case of confined diffusion, where the particle is free to randomly diffuse inside an area surrounded by impermeable walls, the effects of the averaging over the camera's frame time (of a single frame) are apparent. Fig. 2 A shows typical trajectories for confined diffusion within 42-, 120-, and 240-nm length square compartments at frame times between 25 μs and 33 ms. The case for 120-nm length compartments simulate diffusion observed in an ECV304 cell line (a sub-line of T24). For the 120-nm compartments, at the shortest frame time of 25 μs, the trajectory quite faithfully reports confinement in a square compartment. At longer frame times, the points near the compartment boundary are lost because as the particle bounces off the boundary, they exhibit a more centralized average position (averaged over the exposure time in a frame), and at a frame time of 33 ms, the confinement area appears circular and of a much reduced area. For the 42-nm compartments, even at an exposure time of 25 μs, there is some reduction in the observed area of diffusion (Fig. 2 B).

FIGURE 2.

Diffusion in a confined area (without escape) appears centralized within a compartment away from the compartment boundaries due to time-averaging over the exposure time during a single frame. (A) Typical 1000-frame trajectories of a molecule trapped in a square compartment of length 42 (top), 120 (middle), and 240 (bottom) nm observed at frame times of 0.025, 0.11, 0.2, 2, and 33 ms. Compartment sizes corresponds approximately to those found experimentally: 240 nm for NRK cells; 120 nm for ECV cells (a sub-line of T24 cells), and 42 nm for FRSK, CHO, and PtK2 cells. (B) Magnified image of diffusion in a 42-nm length square compartment as observed at a frame time of 25 μs, showing that, for such small domains, the apparent area of diffusion is considerably reduced even at the shortest frame time available for single-particle tracking using the 40-nmφ colloidal gold probe.

The MSD-t plot of a particle trapped in the 120-nm length compartments observed at frame times of 25 μs and 33 ms are shown in Fig. 3 A. The asymptotic value of Eq. 2 at long times, L²/6, is found to be much greater in the 25-μs/frame observations than in the 33-ms/frame observations, reflecting the averaging observed in the trajectories seen in Fig. 2 (note the vastly different scales of the y axis in Fig. 3 A, left and right).

FIGURE 3.

Parameters characterizing confined diffusion are severely affected by time-averaging over the frame time. (A) The MSD-t plots for particles trapped within a 120-nm length square compartment at frame times of 25 μs (left) and 33 ms (right). MSDs calculated from the trajectories shown in Fig. 2 (single-molecule MSDs), plotted as a function of the time interval. MSD grows rapidly and then levels off. The theoretical plateau value is 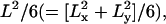which is 4800 nm² (because both L_x and L_y are 120 nm). At a frame time of 25 μs (left figure), this is very close to the observed value. However, at a frame time of 33 ms, the limiting plateau value is severely suppressed (right figure; note the greatly reduced value in the y axis, despite the expanded x axis from the left figure by 1000-fold), corresponding to the centralized distribution of the observed points at this frame time. (B) Apparent microscopic diffusion coefficient D_2–4, plotted against frame time. The solid line is not a fitting, but the predicted apparent diffusion coefficient from Eq. 1 (see the text). The set diffusion coefficient in the simulation was 9 μm²/s. (C) The compartment size determined by fitting the MSD-t curve (like those shown in A) using Eq. 2 displayed as a function of the frame time (at least 100 simulations at each frame time). Note that both the apparent diffusion coefficient and compartment size are severely underestimated at longer frame rates, as expected from the trajectories in Fig. 2 and the MSD-t curves in A. In B and C, error bars are mostly hidden by the data markers.

Fig. 3 B shows the apparent mean microscopic diffusion coefficient (D_2–4, as defined in the previous section, called apparent because the trajectories obtained at slow rates are severely distorted as seen in Fig. 2; this value tends to represent the initial slope in the MSD-t plot in Fig. 3 A) as a function of the camera frame time for the 120-nm square compartments. At longer frame times, severe reductions in the apparent diffusion coefficient occur. This is again due to the particle's position being averaged to a centrally located position in each frame. In fact, even at the shortest frame time used here (25 μs per frame), a slight reduction from the set 9 μm²/s is observed.

This effect can be predicted using the expected MSD for a particle permanently trapped in a square compartment, if the compartment size is known. From Eq. 1, one can determine the expected displacements for the second, third, and fourth frame time differences at a given acquisition rate. For example, for video rate acquisition in a compartment of known size (experimentally determined at higher acquisition rates), the displacements are determined from Eq. 1 for time differences of 66, 99, and 132 ms. A linear fit to these displacements versus time at these three points determines the apparent diffusion coefficient, D_2–4, at that acquisition rate. The solid line on Fig. 3 B shows this prediction, which fits the data well.

Fig. 3 C shows the apparent confinement size determined from a fit of Eq. 1 to the MSD-t plots of motion in a 120-nm compartment. For example, the 120-nm compartments are found on average to be 115 nm when observed with a 25-μs exposure time, but reduce to 16 nm at a 33-ms exposure time due to averaging at the camera.

Fig. 4 A shows the 100,000 positions determined through tracking the diffusion of a particle in a 120-nm compartment observed at frame times of 25 μs, 2 ms, and 33 ms. The effect of averaging is apparent (Fig. 4 A). Fig. 4 B shows the histograms for the apparent positions determined in the x direction for these frame rates, clearly showing the centralized pseudo-Gaussian distributions of the probability density of finding a particle at a given position at longer frame times. From these probability density distributions, the apparent effective potential for individual molecules can be evaluated (from U(x) = −k_BT log(P(x)), where U(x) is the effective potential, P(x) is the probability of finding the particle at position x, and k_BT is the thermal energy). As can be seen in Fig. 4 C, at a frame time of 25 μs, the effective potential almost correctly reports a square-well potential, whereas, at frame times of 2 ms and 33 ms, one might erroneously conclude that the particle is trapped in a quadratic potential. This artifact implies that one must pay keen attention to the intricate interplays among the frame time, the compartment size, and the diffusion coefficient. Determination of the spring constant of the optical trap is often carried out in a protocol similar to that described here. It is well known that the spring constant can be enormously overestimated if the detector does not have a sufficient time-resolution or a shutter that limits the exposure time (for particles always trapped in a single potential, the data acquisition rate is not important as long as the trajectory is sufficiently long, but the exposure time should be short).

FIGURE 4.

Long frame times may erroneously lead to apparent quadratic trapping potentials from the square well potential. (A) The 100,000 consecutive expected positions of a simulated molecule undergoing a free diffusion but confined within a 120-nm length square compartment at frame times of 0.025 (black), 2 (red), and 33 ms (blue). At longer frame times, the simulated molecule appears to be preferentially localized toward the center of the compartment due to averaging during a single frame time. (B) Probability distribution of finding the simulated molecule at different frame times. (C) Apparent effective trapping potential the particle is moving in. At the shortest frame time of 25 μs, the square-well potential is obtained quite faithfully, but, at longer frame times, the molecule is incorrectly reported to be held in quadratic potentials.

In the Supplemental Material (Fig. S1 and its figure legend), we reanalyze the findings of a recent publication (Daumas et al., 2003). In that publication, the authors interpret the results of standard video-rate single-particle tracking of the μ-opioid receptor on NRK cells to propose a model for diffusion of the receptor in a quadratic trapping potential. They found total confinement without hopping, which Suzuki et al. (2005) found is due to high levels of artificial crosslinking due to prolonged on-ice preincubation of the probe with the cells. From the above analysis, we propose that one cannot make these conclusions from data collected at standard video rate. This serves as a demonstration of the pitfalls of overinterpreting data, without heed to the limitations of the technique used.

Hop diffusion

It has been shown previously that membrane proteins (Kusumi et al., 1993; Sako and Kusumi, 1994; Tomishige et al., 1998) and even lipids (Fujiwara et al., 2002; Murase et al., 2004) undergo temporary confinement within 30–700-nm compartments (i.e., the plasma membrane is partitioned into small compartments throughout the whole cell and the compartment size is cell-type-dependent) with infrequent intercompartmental hops. The confinement is most likely due to the underlying actin-based membrane skeleton and various transmembrane proteins that are immobilized to the skeleton (Sako and Kusumi, 1994, 1995; Fujiwara et al., 2002; Murase et al., 2004).

Shown in Fig. 5 are representative simulated trajectories obtained at frame times of 0.025, 0.11, 0.2, 2, and 33 ms for 1000 frames for 120-nm compartments with a probability of barrier passage per attempt of 0.0008, which results in an average (median) residency time of 77 ms (23 ms) determined at a frame time of 25 μs. Note that when the frame time becomes comparable to or longer than the average residency time, at a frame time of 33 ms in this case, the motion looks like simple Brownian diffusion, although hop diffusion belies it. Since a hop from a compartment to an adjacent one occurs in a random direction, and since, at slower frame rates, many hops may occur during a single frame time, it is obvious that simple Brownian motion will be observed. At a frame time of 2 ms or shorter, the square lattice of the underlying compartments becomes visible, although the diffusion within the compartments does not quite fill the compartment space until a frame time as short as 200 μs is achieved.

FIGURE 5.

Hop diffusion trajectories observed at various frame times. Typical 1000-frame trajectories simulated for a particle undergoing hop diffusion over 120-nm length square compartments with a probability of 0.008 to pass the compartment boundary at each attempt, which were observed at frame times of 0.025, 0.110, 0.2, 2, and 33 ms. Note that each trajectory contains 1000 determined positions, and thus the total length of each trajectory is different from each other. The scale is the same except for the 33-ms trajectory. With an increase of the frame time, like the case of confined diffusion, the determined points within a compartment become more centralized due to time-averaging during the frame exposure time (thus, more space between two compartments is formed), and the diffusion is dominated by the hops between the compartments. In the case of the 2-ms frame time, hop movement between the same two compartments is also apparent (directly seen in the trajectory). In addition, since the total length of the trajectory is 2 s, and the mean residency time is 23 ms, there may be ∼87 hops on average. Here, this number of hops occurs over 20 compartments.

Fig. 6 A shows the MSD-t plots for the trajectories observed at frame times of 25 μs and 33 ms. At a frame time of 33 ms (Fig. 6 A, right figure), the MSD grows linearly in time, showing that if the experiments were performed only at this rate or slower, it is very likely that one might reach an erroneous conclusion that the molecule underwent simple Brownian diffusion. Meanwhile, at a 25 μs/frame (Fig. 6 A, left figure), the MSD-t curve shows two distinct linear regimes as expected: the linear regime at short times is indicative of the fast diffusion within a compartment, whereas the regime at much longer times is due to the slow intercompartmental transitions.

FIGURE 6.

Parameters characterizing hop diffusion are severely affected by time-averaging over the frame time, the number of observations made during the residency period within a compartment, and the total observation time, which, if inappropriately chosen, may lead to an erroneous conclusion that the diffusion is simple Brownian. (A) MSDs for single trajectories of hop diffusion (those shown in Fig. 5) observed at frame times of 25 μs (left) and 33 ms (right). Note that both x and y axes are expanded 1000-fold in the figure on the right (for 33 ms). At a frame time of 33 ms (right), the plot can be fitted with a linear line, showing (apparent) simple Brownian character. However at a frame time of 25 μs, typical hop diffusion characteristics are apparent: fast rise in the short-time regime and slower linear growth of MSD with time in the long-time regime, with a slope comparable to that found in the 33-ms MSD-t plot. (B) Apparent microscopic diffusion coefficient D_2–4 plotted against the frame time (at least 100 simulations for each frame time). The set diffusion coefficient in the simulation was 9 μm²/s. At short frame times, the diffusion coefficient within a compartment can be detected with reasonable levels of fidelity. See the trajectories in Fig. 5. It is clear that at shorter frame times, the diffusion coefficient within a compartment dominates. At much longer frame times, the apparent diffusion coefficient levels off. In this time regime, the diffusion coefficient within a compartment (set at 9 μm²/s) becomes negligible, and the apparent diffusion coefficient is determined by the hop diffusion between the compartments, i.e., the compartment size and the residency time within a compartment (see trajectories in Fig. 5). (C) The plot of log(MSD/time) against log(time), covering six orders of magnitude in time. Note that the time here is not frame time, but the actual time interval of the observation of simulated particles. The individual solid curves are those obtained for each frame time. The vertical broken lines show the time taken to first sense the barriers (at 0.1 ms) and the median residency time within a compartment (at 23 ms). Very clear anomalous diffusion (the best fit for the α-value ∼0.23, i.e., a slope of −0.77) is observed in between these lines, whereas simple Brownian diffusion is observed at time-windows below and above these crossover timescales (the slope ∼0).

Fig. 6 B shows that the apparent diffusion coefficient within a compartment decreases with an increase of the frame (exposure) time, due to time-averaging over a single frame, in a similar way found in the case of confined diffusion. In fact, a slight reduction from the set 9 μm²/s is observed even at the shortest frame time used here (25 μs). In the case of totally confined diffusion (Fig. 3 B), the diffusion coefficient drops toward zero as the frame time is increased. In contrast, in the case of hop diffusion, the diffusion coefficient decreases with an increase of the frame time up to ∼2 ms/frame, but then levels off at a constant value of 0.14 μm²/s, when the frame time becomes longer. This is due to the random hop movement between the compartments, and in this time regime, the observed diffusion coefficient D_2–4 could be predominantly determined by the hop movement between the compartments without too much influence of the diffusion coefficient within the compartments. See the 2-ms/frame trajectory shown in Fig. 5. The particle's movement is dominated by the random hops between the compartments rather than the diffusion within a compartment. The time zone used for the determination of D_2–4 with a frame time of 2 ms is 8 ms. Therefore, these results indicate that if the diffusion coefficients are estimated in a time regime longer than 8 ms in the MSD-t plot, where the plot is expected to be linear with a slope given as 4D_MACRO (see Methods), then D_MACRO, the macroscopic diffusion coefficient describing the hop diffusion over the compartments, can be determined. This is consistent with the MSD-t plot shown in Fig. 6 A (left) determined for a time-resolution (frame time) of 25 μs.

As described in Methods, the residency time within a compartment (τ) can be calculated from the compartment size (L = 0.12 μm) and D_MACRO, through τ = L²/[4D_MACRO]), giving an average (median) residency time of 77 ms (23 ms) (averaged over all of the trajectories obtained for all of the frame times employed in this study). To examine the consistency, using the limiting value of D_2–4 in the long frame time regime over 2 ms, which is 0.14 μm²/s, the average residency time is calculated, using L²/[4(average D_2–4 determined using frame times over 2 ms) = (0.12)²/4/0.14], which turned out to be ≈30 ms. This value agrees well with the residency time of 77 ms (median: 23 ms), directly determined from the trajectories in which hop diffusion is apparent.

Diffusion anomaly is often discussed using the relationship: MSD = Ct^α (0 ≤ α ≤ 1, 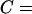constant), where α parameterizes the level of anomaly (Saxton, 1994, 1996; Feder et al., 1996). In the case of simple Brownian diffusion, α = 1. For the sake of clarity, another plot, log(MSD/t) versus log(t) [log(MSD/t) = (α − 1)log(t) + C′, C′ = constant], has become a standard method. In this display, the plot becomes flat (the slope α − 1 = 0), when α = 1 (when the diffusion is simple Brownian). When diffusion is anomalous, α becomes <1, giving the plot of log(MSD/t) versus log(t) a negative slope (α − 1 < 0).

Fig. 6 C shows this plot (we have actually plotted log(MSD/4t) versus log(t) so that the ordinate may be directly compared with the diffusion coefficient) in a time range covering ≈6 orders of magnitude (2 μs−2 s). The slope is found to be almost zero at both short and long times in this plot, showing simple Brownian nature at short and long time regimes, as expected for the case of hop diffusion. Between these two regimes, the slope is negative, a clear indication of anomalous diffusion.

A crossover between the anomalous diffusion time-regime and the short-term apparent simple Brownian regime is found at ≈100 μs (see the vertical dotted line on the left in Fig. 6 C). This time is comparable to that required for the particle to first sense the compartment boundaries. Assuming that the particle starts diffusion at the center of the compartment at time 0, it will cover an area of 60 nm in radius (this number is used because the compartment assumed here is 120-nm-long square) in 100 μs ([0.06]²/4/9), thus confirming that the lower crossover is induced by the initial encounters with the compartment boundaries.

A second crossover occurs between the anomalous diffusion time-regime and the long-term apparent simple Brownian regime (≈20 ms, see the vertical dotted line on the right in Fig. 6 C). This value is comparable to the median residency time in a compartment, 23 ms (the mean residency time is 77 ms, which is also close to the above crossover point). This coincidence suggests that at the longer time regime, the detected movement is dominated by the random hops of molecules between the compartments rather than the diffusion within a compartment, as clearly seen in 2-ms/frame trajectories shown in Fig. 5. There, movement within a compartment is quite well-averaged over the frame exposure time to give an averaged centralized location of molecules, whereas the hops between the compartments are clearly seen. Note that the crossover points determined in the plot of D_2–4 versus frame time (Fig. 6 B) and that in the plot of log(MSD/4t) versus log(t) (Fig. 6 C) appear to be different by a factor ∼10–100. In the latter plot, time indicates the time interval during which the MSD is calculated for each trajectory and then averaged over all of the trajectories obtained for the same frame time. Therefore, the x axis of these two figures should not be confused.

47-nm compartments found in PtK2 cells at a frame time of 25 μs

From simulation, we have predicted that the camera's frame time will have profound influences on the results of single-particle/molecule tracking experiments. To substantiate the simulation results described above, we have examined the diffusion of a transmembrane protein, transferrin receptor, in PtK2 cells. Previously, Murase et al. (2004) have shown that an unsaturated phospholipid (DOPE) undergoes hop diffusion in the plasma membrane of PtK2 cells in culture with very small compartments of ∼45 nm on average. In the present work, we describe the results of systematic variations of the frame time over 33, 0.22, and 0.025 ms. It is an attempt to find the appropriate frame time for the observation of the diffusion of transferrin receptor in this cell type, and will serve as a model case for the diffusion studies of other membrane molecules in different cell types.

We have labeled transferrin receptor with 40-nm diameter colloidal gold particles. The use of the colloidal gold labels allows for high-speed single-particle tracking, up to a frame time of 25 μs. Such a short frame time cannot be accomplished using single fluorescent-molecule imaging due to limited signal/noise ratio of the images. Possible detrimental influences of the use of such large (on molecular scales) probes include crosslinking of the molecules underneath the gold probe and interactions between the gold probe and the extracellular matrix, extracellular domains of other membrane proteins, or lipid molecules in the extracellular leaflet of the membrane. It has been shown that removal of substantial portions on the extracellular domains of membrane molecules and the extracellular matrix does not affect the diffusion of the gold-labeled lipid in FRSK (Murase et al., 2004) and NRK cells (Fujiwara et al., 2002), indicating that the most serious problem with colloidal gold probes is their tendency to crosslink their target molecules. A careful titration of the concentrations used (and in the case of antibody-labeling, using the Fab fragment of the antibody) can be done to minimize the crosslinking effects of the gold. Since the diffusion measurement is very sensitive to clustering of membrane molecules in the compartmentalized plasma membrane (in a marked contrast with that predicted and found in the case of two-dimensional continuum fluids, like reconstituted membranes and liposomal membranes; see Iino et al., 2001; Murase et al., 2004; Kusumi et al., 2005a,b), the diffusion coefficient can be measured as a function of the concentration of the ligand (or the Fab fragment of an antibody) when the colloidal gold probes are prepared. The diffusion coefficient will increase as the ligand concentration is decreased, and, if one is lucky with the ligand, cell, and/or the conjugation method, it may reach a plateau value before the colloidal gold probe loses the specific binding affinity to the specific target molecule. Normally, the limiting (the maximal) diffusion coefficient with the colloidal gold probe is compared with the diffusion coefficient determined with a single fluorophore probe, both evaluated at identical frame times, usually at the standard video rate. This is because, with fluorescent probes, the frame time must be sufficiently long to gain a reasonable signal/noise ratio, and the total observation time is severely limited due to photobleaching. The plateau value with colloidal gold probes may be comparable to the diffusion coefficient determined by fluorescent probes, and if this occurs, it ensures that the gold labels are not affecting the motion of the molecule under study.

Here we compared the diffusion of gold-labeled transferrin with Alexa555-transferrin, both attached on the PtK2 cell surface, and both observed at a frame time of 33 ms. To take more averages over single trajectories to reduce the statistical variations (see Eq. 1), in particular for single fluorescent molecule trajectories, which have limited lengths due to photobleaching, the microscopic diffusion coefficient was evaluated using the first, second, and third points in the MSD-t plot, defined as D_1–3. D_1–3 for the Alexa-labeled transferrin was found to be 0.55 ± 0.04 μm²/s (n = 37). For the gold-labeled transferrin, D_1–3 was found to be 0.34 ± 0.03 μm²/s (n = 31). Note that these diffusion coefficients are ∼20-fold smaller than those found in synthetic lipid bilayers or on membrane blebs (balloon-like structures of the plasma membrane, where the membrane skeleton is scarce) in living cells (Tank et al., 1982; Fujiwara et al., 2002; Murase et al., 2004). Since the gold-labeled transferrin exhibited a microscopic diffusion coefficient that is 1.6-fold smaller than that of Alexa-labeled transferrin on PtK2 cells, it is concluded that these gold probes induced slight crosslinking of transferrin receptor. We expect that this crosslinking may slow intercompartmental hops, thus lowering the apparent diffusion coefficient, but will not significantly affect the apparent size of the compartments (if they are visible). The low signal/noise ratio for single fluorophore image precludes simultaneously accomplishing both higher framing rates and sufficient duration of observation of single molecules, which is required for the detection of hop diffusion in the cell membrane (Kusumi et al., 2005a,b). Thus, from here on, we will concentrate on results determined through observing gold-labeled transferrin.

The frame time has been systematically varied from the standard video's 33 ms to 220 μs and 25 μs. Fig. 7 A shows typical trajectories of the gold-labeled transferrin receptor at each observation frame time. Note that the trajectory at the shortest frame time appears to be compartmentalized as compared to the trajectory at standard video rate, which appears to be random Brownian motion. Classification of trajectories by a statistical analysis (Kusumi et al., 1993; Fujiwara et al., 2002) finds that, with a decrease of the frame time, the number of trajectories classified as undergoing simple Brownian motion decreases from 77% at standard video rate to 7% at a frame time of 25 μs.

FIGURE 7.

Experimental diffusion observations of gold-tagged transferrin receptor in the plasma membrane of the live PtK2 cells at various frame times reveal its rapid hop diffusion over small compartments. (A) Typical experimental trajectories obtained at frame times of 0.025, 0.22, and 33 ms. In the case of 0.025-ms trajectory, various plausible compartments detected by a computer program developed previously (Fujiwara et al., 2002) are shown in different colors in the order of purple, blue, green, yellow, and red. (B) Apparent microscopic diffusion coefficient, D_1–3, for transferrin receptor plotted against the frame time of the camera (red triangles). Also shown are the results of Monte Carlo simulation (blue squares) for 54-nm compartments with underlying diffusion coefficient of 9 μm²/s and probability of passing a barrier of 0.0045. The standard error of the mean for each point is within the extent of the data markers. Even in the shorter frame-time regime, the diffusion coefficient is changing rapidly, implying that even a frame time of 25 μs is not sufficient to obtain the intrinsic diffusion coefficient in such a small compartment. (C) Distribution of the compartment size as determined from the transferrin receptor trajectories observed at a frame time of 25 μs.

D_1–3 increases from 0.34 ± 0.03 μm²/s (n = 31) at a 33-ms frame time to 2.2 ± 0.2 μm²/s (n = 32) at a 25-μs frame time (Fig. 7 B, triangles). The average compartment size for transferrin receptor in PtK2 cells (see Fig. 7 C) was determined to be 47 ± 3 nm (n = 30) by a fit to the MSD-t plots at a frame time of 25 μs, using an equation developed for diffusion through an infinite array of partially permeable barriers (Powles et al., 1992). The average residency time determined for gold-tagged transferrin, again using the relationship, 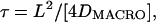was 2.8 ms. Since this value is influenced by the crosslinking by gold probes, to obtain the correct residency time for transferrin receptor, D_MACRO, the macroscopic diffusion coefficient determined by Alexa-transferrin has to be used. Since the residency time for gold-tagged transferrin is 2.8 ms, D_1–3, determined by using the first, second, and third frames at the video rate, representing the diffusion coefficient in a time window ∼100 ms, is thought to approximate D_MACRO sufficiently well. Using the D_1–3 for Alexa-transferrin determined at video rate (0.55 μm²/s), the average residency time of 1.7 ms was obtained.

Although a residency time of 1.7 ms may seem very short, it would still be restrictive enough to induce a 20-fold decrease of the long-range diffusion coefficient over the coefficient for free diffusion within a compartment. The experimental distribution of compartment sizes on PtK2 cells is shown in Fig. 7 C. These surprisingly small compartments are hidden at slower frame rates due to the short average residency time in each compartment.

We found that these results can be simulated very well, assuming the hop diffusion for 54-nm compartments with the microscopic diffusion coefficient within a compartment of 9 μm²/s, a probability of passing the boundaries of 0.0045. The predicted values for D_1–3 was 2.02 ± 0.01 and 0.347 ± 0.004 μm²/s for frame times of at 25 μs and 33 ms, respectively (n = 100 for each case), in agreement with the experimentally determined values, as shown in Fig. 7 B (squares). Furthermore, the Monte Carlo simulations predicted an apparent compartment size of 48.7 ± 0.6 nm (n = 100) at a frame time of 25 μs, in agreement with the observed compartment size. These results clearly show that even at a very short frame time of 25 μs, the time-averaging over a frame time is quite apparent when the compartment size is small, and that at the normal video frame time, all of the hop diffusion characteristics, including short residency times in small compartments, are totally hidden.

GENERAL DISCUSSION

We have shown how the characteristic time (length) scales present in hop diffusion can be investigated through a systematic variation of the observation rate (camera frame rate and exposure time). Three regimes become apparent with an anomalous diffusion regime being bracketed by normal diffusion at both high and low frame time observations (Fig. 6 C). These results clearly indicate that the hop diffusion can be easily mistaken as slow simple Brownian diffusion, if observation is made only at slower rates, like the standard video rate. Similar observations have been made experimentally, covering a time of approximately five orders of magnitude, with the shortest time-window of 50 μs (at least two points are needed to determine the MSD).

While varying the frame time, we have emphasized that a keen awareness of the effects of the exposure time (of a single frame) at the detector is required. The time-averaging inherent in the imaging of a diffusing particle can have severe effects on the apparent characteristics of the motion reported. Although pure simple Brownian motion is unaffected by this time-averaging, the apparent motion of particles undergoing confined or hop diffusion motion is strongly affected. Within a compartment, the average position is away from the compartment boundaries and centralized. In an extreme case, the particle appears almost stationary (imagine determining the average position of a membrane molecule totally trapped in a submicron compartment every 1 h using a time-average of 1 h/frame, or see Figs. 2 and 4 for the 33-ms case, and Fig. 5 for the 2-ms case), trapped in a very high trapping potential.

In the case of hop diffusion, the issue of frame time becomes more complicated. As assumed in this article, with camera systems where the repetition rate of the observation for coordinate determination (the frame rate of the camera) and the time-window for each observation (the frame exposure time of the camera) are tightly coupled, the distinction of the frame rate and frame time may not be clear. However, these two represent different concepts, and this difference becomes important in understanding their effects on hop diffusion.

First, for monitoring movement within a compartment of a molecule undergoing hop diffusion, the issue is the time-averaging during a single frame, just like the case of confined diffusion, and thus frame time is the key concept here. Second, however, to detect the hop movement between the compartments, one has to make sufficient numbers of determinations of the particle's coordinate during the residency time within the compartment. Therefore, the critical concept related to this problem is the frame rate. For example, the trajectory shown in Fig. 5 at a frame time of 2-ms suggests that ∼50 determinations have to be made before a compartment is detected as such (1000-frame trajectory covering 20 compartments), which is in general agreement with our experience in actual experiments (although more determinations will be better). The third consideration is the total observation time window. If this is not long enough, the hop event may not take place during the observation period.

Therefore, in actual experiments for the detection of hop diffusion, 1), the exposure time of each frame (frame time), 2), the frequency of the observation (frame rate, but this cannot be greater than the inverse of the frame time), and 3), the total duration of the observation, have to be coordinated within the given experimental boundary conditions, such as the photobleaching time of the probe, photodamage to the cells, excitation light intensity, available size of the memory, and so on. If these three conditions are not simultaneously satisfied, direct monitoring of hop diffusion cannot be done. This may be the reason why many researchers have difficulty detecting the hop diffusion.

For example, in the case of single fluorescent molecule imaging, satisfying all of these three requirements is not a simple matter, due to photobleaching of the probe under the high illumination conditions that may be required for accomplishing short frame exposure time (single frame). Often, the short frame time is first achieved, but then one has to choose either the total length of observation (using time-lapse recording, sacrificing the frame rate) or the high frame rate (sacrificing the total observation time, and depending on one's luck of accidentally obtaining a long trajectory). Unless a good compromise among these three experimental variables could be found, clear hop diffusion cannot be found. These effects limit what can be implied about the motion of fast diffusing membrane-associated molecules when observed at video rates of 33 ms per frame (NTSC) (or similarly, 40 ms per frame, PAL).

Insight into the effects of the membrane-skeleton-based compartmentalization of the plasma membrane on the diffusivity and function of membrane molecules can still be made, even at standard video rates, perhaps by observing the diffusion in membrane blebs or by the careful application of actin stabilizing/destabilizing drugs. We recommend the observation in the blebbed membranes because the interpretation of drug-induced effects is complicated. For example, application of latrunculin or cytochalasin D for a very short period of time (finishing experiments within 15 min after the application of the drugs) induced slight increases of the compartment size concomitantly with slight decreases of the hop rate, resulting in a slight increase of the macroscopic diffusion coefficient determined at video rate by a factor of only between 1 and 2, depending on the cell type (Fujiwara et al., 2002; Murase et al., 2004). A clear example is found in Murase et al. (2004; compare to their Table 5): after cyto chalasin treatment, the average compartment size increased from 45 to 87 nm, but the hop rate for gold-tagged DOPE decreased from an average of once every 15 ms to once every 39 ms, thus only slightly changing the macroscopic diffusion coefficient, from 0.042 to 0.046 μm²/s. After ensemble-averaging over many molecules observed by FRAP, or too-long-term-averaging in low time-resolution single-molecule tracking, such small changes in the motional characteristics of the membrane molecules may easily be missed (furthermore, the use of high concentrations of actin-depolymerizing drugs and/or the long incubation periods often employed in cell biological studies may complicate the results), and thus high-speed single-molecule tracking methods may be the best observation choice. For further details, see the online Supplemental Material in Murakoshi et al. (2004) and Kusumi et al. (2005a,b).

Knowledge that the underlying diffusion coefficient may be as high as 10 μm²/s and that compartmentalization may occur on very small length and timescales (over 10's of nanometers and over milliseconds), coupled with changes in the diffusion coefficient as determined at standard video rates, will allow for a clearer interpretation of the mechanisms involved in such processes as signal transduction and the initiation of cell-cell adhesion in the plasma membrane. For example, the reduction of diffusion coefficient upon oligomerization of acetylcholine receptor (Peng et al., 1989) or Fcɛ receptor (McCloskey, 1993), or upon liganding of luteinizing hormone receptors (Roess et al., 2000) has been detected at lower time-resolutions and/or using bulk FRAP assays (but still at the level of single cells), and the argument for the essential role of immobilization of Fcɛ receptor for initiating its signaling cascade has been advanced (Schweitzer-Stenner et al., 1997). E-cadherin molecules on the free cell surface, which are not engaged in cell-cell adhesion, unlike those in adherens junctions, have been found to be in oligomeric forms of various sizes, and their macroscopic diffusion rates observed at a 100-ms time-window varies greatly, depending on the size of oligomers (Iino et al., 2001). The two-dimensional continuum fluid model (Saffman and Delbrück, 1975) based on the fluid mosaic model (Singer and Nicolson, 1972) cannot explain such large decreases of diffusion coefficient upon oligomerization or liganding.

The partitioning of the plasma membrane into many small (several 10s of nanometers) compartments by the membrane skeleton fences and the anchored-protein pickets offers a clear explanation about why the diffusion in the plasma membrane is very sensitive to the formation of molecular complexes, in contrast to the prediction from the two-dimensional continuum fluid model. Monomers of membrane molecules may hop across the picket line with relative ease, but upon molecular complex formation, the complexes as a whole, rather than single molecules, have to hop across the picket-fence line all at once, and therefore, these complexes are likely to have a much slower rate of hopping between the compartments. In addition, molecular complexes are, due to the avidity effect, more likely to be bound or tethered to the membrane skeleton, perhaps temporarily, which also induces (temporary) immobilization or trapping of molecular complexes. Such enhanced confinement and binding effects induced by oligomerization or molecular complex formation are collectively termed oligomerization-induced trapping (Kusumi and Sako, 1996; Iino et al., 2001). Therefore, for the understanding of the data obtained at low time-resolutions and/or for many molecules collectively, even if the data suggest apparent simple Brownian diffusion, the partitioned model of the plasma membrane and rapid hop diffusion of membrane molecules between the membrane compartments of several tens of nanometers at a frequency of every 1–10 ms on average should always be considered.

This oligomerization-induced trapping might be critically important in the temporary confinement of a cytoplasmic signal at the very early stages of signal transduction. When an extracellular signal is received by a receptor molecule, the receptor often forms oligomers and signaling complexes. Due to the oligomerization-induced trapping, these oligomeric complexes tend to be trapped in the same membrane skeleton compartment as that where the extracellular signal was received. Therefore, the membrane skeleton fence and the anchored transmembrane-protein pickets temporarily help to confine the cytoplasmic signal to the place where the extracellular signal was received. Although such spatial confinement may last only several to several tens of seconds, it may have an important consequence, perhaps leading to signals that induce local or polarized reorganization of the cytoskeleton or chemotactic events.

Single-molecule tracking is a powerful tool, but its various limitations must be fully understood before it may be used to truly investigate structure in the plasma membrane of live cells. In the present report, we dealt with the time-averaging over a single frame as well as the density of observation points in time (with a brief reference to the total observation time). As the frame time and frame rates of available cameras are improved continually, and as various probe technologies are making impressive progress (Pinaud et al., 2004), we expect these limitations to be reduced in the coming time, which will lead to a number of very interesting observations in the near future.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.