Nano- to Microscale Dynamics of P-Selectin Detachment from Leukocyte Interfaces. II. Tether Flow Terminated by P-Selectin Dissociation from PSGL-1

Abstract

We have used a biomembrane force probe decorated with P-selectin to form point attachments with PSGL-1 receptors on a human neutrophil (PMN) in a calcium-containing medium and then to quantify the forces experienced by the attachment during retraction of the PMN at fixed speed. From first touch to final detachment, the typical force history exhibited the following sequence of events: i), an initial linear-elastic displacement of the PMN surface, ii), an abrupt crossover to viscoplastic flow that signaled membrane separation from the interior cytoskeleton and the beginning of a membrane tether, and iii), the final detachment from the probe tip most often by one precipitous step of P-selectin:PSGL-1 dissociation. Analyzing the initial elastic response and membrane unbinding from the cytoskeleton in our companion article I, we focus in this article on the regime of tether extrusion that nearly always occurred before release of the extracellular adhesion bond at pulling speeds ≥1 μm/s. The force during tether growth appeared to approach a plateau at long times. Examined over a large range of pulling speeds up to 150 μm/s, the plateau force exhibited a significant shear thinning as indicated by a weak power-law dependence on pulling speed, 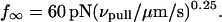Using this shear-thinning response to describe the viscous element in a nonlinear Maxwell-like fluid model, we show that a weak serial-elastic component with a stiffness of ∼0.07 pN/nm provides good agreement with the time course of the tether force approach to the plateau under constant pulling speed.

INTRODUCTION

As a vital part of cellular function in the inflammatory response, transient bonds between selectins and sialo-mucin glycoproteins enable leukocytes to perform a “rolling” exploration of vessel walls (Vestweber and Blanks, 1999; McEver, 2001, 2002). Most of our knowledge about how selectin bonds behave under stress has come from observing the rolling and tethering of receptor-bearing particles (cells or microspheres) in flow chambers with walls decorated by adhesive ligands (Lawrence and Springer, 1991; Brunk and Hammer, 1997). These experiments have shown that at a given shear rate, the average cell-rolling speed correlates with the mean distance between adhesion sites (i.e., surface density) and the mean lifetime of the adhesion bonds, which can be reduced significantly by the hydrodynamic force exerted on the cell or particle (Kaplanski et al., 1993; Alon et al., 1995, 1997). Complicating the dynamics in cell rolling, the force experienced by an adhesive bond depends on the lateral separation distance between the attachment site and the center of cell-surface contact, acting as a moment arm or lever to reduce the bond force. Immediately after attachment, the normal component of adhesion force causes the cell surface structure to flatten against the substrate, creating an initial separation between the cell center and the attachment site. However, this initial distance is quickly augmented by the rapid growth of a membrane nanotube or “tether” between the cell and the adhesion site, significantly lowering the load on the adhesive bond and prolonging its lifetime. Hence, the formation and growth of a tether during the lifetime of an adhesive bond is recognized as a key factor in the dynamics of leukocyte interactions with vessel walls and has been studied extensively using flow-chamber experiments (Schmidtke and Diamond, 2000; Park et al., 2002; Ramachandran et al., 2004).

To examine the formation and growth of a single tether in the context of a selectin-mediated interaction important in leukocyte function, we have detached polymorphonuclear granulocytes (PMNs) from point bonds to recombinant P-selectin immobilized on the tip of an ultrasensitive force probe. Measuring the probe force with a sensitivity of 1 pN at time intervals of 0.0006 s, we quantified the full history of force up to final rupture of each P-selectin attachment while retracting the PMN at a preset speed between 0.4 and 150 μm/s. Subtracting out the biomembrane force probe (BFP) tip deflection to expose the time-dependent cell extension, we observed two well-defined regimes of PMN deformation, each representing a very different type of material behavior. The first regime was a brief elastic-like extension of the cell surface revealed by a steady linear rise in force that ended after a displacement of ∼200–500 nm, depending on the pulling speed. As described in our companion article I (Evans et al., 2005), the abrupt termination of the elastic regime signaled a cohesive failure in the membrane linkage to the PMN cytoskeleton. When analyzed over the full range of pulling speeds, the most frequent force for separation of the membrane from the cytoskeleton was found to be proportional to the logarithm of the force rate (pN/s) experienced by an attachment during the initial elastic regime, agreeing with the model for kinetically limited rupture of a weak chemical bond (Evans and Ritchie, 1997; Evans and Williams, 2002). Triggered by the membrane unbinding event, a second regime began that exhibited a transient approach to a plateau in force accompanied by fluid-like extrusion of a membrane tether, quickly distancing the cell from the probe tip by as much as a few micrometers. The primary focus of this article is on the rheology of single tether growth observed in the majority of tests before a single precipitous step of detachment from the probe tip. In the Appendix, we describe some exotic force histories that showed more than one step of detachment, most likely arising from multiple sites of bonding between the PMN and the probe tip.

When examined at comparable pulling speeds, we found that the forces driving single tether growth after membrane separation from the cytoskeleton were similar in magnitude to the results from other PMN experiments (Shao and Hochmuth, 1996; Schmidtke and Diamond, 2000; Marcus and Hochmuth, 2002). In the studies by Hochmuth and co-workers, a PMN was point attached to a microsphere coated with monoclonal antibodies and then pulled away from the rigidly held microsphere by a step aspiration of the whole cell into a large micropipette. Varying pipette suction, they examined tether growth rates from ∼0.1 to 10 μm/s. By comparison, Schmidtke and Diamond (2000) used high-speed video microscopy to quantify the rates of tether growth from flowing PMNs when captured by transient bonds to P-selectin on spread platelets in a flow chamber. Varying the shear rate, Schmidtke and Diamond extended the range of tether growth rates from ∼10 to 40 μm/s. Encompassing and further extending the range of pulling speeds up to 150 μm/s, we find that the apparent plateau forces driving single tether growth from PMNs after initial transients increase as a weak-fractional power law of the pulling speed and that the results from the earlier experiments also correlate with this shear-thinning behavior.

MATERIALS AND METHODS

Referring to article I (Evans et al., 2005) for details of the preparations, we will only note a few important aspects here. Used as the targets for P-selectin attachment, the PMNs were obtained from finger-prick blood samples and suspended in a hypotonic 150 mOsm HEPES buffer that contained 1 mM calcium. As noted in article I, the PMNs equilibrated after a few minutes to a size very close to that in isotonic buffer through osmotic regulation and exhibited nearly the same cell deformability, with the same large reservoir of excess membrane area, as in isotonic conditions.

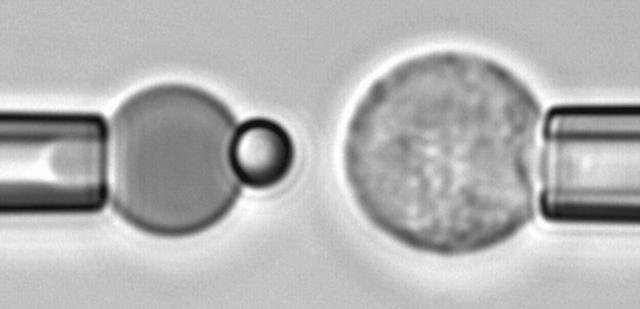
The force transducer in the biomembrane force probe (Fig. 1, left) was created by aspiration of a PEG-biotinylated red blood cell into a smooth spherical shape by micropipette suction. Then, a PEG-biotinylated glass microsphere, previously coated with streptavidin, was attached to the PEG-biotinylated cell to complete the BFP “assembly”. For the tests reported here, the glass tip was also sparsely functionalized with PEG-linked recombinant P-selectin proteins (Glycotech, Rockville, MD) using covalent chemistry. With the BFP-holding pipette kept stationary and the pressurized red cell capsule responding like a linear spring, axial deflections of the BFP tip were converted to compressive or tensile forces using the BFP spring constant k_f, set precisely by the pipette suction pressure. The determination of the BFP spring constant is based on the following mechanical features. First, when prevented from adhesion to the glass tube by coating with albumin, pipette pressurization of the red cell can be used to produce a smooth-outer sphere and a state of uniform membrane tension . The level of tension is proportional to the aspiration pressure and the pipette radius 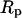. The specific expression for tension involves a secondary dependence on the radius 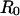of the outer spherical portion of the cell as given by,

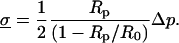(1)

FIGURE 1.

Video micrograph of a biomembrane force probe (left) and a PMN target held in an opposing micropipette (right). The exposed spherical segment of the BFP red cell has a diameter of ∼6 μm.

Second, when extended or compressed along the axis of cylindrical symmetry, the outer portion of the cell remains a surface described by a constant mean curvature. When pulled or pushed by small axial forces, the shape deviates slightly from a sphere with small changes in axial length that are directly proportional to the axial force (Evans et al., 1995; Simson et al., 1998). The coefficient of proportionality between force and deflection defines the BFP spring constant (k_f). The expression for the spring constant depends mainly on the transducer membrane tension,

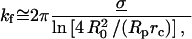(2)

with a weak logarithmic dependence on the characteristic dimension of the cell 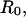the pipette radius 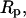and the radius 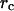of the adhesive contact between the glass bead and the cell (Evans et al., 1995).

Taken from the dilute suspension in the microscope chamber, a PMN was selected by a second micropipette (Fig. 1, right) and perfectly aligned with the BFP to ensure axial symmetry. The PMN was moved to/from contact with the BFP tip by a linear piezo translator with subnanometer resolution in position. Throughout these maneuvers, custom-designed software was used to acquire and analyze a thin slice of the video-microscope image along the axis of symmetry at a frame rate of ∼1500/s. Repeated hundreds of times, each test cycle consisted of bringing the PMN into a soft feedback-controlled contact with the BFP tip, holding the contact at a small impingement force for a brief period of time (“touch”), and then retracting the PMN at a constant speed. After a few hundred tests, a fresh PEG-biotinylated red cell and probe bead were used to assemble a new BFP for another series of adhesion tests with fresh PMNs.

RESULTS

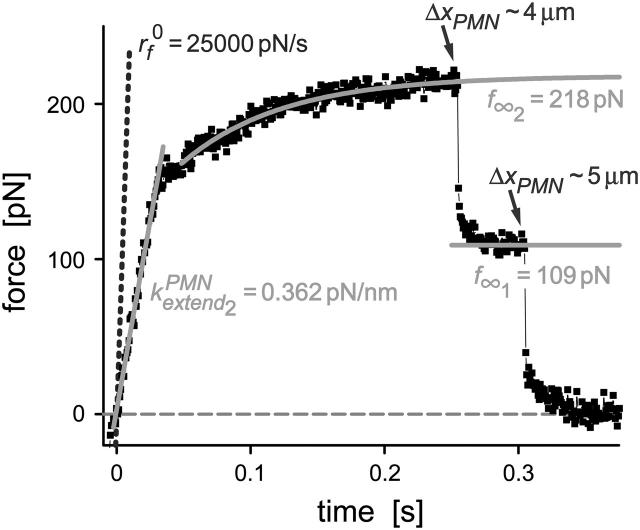
Using BFP tips linked sparsely with either mono-P-selectin or a P-selectin Fc chimera, 30–70% of touches to PMN surfaces resulted in point attachments. Testing hundreds of attachments with each of nearly 60 PMNs, we found that the majority of touches to PMNs with the mono- and dimeric P-selectin tips resulted in a similar type of force history, ending in a single precipitous step of detachment as if held by a single molecular bond (cf. Fig. 2). Still, because two-thirds of the tests were performed with the P-selectin Fc dimer, and half of these tests had tips with P-selectin concentrations sufficient to produce attachments in 60–70% of touches, a few attachments in these tests showed obvious features of multiple sites of bonding. We briefly describe some of these cases in the section on force relaxation at constant length and in the Appendix. However, as in our article I on membrane separation from the cytoskeleton (Evans et al., 2005), we will focus on the flow properties of tethers observed in the large fraction (79%) of tests that showed a single step of P-selectin detachment like the examples appearing in Fig. 2. Thus, we expect these cases to primarily reflect PMN attachment to a single P-selectin site on the probe tip.

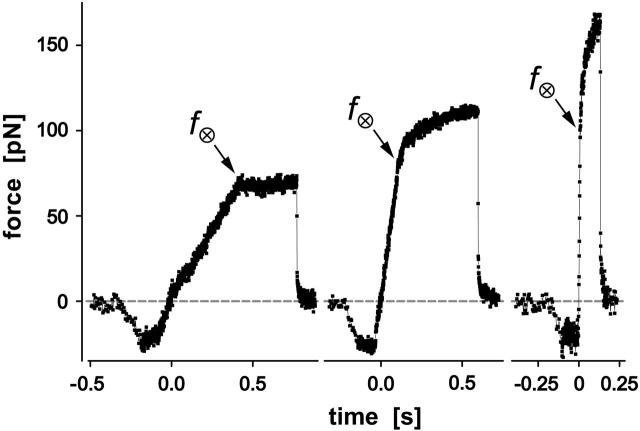
FIGURE 2.

Examples of BFP force-time curves obtained for P-selectin:PMN attachments at three different pulling speeds (v_pull ∼ 2, 15, 50 μm/s). Negative forces represent the initial indentation of the PMN at touch regulated by feedback control. Labeled by the force f_⊗, termination of the initial elastic regime marked the onset of the tether flow regime. The final precipitous drop in force revealed the BFP recoil upon release of the PMN tether by P-selectin dissociation from PSGL-1. (The data shown here and in the following figures were obtained at 1500/s framing rate without averaging.)

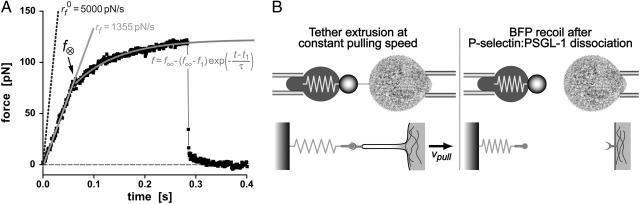
The force-time traces in Fig. 2 show representative cycles of PMN “touch” to the probe and then “retraction” after contact under conditions of slow and fast pulling speeds. The PMN approach to the tip was stopped when a preset level of impingement force was detected (e.g., the negative forces of 15–20 pN in Fig. 2). After a brief pause (∼0.1 s), the piezo translator connected to the PMN-holding pipette was reversed, pulling the PMN away at a preset steady speed v_pull. The tensile loading of a PMN attachment to the tip began when the force crossed zero during retraction, defined as time 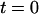, and ended at the time of final P-selectin dissociation. Highlighted by representative expressions in Fig. 3 A, two prominent regimes of PMN deformation were readily distinguished in the force histories. In the first regime, the force rose linearly in time from t = 0, revealing an initial elastic-like stiffness of k_i ≈ 0.2–0.3 pN/nm for point deformation of the PMN surface. Examined in detail in article I (Evans et al., 2005), this regime terminated abruptly at a (most frequent) force f_⊗ proportional to the logarithm of the initial loading rate r_f [slope Δf/Δt = (k_i k_f) v_pull / (k_i + k_f)] experienced by the attachment, i.e., f_⊗ ≅ (17 pN) ln [r_f / (12–27 pN/s)]. With the PMN still attached to the BFP, the end of the first regime signaled the separation of the membrane from the PMN cytoskeleton and the onset of a second regime that exhibited a Maxwell-like relaxation to an apparent plateau force as seen in Figs. 2 and 3 A. The second regime was accompanied by the growth of a tether and a rapid distancing of the PMN from the probe tip as illustrated schematically in Fig. 3 B. Often reaching lengths of several micrometers, tethers were barely detectable in the optical microscope except for the small funnel-shaped extension of the cell body at the attachment site.

FIGURE 3.

(A) Functional relations and parameters used to model the two regimes of force response observed under constant speed retraction of a PMN from attachment to a P-selectin probe tip. Beginning with an initial elastic-like regime, the PMN attachment force closely follows the solid straight line with a significantly diminished slope (loading rate) relative to the nominal loading rate defined by the BFP spring constant times the pulling speed (dotted line). The reduction in slope is due to the soft response of the PMN cortex. The crossover force f_⊗ marks the event of membrane separation from the cytoskeleton and the onset of viscous tether growth. The force driving tether flow appears to follow an exponential-like transient in time approaching a plateau in force f_∞ (curved solid line). (B) Schematic of tether extrusion and BFP recoil at final detachment. The spring overlay symbolizes the Hookean elastic response of the BFP red cell at small axial deformations. The schematic below shows the corresponding microscale deformation of the PMN structure. The complementary pin and Y-shaped symbols represent the specific P-selectin and PSGL-1 interaction.

Tether extraction and force response under constant pulling speed

Table 1 summarizes the numbers of cells and tethers examined at each pulling speed. Unless prematurely terminated by P-selectin dissociation from PSGL-1, the force response 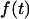during tether growth had the appearance of an exponential-like relaxation that approached a speed-dependent plateau and that could be well matched through a nonlinear fit using the expression (cf. Fig. 3 A),

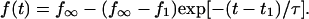(3)

TABLE 1.

Summary of the number of tethers and cells examined at various pulling speeds

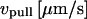	0.4	2	4.5	10	15	16.7	33.3	50	150
Number of tethers	7	107	17	213	99	163	90	407	128
Number of PMNs	4	17	3	15	5	18	5	31	17

An arbitrary starting point in time, t₁, was chosen to obtain the best fit of the exponential to each force transient. In addition to the initial force, 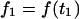, the plateau force 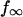and the apparent relaxation time 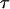were adjustable parameters in the fit. The exponential function in Eq. 3 was found to provide good agreement with the observed transients measured during tether formation at all nine pulling speeds listed in Table 1. As shown by the cumulated fitting results plotted in Fig. 4, A and B, a substantial spread was found in the values of the plateau force and the apparent relaxation time.

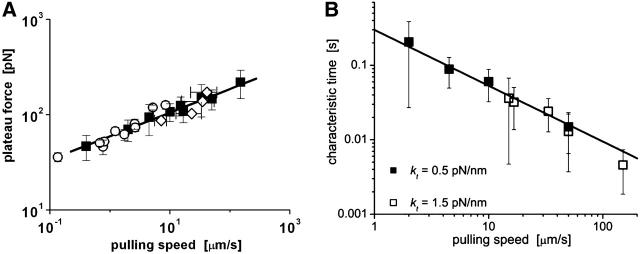
FIGURE 4.

(A) The plateau forces f_∞ (solid squares) obtained from fits to each tethering regime are plotted as functions of PMN retraction speed on a log-log scale. The solid line is a power law fit to the BFP data defined by, f_∞ ≈ 60pN (v_pull/μm/s)^0.25. Open circles are data replotted from Shao and Hochmuth (1996). Open diamonds are data measured previously by Schmidtke and Diamond (2000). (B) Log-log plot of the apparent relaxation times for approach to a plateau in tethering force as function of the tether-pulling speed. The solid line is an inverse power law fit to the BFP data defined by, τ ≈ 0.3 s (μm/s / v_pull)^0.75. (Error bars denote standard deviations.)

Even though approaching a fluid-like plateau f_∞ at long times, the tether force was not a linear function of the pulling speed. Clearly non-Newtonian, the data in Fig. 4 A exhibit a shear-thinning response where the plateau force increases weakly with the extrusion speed,

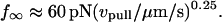(4)

Moreover, the earlier data (Shao and Hochmuth,1996; Schmidtke and Diamond, 2000) are seen in Fig. 4 A to also correlate with this dependence in different ranges of pulling speed. As further evidence for shear thinning, the apparent relaxation time for approach to the plateau force was found to decrease as an inverse power law of the pulling speed as shown in Fig. 4 B.

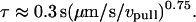(5)

Although examined over nearly three orders of magnitude in tether flow rate, it is important to emphasize that the expressions given in Eqs. 4 and 5 are purely convenient phenomenological parameterizations for pulling speeds >0.4 μm/s. As discussed later in the section on force relaxation at constant tether length, and in the Conclusions, important deviations can arise at a slow pulling speed.

Phenomenological model of tether flow

At first glance, a simple Maxwell-like exponential relaxation seems to be inconsistent with a viscoelastic flow that exhibits a shear-thinning response to pulling speed. However, we will demonstrate that when initiated at a high force, the transient approach to a force plateau can be closely approximated by an exponential relaxation provided that the plateau force and relaxation time possess an appropriate complementary power-law dependence on pulling speed. Generalizing the ansatz defining a Maxwell fluid, we start from the assumption that the tethering force can be described by a velocity- or extension-rate-dependent function, i.e., 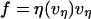, where the viscous damping coefficient 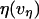is not constant, but instead is assumed to obey an inverse power-law dependence on the extension rate 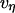, i.e., 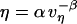. Next, this viscous component is coupled in series to a linear elastic element that includes the tether material, the force transducer, and other possible elastic contributions. The instantaneous extension x_e of the elastic component is proportional to force, x_e = (1/k_e) f, where k_e is the effective stiffness of all the serial elastic contributions. The total rate of extension for the combined elements is defined by, v_η + dx_e/dt, or in terms of the force and its time derivative, by (f/α)^1/(1-β) + (1/k_e) df/dt. Thus, under conditions of constant pulling speed, the rate of extension, v_pull = v_η + dx_e/dt, leads to a nonlinear first-order differential equation that predicts the force history,

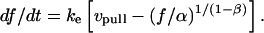(6)

Equation 6 approaches a stationary limit at long times, 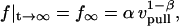that can be made consistent with the speed dependence found for the plateau force (cf. Fig. 4 A and Eq. 4) using the values of 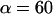pN (s/μm)^0.25 and 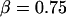in the shear-thinning expression for viscous damping 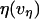. In addition, the first-order expansion of Eq. 6 local to the plateau force follows a terminal exponential relaxation characterized by the time constant, 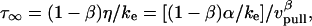that exhibits the appropriate inverse power-law dependence on pulling speed and exponent 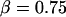seen in Fig. 4 B and Eq. 5. Further comparison of this linearized approximation to the empirical result in Eq. 5 yields a value of ∼0.3 s (μm/s)^0.75 for the prefactor 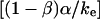. Thus, with the value of 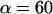pN (s/μm)^0.25 implied by the plateau-force data in Fig. 4 A, the terminal relaxation indicates that the serial elastic coefficient should be of order, k_e ∼ 0.05 pN/nm.

Clearly, the most critical check for consistency of this nonlinear Maxwell model with the experiment is to show that the model matches the diversity of tether-force transients observed in experiments, beginning from random forces f_⊗ above or below the apparent plateau f_∞, and depending only on the pulling speed. Using the values of 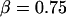and 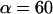pN (s/μm)^0.25, we found that numerical solutions computed with Eq. 6 closely matched the tether transients at all pulling speeds for a single value of effective elastic coefficient 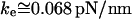. Most important, and demonstrated in Fig. 5, the solutions computed for the tether relaxation using Eq. 6 approached the plateau force from above or below—set only by the initial force f_⊗ for membrane separation from the cytoskeleton and by the pulling speed. Moreover, as shown in Fig. 5, the exponential approximation in Eq. 3, combined with Eqs. 4 and 5, closely follows the direct numerical solutions using Eq. 6.

FIGURE 5.

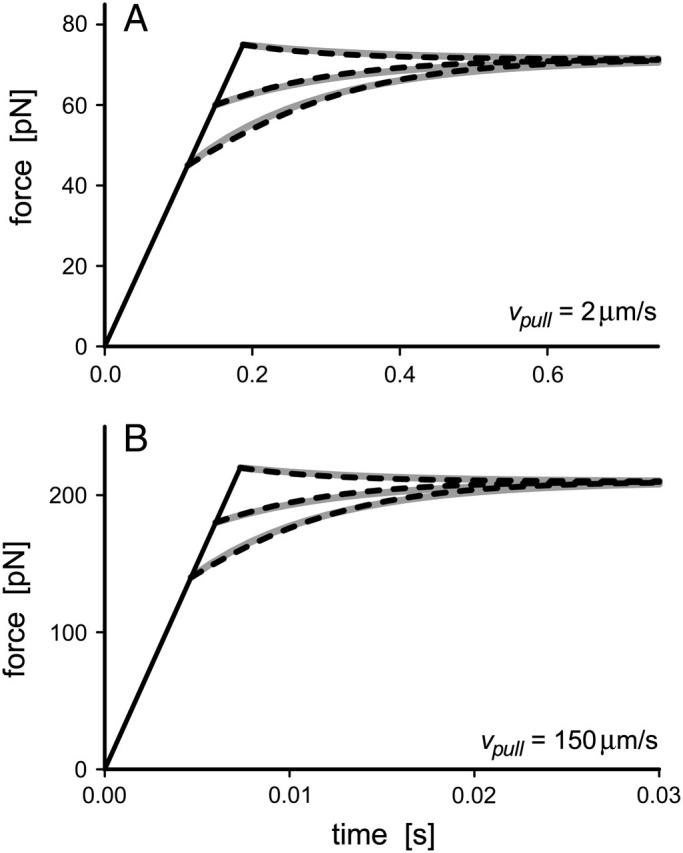
Comparison of the numerical solutions for the nonlinear Maxwell model (Eq. 6; dashed curves) to the exponential approximations (Eq. 3; gray solid curves) used to fit tether-force transients at constant pulling speeds of 2 μm/s in panel A and 150 μm/s in panel B.

Thus, beginning at the loading rate-dependent force 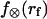for membrane separation from the cytoskeleton, the tether force transient under constant speed retraction was found to agree well with the nonlinear Maxwell flow modeled by Eq. 6. Consistent with the measurements of plateau forces summarized in Fig. 4 A, the viscous flow element in the model is characterized by a very strong power-law dependence on tether pulling force, 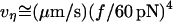; and a soft elastic extension, 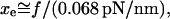seems to account for the apparent relaxation times summarized in Fig. 4 B.

Termination of attachments by P-selectin:PSGL-1 dissociation

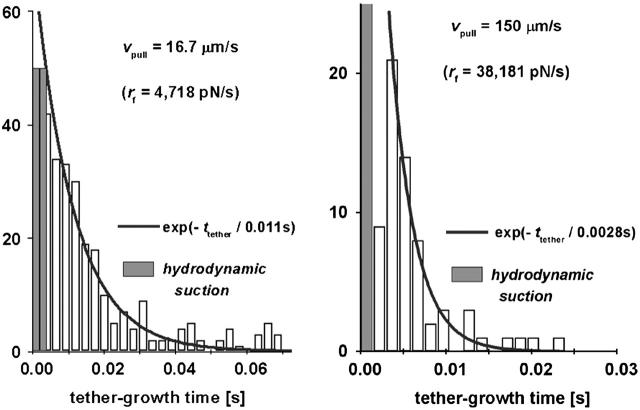
Excluding tests that exhibited obvious features of multiple sites of attachment (see Appendix), the growth times (t_tether) of tethers were collected into histograms at all pulling speeds to characterize the statistics of final PMN detachment. The examples in Fig. 6 demonstrate that the distributions of tether-growth times exhibited an exponential-like decay consistent with the Bell (1978) model for dissociation of an ideal bond held at constant force. Based on the assumption that PSGL-1 remained embedded in the membrane, we hypothesized that the exponential decay in tether-growth times should correlate with the rate of P-selectin dissociation from PSGL-1 under force, which we had quantified in a separate study using P-selectin and PSGL-1 immobilized on glass microspheres (Evans et al., 2004). However, in contrast to the precise loading of bonds in the probe tests using microspheres, the steady-speed retraction of PMNs with soft material properties applied a varied history of force loading to cell attachments. As shown by the typical force response in Fig. 3 A, pulling a PMN from the BFP tip began with a steady ramp of force ending at the level f_⊗ after which, the force changed little throughout the tether growth phase, approaching a plateau in force from above or below as illustrated in Fig. 5. The simplest generic approximation to this tether force history is a force that increases with a steady ramp r_f = Δf/Δt up to the time t_⊗ = f_⊗/r_f expected for membrane separation from the cytoskeleton, then remains essentially constant until P-selectin dissociates from PSGL-1. Thus, the estimate for tether-growth time is the most frequent time t_bond(f_⊗) for dissociation of P-selectin from PSGL-1 at the force f_⊗. With f_⊗ defined by the logarithmic dependence on the loading rate r_f described in article I, both the tether growth time, t_tether ≈ t_bond(f_⊗), and the total time of attachment, t_attach ≈ t_⊗ + t_bond(f_⊗), can be predicted from the elastic loading rate at a particular pulling speed.

FIGURE 6.

Histograms of tether growth times for two fast pulling speeds. The solid curves are exponentials that best match the data. The time constants listed on each figure are consistent with the dissociation of a monomeric P-selectin bond to PSGL-1 when held at the most frequent force found for membrane separation from the cytoskeleton. (The shaded bins represent the range of observations obscured by nonspecific forces arising from hydrodynamic coupling between the probe tip and the cell surface at fast pulling speeds, discussed in the Materials and Methods section of article I.)

Ignoring the slowest tests performed at v_pull ∼ 0.4 μm/s where almost no tethers were observed, we analyzed the total times of attachment for retraction speeds >2 μm/s, which nearly always produced a period of tether growth. Including the ramp time and the tether-growth time, the total times for attachments to PMNs are plotted in Fig. 7 as functions of the loading rates applied during the initial elastic regime. The loading rates, r_f > 240 pN/s, for these data correspond to the loading conditions in bead-bead tests (Evans et al., 2004) where the lifetimes of P-selectin:PSGL-1 bonds were found to decrease as a single exponential of force as given by, t_bond (f) ≈ 3 s exp(−f / 18 pN)]. Hence, if held by a single P-selectin bond at a force equal to the membrane separation force f_⊗, the tether-growth time is predicted to diminish essentially as the inverse of the loading rate, t_bond (f_⊗) ≈ 31–68 s (pN/s / r_f)^17/18, which agrees well with the exponential decay times shown by the particular cases in Fig. 6. However, examining the total times for survival of all PMN attachments, the results seem to correlate best with the random dissociation of two monomeric P-selectin:PSGL-1 interactions as shown in Fig. 7, and defined by ∼1.5 t_bond (f_⊗). The nearly twofold larger lifetime suggests that the Fc P-selectin chimera used in most tests formed an uncorrelated dimeric attachment to a PSGL-1 homodimer on PMN surfaces.

FIGURE 7.

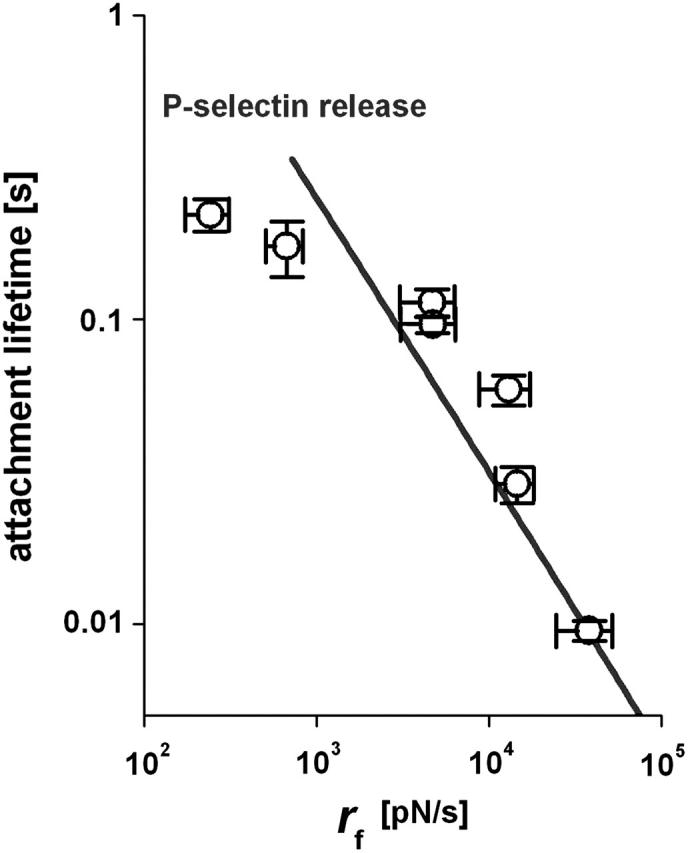
The mean values measured for the lifetimes of all attachments are plotted as a function of the initial elastic loading rates produced by retraction of the PMNs at pulling speeds >1 μm/s. The solid curve shows the attachment lifetime expected for an uncorrelated dimeric P-selectin connection to PSGL-1. (Error bars denote means ± SE.)

Absence of tethers at slow pulling speeds and the onset of tether growth at fast speeds

Very few attachments were detected at the slowest pulling speed v_pull of 0.4 μm/s, equivalent to an initial loading rate r_f of only 45 pN/s, and those attachments seemed to nearly always (92%) fail without evidence of tether formation. By comparison, both the attachment frequency and the frequency of tether formation increased significantly at a pulling speed of 2 μm/s, corresponding to an initial loading rate of ∼242 pN/s. Thus, at the slowest rate, P-selectin bonds to PMNs appeared to dissociate rapidly at forces below the level required for membrane separation from the PMN cytoskeleton. The absence of tethers and premature dissociation of P-selectin from PMNs are consistent with recent observations demonstrating very fast P-selectin dissociation from PSGL-1 under very slow loading when immobilized on glass beads (Evans et al., 2004). First discovered using a combination of flow-chamber and atomic force microscope experiments, the lifetimes of PSGL-1:P-selectin attachments have been observed to actually increase with initial application of small forces, and then to decrease at higher forces (Marshall et al., 2003). This behavior has been labeled a “catch-slip bond”, following a phenomenological model proposed by Dembo et al. (1988).

By probing bonds between PSGL-1 and P-selectin on microspheres with a new method of force spectroscopy, we were able to establish that this “catch-slip bond” behavior actually stems from a switch between one P-selectin:PSGL-1 dissociation pathway to another dissociation pathway near a loading rate of r_f ∼ 300 pN/s. Shown by the jump from open to solid triangles in Fig. 8 (data from Evans et al., 2004), the switch between dissociation pathways at this loading rate produces a sudden transition in the most frequent forces for rupture of P-selectin:PSGL-1 bonds. Adding the most frequent forces for membrane separation from the PMN cytoskeleton to Fig. 8 (circles; taken from our article I), a striking hierarchy appears at fast loading rates with the force level for the kinetically limited failure of the P-selectin:PSGL-1 bond always exceeding the force level for membrane separation from the cytoskeleton. This hierarchy clearly illustrates how the two failure events act sequentially to first trigger and then terminate tether growth.

FIGURE 8.

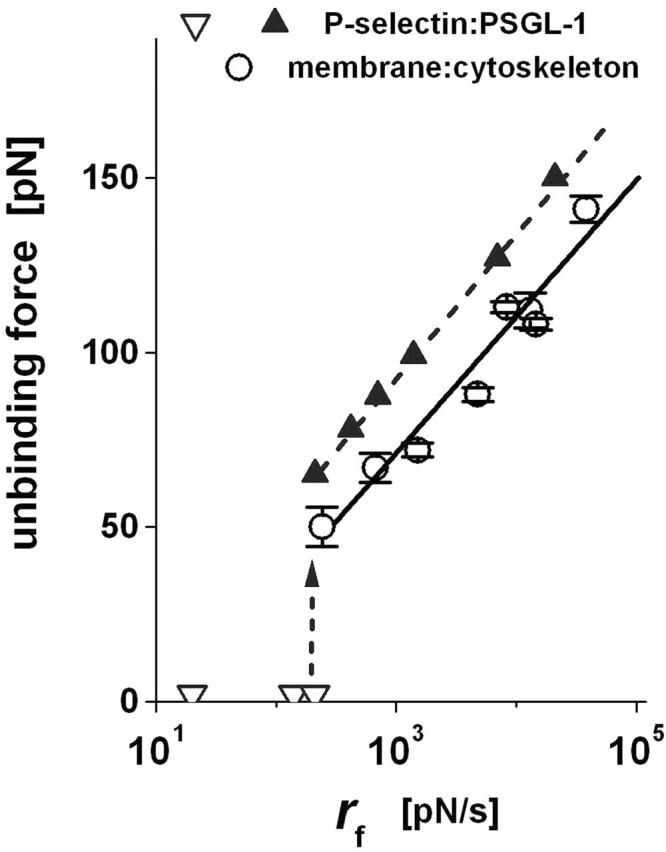
The most frequent forces for breaking P-selectin:PSGL-1 bonds measured in tests with the molecules immobilized on glass beads (solid triangles; data taken from Evans et al., 2004) are compared to the most frequent forces for membrane unbinding from the PMN cytoskeleton as described in article I (open circles; Evans et al., 2005). The parallel hierarchy of these failure events at fast loading rates accounts for the correlation between the onset of tether formation and subsequent termination by P-selectin dissociation. (Error bars denote means ± SE, which lie within the data symbols for the bead-bead tests.)

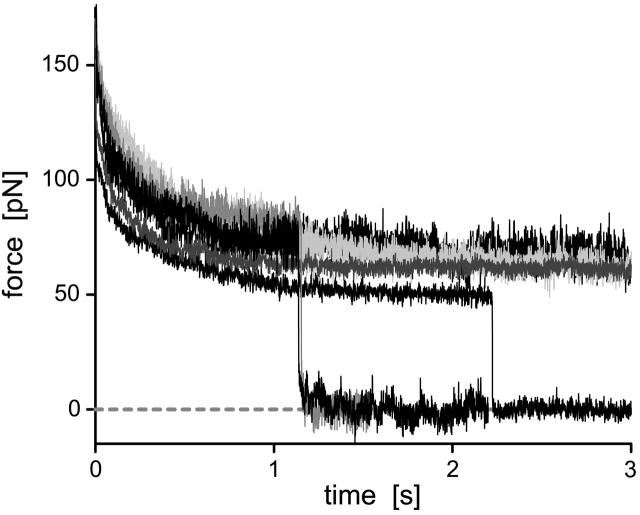
Tether-force relaxation at constant length

Very rarely, a PMN tether was observed to remain attached to the BFP tip at the end of the piezo cycle. With the PMN-holding pipette stationary at this point, the force relaxed to levels ranging between 50 and 100 pN as illustrated by the examples in Fig. 9. Although clearly requiring several P-selectin:PSGL-1 bonds to sustain these persistent attachments, the force relaxation was found to be consistent for the most part with the same shear-thinning behavior exhibited by the tether-force transient produced under constant pulling speed. The analytical expression predicting the force relaxation at constant length follows from integration of Eq. 6, beginning from a force f(0) at t = 0 and setting v_pull = 0:

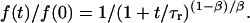(7)

FIGURE 9.

Examples of force relaxation for six tethers held at constant lengths. The long survival of these tethers at high forces implies that the attachments were sustained by many P-selectin bonds.

The integration results in a characteristic timescale for relaxation at constant length, 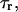defined by an expression,

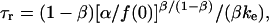(8)

which is slightly different from the relaxation time for the terminal-exponential approach to a plateau force under constant pulling speed.

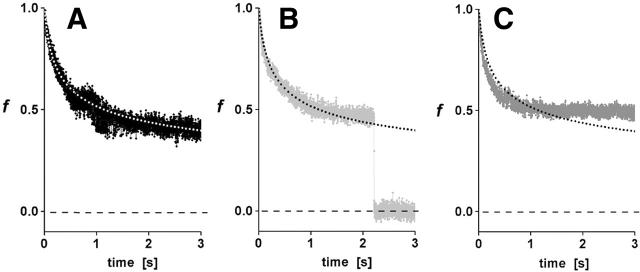
Using the values of α and k_e derived from analysis of the transient approaches to plateau forces under constant pulling speed, the shear-thinning model was found to best match the force relaxation given a slightly larger exponent, β = 0.8, as demonstrated by comparison to specific examples in Fig. 10, A–C. However, at long times, it seems clear that some other process takes over and arrests the flow (cf. Fig. 10 C), preventing the continued relaxation to zero force as predicted by the Maxwell-like model. Still, the simple model is able to capture the relaxation at constant length over a very large time frame (≥1 s), equivalent to 100-fold decrease in the internal viscous flow implied by the model. From the viewpoint of mechanics, the final stationary tether force is related to the magnitude of axial tension in the tether membrane and the tether diameter, the diameter being stabilized by compressional rigidity of the cytoplasmic lumen and the membrane bending rigidity. The usual view is that only membrane bending rigidity acts to stabilize the cylinder as for a pure lipid bilayer. However, we found that this type of stationary threshold based on a bilayer-stabilized tether (unless very small) could not be made compatible with the observed tether-force approach to a speed-dependent plateau and the time course of relaxation at constant tether length. Thus, it seems possible that actin or other stiff structures lining the lumen may act to strongly resist compression, leading to larger tether diameters and bigger pulling forces than expected from vesicle membrane mechanics.

FIGURE 10.

As representative examples from the data in Fig. 9, three force relaxations at constant length are plotted on a normalized scale and compared with the prediction in Eq. 7 (dotted curves) based on the nonlinear Maxwell model. Although the model predicts that the tether force should go to zero at zero pulling speed, some other process appears to take over and arrest flow at long times. Still, the simple model is able to capture the force relaxation at constant length over a very large time frame (≥1 s), equivalent to 100-fold decrease in the internal viscous flow implied by the model.

CONCLUSIONS

Taken together with article I, we have quantified the nano- to microscale dynamics associated with detachment of P-selectin from PSGL-1 on a PMN surface. We have shown that the detachment process is characterized by a well-defined sequence of regimes beginning with elastic-like deformation of the cell, abrupt onset of tether formation triggered by membrane separation from the cytoskeleton, and ending with P-selectin dissociation from PSGL-1. The attachment to a PMN and the formation of a tether became routine events only at pulling speeds producing initial loading rates ≥240 pN/s, in close agreement with the recently discovered “catch-bond”-like switch from a fast-to-slow pathway for P-selectin:PSGL-1 dissociation (Marshall et al., 2003; Evans et al., 2004). Focusing in this article on the rheology of tether growth, we have demonstrated that the tether forces exhibit a shear-thinning response to pulling speed over the range from 0.4 to 150 μm/s. Although examined over different segments of this range in pulling speed, the earlier results for pulling tethers from PMNs using monoclonal antibody attachments (Shao and Hochmuth, 1996; Shao et al., 1998; Marcus and Hochmuth, 2002) and the results for tethers pulled from PMNs under flow while attached to spread platelets (Schmidtke and Diamond, 2000) are also consistent with the shear-thinning behavior found here. Combining the kinetic parameters obtained for membrane separation from of the cytoskeleton and for dissociation of the P-selectin:PSGL-1 bond under force with the shear-thinning properties describing tether growth, our collaborators have performed detailed numerical simulations of cell rolling and transient tethering to walls in a flow chamber (King et al., 2005). The results of their simulations support the conclusion that mixtures of single and double adhesion bonds are sufficient to account for the experimental dependence of the rolling speeds on shear rates measured in recent studies of leukocyte rolling on P-selectin substrates (Park et al., 2002).

Although we find that the approach to a speed-dependent plateau force correlates well with a nonlinear Maxwell fluid model, tethers still seem capable of sustaining force if held at constant length for long times. In many tests of tether extrusion from cells, extrapolations to an apparent force threshold have been treated as determined by the membrane bending stiffness and lateral tension in the cell plasma membrane, equivalent to the elastic behavior of lipid bilayer vesicles (Božič et al., 1992; Evans and Yeung, 1994; Heinrich and Waugh, 1996). On the other hand, when exceeding this lipid bilayer estimate, the threshold force is sometimes assumed to involve the membrane tension augmented by an energy of adhesion per area of contact with the cytoskeleton (Hochmuth et al., 1996; Hwang and Waugh, 1997). However, intrigued by the similarity of our results and the power-law viscous behavior found many years ago in viscometric tests of F-actin solutions (Stossel, 1984; Janmey et al., 1988), we speculate that there could be an alternative explanation for a persistent tether force at constant length. This explanation is analogous to a conclusion stated by Janmey et al. (1994) in regard to the inverse power-law dependence of viscosity observed for F-actin solutions. Quoting from their article, the shear-thinning behavior was attributed to a “critical disruption of some complex structure within the solution characteristic of an indeterminate fluid. The … disruption during such flow is likely to be the breaking of individual filaments and their ordering into bundles or filaments aligned with the flow field ….” Hence, it could be that the weak increase in tether force with faster pulling speed and the apparent relaxation to a force threshold when pulling has stopped may be consequences of breaking and reforming protein bonds within the F-actin cytoskeleton. Yet, we agree with a comment of one reviewer that “it is not clear whether the cytoskeleton makes this contribution through its interaction with the membrane or through … bonds within” its structure.

APPENDIX: MULTIPLE-POINT ATTACHMENTS

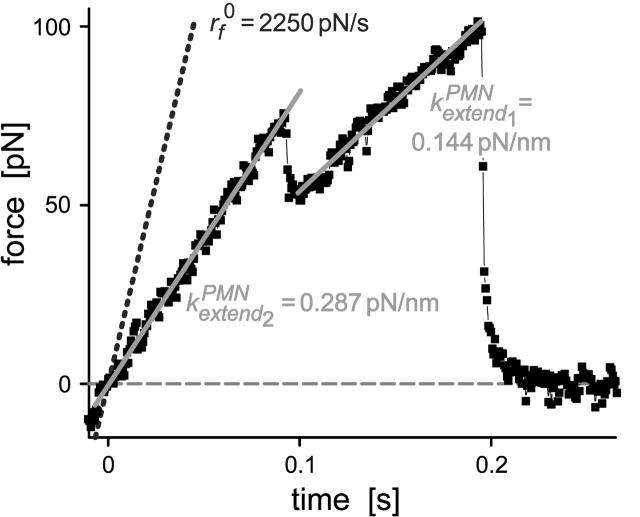
The P-selectin density on the probe tip and the PMN touching force were adjusted to produce one to two PMN attachments per three touches to the probe tip. Although this is a much higher attachment frequency than normally used in testing single bonds between microspheres, the approach enabled us to minimize the period of time a PMN was held in the pipette while providing many tests of attachments to the same cell. Therefore, we were not surprised to find that a small number of PMN contacts to the probe exhibited obvious features of multiple-point attachments. Some of the multiple attachments were revealed by a split of the initial elastic response into a hierarchy of linear regimes with different slopes (cf. Fig. A1), connected by a precipitous drop in force from higher-to-lower slope regimes. Other types of multiple attachments were identified by the appearance of quantized reductions in force before final detachment, implying that the cell was connected to the probe tip by a parallel set of tethers (cf. Fig. A2).

FIGURE A1.

Example of a parallel elastic deformation of the PMN surface that appears to arise from pulling at separate sites of attachment. The linear fits (solid lines) to the hierarchy of elastic regimes start at the origin, indicating that the deformation fields local to each bond were independent. In this case, the two elastic regimes are found to differ by a factor of two in stiffness. The nominal loading ramp 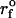was set by a BFP spring constant of 0.5 pN/nm and pulling speed of 4.5 μm/s (dotted line).

FIGURE A2.

Example of a sequential detachment of two parallel tethers pulled from a PMN surface. The force levels appear to be quantized values of the average plateau force (<f_∞> ≈ 108.5 pN) expected for pulling a single tether at this speed (16.7 μm/s). The tether length immediately before each failure is noted on the figure. The nominal loading ramp 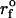was set by a BFP spring constant of 1.5 pN/nm and the pulling speed (dotted line).

The multiple-point attachment that showed a hierarchy of two initial elastic regimes (cf. Fig. A1) most likely revealed the sequential dissociation of two P-selectin bonds at widely separated sites where the second dissociation resulted in complete detachment. Interestingly, the sequence of a stiff elastic regime followed by a softer regime indicates that the deformation field local to each bond was essentially independent of the other—acting like parallel springs. In the second case (cf. Fig. A2), the multiple-point attachment showed two nearly equal reductions in force, the last coincident with complete detachment. This response was most likely due to the presence of two parallel tethers. Adding support to the rheological model of a speed-dependent tether force, pulling the two putative tethers essentially produced a twofold greater force than for a single tether and resulted in detachment through quantized reductions of force.