Ligand Accumulation in Autocrine Cell Cultures

Abstract

Cell-culture assays are routinely used to analyze autocrine signaling systems, but quantitative experiments are rarely possible. To enable the quantitative design and analysis of experiments with autocrine cells, we develop a biophysical theory of ligand accumulation in cell-culture assays. Our theory predicts the ligand concentration as a function of time and measurable parameters of autocrine cells and cell-culture experiments. The key step of our analysis is the derivation of the survival probability of a single ligand released from the surface of an autocrine cell. An expression for this probability is derived using the boundary homogenization approach and tested by stochastic simulations. We use this expression in the integral balance equations, from which we find the Laplace transform of the ligand concentration. We demonstrate how the theory works by analyzing the autocrine epidermal growth factor receptor system and discuss the extension of our methods to other experiments with cultured autocrine cells.

INTRODUCTION

For any cellular system in which functional responses are at least partially governed by receptor-mediated signals, proper understanding of signal-response relationships requires that the investigator to quantify dynamic properties of receptor activation by ligand binding. Traditionally, for cells responding to exogenous soluble ligands such as cytokines and growth factors, this has been accomplished by a combination of quantitative experiment and mathematical modeling of essential ligand/receptor binding and endocytic trafficking processes, using ligand-labeling techniques (e.g., see Lauffenburger and Linderman, 1993). An analogous capability is desired for cellular systems involving endogenous cytokines or growth factor operating in autocrine and/or paracrine fashion, but the experiment and modeling approach is not nearly as straightforward due to the challenges in labeling self-produced ligands. Nonetheless, it remains very important for an experimental cell biologist to be able to estimate key system properties (characterized by model parameters; see Table 1) from a conveniently accessible set of experiments without labeled ligands.

TABLE 1.

Parameters of the model

Parameter	Description	Value	Reference
D	Ligand diffusivity	10−6 cm2 s−1	Lauffenburger and Linderman (1993)
h	Height of the extracellular medium	0.2 cm	This article
ke	Complex internalization rate constant	0.28 min−1	Hendriks et al. (2003b)
kon	Forward binding rate constant	∼108 M−1 min−1	Hendriks et al. (2003b)
koff	Complex dissociation rate constant	0.24 min−1	Hendriks et al. (2003b)
Q	Ligand release rate per cell	800 mol × min−1 cell−1 = 2.21 × 10−23 mol × s−1 cell−1	This article
R0	Number of receptors per cell	1 × 105 receptors × cell−1	This article
rcell	Radius of the cell	0.0025 cm	This article

Low levels of autocrine signals prevent direct measurement of their concentrations and require a theory that can relate these concentrations to measurable parameters of the assay (DeWitt et al., 2001; Wiley et al., 2003). Here we develop such a theory. The key quantity of our analysis is the survival probability of a single secreted ligand, i.e., the probability that the ligand has not been recaptured for time t after its release from the cell surface. Using the boundary homogenization approach, we derive an approximate expression for this probability and use it to find the Laplace transform of ligand concentration as a function of time.

We analyze the kinetics of ligand accumulation in the medium covering autocrine cells that occupy a fraction σ of the cell-culture dish as shown in Fig. 1. The cells release ligands with a rate Q(t) and express a constant level of receptors, R₀, that bind the ligands with the forward binding constant k_on; bound ligands dissociate with the rate constant k_off and are internalized with the rate constant k_e. All of these parameters can be measured experimentally. For example, ligand secretion is assayed by blocking ligand capture with anti-receptor antibodies (DeWitt et al., 2001; Dong and Wiley, 1999; Oehrtman et al., 1998; Wiley et al., 2003).

FIGURE 1.

Schematic representation of a cell-culture assay: a random dispersion of cells on the bottom of the cell-culture dish is covered by a layer of liquid medium. A released ligand can be captured by the cell surface receptors on the parent cell (autocrine trajectory) or on its neighbors (paracrine trajectory). Cells are modeled by disklike traps of radius r_cell.

All previous approaches to quantitative analyses of autocrine loops have been based either on a single-cell approximation (Goldstein and Dembo, 1995; Shvartsman et al., 2002) or, alternatively, relied on compartmental models (DeWitt et al., 2001, 2002; Forsten and Lauffenburger 1992a,b, 1994; Lauffenburger et al., 1998; Oehrtman et al., 1998). Clearly, single-cell approximation cannot take into account the effects of cell density. At the same time, compartmental models used ad hoc descriptions for ligand transport in the medium, and relied on arbitrary decomposition of the liquid medium by a series of stirred compartments. The validity of these approximations has never been tested due to the computational difficulties associated with the analysis of the full problem with randomly placed autocrine cells. The homogenization-based biophysical framework presented in this article goes beyond single-cell and compartmental approximations and is computationally efficient. It enables direct prediction of the operation of autocrine loops in cell-culture assays, based on the measurable parameters of autocrine systems.

Model formulation

We model the cell culture by a random two-dimensional dispersion of non-overlapping disks with the surface trapping rate κ_cell that is simply related to the ligand-receptor binding constant, receptor expression level, and cell area A: κ_cell = k_on R₀/(N_Av A), where N_Av is the Avogadro's number (Lauffenburger and Linderman, 1993). The disks are placed on the reflective surface that models the bottom of the cell-culture dish, Fig. 1. Ligands are modeled by point Brownian particles that are released from the cell surfaces into the medium layer of height h where they move with a constant diffusivity D. We consider the situation when a layer of fresh medium is added to autocrine cells that secrete, bind, and internalize ligands (DeWitt et al., 2001, 2002; Dong et al., 1999; Dong and Wiley, 1999). We assume that autocrine loops operate in a ligand-limited regime, where receptors are in excess and their level is not significantly affected by ligand binding and internalization. This assumption is experimentally justified, at least for a variety of cell lines with epidermal-growth-factor receptor (EGFR) autocrine loops (DeWitt et al., 2001; Oehrtman et al., 1998; Wiley et al., 1998).

The problem of finding the kinetics of ligand accumulation is intractable analytically even in the ligand-limited regime because of the heterogeneous and random boundary condition on the surface of the dish,

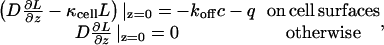(1)

where L(x,y,z,t) is the ligand concentration, c(t) = C(t)/A is the density of ligand-receptor complexes on the surface of the cell containing C(t) complexes, and q(t) = Q(t)/A is the flux density of ligands secreted by the cell. This article shows how to handle this complex boundary condition and derive an expression for the ligand concentration as a function of time.

We define the ligand concentration as the ratio of the total amount of the ligand in the medium layer to the medium volume. The concentration accumulated in the medium (averaged over the height of the liquid layer) by time t, L(t), is given by

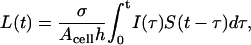(2)

where I(t) is the ligand release rate per cell and S(t) denotes the ligand survival probability which is the probability that a ligand released from the cell surface has not been recaptured for time t. The ligand source I(t) is a sum of two terms, which describe ligand secretion and dissociation of ligand-receptor complexes:

(3)

The balance equation for the cell surface ligand-receptor complexes accounts for binding of ligands released at all times <t, and for the decrease in the number of complexes due to the dissociation and endocytosis:

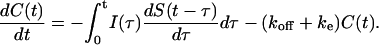(4)

This equation is complemented by the initial condition C(0) = 0, which corresponds to the typical situation where autocrine cells are covered by fresh medium and the previously accumulated cell surface ligand is stripped from the cells (DeWitt et al., 2001, 2002; Dong et al., 1999; Dong and Wiley, 1999).

Solving Eqs. 2 and 4 by the Laplace transform method, we find that the Laplace transform of the ligand concentration is given by

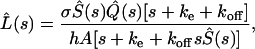(5)

where 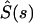and are the Laplace transforms of the ligand survival probability and of the ligand secretion rate, respectively.

Ligand survival probability

To finish the derivation, we have to find the ligand survival probability. Below, we derive an approximate expression for the Laplace transform of S(t). This expression is extremely accurate, as shown by comparison with the results of Brownian dynamics simulations.

Ligands released from the cell surface can be separated into two groups depending on whether they are recaptured by the same cell or by other cells. The former and latter are termed autocrine and paracrine ligands, respectively. The autocrine fraction of the ligands, P_au, is given by

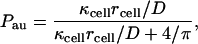(6)

where r_cell is the cell radius (Batsilas et al., 2003).

As we have shown before, using Brownian dynamics simulations, trajectories of autocrine ligands are localized near the cell surface (Batsilas et al., 2003). Therefore, one can derive the Laplace transform of the survival probability of autocrine ligands, S_au(t), by solving the one-dimensional problem discussed in the Appendix with κ = κ_cell. The expression for the Laplace transform is given in Eq. A10.

To find the survival probability of paracrine ligands, S_para(t), we homogenize the non-uniform boundary condition on the dish surface (Fig. 2). The non-uniform boundary condition can be replaced by a uniform boundary condition with the effective trapping rate, κ_eff, given by

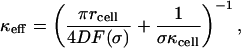(7)

where F(σ) is the dimensionless function of the cell-surface fraction σ of the form F(σ) = σ(1 + 3.8σ^1.25)/(1−σ): F(σ) ≈ σ when σ → 0 and diverges as σ → 1 (Berezhkovskii et al., 2004a,b). After the boundary homogenization, the Laplace transform of S_para(t) again can be found by using Eq. A10 from the Appendix, in which now we take κ = κ_eff.

FIGURE 2.

Schematic representation of the boundary homogenization procedure. The original cell-culture system is approximated by a much simpler one: a ligand-source cell with the surface trapping rate κ_cell is located on a uniformly absorbing plane with the effective trapping rate κ_eff. The ligand survival probability can be considered as a sum of two terms: Trajectories that eventually end up on the parent cell contribute to the first term, whereas all other trajectories contribute to the second term.

Keeping in mind that a ligand can be recaptured by either the parent cell (with probability P_au) or by other cells (with probability (1–P_au)), we write the survival probability as

(8)

To check this formula we performed extensive Brownian dynamics simulations using the previously described adaptive time-step algorithm (Batsilas et al., 2003). We found excellent agreement between the ligand survival probability predicted by Eq. 8 and the simulation results (see Fig. 3 for a representative example of analysis over a wide range of cell and receptor densities).

FIGURE 3.

Comparison of the ligand survival probabilities found in the Brownian dynamics simulations (dashed curves) and predicted by the analytical solution in Eq. 8 (solid curves). The calculations were done for the three values of R₀ and different values of cell density σ of 0.05, 0.25, and 0.4. The parameters of the upper panel correspond to κ_cell = 9.69 × 10⁻⁵ cm × s⁻¹, the middle one to κ_cell = 1.09 × 10⁻³ cm × s⁻¹, and the lower one to κ_cell = 5.02 × 10⁻³ cm × s⁻¹. The rest of the parameters are k_on = 10⁸ M⁻¹ min⁻¹, r_cell = 0.001 cm, h = 0.3 cm, and D = 10⁻⁶ cm² × s⁻¹.

Substituting the Laplace transform of S(t) in Eq. 8 into Eq. 5 we arrive at our final expression for the Laplace transform of the ligand concentration, which is the main result of this note.

Reduction to compartmental models

In addition to its utility in the data analysis and prediction of the experimentally inaccessible capture probabilities and statistical properties of ligand trajectories, our theory enables the systematic derivation of compartmental (ODE-based) models of autocrine systems. In a compartmental model, it is assumed that the survival probability of a ligand is a single-exponential function of time as

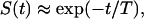(9)

where T is the average lifetime of a free secreted ligand that can be found using S(t) given in Eq. 8,

(10)

This relation together with those in Eqs. 6 and 7 allows one to find time T as a function of measurable parameters of the cells and the assay. For example, when most of the ligand is trapped outside the parent cell (P_au ≪ 1), S(t) ≈ exp(−tσκ_cell/h).

When S(t) is single-exponential, the integral evolution equation for the ligand concentration in Eq. 2 can be replaced by a differential equation as

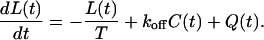(11)

In addition, the integro-differential balance equation for the number of ligand-receptor complexes given in Eq. 4 also simplifies and takes the form

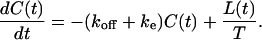(12)

Moreover, in the case of single-exponential S(t), the Laplace transform in Eq. 5 can be inverted analytically.

Reduction to compartmental models converts the set of integro-differential equations for ligands and complexes into a system of ODEs, which is similar to that in the previously published compartmental models of autocrine loops (Forsten and Lauffenburger, 1992b; Oehrtman et al., 1998). Notice that our modeling framework enables the systematic assessment of the accuracy of such an approximation by comparison with the results of direct Brownian dynamics simulations and more precise description given by the expression in Eq. 8. For the molecular and cellular parameters of autocrine EGFR systems, we found that the single-exponential survival probability consistently overestimates the true survival probability at short time and underestimates at long times (see Fig. 4). In general, compartmental models based on the monoexponential approximation for ligand survival probability will be accurate for thin medium layer and slow ligand binding.

FIGURE 4.

Comparison of the single-exponential approximation of the survival probability given in Eq. 10 with the time-dependence of S(t) predicted by Eq. 8 for three values of R₀. Other parameters are σ = 0.4, k_on = 10⁸ M⁻¹ min⁻¹, r_cell = 0.001 cm, h = 0.3 cm, and D = 10⁻⁶ cm² × s⁻¹.

Analysis of experiments

To illustrate our theory, we apply it to experiments with cultured autocrine human mammary epithelial cells (HMECs) (Hendriks et al., 2003b). HMECs, expressing ∼100,000 EGF receptors/cell and secreting ∼800 molecules of EGF/min, were plated with the density of ∼100,000 cells per well with the area of 10 cm² and covered by 2 ml of liquid medium. The ligand concentration in the medium was assayed by ELISA as described previously (DeWitt et al., 2001, 2002). In terms of our model, these parameters of the assay translate into the cell coverage σ = 0.196 (based on the average HMEC radius of ∼25 μm) and the medium height h = 0.2 cm. Given these parameters and ligand diffusivity of D = 10⁻⁶ cm²/s, we determined the molecular and cellular parameters of the HMEC autocrine loops that are consistent with the experimental data. Specifically, we used the numerical inversion of Laplace transform in the Eq. 5 for the evolution of ligand concentration, supplied with the expression for ligand survival probability given by Eqs. 8 and A10, to determine the values of k_on, k_off, and k_e, consistent with the experimentally measured time-course of ligand accumulation in the medium.

Note that the computational analysis of this problem is possible only as a result of the homogenization-based multiscale model described above. This allowed us to perform a global analysis of the goodness of fit in the three-dimensional parameter space (k_on, k_off, k_e). The three-dimensional cube in the parameter space was defined based on the experimentally available ranges for the molecular and cellular parameters for the EGFR/EGF system (DeWitt et al., 2001, 2002; Hendriks et al., 2003b). An example of this calculation is shown in Fig. 5 (for presentation purposes, we show only the two-dimensional cut through the sampled three-dimensional parameter space). The shaded area in the (k_on, k_off) space, for the experimentally determined value of k_e = 0.28 min⁻¹ (Hendriks et al., 2003a,b,c) and R₀ = 10⁵ receptors/cell, denotes the domain of parameters where maximal relative error between the model prediction and experiments is <50%. We then determined whether the values of k_on and k_off, independently measured for this system (Hendriks et al., 2003b), are within the range of parameters consistent with data. As a result, we have found that the smallest k_on, consistent with R₀ = 10⁵ receptors/cell, k_off = 0.24, and k_e = 0.28, exceeds the previously measured value of k_on ∼ 10⁸ M⁻¹ min⁻¹ by a factor of 5–8, depending on the assumed value of the relative error (see Fig. 5). Given the large experimental error associated with determination of the cellular and molecular parameters of autocrine systems this discrepancy is acceptable.

FIGURE 5.

(a) Diagram showing the area on the (k_on, k_off)-plane where the relative error between the model prediction and experimental measurements is <50%. The relative error is defined as e = max|(L_exp(t_i) − L_comp(t_i))/L_exp(t_i)|, where i stands for the measurement number. (b) Comparison between the experimentally measured concentration of EGF and L(t) computed at fixed values of k_e = 0.28 min⁻¹, k_off = 0.24 min⁻¹, and k_on = 8.6 × 10⁸ M⁻¹ min⁻¹ corresponding to the relative error e = 15%. Average ligand concentration measurements are shown by open symbols with the error bars representing the standard deviation from duplicate samples. The computation results are shown by solid and dashed curves. Parameters of the cell-culture assay are h = 0.2 cm, N_cells = 10⁵ cells/well, r_cell = 0.0025 cm, σ = 0.196, R₀ = 10⁵ receptors/cell, Q = 800 mol × min⁻¹ × cell⁻¹, and D = 10⁻⁶ cm² × s⁻¹.

CONCLUSIONS

To summarize, we have developed a stochastic biophysical theory of ligand accumulation in cell-culture assays, which directly links the bulk concentrations of autocrine ligands to the measurable parameters of autocrine cells and cell-culture experiments. Previous analyses of autocrine cell cultures were based on compartmental models (Oehrtman et al., 1998), confluent monolayer approximation (Shvartsman et al., 2001), or required experimental input from independent assays (DeWitt et al., 2001). Our approach goes beyond these approximations, and can be used over a broad range of both the cell and culture parameters. Our theory can be generalized to experiments with co-cultures of autocrine and paracrine cells. For example, in experiments by Pierce et al. (2001), autocrine donor cells that produced EGFR ligands were plated together with acceptor cells that could bind EGFR ligands. To analyze experiments of this type, the boundary homogenization procedure must be adapted to the case when traps with two different trapping rates cover a reflecting boundary. The approach described in this article can be extended to account for more complex dynamics of secreted signals in the extracellular medium, e.g., degradation in the case of cell communication mediated by Nitric Oxide (Nalwaya and Deen, 2004), or reversible binding to ligand decoys in the case of cell communication by secreted growth factors (Oehrtman et al., 1998). Finally, our models can be naturally extended to the case when autocrine ligand-receptor binding stimulates further ligand release, as in experiments with autocrine cancer cells (Shvartsman et al., 2002).

APPENDIX: DERIVATION OF THE EXPRESSION FOR THE SURVIVAL PROBABILITY

Consider a particle that diffuses between partially absorbing and perfectly reflecting planes separated by distance h. The particle starts from the point located at distance z₀ from the partially absorbing boundary, which corresponds to the plane z = 0. The particle propagator in the z direction, which is perpendicular to the boundaries, or its Green's function, G(z,t|z₀), satisfies the diffusion equation

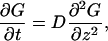(A1)

with boundary conditions

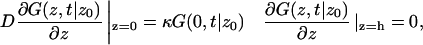(A2)

and the initial condition

(A3)

The particle survival probability, S(t|z₀), is given by

(A4)

The propagator considered as a function of z₀ satisfies

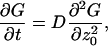(A5)

and the initial condition in Eq. A3 and boundary conditions on the planes

(A6)

Using the definition of survival probability, one can check that S(t|z₀) satisfies

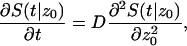(A7)

with boundary conditions

(A8)

and the initial condition S(0|z₀) = 1. Solving the problem by the Laplace transform method, we find

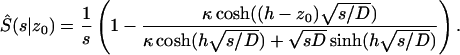(A9)

Setting z₀ = 0, we arrive at

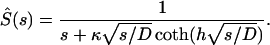(A10)

This expression is used to find the Laplace transforms of the survival probabilities of autocrine and paracrine ligands.