Abstract
The proteasome is the major protease for intracellular protein degradation. The influx rate of protein substrates and the exit rate of the fragments/products are regulated by the size of the axial channels. Opening the channels is known to increase the overall degradation rate and to change the length distribution of fragments. We develop a mathematical model with a flux that depends on the gate size and a phenomenological cleavage mechanism. The model has Michaelis-Menten kinetics with a Vmax that is inversely related to the length of the substrate, as observed in the in vitro experiments. We study the distribution of fragment lengths assuming that proteasomal cleavage takes place at a preferred distance from the ends of a protein fragment, and find multipeaked fragment length distributions similar to those found experimentally. Opening the gates in the model increases the degradation rate, increases the average length of the fragments, and increases the peak in the distribution around a length of 8–10 amino acids. This behavior is also observed in immunoproteasomes equipped with PA28. Finally, we study the effect of re-entry of processed fragments in the degradation kinetics and conclude that re-entry is only expected to affect the cleavage dynamics when short fragments enter the proteasome much faster than the original substrate. In summary, the model proposed in this study captures the known characteristics of proteasomal degradation, and can therefore help to quantify MHC class I antigen processing and presentation.
INTRODUCTION
The proteasome is a barrel-shaped multi-subunit protease involved in most cytosolic proteolysis. The proteasome degrades (partially) unfolded and nonfunctional intracellular proteins. The 20S core particle of the proteasome is characterized by an internal chamber equipped with catalytic sites at the β-subunits (Whitby et al., 2000; Groll et al., 1997; Forster and Hill, 2003; Lowe et al., 1995). The α-subunits, organized in a ring-shaped structure, function as a gate by forming an axial channel that regulates the influx and efflux of proteins via the opening and closing of the entrance of the proteolytic chambers. Closing the channel may therefore favor the degradation of substrates by restricting the release of degradation products (Kohler et al., 2001; Kisselev et al., 2002; Groll and Huber, 2003). The size of the axial channel can be controlled by regulatory particles like PA28, or its homologs, and 19S. An open channel facilitates the uptake of substrate, and the release of fragments (DeMartino and Slaughter, 1999; Rechsteiner et al., 2000; Cascio et al., 2002; Dick et al., 1996; Groettrup et al., 1996; Kloetzel, 2004; Van Hall et al., 2000; Kohler et al., 2001). Using open-channel eukaryotic proteasome mutants, Kohler et al. (2001) showed that the opening of the channel strongly influences the kinetics and the length distribution of the fragments obtained in vitro. Opening the channel increases the degradation rate and increases the median length of resulting fragments by 40%. These results support the notion that the axial channel of the proteasome and its regulation play a pivotal role in the degradation of endogenous proteins. In this article we develop a mathematical model of the proteasome degradation dynamics to get more insight into the effects of the gate size on the kinetics of protein degradation and the lengths of the protein fragments that are produced.
Theoretical models for the kinetics of proteasome degradation have been published before. Several of these concentrate on the degradation of short peptides (Stein et al., 1996; Stohwasser et al., 2000; Schmidtke et al., 2000), and will not be discussed here. The group of Holzhutter has published two theoretical models for the degradation of long substrates (Holzhutter and Kloetzel, 2000; Peters et al., 2002) that are relevant for the model developed here. Recently these models have been simplified into a simple caricature model illustrating the complexity of proteasomal degradation (Hadeler et al., 2004). These models consider specific proteins with predefined cleavage sites, and are fitted to experimental data obtained with these proteins after proteasomal degradation (Holzhutter and Kloetzel, 2000; Peters et al., 2002).
With the model proposed here we attempt to generalize these previous models by not considering one protein with a particular sequence. Instead, the protein substrates considered here are completely characterized by their length. Nevertheless, various characteristics of the previous models have been adopted in our novel model. First, we will also assume preferential cleavage of fragments of approximately nine amino acids (aa) (Holzhutter and Kloetzel, 2000; Peters et al., 2002) by assuming that cleavage most likely occurs around the ninth position from one end of the substrate. Second, we adopt the notion that the rate at which fragments exit from the proteasome decreases with the length of the fragment. Holzhutter and Kloetzel (2000) assumed an exponential relation between the efflux rate and the fragment length. Because we consider long substrates we will use a shifted exponential, or a similar declining Hill function for this relation, and assume that long fragments hardly leave the proteasome. One underlying mechanistic reason could be the partial refolding, or the bending, of long fragments inside the core particle (CP), which is feasible for amino acid sequences longer than 30–40 aa. Additionally, secondary binding sites may stabilize the binding of long substrates (Bogyo et al., 1998).
The proteasomal degradation of our new model exhibits Michaelis-Menten kinetics. The Michaelis-Menten constant Km and the maximum velocity of degradation Vmax are both decreasing functions of the substrate length, which is in agreement with experimental data (Kisselev et al., 1998, 2000). By tuning the parameters of the model, we can obtain a three-peak length distribution of products as observed experimentally (Kohler et al., 2001; Cascio et al., 2002; Saric et al., 2004; Wang et al., 1999). The first peak corresponds to 2–3 aa, the second to 8–10 aa, and the third is a wide peak at ∼20–30 aa. The opening of the gate changes the residence time of fragments inside the CP, and thereby changes the ratio of small over long fragments observed outside. Finally, we find that the re-entry of intermediate products does not strongly influence the initial dynamics unless the influx rate depends on the length of the peptides.
MODEL
The model describes the rates at which the concentrations of fragments of length k change over time. The concentrations change by proteasomal cleavage, making two short fragments out of a long one, and by the influx and efflux of fragments through the gates. A major characteristic of our model is that the dynamics do not depend on the actual amino acid sequence and orientation of the fragment. Influx, efflux, and cleavage only depend on the length of the fragment. Let nk be the concentration of fragments of length k inside the proteolytic chambers, and let Nk be the fragments of length k outside. The dynamics of nk and Nk are given as
 |
(1) |
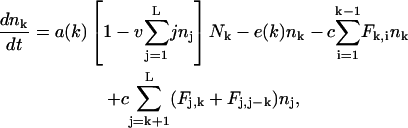 |
(2) |
for k = 1,2,…L. The substrate NL is an outside fragment of length k = L. The first term of Eq. 1 describes the influx of fragments into the proteasome. For the influx function a(k) we will first consider the case where there is no re-entry of fragments other than the substrate, i.e., we set 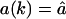 for k = L, and a(k) = 0 otherwise. Later (see Re-entry, below) we also allow other fragments to enter. The influx of substrate into the proteolytic chambers is a rate-limiting factor in protein degradation (Dorn et al., 1999; Liu et al., 2003; Lee et al., 2002; Huffman et al., 2003; Akopian et al., 1997). Experimental data suggest that the influx is limited by the maximum number of amino acids that can be accommodated in the proteasome (Groll et al., 1997; Whitby et al., 2000; Forster and Hill, 2003; Huffman et al., 2003; Hutschenreiter et al., 2004) (see also Re-entry, below). In our model the influx rate therefore decreases when the total number of amino acids inside,
for k = L, and a(k) = 0 otherwise. Later (see Re-entry, below) we also allow other fragments to enter. The influx of substrate into the proteolytic chambers is a rate-limiting factor in protein degradation (Dorn et al., 1999; Liu et al., 2003; Lee et al., 2002; Huffman et al., 2003; Akopian et al., 1997). Experimental data suggest that the influx is limited by the maximum number of amino acids that can be accommodated in the proteasome (Groll et al., 1997; Whitby et al., 2000; Forster and Hill, 2003; Huffman et al., 2003; Hutschenreiter et al., 2004) (see also Re-entry, below). In our model the influx rate therefore decreases when the total number of amino acids inside, 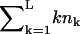 , increases. The maximum filling of the proteasome is normalized to 1 by a scaling parameter v, determining the maximum number of amino acids that can be accommodated within the CP.
, increases. The maximum filling of the proteasome is normalized to 1 by a scaling parameter v, determining the maximum number of amino acids that can be accommodated within the CP.
Proteasomes degrade a wide range of different substrates, including nonprotein substrates such as synthetic linear polymers, and generally the degradation rate decreases if the length of the substrate is increased (Hortin and Murthy, 2002; Peters et al., 2002). We assume that the influx rate does not strongly depend on the amino acid composition of the substrate.
Very little is known about the efflux of fragments from the proteasome. Previous mathematical models have assumed that long fragments, e.g., lengths up to 40 aa, have a slower efflux than short fragments, e.g., lengths starting at 20 aa, and have modeled this with a declining exponential function (Holzhutter and Kloetzel, 2000). This seems a natural assumption because long peptides will have more residues binding to the CP (Holzhutter and Kloetzel, 2000), which will impair their passage through the narrow pore. Because we consider long substrates, i.e., lengths up to 150 aa, we required a function that allowed short fragments to have a high efflux, fragments of an intermediate length to have a length-dependent efflux, and long fragments to have a slow efflux. One possibility is to use a similar shifted exponential function 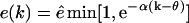 that switches from maximum efflux, ê, to an exponentially declining efflux at a fragment length of θ aa. Another possibility is a steep Hill function, e.g.,
that switches from maximum efflux, ê, to an exponentially declining efflux at a fragment length of θ aa. Another possibility is a steep Hill function, e.g.,
 |
(3) |
that switches at a fragment length of  from the maximal efflux rate ê for short fragments to an efflux close to zero for long fragments. In Fig. 1 A we depict this function for θ = 25 and
from the maximal efflux rate ê for short fragments to an efflux close to zero for long fragments. In Fig. 1 A we depict this function for θ = 25 and 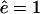 . We have tried both and have found very similar results (not shown). Thus, the basic assumption of our model is that fragments on an intermediate length, i.e., ∼25 aa, have a length-dependent efflux. The rate of efflux of shorter fragments is ê, and long fragments have a negligible rate of efflux. This is described phenomenologically by Eq. 3.
. We have tried both and have found very similar results (not shown). Thus, the basic assumption of our model is that fragments on an intermediate length, i.e., ∼25 aa, have a length-dependent efflux. The rate of efflux of shorter fragments is ê, and long fragments have a negligible rate of efflux. This is described phenomenologically by Eq. 3.
FIGURE 1.
A graphical representation of the model assumptions. (A) The efflux rate as given in Eq. 3. (B) Binomial (dashed lines) and Gaussian (solid lines) distributions for the cleavage probability. For the binomial distribution p = 0.25, μ = 9 and for the Gaussian distribution μ = 9, σ = 3. (C) Schematic representation of the phenomenological cleavage machinery given in Eq. 5 for different sequence lengths. The cleavage probability is peaked at μ = 9 residues from one end of the substrate.
The first two terms of Eq. 2 are the same influx and efflux terms as discussed above. The last terms describe the cleavage machinery located in the core of the proteasome. Fragments of length k are cut at a maximum rate c and with probability 0 < Fk,i < 1 into two fragments of length i and k–i. Two terms account for the loss and for the gain of each fragment of length k. The negative term corresponds to a loss for fragments of length k which are cut in shorter fragments, and the positive term is a gain because fragments of length j > k can be cleaved into a fragment of length k. The standard parameters that are used in the simulations are given in Table 1, and will be discussed in more detail in Results, below.
TABLE 1.
Parameter values
| Parameter | Description | Dimension | Default value |
|---|---|---|---|
| L | Length of the substrate | Amino acids | 100 |
| NL(0) | Initial substrate concentration | Mol | 100 |
| â | Rate of influx | Time−1 | 0.1 |
| ê | Rate of efflux | Time−1 | 1 |
| c | Cleavage rate | Time−1 | 1 |
| θ | Critical fragment length | Amino acids | 25 |
| μ | Preferred cleavage position | Amino acids | 9 |
| σ | Std of cleavage position | Amino acids | 3 |
| v | Scaling factor | — | 1/200 |
Cleavage mechanism
Our main assumption for the cleavage mechanism is that the proteasome cleaves proteins starting around their N-termini or C-termini. To allow for cleavages, the protein has to bind into a groove close to a catalytic site (Lowe et al., 1995; Seemuller et al., 1995; Groll and Huber, 2003; Heinemeyer et al., 1997), and the minimal size of a binding motif is ∼3–4 aa (Lowe et al., 1995; Seemuller et al., 1995; Groll and Huber, 2003; Heinemeyer et al., 1997; Kesmir et al., 2003). Because Groll and Huber (2003) concluded from a variety of experiments that there is a preferred length of 7–9 aa for docking substrates in the binding grooves, we assume that the proteasome starts at a distance 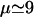 from one end of the protein/peptide, and scans the substrate chain in both directions until a cleavage site is found. Letting p be the probability to find a cleavage site, the chance to cut at site i has its maximum p at μ, and is given by Pi = p(1 – p)|i–μ|. Since possible cleavage sites are expected to be found on average once in four aa (Kesmir et al., 2002; 2003), we choose
from one end of the protein/peptide, and scans the substrate chain in both directions until a cleavage site is found. Letting p be the probability to find a cleavage site, the chance to cut at site i has its maximum p at μ, and is given by Pi = p(1 – p)|i–μ|. Since possible cleavage sites are expected to be found on average once in four aa (Kesmir et al., 2002; 2003), we choose 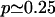 . This probability distribution is depicted in Fig. 1 B by the dashed line. Using this cleavage function we were able to reproduce degradation kinetics found experimentally, but the fragment distribution had very sharp peaks (data not shown). Indeed it seems unrealistic that the cleavage probability has the sharp peak at μ = 9 depicted in Fig. 1 B. To round the peak, one can model the cleavage probability with a phenomenological Gaussian distribution of
. This probability distribution is depicted in Fig. 1 B by the dashed line. Using this cleavage function we were able to reproduce degradation kinetics found experimentally, but the fragment distribution had very sharp peaks (data not shown). Indeed it seems unrealistic that the cleavage probability has the sharp peak at μ = 9 depicted in Fig. 1 B. To round the peak, one can model the cleavage probability with a phenomenological Gaussian distribution of
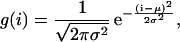 |
(4) |
where the mean μ provides the most likely cutting position, and the standard deviation σ defines the range of likely cleavage positions. This distribution is similar to the previous one but it has a rounder peak (see Fig. 1 B, where the solid line depicts Eq. 4 with μ = 9 and σ = 3). Thus, the probability of cutting a peptide of length k at position i is
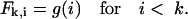 |
(5) |
The cleavage probability should be very low for the first 3–4 residues of the protein due to the binding of the substrate before cleavage (see above). Hence the standard deviation, σ, should be small. Choosing μ = 9 and σ = 3 implies that we expect at least one cleavage site in every μ + 2σ = 15 consecutive residues, which seems a fair assumption. Because σ < μ we obtain that the proteasome has a low probability to cut in the very first positions (see Fig. 1).
We have tested various forms of the cleavage matrix F. For instance, one could argue that cleavage should take place at both ends of the protein, and we have modeled this by filling the F matrix with two Gaussians centered at distance μ from the N- and the C-termini. This hardly changes the results, and the main effect is an increase of the cleavage rate, which can be compensated for by normalizing the F matrix, or by changing the c parameter. One can easily see that such a symmetric F matrix basically doubles the rate at which fragments of a particular length, e.g., a length of μ aa, are produced. We have also tested forms of the matrix where long substrates were only cut at one end, whereas short fragments could be cleaved at both ends. This also delivered very similar results. In the end we have therefore chosen the simple form defined by Eq. 5 and illustrated in Fig. 1.
The results shown in the figures were obtained by numerical integration of the model, i.e., Eqs. 1 and 2, with the variable time-step, fourth-order Runge-Kutta integrator, provided by Press et al. (1988).
RESULTS
The model has three rate parameters: the cleavage rate c, the maximum influx rate â, and the maximum efflux rate ê. A normal timescale of proteasome experiments is minutes. However, experimental results on proteasome degradation are typically compared for a certain level of substrate degradation, rather than at a specific point in time. Since time is not an important issue, and because we have three rate parameters in our model one can always rescale the time such that c = 1 per time unit. Increasing the cleavage rate will therefore be the same as decreasing the flux through the gates (i.e., as decreasing â and ê).
Kinetics
Experimental data suggest that the in vitro degradation rate of substrates by the proteasome obeys Michaelis-Menten kinetics (Reidlinger et al., 1997; Djaballah and Rivett, 1992; Hortin and Murthy, 2002; Realini et al., 1997; Orlowski et al., 1991; Cardozo et al., 1999; 1994; Akopian et al., 1997; Kisselev et al., 2002). For long substrates the maximum degradation rate and the Michaelis-Menten constant are known to decrease with the length of the substrate (Kisselev et al., 1999; 2000; Akopian et al., 1997; Cascio et al., 2002). Our model also exhibits Michaelis-Menten kinetics (see Fig. 2). For various initial substrate concentrations, Fig. 2 depicts the depletion of the substrate (L = 100) in the solution (Fig. 2 A), and the corresponding filling of the proteasome (Fig. 2 B). There is a rapid initial phase during which the proteasome fills up by influx of the substrate and degradation starts concomitantly. When the initial substrate concentration is low this initial phase accounts for a significant depletion of the substrate concentration NL (see Fig. 2 A). Otherwise, the substrate concentration remains high and the filling of the proteasome approaches a quasi-steady state corresponding to a maximum degradation rate.
FIGURE 2.
Michaelis-Menten kinetics. (A) Substrate consumption; each curve is the timecourse for a different initial concentration, NL(0). (B) Filling of the proteasome core particle (in amino acids) for each curve shown in A. (C) Michaelis-Menten log-log plot; each symbol-curve denotes a substrate of a different length (see legend) obtained from the model presented in Eqs. 1 and 2 in conditions where the proteasome is in a bath of substrate to prevent substrate-limiting effects. Solid lines are nonlinear parameter fits with the Michaelis-Menten function. The solid line is given by the initial slope 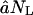 and the dashed-dot line is Vmax, predicted by the simplified model in the Appendix for the standard parameter values (see Table 1), and an average efflux
and the dashed-dot line is Vmax, predicted by the simplified model in the Appendix for the standard parameter values (see Table 1), and an average efflux 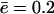 (see Eq. 6). (D) Vmax as a function of the substrate length increases for substrate shorter than 10 aa and decreases for substrates longer than that. The initial substrate concentration was set to N(t) = NL(0) = 6000 to ensure the degradation rate approached Vmax for all of the different substrate lengths.
(see Eq. 6). (D) Vmax as a function of the substrate length increases for substrate shorter than 10 aa and decreases for substrates longer than that. The initial substrate concentration was set to N(t) = NL(0) = 6000 to ensure the degradation rate approached Vmax for all of the different substrate lengths.
To study the Michaelis-Menten kinetics, we fix the substrate concentration by fixing N(t) = N(0) and let the model approach the corresponding steady state. At the steady state we measure the degradation rate as the loss of substrate molecules from the solution per unit of time, and depict this as a function of the substrate concentration and the length of the substrate, L (see Fig. 2 C). This reveals a family of Michaelis-Menten curves for the various lengths of the substrate. The longer the substrate, the smaller the maximum degradation rate, Vmax, and the smaller the Michaelis-Menten constant, Km. The degradation rate at low substrate concentrations is fairly independent of the length of the substrate (see Fig. 2 C and Appendix). More formally, one can illustrate the Michaelis-Menten kinetics by a quasi-steady-state approximation. In the Appendix, we develop a simplified model of three differential equations for the substrate concentration inside, n(t), and outside N(t), and for the total concentration of fragments inside, p(t), by a quasi-steady-state assumption for the internal dynamics, i.e., by assuming dn/dt = dp/dt = 0. For sufficiently long substrates, we arrive at the equation
 |
(6) |
and â is the influx rate of the substrate and  is an average efflux rate of the fragments (for details, see the Appendix). The latter should be taken as an average of the length-dependent efflux of the full model (see Eq. 3 and the Appendix). The simplified model has a Michaelis-Menten constant
is an average efflux rate of the fragments (for details, see the Appendix). The latter should be taken as an average of the length-dependent efflux of the full model (see Eq. 3 and the Appendix). The simplified model has a Michaelis-Menten constant 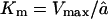 . This approximation is in good agreement with the kinetics of the full model for long substrates (see Fig. 2 D). For low concentrations of substrate, i.e., for N ≪ Km,
. This approximation is in good agreement with the kinetics of the full model for long substrates (see Fig. 2 D). For low concentrations of substrate, i.e., for N ≪ Km, 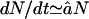 , the degradation rate is indeed independent of the length of the substrate. The line
, the degradation rate is indeed independent of the length of the substrate. The line  is depicted by the solid line in Fig. 2 C and is in excellent agreement with the simulations of the full model. For the current parameter settings, Vmax is approached rapidly, e.g., within 10 time units (results not shown). The plateau level in Fig. 2 C depicted as a dot-dashed line is the Vmax value obtained from the simplified model for a substrate of length L = 100 and average efflux
is depicted by the solid line in Fig. 2 C and is in excellent agreement with the simulations of the full model. For the current parameter settings, Vmax is approached rapidly, e.g., within 10 time units (results not shown). The plateau level in Fig. 2 C depicted as a dot-dashed line is the Vmax value obtained from the simplified model for a substrate of length L = 100 and average efflux 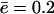 per time-unit. In this model, Vmax itself is a saturation function of the cleavage rate c and the efflux rate
per time-unit. In this model, Vmax itself is a saturation function of the cleavage rate c and the efflux rate  (see Eq. 6). This means that the efflux and the cleavage play similar roles in limiting the maximum rate of degradation. At high cleavage rates the degradation rate is limited by the efflux, and at high efflux rates it is limited by the cleavage.
(see Eq. 6). This means that the efflux and the cleavage play similar roles in limiting the maximum rate of degradation. At high cleavage rates the degradation rate is limited by the efflux, and at high efflux rates it is limited by the cleavage.
For short substrates the expression for the Vmax and the Michaelis-Menten constant become somewhat more complicated because one can no longer ignore the efflux of uncleaved substrate molecules (see Appendix). Very short substrates, i.e., those shorter than μ + σ aa, will have a slower overall cleavage rate than longer substrates (see Eq. 4 and Fig. 1). Decreasing this cleavage rate will decrease the Vmax. This is studied in Fig. 2 D where we simulate the model again for a fixed substrate concentration. To ensure that even short substrates have approached their high Vmax, the substrate concentration is fixed at N(t) = 6000; higher values gave similar results (not shown). One indeed sees that Vmax first increases with the substrate length, which is due to the increase of the overall cleavage rate, and then decreases with the length of the substrate, which is explained by Eq. 6. This is in good agreement with experimental results (Akopian et al., 1997; Dolenc et al., 1998; Kisselev et al., 1998, 1999, 2000). Dolenc et al. (1998), working with short substrates, demonstrated that the ratio of the observed degradation rate and the observed Michaelis-Menten constant increased with the length of the substrate. We find a similar relation in the Appendix in Eq. 10, and predict that this ratio should approach saturation when longer substrates would be tested.
Length distribution of the fragments
In vitro experiments generate cleavage products that range from 2 to 35 aa (Nussbaum et al., 1998; Kisselev et al., 1998, 1999; Kohler et al., 2001; Cascio et al., 2001). Using size-exclusion chromatography and on-line fluorescence detection, Kohler et al. (2001) showed that the products generated by the wild-type (WT) proteasome have a length distribution with three broad peaks corresponding to lengths of 2–3, 8–10, and 20–30 aa, respectively. Other approaches, such as mass spectrometry, are not quantitative and fail to detect short peptides. We have searched the parameter space of our model to identify the regimes that result in similar fragment length distributions.
Parameter sweep
In Fig. 3 we show how the fragment length distribution depends on the size of the gate, i.e., on the influx and efflux rates â and ê, as calculated with the model Eqs. 1 and 2. In each panel, the distribution is depicted for the time-point at which 20% of the substrate is degraded. The time at which this is achieved is indicated in each panel. For an intermediate efflux rate, we obtain three-peaked distributions similar to those observed in experiments (Kohler et al., 2001) for a wide range of influx rates. Note that the first has its maximum at 1 aa but we call this decreasing slope a peak, for simplicity. In our model, the three-peaked distributions are the result of the cleavage machinery, which tends to cut fragments of 8–10 aa, and the efflux of products, which favors the short fragments. The distribution is insensitive to 100-fold variation of the influx rate â (see Fig. 3). One can indeed see from Eq. 2 that the influx becomes unimportant whenever the proteasome fills up. The influx rate will therefore only become important when it becomes the rate-limiting factor.
FIGURE 3.
The length distributions of the fragments outside for various different values of the influx and efflux rates. From left to right, the efflux rate ê increases from 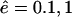 to 10. From top to bottom, the influx rate â increases from
to 10. From top to bottom, the influx rate â increases from  to 1. Each panel shows the distribution of fragments outside at the time-point where 20% of the substrate had been degraded. This time is indicated in each panel. E could represent a WT proteasome and I an open-channel mutant (see also Fig. 4). Note that the distributions are relatively insensitive to the variation in the influx rate â.
to 1. Each panel shows the distribution of fragments outside at the time-point where 20% of the substrate had been degraded. This time is indicated in each panel. E could represent a WT proteasome and I an open-channel mutant (see also Fig. 4). Note that the distributions are relatively insensitive to the variation in the influx rate â.
In the first column of Fig. 3, A, D, and G, the efflux is slow compared to the cleavage ( ). As a consequence, most substrate molecules are fragmented extensively before they are exported, and one observes short fragments in the solution. Increasing the efflux rate 10-fold (see the second column of Fig. 3, B, E, and H) gives a similar timescale to the efflux and to the cleavage, and allows for a three-peak distribution (see below). Another 10-fold increase of the efflux rate (see Fig. 3, C, F, and I) makes cleavage the limiting factor. The ratio of long to short fragments increases (which will later be interpreted as opening the gate, see below). Because the residence time of fragments in the CP is short, there is less fragmentation, and the first peak at 1–3 aa decreases.
). As a consequence, most substrate molecules are fragmented extensively before they are exported, and one observes short fragments in the solution. Increasing the efflux rate 10-fold (see the second column of Fig. 3, B, E, and H) gives a similar timescale to the efflux and to the cleavage, and allows for a three-peak distribution (see below). Another 10-fold increase of the efflux rate (see Fig. 3, C, F, and I) makes cleavage the limiting factor. The ratio of long to short fragments increases (which will later be interpreted as opening the gate, see below). Because the residence time of fragments in the CP is short, there is less fragmentation, and the first peak at 1–3 aa decreases.
Three-peaked distribution
When the efflux rate and the cleavage rate have a similar timescale we observe three peaks in the distribution of fragments (see Fig. 3 and the WT curves in Fig. 4). Similar to what is observed experimentally (Kohler et al., 2001), the third peak is much smaller than the other two, and the second peak is larger than the first peak. The average fragment length is 7.3 aa, and the third peak is centered around a length of 23 aa. The fractions of small fragments (1–5 aa), intermediate fragments (6–11 aa), and long fragments (>11 aa) are 36.5%, 51%, and 12.5%, respectively. These fractions are compatible with the experimental observations of Kisselev et al. (1998, 1999) and Kohler et al. (2001). In our model, the first peak corresponding to the small fragments reflects an efficient cleavage mechanism where fragments are repeatedly cleaved before they are released from the CP. These rest products do not collapse to single amino acids because cleavage of very short fragments is improbable in our model (see Fig. 1 B). The second peak, corresponding to fragments with a length of 8–10 aa, is the result of the preference to cut at μ = 9 aa (see Cleavage Mechanism, above). Fragments are found in a broad peak at ∼9 aa, because of the variation in the cleavage (i.e., standard deviation of the Gaussian function). The third peak at ∼25 aa found in the WT distribution is due to the efflux function. This function blocks the efflux of fragments longer than 30 aa. Fragments of ∼25 aa do move out, and thereby reduce the production of fragments of 15–20 aa, which shows up as a peak centered at ∼25 aa. Short fragments, i.e., <10 aa, are always produced by the cleavage of any other sufficiently long fragment.
FIGURE 4.
Fragment length distributions depend on the gate opening. (A) The solid line corresponds to the WT proteasome at time t = 66, and the dashed line to the open-channel mutant at time t = 56. At these time-points 20% of substrate is degraded. The stars depict the distribution of the open-channel mutant at t = 66 (when 23% of substrate is degraded). This illustrates that the degradation rate is higher for the open-channel mutant. The average length of the products is 9.1 aa for the mutant and 7.3 aa for the WT proteasome. (B) Same as A, but at time-points when 80% of the substrate is degraded. The average lengths are the same as in A, and the peaks are located at similar lengths. The stars depict the distribution of the open-channel mutant at t = 279, when 92% of substrate is degraded. Parameters: open-channel mutant  , and WT
, and WT 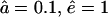 .
.
Gate opening
Comparing WT eukaryotic proteasomes with open-channel mutants Kohler et al. (2001) showed that: 1), mutants degrade substrates faster; 2), the average length of resulting fragments is 23% longer than when the same substrate is degraded with the WT proteasome; and 3), the main effect of opening the gate is to increase the number of long fragments and to decrease the number of short (2–3 aa long) fragments. In Fig. 4 we report the effect of the gate size by increasing the influx and efflux rate threefold from a WT with 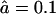 and
and 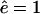 to an open-channel mutant with
to an open-channel mutant with 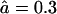 and
and 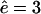 . The fragment length distributions are compared at time-points where 20% (Fig. 4 A) or 80% (Fig. 4 B) of the substrate is degraded. For these parameters the WT proteasome delivers the three-peaked distribution discussed above (see Fig. 4).
. The fragment length distributions are compared at time-points where 20% (Fig. 4 A) or 80% (Fig. 4 B) of the substrate is degraded. For these parameters the WT proteasome delivers the three-peaked distribution discussed above (see Fig. 4).
In the open-channel mutant the flux of fragments through the axial channel is increased. As a consequence, the ratio of small over long fragments decreases (see Fig. 4 A, dashed lines). In terms of the three-peaked distribution this results in a decrease in the first peak, and an increase in the second and the third peaks. The average length of the outside fragments increases from 7.3 aa for the WT to 9.1 aa for the open-channel mutant. With the mutant, 20% substrate degradation is achieved at t = 56, and with WT this takes until t = 66. This corresponds to 18% increase in the degradation rate. Fragments are produced with the same frequency during the degradation process; the positions of the peaks remain similar between the distribution at 20% and 80% substrate degradation. Comparing the open-channel mutant in the model with the WT discussed above, the average fragment length has increased by 24.6% (from 7.3 to 9.1 aa). The third peak is now located at 27 aa, and the distributions of small, intermediate, and long fragments in the mutant are 22%, 58%, and 20%, respectively. These results are in good agreement with the data of Kohler et al. (2001).
Re-entry
In vivo the processed fragments of the proteasome degradation are exposed to amino peptidases and other proteases in the cytosol (Reits et al., 2004). This strongly reduces the possibility that fragments can enter the proteasome and be further degraded. However, re-entry of fragments is possible in vitro, and this is a controversial point regarding the validity of in vitro experiments for the understanding of in vivo proteasomal activity.
All results discussed above were obtained in the absence of re-entry because only the substrate had a non-zero influx rate  . To study the effect of re-entry of processed fragments we first give all fragments the same influx rate
. To study the effect of re-entry of processed fragments we first give all fragments the same influx rate 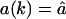 for k = 1,2,…L. Fig. 5, A and B, show how re-entry affects the timecourse and the length distribution of fragments. Re-entry slightly reduces the degradation rate at late time-points, e.g., after 50% of the substrate has been degraded, when the concentration of some fragments in the solution exceeds that of the substrate (see Fig. 5 A). In open-channel mutants this late effect of re-entry is even weaker (not shown). The effect of re-entry increases when time proceeds, e.g., when the substrate is >80% degraded, because the products start to dominate in the solution (see Fig. 5 A). Comparing the number of fragments of length 8–10 aa illustrates that the effect of re-entry on the degradation process is small. The length distribution at 80% substrate degradation is shown in Fig. 5 B. During the course of the degradation, the positions of the peaks shift to smaller fragments as a result of the reprocessing of products. The average fragment length shifts from 7.3 aa to 6 aa.
for k = 1,2,…L. Fig. 5, A and B, show how re-entry affects the timecourse and the length distribution of fragments. Re-entry slightly reduces the degradation rate at late time-points, e.g., after 50% of the substrate has been degraded, when the concentration of some fragments in the solution exceeds that of the substrate (see Fig. 5 A). In open-channel mutants this late effect of re-entry is even weaker (not shown). The effect of re-entry increases when time proceeds, e.g., when the substrate is >80% degraded, because the products start to dominate in the solution (see Fig. 5 A). Comparing the number of fragments of length 8–10 aa illustrates that the effect of re-entry on the degradation process is small. The length distribution at 80% substrate degradation is shown in Fig. 5 B. During the course of the degradation, the positions of the peaks shift to smaller fragments as a result of the reprocessing of products. The average fragment length shifts from 7.3 aa to 6 aa.
FIGURE 5.
Effect of the re-entry of fragments. (A, B) Comparison of the timecourse and fragment-length distribution without re-entry and with re-entry employing a constant influx rate for all the fragments: 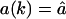 . (A) Timecourse of the degradation process: the solid line is the substrate depletion with re-entry (
. (A) Timecourse of the degradation process: the solid line is the substrate depletion with re-entry ( for k = 1,2,…,L), and dashed lines depict the same without re-entry. The solid symbols depict the timecourses of fragments with re-entry, and the empty symbols those of the same fragment lengths without re-entry. (B) Length distribution of fragment with re-entry (solid line) and without re-entry (dashed line). C and D are the same as A and B, but with a length-dependent influx rate
for k = 1,2,…,L), and dashed lines depict the same without re-entry. The solid symbols depict the timecourses of fragments with re-entry, and the empty symbols those of the same fragment lengths without re-entry. (B) Length distribution of fragment with re-entry (solid line) and without re-entry (dashed line). C and D are the same as A and B, but with a length-dependent influx rate 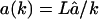 for k = 1,2,…,L. Because short fragments rapidly re-enter the CP, there are fewer fragments outside. (D) The distribution shifts to the left increasing the first peak, 1–3 aa, whereas the second (8–10 aa) and the third (20–30 aa) peak disappear.
for k = 1,2,…,L. Because short fragments rapidly re-enter the CP, there are fewer fragments outside. (D) The distribution shifts to the left increasing the first peak, 1–3 aa, whereas the second (8–10 aa) and the third (20–30 aa) peak disappear.
Re-entry becomes more important if we allow small fragments to have a faster influx than large fragments. For instance, this would be the case if the fragments are actively transported through the axial channel. One would then expect the transportation time to be proportional to the length of the substrate, and the influx rate would be inversely related to the substrate length, e.g., 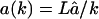 for k = 1,2,…L. Note that this function preserves the influx rate â for substrates of length L that was used above. With such a length-dependent influx rate, the re-entry of products markedly slows down the degradation of the substrate (Fig. 5 C). As a consequence of the re-entry, the peak at a length of 8–10 residues vanishes, and >50% of fragments outside are smaller than 4 aa (see Fig. 5 D). Allowing for re-entry, the average fragment length shifts from 7.3 to 4.7 aa.
for k = 1,2,…L. Note that this function preserves the influx rate â for substrates of length L that was used above. With such a length-dependent influx rate, the re-entry of products markedly slows down the degradation of the substrate (Fig. 5 C). As a consequence of the re-entry, the peak at a length of 8–10 residues vanishes, and >50% of fragments outside are smaller than 4 aa (see Fig. 5 D). Allowing for re-entry, the average fragment length shifts from 7.3 to 4.7 aa.
Summarizing, these results suggest that for in vitro experiments, re-entry could indeed be an issue: if the transport rate of substrates inside the CP is dependent on the length, the experiments should be terminated when <10% of the substrate is degraded to exclude the possibility of re-entry. At the moment many groups use 20% as the typical stopping criteria (Cascio et al., 2001; Kisselev et al., 1999). An accurate analysis of the transport rates through the proteasome channel is required to resolve this issue further.
DISCUSSION AND CONCLUSION
This work provides insights on the effect of the size of the axial channel on proteasome degradation. A realistic choice for the model parameters is hard to obtain. The model is phenomenological and is designed to qualitatively capture salient features of the kinetics of degradation like the Michaelis-Menten saturation and the three-peaked distribution. The experimental data that are currently available are not adequate for a mechanistic and realistic description of how the gate size influences the transport of fragments in and out. One main result of the model is that the residence time inside the CP, which depends on the gate size of the axial channel, drastically affects the fragment length distribution and the proteasome kinetics. We now understand how a three-peaked fragment length distribution that is observed in the experiments can be obtained. In the model the first peak is due to efficient fragmentation to the minimal length before the fragment is released from the proteasome. The second peak is a consequence of the fact that the cleavage probability has its maximum at the μ = 9, which delivers many fragments of ∼9 aa from a single substrate molecule. The third peak between 20 and 30 residues results from the threshold in the efflux function Eq. 3.
Very little is known about the effects of size, charge, and hydrophobicity on the transport of peptides through large aqueous pores. We therefore prefer our simple phenomenological function for the efflux (Eq. 3) over complicated mechanistic functions.
The threshold parameter θ in the exit function was shown to be important for the existence of the third peak. Choosing considerably lower values of θ the third peak moves to the left and disappears by merging with the second peak. For larger values of θ, the peak will always be present, and located around a length of θ, provided θ remains smaller than the substrate length. We have shown the three-peaked length-distributions for a substrate of 100 aa. Intuitively, one would expect that the fraction of short fragments, i.e., those of ∼μ = 9 aa, decreases when shorter substrates were studied. Long substrates are sequentially cleaved at a preferred length of μ = 9 aa, which delivers many fragments of that length. Simulations have confirmed this; short substrates, e.g., L = 50 aa, can also give a three-peak distribution, but a smaller relative size of the second peak (results not shown).
The cleavage mechanism in our model is also phenomenological and basically assumes that cleavage occurs, independently on the substrate orientation, at some preferred distance from one end (see Eq. 5), and requires a minimal substrate length to efficiently cleave the sequence. This was inspired from crystallographic structure (Lowe et al., 1995; Seemuller et al., 1995; Groll and Huber, 2003; Groll et al., 1997) describing a binding pocket nearby the active site where the substrate docks before the cut takes place and from enzymatic studies with inhibitors, suggesting that a minimal length of 3–4 aa is required to dock to the active site and efficiently cleave the substrate (Lowe et al., 1995; Seemuller et al., 1995; Groll and Huber, 2003; Groll et al., 1997; Bogyo et al., 1998). Additionally, at least for two special models, it has been shown that both in vitro and in vivo initiation of proteolysis occurs close to the C-terminus of proteins (Zhang et al., 2004; Navon and Goldberg, 2001). This result supports our hypothesis of a high cleavage probability at the ends of the substrate. To study the effects of our Gaussian cleavage probability function, we have also considered other functions, including a simple uniform cleavage probability. This failed to deliver a three-peaked distribution, but had very similar Michaelis-Menten kinetics (not shown).
A major simplification of the model was to ignore the substrate specificity of the proteasome. This allowed us to find an expression for the relationship between the maximal degradation rate, Vmax, and the length of the substrate (see Eq. 6). Goldberg and colleagues reported decreasing kinetics constants Km and Vmax for substrates longer that 70 aa, whereas for short peptides the degradation rate increases with increasing substrate length (Kisselev et al., 2002, 2000, 1999, 1998; Akopian et al., 1997; Dolenc et al., 1998). These observations fit well with the model results. Fig. 2 D shows a similar non-monotonic relation between Vmax and the substrate length, and the Appendix explains these results in terms of a conventional Michaelis-Menten quasi-steady-state assumption.
Additionally, the Michaelis-Menten function, i.e., Eq. 6, showed that the degradation rate can be either efflux-limited or cleavage-limited. Kinetically, one can therefore distinguish between the efflux-limited case, where the cleavage is fast and the efflux is slow, and the cleavage-limited case, where the cleavage is slow and efflux is fast (see Fig. 3). When efflux is limiting, the residence time is long, and long fragments are cleaved repeatedly into small products. When the cleavage is limiting, long fragments will be produced. Since open-channel mutants have an increased degradation rate (Kohler et al., 2001), one can conclude that in the WT proteasome the efflux was the limiting factor. On the other hand, experiments with mutant proteasomes, in which the catalytic site threonine was replaced with serine (Kisselev et al., 2000), showed that the Vmax decreases strongly and longer fragments are produced when compared to the WT. This suggests that in this mutant proteasome cleavage is the rate-limiting factor (see Eq. 6 and Results). It has been proposed that the regulatory 19S cap, which binds to the CP forming the 26S proteasome, increases the enzymatic activity (Hoffman and Rechsteiner, 1996), and facilitates the binding of the substrates. The 26S proteasome exhibits a fragment length distribution similar to 20S proteasome but the average length of the fragments is shorter (Kisselev et al., 1999; Emmerich et al., 2000). These results are in agreement with our model, which predicts that an increased efficiency in the cleavage activity limits the capacity of long fragments to go out, increasing the frequency of shorter products. The 26S can be therefore described as a proteasome with higher cleavage efficiency with respect to 20S and therefore releases fewer longer fragments. Stimulation of cells with interferon-γ leads to a replacement of the catalytic β-subunits of the proteasome. The change in activity of the so-called immunoproteasome with the interferon-γ induced subunit PA28 remains controversial (Cascio et al., 2002; Sijts et al., 2000; Van Hall et al., 2000; Kloetzel, 2004). Some forms of the immunoproteasome, i.e., immuno-20S with PA28 and 26S immunoproteasome, cleave short fluorogenic peptides and long substrates faster than the constitutive forms of the proteasome (Eleuteri et al., 1997; Glickman, 2000; Cardozo and Michaud, 2002; Tenzer et al., 2004; Kloetzel, 2004; Peters et al., 2002). Other experiments have shown that the immunoproteasome and the constitutive proteasome have similar rates of substrate turnover (Cascio et al., 2001; Toes et al., 2001), but do agree that these tend to generate longer products (Toes et al., 2001; Cascio et al., 2001).
Our results suggest that the faster turnover and longer fragments documented for some forms of the immunoproteasome can be explained with an open-gate configuration. Above we already discussed that the maximum degradation rate, Vmax, saturates and can be limited by either the cleavage c or the efflux rate 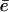 . In the cleavage-limited case, augmenting the efflux
. In the cleavage-limited case, augmenting the efflux 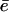 of the products in Eq. 6 will hardly increase the degradation rate, and hence the average fragment length will remain the same.
of the products in Eq. 6 will hardly increase the degradation rate, and hence the average fragment length will remain the same.
Recently it was suggested that, in vivo, the proteasome may be only one of the several proteases involved in the production of short peptides (Kloetzel, 2004; Reits et al., 2004), and the fragments produced by proteasomal cleavage might be longer than was previously appreciated. Our model has addressed in vitro data, and it remains unclear why the fragment lengths produced in vitro and in vivo would be so different.
Finally, our model can be used to achieve a more quantitative picture of the MHC class I antigen processing and presentation pathway. Based on estimates coming from the average turnover of proteins in a cell, Yewdell and colleagues argue that the efficiency of antigen processing is low, meaning that most of the potential MHC ligands are destroyed by the proteasome (Yewdell, 2001; Yewdell et al., 2003). Kisselev et al. (1999) report that two-thirds of the proteasome products are too short for antigen presentation. We also find that at least 50% of the fragments generated by the proteasome are shorter than eight amino acids (see Fig. 4) and therefore cannot be used for antigen presentation. The longer fragments produced by some forms of the immunoproteasome can be explained by an opened gate. For such immunoproteasomes we predict not only longer fragments, but also an elevated steady-state level of fragments from 8 to 35 aa (see Fig. 4). Such an immunoproteasome would markedly increase the number of possible MHC ligands.
Acknowledgments
We thank three anonymous referees for excellent suggestions.
F.L. and M.O.G. thank the Volkswagen Foundation for funding. C.K. and R.d.B. acknowledge the financial support from the Netherlands Organization for Scientific Research (grants 050-50-202 and 016-04-603).
APPENDIX
To simplify the mathematical model, let N be the concentration of substrate outside and n the concentration of substrate inside the CP. The length of the substrate is L. Define p as the total product concentration present at time t in the CP, and for simplicity, approximate the length of these products also to L. The equations for the substrate dynamics are
 |
(7) |
where â is the influx rate of the substrate, c is the cleavage rate, and v is the scaling factor for the volume of the proteasome (see Table 1). Let ε be the slow exit rate of the substrate. Long substrates hardly exit the proteasome without being cleaved, i.e., ε = 0. However, for short substrates, ε can be larger than zero. This simplified model resembles the full model, given that the average efflux rate of the fragments is 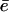 (see Results, above). Assuming that the substrate and the products inside the CP are in the quasi-steady state (i.e., dn/dt = dp/dt = 0), one obtains
(see Results, above). Assuming that the substrate and the products inside the CP are in the quasi-steady state (i.e., dn/dt = dp/dt = 0), one obtains
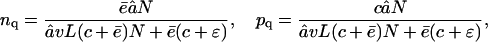 |
where nq and pq are the quasi-steady-state concentrations of the substrate and the products, respectively. This leads to
 |
which is a Michaelis-Menten function with a maximum degradation rate of
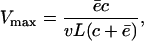 |
(8) |
which is approached when N → ∞. Conversely, when N ≪ Km the loss of substrates, dN/dt, approaches a linear degradation rate  . The Michaelis-Menten constant, i.e., the substrate concentration at which dN/dt is half of the maximum, is
. The Michaelis-Menten constant, i.e., the substrate concentration at which dN/dt is half of the maximum, is 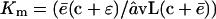 .
.
For long substrates, i.e., when ɛ → 0, the Michaelis-Menten constant simplifies to 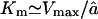 , which is given as Eq. 6 in the text. The linear degradation rate at low substrate concentrations simplifies to
, which is given as Eq. 6 in the text. The linear degradation rate at low substrate concentrations simplifies to  .
.
For very short substrates, i.e., when L < μ + σ, the cleavage rate increases with the substrate length; see Fig. 1 C and Eq. 8. For such short substrates the overall cleavage rate is  , which is a cumulative Gaussian function that increases sigmoidally with the length of the substrate L, and approaches the maximum overall cleavage rate c when
, which is a cumulative Gaussian function that increases sigmoidally with the length of the substrate L, and approaches the maximum overall cleavage rate c when  . This means that for short substrates Eq. 8 becomes
. This means that for short substrates Eq. 8 becomes
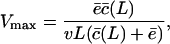 |
(9) |
which has a numerator increasing sigmoidally with the substrate length L. Because 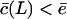 for small substrates, Vmax will first increase with the substrate length. When
for small substrates, Vmax will first increase with the substrate length. When 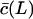 has approached c, Vmax can only decrease when the substrate length is increased because Vmax in Eq. 8 is inversely related to L. This non-monotonic behavior is confirmed by the simulations of the full model in Fig. 2 D. Finally, because some authors (Dolenc et al., 1998) express the ratio of the maximum degradation rate and the saturation constant, it is interesting to see that
has approached c, Vmax can only decrease when the substrate length is increased because Vmax in Eq. 8 is inversely related to L. This non-monotonic behavior is confirmed by the simulations of the full model in Fig. 2 D. Finally, because some authors (Dolenc et al., 1998) express the ratio of the maximum degradation rate and the saturation constant, it is interesting to see that
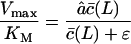 |
(10) |
increases with the substrate length L and approaches a maximum when 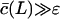 .
.
References
- Akopian, T. N., A. F. Kisselev, and A. L. Goldberg. 1997. Processive degradation of proteins and other catalytic properties of the proteasome from Thermoplasma acidophilum. J. Biol. Chem. 272:1791–1798. [DOI] [PubMed] [Google Scholar]
- Bogyo, M., S. Shin, J. S. McMaster, and H. L. Ploegh. 1998. Substrate binding and sequence preference of the proteasome revealed by active-site-directed affinity probes. Chem. Biol. 5:307–320. [DOI] [PubMed] [Google Scholar]
- Cardozo, C., and C. Michaud. 2002. Proteasome-mediated degradation of τ-proteins occurs independently of the chymotrypsin-like activity by a nonprocessive pathway. Arch. Biochem. Biophys. 408:103–110. [DOI] [PubMed] [Google Scholar]
- Cardozo, C., C. Michaud, and M. Orlowski. 1999. Components of the bovine pituitary multicatalytic proteinase complex (proteasome) cleaving bonds after hydrophobic residues. Biochemistry. 38:9768–9777. [DOI] [PubMed] [Google Scholar]
- Cardozo, C., A. Vinitsky, C. Michaud, and M. Orlowski. 1994. Evidence that the nature of amino acid residues in the P3 position directs substrates to distinct catalytic sites of the pituitary multicatalytic proteinase complex (proteasome). Biochemistry. 33:6483–6489. [DOI] [PubMed] [Google Scholar]
- Cascio, P., M. Call, B. M. Petre, T. Walz, and A. L. Goldberg. 2002. Properties of the hybrid form of the 26S proteasome containing both 19S and PA28 complexes. EMBO J. 21:2636–2645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cascio, P., C. Hilton, A. F. Kisselev, K. L. Rock, and A. L. Goldberg. 2001. 26S proteasomes and immunoproteasomes produce mainly N-extended versions of an antigenic peptide. EMBO J. 20:2357–2366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeMartino, G. N., and C. A. Slaughter. 1999. The proteasome, a novel protease regulated by multiple mechanisms. J. Biol. Chem. 274:22123–22126. [DOI] [PubMed] [Google Scholar]
- Dick, T. P., T. Ruppert, M. Groettrup, P. M. Kloetzel, L. Kuehn, U. H. Koszinowski, S. Stevanovic, H. Schild, and H. G. Rammensee. 1996. Coordinated dual cleavages induced by the proteasome regulator PA28 lead to dominant MHC ligands. Cell. 86:253–262. [DOI] [PubMed] [Google Scholar]
- Djaballah, H., and A. J. Rivett. 1992. Peptidylglutamyl-peptide hydrolase activity of the multicatalytic proteinase complex: evidence for a new high-affinity site, analysis of cooperative kinetics, and the effect of manganese ions. Biochemistry. 31:4133–4141. [DOI] [PubMed] [Google Scholar]
- Dolenc, I., E. Seemuller, and W. Baumeister. 1998. Decelerated degradation of short peptides by the 20S proteasome. FEBS Lett. 434:357–361. [DOI] [PubMed] [Google Scholar]
- Dorn, I. T., R. Eschrich, E. Seemuller, R. Guckenberger, and R. Tampe. 1999. High-resolution AFM-imaging and mechanistic analysis of the 20S proteasome. J. Mol. Biol. 288:1027–1036. [DOI] [PubMed] [Google Scholar]
- Eleuteri, A. M., R. A. Kohanski, C. Cardozo, and M. Orlowski. 1997. Bovine spleen multicatalytic proteinase complex (proteasome). Replacement of X, Y, and Z subunits by LMP7, LMP2, and MECL1 and changes in properties and specificity. J. Biol. Chem. 272:11824–11831. [DOI] [PubMed] [Google Scholar]
- Emmerich, N. P., A. K. Nussbaum, S. Stevanovic, M. Priemer, R. E. Toes, H. G. Rammensee, and H. Schild. 2000. The human 26S and 20S proteasomes generate overlapping but different sets of peptide fragments from a model protein substrate. J. Biol. Chem. 275:21140–21148. [DOI] [PubMed] [Google Scholar]
- Forster, A., and C. P. Hill. 2003. Proteasome degradation: enter the substrate. Trends Cell Biol. 13:550–553. [DOI] [PubMed] [Google Scholar]
- Glickman, M. H. 2000. Getting in and out of the proteasome. Semin. Cell Dev. Biol. 11:149–158. [DOI] [PubMed] [Google Scholar]
- Groettrup, M., A. Soza, M. Eggers, L. Kuehn, T. P. Dick, H. Schild, H. G. Rammensee, U. H. Koszinowski, and P. M. Kloetzel. 1996. A role for the proteasome regulator PA28α in antigen presentation. Nature. 381:166–168. [DOI] [PubMed] [Google Scholar]
- Groll, M., L. Ditzel, J. Lowe, D. Stock, M. Bochtler, H. D. Bartunik, and R. Huber. 1997. Structure of 20S proteasome from yeast at 2.4 Å resolution. Nature. 386:463–471. [DOI] [PubMed] [Google Scholar]
- Groll, M., and R. Huber. 2003. Substrate access and processing by the 20S proteasome core particle. Int. J. Biochem. Cell Biol. 35:606–616. [DOI] [PubMed] [Google Scholar]
- Hadeler, K. P., C. Kuttler, and A. K. Nussbaum. 2004. Cleaving proteins for the immune system. Math. Biosci. 188:63–79. [DOI] [PubMed] [Google Scholar]
- Heinemeyer, W., M. Fischer, T. Krimmer, U. Stachon, and D. H. Wolf. 1997. The active sites of the eukaryotic 20S proteasome and their involvement in subunit precursor processing. J. Biol. Chem. 272:25200–25209. [DOI] [PubMed] [Google Scholar]
- Hoffman, L., and M. Rechsteiner. 1996. Nucleotidase activities of the 26S proteasome and its regulatory complex. J. Biol. Chem. 271:32538–32545. [DOI] [PubMed] [Google Scholar]
- Holzhutter, H. G., and P. M. Kloetzel. 2000. A kinetic model of vertebrate 20S proteasome accounting for the generation of major proteolytic fragments from oligomeric peptide substrates. Biophys. J. 79:1196–1205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hortin, G. L., and J. Murthy. 2002. Substrate size selectivity of 20S proteasomes: analysis with variable-sized synthetic substrates. J. Protein Chem. 21:333–337. [DOI] [PubMed] [Google Scholar]
- Huffman, H. A., M. Sadeghi, E. Seemuller, W. Baumeister, and M. F. Dunn. 2003. Proteasome-cytochrome c interactions: a model system for investigation of proteasome host-guest interactions. Biochemistry. 42:8679–8686. [DOI] [PubMed] [Google Scholar]
- Hutschenreiter, S., A. Tinazli, K. Model, and R. Tampe. 2004. Two-substrate association with the 20S proteasome at single-molecule level. EMBO J. 23:2488–2497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kesmir, C., A. K. Nussbaum, H. Schild, V. Detours, and S. Brunak. 2002. Prediction of proteasome cleavage motifs by neural networks. Protein Eng. 15:287–296. [DOI] [PubMed] [Google Scholar]
- Kesmir, C., V. Van Noort, R. J. De Boer, and P. Hogeweg. 2003. Bioinformatic analysis of functional differences between the immunoproteasome and the constitutive proteasome. Immunogenetics. 55:437–449. [DOI] [PubMed] [Google Scholar]
- Kisselev, A. F., T. N. Akopian, and A. L. Goldberg. 1998. Range of sizes of peptide products generated during degradation of different proteins by archaeal proteasomes. J. Biol. Chem. 273:1982–1989. [DOI] [PubMed] [Google Scholar]
- Kisselev, A. F., T. N. Akopian, K. M. Woo, and A. L. Goldberg. 1999. The sizes of peptides generated from protein by mammalian 26 and 20S proteasomes. Implications for understanding the degradative mechanism and antigen presentation. J. Biol. Chem. 274:3363–3371. [DOI] [PubMed] [Google Scholar]
- Kisselev, A. F., D. Kaganovich, and A. L. Goldberg. 2002. Binding of hydrophobic peptides to several non-catalytic sites promotes peptide hydrolysis by all active sites of 20S proteasomes. Evidence for peptide-induced channel opening in the α-rings. J. Biol. Chem. 277:22260–22270. [DOI] [PubMed] [Google Scholar]
- Kisselev, A. F., Z. Songyang, and A. L. Goldberg. 2000. Why does threonine, and not serine, function as the active site nucleophile in proteasomes? J. Biol. Chem. 275:14831–14837. [DOI] [PubMed] [Google Scholar]
- Kloetzel, P. M. 2004. Generation of major histocompatibility complex class I antigens: functional interplay between proteasomes and TPPII. Nat. Immunol. 5:661–669. [DOI] [PubMed] [Google Scholar]
- Kohler, A., P. Cascio, D. S. Leggett, K. M. Woo, A. L. Goldberg, and D. Finley. 2001. The axial channel of the proteasome core particle is gated by the Rpt2 ATPase and controls both substrate entry and product release. Mol. Cell. 7:1143–1152. [DOI] [PubMed] [Google Scholar]
- Lee, C., S. Prakash, and A. Matouschek. 2002. Concurrent translocation of multiple polypeptide chains through the proteasomal degradation channel. J. Biol. Chem. 277:34760–34765. [DOI] [PubMed] [Google Scholar]
- Liu, C. W., M. J. Corboy, G. N. DeMartino, and P. J. Thomas. 2003. Endoproteolytic activity of the proteasome. Science. 299:408–411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lowe, J., D. Stock, B. Jap, P. Zwickl, W. Baumeister, and R. Huber. 1995. Crystal structure of the 20S proteasome from the archaeon T. acidophilum at 3.4 A resolution. Science. 268:533–539. [DOI] [PubMed] [Google Scholar]
- Navon, A., and A. L. Goldberg. 2001. Proteins are unfolded on the surface of the ATPase ring before transport into the proteasome. Mol. Cell. 8:1339–1349. [DOI] [PubMed] [Google Scholar]
- Nussbaum, A. K., T. P. Dick, W. Keilholz, M. Schirle, S. Stevanovic, K. Dietz, W. Heinemeyer, M. Groll, D. H. Wolf, R. Huber, H. G. Rammensee, and H. Schild. 1998. Cleavage motifs of the yeast 20S proteasome β subunits deduced from digests of enolase 1. Proc. Natl. Acad. Sci. USA. 95:12504–12509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orlowski, M., C. Cardozo, M. C. Hidalgo, and C. Michaud. 1991. Regulation of the peptidylglutamyl-peptide hydrolyzing activity of the pituitary multicatalytic proteinase complex. Biochemistry. 30:5999–6005. [DOI] [PubMed] [Google Scholar]
- Peters, B., K. Janek, U. Kuckelkorn, and H. G. Holzhutter. 2002. Assessment of proteasomal cleavage probabilities from kinetic analysis of time-dependent product formation. J. Mol. Biol. 318:847–862. [DOI] [PubMed] [Google Scholar]
- Press, W. H., B. P. Plannery, S. A. Teukolsky, and W. T. Vetterling. 1988. Numerical Recipes in C. The Art of Scientific Computing. Cambridge University Press, Cambridge, UK.
- Realini, C., C. C. Jensen, Z. Zhang, S. C. Johnston, J. R. Knowlton, C. P. Hill, and M. Rechsteiner. 1997. Characterization of recombinant REGα, REGβ, and REGγ proteasome activators. J. Biol. Chem. 272:25483–25492. [DOI] [PubMed] [Google Scholar]
- Rechsteiner, M., C. Realini, and V. Ustrell. 2000. The proteasome activator 11S REG (PA28) and class I antigen presentation. Biochem. J. 345:1–15. [PMC free article] [PubMed] [Google Scholar]
- Reidlinger, J., A. M. Pike, P. J. Savory, R. Z. Murray, and A. J. Rivett. 1997. Catalytic properties of 26S and 20S proteasomes and radiolabeling of MB1, LMP7, and C7 subunits associated with trypsin-like and chymotrypsin-like activities. J. Biol. Chem. 272:24899–24905. [DOI] [PubMed] [Google Scholar]
- Reits, E., J. Neijssen, C. Herberts, W. Benckhuijsen, L. Janssen, J. W. Drijfhout, and J. Neefjes. 2004. A major role for TPPII in trimming proteasomal degradation products for MHC class I antigen presentation. Immunity. 20:495–506. [DOI] [PubMed] [Google Scholar]
- Saric, T., C. I. Graef, and A. L. Goldberg. 2004. Pathway for degradation of peptides generated by proteasomes: a key role for thimet oligopeptidase and other metallopeptidases. J. Biol. Chem. 279:46723–46732. [DOI] [PubMed] [Google Scholar]
- Schmidtke, G., S. Emch, M. Groettrup, and H. G. Holzhutter. 2000. Evidence for the existence of a non-catalytic modifier site of peptide hydrolysis by the 20 S proteasome. J. Biol. Chem. 275:22056–22063. [DOI] [PubMed] [Google Scholar]
- Seemuller, E., A. Lupas, D. Stock, J. Lowe, R. Huber, and W. Baumeister. 1995. Proteasome from Thermoplasma acidophilum: a threonine protease. Science. 268:579–582. [DOI] [PubMed] [Google Scholar]
- Sijts, A. J., T. Ruppert, B. Rehermann, M. Schmidt, U. Koszinowski, and P. M. Kloetzel. 2000. Efficient generation of a hepatitis B virus cytotoxic T lymphocyte epitope requires the structural features of immunoproteasomes. J. Exp. Med. 191:503–514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stein, R. L., F. Melandri, and L. Dick. 1996. Kinetic characterization of the chymotryptic activity of the 20S proteasome. Biochemistry. 35:3899–3908. [DOI] [PubMed] [Google Scholar]
- Stohwasser, R., U. Salzmann, J. Giesebrecht, P. M. Kloetzel, and H. G. Holzhutter. 2000. Kinetic evidences for facilitation of peptide channelling by the proteasome activator PA28. Eur. J. Biochem. 267:6221–6230. [DOI] [PubMed] [Google Scholar]
- Tenzer, S., L. Stoltze, B. Schonfisch, J. Dengjel, M. Muller, S. Stevanovic, H. G. Rammensee, and H. Schild. 2004. Quantitative analysis of prion-protein degradation by constitutive and immuno-20S proteasomes indicates differences correlated with disease susceptibility. J. Immunol. 172:1083–1091. [DOI] [PubMed] [Google Scholar]
- Toes, R. E., A. K. Nussbaum, S. Degermann, M. Schirle, N. P. Emmerich, M. Kraft, C. Laplace, A. Zwinderman, T. P. Dick, J. Muller, B. Schonfisch, C. Schmid, et al. 2001. Discrete cleavage motifs of constitutive and immunoproteasomes revealed by quantitative analysis of cleavage products. J. Exp. Med. 194:1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Hall, T., A. Sijts, M. Camps, R. Offringa, C. Melief, P. M. Kloetzel, and F. Ossendorp. 2000. Differential influence on cytotoxic T lymphocyte epitope presentation by controlled expression of either proteasome immunosubunits or PA28. J. Exp. Med. 192:483–494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, R., B. T. Chait, I. Wolf, R. A. Kohanski, and C. Cardozo. 1999. Lysozyme degradation by the bovine multicatalytic proteinase complex (proteasome): evidence for a nonprocessive mode of degradation. Biochemistry. 38:14573–14581. [DOI] [PubMed] [Google Scholar]
- Whitby, F. G., E. I. Masters, L. Kramer, J. R. Knowlton, Y. Yao, C. C. Wang, and C. P. Hill. 2000. Structural basis for the activation of 20S proteasomes by 11S regulators. Nature. 408:115–120. [DOI] [PubMed] [Google Scholar]
- Yewdell, J. W. 2001. Not such a dismal science: the economics of protein synthesis, folding, degradation and antigen processing. Trends Cell Biol. 11:294–297. [DOI] [PubMed] [Google Scholar]
- Yewdell, J. W., E. Reits, and J. Neefjes. 2003. Making sense of mass destruction: quantitating MHC class I antigen presentation. Nat. Rev. Immunol. 3:952–961. [DOI] [PubMed] [Google Scholar]
- Zhang, M., A. I. MacDonald, M. A. Hoyt, and P. Coffino. 2004. Proteasomes begin ornithine decarboxylase digestion at the carboxy terminus. J. Biol. Chem. 279:20959–20965. [DOI] [PubMed] [Google Scholar]







