Measuring Forces between Protein Fibers by Microscopy

Abstract

We propose a general scheme for measuring the attraction between mechanically frustrated semiflexible fibers by measuring their thermal fluctuations and shape. We apply this analysis to a system of sickle hemoglobin (HbS) fibers that laterally attract one another. These fibers appear to “zip” together before reaching mechanical equilibrium due to the existence of cross-links into a dilute fiber network. We are also able to estimate the rigidities of the fibers. These rigidities are found to be consistent with sickle hemoglobin “single” fibers 20 nm in diameter, despite recent experiments indicating that fiber bundling sometimes occurs. Our estimate of the magnitude of the interfiber attraction for HbS fibers is in the range 8 ± 7 kBT/μm, or 4 ± 3 k_BT/μm if the fibers are assumed, a priori to be single fibers (such an assumption is fully consistent with the data). This value is sufficient to bind the fibers, overcoming entropic effects, although extremely chemically weak. Our results are compared to models for the interfiber attraction that include depletion and van der Waals forces. This technique should also facilitate a similar analysis of other filamentous protein assembles in the future, including β-amyloid, actin, and tubulin.

INTRODUCTION

Sickle cell anemia is a blood disorder in which a genetic mutation leads to the transcription of sickle hemoglobin (HbS). A good review of sickle cell anemia, from its molecular basis to the formation of an intracellular sickle hemoglobin gel and the associated pathologies can be found in Eaton and Hofrichter (1990). The main pathology of sickle cell anemia is caused by the physical properties of the sickle hemoglobin gel that forms inside the red blood cells under low oxygen conditions. A consequence of this is that the rigidified red blood cells are unable to circulate through narrow blood vessels and perform their role in oxygen transportation. This exacerbates the deoxygenation of the blood still further, leading to an episode in sufferers of the disease known clinically as a sickle cell crisis.

It has been known for some time that sickle hemoglobin (HbS) differs from normal hemoglobin (HbA) by the presence of a 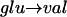substitution at the protein's β6 site. This val substitution leads to the assembly of long, twisted, multistranded fibers at physiological concentrations of deoxygenated HbS. These compose the gel that rigidifies red blood cells. An important result is that under a variety of conditions, a common structure of a 21-nm diameter fiber has been observed. This is referred to as a single fiber.

This single fiber has been found to have a very well-defined structure, being composed of seven double strands of HbS, packed together and twisted about a common axis, with a pitch length of ∼270 nm. Furthermore, single fibers have been observed to form bundles, or macrofibers in HbS gels, and so can be regarded as a fundamental building block of higher order structures.

It has been known for some time that HbS fibers “zip” together to form larger bundles (Briehl, 1995). This is indicative of an attraction between them, and because these fibers compose the gel that is the primary cause of sickle cell crises (Eaton and Hofrichter, 1990), an important step in characterizing the microstructure of these gels is to calculate the strength of this attraction between single fibers.

In what follows we will estimate the magnitude of the interfiber attraction by analyzing a system in which two fibers are observed to partially zip together, in real time. The details of the technique used to provide this data are given in Materials and Methods. These two fibers are mechanically constrained from undergoing complete zippering due to constraining cross-links in the gel. As a result the region of contact between the two fibers extends, eventually reaching a frustrated mechanical equilibrium in which the two fibers form the arms of a “Y” shape (see Figs. 1 and 2). The shape of the fibers gives information about how the energy of attraction per unit length (a force) between the fibers balances the mechanical forces due to the distortion of the fibers. This analysis provides an estimate of the interfiber attraction, σ.

FIGURE 1.

A snapshot of the system obtained using DIC microscopy. Two fibers are observed to merge. The zippered, or adhered, portion of the two fibers forms the stem of the Y shape, on the right, and is referred to as the (composite) third fiber. The distant contacts between these fibers and the gel/network in which they reside, and that stabilize this shape, are not imaged here.

FIGURE 2.

A sketch outlining the basic principle of our analysis. At equilibrium variation of the stored mechanical energy in the fibers balances the variation of interfiber attraction with respect to change in the length of the zippered “stem” (a force balance condition). The inset box indicates how zippering proceeds and results in bending of the fibers. The more rigid, and more tense, the fibers are, the less they will adhere.

Although the focus of this analysis is the frustrated system of fibers described above, our aim is to evaluate the attraction per unit length between single fibers in general (We find that our estimates of the rigidities of our fibers are consistent with HbS single fibers). Therefore, the calculated parameter, σ, that measures the interfiber attraction, will have significance beyond situations where fibers have such constraints. It is an important control parameter for the gel, which has a number of interpretations. For example, it quantifies the thermodynamic stability of macrofibers, gives a surface energy useful to thermodynamic models (Turner et al., 2003) and reveals the extent to which the interfiber attraction under examination stabilizes the gel.

Despite the application of our analysis to a sickle hemoglobin system, it should enjoy wider application to the study of interactions between other filamentous protein assembles, e.g., β-amyloid, actin, tubulin, etc. The mathematics of this analysis is treated in the various parts of the “Quantitative analysis” section.

To calculate the equilibrium force between our fibers we calculate the mechanical energy stored in the fibers, which in turn depends on how much of the contour length of each fiber comes into contact with its partner. Given that the fibers are at mechanical equilibrium with respect to variations in their zippered length, the change in mechanical energy with this length is equivalent to the attraction energy per unit length (force) between the fibers.

The subsection “Fiber Hamiltonans” introduces a free energy for the system and shows how the interfiber attraction, σ, can be expressed in terms of Hamiltonians for the fibers. The forms adopted for these Hamiltonians is also justified in this subsection. The subsection “Variational minimizations of the Hamiltonian to find the equilibrium fiber shape” outlines how variational minimization of the fiber Hamiltonians can be used to derive an expression for the shapes of the fibers in mechanical equilibrium.

The next step in our analysis is to estimate the rigidities of the fibers. Both isolated fibers and those cross-linked into a gel undergo thermal fluctuations, according to the principle of equipartition of energy. Equipartition of energy may be exploited to estimate the rigidities of interacting fibers using a similar approach to work carried out to measure the rigidities of microtubules and actin filaments (Gittes et al., 1993) or of freely suspended HbS fibers (Wang et al., 2002). The rigidity estimates that we obtain for the fibers that comprise our mechanically frustrated structure, are consistent with single fibers, (fibers composed of seven twisted double strands of HbS) rather than bundles of several such fibers, as discussed elsewhere (Wang et al., 2002; Turner et al., 2002). In the subsection “Evaluating rigidities and persistence lengths from fluctuations of the fibers” we indicate how an analysis of fibers' fluctuations are used to estimate their rigidities.

This study provides an estimate of the attractive force between sickle hemoglobin fibers that includes the effects of tensions and torques that act on the observed fibers. Such forces may always be present due to the cross-linked contacts between the fibers and the cross-linked network in which they reside. Our analysis will impose global force and torque balance conditions to close our system of equations, as detailed in the subsection “Calculating σ, the energy of attraction between zippered fibers per unit length,” and thus estimates for the interfiber attraction, σ, may then be calculated.

The Results section presents the results of calculations using the analysis of section 3, when applied to our data of a system of mechanically constrained sickle hemoglobin fibers. Confidence intervals for the fibers' rigidities and the estimate of the interfiber attraction, σ, are given.

The Discussion section discusses the results, and their implications for sickle hemoglobin gels. A comparison is made between this experimentally derived estimate of the interfiber attraction and models for physical interactions due to depletion and Van der Waals attractions, renormalized by thermal fluctuations (Jones et al., 2003).

MATERIALS AND METHODS

Hemoglobin S was purified chromatographically on DE-52, deoxygenated with sodium dithionite in an anaerobic atmosphere and sealed into slides, all near 4°C, as previously described (Briehl and Guzman, 1994). Optical pathlengths were ∼10 μm. Fiber and gel formation was then induced, under microscopic observation, by warming to ∼24°C. Studies were done in 0.1 M potassium phosphate, pH 7.2, using 3.2 mM hemoglobin (20.6 gm/dl). Observations were made by video enhanced differential interference contrast (DIC) microscopy using a Zeiss Axioplan microscope with a 100× plan-neofluar oil objective. Images were obtained with a Hamamatsu Newvicon camera and recorded with a Panasonic super VHS video cassette recorder. Under DIC observation 20-nm diameter single HbS fibers, which cannot be seen by bright field microscopy, appear ∼20 times wider than actual size, so that diameters and hence sizes of fibers cannot be ascertained by direct observation.

QUANTITATIVE ANALYSIS

The aim of this analysis is to calculate the attraction between the fibers per unit length, σ (or equivalently the mechanical energy derivative with respect to the adjacent length of the fibers). In doing so, we also estimate the rigidities of the fibers. The analysis is broken down into the following subsections:

1. Hamiltonians for the mechanical energy in the fibers are introduced and related to the interfiber attraction, σ.

2. A variational minimization of the Hamiltonian is performed to calculate the shapes of the fibers at mechanical equilibrium. Alternative choices of boundary conditions are justified.

3. An analysis of thermal fiber fluctuations is performed to estimate fiber rigidities.

4. Finally global force and torque balance conditions are applied to the system to obtain a closed system of equations and therefore to calculate the contribution of the zippered portion of the fibers to the interfiber attraction.

Fiber Hamiltonians

Referring to Figs. 1 and 2 we see that we may consider the system as being composed of three fiber branches, each representing one arm of a Y shape and joined at the zippering point (defined to be the origin). We label the free arm of the upper fiber as fiber 1, the free arm of the lower fiber as fiber 2, and the zippered portion of the fibers to be the composite fiber 3.

Referring again to Fig. 2, the energy of this mechanically constrained system can be expressed as

(1)

where L₃ is the length of the zippered “stem” of the fibers at mechanical equilibrium. The term, σ, is the attraction per unit of zippered length that holds the fibers together, whereas each H_p is the mechanical energy stored in each fiber.

Zippering will cease when there is an energy minimum with respect to the zippered distance, 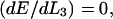and hence the interfiber attraction can be expressed as

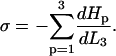(2)

The terms H_p above are Hamiltonians for the energy stored in each of the fibers. To calculate σ we must adopt forms of H_p that express the fibers' mechanical energy in terms of their shape. To do this we describe the shape of each of these fibers in the focal plane by a function u_p(x) (with p ∈ {1, 2, 3}), which measures the displacement of the fiber at x from the x axis (see Fig. 4). This x axis is chosen to pass through the zippering point so that the gradients are zero (u′_p(x) = 0) at the zippering point. Here, and in what follows a prime (′) denotes differentiation with respect to x.

The Hamiltonian that describes the fiber energy must include the contributions associated with bending and tension of the fibers. These terms are included as the leading terms of a truncating expansion of those powers of derivatives of the fiber shape that do not vanish due to symmetry considerations. Thus, we implicitly use a small gradient approximation for our model Hamiltonians that is consistent with the structure of Fig. 2. In this scheme is the bending energy of a fiber per unit length and gives the corresponding contribution due to the action of tension. Both the terms act to raise the energy if the fiber is not straight. Here the parameter, γ, is the tension acting along the fibers, and κ is the fiber rigidity, which is related to the persistence length l_p of the fiber by κ = k_BTl_p.

In addition to the terms representing the energy cost of bending and tension in the fibers, the boundary conditions acting upon the fibers must be incorporated into our model. This is because if the fiber ends were free then both the state of minimum mechanical energy and maximum attractive interaction would correspond to fully zipped, parallel fibers collinear with the x axis (say). Formally there are a number of equivalent ways to incorporate the boundary conditions. One way is to specify the gradient φ_p and displacement Δ_p of the fibers at x = L, where L is chosen to be near the edge of the microscopic field. Alternatively, we may employ the Lagrange multipliers μ and λ for the effective forces and torques, respectively, that act on the fibers to maintain the observed fiber shape. To obtain closure for our equations, we must use both sets of boundary conditions, as explained in the following subsection.

Dropping the p index for the fibers for notational simplicity, we employ the following expression for the Hamiltonian yielding the total energy of each fiber

(3)

Here

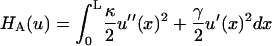(4)

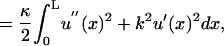(5)

where k is defined to be

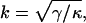(6)

and the boundary conditions are specified in

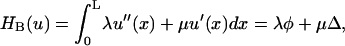(7)

where λ and μ are Lagrange multipliers for the torque and force acting on the fiber at x = L.

Variational minimization of the Hamiltonian to find the equilibrium fiber shape

A variational minimization of the above Hamiltonians was performed (as detailed in Appendix A), to calculate the shape of the fibers in mechanical equilibrium (without fluctuations).

For fibers 1 and 2, which are clearly visible at x = L, we can measure the boundary conditions u₀(x = L) = Δ and u′₀(x = L) = φ from our data. These are then used to express the fiber shapes in the form u₀(x, k, L, Δ, φ) as

(8)

It is useful to note that this form of u₀(x, k, L, Δ, φ) does not depend explicitly on the fiber rigidity κ. Hence the variables k, L, Δ, φ can be obtained by a simple least-squares fit to the above equation for the fiber shape(s), as detailed in Appendix C.

However, from our microscopic data we are not able to clearly see the end of composite fiber 3. It is for this reason that the following expression must also be derived for the fiber shape u₀(x, k, L, λ, μ, κ) in terms of Lagrange multipliers λ and μ for the torque and force acting at x = L;

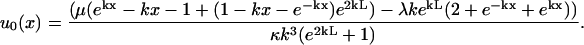(9)

Hence the shape of composite fiber 3 must here be established using a force and torque balance analysis, rather than from direct measurement from the data.

For fibers 1 and 2, these Lagrange multipliers can be related to the measured quantities u₀(x = L) = Δ and u′₀(x = L) = φ by

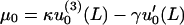(10)

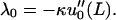(11)

The mathematical equivalence of the two alternate forms for u₀, Eqs. 8 and 9 can be derived using Eqs. 10 and 11.

Evaluating rigidities and persistence lengths from fluctuations of the fibers

We next wish to relate thermal fiber fluctuations to the fiber rigidity(s). Variational minimization of our model Hamiltonians, as described above, indicates that when Eqs. 10 and 11 are satisfied then for small fluctuations δu about an equilibrium fiber shape u₀, the terms in the Hamiltonian involving u₀ and δu decouple and can therefore be considered separately. Hence

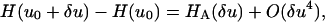(12)

where the O(δu⁴) term can be neglected for small fluctuations. This result is completely natural: one should expect a harmonic (Hookian) response for small fluctuations. The principle of equipartition of energy is then applied (for details see Appendix B), to obtain the following

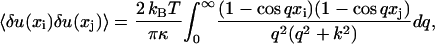(13)

where . This equation represents the thermal contribution to the covariance of deviations of points on the fiber from their average positions at the points x_i and x_j on [0, L] provided that the fiber is cross-linked into the network at a distance Λ far larger than L from the imaged portion.

The values of the fiber rigidities extracted by this method, are described in Appendix C where they are found to be close to the estimated rigidity of single hemoglobin fibers (κ = 130 k_BT μm).

Calculating σ, the energy of attraction between zippered fibers per unit length

In the “Fibers Hamiltonians” subsection we saw how the interfiber attraction, σ, can be related to the chosen Hamiltonians at a point of equilibrium with respect to the adjacent length of fibers L₃ by Eq. 2;

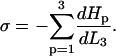The corresponding fiber shapes at this equilibrium have the form u₀, as mentioned in Appendix A. To establish the contribution to the above expression from the composite third fiber, it is necessary to use the form for u₀ for this fiber that involves the Lagrange multipliers for the forces and torques (rather than measured displacement and gradient), which are calculated using the following force and torque balance equations for the system. This is necessary because for the particular microscopic data we are analyzing, the composite third fiber is not clearly visible (and in general fiber 3 will exhibit the smallest displacement and so its shape will anyway have the worst signal/noise properties). Fig. 4 illustrates the forces F_p and torques τ_p acting on each fiber at x = L. Force balance yields two conditions from the vector identity

(14)

whereas torque balance is a scalar identity

(15)

We also adopt the approximation

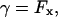(16)

which is valid provided u₀ everywhere has a small gradient.

Calculation of using the form u₀(x, k, L, λ, μ, κ) gives the result

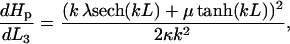(17)

where λ and μ must be calculated from κ, Δ, φ, k using Eqs. 10 and 11 for fibers 1 and 2, whereas for the composite fiber 3, λ, and μ are calculated from force and torque balance as follows.

The following sign convention is employed for the Lagrange multipliers

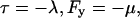(18)

and the linear small gradient approximation 16 allows us to write Eqs. 14 and 15 as

(19)

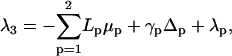(20)

if we choose L₃ = 0.

From Eq. 17 for , we see that L₃ = 0 then simplifies the equation to

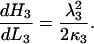(21)

Then from Eq. 2.

To calculate κ₃, the rigidity of the composite third fiber, we use two models that are bounds for its value. One corresponds physically to a case where zippered fibers may be able to smoothly slide past each other so that the rigidities sum

(22)

and would correspond to an upper bound for κ₃.

An upper bound for κ₃ can be specified by the model

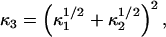(23)

which would physically correspond to the case where the composite fiber formed a cylinder with a cross-sectional area equal to the sum of the cross-sectional areas of fibers 1 and 2, also modeled as cylinders.

RESULTS

As outlined in Appendix C, the confidence intervals for the rigidities of fibers 1 and 2 are

(24)

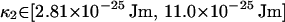(25)

which correspond (using κ = k_BTl_p) to the fiber persistence lengths

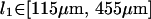(26)

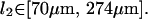(27)

This is entirely consistent with the hypothesis that our system is composed of HbS single fibers, based on literature values for their persistence lengths (Wang et al., 2002), (M. S. Turner, unpublished data).

The confidence interval for the interfiber attractive energy per unit length, σ is

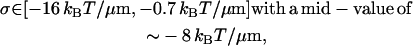(28)

using the model Eq. 22 for the rigidity κ₃ of the composite third fiber, whereas using the model Eq. 23 for κ₃ gives

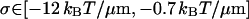(29)

If we assume that our system is composed of single HbS fibers (as is consistent with the fiber persistence lengths Eqs. 26 and 27), then the above ranges for σ become respectively

(30)

when the model Eq. 22 is employed for κ₃, and

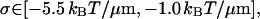(31)

when Eq. 23 is used for κ₃.

These estimates of σ can be used to calculate the strength of attraction between crossed fibers. The energy of attraction will be E = σd, where d is the typical lengthscale over which the attraction acts between the fibers, for which we use the fiber diameter of 21 nm. This would give E ∼ 0.1 k_BT, much less than the characteristic energy scale k_BT in this system. Therefore, we can see that the estimate of our lateral attraction σ that we have calculated is not sufficient to explain cross-links between sickle hemoglobin fibers. There must, therefore, be another mechanism responsible for cross-links of the fibers.

DISCUSSION

This study represents the first measurement of interfiber force between protein filaments of which we are aware. It has potential applications to systems containing other biological fibers, such as actin or amyloid filaments, provided only that they attract laterally (i.e., zip together).

In the case of sickle cell anemia, it is the physical properties of the intracellular sickle cell hemoglobin (HbS) gel that are the cause of the main pathology to the function of red blood cells. To relate these properties of the gel to its fibrillar microstructure, it is necessary to understand the mechanism that stabilizes the various structures encountered at this lengthscale. Because the HbS single fiber that is so ubiquitous in HbS gels has a well-defined structure, and is known to bundle into macrofibers, a calculation of the attraction σ between single fibers provides a very useful parameter for understanding these gels. Indeed, the estimates of the rigidity that we extract are consistent with the fibers under scrutiny themselves being single fibers.

As illustrated in Fig. 5, our estimates for σ (28, 29, 30, and 31) give us information that may help in understanding a number of properties of the gel as follows:

It directly quantifies the magnitude of this lateral attraction in stabilizing the networks of fibers. As calculated in the Results section, our estimate of the interfiber attraction is insufficient to explain observed cross-linking of fibers, and therefore this phenomenon must be due to a separate mechanism. Nevertheless, the lateral attraction σ that we calculate may still play a significant role in stabilizing the gel microstructure. It would be important in any future model or computer simulation of the fiber networks that compose the gel within a red blood cell.

The estimates of σ also give us information on the binding energy between bundles of single sickle hemoglobin fibers that make up the more rigid macrofibers in the gel.

Estimates of σ can additionally be related to the surface energy of sickle hemoglobin as would be important in thermodynamic models (see, e.g., Turner et al., 2003).

Furthermore, our estimates of the rigidities of the fibers (24, 25) can be exploited as a novel way of identifying the type of fiber under observation, despite the limitations of the resolution of the microscopic data. In this case the rigidities estimated are consistent with literature values for single sickle hemoglobin fibers (Wang et al., 2002).

The above confidence intervals for σ indicate that the interfiber attraction is chemically weak but sufficient to overcome entropic effects and therefore are able to stabilize bundles of sickle hemoglobin single fibers, as discussed elsewhere (Jones et al., 2003).

There exists previous work in which depletion and Van der Waals interactions between pairs of hemoglobin fibers were estimated (Jones et al., 2003). The estimate for the interfiber attraction, including effects due to the helical geometry of the fibers and due to thermal bending fiber fluctuations where a hydration layer was introduced as an (arbitrary) 5-Å minimum fiber separation is

As a result of the semiqualitative nature of these theoretical estimates, this number should be regarded as encouragingly close to the improved experimental result described in this study (28, 29, 30, and 31).

It is also worth noting that we have assumed that there is little aggregation of the monomers, apart from those fibers under scrutiny. If there was a significant reduction in the monomer concentration due to aggregation into structures of size intermediate between monomers and single fibers, this would lower the osmotic pressure of HbS in the solution, and reduce the depletion attraction between the fibers. A reduction of the attractive force between fibers would also result from any weak attraction that may exist between monomeric HbS and the fibers.

The analysis of frustrated systems of sickle hemoglobin fibers presented here indicates that depletion forces, as well as Van der Waals forces, may play a significant role in the mechanism of fiber zippering.

APPENDIX A: VARIATIONAL MINIMIZATION OF HAMILTONIANS TO FIND EQUILIBRIUM FIBER SHAPE U₀

The mechanical equilibrium shape of the fibers will be that which minimizes the fibers' respective Hamiltonians H (in the absence of thermal fluctuations). In this way we determine the equilibrium fiber shape u₀ using variational minimization to the integral Eq. 3. This is consistent with the treatment given in, e.g., Landau and Lifshitz (1986).

Consider the fiber shape u(x) = u₀(x) + δu(x) where δu(x) is a small deviation (fluctuation) about the equilibrium fiber shape, u₀(x). Then we have that

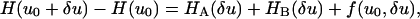(32)

where the functional f(u₀, δu) includes only cross terms linear in both u₀ and δu. Performing a variational minimization of Eq. 32 using the boundary conditions δu(0) = 0, and δu′(0) = 0 while neglecting terms quadratic in δu gives a fourth-order ordinary differential equation in x for the fiber shape. It also relates the Lagrange multipliers μ and λ for the effective forces and torques acting at x = L to the equilibrium fiber shape u₀. Our ordinary differential equation for the fiber shape is

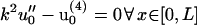(33)

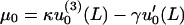(34)

(35)

where a new characteristic inverse length k appears defined by

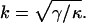(36)

The boundary conditions u₀(0) = 0, and u′₀(0) = 0 at the zip point are used to determine u₀. These boundary conditions, together with the boundary conditions Eqs. 34 and 35 (for the Lagrange multipliers for the effective force and torque at x = L), yield the following solution to Eq. 33 for the average fiber shape of the form u₀(x, k, L, λ, μ, κ) given in Eq. 9

Some of the utility of this form lies in the fact that the displacement of the zippered part of the system (composite fiber 3) was not clearly observed in our experimental procedure (in general, fiber 3 will exhibit the smallest displacement and its shape will anyway have the worst signal/noise properties). Hence, the shape of composite fiber 3 must here be established using a force and torque balance analysis, rather than from direct measurement from the data.

If instead of solving Eq. 33 using the boundary conditions Eqs. 34 and 35, we use the (measured) boundary conditions u₀(x = L) = Δ and u′₀(x = L) = φ then we obtain u₀(x, k, L, Δ, φ) given by Eq. 8, which does not depend explicitly on the fiber rigidity κ. Hence the variables k, L, Δ, φ can be obtained by a simple least-squares fit to the above equation for the fiber shape(s), as detailed in Appendix C.

APPENDIX B: CORRELATION FUNCTIONS IN FOURIER SPACE

Initially it may seem that the way to proceed in analyzing the statistical mechanics of fiber fluctuations would be to consider the Hamiltonian H_A(δu) as defined in Eq. 4, where the range of the integration is over [0, L]. In fact this is not possible because our analysis of fluctuations relies on the use of a Fourier series expansion for the fluctuations in the fiber slope u′, to exploit the orthogonality of its Fourier amplitudes. There is no such choice of Fourier series for either δu or its derivatives that satisfies the boundary conditions δu(x = 0) = δu′(x = 0) = 0 but δu(x = L) and δu′(x = L) unspecified and with uncorrelated Fourier coefficients.

We, therefore, specify our Hamiltonian over the much larger, but still finite, domain x ∈ [0, Λ] on which an orthogonal Fourier series can be chosen that does not explicitly violate our boundary conditions for δu at x = L. If Λ is far enough away from L then choosing a Fourier series that constrains the gradient δu′(x = Λ) will have a negligible effect on the fiber shape at x = L. We therefore define

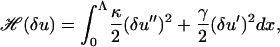(37)

as our Hamiltonian for the fiber fluctuations. Because Eq. 37 only contains derivatives of δu we define

(38)

We consider w(x) as being odd on the extended domain [−Λ, Λ] so that w(x) may be expressed as a Fourier sine series, which ensures w(0) = 0, consistent with our assumed boundary conditions for δu′ at x = 0.

Because the set 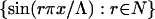is orthogonal on [0, Λ] then the Fourier series

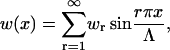(39)

can be substituted into the Hamiltonian Eq. 37. Exploiting these orthogonality properties allows the Hamiltonian to be expressed in a form quadratic in the Fourier coefficients, w_r.

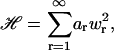(40)

where . We now wish to calculate the ensemble average of the quantity w_nw_m, which is the product of two of the Fourier modes in the series for w(x). This is given by

(41)

where and Z is the partition function,

(42)

Because the exponential term in both Eqs. 41 and 42 may be written 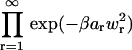, we can factorize 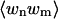and divide out all terms for which r ≠ n, m. Thus

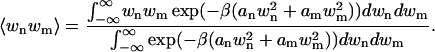(43)

If n ≠ m further factorization is possible, which gives a zero ensemble average by symmetry. If, however, n = m, then as usual we have

Thus

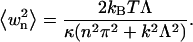(44)

Using the result that for n ≠ m and the definition Eq. 38 gives

(45)

where δu(x_i) and δu(x_j) are displacements at two points on the same fiber. As Λ becomes larger, the above sum will tend to the result Eq. 13.

APPENDIX C: ANALYSIS OF THE DATA

Fitting the parameters Δ, φ, k to the data

The parameters Δ, φ and k were fitted to fibers 1 and 2 using measurements taken from the data. (This procedure could not be carried out for the composite third fiber because it was not clearly visible, and so a force and torque balance analysis was applied to the system instead to calculate the mechanical contribution of the third fiber to the interfiber attraction σ.) Twelve images from the video data were selected for the analysis on the grounds of clearly showing a sufficiently large enough region of the system, and also being separated by sufficient time intervals (>1 s) for the fluctuations to be temporally uncorrelated.

For each of these 12 images an x axis was chosen so as to pass through the zip point, tangentially to the fibers, consistent with the assumed boundary conditions u₀(x = 0) = u′₀(x = 0) = 0. Next the perpendicular distances y_i of the fiber from the x axis are measured at six equally spaced points for x ∈ [0, L] (Fig. 3), the last of these points being at x = L. This allows us to specify Δ and φ for each fiber. We then perform a least-squares fit of the model fiber shape to the y_i using the form u₀ = u₀(x, k, L, Δ, φ) to fit a value of k to each fiber in each image.

FIGURE 3.

This sketch shows how the x axis is defined so as to pass tangentially through the point at which adjacent fibers part from each other. This point is referred to as the “zip” point. The thick dashed lines represent fiber that is not in the focal plane and indicate that the system is constrained by boundary conditions that lie outside of the field of visualization of the data. The narrow dashed lines indicate positions where the fiber displacements were measured, see Table 1.

FIGURE 4.

Sketch of the forces and torques acting on the fibers. At equilibrium the two components of force and the (scalar) force moment must balance.

FIGURE 5.

Diagrammatic summary of the various physical properties controlled by interfiber attraction (σ), which is related to the surface energy of the fiber. Sketch 1 represents a network of sickle hemoglobin fibers, bound together by interfiber forces. Sketch 2 represents a bundle of HbS fibers that is also stabilized by interfiber forces. Sketch 3 represents the fact that the interfiber forces can be related to the surface energy of a fiber, which is necessary to determine a thermodynamic model of the fibers (e.g., Turner et al., 2003).

This procedure gives for each of the twelve images, a set {Δ, φ, k}, where each k extracted corresponds to a tension γ = k²κ. The resulting values of the parameters {Δ, φ, k} are displayed in Table 1.

TABLE 1.

Fitted values of k, Δ, φ to each image for fibers 1 and 2

Image	Time (s)	k1 (μm−1)	Δ1 (μm)	φ1	k2 (μm−1)	Δ2 (μm)	φ2
1	00:28:30:37	−0.167	3.97	0.55	0.741	−3.86	−0.40
2	00:28:31:04	0.102	3.44	0.40	0.396	−4.38	−0.50
3	00:28:32:14	0.255	4.28	0.45	0.284	−3.76	−0.45
4	00:28:32:94	0.123	3.97	0.50	0.740	−3.76	−0.45
5	00:28:34:28	−0.128	4.17	0.45	0.313	−2.92	−0.35
6	00:28:39:68	−0.143	3.55	0.40	0.429	−3.34	−0.40
7	00:28:41:58	0.165	3.97	0.40	0.277	−2.92	−0.40
8	00:28:42:12	0.419	3.13	0.30	0.588	−4.38	−0.50
9	00:28:42:85	0.103	2.82	0.35	0.282	−4.49	−0.50
10	00:28:44:08	0.281	3.23	0.30	0.462	−3.76	−0.40
11	00:28:44:75	0.145	3.03	0.35	0.286	−4.07	−0.50
12	00:28:45:35	0.302	3.23	0.40	0.137	−4.28	−0.50

If we assume that these variables are Gaussian distributed, then 95% Student's t-test confidence intervals for the values of these variables are

Establishing confidence intervals for the fiber rigidities; multivariate Gaussian distribution

By considering the form of the ensemble average and examining the form of the Hamiltonian H(δu) Eq. 37, it can be seen that the measurements y_i have a multivariate (i.e. correlated) Gaussian distribution. The probability density function of this distribution is Cowan (1998)

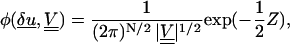(46)

where

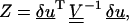(47)

is a quantity that has a χ-squared statistical distribution (Cowan, 1998). Here N is the number of data points (in this case 6), and δu is a vector of the fiber fluctuation measured at six points x_i, defined by δu_i = y_i(x_i) −u₀(x_i, k, L, Δ, φ).

The covariance matrix 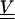is defined by

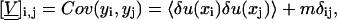(48)

where 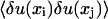is the covariance of thermal fiber fluctuations as defined in Eq. 13. The quantity mδ_ij represents the noise arising from the error of measurement, which only contributes to diagonal elements of the covariance matrix 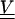. The greatest accuracy that our method of measurement of y_i gives us is ±50 nm. If the measurement is uniformly distributed in this interval, then its variance is (29 nm)². This is the value we use for m in the above equation.

So for each fiber in each image we calculate the statistic

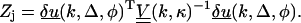(49)

Because the previous subsection of this appendix fitted values for the parameters {Δ, φ, k} as shown in Table 1 then the only unknown parameter in Eq. 13 is therefore κ. To establish a meaningful confidence interval for κ we need to consider the statistics of all of the images together. This is achieved by taking the sum of the χ-squared variables over all of the images.

(50)

We utilize the fact that the sum of independent χ-squared variables is also a χ-squared variable, which is justified because fiber fluctuations in different data images are independent, although they share the same distribution, which depends on the underlying values of the parameters {k, κ, Δ, φ}.

This has a χ-squared distribution, and because there are 72 measurements, but three fitted parameters {k, Δ, φ} we construct a 95% confidence interval for κ by comparing Z_tot to a χ-squared distribution on 69 degrees of freedom.

The values of {k, Δ, φ} that are used are taken from the confidence intervals of the previous subsection. The calculation of Z_tot Eq. 50 is repeated for each combination of the bounds of these confidence intervals. It is in this way that uncertainty in the values of {k, Δ, φ} is incorporated into our confidence interval for κ. Because this generates a slightly different confidence interval for each repetition, the maximum and minimum values of these confidence intervals are taken as bounds for κ, which are

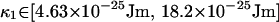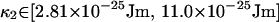The corresponding persistence lengths of the fibers from κ = k_BTl_p are

This is entirely consistent with the hypothesis that our system is composed of HbS single fibers, based on literature values for their persistence lengths.

Modeling the forces that act on a frustrated system of fibers; the small gradient (small curvature) approximation

Given the confidence interval for κ for each fiber, based on an analysis of all of the images together, and for each fiber in each image we now have fitted values for {k, Δ, φ}. These are now used to generate values for σ to establish its bounds.

Given that for each fiber, there is a confidence interval of the form κ ∈ [κ min, κ max ], each one of these bounds in turn is used to calculate values of λ and μ using Eqs. 10 and 11, and the set of values of {k, Δ, φ} that were fitted to each fiber in each image. Therefore, for each bound for κ, a set {k, λ, μ} is generated for each fiber in each image. Equations 19 and 20 are then applied where γ = κk² to calculate λ and μ for the composite third fiber, which has L₃ ≡ 0 and κ₃ given in Eqs. 22 and 23. Then the contribution to σ from each fiber was evaluated using Eqs. 17 and 21, for each of the bounds of κ ∈ [κmin, κmax]. The interfiber attraction σ is then the sum of these contributions.

Of all of the values of σ generated by the above procedure, the upper and lower bounds are taken, giving the following bounds for our attraction, σ when we use a model Eq. 22 for κ₃.

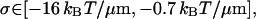(51)

whereas using the model Eq. 23 for κ₃ gives

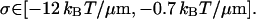(52)

If we assume that the persistence length of the fibers analyzed is 130 μm, then the corresponding ranges for σ are

(53)

when model Eq. 22 is employed for κ₃, and

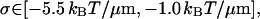(54)

when Eq. 23 is used for κ₃.