Exploring the Helix-Coil Transition via All-Atom Equilibrium Ensemble Simulations

Abstract

The ensemble folding of two 21-residue α-helical peptides has been studied using all-atom simulations under several variants of the AMBER potential in explicit solvent using a global distributed computing network. Our extensive sampling, orders of magnitude greater than the experimental folding time, results in complete convergence to ensemble equilibrium. This allows for a quantitative assessment of these potentials, including a new variant of the AMBER-99 force field, denoted AMBER-99φ, which shows improved agreement with experimental kinetic and thermodynamic measurements. From bulk analysis of the simulated AMBER-99φ equilibrium, we find that the folding landscape is pseudo-two-state, with complexity arising from the broad, shallow character of the “native” and “unfolded” regions of the phase space. Each of these macrostates allows for configurational diffusion among a diverse ensemble of conformational microstates with greatly varying helical content and molecular size. Indeed, the observed structural dynamics are better represented as a conformational diffusion than as a simple exponential process, and equilibrium transition rates spanning several orders of magnitude are reported. After multiple nucleation steps, on average, helix formation proceeds via a kinetic “alignment” phase in which two or more short, low-entropy helical segments form a more ideal, single-helix structure.

INTRODUCTION

Although protein folding has been a primary focus of biophysical study for the last few decades, a complete quantitative understanding of the most elementary and ubiquitous of protein structural elements remains a great challenge. This is true even of the α-helix, the fastest folding and most geometrically simple of protein substructures. In the past, limitations in our understanding were induced predominantly by limited computational power and the limited temporal resolution of experimental approaches. As new experimental techniques begin to reach the short timescales necessary to study fundamental folding processes, the barrier between theory and experiment often now lies in the quality of the computation itself. At its most fundamental level, much of biocomputation depends on the accuracy of atomistic potential sets such as AMBER, CHARMM, and OPLS, and the quality of the sampling performed. Indeed, previous potential set assessment consisted primarily of too few simulations to adequately compare to bulk experimental results.

Recently it has been shown that a large, extremely heterogeneous ensemble of individual molecular dynamics (MD) trajectories can average out to give a very simple (and perhaps oversimplified) picture of biomolecular assembly on the bulk level (Shimada and Shakhnovich, 2002; Sorin et al., 2004), supporting a recent suggestion that unobserved intermediates can be present even in the simplest of “two-state” systems (Daggett and Fersht, 2003). The most comprehensive test of any force field will therefore include characterization of the predictions made by that potential on an ensemble level, a daunting computational task even for the most elementary of systems. Still, a distributed computing effort can greatly advance computational studies of protein and nucleic acid folding (Pande et al., 2003; Snow et al., 2002; Sorin et al., 2004, 2003; Zagrovic et al., 2001) as well as the validation of solute and solvent force-field accuracy and applicability (Rhee et al., 2004; Shirts et al., 2003; Zagrovic and Pande, 2003a), by greatly increasing the possible sampling time used to evaluate the accuracy and predictive power of current models.

We now apply our global distributed computing network (http://folding.stanford.edu) to assess biomolecular potentials in an absolute sense on all aspects of the helix-coil transition. Here we report the first absolute convergence to equilibrium in silico between all-atom native and unfolded ensembles for two helical polymers in explicit solvent, thus allowing simultaneous evaluation of the thermodynamic, kinetic, and structural predictions defined by each force field studied. This result has three major implications. First, the ability to reach absolute convergence allows one to test the validity of other sampling methods, such as replica exchange techniques. Second, it signals the oncoming ability to test and improve computational models (such as potential sets) through direct, quantitative comparison to bulk experiment. Finally, such comparisons offer direct insight into biopolymeric self-assembly through the successes and failures of current models alike. We take a step in this direction by considering the most elementary protein subunit: the α-helix.

What are the general rules of helix formation? Although some ultrafast kinetics measurements of the helix-coil transition have been adequately modeled as a two-state dynamics (Lednev et al., 1999a, 2001; Thompson et al., 1997, 2000; Williams et al., 1996), other experimental results show evidence for a multiphasic kinetics (Huang et al., 2001; Kimura et al., 2002; Yoder et al., 1997). Furthermore, Huang et al. have recently demonstrated a dependence of relaxation rates in laser temperature-jump (T-jump) experiments on both the initial and final temperatures, thus suggesting that the helix-coil transition is a conformational diffusion search process (Huang et al., 2002). With this ongoing debate and the small molecular size of helical polypeptides relative to more complex protein structures, a significant amount of interest in helix-coil processes has been generated in the simulation community within the last decade.

The Caflisch and Duan groups have extensively studied helix formation in implicit solvent. Ferrara et al. (2000) studied helix formation in the (AAQAA)₃ peptide with the CHARMM united atom force field (Brooks et al., 1983) using a distance-dependent dielectric continuum solvent model at temperatures from 270 to 420 K, totaling 1.42 μs. They reported a single free energy minimum at all temperatures and multiple folding pathways resulting in non-Arrhenius kinetics (Ferrara et al., 2000), supporting the diffusion search model of the helix-coil transition mentioned above. In contrast, Duan and co-workers (Chowdhury et al., 2003) reported three distinct kinetic phases in helix folding after collecting 32 100-ns trajectories of the AK16 peptide [Ace-YG(AAKAA)₂AAKA-NH₂] under a variant of the AMBER-94 potential using a generalized Born (GB) continuum solvent model. They observed subnanosecond nucleation, propagation to helical intermediates on the nanosecond timescale, and a transition state defined by a helix-turn-helix motif with significant hydrophobic interactions between opposing helical segments, suggesting that the rate-limiting step in helix formation is the breaking of these hydrophobic contacts. Similar behavior for the polyalanine based helix-forming F_s peptide was reported using GB solvent, with the helix-turn-helix motif being the predominant population at 300 K (Zhang et al., 2004).

Hummer and co-workers employed an explicit solvent representation to simulate the folding of the polyalanine pentamer (A₅) under the AMBER-94 force field at multiple temperatures (Hummer et al., 2000, 2001), reporting barrierless helix formation modeled as a diffusive search process. Although the studies of Hummer et al. strongly suggest that the nucleation process is in fact a diffusive search for the helical region of the phase space, this small peptide may not be representative of the dynamics expected of larger helix-forming peptides and, prior to this report, the effects of the heliophilicity inherent to the AMBER-94 potential remained unclear.

Garcia and co-workers studied two 21-residue helical peptides, for which we report equilibrium simulation results herein: the capped alanine homopolymer A₂₁ (Ace-A₂₁-NMe), which is naturally insoluble in water, and the F_s peptide (Ace-A₅[AAAR⁺A]₃A-NMe), a soluble α-helical arginine-substituted analog of A₂₁. Using a replica exchange molecular dynamics (REMD) methodology, with a total sampling time of ∼1.7 μs, they showed that AMBER-94 overstabilizes helical conformations in both peptides (Garcia and Sanbonmatsu, 2001) by comparing the Lifson-Roig (LR) helix-coil parameters (Lifson and Roig, 1961; Qian and Schellman, 1992) derived from simulation to the experimentally determined values. In response to the poor agreement resulting from that comparison, they introduced a modified potential (which we refer to herein as “AMBER-GS”) in which the φ and ψ torsion potentials in the original AMBER-94 are set to zero, and found much better agreement with experimental helix-coil parameters. In comparing the two sequences they reported a shielding of backbone carbonyl oxygen atoms from the surrounding aqueous media by the large arginine (Arg) side chains four residues downstream acting to stabilize helical polyalanine based peptides with such insertions, as suggested in previous studies (Vila et al., 2000; Wu and Wang, 2001). Additionally, Nymeyer and Garcia compared GB implicit solvation with an explicit (TIP3P) representation of the solvent and showed that the implicit model significantly favors a nonnative, compact helical bundle in simulations of F_s (Nymeyer and Garcia, 2003), suggesting that an explicit representation of the solvent may be needed to most accurately capture helix-coil dynamics in simulation.

The work of the Garcia group in this area has been seminal. Specifically, Garcia and Sanbonmatsu applied new methodology (in their case, replica exchange molecular dynamics) to greatly advance the sampling possible and to make quantitative predictions of helix properties. We expect that others will follow in their footsteps and use advanced sampling methods to further improve contemporary force fields. Moreover, improved sampling methods and improved models will go hand in hand: as sampling methodology advances, so too will our ability to improve upon the accuracy of the models employed. Still, several questions remain regarding simulation methods on the helix-coil transition, and recent work has suggested that typically used REMD convergence protocols may not be sufficient to quantitatively assess thermodynamic equilibrium (Rhee and Pande, 2003). Also, greatly increased statistics should have a significant impact on our ability to compare with bulk experiments.

Indeed, one of the goals of the following report is to use a degree of sampling that was previously not possible to improve our ability to predict helix-coil properties, and to then use these predictions to improve upon the accuracy of biomolecular potential sets as applied to a model helix-coil system. Specifically, we seek to better understand helix-coil dynamics by performing ensemble level helix-coil equilibrium simulations, which begin in nonequilibrium (1000 fully native and 1000 fully unfolded starting conformations per force field, per polymer) and converge to thermodynamic equilibrium at a biologically relevant temperature (305 K, the approximate F_s midpoint temperature detected by circular dichroism, Thompson et al., 1997; and ultraviolet resonance Raman, Ianoul et al., 2002). Additional nonambient temperatures were also studied to probe the ability of these force fields to adequately account for the temperature dependence of helical character. The resulting analyses thus make it possible to greatly increase our understanding of both the helix-coil transition and the dependence of simulation results on the force field employed.

We report below the unbiased, all-atom equilibrium ensemble simulations of A₂₁ and F_s, the latter of which has been characterized experimentally on the nanosecond to microsecond regime (Lednev et al., 1999b, 2001; Lockhart and Kim, 1992, 1993; Thompson et al., 1997, 2000; Williams et al., 1996; Yoder et al., 1997) using standard versions of the AMBER-94 (Cornell et al., 1995), AMBER-96 (Kollman et al., 1997), and AMBER-99 (Wang et al., 2000) potentials. Additionally, the effect of modifying backbone torsional potentials in these force fields was probed. In standard molecular mechanics force fields, such as AMBER, torsional potential energies are defined by sum of one or more periodic functions,

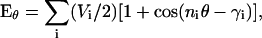(1)

where V_i is the amplitude, n_i is the multiplicity, and γ_i is the phase for the i^th term in the expansion, and θ is the torsion angle. The (φ,ψ) potential energy surface for a given force field is then the sum of these terms for the backbone φ and ψ torsions, as shown in Fig. 1 for the AMBER potentials discussed in this work.

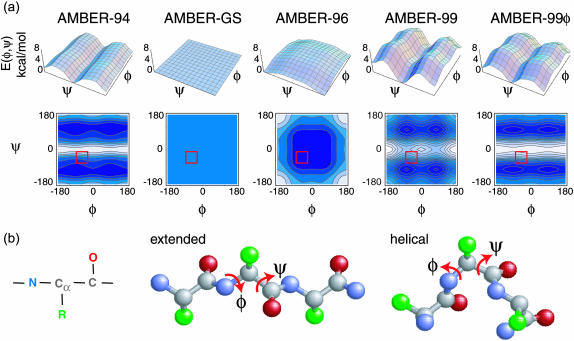
FIGURE 1.

Backbone torsion potentials of the force fields studied. (a) The (φ,ψ) potentials for the AMBER all-atom force fields assessed in this study are shown in three-dimensional form and scaled to represent relative energy differences between them. Contours are drawn at nkT levels for 0 ≤ n ≤ n_max, and red boxes indicate the region of the phase space considered helical for Lifson-Roig calculations based on assessing the dependence of LR parameters on the (φ,ψ) cutoff as described in the text. The AMBER-GS potential is zero for the entire space and the helical regime lies on the maximum energy plateau of the AMBER-96 potential. AMBER-99 includes rotational barriers greater than kT along φ that are not present in the heliophilic AMBER-94. These barriers are removed in our AMBER-99φ variant. (b) The peptide unit: heavy-atom ball-and-stick representations of the peptide backbone showing the rotatable backbone φ and ψ torsions for the fully extended peptide and the ideal helix conformation.

The force field of Cornell et al., most commonly referred to as AMBER-94 (Cornell et al., 1995), is one of the most widely used of contemporary all-atom potentials and has become well characterized in the literature. The AMBER-96 potential (Kollman et al., 1997) differs from AMBER-94 only due to changes in backbone (φ,ψ) torsion potentials. As expected from the energetic maximum in AMBER-96 that includes the helical region of the phase space (Fig. 1), this potential favors extended conformations (Ono et al., 2000): these ensembles rapidly unfolded and were therefore not considered in quantitative aspects of the following analysis. As noted above, the AMBER-GS potential introduced by Garcia and Sanbonmatsu (2001) also differs only slightly from the force field of Cornell et al. (1995). The published modification made by Garcia and co-workers was the removal of φ and ψ torsional terms from the original AMBER-94 potential (Fig. 1), and this modification was reported to greatly decrease the known heliophilicity inherent to AMBER-94 (Garcia and Sanbonmatsu, 2001).

However, Garcia and Sanbonmatsu made an additional modification to the Cornell force field in producing the AMBER-GS potential used in their original study (Garcia and Sanbonmatsu, 2001), which was detailed in a later publication (Nymeyer and Garcia, 2003): 1–4 van der Waals interactions, which account for hard-core repulsion and soft-core attraction between atoms separated by three covalent bonds, were scaled differently than in the standard AMBER potentials (i.e., not reduced by a factor of 2 in their simulations; A. Garcia, personal communication). Recent reports remove (φ,ψ) terms from AMBER-94 but do not remove the standard AMBER scaling of 1–4 van der Waals interactions (Rhee et al., 2004; Zaman et al., 2003). This study follows suit in retaining the standard AMBER scaling rules and we therefore use the “AMBER-GS” moniker to refer to the Cornell force field with (φ,ψ) torsion terms removed. We have also examined the effects of modifying backbone torsions and scaling terms and find only minor differences in helical content between the scaled and nonscaled ensemble properties for AMBER-GS (Sorin and Pande, 2005). Assessment of the AMBER-94 and AMBER-GS potential sets described below, as judged by the ability to accurately predict experimentally observed rates, LR equilibrium helical parameters (Lifson and Roig, 1961; Qian and Schellman, 1992), and ensemble averaged structural features, shows that the both potentials significantly overstabilize helical conformations, with AMBER-GS increasing the heliophilicity over the original AMBER-94 potential.

The AMBER-99 potential (Wang et al., 2000) includes additional differences in torsional and angle potentials, distinguishing this force field from the former three. Most notably, AMBER-99 includes additional energetic barriers (greater than kT in magnitude) about the φ torsion angle (Fig. 1). Because the AMBER-99 potential was parameterized based on the alanine dimer and trimer, one might expect this force field to perform well in comparison to its predecessors for polyalanine-based helix-forming sequences. However, we show below that this force field greatly understabilizes polyalanine-based helices. Indeed, a test of the solvated F_s peptide in AMBER-99 using the AMBER molecular dynamics package shows that this helical peptide unfolds on the subnanosecond timescale (data not shown) followed by sporadic formation of 3₁₀ and α-helical nuclei, which most often occur near the terminal regions. Interestingly, Simmerling and co-workers (Okur et al., 2003) studied the β-forming tryptophan zipper sequence SWTWENGKTWK and the α-helical sequence IDYWLAHKALA using AMBER-99, reporting the apparent stabilization of nonnative helical structure in the terminal regions for both sequences. Thus, while this potential understabilizes model polyalanine-based α-helical peptides, a favoring of terminal helical backbone conformations is apparent.

In an attempt to rectify these differences and inadequacies, we considered the torsional potentials in (φ,ψ) space and tested a new potential, which we refer to as “AMBER-99φ.” The central idea in our modification of the original AMBER-99 potential is that the low overall helical content predicted by that potential, in comparison to the AMBER-94 force field, results primarily from the added barriers about the φ rotation degree of freedom, which is apparent in Fig. 1. We thus removed these φ barriers in AMBER-99 by employing the original AMBER-94 φ torsion potential with the goal of better reproducing experimental helix thermodynamics and kinetics for F_s. We show below that this one modification to the heliophobic AMBER-99 potential results in a significant improvement over the original AMBER force fields in studies of the helix-coil transition in polyalanine-based peptides. The AMBER-99φ simulation ensembles are therefore used to gain insight into the helix-coil transition from an equilibrium ensemble perspective. Although it is unclear whether our torsional modification is an improvement for nonhelical peptides, the goal of this study was to best reproduce experimental properties to better understand the helix-coil transition. Indeed, one of the next steps in force-field evolution will be to test and further develop models for their ability to predict both α-helical and β-sheet properties and propensities.

METHODS

Simulation protocol

The capped A₂₁ (Ace-A₂₁-NMe) and F_s (Ace-A₅[AAAR⁺A]₃A-NMe) peptides were each simulated using the AMBER-94 (Cornell et al., 1995), AMBER-96 (Kollman et al., 1997), AMBER-GS (Garcia and Sanbonmatsu, 2001), AMBER-99 (Wang et al., 2000), and AMBER-99φ all-atom potentials ported into the GROMACS molecular dynamics suite (Lindahl et al., 2001) as modified for the Folding@Home (Zagrovic et al., 2001) infrastructure (http://folding.stanford.edu). The default scaling factors of 1/2 and 1/1.2 were applied to 1–4 Lennard-Jones and Coulombic interactions, respectively, as described for AMBER all-atom potentials (Cornell et al., 1995; Duan et al., 2003; Kollman et al., 1997; Wang et al., 2000).

For both the A₂₁ and F_s sequences a canonical helix (φ =−57°, ψ=−47°) and a random coil configuration with no helical content were generated and centered in 40-Å cubic boxes. The charged F_s peptide was neutralized with three Cl⁻ ions placed randomly around the solute with minimum ion-ion and ion-solute separations of 5 Å. Each system was then solvated with the following total number of TIP3P (Jorgensen et al., 1983) water molecules: native A₂₁, 2091; unfolded A₂₁, 2082; native F_s, 2075; unfolded F_s, 2065. After energy minimization using a steepest descent algorithm, and solvent annealing for 500 ps of MD with the peptide conformation held fixed, these four starting conformations served as the starting point for 1000 independent MD trajectories in each AMBER potential and temperature reported, which were simulated on ∼20,000 personal CPUs. Table 1 details the sampling obtained for each F_s peptide ensemble studied including the maximum individual simulation length in nanoseconds (Maximum) and total ensemble sampling time in microseconds (Total).

TABLE 1.

Simulated ensemble statistics for F_s

H/C*†	Force field	T (K)	Maximum (ns)	Total time (μs)	>EQ‡ (μs)
H	99φ	273	200	136.27	96.18
C	99φ	273	200	137.27	97.20
H	99φ	305	165	70.21	31.40
C	99φ	305	170	71.48	32.53
H	99φ	337	200	131.06	90.99
C	99φ	337	200	128.35	88.35
H	99	273	100	31.49	14.40
C	99	273	110	31.94	14.79
H	99	305	75	29.23	12.76
C	99	305	90	29.79	12.93
H	99	337	70	21.37	6.48
C	99	337	70	21.77	6.87
H	94	273	200	74.26	35.05
C	94	273	200	61.85	23.11
H	94	305	201	73.12	34.18
C	94	305	245	71.79	32.73
H	94	337	185	55.32	17.34
C	94	337	185	55.53	16.80
H	GS	273	200	128.66	88.65
C	GS	273	200	131.08	91.08
H	GS	305	200	124.32	84.26
C	GS	305	200	124.11	84.06
H	GS	337	200	124.30	84.23
C	GS	337	200	122.98	82.96
Total	–	–	–	1987.5	1179.3

^*Similar statistics for A₂₁ were collected.

^†Starting states are: full helix (H); random coil (C).

^‡Equilibrium sampling is chosen conservatively as stated in the text.

All simulations reported herein were conducted under NPT conditions (Berendsen et al., 1984) at 1 atm and temperatures ranging from 273 to 337 K. Long-range electrostatic interactions were treated using the reaction field method with a dielectric constant of 80, and 9-Å cutoffs were imposed on all Coulombic and Lennard-Jones interactions. Nonbonded pair lists were updated every 10 steps, and covalent bonds involving hydrogen atoms were constrained with the LINCS algorithm (Hess et al., 1997). An integration step size of 2 fs was used with coordinates stored every 100 ps.

Lifson-Roig calculations

To compare the predicted thermodynamics to experiment we fit our results to the classical LR helix-coil counting theory (Lifson and Roig, 1961; Qian and Schellman, 1992). In this model residue states are defined in terms of the backbone torsional (φ,ψ) space. We followed the definition of Garcia and Sanbonmatsu where a residue is considered helical if φ=−60(±30)° and ψ=−47(±30)° and nonhelical otherwise (Garcia and Sanbonmatsu, 2001), thus allowing our results to be directly compared to the results of their REMD simulations. In addition, we considered the dependence of the LR parameters on the cutoffs applied to the helical portion of the (φ,ψ) space by performing the same calculations outlined below using φ=−60(±n)° and ψ=−47(±n)° with n ranging from 10 to 50° to define helical residues. As outlined in the Results section, the optimal cutoff was determined to be ∼30° based on the minimum variance point for w.

In LR theory, as described by Qian and Schellmen, a helical hydrogen bond requires three consecutive residues to be constrained in helical conformations, giving a maximal helix length of n−2 residues, where n is the total number of amino acids in the peptide (Qian and Schellman, 1992). Each residue has a statistical weight of being in the helical state given by the integral of the Boltzmann weight of all residue (φ,ψ) conformations,

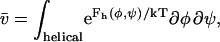(2)

and a statistical weight for the nonhelical state given by

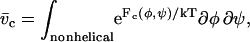(3)

where the subscripts h and c refer to the helix and coil states, respectively, and F_x(φ,ψ) is the free energy of the state x dependent on (φ,ψ). Because the formation of a helical segment consisting of three or more helical residues restricts motion in (φ,ψ) space, an additional parameter is used to specify the statistical weight of a residue both being helical and participating in a helical segment,

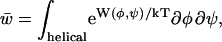(4)

where W includes the conformational free energy of the residue and the interaction of that residue with its neighbors when participating in a helix. Taking the coil state as reference gives the normalized weights of 1, 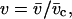and 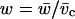with each residue in a given molecular conformation assigned a specific statistical weighting: helical residues that terminate a helical segment are assigned weight v, those that do not terminate the helix are assigned w, and nonhelical residues are assigned a weight of 1. The longest helical segment in a chain of length n thus has a statistical weight of 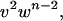where v² and w are the nucleation and propagation constants in LR theory, which can be related to σ and s in Zimm-Bragg theory (Qian and Schellman, 1992). The equilibrium constants for nucleation and propagation are given by 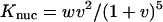and 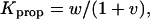respectively.

Based on the weighting scheme above, a weight matrix for the central residue in the eight possible helix-coil conformational triplets is simplified as

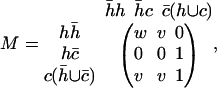(5)

where bars specify the central residue in the triplet and ∪ represents the combined helical and nonhelical portion of the (φ,ψ) space. This leads to the molecular partition function

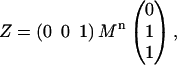(6)

which was used to calculate the helical properties of our simulated ensembles. Namely, the mean number of helical hydrogen bonds is given by

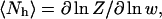(7)

and the mean number of helical segments of two or more residues is given by

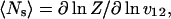(8)

where v₁₂ is the v in the first row and second column of the weight matrix (Eq. 5). The mean number of helical residues is related to these quantities by

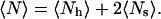(9)

Combining these relations thereby allows for the simultaneous evaluation of v and w for given values of 〈N〉 and 〈N_s〉, which are extracted from the simulated ensembles. For additional analysis, we also follow the N_c metric, defined as the longest contiguous helical segment in a given conformation.

Cluster analysis

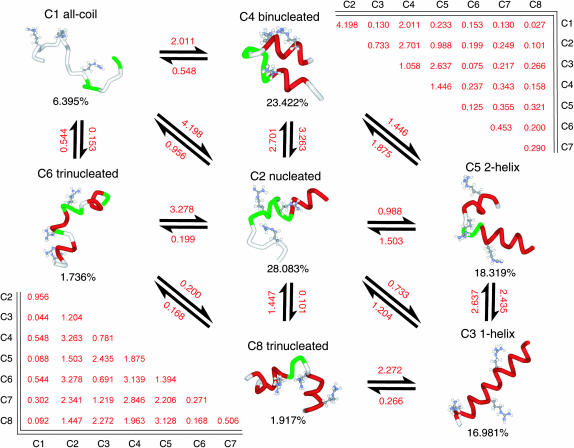
To define thermodynamic microstates in an unbiased manner using the LR parameters and radius of gyration (R_g) values calculated from our equilibrium data sets, conformations were clustered using a modified version of the K_means algorithm (Hastie et al., 2001). In our “shrinking-K_means” algorithm, a large initial number of cluster centers are randomly placed within the hypercube defined by the data. Void centers, those to which no conformations are assigned in a given iteration, are removed from the analysis and replaced with new randomly placed cluster centers for use in the next iteration. Convergence is reached when a significant number of iterations have been made with no change in the cluster assignments for the data set. This method thus allows for clustering without a priori knowledge of the number of clusters present in the data set. Because the K_means algorithm is inherently heuristic, optimization is achieved by performing multiple clustering attempts and maximizing the mean-squared difference (MSD) between the distance of the conformations from their assigned centers and nearest nonassigned centers. This maximized MSD favors fewer clusters in the final result, avoiding the splitting of microstates into separate clusters, and thus counteracting the initialization of additional centers in the shrinking-K_means method. The motivations for, and benefits of, applying K_means clustering to large data sets have been described recently by Elmer and Pande (2004).

After several trials to determine an upper bound on the number of clusters present in our equilibrium simulations, the shrinking-K_means algorithm was initiated with 25 randomly placed cluster centers, with each conformation represented by a vector composed of the corresponding N, N_c, N_s, and R_g values for that conformation. Because each defined microstate should be represented by a consistent number of helical segments within each conformation, the N_s metric was weighted by a factor of 20 to avoid the mixing of this metric within microstates (without affecting the clustering in other dimensions). The clustering reported herein maximized the MSD in 10 independent clustering trials.

RESULTS AND DISCUSSION

This section has been partitioned into several parts. We begin by demonstrating that our simulations reach conformational equilibrium in the absolute sense at the ensemble level (i.e., the behavior of ensembles started folded and unfolded converge), with the only exception being the AMBER-GS ensembles that take significantly longer to fully equilibrate compared to other force fields, and then consider the backbone torsional space sampled by each AMBER potential. The force fields are then assessed via comparison of our equilibrium results to several experimental measurements, which show that the AMBER-99φ potential best reproduces the known experimental properties of polyalanine-based helix-coil equilibrium at ambient temperature (nonambient temperatures are also probed). The remaining sections focus predominantly on extracting information about helix-coil equilibria from the AMBER-99φ ensembles, with further comparisons between these potentials included where appropriate. These sections first examine the macrostates present in equilibrium from a bulk perspective, and then delve deeper into the conformational diversity of the equilibrium via conformational clustering. The kinetics of the resulting microstates is followed and the ensemble folding and unfolding mechanisms are discussed.

Helix-coil convergence

Table 1 provides an overview of the sampling time achieved for F_s under these force fields, which totals nearly 2 ms. Similar statistics were collected for A₂₁, giving an aggregate sampling time of nearly 4 ms (not including the rapidly denaturing AMBER-96 ensembles described above), orders of magnitude greater than both the experimentally determined folding time and all previous helix-coil simulations in explicit solvent combined. Thermodynamic convergence was tested by monitoring several ensemble averaged helical metrics including the total number of residues participating in helices (N), the largest contiguous helical segment length (N_c), and the number of helical segments (N_s) using the Lifson-Roig counting method. Additional structural metrics were also monitored, including the all-atom root-mean-squared deviation (RMSD), radius of gyration (R_g), α-helical fraction (θ_a), 3₁₀-helical fraction 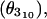and dwell time averages per residue in the helix (τ_helix) and coil (τ_coil) states. These were used to verify that each equilibrium represented true ensemble equilibrium and that the ensemble averaged signals were not masking discrepancies on the residue level.

The ensemble averaged signals for native and folding ensembles of both peptides demonstrate absolute convergence, as plotted in Fig. 2; of the four potentials, only the AMBER-GS variant did not reach absolute equilibrium on the 100-ns timescale, and additional sampling was thus required. Still, the native and folding ensembles do approach convergence for the AMBER-GS variant on the longer timescale simulated, and we therefore make direct comparisons between the four force fields. The comparison of 〈N_s〉 in Fig. 2 shows an initial rapid gain in the mean number of helical segments in the AMBER-GS folding ensembles not seen in the kinetics of the other force fields. This kinetic favoring of nucleation events is interpreted as a result of the lack of barriers to (φ,ψ) rotation that would otherwise oppose helix-friendly nonbonded interactions. In contrast to the other force fields tested, the heliophobic AMBER-99 required less sampling to reach equilibrium due to the rapid unfolding to low helical content described above (similar to the observations reported above using the AMBER-96 potential).

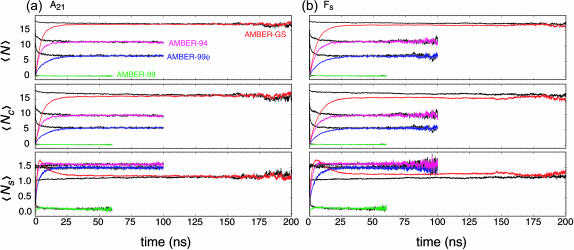
FIGURE 2.

Convergence of ensemble-averaged helical metrics. Time evolution of the (a) A₂₁ and (b) F_s folding ensembles under the AMBER-94 (magenta), AMBER-GS (red), AMBER-99 (green), and AMBER-99φ (blue) potentials. The plots include, from top to bottom, the mean α-helix content, mean contiguous helical length, and mean number of helical segments per conformation according to classical LR counting theory. Native ensembles that converge with corresponding color-coded folding ensembles are shown in black. Signal noise in the longer time regime is due to fewer simulations reaching that timescale (additional data at long times have been removed for visual clarity). The relative helical character remains essentially unchanged with Arg insertions in each force field. Although the AMBER-GS F_s ensemble did not reach absolute equilibrium on the timescales simulated, that force field clearly predicts greater helical content than the other AMBER potentials.

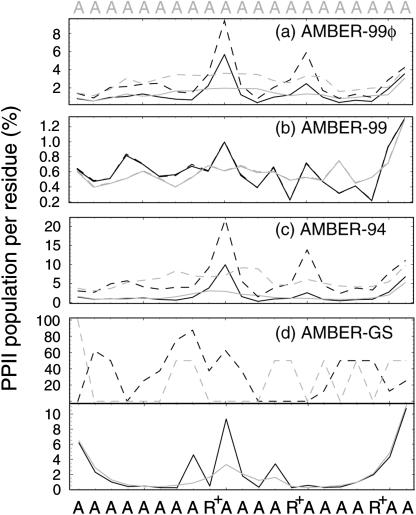
A comparison of the observed ensemble convergence on the residue level is shown in Fig. 3, which plots the ensemble convergence kinetics in the form of probabilities of having helical (φ,ψ) per residue for the folding ensembles (left) and native ensembles (right) of both peptides throughout the first 50 ns of sampling. The degree of convergence in AMBER-94, AMBER-99, and AMBER-99φ simulations is readily apparent, whereas the AMBER-GS folding ensemble has yet to reach the almost fully helical ensemble values predicted by the stability of the native AMBER-GS simulations.

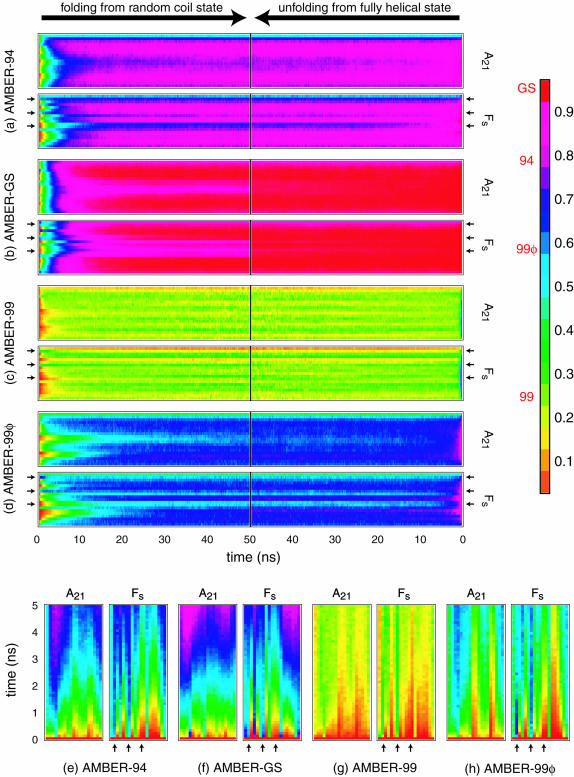
FIGURE 3.

Ensemble convergence at the residue level. Probabilities of each residue having helical (φ,ψ) as a function time for the folding (left) and native (right) ensembles are shown. Small black arrows indicate the positions of ARG substitutions in F_s. In each plot the sequence runs from the N-terminal (bottom) to the C-terminal (top). Note that these probabilities do not represent the probabilities of taking part in a helical segment, as defined in LR theory as three or more contiguous helical residues. Red labels to the left of the key indicate the regime of helicity represented by each force field. Lower panels (e–h) magnify the first 5 ns of folding in each force field for inspection of nucleation trends, with the sequence running from C-terminal (left) to N-terminal (right).

Sampling backbone torsional space

As outlined above, our equilibrium simulations contradict the REMD results reported by Garcia and Sanbonmatsu, who found that removing (φ,ψ) torsions from AMBER-94 to produce the AMBER-GS variant led to decreased heliophilicity and better agreement with experimental LR parameters. In contrast, we find that removing the (φ,ψ) torsions from AMBER-94 (as in AMBER-GS) leads to a more helix-friendly potential. This observation can be understood by physical arguments: only a small portion of the helical region, as defined by Garcia and co-worker (Garcia and Sanbonmatsu, 2001) and described in the following section, lies in the energetic minimum of ψ rotational space of the AMBER-94 potential. Removing the potential within the helical window in AMBER-94 (Fig. 1, red box), which is energetically downhill and favors nonhelical conformations, thus allows helix-friendly nontorsional terms (i.e., electrostatics and atomic dispersion) to dominate.

Furthermore, our results show that the AMBER-GS helix-coil dynamics occur on a significantly longer timescale than the other AMBER force fields (Fig. 2). It is thus possible that REMD simulations employing this force field do not reach absolute convergence due to the long timescales involved. For instance, it has been shown that REMD offers only ∼1 order of magnitude decrease in necessary sampling time in the folding of BBA5 (Rhee and Pande, 2003). Thus, although high temperature is a driving force for rapid unfolding in REMD simulations, allowing insufficient time for refolding may taint the apparent equilibrium in favor of less helical conformations. To demonstrate the difference in (φ,ψ) distributions with changes in backbone torsional potentials, our equilibrium backbone sampling of the AMBER force fields is shown in Fig. 4.

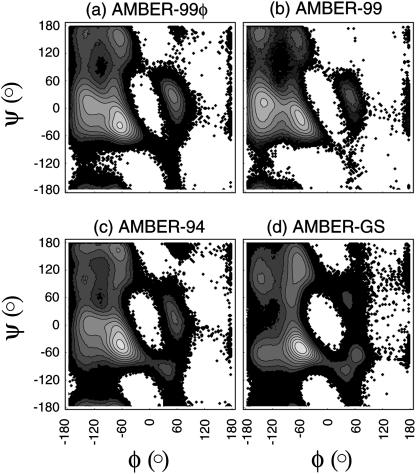
FIGURE 4.

Sampling the (φ,ψ) free energy landscape. The equilibrium sampling of backbone torsional space using the (a) AMBER-99φ, (b) AMBER-99, (c) AMBER-94, and (d) AMBER-GS potentials for all residues in the F_s peptide are shown. Each map consists of ∼40,000 equilibrium conformations with backbone torsional values binned in 3° intervals and contours representing kT units at 305 K. Minima in each landscape are described in the text.

For comparison to both quantum mechanical sampling of the alanine dimer and a survey of the Protein Data Bank, we reference the recent studies of MacKerell et al., which reported grid-based corrections to the (φ,ψ) potential for the CHARMM22 force field (MacKerell et al., 2004a,b). Although each of the AMBER force fields in Fig. 4 shows better agreement with these distributions than the CHARMM22 potential, significant deficiencies are apparent. The AMBER-GS potential underweights the minimum representing left-handed helices near (φ,ψ) = {57°,47°}, while producing additional minima in the (φ,ψ) = {60°,−120°} region. These deficiencies are also apparent in the AMBER-94 equilibrium sampling to different relative magnitudes. Additionally, the AMBER-GS potential predicts a significantly smaller and deeper minimum in the region surrounding the helical regime than all other force fields. In contrast, the AMBER-99 potential underweights the minimum representing polyproline (PP) conformations near (φ,ψ) = {−75°,145°}, instead favoring extended β-structure (β_ext) in the region (φ,ψ) = {−160°,170°}. This trend is reversed in the AMBER-99φ variant, resulting in the expected favoring of PP structure over extended β_ext structure. Both AMBER-94 and AMBER-GS show detectable β-populations not seen in AMBER-99 and AMBER-99φ sampling. Of these force fields, the best agreement with the Protein Data Bank and quantum mechanical sampling is achieved by the AMBER-99φ variant, which captures disributions that are underweighted by other force fields without overweighting other regions of the phase space.

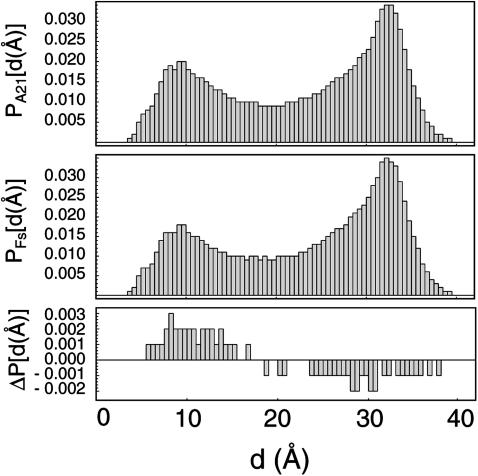
A significant literature has recently begun to develop around studying the existence of polyproline conformations in polyalanine systems (Drozdov et al., 2003; Garcia, 2004; Kentsis et al., 2004; Mezei et al., 2004; Shi et al., 2002; Weise and Weisshaar, 2003; Zagrovic et al., 2005). Although there has been no definitive characterization of the PP content in such systems, PPII structure has been suggested as a predominant conformer in the alanine dipeptide (Drozdov et al., 2003; Weise and Weisshaar, 2003) and in the unfolded state of larger polyalanine sequences (Garcia, 2004; Shi et al., 2002), and further study in this area is ongoing. Fig. 5 shows the PPII content profiles for both peptides in the force fields studied, including all equilibrium data for the two peptides (solid lines), as well as analogous calculated PPII propensities in the unfolded state (dashed lines). PPII structure was analyzed in accord with the method outlined previously by Garcia using backbone torsional values of−120° ≤ φ ≤−30° and 60° ≤ ψ ≤ 180° to allow direct comparison to previously published results (Garcia, 2004). For simplicity, the “unfolded state” is defined as all conformations in which two-thirds or more of the sequence (14 residues or more) are nonhelical using the definition from LR theory. Although this definition is somewhat arbitrary, the proper portion of (φ,ψ) space used to define PPII structure is also somewhat arbitrary (Garcia, 2004), and the results shown in Fig. 5 are thus meant to serve solely as a qualitative description of the observed PPII populations in the equilibrium and unfolded ensembles.

FIGURE 5.

Polyproline structural content. PP-type conformational probabilities per residue are shown for both A₂₁ (gray) and F_s (black) using the equilibrium sampling (solid lines) and the unfolded state (dashed lines). As described in the text, the AMBER-99 ensembles remain essentially unchanged due to the favoring of extended conformations in that force field. Two parts are shown in panel d to distinguish the PPII content of the unfolded state (top) from that observed in the equilibrium sampling (bottom). Due to the small proportion of highly unfolded configurations in the AMBER-GS ensembles, too few unfolded conformations to quantitatively access PPII presence were analyzed. However, it is clear from the top plot in panel d that unfolded conformations in that force field favor PPII structure to a significant degree.

As shown there, the AMBER-99φ and AMBER-94 potentials yield similar PPII populations, with AMBER-94 predicting roughly twice the occurrence of such conformations, and both show a significant increase in PPII presence when only the unfolded state is considered. Our results thus suggest that PPII structure does indeed exist in the unfolded state of polyalanine sequences. However, the overall abundance of PPII structure is low in both cases, with a maximum likelihood of ∼8% using the AMBER-99φ force field. In contrast to the AMBER-99φ and AMBER-94 ensembles, the AMBER-99 ensembles remain unchanged due to the favoring of extended conformations in that force field and the lack of highly unfolded configurations in the AMBER-GS ensembles yield too few conformations to quantitatively access PPII presence. Still, it is apparent from Fig. 5 d that the unfolded state in the AMBER-GS potential contains a more appreciable amount of PPII character, in agreement with the REMD results of Garcia, who reported ∼25% PPII content in polyalanine peptides using the AMBER-GS potential (Garcia, 2004).

The observation that the AMBER-GS potential overstabilizes polyalanine helices to a greater extent than AMBER-94 may also appear contradictory to a recent study by Zaman et al., who studied the propensity of various force fields to favor helical (φ,ψ) values (Zaman et al., 2003). They reported a twofold favoring of helical backbone torsions in AMBER-94 when compared to AMBER-GS in an implicit solvent model for the central residue in the capped alanine trimer (Ace-A₃-NMe), and we have observed a comparable trend for the same system in explicit TIP3P solvent (data not shown). To understand this difference, two factors that affect the propensity to form helical backbone conformations must be considered: i), the study of Zaman et al. (2003) showed a strong backbone conformational dependence upon nearest-neighbor conformation and identity (violating Flory's isolated pair hypothesis), and ii), long-range interactions that favor helical conformations are not present in the trimers examined in that study.

Based on our results, we suggest that the results obtained in studying smaller systems might be inaccurate when extrapolated to larger sequences. Our results, alongside the results of Zaman et al. (2003), suggest that the torsional space sampled depends not only on nearest-neighbor influences, but also on the ability to form secondary structure and therefore, to a certain degree, on the length of the peptide. We thus postulate that the generalized parameterization of backbone torsions using experimental data and/or quantum calculations based solely on dimers/trimers may produce torsional potentials that are inadequate for larger protein sequences, as we report herein using the AMBER-99 potential. Indeed, at the atomic level even the simple α-helix is a complex system of interactions that may not be easily generalizable.

Assessing the potentials at ambient temperature

The start of conformational equilibrium for each pair of native and folding ensembles was conservatively taken as 20 ns for AMBER-99 ensembles and 40 ns for all other ensembles (see Fig. 2). The amount of data present in each ensemble after this point is specified in Table 1 for F_s, and the simulated kinetic and thermodynamic properties that were compared to the published experimental results for F_s are shown in Table 2. For comparison between force fields are the ensemble averaged RMSD and radius of gyration for each ensemble. As shown in Table 2, an experimental radius of gyration of 9 Å was found using small angle x-ray scattering for a sequence of similar size and identity at ∼283 K (B. Zagrovic, unpublished data). Although AMBER-94 and AMBER-GS predict somewhat extended molecular sizes due to their overweighting of helical conformations, and AMBER-99 predicts a significantly compact molecular size due to favoring of nonhelical conformations, our modified AMBER-99φ shows the best agreement with experiment.

TABLE 2.

Comparison of 305-K equilibrium ensemble simulation results to experimental values

	AMBER-94		AMBER-GS		AMBER-99		AMBER-99φ
Metric	A21	Fs	A21	Fs	A21	Fs	A21	Fs	Experimental (Fs)
v*	0.35	0.36	0.68	0.70	0.06	0.06	0.26	0.26	0.036
w*	1.66	1.67	3.70	3.70	0.70	0.70	1.27	1.26	∼1.3
〈% 310〉eq	6.40	6.40	0.15	0.04	16.0	16.5	17.8	17.3	∼16%
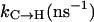	0.15	0.11	0.12	0.08	0.00	0.00	0.06	0.05	0.06
〈τcoil (ns)〉	0.21	0.24	0.32	0.38	0.81	0.89	0.26	0.28	0.3
〈Rg (Å)〉eq	9.32	9.40	9.56	9.55	7.32	7.97	9.02	9.24	9†
〈RMSD (Å)〉eq	3.60	4.00	1.88	2.59	7.85	7.68	5.13	5.31	–

^*Calculated using 30° cutoffs as described in the text.

^†Measured at ∼283 K.

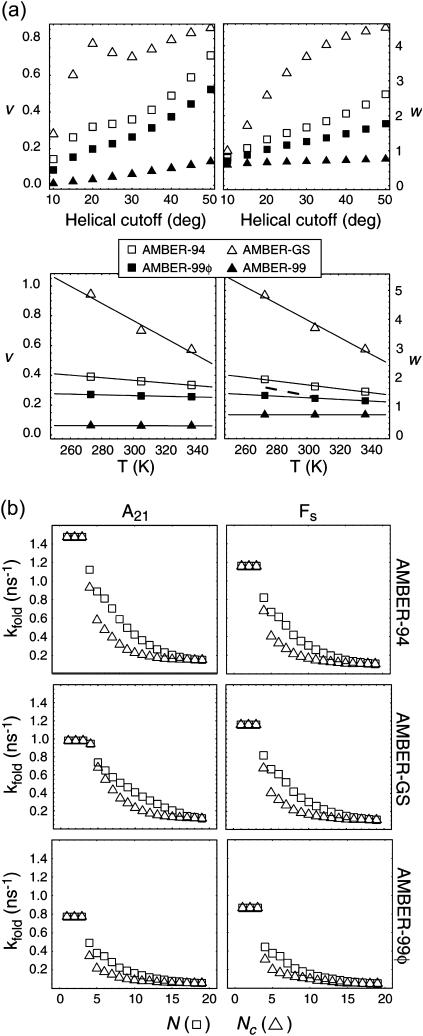
The primary comparison between helix simulation and experiment is the ability of a given force field to reproduce experimentally measured helix-coil parameters, and we make such a comparison to the LR nucleation v and propagation w parameters. For each force field, we evaluated these parameters using cutoffs of n degrees from the ideal helical torsions, with helical residues defined by φ=−60(±n)° and ψ=−47(±n)°. To characterize the dependence of the LR parameters on the cutoff used and thereby determine the most adequate cutoff, we tested values of n ranging from 10 to 50° and looked for points of minimum variance within the cutoff dependence plots. Because both the nucleation and propagation equilibrium constants are directly proportional to w, the appearance of a minimum variance region in the AMBER-94 and AMBER-99φ potentials implies a free energy barrier, and this is used to distinguish conformations that strongly contribute to the helix-coil parameters from those that do not. The inflection points shown in the figure occur at 25–30°, supporting the use of a 30° cutoff by Garcia et al. (Garcia and Sanbonmatsu, 2001) and used in further LR calculations reported below. The lack of backbone torsion potentials in AMBER-GS results in a cutoff dependence void of inflection points, as shown in Fig. 6.

FIGURE 6.

Simulated LR parameters and detection of intermediates. (a) The values shown are from simulations under the AMBER-94 (□), AMBER-GS (▵), AMBER-99φ (▪), and AMBER-99 (▴) potentials. The top frames demonstrate the dependence of the LR parameters on the (φ,ψ) cutoff in determination of residue helicity at 305 K, with minimum variance points lying in the 25–30° regime. The bottom frames show the calculated LR parameters at 273, 305, and 337 K using a 30° cutoff. Although the LR parameters derived from the AMBER-99 potential exhibit a negligible temperature dependence, changing only the φ torsional potential between the AMBER-99 and AMBER-99φ potentials results in a more realistic temperature dependence of w(T). The experimentally determined temperature dependence of w (Rohl and Baldwin, 1997) is approximated by the dashed line. (b) Comparison of single exponential fits of N and N_c values for both peptides in the three folding potentials employed. In each case, the lack of simultaneous rates for these two metrics signifies the existence of one or more kinetic intermediates. The fits for small values of N and N_c are somewhat ambiguous (based on the fitting method), and should therefore not be taken as quantitative measures; refer to Table 3 and the relevant portion of the text for nucleation kinetics.

As shown in Table 2, all AMBER force fields studied overestimate the nucleation parameters by roughly an order of magnitude. Of these potentials, we see the largest v values predicted by AMBER-GS and AMBER-94, respectively, and this trend is also observed in strong overestimates of the propagation parameter w. Although AMBER-99 best predicts the nucleation parameter, the lack of helix stabilization within that force field results in a disparagingly low propagation parameter. In comparison, AMBER-99φ yields the best agreement with w while predicting the lowest v of the heliophilic potentials. The equilibrium constants for nucleation and propagation calculated using v and w at 305 K (the approximate F_s midpoint temperature) are K_nuc = 0.0465 and K_prop = 1.23 from AMBER-94 simulation and K_nuc = 0.1277 and K_prop = 2.18 from AMBER-GS simulation, compared to K_nuc = 0.0270 and K_prop = 1.00 from AMBER-99φ simulation. The resulting structural difference is apparent in the mean length of helical segments, 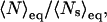which is ∼14.3 for AMBER-GS ensembles, ∼7.15 for AMBER-94 ensembles, and only ∼4.5 for AMBER-99φ ensembles.

Two features of the simulated LR parameters shown in Table 2 are notable in comparison to the values of v and w calculated by the AMBER-94 REMD methodology used by Garcia and co-worker, who reported v=0.30 and w=1.68 for A₂₁ and v=0.27 and w=2.12 for F_s, both at 300 K (Nymeyer and Garcia, 2003). First of all, the LR parameters predicted using REMD are very similar to our equilibrium values for A₂₁. However, unlike the findings of Garcia and Sanbonmatsu), we observe no significant difference in these parameters when comparing the polyalanine peptide with the Arg substituted F_s. As noted above, we expect that our significant increase in sampling accounts for this difference and underlines the potential limitations inherent to REMD methods (Rhee and Pande, 2003). Still, LR parameters determined by experiment may not be adequately characterized by the coupling of simulation and LR theory using a simple cutoff placed on the helical portion of the (φ,ψ) space due to the added complexity of the experimental system and method employed. With this in mind, we consider additional metrics below in assessing these force fields.

Because LR theory does not differentiate between helical types (the 3₁₀-helix falls within the helical portion of the (φ,ψ) space), the Dictionary of Secondary Structure in Proteins (Kabsch and Sander, 1983) was used to evaluate 3₁₀-helix content, which reveals significant disparity between these force fields. From nuclear Overhauser effect spectroscopy studies of the alanine-based peptides 3K [Ace-(A₄K)₃A-NH₂] and MW (Ace-AMAAKAWAAKAAAARA-NH₂), Millhauser et al. suggested that 3₁₀-helix populations were significant, particularly near the termini (Millhauser et al., 1997). In MD simulations of the MW peptide by Armen et al. using the ENCAD force field, nuclear Overhauser effects comparable to those reported by Millhauser et al. (1997) were observed with a 3₁₀-helix fraction of ∼16% (Armen et al., 2003). As shown in Table 2, AMBER-99 outperforms both the AMBER-94 and AMBER-GS potentials with a 3₁₀ content of ∼16% for both peptides, with 3₁₀ conformations occurring predominantly near the termini, and the AMBER-99φ ensembles agree with this estimate at ∼17%. In comparison, AMBER-94 and AMBER-GS significantly underestimate the mean 3₁₀ population at only 6.4% and < 1%, respectively.

To compare the overall folding rates predicted by these force fields with experiment, we follow the experimental analysis commonly done in fitting ultrafast kinetics measurements and assume two-state behavior (Lednev et al. 1999a, 2001; Thompson et al., 1997, 2000; Williams et al., 1996). The actual thermodynamic states present in equilibrium are not known a priori, which makes this assumption attractive. Additionally, formation of a fully helical conformation will be the upper bound on the folding time measured in experiment because: i), significantly faster modes are not yet resolvable experimentally and ii), kinetic modes that are slightly faster but on the same timescale as complete folding will remain unresolvable and thus contribute to the slowest mode on that timescale (i.e., complete folding). For these reasons, we define the folding rates as the rates of complete helix formation 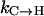for each ensemble, which are compared to the result from laser T-jump infrared measurements of Williams et al. (1996) in Table 2. As shown there, the rate from AMBER-99φ agrees well with that extracted from experiment whereas the predictions of AMBER-94 and AMBER-GS are roughly twice as fast as the experimentally derived folding rate.

Assessing the potentials at nonambient temperatures

Although our AMBER-99φ variant clearly captures helix-coil equilibrium much better near biological (ambient) temperatures than the other variants studied, the accuracy of a force field is also dependent on the temperature of the simulation, and we therefore probed the ability of these force fields to reproduce the correct trend in the LR propagation parameter w as determined experimentally by Baldwin and co-workers (Rohl and Baldwin, 1997). Data from their circular dichroism and NH exchange experiments were fit to the van't Hoff equation,

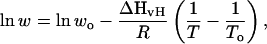(10)

where T_o and w_o were taken as 273 K and w(273 K), yielding enthalpy changes of approximately −1.25 kcal/mol. For direct comparison, additional equilibrium ensemble simulations were collected at 273 and 337 K (Table 1). Differences between the measurement of v and w in experiment and our method of calculation will clearly affect the accuracy of the predicted LR parameters, and thus make these comparisons somewhat less significant than the comparison of other metrics such as folding rate and mean R_g. Still, insight into the temperature dependence of these predicted parameters may offer insight into the applicability of these force fields at nonambient temperatures.

The resulting temperature dependence of v and w for the potentials studied are shown in the lower panels of Fig. 6 a. The LR parameters derived from AMBER-GS simulation show the greatest temperature dependencies of the four potentials, whereas AMBER-99 erroneously exhibits essentially constant values of v and w. Fitting the AMBER-GS data to Eq. 10 results in a slightly overestimated enthalpy change of −1.4 kcal/mol. From the plot, this level of agreement may be fortuitous due to the overestimated LR parameters under the AMBER-GS potential. In comparison, the less heliophilic AMBER-94 and AMBER-99φ potentials underestimate the enthalpy change at −0.7 and −0.4 kcal/mol, respectively. Thus, even the more accurate force fields at near-ambient temperatures poorly capture the extreme temperatures studied. It has been shown that, like many other water models, TIP3P does not adequately capture the character of true water outside the ambient temperature regime (Horn et al., 2004) and although it is unclear to what degree the TIP3P water model influences this lack of accuracy at nonambient temperatures, it is clear that the use of such models is insufficient to assess the dynamics outside this range.

For this reason, we assess only our 305 K simulation ensembles below, and are currently working on assessing force-field accuracy under more adequate representations of explicit water at nonambient temperatures (E. J. Sorin and V. S. Pande, unpublished data). Based on the more accurate folding rate prediction under AMBER-99φ and the ability of this force field to more accurately reproduce ensemble thermodynamic character, as outlined above, we assess the specifics of the helix-coil equilibrium below focusing on the results obtained in our AMBER-99φ simulations. Further comparison between these force fields is also included to probe the effects of modifying or eliminating the backbone torsional potentials.

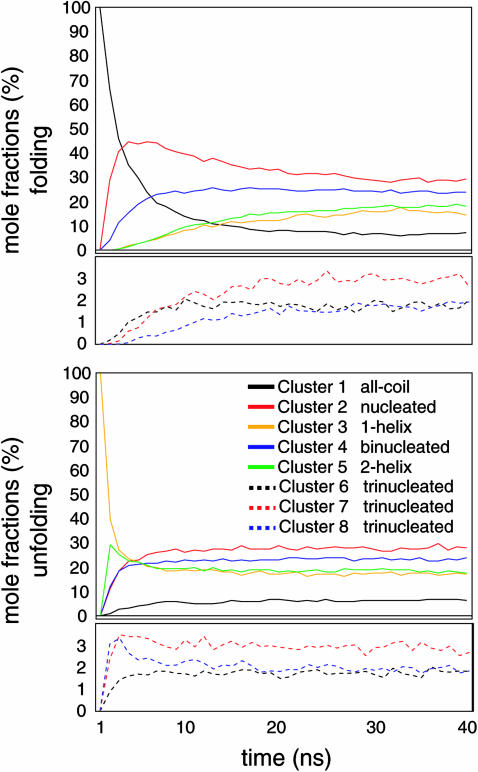
Helix nucleation dynamics

Because the definition of a helix is somewhat subjective and the accuracy of applying a two-state model is questionable, the folding kinetics was followed along both the N and N_c metrics. For each possible value (1 ≤ N, N_c ≤ 19), the population as a function of time was fit to a single exponential and the resulting rate of formation was extracted for each ensemble. The common thread shared by all force field/peptide permutations is the occurrence of multiple nucleation events, on average, during the folding process. That is, the rate of increase in N_c drops off much faster than the rate of increase in N, as shown in Fig. 6 b, suggesting the presence of one or more kinetic intermediates during helix formation. Were a single nucleation event to occur during folding, we would expect changes in these two metrics to be identical. This distinction in rates thus results from the nucleation and “alignment” of multiple short helical regions to form a longer, more ideally helical structure, as described recently for longer helices (Kimura et al., 2002). Additionally, the observation that small α-helical regions are the structural motif most similar to the random flight chain (Zagrovic and Pande, 2003b), RMSD = 0.8 Å for C_α atoms in an eight-residue helix, suggests that these short helical regions may be less entropically penalized than longer helical segments, as postulated previously (Banavar et al., 2002; Pappu et al., 2000; Zaman et al., 2003). This is also supported by the result that AMBER99φ yields a mean helical segment length of only ∼4.5 residues and undergoes multiple nucleation steps, on average, during the folding process.

Based on these observations, complete helix nucleation should not be expected to occur as a simple exponential process. Rather, the occurrence of the first nucleus should appear with exponential kinetics and each subsequent n^th nucleation event should be dependent upon the (n−1)^th rate, giving an n^th order exponential for the n^th nucleation rate (i.e., longer peptides will allow more nucleation events on average than shorter ones). With this in mind, we examined each simulated ensemble and recorded each occurrence of a purely random coil conformation (by LR statistics this includes all conformations in which no three consecutive residues are in helical (φ,ψ) space). We then defined nucleation as the formation of three or more contiguous helical residues lasting for 500 ps or longer, and histograms of the time taken for each random coil to undergo nucleation were generated. To avoid bias that might be introduced by the random coil starting conformation within any or all of the potentials examined, the first 5 ns of simulation time was excluded from this analysis. A similar search for the occurrence of secondary helix nuclei was also undertaken. We then fit the rates of initial nucleation to a single exponential, 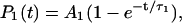and the sum of the nucleation probabilities was fit to the biexponential

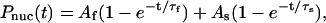(11)

where τ_x is the inverse rate of the x^th nucleation component and the subscripts f and s refer to the fast and slow components, respectively. The resulting fits for each ensemble are shown in Table 3, where k_x = 1/τ_x. Although these fits are excellent overall, the modestly lower R² for the AMBER-GS ensembles results from the lack of a significant number of random coils after the initial 5 ns of simulation. Results for AMBER-99 are not shown as that force field favored unfolding of the helical ensemble.

TABLE 3.

Simulated nucleation parameters at 305 K

Force field	Peptide	k1 (ns−1)	R2	Af	kf (ns−1)	As	ks (ns−1)	R2
AMBER-99φ	A21	15.10	0.999	0.945	16.43	0.054	4.87	0.999
	Fs	13.49	0.999	0.886	15.63	0.111	5.38	0.999
AMBER-94	A21	18.75	0.999	0.744	22.83	0.255	12.22	0.999
	Fs	16.17	0.999	0.682	20.74	0.316	10.72	0.999
AMBER-GS	A21	9.00	0.991	0.608	16.95	0.392	4.51	0.997
		Fs	12.14	0.982	0.756	24.34	0.243	3.193	0.998

As shown in Table 3, all three force fields predict initial nucleation, as defined above, to occur on the tens of picoseconds timescale, with the AMBER-94 potential yielding the fastest initial nucleation rate. However, the biexponential fits highlight the differences between the potentials. First of all, whereas AMBER-99φ heavily favors the faster nucleation mode (which is predominantly determined by the initial nucleation event), AMBER-94 and AMBER-GS only moderately favor this mode (i.e., secondary nucleation is kinetically favored in these force fields relative to AMBER-99φ). Interestingly, AMBER-94 follows the trend of AMBER-99φ, with arginine substitutions resulting in a lower weighting of the fast nucleation mode, yet the relative rates are more rapid for both modes under the AMBER-94 potential. In contrast, the AMBER-GS potential reverses this trend and shows a significant difference (∼30%) between the A₂₁ and F_s fast mode rates, while predicting slow nucleation modes that are in strong agreement with the AMBER-99φ results. Each force field thus predicts nucleation rates that are in reasonable agreement with, but somewhat faster than, the AMBER-94 simulation results of Hummer et al. who put the nucleation event on the 100-ps timescale (Hummer et al., 2001) and the upper bound of 100 ps set by experiment (Thompson et al., 2000). Of the three, the AMBER-99φ potential predicts the slowest of both modes, with time constants of ∼60 ps and ∼200 ps, respectively.

The lower panels in Fig. 3 magnify the first 5 ns of each of the eight folding ensembles to better characterize the nucleation trends described herein. We note that although the modification of the AMBER-99 potential we have introduced increases the probability of being in helical (φ,ψ) conformations per residue, it does not significantly alter the overall shape of the time evolution of helical residues, as shown in Fig. 3, g and h. Although there are no single points of significantly increased nucleation likelihood, the two Arg residues nearest the C-terminal serve as likely nucleation centers, thus explaining the reweighting of fast and slow nucleation modes upon Arg insertions in the AMBER-94 and AMBER-99φ potentials. In contrast, the first Arg residue maintains one of the lowest helical probabilities during the transition, a trend that appears in each AMBER potential and is therefore interpreted as a specific sequence effect on the folding dynamics. Moreover, the possibility of nucleating anywhere along the sequence with higher likelihoods at substitution positions and rapid secondary nucleation steps indicates a complex folding mechanism in which many potential pathways to the native helical conformation are possible.

In comparison, we had previously examined similar helices using the OPLS united atom force field (Jorgensen and Tirado-Rives, 1988) and GB/SA continuum solvent (Qiu et al., 1997) with water-like viscosity (Pande et al., 2003). Although the collected statistics under that model were very limited, the model predicted blocking of helix propagation by Arg insertions relative to the polyalanine peptide, with F_s folding slower and to a lesser extent than polyalanine. This is consistent with both the study of Garcia and co-workers, which described a favoring of compact structure on the part of the implicit solvent (Nymeyer and Garcia, 2003), and the observation of a compact transition state by Duan and co-workers (Chowdhury et al., 2003). Such contradictory reports highlight the differences in helix dynamics observed under implicit and explicit representations of the solvent, and we are currently working on gaining a better understanding the effects of implicit and explicit solvation models on helix formation (E. J. Sorin and V. S. Pande, unpublished data).

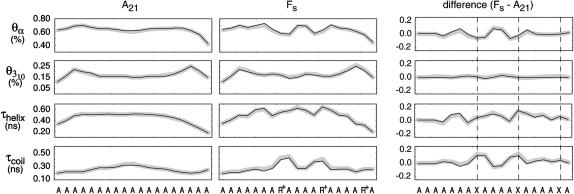
Equilibrium residue properties

Fig. 7 demonstrates the convergence observed between native (black) and folding (gray) ensembles on the residue level for both A₂₁ (left) and F_s (right) under the AMBER-99φ potential. Included are the fractional α-helicity, the fractional 3₁₀-helicity, and the mean dwell times in the helix and coil states per residue. For each property, the change upon Arg insertion is shown to the right. Vertical dashed lines are present for visual clarity in comparing the locations of Arg substitutions between A₂₁ and F_s. The 3₁₀-helix fractions per residue shown in Fig. 7 demonstrate the significance of non-α-helical populations near the termini, in agreement with the previously mentioned studies of Millhauser et al. (1997) and Armen et al. (2003). Additionally, no significant π-helix or β-structure was observed in any of the simulated ensembles, the former of which is a known artifact inherent to certain force fields (Feig et al., 2003; Hiltpold et al., 2000).

FIGURE 7.

Equilibrium residue properties. From top to bottom are the mean α-helicity, 3₁₀ helicity, helix dwell time, and coil dwell time per residue for the A₂₁ (left) and F_s (right) sequences under the AMBER-99φ potential at 305 K. The difference is shown for each ensemble property on the right, with dashed vertical lines representing locations of ARG insertions. The 3₁₀-helicity is based on Dictionary of Secondary Structure in Proteins assignments, whereas all other frames are based on LR counting theory. The native and folding ensembles are shown in black and gray, respectively, and highlight the degree of convergence between the ensembles on the residue level.

Although these three substitution positions might be expected to share similar kinetic and thermodynamic characteristics, differences are readily apparent. For instance, Garcia and Sanbonmatsu have suggested that the backbone carbonyl oxygen four residues upstream are significantly shielded from water by the large Arg side chains at each position i in F_s (Garcia and Sanbonmatsu, 2001), thus increasing the helicity at each i^th − 2 position. As shown in Fig. 7, we observe such a trend for the first two substitution positions but not the third, suggesting that this effect is not entirely correlated with helical stability.

Fig. 7 also shows that the substitution of Arg residues in F_s results in slightly longer helix dwell times for surrounding ALA residues, but also significantly increases the coil dwell times at (and near) the sites of substitution. For all potentials other than AMBER-99, the mean residue dwell times in the coil state listed in Table 2 (low near termini, higher for central residues) fair well in comparison to values reported by Thompson et al. (1997, 2000), with AMBER-99φ dwell times being slightly longer than those predicted by AMBER-94 and slightly shorter than those predicted by AMBER-GS.

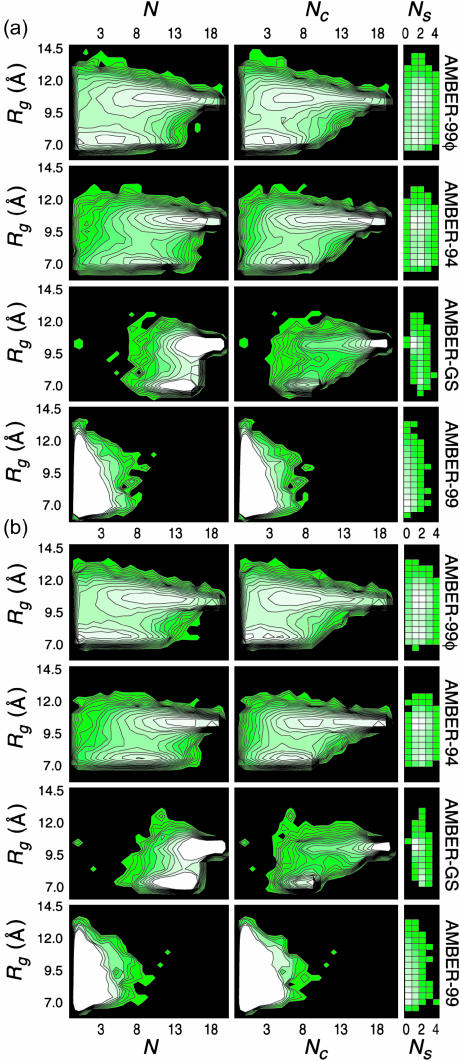
Macrostate assessment and free energy landscapes

The conformational free energy landscapes for A₂₁ and F_s under the four AMBER potentials are projected onto the R_g, N, N_c, and N_s folding metrics in Fig. 8. These surfaces are derived from the equilibrium helix-coil sampling reported above and therefore represent true equilibrium free energy contours as projected onto these reaction coordinates. By definition, this description inherently expresses the relative populations of all microstates present in the reported equilibria, and thus represents the thermodynamic reversible work function (i.e., constant temperature Helmholtz free energy) for the helix-coil system under the models studied. The inclusion of R_g allows for the differentiation of overall molecular size that the LR counting method does not consider without the ambiguity inherent to calculating RMSD values for helical sequences in solution (which can be highly misleading due to fluctuations within a single residue resulting in long-range distance differences). The resulting folding landscapes are nearly identical for the two sequences within each potential, yet large differences in the conformational sampling are apparent between the potentials. As discussed above, the AMBER-94 and AMBER-GS potentials sample predominantly the native regime of the conformational space, whereas the AMBER-99 potential predominantly samples the unfolded regime. The AMBER-99φ variant reveals a free energy landscape quite similar to that predicted by AMBER-94, yet with significantly lower overall helical content.

FIGURE 8.

Folding landscape characterization. Free energy surfaces for (a) A₂₁ and (b) F_s under the four AMBER potentials as projected onto the R_g, N, N_c, and N_s folding metrics. Each landscape was generated using ∼40,000 peptide conformations randomly chosen from the equilibrium simulation ensembles. Contours represent 0.25 kcal/mol intervals with each conformation assigned a statistical free energy−RT Log P, where P is the probability of the conformation within the ensemble sampled. The radius of gyration was binned in 0.5 Å intervals for all plots.

We compare these landscapes for small values of N to the explicit solvent AMBER-94 nucleation studies of A₅ reported by Hummer et al. who modeled the resulting kinetics as a barrierless diffusive search (Hummer et al., 2000). By the LR counting method, which requires three consecutive helical residues to constitute a helical segment, regions of N ≤ 5 must describe a single helical region, and that region of each landscape (the left most portion of each plot, for 0 ≤ N ≤ 5) is thus representative of the landscape valid for A₅ (R_g would of course be limited by the size of the A₅ peptide, and this axis would thus decrease in relative magnitude). The region sampled by Hummer et al. is composed of a single basin in which conformational diffusion would occur without barrier crossing events in both the AMBER-94 and AMBER-99φ potentials, extending downhill to N=5, consistent with ultraviolet Raman studies (Lednev et al., 2001). This observation for short helical segments is also consistent with ALA not undergoing an enthalpic penalty associated with side-chain perturbation of stabilizing water-backbone interactions (Huang et al., 2002; Wu and Wang, 2001) as well as the lack of a significant entropic barrier separating purely coil conformations from those with relatively short helical segments described above.

Chowdhury et al. (2003) simulated the folding of the capped 16-residue alanine-based peptide Ace-YG(AAKAA)₂AAKA-NH₂ using a modified version (Duan et al., 2003) of the AMBER-94 force field with a GB continuum representation of the solvent and reported transient multinucleated, helix-turn-helix structures that were interpreted as representing the helix-coil transition state ensemble (TSE). The free energy landscapes for AMBER-94 and AMBER-99φ in Fig. 8 show TSE regions that are crossed in a direction predominantly parallel to the R_g degree of freedom, specifying that a straightening of nonlinear structures to near-native length occurs as the TSE is passed. In the AMBER-94 potential, the “unfolded” basin corresponds to N ≤ 13 and N_c ≤ 8, implying a population dominated by multinucleated helices, shown directly as a favoring of N_s=2 conformers in the low R_g regime. Crossing the TSE in the folding direction includes simultaneous alignment and propagation of multiple helical segments, in tandem with an increase in R_g, with N_s=1 being predominant in the “native” basin. The TSE detected in our AMBER-94 equilibrium ensembles therefore appears to be in qualitative agreement with that reported by Chowdhury et al. (2003).

Because this study and that of Chowdhury et al. (2003) differ in the solvation model employed (TIP3P and GB, respectively), and in light of the study of Nymeyer and Garcia (2003), which suggests that GB does not accurately characterize the free energy landscape for F_s, we have tested this apparent agreement by performing P_fold calculations using our AMBER-94 and AMBER-99φ ensembles. As described elsewhere (Du et al., 1998; Pande and Rokhsar, 1999), P_fold is the probability that a given conformation will fold before unfolding, and therefore connects the observed kinetics (folding likelihood) to the underlying thermodynamics (free energy landscape) of the system. Because P_fold assumes definitions of the folded and unfolded states, we partitioned the free energy landscapes shown in Fig. 8 along the R_g, N, and N_c degrees of freedom such that the native and unfolded regimes were best separated (i.e., R_g cutoff of 9 Å, with cutoffs in N and N_c based on the plots in Fig. 8), and the radius of gyration was binned in 0.1 Å intervals. The folding “committor” (Bolhuis et al., 2000; Du et al., 1998) for each bin, P_fold(R_g, N, N_c), was then calculated by following all conformations within all trajectories in the ensemble data forward in time and determining the probability of conformations within each {R_g, N, N_c} bin folding before unfolding.

One concern with this approach is that our chosen degrees of freedom may not be kinetically relevant (Bolhuis et al., 2000; Du et al., 1998; Geissler et al., 1999). For example, it is possible that a given degree of freedom, such as N_c, might overlap with both the folded and unfolded basin. In this case, conformations with the same value of N_c could have radically different kinetic properties (i.e., some near the folded state with P_fold ∼ 1 and some near the unfolded state with P_fold ∼ 0). Ideally, one would therefore calculate distributions of P_fold committors over a given value used in a projection, which has the benefit of exposing whether the projection involves kinetically similar or different conformations (Bolhuis et al., 2000; Du et al., 1998; Geissler et al., 1999; Radhakrishnan and Schlick, 2004). Indeed, kinetically different conformations could be seen via a bimodal P_fold committor distribution. For instance, the use of folding committors has recently been employed to assess the rotamer character of specific residues contributing to the TSE of DNA polymerase-β on the tens of picoseconds timescale (Radhakrishnan and Schlick, 2004). Unfortunately, this is not computationally tractable in our case due to the structural heterogeneity observed in our equilibrium data: a similar sampling conducted on the tens of nanoseconds timescale for thousands to millions of nonidentical conformations is not yet feasible, even with the resources available to us at this time.

With these above factors in mind, to gauge the error involved in our P_fold values we use the following approach. Because we can only calculate the committor value after a given projection and not before the projection as discussed above, we are averaging a binary outcome (i.e., only folding or unfolding events are possible) and the mean ± standard error (SE) in the P_fold estimator for each bin is calculated following a binomial distribution according to mean ± SE=[p(1−p)/n]^1/2, where p is the P_fold committor and n is the number of configurations followed from the sampled bin. Because the conformations in a given {R_g, N, N_c} bin will be very similar in molecular size and helical content, we argue that our partitioning of the conformational space into small bins along these three reaction coordinates will distinguish folding character between bins, thus minimizing the likelihood that non-TSE bins will be incorrectly identified as belonging to the TSE due to averaging of conformations with high and low P_fold values within a given bin.

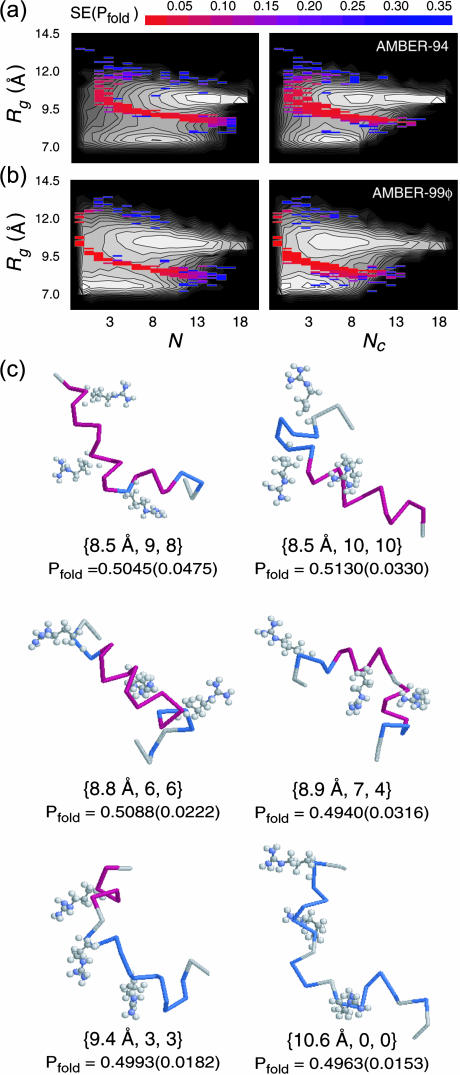
Fig. 9 shows the free energy landscapes along these three reaction coordinates in grayscale with the putative TSE region (bins) overlaid in color. The TSE in each of these potentials was identified by looking for bins with 0.45 < P_fold(R_g, N, N_c) < 0.55, and bins meeting this criteria were projected onto the two-dimensional planes shown in Fig. 9 without any averaging along the third (orthogonal) reaction coordinate. As defined by the color scale in the figure, red and blue bins represent the high-confidence and low-confidence TSE regions, respectively, and the lack of confidence in the blue bins stems predominantly from a limited sampling within those bins. Our ability to sample absolute equilibrium under the models studied results in a significant coincidence of features between the free energy landscapes in Fig. 8 and the TSE bins in Fig. 9, supporting this method of TSE detection.

FIGURE 9.

P_fold detection of the putative transition state ensemble. The (a) AMBER-94 and (b) AMBER-99φ ensembles were used to generate P_fold values on the conformational grid defined by R_g, N, and N_c, with the radius of gyration binned in 0.1 Å intervals and cutoffs in the two-state approximation taken from the free energy landscapes in Fig. 8, which are shown here in grayscale. The TSE region was defined by bins with 0.45 < P_fold < 0.55, and the mean ± SE in P_fold outlines the confidence level of putative TSE regions. (c) As described in the text, the TSE consists of a diverse set of conformations with varying molecular size and helical content, ranging from relatively extended to collapsed structures with one or more nucleation sites or helical segments present. Representations for several putative TSE conformations with low SE are shown, with violet and cyan representing residues in helical and turn conformations, respectively. The bin {R_g, N, N_c} and P_fold(mean ± SE) are shown below each TSE member. These examples, which represent a small portion of the very heterogeneous TSE, only highlight the conformational diversity within the TSE region.

From Fig. 9 a, the AMBER-94 TSE is much more diverse than suggested by the implicit solvent study of Chowdhury et al. (2003). Indeed, a continuum of structures ranging from compact to relatively extended is observed. However, crossing the transition state region from more collapsed structures, which Nymeyer and Garcia showed to be favored by the implicit solvent model employed (Nymeyer and Garcia, 2003), does appear to consist predominantly of an increase in molecular size. Although it is therefore not surprising that Chowdhury et al. (2003) observed the TSE to have such a strict conformational definition, an accurate representation of the AMBER-94 TSE should not require the tightly packed helix-turn-helix motif they reported, in which interactions between antiparallel helical stretches are necessarily present.

In contrast to the AMBER-94 landscape, the AMBER-99φ “unfolded” basin corresponds roughly to N ≤ 8 and N_c ≤ 5 and a roughly equal mix of helices with N_s = 1 and N_s = 2 are present in the “unfolded” region. Crossing the TSE in the folding direction results in a population defined by energetic minima centered at N_c,MIN < N_MIN, thereby including a significant population of multinucleated helical conformations. The AMBER-99φ TSE thus includes multiple conformational state types: part of the unfolded population includes a single helical segment of N ≤ 8 and propagation occurs as the polymer becomes less compact; a second part of the unfolded population consists of conformations with multiple nucleated or short helical regions (N ≤ 5) and these may undergo a second nucleation step followed by an alignment of helical segments. The AMBER-99φ potential thus predicts a TSE similar to that predicted by AMBER-94, with great diversity including single- and multinucleated moieties with a broad range of gyration radii, yet with lower overall helical content than predicted by the AMBER-94 potential. Several members of the AMBER-99φ TSE are shown in Fig. 9 c to demonstrate this diversity. We thus find that helix folding does not occur via a simple free energy bottleneck, wherein the transition state is a saddle point on the free energy surface with two states separated by a free energy barrier. Instead, the P_fold ∼ 1/2 region for the helix-coil transition is better characterized as a turning point within the free energy basin surrounding the native regime of the phase space, akin to diffusional dynamics. Crossing this turning point in either direction reverses the likelihood of folding versus unfolding.

Interestingly, the helix-coil landscape appears to be two-state for all force fields in which helical conformations are stable. Because fluorescence and other probes that measure specific distances are often used to assess biomolecular dynamics, end-to-end distance distributions for A₂₁ and F_s were also examined, as illustrated in Fig. 10. While a small population with very low end-to-end distance is present (i.e., d < 5 Å), a relatively well-defined two-state character is observed for both equilibrium ensembles. Based on the structural diversity of the TSE described above, it is clear that such measurements capture solely the dynamics related to changes in molecular size rather than the actual helix-coil dynamics of interest. Because both of these analyses may mask the finer detail of the underlying free energy landscape, a microstate analysis is described in the next section.

FIGURE 10.

Equilibrium end-to-end distance distributions for A₂₁ (top) and F_s (bottom) under the AMBER-99φ force field at 305 K as measured from the N-acetyl carbon to the C-terminal nitrogen. The difference is shown in the bottom panel, with A₂₁ favoring more collapsed conformations by ∼10% over F_s and F_s favoring more extended conformations. For reference, the ideal helix has an end-to-end distance of ∼31 Å using this measurement.

Microstate assessment and Markovian state models

Although the macrostate analysis above demonstrates the pseudo-two-state appearance of helix-coil equilibrium, that assessment also depicts two conformationally diverse macrostates. To better explore the structural diversity of the equilibrium under the AMBER-99φ potential without assuming two-state behavior, the modified K_means algorithm described above was used to cluster the F_s data into microstates based on the calculated R_g and LR helix-coil parameter values, the results of which are shown in Table 4. A total of 397,700 equilibrium conformations were included in this clustering, representing nearly 40 μs of equilibrium sampling with 100-ps resolution. Free energies per microstate relative to the pure coil (cluster 1) were calculated as ΔG_eq=−RT ln (P_n/P₁), where P_n is the probability of a conformation occurring in cluster n. To compare sampling of these microstates between the AMBER force fields, the analogous AMBER-94, AMBER-GS, and AMBER-99 F_s equilibrium ensembles were fit to the clusters in Table 4 and the resulting populations are also shown.

TABLE 4.

Cluster assignments for AMBER-99φ equilibrium helix-coil ensembles at 305 K

Cluster	Ns	N	Nc	Rg (Å)	%eq	ΔGeq (kcal/mol)	%99	%94	%GS
1	0	0	0	8.35	6.395	0	85.912	0.400	∼0
2	1	3.572	3.572	8.858	28.083	−0.897	13.279	7.408	0.014
3	1	12.086	12.086	9.943	16.981	−0.592	0.031	38.234	79.335
4	2	5.140	3.516	9.005	23.422	−0.787	0.076	11.213	0.070
5	2	10.822	7.930	9.673	18.319	−0.638	0.005	35.783	20.011
6	3	4.360	2.065	9.278	1.736	0.790	0.012	0.691	∼0
7	3	7.180	3.923	9.523	2.935	0.472	0.002	2.672	0.051
8	3	10.326	6.224	9.951	1.917	0.730	0	3.395	0.508
9	4	5.566	2.200	7.737	0.036	3.139	∼0	0.041	∼0
10	4	5.817	2.265	10.279	0.102	2.508	0	0.054	∼0
11	4	8.354	4.007	10.073	0.074	2.703	0	0.110	∼0
12	5	5.750	1.750	9.60	0.001	5.311	0	∼0	∼0

Although several high energy microstates are present in very limited populations, each representing multinucleated species N_s > 3 with little propagated helical structure to stabilize the existing nuclei, these make up only ∼0.2% of the equilibrium data set and the 0 ≤ N_s ≤ 2 microstates dominate the equilibrium. Because we use a heuristic clustering algorithm and a cutoff in the LR calculations outlined above, we cannot rule out the possibility that these minor clusters are detected as artifacts of the analysis, and may actually represent minor populations of other clusters. The incorporation of these data into the larger clusters would not significantly alter the results reported herein and, for brevity, we focus on the eight predominant microstates.

Based on this clustering scheme, a more definitive view of the folding and unfolding kinetics is provided in Fig. 11, which shows the evolution of mole fractions for the eight low-energy microstates listed in Table 4 as calculated in 1 ns windows before reaching equilibrium. The folding of the all-coil state (top) initiates via nucleation and propagation to form small single-helical stretches (cluster 2), which subsequently generate the diverse equilibrium macrostate characterized in Table 4 either through further propagation or additional nucleation events. In contrast, the unfolding of the all-helix state (bottom) initiates predominantly via breakage of long helices into multiple helical segments. This unfolding mechanism may be thought of in terms of a nucleation-propagation mechanism wherein the nucleation of the coil state occurs in the presence of helical residues, and propagation of coil conformations occurs further until reaching the equilibrium macrostate described by Table 4. Such nucleation of the coil state can occur near the central region of the helix, producing conformations consisting of two helices (cluster 5, 2-helix) or near the termini producing frayed helical structures. Additional coil nucleation and/or propagation then result in all-coil conformers and those consisting of multiple shorter helices. One would thus expect parameters describing the nucleation-propagation mechanism for helix formation and coil formation to be equivalent at the midpoint temperature.

FIGURE 11.

Microstate helix-coil kinetics. The time evolution of mole fractions calculated over each 1 ns window before reaching equilibrium are shown for the eight dominant clusters listed in Table 4 for the folding (top) and unfolding (bottom) F_s ensembles in AMBER-99φ. From the initially increasing species in each plot, the apparent bulk unfolding mechanism is not equivalent to the reverse of the folding mechanism: folding initiates via nucleation and propagation of small single-helix structures (red) followed by evolution to the diverse equilibrium populations described in the text; in contrast, unfolding begins predominantly with the breaking of single-helix segments into multiple shorter helices (green), and may be considered as nucleation and propagation of the coil state within helical regions.

The resulting network of potential pathways and rates between each microstate are shown in partial form in Fig. 12 for the AMBER-99φ equilibrium ensemble. As required by true ensemble equilibrium, the transition probability matrix resulting from our equilibrium simulations yields steady-state concentrations of each microstate, and the rates shown in Fig. 12 were derived from this matrix. Conversion rates ranging from the tens of picoseconds to the tens of nanoseconds regimes are apparent at 305 K, and this range is expected to widen under denaturing conditions such as temperature-jump perturbation.

FIGURE 12.

Network for helix conformational diffusion. F_s structures representing seven of the eight predominant microstates are shown on a simplified network of configurational dynamics. Notation above and below each structure specify the cluster and the equilibrium mole fraction (%) in the AMBER-99φ potential. Equilibrium rates between microstates derived from the transition probability matrix are shown in red (ns⁻¹) and are based on 100-ps temporal resolution. The residue coloration scheme includes random coil (white), turn (green), and helix (red).

Our equilibrium ensemble simulations using the AMBER-99φ potential thus predict a helix-coil free energy landscape for moderate sized alanine-based peptides composed of two broad, shallow energy basins, each of which includes a diverse, conformationally diffuse population. In the “unfolded” regime, a continuum of conformations including random coil, single short helical segments, and multinucleated species exists. Similarly, the “native” regime represents a continuum ranging from short multinucleated regions to ideal single helical stretches. These broad basins are separated by a small free energy barrier that represents the single (rate limiting) barrier in helix formation and unfolding, as in the kinetic zipper model of Eaton and co-workers (Thompson et al., 1997, 2000). Although the diverse stochastic folding mechanism observed in our simulations may be simplified as two competing parallel pathways, as outlined above, a more apt description of helix-coil kinetics should include possible back-reactions and conversions to neighboring microstates, appearing more as a diffusion search process than a simple exponential barrier crossing.

CONCLUSION

Our equilibrium ensemble simulations quantitatively demonstrate that the AMBER-99φ potential significantly outperforms other AMBER all-atom force fields in reproducing experimental helix-coil kinetics and thermodynamics. In the process of making this comparison, insight into the helix-coil transition has been gained. Notably, we report a kinetic alignment phase during helix formation in which conformations containing multiple short helical segments extend and these regions merge to produce a more “ideal” helix. The building blocks of this ideal helical conformation average only ∼4.5 residues in length, by Lifson-Roig counting, and thus closely follow the statistics of a random flight chain (Zagrovic and Pande, 2003b). The diffusive search for these short helical conformations thus includes no appreciable entropic barrier, which is somewhat contradictory to the more general helix-coil philosophy.

Although the kinetics of helix formation have been described as being much more complex than the rigorous two-state model that is often assumed, helix-coil equilibrium does in fact appear to consist of two broad energetic basins separated by a rate-limiting free energy barrier. However, complexity is added by the significant conformational diffusion within these basins: in the “unfolded” regime a spectrum of conformations exists, ranging from those that are purely coil to those that include one or more short helical segments separated by turn regions; in the “native” regime a second spectrum exists that includes similar diversity in overall helical content along a relatively linear conformation. How these regions of great conformational variability change the predicted two-state behavior of course depends on the experimental methods and perturbations applied, and it is therefore not surprising that a wide range of seemingly contradictory behavior has been reported for various helix forming sequences, including relaxation rates that span several orders of magnitude.

The efforts reported herein demonstrate how significant improvements in sampling, such as from distributed computing efforts, can provide a foundation for the absolute assessment of biomolecular potentials, which continue to require validation at both the bulk and single molecule levels, by offering a quantitative comparison of several molecular mechanical potential sets and modifying a recently parameterized and heliophobic force field to gain quantitative agreement with several experimental metrics. Indeed, our AMBER-99φ variant has outperformed its predecessors at reproducing the experimentally determined Lifson-Roig parameters, helix folding rate, 3₁₀ helical fraction, and mean radius of gyration. Still, the imperfect agreement between experimentally determined LR parameters and those calculated from our equilibrium simulations demonstrates the appeal of a more accurate force field, and we are currently working on accomplishing this goal via optimization of the backbone torsional potential to reproduce experimental v and w values. Our efforts have also shown that an adequate temperature-dependent thermodynamics is lacking in all of these force fields, and it remains unknown to what degree the inaccuracies inherent to most explicit solvent models (such as TIP3P) are responsible for this behavior. Applications of such potentials at temperatures outside the ambient/biological regime are therefore inherently missing the true equilibrium character of the helix-coil system. Extending our force-field modifications to a broader range of applicability will thus be a future necessity. Indeed, the successes and failures of the force fields studied herein reveal the complexity of even the simplest of biomolecular structure and dynamics, and it will be exciting to see the future development of potentials that can adequately account for such complexity.